[논문] LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS

논문 출처
Hu, E., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., Wang, L., & Chen, W.
LoRA: Low-Rank Adaptation of Large Language Models.
arXiv preprint (arXiv:2106.09685), Version 2.
🔗 원문 링크 (arXiv:2106.09685)

저자

• Edward Hu (Microsoft Corporation) – edwardhu@microsoft.com
• Yelong Shen (Microsoft Corporation) – yeshe@microsoft.com
• Phillip Wallis (Microsoft Corporation) – phwallis@microsoft.com
• Zeyuan Allen-Zhu (Microsoft Corporation) – zeyuana@microsoft.com
• Yuanzhi Li (Carnegie Mellon University) – yuanzhil@andrew.cmu.edu
• Shean Wang (Microsoft Corporation) – swang@microsoft.com
• Lu Wang (Microsoft Corporation) – luw@microsoft.com
• Weizhu Chen (Microsoft Corporation) – wzchen@microsoft.com

---

∗ 공동 기여(Equal contribution).

---

(Version 2)

---

V1과 비교했을 때, 이번 초안에는 더 나은 베이스라인(baselines),
GLUE 실험, 그리고 어댑터 지연(adapter latency) 에 대한
추가 내용이 포함되어 있다.

---

초록 (Abstract)

자연어 처리(NLP)의 주요 패러다임 중 하나는
일반 도메인 데이터에 대한 대규모 사전학습(pre-training) 과
특정 작업이나 도메인에 대한 적응(adaptation) 으로 구성된다.

하지만 모델이 커질수록,
모든 파라미터를 다시 학습시키는 전체 미세조정(full fine-tuning) 은
점점 더 비현실적이 된다.

예를 들어, GPT-3 (175B) 모델의 경우,
각각 1,750억 개의 파라미터를 가진 미세조정된 모델 인스턴스를
독립적으로 배포하는 것은 막대한 비용이 든다.

이를 해결하기 위해 우리는 LoRA (Low-Rank Adaptation) 를 제안한다.

LoRA는 사전학습된 모델의 가중치를 고정(freeze) 한 채,
트랜스포머(Transformer) 아키텍처의 각 층(layer) 에
학습 가능한 저랭크 분해 행렬(rank decomposition matrices) 을 삽입함으로써,
전이 학습(transfer learning) 시 필요한 학습 가능한 파라미터 수를 크게 줄인다.

---

전이 학습(Transfer Learning)이란?

• 전이 학습(Transfer Learning) 은
  하나의 작업(task)이나 도메인(domain)에서 학습된 지식을
  다른 작업으로 이전(transfer) 하여 활용하는 학습 방법이다.

• 일반적으로 대규모 데이터로 사전학습(pre-training) 된 모델은
  언어, 문맥, 구조 등에 대한 일반적인 표현(representation) 을 이미 학습하고 있다.
  이러한 모델을 새로운 응용 문제(예: 감정 분석, 질의응답, 번역 등)에 적용할 때는
  모델의 일부 파라미터만 조정하거나,
  특정 층(layer)만 미세조정(fine-tuning) 하는 방식으로 수행된다.

• 따라서 처음부터 모델을 다시 학습시키지 않고,
  이미 학습된 지식(knowledge) 을 바탕으로
  새로운 작업에 빠르게 적응(adapt) 하는 것이
  전이 학습의 핵심 개념이다.

• LoRA 역시 이러한 전이 학습의 한 형태로,
  전체 모델을 다시 학습하지 않고
  필요한 부분만 효율적으로 조정하여 성능을 유지한다.

---

GPT-3 (175B)를 Adam 옵티마이저로 미세조정했을 때와 비교하면,
LoRA는 학습 가능한 파라미터 수를 최대 10,000배까지 줄이고,
GPU 메모리 요구량을 약 3배 절감할 수 있다.

그럼에도 불구하고, LoRA는
RoBERTa, DeBERTa, GPT-2, GPT-3 등의 모델에서
미세조정(full fine-tuning)과 동등하거나 더 우수한 성능을 보인다.

또한, 학습 가능한 파라미터가 더 적고,
학습 처리량(training throughput) 이 더 높으며,
어댑터(adapters) 방식과 달리
추론(inference) 시 지연(latency) 도 추가되지 않는다.

---

어댑터(Adapter) 방식이란?

• 어댑터(Adapter) 는 대형 사전학습 모델(pre-trained model)의
  모든 파라미터를 다시 학습시키지 않고,
  각 층(layer) 사이에 작은 학습 가능한 모듈(small trainable modules) 을 추가하여
  새로운 작업에 맞게 모델을 미세조정(fine-tuning)하는 방법이다.

• 이 방식은 원래의 모델 파라미터를 거의 그대로 유지한 채,
  적은 추가 파라미터(parameter-efficient) 만 학습할 수 있다는 장점이 있다.
  따라서 전체 모델을 다시 학습시키는 것보다 훨씬 효율적이며,
  서로 다른 작업 간에 공유(reuse) 도 용이하다.

• 그러나 어댑터는 추론(inference) 단계에서
  각 층에 추가된 모듈을 통과해야 하므로,
  추가적인 지연(latency) 이 발생할 수 있다는 단점이 있다.

어댑터 방식은 “모델 전체를 다시 학습하지 않고 필요한 부분만 추가 학습하는”
파라미터 효율적 미세조정(Parameter-Efficient Fine-Tuning, PEFT) 기법이다.
하지만 LoRA는 어댑터와 달리 추론 시 지연이 거의 없고,
동일한 효율성을 유지하면서 더 단순한 구조를 제공한다.

---

아울러 우리는
언어 모델 적응에서의 랭크 결핍(rank-deficiency) 현상에 대한
실증적 분석을 제공하여,
LoRA의 효율성에 대한 통찰(insight) 을 제시한다.

---

왜 ‘랭크 결핍(Rank-Deficiency)’이라고 부를까?

• “랭크 결핍”은 원래 선형대수학에서 행렬의 랭크(rank) 가
  최대치보다 낮을 때, 즉 선형 독립 성분이 부족할 때를 의미하는 부정적 용어이다.
  예를 들어, $n \times n$ 행렬의 랭크가 $n$보다 작다면
  그 행렬은 정보 손실(loss of information) 이 있거나,
  역행렬이 존재하지 않는(singular) 상태로 본다.

• 하지만 언어 모델의 관점에서는 이 “결핍”이 반드시 나쁜 것이 아니다.
  오히려 모델이 실제로는 낮은 차원(low-rank) 의 표현만으로도
  충분히 의미 있는 정보를 학습하고,
  복잡한 패턴을 표현할 수 있음을 보여주는 구조적 효율성(structural efficiency) 의 신호이기도 하다.

• LoRA는 바로 이 특성을 적극적으로 이용한다.
  즉, 언어 모델이 본질적으로 랭크 결핍 구조를 가진다는 점을 활용하여,
  전체 파라미터를 모두 학습하지 않고도
  필요한 저차원 방향만 학습함으로써 동일한 효과를 얻는다.

• 따라서 “랭크 결핍”이라는 단어는 수학적으로는 제약(constraint)을 뜻하지만,
  LoRA의 맥락에서는 “낮은 차원 구조로도 충분히 잘 작동하는 현상” 이라는
  긍정적인 의미로 재해석된다.

---

마지막으로, 우리는
PyTorch 모델에 LoRA를 통합할 수 있는 패키지를 공개하였으며,
RoBERTa, DeBERTa, GPT-2용 구현 및 모델 체크포인트를
다음 링크에서 제공한다.

🔗 https://github.com/microsoft/LoRA

1. 서론 (Introduction)

자연어 처리(NLP)의 많은 응용들은
하나의 대규모 사전학습 언어 모델(pre-trained language model) 을
여러 개의 전이(또는 하위) 응용 프로그램(downstream applications) 에
적응시키는 것에 의존한다.

이러한 적응(adaptation)은 일반적으로
모든 사전학습된 모델의 파라미터를 업데이트하는 미세조정(fine-tuning) 을 통해 수행된다.

그러나 미세조정의 주요 단점은,
새로운 모델이 원래 모델과 동일한 수의 파라미터를 갖게 된다는 점이다.

모델 규모가 몇 달마다 더 커지는 현 상황에서,
이 문제는 단순히 GPT-2 (Radford et al.)나 RoBERTa large (Liu et al., 2019) 수준에서는
“약간의 불편함”에 불과할 수 있었지만,
1,750억 개의 학습 가능한 파라미터를 가진 GPT-3 (Brown et al., 2020)¹ 의 경우에는
중대한 배포(deployment)상의 도전 과제로 변하게 되었다.

---

¹GPT-3 (175B)는 퓨샷 학습(few-shot learning) 만으로도
일정 수준 이상의 성능을 달성하지만,
부록 A(Appendix A) 에서 보여지듯이
미세조정(fine-tuning) 을 통해 그 성능이 크게 향상된다.

---

많은 연구자들이 이 문제를 완화하기 위해
일부 파라미터만 적응(adapt) 시키거나,
새로운 작업(task) 을 위해 외부 모듈(external modules) 을 학습하는 방법을 시도해왔다.

이러한 방식에서는 각 작업마다
사전학습된 모델에 더해 작업별 파라미터(task-specific parameters) 만
저장하고 불러오면 되므로,
배포(deployment) 시 운영 효율성(operational efficiency) 이 크게 향상된다.

그러나 기존 기법들은 종종
모델의 깊이(model depth) 를 확장함으로써 추론 지연(inference latency) 을 유발하거나
(Loulsby et al., 2019; Rebuffi et al., 2017),
모델이 처리할 수 있는 시퀀스 길이(sequence length) 를 줄이는 문제를 발생시킨다
(Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021) (3장 참조).

더 중요한 점은, 이러한 방법들이 종종
미세조정(fine-tuning) 기반의 베이스라인(baseline) 수준의 성능을 달성하지 못해,
효율성과 모델 품질 간의 트레이드오프(trade-off) 를 초래한다는 것이다.

우리는 Li et al. (2018a) 및 Aghajanyan et al. (2020)에서 제시된 결과로부터 영감을 얻었다.
이들 연구는 과도하게 매개변수화된(over-parameterized) 모델이 실제로는
낮은 고유 차원(low intrinsic dimension) 상에 존재함을 보여준다.

이에 기반하여 우리는,
모델 적응(model adaptation) 과정에서 발생하는 가중치 변화(weight change) 역시
낮은 내재적 랭크(intrinsic rank) 를 가진다고 가정(hypothesis)한다.
이 가정으로부터 우리가 제안한 LoRA (Low-Rank Adaptation) 방법이 도출된다.

LoRA는 사전학습된 가중치를 그대로 고정(freeze) 시킨 채,
적응 과정에서의 밀집층(dense layer) 변화량을
랭크 분해 행렬(rank decomposition matrices) 형태로 학습하도록 설계된다.
즉, 밀집층 자체를 직접 학습하는 대신,
그 변화(change)를 저랭크 행렬 형태로 간접적으로 최적화한다는 것이다
(그림 1 참고).

---

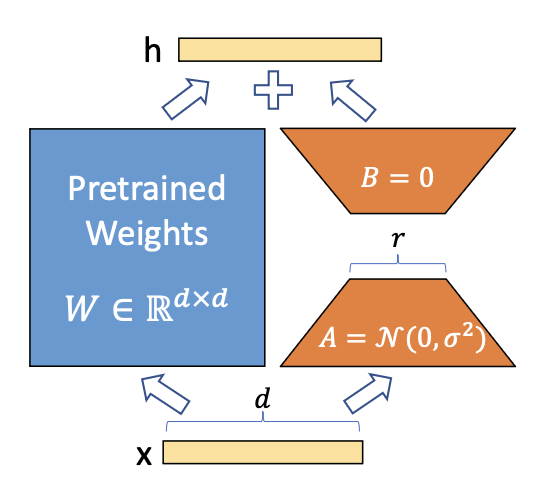
그림 1: 우리의 재매개변수화(reparametrization) 방식.
우리는 A와 B만 학습한다.

---

재매개변수화(Reparametrization)와 랭크 분해 행렬 학습이란?

• 재매개변수화(Reparametrization) 는
  기존의 가중치 행렬 $W$ 를 직접 학습하지 않고,
  그것을 다른 형태의 파라미터(예: $A$, $B$) 로 다시 표현하여 학습하는 방법이다.
  즉, $W$ 대신 $W + \Delta W$ 형태로 모델을 표현하고,
  이때 $\Delta W = B A$ 로 두어 $A$, $B$ 두 행렬만 학습한다.

• 이렇게 하면, 원래의 거대한 가중치 행렬 $W \in \mathbb{R}^{d \times d}$ 을
  직접 업데이트할 필요가 없다.
  대신, 저랭크(rank $r$) 제약을 가진 두 행렬 $A \in \mathbb{R}^{r \times d}$,
  $B \in \mathbb{R}^{d \times r}$ 을 통해
  $W$ 의 변화를 근사(approximation)하게 된다.

• 그림에서처럼, $A$ 는 초기값을 정규분포 $\mathcal{N}(0, \sigma^2)$ 로 설정하고,
  $B$ 는 0으로 초기화된다.
  학습 과정에서는 $A$와 $B$만 최적화되고,
  원래의 사전학습 가중치 $W$ 는 고정(freeze) 되어 유지된다.

• 이러한 방식은 모델의 전체 구조를 바꾸지 않으면서도
  적은 수의 학습 파라미터로 동일한 효과를 얻을 수 있게 해주며,
  이를 통해 저장 공간과 계산량을 크게 절약할 수 있다.

• 요약하자면, LoRA의 재매개변수화는
  거대한 파라미터 행렬을 저차원(rank-$r$) 공간으로 분해해
  효율적으로 학습하는 저랭크 근사(low-rank approximation) 기반의 접근법이다.

---

GPT-3 (175B)를 예로 들면,
전체 랭크($d$)가 12,288에 달하더라도
매우 낮은 랭크(예: $r=1$ 또는 $r=2$) 만으로 충분함을 보여준다.
이는 LoRA가 저장(storage) 및 계산(compute) 양 측면에서
매우 효율적인 방법임을 의미한다.

LoRA는 여러 가지 핵심적인 이점을 가진다.

• 사전학습된 모델(pre-trained model) 은 여러 다른 작업(tasks)을 위한
  작은 LoRA 모듈들을 구축하는 데 공유되고 사용될 수 있다.
  우리는 공유된 모델을 고정(freeze)한 상태로 유지하고,
  그림 1의 행렬 A와 B를 교체함으로써 작업을 효율적으로 전환할 수 있다.
  이는 저장 공간 요구량(storage requirement)과
  작업 전환 시 오버헤드(task-switching overhead)를 크게 줄여준다.

• LoRA는 학습을 더욱 효율적으로 만들고,
  적응형 옵티마이저(adaptive optimizer)를 사용할 때
  하드웨어 진입 장벽(hardware barrier to entry)을 최대 3배까지 낮춘다.
  이는 대부분의 파라미터에 대해 그래디언트를 계산하거나
  옵티마이저 상태(optimizer state)를 유지할 필요가 없기 때문이다.
  대신, 우리는 삽입된 훨씬 작은 저랭크 행렬(low-rank matrices) 만 최적화한다.

• 우리의 단순한 선형(linear) 설계는,
  배포(deployment) 시 학습 가능한 행렬(trainable matrices)을
  고정된 가중치(frozen weights)와 병합(merge)할 수 있게 하며,
  완전히 미세조정된 모델(fully fine-tuned model)과 비교했을 때
  추론 지연(inference latency) 을 전혀 초래하지 않는다.

• LoRA는 많은 기존 기법들과 직교적(orthogonal) 이며,
  프리픽스 튜닝(prefix-tuning) 과 같은
  여러 방법들과 결합될 수 있다.
  이에 대한 예시는 부록 E(Appendix E) 에서 제시한다.

---

‘직교적(Orthogonal)’이라는 표현의 의미

• 여기서 직교적(orthogonal) 이라는 표현은
  수학적 의미의 “서로 독립적(independent)”이라는 개념에서 유래한다.
  즉, LoRA가 다른 방법들과 간섭하지 않고 동시에 사용할 수 있다 는 뜻이다.

• 어떤 기법이 직교적이라는 것은
  그것이 다른 학습 기법의 구조나 원리에 의존하지 않으며,
  별도로 적용하거나 함께 결합(combine) 해도
  서로의 작동 방식에 영향을 주지 않는다는 의미이다.

• 따라서 LoRA는 프리픽스 튜닝(prefix-tuning), 프로프트 튜닝(prompt tuning),
  어댑터(adapter) 등과 같은 다른 파라미터 효율적 학습 기법(PEFT) 들과
  함께 사용될 수 있으며, 이러한 결합은
  추가적인 성능 향상이나 효율성 개선을 가능하게 한다.

---

용어 및 표기 규칙 (Terminologies and Conventions)

우리는 트랜스포머(Transformer) 아키텍처를 자주 참조하며,
그 구조에서 일반적으로 사용되는 용어와 표기 규칙(conventions)을 따른다.

트랜스포머 층의 입력 및 출력 차원 크기를 \(d_{\text{model}}\)이라고 부른다.

\(W_q, \; W_k, \; W_v, \; W_o\)는 각각 셀프-어텐션(self-attention) 모듈 내의
쿼리(query), 키(key), 밸류(value), 출력(output) 투영 행렬을 의미한다.

\(W \; \text{또는} \; W_0\)는 사전학습된(pre-trained) 가중치 행렬을,
\(\Delta W\)는 적응(adaptation) 중 누적된 그래디언트 업데이트(accumulated gradient update) 를 나타낸다.

\(r\)은 LoRA 모듈의 랭크(rank) 를 의미한다.

우리는 Vaswani et al. (2017) 및 Brown et al. (2020) 의 표준 규칙을 따르며,
모델 최적화(model optimization)에는 Adam 옵티마이저
(Loshchilov & Hutter, 2019; Kingma & Ba, 2017)를 사용한다.

또한, 트랜스포머의 MLP 피드포워드(feedforward) 차원은
\(d_{\text{ffn}} = 4 \times d_{\text{model}}\)로 설정한다.

2. 문제 정의 (Problem Statement)

우리의 제안은 학습 목표(training objective) 에 구애받지 않지만,
본 연구에서는 언어 모델링(language modeling) 을 주요 동기 사례로 삼는다.

아래는 언어 모델링 문제에 대한 간단한 설명이며,
특히 작업별 프롬프트(task-specific prompt) 가 주어졌을 때
조건부 확률(conditional probability) 을 최대화하는 과정을 다룬다.

사전학습된 자기회귀 언어 모델(autoregressive language model)
$P_\Phi(y|x)$ 이 주어졌다고 가정하자.
이 모델은 매개변수 Φ로 정의된다.

예를 들어, $P_\Phi(y|x)$ 는 GPT (Radford et al.; Brown et al., 2020) 과 같은
트랜스포머(Transformer) 기반의 일반적 다중작업 학습기(generic multi-task learner) 일 수 있다
(Vaswani et al., 2017).

이제 이 사전학습된 모델을
요약(summarization), 기계 독해(MRC, Machine Reading Comprehension),
자연어 → SQL 변환(NL2SQL) 과 같은
조건부 텍스트 생성(conditional text generation) 작업에 적응(adapt)시키는 것을 고려하자.

각 전이 학습(downstream) 작업은
컨텍스트-타깃(context–target) 쌍으로 이루어진 학습 데이터셋으로 표현된다.

\[Z = \{(x_i, y_i)\}_{i=1}^N\]

여기서 $x_i$와 $y_i$는 모두 토큰(token) 시퀀스이다.

예를 들어, NL2SQL의 경우 $x_i$는 자연어 질의(natural language query)이고,
$y_i$는 그에 대응하는 SQL 명령문(SQL command) 이다.

요약(summarization)의 경우 $x_i$는 기사(article)의 본문(content)이고,
$y_i$는 그 요약(summary)이다.

전체 미세조정(full fine-tuning)에서는
모델이 사전학습된 가중치(pre-trained weights) $\Phi_0$ 로 초기화되고,
다음의 조건부 언어 모델링 목표(conditional language modeling objective) 를
최대화하기 위해 그래디언트를 반복적으로 따라가며
$\Phi_0 + \Delta \Phi$ 로 업데이트된다.

\[\max_{\Phi} \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log \big(P_{\Phi}(y_t \mid x, y_{<t})\big) \tag{1}\]

---

전체 미세조정(Full Fine-Tuning)의 의미

• 전체 미세조정(full fine-tuning) 은 사전학습(pre-training)이 끝난 모델의
  모든 파라미터(parameter) 를 다시 학습 가능한 상태로 두고,
  새로운 작업(task)에 맞게 전체를 재학습시키는 방식이다.

• 위 식에서 $\Phi_0$ 는 사전학습(pre-trained)으로 얻은 원래의 가중치(weight)이며,
  $\Delta \Phi$ 는 새로운 작업에 맞게 학습을 통해 추가로 얻어지는
  가중치의 변화량(weight update) 을 의미한다.
  즉, 최종 가중치는 $\Phi = \Phi_0 + \Delta \Phi$ 형태로 표현된다.

• 모델은 주어진 데이터셋 $Z = {(x_i, y_i)}$ 에 대해,
  각 토큰 시점 $t$ 에서 이전 토큰들 $y_{<t}$ 과 입력 $x$ 가 주어졌을 때,
  다음 토큰 $y_t$ 가 등장할 확률 $P_{\Phi}(y_t \mid x, y_{<t})$ 을
  최대화하는 방향으로 학습된다.

• 식 (1)은 이러한 과정을 확률적 언어 모델링(objective) 의 형태로 나타낸 것이다.
  즉, 모든 학습 데이터 $(x, y)$ 와 각 시점 $t$ 에 대한
  로그 확률의 합(log-likelihood sum)을 최대화함으로써,
  모델이 주어진 문맥(context)에서 다음 단어를 예측하도록 학습한다.

• 이 접근 방식은 성능은 높지만,
  파라미터 수가 매우 큰 모델(예: GPT-3)에서는
  모든 가중치를 업데이트해야 하므로 비용(cost) 과 메모리(memory) 측면에서
  매우 비효율적이라는 한계를 가진다.

---

전체 미세조정의 주요 단점 중 하나는
각 전이 학습(downstream) 작업마다
서로 다른 파라미터 집합 $\Delta \Phi$ 를 학습해야 한다는 점이다.

이때 그 차원(dimensions) $\mid\Delta\Phi\mid$ 는
원래 모델의 파라미터 수 $\mid \Phi_0 \mid$ 와 동일하다.

따라서 사전학습 모델이 매우 클 경우
(예: $|\Phi_0| \approx 175$B인 GPT-3)
많은 개수의 미세조정된 모델 인스턴스를
저장하거나 배포하는 것은 매우 어렵거나 거의 불가능하다.

이 논문에서는 보다 파라미터 효율적(parameter-efficient) 인 접근을 채택한다.

즉, 작업별 파라미터 변화량(increment) $\Delta \Phi = \Delta \Phi(\Theta)$ 를
훨씬 더 작은 크기의 파라미터 집합 $\Theta$ 로 표현한다.

여기서 $\mid \Theta \mid \ll \mid \Phi_0 \mid$ 이다.

따라서 $\Delta \Phi$ 를 찾는 문제는
이제 $\Theta$ 위에서 최적화하는 문제로 바뀐다.

\[\max_{\Theta} \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log \big(P_{\Phi_0 + \Delta \Phi(\Theta)}(y_t \mid x, y_{<t})\big) \tag{2}\]

---

$\Theta$의 의미와 식 (2)의 해석

• 식 (2)에서 등장하는 $\Theta$는
  LoRA가 새로 도입한 학습 가능한 파라미터들의 집합(set of trainable parameters) 이다.
  이 파라미터들은 기존의 모델 가중치 $\Phi_0$와는 별도로,
  가중치 변화량(weight update) $\Delta \Phi$를 저차원 공간에서 표현하기 위해 사용된다.

• 구체적으로, LoRA는 기존의 거대한 가중치 행렬 $W \in \mathbb{R}^{d \times d}$ 를
  그대로 학습하지 않고,
  그 변화량을 두 개의 저랭크 행렬(low-rank matrices) $A \in \mathbb{R}^{r \times d}$,
  $B \in \mathbb{R}^{d \times r}$ 의 곱으로 근사한다.
  \(\Delta W = B A\)
  이때 $\Theta$는 바로 이 행렬들 $A$와 $B$ — 즉,
  LoRA 모듈 내에서 새롭게 학습되는 모든 파라미터들의 집합을 의미한다.

• 따라서 $\Delta \Phi(\Theta)$는 “$\Theta$로부터 계산된 전체 가중치 변화량”이다.
  다시 말해, $\Theta$를 학습하면 그에 따라 $\Delta \Phi$가 결정된다.
  학습의 초점은 이제 $\Phi$ 전체가 아니라,
  이 작은 저차원 파라미터 공간 $\Theta$ 위로 옮겨지는 것이다.

• 식 (2)는 이러한 과정을 수식으로 표현한 것으로,
  모델은 여전히 조건부 확률
  $P(y_t \mid x, y_{<t})$을 최대화하지만,
  이때의 파라미터는 사전학습된 가중치 $\Phi_0$ 와
  $\Theta$로부터 유도된 변화량 $\Delta \Phi(\Theta)$ 를 합친 형태로 쓰인다.

• 요약하면,
  $\Theta$ = LoRA에서 새로 추가된 학습 가능한 저랭크 행렬 파라미터의 집합이며,
  이 $\Theta$를 학습함으로써
  거대한 모델 전체의 가중치를 직접 업데이트하지 않고도
  새로운 작업에 적응할 수 있게 되는 것이다.

---

이후의 섹션에서는
$\Delta \Phi$ 를 계산 및 메모리 효율적으로 표현하기 위한
저랭크 표현(low-rank representation) 방식을 제안한다.

특히, 사전학습 모델이 GPT-3 (175B) 인 경우,
학습 가능한 파라미터 수 $|\Theta|$ 는
$|\Phi_0|$ 의 0.01% 수준까지 줄일 수 있다.

---

3. 기존 방법들은 충분하지 않은가? (Aren’t Existing Solutions Good Enough?)

우리가 해결하려는 문제는 결코 새로운 것이 아니다.
전이 학습(transfer learning) 이 등장한 이후,
수많은 연구들이 모델 적응(model adaptation)을
더 파라미터 효율적(parameter-efficient) 이고
계산 효율적(compute-efficient) 으로 만드는 방법을 제시해 왔다.
이와 관련된 잘 알려진 연구들에 대해서는 6장(Section 6) 에서 요약한다.

언어 모델링(language modeling) 을 예로 들면,
효율적인 적응을 위한 대표적인 두 가지 전략이 존재한다.

첫 번째는 어댑터 층(adapter layers) 을 추가하는 방식이고,
(Houlsby et al., 2019; Rebuffi et al., 2017; Pfeiffer et al., 2021; Rücklé et al., 2020).

두 번째는 입력층 활성화(input layer activations) 의
일부 형태를 최적화(optimization)하는 접근이다.
(Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021).

그러나 두 전략 모두 한계를 가진다.
특히 대규모 모델 환경(large-scale setting) 이나
지연(latency)에 민감한 실제 서비스(production scenario) 에서는
이러한 기존 방법들이 충분히 효과적이지 않다.

어댑터 층(Adapter Layers)은 추론 지연(Inference Latency)을 초래한다

어댑터(adapter)에는 여러 가지 변형(variants)이 존재한다.
우리는 그중 두 가지 대표적인 설계(design) 에 초점을 맞춘다.

첫째, Houlsby et al. (2019) 이 제안한 방식으로,
각 트랜스포머 블록(Transformer block) 에 두 개의 어댑터 층(adapter layers) 을 포함한다.

둘째, Lin et al. (2020) 의 보다 최근 설계로,
각 블록에 하나의 어댑터 층만 포함하지만,
추가적인 LayerNorm (Ba et al., 2016) 을 사용한다.

전체 지연(latency)을 줄이기 위해
일부 층을 가지치기(pruning) 하거나
멀티태스크 환경(multi-task setting) 을 활용할 수도 있지만
(Rücklé et al., 2020; Pfeiffer et al., 2021),
어댑터 층에서 발생하는 추가 연산량(extra compute) 자체를
근본적으로 제거할 방법은 없다.

처음에는 이것이 큰 문제가 아닌 것처럼 보일 수 있다.
왜냐하면 어댑터 층은 일반적으로
좁은 병목 차원(bottleneck dimension) 을 사용하여
원래 모델의 1% 미만의 파라미터만 추가하기 때문이다.
이로 인해 추가되는 연산량(FLOPs)은 제한적이다.

그러나 대규모 신경망(large neural networks) 은
하드웨어 병렬 처리(hardware parallelism) 를 통해
낮은 지연(latency)을 유지한다.
문제는 어댑터 층이 순차적으로(sequentially) 처리되어야 한다는 점이다.

따라서 온라인 추론(online inference) 환경처럼
배치 크기(batch size) 가 1에 가까운 상황에서는
이 순차적 처리로 인해 지연이 뚜렷하게 나타난다.

예를 들어, 모델 병렬화(model parallelism)가 적용되지 않은 일반적인 환경에서,
단일 GPU 위에서 GPT-2 (Radford et al.) medium 모델을
어댑터와 함께 실행하면,
병목 차원이 매우 작더라도(표 1 참조)
추론 지연(latency)이 눈에 띄게 증가함을 확인할 수 있다.

---

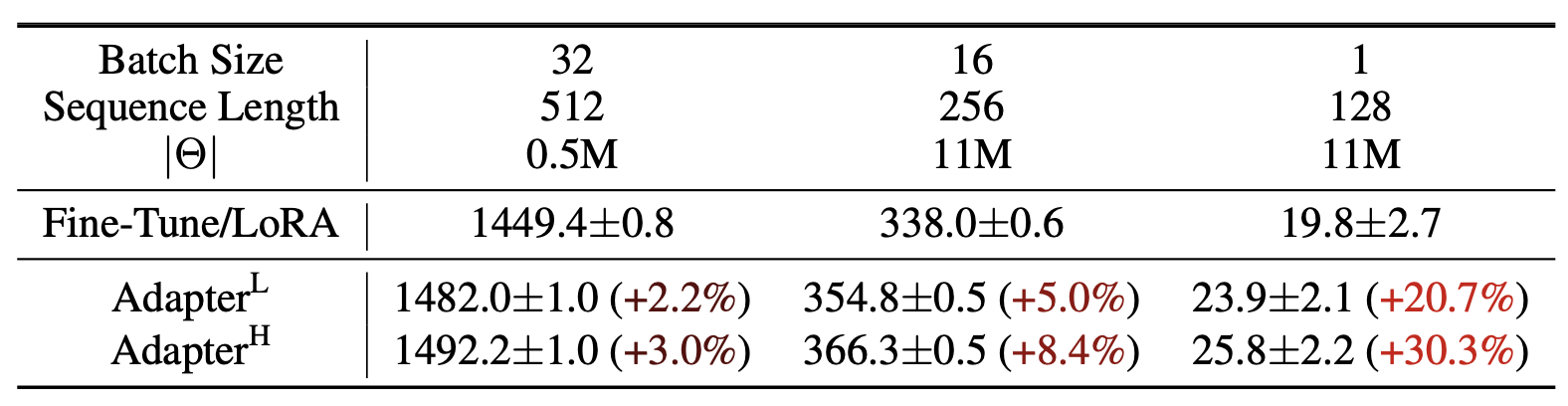
표 1

GPT-2 medium에서 단일 순전파(single forward pass) 시의
추론 지연 시간(inference latency) 을 밀리초 단위로 측정한 결과이다.
100회의 실험을 평균하여 산출했으며,
NVIDIA Quadro RTX8000 GPU를 사용하였다.

기호 “$|\Theta|$”는 어댑터 층(adapter layers) 에서의
학습 가능한 파라미터 수(trainable parameters) 를 나타낸다.

Adapter^L과 Adapter^H는
두 가지 어댑터 튜닝(adapter tuning) 변형이며,
이에 대한 설명은 5.1절(Section 5.1) 에 제시되어 있다.

어댑터 층으로 인해 발생하는 추론 지연은
온라인 환경(online setting) 이나
짧은 시퀀스 길이(short-sequence-length) 의 경우 특히 두드러질 수 있다.
자세한 실험 결과는 부록 B(Appendix B) 를 참조하라.

---

이 문제는 Shoeybi et al. (2020), Lepikhin et al. (2020)에서처럼
모델을 여러 GPU에 샤딩(sharding) 해야 할 때 더 심각해진다.

추가된 네트워크 깊이로 인해
AllReduce 및 Broadcast와 같은
동기식 GPU 연산(synchronous GPU operations) 이 더 많이 필요하기 때문이다.

이는 우리가 어댑터 파라미터를 여러 번 중복 저장(redundantly store) 하지 않는 한
피할 수 없는 문제이다.

---

AllReduce와 Broadcast 연산의 의미

• AllReduce 와 Broadcast 는
  다중 GPU 환경에서 모델 학습이나 추론 시 데이터를 동기화(synchronize) 하기 위해 사용되는
  대표적인 통신 연산(communication operations) 이다.

• AllReduce 연산은
  여러 GPU가 각각 계산한 값을 서로 교환(exchange)하고,
  이를 더하거나(예: gradient 합산), 평균내는 등의 연산을 통해
  모든 GPU가 동일한 결과를 갖도록 만드는 과정이다.
  예를 들어, 모델 병렬 학습 시 각 GPU가 계산한 그래디언트를
  전체적으로 합산하여 모든 GPU에 동일하게 반영하는 데 사용된다.
  \(\text{AllReduce: } x_i \rightarrow \sum_i x_i \quad \text{(모든 GPU 간 합산 후 동기화)}\)

• Broadcast 연산은
  한 GPU(일반적으로 “마스터 GPU”)에서 계산된 값을
  다른 모든 GPU로 복사(copy)하여 전달하는 과정이다.
  이는 모델 파라미터나 중간 결과를 여러 장치에 동일하게 배포(distribute)할 때 사용된다.
  \(\text{Broadcast: } x_1 \rightarrow (x_1, x_1, x_1, \dots)\)

• 이러한 연산들은 모두 동기식(synchronous) 으로 수행되기 때문에,
  하나의 GPU라도 작업이 지연되면 전체 연산이 멈추게 된다.
  따라서 네트워크 깊이가 깊어질수록,
  또는 어댑터 층이 추가될수록
  GPU 간 통신 부담(communication overhead) 이 커지고
  결과적으로 추론 지연(latency) 도 증가하게 된다.

---

프롬프트 직접 최적화의 어려움 (Directly Optimizing the Prompt is Hard)

다른 방향의 접근법인 프리픽스 튜닝(prefix tuning) (Li & Liang, 2021)은
다른 형태의 어려움을 겪는다.

우리는 프리픽스 튜닝이 최적화(optimization) 하기 어렵고,
학습 가능한 파라미터 수(trainable parameters) 에 따라
그 성능이 단조적으로(non-monotonically) 변하지 않는다는 것을 관찰했다.
이는 원 논문(original paper)에서도 보고된 바와 동일한 현상이다.

보다 근본적으로,
시퀀스 길이(sequence length) 의 일부를
적응(adaptation)을 위해 예약(reserve)해야 한다는 점이 문제이다.

이로 인해 전이 학습(downstream task)을 처리할 수 있는
실제 시퀀스 길이(available sequence length) 가 줄어들게 된다.

우리는 이러한 제약이
프롬프트 튜닝(prompt tuning)의 성능을
다른 방법들에 비해 떨어뜨리는 요인 중 하나라고 추정한다.

작업별 성능(task performance)에 대한 자세한 연구는
5절(Section 5) 에서 다룬다.

---

시퀀스 길이 예약이 의미하는 것

• 프리픽스 튜닝(prefix tuning)에서는
  모델이 새로운 작업(task)에 적응할 수 있도록
  입력 시퀀스의 맨 앞부분에 학습 가능한 토큰들(trainable tokens),
  즉 프리픽스(prefix) 를 추가한다.

• 이 프리픽스는 모델의 파라미터를 직접 수정하지 않고도
  입력에 “작업별 힌트(task-specific context)”를 주는 역할을 한다.
  하지만 이 추가된 프리픽스 토큰들이
  전체 시퀀스 길이 안에 포함되기 때문에,
  모델이 실제 입력 데이터(예: 문장, 문단 등)를 처리할 수 있는
  토큰 수(token capacity) 가 줄어들게 된다.

• 예를 들어, 모델의 최대 시퀀스 길이가 512라면
  프리픽스로 20개의 토큰을 사용했을 때
  실제 작업 입력에는 492개의 토큰만 사용할 수 있다.
  즉, 적응을 위한 공간이 늘어날수록
  입력 데이터에 할당할 수 있는 공간이 줄어드는 구조적 제약이 생긴다.

• 이러한 이유로 프리픽스 튜닝은
  특히 긴 문맥(long-context)이나 복잡한 입력을 처리해야 하는 작업에서
  성능이 저하될 가능성이 있다.

---

4. 우리의 방법 (Our Method)

이 절에서는 LoRA의 간단한 설계(simple design) 와
그 실용적 장점(practical benefits) 에 대해 설명한다.

여기서 제시하는 원칙(principles)은
딥러닝 모델의 모든 밀집층(dense layers) 에 적용 가능하지만,
본 연구에서는 트랜스포머(Transformer) 기반 언어 모델의
특정 가중치(weights)에만 초점을 맞춘다.
이는 LoRA의 주요 동기 사례(motivating use case)이기 때문이다.

4.1 저랭크 기반의 파라미터화된 갱신 행렬 (Low-Rank-Parametrized Update Matrices)

신경망(neural network)은 여러 개의 밀집층(dense layer) 으로 구성되어 있으며,
각 층은 행렬 곱(matrix multiplication) 연산을 수행한다.
이 층들의 가중치 행렬(weight matrix)은 일반적으로 풀 랭크(full-rank) 구조를 가진다.

---

풀 랭크(Full-Rank)란 무엇인가?

• 풀 랭크(full-rank) 행렬이란,
  행렬이 가질 수 있는 최대 차수(rank) 를 모두 가진 경우를 의미한다.
  즉, $d \times k$ 크기의 행렬이라면
  그 랭크(rank)가 $\min(d, k)$ 인 상태를 말한다.

• 행렬의 랭크(rank) 는
  행 또는 열이 서로 선형적으로 독립(linearly independent) 한 정도를 나타내며,
  이는 곧 행렬이 표현할 수 있는 정보의 다양성(information diversity) 을 의미한다.

• 예를 들어,
  어떤 가중치 행렬이 풀 랭크라면
  모든 출력 방향(output direction)을
  입력 공간(input space)의 선형 조합(linear combination)으로 표현할 수 있다.
  즉, 정보 손실 없이 입력을 변환할 수 있는 완전한 표현 능력(full representational capacity) 을 가진다.

• 반대로, 랭크가 낮은 행렬(저랭크 행렬, low-rank matrix)은
  일부 방향으로의 변환 능력이 제한되어 있으며,
  이는 계산량을 줄이는 대신 표현력(expressiveness) 을 희생한다.

• LoRA는 이러한 특성을 이용하여,
  기존의 풀 랭크 행렬을 직접 학습하는 대신
  저랭크 근사(low-rank approximation) 를 통해
  훨씬 적은 파라미터로 유사한 변환을 수행하도록 설계된 것이다.

---

특정 작업(task)에 적응(adaptation)할 때,
Aghajanyan et al. (2020) 은
사전학습된 언어 모델(pre-trained language model)이
낮은 “내재 차원(intrinsic dimension)” 을 가지고 있으며,
무작위 투영(random projection)을 통해
더 작은 부분공간(subspace)으로 축소되더라도
효율적으로 학습할 수 있음을 보였다.

이 결과에 영감을 받아,
우리는 적응 과정에서의 가중치 변화(weight update) 역시
낮은 내재 랭크(intrinsic rank) 를 가진다고 가정(hypothesize)한다.

사전학습된 가중치 행렬이 $W_0 \in \mathbb{R}^{d \times k}$ 일 때,
그 갱신(update)을 저랭크 분해(low-rank decomposition) 형태로 제한한다.

\[W_0 + \Delta W = W_0 + BA\]

여기서 $B \in \mathbb{R}^{d \times r}$, $A \in \mathbb{R}^{r \times k}$이며,
랭크 $r \ll \min(d, k)$ 이다.

---

$d$와 $k$의 의미

• 여기서 $d$와 $k$는 각각 행렬의 차원(dimension) 을 나타낸다.
  구체적으로, $W_0 \in \mathbb{R}^{d \times k}$ 는
  입력 벡터(input vector) 를 출력 벡터(output vector) 로 변환하는
  가중치 행렬(weight matrix) 이다.

• $k$는 입력 차원(input dimension),
  즉 한 데이터 샘플(토큰 등)을 표현하는 벡터의 크기이다.
  반면 $d$는 출력 차원(output dimension) 으로,
  변환 후 벡터가 표현되는 공간의 크기를 의미한다.

• 예를 들어,
  트랜스포머의 셀프-어텐션(self-attention) 구조에서
  쿼리(query)나 밸류(value) 투영 행렬이
  $W_q, W_v \in \mathbb{R}^{d \times k}$ 라면,
  입력 임베딩의 차원이 $k$이고,
  어텐션 공간의 출력 차원이 $d$가 된다.

• LoRA에서는 이 가중치 행렬의 업데이트를
  $B \in \mathbb{R}^{d \times r}$, $A \in \mathbb{R}^{r \times k}$ 로 분해하여
  저랭크 근사(low-rank approximation) 를 수행한다.
  여기서 $r$은 $d$와 $k$보다 훨씬 작은 값으로 설정되어,
  계산량과 파라미터 수를 크게 줄이면서도
  원래의 표현력을 최대한 보존할 수 있도록 한다.

---

학습 과정 동안 $W_0$는 고정(frozen) 되어
그래디언트 업데이트를 받지 않으며,
$A$와 $B$만이 학습 가능한 파라미터(trainable parameters) 를 포함한다.

$W_0$와 $\Delta W = BA$ 는
모두 동일한 입력(input)을 곱하고,
그 결과(output) 벡터는 좌표 단위로 합산(coordinate-wise summation) 된다.

$h = W_0 x$ 라고 할 때, 수정된 순전파(modified forward pass)는 다음과 같다:

\[h = W_0 x + \Delta W x = W_0 x + BAx \tag{3}\]

이 재매개변수화(reparametrization)는 그림 1(Figure 1) 에 시각화되어 있다.

초기화 시, $A$는 정규분포(random Gaussian) 로 $B$는 0(zero) 으로 설정하여,
학습 초기에 $\Delta W = BA = 0$ 이 되도록 한다.

그 후, $\Delta W x$를 $\dfrac{\alpha}{r}$로 스케일링(scale)한다.
여기서 $\alpha$는 랭크 $r$에 따라 설정되는 상수(constant)이다.

Adam 옵티마이저를 사용할 때, $\alpha$ 값을 조정하는 것은
초기화 스케일을 적절히 설정했을 경우 학습률(learning rate) 을 조정하는 것과 유사하다.
따라서 우리는 시도하는 첫 번째 랭크 $r$에 대해 $\alpha$를 설정하고 이후 추가 조정은 하지 않는다.

이러한 스케일링은 $r$ 값을 변화시킬 때마다 하이퍼파라미터를 다시 조정해야 하는 필요성을 줄여준다
(Yang & Hu, 2021).

---

$\alpha$를 고정해도 되는 이유

• LoRA에서는 학습 중 가중치 갱신항 $\Delta W x = BAx$에
  $\dfrac{\alpha}{r}$이라는 스케일링 계수를 곱해 사용한다.
  따라서 전체 식은 다음과 같이 표현된다.

  \[h = W_0x + \frac{\alpha}{r}BAx\]

• 이렇게 하면 랭크 $r$이 달라져도
  업데이트의 크기(scale)가 자동으로 보정된다.
  예를 들어 $r$이 커지면 자유도가 늘어나고 $\Delta W$의 크기가 커지지만,
  동시에 $\dfrac{1}{r}$로 나누어 주기 때문에 변화폭이 일정하게 유지된다.

• 논문에서 “$\alpha$를 처음 시도하는 $r$ 값으로 고정한다”고 말하는 이유는
  바로 이 자동 보정 덕분이다.
  $\alpha$를 한 번 정하면 이후 다른 $r$ 값을 실험하더라도
  $\dfrac{\alpha}{r}$ 항이 알아서 균형을 맞춰주므로
  $\alpha$나 학습률을 다시 튜닝할 필요가 없다.

• 즉, $\alpha$는 고정된 상수이지만
  실제 적용은 $\dfrac{\alpha}{r}$ 형태로 이루어지기 때문에
  랭크가 달라져도 학습 안정성(stability) 을 유지할 수 있는 것이다.

---

전체 미세조정의 일반화 (A Generalization of Full Fine-Tuning)

보다 일반적인 형태의 미세조정(fine-tuning) 은
사전학습된 파라미터 중 일부만을 학습 대상으로 삼는 방식을 허용한다.

LoRA는 이보다 한 단계 더 나아가,
적응(adaptation) 과정에서 가중치 행렬(weight matrix)에 적용되는
누적 그래디언트 업데이트(accumulated gradient update) 가
풀 랭크(full-rank) 일 필요가 없다고 가정한다.

이는 곧 LoRA를 모든 가중치 행렬에 적용하고
모든 바이어스(bias)² 를 함께 학습시킬 때,
사전학습된 가중치 행렬의 랭크(rank) 와
LoRA의 랭크 $r$ 를 동일하게 설정하면
전체 미세조정(full fine-tuning) 과 거의 동일한 수준의
표현력(expressiveness) 을 복원할 수 있음을 의미한다.

---

² 바이어스는 가중치에 비해 차지하는 파라미터 수가 매우 적다.

---

즉, 학습 가능한 파라미터의 수를 점진적으로 늘려감에 따라,
LoRA의 학습은 원래 모델의 학습과 점점 수렴(converge) 하게 된다.

반면,
어댑터(adapter) 기반 방법은
이론적으로 MLP(다층 퍼셉트론) 에 수렴하며,
프리픽스(prefix) 기반 방법은
긴 입력 시퀀스(long input sequences) 를 처리하지 못하는 모델로 수렴한다.³

---

³ 이는 복잡한(hard) 작업에 적응할 때 불가피한 현상이다.

---

추가적인 추론 지연이 없음 (No Additional Inference Latency)

프로덕션 환경(production environment)에서 모델을 배포할 때,
다음과 같이 명시적으로 계산하여 저장할 수 있다.

\[W = W_0 + BA\]

그 후 일반적인 방식으로(in the usual way) 추론(inference)을 수행하면 된다.
여기서 $W_0$와 $BA$는 모두 $\mathbb{R}^{d \times k}$ 공간에 속한다.

다른 전이 학습(downstream) 작업으로 전환해야 하는 경우에는,
$BA$를 빼서 원래의 $W_0$를 복원한 뒤,
새로운 작업에 해당하는 $B’A’$를 더하면 된다.
이 연산은 매우 빠르며 메모리 오버헤드(memory overhead) 도 거의 없다.

가장 중요한 것은, 이러한 설계에 의해
LoRA는 추론 중(inference) 완전 미세조정(fine-tuned) 모델과 비교했을 때
어떠한 추가적인 지연(latency)도 유발하지 않는다는 점이다.

4.2 트랜스포머에 LoRA 적용하기 (Applying LoRA to Transformer)

이론적으로, LoRA는
신경망(neural network) 내의 임의의 가중치 행렬(weight matrix) 부분집합에
적용하여 학습 가능한 파라미터 수를 줄일 수 있다.

트랜스포머(Transformer) 아키텍처에서는
셀프-어텐션(self-attention) 모듈에
4개의 가중치 행렬 $W_q, W_k, W_v, W_o$ 가 있고,
MLP 모듈에는 2개의 가중치 행렬이 존재한다.

우리는 $W_q$ (또는 $W_k$, $W_v$)를
출력 차원이 일반적으로 어텐션 헤드(attention heads) 로 분할되어 있더라도,
단일 행렬(single matrix) $d_{\text{model}} \times d_{\text{model}}$ 크기의 행렬로 간주한다.

본 연구에서는 단순성과 파라미터 효율성(parameter-efficiency)을 위해
전이 학습(downstream task) 시
어텐션 가중치(attention weights) 만 적응(adapt)시키고,
MLP 모듈은 고정(freeze) 시켜 학습하지 않는다.

또한, 7.1절(Section 7.1) 에서
트랜스포머 내 서로 다른 유형의 어텐션 가중치 행렬에
LoRA를 적용할 때의 효과를 추가로 분석한다.

한편, MLP 층, LayerNorm 층, 바이어스(biases) 에
LoRA를 적용하는 것에 대한 실증적 연구(empirical investigation)는
향후 연구(future work) 로 남겨둔다.

실용적 이점과 한계 (Practical Benefits and Limitations)

가장 큰 이점은 메모리(memory) 와 저장 공간(storage) 사용량의 감소이다.

대규모 트랜스포머(Transformer)를 Adam 옵티마이저로 학습할 때,
$r \ll d_{\text{model}}$ 인 경우
고정된 파라미터(frozen parameters)에 대한 옵티마이저 상태(optimizer states)를
저장할 필요가 없으므로 VRAM 사용량을 최대 2/3까지 줄일 수 있다.

예를 들어, GPT-3 (175B) 모델의 경우
학습 중 VRAM 소비량이 1.2TB에서 350GB로 감소한다.

$r = 4$이고 쿼리(query) 및 밸류(value) 투영 행렬만을 적응시킬 때,
체크포인트(checkpoint) 크기는 약 10,000배 감소한다
(350GB → 35MB)⁴.

---

⁴ 배포(deployment) 시에는 여전히 350GB 크기의 기본 모델이 필요하다.
그러나 100개의 적응된 모델(adapted models)을 저장하더라도
필요한 용량은 350GB + (35MB × 100) ≈ 354GB에 불과하다.
이는 각각의 모델을 별도로 저장했을 때 필요한 100 × 350GB ≈ 35TB에 비해
극적으로 작다.

---

이로 인해 훨씬 적은 수의 GPU로 학습이 가능해지고,
입출력 병목(I/O bottleneck) 문제를 피할 수 있다.

또한, LoRA 가중치만 교체하면
모든 파라미터를 교체할 필요 없이
배포 중에도 낮은 비용으로 작업 간 전환(task switching) 이 가능하다.

이 덕분에 VRAM에 사전학습된 가중치를 저장한 채로
다양한 맞춤형(customized) 모델을
실시간(on the fly) 으로 교체하여 사용할 수 있다.

마지막으로, GPT-3 (175B) 에서 전체 미세조정(full fine-tuning)과 비교했을 때
약 25%의 학습 속도 향상(speedup) 이 관찰되었다.⁵

이는 전체 파라미터 중 대다수에 대해
그래디언트를 계산할 필요가 없기 때문이다.

---

⁵ GPT-3 (175B) 의 경우,
전체 미세조정(full fine-tuning) 의 학습 처리 속도(training throughput)는
V100 GPU당 32.5 tokens/s 이다.
동일한 모델 병렬화(model parallelism) 분할 수(weight shards)를 사용했을 때,
LoRA 의 처리 속도는 V100 GPU당 43.1 tokens/s 로 향상된다.

---

LoRA에도 몇 가지 한계점(limitations)이 존재한다.

예를 들어, 추가적인 추론 지연(inference latency)을 제거하기 위해
$A$와 $B$를 $W$에 흡수(absorb)하기로 선택한 경우,
서로 다른 작업(tasks)에 대해 서로 다른 $A$와 $B$를 가진 입력들을
하나의 순전파(single forward pass) 에서 배치(batch) 처리하는 것은 간단하지 않다.

그러나 지연(latency)이 중요하지 않은 시나리오에서는,
가중치(weights)를 병합하지 않고
배치 내의 각 샘플(sample)에 사용할 LoRA 모듈을
동적으로 선택(dynamically choose) 하는 것이 가능하다.

---

왜 서로 다른 작업을 한 번에 배치 처리하기 어려운가?

• LoRA에서는 각 작업(task)마다 고유한 $A$와 $B$ 행렬을 가진다.
  즉, “작업 A용 LoRA”와 “작업 B용 LoRA”는 서로 다른 파라미터 집합을 사용한다.

• 그런데 만약 $A$와 $B$를 기본 가중치 $W$에 미리 흡수(absorb) 해버리면
  LoRA가 원래의 모델 구조에 완전히 통합되어 버린다.
  이렇게 되면 한 번의 순전파(forward pass)에서
  여러 작업이 서로 다른 $A$와 $B$를 동시에 사용하는 것이 불가능해진다.
  (즉, 한 모델이 한 가지 LoRA 설정만 사용할 수 있는 셈이다.)

• 반면, 지연(latency) 이 중요하지 않은 상황이라면
  $A$와 $B$를 미리 합치지 않고 그대로 분리해 둔 채로
  배치 내 각 샘플(sample) 이 서로 다른 LoRA 모듈을
  동적으로 선택(dynamically select) 하여 사용할 수 있다.
  예를 들어, 같은 배치에 “요약 작업용 LoRA”와 “번역 작업용 LoRA”가 섞여 있어도
  각 입력마다 대응되는 LoRA 모듈을 지정해 처리할 수 있다는 뜻이다.

• 그러나 이 방식은 LoRA 모듈을 매번 선택하고 적용해야 하므로
  연산 효율이 떨어지고, 실제 서비스 환경(online inference)에서는
  속도 저하(latency increase)가 발생할 수 있다.

---

5. 실증 실험 (Empirical Experiments)

우리는 RoBERTa (Liu et al., 2019), DeBERTa (He et al., 2021),
그리고 GPT-2 (Radford et al., b)에서 LoRA의 전이 학습(downstream) 성능을 평가하고,
그 후 이를 GPT-3 (175B) (Brown et al., 2020)로 확장한다.

본 실험은 자연어 이해(NLU, Natural Language Understanding) 부터
자연어 생성(NLG, Natural Language Generation) 까지
넓은 범위의 작업(tasks)을 포함한다.

구체적으로,
RoBERTa와 DeBERTa는 GLUE 벤치마크(GLUE benchmark) (Wang et al., 2019)를 기준으로 평가한다.

GPT-2의 경우, Li & Liang (2021) 의 설정을 그대로 따라
직접적인 비교(direct comparison)를 수행하며,
대규모 실험(large-scale experiments)을 위해
GPT-3에는 다음 두 작업을 추가한다:

• WikiSQL (Zhong et al., 2017): 자연어 질의(NL)를 SQL 쿼리로 변환
• SAMSum (Gliwa et al., 2019): 대화 요약(conversation summarization)

사용된 데이터셋에 대한 더 자세한 내용은 부록 C(Appendix C) 를 참고한다.

모든 실험은 NVIDIA Tesla V100 GPU 환경에서 수행하였다.

5.1 베이스라인 (Baselines)

다른 베이스라인(baseline)들과의 폭넓은 비교를 위해,
우리는 기존 연구에서 사용된 설정(setup)을 재현(replicate)하고,
가능한 경우 그들이 보고한 수치(reported numbers)를 그대로 활용하였다.
그러나 이러한 방식은 일부 베이스라인이
특정 실험에서만 등장할 수도 있음을 의미한다.

미세조정(Fine-Tuning, FT) 은
적응(adaptation)을 위한 일반적인 접근법이다.
미세조정 과정에서 모델은
사전학습된 가중치(pre-trained weights) 와 바이어스(biases) 로 초기화되고,
이후 모든 모델 파라미터(model parameters) 가
그래디언트 업데이트(gradient updates) 를 받는다.

단순한 변형으로는,
일부 층(layers)만 업데이트하고
나머지 층을 고정(freeze) 하는 방식이 있다.
이 중 하나로, Li & Liang (2021) 이 GPT-2에서 보고한
FT^Top2 베이스라인을 포함하였다.
이는 마지막 두 개의 층만 적응(adapt) 시키는 미세조정 방식이다.

Bias-only (또는 BitFit) 은
모델의 바이어스 벡터(bias vectors) 만 학습시키고,
그 외의 모든 파라미터는 고정(freeze) 시키는 베이스라인이다.
이 접근은 BitFit (Zaken et al., 2021) 에서도
동일한 방식으로 연구된 바 있다.

---

Bias-only (BitFit) 방식의 의미

• 바이어스(bias) 는 각 뉴런의 출력값을 조정하는 상수 항(constant term) 으로,
  모델이 입력값에 관계없이 특정 방향으로 출력을 이동(shift)시키는 역할을 한다.

• Bias-only 학습 또는 BitFit 방식은
  가중치(weight)는 그대로 둔 채,
  이 바이어스 항만 미세하게 조정(fine-tune)함으로써
  새로운 작업(task)에 적응하도록 하는 매우 단순한 접근이다.

• 이 방법의 장점은 학습해야 할 파라미터 수가 극도로 적다는 점이다.
  전체 파라미터 중 바이어스 항은 0.1% 이하에 불과하므로,
  적은 자원으로도 빠르게 전이 학습이 가능하다.

• 반면, 모델의 표현력(expressive power) 은 제한된다.
  가중치 행렬을 전혀 수정하지 않기 때문에,
  복잡한 작업에서는 충분한 적응력을 확보하기 어렵다.

• 즉, BitFit은 효율성과 단순성을 극대화하지만,
  성능 향상 폭은 제한적인 파라미터 효율적 미세조정(PEFT) 기법이다.

---

Prefix-embedding tuning (PreEmbed) 은
입력 토큰들 사이에 특수 토큰(special tokens) 을 삽입하는 방식이다.
이 특수 토큰들은 학습 가능한 단어 임베딩(trainable word embeddings) 을 가지며,
일반적으로 모델의 기존 어휘(vocabulary)에는 포함되지 않는다.

이러한 특수 토큰을 어디에 위치시킬지 는
모델의 성능에 영향을 줄 수 있다.
본 논문에서는 두 가지 방식에 초점을 맞춘다.

• 프리픽싱(prefixing) : 특수 토큰을 프롬프트(prompt) 앞에 추가하는 방식
• 인픽싱(infixing) : 특수 토큰을 프롬프트 뒤에 추가하는 방식

이 두 방법은 Li & Liang (2021) 에서 모두 논의되었다.

프리픽스(prefix) 토큰의 개수를 $l_p$,
인픽스(infix) 토큰의 개수를 $l_i$ 라고 할 때,
학습 가능한 파라미터의 수는 다음과 같다.

\[|\Theta| = d_{\text{model}} \times (l_p + l_i)\]

---

Prefix-embedding tuning 방식의 개념

• Prefix-embedding tuning (PreEmbed) 은
  모델이 입력(prompt)을 해석하기 전에
  학습 가능한 임베딩 벡터(learnable embedding vectors) 를
  인위적으로 삽입해 주는 방식이다.
  이 임베딩은 마치 “작업(task)별 가이드 문장”처럼 동작하며,
  모델이 어떤 문맥(context)에서 작동해야 하는지를 미리 조정한다.

• 이 접근법은 프롬프트(prompt) 기반 학습(prompt-based learning) 의 한 형태로,
  사전학습된 언어모델이 기존에 학습한 지식을 그대로 유지한 채
  새로운 작업에 적응할 수 있도록 돕는다.

• 예를 들어, “문장 요약” 작업을 학습할 때
  입력 앞에 [SUMMARIZE] 같은 토큰을 추가하면,
  모델은 이 임베딩을 통해 해당 문맥을 “요약” 문제로 인식하게 된다.

• 프리픽싱(prefixing) 과 인픽싱(infixing) 은
  이러한 특수 토큰을 어디에 삽입하느냐의 차이에 불과하다.
  • 프리픽싱(prefixing): 입력 앞에 붙여 모델이 가장 먼저 인식하도록 함
  • 인픽싱(infixing): 입력 뒤쪽에 붙여 문맥 정보를 보완하도록 함

• 학습 가능한 파라미터 수는
  각 특수 토큰의 임베딩 크기($d_{\text{model}}$)와
  토큰의 개수($l_p$, $l_i$)에 비례하며,
  수식으로는 다음과 같이 표현된다.
  \(|\Theta| = d_{\text{model}} \times (l_p + l_i)\)

• 즉, PreEmbed는 가중치(weight) 나 레이어(layer) 를 바꾸지 않고도
  문맥을 조절(contextual adaptation) 하는 방법으로,
  추가 파라미터가 매우 적고 구조 변경이 필요 없는 장점이 있다.

---

Prefix-layer tuning (PreLayer) 은
Prefix-embedding tuning 의 확장(extension)이다.
이 방법은 단지 특수 토큰의 단어 임베딩(word embeddings)
또는 임베딩 층 이후의 활성값(activations) 만 학습하는 것이 아니라,
각 트랜스포머 층(Transformer layer) 이후의
활성값 전체를 학습한다.

이때 이전 층에서 계산된 활성값들은
단순히 학습 가능한 값으로 치환(replace) 된다.

그 결과, 학습 가능한 파라미터의 총 수는 다음과 같다.

\[|\Theta| = L \times d_{\text{model}} \times (l_p + l_i)\]

여기서 $L$은 트랜스포머 층의 개수(number of Transformer layers) 를 의미한다.

---

Prefix-layer tuning 방식의 개념

• Prefix-layer tuning (PreLayer) 은
  Prefix-embedding tuning 보다 한 단계 더 깊은 수준에서
  모델의 내부 표현(internal representation)을 조정하는 방법이다.

• PreEmbed가 입력 임베딩(input embedding) 수준에서만
  “특수 토큰의 표현”을 학습하는 반면,
  PreLayer는 트랜스포머의 각 층(layer) 마다
  새로운 학습 가능한 활성값(learnable activations) 을 삽입한다.

• 즉, 원래는 이전 층의 출력을 다음 층의 입력으로 사용하지만,
  PreLayer에서는 이 출력을 완전히 교체(replace) 하여
  “학습 가능한 프리픽스(prefix)”로 대체한다.
  이로써 모델은 각 층에서 독립적으로
  새로운 문맥 정보를 주입(inject)할 수 있게 된다.

• 결과적으로, PreLayer는
  트랜스포머 전체를 관통하는 계층적 프리픽스 구조(hierarchical prefixing) 를 형성하며,
  더 강력한 조정 능력을 제공한다.
  하지만 동시에, 학습해야 할 파라미터 수도 늘어난다.

• 실제로, 전체 학습 가능한 파라미터 수는
  트랜스포머 층의 개수 $L$에 비례하여 증가한다.
  \(|\Theta| = L \times d_{\text{model}} \times (l_p + l_i)\)

• 정리하자면,
  PreLayer는 각 층의 출력 공간에서 직접 적응(adaptation)을 수행하는 기법으로,
  PreEmbed보다 훨씬 유연하지만,
  그만큼 계산량(computation) 과 메모리 요구량(memory usage) 이 커지는 단점이 있다.

---

어댑터 튜닝(Adapter tuning) 은 Houlsby et al. (2019) 에 의해 제안된 방법으로,
셀프-어텐션(self-attention) 모듈(및 MLP 모듈)과
그 뒤의 잔차 연결(residual connection) 사이에
어댑터 층(adapter layer) 을 삽입한다.

각 어댑터 층은 두 개의 완전연결층(fully connected layers) 과
그 사이에 위치한 비선형 함수(non-linearity) 로 구성되며,
각 층에는 바이어스(bias) 도 포함된다.
이 원래의 설계를 Adapter^H 라고 부른다.

최근 Lin et al. (2020) 은
더 효율적인 설계를 제안하였는데,
이는 MLP 모듈 뒤와 LayerNorm 이후에만
어댑터 층을 적용하는 방식이다.
이 설계를 Adapter^L 이라고 한다.

또한, Pfeiffer et al. (2021) 이 제안한
매우 유사한 또 다른 변형이 있으며,
이를 Adapter^P 라고 부른다.

우리는 또한 Rücklé et al. (2020) 이 제안한
AdapterDrop (Adapter^D) 베이스라인도 포함한다.
이 방법은 일부 어댑터 층을 제거(drop)하여
효율성을 더욱 높인다.

비교 가능한 베이스라인의 수를 최대화하기 위해,
가능한 경우 기존 연구에서 보고된 수치(reported results)를 인용하였으며,
표에서 별표(*)로 표시된 행이 이에 해당한다.

모든 경우에서 학습 가능한 파라미터의 수는 다음과 같이 주어진다.

\[|\Theta| = \hat{L}_{\text{Adpt}} \times (2 \times d_{\text{model}} \times r + r + d_{\text{model}}) + 2 \times \hat{L}_{\text{LN}} \times d_{\text{model}}\]

여기서
\(\hat{L}_{\text{Adpt}}\) 는 어댑터 층의 개수(number of adapter layers),
\(\hat{L}_{\text{LN}}\) 은 학습 가능한 LayerNorm의 개수(number of trainable LayerNorms) 를 의미한다.
(예: AdapterL의 경우 LayerNorm을 학습시킴)

---

어댑터(Adapter) 튜닝의 구조적 특징

• 어댑터(Adapter) 는 대형 언어모델의 모든 파라미터를 미세조정하지 않고,
  기존 층(layer) 사이에 작은 모듈을 삽입하여 새로운 작업에 적응하도록 하는 기법이다.
  즉, 모델의 주요 가중치는 그대로 두고,
  작고 얕은(subnetwork) 네트워크만 추가 학습하는 형태이다.

• 어댑터 층은 일반적으로 다음과 같은 구조를 가진다.

  \[h' = h + f(W_{\text{up}} \, \sigma(W_{\text{down}} h))\]

  여기서
  $W_{\text{down}}$ 은 차원 축소(bottleneck) 를 위한 작은 행렬,
  $W_{\text{up}}$ 은 다시 확장(projection back) 하는 행렬이며,
  $\sigma$ 는 비선형 함수(예: ReLU, GELU)이다.
  이렇게 “입력 → 축소 → 비선형 변환 → 복원” 과정을 거치면서
  모델은 작은 파라미터만으로 새로운 표현을 학습할 수 있다.

• Adapter^H (Houlsby-style) 는
  셀프-어텐션과 MLP 모듈 모두 뒤에 어댑터를 삽입하여
  비교적 풍부한 적응 표현을 학습하지만, 연산량이 다소 증가한다.

• Adapter^L (Lin-style) 은
  MLP 뒤쪽과 LayerNorm 이후에만 어댑터를 적용하여
  파라미터 수와 연산량을 줄인 효율적인 변형이다.

• Adapter^P (Pfeiffer-style) 은 AdapterL과 구조가 매우 유사하며,
  위치와 초기화 방식의 세부 차이만 존재한다.

• Adapter^D (AdapterDrop) 은
  일부 어댑터 층을 제거(drop)함으로써
  훈련 효율을 높이는 방법으로,
  메모리 사용량과 추론 시간을 줄일 수 있다.

• 이처럼 어댑터 계열의 방법들은
  추가되는 파라미터 수가 매우 적고,
  기존 모델의 표현을 크게 손상시키지 않으면서
  새로운 작업으로 빠르게 적응할 수 있다는 장점이 있다.
  그러나 모든 층을 순차적으로 거치므로,
  추론 시 지연(latency) 이 발생한다는 한계도 존재한다.

---

한편, LoRA 는 기존 가중치 행렬(weight matrix)에
랭크 분해(rank decomposition) 행렬 쌍을 병렬로 추가하여 학습 가능한 구조를 만든다.
4.2절 에서 언급한 바와 같이,
대부분의 실험에서는 단순화를 위해
$W_q$ 와 $W_v$ 에만 LoRA를 적용하였다.

LoRA의 학습 가능한 파라미터 수는
랭크 $r$ 과 원래 가중치의 형태(shape)에 따라 결정된다.

\[|\Theta| = 2 \times \hat{L}_{\text{LoRA}} \times d_{\text{model}} \times r\]

여기서
$\hat{L}_{\text{LoRA}}$ 는 LoRA가 적용된 가중치 행렬의 개수를 의미한다.

---

LoRA의 구조적 특징과 파라미터 효율성

• LoRA (Low-Rank Adaptation) 의 핵심 아이디어는
  기존의 가중치 행렬 $W$ 를 직접 수정하지 않고,
  그 변화량(update)을 저랭크 행렬 쌍 $A$, $B$ 의 곱으로 근사하는 것이다.
  즉,

  \[W' = W + BA\]

  와 같이 표현되며, 여기서 $B \in \mathbb{R}^{d_{\text{model}} \times r}$,
  $A \in \mathbb{R}^{r \times d_{\text{model}}}$,
  그리고 $r \ll d_{\text{model}}$ 이다.

• 이 구조 덕분에 LoRA는 학습해야 할 파라미터 수를 대폭 줄이면서도,
  원래의 모델 표현력을 유지할 수 있다.
  왜냐하면, 모델의 변화량 $\Delta W$ 를
  고차원(full rank) 공간이 아니라
  저차원(low-rank) 부분공간(subspace) 내에서만 학습하기 때문이다.

• 대부분의 실험에서 LoRA는
  쿼리($W_q$) 와 밸류($W_v$) 투영 행렬에만 적용되었다.
  이는 어텐션(attention) 계산에서
  가장 중요한 정보 흐름을 담당하는 두 행렬에 집중함으로써,
  효율성과 성능의 균형을 맞추기 위한 설계이다.

• LoRA의 총 학습 파라미터 수는
  다음과 같이 간단히 계산된다.

  \[|\Theta| = 2 \times \hat{L}_{\text{LoRA}} \times d_{\text{model}} \times r\]

  여기서 $\hat{L}_{\text{LoRA}}$ 는 LoRA가 적용된
  가중치 행렬(weight matrices)의 개수를 의미한다.

• 즉, LoRA는 랭크 $r$ 값을 작게 설정함으로써
  전체 파라미터의 0.1% 이하만을 학습하면서도,
  완전 미세조정(full fine-tuning) 수준의 성능을 유지할 수 있는
  매우 효율적인 전이 학습(parameter-efficient transfer learning) 기법이다.

---

5.2 RoBERTa Base/Large

RoBERTa (Liu et al., 2019) 는
BERT (Devlin et al., 2019a) 에서 제안된
사전학습 방식을 개선한(pre-training recipe optimized) 모델로,
학습 가능한 파라미터 수를 크게 늘리지 않으면서도 BERT의 성능을 향상시킨 모델이다.

최근 몇 년간 RoBERTa는
GLUE 벤치마크 (Wang et al., 2019) 와 같은
NLP 리더보드에서 훨씬 더 큰 모델들에 의해 추월당했지만,
그럼에도 불구하고 모델 크기 대비 경쟁력 있고 인기 있는 사전학습 모델로
여전히 많은 연구자들(practitioners) 사이에서 사용되고 있다.

우리는 HuggingFace Transformers 라이브러리 (Wolf et al., 2020) 에서
사전학습된 RoBERTa Base (125M) 와 RoBERTa Large (355M) 모델을 사용하였으며,
GLUE 벤치마크의 여러 과제(tasks)에 대해
다양한 효율적 적응 기법(efficient adaptation approaches) 의 성능을 비교 평가하였다.

또한 Houlsby et al. (2019) 과 Pfeiffer et al. (2021) 의 설정을 재현(replicate)하여
동일한 조건에서 비교하였다.

공정한 비교(fair comparison)를 위해,
어댑터(Adapter) 방식과 LoRA를 비교할 때
다음 두 가지 주요 변경 사항을 적용하였다.

1. 모든 과제에서 동일한 배치 크기(batch size) 를 사용하고,
   시퀀스 길이(sequence length) 는 128로 설정하여
   어댑터 베이스라인(adapter baselines)의 설정과 일치시켰다.
2. MRPC, RTE, STS-B 과제의 경우,
   MNLI로 이미 적응된 모델이 아닌,
   사전학습된(pre-trained) 모델에서 직접 초기화하였다.
   (이는 미세조정(fine-tuning) 베이스라인의 설정과 다르다.)

Houlsby et al. (2019) 의 이보다 더 제한된 설정을 따른 실행(run)들은
† 기호로 표시된다.

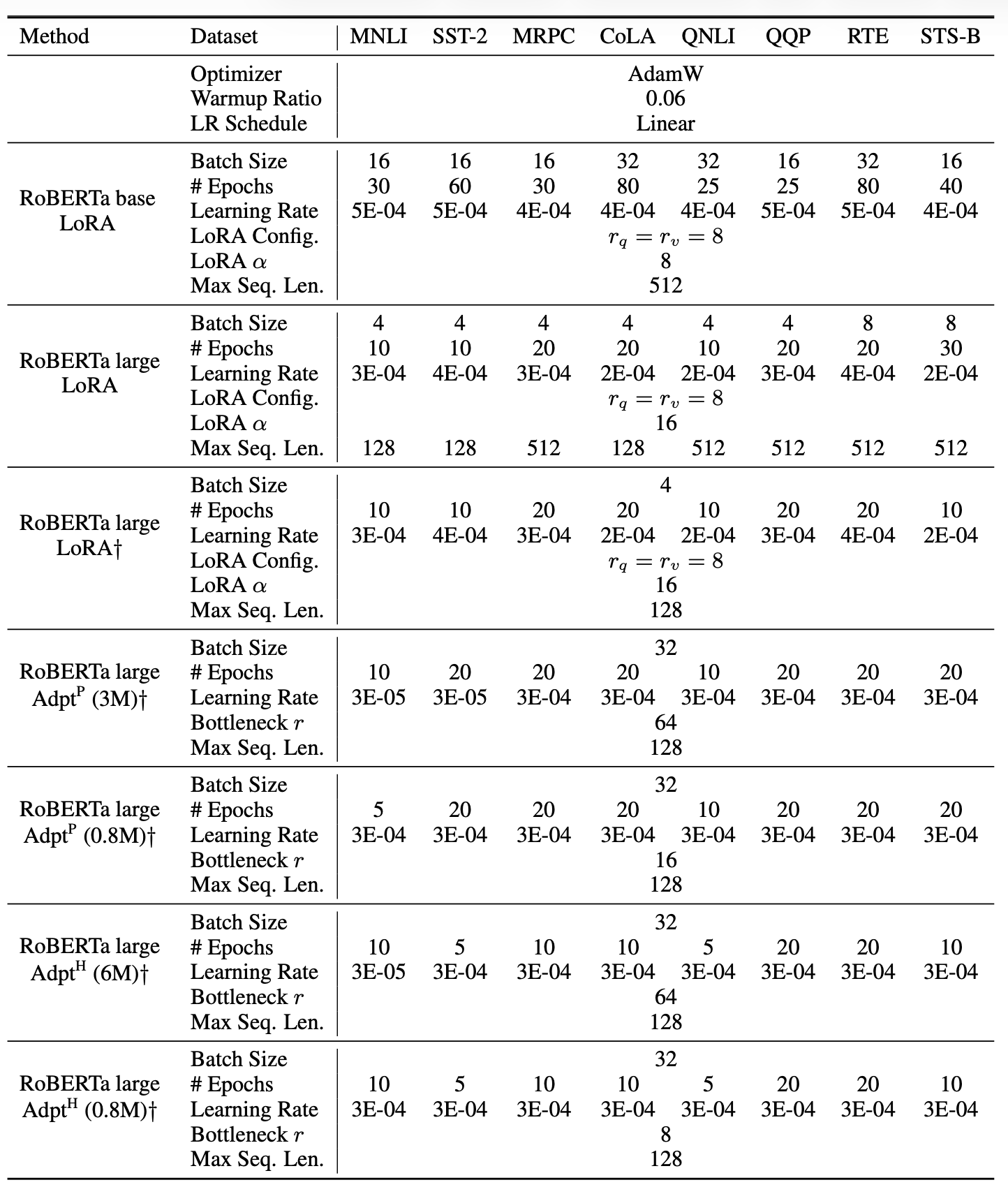
결과는 표 2 (상단 3개 구간) 에 제시되어 있으며,
사용된 하이퍼파라미터(hyperparameter) 의 세부 내용은
부록 D.1 (Section D.1) 에서 확인할 수 있다.

---

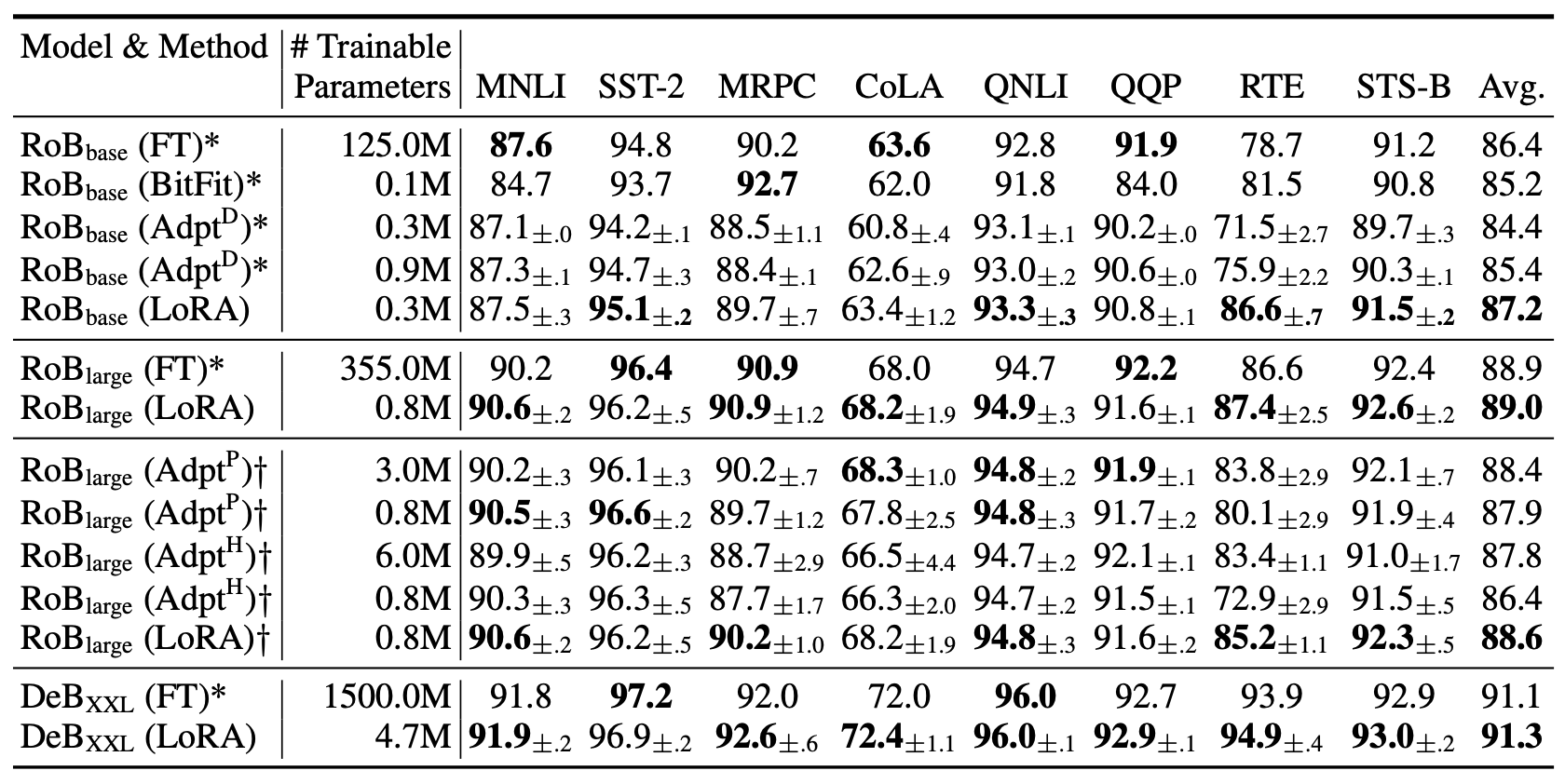
표 2

GLUE 벤치마크에서 서로 다른 적응(adaptation) 방법을 적용한
RoBERTa-base, RoBERTa-large, 그리고 DeBERTa-XXL 모델의 성능 비교.

MNLI는 전체 정확도(overall accuracy, matched 및 mismatched 포함),
CoLA는 Matthew’s 상관 계수(Matthew’s correlation),
STS-B는 피어슨 상관 계수(Pearson correlation),
그 외 과제들은 정확도(accuracy) 를 기준으로 평가하였다.

모든 지표(metric)는 값이 높을수록 더 우수하다.

별표(*)는 기존 연구에서 발표된 수치(published results) 를,
더거 기호(†)는 공정한 비교(fair comparison) 를 위해
Houlsby et al. (2019) 과 유사한 설정으로 구성된 실행(run)을 나타낸다.

---

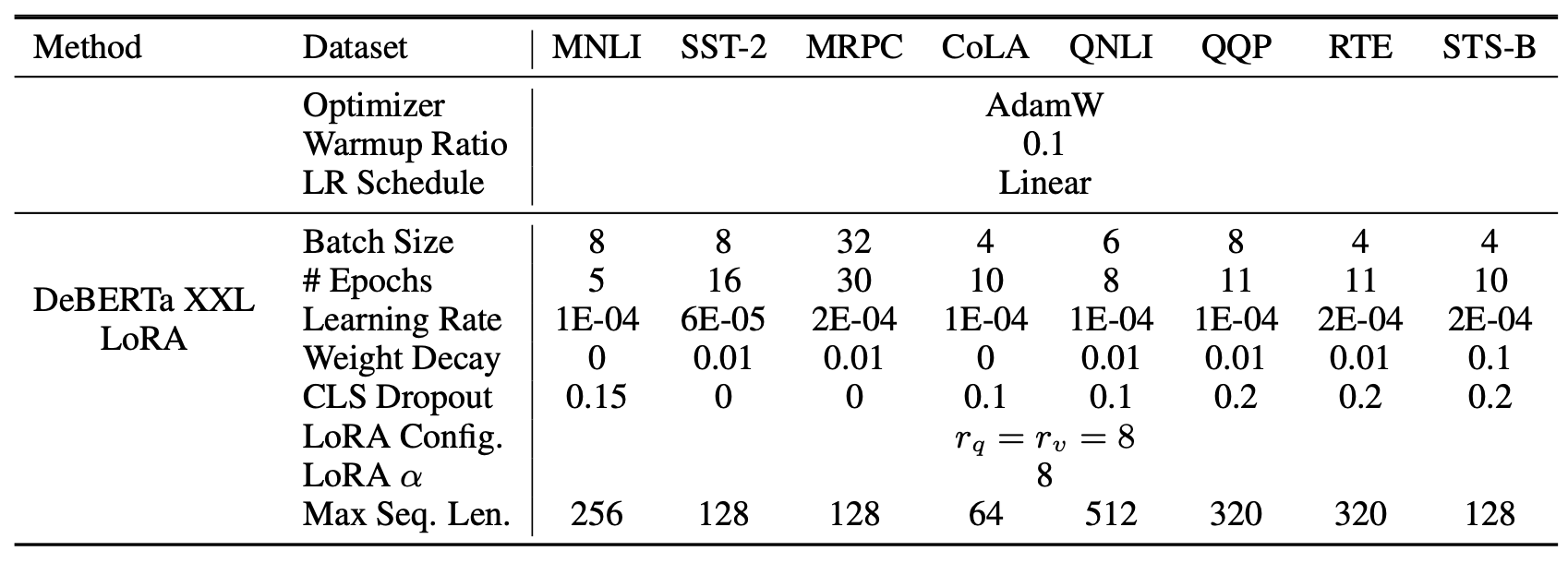
5.3 DeBERTa XXL

DeBERTa (He et al., 2021) 는
BERT의 보다 최근 변형(modern variant)으로,
훨씬 더 대규모 데이터로 학습되었으며,
GLUE (Wang et al., 2019) 와 SuperGLUE (Wang et al., 2020) 와 같은
벤치마크에서 매우 경쟁력 있는 성능을 보인다.

우리는 LoRA가
완전 미세조정(full fine-tuning) 된 DeBERTa XXL (1.5B) 모델의
GLUE 벤치마크 성능을 여전히 따라잡을 수 있는지를 평가하였다.

그 결과는 표 2 (하단 구간) 에 제시되어 있으며,
사용된 하이퍼파라미터(hyperparameters) 의 세부 내용은
부록 D.2 (Section D.2) 에서 확인할 수 있다.

5.4 GPT-2 Medium/Large

LoRA가 자연어 이해(NLU) 에서
전체 미세조정(full fine-tuning) 의 경쟁력 있는 대안이 될 수 있음을 보여주었으므로,
우리는 이제 LoRA가 GPT-2 Medium 및 Large (Radford et al., b) 와 같은
자연어 생성(NLG) 모델에서도 여전히 우수한지를 알아보고자 한다.

직접적인 비교를 위해,
우리의 설정은 Li & Liang (2021) 과 가능한 한 유사하게 유지하였다.

지면 제약(space constraint)으로 인해,
이 절에서는 E2E NLG Challenge 에 대한 결과만 제시하며,
그 내용은 표 3 에 나와 있다.

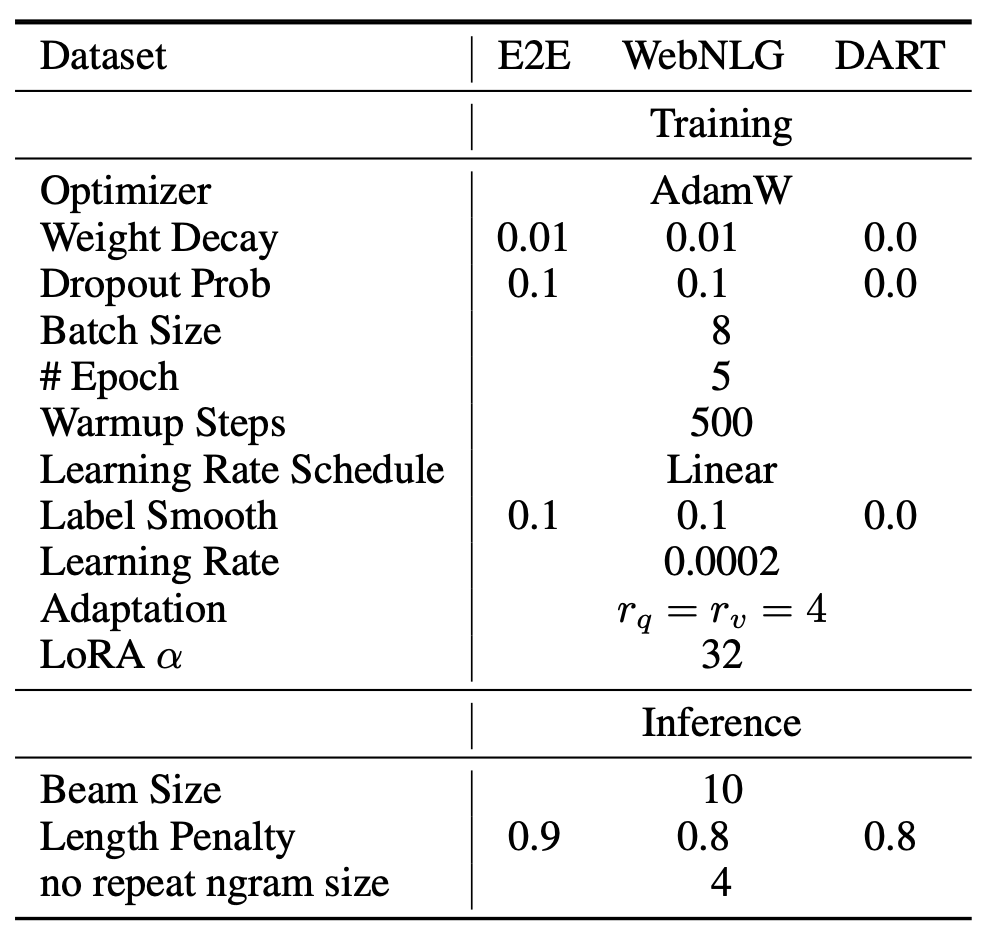
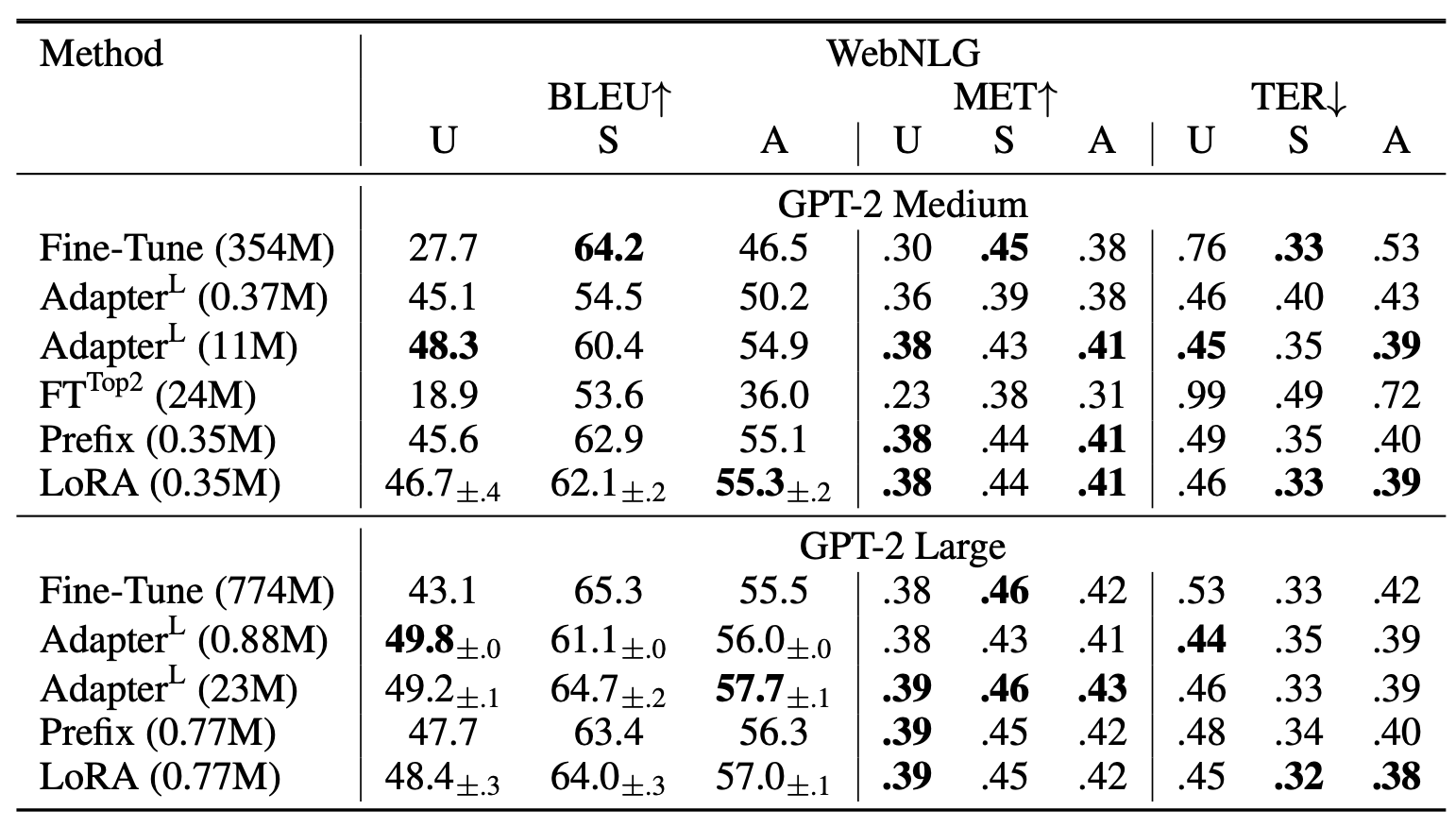
WebNLG (Gardent et al., 2017) 및 DART (Nan et al., 2020) 의 결과는
부록 F.1 (Section F.1) 에서 확인할 수 있으며,
사용된 하이퍼파라미터(hyperparameters) 의 목록은
부록 D.3 (Section D.3) 에 포함되어 있다.

---

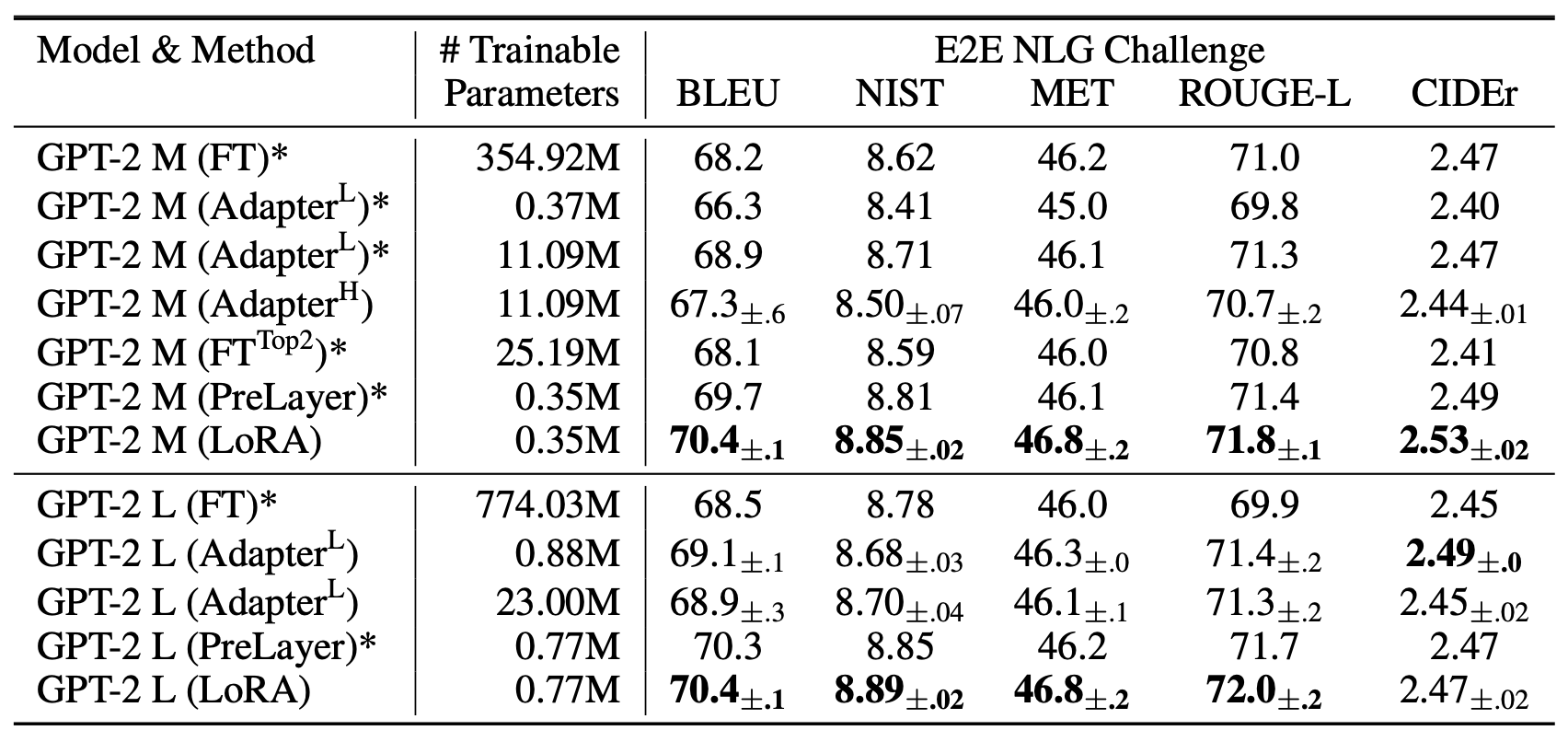
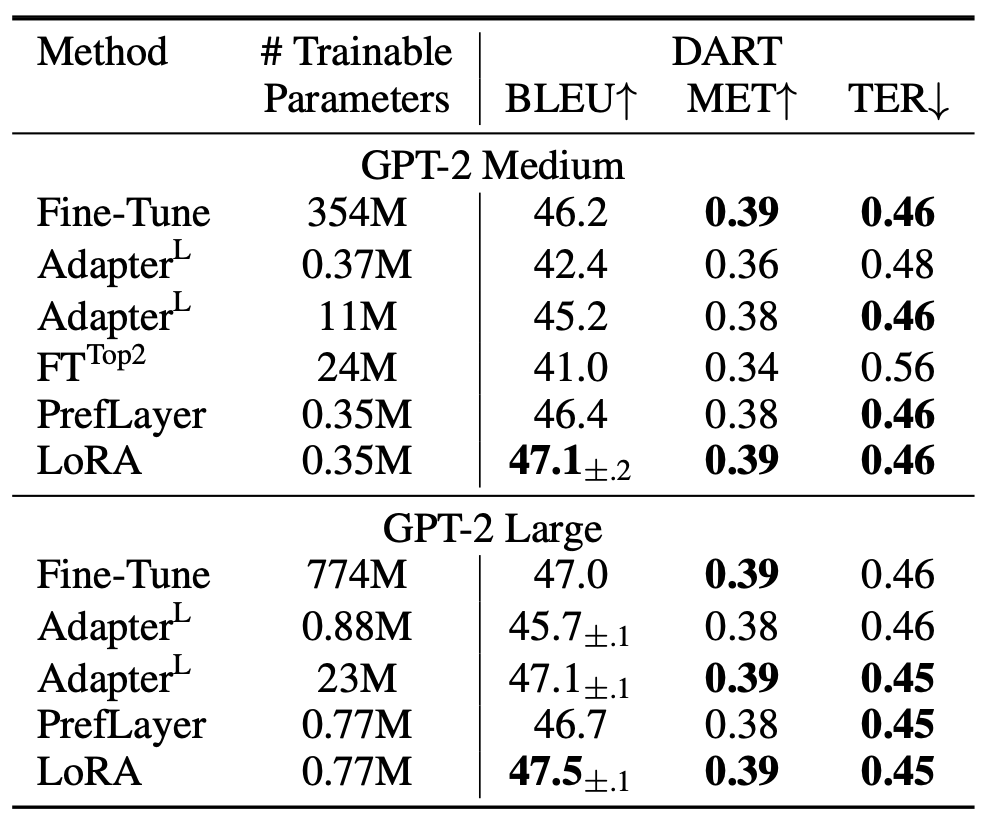
표 3

E2E NLG Challenge에서 서로 다른 적응(adaptation) 방법을 적용한
GPT-2 Medium (M) 과 Large (L) 모델의 성능 비교.

모든 평가 지표(metric)에 대해 값이 높을수록 성능이 좋다.
LoRA는 유사하거나 더 적은 학습 가능한 파라미터 수로
여러 베이스라인보다 우수한 성능을 보였다.

우리가 수행한 실험에 대해서는 신뢰 구간(confidence intervals) 이 함께 제시되어 있으며,
별표(*)는 기존 연구에서 발표된 수치(published results) 를 나타낸다.

---

5.5 GPT-3 175B로의 확장 (Scaling Up to GPT-3 175B)

LoRA의 최종적인 스트레스 테스트(stress test) 로서,
우리는 1750억 개의 파라미터(parameter) 를 가진 GPT-3 모델로 확장하였다.

높은 학습 비용(training cost)으로 인해,
모든 항목마다 개별적인 표준편차(standard deviation)를 제공하는 대신,
특정 과제(task)에 대해 무작위 시드(random seeds) 를 기준으로 한
일반적인 표준편차(typical standard deviation) 만을 보고한다.
사용된 하이퍼파라미터(hyperparameters) 의 세부 사항은
부록 D.4 (Section D.4) 에 제시되어 있다.

표 4 에서 보이듯,
LoRA는 세 개의 데이터셋 모두에서
미세조정(fine-tuning) 베이스라인과 비슷하거나 그 이상의 성능을 보였다.

그러나 그림 2(Figure 2) 에서 볼 수 있듯이,
모든 방법이 학습 가능한 파라미터 수가 많아질수록
단조롭게(monotonically) 성능이 향상되는 것은 아니다.

우리는 Prefix-embedding tuning 에서
256개 이상의 특수 토큰(special tokens) 을 사용하거나,
Prefix-layer tuning 에서
32개 이상의 특수 토큰 을 사용할 경우,
성능이 유의미하게 하락(significant performance drop) 하는 것을 관찰했다.
이 결과는 Li & Liang (2021) 에서 보고된 유사한 관찰과 일치한다.

이 현상에 대한 심층 분석(thorough investigation) 은
본 연구의 범위를 벗어나지만,
우리는 특수 토큰의 수가 많아질수록
입력 분포(input distribution)가
사전학습 데이터 분포(pre-training data distribution) 에서
더 멀어지기 때문일 것으로 추정한다.

또한, 우리는 Section F.3 에서
적은 데이터 환경(low-data regime) 에서의
다양한 적응(adaptation) 방법의 성능을 별도로 분석하였다.

---

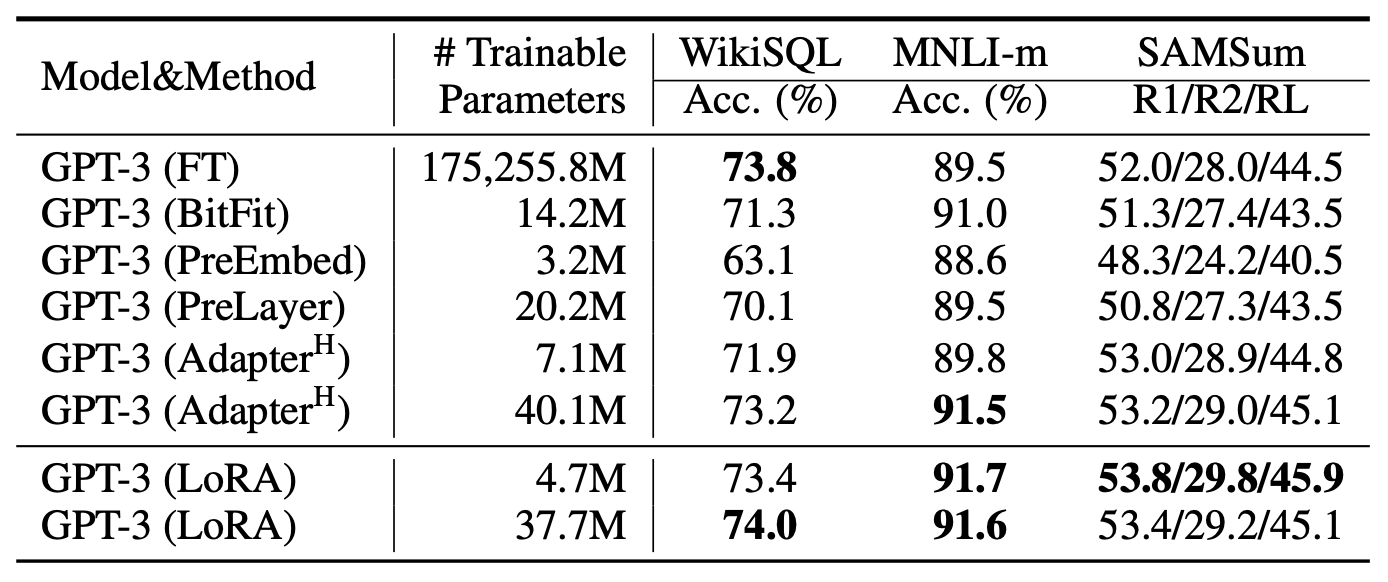
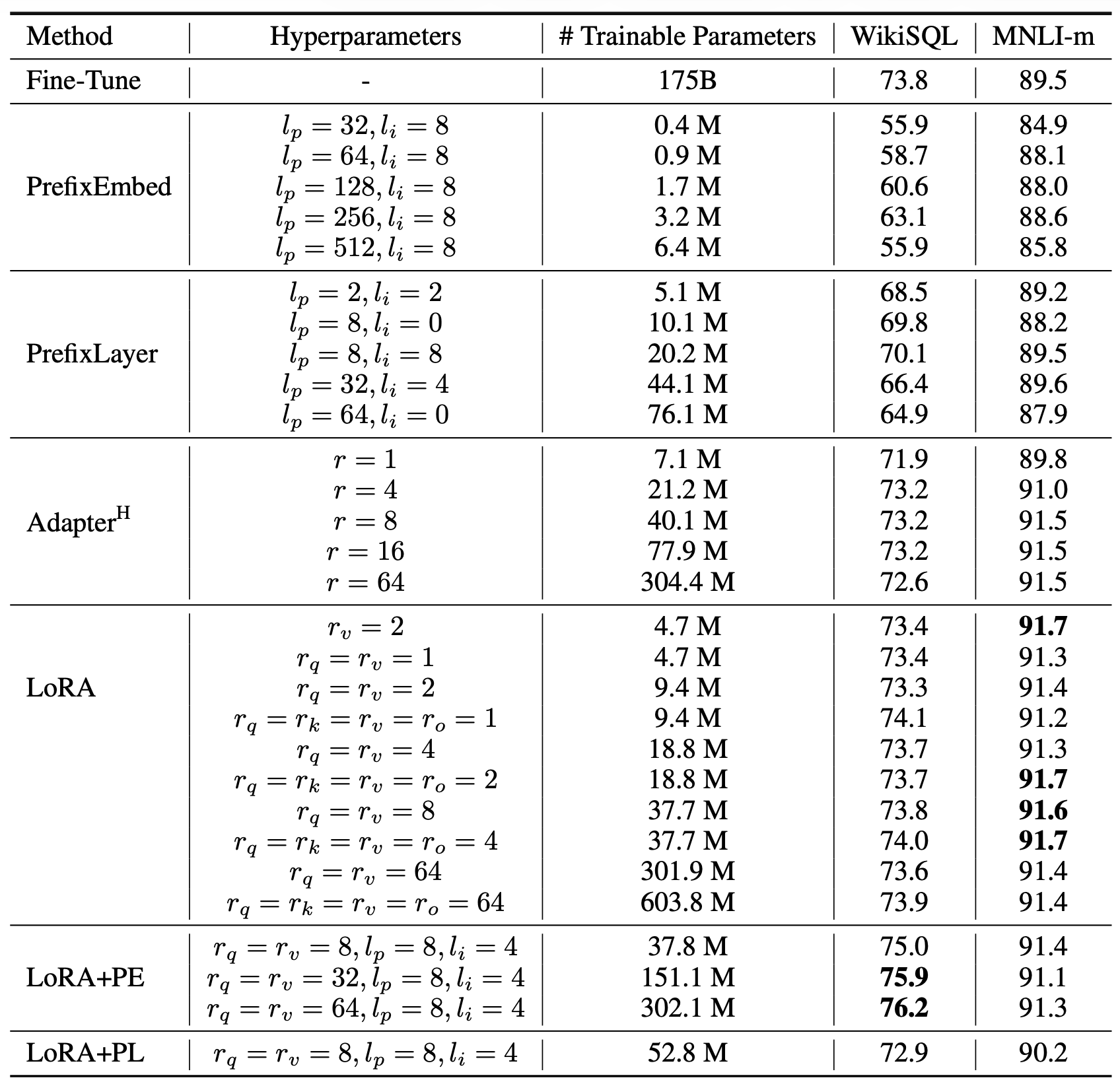
표 4

GPT-3 175B 에서 서로 다른 적응(adaptation) 방법의 성능 비교.

WikiSQL 에 대해서는 논리 형태(logical form) 검증 정확도(validation accuracy),
MultiNLI-matched 에 대해서는 검증 정확도(validation accuracy),
그리고 SAMSum 에 대해서는 Rouge-1 / Rouge-2 / Rouge-L 점수를 보고한다.

LoRA는 전체 미세조정(full fine-tuning) 을 포함한
이전 접근 방식들보다 더 우수한 성능을 보였다.

결과의 변동 범위(fluctuation range)는 다음과 같다.

• WikiSQL: 약 ±0.5%
• MNLI-m: 약 ±0.1%
• SAMSum: 세 지표 각각 약 ±0.2 / ±0.2 / ±0.1

---

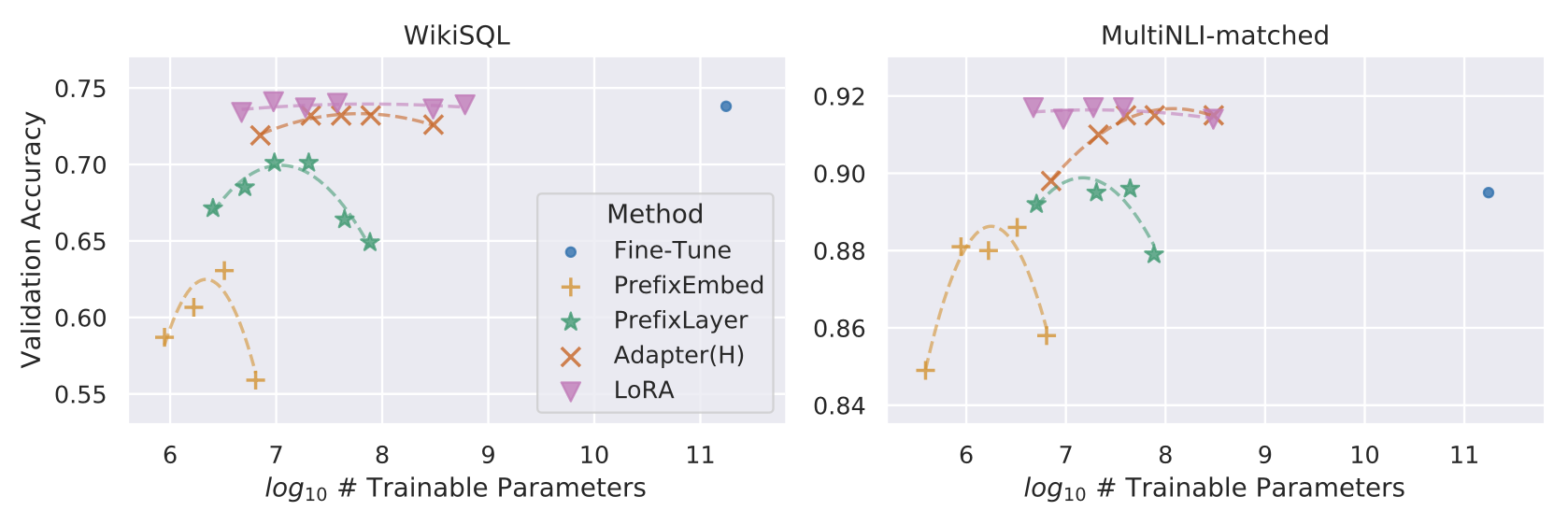
그림 2

GPT-3 175B 에서 WikiSQL 및 MNLI-matched 데이터셋에 대한
여러 적응(adaptation) 방법들의 학습 가능한 파라미터 수(trainable parameters) 와
검증 정확도(validation accuracy) 간의 관계를 나타낸 그래프.

LoRA는 더 나은 확장성(scalability) 과
과제 성능(task performance) 을 보인다.

도표에 사용된 데이터 포인트의 세부 내용은
부록 F.2 (Section F.2) 에 제시되어 있다.

---

6. 관련 연구 (Related Works)

트랜스포머 언어모델 (Transformer Language Models)

트랜스포머(Transformer) (Vaswani et al., 2017)는
셀프-어텐션(self-attention) 을 적극적으로 활용하는
시퀀스-투-시퀀스(sequence-to-sequence) 구조의 아키텍처이다.

Radford et al. (a) 는 트랜스포머 디코더(decoder)들을
여러 층으로 쌓은 구조를 이용해
이를 자기회귀 언어모델(autoregressive language modeling) 에 적용하였다.

그 이후로, 트랜스포머 기반 언어모델들은
자연어처리(NLP) 분야를 지배하게 되었으며,
다양한 과제에서 최첨단(state-of-the-art) 성능을 달성하였다.

BERT (Devlin et al., 2019b) 와 GPT-2 (Radford et al., b) 를 계기로
새로운 패러다임이 등장하였다.
이 두 모델은 모두 대규모 텍스트 데이터로 학습된
대형 트랜스포머 언어모델(large Transformer language models) 로,
일반 도메인 데이터(general domain data) 에 대한 사전학습(pre-training) 후
과제별 데이터(task-specific data) 로 미세조정(fine-tuning) 을 수행하면,
단순히 과제 데이터로만 학습하는 것보다
훨씬 큰 성능 향상이 가능함을 보여주었다.

또한, 더 큰 규모의 트랜스포머 모델을 학습시키는 것은
일반적으로 성능 향상으로 이어지며,
지속적인 연구 주제로 남아 있다.

현재까지 학습된 단일 트랜스포머 언어모델 중
가장 큰 모델은 GPT-3 (Brown et al., 2020) 로,
1750억 개의 파라미터(175B parameters) 를 가지고 있다.

프롬프트 엔지니어링과 미세조정 (Prompt Engineering and Fine-Tuning)

GPT-3 (175B) 는 몇 개의 추가 학습 예시(few-shot examples)만으로도
그 동작(behavior)을 조정할 수 있지만,
그 결과는 입력 프롬프트(input prompt) 에 크게 의존한다 (Brown et al., 2020).

이로 인해, 원하는 과제에서 모델의 성능을 극대화하기 위해
프롬프트를 어떻게 구성하고(format) 작성할지를
경험적으로 탐색하는 실천적 기술(empirical art) 이 필요하게 되었으며,
이를 프롬프트 엔지니어링(prompt engineering)
또는 프롬프트 해킹(prompt hacking) 이라고 부른다.

반면, 미세조정(fine-tuning) 은
일반 도메인 데이터(general domain data) 로 사전학습된 모델을
특정 과제(specific task) 에 맞추어 다시 학습시키는 방법이다
(Devlin et al., 2019b; Radford et al., a).

그 변형(variant) 중 일부는
모델의 전체 파라미터가 아니라 일부 파라미터(subset of parameters) 만 학습하는 방법도 포함한다
(Devlin et al., 2019b; Collobert & Weston, 2008).
그러나 실무자(practitioners)들은
전이 학습(downstream task)의 성능을 최대화하기 위해
대부분의 경우 모든 파라미터를 다시 학습(retrain all parameters) 한다.

하지만 GPT-3 (175B) 는 규모가 매우 크기 때문에,
기존 방식의 미세조정(fine-tuning)을 수행하기 어렵다.
그 이유는 다음과 같다:

• 체크포인트(checkpoint) 크기가 매우 크고,
• 사전학습(pre-training) 과 동일한 수준의 메모리 사용량(memory footprint) 을 요구하며,
• 이로 인해 하드웨어 진입 장벽(hardware barrier to entry) 이 높기 때문이다.

파라미터 효율적 적응 (Parameter-Efficient Adaptation)

여러 연구에서는 신경망(neural network) 내의 기존 층(layers)들 사이에
어댑터 층(adapter layers) 을 삽입하는 방법을 제안하였다
(Houlsby et al., 2019; Rebuffi et al., 2017; Lin et al., 2020).

우리의 방법(LoRA)은 이와 유사한 병목 구조(bottleneck structure) 를 사용하여,
가중치 업데이트(weight updates)에 저랭크 제약(low-rank constraint) 을 부과한다.

그러나 핵심적인 기능적 차이(key functional difference)는,
우리의 학습된 가중치(learned weights)가
추론(inference) 중 기존의 주요 가중치(main weights) 와 병합(merge) 될 수 있어,
추가적인 지연(latency) 을 발생시키지 않는다는 점이다.
이는 어댑터 층(adapter layers)에서는 불가능하다 (3절 참조).

어댑터의 최근 확장형(comtemporary extension) 인 COMPACTER (Mahabadi et al., 2021) 는,
Kronecker 곱(Kronecker products) 과
일부 사전 정의된 가중치 공유 체계(predetermined weight sharing scheme) 를 사용하여
어댑터 층(adapter layers)을 매개변수화(parametrize)하는 방식이다.

---

COMPACTER와 Kronecker 곱을 이용한 어댑터 효율화

• COMPACTER (Mahabadi et al., 2021) 는
  기존 어댑터(Adapter) 구조의 파라미터 효율성을 한층 더 높이기 위해 제안된
  최근 확장형(modern extension) 방식이다.

• 일반적인 어댑터 층은
  두 개의 완전연결층(fully connected layers)을 추가하여
  비선형 변환을 수행하지만,
  각 층마다 독립적인 가중치 행렬(weight matrix) 을 학습해야 한다.
  이로 인해 층 수가 많아질수록 중복된 파라미터(redundant parameters) 가 급격히 증가한다.

• COMPACTER는 이러한 비효율성을 줄이기 위해
  가중치 행렬을 Kronecker 곱(Kronecker product) 형태로 분해하여 표현한다.
  예를 들어,

  \[W_{\text{adapter}} = A \otimes B\]

  와 같이 나타낼 수 있으며,
  여기서 $\otimes$ 는 크로네커 곱(Kronecker product) 연산을 의미한다.

• Kronecker 곱은
  두 행렬 $A$와 $B$를 결합해 더 큰 블록 행렬(block matrix)을 구성하는 연산이다.
  예를 들어,

  \[A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}, \quad B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}\]

  일 때,

  \[A \otimes B = \begin{bmatrix} a_{11}B & a_{12}B \\ a_{21}B & a_{22}B \end{bmatrix}\]

  와 같이 표현된다.

• 이를 통해 하나의 큰 행렬을 두 개의 작은 행렬로 표현할 수 있으므로,
  필요한 파라미터 수를 크게 줄이면서도
  원래의 변환 능력(expressive power) 을 유지할 수 있다.

• 또한 COMPACTER는 가중치 공유(weight sharing) 를 적용하여
  여러 어댑터 층이 일부 파라미터를 공유하도록 설계되었다.
  이를 통해 저장 공간 절약과 학습 안정성 향상을 동시에 달성한다.

• 정리하자면, COMPACTER는
  저랭크 근사(low-rank approximation) 와
  크로네커 곱 기반 파라미터화(Kronecker parameterization) 를 결합한
  차세대 어댑터 구조(next-generation adapter architecture) 로,
  기존 어댑터 대비 훨씬 적은 파라미터로도
  유사한 성능을 달성할 수 있다.

---

이와 유사하게,
LoRA를 다른 텐서 곱(tensor product) 기반 방법들과 결합하면
파라미터 효율성(parameter efficiency)을 더욱 향상시킬 수 있을 것으로 예상되며,
이는 향후 연구로 남긴다.

보다 최근에는,
미세조정(fine-tuning) 대신
입력 단어 임베딩(input word embeddings) 을 직접 최적화하는 방법이 제안되었다.
이는 본질적으로 프롬프트 엔지니어링(prompt engineering) 의
연속적이고 미분 가능한 일반화(continuous and differentiable generalization) 로 볼 수 있다
(Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021).

---

“연속적이고 미분 가능한 일반화”의 의미

• 전통적인 프롬프트 엔지니어링(prompt engineering) 은
  사람이 직접 단어(토큰)를 조합해 입력 문장을 설계하는 이산적(discrete) 과정이다.
  예를 들어,
  “요약해줘(Summarize this article:)” 같은 문구를 바꾸어가며
  모델의 출력을 경험적으로 조정한다.

• 반면, 연속적이고 미분 가능한 일반화(continuous and differentiable generalization) 는
  이런 텍스트 기반 프롬프트를
  연속적인 벡터 공간(continuous vector space) 에서 직접 학습하는 접근이다.
  즉, 단어 대신 임베딩 벡터(embedding vectors) 자체를
  모델의 학습 대상(trainable parameters) 으로 두고
  역전파(backpropagation)를 통해 자동으로 최적화한다.

• 이 접근은 사람이 문장을 바꿔가며 시도하는 대신,
  모델이 스스로 최적의 프롬프트 벡터를 찾아가는 과정이라 할 수 있다.
  따라서 “연속적(continuous)”이라는 말은
  입력이 이산적인 단어가 아닌 실수 벡터로 표현된다는 뜻이고,
  “미분 가능(differentiable)”은
  이 벡터가 경사하강법(gradient descent) 을 통해
  학습될 수 있다는 의미이다.

• 결과적으로, 이러한 방법은
  사람이 직접 프롬프트를 설계하지 않아도 되며,
  모델이 학습 과정에서 프롬프트를 자동으로 최적화(auto-tune) 하는
  보다 일반적이고 수학적인 확장 형태라고 할 수 있다.

---

우리의 실험 섹션에서는
Li & Liang (2021) 과의 비교 결과를 포함하였다.

그러나 이러한 연구 방향(line of works)은
프롬프트 내에 더 많은 특수 토큰(special tokens) 을 사용함으로써만 확장될 수 있으며,
위치 임베딩(positional embeddings) 을 학습하는 경우
이 특수 토큰들이 과제 토큰(task tokens)을 위한
사용 가능한 시퀀스 길이(sequence length) 를 차지하게 된다.

딥러닝에서의 저랭크 구조 (Low-Rank Structures in Deep Learning)

저랭크(low-rank) 구조는 머신러닝 전반에서 매우 흔히 나타나는 특성이다.
많은 머신러닝 문제들은 내재적인(intrinsic) 저랭크 구조를 가지고 있으며
(Li et al., 2016; Cai et al., 2010; Li et al., 2018b; Grasedyck et al., 2013),
이는 데이터나 모델의 표현이 실제 차원보다
더 작은 유효 차원(subspace) 위에서 작동함을 의미한다.

또한, 많은 딥러닝 과제들 — 특히 과도하게 매개변수화된(over-parametrized)
신경망의 경우 — 학습이 완료된 후 모델이
저랭크 특성(low-rank property) 을 자연스럽게 갖게 되는 것으로 알려져 있다
(Oymak et al., 2019).

일부 선행 연구들은 신경망을 학습할 때부터
명시적으로 저랭크 제약(low-rank constraint) 을 부여하기도 했다
(Sainath et al., 2013; Povey et al., 2018; Zhang et al., 2014;
Jaderberg et al., 2014; Zhao et al., 2016; Khodak et al., 2021; Denil et al., 2014).
그러나, 우리의 지식으로는 이러한 연구들 중
“고정된(frozen) 모델”에 대해 저랭크 갱신(update)을 적용하여
하위 과제(downstream task)에 적응(adaptation)시키는 방법을
고려한 연구는 없었다.

이론적 관점에서도, 여러 연구들에서
저랭크 구조를 가진 개념 계층(concept class) 의 경우,
신경망이 기존의 고전적 학습 방법(classical learning methods) —
예를 들어 유한 폭(finite-width)에서 근사된 신경접선커널(NTK, Neural Tangent Kernel) —
보다 더 우수한 성능을 보임이 보고되었다
(Allen-Zhu et al., 2019; Li & Liang, 2018;
Ghorbani et al., 2020; Allen-Zhu & Li, 2019, 2020a).

---

신경접선커널(NTK, Neural Tangent Kernel)이란?

• 신경접선커널(NTK) 은
  딥러닝 모델, 특히 심층 신경망(deep neural networks) 의 학습 과정을
  수학적으로 근사(approximate) 하기 위해 제안된 이론적 개념이다.

• 기본 아이디어는,
  신경망의 출력 함수(output function) 를
  파라미터 공간(parameter space)에서의 1차 테일러 전개(Taylor expansion) 로
  근사하는 것이다.
  즉, 모델이 학습 과정에서 변화하는 양상을
  커널 함수(kernel function) 형태로 표현할 수 있다는 것이다.

• 수식적으로, NTK는 다음과 같이 정의된다.

  \[K(x, x') = \nabla_\theta f_\theta(x)^\top \nabla_\theta f_\theta(x')\]

  여기서
  $f_\theta(x)$ 는 파라미터 $\theta$ 를 가진 신경망의 출력,
  $\nabla_\theta f_\theta(x)$ 는 $\theta$ 에 대한 그라디언트(gradient)이다.
  즉, NTK는 입력 $x$와 $x’$에 대해
  모델 파라미터가 출력에 미치는 민감도(sensitivity) 의 내적(inner product)을 계산한다.

• NTK는 신경망이 충분히 큰 폭(무한 폭, infinite width) 을 가질 때,
  그 학습 과정이 선형화(linearized) 되어
  커널 회귀(kernel regression)와 동일하게 동작함을 보인다.
  이 때문에 NTK는
  “딥러닝이 실제로 왜 작동하는가”를 수학적으로 이해하기 위한
  핵심 이론 중 하나로 간주된다.

• 그러나 실제 신경망은 유한 폭(finite-width)이므로,
  NTK 근사로는 설명되지 않는
  비선형 표현 학습(nonlinear representation learning) 이 가능하다.
  논문에서 언급한 바와 같이,
  이러한 이유로 저랭크 구조(low-rank structure) 를 가진 과제에서는
  NTK보다 진짜 신경망(neural networks) 이
  훨씬 더 우수한 성능을 보일 수 있다.

---

또한, Allen-Zhu & Li (2020b) 는
저랭크 적응(low-rank adaptation) 이
적대적 학습(adversarial training) 환경에서도 유용할 수 있음을
이론적으로 제시하였다.

종합하면, 본 논문에서 제안한 저랭크 적응 갱신(low-rank adaptation update) 은
기존 문헌에 의해 충분히 동기부여(motivated)된 개념이라 할 수 있다.

7. 저랭크 갱신(low-rank updates)의 이해

LoRA가 보여준 경험적(실증적) 우수성(empirical advantage) 을 바탕으로,
본 절에서는 하위 과제(downstream tasks)로부터 학습된
저랭크 적응(low-rank adaptation) 의 특성을
더 깊이 있게 설명하고자 한다.

저랭크 구조(low-rank structure)는
단순히 하드웨어 접근 장벽(hardware barrier to entry) 을 낮추어
여러 실험을 병렬적으로 수행할 수 있게 하는 것뿐만 아니라,
갱신된 가중치(update weights) 가
사전학습된 가중치(pre-trained weights) 와
어떻게 상관(correlated)되어 있는지를
더 잘 해석할 수 있도록 한다는 장점도 지닌다.

우리는 GPT-3 175B 모델에 초점을 맞추어 연구를 진행하였으며,
이 모델에서 최대 10,000배에 달하는 학습 파라미터 수의 감소를 이루면서도
과제 성능(task performance)에 부정적인 영향을 주지 않았다.

우리는 다음의 질문들에 답하기 위해 일련의 실증적 연구(sequence of empirical studies) 를 수행한다.

1) 파라미터 예산 제약(parameter budget constraint) 이 주어졌을 때,
사전학습된 트랜스포머(pre-trained Transformer)의
가중치 행렬(weight matrices) 중
어떤 부분집합(subset) 을 적응(adapt)시켜야
하위 과제(downstream performance)를 최대화할 수 있는가?

2) “최적의(optimal)” 적응 행렬(adaptation matrix) $\Delta W$ 는
실제로 랭크 결핍(rank-deficient) 한가?
그렇다면, 실무적으로 사용하기에 좋은 랭크(rank)는 얼마인가?

3) $\Delta W$ 와 $W$ 사이에는 어떤 관계가 있는가?
$\Delta W$ 는 $W$ 와 높은 상관관계를 가지는가?
$\Delta W$ 의 크기는 $W$ 와 비교했을 때 얼마나 큰가?

우리는 (2)와 (3)에 대한 우리의 답변이,
사전학습된 언어모델(pre-trained language models) 을
하위 과제(downstream tasks) 에 활용하는 데 있어
근본적인 원리(fundamental principles) 를 밝히는 데 도움이 된다고 믿는다.
이는 자연어 처리(NLP) 에서 매우 중요한 주제이다.

7.1 트랜스포머의 어떤 가중치 행렬(weight matrices)에 LoRA를 적용해야 하는가?

제한된 파라미터 예산(parameter budget) 이 주어졌을 때,
하위 과제(downstream tasks)에서 최상의 성능을 얻기 위해
어떤 유형의 가중치(weights)를 LoRA로 적응(adapt) 시켜야 하는가?

4.2절 에서 언급한 바와 같이,
우리는 셀프-어텐션(self-attention) 모듈 내의 가중치 행렬만을 고려한다.

GPT-3 175B 모델에 대해,
우리는 파라미터 예산을 1,800만 개(약 FP16 기준 35MB) 로 설정하였다.
이는 모든 96개 층(layers)에 대해,
하나의 어텐션 가중치 유형만 적응할 경우 랭크 $r = 8$,
두 가지 유형을 동시에 적응할 경우 랭크 $r = 4$ 에 해당한다.

그 결과는 표 5(Table 5) 에 제시되어 있다.

---

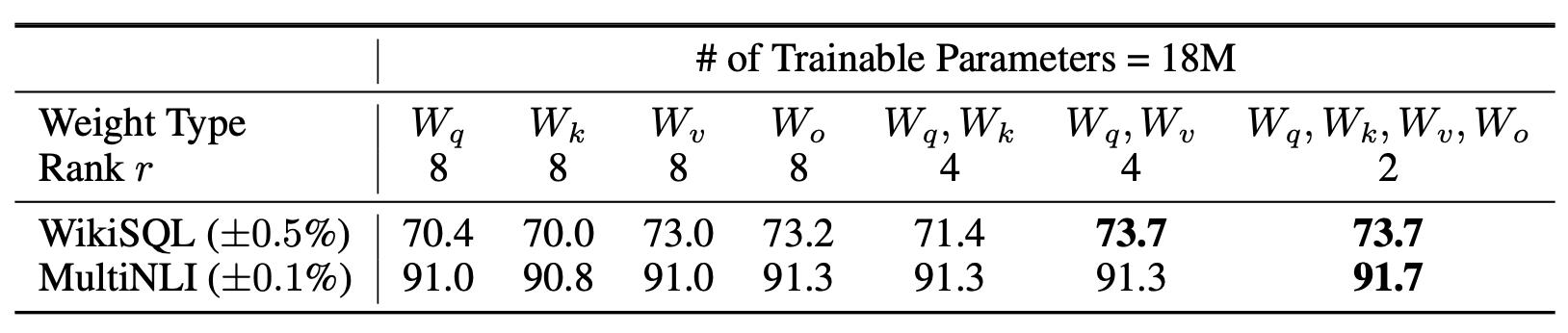
표 5

동일한 수의 학습 가능한 파라미터(trainable parameters)를 사용했을 때,
GPT-3 내의 서로 다른 유형의 어텐션 가중치(attention weights) 에
LoRA 를 적용한 후의 WikiSQL 및 MultiNLI 검증 정확도(validation accuracy).

$W_q$ 와 $W_v$ 를 모두 적응(adapt)시킨 경우,
전반적으로 가장 우수한 성능을 보였다.

또한, 주어진 데이터셋 내에서는
무작위 시드(random seeds) 간의 표준편차(standard deviation)가
일관되게 나타남을 확인하였으며,
그 값은 첫 번째 열(column) 에 보고하였다.

---

7.2 LoRA에서 최적의 랭크(rank) $r$ 는 무엇인가?

이제 우리는 모델 성능에 대한 랭크 $r$ 의 영향을 살펴본다.

우리는 비교를 위해
$\lbrace W_q, W_v \rbrace$,
$\lbrace W_q, W_k, W_v, W_c \rbrace$,
그리고 $W_q$ 단독으로 적응(adapt)시킨 경우를 포함한다.

---

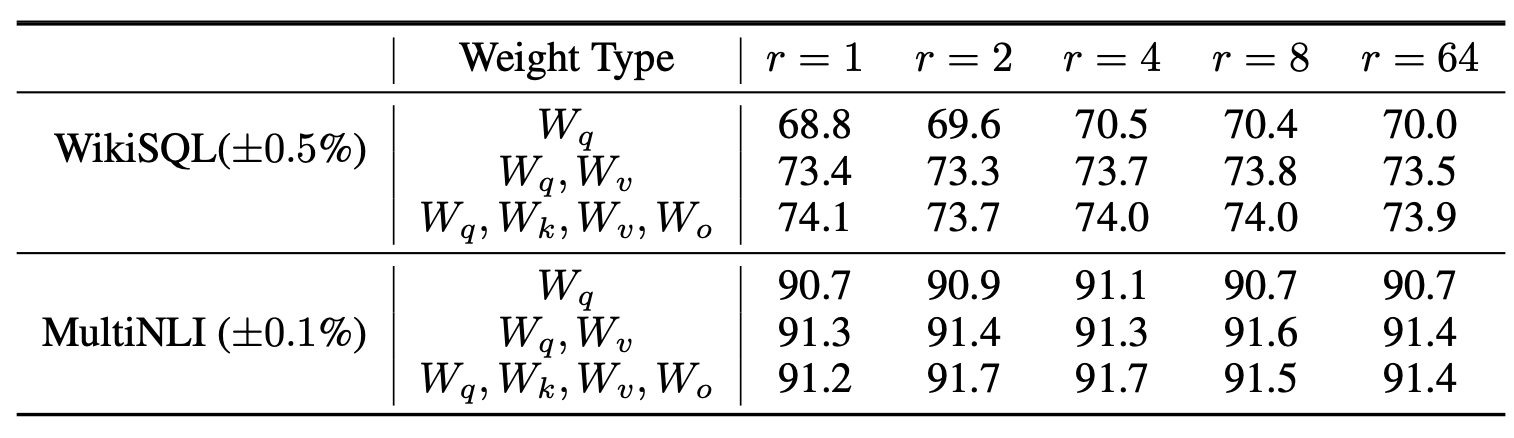
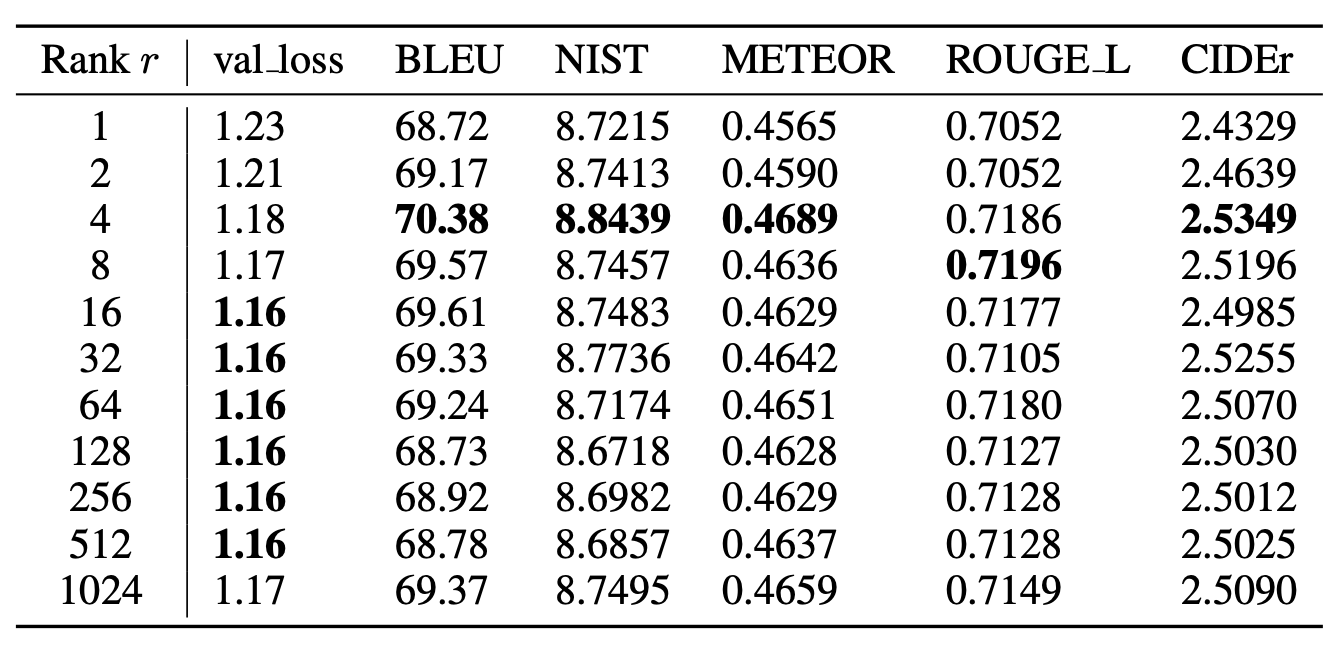
표 6

서로 다른 랭크(rank) $r$ 값에 따른 WikiSQL 및 MultiNLI 검증 정확도(validation accuracy).

흥미롭게도, 두 데이터셋 모두에서
$W_q$ 와 $W_v$ 를 함께 학습할 경우
랭크 $r = 1$ 과 같이 매우 작은 값만으로도 충분하였다.
반면, $W_q$ 만 단독으로 학습할 때는
더 큰 $r$ 값이 필요했다.

유사한 실험은 부록 H.2(Section H.2) 에서
GPT-2 모델을 대상으로 수행하였다.

---

표 6은 놀랍게도 LoRA 가 매우 작은 랭크 $r$ 값에서도
이미 경쟁력 있는 성능을 보임을 보여준다
(특히 ${ W_q, W_v }$ 를 함께 학습할 때는 $W_q$ 단독 학습보다 더욱 그렇다).

이 결과는 갱신 행렬(update matrix) $\Delta W$ 이
매우 작은 “내재적 랭크(intrinsic rank)” 를 가질 수 있음을 시사한다.⁶

---

⁶그러나, 모든 과제(task)나 데이터셋(dataset)에 대해
작은 랭크 $r$ 이 항상 잘 작동할 것이라고 기대하지 않는다.

다음의 사고 실험(thought experiment)을 고려해보자.
만약 하위 과제(downstream task)가
사전학습(pre-training)에 사용된 언어(language)와
전혀 다른 언어로 이루어져 있다면,
전체 모델을 다시 학습(retraining the entire model) 하는 것이 —
즉, $r = d_{\text{model}}$ 인 LoRA에 해당하는 경우 —
작은 $r$ 값을 가진 LoRA보다
확실히 더 나은 성능을 낼 것이다.

---

이 발견을 뒷받침하기 위해,
우리는 서로 다른 랭크 $r$ 값 및
서로 다른 무작위 시드(random seeds) 로 학습된
부분공간(subspaces) 간의 중첩(overlap)을 확인하였다.

그 결과, $r$ 값을 늘린다고 해서
더 의미 있는 부분공간을 포착하는 것은 아님을 확인하였다.
이는 저랭크 적응 행렬(low-rank adaptation matrix) 만으로도
충분하다는 점을 시사한다.

서로 다른 $r$ 간의 부분공간 유사도(Subspace similarity)

같은 사전학습 모델을 사용하여 랭크 $r = 8$과 $r = 64$로 학습된 적응 행렬 $A_{r=8}$ 및 $A_{r=64}$ 가 주어졌을 때,
우리는 특이값 분해(singular value decomposition)를 수행하고,
우측-특이(unitary) 행렬 $U_{A_{r=8}}$ 및 $U_{A_{r=64}}$ 를 얻는다.⁷

---

⁷유사한 분석은 $B$와 좌측-특이 유니터리 행렬(left-singular unitary matrices) 에 대해서도 수행될 수 있으나,
우리의 실험에서는 $A$ 를 사용한다.

---

우리가 답하고자 하는 질문은 다음과 같다:
$U_{A_{r=8}}$ 에서 상위 $i$개의 특이벡터( $1 \le i \le 8$ )가 생성하는 부분공간이,
$U_{A_{r=64}}$ 에서 상위 $j$개의 특이벡터( $1 \le j \le 64$ )가 생성하는 부분공간에
얼마나 포함되는가?

우리는 이 양을 그라스만 거리(Grassmann distance)에 기반한 정규화된 부분공간 유사도로 측정한다
(보다 공식적인(formal) 논의는 부록 G(Appendix G) 참조):

\[\phi(A_{r=8}, A_{r=64}, i, j) = \frac{ \left\lVert U_{A_{r=8}}^{\,i\top}\, U_{A_{r=64}}^{\,j} \right\rVert_F^{2} }{ \min(i, j) } \in [0, 1] \tag{4}\]

여기서 $U_{A_{r=8},\, i}$ 는 $U_{A_{r=8}}$ 의 상위 $i$개 특이벡터에 해당하는 열들(columns)을 의미한다.

$\phi(\cdot)$ 의 범위는 $[0, 1]$이며, 값이 1이면 부분공간이 완전히 겹침(complete overlap)을,
값이 0이면 완전 분리(complete separation)를 뜻한다.

---

그라스만 거리(Grassmann distance)란?

• 그라스만 거리(Grassmann distance) 는
  두 부분공간(subspaces) 사이의 유사도(similarity) 또는 거리(distance)를
  측정하기 위한 수학적 도구이다.
  즉, 두 벡터 부분공간이 서로 얼마나 “겹치는지(overlap)”를 수치적으로 표현한다.

• 두 부분공간이 동일하다면(즉, 완전히 같은 방향을 공유한다면)
  그라스만 거리는 0이 되고,
  서로 완전히 독립(orthogonal)이라면 거리는 최대가 된다.
  LoRA 논문에서는 이 개념을 반대로 활용하여,
  “정규화된 부분공간 유사도(normalized subspace similarity)”
  $\phi(\cdot)$ 를 0에서 1 사이의 값으로 정의하였다.

  • $\phi = 1$ → 두 부분공간이 완전히 일치 (완전한 중첩)
  • $\phi = 0$ → 두 부분공간이 완전히 분리 (전혀 겹치지 않음)

• 본 논문에서는 $A_{r=8}$ 과 $A_{r=64}$ 로부터 얻은
  특이벡터(singular vectors) 들이 생성하는 부분공간을 비교함으로써,
  랭크(r) 가 커질수록 학습된 부분공간이
  의미 있게 확장되는지(=더 많은 정보를 학습하는지)를 검증한다.

• 결론적으로, $\phi$ 값이 랭크 증가에 따라 크게 변하지 않는다면
  이는 “이미 작은 랭크에서도 충분히 표현 가능한(subspace already saturated)”
  저랭크 적응(low-rank adaptation)이 가능함을 시사한다.

---

$i$ 와 $j$ 를 변화시킬 때 $\phi$ 가 어떻게 변하는지는 그림 3(Figure 3) 을 참조하라.
지면 제약으로 인해 우리는 96개 층 중 48번째 층만을 살펴보지만,
그 결론은 다른 층들에도 동일하게 성립하며, 이는 부록 H.1(Section H.1) 에 제시되어 있다.

---

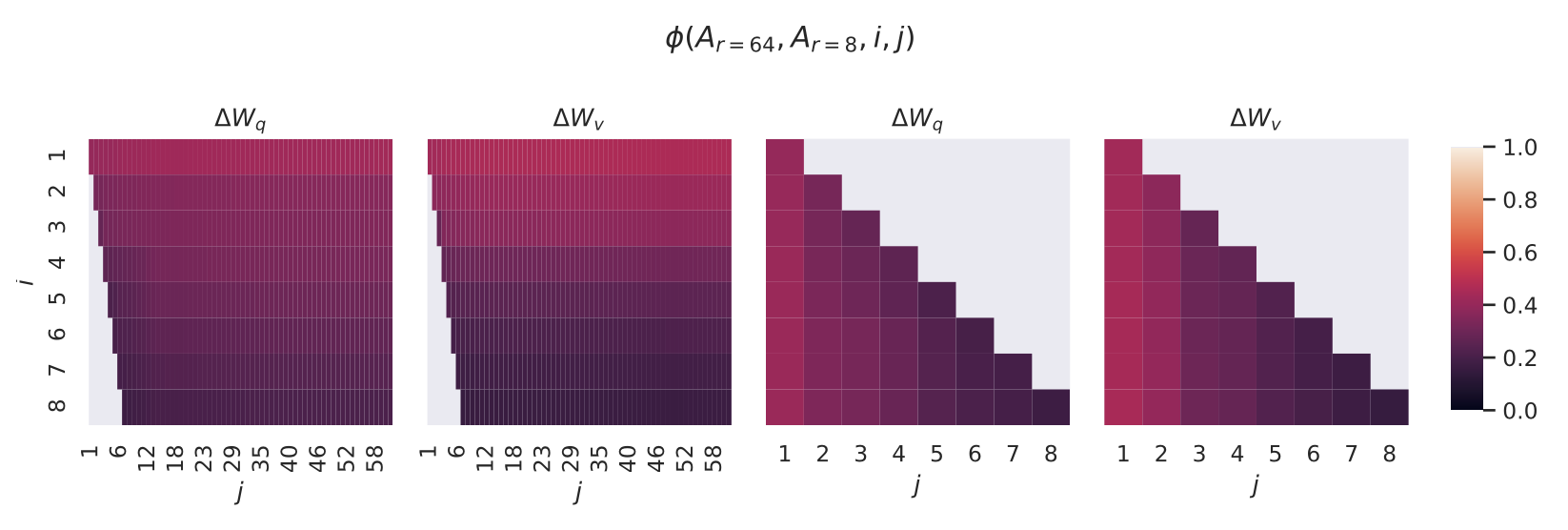
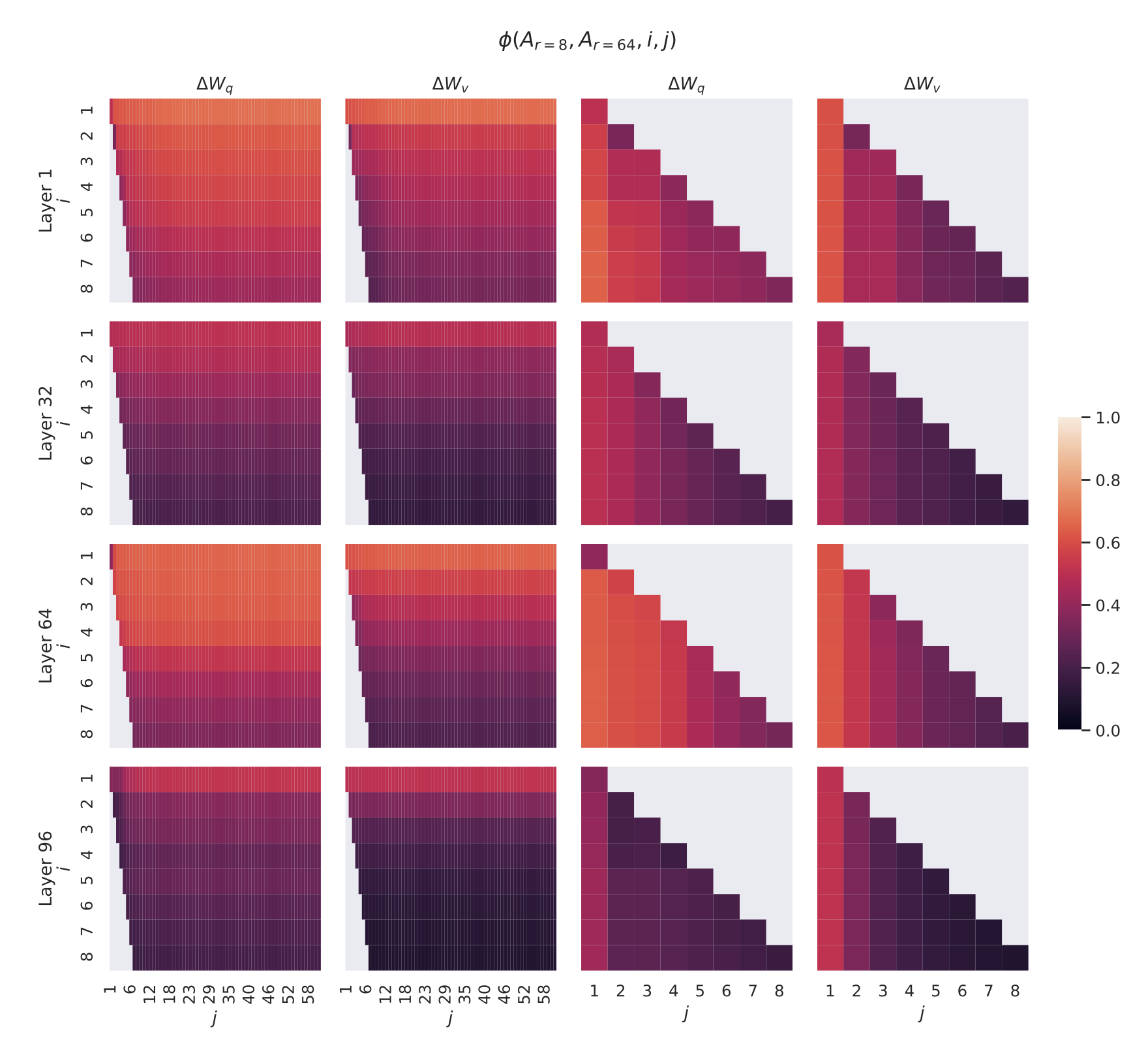
그림 3

$\Delta W_q$ 와 $\Delta W_v$ 에 대해,
$A_{r=8}$ 과 $A_{r=64}$ 의 열 벡터(column vectors) 간 부분공간 유사도(subspace similarity) 를 나타낸다.

세 번째와 네 번째 그림은,
앞의 두 그림에서 왼쪽 아래 삼각형(lower-left triangle) 부분을
확대(zoom-in)한 것이다.

결과적으로,
$r=8$ 에서의 상위 방향(top directions)은
$r=64$ 의 부분공간에 포함되며,
그 반대의 관계도 성립한다.

---

우리는 그림 3 으로부터 중요한 관찰을 얻을 수 있다.

가장 상위의 특이벡터(singular vector) 에 해당하는 방향들은
$A_{r=8}$ 과 $A_{r=64}$ 사이에서 상당히 큰 중첩(overlap) 을 보이지만,
그 외의 방향들은 그렇지 않다.

구체적으로,
$A_{r=8}$ 의 $\Delta W_v$ (또는 $\Delta W_q$) 와
$A_{r=64}$ 의 $\Delta W_v$ (또는 $\Delta W_q$) 는
정규화된 유사도(normalized similarity) 가 0.5 이상인
1차원 부분공간(subspace of dimension 1) 을 공유한다.
이는 GPT-3의 하위 과제(downstream tasks)에서
$r = 1$ 인 경우에도 우수한 성능을 보이는 이유를 설명해 준다.

$A_{r=8}$ 과 $A_{r=64}$ 모두 동일한 사전학습된(pre-trained) 모델로부터 학습되었기 때문에,
그림 3은 두 행렬에서 가장 상위의 특이벡터 방향(top singular-vector directions) 이
가장 유용한(informative) 정보를 담고 있음을 보여준다.

반면, 그 외의 방향들은
학습 중에 누적된 무작위 잡음(random noise) 을 주로 포함할 가능성이 크다.

따라서, 적응 행렬(adaptation matrix) 은
실제로 매우 낮은 랭크(low rank) 로도 충분히 표현될 수 있음을 알 수 있다.

서로 다른 랜덤 시드 간의 부분공간 유사도(Subspace similarity between different random seeds)

이를 추가로 확인하기 위해,
$r = 64$ 에서 두 개의 서로 다른 랜덤 시드(random seeds) 로 학습된
결과 간의 정규화된 부분공간 유사도(normalized subspace similarity) 를
그린 것이 그림 4 이다.

$\Delta W_q$ 는 $\Delta W_v$ 보다 더 높은
내재적 랭크(intrinsic rank) 를 가지는 것으로 보인다.

그 이유는 두 번의 학습(run) 모두에서
$\Delta W_q$ 의 특이값(singular value) 방향 중
공통적으로 학습된 방향이 더 많기 때문이다.

이 현상은 표 6 에서의 실험적 관찰과도 일치한다.

비교를 위해,
우리는 두 개의 무작위 가우시안 행렬(random Gaussian matrices) 에 대해서도
같은 유사도 계산을 수행했는데,
이 경우 두 행렬은 서로 공통된 특이값 방향(singular value directions) 을
전혀 공유하지 않는 것으로 나타났다.

---

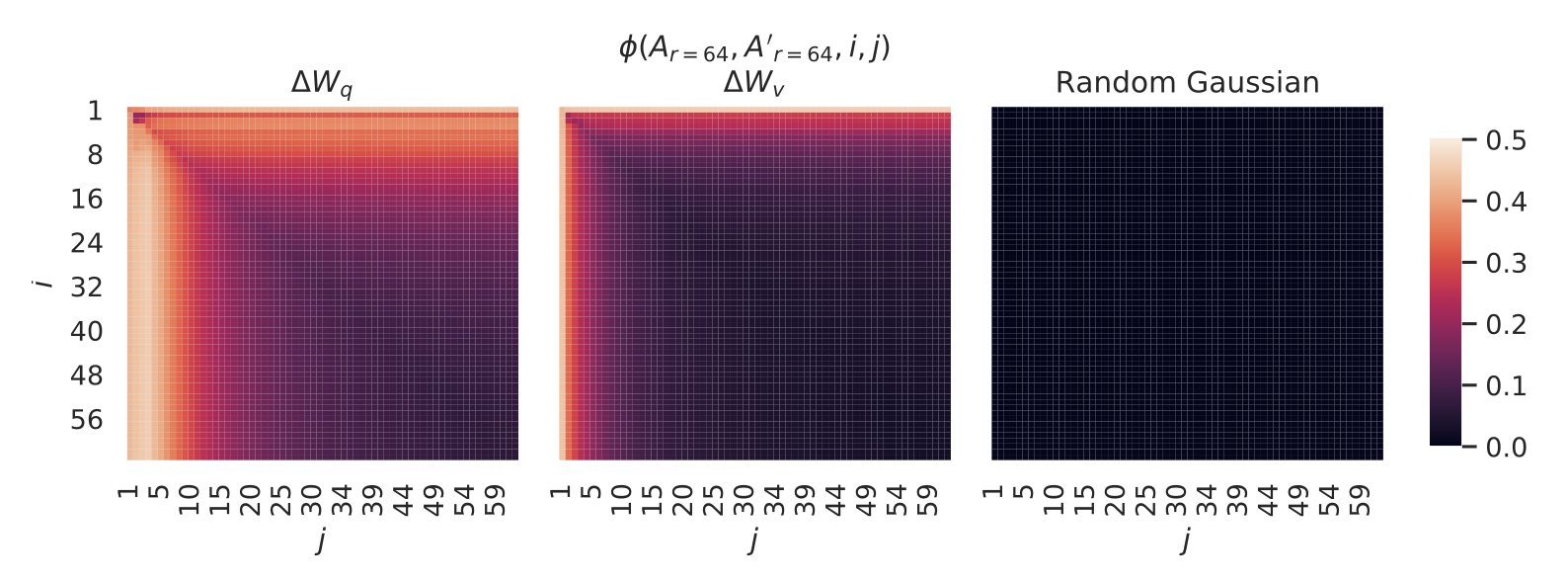
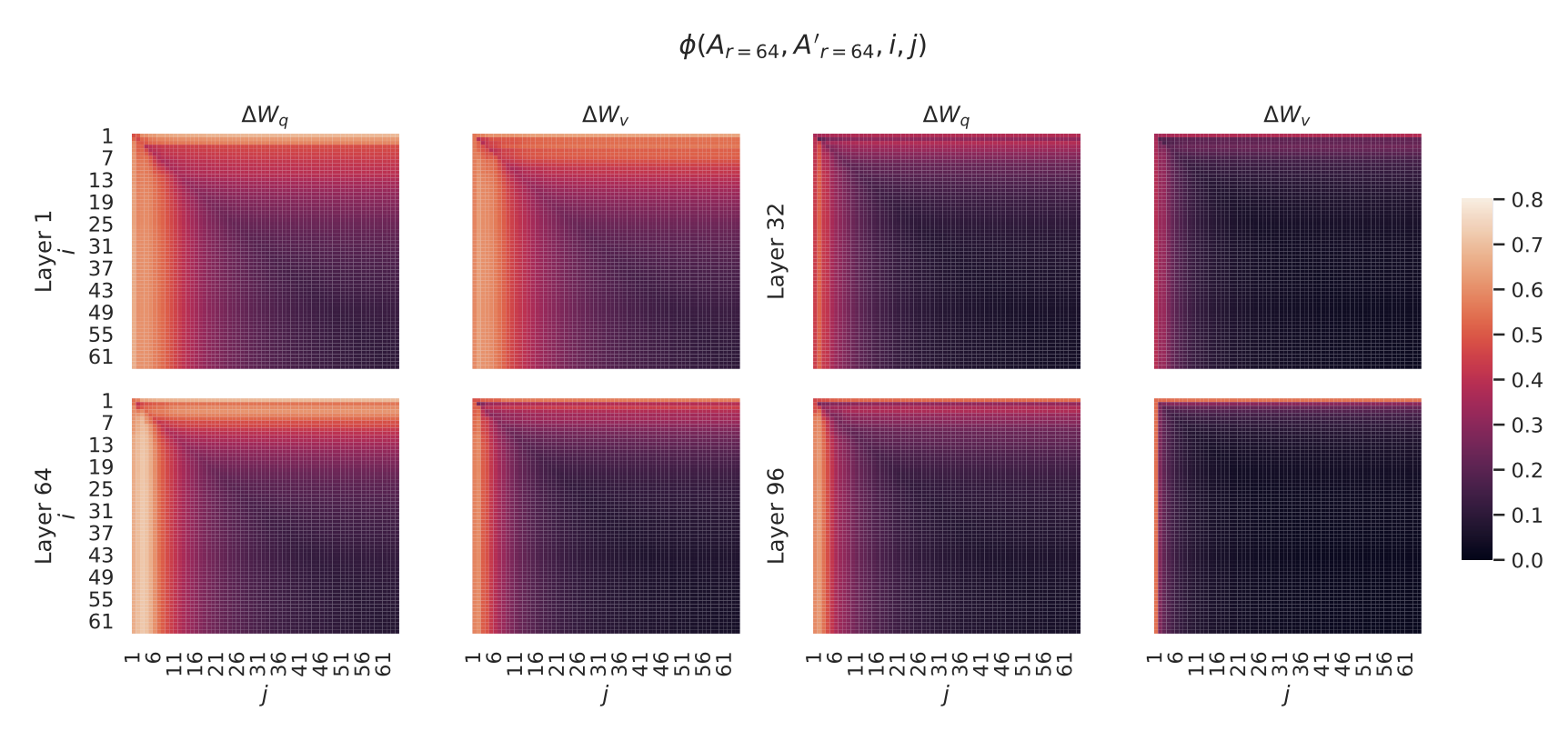
그림 4

왼쪽(Left) 및 가운데(Middle) —
$r = 64$ 인 $A_{r=64}$ 의 열 벡터(column vectors) 에 대해,
두 개의 서로 다른 랜덤 시드(random seeds) 로 학습된
$\Delta W_q$ 와 $\Delta W_v$ 간의 정규화된 부분공간 유사도(normalized subspace similarity) 를 나타낸다.
(48번째 층 기준)

오른쪽(Right) —
두 개의 무작위 가우시안 행렬(random Gaussian matrices) 의
열 벡터들 간의 동일한 히트맵(heat map) 을 보여준다.

다른 층(layer)에 대한 결과는 부록 H.1 (Section H.1) 을 참조하라.

---

7.3 적응 행렬(ADAPTATION MATRIX) $\Delta W$은 기존 가중치(W)와 어떻게 비교되는가?

우리는 $\Delta W$ 와 $W$ 사이의 관계를 더 조사한다.
특히, $\Delta W$ 가 $W$ 와 높은 상관관계(highly correlate) 를 가지는가?
(즉, 수학적으로 말하면, $\Delta W$ 가 $W$ 의 상위 특이 방향(top singular directions) 에
주로 포함되어 있는가?)

또한, $W$ 의 해당 방향들과 비교했을 때
$\Delta W$ 의 “크기(size)” 는 어느 정도인가?

이것은 사전학습된 언어모델(pre-trained language models)이
적응(adaptation)하는 근본적인 메커니즘(underlying mechanism) 을 밝히는 데 도움이 될 수 있다.

이 질문들에 답하기 위해,
우리는 $\Delta W$ 의 왼쪽 및 오른쪽 특이벡터 행렬(left/right singular-vector matrices) 을
각각 $U$ 와 $V$ 라 할 때,
$W$ 를 $\Delta W$ 의 $r$차원 부분공간($r$-dimensional subspace) 으로
다음 계산을 통해 사영(project)한다.

\[U^{\top} W V^{\top}\]

그다음, 우리는
$| U^{\top} W V^{\top} |_F$ 와 $| W |_F$ 간의
프로베니우스 노름(Frobenius norm) 을 비교한다.

비교를 위해, 우리는 또한
$U$, $V$ 를 $W$ 의 상위 $r$개의 특이벡터(top $r$ singular vectors)
또는 무작위 행렬(random matrix) 으로 교체하여
$| U^{\top} W V^{\top} |_F$ 를 계산한다.

우리는 표 7(Table 7) 로부터 여러 가지 결론을 도출한다.

---

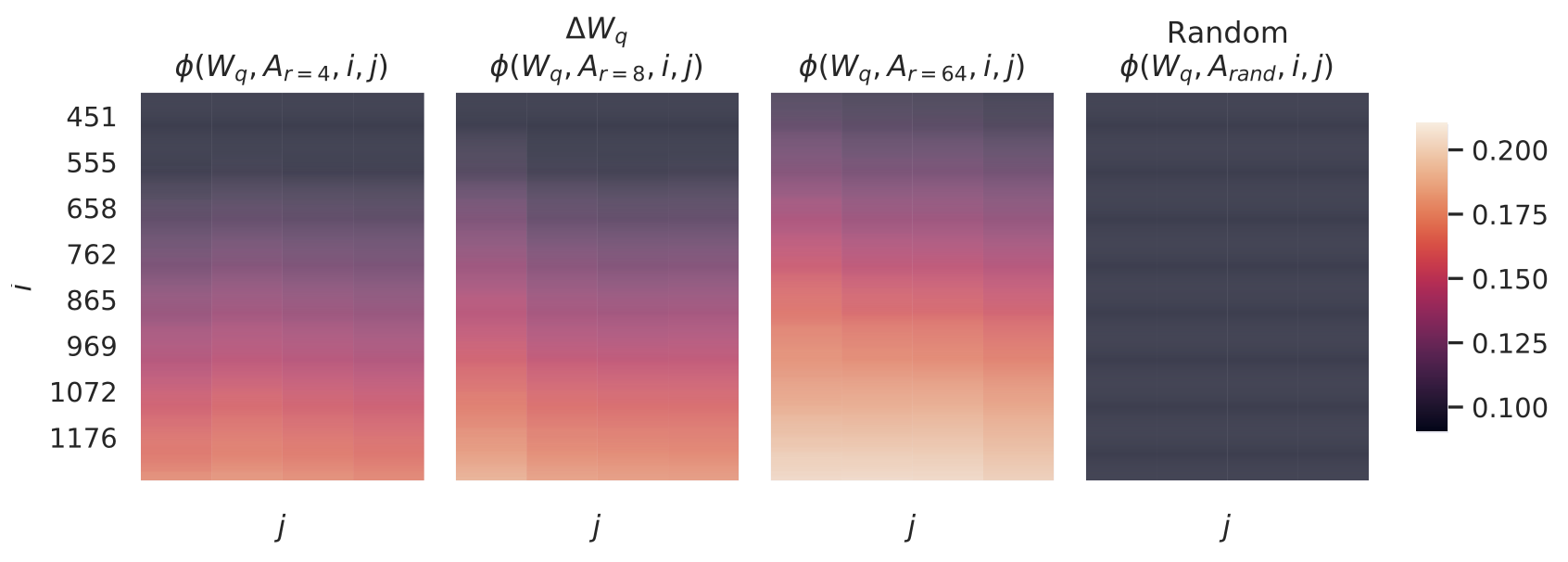
표 7(Table 7)

$U$ 와 $V$ 가 각각 (1) $\Delta W_q$, (2) $W_q$, (3) 무작위 행렬(random matrix) 의
왼쪽/오른쪽 상위 $r$개의 특이벡터 방향(left/right top $r$ singular vector directions) 일 때,
$| U^{\top} W_q V^{\top} |_F$ 의 프로베니우스 노름(Frobenius norm) 을 나타낸다.

여기서 가중치 행렬(weight matrices)은
GPT-3의 48번째 층(48th layer) 에서 추출되었다.

---

첫째, $\Delta W$ 는 무작위 행렬(random matrix) 과 비교했을 때
$W$ 와 더 강한 상관관계(stronger correlation) 를 보인다.
이는 $\Delta W$ 가 이미 $W$ 안에 존재하는 일부 특징(feature)을
증폭(amplify) 시킨다는 것을 의미한다.

둘째, $\Delta W$ 는 $W$ 의 상위 특이 방향(top singular directions) 을 단순히 반복(repeat)하는 것이 아니라,
$W$ 에서 강조되지 않았던 방향들을 선택적으로 증폭한다(amplify).

셋째, 그 증폭 계수(amplification factor)는 상당히 크다.
예를 들어, $r = 4$ 인 경우,
\(21.5 \approx 6.91 / 0.32\)
이다.
$r = 64$ 에서 증폭 계수가 더 작아지는 이유에 대해서는 부록 H.4 (Section H.4) 를 참조하라.

또한, 부록 H.3 (Section H.3) 에서는
$W_q$ 로부터 더 많은 상위 특이 방향(top singular directions)을 포함시킬 때
상관관계가 어떻게 변하는지를 시각화하였다.

이 결과는,
저랭크 적응 행렬(low-rank adaptation matrix) 이
일반 사전학습 모델(general pre-training model) 에서 이미 학습되었지만
충분히 강조되지 않았던 중요한 특징들을
특정 하위 과제(downstream tasks) 에 맞게 선택적으로 증폭할 가능성이 있음을 시사한다.

8. 결론 및 향후 연구 (Conclusion and Future Work)

거대한 언어 모델을 미세조정(fine-tuning)하는 것은,
필요한 하드웨어 요구량(hardware requirement) 과
서로 다른 과제(task)에 대한 독립적인 인스턴스(instance) 를
호스팅하기 위한 저장(storage) 및 전환 비용(switching cost) 측면에서
매우 비용이 많이 든다(prohibitively expensive).

우리는 LoRA 를 제안하였다.
이는 효율적인 적응(adaptation) 전략으로서,
추론 지연(inference latency) 을 유발하지 않으며,
입력 시퀀스 길이(input sequence length) 를 줄이지 않으면서도
높은 모델 품질(model quality) 을 유지한다.

중요하게도, LoRA는 모델 파라미터의 대다수를 공유함으로써,
서비스 환경에서 빠른 과제 전환(task-switching) 을 가능하게 한다.

비록 우리는 트랜스포머(Transformer) 언어 모델에 초점을 맞추었지만,
여기서 제안된 원칙들은 밀집층(dense layers) 을 가진
어떠한 신경망(neural networks)에도 일반적으로 적용될 수 있다.

향후 연구에는 여러 가지 방향이 존재한다.

1. LoRA를 다른 효율적인 적응 방법들과 결합하는 것
   LoRA는 다른 효율적인 적응 방법들과 결합될 수 있으며,
   잠재적으로 직교적인(orthogonal) 개선을 제공할 수 있다.

2. 미세조정(fine-tuning)과 LoRA의 작동 메커니즘에 대한 이해
   사전학습(pre-training) 동안 학습된 특징(feature)들이
   어떻게 하위 과제(downstream tasks)에서 잘 작동하도록 변환되는지는
   아직 명확하지 않다.
   우리는 LoRA가 이러한 문제를
   전체 미세조정(full fine-tuning) 보다 더 다루기 쉽게 만들 것이라고 믿는다.

3. LoRA를 적용할 가중치 행렬의 선택 방법
   우리는 대부분의 경우 경험적 휴리스틱(heuristics)에 의존하여
   LoRA를 적용할 가중치 행렬을 선택한다.
   이를 더 원리적인(principled) 방식으로 수행할 수 있는지가
   탐구될 가치가 있다.

4. $\Delta W$의 랭크 결핍(rank-deficiency)
   $\Delta W$ 의 랭크 결핍은
   $W$ 또한 랭크 결핍일 수 있음을 시사하며,
   이는 향후 연구에 대한 또 다른 영감을 제공할 수 있다.

참고문헌 (References)

[1] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning.
arXiv preprint arXiv:2012.13255, 2020.

[2] Zeyuan Allen-Zhu and Yuanzhi Li. What Can ResNet Learn Efficiently, Going Beyond Kernels?
In NeurIPS, 2019. Full version: https://arxiv.org/abs/1905.10337.

[3] Zeyuan Allen-Zhu and Yuanzhi Li. Backward feature correction: How deep learning performs deep learning.
arXiv preprint arXiv:2001.04413, 2020a.

[4] Zeyuan Allen-Zhu and Yuanzhi Li. Feature purification: How adversarial training performs robust deep learning.
arXiv preprint arXiv:2005.10190, 2020b.

[5] Zeyuan Allen-Zhu, Yuanzhi Li, and Zhao Song. A convergence theory for deep learning via over-parameterization.
In ICML, 2019. Full version: https://arxiv.org/abs/1811.03962.

[6] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. Layer normalization.
arXiv preprint arXiv:1607.06450, 2016.

[7] Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. Language Models are Few-Shot Learners.
arXiv preprint arXiv:2005.14165, 2020.

[8] Jian-Feng Cai, Emmanuel J. Candès, and Zuowei Shen. A singular value thresholding algorithm for matrix completion.
SIAM Journal on Optimization, 20(4):1956–1982, 2010.

[9] Daniel Cer, Mona Diab, Eneko Agirre, Inigo Lopez-Gazpio, and Lucia Specia. SemEval-2017 Task 1: Semantic textual similarity—multilingual and crosslingual focused evaluation.
In Proceedings of SemEval-2017, 2017. doi: 10.18653/v1/S17-2001. Link.

[10] Ronan Collobert and Jason Weston. A unified architecture for natural language processing: deep neural networks with multitask learning.
In ICML ’08, pp. 160–167. ACM, 2008. doi: 10.1145/1390156.1390177. Link.

[11] Misha Denil, Babak Shakibi, Laurent Dinh, Marc’Aurelio Ranzato, and Nando de Freitas. Predicting parameters in deep learning.
arXiv preprint arXiv:1306.0543, 2014.

[12] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding.
arXiv preprint arXiv:1810.04805, 2019b.

[13] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of deep bidirectional transformers for language understanding.
2019a.

[14] William B. Dolan and Chris Brockett. Automatically constructing a corpus of sentential paraphrases.
In Proceedings of IWP2005, 2005. Link.

[15] Claire Gardent, Anastasia Shimorina, Shashi Narayan, and Laura Perez-Beltrachini. The WebNLG challenge: Generating text from RDF data.
In INLG, pp. 124–133, 2017.

[16] Behrooz Ghorbani, Song Mei, Theodor Misiakiewicz, and Andrea Montanari. When do neural networks outperform kernel methods?
arXiv preprint arXiv:2006.13409, 2020.

[17] Bogdan Gliwa, Iwona Mochol, Maciej Biesek, and Aleksander Wawer. SAMSung corpus: A human-annotated dialogue dataset for abstractive summarization.
CoRR, abs/1911.12237, 2019.

[18] Lars Grasedyck, Daniel Kressner, and Christine Tobler. A literature survey of low-rank tensor approximation techniques.
GAMM-Mitteilungen, 36(1):53–78, 2013.

[19] Jihun Ham and Daniel D. Lee. Grassmann discriminant analysis: a unifying view on subspace-based learning.
In ICML, pp. 376–383, 2008. Link.

[20] Karen Hambardzumyan, Hrant Khachatrian, and Jonathan May. WARP: Word-level Adversarial ReProgramming.
arXiv preprint arXiv:2101.00121, 2020.

[21] Pengcheng He, Xiaodong Liu, Jianfeng Gao, and Weizhu Chen. DeBERTa: Decoding-enhanced BERT with disentangled attention.
2021.

[22] Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin de Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. Parameter-Efficient Transfer Learning for NLP.
arXiv preprint arXiv:1902.00751, 2019.

[23] Max Jaderberg, Andrea Vedaldi, and Andrew Zisserman. Speeding up convolutional neural networks with low rank expansions.
arXiv preprint arXiv:1405.3866, 2014.

[24] Mikhail Khodak, Neil Tenenholtz, Lester Mackey, and Nicolò Fusi. Initialization and regularization of factorized neural layers.
2021.

[25] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization.
arXiv preprint arXiv:1412.6980, 2017.

[26] Dmitry Lepikhin, HyoukJoong Lee, Yuanzhong Xu, Dehao Chen, Orhan Firat, Yanping Huang, Maxim Krikun, Noam Shazeer, and Zhifeng Chen. GShard: Scaling giant models with conditional computation and automatic sharding.
arXiv preprint arXiv:2006.16668, 2020.

[27] Brian Lester, Rami Al-Rfou, and Noah Constant. The Power of Scale for Parameter-Efficient Prompt Tuning.
arXiv preprint arXiv:2104.08691, 2021.

[28] Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the Intrinsic Dimension of Objective Landscapes.
arXiv preprint arXiv:1804.08838, 2018a.

[29] Xiang Lisa Li and Percy Liang. Prefix-Tuning: Optimizing Continuous Prompts for Generation.
arXiv preprint arXiv:2101.00190, 2021.

[30] Yuanzhi Li and Yingyu Liang. Learning overparameterized neural networks via stochastic gradient descent on structured data.
In NeurIPS, 2018.

[31] Yuanzhi Li, Yingyu Liang, and Andrej Risteski. Recovery guarantee of weighted low-rank approximation via alternating minimization.
In ICML, pp. 2358–2367. PMLR, 2016.

[32] Yuanzhi Li, Tengyu Ma, and Hongyang Zhang. Algorithmic regularization in over-parameterized matrix sensing and neural networks with quadratic activations.
In COLT, pp. 2–47. PMLR, 2018b.

[33] Zhaojiang Lin, Andrea Madotto, and Pascale Fung. Exploring versatile generative language model via parameter-efficient transfer learning.
In Findings of EMNLP 2020, pp. 441–459, 2020. doi: 10.18653/v1/2020.findings-emnlp.41. Link.

[34] Xiao Liu, Yanan Zheng, Zhengxiao Du, Ming Ding, Yujie Qian, Zhilin Yang, and Jie Tang. GPT Understands, Too.
arXiv preprint arXiv:2103.10385, 2021.

[35] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. RoBERTa: A robustly optimized BERT pretraining approach.
2019.

[36] Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization.
arXiv preprint arXiv:1711.05101, 2017; 2019.

[37] Rabeeh Karimi Mahabadi, James Henderson, and Sebastian Ruder. COMPACTER: Efficient low-rank hypercomplex adapter layers.
2021.

[38] Linyong Nan, Dragomir Radev, Rui Zhang, Amrit Rau, Abhinand Sivaprasad, Chiachun Hsieh, Xiangru Tang, Aadit Vyas, Neha Verma, Pranav Krishna, et al. DART: Open-domain structured data record to text generation.
arXiv preprint arXiv:2007.02871, 2020.

[39] Jekaterina Novikova, Ondřej Dušek, and Verena Rieser. The E2E dataset: New challenges for end-to-end generation.
arXiv preprint arXiv:1706.09254, 2017.

[40] Samet Oymak, Zalan Fabian, Mingchen Li, and Mahdi Soltanolkotabi. Generalization guarantees for neural networks via harnessing the low-rank structure of the Jacobian.
arXiv preprint arXiv:1906.05392, 2019.

[41] Jonas Pfeiffer, Aishwarya Kamath, Andreas Rücklé, Kyunghyun Cho, and Iryna Gurevych. AdapterFusion: Non-destructive task composition for transfer learning.
2021.

[42] Daniel Povey, Gaofeng Cheng, Yiming Wang, Ke Li, Hainan Xu, Mahsa Yarmohammadi, and Sanjeev Khudanpur. Semi-orthogonal low-rank matrix factorization for deep neural networks.
In Interspeech, pp. 3743–3747, 2018.

[43] Alec Radford, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. Improving Language Understanding by Generative Pre-Training.
pp. 12, a.

[44] Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language Models are Unsupervised Multitask Learners.
pp. 24, b.

[45] Pranav Rajpurkar, Robin Jia, and Percy Liang. Know what you don’t know: Unanswerable questions for SQuAD.
CoRR, abs/1806.03822, 2018. Link.

[46] Sylvestre-Alvise Rebuffi, Hakan Bilen, and Andrea Vedaldi. Learning multiple visual domains with residual adapters.
arXiv preprint arXiv:1705.08045, 2017.

[47] Andreas Rücklé, Gregor Geigle, Max Glockner, Tilman Beck, Jonas Pfeiffer, Nils Reimers, and Iryna Gurevych. AdapterDrop: On the efficiency of adapters in Transformers.
2020.

[48] Tara N. Sainath, Brian Kingsbury, Vikas Sindhwani, Ebru Arisoy, and Bhuvana Ramabhadran. Low-rank matrix factorization for deep neural network training with high-dimensional output targets.
In ICASSP 2013, pp. 6655–6659. IEEE, 2013.

[49] Mohammad Shoeybi, Mostofa Patwary, Raul Puri, Patrick LeGresley, Jared Casper, and Bryan Catanzaro. Megatron-LM: Training multi-billion parameter language models using model parallelism.
arXiv preprint arXiv:1909.08053, 2020.

[50] Richard Socher, Alex Perelygin, Jean Wu, Jason Chuang, Christopher D. Manning, Andrew Ng, and Christopher Potts. Recursive deep models for semantic compositionality over a sentiment treebank.
In EMNLP 2013, pp. 1631–1642, 2013. Link.

[51] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is All You Need.
In NeurIPS 2017, pp. 6000–6010, 2017.

[52] Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. GLUE: A multi-task benchmark and analysis platform for natural language understanding.
2019.

[53] Alex Wang, Yada Pruksachatkun, Nikita Nangia, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. SuperGLUE: A stickier benchmark for general-purpose language understanding systems.
2020.

[54] Alex Warstadt, Amanpreet Singh, and Samuel R. Bowman. Neural network acceptability judgments.
arXiv preprint arXiv:1805.12471, 2018.

[55] Adina Williams, Nikita Nangia, and Samuel Bowman. A Broad-Coverage Challenge Corpus for Sentence Understanding through Inference.
In NAACL 2018 (Long Papers), pp. 1112–1122, 2018. doi: 10.18653/v1/N18-1101. Link.

[56] Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Rémi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander M. Rush. Transformers: State-of-the-art natural language processing.
In EMNLP 2020: System Demonstrations, pp. 38–45, 2020. Link.

[57] Greg Yang and Edward J. Hu. Feature Learning in Infinite-Width Neural Networks.
arXiv preprint arXiv:2011.14522, 2021.

[58] Elad Ben Zaken, Shauli Ravfogel, and Yoav Goldberg. BitFit: Simple parameter-efficient fine-tuning for transformer-based masked language models.
2021.

[59] Yu Zhang, Ekapol Chuangsuwanich, and James Glass. Extracting deep neural network bottleneck features using low-rank matrix factorization.
In ICASSP 2014, pp. 185–189. IEEE, 2014.

[60] Yong Zhao, Jinyu Li, and Yifan Gong. Low-rank plus diagonal adaptation for deep neural networks.
In ICASSP 2016, pp. 5005–5009. IEEE, 2016.

[61] Victor Zhong, Caiming Xiong, and Richard Socher. Seq2SQL: Generating structured queries from natural language using reinforcement learning.
CoRR, abs/1709.00103, 2017. Link.

---

A. 대규모 언어 모델들은 여전히 파라미터 업데이트가 필요하다

Few-shot 학습 또는 프롬프트 엔지니어링은
훈련 샘플이 소수만 있을 때 매우 유리하다.

그러나 실제로는,
성능이 중요한 응용 분야에서는 수천 개 이상의
훈련 예시를 선별(curate)할 여유가 있는 경우가 많다.

표 8(Table 8)에서 보듯이,
파인튜닝(fine-tuning)은 데이터셋의 크기와 관계없이
few-shot 학습에 비해 모델 성능을 현저하게 향상시킨다.

우리는 GPT-3 논문(Brown et al., 2020)에 제시된
RTE에 대한 GPT-3 few-shot 결과를 사용하였다.

또한 MNLI-matched의 경우,
각 클래스당 두 개의 데모(demonstration)를 사용하였으며
총 여섯 개의 in-context 예시를 사용하였다.

---

표 8.

파인튜닝(fine-tuning)은 GPT-3 (Brown et al., 2020)에서
few-shot 학습을 현저하게 능가한다(significantly outperforms).

---

B. 어댑터 레이어(Adapter Layers)가 유발하는 추론 지연(Inference Latency)

어댑터 레이어는 사전 학습된(pre-trained) 모델에
순차적(sequential) 으로 추가되는 외부 모듈이다.

반면, 우리가 제안하는 LoRA는
병렬적(parallel) 으로 추가되는 외부 모듈로 볼 수 있다.

그 결과, 어댑터 레이어는 기본(base) 모델 외에
추가적으로 계산되어야 하므로
불가피하게 추가적인 지연(latency) 을 초래한다.

Rücklé et al. (2020)이 지적한 바와 같이,
모델의 배치 크기(batch size) 및/또는
시퀀스 길이(sequence length) 가 충분히 커서
하드웨어 병렬성을 완전히 활용할 수 있는 경우에는
어댑터 레이어로 인한 지연이 완화될 수 있다.

우리는 GPT-2 medium 모델에 대해
유사한 지연(latency) 실험을 수행하여
그들의 관찰 결과를 확인하였으며,
특히 배치 크기가 작은 온라인 추론(online inference) 과 같은
특정 시나리오에서는 추가 지연이 상당할 수 있음을 지적한다.

우리는 NVIDIA Quadro RTX8000에서
100회의 반복 실험 평균을 통해
단일 순전파(single forward pass) 의 지연 시간을 측정하였다.

입력 배치 크기(batch size),
시퀀스 길이(sequence length),
그리고 어댑터 병목 차원(adapter bottleneck dimension, r)을 변화시키며 측정하였다.

두 가지 어댑터 설계를 시험하였다.
첫 번째는 Houlsby et al. (2019)이 제안한 원래 설계로, 이를 Adapter^H라 부른다.
두 번째는 Lin et al. (2020)이 제안한
보다 효율적인 최신 변형으로, 이를 Adapter^L이라 부른다.

각 설계에 대한 세부 내용은 5.1절(Section 5.1) 을 참조하라.

그림 5(Figure 5) 에서는
어댑터가 없는 베이스라인(no-adapter baseline)에 비한
성능 저하(지연 증가)를 백분율(%)로 나타내었다.

---

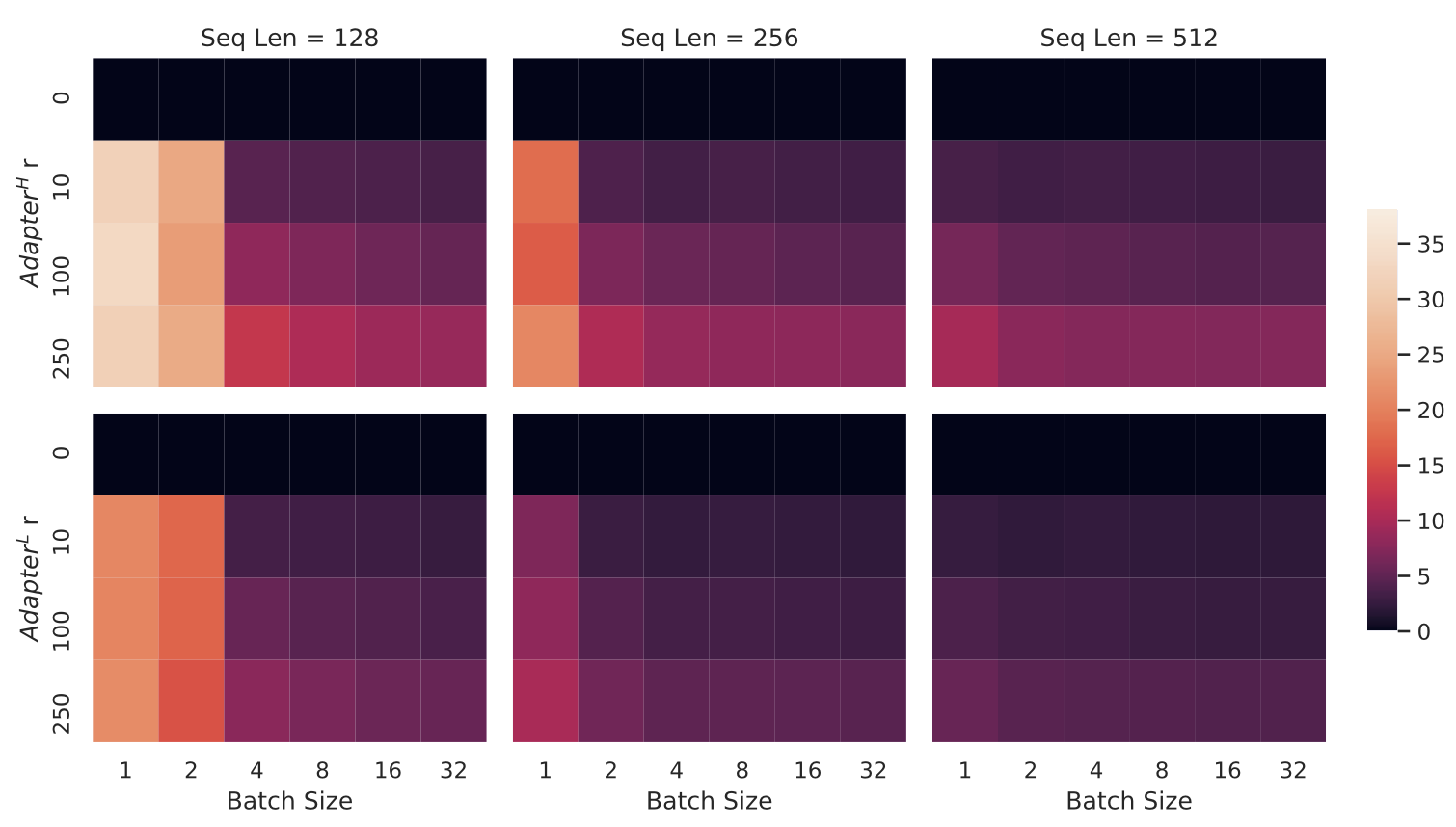
그림 5.

어댑터가 없는 베이스라인(no-adapter baseline, r = 0)과 비교한
추론 지연(inference latency)의 감속 비율(percentage slow-down).

상단 행(top row)은 Adapter^H의 결과를,
하단 행(bottom row)은 Adapter^L의 결과를 나타낸다.

배치 크기(batch size)와 시퀀스 길이(sequence length)가 커질수록
지연(latency)은 완화되는 경향을 보이지만,
온라인 환경(online scenario) 이며
시퀀스 길이가 짧은 경우(short-sequence-length scenario) 에는
지연이 30% 이상까지 증가할 수 있다.

시각적 구분을 용이하게 하기 위해
컬러맵(colormap)을 조정하였다.

---

C. 데이터셋 세부 사항 (Dataset Details)

GLUE Benchmark는
자연어 이해(Natural Language Understanding, NLU) 과제들을
폭넓게 포함하는 벤치마크 컬렉션이다.

이 벤치마크에는 다음과 같은 과제들이 포함되어 있다.

• MNLI (추론, inference) — Williams et al. (2018)
• SST-2 (감정 분석, sentiment analysis) — Socher et al. (2013)
• MRPC (의미 중복 문장 판별, paraphrase detection) — Dolan & Brockett (2005)
• CoLA (언어적 허용성, linguistic acceptability) — Warstadt et al. (2018)
• QNLI (추론, inference) — Rajpurkar et al. (2018)
• QQP⁸ (질문-답변 일치 여부, question-answering)
• RTE (추론, inference)
• STS-B (문장 간 의미적 유사도, textual similarity) — Cer et al. (2017)

이처럼 폭넓은 범위를 다루는 GLUE benchmark는
RoBERTa, DeBERTa와 같은
자연어 이해 모델(NLU models)을 평가하기 위한
표준적인 지표(standard metric)로 널리 사용된다.

각 개별 데이터셋은
서로 다른 완화된(permissive) 라이선스 하에 배포된다.

---

⁸https://quoradata.quora.com/First-Quora-Dataset-Release-Question-Pairs

---

WikiSQL은 Zhong et al. (2017)에 의해 소개되었으며,
56,355개의 학습 예시와 8,421개의 검증 예시로 구성되어 있다.

이 과제의 목적은 자연어 질문(natural language question) 과
테이블 스키마(table schema) 로부터
SQL 쿼리(SQL queries) 를 생성하는 것이다.

문맥(context)은
\(x = \{\text{table schema, query}\}\)
로 인코딩하며,
목표(target)는
\(y = \{\text{SQL}\}\)
로 인코딩한다.

이 데이터셋은 BSD 3-Clause License 하에 배포된다.

---

SAMSum은 Gliwa et al. (2019)에 의해 소개되었으며,
14,732개의 학습 예시와 819개의 테스트 예시를 포함한다.

이 데이터셋은 두 사람 간의 대화(chat conversation) 와
언어학자들이 작성한 요약문(abstractive summary) 으로 구성되어 있다.

문맥(context)은
\n으로 연결된 발화(utterances)를 이어붙이고,
그 뒤에 \n\n을 추가하여 인코딩하며,
목표(target)는
\(y = \{\text{summary}\}\)
로 인코딩한다.

이 데이터셋은 비상업적 사용 제한(non-commercial licence) 인
Creative Commons BY-NC-ND 4.0 하에 배포된다.

---

E2E NLG Challenge는 Novikova et al. (2017)에 의해
엔드투엔드(end-to-end) 데이터 기반
자연어 생성(NLG) 시스템을 훈련하기 위한 데이터셋으로 처음 소개되었다.
이 데이터셋은 데이터-텍스트(data-to-text) 평가에 일반적으로 사용된다.

E2E 데이터셋은 약

• 42,000개의 학습 예시,
• 4,600개의 검증 예시,
• 4,600개의 테스트 예시로 구성되어 있으며,
  모두 레스토랑 도메인(restaurant domain) 에 속한다.

각 입력 테이블(source table)은 여러 개의 참조(reference)를 가질 수 있다.

각 샘플 입력 $(x, y)$ 는
슬롯-값 쌍(slot-value pairs) 의 시퀀스와
해당하는 자연어 참조 텍스트(natural language reference text) 로 구성된다.

이 데이터셋은 Creative Commons BY-NC-SA 4.0 하에 배포된다.

---

DART는 Nan et al. (2020)에 의해 기술된
오픈 도메인(open-domain) 데이터-텍스트 데이터셋이다.

DART의 입력은
개체(ENTITY) — 관계(RELATION) — 개체(ENTITY)
삼중항(triple)의 시퀀스로 구성된다.

총 82,000개의 예시로 이루어진 DART는
E2E보다 훨씬 크고 복잡한
데이터-텍스트 생성 과제를 포함한다.

이 데이터셋은 MIT License 하에 배포된다.

---

WebNLG는 Gardent et al. (2017)에 의해 소개된
또 다른 대표적인 데이터-텍스트 평가용(data-to-text evaluation) 데이터셋이다.

총 22,000개의 예시로 구성된 WebNLG 데이터셋은
14개의 고유한 범주(distinct categories) 를 포함하며,
그 중 9개 범주는 학습 과정에서 등장한다.

이 중 9개 범주는 학습 단계에서 등장하며,
나머지 5개 범주는 학습 중 보이지 않지만 테스트 세트에는 포함된다.

따라서 평가 시에는 일반적으로

• 학습 중 등장한 범주(S, seen),
• 등장하지 않은 범주(U, unseen),
• 전체(A, all)
  로 나누어 수행한다.

각 입력 예시는
주어(SUBJECT) — 속성(PROPERTY) — 목적어(OBJECT)
삼중항(triple)의 시퀀스로 표현된다.

이 데이터셋은 Creative Commons BY-NC-SA 4.0 하에 배포된다.

D. 실험에 사용된 하이퍼파라미터

D.1 RoBERTa

우리는 AdamW 옵티마이저를 사용하여
선형 학습률 감쇠 스케줄(linear learning rate decay schedule) 로 훈련을 수행하였다.

LoRA에 대해서는
학습률(learning rate),
훈련 epoch 수,
배치 크기(batch size)를 변화시키며 실험하였다.

Liu et al. (2019)을 따라,
MRPC, RTE, STS-B 과제에 적응할 때에는
기존의 초기화 방법을 사용하는 대신,
MNLI에서의 최적 체크포인트(best MNLI checkpoint) 로부터
LoRA 모듈을 초기화하였다.

모든 과제에서 사전학습된(pre-trained) 모델은 고정(frozen) 상태로 유지되었다.

모든 결과는 5개의 서로 다른 랜덤 시드(random seed) 에 대해
중앙값(median) 을 보고하였으며,
각 실험(run) 결과는 가장 성능이 좋은 epoch(best epoch) 에서의 값을 사용하였다.

공정한 비교를 위해,
Houlsby et al. (2019) 및 Pfeiffer et al. (2021)의 설정과 동일하게,
모델의 시퀀스 길이(sequence length) 를 128로 제한하고,
모든 과제에서 고정된 배치 크기(fixed batch size) 를 사용하였다.

특히, MRPC, RTE, STS-B 과제에 적응할 때에는
이미 MNLI에 적응된 모델이 아니라,
사전학습된 RoBERTa large 모델(pre-trained RoBERTa large model) 로부터 시작하였다.

이러한 제한된 설정(restricted setup) 으로 수행된 실험들은
표에서 †(dagger) 로 표시하였다.

우리의 실험에서 사용된 하이퍼파라미터는
표 9(Table 9) 에 제시되어 있다.

---

표 9.

GLUE 벤치마크에서 RoBERTa에 사용된 하이퍼파라미터(hyperparameters).

---

D.2 DeBERTa

우리는 다시 AdamW 옵티마이저를 사용하여
선형 학습률 감쇠 스케줄(linear learning rate decay schedule) 로 훈련을 수행하였다.

He et al. (2021)을 따라,
학습률(learning rate),
드롭아웃 확률(dropout probability),
워밍업 스텝 수(warm-up steps),
배치 크기(batch size) 를 조정하였다.

공정한 비교를 위해,
He et al. (2021)에서 사용한 것과 동일한
모델 시퀀스 길이(model sequence length) 를 사용하였다.

또한 He et al. (2021)을 따라,
MRPC, RTE, STS-B 과제에 적응할 때에는
기존의 초기화 방식을 사용하지 않고,
MNLI에서의 최적 체크포인트(best MNLI checkpoint) 로부터
LoRA 모듈을 초기화하였다.

모든 과제에서 사전학습된(pre-trained) 모델은 고정(frozen) 상태로 유지되었다.

결과는 5개의 랜덤 시드(random seed) 에 대한 중앙값(median) 으로 보고하였으며,
각 실험(run)의 결과는 가장 성능이 좋은 epoch(best epoch) 에서의 값을 사용하였다.

우리의 실험에서 사용된 하이퍼파라미터(hyperparameters) 는
표 10(Table 10) 에 제시되어 있다.

---

표 10.

GLUE 벤치마크에 포함된 과제들에 대해
DeBERTa XXL 모델에 사용된 하이퍼파라미터(hyperparameters).

---

D.3 GPT-2

모든 GPT-2 모델은 AdamW 옵티마이저(Loshchilov & Hutter, 2017)를 사용하여
선형 학습률 스케줄(linear learning rate schedule) 로
총 5 epoch 동안 훈련하였다.

배치 크기(batch size), 학습률(learning rate),
그리고 빔 서치(beam search) 의 빔 크기(beam size)는
Li & Liang (2021)에 기술된 설정을 따랐다.

이에 따라 LoRA에 대해서도 위의 하이퍼파라미터들을 조정하였다.

결과는 3개의 랜덤 시드(random seed) 에 대한 평균(mean) 으로 보고하였으며,
각 실험(run)의 결과는 가장 성능이 좋은 epoch(best epoch) 에서의 값을 사용하였다.

GPT-2에서 LoRA에 사용된 하이퍼파라미터는
표 11(Table 11) 에 제시되어 있다.

기타 기준선 모델(baseline) 에 사용된 하이퍼파라미터는
Li & Liang (2021)을 참조하라.

---

표 11.

E2E, WebNLG, 그리고 DART 과제에서
GPT-2 LoRA에 사용된 하이퍼파라미터(hyperparameters).

---

D.4 GPT-3

모든 GPT-3 실험에서는 AdamW 옵티마이저(Loshchilov & Hutter, 2017)를 사용하여
2 epoch 동안 훈련하였으며,
배치 크기(batch size) 는 128 샘플,
가중치 감쇠(weight decay) 계수는 0.1로 설정하였다.

시퀀스 길이(sequence length)는 다음과 같이 설정하였다.

• WikiSQL (Zhong et al., 2017): 384
• MNLI (Williams et al., 2018): 768
• SAMSum (Gliwa et al., 2019): 2048

모든 방법(method) – 데이터셋(dataset) 조합에 대해
학습률(learning rate) 을 조정하였다.

사용된 하이퍼파라미터의 세부 사항은 D.4절(Section D.4) 를 참조하라.

프리픽스 임베딩 튜닝(prefix-embedding tuning) 의 경우,
최적의
\(l_p = 256, \quad l_i = 8\)
값을 사용하였으며,
총 3.2M개의 학습 가능한 파라미터(trainable parameters) 를 가진다.

프리픽스 레이어 튜닝(prefix-layer tuning) 에서는
\(l_p = 8, \quad l_i = 8\)
로 설정하여,
총 20.2M개의 학습 가능한 파라미터로
가장 우수한 전체 성능(overall best performance)을 얻었다.

LoRA의 경우, 두 가지 파라미터 예산(parameter budgets) 을 제시한다.

• 4.7M개 파라미터:
  $r_q = r_v = 1$ 또는 $r_v = 2$
• 37.7M개 파라미터:
  $r_q = r_v = 8$ 또는 $r_q = r_k = r_v = r_o = 2$

각 실험(run)에서는 가장 높은 검증 성능(best validation performance) 을 보고하였다.

GPT-3 실험에서 사용된 학습 하이퍼파라미터(training hyperparameters) 는
표 12(Table 12) 에 제시되어 있다.

---

표 12.

다양한 GPT-3 적응 방법(GPT-3 adaptation methods) 에 사용된
학습 하이퍼파라미터(training hyperparameters).

학습률(learning rate)을 조정한 이후에는
모든 데이터셋에 동일한 하이퍼파라미터를 사용하였다.

---

E. LoRA와 프리픽스 튜닝(Prefix Tuning)의 결합

LoRA는 기존의 프리픽스 기반(prefix-based) 접근법들과
자연스럽게 결합될 수 있다.

이 절에서는 WikiSQL과 MNLI 데이터셋을 대상으로,
LoRA와 프리픽스 튜닝의 변형(prefix-tuning variants)을 결합한
두 가지 방법을 평가한다.

LoRA+PrefixEmbed (LoRA+PE) 는
LoRA를 프리픽스 임베딩 튜닝(prefix-embedding tuning) 과 결합한 방식이다.

여기서는
\(l_p + l_i\)
개의 특수 토큰(special tokens) 을 삽입하고,
이들의 임베딩(embeddings) 을
학습 가능한 파라미터(trainable parameters) 로 취급한다.

프리픽스 임베딩 튜닝(prefix-embedding tuning)에 대한
자세한 내용은 5.1절(Section 5.1) 을 참조하라.

LoRA+PrefixLayer (LoRA+PL) 은
LoRA를 프리픽스 레이어 튜닝(prefix-layer tuning) 과 결합한 방식이다.

마찬가지로
\(l_p + l_i\)
개의 특수 토큰(special tokens) 을 삽입한다.

그러나 이 토큰들의 은닉 표현(hidden representations) 이
자연스럽게 변화하도록(evolve naturally) 두는 대신,
각 Transformer 블록(Transformer block) 이후마다
이들을 입력과 무관한 벡터(input-agnostic vector) 로 교체(replace) 한다.

따라서,
임베딩(embeddings) 과 이후의
Transformer 블록 활성화(activations) 모두
학습 가능한 파라미터(trainable parameters) 로 취급된다.

---

‘입력과 무관한 벡터(input-agnostic vector)’의 의미

• 일반적인 프리픽스 튜닝(prefix tuning) 에서는
  삽입된 특수 토큰(special tokens) 들이
  Transformer 블록을 거치며
  입력 문맥(input context)에 따라 자연스럽게 변화(evolve) 하도록 학습된다.
  즉, 각 층의 은닉 표현(hidden representation) 이
  입력 문장에 반응하여 동적으로 바뀐다.

• 반면, 입력과 무관한 벡터(input-agnostic vector) 로 교체한다는 것은
  각 블록 이후마다 이 토큰들의 은닉 표현을
  입력 내용에 따라 변화시키지 않고,
  항상 동일한 형태의 벡터로 대체한다는 뜻이다.
  이 벡터는 입력과 관계없이
  모델이 학습 과정에서 최적화(optimization) 하는
  학습 가능한 파라미터(trainable parameter) 로 존재한다.

• 여기서 “입력과 무관하다”는 것은
  입력에 따라 값이 달라지지 않는다는 의미이지,
  학습되지 않는다는 뜻이 아니다.
  이 벡터들은 훈련 중에 역전파(backpropagation) 를 통해
  손실(loss)을 줄이는 방향으로 지속적으로 업데이트된다.

• 이렇게 하면 프리픽스 토큰이
  입력 문맥에 따라 불안정하게 바뀌는 대신,
  각 Transformer 층마다 고정된 조정 신호(adjustment signal) 를 제공하여
  모델의 동작을 안정적으로 보정(stabilize) 한다.

• 따라서 모델은 입력 데이터에 따라 이 토큰을 재활용하지 않고,
  각 층의 출력이 지나갈 때마다
  입력에는 무관하지만 학습에는 참여하는 벡터를 삽입하는 방식으로
  안정적이고 효율적인 튜닝을 수행할 수 있다.

• 요약하자면,
  “입력과 무관한 벡터로 교체한다” 는 것은
  프리픽스 토큰이 입력마다 달라지지 않고,
  층(layer)마다 일정한 학습 가능한 조정 패턴(trainable adjustment pattern) 을
  제공하도록 설계한다는 의미이다.

---

프리픽스 레이어 튜닝(prefix-layer tuning)에 대한
자세한 내용 역시 5.1절(Section 5.1) 을 참조하라.

표 15(Table 15)에는 LoRA+PE 및 LoRA+PL 조합을
WikiSQL과 MultiNLI 데이터셋에서 평가한 결과를 제시하였다.

우선, LoRA+PE는 WikiSQL에서
기존의 LoRA 및 프리픽스 임베딩 튜닝(prefix-embedding tuning)
두 방법 모두를 유의미하게 능가(significantly outperforms) 한다.
이는 LoRA가 프리픽스 임베딩 튜닝과 비교적 독립적(orthogonal) 임을 시사한다.

반면 MultiNLI에서는
LoRA+PE 조합이 단독 LoRA보다 나은 성능을 보이지 않았다.
이는 LoRA 자체가 이미 인간 베이스라인(human baseline) 에 근접한
높은 성능을 달성했기 때문일 가능성이 있다.

다음으로, LoRA+PL은
더 많은 학습 가능한 파라미터(trainable parameters) 를 사용했음에도 불구하고
단독 LoRA보다 약간 낮은 성능(slightly worse) 을 보였다.

그 이유로는 프리픽스 레이어 튜닝(prefix-layer tuning) 이
학습률(learning rate) 설정에 매우 민감(sensitive)하기 때문에,
LoRA+PL 조합에서는
LoRA 가중치(weight) 의 최적화(optimization)가
더 어렵게 이루어졌기 때문이라고 분석하였다.

---

F. 추가 실증 실험 (Additional Empirical Experiments)

F.1 GPT-2에 대한 추가 실험

우리는 Li & Liang (2021) 의 설정을 따라
DART (Nan et al., 2020) 및 WebNLG (Gardent et al., 2017) 데이터셋에 대해
실험을 반복하였다.

그 결과는 표 13(Table 13) 에 제시되어 있다.

5절(Section 5) 에 보고된 E2E NLG Challenge 실험 결과와 유사하게,
LoRA는 동일한 학습 가능한 파라미터 수(trainable parameters) 를 사용할 때
프리픽스 기반(prefix-based) 접근법들보다 더 나은 성능을 보이거나,
적어도 동등한 수준(on-par) 의 성능을 달성하였다.

---

표 13.

DART 데이터셋에서 서로 다른 적응 방법(adaptation methods) 을 적용한 GPT-2의 결과.

모든 적응 방법에서 MET 및 TER의 분산(variance)은
0.01 미만으로 매우 작게 나타났다.

---

표 14.

WebNLG 데이터셋에서 서로 다른 적응 방법(adaptation methods) 을 적용한 GPT-2의 결과.

모든 실험에서 MET 및 TER의 분산(variance)은
0.01 미만으로 매우 작게 나타났다.

표 내의 표기는 다음을 의미한다.

• “U” : 학습 시 등장하지 않은 미등장 범주(unseen categories)
• “S” : 학습 시 등장한 등장 범주(seen categories)
• “A” : 테스트 세트 전체에 해당하는 모든 범주(all categories)

---

F.2 GPT-3에 대한 추가 실험 (Additional Experiments on GPT-3)

서로 다른 적응 방법(adaptation methods) 을 적용한
GPT-3의 추가 실험 결과를 표 15(Table 15) 에 제시하였다.

이 실험의 초점은
성능(performance) 과 학습 가능한 파라미터 수(number of trainable parameters) 사이의
트레이드오프(trade-off) 를 파악하는 데 있다.

---

표 15.

WikiSQL 및 MNLI 데이터셋에서
서로 다른 적응 방법(adaptation approaches) 에 대한 하이퍼파라미터 분석(hyperparameter analysis) 결과.

프리픽스 임베딩 튜닝(PrefixEmbed) 과
프리픽스 레이어 튜닝(PrefixLayer) 은
학습 가능한 파라미터 수(number of trainable parameters) 가 증가할수록
성능이 오히려 저하되는 경향을 보인다.

반면, LoRA의 성능은 안정적으로 유지(stabilizes) 된다.

성능 평가는 검증 정확도(validation accuracy) 를 기준으로 측정하였다.

---

F.3 저데이터 환경(Low-Data Regime)

저데이터 환경에서 서로 다른 적응 방법(adaptation approaches) 의 성능을 평가하기 위해,
우리는 MNLI 전체 학습 세트(full training set) 로부터
100개, 1,000개, 10,000개의 학습 예시를 무작위로 샘플링하여
저데이터 MNLI 과제(MNLI-n tasks) 를 구성하였다.

표 16(Table 16)** 에는
MNLI-n에서의 다양한 적응 방법들의 성능이 제시되어 있다.

---

표 16.
GPT-3 175B 모델을 사용하여
MNLI 데이터셋의 하위 집합(subset)에서
서로 다른 방법들의 검증 정확도(validation accuracy) 를 비교한 결과.

여기서 MNLI-n 은
$n$개의 학습 예시(training examples)를 포함한
MNLI의 하위 집합을 의미한다.

모든 방법은 전체 검증 세트(full validation set) 를 사용하여 평가하였다.

LoRA 는 파인튜닝(fine-tuning) 을 포함한
다른 방법들에 비해 샘플 효율성(sample-efficiency) 측면에서
더 우수한 성능을 보였다.

---

놀랍게도, PrefixEmbed 와 PrefixLayer 는
MNLI-100 데이터셋에서 매우 낮은 성능을 보였다.

• PrefixEmbed 는 무작위 추측(random chance, 33.3%)보다 약간 나은
  37.6% 수준에 불과했다.
• PrefixLayer 는 PrefixEmbed보다 나았지만,
  여전히 Fine-Tuning 이나 LoRA 에 비해 상당히 낮은 성능을 보였다.

학습 예시 수가 증가함에 따라
프리픽스 기반(prefix-based) 접근법과
LoRA / Fine-Tuning 간의 성능 격차는 줄어들었는데,
이는 GPT-3 모델에서는
프리픽스 기반 접근법이 저데이터(low-data) 과제에 적합하지 않을 수 있음을 시사한다.

또한 LoRA 는

• MNLI-100 및 MNLI-Full 환경에서는 Fine-Tuning보다 더 나은 성능을 보였고,
• MNLI-1k 및 MNLI-10k 환경에서는
  랜덤 시드(random seed)에 따른 ±0.3의 분산을 고려할 때
  유사한 성능(comparable performance) 을 달성하였다.

표 17(Table 17) 에는
MNLI-n에서의 각 적응 방법별 학습 하이퍼파라미터(training hyperparameters) 가 제시되어 있다.

---

표 17.

MNLI(m)-n에서
서로 다른 GPT-3 적응 방법(adaptation methods) 에 사용된
하이퍼파라미터(hyperparameters).

---

특히 PrefixLayer 는
MNLI-100 데이터셋에서
학습률이 너무 크면 손실(training loss)이 감소하지 않았기 때문에,
더 작은 학습률(smaller learning rate) 을 사용하였다.

G. 부분공간 간 유사도 측정 (Measuring Similarity Between Subspaces)

이 논문에서는 다음의 척도(measure)를 사용하여
부분공간(subspace) 간의 유사도를 측정한다.

\[\phi(A, B, i, j) = \psi(U_A^i, U_B^j) = \frac{ \| (U_A^i)^{\top} U_B^j \|_F^2 }{ \min\{i, j\} }\]

여기서 $U_A^i \in \mathbb{R}^{d \times i}$ 와
$U_B^j \in \mathbb{R}^{d \times j}$ 는
각각 행렬 $A$와 $B$의 좌측 특이행렬(left singular matrix) 로부터
열(column)을 취해 얻은 직교정규 행렬(column orthonormal matrix) 이다.

우리는 이 유사도가
부분공간들 간의 거리를 측정하는
표준 Projection Metric의 단순한 역(reverse) 형태임을 지적한다.

이 지표는 Ham & Lee (2008) 에서 사용된 것과 동일하다.

보다 구체적으로(concretely),
행렬 $(U_A^i)^{\top} U_B^j$ 의 특이값(singular values) 을
$\sigma_1, \sigma_2, \dots, \sigma_p$ 라 하자.
이때 $p = \min{i, j}$ 로 둔다.

우리는 Ham & Lee (2008) 에서 정의한
Projection Metric 이 다음과 같음을 알고 있다.

\[d(U_A^i, U_B^j) = \sqrt{\, p - \sum_{i=1}^{p} \sigma_i^2 \,} \in [0, \sqrt{p}]\]

우리의 유사도(similarity) 는 다음과 같이 정의된다.

\[\phi(A, B, i, j) = \psi(U_A^i, U_B^j) = \frac{\sum_{i=1}^{p} \sigma_i^2}{p} = \frac{1}{p}\left( 1 - d(U_A^i, U_B^j)^2 \right)\]

이 유사도는 다음 조건을 만족한다.

• 만약 $U_A^i$ 와 $U_B^j$ 가 동일한 열 공간(column span) 을 공유한다면,
  $\phi(A, B, i, j) = 1$ 이 된다.
• 만약 두 행렬이 완전히 직교(orthogonal) 하다면,
  $\phi(A, B, i, j) = 0$ 이 된다.
• 그 외의 경우에는
  \(\phi(A, B, i, j) \in (0, 1)\)
  의 범위에 속한다.

H. 저랭크 행렬(Low-Rank Matrices)에 대한 추가 실험

우리는 저랭크 갱신 행렬(low-rank update matrices) 에 대한
추가적인 실험 결과를 제시한다.

H.1 LoRA 모듈 간의 상관관계

그림 6(Figure 6) 및 그림 7(Figure 7) 은
그림 3(Figure 3) 과 그림 4(Figure 4) 에 제시된 결과가
다른 계층(layers)에서도 일반화되는(generalize) 양상을 보여준다.

---

그림 6.

96층(96-layer) Transformer의
1번째, 32번째, 64번째, 96번째 층에서의
$\Delta W_q$ 와 $\Delta W_v$ 에 대해,

$A_{r=8}$ 과 $A_{r=64}$ 의 열 벡터(column vectors) 간
정규화된 부분공간 유사도(normalized subspace similarity) 를 나타낸 그림.

---

그림 7.

96층(96-layer) Transformer의
1번째, 32번째, 64번째, 96번째 층에서의
$\Delta W_q$ 와 $\Delta W_v$ 에 대해,

서로 다른 랜덤 시드(random seed)로 학습된 두 실험(run)에서의
$A_{r=64}$ 열 벡터(column vectors) 간
정규화된 부분공간 유사도(normalized subspace similarity) 를 나타낸 그림.

---

H.2 GPT-2에서의 r의 영향

우리는 GPT-2 에서의 r의 영향(Section 7.2) 을
다시 실험하였다.

E2E NLG Challenge 데이터셋을 예시로 사용하여,
총 26,000 스텝(step) 동안 학습한 후
서로 다른 r 값 선택에 따른
검증 손실(validation loss) 및 테스트 지표(test metrics) 를 보고하였다.

그 결과는 표 18(Table 18) 에 제시되어 있다.

---

표 18.

GPT-2 Medium 모델을 사용하여
서로 다른 랭크(rank) r 값에서 LoRA가
E2E NLG Challenge 데이터셋에서 달성한
검증 손실(validation loss) 및 테스트 세트 지표(test set metrics).

GPT-3에서는 많은 과제에서 $r = 1$ 만으로 충분한 반면,
여기서는 검증 손실이 $r = 16$일 때,
BLEU 점수가 $r = 4$일 때 각각 최고 성능을 보였다.

이는 GPT-2 Medium이
GPT-3 175B와 유사한 내재적 적응 랭크(intrinsic rank for adaptation) 를
가지고 있음을 시사한다.

또한, 일부 하이퍼파라미터는
$r = 4$ 설정에서 튜닝되었으며,
이는 다른 기준선(baseline)의 파라미터 수(parameter count) 와 일치하도록 조정된 것이다.
따라서 다른 $r$ 값들에 대해서는
이 설정이 최적(optimal) 이 아닐 수도 있다.

---

GPT-2 Medium 모델의 최적 랭크(optimal rank)는
사용된 평가 지표(metric)에 따라 4와 16 사이에 위치하며,
이는 GPT-3 175B 모델에서의 결과와 유사하다.

한편, 모델 크기(model size) 와
적응에 적합한 최적 랭크(optimal rank for adaptation) 간의 관계는
여전히 미해결된(open) 연구 문제로 남아 있다.

H.3 W와 $\Delta W$ 간의 상관관계

그림 8(Figure 8) 은
$r$ 값이 달라질 때
W 와 $\Delta W$ 간의 정규화된 부분공간 유사도(normalized subspace similarity) 를 보여준다.

---

그림 8.

$r$ 값이 달라질 때의
$W_q$의 특이 방향(singular directions) 과
$\Delta W_q$의 특이 방향 간의
정규화된 부분공간 유사도(normalized subspace similarity),
그리고 무작위 기준선(random baseline) 과의 비교를 보여준다.

$\Delta W_q$ 는
$W$에서 충분히 강조되지 않았지만 중요한 방향들을
증폭(amplify) 하는 경향을 보인다.

또한 $r$ 값이 커질수록,
$\Delta W$ 는 이미 $W$에서 강조된 방향들을
더 많이 포착(pick up)하는 경향이 나타난다.

---

특히, $\Delta W$ 는 W의 상위 특이방향(top singular directions) 을
포함하지 않음을 다시 확인할 수 있다.
ΔW의 상위 4개 방향과 W의 상위 10% 방향 간 유사도는
0.2를 거의 넘지 않기 때문이다.

이 결과는 $\Delta W$ 가
W에서 강조되지 않았던 과제 특이적(task-specific) 방향들을
포함하고 있음을 시사한다.

흥미로운 다음 연구 질문은 다음과 같다.

• “모델이 잘 적응하도록 하기 위해,
• 이러한 과제 특이적 방향(task-specific directions) 을
• 얼마나 강하게 증폭(amplify)해야 하는가?”

H.4 증폭 계수 (Amplification Factor)

자연스럽게 다음과 같은 특징 증폭 계수(feature amplification factor) 를 고려할 수 있다.

\[\frac{ \| \Delta W \|_F }{ \| U^{\top} W V^{\top} \|_F },\]

여기서 $U$ 와 $V$ 는 $\Delta W$의 특이값 분해(SVD) 로부터 얻은
좌·우 특이행렬(left- and right-singular matrices)이다.
(참고로, $UU^{\top}WV^{\top}V$ 는 $W$를 $\Delta W$가 생성하는 부분공간(subspace)에
투영(projection)한 결과를 의미한다.)

직관적으로, $\Delta W$ 가 주로 과제 특이적 방향(task-specific directions) 을 포함할 때,
이 양은 그 방향들이 $\Delta W$ 에 의해 얼마나 증폭(amplified) 되는지를 나타낸다.

Section 7.3 에서 보인 바와 같이,
$r = 4$일 때 이 증폭 계수(amplification factor) 는 최대 20에 달한다.

즉, 각 층(layer)마다 (대략적으로 말하면) 네 개의 특징 방향(feature directions)이 존재하며,
이들은 사전학습된 모델(pre-trained model) $W$의 전체 특징 공간(feature space) 중에서
특히 큰 비율(20배)로 증폭되어야
하류 과제(downstream task)에서 보고된 정확도를 달성할 수 있다는 뜻이다.

또한, 서로 다른 하류 과제들마다
증폭되어야 하는 특징 방향(feature directions)의 집합은
서로 크게 다를 것으로 예상된다.

그러나 $r = 64$의 경우,
이 증폭 계수는 약 2 정도에 불과하며,
이는 $\Delta W$에서 학습된 대부분의 방향들이
크게 증폭되지 않는다는 것을 의미한다.

이는 놀라운 일이 아니며,
오히려 과제 특이적 방향(task-specific directions) 을 표현하기 위해 필요한
내재적 랭크(intrinsic rank) 가 낮다는 점을 다시 한 번 입증한다.

대조적으로, $r = 4$인 랭크-4 버전(rank-4 version) 의 $\Delta W$ 에서는
이러한 방향들이 약 20배 더 큰 비율로 증폭된다.