[논문] ANOMALY TRANSFORMER: TIME SERIES ANOMALY DETECTION WITH ASSOCIATION DISCREPANCY
논문 출처
Xu, J., Wu, H., Wang, J., & Long, M.
Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy.
International Conference on Learning Representations (ICLR 2022).
🔗 원문 링크 (arXiv:2110.02642)
저자
- Jiehui Xu (Tsinghua University, BNRist, School of Software) - xjh20@mails.tsinghua.edu.cn
- Haixu Wu (Tsinghua University, BNRist, School of Software) - whx20@mails.tsinghua.edu.cn
- Jianmin Wang (Tsinghua University, BNRist, School of Software) - jimwang@tsinghua.edu.cn
- Mingsheng Long (Tsinghua University, BNRist, School of Software) - mingsheng@tsinghua.edu.cn
∗ 공동 기여(Equal contribution).
초록 (Abstract)
시계열(time series)에서 이상 시점(anomaly points)을 비지도(unsupervised) 방식으로 탐지하는 것은 도전적인 문제이며,
모델은 구별 가능한 기준(distinguishable criterion)을 도출할 수 있어야 한다.
기존의 방법들은 주로 포인트 단위 표현(pointwise representation)이나
쌍별 연관성(pairwise association)을 학습하는 방식으로 이 문제에 접근해 왔다.
그러나 어느 쪽도 복잡한 동적 패턴(intricate dynamics)을 설명하기에는 충분하지 않았다.
포인트 단위 표현과 쌍별 연관성
포인트 단위 표현 (Pointwise Representation)
각 시점(time point)을 독립적으로 표현하는 방식이다.
예를 들어, 한 시점의 센서 값이나 그 주변 몇 개의 값만을 사용하여 특징 벡터를 만든다.
→ 문제: 각 시점을 따로 보므로, 전체적인 시간적 맥락을 반영하기 어렵다.쌍별 연관성 (Pairwise Association)
두 시점 사이의 관계를 모델링하는 방식이다.
예를 들어, $t$ 시점과 $t+k$ 시점 사이의 상관관계(correlation)나 유사도(similarity)를 계산한다.
→ 문제: 쌍 단위 관계만 보므로, 더 복잡한 다중 시점 간의 상호작용(dynamics)을 포착하기 어렵다.
최근 Transformer는 포인트 단위 표현과 쌍별 연관성을 통합적으로 모델링하는 데에 뛰어난 성능을 보여주었다.
그리고 우리는 각 시점의 셀프 어텐션 가중치 분포(self-attention weight distribution)가
전체 시계열과의 풍부한 연관성(rich association)을 내포할 수 있음을 발견하였다.
셀프 어텐션 가중치 분포와 시계열의 연관성
셀프 어텐션(self-attention)은 입력 시퀀스 내의 각 시점(time point)이
다른 모든 시점들과 얼마나 관련되어 있는지를 학습하는 메커니즘이다.구체적으로, 한 시점의 가중치 분포(weight distribution) 는
그 시점이 전체 시계열(whole series)의 어느 부분에 주의를 기울이고 있는지를 보여준다.
- 예를 들어, 주기적인 패턴(periodic pattern)이 있는 시계열에서는
어텐션이 일정한 간격의 시점들에 반복적으로 집중하는 경향을 보인다.- 반대로, 이상(anomaly)이 있는 구간에서는
특정 시점의 어텐션 가중치가 불균형하게 쏠리거나 급격히 변한다.
우리의 핵심 관찰은,
이상 시점(anomalies)들이 드물기 때문에,
이상 시점에서 전체 시계열(whole series)로의
자명하지 않은 연관성(nontrivial associations) 을 형성하는 것이 극도로 어렵다는 것이다.
따라서 이상 시점들의 연관성은 주로 인접한 시점(adjacent time points)에 집중하게 된다.
이웃한 시점에 연관성이 집중되는 경향(adjacent-concentration bias)은,
정상(normal) 시점과 이상(abnormal) 시점을 본질적으로 구별할 수 있는
연관성 기반 기준(association-based criterion) 을 의미한다.
우리는 이를 연관성 불일치(Association Discrepancy) 를 통해 강조한다.
기술적으로, 우리는 연관성 불일치를 계산하기 위한
새로운 Anomaly-Attention 메커니즘을 갖춘 Anomaly Transformer를 제안한다.
연관성 불일치가 정상(normal)과 이상(abnormal)을 더 잘 구별할 수 있게 하기 위해,
미니맥스 전략(minimax strategy)이 고안되었다.
Anomaly Transformer는 세 가지 응용 분야, 즉 서비스 모니터링, 우주 및 지구 탐사, 수자원 관리에서의,
여섯 가지 비지도 시계열 이상 탐지 벤치마크에서 최첨단(state-of-the-art) 성능을 달성하였다.
1 서론 (Introduction)
현실 세계의 시스템들은 항상 연속적인 방식으로 작동하며, 산업 장비, 우주 탐사선 등과 같이,
다중 센서(multi-sensors)에 의해 모니터링되는 연속적인 측정값(successive measurements)을 생성한다.
대규모 시스템 모니터링 데이터에서 오작동을 발견하는 일은 시계열에서 비정상 시점을 탐지하는 문제로 환원될 수 있으며,
이는 보안(security)을 보장하고 재정적 손실(financial loss)을 방지하는 데 매우 중요하다.
그러나 이상 시점(anomalies)은 일반적으로 드물고 방대한 정상 시점(normal points)에 의해 가려져 있기 때문에,
데이터를 라벨링(data labeling)하는 것은 어렵고 비용이 많이 든다.
따라서 우리는 비지도 환경에서의 시계열 이상 탐지(time series anomaly detection)에 초점을 맞춘다.
비지도 시계열 이상 탐지는 실제 환경에서 매우 도전적인 문제이다.
모델은 비지도 작업(unsupervised tasks)을 통해 복잡한 시간적 동역학(complex temporal dynamics)으로부터
유의미한 표현(informative representations)을 학습해야 한다.
또한 풍부한 정상 시점 속에서 드문 이상 시점을 탐지할 수 있는
구별 가능한 기준(distinguishable criterion)을 도출해야 한다.
다양한 고전적 이상 탐지 방법들은 여러 가지 비지도 패러다임을 제시해 왔다.
예를 들어, LOF (Local Outlier Factor, Breunig et al., 2000)에서 제안된
밀도 추정(density-estimation) 기반 방법과,
OC-SVM (One-Class SVM, Schölkopf et al., 2001)과
SVDD (Support Vector Data Description, Tax & Duin, 2004)에서 제시된
클러스터링(clustering) 기반 방법 등이 있다.
그러나 이러한 고전적 방법들은 시간적 정보를 고려하지 않으며,
보지 못한 실제 시나리오(unseen real scenarios)로 일반화하기 어렵다.
신경망(neural networks)의 표현 학습 능력(representation learning capability)에 힘입어,
최근의 딥러닝 기반 모델들(Su et al., 2019; Shen et al., 2020; Li et al., 2021)은 우수한 성능을 달성하였다.
이 중 주요한 접근 방식은,
잘 설계된 순환 신경망(recurrent networks)을 통해
포인트 단위 표현(pointwise representations)을 학습하는 것에 집중하고,
재구성(reconstruction) 또는 자기회귀(autoregressive) 과제를 통해
자기지도(self-supervised) 방식으로 학습하는 것이다.
이때 자연스럽고 실용적인 이상 기준(anomaly criterion)은
포인트 단위의 재구성 오차(reconstruction error) 또는 예측 오차(prediction error)이다.
그러나 이상 시점(anomalies)은 드물기 때문에,
포인트 단위 표현은 복잡한 시간적 패턴을 설명하기에는 충분하지 않으며,
정상 시점(normal time points)에 의해 지배되어 이상 시점이 잘 구별되지 않는다.
또한 재구성 오차나 예측 오차는 포인트 단위(point by point)로 계산되기 때문에,
시간적 맥락(temporal context)에 대한 포괄적인 설명을 제공할 수 없다.
또 다른 주요 방법 범주는
명시적인 연관성 모델링(explicit association modeling)에 기반하여 이상을 탐지하는 것이다.
벡터 자기회귀(vector autoregression)와 상태 공간 모델(state space models)이 이 범주에 속한다.
그래프(graph) 역시 명시적인 연관성을 포착하는 데 사용되었다.
서로 다른 시점(time points)을 정점(vertices)으로 하여 시계열(time series)을 표현하고,
랜덤 워크(random walk)를 통해 이상을 탐지하는 방식이다 (Cheng et al., 2008; 2009).
그래프와 랜덤 워크를 이용한 이상 탐지 방식
그래프 기반 이상 탐지(graph-based anomaly detection)는
시계열(time series)의 구조적 관계(structural relationship) 를 명시적으로 표현하는 접근이다.
- 그래프 구성 단계
- 각 시점(time point)을 그래프의 정점(vertex)으로 설정한다.
- 시점 간의 유사도(similarity)나 상관관계(correlation)를 계산하여
유사도가 높을수록 간선(edge)의 가중치(weight)를 크게 부여한다.예를 들어,
\[w_{ij} = \exp(-\|x_i - x_j\|^2)\]와 같이 두 시점 $i, j$의 유사도에 기반해 간선 가중치를 정의할 수 있다.
- 랜덤 워크(Random Walk) 수행
- 그래프 위에서 임의의 정점에서 시작해
연결된 간선을 따라 확률적으로 이동하는 과정을 반복한다.- 정상 시점(normal points)은 다른 시점들과의 연결이 강하고 고르게 분포되어 있어,
랜덤 워크가 안정적인 확률 분포(stationary distribution)에 수렴한다.- 반면 이상 시점(anomalies)은 연결이 약하거나 불균형하여
방문 확률이 비정상적으로 낮거나 높게 나타난다.- 이상 탐지(Detection)
- 최종적으로 각 정점의 방문 확률 분포를 분석하여,
정상 패턴과 확연히 다른 확률 특성을 보이는 정점을 이상으로 판단한다.이러한 방식은 포인트 단위 오차(pointwise error)를 계산하는 방법보다
더 전역적(global) 인 관점에서 시계열의 구조적 이상을 포착할 수 있다는 장점이 있다.
일반적으로 이러한 고전적 방법들을 통해, 유의미한 표현을 학습하거나, 세밀한 연관성을 모델링하는 것은 어렵다.
최근에는 그래프 신경망(Graph Neural Network, GNN)이,
다변량 시계열(multivariate time series)에서 여러 변수 간의 동적인 그래프를 학습하는 데 적용되었다
(Zhao et al., 2020; Deng & Hooi, 2021).
그래프 신경망(GNN)을 활용한 시계열 이상 탐지
그래프 신경망(Graph Neural Network, GNN)은
그래프 구조에서 노드(정점) 간의 관계를 학습할 수 있는 신경망으로,
시계열 데이터에서 변수 간 상호의존성(inter-dependency) 을 모델링하는 데 효과적이다.
- 다변량 시계열에서의 그래프 구성
- 각 변수(variable)를 그래프의 정점(vertex)으로 설정한다.
예를 들어, 센서 네트워크에서는 센서 하나가 하나의 정점이 된다.- 변수 간의 유사도(similarity), 상관계수(correlation), 또는 인과성(causality)을 기반으로
간선(edge)을 정의한다.- 이렇게 구성된 그래프는 시간에 따라 변하므로 동적 그래프(dynamic graph) 로 표현된다.
- GNN의 학습 방식
각 정점은 자신과 인접한 노드들의 정보를 반복적으로 집계(aggregation)하여
\[h_i^{(l+1)} = \sigma\left(\sum_{j \in \mathcal{N}(i)} w_{ij} \, h_j^{(l)}\right)\]
새로운 임베딩(embedding)을 생성한다.여기서 $h_i^{(l)}$는 $l$번째 층에서의 정점 $i$의 표현,
$\mathcal{N}(i)$는 인접 노드 집합, $\sigma$는 비선형 활성화 함수이다.이 과정을 통해 모델은 변수들 간의 관계 구조를 단계적으로 학습한다.
- 이상 탐지로의 적용
- 학습된 그래프 표현을 기반으로, 정상 상태에서는 강한 연결성을 보이지만
이상이 발생하면 연결 구조가 급격히 약화되거나 변형된다.- 이러한 구조적 변화를 이상 지표(anomaly indicator)로 사용한다.
요약하자면, GNN은 시계열의 시간 축뿐 아니라
변수 간의 관계 축(relationship axis) 까지 함께 고려함으로써,
다변량 시계열에서의 복잡한 이상 패턴을 보다 정교하게 탐지할 수 있게 해준다.
이러한 접근은 표현력이 더 풍부하긴 하지만,
학습된 그래프는 여전히 단일 시점(single time point)에 한정되어 있으며,
복잡한 시간적 패턴(complex temporal patterns)을 다루기에는 충분하지 않다.
한편, 부분 시퀀스(subsequence) 기반 방법들은
부분 시퀀스들 간의 유사성(similarity)을 계산하여 이상을 탐지한다 (Boniol & Palpanas, 2020).
부분 시퀀스(subsequence) 기반 이상 탐지 방식
부분 시퀀스 기반 방법은 시계열 전체를 한 번에 분석하는 대신,
시계열을 일정 길이의 작은 구간(subsequence)으로 나누어
각 구간 간의 유사성(similarity)을 비교함으로써 이상을 탐지하는 접근이다.
- 부분 시퀀스 분할(Subsequence Segmentation)
길이가 $T$인 시계열을 슬라이딩 윈도우(sliding window) 기법을 이용해
\[X = [x_1, x_2, \dots, x_T] \rightarrow \{[x_1,\dots,x_k], [x_2,\dots,x_{k+1}], \dots\}\]
여러 개의 부분 시퀀스로 분할한다.
예:이렇게 하면 시계열의 지역적(local) 패턴을 세밀하게 분석할 수 있다.
- 유사성 계산(Similarity Computation)
- 각 부분 시퀀스 간의 거리를 계산하여 패턴의 유사성을 측정한다.
자주 사용되는 거리 척도는 다음과 같다.
- DTW (Dynamic Time Warping): 시간적 변형을 고려한 유사도 측정
- Euclidean Distance: 단순한 시점별 차이 계산
- 정상적인 부분 시퀀스들은 서로 높은 유사도를 보이지만,
이상이 포함된 부분 시퀀스는 다른 구간들과의 유사도가 급격히 낮아진다.- 이상 탐지(Anomaly Detection)
- 각 부분 시퀀스의 평균 유사도 점수를 계산한 뒤,
특정 임계값(threshold) 이하의 점수를 가진 시퀀스를 이상으로 판단한다.이러한 방법은 시계열의 지역적 이상(local anomaly) 을 효과적으로 탐지할 수 있지만,
시계열 전체의 전역적 구조(global temporal structure)를 반영하기 어렵다는 한계가 있다.
특히, 시점 간 장기 의존성(long-term dependency)을 포착하기 힘들기 때문에
Transformer와 같은 전역적 모델의 필요성이 대두되었다.
이러한 방법들은 더 넓은 시간적 맥락(wider temporal context)을 탐색할 수는 있지만,
각 시점과 전체 시계열 간의 세밀한 시간적 연관성(fine-grained temporal association)은 포착하지 못한다.
본 논문에서는 Transformer (Vaswani et al., 2017)를 비지도 환경에서의 시계열 이상 탐지에 적용하였다.
Transformer는 자연어 처리(Brown et al., 2020), 머신 비전(machine vision, Liu et al., 2021),
시계열 분석(time series, Zhou et al., 2021) 등 다양한 분야에서 큰 성과를 거두었다.
이러한 성공은 전역 표현(global representation)과 장기 관계(long-range relation)를 통합적으로 모델링할 수 있는
Transformer의 강력한 표현 능력에 기인한다.
Transformer를 시계열에 적용한 결과,
각 시점의 시간적 연관성은 셀프 어텐션 맵(self-attention map)으로부터 얻어질 수 있음을 확인하였다.
이는 시간 축을 따라 각 시점이 전체 시계열의 다른 시점들과 맺는 연관성 가중치(association weights)의 분포로 표현된다.
이러한 연관성 분포는, 시계열의 시간적 맥락에 대한 더 풍부하고 유의미한 정보를 제공할 수 있으며,
특히 시계열의 주기(period)나 추세(trend)와 같은 동적 패턴(dynamic patterns)을 드러낸다.
우리는 이러한 연관성 분포를 시리즈 연관성(series-association) 이라고 부르며,
Transformer를 통해 원시 시계열(raw series)로부터 도출할 수 있다.
더 나아가 우리는, 이상 시점(anomalies)들이 드물고 정상 패턴(normal patterns)이 지배적이기 때문에,
이상 시점이 전체 시계열과 강한 연관성(strong associations)을 형성하기 어렵다는 것을 관찰하였다.
이상 시점의 연관성(association)은 시계열의 연속성(continuity)으로 인해,
유사한 비정상 패턴을 포함할 가능성이 높은 인접한 시점(adjacent time points)에 집중되는 경향을 보인다.
이러한 인접 집중(adjacent-concentration) 의 귀납적 편향(inductive bias)을
우리는 사전 연관성(prior-association) 이라고 부른다.
반면, 지배적인 정상 시점(normal time points)은 인접한 구간에 한정되지 않고,
전체 시계열(whole series)과의 유의미한 연관성(informative associations)을 형성할 수 있다.
이러한 관찰에 기반하여, 우리는 연관성 분포(association distribution)가 지니는
정상 시점과 이상 시점 간의 고유한 구별 가능성(distinguishability)을 활용하고자 한다.
이를 통해 각 시점에 대해 새로운 이상 기준(anomaly criterion)을 정의할 수 있다.
이 기준은 각 시점의 사전 연관성(prior-association) 과 시리즈 연관성(series-association) 간의 거리를 정량화하여 산출되며,
이를 연관성 불일치(Association Discrepancy) 라고 명명한다.
앞서 언급했듯이, 이상 시점의 연관성은 인접한 시점에 집중되는 경향이 있기 때문에,
이상 시점은 정상 시점에 비해 더 작은 연관성 불일치(association discrepancy)를 나타내게 된다.
기존의 방법들을 뛰어넘어, 우리는 Transformer를 비지도 시계열 이상 탐지에 도입하고,
연관성 학습(association learning)을 위한 Anomaly Transformer 를 제안한다.
연관성 불일치(Association Discrepancy)를 계산하기 위해,
셀프 어텐션(self-attention) 메커니즘을 새롭게 설계하여 Anomaly-Attention 구조를 제안한다.
이 메커니즘은 이중 분기(two-branch) 구조를 가지며,
각 시점의 사전 연관성(prior-association)과 시리즈 연관성(series-association) 을 각각 모델링한다.
사전 연관성은 학습 가능한 가우시안 커널을 사용하여 각 시점의 인접 집중(adjacent-concentration) 특성을 반영하고,
시리즈 연관성은 원시 시계열로부터 학습된 셀프 어텐션 가중치(self-attention weights)를 사용한다.
또한 두 개의 분기 사이에는 미니맥스 전략(minimax strategy) 이 적용되며,
이를 통해 연관성 불일치의 정상 시점(normal)–이상 시점(abnormal)간 구별 가능성(distinguishability)을 강화하고,
새로운 연관성 기반 기준(association-based criterion)을 도출한다.
Anomaly Transformer는 세 가지 실제 응용 분야에 걸친 여섯 가지 벤치마크에서 우수한 성능을 달성하였다.
본 논문의 주요 기여는 다음과 같다.
연관성 불일치(Association Discrepancy)에 대한 핵심 관찰에 기반하여,
사전 연관성과 시리즈 연관성을 동시에 모델링하는,
Anomaly-Attention 메커니즘을 갖춘 Anomaly Transformer를 제안하였다.연관성 불일치의 정상–이상 간 구별 가능성을 강화하기 위해
미니맥스 전략(minimax strategy) 을 도입하고,
이를 통해 새로운 연관성 기반 이상 탐지 기준을 제시하였다.제안한 모델은 세 가지 실제 응용 분야의 여섯 가지 벤치마크에서
최첨단(state-of-the-art) 이상 탐지 성능을 달성하였으며,
이는 광범위한 제거 실험(ablation study)과 사례 분석(case study)을 통해 검증되었다.
2 관련 연구 (Related Work)
2.1 비지도 시계열 이상 탐지 (Unsupervised Time Series Anomaly Detection)
중요한 실제 세계의 문제(real-world problem)로서, 비지도 시계열 이상 탐지는 광범위하게 연구되어 왔다.
이상(anomaly) 판별 기준에 따라 분류하면 이러한 접근 방식들은 대체로,
- 밀도 추정(density-estimation)
- 클러스터링 기반(clustering-based)
- 재구성 기반(reconstruction-based)
- 자기회귀 기반(autoregression-based)
방법으로 구분된다.
밀도 추정(density-estimation) 기반 방법에는,
대표적인 고전적 접근법인 LOF (Local Outlier Factor, Breunig et al., 2000) 과
COF (Connectivity Outlier Factor, Tang et al., 2002) 가 있다.
이들은 각각 지역 밀도(local density) 와 지역 연결성(local connectivity) 을 계산하여 이상치(outlier)를 판별한다.
밀도 추정 기반 이상 탐지의 개념
밀도 추정(density estimation) 기반 방법은
데이터가 얼마나 밀집되어 있는가(= 주변 데이터와 얼마나 가까운가) 를 기준으로
이상 여부를 판단하는 접근이다.
- 기본 아이디어
- 정상(normal) 데이터는 주변에 유사한 점들이 많아 밀도(density) 가 높다.
- 반면 이상치(outlier)는 주변에 유사한 점이 거의 없어 밀도 가 낮다.
- 따라서 “밀도가 낮은 데이터”를 이상으로 간주한다.
- LOF (Local Outlier Factor)
- 각 데이터 포인트의 지역 밀도(local density) 를 계산하고,
이웃들과 비교하여 얼마나 밀도가 떨어지는지를 평가한다.- LOF 값이 높을수록 주변보다 상대적으로 고립되어 있다는 뜻이며,
이상치일 가능성이 크다.- COF (Connectivity Outlier Factor)
- LOF와 유사하지만, 단순한 거리 대신
연결성(connectivity) 을 기반으로 이상 여부를 판단한다.- 즉, 한 점이 다른 점들과 얼마나 잘 연결되어 있는지를 측정하여
연결성이 약한 점을 이상으로 본다.
또한 DAGMM (Zong et al., 2018) 과 MPPCACD (Yairi et al., 2017) 는
가우시안 혼합 모델(Gaussian Mixture Model, GMM)을 결합하여
표현 공간(representation space)에서의 밀도(density)를 추정한다.
가우시안 혼합 모델(Gaussian Mixture Model, GMM)
가우시안 혼합 모델(Gaussian Mixture Model, GMM) 은
확률적 밀도 추정(probabilistic density estimation) 에 기반한 대표적인 통계적 모델로,
여러 개의 가우시안 분포(Gaussian distributions) 를 결합하여
복잡한 데이터 분포를 근사(approximation)하는 방법이다.
- 핵심 개념
- GMM은 데이터가 단일 가우시안 분포로 설명되지 않고,
여러 개의 서로 다른 가우시안 분포가 혼합되어 생성되었다고 가정한다.- 즉, 각 데이터 포인트 $x_i$는
$K$개의 가우시안 성분(component) 중 하나에서
확률적으로 생성된 것으로 본다.모델의 전체 확률 밀도함수는 다음과 같이 표현된다.
\[p(x) = \sum_{k=1}^{K} \pi_k \, \mathcal{N}(x \mid \mu_k, \Sigma_k)\]여기서
- $\pi_k$: 혼합 가중치(mixing weight), $\sum_k \pi_k = 1$
- $\mu_k$: 각 성분의 평균(mean vector)
- $\Sigma_k$: 각 성분의 공분산 행렬(covariance matrix)
- 학습 과정 (EM 알고리즘)
- GMM의 파라미터 ${\pi_k, \mu_k, \Sigma_k}$ 는
기댓값-최대화(Expectation-Maximization, EM) 알고리즘으로 추정된다.- E-step: 각 데이터가 어떤 가우시안 성분에 속할 확률(책임도, responsibility)을 계산한다.
- M-step: 해당 확률을 이용해 평균, 공분산, 혼합 가중치를 갱신한다.
- 이를 반복하여 로그우도(log-likelihood)가 수렴할 때까지 학습한다.
- 이상 탐지(Anomaly Detection)에서의 활용
- 학습된 GMM은 정상 데이터의 확률 밀도를 모델링하므로,
새로운 샘플의 로그 확률값(log-probability) 이 매우 낮으면
해당 샘플을 이상치(anomaly) 로 판단할 수 있다.즉,
\[\log p(x) < \tau \quad \Rightarrow \quad x \text{는 이상치로 간주}\]와 같이 임계값 $\tau$를 기준으로 이상을 탐지한다.
- 특징 및 장점
- 데이터의 다봉(multimodal) 구조를 포착할 수 있다.
- 비지도 학습(unsupervised learning) 기반으로 라벨 없이도 분포를 추정 가능하다.
- 이상 탐지, 클러스터링, 음성 인식, 이미지 분할 등 다양한 응용 분야에서 사용된다.
- 한계점
- 각 성분이 정규분포 형태를 따른다는 가정을 전제로 하므로,
복잡한 비정규(non-Gaussian) 분포에서는 정확도가 떨어질 수 있다.- 차원이 높아질수록 공분산 행렬 추정이 어려워지고,
계산량이 급격히 증가한다.
DAGMM과 MPPCACD의 밀도 추정 방식
DAGMM (Deep Autoencoding Gaussian Mixture Model) 과
MPPCACD (Multi-Process Principal Component Analysis Change Detection) 는
고차원 데이터의 은닉 표현(hidden representation) 공간에서
데이터 분포의 밀도를 추정함으로써 이상을 탐지하는 대표적인 딥러닝 기반 밀도 추정 기법이다.
- DAGMM의 핵심 아이디어
- 입력 데이터를 오토인코더(autoencoder)를 통해 저차원 잠재 공간(latent space)으로 압축한다.
- 이 잠재 표현(latent representation)을 이용해
가우시안 혼합 모델(Gaussian Mixture Model, GMM)을 학습한다.- 정상 데이터는 GMM의 고밀도 영역(high-density region)에 위치하지만,
이상치는 저밀도 영역(low-density region)에 위치하게 된다.- 따라서 샘플의 밀도 확률(density probability) 이 낮을수록
이상으로 판단할 수 있다.- MPPCACD의 접근 방식
- 시계열 데이터를 여러 프로세스(subprocess)로 분리한 뒤,
각 프로세스에 대해 주성분 분석(PCA)을 적용한다.- 이렇게 얻은 다중 프로세스 표현을 기반으로
데이터 분포의 변화를 감지(change detection)하고,
밀도 변동이 큰 구간을 이상으로 탐지한다.- 공통적인 특징
- 두 방법 모두 단순한 거리 기반 이상 탐지보다 더 확률적이고 정교한 접근을 취한다.
- 특히 DAGMM은 딥러닝을 통해 특징 공간을 자동 학습하므로,
기존 GMM보다 복잡한 데이터 분포를 잘 포착할 수 있다.- 한계점
- 학습 데이터에 이상치가 포함될 경우 GMM의 분포가 왜곡될 수 있으며,
시계열의 시간적 순서를 직접적으로 반영하지 못한다는 점에서
Transformer 기반 접근법과 같은 시계열 구조적 모델링이 필요하다.
클러스터링 기반(clustering-based) 방법에서는
이상 점수(anomaly score)를 일반적으로 클러스터 중심(cluster center)까지의 거리(distance)로 정의한다.
SVDD (Tax & Duin, 2004) 와 Deep SVDD (Ruff et al., 2018) 는
정상 데이터에서 얻어진 표현들(representations)을 하나의 밀집된 클러스터(compact cluster)로 모은다.
SVDD와 Deep SVDD의 이상 탐지 원리
SVDD (Support Vector Data Description) 와 Deep SVDD 는
정상(normal) 데이터가 어떤 “공간적 경계(boundary)” 안에 존재한다는 가정 하에
이를 기반으로 이상을 판별하는 대표적인 클러스터링 기반 이상 탐지 기법이다.
- SVDD의 기본 아이디어
- 정상 데이터 포인트들이 포함되는 최소 구(minimum hypersphere) 를 찾는다.
구의 중심을 $c$, 반지름을 $R$이라 하면,
\[\min_{R, c} \; R^2 + C \sum_i \xi_i \quad \text{s.t.} \quad \|x_i - c\|^2 \le R^2 + \xi_i, \; \xi_i \ge 0\]
다음 최적화 문제를 푼다:- 즉, 가능한 한 작은 구로 대부분의 정상 데이터를 감싸면서,
구 밖에 위치한 포인트는 이상치로 간주한다.- Deep SVDD의 확장
- 입력 데이터를 신경망을 통해 잠재 공간(latent space)으로 변환한 뒤,
그 공간에서 SVDD의 원리를 적용한다.- 이를 통해 복잡한 비선형 경계를 학습할 수 있어,
단순한 선형 구(sphere)보다 훨씬 강력한 표현력을 가진다.- 학습된 신경망은 정상 데이터의 표현을
하나의 밀집된 중심 영역(compact cluster) 으로 모으는 방향으로 파라미터를 조정한다.- 핵심 아이디어 요약
- 정상 데이터는 중심 근처의 밀집된 영역에 분포하고,
이상 데이터는 이 경계 밖(outside the boundary)에 존재한다.- 따라서 새로운 샘플이 학습된 구의 경계 밖에 위치하면
이상치(anomaly)로 판별된다.- 한계점
- SVDD 계열 방법은 데이터 간 시간적 관계를 고려하지 않기 때문에
시계열 데이터의 동적 특성을 모델링하기에는 한계가 있다.
이런 점에서 Transformer 기반 모델은
“정상 패턴의 공간적 경계”뿐 아니라
“시간적 연관성(temporal association)”까지 함께 학습할 수 있다는 강점을 가진다.
THOC (Shen et al., 2020) 는
계층적 클러스터링 메커니즘(hierarchical clustering mechanism)을 이용해
중간 계층(intermediate layers)에서의 다중 스케일 시간적 특징(multi-scale temporal features)을 통합(fuse)하고,
다층 간 거리(multi-layer distances)를 기반으로 이상을 탐지한다.
THOC의 계층적 이상 탐지 구조
THOC (Temporal Hierarchical One-Class Network) 은
시계열 데이터에서 서로 다른 시간적 범위의 패턴을 포착하기 위해
계층적 클러스터링(hierarchical clustering) 개념을 신경망 구조에 통합한 모델이다.
- 핵심 아이디어
- 시계열 데이터는 단일 시간 스케일로만 보면 놓치기 쉬운
다양한 수준(level)의 패턴 — 예를 들어,
짧은 주기(short-term) 진동부터 긴 주기(long-term) 추세까지 — 를 포함한다.- THOC는 여러 계층(intermediate layers)에서 추출된 특징들을
통합적으로 분석하여 이러한 다중 스케일(multi-scale) 패턴을 학습한다.- 모델 구조
- 하위 계층(lower layer)은 빠르게 변하는 단기 패턴(short-term dynamics)을,
상위 계층(higher layer)은 느린 장기 패턴(long-term dependencies)을 포착한다.- 각 계층의 표현(feature representations)을 클러스터링(clustering) 하여
정상 데이터가 형성하는 군집(cluster) 구조를 파악한다.- 이상 탐지 방식
- 입력 시계열을 각 계층의 군집 구조에 투영한 뒤,
“해당 계층의 중심(cluster center)”으로부터의 거리(distance)를 계산한다.- 모든 계층의 거리 정보를 통합하여
다층 간 거리(multi-layer distances) 로 이상 점수를 산출한다.- 정상 데이터는 여러 계층에서 일관된 군집 중심에 가깝게 위치하지만,
이상 데이터는 특정 계층에서 중심으로부터 멀어지거나
계층 간 일관성이 깨지는 형태를 보인다.- 특징과 의의
- THOC는 기존 단일 스케일 모델이 포착하지 못한
복합적인 시간적 구조(temporal hierarchy)를 반영한다.- 즉, 시간적 다층 표현(time-scale hierarchy) 을 활용하여
더 안정적이고 세밀한 이상 탐지가 가능하다.- 한계점
- 그러나 여전히 포인트 간의 명시적 연관성(association)을 직접 모델링하지 않으며,
Transformer 기반의 전역적 어텐션(attention) 메커니즘처럼
시점 간 관계를 정량적으로 표현하지는 못한다.
ITAD (Shin et al., 2020) 는 분해된 텐서(decomposed tensors)에 대한 클러스터링(clustering)을 수행한다.
ITAD의 텐서 분해 기반 이상 탐지
ITAD (Interpretable Tensor-based Anomaly Detection) 는
다차원 시계열(multivariate time series)을 텐서(tensor) 형태로 표현하고,
그 내부 구조를 분해(decomposition)하여 이상을 탐지하는 방법이다.
- 텐서 표현 (Tensor Representation)
- 시계열 데이터를 3차원 텐서로 변환한다.
예를 들어,
- 첫 번째 축: 시간(time)
- 두 번째 축: 변수(feature or sensor)
- 세 번째 축: 관측 구간(window or segment)
- 이렇게 하면 데이터의 시간적(time), 공간적(spatial), 변수 간 관계(inter-variable) 를
하나의 구조 안에 함께 표현할 수 있다.- 텐서 분해 (Tensor Decomposition)
- 텐서 내부의 패턴을 저차원 성분(low-rank components)으로 분리하여
주요 구조(main structure)와 노이즈(noise)를 구분한다.- 대표적인 방법은 CP 분해(Canonical Polyadic Decomposition) 또는
Tucker 분해(Tucker Decomposition) 로,
데이터의 핵심 패턴(core pattern)을 추출할 수 있다.- 클러스터링 및 이상 탐지 (Clustering and Detection)
- 분해된 저차원 표현(latent representation)을 클러스터링하여
정상 데이터의 구조적 패턴을 학습한다.- 새로운 데이터가 기존 클러스터 구조와 크게 다를 경우,
그 점을 이상(anomaly)으로 판단한다.- 의의와 장점
- ITAD는 단순히 개별 시점(point)이나 쌍(pair) 수준이 아니라,
시계열 전체의 다차원적 구조(multidimensional structure) 를 반영할 수 있다.- 특히 “어떤 축(시간, 변수, 구간)”에서 이상이 발생했는지
해석 가능한(interpretable) 형태로 파악할 수 있다는 점에서 의미가 크다.- 한계점
- 텐서 분해는 계산 비용이 크고,
복잡한 시계열에서의 비선형 관계를 충분히 포착하기 어렵다.- 따라서 최근 연구에서는 Transformer 기반 모델처럼
비선형적이고 전역적인 연관성(global association) 을 학습할 수 있는 접근이 주목받고 있다.
재구성 기반(reconstruction-based) 모델들은 재구성 오차(reconstruction error)를 통해 이상을 탐지하려고 시도한다.
Park et al. (2018)은, 시간적 모델링(temporal modeling)을 위해 LSTM 백본(backbone)을 사용하고,
재구성을 위해 변분 오토인코더(Variational AutoEncoder, VAE) 를 사용하는 LSTM-VAE 모델을 제시하였다.
LSTM-VAE 모델의 구조와 동작 원리
LSTM-VAE (Long Short-Term Memory – Variational AutoEncoder) 는
시계열 데이터의 시간적 의존성(temporal dependency)과
데이터 분포의 잠재 구조(latent structure)를 동시에 학습하기 위해
LSTM과 VAE를 결합한 모델이다.
- 구조 개요
- LSTM 인코더(encoder): 입력 시계열 데이터를 순차적으로 처리하여
시간적 패턴(temporal pattern)을 포착하고,
이를 잠재 공간(latent space)의 확률 분포로 매핑한다.VAE의 잠재 변수(latent variables):
\[z = \mu + \sigma \odot \epsilon\] \[(\epsilon \sim \mathcal{N}(0, 1))\]
인코더가 출력한 분포(평균과 분산)를 사용해 잠재 변수 $z$를 샘플링한다.
이때, VAE의 핵심인 재매개변수화 기법(reparameterization trick)을 이용한다.
- LSTM 디코더(decoder): 잠재 변수 $z$를 입력받아
원래의 시계열을 재구성(reconstruct)한다.학습 목적 함수(Objective Function)
\[\mathcal{L} = \text{Reconstruction Loss} + \text{KL Divergence}\]
LSTM-VAE는 다음 손실 함수를 최소화하며 학습된다.
- Reconstruction Loss: 입력 시계열과 복원된 시계열 간의 차이.
- KL Divergence: 잠재 분포가 표준 정규분포에 가깝도록 제약하는 항.
- 이상 탐지 메커니즘
- 모델이 정상(normal) 시계열 패턴에 맞춰 학습되면,
정상 데이터는 낮은 재구성 오차를 보인다.- 반면, 이상(anomalous) 패턴은 잠재 분포에 적합하지 않아
높은 재구성 오차(reconstruction error) 를 보이게 된다.- 이 오차를 이상 점수(anomaly score)로 사용하여 이상 여부를 판단한다.
- 핵심 의의
- LSTM은 시계열의 시간적 구조(temporal structure) 를,
VAE는 데이터의 확률적 표현(probabilistic representation) 을 담당하여
두 기법의 장점을 결합한다.- 따라서 LSTM-VAE는
“시간적 패턴 + 확률적 이상성”을 모두 반영하는
강력한 비지도 이상 탐지 모델이다.
OmniAnomaly (Su et al., 2019) 는
정규화 흐름(normalizing flow)을 통해 LSTM-VAE 모델을 더욱 확장하였으며,
탐지를 위해 재구성 확률(reconstruction probabilities)을 사용한다.
OmniAnomaly의 구조와 핵심 개념
OmniAnomaly (Su et al., 2019) 는
기존 LSTM-VAE 구조를 기반으로 하지만, 정규화 흐름(normalizing flow) 을 도입하여
잠재 공간(latent space)의 확률 분포를 보다 유연하게 모델링한 고도화된 시계열 이상 탐지 모델이다.
- 핵심 아이디어
- 기존 LSTM-VAE는 잠재 변수가 정규분포 $\mathcal{N}(0, I)$ 를 따른다고 가정하지만,
실제 시계열 데이터의 잠재 분포는 훨씬 복잡하다.- OmniAnomaly는 정규화 흐름(normalizing flow) 을 사용하여
단순한 분포를 점진적으로 변환(transform)함으로써
복잡한 분포를 정밀하게 표현할 수 있다.- 정규화 흐름(Normalizing Flow)의 개념
잠재 변수 $z_0$를 여러 개의 가역 변환 함수(invertible transformation) $f_i$를 통해
\[z_K = f_K \circ f_{K-1} \circ \cdots \circ f_1 (z_0)\]
다음과 같이 변환한다:이러한 변환 과정을 통해 단순한 분포(예: 정규분포)를
실제 데이터의 복잡한 분포 형태로 정밀하게 매핑할 수 있다.- 모델 구성
- LSTM 인코더: 시계열의 시간적 의존성을 학습하고,
입력 데이터를 잠재 변수 $z_0$로 압축한다.- Normalizing Flow 변환: $z_0$를 여러 단계의 비선형 변환을 거쳐
더 복잡한 잠재 변수 $z_K$로 변환한다.- LSTM 디코더: $z_K$로부터 원래 시계열을 재구성(reconstruct)한다.
- 이상 탐지 방식
- OmniAnomaly는 단순한 재구성 오차 대신,
각 시점의 재구성 확률(reconstruction probability) 을 사용한다.- 즉, 데이터가 학습된 잠재 분포에서 발생할 확률이 낮을수록
그 데이터가 이상일 가능성이 높다고 판단한다.- 특징 및 장점
- 복잡한 데이터 분포를 정밀하게 추정할 수 있어
비선형적이고 비정상적인 시계열(anomalous time series)에 강하다.- 확률 기반(probabilistic) 탐지 방식을 사용하므로
이상 여부를 더 안정적으로 평가할 수 있다.- 요약
- LSTM → 시간적 패턴 학습
- VAE → 잠재 공간 확률 모델링
- Normalizing Flow → 복잡한 분포 표현 강화
- 이 세 요소가 결합되어, OmniAnomaly는
“정확한 확률적 이상 탐지(probabilistic anomaly detection)” 를 실현한다.
InterFusion (Li et al., 2021) 은
백본(backbone)을 계층적 VAE(hierarchical VAE)로 새롭게 설계하여,
다중 시계열(multiple series)간의 상호 의존성(inter-dependency)과 내부 의존성(intra-dependency)을 동시에 모델링한다.
InterFusion의 계층적 VAE 구조와 이상 탐지 원리
InterFusion (Li et al., 2021) 은
복수의 시계열(multivariate time series)에서 발생하는
변수 간 상호 작용(interaction)과 내부 패턴(internal temporal structure)을 동시에 학습하기 위해
계층적 변분 오토인코더(Hierarchical Variational AutoEncoder, HVAE) 를 적용한 모델이다.
- 기본 아이디어
- 기존 VAE는 모든 입력을 하나의 잠재 변수(latent variable)로 요약하지만,
InterFusion은 두 단계의 잠재 구조(latent hierarchy)를 도입한다.
- 전역 잠재 변수(global latent variable):
여러 시계열 간의 공통 패턴(inter-dependency) 을 학습.- 국소 잠재 변수(local latent variable):
각 시계열 내부의 개별 패턴(intra-dependency) 을 학습.- 이를 통해 모델은 “각 변수 내부의 변화”와 “변수 간의 관계”를
동시에 이해할 수 있게 된다.- 모델 구조
- 인코더(encoder):
입력 시계열 데이터를 두 수준의 잠재 변수 $(z_g, z_l)$ 로 인코딩한다.
- $z_g$: 여러 시계열 간의 전역 패턴(global dependencies).
- $z_l$: 개별 시계열의 지역적 패턴(local dependencies).
- 디코더(decoder):
두 잠재 변수에서 다시 전체 시계열을 재구성(reconstruct)한다.
이때 전역 정보와 지역 정보가 결합되어
복합적 시계열 패턴을 복원한다.- 이상 탐지 메커니즘
- 학습 과정에서 모델은 정상(normal) 시계열의 전역–지역 패턴을 학습한다.
- 새로운 입력이 주어졌을 때,
복원된 시계열과의 재구성 오차(reconstruction error) 또는
잠재 확률(likelihood) 을 측정한다.- 전역/지역 수준에서 어느 한쪽이라도 큰 불일치(discrepancy)가 발생하면,
해당 시점은 이상(anomaly)으로 간주된다.- 의의와 장점
- InterFusion은 단순히 한 시계열 내의 이상만 보는 것이 아니라,
여러 시계열 간의 상호 의존성(inter-series dependency) 까지 함께 분석한다.- 따라서 산업 설비, 센서 네트워크, 금융 데이터 등
복수 변수 간 관계가 중요한 환경에서 특히 효과적이다.- 한계점 및 발전 방향
- HVAE 구조는 복잡하고 계산량이 많으며,
긴 시계열에서 전역적 관계(global temporal association)를
완전히 포착하기는 어렵다.- 이런 한계를 극복하기 위해 Transformer 기반 접근법에서는
어텐션(attention) 을 통해 전 시점 간의 연관성을 직접 학습하도록 설계한다.
GANs (Generative Adversarial Networks, Goodfellow et al., 2014) 또한
재구성 기반 이상 탐지(reconstruction-based anomaly detection)에 사용된다.
자기회귀(autoregression) 기반 모델들은 예측 오차(prediction error)를 통해 이상을 탐지한다.
VAR 는 ARIMA (Anderson & Kendall, 1976) 를 확장한 것으로,
시차 의존 공분산(lag-dependent covariance)에 기반하여 미래를 예측한다.
자기회귀 모델은 또한 LSTM (Hundman et al., 2018; Tariq et al., 2019)으로 대체될 수도 있다.
이 논문은 새로운 연관성 기반 기준(association-based criterion)을 특징으로 한다.
무작위 이동(random walk) 방식이나
부분 시퀀스(subsequence) 기반 방법(Cheng et al., 2008; Boniol & Palpanas, 2020)과는 달리,
우리의 기준(criteria)은 시간적 모델(temporal model)을 상호 연계적으로 설계(co-design)하여
보다 풍부한 시간 시점 간 연관(time-point association)을 학습하도록 구현되었다.
2.2 시계열 분석을 위한 Transformer (Transformers for Time Series Analysis)
최근 Transformer (Vaswani et al., 2017)는 자연어 처리(Devlin et al., 2019; Brown et al., 2020),
오디오 처리(Huang et al., 2019), 컴퓨터 비전(Dosovitskiy et al., 2021; Liu et al., 2021) 등
순차 데이터(sequential data) 처리에서 강력한 성능을 보여주었다.
시계열 분석(time series analysis)의 경우,
Transformer는 셀프 어텐션(self-attention) 메커니즘의 장점을 활용하여
신뢰할 수 있는 장기 시간 의존성(long-range temporal dependencies)을
발견하는 데 사용되고 있다 (Kitaev et al., 2020; Li et al., 2019b; Zhou et al., 2021; Wu et al., 2021).
특히 시계열 이상 탐지(time series anomaly detection)를 위해 GTA (Chen et al., 2021) 는,
그래프 구조(graph structure)를 사용하여 여러 IoT 센서 간의 관계를 학습하고,
Transformer를 통해 시간적 모델링(temporal modeling)을 수행하여,
재구성 기준(reconstruction criterion)을 기반으로 이상을 탐지한다.
그래프 기반 시계열 이상 탐지: GTA (Graph Transformer for Anomaly Detection)
GTA (Graph Transformer for Anomaly Detection, Chen et al., 2021) 는
그래프 신호 처리(graph signal processing) 와 트랜스포머(Transformer) 의 장점을 결합한
대표적인 그래프 기반 시계열 이상 탐지(Graph-based Time Series Anomaly Detection) 모델이다.
- 핵심 아이디어
- 여러 IoT 센서 노드(sensor node) 를 그래프 구조(graph structure) 로 표현하여,
각 노드 간의 공간적 상관관계(spatial correlation) 를 학습한다.- 동시에, 트랜스포머를 이용하여 시간적 의존성(temporal dependency) 을 모델링한다.
- 이렇게 학습된 그래프-시계열 표현은
센서 간 상호작용(interaction)과 시점 간 연속성(temporal continuity)을 동시에 포착한다.- 모델 구조 요약
- 그래프 인코더(Graph Encoder):
그래프 인접 행렬(adjacency matrix)을 기반으로 노드 간 관계를 학습한다.- 트랜스포머 기반 시간 인코더(Temporal Transformer Encoder):
각 노드의 시계열 데이터를 입력받아,
시점 간의 복잡한 의존성을 주의(attention) 메커니즘으로 학습한다.- 디코더(Decoder):
인코딩된 표현으로부터 원래의 시계열 신호를 재구성(reconstruction)한다.- 이상 탐지 메커니즘
- 모델이 입력 시계열을 복원(reconstruct)할 때 발생하는
재구성 오차(reconstruction error) 를 이용하여 이상을 탐지한다.- 정상 데이터는 모델이 잘 복원하지만,
이상 데이터는 복원 오차가 커지므로 이를 이상 점수(anomaly score) 로 사용한다.즉,
\[\text{Anomaly Score}(x_t) = \|x_t - \hat{x}_t\|^2\]와 같이 정의되며, 오차가 클수록 이상일 확률이 높다.
- 특징 및 의의
- 공간적 상관(spatial correlation) 과 시간적 패턴(temporal pattern) 을 동시에 고려함으로써,
단일 시계열 모델보다 복잡한 IoT 네트워크 환경에 더 잘 대응한다.- 그래프 구조 학습(graph learning) 과 트랜스포머의 주의 메커니즘(attention mechanism) 을 결합하여,
센서 간 관계가 명시적으로 주어지지 않아도 데이터로부터 동적으로 학습할 수 있다.- 결과적으로 GTA는 다변량 시계열(multivariate time series) 이상 탐지에
강력한 성능을 보이는 대표적인 딥러닝 기반 접근법으로 평가된다.
기존 Transformer의 사용 방식과 달리,
Anomaly Transformer 는 연관성 불일치(association discrepancy)에 대한 핵심 관찰(key observation)에 기반하여,
셀프 어텐션 메커니즘(self-attention mechanism)을 Anomaly-Attention 으로 새롭게 설계하였다.
3 방법 (Method)
시스템이 $d$개의 연속적인 측정값(successive measurements)을 모니터링하고,
시간에 따라 일정한 간격으로 관측값(observations)을 기록한다고 가정하자.
관측된 시계열(time series) $X$는 시간 시점들의 집합 ${x_1, x_2, \dots, x_N}$ 으로 표현되며,
각 시점의 관측값 $x_t \in \mathbb{R}^d$는 시간 $t$에서의 측정값을 나타낸다.
비지도 시계열 이상 탐지(unsupervised time series anomaly detection)의 목표는,
라벨(labels) 없이 각 시점 $x_t$ 가 이상(anomalous)인지 아닌지를 판별하는 것이다.
앞서 언급했듯이, 비지도 시계열 이상 탐지의 핵심은,
유의미한 표현(informative representations)을 학습하고,
구별 가능한 기준(distinguishable criterion)을 찾는 데 있다.
이를 위해 우리는 Anomaly Transformer 를 제안한다.
이 모델은 더 유의미한 연관성(informative associations)을 학습하고,
본질적으로 정상(normal)과 이상(abnormal)을 구별할 수 있는
연관성 불일치(Association Discrepancy) 를 학습함으로써 이 문제를 해결한다.
기술적으로는,
각 시점의 사전 연관성과 시리즈 연관성을 표현하기 위해 새로운 Anomaly-Attention 메커니즘을 제안하며,
보다 구별력 있는 연관성 불일치를 얻기 위해 미니맥스 최적화 전략을 함께 사용한다.
이러한 구조적 설계와 결합하여,
학습된 연관성 불일치(association discrepancy)에 기반한 연관성 기반 기준(association-based criterion) 을 도출한다.
3.1 Anomaly-Attention
이상 탐지에 대한 Transformer (Vaswani et al., 2017)의 한계로 인해,
우리는 기본 구조(vanilla architecture)를,
Anomaly-Attention 메커니즘을 포함한 Anomaly-Transformer로 새롭게 설계하였다 (그림 1).
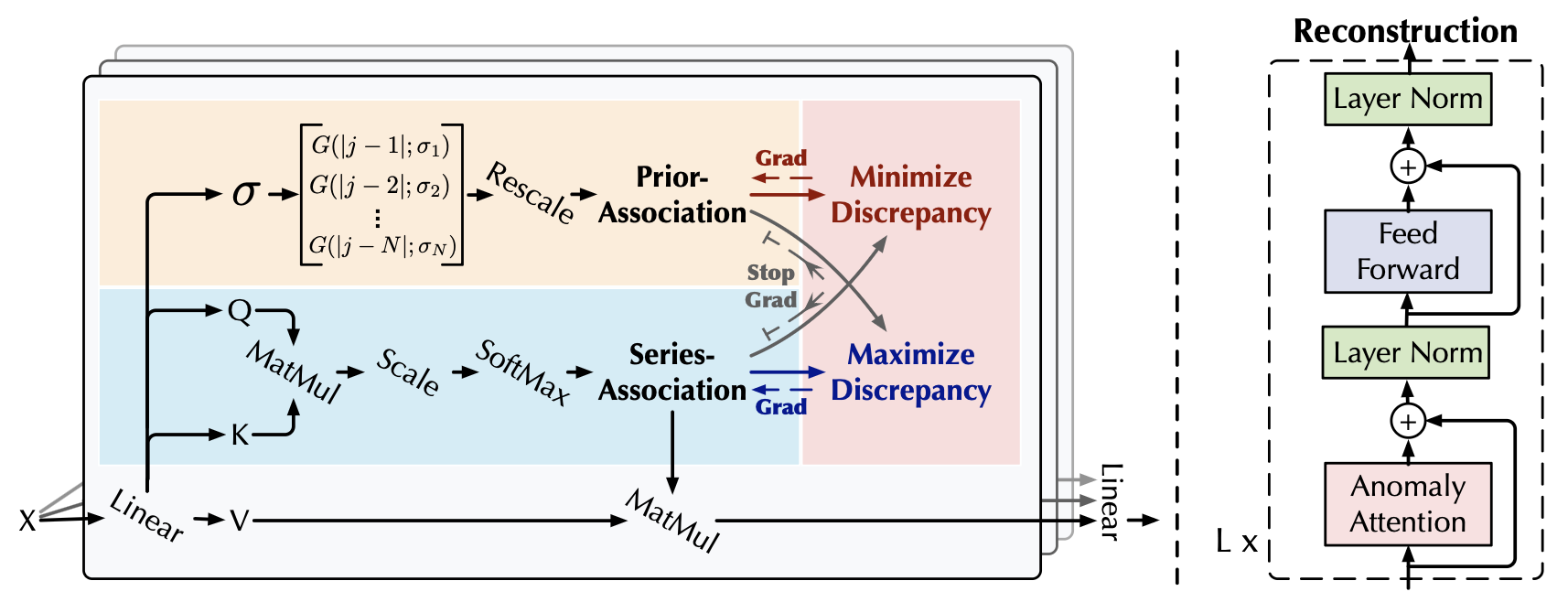
그림 1 : Anomaly-Transformer
Anomaly-Attention(왼쪽)은 사전 연관성(prior-association)과 시리즈 연관성(series-association)을 동시에 모델링한다.
우리의 모델은, 재구성 손실(reconstruction loss) 외에도,
특별히 설계된 정지-그래디언트(stop-gradient) 메커니즘(회색 화살표)을 포함한 미니맥스 전략 을 통해 최적화된다.
이 메커니즘은 사전 연관성과 시리즈 연관성을 제약하여,
더욱 더 잘 구별할 수 있는 연관성 불일치(distinguishable association discrepancy)를 학습하도록 돕는다.
전체 구조 (Overall Architecture)
Anomaly Transformer는 Anomaly-Attention 블록과 피드포워드(feed-forward) 계층을 번갈아 쌓은 구조를 가진다.
이러한 적층 구조(stacking structure)는
깊은 다단계 특징(deep multi-level features)으로부터 내재된 연관성(underlying associations)을 학습하는 데 도움이 된다.
모델이 $L$개의 계층을 가지고 있고, 길이가 $N$인 입력 시계열 $X \in \mathbb{R}^{N \times d}$ 를 가진다고 가정하자.
$l$번째 계층의 수식(overall equations)은 다음과 같이 정의된다(formulized):
\[Z^{(l)} = \text{Layer-Norm}(\text{Anomaly-Attention}(X^{(l-1)}) + X^{(l-1)}) \tag{1}\] \[X^{(l)} = \text{Layer-Norm}(\text{Feed-Forward}(Z^{(l)}) + Z^{(l)})\]여기서 $X^{(l)} \in \mathbb{R}^{N \times d_{\text{model}}}$, $l \in {1, \dots, L}$은 $d_{\text{model}}$ 개의 채널을 가진 $l$번째 계층의 출력을 나타낸다.
초기 입력 $X^{(0)} = \text{Embedding}(X)$는 임베딩된 원시 시계열(embedded raw series)을 나타낸다.
$Z^{(l)} \in \mathbb{R}^{N \times d_{\text{model}}}$은 $l$번째 계층의 은닉 표현(hidden representation)이다.
$\text{Anomaly-Attention}(\cdot)$은 연관성 불일치(association discrepancy)를 계산하기 위한 것이다.
Anomaly-Attention
단일 분기(single-branch) 구조의 셀프 어텐션 메커니즘(Self-Attention mechanism, Vaswani et al., 2017)은
사전 연관성(prior-association) 과 시리즈 연관성(series-association)을 동시에 모델링할 수 없다.
이에 우리는 이중 분기(two-branch) 구조를 가진 Anomaly-Attention 을 제안한다 (그림 1).
사전 연관성의 경우, 상대적인 시간 거리(relative temporal distance)에 따른 사전 확률(prior)을 계산하기 위해,
학습 가능한 가우시안 커널(learnable Gaussian kernel) 을 사용한다.
가우시안 커널의 단봉(unimodal) 특성 덕분에,
이 설계는 인접한 시점(adjacent horizon)에 더 많은 주의를 기울일 수 있게 한다.
또한 우리는 가우시안 커널에 대해 학습 가능한 스케일 파라미터(learnable scale parameter) $\sigma$ 를 도입하여,
이 사전 연관성이 시계열의 다양한 패턴, 예를 들어 이상 구간의 길이가 다른 경우 등에 적응할 수 있도록 한다.
시리즈 연관성 분기는 원시 시계열(raw series)로부터 연관성을 학습하며,
이를 통해 가장 효과적인 연관성(effective associations)을 적응적으로 찾아낼 수 있다.
이 두 가지 형태는 모두 각 시점의 시간적 의존성(temporal dependencies)을 보존하며,
단순한 포인트 단위 표현(point-wise representation)보다 더 유의미하다(informative).
또한, 이 두 연관성은 각각,
인접 집중 사전(adjacent-concentration prior) 및 학습된 연관성(learned associations)을 반영하며,
그 불일치(discrepancy)는 정상(normal)과 이상(abnormal)을 구별할 수 있는 특성을 가진다.
$l$번째 계층(layer)에서의 어노말리 어텐션은 다음과 같다:
초기화 (Initialization)
\[Q, K, V, \sigma = X^{(l-1)} W_Q^{(l)}, \; X^{(l-1)} W_K^{(l)}, \; X^{(l-1)} W_V^{(l)}, \; X^{(l-1)} W_\sigma^{(l)}\]사전 연관성 (Prior-Association)
- 상대적 시간 거리(relative temporal distance)에 대한 학습 가능한 가우시안 커널을 사용한다.
- 가우시안의 단봉(unimodal) 성질로 인해 인접 구간에 본질적으로 더 많은 주의를 기울인다.
- 또한 가우시안 커널의 학습 가능한 스케일 파라미터 $\sigma$ 를 사용하여,
서로 다른 길이의 이상 구간 등 다양한 시계열 패턴에 적응하도록 한다.
시리즈 연관성 (Series-Association)
\[S^{(l)} = \text{Softmax}\left( \frac{Q K^T}{\sqrt{d_{\text{model}}}} \right)\]재구성 (Reconstruction)
\[Z^{(l)} = S^{(l)} V\]여기서, $Q, K, V \in \mathbb{R}^{N \times d_{\text{model}}}$, $\sigma \in \mathbb{R}^{N \times 1}$은 각각,
셀프 어텐션의 쿼리(query), 키(key), 값(value), 그리고 학습된 스케일(learned scale)을 나타낸다.
또한, $W_Q^{(l)}, W_K^{(l)}, W_V^{(l)} \in \mathbb{R}^{d_{\text{model}} \times d_{\text{model}}}$, $W_\sigma^{(l)} \in \mathbb{R}^{d_{\text{model}} \times 1}$은,
$l$번째 계층에서 각각 $Q, K, V, \sigma$ 를 위한 파라미터 행렬(parameter matrices)이다.
사전 연관성 $P^{(l)} \in \mathbb{R}^{N \times N}$은 학습된 스케일(learned scale) $\sigma \in \mathbb{R}^{N \times 1}$ 에 기반하여 생성된다.
여기서 $i$번째 원소 $\sigma_i$ 는 $i$번째 시점(time point)에 해당한다.
구체적으로, $i$번째 시점이 $j$번째 시점과 맺는 연관성 가중치(association weight)는
거리 $|j - i|$ 에 대해 다음의 가우시안 커널(Gaussian kernel) 로 계산된다:
그 후, 각 시점별 연관성 가중치를 정규화하기 위해 $\text{Rescale}(\cdot)$ 함수를 사용하여,
각 행(row)의 합으로 나누어 이산 확률 분포(discrete distribution) $P^{(l)}$ 로 변환한다.
시리즈 연관성은 $S^{(l)} \in \mathbb{R}^{N \times N}$ 으로 표현된다.
$\text{Softmax}(\cdot)$ 는 마지막 차원(last dimension)을 따라 어텐션 맵(attention map)을 정규화하며,
$S^{(l)}$의 각 행은 하나의 이산 확률 분포(discrete distribution) 를 형성한다.
$\widehat{Z}^{(l)} \in \mathbb{R}^{N \times d_{\text{model}}}$은 $l$번째 계층의 Anomaly-Attention을 거친 후의 은닉 표현(hidden representation) 이다.
우리는 식 (2)를 단순화하기 위해 Anomaly-Attention(·) 표현을 사용하였다.
멀티헤드 버전에서는, 학습된 스케일이 $\sigma \in \mathbb{R}^{N \times h}$로 확장되며, 여기서 $h$는 헤드(head)의 개수를 나타낸다.
$m$번째 헤드의 쿼리(query), 키(key), 값(value)은 각각 $Q_m, K_m, V_m \in \mathbb{R}^{N \times \frac{d_{\text{model}}}{h}}$ 로 정의된다.
모듈은 여러 헤드에서 얻은 출력 \(\{\widehat{Z}^{(l)}_m \in \mathbb{R}^{N \times \frac{d_{\text{model}}}{h}}\}_{1 \leq m \leq h}\)을 연결(concatenate)하여,
최종 결과인 \(\widehat{Z}^{(l)} \in \mathbb{R}^{N \times d_{\text{model}}}\)을 얻는다.
연관성 불일치 (Association Discrepancy)
우리는 연관성 불일치를,
사전 연관성 과 시리즈 연관성 간의 대칭화된 KL 발산(symmetrized KL divergence) 으로 공식화(formalize)한다.
KL 발산(Kullback–Leibler Divergence)의 의미
1) 정의 (Definition)
\[\text{KL}(P \| Q) = \sum_i P(i) \log \frac{P(i)}{Q(i)}\]
두 확률 분포 $P$와 $Q$ 사이의 KL 발산은
한 분포가 다른 분포와 얼마나 “다른지”를 측정하는 비대칭적 거리 척도이다.
수식으로는 다음과 같이 정의된다:여기서
- $P(i)$ : 실제(참) 분포에서의 확률
- $Q(i)$ : 근사(모델) 분포에서의 확률
즉, $P$를 참 분포(ground truth)로,
$Q$를 $P$를 근사하려는 모델 분포로 볼 때,
$Q$가 $P$를 얼마나 “잘 따라가는지”를 측정한다.2) 직관 (Intuition)
- 만약 $P$와 $Q$가 완전히 동일하면,
$\text{KL}(P | Q) = 0$
(즉, 두 분포 간 정보 손실이 없음).- 반대로, $Q$가 $P$와 매우 다를수록 KL 발산 값은 커진다.
이는 $Q$가 $P$의 확률 질량(probability mass)을
잘못된 위치에 두고 있음을 의미한다.3) 대칭화 (Symmetrization)
\[\text{Sym-KL}(P, S) = \text{KL}(P \| S) + \text{KL}(S \| P)\]
KL 발산은 일반적으로 비대칭이므로,
본 논문에서는 이를 대칭화(symmetrization)하여 다음과 같이 정의하였다:이를 통해 “한쪽 기준으로 본 차이”가 아니라
양쪽 기준에서의 정보 차이(Information Discrepancy) 를 동시에 반영한다.
이는 두 확률 분포 사이의 정보 이득(information gain) 을 나타낸다 (Neal, 2007).
정보 이득 (Information Gain)
정보 이득(information gain) 은 한 확률 분포에서 다른 확률 분포로 변화할 때,
얻어진 정보량의 증가(즉, 불확실성의 감소) 를 정량적으로 나타내는 개념이다.
- 핵심 개념
- 정보 이득은 두 확률 분포 간의 차이를 측정하는 지표로,
주로 KL 발산(Kullback–Leibler divergence) 으로 정의된다.예를 들어, 실제 분포 $P$ 와 근사 분포 $Q$ 사이의 정보 이득은 다음과 같이 표현된다.
\[D_{KL}(P \,\|\, Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}\]또는 연속 확률 변수의 경우,
\[D_{KL}(P \,\|\, Q) = \int P(x) \log \frac{P(x)}{Q(x)} \, dx\]- 이는 $Q$가 $P$를 얼마나 잘 근사하는지를 나타내며,
값이 클수록 두 분포 간의 차이(즉, 정보 이득)가 크다는 뜻이다.- 직관적 해석
- 정보 이득은 “새로운 정보가 기존의 불확실성을 얼마나 줄였는가”를 의미한다.
- 예를 들어, 모델이 새로운 관측치를 통해 기존 예측의 불확실성을 줄였다면,
그만큼의 정보 이득이 발생했다고 볼 수 있다.- 응용 예시
의사결정나무(Decision Tree) 에서는
\[\text{Information Gain} = H(\text{전체}) - H(\text{분할 후})\]
특정 속성(attribute)을 기준으로 데이터를 분할했을 때,
엔트로피(entropy)가 얼마나 감소했는지를 “정보 이득”으로 정의한다.
즉,로 계산되며, 정보 이득이 클수록 그 속성이 더 유용한 분류 기준이 된다.
- 요약
- 정보 이득 = 불확실성 감소량 = 새로운 정보로 얻은 지식의 양
- 확률 분포 간의 차이, 또는 학습 전후의 예측 능력 향상을 수치적으로 나타내는 핵심 개념이다.
다층 특성(multi-level features)에서 얻은 연관성들을 보다 유의미한 척도(informative measure)로 결합하기 위해,
여러 계층에서의 연관성 불일치를 평균한다.
그 정의는 다음과 같다:
\[\text{AssDis}(P, S; X) = \frac{1}{L} \sum_{l=1}^{L} \left[ \text{KL}(P^{(l)}_{i,:} \,\|\, S^{(l)}_{i,:}) + \text{KL}(S^{(l)}_{i,:} \,\|\, P^{(l)}_{i,:}) \right], \quad i = 1, \dots, N\]여기서 $\text{KL}(\cdot | \cdot)$은 $P^{(l)}$ 과 $S^{(l)}$ 의 각 행(row)에 해당하는 두 개의 이산 확률 분포간의 KL 발산 을 계산한 것이다.
$\text{AssDis}(P, S; X) \in \mathbb{R}^{N \times 1}$은 시계열 $X$의 각 시점에 대한 포인트 단위의 연관성 불일치를 나타낸다.
즉, $i$번째 원소는 $X$의 $i$번째 시점에 해당한다.
이전의 관찰에서, 이상 시점은 정상 시점보다 더 작은 $\text{AssDis}(P, S; X)$ 값을 보이는 경향이 있었다.
따라서 $\text{AssDis}$ 는
본질적으로(normal-abnormal) 구별 가능한 지표(distinguishable measure)가 된다.
앞선 관찰에서 알 수 있듯이, 이상 시점은 정상 시점에 비해 더 작은 연관 불일치(Association Discrepancy) 값을 나타낸다.
이로 인해 AssDis는 본질적으로 구분 가능한(inherently distinguishable) 특성을 가진다.
3.2 미니맥스 연관성 학습 (Minimax Association Learning)
비지도 작업(unsupervised task)에 대해, 우리 모델은 재구성 손실(reconstruction loss) 을 통해 최적화된다.
재구성 손실은 시리즈 연관성 이 가장 유의미한 연관성(informative associations)을 찾도록 유도한다.
정상 시점과 이상 시점 간의 차이를 더욱 확대하기 위해,
우리는 추가적인 손실 항(additional loss)을 도입하여 연관성 불일치 를 더 크게 만든다.
사전 연관성(prior-association)은 단봉(unimodal) 특성을 가지므로,
불일치 손실(discrepancy loss) 은 시리즈 연관성이 인접 영역 이외의 부분에 더 많은 주의를 기울이도록 유도한다.
왜 불일치 손실이 시리즈 연관성을 비인접 영역으로 확장시키는가?
1) 사전 연관성은 가우시안(단봉) 분포
사전 연관성(Prior)은 가우시안 커널로 정의된다:
\[P_{i,j} \propto \exp\!\left(-\frac{|i-j|^2}{2\sigma_i^2}\right)\]중심 시점 $i$ 주변(인접 시점)에 값이 크고, 멀수록 급감 → 인접 집중 성향을 가짐.
2) 시리즈 연관성은 학습적으로 자유롭게 형성됨
- 시리즈 연관성 $S$ 는 데이터로부터 학습된 어텐션(attention) 분포로,
시점 $i$가 모든 시점 $j$와 맺는 실제 관계 강도를 나타낸다.3) 불일치 손실(discrepancy loss)은 $P$와 $S$의 차이를 키움
총손실은 다음과 같이 정의된다:
\[\mathcal{L}_{\text{Total}} = \|X - \hat{X}\|_F^2 - \lambda \, \|\text{AssDis}(P, S; X)\|_1\]두 번째 항의 $-\lambda$ 항은 $\text{AssDis}$ 값을 크게 만드는 방향으로 학습을 유도한다.
즉, $P$와 $S$가 서로 더 달라지도록 유도한다.4) 결과적으로 $S$는 비인접 영역으로 확장됨
- $P$는 이미 인접(local) 시점에 집중되어 있으므로,
$S$가 $P$와 달라지기 위해서는 멀리 떨어진 시점(비인접, global) 에
더 많은 가중치를 부여해야 한다.- 따라서 $S$는 전역적(global) 관계를 더 적극적으로 학습하게 되고,
정상(normal)과 이상(abnormal)의 구조적 차이를 더 뚜렷하게 만든다.5) 이상 탐지 관점에서의 효과
- 정상 시점: 전 구간에 걸쳐 안정적인 연관성을 형성할 수 있음 →
$S$가 전역으로 확장되어도 일관된 패턴 유지.- 이상 시점: 주변 외에는 연관성이 약함 →
$S$가 비인접 영역으로 확장될수록
$P$와 $S$의 불일치 $\text{AssDis}(P, S; X)$ 가 상대적으로 작게 나타남 →
이상이 명확히 구분됨.
이로 인해 이상 시점의 재구성이 더 어려워지고, 결과적으로 이상 시점을 더 명확하게 식별할 수 있게 된다.
입력 시계열 $X \in \mathbb{R}^{N \times d}$에 대한 손실 함수(loss function)는 다음과 같이 정의된다:
\[\mathcal{L}_{\text{Total}}(X, P, S, \lambda; \hat{X}) = \| X - \hat{X} \|_F^2 - \lambda \times \| \text{AssDis}(P, S; X) \|_1 \tag{4}\]여기서,
- $\hat{X} \in \mathbb{R}^{N \times d}$ : 입력 $X$의 재구성(reconstruction)
- $| \cdot |_F$ : 프로베니우스 놈(Frobenius norm)
- $| \cdot |_k$ : $k$-놈($k$-norm)
- $\lambda$ : 두 손실 항의 균형을 조절하는 하이퍼파라미터(trade-off parameter)
프로베니우스 놈(Frobenius Norm)과 $k$-놈($k$-Norm)의 의미
1) 프로베니우스 놈 (Frobenius Norm)
\[\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} |A_{ij}|^2} = \sqrt{\mathrm{trace}(A^\top A)}\]
- 행렬 $A \in \mathbb{R}^{m \times n}$ 의 모든 원소를 제곱한 뒤 더하고, 그 제곱근을 취한 값이다.
- 즉, 행렬의 “전체 크기(energy)” 또는 “유클리드 거리(Euclidean length)”를 측정한다.
- 직관적 의미:
행렬을 하나의 벡터로 펼쳤을 때, 그 벡터의 $L_2$-노름(L2 norm)과 동일하다.- Anomaly Transformer에서의 역할:
재구성 손실 $|X - \hat{X}|_F^2$ 은
원본 시계열 $X$와 복원된 시계열 $\hat{X}$ 간의 전체 오차 에너지를 측정한다.
이 값이 작을수록 모델이 원본 패턴을 잘 복원하고 있음을 의미한다.2) $k$-놈 ($k$-Norm)
\[\|x\|_k = \left( \sum_{i=1}^{n} |x_i|^k \right)^{1/k}\]
- 벡터 $x = [x_1, x_2, \dots, x_n]$ 의 $k$-놈은 다음과 같이 정의된다:
- $k$ 값에 따라 다른 성질을 가진다:
- $k = 1$ → L1 놈: 절댓값의 합 → 희소성(sparsity)을 유도.
- $k = 2$ → L2 놈: 제곱합의 제곱근 → 거리 기반 유사도에 적합.
- $k = \infty$ → 최대 놈(Max Norm): 벡터 내 절댓값의 최댓값.
- Anomaly Transformer에서의 사용:
$|\text{AssDis}(P, S; X)|_1$ 은
각 시점의 연관성 불일치를 절댓값 기준으로 합산하여,
전체적으로 얼마나 큰 차이가 존재하는지를 평가한다.
즉, 이상 정도의 전역 척도(global measure) 로 사용된다.
$\lambda > 0$ 일 때, 최적화 과정은 연관성 불일치를 확대하도록 유도된다.
또한, 연관성 불일치가 더욱 구별 가능하도록 하기기 위해 미니맥스 전략이 제안된다.
미니맥스 전략 (Minimax Strategy)
연관성 불일치를 직접적으로 최대화하면,
가우시안 커널의 스케일 파라미터가 극단적으로 감소하여(Neal, 2007), 사전 연관성을 무의미하게 만든다.
연관성 학습(association learning)을 더 잘 제어하기 위해, 우리는 미니맥스 전략을 제안한다 (그림 2).
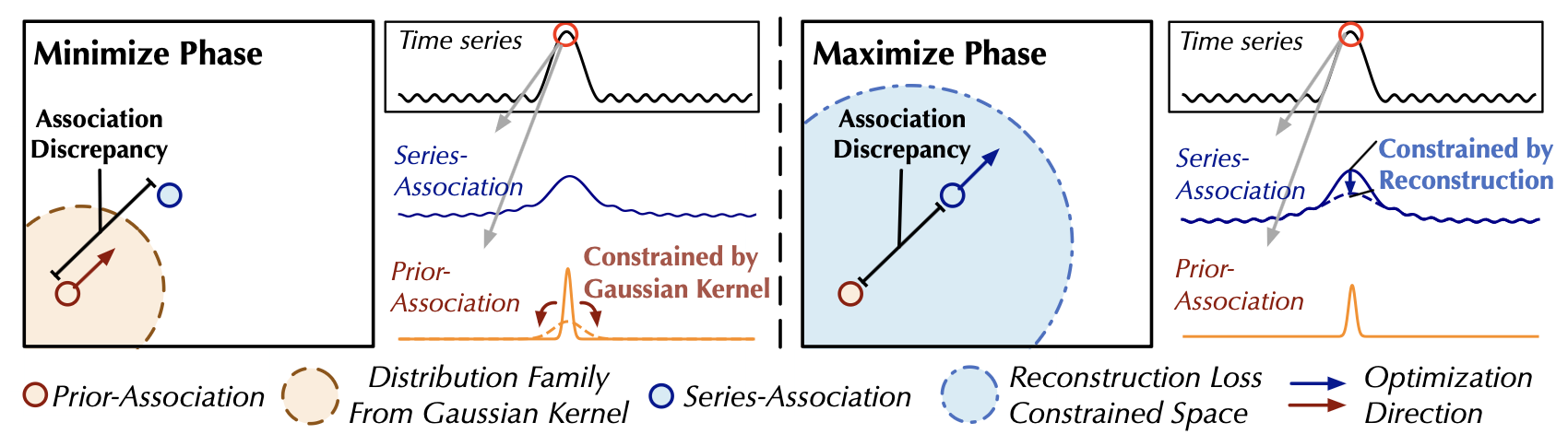
그림 2. 미니맥스 연관성 학습 (Minimax Association Learning)
최소화 단계(minimize phase)에서는,
사전 연관성이 가우시안 커널에 의해 유도된 분포 계열(distribution family) 내에서 연관성 불일치를 최소화한다.
최대화 단계(maximize phase)에서는,
시리즈 연관성이 재구성 손실(reconstruction loss) 하에서 연관성 불일치를 최대화한다.
구체적으로 최소화 단계에서는, 사전 연관성 $P^{(l)}$이,
원시 시계열로부터 학습된 시리즈 연관성 $S^{(l)}$를 근사하도록 유도된다.
이 과정은 사전 연관성이 다양한 시간적 패턴(temporal patterns)에 적응할 수 있도록 만든다.
최대화 단계에서는 연관성 불일치를 확대하도록, 시리즈 연관성을 최적화한다.
이 과정은 시리즈 연관성이 비인접 영역(non-adjacent horizon)에 더 많은 주의를 기울이도록 만든다.
따라서 재구성 손실(reconstruction loss)을 통합하면, 두 단계의 손실 함수는 다음과 같다:
최소화 단계 (Minimize Phase):
\[\mathcal{L}_{\text{Total}}(X, P, S_{\text{detach}}, -\lambda; X) \tag{5}\]최대화 단계 (Maximize Phase):
\[\mathcal{L}_{\text{Total}}(X, P_{\text{detach}}, S, \lambda; X)\]여기서 $\lambda > 0$이고, *detach는 연관성에 대한 그래디언트 역전파(gradient backpropagation)를 중지함을 의미한다 (그림 1).
미니맥스 손실의 의미
위의 두 식은 미니맥스 학습 전략(minimax learning strategy) 을 수식으로 표현한 것이다.
최소화 단계(Minimize Phase) 에서는
사전 연관성 $P$ 이 시리즈 연관성 $S$ 를 따라가도록(approximate) 학습된다.
이때 $S_{\text{detach}}$ 는 그래디언트 전파가 차단되어(backpropagation detached)
$S$ 는 고정된 기준(reference) 역할만 수행한다.
즉, $P$ → $S$ 로 수렴하도록 만드는 단계이다.최대화 단계(Maximize Phase) 에서는
반대로 시리즈 연관성 $S$ 가 고정된 $P_{\text{detach}}$ 를 기준으로
연관성 불일치(Association Discrepancy) 를 확대(enlarge)하도록 학습된다.
이 과정은 $S$ 가 비인접 영역(non-adjacent area) 에
더 많은 주의를 기울이게 만들어,
이상(anomalies)과 정상(normals)을 더 명확히 구분할 수 있도록 돕는다.
$P$가 최소화 단계에서 $S_{\text{detach}}$를 근사하므로,
최대화 단계에서는 시리즈 연관성에 더 강한 제약(stronger constraint)을 적용하게 된다.
이는 시점(time points)들이 비인접 영역(non-adjacent area)에 더 많은 주의를 기울이도록 강제한다.
재구성 손실 하에서, 이러한 과정은 정상(normal) 시점에 비해 이상(anomalies) 시점이 달성하기 훨씬 더 어렵다.
따라서 연관성 불일치의 정상-이상 구별 가능성(normal-abnormal distinguishability)을 증폭시킨다.
연관성 기반 이상 판단 기준 (Association-based Anomaly Criterion)
우리는 정규화된 연관성 불일치를 재구성 기준(reconstruction criterion)과 결합하여,
시간적 표현(temporal representation)과 구별 가능한 연관성 불일치(distinguishable association discrepancy)
양쪽의 이점을 모두 활용하도록 한다.
입력 시계열 $X \in \mathbb{R}^{N \times d}$의 최종 이상 점수(anomaly score)는 다음과 같이 정의된다:
\[\text{AnomalyScore}(X) = \text{Softmax} \big(-\text{AssDis}(P, S; X)\big) \odot \| X_{i,:} - \hat{X}_{i,:} \|_2^2, \quad i = 1, \dots, N \tag{6}\]여기서,
- $\odot$ : 원소별 곱(element-wise multiplication)
- $\text{AnomalyScore}(X) \in \mathbb{R}^{N \times 1}$: 시계열 $X$의 각 시점별 이상 기준(point-wise anomaly criterion)
더 나은 재구성을 위해, 이상 시점은 일반적으로 연관성 불일치를 감소시키는 경향이 있다.
이러한 경우에도, 이 식은 여전히 높은 이상 점수(higher anomaly score)를 유도한다.
이상 점수(Anomaly Score)의 구성 원리
위 식은 재구성 오차(reconstruction error) 와
연관성 불일치(association discrepancy) 를 결합하여
각 시점별로 이상 여부를 정량화하는 기준을 정의한다.
먼저, $\text{AssDis}(P, S; X)$ 는 각 시점의
사전 연관성(prior-association) 과 시리즈 연관성(series-association) 간의
불일치를 측정한다.
이 값이 작을수록(즉, $-\text{AssDis}$ 가 클수록)
해당 시점이 이상일 가능성이 높다는 것을 의미한다.
이를 Softmax 로 정규화하여
“연관성 기반 가중치(association-based weight)” 로 변환한다.다음으로, $| X_{i,:} - \hat{X}_{i,:} |_2^2$ 는
원본 시계열과 재구성된 시계열 간의
2-노름 제곱(Euclidean squared distance), 즉 재구성 오차를 나타낸다.
이 값이 클수록 해당 시점이 재구성하기 어려운(즉, 비정상적인) 시점이다.두 요소를 원소별 곱($\odot$)으로 결합함으로써,
모델은 “재구성이 어렵고, 동시에 연관성 패턴이 비정상적인 시점”을
더 높은 이상 점수로 평가하게 된다.따라서, $\text{AnomalyScore}(X)$ 는
단순한 오차 기반 기준보다 더 정교하고 해석 가능한(an interpretable)
이상 탐지 지표로 작동한다.
따라서, 이 설계는 재구성 오차와 연관성 불일치가 서로 협력하여 이상 탐지 성능을 향상시키도록 만든다.
4 실험 (Experiments)
우리는 세 가지 실제 응용 분야에 대해 여섯 개의 벤치마크 데이터셋을 사용하여
Anomaly Transformer 를 광범위하게 평가하였다.
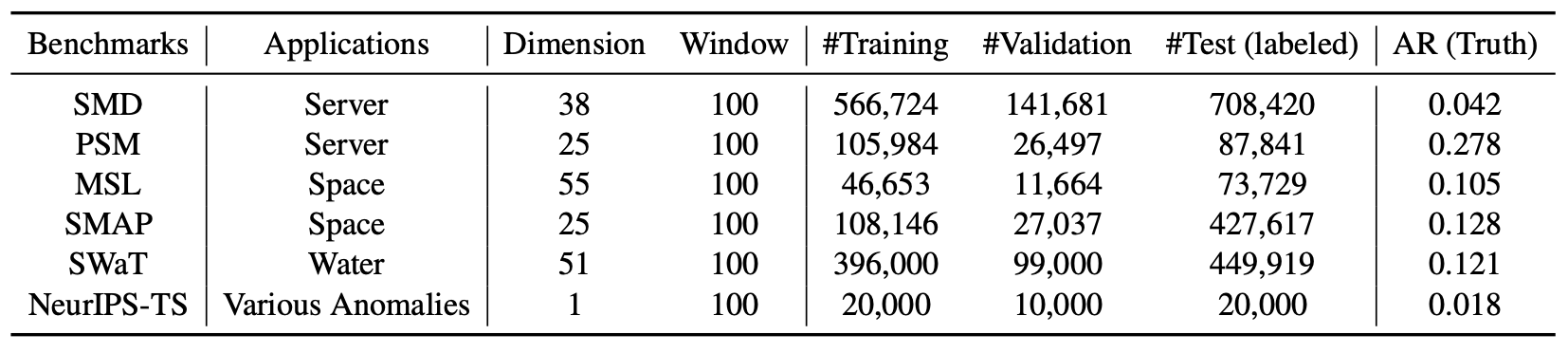
데이터셋
여섯 개의 실험용 데이터셋은 다음과 같다.
(1) SMD (Server Machine Dataset, Su et al., 2019)
대형 인터넷 회사로부터 수집된 5주간의 데이터셋으로, 38차원을 가진다.
(2) PSM (Pooled Server Metrics, Abdulaal et al., 2021)
eBay의 여러 애플리케이션 서버 노드로부터 내부적으로 수집된 데이터셋이며, 26차원을 가진다.
(3) MSL(Mars Science Laboratory rover) 및 SMAP(Soil Moisture Active Passive satellite)는
NASA (Hundman et al., 2018)에서 공개한 공공 데이터셋이다.
각각 55차원과 25차원을 가지며,
우주선 모니터링 시스템의 ISA (Incident Surprise Anomaly) 보고서에서
파생된 텔레메트리 이상 데이터(telemetry anomaly data) 를 포함한다.
(4) SWaT (Secure Water Treatment, Mathur & Tippenhauer, 2016)
지속적으로 운영 중인 중요 인프라 시스템의 51개 센서로부터 얻어진 데이터셋이다.
(5) NeurIPS-TS (NeurIPS 2021 Time Series Benchmark)
Lai et al. (2021) 에 의해 제안된 데이터셋으로,
다섯 가지 시계열 이상 시나리오(time series anomaly scenarios)를 포함한다.
이 시나리오들은 행동 기반 분류체계(behavior-driven taxonomy)에 따라 다음과 같이 구분된다:
- point-global
- pattern-contextual
- pattern-shapelet
- pattern-seasonal
- pattern-trend
통계적 세부 사항은 부록(Appendix) 의 표 13(Table 13) 에 요약되어 있다.
구현 세부 사항 (Implementation Details)
Shen et al. (2020)에서 잘 확립된 프로토콜을 따라,
우리는 겹치지 않는 슬라이딩 윈도우(non-overlapped sliding window)를 사용하여 하위 시계열(sub-series) 집합을 얻는다.
모든 데이터셋에 대해 슬라이딩 윈도우의 크기는 100으로 고정되어 있다.
각 시점(time point)은, 이상 점수(anomaly score, 식 (6) 참고)가
특정 임계값(threshold) $\delta$ 보다 클 경우 이상(anomaly) 으로 라벨링된다.
임계값 $\delta$ 는 검증 데이터셋의 전체 시점(time points) 중 비율 $r$ 만큼이 이상 시점(anomaly)으로 표시되도록 설정된다.
주요 결과(main results)에서는 다음과 같이 설정하였다:
- SWaT: $r = 0.1\%$
- SMD: $r = 0.5\%$
- 나머지 데이터셋: $r = 1\%$
우리는 널리 사용되는 조정 전략(adjustment strategy) (Xu et al., 2018; Su et al., 2019; Shen et al., 2020)을 채택하였다.
즉, 특정 연속된 이상 구간(successive abnormal segment) 내에서 어떤 시점이 탐지되면,
그 구간 내의 모든 이상 시점들이 올바르게 탐지된 것으로 간주한다.
이 전략은, 실제 환경에서 이상 시점 하나가 경보를 발생시키면, 결국 전체 구간(segment)이 주목되게 된다는 점에 근거한다.
Anomaly Transformer 는 3개의 계층(layers) 으로 구성되어 있다.
은닉 상태(hidden states)의 채널 수 $d_{\text{model}}$ 은 512로 설정되었으며, 헤드(head) 의 수는 8이다.
하이퍼파라미터 $\lambda$ (식 (4) 참고)는 손실 함수의 두 부분 간의 균형을 맞추기 위해 모든 데이터셋에서 3으로 설정되었다.
ADAM 옵티마이저 (Kingma & Ba, 2015)를 사용하였으며, 초기 학습률(initial learning rate)은 $10^{-4}$ 로 설정하였다.
훈련 과정은, 배치 크기(batch size) 32로 설정하였고, 10 epoch 이내에서 조기 종료(early stopping)되었다.
모든 실험은 단일 NVIDIA TITAN RTX 24GB GPU 환경에서 PyTorch (Paszke et al., 2019)를 사용하여 구현되었다.
베이스라인 모델 (Baselines)
우리는 18개의 베이스라인 모델(baseline models) 과 우리 모델을 폭넓게 비교하였다.
이들은 다음과 같은 여러 범주로 구성된다:
재구성 기반 모델 (Reconstruction-based models):
InterFusion (2021), BeatGAN (2019), OmniAnomaly (2019), LSTM-VAE (2018)밀도 추정 기반 모델 (Density-estimation models):
DAGMM (2018), MPPCACD (2017), LOF (2000)클러스터링 기반 모델 (Clustering-based models):
ITAD (2020), THOC (2020), Deep-SVDD (2018)자기회귀 기반 모델 (Autoregression-based models):
CL-MPPCA (2019), LSTM (2018), VAR (1976)고전적 모델 (Classic models):
OC-SVM (2004), IsolationForest (2008)
또한, 변화점 탐지(change point detection) 및 시계열 분할(time series segmentation) 에 기반한
3개의 추가 베이스라인 모델은 부록(Appendix I) 에서 다루었다.
이 중 InterFusion (2021)과 THOC (2020)은 최첨단(state-of-the-art) 딥러닝 모델이다.
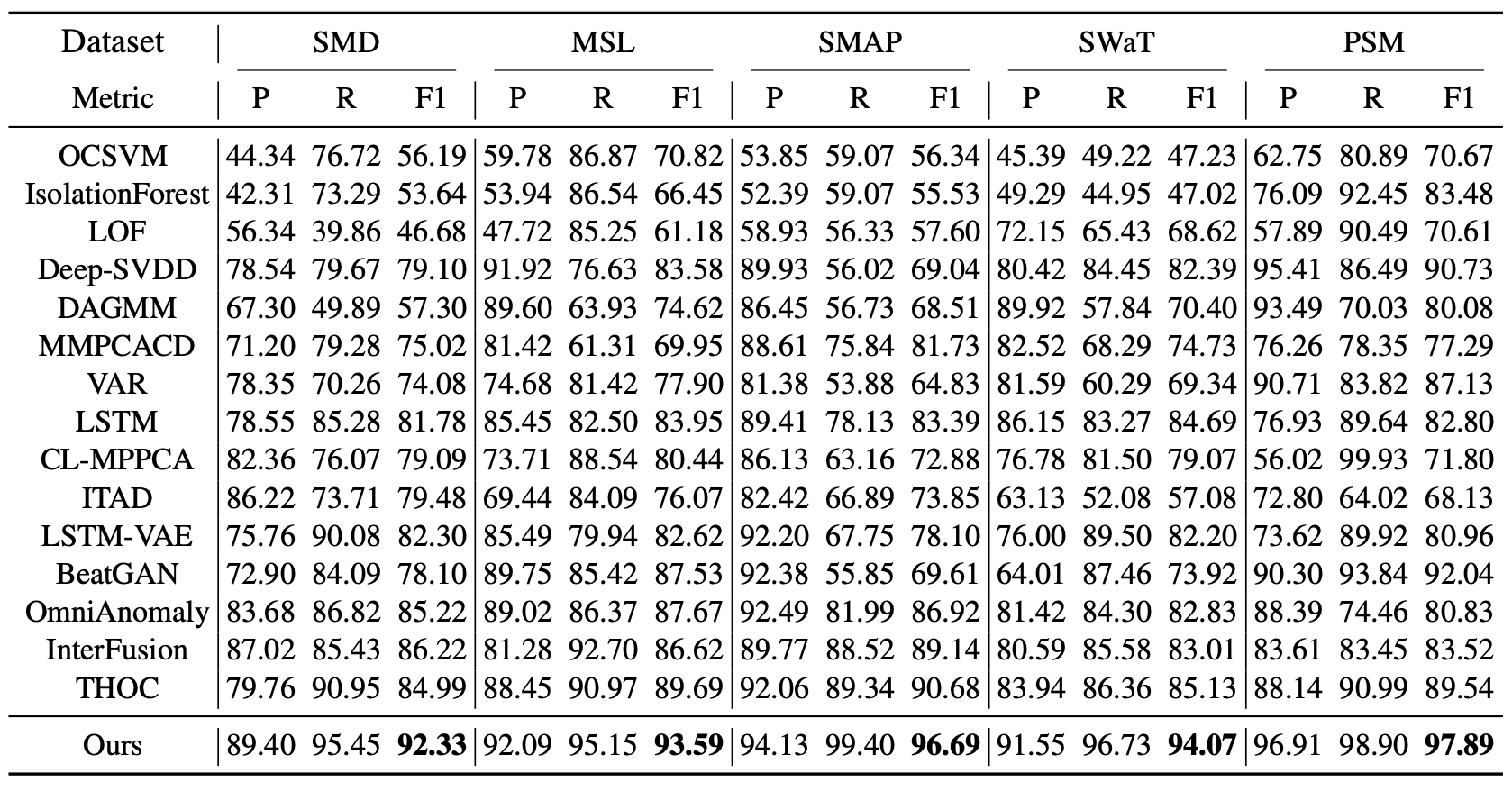
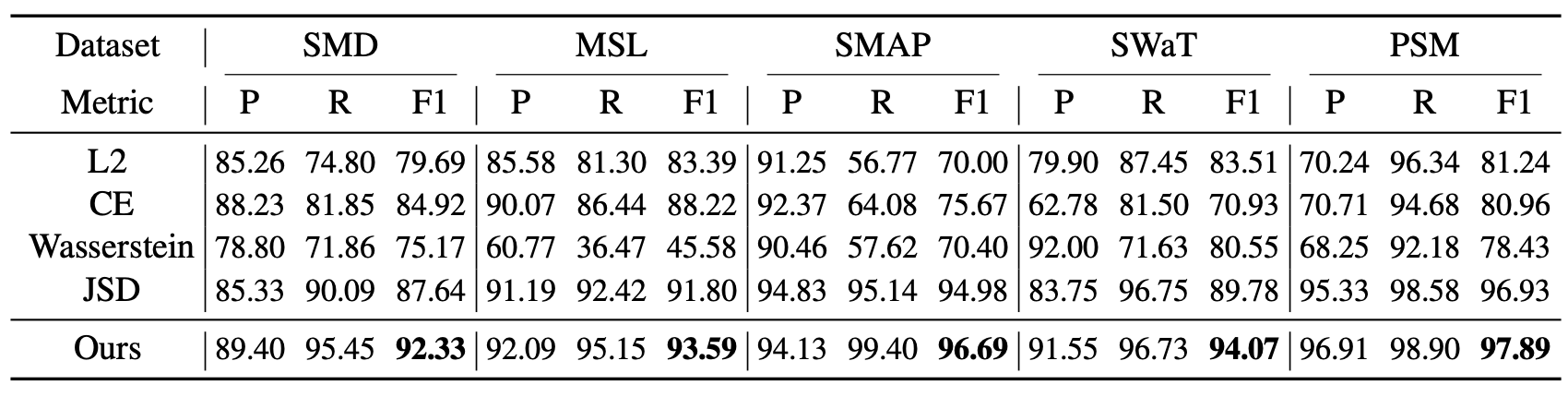
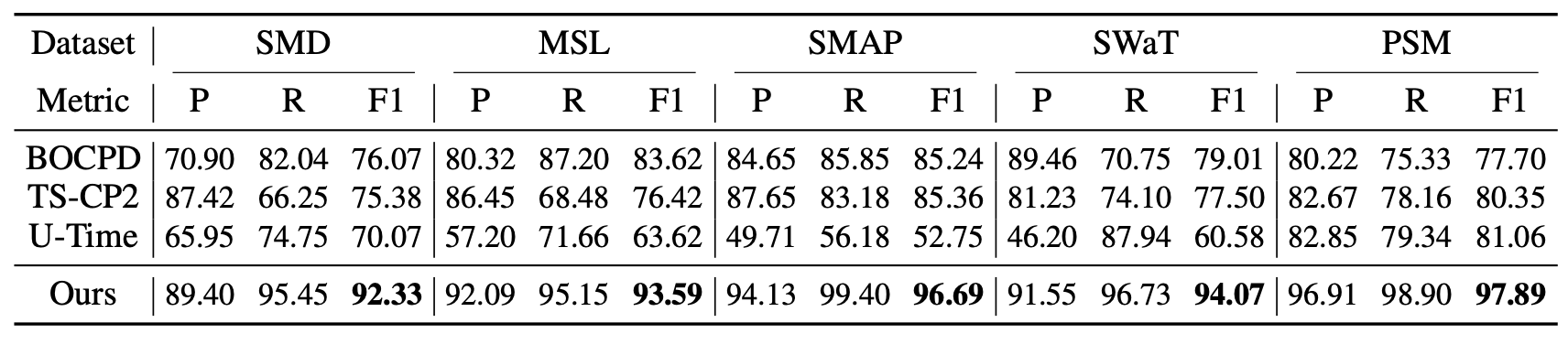
표 1. 다섯 개 데이터셋에서의 Anomaly Transformer (본 연구, Ours) 의 정량적 결과.
여기서 P, R, F1 은 각각
정밀도(Precision), 재현율(Recall), 그리고 F1-점수(F1-score) (단위: %)를 나타낸다.
F1-점수는 정밀도와 재현율의 조화 평균(harmonic mean) 으로 계산된다.
이 세 가지 지표 모두에서, 값이 높을수록 더 나은 성능을 의미한다.
4.1 주요 결과 (Main Results)
실세계 데이터셋 (Real-world datasets)
우리는 10개의 경쟁 베이스라인 모델들과 함께, 5개의 실세계 데이터셋에서 우리 모델을 폭넓게 평가하였다.
표 1(Table 1)에 나타난 바와 같이,
Anomaly Transformer는 모든 벤치마크에서 일관된 최첨단(state-of-the-art) 성능을 달성하였다.
우리는 시간적 정보(temporal information) 를 고려하는 딥러닝 모델들이
Deep-SVDD (Ruff et al., 2018) 나 DAGMM (Zong et al., 2018) 과 같은
일반적인 이상 탐지 모델들보다 더 우수한 성능을 보인다는 것을 관찰하였다.
이는 시간적 모델링(temporal modeling) 의 유효성을 입증한다.
제안된 Anomaly Transformer는, RNN으로부터 학습된 포인트 단위 표현(point-wise representation)을 넘어,
더 풍부하고 유의미한 연관성(associations)을 모델링한다.
표 1의 결과는, 시계열 이상 탐지에서 연관성 학습(association learning)의 이점을 뒷받침하는 설득력 있는 증거를 제공한다.
또한, 그림 3에 ROC 곡선(Receiver Operating Characteristic curve)을 통한 보다 완전한 비교를 수행하였다.
Anomaly Transformer 는 모든 다섯 개 데이터셋에서 가장 높은 AUC (Area Under Curve) 값을 기록하였다.
그림 3. 다섯 개 데이터셋에 대한 ROC 곡선(Receiver Operating Characteristic curves)
가로축(horizontal-axis)은 거짓 양성률(false-positive rate),
세로축(vertical-axis)은 진짜 양성률(true-positive rate) 을 나타낸다.
AUC 값(AUC, area under the ROC curve)이 높을수록 더 나은 성능을 의미한다.
사전 정의된 임계값 비율(predefined threshold proportion) $r$은
${0.5\%, 1.0\%, 1.5\%, 2.0\%, 10\%, 20\%, 30\%}$ 로 설정되었다.
이는 다양한 사전 설정 임계값 하에서,
우리 모델이 거짓 양성률(false positive rate) 과 진짜 양성률(true positive rate) 에 대해 우수한 성능을 보임을 의미하며,
이는 실제 응용 사례(real-world applications)에서 매우 중요한 특성이다.
NeurIPS-TS 벤치마크
이 벤치마크는 Lai et al. (2021) 에 의해 제안된 정교하게 설계된 규칙(well-designed rules)에 따라 생성되었으며,
모든 유형의 이상 시점을 포함하고, 포인트 단위(point-wise) 및 패턴 단위(pattern-wise) 이상 시점을 모두 포괄한다.
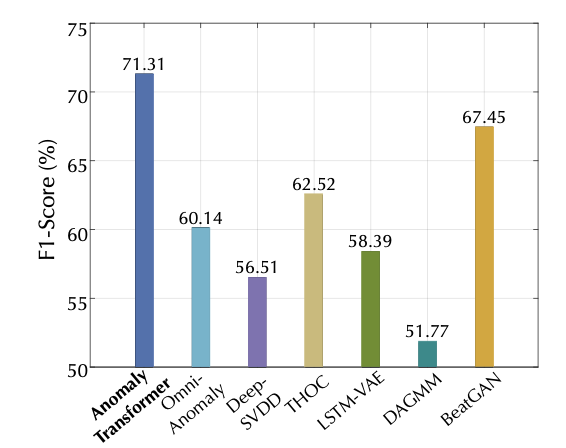
그림 4에 나타난 바와 같이, Anomaly Transformer는 이 벤치마크에서도 여전히 최첨단(state-of-the-art) 성능을 달성하였다.
이는 다양한 형태의 이상(anomalies)에 대해 우리 모델의 효과성(effectiveness)을 검증한다.
그림 4. NeurIPS-TS 데이터셋에 대한 결과
제거 실험 (Ablation Study)
제거 실험 (Ablation Study)이란?
제거 실험(Ablation Study) 은 모델을 구성하는 여러 요소 중
특정 구성 요소(component) 를 제거하거나 변경했을 때
성능이 어떻게 변하는지를 분석하는 실험이다.예를 들어, 모델에서 특정 모듈이나 손실 항을 제거한 버전을
원본 모델과 비교함으로써,
해당 요소가 전체 성능에 기여하는 정도를 정량적으로 평가할 수 있다.이 방식은 마치 “조직 절제(ablation)”처럼
하나의 부분을 제거하고 그 영향을 관찰한다는 점에서 이름이 유래되었다.제거 실험은 다음과 같은 목적을 가진다:
- 모델의 각 구성 요소의 중요성을 검증한다.
- 불필요하거나 중복된 부분을 식별하여 모델을 단순화할 수 있다.
- 제안된 새로운 기법의 실제 효과를 명확히 입증할 수 있다.
따라서, 논문에서 제거 실험은
“이 설계가 정말 필요한가?”
“이 모듈이 성능을 실제로 향상시키는가?”
와 같은 질문에 대한 객관적 근거를 제공하는 핵심 분석 과정이다.
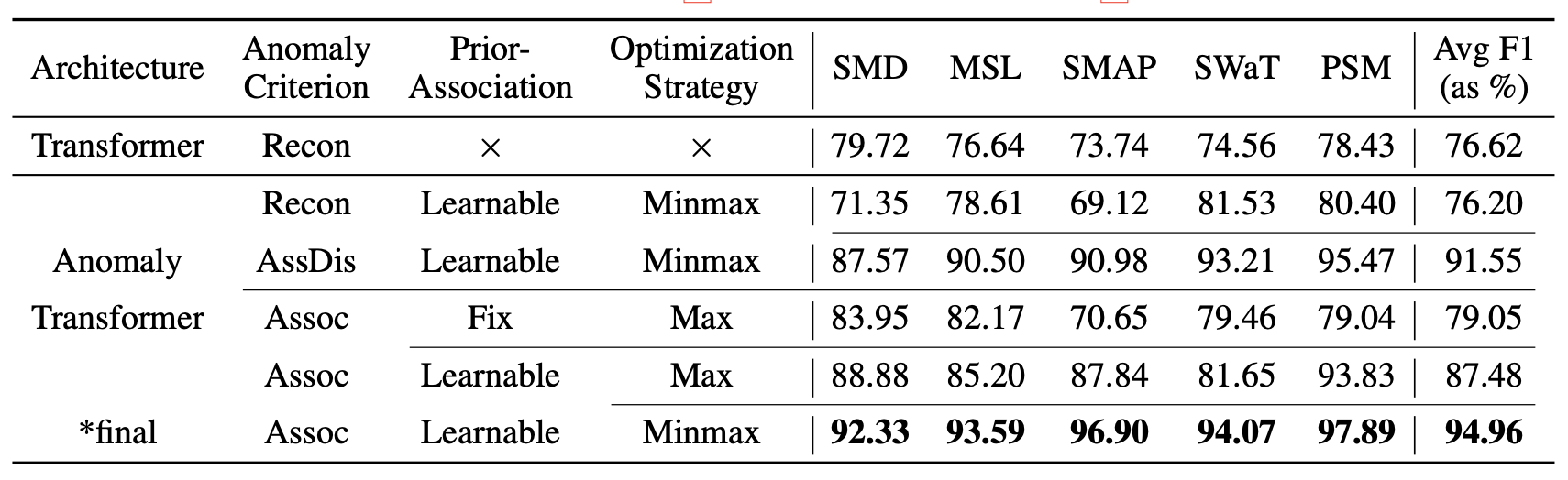
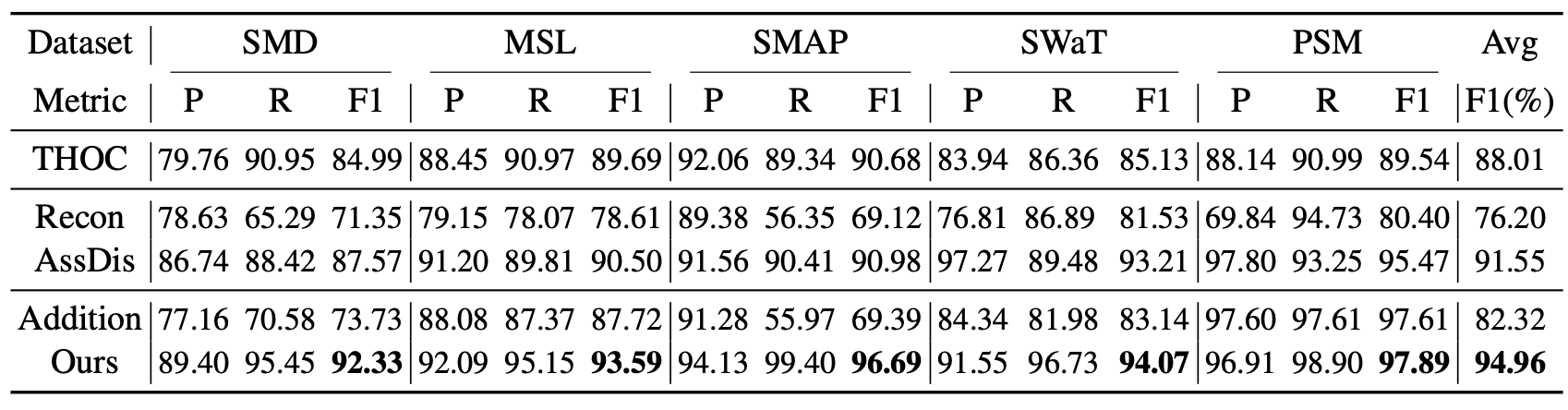
표 2(Table 2)에 나타난 바와 같이, 우리는 모델의 각 구성 요소가 미치는 영향을 추가로 조사하였다.
표 2. 이상 기준(anomaly criterion), 사전 연관성(prior-association),
그리고 최적화 전략(optimization strategy)에 대한 제거 실험 결과(F1-score).
Recon, AssDis, Assoc 은 각각
순수한 재구성 성능(pure reconstruction performance),
순수한 연관성 불일치(pure association discrepancy),
그리고 제안된 연관성 기반 기준(association-based criterion) 을 의미한다.
Fix 는 사전 연관성(prior-association)의
학습 가능한 스케일 파라미터(learnable scale parameter) $\sigma$ 를
1.0으로 고정(fix)한 설정을 의미한다.
Max 와 Minimax 는 각각
연관성 불일치(association discrepancy)에 대해
최대화 방식(maximization, 식 (4)) 과
미니맥스 방식(minimax, 식 (5)) 을 적용한 전략을 의미한다.
우리의 연관성 기반 기준(association-based criterion)은
널리 사용되는 재구성 기준(reconstruction criterion)을 일관되게 능가하였다.
구체적으로, 연관성 기반 기준은 평균 F1-점수(F1-score)에서 18.76%의 절대 향상(76.20 → 94.96) 을 가져왔다.
또한, 연관성 불일치(association discrepancy)를 기준으로 직접 사용하는 경우에도
여전히 우수한 성능(F1-score: 91.55%)을 달성하였으며,
이전의 최첨단(state-of-the-art) 모델인 THOC (F1-score: 88.01%, 표 1에서 계산)을 능가하였다.
그뿐만 아니라, 학습 가능한 사전 연관성(learnable prior-association)(식 (2)의 $\sigma$에 해당)과
미니맥스 전략(minimax strategy)은 모델의 성능을 각각
8.43% (79.05 → 87.48), 7.48% (87.48 → 94.96)만큼 추가로 향상시켰다.
마지막으로, 제안된 Anomaly Transformer는 순수한 Transformer에 비해
18.34%의 절대적 개선(76.62 → 94.96)을 달성하였다.
이 결과들은, 우리의 설계에 포함된 각 모듈이 효과적이며 필수적임을 검증한다.
연관성 불일치에 대한 추가적인 제거 실험 결과는 부록 D(Appendix D)에 제시되어 있다.
4.2 모델 분석 (Model Analysis)
우리 모델이 어떻게 작동하는지를 직관적으로 설명하기 위해(intuitively explain),
세 가지 핵심 설계(key designs)에 대한 시각화(visualization) 및 통계적 결과(statistical results) 를 제공한다.
이 세 가지 핵심 설계는 다음과 같다:
- 이상 기준 (Anomaly Criterion)
- 학습 가능한 사전 연관성 (Learnable Prior-Association)
- 최적화 전략 (Optimization Strategy)
이상 기준 시각화 (Anomaly Criterion Visualization)
연관성 기반 기준(association-based criterion)이 어떻게 작동하는지 보다 직관적으로 이해하기 위해,
그림 5(Figure 5)에 일부 시각화 결과를 제시하고,
서로 다른 유형의 이상(anomalies)에 대한 기준의 성능을 탐구하였다.
이상의 분류 체계(taxonomy)는 Lai et al. (2021) 로부터 인용되었다.
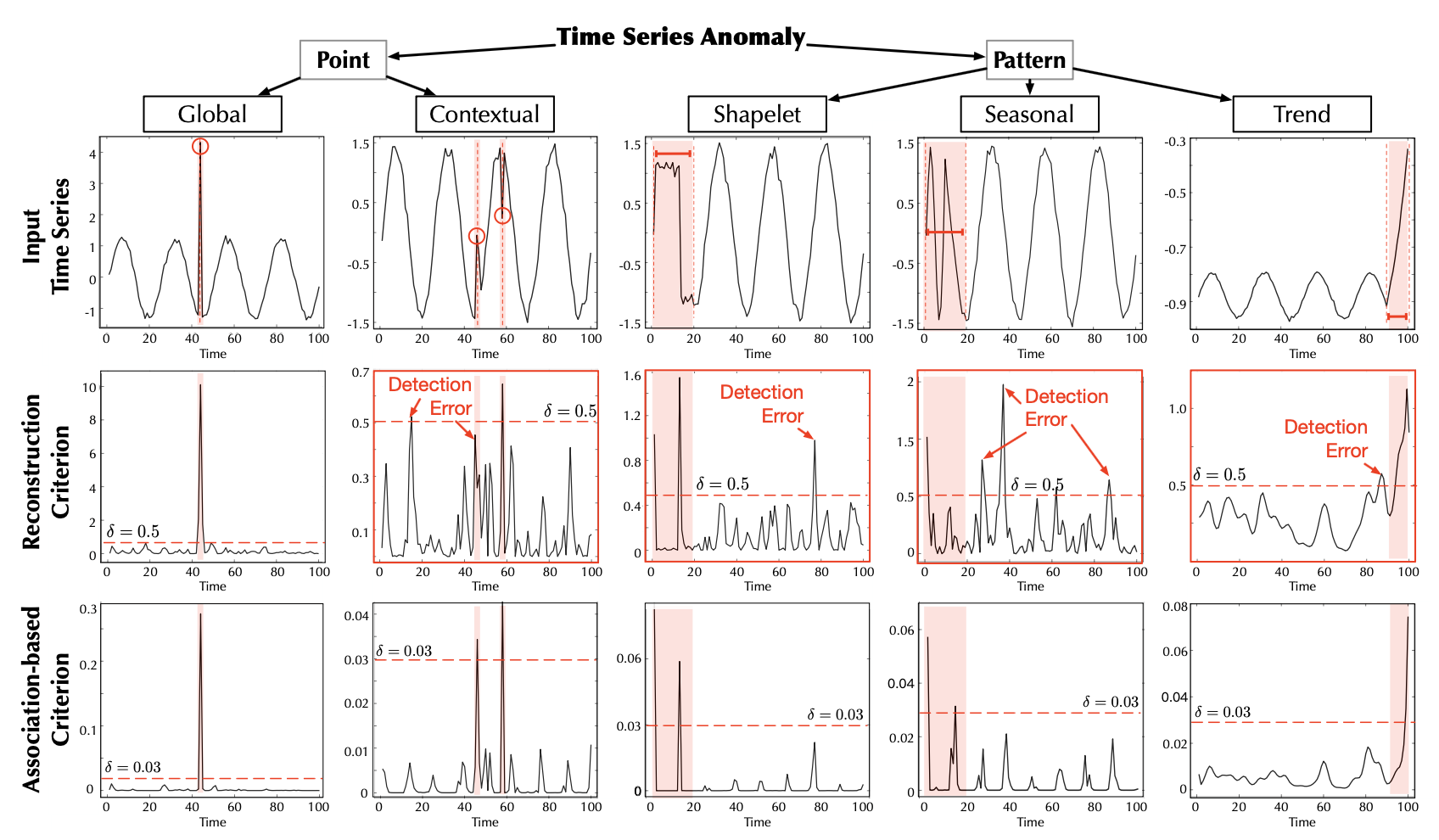
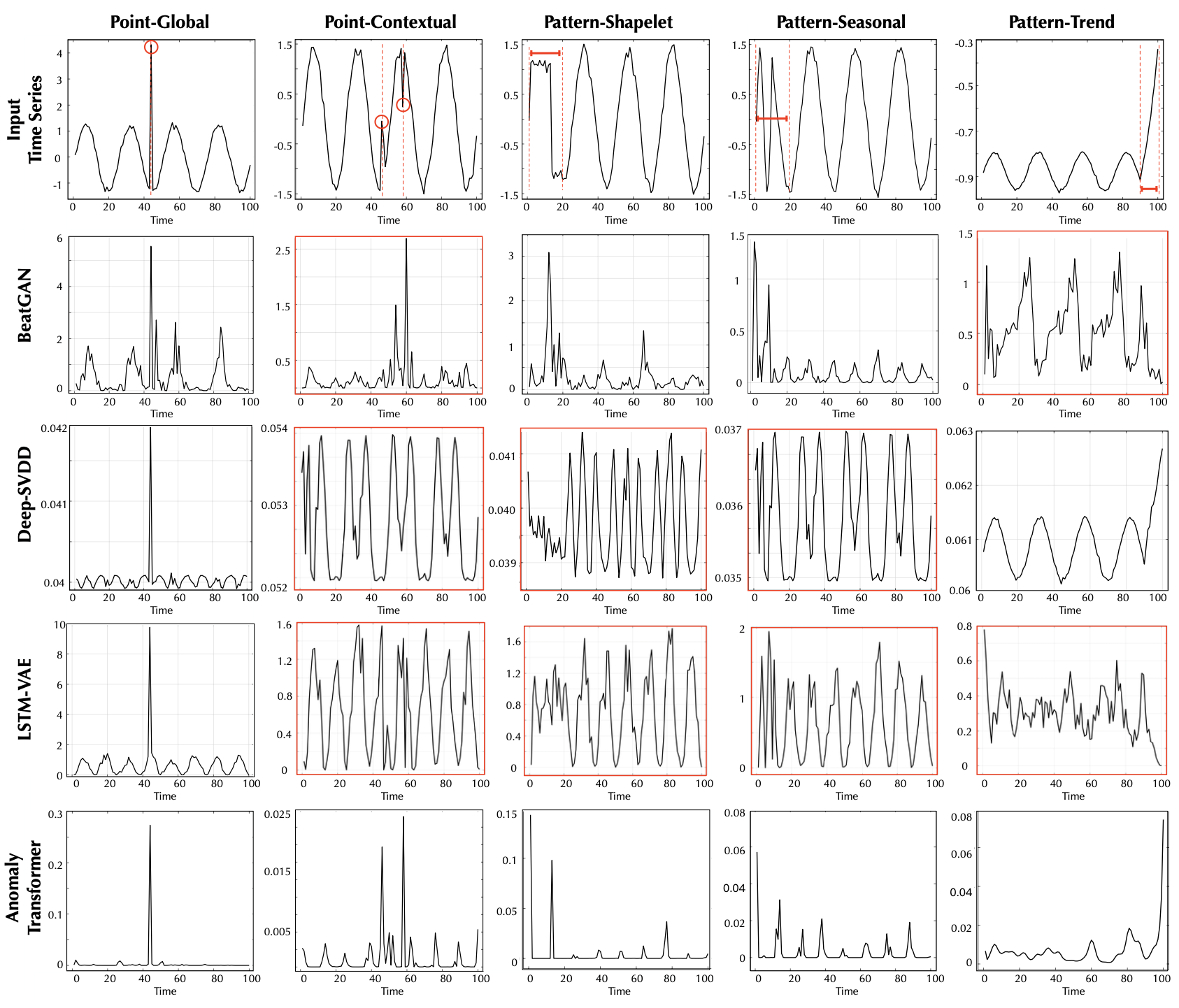
그림 5. 서로 다른 이상 범주(anomaly categories)의 시각화 (Lai et al., 2021)
우리는 NeurIPS-TS 데이터셋으로부터의
원시 시계열(raw series)을 첫 번째 행(first row)에,
그에 대응하는 재구성 결과(reconstruction)를 두 번째 행(second row)에,
그리고 연관성 기반 기준(association-based criteria)을 세 번째 행(third row)에 표시하였다.
포인트 단위 이상(point-wise anomalies)은 빨간색 원(red circles) 으로,
패턴 단위 이상(pattern-wise anomalies)은 빨간색 구간(red segments) 으로 표시하였다.
잘못 탐지된 사례는 빨간색 상자(red boxes) 로 표시하였다.
우리는 제안된 연관성 기반 기준이 전반적으로 더 구별 가능(distinguishable) 하다는 것을 확인하였다.
구체적으로, 연관성 기반 기준은 정상 구간(normal part)에 대해 일관되게 작은 값을 얻을 수 있으며,
이는 point-contextual 및 pattern-seasonal 사례들에서 뚜렷한 대비를 보인다 (그림 5 참고).
반면, 재구성 기준(reconstruction criterion) 의 불안정한 곡선(jitter curves)은
탐지 과정을 혼란스럽게 만들며, 앞서 언급된 두 가지 경우에서 탐지에 실패한다.
이러한 결과는 우리의 기준이 이상(anomalies)을 명확히 강조하고,
정상(normal)과 비정상(abnormal) 시점 간에 뚜렷한 값의 차이를 제공함으로써,
탐지를 더욱 정밀하게 하고 거짓 양성률(false-positive rate)을 줄임을 검증한다.
사전 연관성 시각화 (Prior-Association Visualization)
미니맥스 최적화(minimax optimization) 과정 동안, 사전 연관성은 시리즈 연관성에 근접하도록 학습된다.
따라서, 학습된 $\sigma$ 값은 시계열(time series)의 인접 집중(adjacent-concentrating) 정도를 반영할 수 있다.
그림 6에서 볼 수 있듯이, $\sigma$ 값은 시계열의 다양한 데이터 패턴(data patterns)에 적응(adapt)하도록 변화한다.
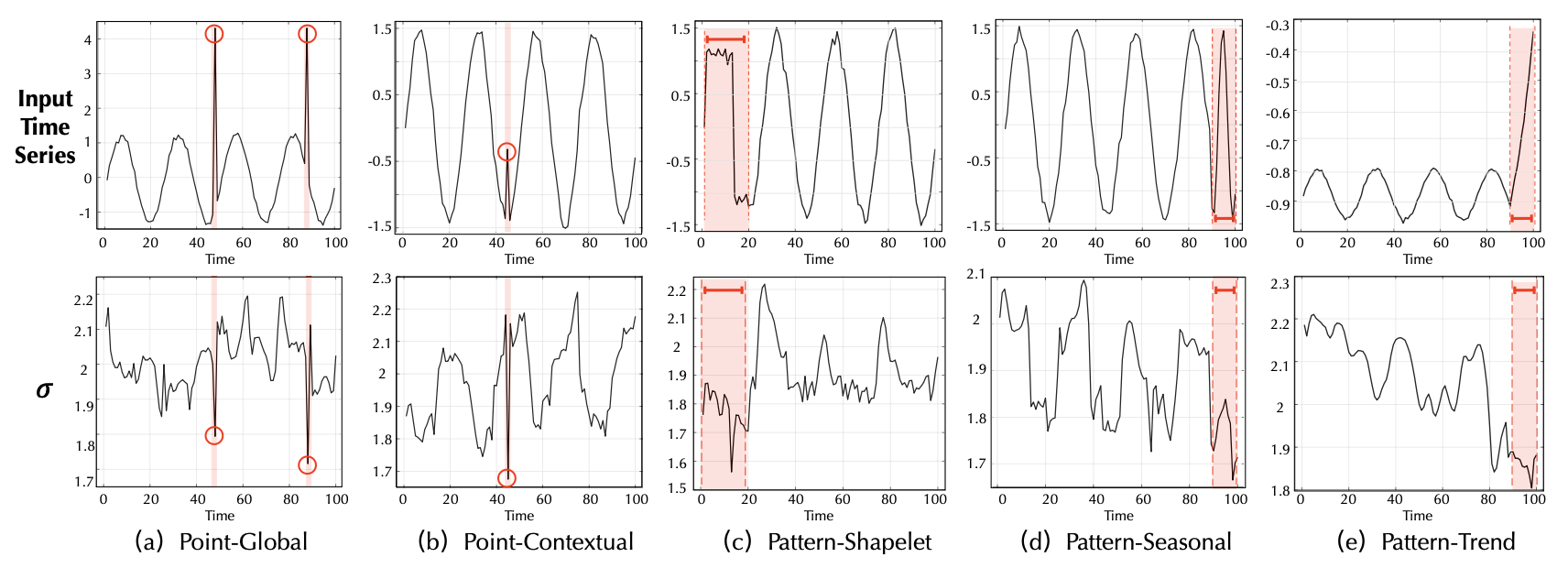
그림 6. 서로 다른 유형의 이상 유형에 대해 학습된 스케일 파라미터(scale parameter) $\sigma$ 의 시각화
이상 구간은 빨간색(red) 으로 강조 표시되어 있다
특히, 이상 시점의 사전 연관성은 일반적으로 정상 시점에 비해 더 작은 $\sigma$ 값을 가지며,
이는 이상(anomalies)에 대한 인접 집중 유도 편향(adjacent-concentration inductive bias)과 일치한다.
최적화 전략 분석 (Optimization Strategy Analysis)
재구성 손실(reconstruction loss)만을 사용한 경우,
이상 시점과 정상 시점은 인접 시점에 대한 연관 가중치(association weights)에서 유사한 거동(behavior)을 보이며,
대비값(contrast value)이 1에 가까운 결과로 나타난다 (표 3(Table 3)).
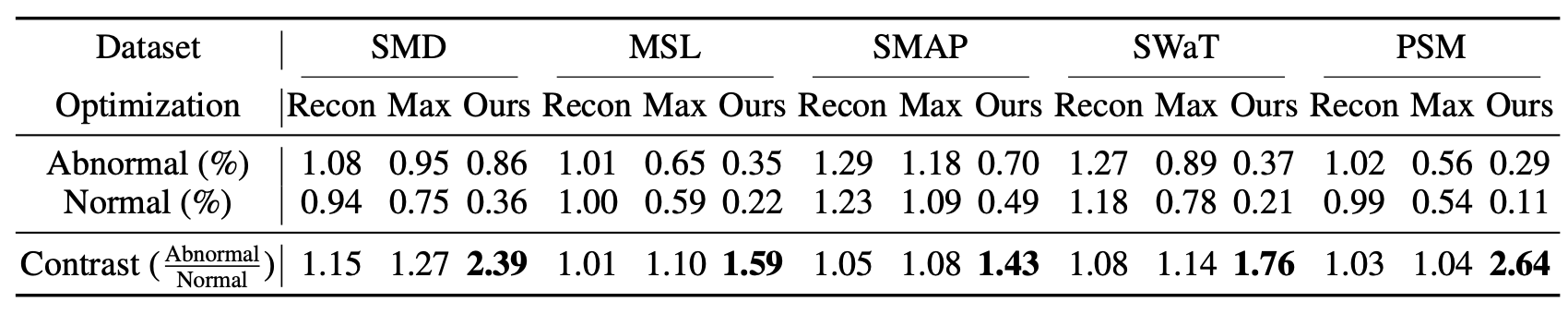
표 3. 이상 시점과 정상 시점에 대한 인접 연관 가중치(adjacent association weights) 의 결과.
Recon, Max, Minimax 는 각각
재구성 손실(reconstruction loss),
직접 최대화(direct maximization),
미니맥스 전략(minimax strategy) 에 의해
감독되는 연관 학습 과정(association learning process)을 의미한다.
더 높은 대비값(contrast value) — 즉 $\dfrac{\text{Abnormal}}{\text{Normal}}$ — 은
정상 시점과 이상 시점 간의 더 강한 구별 가능성(distinguishability) 을 의미한다.
연관성 불일치를 최대화하면,
시리즈 연관성이 비인접 영역(non-adjacent area)에 더 많은 주의를 기울이도록 강제한다.
그러나 더 나은 재구성(reconstruction)을 얻기 위해,
이상 시점들은 정상 시점보다 훨씬 큰 인접 연관 가중치(adjacent association weights)를 유지해야 하며,
이는 더 큰 대비값(contrast value)에 해당한다.
하지만 연관성 불일치를 직접 최대화(direct maximization)하는 방식은
가우시안 커널(Gaussian kernel)의 최적화에 어려움을 초래하며,
정상과 이상 시점 간의 차이를 기대만큼 강하게 증폭시키지 못한다 (SMD: 1.15 → 1.27).
반면, 미니맥스 전략(minimax strategy)은 사전 연관성을 함께 최적화하여,
시리즈 연관성에 더 강력한 제약(stronger constraint)을 부여한다.
이로써 보다 구별 가능한 대비값(distinguishable contrast values)을 얻을 수 있으며,
직접 최대화 방식보다 더 우수한 성능을 달성한다 (SMD: 1.27 → 2.39).
5 결론 및 향후 연구 (Conclusion and Future Work)
본 논문은 비지도 시계열 이상 탐지 문제 를 다루었다.
기존 연구들과 달리, 우리는 Transformer를 통해
더 풍부하고 유의미한 시점 간 연관성(time-point associations)을 학습하였다.
연관성 불일치(association discrepancy) 에 대한 핵심 관찰(key observation)에 기반하여,
우리는 Anomaly Transformer 를 제안한다.
이 모델은 연관성 불일치를 구체화하기 위해,
이중 분기(two-branch) 구조의 Anomaly-Attention을 포함한다.
또한, 정상(normal) 시점과 이상(abnormal) 시점 간의 차이를 더욱 증폭시키기 위해
미니맥스 전략(minimax strategy) 을 도입하였다.
우리는 연관 불일치(association discrepancy)를 도입함으로써,
재구성 성능(reconstruction performance)과 연관 불일치가 협력적으로 작동하는
연관 기반 기준(association-based criterion)을 제안한다.
Anomaly Transformer는 광범위한 실증적 연구에서 최첨단(state-of-the-art) 성능을 달성하였다.
향후 연구(Future Work)로는, 자기회귀(autoregression) 및 상태공간 모델(state space models)의
고전적 분석(classic analysis)에 기반한 Anomaly Transformer의 이론적 연구(theoretical study)가 포함될 것이다.
감사의 글 (Acknowledgements)
이 연구는 다음의 지원을 받아 수행되었다.
- 국가 차세대 인공지능 중대형 프로젝트 (National Megaproject for New Generation AI) — 과제 번호: 2020AAA0109201
- 중국 국가 자연과학재단 (National Natural Science Foundation of China) — 과제 번호: 62022050, 62021002
- 베이징 노바 프로그램 (Beijing Nova Program) — 과제 번호: Z201100006820041
- BNRist 혁신 기금 (BNRist Innovation Fund) — 과제 번호: BNR2021RC01002
참고문헌 (References)
[1] Ahmed Abdulaal, Zhuanghua Liu, and Tomer Lancewicki. Practical approach to asynchronous multivariate time series anomaly detection and localization. In KDD, 2021.
[2] Ryan Prescott Adams and David J. C. MacKay. Bayesian online changepoint detection.
arXiv preprint arXiv:0710.3742, 2007.
[3] O. Anderson and M. Kendall. Time-series. 2nd edn. J. R. Stat. Soc. (Series D), 1976.
[4] Paul Boniol and Themis Palpanas. Series2graph: Graph-based subsequence anomaly detection for time series. Proc. VLDB Endow., 2020.
[5] Markus M. Breunig, Hans-Peter Kriegel, Raymond T. Ng, and Jörg Sander. LOF: identifying density-based local outliers. In SIGMOD, 2000.
[6] Tom Brown et al. Language models are few-shot learners. In NeurIPS, 2020.
[7] Zekai Chen, Dingshuo Chen, Zixuan Yuan, Xiuzhen Cheng, and Xiao Zhang.
Learning graph structures with transformer for multivariate time series anomaly detection in IoT.
arXiv preprint arXiv:2104.03466, 2021.
[8] Haibin Cheng, Pang-Ning Tan, Christopher Potter, and Steven A. Klooster.
A robust graph-based algorithm for detection and characterization of anomalies in noisy multivariate time series. ICDM Workshops, 2008.
[9] Haibin Cheng, Pang-Ning Tan, Christopher Potter, and Steven A. Klooster.
Detection and characterization of anomalies in multivariate time series. In SDM, 2009.
[10] Shohreh Deldari, Daniel V. Smith, Hao Xue, and Flora D. Salim.
Time series change point detection with self-supervised contrastive predictive coding. In WWW, 2021.
[11] Ailin Deng and Bryan Hooi.
Graph neural network-based anomaly detection in multivariate time series. In AAAI, 2021.
[12] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova.
BERT: Pre-training of deep bidirectional transformers for language understanding. In NAACL, 2019.
[13] Alexey Dosovitskiy et al. An image is worth 16x16 words: Transformers for image recognition at scale. In ICLR, 2021.
[14] Ian Goodfellow et al. Generative adversarial nets. In NeurIPS, 2014.
[15] Cheng-Zhi Anna Huang et al. Music Transformer. In ICLR, 2019.
[16] Kyle Hundman et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding. In KDD, 2018.
[17] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In ICLR, 2015.
[18] Nikita Kitaev, Lukasz Kaiser, and Anselm Levskaya. Reformer: The efficient transformer. In ICLR, 2020.
[19] Kwei-Herng Lai, D. Zha, Junjie Xu, and Yue Zhao. Revisiting time series outlier detection: Definitions and benchmarks. In NeurIPS Dataset and Benchmark Track, 2021.
[20] Dan Li et al. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In ICANN, 2019.
[21] Shiyang Li et al. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In NeurIPS, 2019.
[22] Zhihan Li et al. Multivariate time series anomaly detection and interpretation using hierarchical inter-metric and temporal embedding. In KDD, 2021.
[23] F. Liu, K. Ting, and Z. Zhou. Isolation Forest. In ICDM, 2008.
[24] Ze Liu et al. Swin Transformer: Hierarchical vision transformer using shifted windows. In ICCV, 2021.
[25] Aditya P. Mathur and Nils Ole Tippenhauer. SWaT: A water treatment testbed for research and training on ICS security. In CySWATER, 2016.
[26] Radford M. Neal. Pattern recognition and machine learning. Technometrics, 2007.
[27] Daehyung Park, Yuuna Hoshi, and Charles C. Kemp.
A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder. RA-L, 2018.
[28] Adam Paszke et al. PyTorch: An imperative style, high-performance deep learning library. In NeurIPS, 2019.
[29] Lukas Ruff et al. Deep one-class classification. In ICML, 2018.
[30] T. Schlegl et al. F-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med. Image Anal., 2019.
[31] B. Schölkopf et al. Estimating the support of a high-dimensional distribution. Neural Comput., 2001.
[32] Lifeng Shen, Zhuocong Li, and James T. Kwok.
Time-series anomaly detection using temporal hierarchical one-class network. In NeurIPS, 2020.
[33] Youjin Shin et al. ITAD: Integrative tensor-based anomaly detection system for reducing false positives of satellite systems. In CIKM, 2020.
[34] Ya Su et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. In KDD, 2019.
[35] Jian Tang et al. Enhancing effectiveness of outlier detections for low density patterns. In PAKDD, 2002.
[36] Shahroz Tariq et al. Detecting anomalies in space using multivariate convolutional LSTM with mixtures of probabilistic PCA. In KDD, 2019.
[37] D. Tax and R. Duin. Support vector data description. Mach. Learn., 2004.
[38] Robert Tibshirani, Guenther Walther, and Trevor Hastie. Estimating the number of clusters in a dataset via the gap statistic. J. R. Stat. Soc. (Series B), 2001.
[39] Ashish Vaswani et al. Attention is all you need. In NeurIPS, 2017.
[40] Haixu Wu, Jiehui Xu, Jianmin Wang, and Mingsheng Long.
Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. In NeurIPS, 2021.
[41] Haowen Xu et al. Unsupervised anomaly detection via variational auto-encoder for seasonal KPIs in web applications. In WWW, 2018.
[42] Takehisa Yairi et al.
A data-driven health monitoring method for satellite housekeeping data based on probabilistic clustering and dimensionality reduction. IEEE Trans. Aerosp. Electron. Syst., 2017.
[43] Hang Zhao et al. Multivariate time-series anomaly detection via graph attention network. In ICDM, 2020.
[44] Bin Zhou et al. BeatGAN: Anomalous rhythm detection using adversarially generated time series. In IJCAI, 2019.
[45] Haoyi Zhou et al. Informer: Beyond efficient transformer for long sequence time-series forecasting. In AAAI, 2021.
[46] Bo Zong et al. Deep autoencoding Gaussian mixture model for unsupervised anomaly detection. In ICLR, 2018.
A. 매개변수 민감도 (Parameter Sensitivity)
우리는 본문 전체에서 윈도우 크기를 100으로 설정하였다.
이 값은 시간적 정보, 메모리, 그리고 계산 효율성을 함께 고려한 결과이다.
또한, 우리는 손실 가중치(loss weight) $\lambda$ 를
훈련 곡선(training curve)의 수렴 특성(convergence property) 에 기반하여 설정하였다.
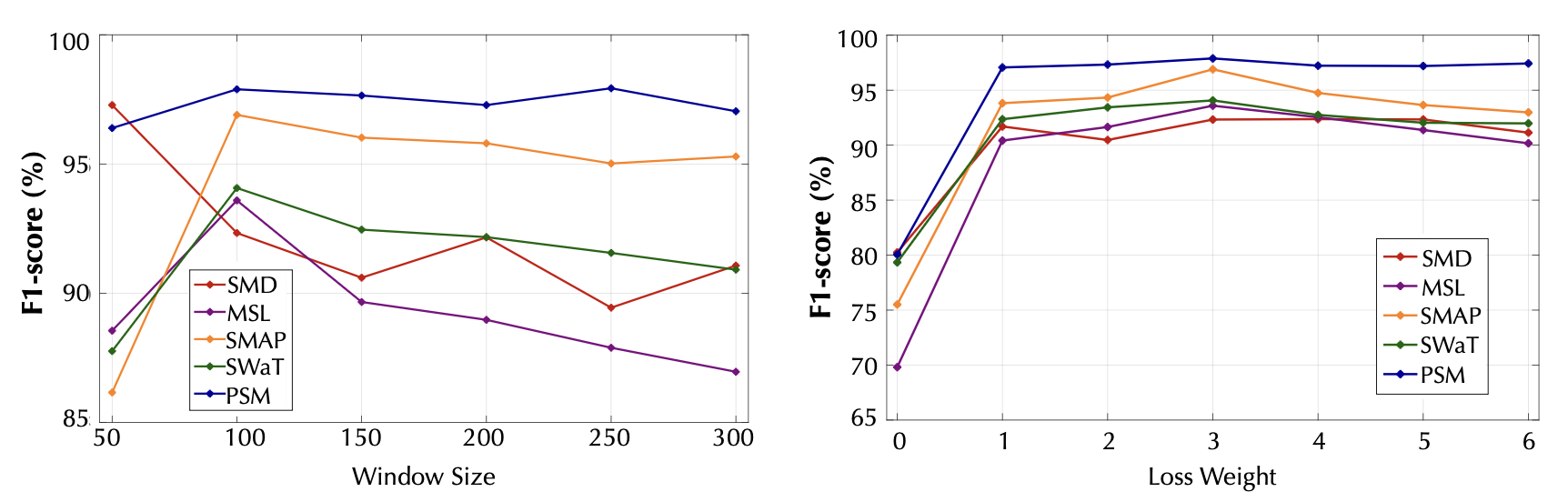
더 나아가, 그림 7은 모델의 성능과 손실 가중치의 관계를 보여준다.
우리 모델의 F1-점수(F1-score)는 안정적임을 확인할 수 있다 (그림 7 왼쪽).
그림 7
슬라이딩 윈도우 크기(왼쪽)와 손실 가중치(loss weight) $\lambda$(오른쪽)에 대한
매개변수 민감도(parameter sensitivity)를 나타낸다.
$\lambda = 0$ 인 경우에도,
모델은 여전히 연관성 기반 기준(association-based criterion)을 사용하지만,
재구성 손실(reconstruction loss)에 의해서만 학습(supervised)된다.
더 큰 윈도우 크기는 더 많은 메모리 비용을 필요로 하지만, 슬라이딩 윈도우의 개수는 감소하게 된다.
특히, 성능만 고려할 경우, 윈도우 크기와 성능의 관계는 데이터의 패턴(data pattern)에 따라 달라질 수 있다.
예를 들어, SMD 데이터셋의 경우, 윈도우 크기가 50일 때 더 나은 성능을 보인다.
또한, 우리는 식 (5)의 손실 항에서, 재구성 손실과 연관성 항의 균형을 맞추기 위해 $\lambda$ 값을 사용하였다.
실험 결과, $\lambda$ 값은 2에서 4 사이의 범위에서 안정적이며 조정이 용이함을 확인하였다.
이러한 결과는 모델의 민감도(sensitivity)가 안정적임을 검증하며, 이는 실제 응용 사례에서 매우 중요한 특성이다.
B 구현 세부사항 (Implementation Details)
우리는 알고리즘 1에서 Anomaly-Attention의 의사코드(pseudo-code)를 제시한다.
알고리즘 1. Anomaly-Attention 메커니즘 (multi-head version)
입력 (Input):
- $X \in \mathbb{R}^{N \times d_{\text{model}}}$ : 입력 시계열
- $D = (j - i)^2 \in \mathbb{R}^{N \times N}$ : 상대적 거리 행렬 (relative distance matrix),
단 $i, j \in {1, \dots, N}$
계층 파라미터 (Layer params):
- MLP_input : 입력을 위한 선형 변환층 (input projection layer)
- MLP_output : 출력을 위한 선형 변환층 (output projection layer)
| 단계 (Step) | 의사코드 (Pseudo-code) | 주석 (Notes) |
|---|---|---|
| 1 | $Q, K, V, \sigma = \mathrm{Split}(\mathrm{MLP}_{\text{input}}(X), \mathrm{dim}=1)$ | $Q, K, V \in \mathbb{R}^{N \times d_{\text{model}}}, \; \sigma \in \mathbb{R}^{N \times h}$ |
| 2 | for $(Q_m, K_m, V_m, \sigma_m)$ in $(Q, K, V, \sigma)$: | $Q_m, K_m, V_m \in \mathbb{R}^{N \times \frac{d_{\text{model}}}{h}}, \; \sigma_m \in \mathbb{R}^{N \times 1}$ |
| 3 | $\sigma_m = \mathrm{Broadcast}(\sigma_m, \mathrm{dim}=1)$ | $\sigma_m \in \mathbb{R}^{N \times N}$ |
| 4 | $\mathcal{P}_m = \dfrac{1}{\sqrt{2\pi}\sigma_m}\exp!\left(-\dfrac{D}{2\sigma_m^2}\right)$ | $\mathcal{P}_m \in \mathbb{R}^{N \times N}$ |
| 5 | $\mathcal{P}_m = \mathcal{P}_m / \mathrm{Broadcast}(\mathrm{Sum}(\mathcal{P}_m, \mathrm{dim}=1))$ | Rescaled $\mathcal{P}_m \in \mathbb{R}^{N \times N}$ |
| 6 | \(\mathcal{S}_m = \mathrm{Softmax}\!\left(\sqrt{\dfrac{h}{d_{\text{model}}}} \, Q_m K_m^{\top}\right)\) | $\mathcal{S}_m \in \mathbb{R}^{N \times N}$ |
| 7 | $\hat{Z}_m = \mathcal{S}_m V_m$ | \(\hat{Z}_m \in \mathbb{R}^{N \times \frac{d_{\text{model}}}{h}}\) |
| 8 | $\hat{Z} = \mathrm{MLP}_{\text{output}}(\mathrm{Concat}([\hat{Z}_1, \dots, \hat{Z}_h], \mathrm{dim}=1))$ | $\hat{Z} \in \mathbb{R}^{N \times d_{\text{model}}}$ |
| 9 | Return $\hat{Z}$ | Keep $\mathcal{P}_m$ and $\mathcal{S}_m$, $m = 1, \dots, h$ |
C 추가 사례 (More Showcases)
주요 결과(표 1)에 대한 직관적인 비교를 위해, 우리는 여러 베이스라인(baseline)들의 기준을 시각화하였다.
Anomaly Transformer는 가장 구별력(distinguishability) 있는 기준을 보여준다(그림 8).
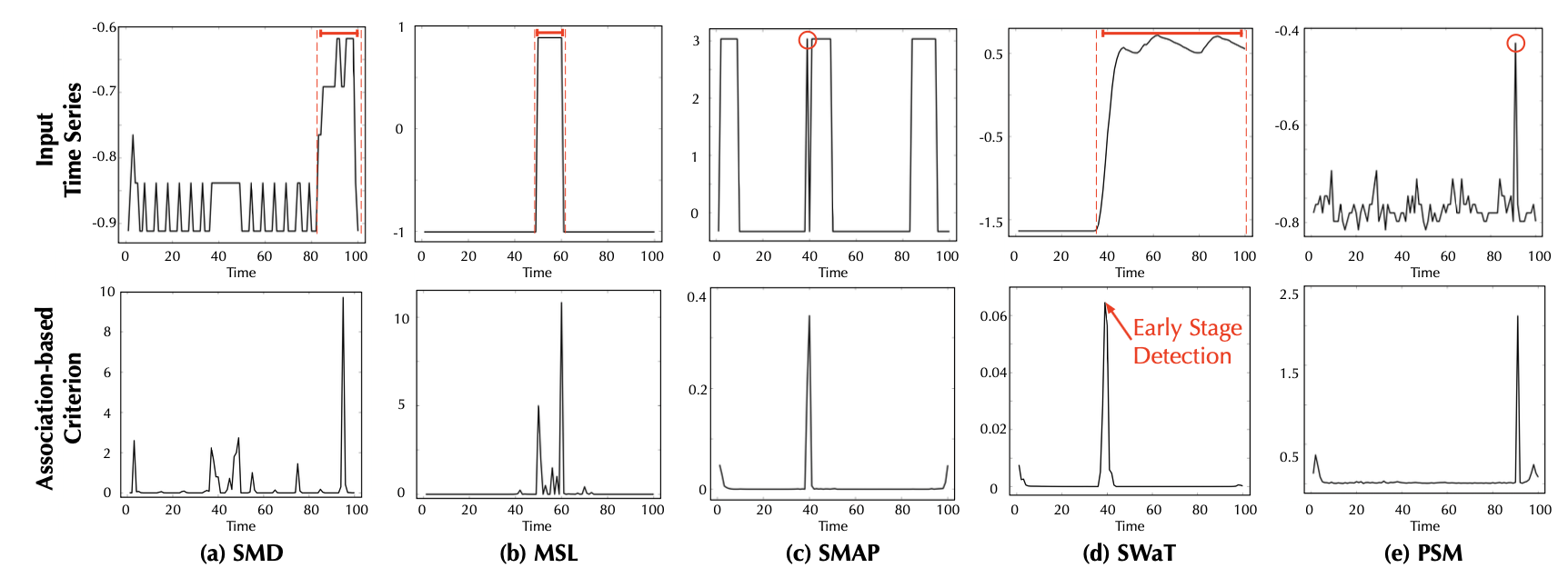
또한, 실세계 데이터셋에서도 Anomaly Transformer는 이상(anomalies)을 정확하게 탐지할 수 있다.
특히 SWaT 데이터셋 (그림 9(d)) 에서 우리 모델은 이상의 초기 단계(early stage)에서도 이를 감지할 수 있음을 보여준다.
이러한 특성은 오작동(malfunction)의 조기 경고(early warning)와 같은 실제 응용 사례에서 매우 의미가 있다.
그림 8. NeurIPS-TS 데이터셋에 대한 학습된 기준(learned criterion)의 시각화
이상 시점(anomalies)은 빨간색 원(red circles) 과 빨간색 구간(red segments) 으로 표시되어 있으며 (첫 번째 행),
베이스라인(baseline) 들의 실패 사례(failure cases)는 빨간색 상자(red boxes) 로 표시되어 있다.
그림 9. 실세계(real-world) 데이터셋에서 학습된 기준(learned criterion)의 시각화
시각화를 위해 데이터의 하나의 차원(one dimension)을 선택하였다.
이 예시들(showcases)은 각각의 데이터셋에 해당하는 테스트 세트(test set)에서 가져온 것이다.
D 연관성 불일치 제거 실험 (Ablation of Association Discrepancy)
우리는 알고리즘 2 에서 연관성 불일치 계산의 의사코드를 제시한다.
D.1 다중 계층 정량화 제거 실험 (Ablation of Multi-level Quantification)
최종 결과(식 (6))를 위해,
우리는 여러 계층(multiple layers)에서의 연관성 불일치(association discrepancy)를 평균화하였다.
또한, 단일 계층(single-layer)만 사용하는 경우에 대해 모델의 성능을 추가로 조사하였다.
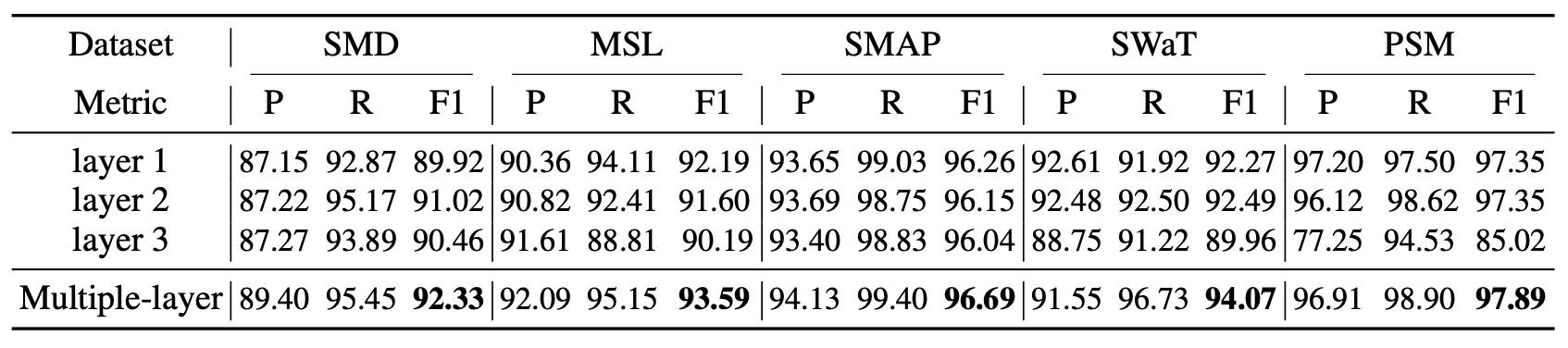
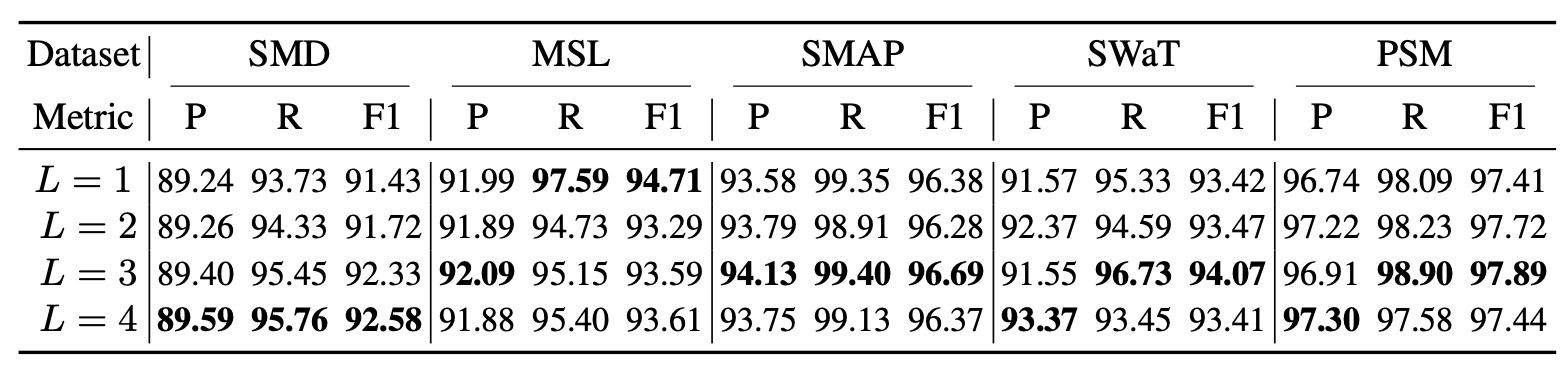
표 4에서 볼 수 있듯이, 다중 계층(multiple-layer) 설계가 가장 우수한 성능을 달성하였으며,
이는 다중 수준 정량화(multi-level quantification)의 효과성을 입증한다.
표 4. 연관성 불일치를 계산할 때 모델 계층(model layers)의 선택에 따른 성능 비교
D.2 통계적 거리 제거 실험 (Ablation of Statistical Distance)
우리는 연관성 불일치(association discrepancy) 를 계산하기 위해
다음과 같은 널리 사용되는 통계적 거리(statistical distances) 들을 선택하였다:
- 대칭화된 쿨백–라이블러 발산 (Symmetrized Kullback–Leibler Divergence, 제안 방식)
- 젠센–섀넌 발산 (Jensen–Shannon Divergence, JSD)
- 바서슈타인 거리 (Wasserstein Distance, Wasserstein)
- 교차 엔트로피 (Cross-Entropy, CE)
- L2 거리 (L2 Distance, L2)
표 5. 연관 불일치(association discrepancy)의 정의를 달리했을 때의 모델 성능 비교
표 5에 나타난 바와 같이, 제안된 연관성 불일치 정의는 가장 우수한 성능을 달성하였다.
우리는 교차 엔트로피(Cross-Entropy, CE) 와 Jensen–Shannon Divergence (JSD) 역시
상당히 우수한 결과를 제공함을 확인하였다.
이 두 방법은 원리상 제안된 정의와 유사하며, 정보 이득(information gain)을 나타내는 데 사용할 수 있다.
반면, L2 거리(L2 distance) 는
이산 확률 분포의 특성을 무시하기 때문에 불일치 계산에 적합하지 않다.
또한, 바서슈타인 거리(Wasserstein distance)는 일부 데이터셋에서 실패하는 경향을 보였다.
그 이유는 사전 연관성과 시리즈 연관성이 위치 인덱스(position index)에서 정확히 일치하기 때문이다.
결과적으로, 바서슈타인 거리는 포인트 단위(point-wise)로 계산되지 않으며,
분포의 오프셋(distribution offset)을 고려하므로 최적화 및 이상 탐지 과정에 잡음(noise)을 유발할 수 있다.
바서슈타인 거리(Wasserstein distance)가 연관 불일치 계산에 적합하지 않은 이유
바서슈타인 거리(Wasserstein distance)는 두 확률 분포 간의 형태 차이(shape difference) 와
질량 이동 비용(transport cost) 을 함께 고려하는 강력한 거리 척도이다.
그러나 Anomaly Transformer에서는 이러한 특성이 오히려 문제를 일으킨다.
- 비교 대상의 성격 차이
- Anomaly Transformer의 연관 불일치는
사전 연관성(prior association) 과 시리즈 연관성(series association) 사이의 차이를 측정한다.- 두 분포는 동일한 시간 인덱스(position index) 위에서 정의되며,
각 시점별(point-wise) 대응 관계를 비교하는 것이 핵심이다.- 바서슈타인 거리의 한계
- 바서슈타인 거리는 두 분포 간의 전역적 이동(offset) 을 고려하기 때문에,
동일한 인덱스 축을 공유하더라도 분포의 중심이 약간만 어긋나면
불필요하게 큰 거리로 계산된다.- 이로 인해, 정상적인 연관 분포에서도
실제 이상과 무관한 잡음(noise) 이 거리 값에 포함될 수 있다.- 결과적 영향
- 바서슈타인 거리는 포인트 단위의 정밀한 대응 관계를 반영하지 못한다.
- 결과적으로, 최적화 과정이 불안정해지고
이상 탐지 기준으로서의 신뢰성이 떨어지는 경향을 보인다.- 요약
- 바서슈타인 거리는 분포의 전역적 형태 차이를 측정하는 데는 유용하지만,
Anomaly Transformer가 요구하는 시점별(point-wise) 연관 비교에는 적합하지 않다.- 따라서 논문에서는 바서슈타인 거리 대신,
대칭 KL 발산(Symmetrized KL Divergence) 을 사용하여
연관 불일치를 더 안정적으로 측정한다.
알고리즘 2. 연관성 불일치 $\text{AssDis}(\mathcal{P}, \mathcal{S}; \mathcal{X})$ 계산 (multi-head version)
입력 (Input):
- $N$ : 시계열 길이 (time series length)
- $L$ : 계층 수 (number of layers)
- $h$ : 헤드 수 (number of heads)
- $\mathcal{P}_{\text{all}} \in \mathbb{R}^{L \times h \times N \times N}$ : 사전 연관성 (prior-association)
- $\mathcal{S}_{\text{all}} \in \mathbb{R}^{L \times h \times N \times N}$ : 시리즈 연관성 (series-association)
| 단계 | 연산(Operation) | 출력 형태(Shape) |
|---|---|---|
| 1 | $\mathcal{P}’ = \mathrm{Mean}(\mathcal{P}, \mathrm{dim}=1)$ | $\mathcal{P}’ \in \mathbb{R}^{L \times N \times N}$ |
| 2 | $\mathcal{S}’ = \mathrm{Mean}(\mathcal{S}, \mathrm{dim}=1)$ | $\mathcal{S}’ \in \mathbb{R}^{L \times N \times N}$ |
| 3 | $\mathcal{R}’ = \mathrm{KL}((\mathcal{P}’, \mathcal{S}’), \mathrm{dim}=-1) + \mathrm{KL}((\mathcal{S}’, \mathcal{P}’), \mathrm{dim}=-1)$ | $\mathcal{R}’ \in \mathbb{R}^{L \times N}$ |
| 4 | $\mathcal{R} = \mathrm{Mean}(\mathcal{R}’, \mathrm{dim}=0)$ | $\mathcal{R} \in \mathbb{R}^{N \times 1}$ |
| 5 | Return $\mathcal{R}$ | 각 시점별 연관성 불일치 (association discrepancy) 결과를 반환 |
D.3 사전 연관성에 대한 제거 실험 (Ablation of Prior-Association)
사전 연관성에 대해, 학습 가능한 스케일 파라미터를 갖는 가우시안 커널 외에도,
학습 가능한 지수 파라미터 $\alpha$ 를 사용하는 멱법칙 커널(power-law kernel) $P(x; \alpha) = x^{-\alpha}$을 적용해 보았다.
이 커널 또한 단봉(unimodal) 분포에 속한다.
표 6에서 볼 수 있듯이, 멱법칙 커널은 대부분의 데이터셋에서 좋은 성능을 달성하였다.
그러나 스케일 파라미터(scale parameter)가 지수 파라미터(power parameter) 보다 최적화가 더 용이하기 때문에,
가우시안 커널이 일관되게 멱법칙 커널 을 능가하는 성능을 보였다.
표 6. 사전 연관성(prior-association)의 정의에 따른 모델 성능 비교
우리의 Anomaly Transformer는 가우시안 커널을 사전 연관성으로 채택하였다.
Power-law는 멱법칙 커널(power-law kernel)을 의미한다.
E. 연관성 기반 기준(Association-based Criterion)에 대한 제거 실험
E.1 계산 (Calculation)
우리는 알고리즘 3 에서 연관성 기반 기준의 의사코드를 제시한다.
알고리즘 3. 연관성 기반 기준 — AnomalyScore(X) 계산
입력 (Input):
- 시계열 길이 $N$ (time series length)
- 입력 시계열 $X \in \mathbb{R}^{N \times d}$
- 재구성된 시계열 $\hat{X} \in \mathbb{R}^{N \times d}$
- 연관성 불일치(association discrepancy) $\mathrm{AssDis}(P, S; X) \in \mathbb{R}^{N \times 1}$
| 단계 | 연산 | 설명 |
|---|---|---|
| 1 | $C_{\text{AD}} = \mathrm{Softmax}\big(-\mathrm{AssDis}(P, S; X), \mathrm{dim}=0\big)$ | $C_{\text{AD}} \in \mathbb{R}^{N \times 1}$ |
| 2 | $C_{\text{Recon}} = \mathrm{Mean}\big((X - \hat{X})^2, \mathrm{dim}=1\big)$ | $C_{\text{Recon}} \in \mathbb{R}^{N \times 1}$ |
| 3 | $C = C_{\text{AD}} \times C_{\text{Recon}}$ | $C \in \mathbb{R}^{N \times 1}$ |
| 4 | Return $C$ | 각 시점별 이상 점수(anomaly score) |
E.2 기준 정의에 대한 제거 실험 (Ablation of Criterion Definition)
우리는 이상 기준(anomaly criterion) 을 정의하는 다양한 방식에 따라 모델의 성능 변화를 탐구하였다.
이에 포함된 실험 조건은 다음과 같다:
- 순수 연관성 불일치(pure association discrepancy)
- 순수 재구성 성능(pure reconstruction performance)
두 기준을 결합한 두 가지 방식: 덧셈(addition) 과 곱셈(multiplication)
Association Discrepancy:
\[\text{AnomalyScore}(X) = \text{Softmax}\big(-\text{AssDis}(P, S; X)\big)\]Reconstruction:
\[\text{AnomalyScore}(X) = \| X_{i,:} - \hat{X}_{i,:} \|_2^2, \quad i = 1, \dots, N\]Addition:
\[\text{AnomalyScore}(X) = \text{Softmax}\big(-\text{AssDis}(P, S; X)\big) + \| X_{i,:} - \hat{X}_{i,:} \|_2^2, \quad i = 1, \dots, N\]Multiplication (Ours):
\[\text{AnomalyScore}(X) = \text{Softmax}\big(-\text{AssDis}(P, S; X)\big) \odot \| X_{i,:} - \hat{X}_{i,:} \|_2^2, \quad i = 1, \dots, N \tag{7}\]
표 7의 결과에서, 우리가 제안한 연관성 불일치(association discrepancy)만을 직접 사용하는 경우에도 우수한 성능을 보이며,
경쟁 베이스라인인 THOC (Shen et al., 2020) 을 일관되게 능가하였다.
또한, 식 (6)에서 사용한 곱셈 결합(multiplication combination) 방식이 가장 뛰어난 성능을 보였으며,
이는 재구성 성능과 연관성 불일치간의 더 나은 협력을 이끌어낸다.
표 7. 기준 정의에 대한 제거 실험 (Ablation of Criterion Definition)
비교를 위해 최첨단(state-of-the-art) 딥러닝 모델인 THOC (Shen et al., 2020) 을 함께 포함하였다.
- AssDis : 순수 연관성 불일치(pure association discrepancy)
- Recon : 순수 재구성 성능(pure reconstruction performance)
- Ours : 제안된 연관성 기반 기준(association-based criterion)으로 곱셈 결합 방식을 적용하였다.
F. 미니맥스 최적화의 수렴 (Convergence of Minimax Optimization)
우리 모델의 전체 손실(식 (4))은 재구성 손실과 연관성 불일치 두 부분으로 구성되어 있다.
연관성 학습(association learning)을 보다 안정적으로 제어하기 위해,
우리는 미니맥스 전략(minimax strategy)을 최적화 과정(식 (5))에 도입하였다.
최소화 단계(minimization phase)에서는
연관성 불일치와 재구성 오차(reconstruction error)를 최소화(minimize)하는 방향으로 학습이 진행된다.최대화 단계(maximization phase)에서는
연관성 불일치를 최대화(maximize)하면서, 동시에 재구성 오차는 최소화 한다.
우리는 학습 과정 동안 두 손실 항의 변화 곡선(change curve)을 시각화하였다.
그림 10과 그림 11에서 볼 수 있듯이, 두 손실 항 모두 제한된 반복(iteration) 내에서 안정적으로 수렴하였다.
이러한 우수한 수렴 특성(convergence property)은 우리 모델의 최적화 과정에서 매우 중요한 요소이다.
그림 10
학습 중 실세계(real-world) 데이터셋에서의 재구성 손실(reconstruction loss)
\(\| X - \hat{X} \|_F^2\) 변화 곡선(change curve).
그림 11
학습 과정(training process) 동안 실세계(real-world) 데이터셋에서의
연관성 불일치(association discrepancy) \(\| \text{AssDis}(P, S; X) \|_1\) 변화 곡선(change curve).
G 모델 파라미터 민감도 (Model Parameter Sensitivity)
본 논문에서는 Transformer (Vaswani et al., 2017; Zhou et al., 2021) 의 관례(convention)를 따라
하이퍼파라미터 $L$ 과 $d_{\text{model}}$을 설정하였다.
또한, 모델 파라미터의 민감도(sensitivity) 를 평가하기 위해
계층 수 $L$ 및 은닉 채널 $d_{\text{model}}$의 다양한 설정(choice)에 따른 성능과 효율성을 조사하였다.
일반적으로 모델의 크기를 증가시키면 더 나은 결과를 얻을 수 있지만,
그에 따라 메모리및 계산 비용 또한 커지게 된다.
표 8. 계층 수 $L$ 의 다양한 설정(choice)에 따른 모델 성능(Model performance)
표 9. 은닉 채널(hidden channels) 수 $d_{\text{model}}$ 의 다양한 설정(choice)에 따른 모델 성능
Mem은 평균 GPU 메모리 사용량을 의미하고,
Time은 학습 과정 동안 100회 반복(iterations)의 평균 실행 시간을 의미한다.
H 임계값 선택 프로토콜 (Protocol of Threshold Selection)
본 논문은 비지도 시계열 이상 탐지에 초점을 맞춘다.
실험적으로, 각 데이터셋은 학습(training), 검증(validation), 테스트(testing) 세트로 구성되어 있으며,
이상 시점(anomalies)는 테스트 세트에만 라벨이 지정되어 있다.
따라서, 우리는 K-Means의 Gap Statistic 방법 (Tibshirani et al., 2001)을 따라 하이퍼파라미터를 선택하였다.
선택 절차는 다음과 같다.
(1) 학습 단계(training phase) 이후,
모델을 라벨이 없는 검증 세트(validation subset)에 적용하여
모든 시점(time points)의 이상 점수(anomaly scores, 식 (6))를 계산한다.(2) 검증 세트에서의 이상 점수 분포(distribution)를 집계한다.
관찰 결과, 이상 점수의 분포는 두 개의 클러스터로 분리되며,
그중 더 큰 이상 점수(anomaly score) 를 가진 클러스터가
$r$개의 시점(time points)을 포함하고 있음을 확인하였다.우리의 모델에서 $r$은 각각 다음과 유사하다:
SWaT: 0.1%, SMD: 0.5%, 기타 데이터셋: 1% (표 10)(3) 실제 응용 사례(real-world applications)에서는
테스트 세트의 크기를 사전에 알 수 없기 때문에,
우리는 임계값(threshold)을 고정된 값 $\delta$로 설정한다.
이때 $\delta$는 검증 집합 내의 $r$개의 시점이
이상 점수 $\delta$보다 큰 값을 가지도록 하여,
이들을 이상치로 탐지하도록 보장한다.
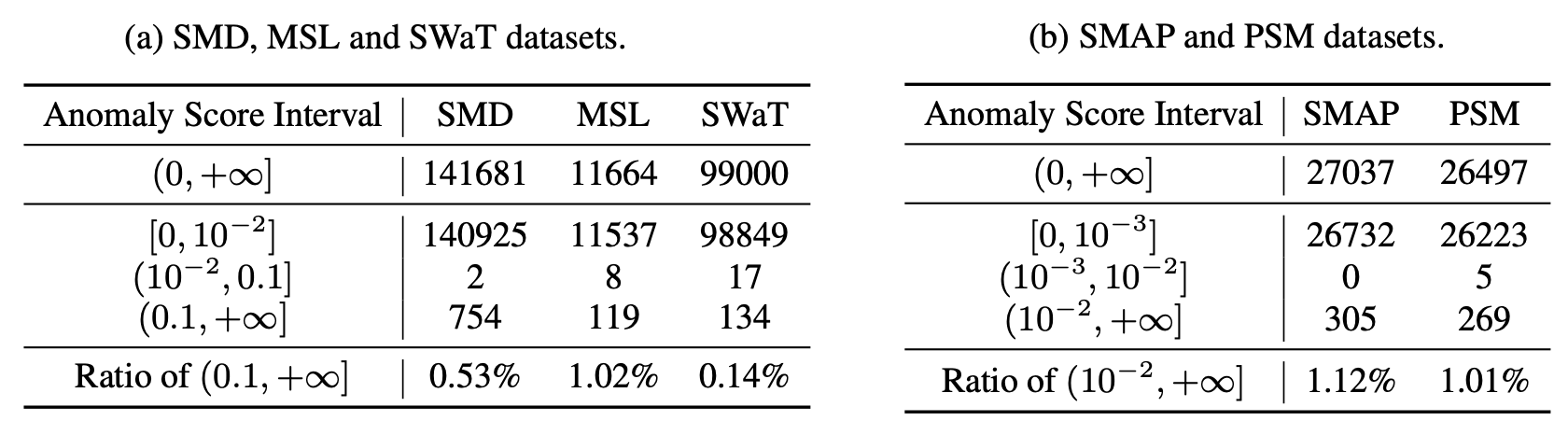
표 10. 검증 세트에서의 이상 점수 분포에 대한 통계적 결과
여기서는 여러 구간(interval) 내에서의 해당 값들을 가지는 시점(time points)의 개수를 계산하였다.
주의할 점은, 임계값(δ)을 직접 설정하는 것도 가능하다는 것이다.
표 10의 구간에 따라,
SMD, MSL, SWaT 데이터셋의 경우 δ = 0.1,
SMAP, PSM 데이터셋의 경우 δ = 0.01 로 고정할 수 있으며,
이러한 설정은 r 값을 사용하는 경우와 거의 유사한 성능 을 보인다.
표 11. 모델 성능
δ에 의한 선택(Choose by δ)은
SMD, MSL 및 SWaT 데이터셋에 대해 δ를 0.1로,
SMAP 및 PSM 데이터셋에 대해 δ를 0.01로 고정함을 의미한다.
r에 의한 선택(Choose by r)은
SWaT에 대해 r을 0.1%,
SMD에 대해 r을 0.5%,
그리고 다른 데이터셋들에 대해 r을 1%로 선택함을 의미한다.
실제(real-world) 응용 환경에서, 선택된 이상치(anomalies)의 개수는 인적 자원(human resources)에 따라 결정된다.
이러한 점을 고려하면,
탐지된 이상치의 개수를 비율 $r$로 설정하는 방식이 보다 실용적이며, 가용한 자원에 따라 결정하기도 더 용이하다.
Gap Statistic과 임계값 δ, r의 선택 방법
Gap Statistic (Tibshirani et al., 2001) 은
비지도 학습(unsupervised learning) 환경에서
임계값(threshold) 또는 클러스터 개수(k) 를
통계적으로 결정하기 위한 방법이다.이 방법은 데이터의 군집 내 분산(within-cluster dispersion) 을
\[\text{Gap}(k) = E^*\big[\log(W_k^*)\big] - \log(W_k)\]
무작위로 생성된 기준 데이터(reference distribution)의 분산과 비교하여
두 값의 차이, 즉 Gap 값(Gap value) 을 계산한다.여기서
- $W_k$: 실제 데이터의 군집 내 분산
- \(E^*[\log(W_k^*)]\): 기준 분포에서 얻은 기대값(expected value)
Gap 값이 최대가 되는 지점을 최적의 임계값(threshold) 또는 클러스터 개수로 선택한다.
본 논문에서는 Gap Statistic 원리를 변형하여,
검증 데이터셋(validation set)에서 얻은 이상 점수(anomaly score) 분포를
두 개의 군집(정상 vs 이상)으로 분리하였다.그 결과, 이상 점수가 큰 군집에 속하는 시점(time points)의 비율을 r로 정의하고,
이 비율에 따라 임계값 δ (delta) 를 설정하였다.예를 들어,
- SWaT 데이터셋에서는 $r = 0.1\%$
- SMD 데이터셋에서는 $r = 0.5\%$
- 나머지 데이터셋에서는 $r = 1\%$
이렇게 설정된 비율 $r$에 대응하는 임계값 δ는
해당 비율의 상위 이상 점수에 해당하는 값으로 고정된다.추가로, δ를 고정값으로 직접 지정하는 방법도 실험적으로 유효하였다.
- SMD, MSL, SWaT: δ = 0.1
- SMAP, PSM: δ = 0.01
두 방법(r 기반 설정과 δ 고정 설정)은
거의 동일한 성능(performance) 을 보였으며,
실제 환경에서는 데이터의 크기나 이상 비율에 따라
두 방식 중 하나를 유연하게 적용할 수 있다.요약하면,
- r 기반 방법: 이상 비율을 기준으로 δ를 동적으로 결정
- δ 고정 방법: 사전에 정의된 δ 값으로 간단하게 임계값 설정
이 두 접근 모두 비지도 시계열 이상 탐지(unsupervised anomaly detection) 상황에서
신뢰성 있고 재현 가능한 임계값 설정 전략으로 활용될 수 있다.
I. 추가 베이스라인 (More Baselines)
시계열 이상 탐지(time series anomaly detection) 방법들 외에도,
변화점 탐지(change point detection) 와 시계열 분할(time series segmentation) 방법들 역시
유용한 비교 기준(valuable baselines)으로 사용될 수 있다.
따라서, 우리는 다음 세 가지 방법을 추가적으로 포함하였다:
- BOCPD (Bayesian Online Change Point Detection) — Adams & MacKay (2007)
- TS-CP2 — Deldari et al. (2021)
- U-Time — Perslev et al. (2019)
이들은 각각 변화점 탐지와 시계열 분할 분야의 대표적인 모델들이다.
그럼에도 불구하고, Anomaly Transformer 는 여전히 가장 우수한 성능을 달성하였다.
BOCPD (Bayesian Online Change Point Detection)
BOCPD 는 Bayesian Online Change Point Detection의 약자로,
시계열 데이터(streaming time series)에서 변화점(change point) 을
온라인(online) 방식으로 탐지하는 알고리즘이다.이 방법은 베이즈 추론(Bayesian inference) 을 기반으로,
각 시점에서 “현재 구간이 새로운 구간으로 바뀌었는가?”를
확률적으로 계산한다.구체적으로,
- 각 시점마다 run length라 불리는 “현재 구간이 지속된 길이”의 분포를 추적한다.
- 새로운 데이터가 들어올 때마다 사후 확률(posterior probability) 을 업데이트하며,
변화점이 발생했을 가능성을 계산한다.BOCPD의 장점은 다음과 같다:
- 실시간(online) 으로 변화점을 감지할 수 있다.
- 베이즈적 불확실성(uncertainty) 을 명시적으로 다룰 수 있다.
- 데이터 분포가 시간이 지남에 따라 바뀌는 비정상(non-stationary) 시계열에도 적용 가능하다.
이러한 특성 덕분에 BOCPD는
시스템 이상 감지, 장비 고장 예측, 시장 구조 변화 탐지 등
다양한 응용 분야에서 활용되고 있다.
TS-CP2 (Time Series Change Point Detection with Contrastive Predictive Coding)
TS-CP2 는 Deldari et al. (2021) 에 의해 제안된
시계열 변화점 탐지(Time Series Change Point Detection) 모델로,
자기지도 학습(self-supervised learning) 기반의
대조 예측 부호화(Contrastive Predictive Coding, CPC) 방식을 사용한다.이 방법의 핵심 아이디어는,
“정상 구간 내의 시계열은 스스로를 잘 예측할 수 있지만,
변화점(change point)이 발생하면 예측이 갑자기 어려워진다”는 점에 있다.구체적으로,
- 모델은 시계열의 잠재 표현(latent representation) 을 학습하여
인접 구간 간의 유사도(similarity) 를 예측한다.- 변화점이 발생하면 두 구간의 표현 간 유사도가 급격히 떨어지므로,
이를 변화 신호(change signal) 로 감지한다.TS-CP2의 장점은 다음과 같다:
- 라벨이 없는 비지도 학습(unsupervised) 설정에서도 동작 가능하다.
- 다차원(multivariate) 시계열에서도 안정적인 성능을 보인다.
- CPC 기반의 표현 학습을 통해 노이즈에 강건하다.
이러한 특성 덕분에 TS-CP2는
복잡한 시계열 환경(예: 센서 네트워크, 금융 데이터, 산업 공정 모니터링 등)에서
구조적 변화(structural change) 를 감지하는 데 효과적으로 사용될 수 있다.
U-Time (Fully Convolutional Network for Time Series Segmentation)
U-Time 은 Perslev et al. (2019) 에 의해 제안된
시계열 분할(time series segmentation) 모델로,
이미지 처리 분야에서 널리 사용되는 U-Net 아키텍처를
시계열 데이터에 맞게 확장한 형태이다.U-Time의 핵심 아이디어는,
시계열 데이터를 연속적인 구간(segment)으로 나누어
각 시점(time point)에 해당하는 클래스(또는 상태) 를 예측하는 것이다.구조적으로, U-Time 은 다음과 같은 특징을 가진다:
- 인코더(Encoder) 가 시계열의 전역적 특징(global features)을 추출한다.
- 디코더(Decoder) 는 업샘플링(up-sampling)을 통해
세밀한 시간적 정보를 복원한다.- 인코더와 디코더 사이에는 skip connection 이 존재하여,
저수준(low-level) 특징과 고수준(high-level) 특징을 결합한다.이러한 구조 덕분에,
U-Time 은 국소적(local) 변화와 전역적(global) 패턴을 동시에 고려할 수 있으며,
복잡한 시계열의 구조적 구간 경계를 효과적으로 탐지할 수 있다.실제로 Perslev 등은 수면 단계 분류(sleep staging) 문제에 이를 적용하여
기존의 RNN 기반 모델보다 빠르고 정확한 성능을 달성하였다.
따라서 U-Time 은
시계열의 세분화(segmentation) 및 이상 구간 탐지(anomaly segmentation) 에서
강력한 기준선(baseline) 모델로 활용된다.
표 12
다섯 개의 실세계(real-world) 데이터셋에서의 Anomaly Transformer (본 연구, Ours) 에 대한 추가 정량적 결과이다.
- P, R, F1 은 각각 정밀도(precision), 재현율(recall), 그리고 F1-점수(F1-score) (단위: %)를 나타낸다.
- F1-score 는 정밀도와 재현율의 조화 평균(harmonic mean) 으로 계산된다.
- 이 세 가지 지표 모두에서 값이 높을수록 성능이 우수함을 의미한다.
J. 한계점 및 향후 연구 (Limitations and Future Work)
윈도우 크기
부록 A의 그림 7에서 볼 수 있듯이, 윈도우 크기가 너무 작을 경우 모델은 연관성 학습에 실패할 수 있다.
그러나 Transformer 구조는 윈도우 크기에 대해 이차 복잡도(quadratic complexity) 를 가지므로,
실제 응용 사례에서는 적절한 균형이 필요하다.
트랜스포머의 이차 복잡도와 Q–K–V 연산 구조
트랜스포머(Transformer)는 셀프-어텐션(self-attention) 메커니즘을 통해
모든 시점 쌍(time-point pair) 간의 연관도를 계산한다.
이때 계산 복잡도는 입력 윈도우(window) 길이 $L$ 에 대해 이차적(quadratic) 으로 증가한다.
복잡도 발생 원리
어텐션은 쿼리(Query), 키(Key), 값(Value) 행렬을 다음과 같이 계산한다.
\(\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^{\top}}{\sqrt{d_k}}\right) V\)여기서 $Q, K, V \in \mathbb{R}^{L \times d}$ 이므로,
$QK^{\top}$ 연산에는 $O(L^2)$ 의 계산량이 필요하다.
(모든 시점 쌍에 대한 유사도를 계산해야 하기 때문)결과적 영향
- 윈도우 크기 $L$ 이 커질수록 연산량과 메모리 사용량이 급격히 증가한다.
- 따라서 실제 시계열 응용에서는
연산 효율과 정보 포착 능력 간의 균형을 고려한 윈도우 설정이 중요하다.
이론적 분석 (Theoretical Analysis)
Transformer는 잘 확립된 딥러닝 모델로서, 그 성능은 이미 여러 선행 연구들에서 탐구되어 왔다.
그러나 여전히 복잡한 딥러닝 모델의 이론적 측면 에 대해서는 충분히 탐구되지 않은 상태이다.
향후 연구에서는 Anomaly Transformer의 이론적 근거(theorem)를 더 잘 정립하기 위해,
자기회귀(autoregression)와 상태 공간 모델(state space models)의 고전적 분석에 기반한
이론적 정당화(theoretical justification) 를 진행할 예정이다.
K. 데이터셋 (Dataset)
다음은 실험에 사용된 데이터셋들의
통계적 세부 정보(statistical details) 이다.
표 13. 벤치마크의 세부 정보
AR은 전체 데이터셋에서의 실제 이상 비율(truth abnormal proportion)을 나타낸다.
L. UCR 데이터셋 (UCR Dataset)
UCR 데이터셋은 KDD 2021 국제 학술대회의 다중 데이터셋 시계열 이상 탐지 대회에서 제공된
매우 도전적이고 포괄적인 데이터셋이다 (Keogh et al., 2021).
이 전체 데이터셋은 총 250개의 하위 데이터셋으로 구성되어 있으며, 다양한 실세계 시나리오를 포괄한다.
각 하위 데이터셋은 단 하나의 이상 구간(anomaly segment)만을 포함하며, 1차원 구조를 가진다.
이들 하위 데이터셋의 길이는 6,684에서 900,000 사이이며, 이미 훈련 세트 와 테스트 세트로 미리 분할되어 있다.
우리는 보다 폭넓은 평가를 위해 UCR 데이터셋에서도 실험을 수행하였다.
표 14에서 보이듯이,
Anomaly Transformer 는 이 도전적인 벤치마크에서도 여전히 최첨단(state-of-the-art) 성능을 달성하였다.
표 14. UCR 데이터셋에서의 정량적 결과
- IF : IsolationForest (2008)
- Ours : 제안된 Anomaly Transformer
- P, R, F1 : 각각 정밀도(precision), 재현율(recall), F1 점수(F1-score) 를 (%) 단위로 표시