[논문] Attention Is All You Need
논문 출처
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., & Polosukhin, I.
Attention Is All You Need.
Advances in Neural Information Processing Systems (NeurIPS 2017).
🔗 원문 링크 (arXiv:1706.03762)
저자
- Ashish Vaswani (Google Brain) - avaswani@google.com
- Noam Shazeer (Google Brain) - noam@google.com
- Niki Parmar (Google Research) - nikip@google.com
- Jakob Uszkoreit (Google Research) - usz@google.com
- Llion Jones (Google Research) - llion@google.com
- Aidan N. Gomez † (University of Toronto) - aidan@cs.toronto.edu
- Łukasz Kaiser (Google Brain) - lukaszkaiser@google.com
- Illia Polosukhin ‡ - illia.polosukhin@gmail.com
∗ 공동 기여. 저자 순서는 무작위이다.
- Jakob은 RNN을 셀프-어텐션으로 대체하자는 아이디어를 제안하고, 이를 검증하기 위한 연구를 시작했다.
- Ashish는, Illia와 함께 최초의 Transformer 모델을 설계하고 구현했으며, 이 연구의 모든 측면에 핵심적으로 관여했다.
- Noam은 scaled dot-product attention, multi-head attention, parameter-free position representation을 제안했으며, 연구의 거의 모든 세부 사항에 깊이 참여했다.
- Niki는 우리의 오리지널 코드베이스와 tensor2tensor에서 수많은 모델 변형을 설계, 구현, 튜닝, 평가하였다.
- Llion은 새로운 모델 변형을 실험했을 뿐만 아니라, 초기 코드베이스와 효율적인 추론 및 시각화를 맡았다.
- Lukasz와 Aidan은 tensor2tensor의 다양한 부분을 설계하고 구현하는 데 수많은 시간을 투자하여, 초기 코드베이스를 대체하고 결과를 크게 개선했으며 연구 속도를 비약적으로 가속시켰다.
† Google Brain에서 수행한 연구 결과임.
‡ Google Research에서 수행한 연구 결과임.본 논문은 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA에서 발표되었다..
Tensor2Tensor(T2T)는 구글 브레인 팀이 공개한 오픈소스 딥러닝 라이브러리로,
주로 시퀀스-투-시퀀스 작업(기계 번역, 요약, 언어 모델링 등)을 쉽게 실험할 수 있도록 설계되었다.주요 특징:
- TensorFlow 기반으로 구현됨
- 다양한 시퀀스 모델(RNN, CNN, Transformer 등)과 대규모 데이터셋을 내장
- GPU/TPU 병렬 학습 지원으로 대규모 실험이 용이
Transformer 논문 역시 초기에는 Tensor2Tensor 코드베이스 안에서 개발되고 검증되었으며,
이 때문에 저자 기여 부분에서 여러 연구자들이 tensor2tensor의 설계·구현·개선을 언급하고 있다.
초록 (Abstract)
현재 널리 사용되는 시퀀스 변환(sequence transduction) 모델들은
인코더와 디코더를 포함하는 복잡한 순환 신경망(recurrent neural networks) 또는
합성곱 신경망(convolutional neural networks)을 기반으로 한다.
가장 성능이 좋은 모델들은 어텐션(attention) 메커니즘을 통해 인코더와 디코더를 연결한다.
어텐션 메커니즘의 역할
기존의 순환 신경망(RNN)이나 LSTM에서는 입력 시퀀스를 순차적으로 처리하기 때문에,
긴 문맥(long context) 정보를 유지하기 어렵다.어텐션 메커니즘(attention mechanism)은 이러한 한계를 극복하기 위해,
출력 시점의 각 단어(또는 시점)가 입력 시퀀스의 모든 위치를 참고하도록 한다.
즉, 모델이 “현재 어떤 입력에 집중해야 하는가?”를 학습하여
중요한 정보에 더 큰 가중치를 부여한다.인코더와 디코더 사이에서는,
인코더가 만든 모든 은닉 상태(hidden states)를 디코더가 한꺼번에 참조할 수 있게 하여,
문맥 정보의 손실을 줄이고 더 정교한 매핑을 가능하게 한다.수식적으로는 다음과 같이 표현된다:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V\]여기서
- $Q$ (Query): 현재 디코더의 상태
- $K, V$ (Key, Value): 인코더의 출력
이러한 구조 덕분에 모델은 멀리 떨어진 단어들 간의 관계나
시계열의 장기 의존성(long-range dependency)을 효과적으로 학습할 수 있다.
우리는 전적으로 어텐션 메커니즘에만 기반한 새로운 단순한 네트워크 아키텍처,
즉 Transformer를 제안한다. 이 아키텍처는 순환과 합성곱을 완전히 제거했다.
두 가지 기계 번역 과제에서의 실험 결과, 제안된 모델은 더 높은 품질을 보이는 동시에
병렬화가 용이하며, 훈련에 필요한 시간도 크게 줄어든다는 것을 보여주었다.
우리 모델은 WMT 2014 영어→독일어 번역 과제에서 28.4 BLEU 점수를 달성했으며,
이는 이전 최고 성능(앙상블 모델 포함)을 2 BLEU 이상 능가한 결과이다.
또한 WMT 2014 영어→프랑스어 번역 과제에서, 단일 모델 기준으로 최고 성능을 경신하며
BLEU 점수 41.0을 달성했다. 이는 8개의 GPU에서 3.5일간 훈련한 결과이며,
문헌에 보고된 기존 최고 성능 모델들의 훈련 비용의 일부만으로 달성한 것이다.
BLEU 점수란?
BLEU(Bilingual Evaluation Understudy)는 기계 번역의 품질을 평가하는 대표적인 지표이다.
예측 번역문과 정답 번역문 사이의 N-gram 정밀도(precision)를 측정하여 계산한다.BLEU의 정의 수식은 다음과 같다:
\[BLEU = BP \cdot \left( \prod_{i=1}^4 \text{precision}_i \right)^{\tfrac{1}{4}}\]
- $\text{precision}_i$: 예측 번역문과 정답 번역문 간의 $i$-gram precision
$BP$: brevity penalty, 짧은 문장이 과도하게 높은 점수를 받는 것을 막기 위한 보정값
\[BP = \min \left( 1, \frac{\text{예측 문장의 단어 수}}{\text{정답 문장의 단어 수}} \right)\]BLEU 점수는 일반적으로 $0 \sim 1$ 범위를 가지며, 백분율(0~100점)로 환산해 보고된다.
값이 높을수록 번역이 더 정확하고 자연스러움을 의미한다.
1 서론 (Introduction)
순환 신경망(Recurrent Neural Networks, RNN), 장단기 메모리(Long Short-Term Memory, LSTM) [12],
그리고 게이티드 순환 신경망(Gated Recurrent Neural Networks) [7]은
언어 모델링, 기계 번역 [29, 2, 5] 등과 같은 시퀀스 모델링과 변환(transduction) 문제에서
확고하게 최첨단(state-of-the-art) 접근법으로 자리 잡아왔다.
이후 언어 모델과 인코더-디코더 아키텍처의 적용 범위를 확장하기 위한 수많은 연구가 이어졌다 [31, 21, 13].
순환 모델은 일반적으로 입력과 출력 시퀀스의 기호 위치를 기준으로 연산을 나누어 수행한다.
입력 시퀀스의 각 위치를 연산 시간 단계에 대응시켜, 일련의 은닉 상태 $h_t$ 들을 만들어낸다.
여기서 $h_t$는 이전 은닉 상태 $h_{t-1}$와 위치 $t$의 입력의 함수이다.
이러한 본질적인 순차적(sequential) 특성 때문에 하나의 학습 샘플 내에서는 병렬화가 불가능하다.
시퀀스 길이가 길어질수록 이 문제가 더 심각해지는데,
GPU 메모리 제약으로 인해 샘플들 간에 동시에 처리할 수 있는 배치 크기가 제한되기 때문이다.
최근 연구에서는 팩터라이제이션(factorization) 트릭 [18]과 조건부 연산(conditional computation) [26]을 통해
계산 효율성이 크게 향상되었으며, 조건부 연산에서는 모델 성능 또한 개선되었다.
그러나 순차적 계산이라는 근본적인 제약은 여전히 남아 있다.
팩터라이제이션 트릭(Factorization Tricks)
순환 신경망(RNN)이나 언어 모델에서 등장하는 거대한 확률 분포(예: 소프트맥스 출력층)를 직접 계산하면 연산량이 매우 커진다.
팩터라이제이션 트릭은 이러한 연산을 작은 부분으로 분해(factorize) 하여 효율적으로 계산하는 기법을 의미한다.
대표적으로 Hierarchical Softmax, Sampled Softmax, Noise-Contrastive Estimation(NCE) 등이 이에 속한다.
즉, 동일한 모델을 더 적은 계산량으로 학습할 수 있도록 하는 최적화 기법이다.
조건부 연산(Conditional Computation)
신경망의 모든 파라미터를 항상 사용하는 대신, 입력에 따라 일부 연산만 선택적으로 활성화하는 방식을 말한다.
예를 들어, 특정 입력에서는 네트워크의 일부 경로만 계산하여 연산량을 줄이고,
중요한 입력에 대해서는 더 많은 계산을 할당할 수 있다.
이는 효율성을 높이는 동시에 모델의 표현력도 유지하거나 향상시킬 수 있어, 최근 대규모 신경망 연구에서 주목받는 방법이다.수식으로 표현하면, 전체 함수 $f(x)$ 대신에
\(f(x) = \sum_i g_i(x) f_i(x)\)
와 같이, 입력 $x$에 따라 선택 함수 $g_i(x)$가 특정 모듈 $f_i$만 활성화되도록 설계한다.
어텐션 메커니즘(attention mechanisms)은 다양한 과제에서
강력한 시퀀스 모델링 및 변환 모델의 핵심적인 요소가 되었다.
이는 입력 또는 출력 시퀀스에서 거리에 상관없이 의존성을 모델링할 수 있도록 한다. [2, 16]
하지만 극히 일부의 경우 [22]를 제외하면, 이러한 어텐션 메커니즘은
항상 순환 신경망과 결합되어 사용되어 왔다.
본 연구에서는 순환 구조를 제거하고, 대신 입력과 출력 간의 전역적 의존성을 학습하기 위해
전적으로 어텐션 메커니즘에 의존하는 모델 아키텍처인 Transformer를 제안한다.
Transformer는 훨씬 더 높은 수준의 병렬화를 가능하게 하며,
단 8개의 P100 GPU에서 12시간 정도의 훈련만으로도
번역 품질에서 새로운 최첨단 성능(state-of-the-art)에 도달할 수 있었다.
2 배경 (Background)
순차적 계산을 줄이려는 목표는 Extended Neural GPU [20], ByteNet [15], ConvS2S [8]의 기반이 되기도 한다.
이들 모델은 모두 합성곱 신경망(convolutional neural networks)을 기본 구성 요소로 사용하여,
입력과 출력의 모든 위치에 대한 은닉 표현(hidden representations)을 병렬적으로 계산한다.
이들 모델에서는 두 임의의 입력 또는 출력 위치 간 신호를 연결하기 위해 필요한 연산의 수가
위치 간 거리(distance)에 따라 증가한다.
ConvS2S의 경우 선형적으로(linearly), ByteNet의 경우 로그(logarithmically) 비율로 증가한다.
이로 인해 먼 위치들 사이의 의존성을 학습하는 것이 더욱 어려워진다 [11].
Transformer에서는 이러한 연산이 상수 개수의 연산(a constant number of operations)으로 줄어든다.
다만 어텐션 가중치가 적용된 위치들을 평균하기 때문에 표현의 세밀함(정밀도)이 줄어드는 비용이 따른다.
우리는 이를 3.2절에서 설명하는 멀티-헤드 어텐션(Multi-Head Attention)으로 보완한다.
Extended Neural GPU
Extended Neural GPU는 2015년 발표된 모델로, 게이티드 순환 유닛(GRU)와 합성곱(convolution)을 결합한 아키텍처이다.
이 모델은 입력 시퀀스를 2차원 격자 구조로 표현하고, 합성곱 연산을 통해 병렬적으로 처리함으로써
전통적인 RNN보다 더 효율적으로 긴 시퀀스를 학습할 수 있도록 설계되었다.
Transformer로 가는 중간 단계의 아이디어 중 하나로 평가된다.
ByteNet
ByteNet은 2016년 발표된 모델로, 합성곱 신경망(CNN) 기반의 시퀀스-투-시퀀스 아키텍처이다.
입력 길이에 따라 연산량이 선형적으로 늘어나는 RNN과 달리,
ByteNet은 직접적인 병렬 처리와 지수적 크기의 수용영역(receptive field)을 활용하여
긴 시퀀스에서도 효율적으로 문맥을 포착할 수 있다.
다만 두 위치 간 의존성을 학습하는 데 필요한 연산이 거리의 로그(logarithmic)에 비례해 증가하는 제약이 있다.
ConvS2S
ConvS2S(Convolutional Sequence to Sequence)는 2017년 발표된 모델로,
완전히 합성곱 네트워크만으로 인코더-디코더 구조를 구성한 기계 번역 모델이다.
합성곱 계층을 깊게 쌓아 넓은 문맥 범위를 처리할 수 있으며,
RNN보다 병렬화가 용이하고 학습 속도가 빠르다는 장점을 가진다.
그러나 입력 위치 간 거리에 비례해 연산량이 선형적으로(linearly) 증가한다는 한계가 있다.
셀프-어텐션(Self-attention)은 때로 인트라-어텐션(intra-attention)이라고도 불리며,
하나의 시퀀스 내 서로 다른 위치들을 연결하여 그 시퀀스의 표현을 계산하는 어텐션 메커니즘이다.
셀프-어텐션은 독해(reading comprehension), 추상적 요약(abstractive summarization),
텍스트 함의(textual entailment), 과제와 무관한 문장 표현 학습(task-independent sentence representations) [4, 22, 23, 19] 등
다양한 작업에서 성공적으로 활용되어 왔다.
엔드-투-엔드 메모리 네트워크(End-to-end memory networks)는
시퀀스 정렬 기반 순환(sequence-aligned recurrence) 대신 순환 어텐션 메커니즘(recurrent attention mechanism)에 기반하며,
단순 언어 질의응답(simple-language question answering)과 언어 모델링(language modeling) 과제에서
우수한 성능을 보인 것으로 보고되었다 [28].
그러나 우리가 아는 한, Transformer는 입력과 출력의 표현을 계산함에 있어
시퀀스 정렬 기반 RNN이나 합성곱을 사용하지 않고 전적으로 셀프-어텐션(Self-attention)에만 의존하는
최초의 변환(transduction) 모델이다.
다음 섹션들에서 우리는 Transformer를 설명하고,
셀프-어텐션(Self-attention)의 필요성을 제시하며,
[14, 15], [8]과 같은 모델들에 비해 가지는 장점을 논의할 것이다.
엔드-투-엔드 메모리 네트워크(End-to-End Memory Networks)
엔드-투-엔드 메모리 네트워크는 2015년 Facebook AI Research에서 제안한 모델로,
메모리(memory) 컴포넌트와 어텐션(attention) 메커니즘을 결합하여,
순환 신경망(RNN)의 시퀀스 정렬 기반 연산 대신 순환 어텐션(recurrent attention)을 사용한다.주요 아이디어는 모델이 외부 메모리를 참조하며 필요한 정보를 읽고 쓸 수 있도록 하여,
긴 문맥에서의 추론(reasoning)을 가능하게 한다는 것이다.
- 순환 어텐션(recurrent attention)이란?
한 번의 어텐션으로 끝나는 것이 아니라, 여러 번 반복적으로(attentive hops)
메모리에 주의를 기울여 필요한 정보를 단계적으로 모으는 방식이다.
→ 예: 질문에 답하기 위해 먼저 인물 정보를 찾고, 다음에 사건 정보를 찾는 식으로 차례대로 집중.대표적인 응용 분야:
- 질의응답(Question Answering, QA) : 긴 문서 속에서 답변에 필요한 정보를 단계적으로 추출
- 언어 모델링(Language Modeling) : 문맥을 메모리에 저장·활용하여 다음 단어를 더 잘 예측
연구 결과, 메모리 네트워크는 단순 언어 질의응답(Simple QA)과 언어 모델링 과제에서
우수한 성능을 보인 것으로 보고되었다 [28].
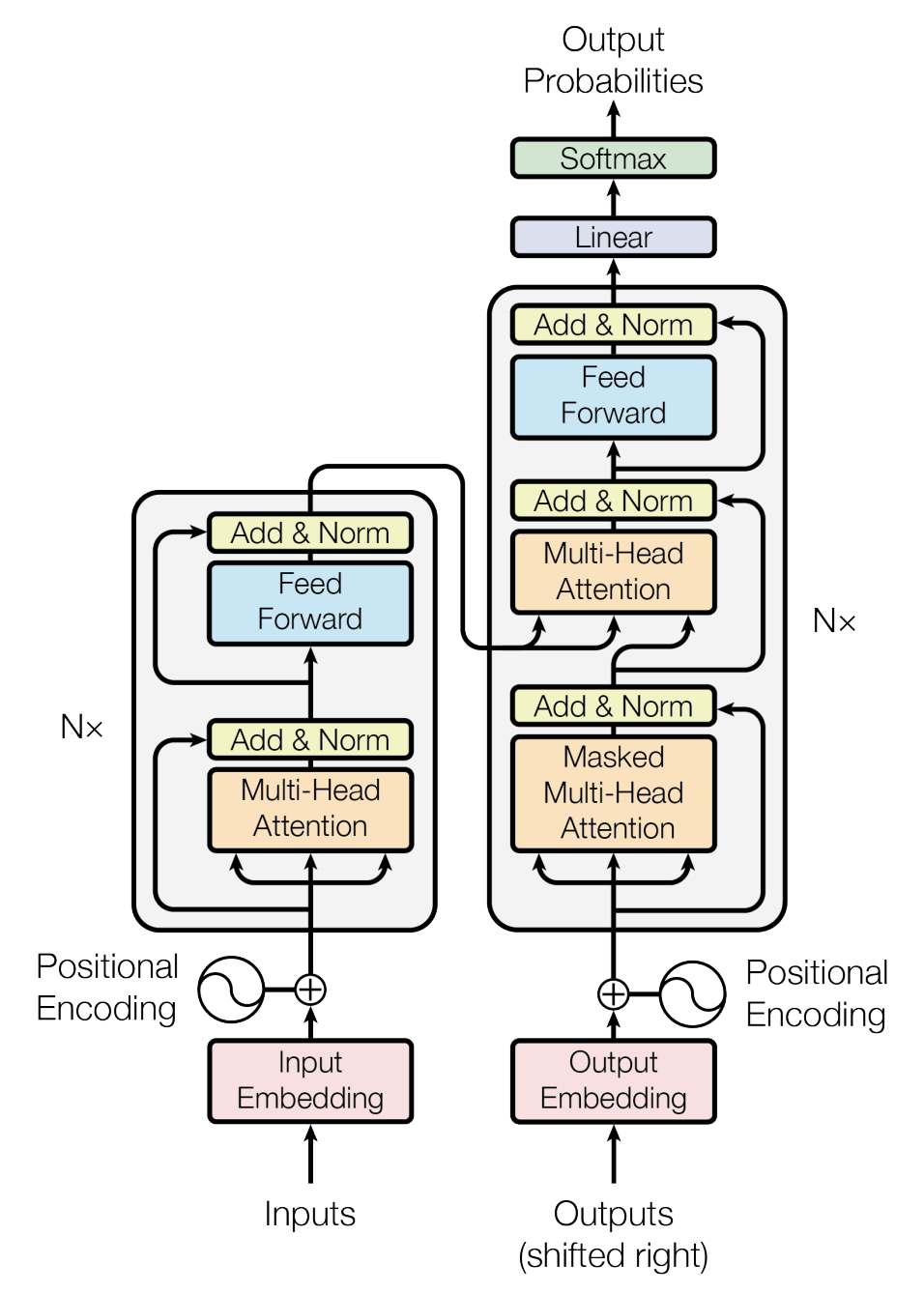
3 모델 아키텍처 (Model Architecture)
대부분의 경쟁력 있는 신경망 기반 시퀀스 변환 모델들은 인코더-디코더 구조를 가진다 [5, 2, 29].
여기에서 인코더는 기호 표현들 $(x_1, \ldots, x_n)$로 이루어진 입력 시퀀스를
연속적 표현들의 시퀀스 $z = (z_1, \ldots, z_n)$로 매핑한다.
$z$가 주어지면, 디코더는 기호들로 이루어진 출력 시퀀스 $(y_1, \ldots, y_m)$을
한 번에 하나씩 순차적으로 생성한다.
각 단계에서 모델은 자기회귀적(auto-regressive) [9]으로 동작하며,
다음 출력을 생성할 때 이전에 생성된 기호들을 추가 입력으로 사용한다.
Transformer는 전체적으로 이러한 아키텍처를 따르며,
인코더와 디코더 모두에서 셀프-어텐션(Self-attention)과 위치별(point-wise) 완전 연결 계층(fully connected layers)을 적층하여 사용한다.
이는 각각 그림 1의 왼쪽과 오른쪽 부분에 나타나 있다.
그림 1. Transformer - 모델 아키텍처
3.1 인코더와 디코더 스택 (Encoder and Decoder Stacks)
인코더(Encoder):
인코더는 $N = 6$개의 동일한 층(layer)으로 이루어진 스택으로 구성된다.
각 층은 두 개의 하위 층(sub-layer)으로 구성된다.
첫 번째 하위 층은 멀티-헤드 셀프-어텐션(Multi-Head Self-Attention) 메커니즘이고,
두 번째 하위 층은 단순한 위치별(position-wise) 완전 연결 피드포워드 네트워크이다.
각 두 개의 하위 층(sub-layer)에는 잔차 연결(residual connection) [10]을 적용하고,
그 뒤에 레이어 정규화(layer normalization) [1]를 수행한다.
즉, 각 하위 층(sub-layer)의 출력은 다음과 같다.
\[\text{LayerNorm}(x + \text{Sublayer}(x))\]
여기서 $\text{Sublayer}(x)$는 해당 하위 층이 구현하는 함수이다.
이러한 잔차 연결(residual connections)을 가능하게 하기 위해,
모델의 모든 하위 층(sub-layer)과 임베딩 층(embedding layer)은
차원 $d_{\text{model}} = 512$의 출력을 생성한다.
디코더(Decoder):
디코더 역시 $N = 6$개의 동일한 층(layer)으로 이루어진 스택으로 구성된다.
각 인코더 층에 포함된 두 개의 하위 층(sub-layer)에 더해,
디코더는 세 번째 하위 층을 추가하는데,
이 층은 인코더 스택의 출력을 대상으로 멀티-헤드 어텐션(Multi-Head Attention)을 수행한다.
인코더와 마찬가지로, 디코더의 각 하위 층(sub-layer)에도
잔차 연결(residual connection)을 적용하고, 그 뒤에 레이어 정규화(layer normalization)를 수행한다.
또한 디코더 스택의 셀프-어텐션(Self-Attention) 하위 층을 수정하여,
각 위치가 이후의 위치들에 주의를 기울이지 못하도록(참조하지 못하도록) 한다.
이러한 마스킹(masking)은 출력 임베딩(output embedding)이 한 위치만큼 어긋나 있다는 사실과 결합되어,
위치 $i$에서의 예측이 $i$보다 작은 위치들의 알려진 출력에만 의존하도록 보장한다.
3.2 어텐션 (Attention)
어텐션 함수(attention function)는 쿼리(query)와 키-값(key-value) 쌍들의 집합을 출력으로 매핑하는 함수로 설명할 수 있으며,
이때 쿼리, 키, 값, 출력은 모두 벡터(vector)이다.
출력은 값(value)들의 가중합(weighted sum)으로 계산되며,
각 값에 할당되는 가중치는 쿼리(query)와 해당 키(key) 간의 호환 함수(compatibility function)에 의해 계산된다.
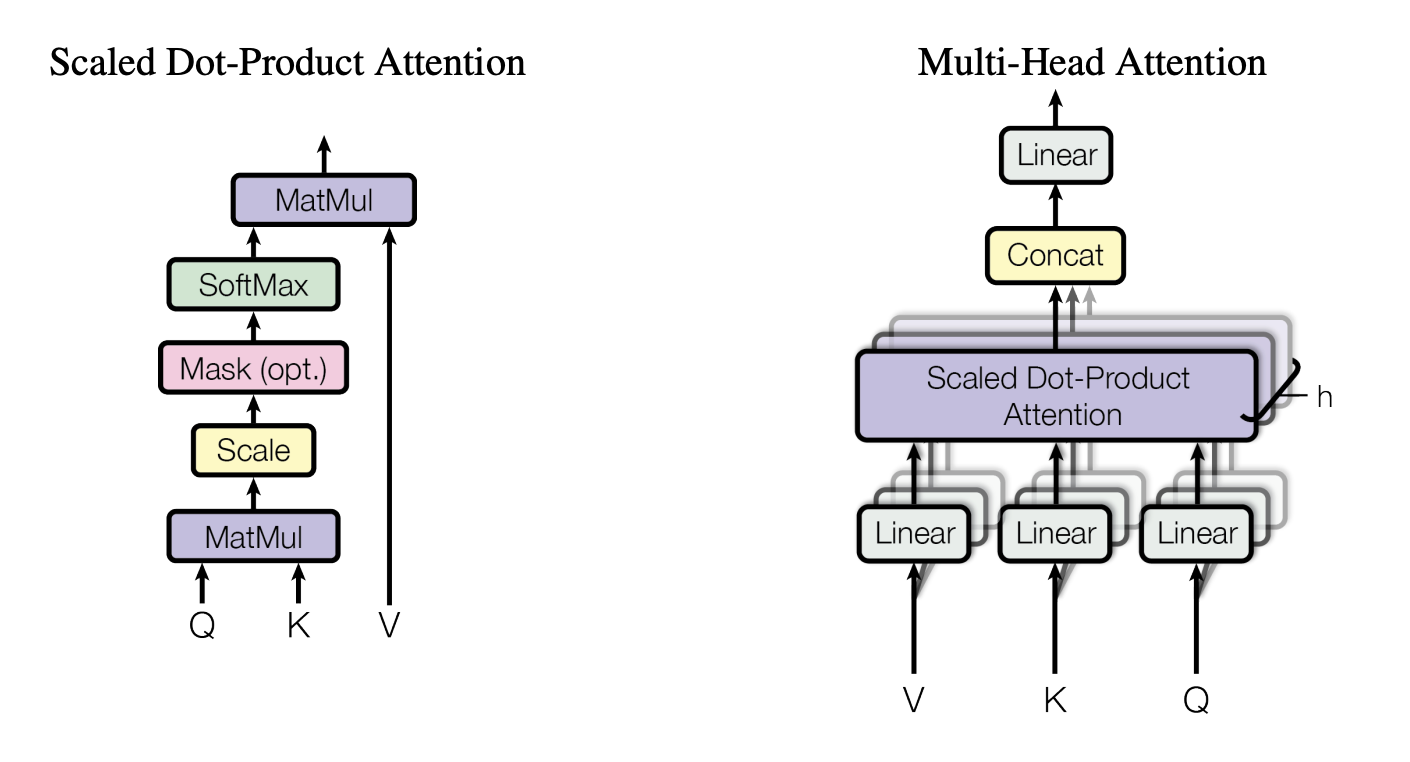
3.2.1 스케일드 닷-프로덕트 어텐션 (Scaled Dot-Product Attention)
우리는 우리가 사용하는 특정한 어텐션 방식을 “스케일드 닷-프로덕트 어텐션(Scaled Dot-Product Attention)”이라고 부른다 (그림 2).
그림 2. (왼쪽) 스케일드 닷-프로덕트 어텐션(Scaled Dot-Product Attention).
(오른쪽) 멀티-헤드 어텐션(Multi-Head Attention)은 여러 개의 어텐션 층을 병렬로 수행한다.
입력은 차원 $d_k$의 쿼리(query)와 키(key), 그리고 차원 $d_v$의 값(value)으로 구성된다.
쿼리를 모든 키들과 내적(dot product)한 뒤,
각 결과를 $\sqrt{d_k}$로 나누고, 소프트맥스(softmax) 함수를 적용하여
값(value)들에 대한 가중치(weights)를 얻는다.
실제로는 여러 개의 쿼리(query) 집합에 대해 어텐션 함수를 동시에 계산하며,
이 쿼리들은 함께 묶여 행렬 $Q$로 표현된다.
키(keys)와 값(values) 또한 각각 행렬 $K$와 $V$로 함께 묶어 표현된다.
출력 행렬은 다음과 같이 계산된다:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \tag{1}\]
가장 흔히 사용되는 두 가지 어텐션 함수는
가산적 어텐션(additive attention) [2]과
내적(곱셈적) 어텐션(dot-product / multiplicative attention)이다.
내적 어텐션(dot-product attention)은
스케일링 계수 $\tfrac{1}{\sqrt{d_k}}$를 제외하면 우리의 알고리즘과 동일하다.
가산적 어텐션(additive attention)은
하나의 은닉층(hidden layer)을 가진 피드포워드 네트워크를 사용하여
호환 함수(compatibility function)를 계산한다.
이 두 방법은 이론적인 복잡도 면에서는 유사하지만,
내적 어텐션(dot-product attention)은 고도로 최적화된 행렬 곱셈(matrix multiplication) 코드로 구현할 수 있기 때문에
실제로는 훨씬 더 빠르고 공간 효율적이다.
$d_k$의 값이 작은 경우에는 두 메커니즘이 비슷한 성능을 보이지만,
$d_k$가 큰 경우에는 스케일링을 적용하지 않은 내적 어텐션(dot-product attention)보다
가산적 어텐션(additive attention)이 더 나은 성능을 보인다 [3].
우리는 $d_k$가 큰 경우, 내적(dot product) 값의 크기가 커져
소프트맥스(softmax) 함수가 기울기(gradient)가 극도로 작은 영역에 놓이게 된다4고 추측한다 [4].
이러한 효과를 상쇄하기 위해, 우리는 내적(dot product)을 $\tfrac{1}{\sqrt{d_k}}$로 스케일링한다.
4왜 내적(dot product)이 커지는지를 설명하기 위해,
$q$와 $k$의 성분들이 평균 0, 분산 1을 갖는 서로 독립인 확률 변수라고 가정하자.
그렇다면 내적 $q \cdot k = \sum_{i=1}^{d_k} q_i k_i$는 평균 0, 분산 $d_k$를 갖게 된다.
3.2.2 멀티-헤드 어텐션 (Multi-Head Attention)
$d_{model}$ 차원의 키(key), 값(value), 쿼리(query)에 대해 단일 어텐션 함수를 수행하는 대신,
우리는 쿼리, 키, 값을 서로 다른 학습된 선형 변환(linear projection)을 통해
각각 $h$번 선형 투영하여, 차원 $d_k$, $d_k$, $d_v$로 매핑하는 것이 유익하다는 것을 발견했다.
이렇게 투영된 각각의 쿼리(query), 키(key), 값(value)에 대해
우리는 어텐션 함수를 병렬로 수행하며,
그 결과 $d_v$ 차원의 출력 값(output value)을 얻게 된다.
이 출력들은 합쳐진 후(concatenate), 다시 한 번 선형 투영(linear projection)되어
최종 출력 값들을 생성하게 되며, 이는 그림 2에 나타나 있다.
멀티-헤드 어텐션(Multi-Head Attention)은
모델이 서로 다른 표현 부분공간(representation subspace)들에서,
서로 다른 위치들의 정보를 동시에 주목(attend)할 수 있도록 한다.
하나의 어텐션 헤드만 사용하는 경우, 평균화(averaging)가 이러한 능력을 방해하게 된다.
\[\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O\] \[\text{head}_i = \text{Attention}(Q W_i^Q, \; K W_i^K, \; V W_i^V)\]
여기서 투영(projection)들은 파라미터 행렬로, 다음과 같이 정의된다:
\[W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k}, \quad W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k}, \quad W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_v},\] \[W^O \in \mathbb{R}^{h d_v \times d_{\text{model}}}.\]이 연구에서 우리는 $h = 8$개의 병렬 어텐션 층(layer), 즉 헤드(head)를 사용한다.
각 헤드마다 우리는 $d_k = d_v = d_{\text{model}} / h = 64$를 사용한다.
각 헤드의 차원이 줄어들기 때문에,
전체 계산 비용은 전체 차원을 사용하는 단일 헤드 어텐션과 유사하다.
3.2.3 본 모델에서의 어텐션 활용 (Applications of Attention in our Model)
Transformer는 멀티-헤드 어텐션(Multi-Head Attention)을 세 가지 방식으로 사용한다:
인코더-디코더 어텐션(encoder-decoder attention) 층에서는,
쿼리(query)는 전 단계의 디코더 층에서 나오며,
키(key)와 값(value)은 인코더의 출력으로부터 나온다.
이를 통해 디코더의 각 위치는 입력 시퀀스의 모든 위치에 주의를 기울일 수 있게 된다.
이는 [31, 2, 8]과 같은 시퀀스-투-시퀀스(sequence-to-sequence) 모델에서의
전형적인 인코더-디코더 어텐션 메커니즘을 모방한 것이다.인코더(encoder)는 셀프-어텐션(self-attention) 층을 포함한다.
셀프-어텐션(self-attention) 층에서는 키(key), 값(value), 쿼리(query)가 모두 같은 곳에서 나오는데,
이 경우 그것은 인코더의 전 단계 층의 출력이다.
인코더의 각 위치는 인코더의 전 단계 층에 있는 모든 위치에 주의를 기울일 수 있다.비슷하게, 디코더(decoder)의 셀프-어텐션(self-attention) 층에서는
디코더의 각 위치가 그 위치를 포함하여, 그 이전까지의 모든 위치에 주의를 기울일 수 있다.
자기회귀(auto-regressive) 특성을 유지하기 위해,
디코더에서는 미래 위치(오른쪽)에서 과거 위치(왼쪽)로의 정보 흐름(leftward information flow)을 차단해야 한다.
우리는 이러한 동작을 스케일드 닷-프로덕트 어텐션(scaled dot-product attention) 내부에서 구현한다.
즉, 소프트맥스(softmax) 입력에서 허용되지 않는 연결(illegal connections)에 해당하는 모든 값을
마스킹(masking)하여 $-\infty$로 설정한다. (그림 2 참조)
3.3 위치별 피드포워드 네트워크 (Position-wise Feed-Forward Networks)
어텐션 하위 층(sub-layer) 외에도,
우리의 인코더와 디코더의 각 층은 완전 연결 피드포워드 네트워크(fully connected feed-forward network)를 포함한다.
이 네트워크는 각 위치에 대해 별도로(separately), 그리고 동일하게(identically) 적용된다.
이는 두 개의 선형 변환(linear transformation)으로 이루어져 있으며,
그 사이에는 ReLU 활성화 함수(activation function)가 위치한다.
\[\text{FFN}(x) = \max(0, \; xW_1 + b_1)W_2 + b_2 \tag{2}\]
선형 변환(linear transformation)은 서로 다른 위치들에 대해서는 동일하게 적용되지만,
층(layer)이 달라지면 서로 다른 파라미터(parameters)를 사용한다.
이를 다른 방식으로 표현하면, 커널 크기 1의 두 개의 합성곱(convolution)으로 볼 수 있다.
입력과 출력의 차원은 $d_{\text{model}} = 512$이고,
내부 층(inner-layer)의 차원은 $d_{ff} = 2048$이다.
FFN과 Conv1D(k=1)의 관계
위치별 피드포워드 네트워크(FFN)는 각 위치에 동일한 선형 변환(linear transformation)을 적용한다.
이는 사실상 커널 크기가 1인 1차원 합성곱(Conv1D with kernel size = 1)과 동일하다.
- Conv1D(k=1)은 커널 사이즈가 1이므로, 각각의 위치에 대해 동일한 가중치를 공유하는 필터를 적용한다.
- 따라서 각 위치별로 독립적으로 연산되지만, 파라미터는 전체 시퀀스에서 공유된다.
- FFN 역시 입력 시퀀스의 각 위치마다 동일한 가중치 행렬을 적용하므로 동등하게 볼 수 있다.
따라서 구현 관점에서는 FFN을 Conv1D(k=1) 두 층을 쌓은 구조로 이해할 수 있다.
3.4 임베딩과 소프트맥스 (Embeddings and Softmax)
다른 시퀀스 변환(sequence transduction) 모델들과 유사하게,
우리는 학습된 임베딩(learned embedding)을 사용하여
입력 토큰(input token)과 출력 토큰(output token)을 $d_{\text{model}}$ 차원의 벡터로 변환한다.
또한 우리는 일반적으로 사용되는 학습된 선형 변환(learned linear transformation)과
소프트맥스(softmax) 함수를 사용하여, 디코더의 출력을
다음 토큰(next-token)의 예측 확률로 변환한다.
우리의 모델에서는 [24]와 유사하게,
두 개의 임베딩 층(embedding layer)과 소프트맥스(softmax) 이전의 선형 변환(pre-softmax linear transformation)이
동일한 가중치 행렬(weight matrix)을 공유한다.
임베딩 층(embedding layer)에서는,
그 가중치(weight)에 $\sqrt{d_{\text{model}}}$을 곱한다.
임베딩과 출력층의 가중치 공유 (Weight Tying)
일반적인 신경망 언어 모델에서는
입력 측(Input Embedding): 단어의 원-핫 벡터(one-hot vector, 차원 $|V|$)를
$d_{\text{model}}$ 차원의 임베딩 벡터로 변환한다.
이때 사용하는 행렬은 $W \in \mathbb{R}^{|V| \times d_{\text{model}}}$ 이다.출력 측(Output Projection): 디코더의 은닉 벡터($d_{\text{model}}$ 차원)를
어휘 분포(vocabulary distribution, 차원 $|V|$)로 변환한다.
보통 새로운 파라미터 $W’ \in \mathbb{R}^{d_{\text{model}} \times |V|}$를 두지만,
Transformer에서는 $W’ = W^\top$로 두어 입력 임베딩과 동일한 행렬을 전치(transpose)하여 사용한다.이렇게 하면
- 파라미터 수가 줄어들어 효율성이 좋아지고,
- 입출력 임베딩 공간을 일관성 있게 공유하므로 학습이 안정된다.
이 기법은 Press & Wolf (2017) [24]에서 제안되었으며,
이후 Transformer를 포함한 최신 언어 모델에서 표준적으로 채택되었다.
왜 $\sqrt{d_{\text{model}}}$을 곱하는가?
임베딩 행렬의 각 원소는 평균 0, 분산 1로 초기화된다.
이 경우, $d_{\text{model}}$ 차원 임베딩 벡터의 기대되는 크기(norm)는
대략 $\sqrt{d_{\text{model}}}$ 정도가 된다.그러나 $\sqrt{d_{\text{model}}}$은 상대적으로 작은 값이기 때문에,
초기 학습 시 어텐션의 softmax가 거의 균등 분포를 내뱉는 문제가 생길 수 있다.따라서 Transformer에서는 임베딩에 $\sqrt{d_{\text{model}}}$을 곱하여
norm 크기를 $\approx d_{\text{model}}$ 수준으로 맞춘다.
이렇게 하면 임베딩 벡터의 스케일이 커져 학습이 안정되고,
softmax가 유의미한 확률 분포를 산출할 수 있다.정리하면:
- 곱하기 전: norm ≈ $\sqrt{d_{\text{model}}}$ (너무 작음)
- 곱한 후: norm ≈ $d_{\text{model}}$ (적정한 크기)
반대로, 어텐션 내적에서는 값이 지나치게 커지므로
$\sqrt{d_k}$으로 나누어 균형을 맞춘다.
즉, 임베딩에서는 곱하고, 어텐션에서는 나눈다.
3.5 위치 인코딩 (Positional Encoding)
우리의 모델은 순환(recurrence)이나 합성곱(convolution)을 포함하지 않기 때문에,
모델이 시퀀스의 순서를 활용할 수 있도록,
시퀀스 내 토큰들의 상대적(relative) 또는 절대적(absolute) 위치에 대한 정보를 주입해야 한다.
이를 위해, 우리는 인코더와 디코더 스택의 가장 아래에서
입력 임베딩(input embedding)에 위치 인코딩(positional encoding)을 더해준다.
위치 인코딩(positional encoding)은 임베딩과 동일한 차원 $d_{\text{model}}$을 가지므로,
두 값을 더할 수 있다.
위치 인코딩(positional encoding)에는 학습되는 방식과 고정된 방식(fixed) 등 여러 선택지가 있다 [8].
본 연구에서는 서로 다른 주파수를 갖는 사인(sine)과 코사인(cosine) 함수를 사용한다:
\[PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\] \[PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\]
여기서 $pos$는 위치(position), $i$는 차원(index of dimension)을 의미한다.
즉, 위치 인코딩(positional encoding)의 각 차원은 하나의 사인파(sinusoid)에 대응한다.
파장의 길이는 $2\pi$에서 $10000 \cdot 2\pi$까지 기하급수적 수열(geometric progression)을 이룬다.
우리는 이 함수를 선택했는데, 그 이유는
어떠한 고정된 오프셋(offset) $k$에 대해서도 $PE_{pos+k}$가
$PE_{pos}$의 선형 함수(linear function)로 표현될 수 있기 때문에,
모델이 상대적 위치(relative position)에 따라 어텐션을 학습하기 쉬울 것이라고 가정했기 때문이다.
사인/코사인 위치 인코딩의 직관적 의미
Transformer에서는 위치 인코딩을
\(PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right), \quad PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\)
로 정의한다.이때 중요한 성질은, 어떠한 고정된 오프셋(offset) $k$에 대해서도
$PE_{pos+k}$가 $PE_{pos}$의 선형 함수(linear function)로 표현될 수 있다는 점이다.예를 들어, 삼각함수 항등식
\(\sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b)\)
\(\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)\)
을 이용하면, $PE_{pos+k}$는 $PE_{pos}$와 상수($\sin(k), \cos(k)$)의 선형 결합으로 나타낼 수 있다.👉 따라서 모델은 단순히 “절대 위치”뿐만 아니라,
두 토큰 간의 “상대적 거리(relative distance)”를 쉽게 학습할 수 있다.
이것이 사인/코사인 기반 위치 인코딩의 핵심 직관이다.
우리는 또한 [8]에 따라 학습된 위치 임베딩(learned positional embedding)을 사용하는 실험도 진행했으며,
두 가지 방식 모두 거의 동일한 결과를 산출함을 확인했다 (표 3의 (E) 행 참조).
우리는 사인(sinusoidal) 기반 방식을 선택했는데,
그 이유는 이 방식이 훈련 중에 관찰된 길이보다 더 긴 시퀀스 길이로도
모델이 일반화(extrapolate)할 수 있도록 해줄 수 있기 때문이다.
4. 왜 셀프-어텐션(Self-Attention)인가?
이 절(section)에서는,
$(x_1, \dots, x_n)$과 같은 가변 길이(variable-length)의 기호 표현 시퀀스를
$(z_1, \dots, z_n)$과 같은 동일 길이의 다른 시퀀스로 매핑하는 데 일반적으로 사용되는
순환 층(recurrent layer)과 합성곱 층(convolutional layer)에 대해,
셀프-어텐션(self-attention) 층의 여러 측면을 비교한다.
여기서 $x_i, z_i \in \mathbb{R}^d$이며, 이는 전형적인 시퀀스 변환 인코더나 디코더의
은닉층(hidden layer)에 해당한다.
셀프-어텐션(self-attention)의 사용을 정당화하기 위해,
우리는 세 가지 바람직한 조건(desiderata)을 고려한다.
첫째는, 각 층(layer)에 대한 총 계산 복잡도(computational complexity)이다.
둘째는, 병렬화할 수 있는 계산의 양으로,
이는 필요한 최소한의 순차적 연산(sequential operations) 수로 측정된다.
셋째는, 네트워크에서 멀리 떨어진 두 위치가 서로 의존 관계를 형성할 때,
그 관계가 전달되는 경로 길이(path length)이다.
장기 의존성(long-range dependency)을 학습하는 것은
많은 시퀀스 변환(sequence transduction) 과제에서 핵심적인 도전 과제이다.
이러한 의존성을 학습하는 능력에 영향을 미치는 핵심 요인 중 하나는,
순방향(forward) 및 역방향(backward) 신호가 네트워크를 통해 지나가야 하는 경로의 길이(path length)이다.
입력 시퀀스와 출력 시퀀스 내 임의의 위치 조합 사이의 이러한 경로가 짧을수록,
장기 의존성(long-range dependency)을 학습하기가 더 쉬워진다 [11].
따라서 우리는 또한, 서로 다른 층(layer) 유형들로 구성된 네트워크에서
임의의 두 입력 및 출력 위치 사이의 최대 경로 길이(maximum path length)를 비교한다.
표 1 서로 다른 층 유형(layer type)에 따른 최대 경로 길이, 층별 복잡도, 최소 순차 연산 수.
여기서 $n$은 시퀀스 길이(sequence length), $d$는 표현 차원(representation dimension),
$k$는 합성곱(convolution)의 커널 크기(kernel size), $r$은 제한된(self-attention restricted) 셀프-어텐션의 이웃 크기(neighborhood size)를 의미한다.
| 층 유형 (Layer Type) | 층별 복잡도 (Complexity per Layer) | 최소 순차 연산 수 (Sequential Operations) | 최대 경로 길이 (Maximum Path Length) |
|---|---|---|---|
| Self-Attention | $O(n^2 \cdot d)$ | $O(1)$ | $O(1)$ |
| Recurrent | $O(n \cdot d^2)$ | $O(n)$ | $O(n)$ |
| Convolutional | $O(k \cdot n \cdot d^2)$ | $O(1)$ | $O(\log_k(n))$ |
| Self-Attention (restricted) | $O(r \cdot n \cdot d)$ | $O(1)$ | $O(n/r)$ |
표 1에서 알 수 있듯이,
셀프-어텐션(self-attention) 층은 모든 위치들을 상수 개수의 순차적 연산(constant number of sequential operations)만으로 연결한다.
반면, 순환 층(recurrent layer)은 $O(n)$의 순차적 연산을 필요로 한다.
계산 복잡도(computational complexity) 측면에서,
시퀀스 길이 $n$이 표현 차원 $d$보다 작을 때, 셀프-어텐션(self-attention) 층은 순환 층(recurrent layer)보다 더 빠르다.
이는 최신(state-of-the-art) 기계 번역 모델에서 사용하는 문장 표현(sentence representation)들,
예를 들어 워드피스(word-piece) [31]나 바이트-페어(byte-pair) [25] 표현 방식에서 대부분 해당된다.
WordPiece와 Byte-Pair Encoding (BPE)
WordPiece와 Byte-Pair Encoding (BPE)는
긴 단어를 더 작은 단위(subword)로 분할하여 표현하는 서브워드 분절 기법이다.
WordPiece [31]: 구글 신경망 번역(GNMT)에서 사용된 방식으로,
자주 등장하는 서브워드를 어휘(vocabulary)에 포함시키고, 드물게 등장하는 단어는 여러 서브워드의 결합으로 표현한다.
예: unbelievable → un + ##believe + ##ableBPE (Byte-Pair Encoding) [25]: 가장 자주 등장하는 바이트 쌍(byte pair)을 반복적으로 병합하여 서브워드 사전을 구축하는 방식.
데이터 압축 기법에서 착안되었으며, 기계 번역 및 언어 모델에서 널리 쓰인다.
예: lower, lowest → low + er, low + est👉 이러한 기법들을 사용하면 어휘 크기를 줄이면서도 희귀 단어(OOV, Out-Of-Vocabulary) 문제를 완화할 수 있다.
특히 문장의 평균 길이가 상대적으로 짧아지므로, $n < d$ 조건에서 Self-Attention이 계산 효율성 측면에서 RNN보다 유리하다.
매우 긴 시퀀스가 포함된 과제에서 계산 성능(computational performance)을 개선하기 위해,
셀프-어텐션(self-attention)은 입력 시퀀스에서 해당 출력 위치를 중심으로
크기 $r$인 이웃(neighborhood)만을 고려하도록 제한할 수 있다.
이 경우 최대 경로 길이(maximum path length)는 $O(n/r)$로 증가하게 된다.
우리는 이러한 접근 방식을 향후 연구에서 더 자세히 탐구할 계획이다.
왜 최대 경로 길이가 $O(n/r)$로 늘어나는가?
제한된(Self-Attention with restriction) 어텐션에서는,
각 위치가 전체 시퀀스가 아니라 자신을 중심으로 반경 $r$ 이웃(neighborhood)만 볼 수 있다.
일반적인 셀프-어텐션: 모든 위치가 직접 연결되므로,
어떤 두 위치 사이의 최대 경로 길이는 $O(1)$.제한된 어텐션: 예를 들어 $n$ 길이 시퀀스에서
맨 앞 위치와 맨 뒤 위치가 서로 의존성을 전달하려면,
한 번에 $r$칸씩만 건너뛸 수 있기 때문에,
총 $n/r$ 단계의 경로를 거쳐야 한다.따라서 최대 경로 길이는 $O(n/r)$가 된다.
이는 계산 효율성을 얻는 대신, 장기 의존성을 학습하는 데 필요한 경로가 길어져
정보 전달이 어려워질 수 있다는 trade-off를 의미한다.
커널 너비 $k < n$인 단일 합성곱(convolution) 층은
모든 입력 및 출력 위치 쌍을 연결하지는 못한다.
이를 달성하기 위해서는,
연속적인 커널(contiguous kernel)의 경우 $O(n/k)$ 개의 합성곱 층(convolutional layer) 스택이 필요하며,
팽창 합성곱(dilated convolution) [15]의 경우 $O(\log_k(n))$ 개가 필요하다.
이로 인해 네트워크 내 임의의 두 위치 사이의 가장 긴 경로의 길이가 증가하게 된다.
합성곱의 커널 크기와 경로 길이 관계
합성곱 신경망(Convolutional Neural Network, CNN)에서 커널 크기 $k$는
한 번의 연산으로 얼마나 넓은 범위를 볼 수 있는지를 결정한다.
커널 크기 $k < n$ (연속 커널, contiguous kernel):
한 번의 합성곱으로는 전체 시퀀스를 연결할 수 없다.
따라서 전체 $n$ 길이 시퀀스를 커버하려면 $O(n/k)$ 층을 쌓아야 한다.팽창 합성곱 (dilated convolution):
커널 간격을 넓혀서 더 빠르게 범위를 확장할 수 있다.
이 경우 필요한 층 수는 $O(\log_k(n))$로 줄어든다.직관적 예시
- 시퀀스 길이 $n=16$, 커널 크기 $k=2$인 경우:
- 연속 커널 → $16/2 = 8$ 층이 필요
- dilated 커널 → $\log_2(16) = 4$ 층이면 충분
👉 따라서 CNN은 병렬화는 가능하지만,
모든 위치를 연결하기 위해 층을 여러 개 쌓아야 하고,
그만큼 경로 길이(path length)가 길어진다는 단점이 있다.
반면, 셀프-어텐션(Self-Attention)은 단일 층에서도 모든 위치를 직접 연결할 수 있어
최대 경로 길이가 $O(1)$이다.
합성곱(convolutional) 층은 일반적으로,
순환(recurrent) 층보다 $k$ 배 더 비용이 많이 든다.
그러나 분리 합성곱(separable convolution) [6]은
복잡도를 크게 줄여서 $O(k \cdot n \cdot d + n \cdot d^2)$로 만든다.
그러나 $k = n$인 경우에도,
분리 합성곱(separable convolution)의 복잡도는
우리 모델에서 사용했던 접근 방식인 셀프-어텐션(self-attention) 층과 위치별(position-wise) 피드-포워드 층의 결합과 동일하다.
일반 합성곱 vs 분리 합성곱 (Separable Convolution)
일반 합성곱 (Standard Convolution):
입력 시퀀스의 모든 위치와 채널에 대해 동시에 합성곱을 적용한다.
연산량은 대략 $O(k \cdot n \cdot d^2)$ 수준으로 크다.분리 합성곱 (Separable Convolution):
연산을 두 단계로 나눈다.
- 공간 방향 합성곱 (Spatial convolution): 커널 크기 $k$를 따라 각 채널에 대해 독립적으로 합성곱 수행 → $O(k \cdot n \cdot d)$
- 채널 방향 합성곱 (Pointwise / $1 \times 1$ convolution): 위치별로 채널을 섞는 연산 → $O(n \cdot d^2)$
최종 연산량: $O(k \cdot n \cdot d + n \cdot d^2)$
직관적 이해
- 일반 합성곱: “모든 채널 × 커널”을 한꺼번에 곱하는 무거운 방식
- 분리 합성곱: “위치 방향(k)” 연산과 “채널 방향(d)” 연산을 분리해서 계산량 절감
결과적으로, 분리 합성곱은 일반 합성곱에 비해 계산 효율성이 크게 향상되어,
특히 커널 크기 $k$가 큰 경우 효과가 두드러진다.
부가적인 이점으로,
셀프-어텐션(self-attention)은 더 해석 가능성 높은(interpretable) 모델을 만들어낼 수 있다.
우리는 우리의 모델에서 나온 어텐션 분포(attention distribution)를 조사하고,
부록(appendix)에서 그 예시들을 제시하고 논의한다.
개별 어텐션 헤드들이 서로 다른 작업을 학습한다는 것이 명확할 뿐만 아니라,
많은 헤드들은 문장의 구문적(syntactic) 및 의미적(semantic) 구조와 관련된 동작을 보이는 것으로 나타난다.
5 학습 (Training)
이 절에서는 우리의 모델들을 위한 학습 방식(training regime)을 설명한다.
5.1 학습 데이터와 배칭 (Training Data and Batching)
우리는 약 450만 개의 문장 쌍으로 이루어진
표준 WMT 2014 영어-독일어 데이터셋에서 학습을 진행하였다.
문장들은 바이트 페어 인코딩(Byte-Pair Encoding, BPE) [3]을 사용하여 인코딩되었으며,
약 37,000개의 토큰으로 이루어진 소스-타깃 공유 어휘집(shared source-target vocabulary)을 가진다.
영어-프랑스어의 경우, 우리는 훨씬 더 큰 규모인 WMT 2014 영어-프랑스어 데이터셋을 사용했으며,
이는 약 3천6백만 개의 문장으로 이루어져 있다.
또한 토큰을 분할하여 32,000개의 단어 조각(word-piece) 어휘집을 구성하였다 [31].
문장 쌍들은 대략적인 시퀀스 길이에 따라 배치(batch)로 묶였다.
각 학습 배치(batch)는 약 25,000개의 소스 토큰(source tokens)과
25,000개의 타깃 토큰(target tokens)을 포함하는 문장 쌍 집합으로 구성되었다.
5.2 하드웨어와 학습 스케줄 (Hardware and Schedule)
우리는 하나의 머신에서 8개의 NVIDIA P100 GPU를 사용하여 모델을 학습시켰다.
논문 전반에서 설명한 하이퍼파라미터들을 사용하는 기본(base) 모델의 경우,
각 학습 스텝(training step)은 약 0.4초가 소요되었다.
우리는 기본(base) 모델을 총 100,000 스텝(steps), 즉 약 12시간 동안 학습시켰다.
대형(big) 모델의 경우 (표 3의 마지막 행에 설명됨),
각 학습 스텝(step)당 소요 시간은 약 1.0초였다.
대형(big) 모델은 총 300,000 스텝(steps) 동안 학습되었으며,
이는 약 3.5일에 해당한다.
5.3 옵티마이저 (Optimizer)
우리는 Adam 옵티마이저(Adam optimizer) [17]를 사용하였으며,
$\beta_1 = 0.9$, $\beta_2 = 0.98$, $\epsilon = 10^{-9}$로 설정하였다.
우리는 학습 과정 동안 학습률(learning rate)을 다음의 수식에 따라 변화시켰다:
\[\text{lrate} = d_{\text{model}}^{-0.5} \cdot \min \left( \text{step_num}^{-0.5},\ \text{step_num} \cdot \text{warmup_steps}^{-1.5} \right) \tag{3}\]
이는 학습률(learning rate)을 처음 warmup_steps 동안은 선형적으로 증가시키고,
그 이후에는 스텝(step) 수의 역제곱근(inverse square root)에 비례하여 감소시키는 것에 해당한다.
우리는 warmup_steps = 4000으로 설정하였다.
5.4 정규화 (Regularization)
우리는 학습 과정에서 세 가지 유형의 정규화(regularization)를 사용하였다.
Residual Dropout
우리는 각 서브-레이어(sub-layer)의 출력에 드롭아웃(dropout) [27]을 적용하였다.
이는 출력이 서브-레이어 입력에 더해지고 정규화(normalization)되기 이전에 수행된다.
추가적으로, 인코더와 디코더 스택 모두에서
임베딩(embedding)과 위치 인코딩(positional encoding)의 합에도 드롭아웃(dropout)을 적용하였다.
기본(base) 모델의 경우, 드롭아웃 비율은 $P_{\text{drop}} = 0.1$로 사용하였다.
Label Smoothing
학습 과정에서 우리는 라벨 스무딩(label smoothing) 기법을 사용하였으며,
그 값은 $\epsilon_{ls} = 0.1$로 설정하였다 [30].
이는 모델이 더 불확실하게 학습되도록 만들기 때문에 퍼플렉서티(perplexity)는 나빠지지만,
정확도(accuracy)와 BLEU 점수는 향상된다.
라벨 스무딩(Label Smoothing)과 Perplexity
라벨 스무딩(Label Smoothing)
일반적인 분류 문제에서는 정답 라벨을 원-핫(One-hot) 벡터로 표현한다.
예를 들어 클래스가 5개이고 정답이 3번 클래스라면:
$[0, 0, 1, 0, 0]$ 과 같이 표현된다.
그러나 이 경우 모델은 지나치게 확신(confident)하게 학습되어,
오버피팅(overfitting)이나 일반화 성능 저하 문제가 발생할 수 있다.라벨 스무딩은 정답 라벨에 작은 확률 질량(probability mass)을 다른 클래스에도 분산시킨다.
예를 들어 $\epsilon_{ls}=0.1$이라면:
$[0, 0, 1, 0, 0] \;\;\;\to\;\;\; [0.025, 0.025, 0.9, 0.025, 0.025]$
이렇게 함으로써 모델이 덜 확신하도록 만들어, 일반화가 향상된다.Perplexity(혼잡도)
Perplexity는 언어 모델의 예측 분포와 실제 정답 분포의 차이를 측정하는 지표이다.
수식은 다음과 같다:
\(\text{Perplexity} = \exp\left( -\frac{1}{N} \sum_{i=1}^N \log p(y_i) \right)\)
여기서 $p(y_i)$는 정답 단어 $y_i$에 대해 모델이 할당한 확률이다.
값이 낮을수록 모델이 정답에 높은 확률을 부여한다는 의미다.라벨 스무딩과의 관계
라벨 스무딩을 적용하면 모델이 정답 클래스에 100% 확신을 갖지 않으므로,
정답 단어의 확률 $p(y_i)$가 낮아져 perplexity는 다소 높아진다.
하지만 이러한 불확실성이 오히려 과적합을 방지하고,
BLEU 점수 및 실제 정확도에서는 더 나은 결과를 보인다.
6 결과 (Results)
6.1 기계 번역 (Machine Translation)
WMT 2014 영어→독일어 번역 과제에서,
대형(big) Transformer 모델(표 2의 Transformer (big))은
이전에 보고된 최고 성능 모델들(앙상블 모델 포함)을 2.0 BLEU 이상 능가하며,
새로운 최첨단(state-of-the-art) BLEU 점수 28.4를 달성하였다.
이 모델의 설정(configuration)은 표 3의 마지막 행(bottom line)에 나와 있다.
학습에는 8개의 P100 GPU를 사용하여 약 3.5일이 소요되었다.
우리의 기본(base) 모델조차도
이전에 발표된 모든 모델들과 앙상블을 능가했으며,
경쟁 모델들의 학습 비용 대비 일부(fraction)에 불과한 비용으로 이를 달성하였다.
WMT 2014 영어→프랑스어 번역 과제에서,
우리의 대형(big) 모델은 BLEU 점수 41.0을 달성하였으며,
이전까지 발표된 모든 단일(single) 모델들을 능가하였다.
또한 이는 이전 최첨단(state-of-the-art) 모델의 학습 비용의 1/4 미만으로 달성된 결과이다.
영어→프랑스어 학습에 사용된 Transformer (big) 모델은
드롭아웃 비율 $P_{\text{drop}} = 0.1$을 사용하였으며,
이는 0.3 대신 적용된 값이다.
기본(base) 모델의 경우,
우리는 10분 간격으로 저장된 마지막 5개의 체크포인트(checkpoints)를 평균하여 얻은 단일(single) 모델을 사용하였다.
대형(big) 모델의 경우,
우리는 마지막 20개의 체크포인트(checkpoints)를 평균하였다.
체크포인트 평균(Checkpoint Averaging) vs 앙상블(Ensemble)
구분 체크포인트 평균 (Checkpoint Averaging) 앙상블 (Ensemble) 방식 여러 시점에서 저장된 모델의
가중치(weight)를 평균하여 하나의 모델을 만든다.여러 개의 완성된 모델이 예측한 출력을 평균한다. 결과 단일 모델 → 추론 시 계산 효율적 다중 모델 → 추론 시 계산 비용 증가 장점 - 추론 비용이 증가하지 않음
- 학습 후반의 진동(oscillation) 완화
- 더 안정적이고 일반화 성능이 향상- 서로 다른 모델의 강점을 결합
- 보통 성능이 가장 높음단점 - 성능 향상은 앙상블에 비해 제한적 - 추론 시 속도 저하 및 메모리 증가 Transformer 논문에서는 체크포인트 평균을 사용하여,
성능 향상을 얻으면서도 추론 효율성을 유지하였다.
우리는 빔 서치(beam search)를 사용했으며,
빔 크기(beam size)는 4, 길이 패널티(length penalty)는 $\alpha = 0.6$으로 설정하였다 [31].
이러한 하이퍼파라미터들은 개발용 데이터셋(development set)에서의 실험을 통해 선택되었다.
빔 서치(Beam Search)와 길이 패널티(Length Penalty)
- 빔 서치(Beam Search)
기계 번역에서 다음 단어를 예측할 때, 단순히 확률이 가장 높은 단어 하나만 고르면
전체 문장의 질이 떨어질 수 있다.
대신 빔 서치는 각 시점에서 상위 beam size 개의 후보를 유지하며
여러 경로를 동시에 탐색한다.
- beam size = 1 → 단순 그리디 탐색(greedy search)
- beam size ↑ → 탐색 폭이 넓어져 더 나은 번역 가능 (하지만 속도 저하)
- 길이 패널티(Length Penalty)
빔 서치에서는 짧은 번역문이 확률적으로 더 높게 나오는 경향이 있다.
이를 보정하기 위해 길이에 따른 패널티(α)를 적용한다.
- $\alpha = 0$ → 패널티 없음 (짧은 번역 선호)
- $\alpha > 0$ → 긴 문장을 더 선호
Transformer 논문에서는 beam size = 4, α = 0.6을 사용하여
짧지 않으면서도 자연스러운 번역 결과를 얻었다.
추론(inference) 시, 우리는 출력의 최대 길이를 입력 길이 + 50으로 설정하였으며,
가능한 경우에는 조기 종료(early termination)를 수행하였다 [31].
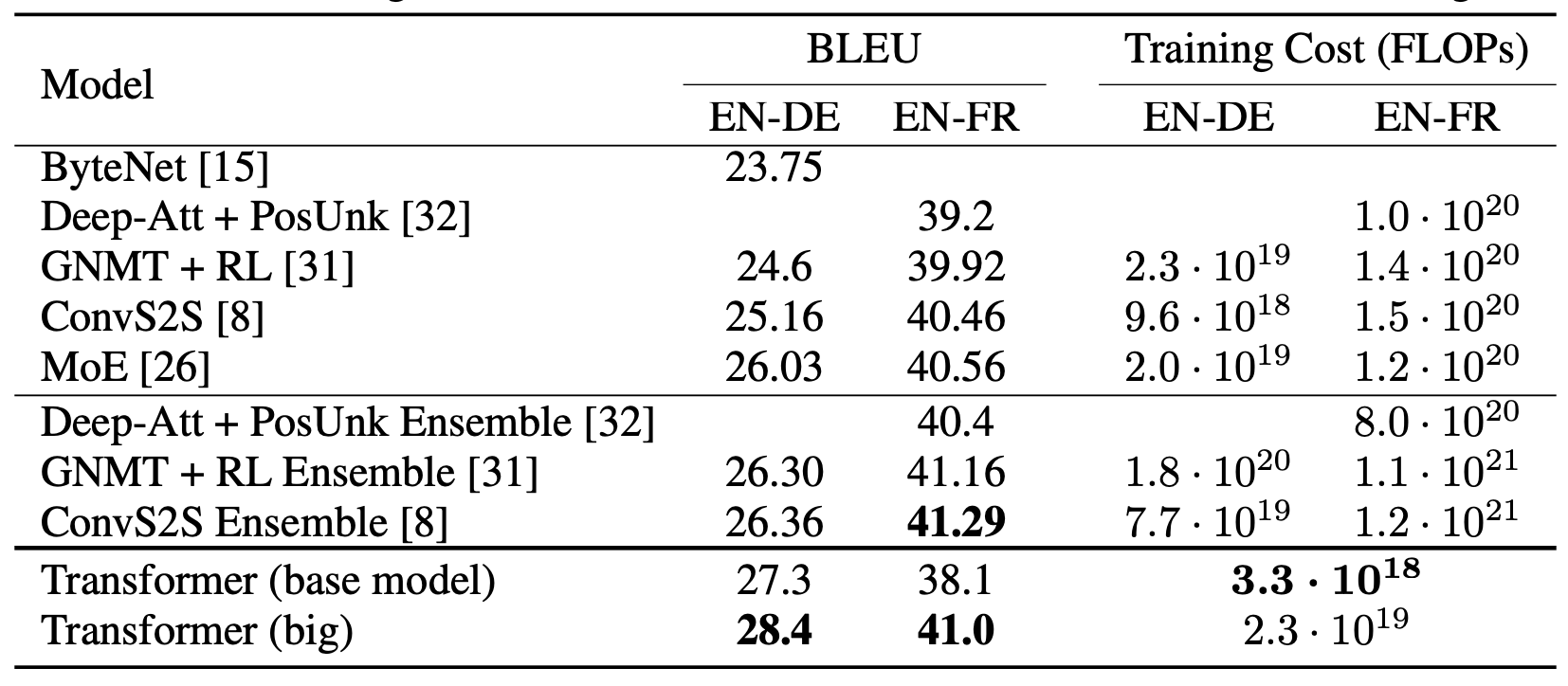
표 2는 우리의 결과를 요약하고,
번역 품질과 학습 비용을 기존 문헌에 보고된 다른 모델 아키텍처들과 비교한 것이다.
표 2: Transformer는 영어→독일어 및 영어→프랑스어 newstest2014 테스트에서,
이전 최첨단(state-of-the-art) 모델들보다 더 높은 BLEU 점수를 달성하였다.
또한 학습 비용은 그에 비해 일부(fraction)에 불과하다.
우리는 모델 학습에 사용된 부동소수점 연산(floating point operations, FLOPs) 수를
학습 시간(training time), 사용된 GPU 수,
그리고 각 GPU의 지속적인(single-precision) 부동소수점 처리 성능 추정치의 곱으로 추정하였다.5
5우리는 각각의 GPU에 대해 다음과 같은 연산 성능 값을 사용하였다:
- K80 : 2.8 TFLOPS
- K40 : 3.7 TFLOPS
- M40 : 6.0 TFLOPS
- P100 : 9.5 TFLOPS
6.2 모델 변형 (Model Variations)
Transformer의 다양한 구성 요소들의 중요성을 평가하기 위해,
우리는 기본(base) 모델을 여러 방식으로 변형시켰다.
그리고 그에 따른 성능 변화를 영어→독일어 번역의 개발용 데이터셋(dev set)인 newstest2013에서 측정하였다.
우리는 이전 절에서 설명한 것과 동일하게 빔 서치(beam search)를 사용했으나,
체크포인트 평균(checkpoint averaging)은 적용하지 않았다.
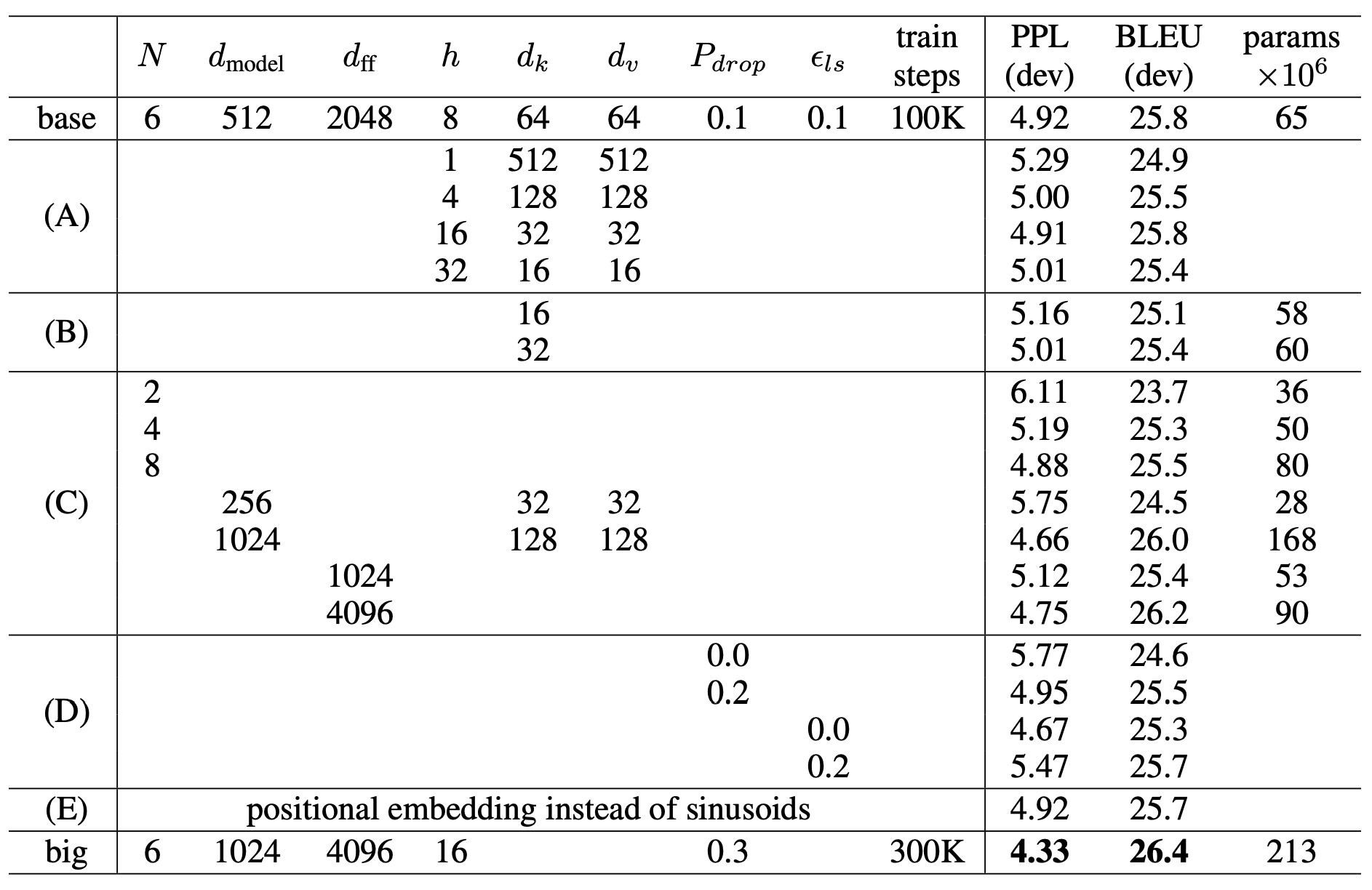
이 결과들은 표 3(Table 3)에 제시하였다.
표 3: Transformer 아키텍처의 변형(Variations).
표에 명시되지 않은 값들은 모두 기본(base) 모델과 동일하다.
모든 평가는 영어→독일어 번역 개발용 데이터셋(newstest2013)에서 수행되었다.
표에 제시된 퍼플렉서티(perplexity)는 바이트 페어 인코딩(Byte-Pair Encoding)에 따른
워드피스(word-piece) 단위로 계산된 것이며, 단어 단위(per-word) 퍼플렉서티와는 비교해서는 안 된다.
표 3의 (A) 행에서는,
우리가 계산량(computation)을 일정하게 유지한 채,
어텐션 헤드(attention heads)의 개수와
어텐션 키(key) 및 값(value)의 차원을 변화시켰다.
(자세한 내용은 3.2.2절에 설명되어 있다.)
단일(single) 헤드 어텐션은 최적 설정 대비 BLEU 점수가 0.9 낮았으며,
헤드 수가 지나치게 많아도 품질이 떨어졌다.
표 3의 (B) 행에서는,
어텐션 키 크기 $d_k$를 줄이는 것이
모델 품질을 저하시킨다는 것을 확인하였다.
이는 호환성(compatibility)을 결정하는 것이 쉽지 않으며,
단순한 내적(dot product)보다 더 정교한 호환 함수(compatibility function)가
도움이 될 수 있음을 시사한다.
우리는 표 3의 (C)와 (D) 행에서,
예상한 대로 더 큰 모델(bigger models)이 더 성능이 좋으며,
드롭아웃(dropout)이 과적합(over-fitting)을 방지하는 데 매우 유용하다는 것을 추가로 관찰하였다.
(E) 행에서는,
우리는 사인(sinusoidal) 기반의 위치 인코딩(positional encoding)을
학습된 위치 임베딩(learned positional embeddings) [8]으로 교체하였으며,
기본(base) 모델과 거의 동일한 결과를 관찰하였다.
7 결론 (Conclusion)
본 연구에서 우리는 Transformer를 제안하였다.
이는 전적으로 어텐션(attention)에만 기반한 최초의 시퀀스 변환(sequence transduction) 모델로서,
인코더-디코더 아키텍처에서 가장 흔히 사용되던 순환 층(recurrent layers)을
멀티-헤드 셀프-어텐션(multi-headed self-attention)으로 대체하였다.
번역 과제에서, Transformer는
순환(recurrent) 또는 합성곱(convolutional) 층에 기반한 아키텍처보다
훨씬 더 빠르게 학습될 수 있다.
WMT 2014 영어→독일어 및 WMT 2014 영어→프랑스어 번역 과제 모두에서,
우리는 새로운 최첨단(state-of-the-art) 성능을 달성하였다.
전자의 과제(영어→독일어)에서는,
우리의 최고 성능 모델이 이전에 보고된 모든 앙상블(ensembles)들까지도 능가하였다.
우리는 어텐션(attention) 기반 모델들의 미래에 대해 매우 고무되어 있으며,
이를 다른 과제들에도 적용할 계획이다.
우리는 Transformer를 텍스트 이외의 입력과 출력 모달리티(modality)를 포함하는 문제들로 확장할 계획이다.
또한 이미지, 오디오, 비디오와 같은 대규모 입력과 출력을 효율적으로 다루기 위해,
지역적(local)이고 제한된(restricted) 어텐션 메커니즘을 탐구할 예정이다.
생성(generation)을 덜 순차적(sequential)으로 만드는 것도 우리의 또 다른 연구 목표이다.
우리의 모델을 학습하고 평가하는 데 사용한 코드는
https://github.com/tensorflow/tensor2tensor
에서 확인할 수 있다.
감사의 글 (Acknowledgements)
우리는 Nal Kalchbrenner와 Stephan Gouws에게
그들의 유익한 의견, 교정, 그리고 영감에 대해 깊이 감사드린다.
참고문헌 (References)
[1] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. Layer normalization.
arXiv preprint arXiv:1607.06450, 2016.
[2] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate.
CoRR, abs/1409.0473, 2014.
[3] Denny Britz, Anna Goldie, Minh-Thang Luong, and Quoc V. Le. Massive exploration of neural machine translation architectures.
CoRR, abs/1703.03906, 2017.
[4] Jianpeng Cheng, Li Dong, and Mirella Lapata. Long short-term memory-networks for machine reading.
arXiv preprint arXiv:1601.06733, 2016.
[5] Kyunghyun Cho, Bart van Merrienboer, Caglar Gulcehre, Fethi Bougares, Holger Schwenk, and Yoshua Bengio.
Learning phrase representations using RNN encoder-decoder for statistical machine translation.
CoRR, abs/1406.1078, 2014.
[6] Francois Chollet. Xception: Deep learning with depthwise separable convolutions.
arXiv preprint arXiv:1610.02357, 2016.
[7] Junyoung Chung, Çaglar Gülçehre, Kyunghyun Cho, and Yoshua Bengio.
Empirical evaluation of gated recurrent neural networks on sequence modeling.
CoRR, abs/1412.3555, 2014.
[8] Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, and Yann N. Dauphin.
Convolutional sequence to sequence learning.
arXiv preprint arXiv:1705.03122, 2017.
[9] Alex Graves. Generating sequences with recurrent neural networks.
arXiv preprint arXiv:1308.0850, 2013.
[10] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun.
Deep residual learning for image recognition.
In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778, 2016.
[11] Sepp Hochreiter, Yoshua Bengio, Paolo Frasconi, and Jürgen Schmidhuber.
Gradient flow in recurrent nets: the difficulty of learning long-term dependencies, 2001.
[12] Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory.
Neural Computation, 9(8):1735–1780, 1997.
[13] Rafal Jozefowicz, Oriol Vinyals, Mike Schuster, Noam Shazeer, and Yonghui Wu.
Exploring the limits of language modeling.
arXiv preprint arXiv:1602.02410, 2016.
[14] Łukasz Kaiser and Ilya Sutskever. Neural GPUs learn algorithms.
In International Conference on Learning Representations (ICLR), 2016.
[15] Nal Kalchbrenner, Lasse Espeholt, Karen Simonyan, Aaron van den Oord, Alex Graves, and Koray Kavukcuoglu.
Neural machine translation in linear time.
arXiv preprint arXiv:1610.10099, 2017.
[16] Yoon Kim, Carl Denton, Luong Hoang, and Alexander M. Rush.
Structured attention networks.
In International Conference on Learning Representations (ICLR), 2017.
[17] Diederik Kingma and Jimmy Ba. Adam: A method for stochastic optimization.
In International Conference on Learning Representations (ICLR), 2015.
[18] Oleksii Kuchaiev and Boris Ginsburg. Factorization tricks for LSTM networks.
arXiv preprint arXiv:1703.10722, 2017.
[19] Zhouhan Lin, Minwei Feng, Cicero Nogueira dos Santos, Mo Yu, Bing Xiang, Bowen Zhou, and Yoshua Bengio.
A structured self-attentive sentence embedding.
arXiv preprint arXiv:1703.03130, 2017.
[20] Samy Bengio and Łukasz Kaiser. Can active memory replace attention?
In Advances in Neural Information Processing Systems (NIPS), 2016.
[21] Minh-Thang Luong, Hieu Pham, and Christopher D. Manning.
Effective approaches to attention-based neural machine translation.
arXiv preprint arXiv:1508.04025, 2015.
[22] Ankur Parikh, Oscar Täckström, Dipanjan Das, and Jakob Uszkoreit.
A decomposable attention model.
In Empirical Methods in Natural Language Processing (EMNLP), 2016.
[23] Romain Paulus, Caiming Xiong, and Richard Socher.
A deep reinforced model for abstractive summarization.
arXiv preprint arXiv:1705.04304, 2017.
[24] Ofir Press and Lior Wolf. Using the output embedding to improve language models.
arXiv preprint arXiv:1608.05859, 2016.
[25] Rico Sennrich, Barry Haddow, and Alexandra Birch.
Neural machine translation of rare words with subword units.
arXiv preprint arXiv:1508.07909, 2015.
[26] Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean.
Outrageously large neural networks: The sparsely-gated mixture-of-experts layer.
arXiv preprint arXiv:1701.06538, 2017.
[27] Nitish Srivastava, Geoffrey E. Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov.
Dropout: A simple way to prevent neural networks from overfitting.
Journal of Machine Learning Research, 15(1):1929–1958, 2014.
[28] Sainbayar Sukhbaatar, Arthur Szlam, Jason Weston, and Rob Fergus.
End-to-end memory networks.
In Advances in Neural Information Processing Systems (NIPS 28), pp. 2440–2448. Curran Associates, Inc., 2015.
[29] Ilya Sutskever, Oriol Vinyals, and Quoc V. Le.
Sequence to sequence learning with neural networks.
In Advances in Neural Information Processing Systems (NIPS), pp. 3104–3112, 2014.
[30] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna.
Rethinking the inception architecture for computer vision.
CoRR, abs/1512.00567, 2015.
[31] Yonghui Wu, Mike Schuster, Zhifeng Chen, Quoc V. Le, Mohammad Norouzi, Wolfgang Macherey, Maxim Krikun, Yuan Cao, Qin Gao, Klaus Macherey, et al.
Google’s neural machine translation system: Bridging the gap between human and machine translation.
arXiv preprint arXiv:1609.08144, 2016.
[32] Jie Zhou, Ying Cao, Xuguang Wang, Peng Li, and Wei Xu.
Deep recurrent models with fast-forward connections for neural machine translation.
CoRR, abs/1606.04199, 2016.