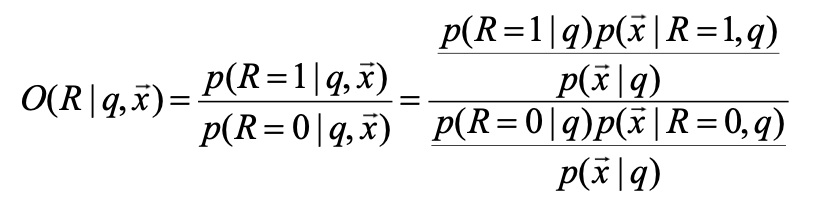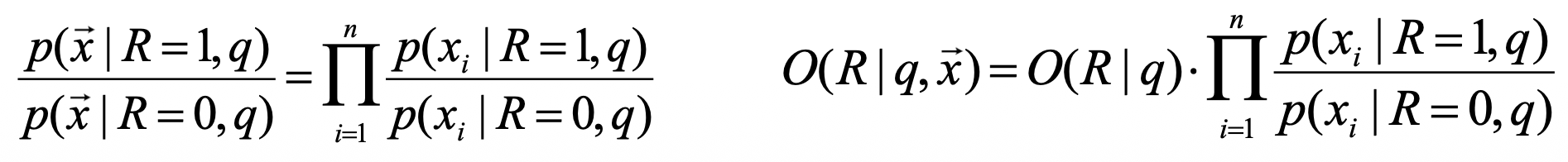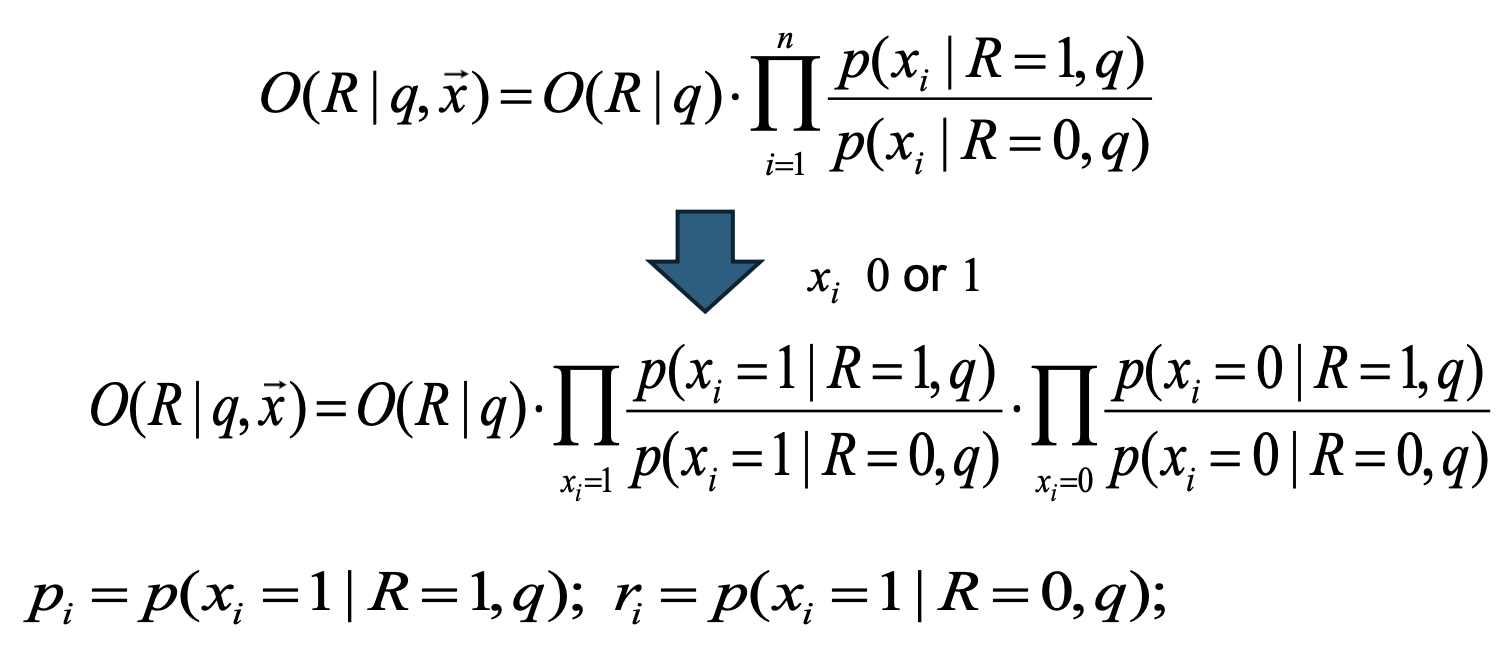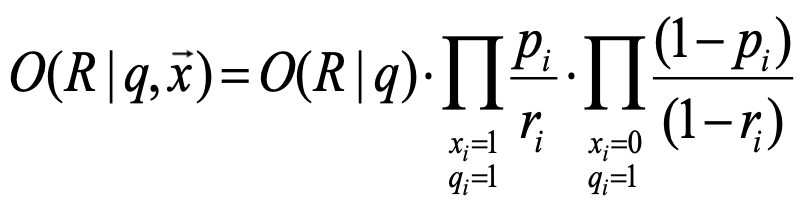[빅데이터와 정보검색] 3주차 검색개요 - 색인과 검색랭킹과 평가(part2)

게시 2025/09/24 업데이트 2025/12/12

By 김성진

85 분읽는 시간

p6. 랭킹 기반 검색 (Ranked Retrieval)

Boolean Query의 장점과 한계
- 불리언 질의: 문서가 질의와 일치하거나, 그렇지 않거나 둘 중 하나
장점
- 자신의 요구사항과 문서 집합을 정확하게 이해하는 전문가에게 유용
- 애플리케이션이 수천 개의 결과를 쉽게 처리할 수 있어 응용 프로그램에 적합
한계
- 대부분의 일반 사용자에게는 적합하지 않음
- 대다수 사용자는 불리언 질의를 작성하는 데 어려움을 느끼거나, 작성하는 것을 번거로워함
- 대부분의 사용자는 수천 개의 결과 목록을 일일이 확인하는 것을 원하지 않음
- 결과 수의 불균형: 결과의 수가 너무 적거나(0개) 혹은 너무 많은(수천 개) 극단적 상황 초래
  
  → 적절한 수의 결과를 얻기 위해서는 상당한 수준의 질의 작성 기술이 필요
  (AND: 종종 너무 적은 결과, OR: 종종 너무 많은 결과)

Boolean Query의 특성
AND / OR / NOT 기반의 필터링 방식으로, 결과는 “포함된다 / 포함되지 않는다”의 이분법적 형태만 제공된다.
문서 간 관련성의 강도를 반영하지 못하는 것이 가장 큰 한계이다.
전문가에게 유용한 이유
도메인 지식이 있는 전문가라면 원하는 조건을 매우 정확하게 지정할 수 있다.
법률·특허·의료처럼 정밀 검색이 필요한 분야에서 Boolean Query는 강력한 도구가 된다.
일반 사용자에게 불편한 이유
대부분의 사용자는 복잡한 연산자를 조합해 질의를 구성하기 어렵다.
원하는 답을 얻기 위해 여러 번 질의를 수정해야 해 사용성이 떨어진다.
결과 수의 불균형 문제
AND를 많이 쓰면 결과가 거의 없거나 0개가 될 수 있다.
OR을 많이 쓰면 결과가 지나치게 많아져 사용자가 감당하기 어렵다.
Ranked Retrieval의 필요성
포함 여부만 보는 것은 한계가 있어 문서의 관련성 점수(relevance score) 를 계산해 정렬해야 한다.
이를 통해 사용자는 상위 몇 개 문서만 확인해도 원하는 정보를 쉽게 얻을 수 있다.

p7. 랭킹 기반 검색 (Ranked Retrieval)

랭킹 기반 검색 시스템

질의에 대한 상위(top) 문서들에 순위를 매겨 반환
자유 텍스트 질의 (Free Text Queries)
- 연산자나 표현식 대신, 사용자가 자연어로 하나 또는 그 이상의 단어를 입력하는 방식
랭킹 기반 검색의 장점: 대량 결과 처리
- 사실상 결과 집합의 크기는 중요하지 않아, 대량의 검색 결과가 나와도 문제 없음
- 상위 k개(약 10개)의 결과만 사용자에게 제시
  
  ← 랭킹 알고리즘이 효과적으로 작동한다는 전제 하에 유효

p8. 랭킹 기반 검색의 기본

문서 순위화의 필요성?
- 검색 사용자에게 가장 유용할 가능성이 높은 문서들을 순서대로 제시
어떻게 문서를 순위화 하나?
- 각 문서에 대해 0과 1 사이의 점수를 부여
- 점수: 문서와 질의가 얼마나 잘 일치하는지를 측정한 결과

문서에 부여되는 0과 1 사이의 점수를 관련성(Relevance) 이라고 부른다.
이 값은 질의(Query)와 문서(Document)가 얼마나 잘 일치하는지를 수치적으로 표현한 것이다.

p9. 유사도 측정 방법

Jaccard coefficient
- 개요
  - 두 집합 A, B의 중복의 정도를 측정
  - $jaccard(A, B) = \mid A ∩ B \mid / \mid A ∪ B \mid $
  - $jaccard(A, A) = 1$
  - $jaccard(A, B) = 0 \quad if A ∩ B = 0$
- 한계점
  - 단어 빈도(term frequency)를 고려하지 않음
  - 문서 집합 내에서 드문 단어가 자주 등장하는 단어보다 더 많은 정보를 담고 있지만, 이러한 정보를 고려하지 않음
  - 문서 길이에 대한 정규화 방식이 필요

가장 단순한 랭킹
Jaccard coefficient는 집합의 교집합/합집합 비율만 계산하는 매우 단순한 방식이다.
구현이 쉽고 직관적이라는 장점이 있다.
문서의 크기가 반영되는 장점
합집합의 크기에 문서가 포함한 단어 수가 그대로 들어가므로
문서가 길수록 유사도 계산에서 자연스럽게 영향이 반영된다.
단어 빈도가 표현되지 못하는 단점
단어가 1번 나오든 100번 나오든 “존재=1”로만 처리된다.
즉, 빈도 정보(term frequency) 를 전혀 반영하지 못한다.
쿼리–문서 유사도 계산 방식
쿼리와 문서를 각각 집합으로 보고
유사도 = |쿼리 ∩ 문서| / |쿼리 ∪ 문서| 로 계산한다.
교집합이 클수록, 합집합이 작을수록 유사도가 높아진다.
벡터 표현 방식
쿼리와 문서는 vocabulary 크기 N의 0/1 벡터로 표현된다.
단어가 존재하면 1, 없으면 0 → 예: 01001...
벡터 AND → 교집합 크기, 벡터 OR → 합집합 크기를 구할 수 있다.
한계점 보충 설명
단어 빈도 고려 불가: 중요한 단어가 반복 등장해도 정보가 반영되지 않는다.
드문 단어와 흔한 단어의 구분 불가: “the”와 “인공지능”이 동일 가중치로 취급된다.
문서 길이 영향 문제: 문서가 길수록 합집합이 커져 유사도가 작게 나올 수 있어
길이 정규화가 필요한 경우가 많다.

p10. Bag of Words Model

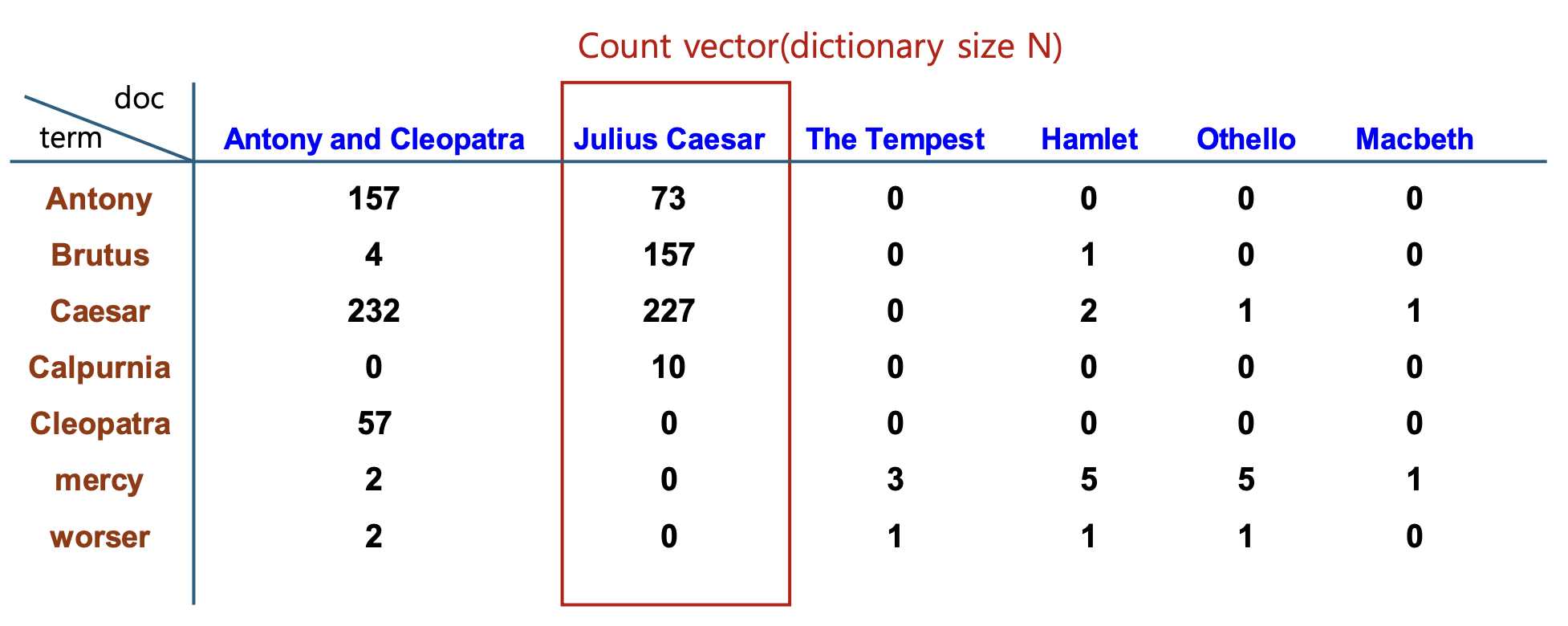
Dictionary와 Term의 문서별 출현빈도 테이블

Bag of Words model : 출현 단어들의 순서관계를 고려하지 않음

Bag of Words라는 말의 유래
“Bag(가방)”이라는 표현은 문서 안의 단어 순서·문법·구조를 모두 무시하고
단지 단어가 몇 번 등장했는지만 기록한다는 의미에서 나온 말이다.
즉, 문서를 “단어가 들어있는 가방”으로 보고,
가방 안에 어떤 단어가 몇 개 들어 있는지만 중요하며 순서는 고려되지 않는다.
예:
“AI is the future”
“the future is AI”
→ 두 문장은 단어 순서가 다르지만 Bag of Words 표현은 동일하다.
위 테이블에 대한 설명
테이블은 각 단어(term)가 여러 문서에서 몇 번 등장했는지(Term Frequency) 를 보여주는 빈도 매트릭스이다.
행(row)은 단어, 열(column)은 문서를 의미한다.
각 셀에는 해당 단어가 해당 문서에서 등장한 횟수가 들어간다.
예: “Caesar”는
Antony and Cleopatra 문서에서 232번 등장
Julius Caesar 문서에서 227번 등장
이런 빈도 매트릭스는 이후 Count Vector, TF-IDF 벡터,
그리고 문서 간 유사도 계산 및 랭킹의 기본 자료가 된다.

p11. Tf-idf

Tf(term frequency)
- 문서 d에 t가 나타나는 횟수: $tf_{t,d}$
- Log frequency weight
\[w_{t,d} = \begin{cases} 1 + \log tf_{t,d}, & \text{if } tf_{t,d} > 0 \\ 0, & \text{otherwise} \end{cases}\] \[score = \sum_{t \in q \cap d} (1 + \log tf_{t,d})\]
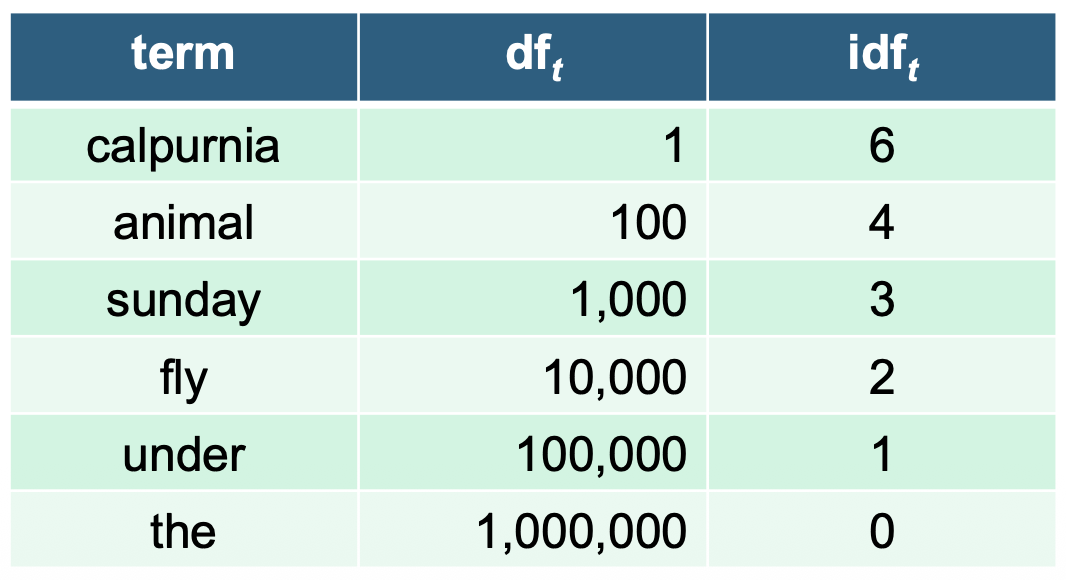
Idf
- T의 문서 빈도(t를 포함하는 문서의 수): $df_t$
- T의 정보성 측정: Inverse document frequency
  \[idf_t = \log \left(\frac{N}{df_t}\right)\]

log의 역할
단어의 빈도 $latex\ tf_{t,d}$ 가 너무 커지면 특정 단어가 과도하게 중요하게 평가되는 것을 막아준다.
로그를 적용하면 빈도 증가 효과가 점점 완만해져, 자주 등장하는 단어라도 영향력이 포화(saturation) 되어 균형 잡힌 가중치를 만들 수 있다.

p12. Tf-idf

Idf
- 질의 랭킹에의 영향: 단일어 질의에는 영향을 미치지 않으나, 2개 이상의 용어로 구성된 질의에는 영향을 미침
- 예) 질의 “carpricious perspn” 에서 “carpricious” 가 “person” 보다 최종 문서 랭킹에 더 큰 비중
정보검색의 가중치 부여방식
\[w_{t,d} = \log(1+tf_{t,d}) \times \log_{10}\left(\frac{N}{df_t}\right)\]
- 문서 내에서 해당 용어가 출현하는 횟수가 많을수록 값이 커지고,
  전체 문서 집합에서 해당 용어가 희귀할수록 값이 커진다.
\[Score(q,d) = \sum_{t \in q \cap d} tf \cdot idf_{t,d}\]

왜 idf는 단일어 질의에 영향이 없나?
단일어 질의 $q={t}$ 의 점수는
$Score(d,q)=tf_{t,d}\cdot idf_t$
로 계산된다.
여기서 $idf_t$ 는 모든 문서에 동일하게 곱해지는 상수이므로
문서 간 순위는 $tf_{t,d}$ 값만으로 결정된다.
반면 다중어 질의 $q={t_1,t_2,\dots}$ 에서는
$Score(d,q)=\sum_i tf_{t_i,d}\,idf_{t_i}$
가 되므로, 단어마다 $idf$ 값이 달라
희귀한 단어(큰 idf) 가 점수에 더 크게 기여 → 문서 순위가 달라진다.
왜 $1+$ 를 $\log$ 안에 넣는가?
$tf_{t,d}=0$ 일 때 $\log(tf_{t,d})$ 는 정의되지 않는다.
이를 피하기 위해
$w_{t,d}=\log(1+tf_{t,d})$
로 정의하면
$tf_{t,d}=0 \Rightarrow w_{t,d}=0$ 으로 자연스럽게 0 가중치가 되고
$tf$ 가 커질수록 증가폭이 완만해져 포화(saturation) 효과도 얻을 수 있다.

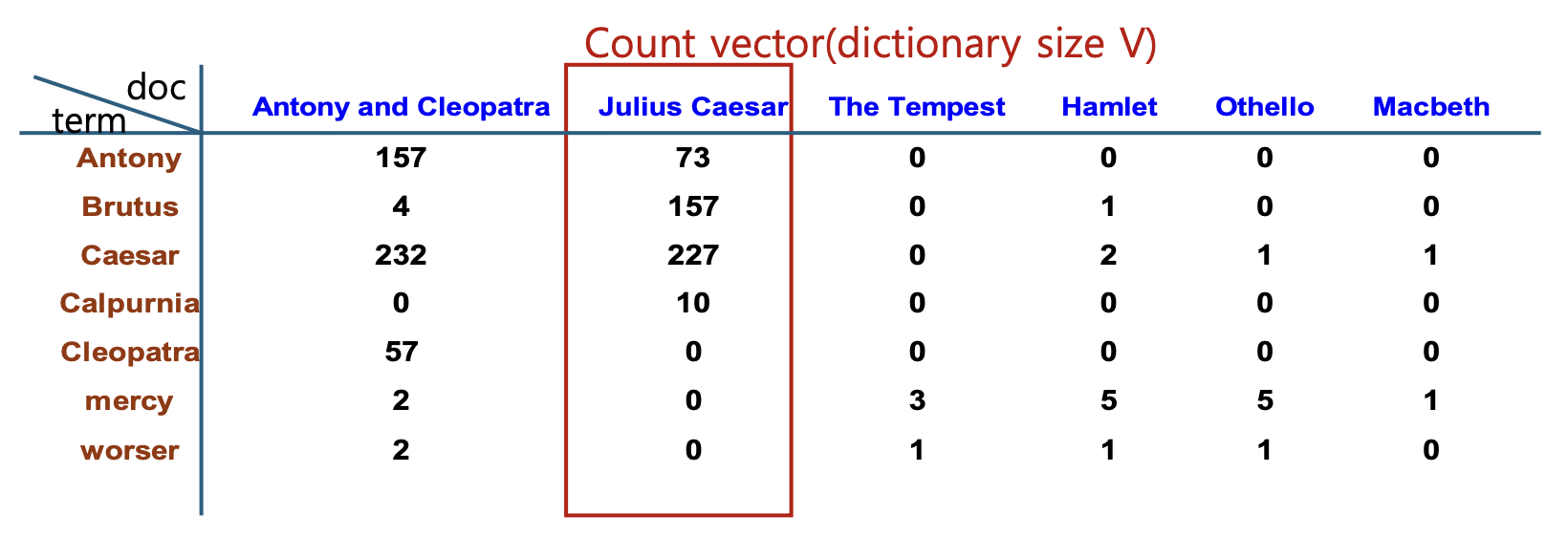
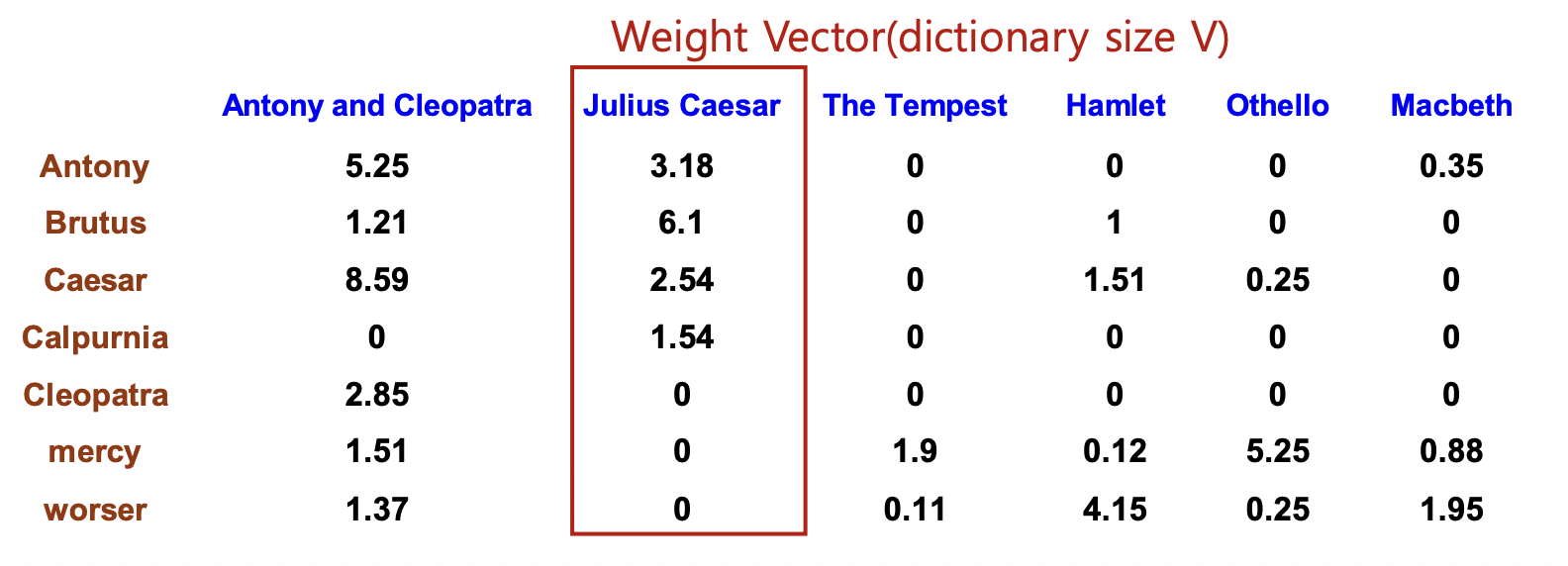
p13. Tf-idf

Count

WeightMatrix
- tf-idf weights

Macbeth 열의 오타
Antony 행과 worser 행의 Macbeth 열 값이 각각 0.35, 1.95로 표기되어 있지만, 위의 Count vector에서 이 두 위치의 tf 값이 0이므로 실제 tf-idf 가중치는 0이어야 한다.
따라서 이는 슬라이드 상의 오타이다.

p14. Vector Space Model

Document Vectors
- $\mid V \mid$-dimensional vector space
- 고차원 벡터, but 희소벡터
Query Vectors
- 질의도 문서와 동일하게 벡터 공간에 벡터로 표현
- 벡터 공간에서 질의와의 근접성(proximity)에 따라 문서의 순위를 매김
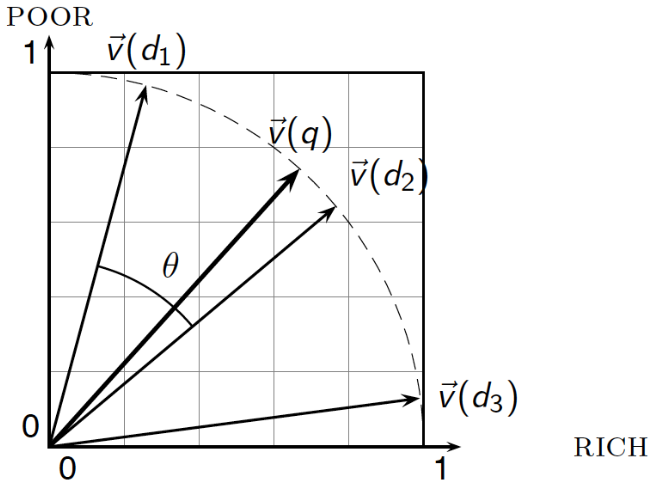
- 근접성(Proximity)?
  - 벡터들의 유사성과 동일
  - 벡터들 간의 거리에 반비례
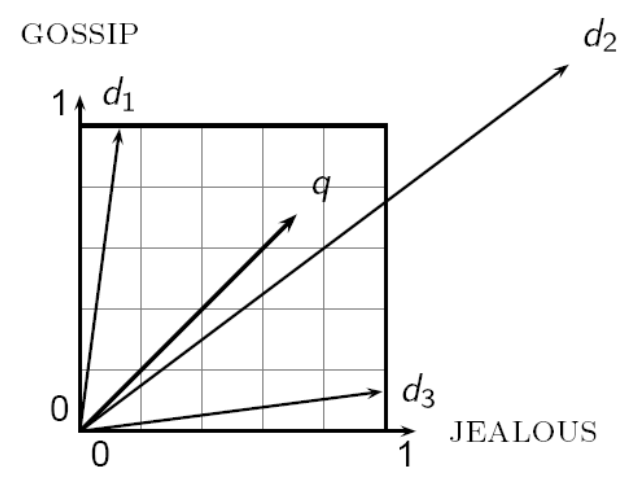
유클리드 거리와 벡터간 각도
- 질의 q와 문서 d2 간 유클리드 거리는 상당히 크지만, 각도는 아주 작음
- 문서의 순위는 질의와의 각도에 따라 결정됨
  - 각도가 작을수록 유사도가 높음

벡터 공간의 의미
문서와 질의를 동일한 차원의 벡터로 표현하면 같은 공간에서 비교할 수 있다.
차원 수는 vocabulary 크기와 같으며, 단어가 10,000개라면 문서·질의 모두 10,000차원 벡터가 된다.
왜 희소 벡터인가?
한 문서가 전체 단어를 모두 포함하는 경우는 거의 없다.
대부분의 차원 값은 0이고 일부 단어에만 값이 존재해 희소(sparse) 벡터가 된다.
근접성(Proximity)과 유사성(Similarity)
벡터 간 유사성은 보통 각도(코사인 유사도) 로 측정한다.
유클리드 거리만 보면 멀어 보일 수 있지만,
각도는 방향성을 기준으로 하므로 의미적 유사성을 더 잘 반영한다.
예시 설명
질의 $q$ 와 문서 $d2$:
유클리드 거리는 멀지만 각도가 작아 실제 유사도는 높다.
질의 $q$ 와 문서 $d1$, $d3$:
각도가 더 크므로 $d2$보다 유사도가 낮다.
정리
문서 순위는 거리보다 각도(코사인 유사도) 에 의해 결정된다.
따라서 랭킹 기반 검색에서는 cosine similarity가 표준적으로 사용된다.

p15. Vector Space Model

코사인 유사도
- 코사인(cosine)
  - 질의와 문서 사이의 각도를 기준으로 내림차순으로 문서의 순위를 매김
  - $\cos(\text{질의}, \text{문서})$ 값을 기준으로 오름차순으로 문서의 순위
  - 코사인 함수는 $[0^\circ, 180^\circ]$ 구간에서 단조 감소 함수

코사인 유사도
- 벡터 크기 정규화
  \[\| \vec{x} \|_2 = \sqrt{\sum_i x_i^2}\]
- 정의
  \[\cos(\vec{q}, \vec{d}) = \frac{\vec{q} \cdot \vec{d}}{\|\vec{q}\|\|\vec{d}\|} = \frac{\sum_{i=1}^{|V|} q_i d_i}{\sqrt{\sum_{i=1}^{|V|} q_i^2} \sqrt{\sum_{i=1}^{|V|} d_i^2}}\]
- 벡터 크기 정규화 코사인 유사도
  \[\cos(\vec{q}, \vec{d}) = \vec{q} \cdot \vec{d} = \sum_{i=1}^{|V|} q_i d_i\]

$q_i$: 질의(query)에서 용어 $i$의 가중치
$d_i$: 문서(document)에서 용어 $i$의 가중치

p16. Vector Space Model

코사인 유사도 계산

초기화
Scores[N] = 0으로 모든 문서 점수를 0에서 시작한다.
Length[N]에는 각 문서의 길이(단어 수 또는 가중치 합)를 저장한다.
질의 단어 반복
for each query term t 를 통해 질의에 포함된 단어 각각에 대해 처리한다.
가중치 계산 및 게시 목록(postings list) 로드
질의 단어의 가중치 w_{t,q}를 계산하고, 단어 t가 등장한 문서들의 postings list 를 가져온다.
게시 목록 반복
for each (d, tf_{t,d}) 형태로, 단어 t가 등장한 문서 d 와 그 문서에서의 등장 횟수(tf)를 순회한다.
점수 업데이트
Scores[d] += w_{t,d} × w_{t,q}
문서 d 의 기존 점수에 문서 가중치와 질의 가중치를 곱해 더한다.
문서 길이 정보 읽기
Length[d] 를 불러와 이후 정규화에 사용한다.
정규화
Scores[d] = Scores[d] / Length[d]
문서 길이로 나누어 문서 크기에 따른 영향력을 제거한다.
상위 K개 문서 반환
최종 점수 배열에서 Top-K 문서를 선택해 반환한다.
정리
전체 과정은 문서-질의 유사도를 계산해 랭킹을 만드는 절차이며,
문서 길이 보정을 포함해 코사인 유사도 기반 계산 흐름을 따른다.

p17. Vector Space Model

Term frequencies

term	SaS	PaP	WH
affection	115	58	20
jealous	10	7	11
gossip	2	0	6
wuthering	0	0	38

Log frequency weighting

term	SaS	PaP	WH
affection	3.06	2.76	2.30
jealous	2.00	1.85	2.04
gossip	1.30	0	1.78
wuthering	0	0	2.58

$dot(SaS, PaP) \approx 12.1$
$dot(SaS, WH) \approx 13.4$
$dot(PaP, WH) \approx 10.1$

After length normalization

term	SaS	PaP	WH
affection	0.789	0.832	0.524
jealous	0.515	0.555	0.465
gossip	0.335	0	0.405
wuthering	0	0	0.588

$cos(SaS, PaP) \approx 0.94$
$cos(SaS, WH) \approx 0.79$
$cos(PaP, WH) \approx 0.69$

Dot Product 계산
두 벡터 $\mathbf{a}, \mathbf{b}$의 내적(dot product)은 다음과 같이 계산된다.
\[\mathbf{a} \cdot \mathbf{b} = \sum_i a_i b_i\]
예를 들어 $dot(SaS, PaP)$의 경우:
\[3.06 \times 2.76 + 2.00 \times 1.85 + 1.30 \times 0 + 0 \times 0 \approx 12.1\]
Cosine Similarity 계산
코사인 유사도는 두 벡터의 내적을 두 벡터 크기의 곱으로 나눈 값이다.
\[\cos(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}\]
여기서 $|\mathbf{a}| = \sqrt{\sum_i a_i^2}$ 는 벡터의 크기이다.
예를 들어 $cos(SaS, PaP)$:
$dot(SaS, PaP) \approx 12.1$
$|SaS| = \sqrt{3.06^2 + 2.00^2 + 1.30^2 + 0^2} \approx 3.86$
$|PaP| = \sqrt{2.76^2 + 1.85^2 + 0^2 + 0^2} \approx 3.22$
따라서,
\[\cos(SaS, PaP) \approx \frac{12.1}{3.86 \times 3.22} \approx 0.94\]

p18. Vector Space Model

Tf-idf 변형들

Term frequency (TF)
- n (natural): $tf_{t,d}$
- l (logarithm): $1 + \log(tf_{t,d})$
- a (augmented): $0.5 + \dfrac{0.5 \times tf_{t,d}}{\max_t(tf_{t,d})}$
- b (boolean):
\[\begin{cases} 1 & \text{if } tf_{t,d} > 0 \\ 0 & \text{otherwise} \end{cases}\]
- L (log ave): $\dfrac{1 + \log(tf_{t,d})}{1 + \log(\text{ave}_{t \in d}(tf_{t,d}))}$
Document frequency (DF)
- n (no): $1$
- t (idf): $\log \dfrac{N}{df_t}$
- p (prob idf): $\max\{0, \log \dfrac{N - df_t}{df_t}\}$
Normalization
- n (none): $1$
- c (cosine): $\dfrac{1}{\sqrt{w_1^2 + w_2^2 + \dots + w_M^2}}$
- u (pivoted unique): $\dfrac{1}{u}$
- b (byte size): $\dfrac{1}{CharLength^\alpha}, \ \alpha < 1$

TF 변형
n (natural): 원시 단순 빈도. 단어가 등장한 횟수를 그대로 사용한다.
l (logarithm): 단어가 지나치게 많이 등장하는 경우 그 영향이 커지는 문제를 완화하기 위해 로그를 취해 포화 효과를 준다.
a (augmented): 문서 길이 차이를 보정하기 위해 최대 빈도로 정규화하여 상대적 비율을 강조한다.
b (boolean): 단어 등장 여부만 고려한다. 단순하지만 단어 빈도 정보가 사라진다.
L (log ave): 각 문서의 평균 빈도로 나누어 문서마다 등장 빈도의 편차를 완화한다.
DF 변형
n (no): DF를 고려하지 않는다. 모든 단어를 동일한 중요도로 간주한다.
t (idf): 드문 단어일수록 가중치를 크게 주어 정보성을 반영한다. 가장 일반적인 방식이다.
p (prob idf): 확률적 IDF로, 단어가 등장하지 않은 문서와 등장한 문서 비율을 이용해 지나치게 흔한 단어의 가중치를 보수적으로 조정한다.
Normalization
n (none): 정규화를 하지 않는다. 문서 길이가 길수록 유리해진다.
c (cosine): 벡터 길이를 1로 정규화한다. 문서 길이 차이를 제거하며 코사인 유사도와 함께 쓰이는 표준 방식이다.
u (pivoted unique): 문서 내 고유 단어 수로 보정한다. 긴 문서일수록 더 다양한 단어를 포함한다는 점을 반영한 방식이다.
b (byte size): 문서 바이트 크기에 따라 정규화한다. 긴 문서에서 생기는 편향을 줄이기 위한 기법이다.

p19. Vector Space Model

코사인 유사도를 활용한 문서 랭킹 과정

벡터 생성
- 질의(Query)를 가중치가 부여된 tf-idf 벡터로 표현: $tf(q, t), idf(t)$
- 각 문서(Document)를 가중치가 부여된 tf-idf 벡터로 표현: $tf(d, t), idf(t)$
유사도 계산 및 순위화
- 질의 벡터와 각 문서 벡터 간의 코사인 유사도 점수를 계산
- 점수를 기준으로 질의에 대한 문서들의 순위 결정
결과 반환
- 가장 높은 순위를 가진 상위 K개의 문서(예: K=10)를 사용자에게 반환

p20. Probabilistic IR

불리언 검색의 문제
- “대박” 아니면 “쪽박”
- 쿼리에 넣은 키워드의 수와 AND, OR 연산 표현의 기술 요구
  - AND 연산이 늘어나면 결과의 수는 줄어듦
  - OR 연산이 늘어나면 결과의 수는 급격히 증가
➡ 따라서 좋은 문서를 랭킹하는 Soft한 방법이 필요
Why Probabilistic IR

Hard 방식: 문서가 질의 조건을 만족하면 1, 만족하지 않으면 0으로 처리한다.
예: Boolean Retrieval (AND, OR 연산으로만 결과 결정)
결과가 극단적으로 나오며, “관련 있음/없음”만 구분할 수 있다.
Soft 방식: 문서와 질의 간의 관련성을 0과 1 사이의 연속적인 값으로 평가한다.
예: Probabilistic IR, Vector Space Model
문서가 질의와 얼마나 유사한지, 관련성이 얼마나 강한지를 수치화하여 랭킹 가능하다.

p21. Probabilistic IR

고전적 확률 기반 정보 검색 모델
- Probability Ranking Principle (PRP): 확률 순위 결정 원칙
- 이진 독립 모델 (≈ Naïve Bayes 텍스트 분류 모델)
  - Independence: terms occur in documents independently (단순화를 위해 용어 간 독립 가정)
- (Okapi) BM25
확률론적 방법
- 정보 검색 분야에서 오래되었지만 현재에도 많이 사용되는 방법
- 문서와 정보 요구 간의 관련성 확률에 따라 순위를 매기는 방식
  - $P(R=1 \mid document_i, query)$

\[p(R=1|x) = \frac{p(x|R=1)p(R=1)}{p(x)}\] \[p(R=0|x) = \frac{p(x|R=0)p(R=0)}{p(x)}\] \[p(R=0|x) + p(R=1|x) = 1\]

$x$: document
$R$: query에 대한 문서의 적합성(relevance)으로
$R=1$이면 적합, $R=0$이면 부적합

용어가 문서에 독립적으로 등장한다(independently)고 가정하는 이유는 계산을 단순화하기 위함이다.
독립 가정을 하면 각 단어의 확률을 곱셈으로 단순 결합할 수 있어 모델이 간단해진다.
하지만 실제로는 단어들이 서로 상관관계를 가진다. 예를 들어 “뉴”와 “욕”은 함께 등장할 확률이 높다.
만약 독립성을 가정하지 않으면, 단어들 간의 공동 확률분포(joint probability distribution)를 모델링해야 하고, 이는 차원이 급격히 커져 계산이 복잡해진다.

p22. Probabilistic IR

The Probability Ranking Principle (PRP)

영문 원문

“If a reference retrieval system’s response to each request is a ranking of the documents in the collection in order of decreasing probability of relevance to the user who submitted the request, where the probabilities are estimated as accurately as possible on the basis of whatever data have been made available to the system for this purpose, the overall effectiveness of the system to its user will be the best that is obtainable on the basis of those data.”

번역본

“만약 어떤 참고 검색 시스템이 각 요청에 대해 응답을 생성하는 방식이, 요청을 제출한 사용자에게 관련될 확률이 감소하는 순서대로 문서 집합 내 문서들을 나열하는 것이라면, 그리고 이러한 확률들이 해당 목적을 위해 시스템에 제공된 모든 데이터를 가능한 한 정확하게 기반으로 추정된다면, 그 시스템의 전반적인 효과성은 해당 데이터에 기초하여 얻을 수 있는 최선의 것이 될 것이다.”

[1960s/1970s] S. Robertson, W.S. Cooper, M.E. Maron;
van Rijsbergen (1979:113); Manning & Schütze (1999:538)
검색 시스템이 각 문서의 관련성 확률을 정확히 추정하여 내림차순으로 순위화할 때
최적의 검색 성능을 달성할 수 있다는 이론적 기반을 제시

p23. Probabilistic IR

확률의 기초 – 베이즈의 정리

\[p(A,B) = p(A \cap B) = p(A|B)p(B) = p(B|A)p(A)\] \[p(A|B) = \frac{p(B|A)p(A)}{p(B)} = \frac{p(B|A)p(A)}{\sum_{X=A,\bar{A}} p(B|X)p(X)}\]

Odds: 어떤 사건이 발생할 확률과 발생하지 않을 확률의 비율

\[O(A) = \frac{p(A)}{p(\bar{A})} = \frac{p(A)}{1-p(A)}\]

베이즈 정리 (Bayes’ Rule)
조건부 확률을 연결하는 기본 공식이다.
어떤 사건 $A$의 사후확률 $p(A \mid B)$를, 사전확률 $p(A)$와 가능도 $p(B \mid A)$로 표현한다.
식:
\[p(A \mid B) = \frac{p(B \mid A)\, p(A)}{p(B)}\]
사전확률 (Prior, $p(A)$)
사건 $A$에 대해, 증거 $B$를 보기 전에 우리가 가진 기존의 믿음
예: “문서가 관련 문서일 확률이 대략 10%다.”
가능도 (Likelihood, $p(B \mid A)$)
사건 $A$가 참일 때 증거 $B$가 관측될 가능성
예: “문서가 관련 문서라면 특정 단어 $B$가 등장할 확률은 0.8이다.”
사후확률 (Posterior, $p(A \mid B)$)
증거 $B$를 관측한 뒤 사건 $A$가 참일 갱신된 확률
예: “이 단어가 나타났다면 문서가 관련 문서일 확률은 40%로 갱신된다.”
요약:
사전확률 = 사건에 대한 초기 믿음
가능도 = 데이터가 그 사건과 얼마나 잘 맞는지
사후확률 = 데이터를 반영한 새로운 믿음
Odds (승산)
사건이 발생할 확률과 발생하지 않을 확률의 비율이다.
식:
\[O(A) = \frac{p(A)}{1 - p(A)}\]
단순한 확률보다 상대적인 발생 가능성을 표현하는 데 유용하며,
특히 Logistic Regression에서 핵심적으로 사용된다.

p24. Probabilistic IR

각 term이 관련성에 어떻게 기여하는지 추정
문서의 관련성 확률을 찾기 위해 결합
확률이 감소하는 순서로 문서를 정렬
정리: 1/0 손실 하에서 손실(베이즈 위험)을 최소화한다는 점에서, PRP를 사용하는 것은 최적이다.
- 1/0 손실 (1/0 loss): 이진 손실 함수로, 결과가 ‘올바른 경우(0)’와 ‘잘못된 경우(1)’ 두 가지로만 구분된다.
  검색에서는 관련 있는 문서를 놓치거나, 관련 없는 문서를 제시할 때 손실이 발생한다고 본다.
- 베이즈 위험 (Bayes risk): 어떤 결정 규칙(문서 순위 결정)을 사용했을 때 예상되는 평균 손실을 의미한다.
  PRP를 따르면 이 평균 손실이 가장 낮아진다는 것을 뜻한다.
- 가장 관련성이 높은 문서들을 우선적으로 보여주는 것이 이론적으로 가장 좋은 결과를 보장한다는 정리로,
  확률에 기반해 순위를 매기는 방식이 사용자의 정보 요구를 가장 효과적으로 충족시킨다는 뜻이다.

1/0 손실 (1/0 loss)
정답이면 손실 0, 틀리면 손실 1인 가장 단순한 손실 함수.
정보 검색에서는
관련 문서를 안 보여주거나
관련 없는 문서를 보여주면
→ 손실 1로 간주한다.
즉, 정확도만을 고려하며 부분적 오류 비용 같은 것은 반영하지 않는다.
베이즈 위험 (Bayes risk)
어떤 결정 규칙을 사용할 때 기대되는 평균 손실을 의미한다.
식:
\[R(\delta) = \mathbb{E}\!\left[\,L(\theta, \delta(X))\,\right]\]
$\delta$: 결정 규칙(문서를 어떤 기준으로 정렬할지).
예: “관련성 확률이 높은 문서부터 보여준다.”
$L$: 손실 함수(판단이 실제 상태와 얼마나 어긋나는지를 수치화).
예: 관련 문서 안 보여주면 1, 관련 없는 문서 보여주면 1.
정보 검색에서는 PRP를 따르면
관련 문서를 놓치거나 불필요한 문서를 보여줄 확률이 최소화되어
기대 손실이 최소(최적) 가 된다.
종합
결정 규칙: 데이터를 보고 문서 순서를 정하는 방식
손실 함수: 그 결정이 실제와 얼마나 다른지 측정
베이즈 위험: 두 요소를 종합해 계산된 평균 손실
따라서 PRP는 베이즈 위험을 최소화하는 최적의 정렬 원리가 된다.

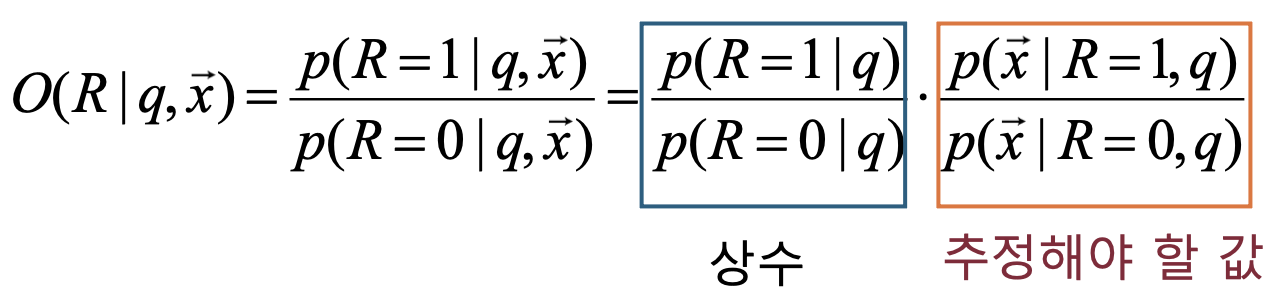
p25. Binary Independence Model

쿼리: 이진 단어 출현 벡터
주어진 쿼리 $q$
• 각 문서 $d$에 대해 다음을 계산: $p(R|q,d)$
• $x$는 문서 $d$를 표현하는 이진 단어 출현 벡터일 때, $p(R|q,x)$를 계산하는 것으로 대체
Odds와 베이즈 룰을 사용하여 정리

Independence 가정 적용

쿼리의 이진 단어 출현 벡터와 독립성 가정
단어가 등장하면 1, 등장하지 않으면 0으로 표시해 벡터로 만든다.
예: 단어 집합 {apple, banana, cat}에서 문서가 “apple, cat”이면 벡터는 $[1,0,1]$.
단어들의 출현 여부가 서로 독립이라고 가정하면
$p(\vec{x}\mid R,q)=\prod_i p(x_i\mid R,q)$ 로 곱으로 분해되어 계산이 단순해진다.
베이즈 룰과 $q$가 조건으로 상시 붙는 경우
일반 베이즈:
\[p(R\mid \vec{x})=\frac{p(R)\,p(\vec{x}\mid R)}{p(\vec{x})}\]
쿼리 $q$가 항상 조건으로 붙으면 모든 항에 $q$가 붙어서
\[p(R\mid q,\vec{x})=\frac{p(R\mid q)\,p(\vec{x}\mid R,q)}{p(\vec{x}\mid q)}\]
$R$이 1인지 0인지 어떻게 아는가?
IR에서는 라벨된 학습 데이터(평가 세트, 사용자 클릭·피드백 등)를 사용해
각 문서–쿼리 쌍에 관련성 $R\in{0,1}$ 을 부여한다.
MNIST와 동일한 원리:
MNIST에서는 숫자 클래스 $Y$ 에 대해
$p(x_j\mid Y=y)$ 같은 분포를 데이터에서 추정한다.
IR에서도
$p(x_i\mid R=1,q)$, $p(x_i\mid R=0,q)$ 를 라벨된 데이터로부터 추정하여
새로운 문서의 관련성 확률을 계산한다.

p26. Binary Independence Model

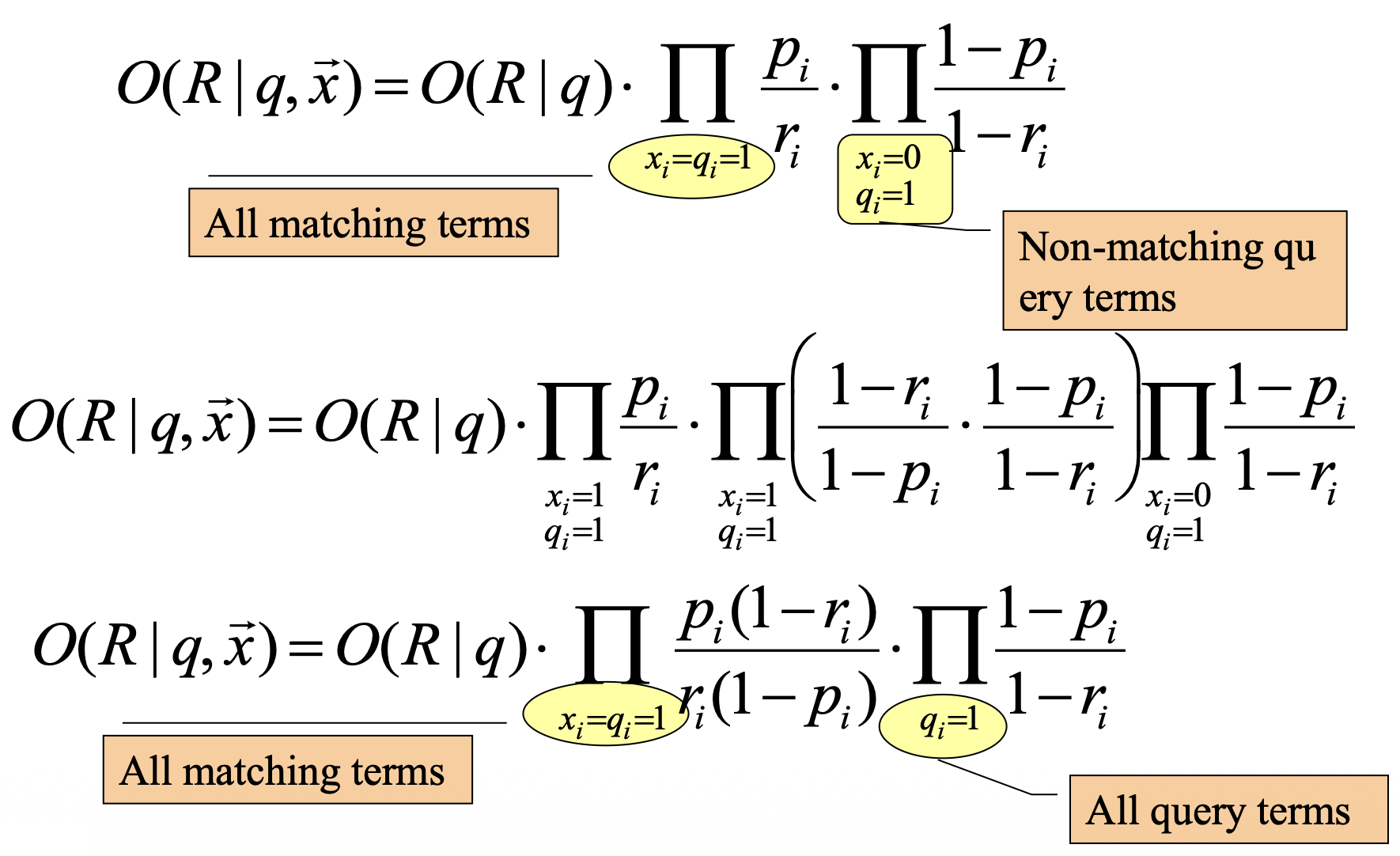
모든 term이 쿼리에 나타나지 않는 경우($q_i=0$)라고 가정하면 $p_i = r_i$

$x_i$가 1인 경우와 0인 경우로 분리하는 이유
원래 식은 모든 term을 곱하는 형태이다.
\[O(R\mid q,\vec{x}) = O(R\mid q)\cdot \prod_{i=1}^n \frac{p(x_i \mid R=1,q)}{p(x_i \mid R=0,q)}\]
각 항은 $x_i=1$일 때의 비율 또는 $x_i=0$일 때의 비율 중 하나를 택한다.
따라서 곱을 $x_i=1$인 경우와 $x_i=0$인 경우로 분리할 수 있다.
\[O(R\mid q,\vec{x}) = O(R\mid q)\cdot \prod_{x_i=1} \frac{p(x_i=1 \mid R=1,q)}{p(x_i=1 \mid R=0,q)} \cdot \prod_{x_i=0} \frac{p(x_i=0 \mid R=1,q)}{p(x_i=0 \mid R=0,q)}\]
두 곱셈 항을 합치면 원래 $n$개의 항과 동일해진다.
모든 term이 쿼리에 나타나지 않는 경우 $q_i=0$이라고 가정하는 이유
쿼리에 없는 term은 관련성 판정에 영향을 주지 않아야 한다.
이를 위해 $q_i=0$일 때 $p_i=r_i$로 두면
$x_i=1$일 때 $\frac{p_i}{r_i}=1$,
$x_i=0$일 때 $\frac{1-p_i}{1-r_i}=1$ 이 되어
곱셈 항에서 모두 1로 사라진다.
따라서 원래 식
\[O(R\mid q,\vec{x}) = O(R\mid q)\cdot \prod_{x_i=1} \frac{p_i}{r_i} \cdot \prod_{x_i=0} \frac{1-p_i}{1-r_i}\]
은 쿼리에 포함된 term($q_i=1$)만 남는 형태로 단순화된다.
\[O(R\mid q,\vec{x}) = O(R\mid q)\cdot \prod_{x_i=1,\, q_i=1} \frac{p_i}{r_i} \cdot \prod_{x_i=0,\, q_i=1} \frac{1-p_i}{1-r_i}\]
즉, 쿼리에 없는 term들은 모두 곱셈에서 기여가 0이 되어(항값 1)
odds 계산에 영향을 미치지 않으며, 최종 식이 간단해진다.

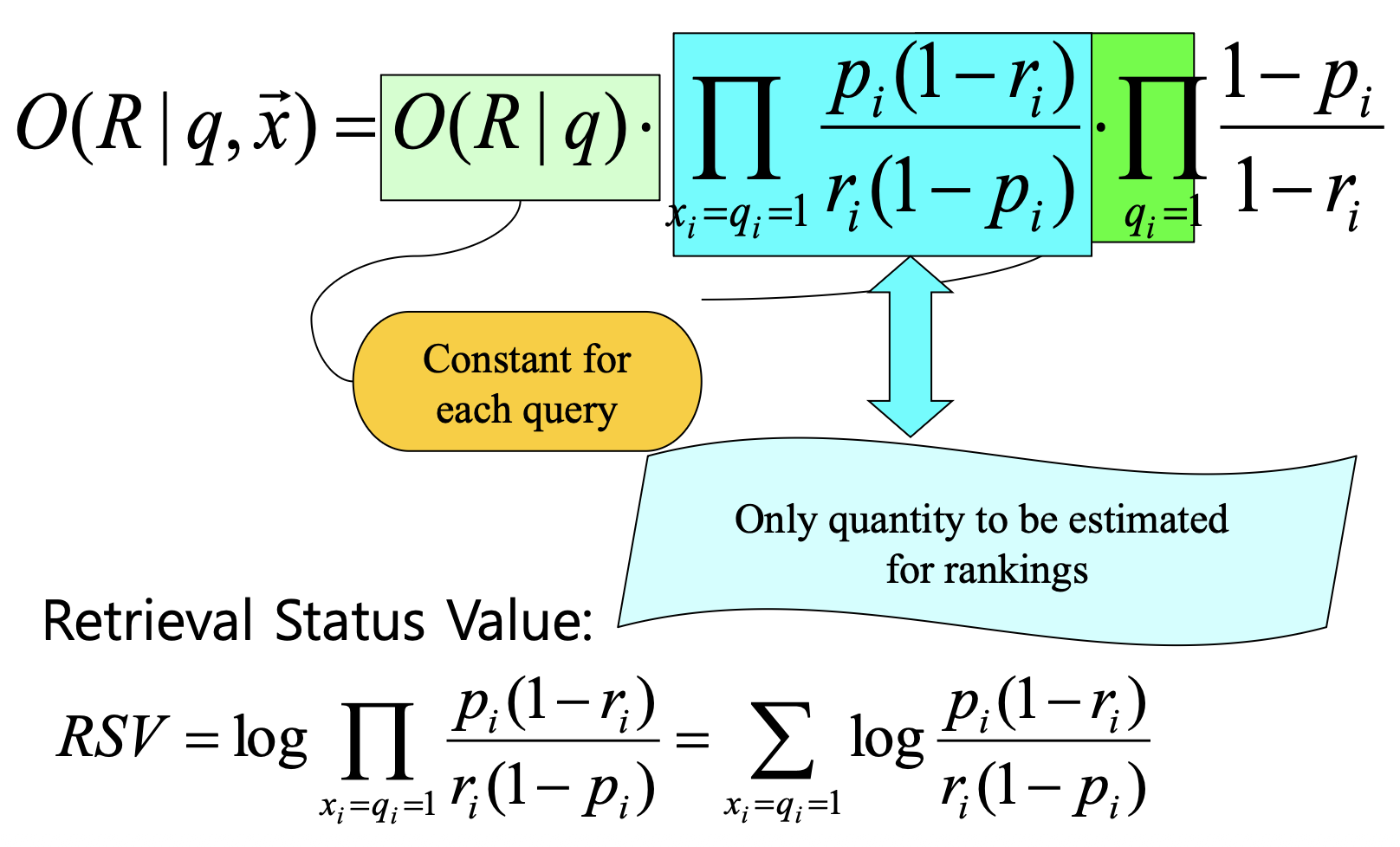
p27. Binary Independence Model

p28. Binary Independence Model

정립(1960년대 초반)
1960년 Maron과 Kuhns가 확률적 색인·관련성 개념을 제시하며 BIM의 기반을 마련했다.
기관: Maron(UC Berkeley), Kuhns(공저자로 기록되나 기관 표기는 문헌마다 상이).
체계화(1970년대)
Robertson & Spärck Jones가 확률적 관련성 프레임워크를 정립하고 RSJ 가중치를 제안해 BIM을 실용적 랭킹 모형으로 만들었다.
기관: Robertson(시티대 → MSR Cambridge), Spärck Jones(케임브리지), van Rijsbergen(글래스고).
적용 확대(1980년대)
Cranfield 계열 컬렉션 등 전통 IR 실험에서 BIM/RSJ 가중치가 대규모로 시험되며 실증 연구가 축적됐다.
관련 피드백과 결합해 문헌 검색·엔터프라이즈 검색에서 강한 성능을 보였다.
실전 전성기(1990년대)
시티대 Okapi 시스템이 BIM을 실전 검색에 적용해 BM11/BM15를 거쳐 BM25를 완성했다.
TREC(NIST)에서 Okapi/BIM 계열이 대표적 베이스라인으로 자리 잡으며, 초기 웹 대규모 컬렉션에서도 견고함이 검증됐다.
기관: Okapi 팀(Centre for Interactive Systems Research), TREC(NIST).
파생과 표준화(2000년대 이후)
LM·LTR·신경 랭킹이 확산되며 “순수 BIM”의 사용은 감소했지만,
BM25는 사실상 업계 표준으로 자리 잡아 Lucene/Elasticsearch 등 대부분의 검색엔진 기본 랭커가 되었다.
활용 분야: 웹 검색, 기업 내 검색, 디지털 라이브러리, e-discovery 등.
현재적 위상과 활용 방식
BIM 자체는 교육·연구에서 “설명 가능한 가벼운 확률적 베이스라인”으로 주로 사용된다.
실무에서는 BM25가 1차 베이스라인으로 널리 쓰이며,
LTR·신경 랭킹 파이프라인에서는 BM25/RSJ 점수를 피처로 사용하거나
초기 후보군 선별(prior), 피드백 가중치 초기값 등으로 결합해 활용된다.

p29. BM25 모델

BM25 (Okapi BM25) ?
- 확률적 정보검색 모델의 대표적 알고리즘
- TF-IDF 모델을 개선한 확률적 정보 검색 랭킹 함수
  - TF-IDF의 한계점을 보완하여 문서의 길이와 단어 빈도수를 더욱 정교하게 반영
  - 문서와 질의(쿼리) 간의 관련성을 점수화하여 검색 결과를 순위 매기는 데 사용
- Best Matching 25의 약자로, 25는 이 모델의 25번째 버전이라는 의미
- 현재 대부분의 검색엔진에서 기본 알고리즘으로 사용
이론적 기반
- 확률 순위 원리 (Probability Ranking Principle)
BIM (Binary Independent Model)
- Term Frequency를 고려하지 않음
- 문서의 길이를 고려하지 않음
- Term 간의 Independence를 가정
BM25 모델의 개선점
- Term Frequency 고려
- 문서의 길이 정규화 적용
- 포화 함수 사용으로 과도한 TF 억제

왜 BM25가 중요한가?
기존 TF-IDF는 단순히 TF×IDF를 곱하는 구조라,
문서 길이가 길거나 특정 단어가 반복될 때 점수가 비정상적으로 커지거나 작아지는 문제가 있었다.
BM25는 이런 비현실적 요소를 보정해 실제 검색 환경에서 합리적인 점수 계산을 제공한다.
BIM과의 차이
BIM(Binary Independent Model)은 단어가 등장했는지 0/1만 반영하여
단어가 얼마나 많이 등장했는지(TF)를 활용하지 못한다.
또한 문서 길이를 고려하지 않아 긴 문서가 지나치게 유리하거나 불리해지는 왜곡이 생긴다.
Independence 가정 역시 실제 언어에서 빈번한 단어 간 상관관계를 반영하지 못한다.
BM25의 개선 아이디어
TF를 반영해 단어가 여러 번 등장할수록 가중치를 부여한다.
긴 문서에 대해 길이 정규화를 적용해 공정하게 비교한다.
단어가 너무 많이 등장해도 점수가 무한정 증가하지 않도록 포화(saturation) 형태로 증가율을 둔화한다.
이론적 기반과 실제 활용
BM25는 PRP(확률 순위 원리)를 실용적으로 구현한 모델이다.
“관련성 확률이 높은 문서를 위에 두는 것이 최적”이라는 원리를 실제 검색 점수로 만든 것이다.
그래서 Elasticsearch/Lucene/Solr 등 대부분의 검색엔진이 기본 랭커로 BM25를 채택한다.
Okapi의 의미
BM25의 Okapi는 런던 시티대의 Okapi 정보검색 시스템에서 유래한다.
이 시스템은 1980~1990년대 문헌 검색 연구에 사용되며 BM25를 포함한 여러 모델을 실험·검증했다.
“Okapi BM25”라는 이름은 BM25가 이 시스템에서 개발·검증되었다는 사실을 반영한다.

p30. BM25 모델

Tf-idf의 한계점

단어 간 의미(시맨틱) 반영 부족
- 단어를 독립적 토큰으로만 다루기 때문에, 동의어(synonym), 다의어(polysemy)를 구분하지 못함.
- 예) “친구”, “동무”, “프렌드” : 동일 의미의 동의어이지만 다르게 취급
문맥(context) 정보 손실
- 단어의 순서, 문법적 관계, 위치 정보를 반영하지 않음
- 예) “dog bites man”, “man bites dog” → tf-idf 값 동일
문서길이 문제
- 긴 문서에서는 tf가 커질 가능성이 높음 → 단순히 길이가 긴 문서가 더 높은 점수를 받을 가능성
- 문서 길이에 따른 보정이 필요
희귀 단어에 대한 과대 평가
- 너무 드물게 등장하는 단어는 높은 IDF 값을 가져 불필요하게 가중치가 커질 수 있음
- 예) 오타 등이 중요 단어처럼 취급될 위험
비선형 관계나 주제 모델링 불가
- 단어 간 관계, 주제(topic) 구조, 잠재 의미(latent semantic)를 반영하지 못함.
- LSA, LDA, Word2Vec, BERT 등 더 발전된 기법들이 등장

p31. BM25 모델

TF-IDF의 한계	BM25의 개선 방식
① 단순 TF 비례 문제 단어가 많이 나올수록 점수가 무한히 커짐 → 긴 문서가 유리	TF Saturation (포화 함수) 적용 → 단어 빈도가 증가할수록 점수가 점점 줄어드는 (log-like) 형태로 제한 $\frac{f}{f+k_1}$ 형태
② 문서 길이 문제 긴 문서는 단어가 더 많이 등장할 확률이 높아 점수 왜곡	길이 정규화(length normalization) 적용 → 문서 길이를 평균 문서 길이(avgdl)과 비교해 보정
③ IDF 계산의 극단성 아주 희귀한 단어가 과도하게 높은 가중치	BM25는 부드럽게 조정된 IDF 사용 $\log \frac{N - df(q) + 0.5}{df(q) + 0.5}$ → 0.5 smoothing을 적용해 희귀 단어에 대한 과도한 점수 상승을 억제하고, 동시에 너무 흔한 단어는 음수 처리하여 “무시”가 아니라 “불리하게 반영”
④ 단순 선형 모델 사용자 질의와 문서의 관련성을 잘 반영 못함	확률적 모델 기반으로 설계 관련성(relevance) 점수를 더 현실적으로 계산

p32. BM25 모델

BM25의 주요 개선점

TF 포화 (TF Saturation) 적용
- TF-IDF는 단어 빈도수(TF)가 높을수록 점수가 선형적으로 증가
- 한 문서에 특정 단어가 아무리 많이 나와도 문서의 관련성 점수가 무한히 커지는 것은 비합리적
- BM25는 TF가 일정 수준 이상이 되면 증가율을 둔화시키는 포화 개념을 도입
- 문서에 단어가 너무 많이 등장하는 경우를 제어하여, 특정 키워드를 반복적으로 사용해 검색 결과를 조작하는 것을 방지하는 효과
부드럽게 조정된 IDF 사용
- TF-IDF는 희귀 단어들이 과도하게 높은 IDF(가중치) 값을 갖는 경향
- BM25는 IDF 계산 시 분자와 분모에 각각 0.5를 더해 극단적인 희귀 단어들의 IDF 값을 완화시킴
문서 길이 정규화 (Document Length Normalization)
- TF-IDF는 문서의 길이가 길수록 TF 값이 높아져 짧은 문서보다 높은 점수를 받는 경향
- BM25는 문서의 길이를 평균 문서 길이와 비교하여 점수를 정규화
  - 평균보다 긴 문서는 페널티를 주고, 짧은 문서는 상대적으로 높은 점수 → 공정성 확보

p33. BM25 모델

Tf 포화(tf saturation)

\[\frac{tf}{k_1 + tf}\]

k1은 문서 내 단어 빈도에 얼마나 가중치를 둘 것인지를 결정하는 중요한 요소
- 높은 k1 값: tf가 증가할수록 점수도 계속해서 거의 선형적으로 증가.
  - 단어가 많이 나올수록 문서의 관련성이 계속해서 커진다고 판단
- 낮은 k1 값: tf가 어느 정도 증가하면 점수 증가율이 급격히 둔화.
  - 일정 횟수 이상 등장하는 단어는 더 이상 점수에 큰 영향을 주지 않는다고 판단

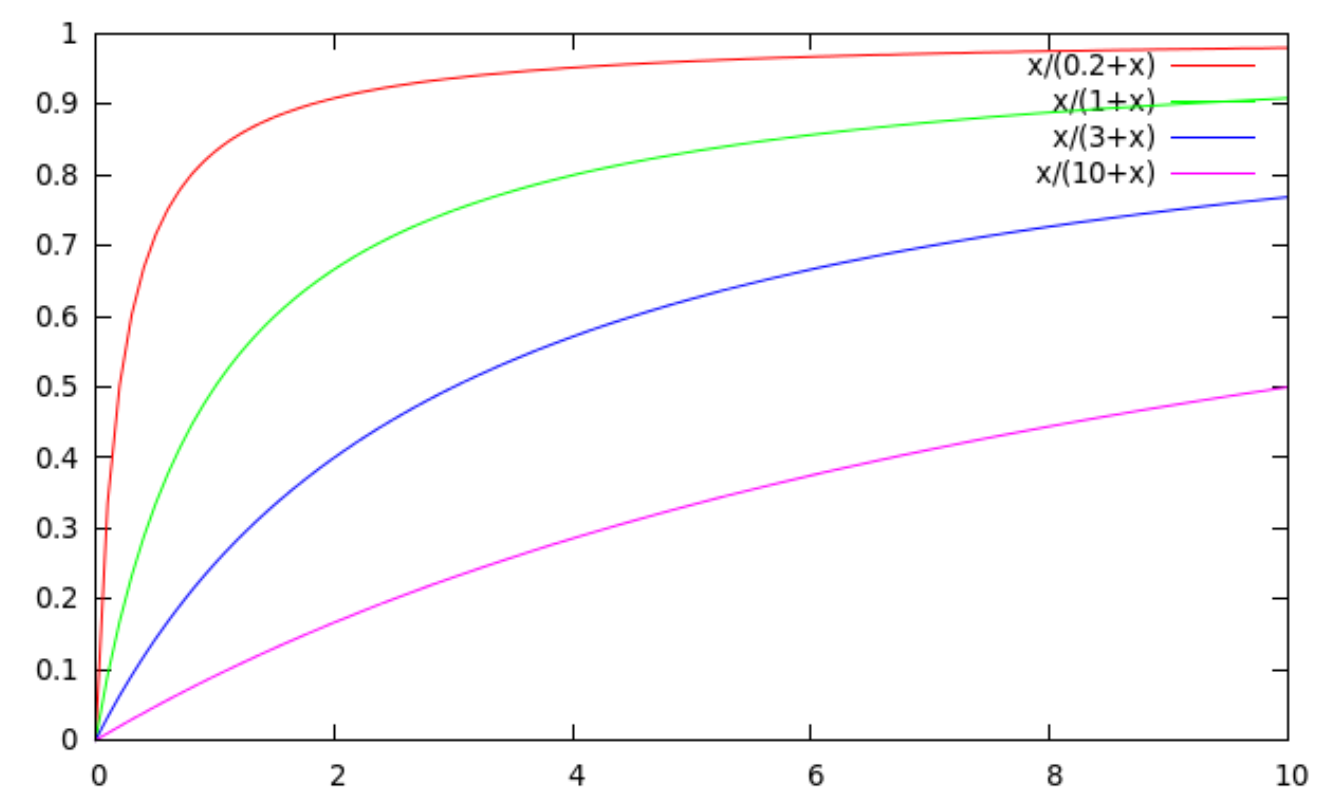
왜 k1이 중요한가?
k1은 문서 내 단어 빈도(tf)에 얼마나 가중치를 줄지 결정하는 핵심 파라미터이다.
k1이 크면 tf가 증가할수록 점수가 계속 상승하고,
k1이 작으면 tf가 조금만 증가해도 점수가 빠르게 포화된다.
높은 k1 값 (선형적 증가 경향)
예: k1 = 10
tf=1 → 1/(10+1)=0.09
tf=5 → 5/(10+5)=0.33
tf=10 → 10/(10+10)=0.50
tf=50 → 50/(10+50)=0.83
→ tf가 커질수록 꾸준히 증가하며 거의 선형에 가까운 패턴을 보인다.
낮은 k1 값 (빠른 포화)
예: k1 = 1
tf=1 → 1/(1+1)=0.50
tf=5 → 5/(1+5)=0.83
tf=10 → 10/(1+10)=0.91
tf=50 → 50/(1+50)=0.98
→ tf가 5 정도만 되어도 거의 포화 상태가 되어 이후 증가율이 매우 둔화된다.
의의
높은 k1: 단어가 많이 등장할수록 관련성이 계속 커진다고 보는 경우 적합.
낮은 k1: 일정 횟수 이상 등장하면 더 이상 중요하지 않다고 보는 경우 적합.
즉, 검색 결과에서 특정 단어를 반복적으로 삽입해 점수를 부풀리는 행위를 억제하는 데도 도움이 된다.

p34. BM25 모델

문서 길이의 정규화

문서 길이가 길어지면 tf의 값이 커지는 경향이 있음
\[dl = \sum_{i \in V} tf_i\]
avdl: 문서 집합 내 평균 문서 길이
문서 길이 정규화 요소
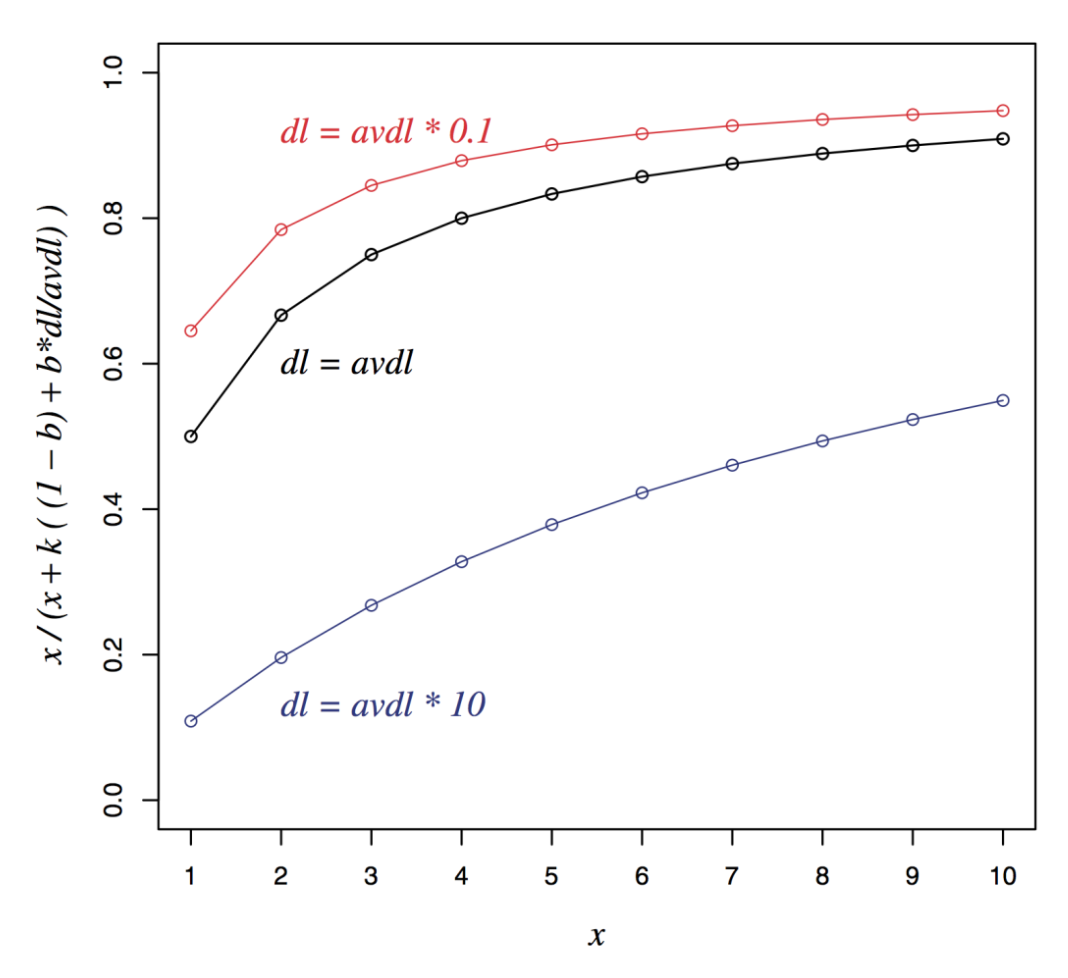
\[B = \left( (1-b) + b \cdot \frac{dl}{avdl} \right), \quad 0 \leq b \leq 1\]
- $b = 1$: 문서 길이를 완전히 보정
- $b = 0$: 문서 길이에 대해 보정하지 않음

차트 해석
그래프는 문서 길이(dl)가 평균 문서 길이(avdl)보다 짧거나 길 때 BM25 점수가 어떻게 달라지는지를 보여준다.
dl = avdl·0.1(빨간선)은 문서가 매우 짧을 때로, 같은 tf라도 점수가 더 높게 나온다.
dl = avdl(검은선)은 기준선처럼 동작하며, 평균 길이 문서에서의 점수 변화를 나타낸다.
dl = avdl·10(파란선)은 문서가 매우 길 때로, 같은 tf라도 점수가 낮아진다.
의미
긴 문서는 자연스럽게 단어가 많이 등장할 수 있으므로 그대로 비교하면 불공정해진다.
BM25는 문서 길이 정규화를 통해 긴 문서에는 패널티를, 짧은 문서에는 상대적 보정을 주어
더 공정한 비교가 가능하도록 한다.
b 파라미터의 역할
b=1: 문서 길이 보정을 완전히 적용해 긴 문서에 강한 패널티를 준다.
b=0: 문서 길이를 전혀 고려하지 않는다.
0 < b < 1: 일반적으로 이 범위에서 균형된 보정이 이루어진다.
실무 활용
b는 보통 0.75 정도가 널리 쓰이며(예: Elasticsearch),
다양한 도메인에서 안정적인 검색 성능을 제공하는 값으로 알려져 있다.

p35. BM25 모델

BM25의 핵심 수식과 구성 요소

\[Score(D, Q) = \sum_{i=1}^{n} \log \left( 1 + \frac{N - df_i + 0.5}{df_i + 0.5} \right) \cdot \frac{(k_1+1)tf_i}{k_1 \left( (1-b) + b \frac{dl}{avdl} \right) + tf_i}\]

질의에 포함된 모든 단어에 대해 계산
idf가 높은 희귀 단어일수록 최종 점수에 더 큰 영향을 줌

\[\frac{(k_1+1)tf_i}{k_1 \left( (1-b) + b \frac{dl}{avdl} \right) + tf_i}\]
TF 포화와 문서 길이 정규화를 동시에 처리하는 핵심 부분
TF가 커질수록 (k1+1)에 수렴하게 되며, dl이 avdl 보다 크면 분모가 커져 점수가 낮아짐

N: 총 문서의 수
dfᵢ: 쿼리 q가 출현한 문서의 수
tfᵢ: 쿼리 q가 출현한 빈도
dl: 문서 d의 길이
avdl: 전체 문서 집합의 평균 길이
k₁: TF 포화도를 조절하는 하이퍼파라미터
- k₁이 작을수록 TF 포화가 빨리 일어남 (일반적으로 1.2 ~ 2.0 사이의 값)
b: 문서 길이 정규화 정도를 조절하는 하이퍼파라미터
- b가 1에 가까울수록 문서 길이에 대한 패널티가 커짐 (일반적으로 0.75)

BM25 수식의 부분별 의미
BM25는 IDF, TF 포화, 문서 길이 정규화라는 세 요소를 결합해 현실적인 검색 순위를 계산한다.
IDF (Inverse Document Frequency)
\[\log \frac{N - df_i + 0.5}{df_i + 0.5}\]
기존 $\log \frac{N}{df_i}$ 대신 분자·분모에 0.5를 더해 극단적 경우(df=0, df=N)에서도 안정적으로 계산되도록 한 smoothing IDF이다.
드문 단어일수록 값이 커져 검색에서 더 중요한 단어로 반영된다.
왜 smoothing인가?
$df_i=0$이면 분모가 0이 되어 계산이 불가능하고, $df_i=N$이면 IDF가 0이 되어 단어의 기여가 사라진다.
이를 방지하기 위해 0.5 보정(smoothing)을 적용해 극단적 상황에서도 점수가 지나치게 왜곡되지 않게 만든다.
TF 포화(TF Saturation)
\[\frac{(k_1+1)tf_i}{k_1\left((1-b) + b\frac{dl}{avdl}\right) + tf_i}\]
단어 빈도(tf)가 커질수록 점수는 증가하지만, 분모에도 tf가 포함되어 있어 증가율이 점점 둔화된다.
→ 특정 단어가 반복 입력되어 점수를 부풀리는 것을 방지하는 역할.
문서 길이 정규화(Document Length Normalization)
\[(1-b) + b \cdot \frac{dl}{avdl}\]
문서 길이가 길수록 단어가 자연스럽게 많이 등장할 수 있으므로 패널티를 주고,
짧은 문서는 상대적으로 보정해 공정한 비교가 가능하도록 한다.
b는 길이 보정 강도(0~1)로, 일반적으로 0.75가 널리 사용된다.
k₁ 파라미터의 역할
k₁이 크면 TF 증가가 점수 증가에 크게 반영되어 선형적 패턴을 띤다.
k₁이 작으면 TF가 조금만 증가해도 점수가 빠르게 포화된다.
일반적으로 1.2~2.0 사이 값이 사용된다.
종합적 의미
IDF: 희귀 단어의 가치 반영(안정성 위해 smoothing 적용)
TF 포화: 과도한 반복 단어의 영향 제한
문서 길이 정규화: 긴 문서 보정 → 공정한 비교
→ BM25는 이 세 요소를 결합하여 현실적인 검색 품질을 제공하는 대표적 랭킹 함수로 자리 잡았다.

p36. BM25 모델

BM25 vs. tf-idf VSM
- Query: “machine learning”
- Query의 term이 출현한 문서 2개
  - Doc1: learning 1024, machine 1
  - Doc2: learning 16, machine 8
tf-idf 계산
\[\log_2 tf \times \log_2 \frac{N}{df}\]
- Doc1: $11 \times 7 + 1 \times 10 = 87$
- Doc2: $5 \times 7 + 4 \times 10 = 75$
BM25 (k₁ = 2)
- Doc1: $7 \times 3 + 10 \times 1 = 31$
- Doc2: $7 \times 2.67 + 10 \times 2.4 = 42.7$

p37. BM25

BM25 vs. TF-IDF 요약

특징	TF-IDF	BM25
TF 처리	선형 증가	포화 함수 적용
문서 길이	정규화 미흡	평균 길이 대비 정규화
장점	직관적이고 단순함	실제 검색 환경에 더 최적화됨
단점	문서 길이에 취약	하이퍼파라미터(k1, b) 튜닝 필요
활용	간단한 검색 및 분석	상용 검색 엔진의 핵심 알고리즘

p38. BM25

Ranking에 Feature 사용

Textual Features
- Zones: 문서제목, 저자, 요약, 본문, anchors 등
- Proximity
Non-textual Features
- File Type
- PageRank
- 파일 생성 시기

Zones (구역, 영역)
문서의 제목·본문·저자·요약·anchor 등으로 구성된 다양한 영역을 의미하며,
동일한 단어라도 어느 zone에 등장했는지에 따라 중요도가 달라진다.
예를 들어, “AI”가 제목에 등장한 경우 본문에만 등장한 경우보다 더 높은 가중치를 줄 수 있다.
Proximity (근접성)
질의어가 문서 내에서 얼마나 가까이 등장하는지 반영하는 특성이다.
단어 간 거리가 짧을수록 의미적 연관성이 높다고 판단하여 점수를 높인다.
예: “인공지능 기술 발전”이 문서에서 연속적으로 등장하면,
서로 멀리 떨어져 등장하는 경우보다 관련성이 높게 평가된다.
Non-textual Features
텍스트 내용 외부의 추가적 특성들을 의미한다.
예: 문서의 파일 형식(PDF/HTML), 웹페이지의 PageRank, 문서의 발행 시점 등.
특히 PageRank는 링크 구조에 기반해 문서의 “전반적 중요도”를 평가하는 대표적 비텍스트 특성이다.

p39. BM25F

존(Zone)을 활용한 랭킹 (Ranking with zones)

각 zone에 ranking function BM25를 적용
전체 term frequency에 대해 weighted combination 기법을 적용하여 zone scores를 계산
- 먼저 각 단어에 대한 evidence를 각 zone별로 결합하고,
- 이후 단어별 evidence를 결합

\[\tilde{tf_i} = \sum_{z=1}^{Z} v_z tf_{zi}, \quad \tilde{dl} = \sum_{z=1}^{Z} v_z len_z, \quad \tilde{avdl} = \text{Average across all documents}\]

$v_z$ : zone weight
$tf_{zi}$ : term frequency in zone $z$
$len_z$ : length of zone $z$
$Z$ : number of zones

Zones의 예시
제목, 저자, 본문, 요약, anchor 등 문서를 이루는 다양한 부분이 각각 zone이 된다.
각 zone은 정보 중요도가 다르기 때문에 검색 점수에 다르게 반영될 수 있다.
가중치 적용 방식
단어 빈도(tf)에 zone별 가중치 (v_z)를 곱해,
중요도가 높은 zone(예: 제목, 헤더)일수록 더 큰 영향력을 갖도록 한다.
예: 제목에 등장한 “AI”는 본문에 등장한 “AI”보다 높은 가중치를 받을 수 있다.
문서 길이 정규화
문서 길이(dl)를 zone별 길이와 가중치를 적용해
weighted document length 방식으로 계산한다.
이를 통해 zone마다 비중을 다르게 고려하면서도 전체 길이 정규화 효과를 유지한다.
이름에 F가 붙는 이유
BM25F의 F는 Field를 의미한다.
즉, 일반 BM25가 문서를 하나의 덩어리로 처리하는 반면,
BM25F는 문서를 여러 필드(zone)로 분해해 각각 가중치를 반영하는 방식으로 점수를 계산한다.

p40. BM25F

\[RSV^{SimpleBM25F} = \sum_{i \in q} \log \frac{N}{df_i} \cdot \frac{(k_1+1)\tilde{tf_i}}{k_1\left((1-b) + b\frac{\tilde{dl}}{\tilde{avdl}}\right) + \tilde{tf_i}}\]

존별 길이 정규화(zone-specific length normalization) (i.e., zone-specific b)

\[\tilde{tf_i} = \sum_{z=1}^Z v_z \frac{tf_{zi}}{B_z}\] \[B_z = \left( (1-b_z) + b_z \frac{len_z}{avlen_z} \right), \quad 0 \leq b_z \leq 1\] \[RSV^{BM25F} = \sum_{i \in q} \log \frac{N}{df_i} \cdot \frac{(k_1+1)\tilde{tf_i}}{k_1 + \tilde{tf_i}}\]

참고: Robertson and Zaragoza (2009: 364)

Zone 정규화 항 $B_z$
\[B_z = (1 - b_z) + b_z \frac{len_z}{avlen_z}, \qquad 0 \le b_z \le 1\]
$len_z$: zone $z$의 길이
$avlen_z$: 모든 문서에서 zone $z$의 평균 길이
$b_z$: zone $z$에 적용되는 정규화 강도
본문처럼 길이가 긴 zone에는 큰 $b_z$로 강하게 보정하고, 제목처럼 짧은 zone에는 작은 $b_z$로 약하게 보정 가능
Zone별 정규화된 단어 빈도 $\tilde{tf_i}$
\[\tilde{tf_i} = \sum_{z=1}^Z v_z \frac{tf_{zi}}{B_z}\]
$tf_{zi}$: zone $z$에서의 단어 $i$의 빈도
$v_z$: zone $z$의 가중치
zone 길이 보정($B_z$)과 중요도($v_z$)를 함께 반영하여 최종 단어 빈도를 계산
기존 BM25F (단순 정규화)
\[RSV^{SimpleBM25F} = \sum_{i \in q} \log \frac{N}{df_i} \cdot \frac{(k_1+1)\tilde{tf_i}}{k_1\left((1-b) + b\frac{\tilde{dl}}{\tilde{avdl}}\right) + \tilde{tf_i}}\]
모든 zone에 동일한 $b$ 값을 적용해 길이 보정을 수행하므로 zone별 특성을 반영하지 못하는 한계가 있음
최종 BM25F (zone-specific $b_z$ 적용)
\[RSV^{BM25F} = \sum_{i \in q} \log \frac{N}{df_i} \cdot \frac{(k_1+1)\tilde{tf_i}}{k_1 + \tilde{tf_i}}\]
zone별 $B_z$로 정규화된 $\tilde{tf_i}$를 사용하여 zone마다 길이와 중요도를 다르게 반영하므로 단순 BM25F보다 정밀한 점수 계산이 가능함

p41. BM25F

비텍스트적 특성(페이지 랭크, 페이지 생성 시기, 페이지 유형 등)을 활용한 랭킹

“관련성 정보는 질의와 독립적이다 (Relevance information is query independent)”
“BIM 방식 도출에서 비질의 용어들을 제거하는 과정에서 모든 비텍스트적 특성을 유지”
BM25 같은 모델에서 확률론적 도출 과정을 거치면서도
문서의 다양한 구조적 정보나 메타데이터 특성들을 손실 없이 활용 가능

\[RSV = \sum_{i \in q} c_i(tf_i) + \sum_{j=1}^{F} \lambda_j V_j(f_j)\]

$\lambda_j$: rescaling을 위해 사용하는 하이퍼파라미터
$V_j(f_j) = \log \frac{p(F_j = f_j \mid R=1)}{p(F_j = f_j \mid R=0)}$

\[RSV^{BM25} + \log(pagerank)\]

non-textual feature의 예시
PageRank, Page Age, Page Type 등 텍스트 외적 요인을 포함하며
이는 query independent한 문서 중요도·신뢰도를 반영함
추가 결합 방식
기본 BM25 점수에 비텍스트 요소를 더해 최종 점수를 계산
$RSV^{BM25} + \log(pagerank)$
PageRank는 웹 링크 구조 기반 중요도를 나타내므로
로그 스케일로 반영하여 값이 과도하게 커지는 것을 방지
$V_j(f_j)$의 의미
특정 feature $f_j$가
관련 문서($R=1$)에서 나타날 확률 대비
비관련 문서($R=0$)에서 나타날 확률의 비율을 로그로 취한 값
따라서 해당 feature가 관련성에 기여하는 정도를 정량적으로 표현
λ 파라미터의 역할
feature별 중요도를 조정하는 scaling 계수
여러 비텍스트 feature를 함께 사용할 때 균형 있는 영향을 부여
정리
BM25F는 텍스트 기반 요소뿐 아니라
문서 구조·메타데이터 등 비텍스트 feature까지 함께 결합할 수 있도록 확장된 모델

p42. IR Evaluation

관련성(Relevance) 측정을 위한 3가지 요소

기준이 되는 문서 집합 (benchmark document collection)
기준이 되는 질의 모음 (benchmark suite of queries)
평가: 각 질의와 각 문서에 대해 관련 있음(Relevant) 또는 관련 없음(Nonrelevant) 으로 판단

p43. 테스트 질의와 평가 컬렉션

Test Queries (테스트 질의)
- 검색 대상 문서 컬렉션의 내용과 실제로 연관되어 있어야 한다.
- 실제 사용자 요구사항을 대표해야 한다.
- 문서에서 무작위로 추출한 질의 용어는 좋지 않은 방법이다.
- 가능하다면 질의 로그에서 샘플을 추출하라.
Public Test Collection (공개 테스트 컬렉션)

p44. 전통적 및 현대 IR 테스트 컬렉션

전통적 테스트 컬렉션

Test Set	데이터 구성 특징	데이터 규모	접근 URL
TREC Robust Track	뉴스 기사, 정부 문서, 어려운 질의	문서: 528,155개 질의: 250개 관련성 판단: 311,410개	Link
TREC Web Track	ClueWeb 컬렉션, 웹페이지, 다양성 평가	문서: 1억 개 (ClueWeb12) 질의: 300개 (2009–2014)	Link
Cranfield Collection	항공공학 논문 초록, 전문 도메인	문서: 1,400개 질의: 225개	Link
CACM Collection	컴퓨터과학 논문 초록, ACM 저널	문서: 3,204개 질의: 64개	Link
Time Collection	Time 잡지 기사, 일반 도메인	문서: 423개 질의: 83개	Link

대규모 현대 테스트셋

Test Set	데이터 구성 특징	데이터 규모	접근 URL
MS MARCO Passage	Bing 검색질의, 웹 패시지, 딥러닝 최적화	패시지: 8,841,823개 질의: 1,010,916개 (train) 질의: 6,980개 (dev)	Link
MS MARCO Document	웹 문서 전문, 실제 검색 환경	문서: 3,213,835개 질의: 367,013개 (train) 질의: 5,193개 (dev)	Link
Natural Questions	Google 검색 질의, 위키피디아, QA 형태	문서: 2,681,468개 질의: 307,373개 답변: long/short answer	Link
DL-Hard	MS MARCO 기반, 어려운 질의 선별	질의: 50개 (매우 어려운 질의) 의기반: MS MARCO 컬렉션	Link

p45. 한국어 일반 도메인 테스트셋

Test Set	데이터 구성 특징	데이터 규모	접근 URL
KorQuAD 1.0	한국어 위키피디아, 기계독해	문서: 1,560개 질의: 70,079개 답변: extractive	Link
KorQuAD 2.1	한국어 위키피디아, 답변 불가능한 질의 포함	문서: 5,668개 질의: 100,000개 답변: extractive / impossible	Link
KLUE-MRC	한국어 자연어 이해 벤치마크, 기계독해	문서: 5,841개 질의: 17,554개 답변: span-based	Link
AI Hub QA	다양한 도메인, 생활 질의응답	질의: 270,000개 답변: 다지선다형 도메인: 일반상식	Link

p46. IR 평가

사용자 요구(User Need)는 질의(Query)로 변환됨
관련성(Relevance)은 질의가 아닌 사용자 요구에 대해 평가
예시:
- 정보 요구(Information Need): 수영장 바닥이 검게 변해서 청소가 필요하다
- 질의(Query): pool cleaner
- 문서가 단순히 해당 단어들을 포함하는지가 아니라, 근본적인 요구사항을 해결하는지를 평가해야 함

사용자의 실제 정보 요구(Information Need)와 그것을 표현한 검색어(Query) 사이에는 차이가 있으며,
문서의 관련성(Relevance)은 검색어의 단순한 키워드 매칭이 아니라
사용자의 근본적인 정보 요구를 얼마나 잘 충족시키는가로 판단해야 한다.

p47. IR 평가

비순위 검색(Unranked Retrieval) 평가

	Relevant	Nonrelevant
Retrieved	tp	fp
Not Retrieved	fn	tn

Precision (정밀도)
\[P = \frac{tp}{tp + fp}\]
Recall (재현율)
\[R = \frac{tp}{tp + fn}\]

순위 검색(Ranked Retrieval) 평가

이진 적합성(Binary Relevance)
- Precision@K (P@K): 상위 K개 검색 결과 중 관련성(Relevance)이 있는 문서의 비율
- Mean Average Precision (MAP): 여러 질의에 대한 Average Precision의 평균
- Mean Reciprocal Rank (MRR): 각 질의에서 첫 번째로 찾은 관련 문서가 높은 순위에 있는 정도
다단계 관련성(Multiple Levels of Relevance)
- Normalized Discounted Cumulative Gain (NDCG):

Highly Relevant: 완전히 요구사항 충족
Relevant: 부분적 유용한 정보 포함
Partially Relevant: 약간의 관련 정보 포함
Not Relevant: 전혀 도움이 되지 않음

p48. IR 평가

Precision@K
- Precision@K = (상위 K개 결과 중 관련 문서 수) / K

순위	1	2	3	4	5	6	7	8	9	10
결과	R	N	R	R	N	R	N	N	R	N

Precision@1 = 1/1 = 1.0 (100%)
Precision@3 = 2/3 = 0.67 (67%)
Precision@5 = 3/5 = 0.6 (60%)
Precision@10 = 5/10 = 0.5 (50%)
장점
- 직관적, 실용적, 간단한 계산
단점
- Recall 무시: 전체 관련 문서 중 얼마나 찾았는지 고려하지 않음
- 순서 무관: 상위 K개 내에서의 순서는 구분하지 않음
- 이진 관련성: 다단계 관련성을 반영하지 못함

K 값	의미	활용 사례
P@1	첫 번째 결과의 정확도	내비게이션 질의, 팩트 체킹
P@5	첫 페이지 상위 결과	일반적인 웹 검색
P@10	첫 페이지 전체 결과	전통적인 검색 엔진 평가
P@20	확장된 결과 집합	연구용 검색, 전문 검색

p49. IR 평가

Mean Average Precision(MAP)
계산과정
- 1단계: Precision@K 계산
- 2단계: Average Precision (AP) 계산
  \[AP = \sum (P(k) \times rel(k)) / \text{전체 관련 문서 수}\]
  - P(k): k번째 위치에서의 Precision@k
  - rel(k): k번째 문서가 관련 문서면 1, 아니면 0
- 3단계: Mean Average Precision 계산
  \[MAP = (1/Q) \times \sum AP(q)\]
  - Q: 전체 질의 수
  - AP(q): 각 질의의 Average Precision
질의 1

순위	1	2	3	4	5	6	7	8	9	10
결과	R	N	R	R	N	R	N	N	R	N
P@k	1.0	0.5	0.67	0.75	0.6	0.67	0.57	0.5	0.56	0.5

AP = (P@1x1 + P@3x1 + P@4x1 + P@6x1 + P@9x1) / 5
= (1.0 + 0.67 + 0.75 + 0.67 + 0.56) / 5 = 3.6 / 5 = 0.73

질의 2

순위	1	2	3	4	5	6	7	8	9	10
결과	N	R	N	R	R	N	N	R	N	N
P@k	0	0.5	0.33	0.5	0.6	0.5	0.43	0.5	0.44	0.4

AP = (P@2x1 + P@4x1 + P@5x1 + P@8x1) / 4
= (0.5 + 0.5 + 0.6 + 0.5) / 4 = 2.1 / 4 = 0.525

MAP

\[MAP = (0.73 + 0.525) / 2 = 0.628\]

p50. IR 평가

MAP의 특징점

장점
- 순위 민감성: 높은 순위의 관련 문서에 더 큰 가중치
- 재현율 고려: 모든 관련 문서를 찾는 능력 반영
- 종합적 평가: 하나의 숫자로 전체 시스템 성능 요약
- 표준화: IR 분야의 널리 인정받는 표준 메트릭
한계점
- 이진 관련성: “관련” vs “비관련”만 구분 → nDCG 같은 다단계 메트릭 사용하여 해결
- 사용자 행동 미반영: 실제 사용자는 상위 몇 개만 확인 → MAP@K 변형 사용
  - MAP@K: 상위 10개 결과만으로 AP 계산

p51. IR 평가

Mean Reciprocal Rank (MRR)

각 질의에 대해 첫 번째 관련 문서의 순위 역수를 계산하고, 이를 모든 질의에 대해 평균

\[\text{Reciprocal Rank}(RR) = \frac{1}{rank_i}\]

$rank_i$ : 첫 번째 관련 문서의 순위

\[MRR = \frac{1}{Q} \times \sum RR_q\]

$Q$: 전체 질의 수
$RR_q$: 각 질의 q의 Reciprocal Rank

질의 1

순위	1	2	3	4	5
결과	N	R	N	R	N

RR = 1/2 = 0.5

질의 2

순위	1	2	3	4	5
결과	R	N	N	R	N

RR = 1/1 = 1.0

질의 3

순위	1	2	3	4	5
결과	N	N	N	R	N

RR = 1/4 = 0.25

MRR

\[MRR = (0.5 + 1.0 + 0.25) / 3 = 1.75 / 3 = 0.583\]

직관적: 사용자가 원하는 답을 얼마나 빨리 찾는지 측정
실용성: 실제 사용자 경험과 직결

p52. IR 평가

nDCG (Normalized Discounted Cumulative Gain)

다단계 관련성과 순위를 모두 고려하는 정보검색 평가 메트릭
구성요소
- Gain: 문의 관련성 수준에 따른 이득
- Cumulative Gain (CG): 상위 k개 문서의 이득합계
- Discounted Cumulative Gain (DCG): 순위에 따른 할인을 적용한 누적 이득
- Ideal DCG (iDCG): 이상적인 순서로 정렬했을 때의 최대 DCG

\[CG@k = \sum_{i=1}^{k} gain_i\] \[DCG@k = \sum_{i=1}^{k} \frac{gain_i}{\log_2(i+1)}\] \[nDCG@k = \frac{DCG@k}{IDCG@k}\]

Gain = relevance_level (0: 관련없음, 1: 약간관련, 2: 관련됨, 3: 매우 관련됨)

p53. IR 평가

순위	1	2	3	4	5	6
관련성	3	2	3	0	1	2

DCG@6 계산

\[DCG@6 = \frac{3}{\log_2(2)} + \frac{2}{\log_2(3)} + \frac{3}{\log_2(4)} + \frac{0}{\log_2(5)} + \frac{1}{\log_2(6)} + \frac{2}{\log_2(7)}\] \[= 3/1.0 + 2/1.585 + 3/2.0 + 0/2.322 + 1/2.585 + 2/2.807\] \[= 3.0 + 1.262 + 1.5 + 0 + 0.387 + 0.712 = 6.861\]

IDCG@6 계산

\[IDCG@6 = \frac{3}{1.0} + \frac{3}{1.585} + \frac{2}{2.0} + \frac{2}{2.322} + \frac{1}{2.585} + \frac{0}{2.807}\] \[= 3.0 + 1.893 + 1.0 + 0.861 + 0.387 + 0 = 7.141\]

nDCG@6 계산

\[nDCG@6 = \frac{6.861}{7.141} = 0.961\]

결과 테이블

k	DCG@k	IDCG@k	nDCG@k
1	3.000	3.000	1.000
2	4.262	4.893	0.871
3	5.762	5.893	0.978
4	5.762	6.754	0.853
5	6.149	7.141	0.861
6	6.861	7.141	0.961

p54. IR 평가

nDCG의 장점

다단계 관련성 지원
- nDCG: 매우관련(3) > 관련(2) > 약간관련(1) > 비관련(0)
순위 할인 (Position Discount)
- 상위 순위는 높은 가중치, 낮은 순위는 낮은 가중치 부여 ($\log_2(i+1)$로 할인)
정규화된 비교
- nDCG 값의 범위: 0 ~ 1
- 서로 다른 질의간의 직접 비교가 가능함

대학원 수업, 빅데이터와 정보검색