[논문] Denoising Diffusion Probabilistic Models
논문 출처
Ho, J., Jain, A., & Abbeel, P.
Denoising Diffusion Probabilistic Models.
Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS), 2020, Vancouver, Canada.
🔗 원문 링크 (arXiv: 2006.11239)
저자
Jonathan Ho
UC Berkeley
jonathanho@berkeley.eduAjay Jain
UC Berkeley
ajayj@berkeley.eduPieter Abbeel
UC Berkeley
pabbeel@cs.berkeley.edu
제34회 신경정보처리시스템 학술대회(Neural Information Processing Systems, NeurIPS)
캐나다 밴쿠버(Vancouver)에서 2020년에 개최.
초록 (Abstract)
우리는 확산 확률 모델(diffusion probabilistic models)을 사용하여
고품질의 이미지 합성 결과를 제시한다.
이 모델은 비평형 열역학(nonequilibrium thermodynamics)의 고찰에서
영감을 받은 잠재 변수(latent variable) 모델의 한 종류이다.
우리의 최상의 결과는,
확산 확률 모델(diffusion probabilistic models)과
랑주뱅 동역학(Langevin dynamics)을 이용한
잡음 제거 점수 매칭(denoising score matching) 사이의
새로운 연결에 따라 설계된 가중 변분 경계(weighted variational bound)에서
훈련함으로써 얻어진다.
또한 우리의 모델은
보통 점진적인 손실 압축 해제(progressive lossy decompression) 방식을
허용하며, 이는 자기회귀 디코딩(autoregressive decoding)의
일반화로 해석될 수 있다.
라벨 정보를 사용하지 않은 CIFAR10 데이터셋(unconditional CIFAR10 dataset)에서
우리는 Inception 점수 9.46과
최첨단의 FID 점수(state-of-the-art FID score) 3.17을 얻었다.
Inception 점수(Inception Score, IS)는
생성된 이미지가 얼마나 명확하고 다양하게 분포하는지를 평가하는 지표이다.사전 학습된 Inception 네트워크로 각 이미지의 클래스 확률을 예측하여
각 이미지의 불확실성(개별 엔트로피)이 낮고,
전체 분포의 다양성(전체 엔트로피)은 높을수록 좋은 점수를 얻는다.FID(Frechet Inception Distance)는
생성된 이미지 분포와 실제 이미지 분포의 유사도를 평가하는 지표이다.Inception 네트워크의 feature 공간에서
두 분포의 평균과 공분산을 비교하여 계산되며,
값이 낮을수록 생성된 이미지가 실제 데이터 분포에 가깝다는 것을 의미한다.
256×256 LSUN 데이터셋에서는
ProgressiveGAN과 유사한 샘플 품질을 얻었다.
ProgressiveGAN(Progressive Growing of GANs)은
2017년에 NVIDIA 연구팀(Karras et al.)이 제안한 생성적 적대 신경망(GAN)의 한 방식이다.핵심 아이디어는 낮은 해상도에서부터 시작하여 점진적으로 층(layer)을 추가하면서
네트워크를 고해상도로 확장해 가는 것이다.이렇게 하면 학습이 안정적(stable) 이고,
세부 구조가 점진적으로 정교해지며,
매우 고품질의 이미지를 생성할 수 있다.ProgressiveGAN은 이후 StyleGAN, StyleGAN2 등의 발전된 모델의
기반이 된 중요한 초기 연구이다.
우리의 구현은 다음에서 확인할 수 있다:
https://github.com/hojonathanho/diffusion
1 서론 (Introduction)
최근 들어 다양한 데이터 유형(data modalities)에서
모든 종류의 심층 생성 모델(deep generative models)들이
고품질의 샘플을 보여주고 있다.
생성적 적대 신경망(Generative Adversarial Networks, GANs),
자가회귀 모델(autoregressive models),
흐름 모델(flows), 그리고
변분 오토인코더(Variational Autoencoders, VAEs)는
주목할 만한 이미지와 오디오 샘플을 합성해왔다 [14, 27, 3, 58, 38, 25, 10, 32, 44, 57, 26, 33, 45].
또한 에너지 기반 모델링(energy-based modeling)과
점수 매칭(score matching)에서도
GANs가 생성한 이미지에 필적하는 결과를 만들어내는
놀라운 발전이 있었다 [11, 55].
그림 1:
CelebA-HQ 256×256 (왼쪽)과
라벨이 없는 CIFAR10(unconditional CIFAR10, 오른쪽)에서 생성된 샘플들.
그림 2:
이 연구에서 고려된 유향 그래프 모델(directed graphical model).
이 논문은 확산 확률 모델(diffusion probabilistic models) [53]의 발전(progress)을 제시한다.
확산 확률 모델(간단히 “확산 모델(diffusion model)”이라 부르기로 한다)은
유한한 시간 후 데이터와 일치하는 샘플을 생성하기 위해
변분 추론(variational inference)을 사용하여 학습된
매개변수화된 마르코프 연쇄(parameterized Markov chain)이다.
이 연쇄의 전이(transition)는 확산 과정을 역전시키도록 학습되는데,
이 확산 과정은 신호가 파괴될 때까지
데이터에 점진적으로 잡음을 추가하는 마르코프 연쇄이다.
확산이 작은 양의 가우시안 잡음으로 구성될 때에는,
샘플링 연쇄의 전이를 조건부 가우시안(conditional Gaussians)으로 설정하는 것으로 충분하며,
이로 인해 특히 단순한 신경망 매개변수화(neural network parameterization)가 가능해진다.
확산 모델(diffusion models)은 정의하기 쉽고 학습 효율도 높지만,
우리의 지식으로는 지금까지 그러한 모델이
고품질 샘플을 생성할 수 있음을 입증한 사례는 없었다.
우리는 확산 모델이 실제로 고품질 샘플을 생성할 수 있음을 보이며,
때로는 다른 종류의 생성 모델들에 대한 기존 결과보다
더 나은 성능을 보이기도 함을 보여준다 (섹션 4).
또한 우리는 확산 모델의 특정한 매개변수화(parameterization)가
훈련 중 여러 잡음 수준에서의 잡음 제거 점수 매칭(denoising score matching) 및
가열된(annealed)* 랑주뱅 동역학(annealed Langevin dynamics)과 동등함을 드러냄을 보여준다 (섹션 3.2) [55, 61].
*여기서 “어닐링(annealing)”은 잡음의 세기를 점진적으로 줄여나가며
시스템이 점차 안정된 상태에 수렴하도록 하는 과정을 의미함
우리는 이러한 매개변수화를 사용했을 때
가장 우수한 샘플 품질 결과를 얻었으며 (섹션 4.2),
따라서 이 등가성(equivalence)을 본 연구의 주요 기여 중 하나로 간주한다.
샘플 품질에도 불구하고,
우리의 모델은 다른 가능도 기반 모델(likelihood-based models)에 비해
경쟁력 있는 로그 가능도(log likelihood)를 가지지 않는다.
(그러나 우리의 모델은
에너지 기반 모델(energy-based models)과 점수 매칭(score matching)에 대해
어닐링된 중요도 샘플링(annealed importance sampling)이 산출하는 것으로 보고된,
가장 큰 추정치보다 더 나은 로그 가능도(log likelihood)를 가진다 [11, 55].)
로그 가능도(log likelihood)는
모델이 주어진 데이터를 얼마나 잘 설명하는지를 나타내는 지표이다.
값이 높을수록 모델이 실제 데이터 분포를 더 정확히 근사한다는 뜻이다.확산 모델은 생성된 이미지의 시각적 품질은 매우 뛰어나지만,
수학적으로 계산되는 확률 기반 평가지표(로그 가능도)는
다른 가능도 기반 모델들보다 낮다는 점을 의미한다.다만, 여기서 언급된 어닐링된 중요도 샘플링(annealed importance sampling) 은
모델의 로그 가능도를 근사적으로 계산하기 위한 고급 통계 기법으로,
여러 단계에 걸쳐 “온도(temperature)”를 서서히 낮추며
분포 간의 차이를 보정하는 방식이다.즉, 이 기법으로 추정된 에너지 기반 모델의 가장 높은 추정치와 비교해도,
확산 모델의 로그 가능도가 그보다 더 우수하다는 점을 강조하고 있다.
우리는 우리의 모델의 무손실 부호화 길이(lossless codelength) 대부분이
지각할 수 없는 이미지 세부 사항들을 설명하는 데 소비된다는 것을 발견했다 (섹션 4.3).
무손실 부호화 길이(lossless codelength)는
데이터를 압축했을 때 정보를 전혀 잃지 않고 표현하는 데 필요한 비트 수를 의미한다.여기서 “지각할 수 없는 이미지 세부 사항”이란
사람의 눈에는 거의 구분되지 않지만
모델이 데이터의 모든 픽셀 값을 완벽히 맞추기 위해
불필요하게 많은 정보를 사용하고 있다는 뜻이다.즉, 확산 모델이 실제로는 시각적으로 중요하지 않은 미세한 잡음 수준의 정보까지
부호화하려고 하기 때문에,
전체 부호화 길이의 대부분이 이런 사소한 세부 묘사에 소모된다는 의미이다.
우리는 이 현상을 손실 압축(lossy compression)의 언어로 보다 정교하게 분석하며,
확산 모델의 샘플링 절차가 점진적 디코딩(progressive decoding)의 일종임을 보여준다.
이 디코딩은 비트 순서(bit ordering)를 따라 진행되는 자가회귀 디코딩(autoregressive decoding)과 유사하지만,
일반적인 자가회귀 모델로는 불가능한 범위까지 훨씬 더 일반화된 형태를 가진다.
이 문장은 다음과 같은 의미를 담고 있다.
먼저, 저자들은 모델이 불필요하게 많은 정보를 부호화하는 현상을
손실 압축(lossy compression), 즉 덜 중요한 정보를 버리고 핵심만 남기는 방식으로
다시 해석하고 있다는 뜻이다.그리고 확산 모델의 샘플링 과정이
일반적인 자기회귀 모델(autoregressive model)처럼
한 단계씩 점진적으로 데이터를 복원하는 “디코딩 과정”과 유사하지만,
그보다 훨씬 유연하고 일반화된 순서(bit ordering) 로 진행된다고 설명한다.즉, 확산 모델은 자기회귀 디코딩보다
더 세밀하고 연속적인 방식으로 데이터를 재구성하는
점진적 복원(decoding) 과정으로 볼 수 있다는 의미이다.
2 배경 (Background)
확산 모델(diffusion models) [53]은
다음 형태의 잠재 변수(latent variable) 모델이다:
여기서 $\mathbf{x}_1, \dots, \mathbf{x}_T$ 는
데이터 $\mathbf{x}_0 \sim q(\mathbf{x}_0)$ 와 동일한 차원을 가지는 잠재 변수(latents)이다.
이 수식은 확산 모델이 잠재 변수 모델(latent variable model) 로 구성된다는 것을 의미한다.
즉, 데이터 $\mathbf{x}_0$ 는 단일 확률 변수로 직접 생성되는 것이 아니라,
여러 단계의 잠재 변수 $\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_T$ 를 거쳐
점진적으로 생성된다는 뜻이다.\(p_\theta(\mathbf{x}_0)\) 는 최종적으로 우리가 얻고자 하는 데이터의 확률 분포이며,
이 분포는 전체 잠재 변수들의 결합 분포 \(p_\theta(\mathbf{x}_{0:T})\) 를
\(\mathbf{x}_1\) 부터 \(\mathbf{x}_T\) 까지 적분(marginalization)하여 얻는다.다시 말해, \(\mathbf{x}_1\)~\(\mathbf{x}_T\) 는
데이터 생성 과정 중간의 “숨겨진 단계(hidden steps)”들이며,
모델은 이 잠재 변수들을 통해 데이터의 복잡한 분포를 학습한다.
결합 분포(joint distribution) $p_\theta(\mathbf{x}_{0:T})$ 는
역방향 과정(reverse process)이라고 불리며,
이는 학습된 가우시안 전이(Gaussian transitions)를 갖는
마르코프 연쇄(Markov chain)로 정의된다.
결합 분포 $p_\theta(\mathbf{x}_{0:T})$ 는
데이터 $\mathbf{x}_0$ 부터 잠재 변수 $\mathbf{x}_T$ 까지의
전체 생성 경로 전체를 아우르는 확률 분포를 의미한다.이를 “역방향 과정(reverse process)”이라고 부르는 이유는,
실제 확산 과정이 데이터를 점점 노이즈로 변환시키는 방향으로 진행되는 반면,
모델은 그 반대 방향으로, 즉 노이즈로부터 데이터를 복원하는 방향으로
학습되기 때문이다.또한 이 역방향 과정은 마르코프 연쇄(Markov chain) 형태로 정의되는데,
이는 각 단계의 상태 $\mathbf{x}_{t-1}$ 이
바로 이전 단계의 상태 $\mathbf{x}_t$ 에만 의존한다는 뜻이다.이때 각 전이 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 는
평균 $\mu_\theta$ 와 공분산 $\Sigma_\theta$ 를 가지는
가우시안 분포(Gaussian transition) 로 모델링되어,
노이즈 제거 과정을 확률적으로 표현한다.
이 연쇄는 다음에서 시작한다:
$p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathbf{I})$
그리고 다음과 같이 표현된다:
\[p_\theta(\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod_{t=1}^{T} p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t), \quad p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) := \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t)) \tag{1}\]이 식은 확산 모델의 생성 과정(generative process) 을 수학적으로 정의한 것이다.
먼저, $p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathbf{I})$ 는
가장 마지막 단계의 잠재 변수 $\mathbf{x}_T$ 가
평균이 0, 공분산이 단위행렬인 표준 가우시안 분포(standard normal distribution) 로부터
샘플링된다는 뜻이다.이후 각 단계는 바로 이전 단계의 변수 \(\mathbf{x}_{t-1}\) 을
현재 변수 \(\mathbf{x}_t\) 로부터 확률적으로 복원하는 과정을 거치며,
이 전이는 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 로 표현된다.특히 이 전이는
평균이 \(\mu_\theta(\mathbf{x}_t, t)\),
공분산이 \(\Sigma_\theta(\mathbf{x}_t, t)\) 인
가우시안 분포 \(\mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t))\) 로
정의된다.이는 모델이 각 단계에서 노이즈를 제거하며
다음 상태를 확률적으로 예측하는 것을 의미한다.전체 생성 과정은 마르코프 성질에 따라
모든 단계의 전이 확률들을 곱한 형태로 나타낼 수 있으며,
이를 통해 최종적으로 데이터 $\mathbf{x}_0$ 까지 점진적으로 복원된다.즉, 모델은
노이즈에서 시작해(\(\mathbf{x}_T\)),
점차 노이즈를 제거하며(\(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\)),
최종적으로 데이터 \(\mathbf{x}_0\) 를 생성하는
확률적 복원 절차(stochastic denoising process) 를 수행한다.
확산 모델(diffusion models)을
다른 유형의 잠재 변수 모델(latent variable models)과 구별하는 것은,
순방향 과정(forward process) 또는 확산 과정(diffusion process) 이라고 불리는
근사 사후분포(approximate posterior) $q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)$ 가
마르코프 연쇄(Markov chain)로 고정되어 있으며,
이는 분산 스케줄(variance schedule) $\beta_1, \dots, \beta_T$ 에 따라
데이터에 점진적으로 가우시안 잡음을 추가한다는 점이다.
\(\mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I})\) 는
이전 상태 \(\mathbf{x}_{t-1}\) 의 일부를 남기고, 나머지를 잡음으로 채워
\(\mathbf{x}_t\) 를 만드는 과정을 나타낸다.$(1 - \beta_t)$ 는 신호를 유지하는 비율,
$\beta_t$ 는 잡음을 추가하는 비율을 의미한다.제곱근(√)은 분산이 일정하게 유지되도록 하기 위한 것이다.
즉, 신호와 잡음의 분산이 $(1 - \beta_t) + \beta_t = 1$ 이 되게 하여
값이 발산하지 않고 안정적으로 확산되도록 한다.결과적으로 $\sqrt{1 - \beta_t}$ 는 “신호 유지 세기”,
$\sqrt{\beta_t}$ 는 “잡음 세기”를 조절하는 계수이다.
학습은 음의 로그 가능도(negative log likelihood)에 대한
통상적인 변분 경계(variational bound)를 최적화함으로써 수행된다:
데이터의 주변 확률(marginal likelihood) 은 다음과 같이 정의된다.
\[p_\theta(\mathbf{x}_0) = \int p_\theta(\mathbf{x}_{0:T}) \, d\mathbf{x}_{1:T}\]이는 모든 잠재 변수 $\mathbf{x}_1, \dots, \mathbf{x}_T$ 를 적분해
데이터 $\mathbf{x}_0$ 의 확률을 계산한 것이다.이 적분은 계산이 어렵기 때문에,
\[\log p_\theta(\mathbf{x}_0) = \log \int q(\mathbf{x}_{1:T} \mid \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)} \, d\mathbf{x}_{1:T}\]
계산 가능한 근사 분포 $q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)$ 를 곱하고 나눈다.이렇게 하면 $q$ 를 기대값(expectation) 형태로 표현할 수 있다.
젠센 부등식(Jensen’s inequality) 을 적용하기 전에,
먼저 그 정의를 간단히 살펴보면 다음과 같다.
함수 $f(x)$ 가 오목(concave) 일 때
\[f(\mathbb{E}[X]) \ge \mathbb{E}[f(X)]\]
확률 변수 $X$ 에 대해 다음이 성립한다:로그 함수 $\log(x)$ 는 오목 함수이므로 다음이 성립한다:
\[\log \mathbb{E}[X] \ge \mathbb{E}[\log X]\]이 성질을 위 식에 적용하면,
로그 안쪽의 적분(기댓값)을 바깥으로 이동시킬 수 있다.따라서 다음의 부등식이 성립한다:
\[\log p_\theta(\mathbf{x}_0) = \log \mathbb{E}_q \left[\frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)}\right] \ge \mathbb{E}_q \left[\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)}\right]\]음의 로그를 취하면 부호가 반대가 되어
식 (3)의 변분 하한(variational lower bound) 형태가 얻어진다.확산 모델은
\[p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T)\prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t), \quad q(\mathbf{x}_{1:T} \mid \mathbf{x}_0) = \prod_{t=1}^T q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\]로 정의되므로, 로그 비율은 다음처럼 전개된다.
\[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)} = -\log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})}\]이를 $q$ 에 대한 기댓값으로 취하면 다음과 같다.
\[\mathbb{E}[-\log p_\theta(\mathbf{x}_0)] \le \mathbb{E}_q \left[ -\log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} \right] =: \mathcal{L}\]
순방향 과정(forward process)의 분산(variances) $\beta_t$ 는
재매개변수화(reparameterization) [33]를 통해 학습되거나,
혹은 하이퍼파라미터(hyperparameters)로 고정될 수 있다.
역방향 과정(reverse process)의 표현력(expressiveness)은
$p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)$ 에서
가우시안 조건부(Gaussian conditionals)를 선택함으로써
부분적으로 보장된다.
이는 $\beta_t$ 가 작을 때
순방향 과정과 역방향 과정이
같은 함수적 형태(functional form)를 가지기 때문이다 [53].
순방향 과정의 분산 $\beta_t$ 는
각 단계에서 데이터에 얼마나 강한 잡음을 추가할지를 결정하는 값이다.
값이 작을수록 한 단계에서 추가되는 잡음의 양이 매우 작아지고,
따라서 $\mathbf{x}_{t-1}$ 과 $\mathbf{x}_t$ 의 관계가 거의 선형적(linear) 관계에 가까워진다.순방향 과정은 다음과 같이 정의된다:
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t \mathbf{I}),\]여기서 $\beta_t$ 는 추가되는 잡음의 분산을 나타낸다.
반면 역방향 과정은
\[p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t))\]로 정의되며,
이는 잡음이 섞인 \(\mathbf{x}_t\) 로부터
원래의 \(\mathbf{x}_{t-1}\) 을 복원하는 확률 분포를 나타낸다.$\beta_t$ 가 매우 작을 경우,
한 단계에서의 확률적 변화가 미소하므로
순방향 분포 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 와
역방향 분포 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 가
모두 근사적으로 선형 가우시안 변환(linear Gaussian transition) 형태를 갖게 된다.
이때 양쪽 모두 평균이 이전 상태의 선형 함수로 표현되고,
공분산도 거의 동일한 크기를 갖는다.수학적으로, $\beta_t \to 0$ 일 때
\[p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) \approx q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0).\]
두 과정의 차이는 고차항(higher-order term) 수준으로 작아지며,
다음 근사 관계가 성립한다:즉, $\beta_t$ 가 충분히 작으면
순방향과 역방향 모두 “가우시안 전이(Gaussian transition)”의 형태를 가지며,
평균(mean)과 분산(variance)의 함수적 형태가 거의 동일하게 된다.
이로 인해 역방향 모델이 학습해야 할 분포의 구조가 단순화되고,
샘플링 과정에서의 수치적 안정성(numerical stability) 또한 높아진다.
순방향 과정의 주목할 만한 성질 중 하나는,
임의의 시점 $t$ 에서 폐형식(closed form)으로
$\mathbf{x}_t$ 를 샘플링할 수 있다는 점이다.
$\alpha_t := 1 - \beta_t$ 및
\(\bar{\alpha}_t := \prod_{s=1}^{t} \alpha_s\) 라는 표기를 사용하면,
다음과 같은 식이 성립한다:
우선 다음과 같이 정의한다:
\[\alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{i=1}^{t} \alpha_i\]순방향 과정은 다음과 같은 가우시안 형태로 표현된다:
\[\mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}, \quad \boldsymbol{\epsilon}_{t-1} \sim \mathcal{N}(0, \mathbf{I})\]이 식을 반복적으로 전개하면 다음과 같다.
첫 번째 단계:
\[\mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}\]두 번째 단계:
\[\mathbf{x}_{t-1} = \sqrt{\alpha_{t-1}}\mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}}\boldsymbol{\epsilon}_{t-2}\]이를 대입하면,
\[\mathbf{x}_t = \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{\alpha_t(1 - \alpha_{t-1})}\boldsymbol{\epsilon}_{t-2} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}\]“서로 다른 분산을 가진 두 가우시안 분포를 결합할 때”
새로운 분산이 두 분산의 합으로 표현된다.예를 들어,
$\mathcal{N}(0, \sigma_1^2\mathbf{I})$ 와 $\mathcal{N}(0, \sigma_2^2\mathbf{I})$ 를 결합하면
결과는 $\mathcal{N}(0, (\sigma_1^2 + \sigma_2^2)\mathbf{I})$ 가 된다.이 원리를 적용하면,
\[\sqrt{(1 - \alpha_t) + \alpha_t(1 - \alpha_{t-1})} = \sqrt{1 - \alpha_t \alpha_{t-1}}\]
단계별 잡음이 합쳐질 때 표준편차는 다음과 같이 단순화된다:위 과정을 계속 반복하면, 일반적으로 다음 형태로 수렴한다:
\[\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})\]위 식은 $\mathbf{x}_t$ 가 원본 데이터 $\mathbf{x}_0$ 와
단일 가우시안 잡음 $\boldsymbol{\epsilon}$ 의 선형 결합(linear combination)으로 표현된다는 것을 의미한다.따라서 $\mathbf{x}_t$ 는 확률 변수 $\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})$ 를 따르며,
평균(mean)은 $\sqrt{\bar{\alpha}_t}\mathbf{x}_0$,
분산(covariance)은 $(1 - \bar{\alpha}_t)\mathbf{I}$ 인 가우시안 분포가 된다.즉, 이 관계를 확률 분포 형태로 쓰면 다음과 같으며,
\[q(\mathbf{x}_t \mid \mathbf{x}_0) = \mathcal{N}\!\left( \mathbf{x}_t; \sqrt{\bar{\alpha}_t}\mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I} \right) \tag{4}\]
이것이 바로 식 (4)이다:
따라서 확률적 경사 하강법(stochastic gradient descent)을 사용하여
$\mathcal{L}$ 의 임의 항(random terms)을 최적화함으로써
효율적인 학습이 가능하다.
추가적인 향상은
식 (3)의 $\mathcal{L}$ 을 다음과 같이 다시 씀으로써
분산 감소(variance reduction)로부터 얻어진다:
(자세한 내용은 부록 A(Appendix A) 를 참고하라.)
식 (5)의 도출 과정
Appendix A에서는 식 (3)에서 제시된 변분 하한(variational lower bound)을
보다 분산이 낮은(reduced variance) 형태로 다시 전개하여
식 (5)를 얻는 과정을 단계별로 설명한다.1. 기본 형태로부터 시작 (식 17)
변분 하한 $\mathcal{L}$ 은 다음과 같이 정의된다.
\[\mathcal{L} = \mathbb{E}_q \left[ -\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)} \right] \tag{17}\]이는 전체 데이터 생성 확률과 근사 분포 간의 로그 비율의 기댓값으로,
변분 하한(VLB, variational lower bound)의 기본 형태를 나타낸다.2. 공통 항 분리 (식 18)
결합 확률 분포 \(p_\theta(\mathbf{x}_{0:T})\) 와 \(q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)\) 는
\[p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod_{t=1}^{T} p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t), \quad q(\mathbf{x}_{1:T} \mid \mathbf{x}_0) = \prod_{t=1}^{T} q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\]
모두 마르코프 연쇄(Markov chain) 구조를 가지므로,
각 조건부 확률의 곱 형태로 전개할 수 있다:이를 식 (17)에 대입하면 다음과 같이 된다.
\[\mathcal{L} = \mathbb{E}_q \left[ -\log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} \right] \tag{18}\]첫 번째 항은 종단 노이즈 분포 $p(\mathbf{x}_T)$ 의 로그 우도를,
두 번째 항은 단계별 전이 확률의 로그 비율을 나타낸다.3. 첫 번째 항과 마지막 항의 분리 (식 19)
$t = 1$ 항을 별도로 분리하여,
\[\mathcal{L} = \mathbb{E}_q \left[ -\log p(\mathbf{x}_T) - \sum_{t > 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} - \log \frac{p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1)}{q(\mathbf{x}_1 \mid \mathbf{x}_0)} \right] \tag{19}\]
마지막 복원 항 $p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1)$ 을 분리해낸다.여기서 마지막 항은 데이터 복원 단계(reconstruction term)를,
나머지 합은 중간 단계의 확률 전이(term transition)를 의미한다.4. 조건부 확률의 재정렬 (식 20–21 유도)
순방향 과정의 확률 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 은
\[q(\mathbf{x}_{t-1}, \mathbf{x}_t \mid \mathbf{x}_0) = q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\, q(\mathbf{x}_t \mid \mathbf{x}_0) = q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\, q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)\]
사후 확률 형태 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)$ 로 변환될 수 있다.
결합 확률의 성질로부터 다음이 성립한다:따라서 다음 관계식을 얻는다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\, q(\mathbf{x}_t \mid \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)} \tag{A}\]식 (A)를 이용하면 분모의 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 를 다음과 같이 바꿀 수 있다:
\[\frac{1}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} = \frac{1}{q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)}\, \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)}\]이를 식 (19)에 대입하면 다음이 된다.
\[\mathcal{L} = \mathbb{E}_q \left[ -\log p(\mathbf{x}_T) - \sum_{t > 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)} \cdot \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)} - \log \frac{p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1)}{q(\mathbf{x}_1 \mid \mathbf{x}_0)} \right] \tag{20}\]여기서 두 번째 로그항은
\[\sum_{t>1} \log \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)} = \log q(\mathbf{x}_1 \mid \mathbf{x}_0) - \log q(\mathbf{x}_T \mid \mathbf{x}_0)\]
$t$ 에 대해 망원급수(telescoping sum) 형태로 대부분 상쇄되어,가 된다.
이후 망원항을 정리하면 식 (21)로 단순화된다.
\[\mathcal{L} = \mathbb{E}_q \left[ -\log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_T \mid \mathbf{x}_0)} - \sum_{t > 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)}{q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)} - \log p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) \right] \tag{21}\]위 식에서
\[-\log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_T \mid \mathbf{x}_0)}\]항은
KL 발산 \(D_{\mathrm{KL}}(q(\mathbf{x}_T \mid \mathbf{x}_0) \parallel p(\mathbf{x}_T))\) 의 형태로 변환되며,
이후 식 (22)로 이어진다.5. KL 발산 형태로 표현 (식 22)
위 식 (20)은 KL 발산의 정의를 이용하여 다음과 같이 정리된다.
\[\mathcal{L} = \mathbb{E}_q \left[ D_{\mathrm{KL}}(q(\mathbf{x}_T \mid \mathbf{x}_0) \parallel p(\mathbf{x}_T)) + \sum_{t > 1} D_{\mathrm{KL}}(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)) - \log p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) \right] \tag{22}\]이 식이 본문에서 제시된 식 (5) 와 동일하다.
즉, 변분 하한을 KL 발산 항들의 합으로 표현한 결과이다.6. 왜 “분산이 낮은(reduced variance)” 형태인가
식 (5)의 각 KL 항은
확률적 샘플링 대신 폐형식(closed-form) 으로 계산 가능한 가우시안 간 KL로 구성된다.기존 ELBO(식 3)는
단일 샘플 \(\mathbf{x}_0 \sim q(\mathbf{x}_0)\) 을 사용하여
\(\log p_\theta(\mathbf{x}_0)\) 를 직접 추정해야 하므로
몬테카를로 추정에 의한 분산이 크다.반면 식 (5)는
- $q(\mathbf{x}_T \mid \mathbf{x}_0)$,
- $q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)$,
- $p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)$
모두 가우시안 분포로 명시적 파라미터화가 되어 있고,
각 KL 항이 닫힌 형태로 계산되므로,
표본 추출에 의한 분산이 발생하지 않는다.즉,
식 (5)는 원래의 ELBO를
“샘플링 기반 추정(Monte Carlo Estimation)”에서
“가우시안 KL 기반의 결정적 계산(Deterministic KL Computation)”으로 변환한 형태이며,
따라서 훨씬 분산이 낮고 안정적인 학습 목표를 제공한다.
식의 각 항에 붙은 레이블(label)은 3절(섹션 3)에서 사용된다.
식 (5)는 KL 발산(KL divergence)을 사용하여
\(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 과
순방향 과정의 사후분포(forward process posterior)
\(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\) 를 직접 비교한다.
이 비교는 $\mathbf{x}_0$ 가 주어졌을 때 계산이 용이하다(tractable).
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\!\left(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}\right), \tag{6}\]여기서
\[\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) := \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}\mathbf{x}_t, \quad \tilde{\beta}_t := \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}\beta_t \tag{7}\]식 (6)의 도출 과정
식 (6)은 순방향 과정
\(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\)
과 초기 상태 \(\mathbf{x}_0\) 의 결합 분포로부터
사후분포 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\)
를 유도하는 과정이다.1. 순방향 과정의 정의
순방향 확산 과정은 다음의 가우시안 형태로 정의된다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}\!\left( \mathbf{x}_t; \sqrt{\alpha_t}\mathbf{x}_{t-1}, (1 - \alpha_t)\mathbf{I} \right)\]이 과정을 $t$ 스텝까지 누적하면,
\[q(\mathbf{x}_t \mid \mathbf{x}_0) = \mathcal{N}\!\left( \mathbf{x}_t; \sqrt{\bar{\alpha}_t}\mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I} \right), \quad \bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s\]
초기 상태 $\mathbf{x}_0$ 로부터의 직접적인 전이 확률은
다음과 같다.2. 사후분포의 정의
우리가 구하고자 하는 것은
\(\mathbf{x}_t\) 와 \(\mathbf{x}_0\) 가 주어졌을 때의
\(\mathbf{x}_{t-1}\) 의 조건부 분포이다.결합 확률의 정의로부터 다음이 성립한다.
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0)\, q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)}\]여기서 마르코프 성질(Markov property), 즉
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0) = q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\]
“현재 상태는 바로 이전 상태에만 의존하고
그보다 앞선 상태에는 직접 의존하지 않는다”는 성질에 의해이므로 식은 다음과 같이 단순화된다.
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\, q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)}\]마지막 항 \(q(\mathbf{x}_t \mid \mathbf{x}_0)\) 은
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \propto q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\, q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)\]
\(\mathbf{x}_{t-1}\) 과 무관한 정규화 상수이므로,
비례식으로 간단히 쓸 수 있다.3. 가우시안 곱의 일반형 정리
두 가우시안 $\mathcal{N}(\mathbf{x}; \mu_1, \Sigma_1)$ 과
\[\mathcal{N}(\mathbf{x}; \tilde{\mu}, \tilde{\Sigma}), \quad \tilde{\Sigma} = (\Sigma_1^{-1} + \Sigma_2^{-1})^{-1}, \quad \tilde{\mu} = \tilde{\Sigma}(\Sigma_1^{-1}\mu_1 + \Sigma_2^{-1}\mu_2)\]
$\mathcal{N}(\mathbf{x}; \mu_2, \Sigma_2)$ 의 곱은
또 다른 가우시안 형태로 표현된다.4. 각 항의 구체적 대입
첫 번째 항 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 는
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}\!\left( \mathbf{x}_t; \sqrt{\alpha_t}\mathbf{x}_{t-1}, (1 - \alpha_t)\mathbf{I} \right)\]
순방향 과정에서 다음의 가우시안 형태로 정의된다.그러나 우리는 \(\mathbf{x}_{t-1}\) 에 대한 사후분포
\(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\) 를 구해야 하므로,
위 확률을 $\mathbf{x}_{t-1}$을 변수로 한 형태로 다시 써야 한다.이를 위해 다음의 확률 밀도 함수를 생각한다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) \propto \exp\!\left( -\frac{1}{2(1 - \alpha_t)} \|\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_{t-1}\|^2 \right)\]제곱항을 $\mathbf{x}_{t-1}$ 에 대해 전개하면,
\[\|\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_{t-1}\|^2 = \alpha_t\|\mathbf{x}_{t-1}\|^2 - 2\sqrt{\alpha_t}\mathbf{x}_t^\top \mathbf{x}_{t-1} + \|\mathbf{x}_t\|^2\]상수항 \(\|\mathbf{x}_t\|^2\) 는 \(\mathbf{x}_{t-1}\) 에 의존하지 않으므로 무시할 수 있다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) \propto \exp\!\left( -\frac{\alpha_t}{2(1 - \alpha_t)} \left\| \mathbf{x}_{t-1} - \frac{\mathbf{x}_t}{\sqrt{\alpha_t}} \right\|^2 \right)\]
남은 부분을 완전제곱(completing the square) 형태로 정리하면,따라서 이는 $\mathbf{x}_{t-1}$ 에 대한 가우시안으로 다음과 같이 다시 쓸 수 있다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}\!\left( \mathbf{x}_{t-1}; \frac{\mathbf{x}_t}{\sqrt{\alpha_t}}, \frac{1 - \alpha_t}{\alpha_t}\mathbf{I} \right)\]확산 계수 $\beta_t = 1 - \alpha_t$ 를 이용하면,
\[\mu_1 = \frac{\mathbf{x}_t}{\sqrt{\alpha_t}}, \quad \Sigma_1 = \frac{\beta_t}{\alpha_t}\mathbf{I}\]
첫 번째 항 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\)의 평균과 분산은 다음과 같이 정리된다.두 번째 항 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)$ 은
\[\mu_2 = \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0, \quad \Sigma_2 = (1 - \bar{\alpha}_{t-1})\mathbf{I}\]5. 평균과 분산의 도출 (식 7)
앞서 얻은 두 항을 다시 상기하자.
첫 번째 항:
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}\!\left( \mathbf{x}_{t-1}; \mu_1 = \frac{\mathbf{x}_t}{\sqrt{\alpha_t}}, \Sigma_1 = \frac{\beta_t}{\alpha_t}\mathbf{I} \right)\]두 번째 항:
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_0) = \mathcal{N}\!\left( \mathbf{x}_{t-1}; \mu_2 = \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0, \Sigma_2 = (1 - \bar{\alpha}_{t-1})\mathbf{I} \right)\]이제 가우시안 곱 정리를 적용하면
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\!\left( \mathbf{x}_{t-1}; \tilde{\mu}_t, \tilde{\Sigma}_t \right)\]
사후분포 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)$ 는
또 다른 가우시안 형태로 표현된다:(1) 공분산 행렬의 계산
가우시안 곱 정리에 따라
\[\tilde{\Sigma}_t = \left(\Sigma_1^{-1} + \Sigma_2^{-1}\right)^{-1}\]
공분산은 다음과 같이 주어진다:각 항을 대입하면,
\[\Sigma_1^{-1} = \frac{\alpha_t}{\beta_t}\mathbf{I}, \quad \Sigma_2^{-1} = \frac{1}{1 - \bar{\alpha}_{t-1}}\mathbf{I}\]따라서
\[\tilde{\Sigma}_t = \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right)^{-1}\mathbf{I}\]분모를 통분하면,
\[\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} = \frac{\alpha_t(1 - \bar{\alpha}_{t-1}) + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}\]여기서 $\beta_t = 1 - \alpha_t$ 이므로,
\[\alpha_t(1 - \bar{\alpha}_{t-1}) + \beta_t = \alpha_t - \alpha_t\bar{\alpha}_{t-1} + 1 - \alpha_t = 1 - \alpha_t\bar{\alpha}_{t-1} = 1 - \bar{\alpha}_t\]따라서,
\[\tilde{\Sigma}_t = \frac{\beta_t(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}\mathbf{I} = \tilde{\beta}_t \mathbf{I}\]즉, 분산 항은 다음과 같이 정리된다.
\[\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}\beta_t\](2) 평균 벡터의 계산
평균은 다음 식으로 계산된다:
\[\tilde{\mu}_t = \tilde{\Sigma}_t \left( \Sigma_1^{-1}\mu_1 + \Sigma_2^{-1}\mu_2 \right)\]각 항을 대입하면,
\[\Sigma_1^{-1}\mu_1 + \Sigma_2^{-1}\mu_2 = \frac{\alpha_t}{\beta_t}\frac{\mathbf{x}_t}{\sqrt{\alpha_t}} + \frac{1}{1 - \bar{\alpha}_{t-1}}\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0\] \[= \frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}}\mathbf{x}_0\]이를 다시 $\tilde{\Sigma}_t$ 와 곱하면:
\[\tilde{\mu}_t = \frac{\beta_t(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \left( \frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}}\mathbf{x}_0 \right)\]분배법칙을 적용하면,
\[\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}\mathbf{x}_t\](3) 결과
최종적으로 사후분포는 다음과 같이 정리된다:
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\!\left( \mathbf{x}_{t-1}; \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t\mathbf{I} \right)\]여기서 \(\tilde{\beta}_t\)와 \(\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0)\)는 위에서 정의한 형태이다.
따라서 식 (5)의 모든 KL 발산은
가우시안 분포 간의 비교로 표현되므로,
고분산의 몬테카를로 추정(Monte Carlo estimates) 대신
폐형식(closed-form) 표현을 이용한
Rao-Blackwellization 방식으로 계산할 수 있다.
위 문장의 의미를 구체적으로 설명하면 다음과 같다.
식 (5)에서 등장하는 모든 KL 발산 항
\[D_{\mathrm{KL}}\big(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\big)\]은 두 확률분포가 모두 가우시안 형태임을 이용해
닫힌 해(closed-form)로 계산할 수 있다.즉, 두 분포가 모두
\[q = \mathcal{N}(\mu_q, \Sigma_q), \quad p = \mathcal{N}(\mu_p, \Sigma_p)\]와 같은 정규분포일 때,
\[D_{\mathrm{KL}}(q \parallel p) = \frac{1}{2} \left[ \mathrm{tr}(\Sigma_p^{-1}\Sigma_q) + (\mu_p - \mu_q)^\top \Sigma_p^{-1}(\mu_p - \mu_q) - k + \log\frac{\det\Sigma_p}{\det\Sigma_q} \right]\]
KL 발산은 다음의 분석적 식으로 바로 계산된다.이처럼 KL 발산을 수치적 샘플링(몬테카를로 추정)을 통해 근사하지 않고
수학적으로 정확한 폐형식(closed-form expression)으로 계산할 수 있기 때문에,
추정 과정에서 발생하는 확률적 노이즈(variance)가 크게 줄어든다.이를 Rao–Blackwellization이라 부르는데,
이는 “기댓값의 분산을 줄이기 위해 조건부 기댓값 형태로 재작성하는 방법”을 의미한다.
즉, $E[f(X)]$ 를 단순 샘플링으로 추정하는 대신
$E[E[f(X)\mid Y]]$ 와 같이 조건부 기댓값을 이용해
더 안정적이고 분산이 낮은 추정치를 얻는 것이다.요약하면,
식 (5)의 각 KL 항이 가우시안 간의 닫힌 해로 표현됨으로써
학습 과정에서 몬테카를로 샘플링에 의존하지 않아도 되며,
그 결과 ELBO 기반 학습보다 분산이 낮고 안정적인 최적화가 가능해진다.
3 확산 모델과 잡음 제거 오토인코더 (Diffusion models and denoising autoencoders)
확산 모델(diffusion models)은
잠재 변수(latent variable) 모델의 한정된 형태처럼 보일 수 있지만,
구현 단계에서 매우 많은 자유도를 가진다.
순방향 과정(forward process)의 분산 $\beta_t$ 와
역방향 과정(reverse process)의 모델의 아키텍처 및
가우시안 분포 매개변수화(parameterization)를 선택해야 한다.
우리의 선택을 정당화하기 위해 (To guide our choices),
우리는 확산 모델(diffusion models) 과 잡음 제거 스코어 매칭(denoising score matching) (섹션 3.2) 사이의
새로운 명시적 연결(explicit connection)을 수립한다.
이 연결은 확산 모델을 위한, 단순화된 가중 변분 하한 목적식(simplified, weighted variational bound objective)
(섹션 3.4)으로 이어진다.
궁극적으로, 제안된 모델 설계는 단순성과
경험적 결과(empirical results)에 의해 정당화된다 (섹션 4).
이 논의는 식 (5)에 의해 정리된다.
3.1 순방향 과정과 $L_T$ (Forward process and $L_T$)
순방향 과정의 분산 $\beta_t$ 는
재매개변수화(reparameterization)를 통해 학습 가능하지만,
여기서는 이를 무시하고 상수로 고정한다
(자세한 내용은 섹션 4 참조).
따라서 본 구현에서는 근사 사후분포 $q$ 가
학습 가능한 파라미터를 가지지 않으며,
이에 따라 $L_T$ 는 학습 과정 동안 상수로 유지되어
무시할 수 있다.
3.2 역방향 과정과 $L_{1:T-1}$ (Reverse process and $L_{1:T-1}$)
이제 $1 < t \leq T$ 인 경우에 대해
\(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t))\) 에서
우리의 선택에 대해 논의한다.
먼저,
$\Sigma_\theta(\mathbf{x}_t, t) = \sigma_t^2 \mathbf{I}$ 로 설정하여
학습되지 않는 시간 의존적 상수(untrained time dependent constants)로 둔다.
실험적으로,
\[\sigma_t^2 = \beta_t\]와
\[\sigma_t^2 = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t\]두 선택 모두 유사한 결과를 보였다.
첫 번째 선택은 $\mathbf{x}_0 \sim \mathcal{N}(0, \mathbf{I})$ 인 경우 최적이며,
두 번째 선택은 $\mathbf{x}_0$ 가 결정론적으로 한 점에 고정된 경우에 최적이다.
이 두 선택은 좌표별 단위 분산(coordinatewise unit variance)을 갖는 데이터에 대해
역방향 과정 엔트로피(reverse process entropy)의
상한과 하한에 각각 대응한다 [53].
위 식은 확산 모델에서 역방향 과정(reverse process)의 분산 선택에 대한 설명이다.
여기서 분산 항 $\Sigma_\theta(\mathbf{x}_t, t)$ 는 학습을 통해 추정하지 않고
실험적으로 설정된 두 가지 상수 형태 중 하나를 사용한다.$\sigma_t^2 = \beta_t$ 와
\(\sigma_t^2 = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t\)
두 설정 모두 유사한 결과를 보였는데,
이는 이론적 근거에 의해 도출된 것이 아니라
여러 실험을 통해 경험적으로 확인된 결과이다.
즉, 특정한 최적화 과정이나 수학적 유도 없이
실제 학습 실험에서 두 설정이 모두 잘 작동한다는 사실에 기반한다.또한, “이 두 선택이 역방향 과정 엔트로피(reverse process entropy)의
상한과 하한에 대응한다”는 의미는
데이터의 각 차원별 분산이 1인 경우(즉, 좌표별 단위 분산)
역방향 과정이 가질 수 있는 불확실성의 범위를
두 설정이 각각 위쪽과 아래쪽에서 제한한다는 뜻이다.
$\sigma_t^2 = \beta_t$ 는 비교적 큰 불확실성을 유지하는 상한에 해당하고,
$\tilde{\beta}_t$ 는 그보다 작은 불확실성을 가지는 하한에 해당한다.
따라서 이 둘은 모델이 잡음을 제거하는 과정에서
엔트로피(불확실성)의 범위를 안정적으로 조절하도록 돕는 역할을 한다.
둘째로, 평균 $\mu_\theta(\mathbf{x}_t, t)$ 을 표현하기 위해,
우리는 $L_t$ 에 대한 다음의 분석에 기초하여 유도된(motivated by)
특정한 매개변수화(parameterization)를 제안한다.
\(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \sigma_t^2 \mathbf{I})\) 일 때,
다음과 같이 쓸 수 있다:
여기서 $C$ 는 $\theta$ 에 의존하지 않는 상수이다.
식 (8)은 변분 하한(ELBO)의 두 번째 항
\[\mathbb{E}_q\!\left[ D_{\mathrm{KL}}\!\big(q(\mathbf{x}_{t-1}\mid \mathbf{x}_t, \mathbf{x}_0) \,\|\, p_\theta(\mathbf{x}_{t-1}\mid \mathbf{x}_t)\big) \right]\]을 전개하여 얻어진다.
먼저, 두 분포 $q$ 와 $p_\theta$ 를 가우시안으로 가정한다:
\[q(\mathbf{x}_{t-1}\mid\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\!\left(\mathbf{x}_{t-1}; \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0),\, \tilde{\beta}_t \mathbf{I}\right), \quad p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t) = \mathcal{N}\!\left(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t),\, \sigma_t^2 \mathbf{I}\right).\]가우시안 간의 KL 발산의 일반식은 다음과 같다:
\[D_{\mathrm{KL}}\!\big( \mathcal{N}(\mu_1, \Sigma_1) \,\|\, \mathcal{N}(\mu_2, \Sigma_2) \big) = \frac{1}{2} \left[ \mathrm{tr}(\Sigma_2^{-1}\Sigma_1) + (\mu_2 - \mu_1)^\top \Sigma_2^{-1}(\mu_2 - \mu_1) - k + \ln\frac{\det\Sigma_2}{\det\Sigma_1} \right].\]여기서 $\Sigma_1 = \tilde{\beta}_t \mathbf{I}$, $\Sigma_2 = \sigma_t^2 \mathbf{I}$ 를 대입하면,
\[D_{\mathrm{KL}}\!\big(q \,\|\, p_\theta\big) = \frac{1}{2\sigma_t^2} \lVert \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t, t) \rVert^2 + C.\]
행렬식(det)과 trace 항이 모두 상수로 정리되어
$\theta$ 와 무관한 부분은 모두 상수 $C$ 로 묶인다.
$\theta$ 가 포함된 유일한 항은 평균 차이 항이다:이제 이를 $\mathbb{E}_q[\cdot]$ 에 대해 기대값을 취하면,
\[L_{t-1} = \mathbb{E}_q \left[ \frac{1}{2\sigma_t^2} \lVert \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t, t) \rVert^2 \right] + C.\]
따라서 $\mu_\theta$ 의 가장 직접적인 매개변수화는
순방향 과정의 사후 평균(forward process posterior mean)인
$\tilde{\mu}_t$ 를 예측하는 모델임을 알 수 있다.
그러나 식 (8)은 $\mathbf{x}_t = \mathbf{x}_t(\mathbf{x}_0, \boldsymbol{\epsilon}) = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}$,
$\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})$ 로 재매개변수화하고
순방향 과정의 사후 분포 식 (7)을 적용하여
다음과 같이 더 확장할 수 있다:
[Step 0] 출발점 — 식 (8)
\[\begin{align} L_{t-1} &= \mathbb{E}_q \!\left[\frac{1}{2\sigma_t^2} \left\lVert \tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0) - \mu_\theta(\mathbf{x}_t,t)\right\rVert^2 \right] + C \tag{8} \end{align}\]
- \(\tilde{\mu}_t\) 는 순방향 과정의 사후 평균, \(\mu_\theta\) 는 역방향 과정의 평균(모델 출력)이다.
- $C$ 는 $\theta$ 와 무관한 상수이다.
[Step 1] 재매개변수화로 기대값의 변수 변경
순방향 과정의 표본 생성식을 사용한다:
\[\mathbf{x}_t=\sqrt{\bar{\alpha}_t}\,\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\,\boldsymbol{\epsilon}, \qquad \boldsymbol{\epsilon}\sim\mathcal{N}(0,\mathbf{I}).\]이를 이용하면 LOTUS(변수변환 하의 기대값 보존)에 의해 \(\mathbb{E}_q[\cdot]\;=\;\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}}[\cdot]\) 로 바뀐다.
LOTUS는 “확률 변수의 변환에 대해, 변환된 확률밀도를 직접 구하지 않아도
기댓값을 계산할 수 있다”는 원리를 의미한다.예를 들어, $\mathbf{z}’ = f(\mathbf{z})$ 이고 $\mathbf{z} \sim q(\mathbf{z})$ 라면,
\[\mathbb{E}_{q_{f}}[h(\mathbf{z}')] = \int h(\mathbf{z}')\, q_{f}(\mathbf{z}')\, d\mathbf{z}' = \int h(f(\mathbf{z}))\, q(\mathbf{z})\, d\mathbf{z}\]
변환된 변수의 기댓값은 다음과 같이 표현할 수 있다.즉, 변환 후의 밀도 $q_f(\mathbf{z}’)$ 를 명시적으로 계산하지 않아도,
원래의 분포 $q(\mathbf{z})$ 와 변환 함수 $f$ 만 알면
기대값을 직접 계산할 수 있다는 뜻이다.[Step 1-1] $\tilde{\mu}_t$ 두 번째 인자에 들어가는 $\mathbf{x}_0$ 를 $\mathbf{x}_t,\boldsymbol{\epsilon}$ 로 치환
위 식을 $\mathbf{x}_0$ 에 대해 정리하면
\[\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \Bigl(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t}\,\boldsymbol{\epsilon}\Bigr).\]따라서
\[\tilde{\mu}_t\bigl(\mathbf{x}_t,\mathbf{x}_0\bigr) = \tilde{\mu}_t\!\Bigl( \mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}), \frac{1}{\sqrt{\bar{\alpha}_t}}\bigl(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}) -\sqrt{1-\bar{\alpha}_t}\,\boldsymbol{\epsilon}\bigr) \Bigr).\][Step 1-2] 위 치환을 식 (8)에 대입하여 식 (9) 도출
\[\begin{align} L_{t-1}-C &= \mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}} \left[ \frac{1}{2\sigma_t^2} \left\lVert \tilde{\mu}_t\!\left( \mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}), \frac{1}{\sqrt{\bar{\alpha}_t}} \Bigl( \mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}) - \sqrt{1-\bar{\alpha}_t}\,\boldsymbol{\epsilon} \Bigr) \right) - \mu_\theta\!\left(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}),t\right) \right\rVert^2 \right] \tag{9} \end{align}\][Step 2] 순방향 사후 평균(식 (7))의 폐형식 대입
순방향 과정의 사후 평균(식 (7))은 다음과 같이 정의된다:
\[\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) := \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}\mathbf{x}_t.\]이제 $\mathbf{x}_0$ 를 $\mathbf{x}_t$ 와 $\boldsymbol{\epsilon}$ 으로 표현하는
\[\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \quad\Longrightarrow\quad \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}\bigl(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\bigr)\]
순방향 과정의 정의식을 위 식에 대입하면 다음과 같이 정리된다:
\[\begin{align} \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) &= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}} \bigl(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\bigr) + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}\mathbf{x}_t \\[6pt] &= \left[ \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{\sqrt{\bar{\alpha}_t}(1 - \bar{\alpha}_t)} + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \right]\mathbf{x}_t - \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}(1 - \bar{\alpha}_t)}\boldsymbol{\epsilon}. \end{align}\]여기서 \(\bar{\alpha}_t = \bar{\alpha}_{t-1}\alpha_t\), \(\beta_t = 1 - \alpha_t\) 를 이용하면
각 항의 계수를 단계적으로 단순화할 수 있다.먼저, $\mathbf{x}_t$ 의 계수를 살펴보면:
\[\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{\sqrt{\bar{\alpha}_t}(1 - \bar{\alpha}_t)} + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}.\]\(\bar{\alpha}_t = \bar{\alpha}_{t-1}\alpha_t\) 이므로 \(\sqrt{\bar{\alpha}_t} = \sqrt{\bar{\alpha}_{t-1}}\sqrt{\alpha_t}\) 이다.
\[\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{\sqrt{\bar{\alpha}_{t-1}}\sqrt{\alpha_t}(1 - \bar{\alpha}_t)} + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} = \frac{\beta_t}{\sqrt{\alpha_t}(1 - \bar{\alpha}_t)} + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}.\]
이를 대입하면:이제 공통 분모 $(1 - \bar{\alpha}_t)$ 로 묶어 정리하면:
\[\frac{1}{1 - \bar{\alpha}_t} \left[ \frac{\beta_t}{\sqrt{\alpha_t}} + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1}) \right].\]괄호 안의 항을 묶어서 계산한다:
\[\frac{\beta_t}{\sqrt{\alpha_t}} + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1}) = \frac{1 - \alpha_t}{\sqrt{\alpha_t}} + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1}) = \frac{1 - \alpha_t + \alpha_t(1 - \bar{\alpha}_{t-1})}{\sqrt{\alpha_t}} = \frac{1 - \alpha_t\bar{\alpha}_{t-1}}{\sqrt{\alpha_t}}.\]따라서 전체 계수는:
\[\frac{1}{1 - \bar{\alpha}_t} \cdot \frac{1 - \alpha_t\bar{\alpha}_{t-1}}{\sqrt{\alpha_t}} = \frac{1 - \bar{\alpha}_t}{(1 - \bar{\alpha}_t)\sqrt{\alpha_t}} = \frac{1}{\sqrt{\alpha_t}}.\]이제 $\boldsymbol{\epsilon}$ 항의 계수를 살펴보면:
\[\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}(1 - \bar{\alpha}_t)}.\]마찬가지로 \(\sqrt{\bar{\alpha}_t} = \sqrt{\bar{\alpha}_{t-1}}\sqrt{\alpha_t}\) 를 대입하면:
\[\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_{t-1}}\sqrt{\alpha_t}(1 - \bar{\alpha}_t)} = \frac{\beta_t}{\sqrt{\alpha_t}} \cdot \frac{\sqrt{1 - \bar{\alpha}_t}}{1 - \bar{\alpha}_t} = \frac{\beta_t}{\sqrt{\alpha_t(1 - \bar{\alpha}_t)}}.\]따라서 두 계수는 각각 다음과 같이 단순화된다:
\[\boxed{ \text{$\mathbf{x}_t$의 계수: } \frac{1}{\sqrt{\alpha_t}}, \quad \text{$\boldsymbol{\epsilon}$의 계수: } \frac{\beta_t}{\sqrt{\alpha_t(1 - \bar{\alpha}_t)}}. }\]따라서 다음의 간결한 형태를 얻는다:
\[\boxed{ \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}\boldsymbol{\epsilon} \right) }.\]따라서 $\tilde{\mu}_t$ 는 $\mathbf{x}_0$ 대신
잡음 변수 $\boldsymbol{\epsilon}$ 만으로 표현할 수 있으며,
이는 모델 학습 시 샘플링이 가능한 형태로 단순화된 표현이다.이를 식 (9)의 $\tilde{\mu}_t(\cdot)$ 위치에 대입한다.
[Step 2-1] 대입 후 정리하여 식 (10) 도출
\[\begin{align} L_{t-1}-C &= \mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}} \left[ \frac{1}{2\sigma_t^2} \left\lVert \frac{1}{\sqrt{\alpha_t}} \Bigl( \mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\boldsymbol{\epsilon} \Bigr) - \mu_\theta\!\left(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}),t\right) \right\rVert^2 \right] \tag{10} \end{align}\]정리하면, (8) → (9)는 재매개변수화에 따른 기대값 변수 변경 및 인자 치환,
(9) → (10)은 순방향 사후 평균의 폐형식(식 (7))을 직접 대입한 단계이다.
식 (10)은 $\mu_\theta$ 가
\[\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}\right)\]을 예측해야 함을 보여준다.
$\mathbf{x}_t$ 가 모델의 입력으로 주어지므로,
다음과 같은 매개변수화를 선택할 수 있다:
여기서 $\boldsymbol{\epsilon}_\theta$ 는
$\mathbf{x}_t$ 로부터 잡음 $\boldsymbol{\epsilon}$ 을 예측하도록 학습되는
함수 근사기(function approximator)이다.
\(\mathbf{x}_{t-1} \sim p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\) 를 샘플링하기 위해서는
다음을 계산한다:
전체 샘플링 절차(Algorithm 2)는
$\boldsymbol{\epsilon}_\theta$ 를 데이터 밀도의 학습된 그래디언트로 사용한다는 점에서
랑주뱅 동역학(Langevin dynamics)과 유사하다.
랑주뱅 동역학(Langevin dynamics)은
\[\mathbf{x}_{t-1} = \mathbf{x}_t + \frac{\eta}{2} \nabla_{\mathbf{x}} \log p(\mathbf{x}_t) + \sqrt{\eta}\,\mathbf{z}, \qquad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I}),\]
확률적 미분 방정식을 이용해 확률 분포로부터 샘플을 생성하는 방법이다.
일반적인 형태는 다음과 같다:여기서 $\nabla_{\mathbf{x}} \log p(\mathbf{x}_t)$ 는
데이터 분포 $p(\mathbf{x})$ 의 로그 확률 밀도에 대한 그래디언트이며,
샘플을 높은 확률 밀도 영역으로 이동시키는 역할을 한다.
즉, 데이터의 확률 밀도를 따라 이동하며 점차 원본 데이터 분포로 수렴하는 과정이다.확산 모델의 역방향 과정은 이와 구조적으로 유사하다.
\(\boldsymbol{\epsilon}_\theta\) 가 학습을 통해
\(\nabla_{\mathbf{x}} \log p(\mathbf{x}_t)\) 를 근사하도록 설계되어 있기 때문이다.
따라서 각 단계에서 모델은
“데이터 확률 밀도의 방향(gradient 방향)”으로
\(\mathbf{x}_t\) 를 조금씩 갱신하며 잡음을 제거한다.
이러한 점에서 전체 샘플링 절차가
랑주뱅 동역학과 유사하다고 할 수 있다.
또한, 위의 매개변수화(식 (11))를 사용할 경우
식 (10)은 다음과 같이 단순화된다:
식 (10)이 매개변수화 (11)로 단순화되어 식 (12)가 되는 과정을 단계별로 전개한다.
1) 식 (10)의 내부 항은 다음과 같다.
\[\frac{1}{\sqrt{\alpha_t}} \Bigl(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\boldsymbol{\epsilon}\Bigr) \;-\; \mu_\theta\!\left(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon}),t\right).\]2) 매개변수화 (11)를 대입한다.
\[\mu_\theta(\mathbf{x}_t,t) = \frac{1}{\sqrt{\alpha_t}} \left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\, \boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\right).\]이를 1)의 두 번째 항에 대입하면
\[\begin{aligned} &\frac{1}{\sqrt{\alpha_t}} \Bigl(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}\Bigr) - \frac{1}{\sqrt{\alpha_t}} \Bigl(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\Bigr) \\ &= \frac{1}{\sqrt{\alpha_t}} \left[ -\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \bigl(\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\bigr) \right] = \frac{\beta_t}{\sqrt{\alpha_t(1-\bar{\alpha}_t)}} \bigl(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)-\boldsymbol{\epsilon}\bigr). \end{aligned}\]3) 노름 제곱에서 스칼라를 밖으로 뺀다.
\[\left\| \frac{\beta_t}{\sqrt{\alpha_t(1-\bar{\alpha}_t)}} \bigl(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)-\boldsymbol{\epsilon}\bigr) \right\|^2 = \frac{\beta_t^2}{\alpha_t(1-\bar{\alpha}_t)} \left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\right\|^2.\]4) 기대값 바깥의 계수와 결합한다.
식 (10)의 계수 $\frac{1}{2\sigma_t^2}$ 와 곱해져
\[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)} \left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\right\|^2\]가 된다.
5) 재매개변수화된 입력을 명시한다. \(\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}\) 이므로 \(\boldsymbol{\epsilon}_\theta\) 의 입력을 \(\boldsymbol{\epsilon}_\theta\!\left(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t\right)\) 로 치환하면,
\[\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}} \!\left[ \frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)} \left\lVert \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta\!\left( \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},\, t \right) \right\rVert^2 \right]\]를 얻는다. 이것이 식 (12)이다.
이는 여러 단계의 잡음 스케일에 대해
각 단계가 인덱스 $t$ 로 구분되는
잡음 제거 점수 매칭(denoising score matching)과 유사하다 [55].
식 (12)는 랑주뱅 형태의 역방향 과정(식 (11))에 대한
변분 하한(variational bound)의 한 항과 동일하다.
따라서, 잡음 제거 점수 매칭과 유사한 목적식을 최적화하는 것은
랑주뱅 동역학과 유사한 샘플링 체인의
유한 시간 주변분포(finite-time marginal)를
변분 추론(variational inference)을 통해 근사하는 것과 동등함을 알 수 있다.
요약하자면, 우리는 역방향 과정의 평균 함수 근사기(mean function approximator)
$\mu_\theta$ 를 학습시켜 $\tilde{\mu}_t$ 를 예측하도록 할 수 있으며,
또는 그 매개변수화를 수정함으로써 $\epsilon$ 을 예측하도록 학습시킬 수도 있다.
($\mathbf{x}_0$ 를 예측하는 방법도 가능하지만,
초기 실험에서는 이 방법이 샘플 품질을 더 나쁘게 만드는 것으로 나타났다.)
우리는 $\epsilon$-예측 매개변수화가
랑주뱅 동역학(Langevin dynamics)과 유사하며,
확산 모델의 변분 하한(variational bound)을
잡음 제거 점수 매칭(denoising score matching)과 유사한 형태의 목적함수로
단순화함을 보였다.
그럼에도 불구하고,
이 방법은 단지 $p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)$ 의
또 다른 매개변수화에 불과하므로,
섹션 4에서는 $\epsilon$ 예측과 $\tilde{\mu}_t$ 예측을 비교하는
소거(ablation) 실험을 통해 그 유효성을 검증한다.
3.3 데이터 스케일링, 역방향 과정 디코더, 그리고 $L_0$
이미지 데이터가 $\lbrace 0, 1, \dots, 255 \rbrace$ 의 정수로 구성되어 있으며
이를 선형적으로 $[-1, 1]$ 범위로 스케일링한다고 가정한다.
이것은 신경망 기반 역방향 과정이
표준 정규 prior $p(\mathbf{x}_T)$ 로부터 시작하여
일관된 스케일의 입력을 다루도록 보장한다.
이산 로그 가능도(discrete log likelihoods)를 얻기 위해,
우리는 역방향 과정의 마지막 항을
가우시안 \(\mathcal{N}(\mathbf{x}_0; \mu_\theta(\mathbf{x}_1, 1), \sigma_1^2 \mathbf{I})\) 로부터
유도된 독립적인 이산 디코더(independent discrete decoder)로 설정한다:
여기서 $D$ 는 데이터의 차원(data dimensionality)이며,
위첨자 $i$ 는 한 좌표의 선택(extraction of one coordinate)을 나타낸다.
식 (13)은 연속적인 가우시안 확률 밀도를
실제 이미지와 같은 이산 데이터(픽셀 값)로 변환하는 과정을 수식으로 표현한 것이다.기본적으로 확산 모델의 마지막 단계는
역방향 과정의 분포를
\(p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) = \mathcal{N}(\mathbf{x}_0; \mu_\theta(\mathbf{x}_1, 1), \sigma_1^2 \mathbf{I})\)
형태의 다변량 가우시안으로 가정한다.여기서 괄호 안의 숫자 $1$ 은
시간 스텝(time step) $t = 1$ 을 의미한다.
즉, 역방향 확산(reverse diffusion)이 $T \to 1$ 로 진행되는 마지막 단계에서,
모델이 \(\mathbf{x}_1\) (거의 잡음이 제거된 샘플)로부터
원본 데이터 \(\mathbf{x}_0\) 를 복원할 때 사용되는 평균(mean)
\(\mu_\theta(\mathbf{x}_1, 1)\) 을 나타낸다.
다시 말해,
$t=1$ 은 모든 잡음이 제거된 최종 복원 단계이며,
$\mu_\theta$ 는 이 단계에서 모델이 예측한
노이즈 없는(noiseless) 데이터의 평균값을 뜻한다.그러나 실제 데이터 $\mathbf{x}_0$ 는
8비트 정수(0~255)로 양자화(quantized)된 이산 픽셀 값이기 때문에
이를 그대로 연속 확률 밀도로 다루면
로그 가능도(log-likelihood)를 직접 계산할 수 없다.따라서 각 좌표(픽셀) $x_0^i$ 에 대해
\[p_\theta(x_0^i \mid \mathbf{x}_1) = \int_{\delta_{-}(x_0^i)}^{\delta_{+}(x_0^i)} \mathcal{N}\bigl(x; \mu_\theta^i(\mathbf{x}_1, 1), \sigma_1^2\bigr)\, dx.\]
해당 픽셀 값이 속하는 구간
$[\delta_-(x_0^i), \delta_+(x_0^i)]$ 내의
가우시안 확률 밀도를 적분하여
이산 확률 질량(probability mass)으로 변환한다:이때, 경계값 $\delta_+(x)$ 와 $\delta_-(x)$ 는
인접한 픽셀 값 간의 구간을 정의한다.예를 들어, 픽셀 값이 $x=0.5$ 라면
그 주변 구간은 $[0.5-\frac{1}{255}, 0.5+\frac{1}{255}]$ 이며,
극단적인 경우 ($x=-1$ 또는 $x=1$) 는
확률이 전체 공간으로 확장되도록
$\pm\infty$ 로 처리한다.이렇게 정의된 각 픽셀의 확률을
\[p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) = \prod_{i=1}^D p_\theta(x_0^i \mid \mathbf{x}_1).\]
모든 좌표 $i=1,\dots,D$ 에 대해 곱하면
최종적인 이미지 전체의 확률이 된다:요약하면,
식 (13)은 연속적인 가우시안 분포를
실제 이산 데이터 공간으로 변환하기 위한 수학적 이산화(discretization)이며,
이를 통해 확산 모델에서 정확한 로그 가능도(log-likelihood)를 계산할 수 있게 된다.
특히, $\mu_\theta(\mathbf{x}_1, 1)$ 은
역방향 과정의 마지막 단계($t=1$)에서
모델이 추정한 원본 데이터의 평균을 나타내므로,
샘플링 과정의 최종 복원 결과를 결정하는 핵심적인 역할을 한다.
(조건부 자기회귀 모델(conditional autoregressive model)과 같은
더 강력한 디코더를 포함시키는 것은 간단하지만,
그 부분은 향후 연구로 남겨둔다.)
여기서 “더 강력한 디코더”란
단순한 가우시안 독립 디코더 대신,
픽셀 간의 상호 의존성을 명시적으로 모델링할 수 있는
조건부 자기회귀 모델(conditional autoregressive model) 같은 구조를 의미한다.예를 들어, 가우시안 디코더는
각 픽셀 $x_0^i$ 의 확률을
다른 픽셀들과 독립적으로(independently) 계산하지만,
자기회귀 디코더는
이전 픽셀들의 값 $\lbrace x_0^1, \dots, x_0^{i-1} \rbrace$ 에 조건부로
$x_0^i$ 를 생성하므로
픽셀 간 통계적 종속성(statistical dependency) 을 포착할 수 있다.이는 복잡한 구조나 세밀한 질감(texture)이 있는 이미지에서
훨씬 더 현실적인 복원을 가능하게 하며,
결과적으로 데이터의 로그 가능도(log-likelihood) 를
더 정확히 추정할 수 있다.따라서 자기회귀 기반의 조건부 디코더는
현재 논문에서 사용된 단순한 독립 가우시안 디코더보다
표현력(expressive power)이 훨씬 강력하지만,
구현 복잡도와 계산 비용이 크기 때문에
본 논문에서는 향후 연구로 남겨둔 것이다.
VAE 디코더 및 자기회귀 모델들에서 사용된
이산화된 연속 분포(discretized continuous distributions) [34, 52]와 유사하게,
여기서의 선택은 변분 하한(variational bound)이
이산 데이터의 무손실 부호 길이(lossless codelength)를 보장하도록 한다.
즉, 데이터에 잡음을 추가하거나
스케일링 연산의 야코비안(Jacobian)을
로그 가능도(log likelihood)에 포함시킬 필요가 없다.
샘플링의 마지막 단계에서,
$\mu_\theta(\mathbf{x}_1, 1)$ 을 잡음 없이(noiselessly) 표시한다.
이 부분은 이산화(discretization)를 적용하는 이유와 그 수학적 의미를 설명하는 내용이다.
“이산화된 연속 분포(discretized continuous distribution)”란
본래 연속적인 확률 분포(예: 가우시안 분포)를
실제 데이터(픽셀 값처럼 이산적인 값)에 맞게
확률 질량(probability mass) 형태로 변환한 분포를 의미한다.
이는 VAE 디코더나 자기회귀 모델에서도 널리 사용되는 방식이다.여기서 말하는 “무손실 부호 길이(lossless codelength)”는
정보 이론적 관점에서의 데이터 압축 효율을 의미한다.
즉, 모델이 학습한 확률 분포로부터 데이터를 인코딩할 때
평균적으로 몇 비트가 필요한지를 나타내는 개념이다.변분 하한(variational bound)은
로그 가능도(log-likelihood)를 근사적으로 최대화하는 목표 함수로,
정보 이론적으로는 데이터 부호화 시 필요한 평균 부호 길이의
하한(lower bound)으로 해석할 수 있다.
따라서 이산 데이터(예: 픽셀 값)에 대해
이산화된 확률 모델을 사용하면
변분 하한이 실제 데이터의 무손실 부호 길이와 일치하게 된다.
즉, 모델이 학습한 확률이
데이터를 얼마나 효율적으로 압축(또는 설명)할 수 있는지를
직접 반영하게 되는 것이다.반대로, 데이터가 연속적인 값으로 모델링될 경우에는
확률 밀도 함수의 단위가 “비트”로 해석될 수 없기 때문에
로그 가능도를 곧바로 부호 길이와 대응시키기 어렵다.
또한 스케일 변환에 따른 야코비안(Jacobian) 항을
로그 가능도 계산에 포함해야 하고,
연속 공간의 불연속성을 보정하기 위해
인위적인 잡음(noise)을 추가해야 하는 문제가 생긴다.하지만 이 논문처럼 이산화(discretization)를 적용하면
이러한 보정 과정이 필요 없다.
데이터가 이미 이산 공간(픽셀 단위)에 정렬되어 있으므로
야코비안 항이나 잡음 추가 없이
확률 질량만으로 정확한 로그 가능도를 계산할 수 있다.마지막으로, “샘플링의 마지막 단계에서 $\mu_\theta(\mathbf{x}_1, 1)$ 을 잡음 없이 표시한다”는 것은
확률적 샘플링(noise sampling)을 하지 않고
모델이 예측한 평균값(mean)을 그대로 출력한다는 의미이다.
즉, $\mathbf{x}_0$ 를 확률적으로 생성하는 대신
모델이 추정한 가장 가능성이 높은(noiseless) 결과를
최종 이미지로 사용하는 것이다.
3.4 단순화된 학습 목적 (Simplified training objective)
위에서 정의한 역방향 과정과 디코더를 이용하면,
식 (12)와 (13)으로부터 유도된 항들로 구성된
변분 하한(variational bound)은
$\theta$ 에 대해 명확하게 미분 가능하며,
학습에 바로 사용할 준비가 된다.
그러나 우리는 샘플 품질 향상과 구현의 단순화를 위해,
다음의 변형된 변분 하한을 사용하는 것이
보다 유익하다는 것을 발견하였다:
여기서 $t$ 는 $1$과 $T$ 사이에서 균등하게(uniform) 선택된다.
식 (14)는 확산 모델의 학습을 단순화한 노이즈 예측(loss) 형태를 나타낸다.
\[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\]
원래의 변분 하한(식 (12))은 각 시점 $t$마다 가중치 항를 포함하지만,
여기서는 그 가중치를 제거하고 단순히
예측된 잡음 $\boldsymbol{\epsilon}_\theta$ 와
실제 잡음 $\boldsymbol{\epsilon}$ 간의 제곱 오차를 최소화한다.즉, 모델은 순방향 과정에서
$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}$
로 만들어진 잡음이 포함된 데이터 $\mathbf{x}_t$ 로부터
원래의 잡음 $\boldsymbol{\epsilon}$ 을 복원하도록 학습된다.이렇게 하면 모델은 각 시점 $t$ 에서
“현재 데이터에 포함된 노이즈의 방향과 크기”를 추정하게 되고,
이를 역방향 과정에서 제거함으로써
점진적으로 깨끗한 샘플을 복원할 수 있게 된다.또한, $t$ 를 $[1, T]$ 사이에서 균등하게 샘플링함으로써
모든 시간 단계의 잡음 수준을 고르게 학습하게 되어,
모델이 다양한 노이즈 조건에서도 안정적으로 작동할 수 있도록 한다.요약하자면, $L_{\text{simple}}(\theta)$ 는
복잡한 변분 하한 대신,
노이즈 복원(denoising) 문제로 단순화한 형태이며,
이는 계산적으로 효율적이고
샘플 품질도 경험적으로 우수한 것으로 보고되었다.
$t = 1$ 인 경우는 $L_0$ 에 해당하며,
이는 식 (13)에서 정의된 이산 디코더의 적분 항을
가우시안 확률 밀도 함수에
빈 폭(bin width)을 곱한 형태로 근사한 것이다.
이때 $\sigma_1^2$ 와 경계 효과(edge effects)는 무시한다.
이 문장은 $t=1$ 일 때의 손실 항 $L_0$ 가
식 (13)에 정의된 이산 디코더의 확률 계산과 어떻게 연결되는지를 설명한다.식 (13)에서는 각 픽셀의 확률을
구간 $[\delta_-(x_0^i), \delta_+(x_0^i)]$ 에서
가우시안 밀도를 적분하여 계산했다.
그러나 실제 계산에서는 이 적분을
“가우시안 확률 밀도 함수의 값 × 구간 폭(bin width)” 으로 근사한다.즉,
\[\int_{\delta_-(x_0^i)}^{\delta_+(x_0^i)} \mathcal{N}(x; \mu_\theta^i(\mathbf{x}_1, 1), \sigma_1^2)\, dx \approx \mathcal{N}(x_0^i; \mu_\theta^i(\mathbf{x}_1, 1), \sigma_1^2) \times \Delta x,\]와 같은 형태로 단순화할 수 있다.
여기서 $\Delta x$ 는 픽셀 간격(즉, bin width)에 해당한다.이렇게 하면 로그 가능도 계산이 훨씬 간단해지며,
이는 곧 $L_0$ 항으로 대응된다.
즉, $L_0$ 는 이산 디코더의 적분 확률을 근사한 형태의 항이다.또한 $\sigma_1^2$ (마지막 단계의 분산 항)과
픽셀 구간의 경계 효과(edge effects)는
로그 가능도에 미치는 영향이 매우 작으므로
계산의 단순화를 위해 무시한다.여기서 픽셀 구간의 경계 효과(edge effects) 란,
픽셀 값이 구간의 경계($x=-1$ 또는 $x=1$) 근처에 있을 때
가우시안 적분 범위가 실제 데이터 공간의 경계를 넘어서는 문제를 말한다.
예를 들어, $x=1$ 근처의 픽셀은
적분 상한 $\delta_+(x)=\infty$ 로 확장되므로
확률 질량이 비정상적으로 커지거나 왜곡될 수 있다.
이러한 효과는 대부분의 픽셀이 중앙 영역($-1 < x < 1$)에 분포해 있기 때문에
전체 로그 가능도에 미치는 영향이 매우 작으며,
계산의 효율성을 위해 무시한다.결과적으로 $t=1$ 일 때의 $L_0$ 는
확률 밀도의 정밀한 적분 대신
가우시안의 점 추정값에 bin 폭을 곱해 근사한
“이산화된 로그 가능도 항”으로 해석할 수 있다.
$t > 1$ 인 경우는 식 (12)의
가중치가 없는(unweighted) 버전에 해당하며,
이는 NCSN(Noise Conditional Score Network)의
잡음 제거 점수 매칭(denoising score matching) 모델 [55]에서
사용된 손실 함수와 유사하다.
($L_T$ 는 등장하지 않는데,
그 이유는 순방향 과정의 분산 $\beta_t$ 가 고정되어 있기 때문이다.)
Algorithm 1은
이 단순화된 목적 함수를 이용한
전체 학습 절차를 보여준다.
우리의 단순화된 목적식 (14)는
식 (12)에서의 가중치(Weighting)를 제거하기 때문에,
이는 표준 변분 하한 [18, 22]과는
재구성(reconstruction)의 서로 다른 측면을 강조하는
가중된 변분 하한(weighted variational bound)이다.
특히, 섹션 4에서 제시된 우리의 확산 과정 설정은
단순화된 목적식이 작은 $t$ 값에 해당하는 손실 항(loss terms)의
가중치를 줄이는(down-weight) 효과를 낳는다.
이러한 항들은 매우 작은 양의 잡음이 포함된 데이터를
복원(denoise)하도록 네트워크를 학습시키는데,
그보다는 작은 $t$ 항들의 비중을 낮추는 것이 바람직하다.
그 이유는 네트워크가 더 큰 $t$ 값, 즉 더 많은 잡음이 포함된
보다 어려운 복원 과제에 집중할 수 있기 때문이다.
우리의 실험에서는 이러한 재가중화(reweighting)가
더 나은 샘플 품질로 이어짐을 확인하였다.
이 부분은 단순화된 목적식($L_{\text{simple}}$)이
본래의 손실 함수에 포함되어 있던 가중항(weight term)을 제거함으로써
시간 스텝 $t$ 에 따른 학습 비중이 어떻게 변하는지를 설명한다.원래의 손실(식 (12))에는
\[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\]와 같은
$t$ 의 함수 형태의 가중항이 포함되어 있었다.
이 항은 $t$ 가 작을수록(즉, 데이터에 잡음이 거의 없는 단계일수록)
상대적으로 큰 값을 가지므로,
본래의 목적식에서는 작은 $t$의 손실 항이 더 크게 반영되었다.그러나 단순화된 목적식 $L_{\text{simple}}$ 에서는
이 가중항을 제거하여
모든 시간 스텝을 동일한 비중으로 평균한다.
이렇게 되면 결과적으로
작은 $t$ (잡음이 거의 없는 구간)에 해당하는 항들의 비중이
상대적으로 줄어드는(down-weight) 효과가 나타난다.이는 의도치 않은 단순화의 부산물이 아니라,
학습 측면에서 오히려 유리한 특성을 제공한다.
왜냐하면 작은 $t$ 구간은 이미 원본 데이터와 거의 동일하여
복원(denoising) 난이도가 낮고,
그보다는 잡음이 더 많이 섞인 큰 $t$ 구간에서의 학습이
모델의 성능 향상에 더 중요한 역할을 하기 때문이다.따라서 단순화된 목적식은
본래의 가중항을 제거함으로써
자연스럽게 쉬운(작은 $t$) 복원 과제의 비중을 낮추고,
어려운(큰 $t$) 복원 과제에 더 많은 학습 자원을 집중시키는 구조로 변한다.
이로 인해 모델은 더 높은 잡음 수준에서의 복원 능력을 학습하게 되고,
결과적으로 샘플 품질이 개선되는 효과를 보인다.
4 실험 (Experiments)
모든 실험에서 $T = 1000$ 으로 설정하여,
샘플링 동안 필요한 신경망 평가 횟수가
이전 연구 [53, 55] 와 일치하도록 하였다.
순방향 과정의 분산은 $\beta_1 = 10^{-4}$ 에서
$\beta_T = 0.02$ 까지 선형적으로 증가하는 상수로 설정하였다.
이 상수들은 데이터가 $[-1, 1]$ 범위로 스케일링된 것에 비해
작은 값을 갖도록 선택되었으며,
이를 통해 역방향 과정과 순방향 과정이
대체로 동일한 함수적 형태를 유지하도록 하였다.
또한, $\mathbf{x}_T$ 에서의 신호 대 잡음비(signal-to-noise ratio)가
가능한 한 작게 유지되도록 하였다
($L_T = D_{\mathrm{KL}}(q(\mathbf{x}_T \mid \mathbf{x}_0)\,|\,\mathcal{N}(0,\mathbf{I})) \approx 10^{-5}$
비트/차원 단위로 실험에서 유지됨).
역방향 과정을 표현하기 위해,
PixelCNN++ [52, 48] 과 유사하되
마스크되지 않은(unmasked) U-Net 백본(backbone)을 사용하였다.
이 문장은 역방향 확산 모델의 아키텍처 선택에 대한 설명이다.
PixelCNN++ 은 원래 자기회귀(autoregressive) 방식으로
이미지를 한 픽셀씩 순차적으로 생성하는 모델로,
픽셀 간의 조건부 확률 $p(x_i \mid x_{<i})$ 을 학습하기 위해
마스크(masked) 합성곱 구조를 사용한다.
이 마스크는 현재 픽셀을 예측할 때
미래 픽셀의 정보가 보이지 않도록 막는 역할을 한다.그러나 확산 모델의 역방향 과정은
한 번에 전체 이미지 $\mathbf{x}_t$ 를 입력받아
동시에 복원해야 하므로
픽셀 단위의 순차적 의존성이 필요하지 않다.
따라서 여기서는 PixelCNN++ 의 아이디어(즉,
잔차 블록 구조, 게이트 활성화, 스킵 연결 등)는 유지하되,
마스크를 제거한(unmasked) 형태의 합성곱 U-Net 을 사용한다.이 U-Net 은 인코더-디코더 구조를 통해
입력 이미지의 전역적(global) 및 지역적(local) 정보를 모두 처리하며,
시간 스텝 $t$ 를 임베딩(embedding) 형태로 받아
잡음의 스케일에 따라 다른 특징(feature)을 학습할 수 있다.요약하면,
PixelCNN++ 의 구조적 장점을 계승하되
픽셀 단위의 순차성 제한(masking)을 제거한
병렬적(global) 복원용 U-Net 을
역방향 확산 모델의 백본으로 채택한 것이다.
그룹 정규화(group normalization)는 전체 네트워크에 적용되었으며 [66],
파라미터는 시간 축 전반에 걸쳐 공유된다.
이 시간적 공유는 Transformer의 사인파 위치 임베딩
(Transformer sinusoidal position embedding) [60]을 사용하여 구현하였다.
이 부분은 확산 모델의 U-Net 네트워크가
시간 축(time dimension)에 따라 어떻게 정규화되고,
시간 정보를 어떻게 통합하는지를 설명한다.먼저 그룹 정규화(group normalization) [66] 는
배치 크기(batch size)에 의존하지 않고
채널 단위로 특징 맵(feature map)을 정규화하는 기법이다.
확산 모델처럼 배치 크기가 작거나
시간 단계 $t$ 별로 입력 분포가 크게 달라지는 경우에도
안정적인 학습을 보장하기 위해
배치 정규화(batch normalization) 대신
그룹 정규화가 사용된다.“파라미터가 시간 축 전반에 걸쳐 공유된다(shared across time)”는 것은,
각 시간 스텝 $t$ 마다 별도의 네트워크를 두는 대신
하나의 네트워크가 모든 $t$ 값을 공통으로 처리한다는 의미이다.
즉, 모델이 시간에 따라 다른 잡음 수준을 다루지만,
그 구조적 파라미터(가중치)는 동일하게 유지된다.대신, 시간에 따른 차이를 반영하기 위해
각 시간 스텝 $t$ 는 사인파 위치 임베딩(sinusoidal positional embedding) [60] 을 통해
벡터 형태로 변환되어 네트워크에 주입된다.
이 방식은 Transformer 모델에서
순서나 위치 정보를 인코딩하는 방법과 동일하며,
$t$ 값을 주기적 함수를 이용해 고차원 벡터로 변환하여
네트워크가 시간적 위치(즉, 잡음 스케일)를 인식할 수 있게 한다.요약하자면,
그룹 정규화는 학습의 안정성을 확보하기 위한 정규화 기법이고,
시간 임베딩은 네트워크가
서로 다른 시간 스텝의 입력을 구분할 수 있도록 하는 메커니즘이다.
두 기법이 결합되어,
하나의 공유된 네트워크가 전체 확산 과정($t = 1 \dots T$)을
일관되게 처리할 수 있도록 설계된 것이다.
또한, $16 \times 16$ 피처맵 해상도에서
셀프-어텐션(self-attention)을 적용하였다 [63, 60].
자세한 내용은 부록 B(Appendix B)에 제시되어 있다.
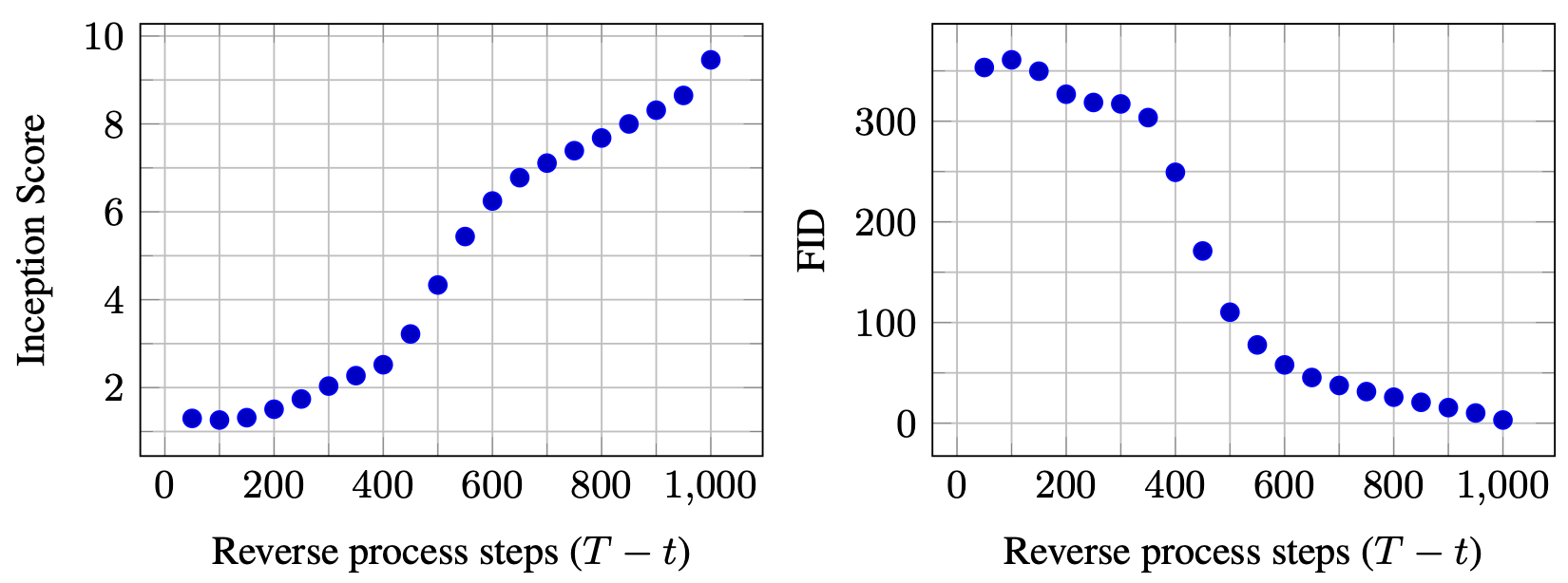
4.1 샘플 품질 (Sample quality)
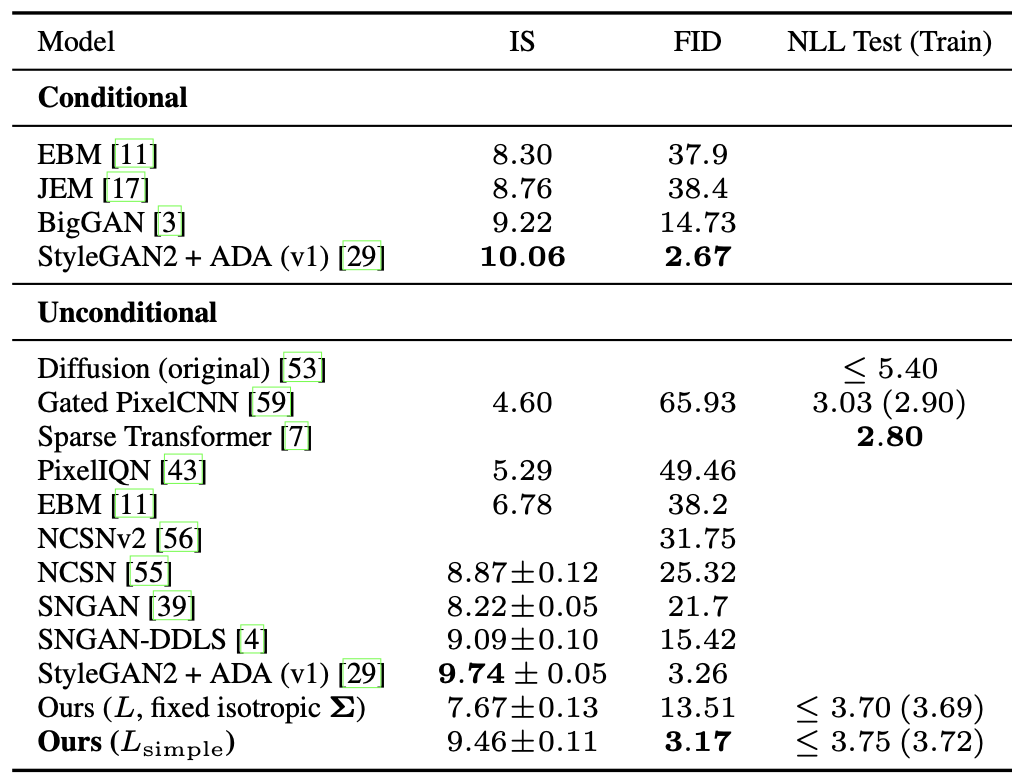
표 1(Table 1)은 CIFAR10 데이터셋에서
Inception 점수, FID 점수, 그리고 음의 로그 우도(negative log likelihood,
즉 무손실 부호 길이 lossless codelengths)를 보여준다.
우리 모델의 FID 점수는 3.17이며,
이는 클래스 조건부(class conditional) 모델을 포함한
대부분의 기존 모델보다 더 나은 샘플 품질을 달성하였다.
FID 점수는 일반적인 관례에 따라
훈련 세트(training set)에 대해 계산되었으며,
테스트 세트(test set)에 대해 계산할 경우
우리의 FID 점수는 5.24로 나타났다.
이 값 또한 문헌에서 보고된
대부분의 훈련 세트 기준 FID 점수보다 우수하다.
표 1: CIFAR10 결과.
NLL(음의 로그 우도)은 비트/차원(bits/dim) 단위로 측정되었다.
우리는 모델을 실제 변분 하한(true variational bound)에 따라 학습시키는 것이
단순화된 목적식(simplified objective)으로 학습시키는 것보다
더 나은 부호 길이(codelengths)를 산출한다는 것을 확인하였다.
이는 예상된 결과이지만, 후자의 단순화된 목적식이
가장 높은 샘플 품질(sample quality)을 제공하였다.
CIFAR10 및 CelebA-HQ $256 \times 256$ 샘플에 대해서는 그림 1(Fig. 1),
LSUN $256 \times 256$ 샘플에 대해서는 그림 3(Fig. 3)과 그림 4(Fig. 4) [71],
그리고 추가적인 내용은 부록 D(Appendix D)를 참고하라.
그림 3: LSUN 교회(Church) 샘플. FID = 7.89
그림 4: LSUN 침실(Bedroom) 샘플. FID = 4.90
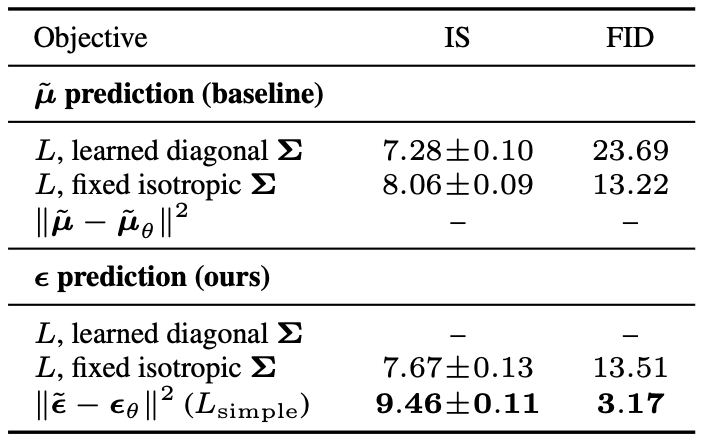
4.2 역방향 과정 매개변수화와 학습 목적의 제거 실험(ablation)
표 2(Table 2)에서는 역방향 과정의 매개변수화(reverse process parameterizations)와
학습 목적(training objectives)이 샘플 품질에 미치는 영향을 보여준다 (섹션 3.2 참조).
표 2: CIFAR10의 비조건부(unconditional) 역방향 과정 매개변수화(reverse process parameterization)와
학습 목적 함수(training objective) 제거(ablation).
빈 항목(blank entries)은 학습이 불안정하였으며,
범위를 벗어난(out-of-range) 점수를 가진 품질이 낮은 샘플을 생성하였다.
우리는 기본(base) 설정에서 $\tilde{\mu}$ 를 예측하는 방식은
비가중 평균제곱오차(unweighted mean squared error)가 아닌
진짜 변분 하한(true variational bound)으로 학습될 때에만 잘 작동하며,
이는 식 (14)와 유사한 단순화된 목적식(simplified objective)에 해당함을 발견하였다.
또한, 역방향 과정의 분산(reverse process variances)을 학습하도록 하는 경우
(즉, 매개변수화된 대각 분산 $\Sigma_\theta(\mathbf{x}_t)$ 를 변분 하한에 포함시키는 경우),
고정된 분산(fixed variances)을 사용하는 경우보다
학습이 불안정해지고 샘플 품질이 저하되는 경향이 있음을 확인하였다.
우리가 제안한 바와 같이 $\boldsymbol{\epsilon}$ 을 예측하는 방식은,
고정된 분산을 갖는 변분 하한으로 학습될 때
$\mu$ 를 예측하는 방식과 거의 비슷한 성능을 보이지만,
단순화된 목적식(simplified objective)으로 학습될 때에는 훨씬 더 우수한 성능을 보인다.
4.3 점진적 부호화(Progressive coding)
표 1은 또한 CIFAR10 모델들의 부호 길이(codelengths)를 보여준다.
학습(train)과 테스트(test) 간의 차이는 최대 0.03 비트/차원(bits per dimension)에 불과하며,
이는 다른 가능도(likelihood) 기반 모델에서 보고된 차이와 유사하다.
이는 우리의 확산(diffusion) 모델이 과적합(overfitting)되지 않았음을 나타낸다
(최근접 시각화(nearest neighbor visualizations)에 대해서는 부록 D를 참조하라).
여전히, 우리의 무손실(lossless) 부호 길이는
에너지 기반 모델(energy-based models) 및
가중 중요도 샘플링(annealed importance sampling)을 사용하는
점수 매칭(score matching) 기법 [11] 에서 보고된 큰 추정치보다는 낫지만,
다른 종류의 가능도 기반 생성 모델(likelihood-based generative models) [7] 과
비교할 만한 수준은 아니다.
우리의 샘플이 높은 품질을 유지하고 있음을 고려할 때,
확산 모델이 손실 압축(lossy compression)에 유리한 귀납적 편향(inductive bias)을
가진다는 결론을 내릴 수 있다.
변분 하한(variational bound)의 항 $L_1 + \cdots + L_T$ 를 속도(rate)로,
$L_0$ 를 왜곡(distortion)으로 간주하면,
CIFAR10에서 가장 높은 품질의 샘플을 생성하는 모델은
속도(rate)가 1.78 bits/dim, 왜곡(distortion)이 1.97 bits/dim으로,
이는 0~255 스케일에서 제곱 평균 제곱근 오차(RMSE)가 0.95에 해당한다.
즉, 손실 없는 부호 길이(lossless codelength)의 절반 이상이
사람이 인지할 수 없는 미세한 왜곡(imperceptible distortions)을 설명하는 데 할당된다.
이 문장은 확산 모델의 학습 목적을 정보 이론적 관점에서 해석한 부분이다.
먼저, 변분 하한(variational bound)을 구성하는 항들 $L_1 + \cdots + L_T$ 는
각 단계에서의 정보 전송량(rate), 즉 데이터를 복원하기 위해 필요한 평균 비트 수로 볼 수 있다.
반면, $L_0$ 는 모델이 복원한 결과가 실제 데이터와 얼마나 차이 나는지를 나타내는
왜곡(distortion) 항으로 해석할 수 있다.이때 “1.78 bits/dim”이라는 속도(rate)는
각 차원(픽셀 값)을 표현하는 데 평균적으로 1.78비트가 필요하다는 뜻이고,
“1.97 bits/dim”의 왜곡(distortion)은
이 부호화 과정에서 생기는 재구성 오차(reconstruction error)를
비트 단위로 측정한 값이다.저자들은 이 값을 다시 실제 픽셀 스케일(0~255 범위)에서
RMSE(root mean squared error) = 0.95 로 환산하였다.
이는 모델이 복원한 이미지가
원본과 거의 구분되지 않을 정도로 매우 작은 오차만을 포함한다는 의미이다.마지막 문장,
“손실 없는 부호 길이(lossless codelength)의 절반 이상이
인지할 수 없는 미세한 왜곡(imperceptible distortions)을 설명하는 데 사용된다”는 말은
모델이 실제로 사용하는 비트 중 상당 부분이
사람이 보지 못할 정도의 아주 미세한 화질 차이를 복원하는 데 쓰인다는 뜻이다.즉, 확산 모델은 시각적으로 구분할 수 없는 수준까지 정밀하게 데이터를 재현하며,
이러한 특성 때문에 정보 이론적으로도 매우 효율적인 압축(encoding) 능력을 보유한다는 점을 보여준다.
점진적 손실 압축(Progressive lossy compression)
우리의 모델이 가지는 속도-왜곡(rate-distortion) 특성을 더 면밀히 탐색하기 위해,
식 (5)와 형태가 유사한 점진적 손실 부호화(progressive lossy code)를 도입하였다
(알고리즘 3, 4 참조).
이는 최소 랜덤 부호화(minimal random coding) [19, 20]과 같은 절차를 통해
$p(\mathbf{x})$ 가 수신자(receiver)에게 사전에 알려진 경우,
$q(\mathbf{x})$ 로부터 샘플 $\mathbf{x} \sim q(\mathbf{x})$ 를
평균적으로 약 $D_{\mathrm{KL}}(q(\mathbf{x}) \,|\, p(\mathbf{x}))$ 비트로 전송할 수 있다고 가정한다.
이를 $\mathbf{x}_0 \sim q(\mathbf{x}_0)$ 에 적용하면,
알고리즘 3과 4는 $\mathbf{x}_T, \ldots, \mathbf{x}_0$ 를 순차적으로 전송하며,
총 기대 부호 길이는 식 (5)와 동일하다.
이 부분은 식 (5)에서 정의된 변분 하한(variational bound)을
점진적 손실 압축(progressive lossy compression) 과정으로 해석하는 내용을 다룬다.먼저, 식 (5)는 전체 변분 하한을 다음과 같은 세 부분으로 나눈다:
- $L_T$: 가장 마지막 단계에서의 KL 발산 항
- $\sum_{t>1} L_{t-1}$: 중간 단계의 KL 발산 항들의 합
- $L_0$: 최종 데이터 복원 항 (로그 가능도 항)
이 세 항은 각각 확산 과정의 단계별 정보 손실이나
전송 효율을 나타내며,
이를 정보 이론적 관점에서 부호화 길이(codelength) 로 해석할 수 있다.저자들은 이를 기반으로,
각 단계의 확률 전이 과정을 실제 “부호화 및 복호화(encoding/decoding)” 절차로 대응시킨다.Algorithm 3 (Sending) 은 데이터 $\mathbf{x}_0$ 를 전송하는 인코더(encoder)에 해당하며,
Algorithm 4 (Receiving) 은 이를 복원하는 디코더(decoder)에 해당한다.구체적으로,
인코더(Algorithm 3)는 실제 데이터 $\mathbf{x}_0$ 로부터
점차 잡음을 추가하면서 $\mathbf{x}_T$ 까지 전송한다.
각 단계에서의 전송은
\(\mathbf{x}_t \sim q(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0)\)
와 같이 확률적으로 이루어진다.반대로 디코더(Algorithm 4)는
받은 $\mathbf{x}_T$ 로부터 역방향 모델
\(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\)
을 이용하여 순차적으로 복원한다.이때 각 전송 단계에서 필요한 비트 수는
\(D_{\mathrm{KL}}(q(\mathbf{x}_t \mid \cdot) \| p_\theta(\mathbf{x}_t \mid \cdot))\)
로 표현된다.
따라서 전체 부호화 과정의 평균 부호 길이는
식 (5)의 변분 하한 전체에 대응하게 된다.즉, 확산 모델의 순방향 과정은
데이터를 점진적으로 압축하면서 손실을 도입하는 과정이며,
역방향 과정은 이 손실 압축으로부터 데이터를 점진적으로 복원하는 과정으로 해석할 수 있다.이 때문에 “progressive lossy compression”이라는 이름이 붙은 것이다.
확산 모델의 샘플링 절차는
데이터를 한 번에 복원하는 것이 아니라,
잡음이 많은 상태($\mathbf{x}_T$)에서부터
점차 신호를 복원하며 세밀한 정보를 추가해가는
점진적 디코딩(progressive decoding) 으로 볼 수 있다.
수신자는 임의의 시점 $t$ 에서 부분적 정보 $\mathbf{x}_t$ 를 완전히 확보하고 있으며,
다음과 같이 점진적으로 $\mathbf{x}_0$ 를 추정할 수 있다:
이는 식 (4)에 의해 유도된다.
(확률적 복원 \(\mathbf{x}_0 \sim p_\theta(\mathbf{x}_0 \mid \mathbf{x}_t)\) 도 가능하지만,
왜곡 계산이 복잡해지므로 여기서는 다루지 않는다.)
식 (15)는 순방향 과정의 표본 생성식에서 $\mathbf{x}_0$ 를 직접 풀어 얻은 식이다.
1) 순방향 과정(식 (4))은 다음과 같다:
\[\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\,\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\,\boldsymbol{\epsilon}, \qquad \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I}).\]2) 위 식을 $\mathbf{x}_0$ 에 대해 정리하면 다음과 같다:
\[\mathbf{x}_0 = \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\,\boldsymbol{\epsilon}}{\sqrt{\bar{\alpha}_t}}.\]3) 학습된 노이즈 예측기 $\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)$ 가
\[\hat{\mathbf{x}}_0 = \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\,\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{\bar{\alpha}_t}}.\]
실제 잡음 $\boldsymbol{\epsilon}$을 근사한다고 가정하면,
이를 위 식에 대입하여 다음의 추정치를 얻는다:즉, 식 (15)는 확산 모델이 예측한 잡음을 이용해
원본 데이터 $\mathbf{x}_0$ 를 복원하는 근사식으로,
역방향 과정에서의 초기 상태 추정(reconstruction) 단계에 해당한다.
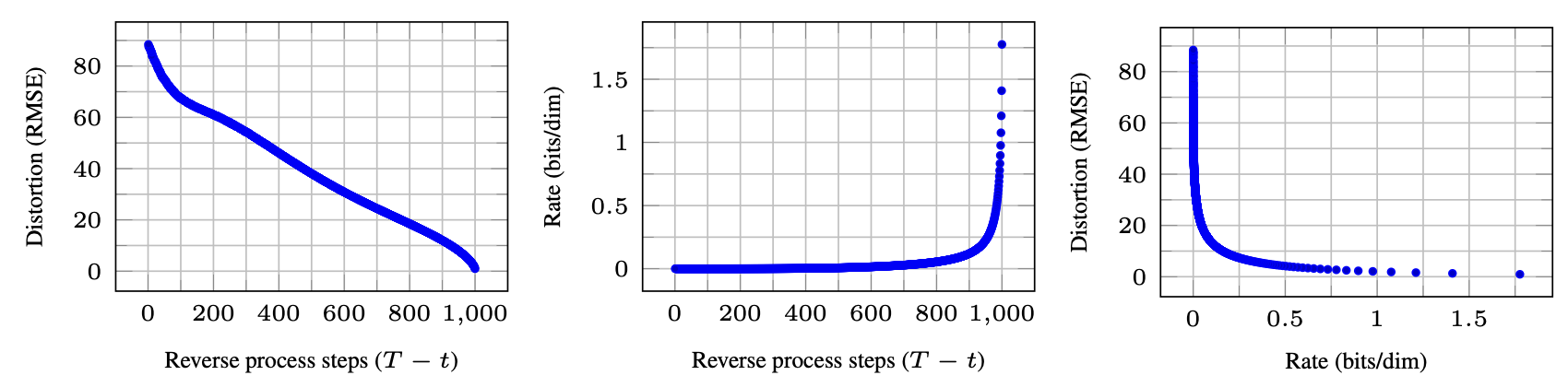
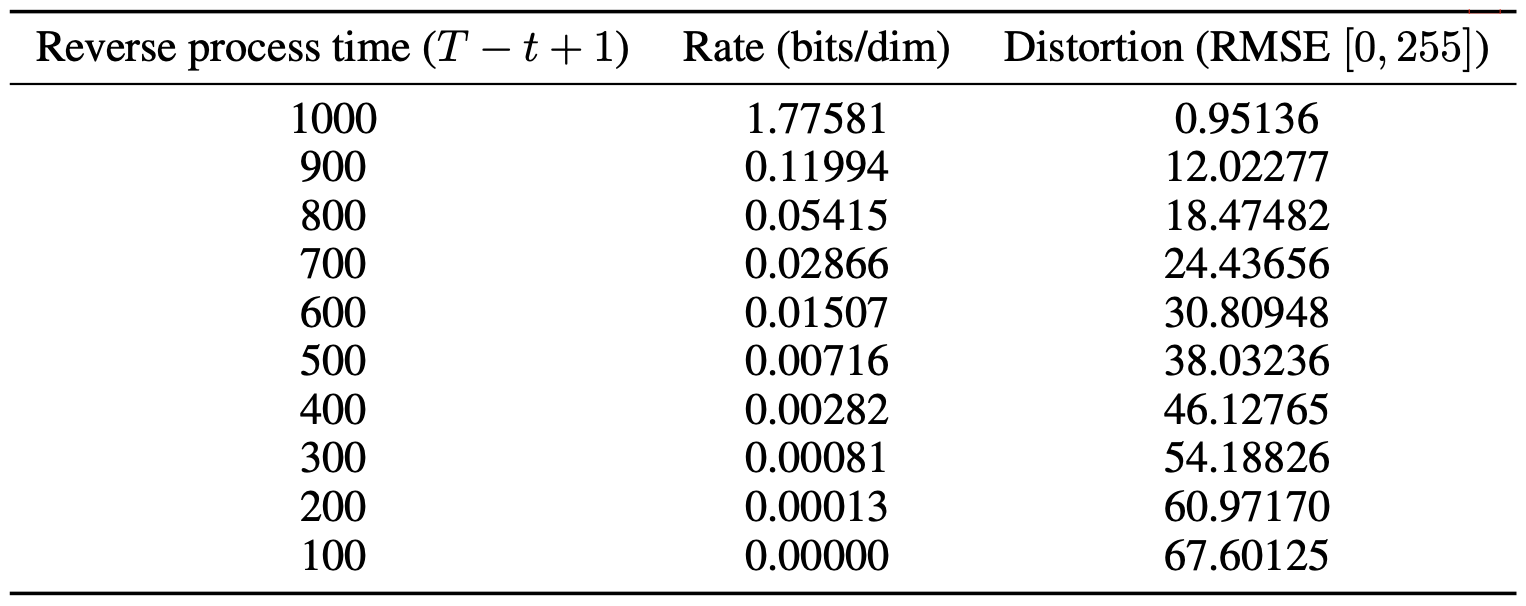
그림 5(Figure 5)는 CIFAR10 테스트 세트에 대한
속도-왜곡(rate-distortion) 그래프를 보여준다.
그림 5: 비조건부(unconditional) CIFAR10 테스트 세트의 시간에 따른
속도-왜곡(rate-distortion) 관계.
왜곡(distortion)은 [0,255] 스케일에서의
제곱 평균 제곱근 오차(RMSE, root mean squared error)로 측정된다.
자세한 내용은 표 4를 참조하라.
각 시점 $t$ 에서 왜곡(distortion)은
제곱 평균 제곱근 오차(root mean squared error)
$\sqrt{\lVert \mathbf{x}_0 - \hat{\mathbf{x}}_0 \rVert^2 / D}$ 로 계산되며,
속도(rate)는 해당 시점까지 수신된 누적 비트 수로 계산된다.
그래프에서 볼 수 있듯, 낮은 속도 구간에서 왜곡이 급격히 감소하며,
이는 대부분의 비트가 실제로 인지 불가능한 미세 왜곡(imperceptible distortions)을
표현하는 데 사용되고 있음을 의미한다.
이 그림은 확산 모델의 역방향 과정(reverse process) 동안
속도(rate) 와 왜곡(distortion) 의 변화를 시각적으로 보여준다.왼쪽 그래프는 시간 $t$ (즉, 역방향 단계 수)에 따라
복원 오차(RMSE)가 점차 감소하는 과정을 나타낸다.
이는 노이즈 제거 단계가 진행될수록
복원된 이미지가 원본 $\mathbf{x}_0$ 에 가까워짐을 의미한다.가운데 그래프는 같은 시간 축에 대해
누적된 부호화 비트 수(rate, bits/dim)를 보여주며,
후반부(노이즈가 거의 제거되는 단계)에서
급격히 증가하는 양상을 보인다.
즉, 복원이 정밀해질수록
더 많은 정보(비트)가 필요함을 나타낸다.오른쪽 그래프는 속도(rate)와 왜곡(distortion) 간의
상호 관계(rate–distortion curve)를 보여준다.
낮은 속도 구간에서는 왜곡이 급격히 감소하지만,
일정 수준 이하로 내려가면
추가적인 비트를 사용해도
왜곡 감소가 거의 이루어지지 않는다.이는 대부분의 비트가
인간이 인식할 수 없는 미세한 왜곡(imperceptible distortions)을
보정하는 데 사용되고 있음을 의미한다.
따라서 확산 모델의 샘플링 과정은
점진적인 복원(progressive decoding)을 수행하며,
초기에는 거친 구조를 복원하고
후반에는 세부적인 시각적 정밀도를 높이는 방향으로 작동한다.
점진적 생성 (Progressive generation)
우리는 무작위 비트로부터의 점진적인 압축 해제(progressive decompression)에 의해
비조건부(unconditional) 점진적 생성 과정을 또한 수행하였다.
즉, 역방향 과정의 결과인 $\hat{\mathbf{x}}_0$ 를 예측하면서,
알고리즘 2를 사용하여 역방향 과정으로부터 샘플링을 수행하였다.
그림 6과 그림 10은 역방향 과정의 진행에 따라
$\hat{\mathbf{x}}_0$ 의 샘플 품질이 어떻게 변화하는지를 보여준다.
그림 6: 비조건부 CIFAR10 점진적 생성 (왼쪽에서 오른쪽으로 시간에 따른 $\hat{\mathbf{x}}_0$).
부록의 그림 10 및 그림 14에서,
시간에 따른 확장된 샘플과 샘플 품질 지표를 확인할 수 있다.
이미지의 대규모 구조(large-scale image features)는 먼저 나타나고,
세부 정보(details)는 나중에 나타난다.
그림 7은 여러 $t$ 값에 대해
\(\mathbf{x}_t\) 를 고정한 상태에서의
확률적 예측 \(\mathbf{x}_0 \sim p_\theta(\mathbf{x}_0 \mid \mathbf{x}_t)\) 을 보여준다.
그림 7: 동일한 잠재 변수(latent)를 조건으로 할 때,
CelebA-HQ 256×256 샘플들은 높은 수준의 속성(high-level attributes)을 공유한다.
오른쪽 아래 사분면은 \(\mathbf{x}_t\) 를,
그 외의 사분면들은 \(p_\theta(\mathbf{x}_0 \mid \mathbf{x}_t)\) 로부터의 샘플을 나타낸다.
$t$ 가 작을 때에는 미세한 세부 정보를 제외한 거의 모든 구조가 유지되며,
$t$ 가 클 때에는 큰 규모의 구조만 보존된다.
아마도 이것은 개념적 압축(conceptual compression)의
단서를 시사하는 것일지도 모른다 [18].
자기회귀 디코딩(autoregressive decoding)과의 연결
변분 하한(식 (5))은 다음과 같이 다시 쓸 수 있다:
\[L = D_{\mathrm{KL}}\bigl(q(\mathbf{x}_T)\,\|\,p(\mathbf{x}_T)\bigr) + \mathbb{E}_q\!\left[\sum_{t \ge 1} D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\,\|\,p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\bigr) \right] + H(\mathbf{x}_0) \tag{16}\](유도 과정은 부록 A를 참고하라.)
\[\begin{align} L &= \mathbb{E}_q \left[ - \log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} \right] \tag{23} \\[8pt] &= \mathbb{E}_q \left[ - \log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} \cdot \frac{q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)} \right] \tag{24} \\[8pt] &= \mathbb{E}_q \left[ - \log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_T)} - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} - \log q(\mathbf{x}_0) \right] \tag{25} \\[8pt] &= D_{\mathrm{KL}}\bigl(q(\mathbf{x}_T) \,\|\, p(\mathbf{x}_T)\bigr) + \mathbb{E}_q \left[ \sum_{t \ge 1} D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t) \,\|\, p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\bigr) \right] + H(\mathbf{x}_0) \tag{26} \end{align}\]위 전개는 변분 하한 $L$ 을 로그 확률 형태로 다시 표현한 것이다.
(1) 식 (23)은 순방향 확률 과정 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 과
역방향 모델 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 간의 로그 비율을 포함한다.(2) 식 (24)는 베이즈 정리(Bayes’ rule) 를 이용해
순방향 확률 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 를
역방향 확률 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 로 변환한 형태이다.베이즈 정리에 따르면,
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\, q(\mathbf{x}_t)} {q(\mathbf{x}_{t-1})}.\]이를 식 (23)의 분모에 대입하면,
\[\frac{1}{q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} = \frac{q(\mathbf{x}_{t-1})} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\, q(\mathbf{x}_t)}.\]따라서 로그 항은 다음과 같이 정리된다:
\[\log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} = \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} + \log \frac{q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)}.\]이렇게 하면 식 (24)가 유도되며,
순방향 과정 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 대신
역방향 형태 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\) 로 표현할 수 있게 된다.(3) 식 (25)는 로그 항을 묶어
$\log \dfrac{p(\mathbf{x}_T)}{q(\mathbf{x}_T)}$ 와
$-\log q(\mathbf{x}_0)$ (데이터의 엔트로피 항)으로 분리한다.(4) 마지막 식 (26)은 KL 발산 정의를 적용한 결과로,
$L$ 이 다음 세 항으로 분해됨을 보여준다: - \(D_{\mathrm{KL}}\bigl(q(\mathbf{x}_T)\,\|\,p(\mathbf{x}_T)\bigr)\) :
종단 분포 간의 차이
- \(\sum_t D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\,\|\,p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\bigr)\) :
각 시점의 전이 분포 차이
- $H(\mathbf{x}_0)$ :
데이터의 엔트로피즉, 변분 하한은 “순방향 확산과 역방향 복원 간의 불일치를 최소화하면서,
데이터의 불확실성을 보존”하는 목적 함수로 해석된다.
이제 확산 과정의 길이 $T$ 를 데이터의 차원 수로 설정하고,
순방향 과정을 다음과 같이 정의하자:
\(q(\mathbf{x}_t \mid \mathbf{x}_0)\) 가
\(\mathbf{x}_0\) 의 처음 $t$ 개 좌표를 마스크(mask)한 상태에서
모든 확률 질량을 $\mathbf{x}_0$ 에 집중하도록 한다.
즉, \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 은
$t$번째 좌표를 마스크하며,
\(p(\mathbf{x}_T)\) 는 모든 질량을 빈(blank) 이미지에 두도록 설정한다.
이를 가정했을 때,
\(p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\) 는
완전히 표현력이 있는(fully expressive) 조건부 분포로 본다.
이러한 설정에서
\(D_{\mathrm{KL}}\bigl(q(\mathbf{x}_T)\,\|\,p(\mathbf{x}_T)\bigr) = 0\) 이 되며,
\(D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\,\|\,p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\bigr)\) 을 최소화하는 것은
$p_\theta$ 가 좌표 $t+1, \dots, T$ 는 그대로 복사하고
$t$번째 좌표를 $t+1, \dots, T$가 주어졌을 때 예측하도록 학습하는 것과 같다.
따라서 이러한 특정한 확산 과정을 사용하여
$p_\theta$ 를 학습하는 것은
결국 자기회귀 모델을 학습하는 것과 동일하다.
이 문장은 확산 모델(diffusion model) 이
자기회귀 모델(autoregressive model) 과
수학적으로 연결될 수 있음을 설명하는 부분이다.먼저, 확산 단계의 총 길이 $T$ 를
데이터의 차원 수(예: 픽셀 개수, 토큰 개수 등)로 설정한다고 가정한다.
이렇게 하면 각 시점 $t$ 에서
하나의 좌표(또는 픽셀, 토큰)를 마스크(mask)하고
남은 좌표만 유지하도록 정의할 수 있다.
순방향 과정 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 은
$t$번째 좌표를 마스크하는 과정을 의미한다.
즉, 점점 더 많은 좌표가 가려지며
최종적으로 $t = T$ 단계에서는
모든 좌표가 마스크되어 빈(blank) 이미지 상태가 된다.반대로, 역방향 과정 $p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)$ 은
마스크된 좌표를 하나씩 복원해 나가는 과정이다.
예를 들어, $t$번째 단계에서
이전에 가려졌던 $t$번째 좌표를
나머지 좌표들 $(t+1, \dots, T)$ 로부터 예측한다.이렇게 정의하면,
- \(p(\mathbf{x}_T)\) 는 “빈 이미지”로 시작하는 분포가 된다.
- \(q(\mathbf{x}_T)\) 도 같은 상태이므로
두 분포의 KL 발산은 \(D_{\mathrm{KL}}(q(\mathbf{x}_T)\,\|\,p(\mathbf{x}_T)) = 0\) 이 된다.이후 남는 학습 항은
\[D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1}\mid\mathbf{x}_t) \,\|\,p_\theta(\mathbf{x}_{t-1}\mid\mathbf{x}_t)\bigr)\]이며, 이 항을 최소화하는 것은
모델 $p_\theta$ 가 각 시점에서
“다음에 복원할 좌표($t$번째)”를
“이미 복원된 좌표들($t+1, \dots, T$)”을 조건으로 예측하도록 학습하는 것과 같다.따라서 이런 설정의 확산 모델은
본질적으로 자기회귀 모델(autoregressive model) 과 동일한 학습 구조를 가지며,
좌표를 한 번에 하나씩 순차적으로 복원(또는 생성)하는 모델로 해석된다.
우리는 따라서 가우시안 확산 모델(식 (2))을
데이터 좌표의 재정렬(reordering)로는 표현할 수 없는
일반화된 비트 순서를 갖는 일종의 자기회귀 모델로 해석할 수 있다.
이전 연구들에서는 이러한 재정렬이
샘플 품질에 영향을 미치는 귀납적 편향(inductive bias)을 도입한다는 것을 보여주었으며 [38],
우리는 가우시안 확산이 유사한 목적을 수행한다고 추측한다.
아마도 마스킹 잡음(masking noise)에 비해
이미지에 가우시안 잡음을 추가하는 것이 더 자연스럽기 때문에,
그 영향은 더 클 수도 있다.
또한 가우시안 확산의 길이(diffusion length)는
데이터의 차원 수와 같아야 할 필요가 없다.
예를 들어, 우리의 실험에서는
$T = 1000$ 을 사용하였는데,
이는 32 × 32 × 3 또는 256 × 256 × 3 이미지의
차원보다 작다.
가우시안 확산은 샘플링 속도를 높이기 위해
더 짧게 만들 수도 있고,
모델의 표현력을 높이기 위해
더 길게 설정할 수도 있다.
4.4 보간 (Interpolation)
우리는 확률적 인코더(stochastic encoder)로서 $q$ 를 사용하여
잠재 공간(latent space)에서 원본 이미지 $\mathbf{x}_0, \mathbf{x}_0’ \sim q(\mathbf{x}_0)$ 를 보간할 수 있다.
즉, $\mathbf{x}_t, \mathbf{x}_t’ \sim q(\mathbf{x}_t \mid \mathbf{x}_0)$ 로부터 샘플링한 뒤,
선형적으로 보간된(latent) 잠재 벡터
$\bar{\mathbf{x}}_t = (1 - \lambda)\mathbf{x}_0 + \lambda\mathbf{x}_0’$ 를
역방향 과정(reverse process)
$\bar{\mathbf{x}}_0 \sim p(\mathbf{x}_0 \mid \bar{\mathbf{x}}_t)$
을 통해 이미지 공간으로 복원한다.
결과적으로, 우리는 역방향 과정을 사용하여
원본 이미지의 손상된 버전(linearly interpolated corrupted versions)으로부터
선형 보간 시 발생하는 인공물(artifacts)을 제거한다.
이 과정은 그림 8 (왼쪽)에 나타나 있다.
그림 8: 500 단계의 확산 과정을 적용한 CelebA-HQ 256×256 이미지의 보간 결과.
우리는 $\lambda$ 의 서로 다른 값들에 대해
잡음(noise)을 고정하여 $\mathbf{x}_t$ 와 $\mathbf{x}_t’$ 이 동일하게 유지되도록 했다.
그림 8 (오른쪽)은
CelebA-HQ 256×256 원본 이미지들($t = 500$)의
보간(interpolation) 및 복원(reconstruction) 결과를 보여준다.
역방향 과정은 고품질의 복원 이미지를 생성하며,
자세(pose), 피부색(skin tone), 헤어스타일(hairstyle), 표정(expression),
배경(background) 등의 속성이
부드럽게 변화하는 자연스러운 보간 결과를 낸다.
단, 안경(eyewear)은 변화하지 않는다.
$t$ 가 더 커질수록 보간은 더 거칠고 다양해지며,
$t = 1000$ 일 때는 완전히 새로운 샘플이 생성된다
(부록 그림 9 참조).
5 관련 연구 (Related Work)
확산 모델(diffusion models)은 흐름(flow) 기반 모델 [9, 46, 10, 32, 5, 16, 23]
또는 변분 오토인코더(VAE) [33, 47, 37]와 유사해 보일 수 있다.
그러나 확산 모델은 $q$ 가 파라미터를 가지지 않도록 설계되어 있으며,
최상위 잠재 변수 $\mathbf{x}_T$ 는 데이터 $\mathbf{x}_0$ 와 거의 0에 가까운 상호정보량(mutual information)을 가진다.
우리의 $\epsilon$-예측(reverse process parameterization)은
다중 잡음 단계(multiple noise levels)에 걸쳐
잡음 제거 점수 매칭(denoising score matching)과
가열된(annealed) 랑주뱅 동역학(Langevin dynamics)을 연결시킨다 [55, 56].
그러나 확산 모델은 로그 가능도(log likelihood)를 직접 계산할 수 있으며,
훈련 절차는 변분 추론(variational inference)을 통해
랑주뱅 샘플러(Langevin dynamics sampler)를 명시적으로 학습시킨다
(자세한 내용은 부록 C 참조).
이 연결성(connection)은 반대 방향의 함의도 지닌다.
즉, 특정 가중된 형태의 잡음 제거 점수 매칭(weighted denoising score matching)은
변분 추론을 사용하여 랑주뱅 형태의 샘플러를 학습하는 것과 동일하다.
마르코프 사슬(Markov chain)의 전이 연산자(transition operator)를 학습하기 위한
다른 방법으로는 infusion training [2], variational walkback [15],
생성 확률적 네트워크(generative stochastic networks) [1],
그리고 그 외의 다양한 방법들 [50, 54, 36, 42, 35, 65]이 있다.
점수 매칭(score matching)과 에너지 기반 모델(energy-based modeling) 간의
이미 알려진 연결성을 고려할 때,
우리의 연구는 최근의 에너지 기반 모델 연구 [67–69, 12, 70, 13, 11, 41, 17, 8]에도
영향을 줄 수 있을 것이다.
우리의 속도-왜곡(rate–distortion) 곡선은
변분 하한(variational bound)을 단 한 번 평가하는 동안
시간에 따라 계산되며,
이는 가중된 중요도 샘플링(annealed importance sampling) [24]에서
왜곡 패널티(distortion penalty)에 대한
속도-왜곡 곡선을 단 한 번의 실행으로 계산할 수 있는 방식과 유사하다.
우리의 점진적 디코딩(progressive decoding) 논증은
합성곱 DRAW(convolutional DRAW) 및 관련 모델 [18, 40]에서도 발견될 수 있으며,
이는 부분 스케일 순서(subscale ordering)나
자기회귀 모델(autoregressive models)의 샘플링 전략을
보다 일반화된 형태로 설계하는 데 도움이 될 수 있다 [38, 64].
6 결론 (Conclusion)
우리는 확산 모델(diffusion models)을 사용하여 고품질의 이미지 샘플을 제시하였으며,
확산 모델과 변분 추론(variational inference) 간의 연결을 발견하였다.
이 연결은 마르코프 연쇄(Markov chain)를 학습하기 위한
잡음 제거 점수 매칭(denoising score matching)과
가열된 랑주뱅 동역학(annealed Langevin dynamics,
그리고 확장적으로는 에너지 기반 모델),
자기회귀 모델(autoregressive models),
그리고 점진적 손실 압축(progressive lossy compression)을 포함한다.
확산 모델은 이미지 데이터에 대해
우수한 귀납적 편향(inductive bias)을 가지는 것으로 보이므로,
우리는 향후 연구에서
이러한 모델이 다른 데이터 모달리티(modality)나
다른 유형의 생성 모델 및 기계학습 시스템의 구성 요소로서
어떤 유용성을 가질 수 있는지를 탐구하고자 한다.
더 넓은 영향 (Broader Impact)
우리의 확산 모델 연구는
기존의 다른 종류의 딥 생성 모델(deep generative models) 연구와
유사한 범위를 갖는다.
예를 들어, GANs, flows, 자기회귀 모델 등에서
샘플 품질을 향상시키기 위한 시도들과 유사하다.
우리의 논문은 이러한 기법 계열 내에서
확산 모델을 일반적으로 유용한 도구로 발전시키는 진전을 보여주며,
따라서 생성 모델이 지금까지 (그리고 앞으로)
사회 전반에 미칠 수 있는 영향력을 더욱 증폭시킬 수 있을 것이다.
불행하게도, 생성 모델의 악용 사례는 이미 널리 알려져 있다.
샘플 생성 기법은 유명 인물의 가짜 이미지나 동영상을
정치적 목적으로 제작하는 데 사용될 수 있다.
소프트웨어 도구가 등장하기 전에도
가짜 이미지는 수작업으로 제작되었지만,
생성 모델과 같은 기술은 그 과정을 훨씬 쉽게 만든다.
다행히도, 현재 CNN 기반 생성 이미지에는
탐지가 가능한 미묘한 결함들이 존재하지만 [62],
생성 모델의 성능이 향상됨에 따라
이러한 탐지는 점점 어려워질 수 있다.
또한 생성 모델은 학습에 사용된 데이터셋의 편향(bias)을 반영한다.
인터넷에서 자동화된 시스템을 통해
대규모 데이터셋이 수집되는 경우,
이러한 편향을 제거하기란 쉽지 않다.
특히 데이터가 라벨이 없는 상태라면 더욱 그렇다.
만약 생성 모델이 편향된 데이터셋으로 학습된 후
그 결과물이 다시 인터넷에 퍼진다면,
이러한 편향은 더욱 강화될 것이다.
한편, 확산 모델은 데이터 압축(data compression)에
유용하게 사용될 가능성도 있다.
데이터 해상도가 높아지고
전 세계 인터넷 트래픽이 증가함에 따라,
인터넷을 통해 대중에게 데이터를 효율적으로 전달하기 위해
압축 기술은 점점 더 중요해지고 있다.
우리의 연구는 라벨이 없는 원시(raw) 데이터를 활용한
표현 학습(representation learning)에 기여할 수 있으며,
이는 이미지 분류(image classification)부터
강화 학습(reinforcement learning)까지
다양한 하위 작업에 적용될 수 있다.
또한 확산 모델은
예술, 사진, 음악 등의 창의적 용도로도
점점 더 활용될 가능성이 있다.
감사의 글 및 연구비 공개 (Acknowledgments and Disclosure of Funding)
본 연구는 ONR PECASE 및 NSF 대학원 연구 펠로십(NSF Graduate Research Fellowship)
보조금 번호 DGE-1752814의 지원을 받았다.
또한 Google의 TensorFlow Research Cloud(TFRC)로부터 Cloud TPU를 제공받았다.
참고문헌 (References)
[1] Guillaume Alain, Yoshua Bengio, Li Yao, Jason Yosinski, Eric Thibodeau-Laufer, Saizheng Zhang, Pascal Vincent.
GSNs: 생성 확률적 네트워크(Generative Stochastic Networks).
Information and Inference: A Journal of the IMA, 5(2):210–249, 2016.
[2] Florian Bordes, Sina Honari, Pascal Vincent.
잡음 주입 학습(Infusion Training)을 통한 노이즈로부터의 샘플 생성 학습.
International Conference on Learning Representations, 2017.
[3] Andrew Brock, Jeff Donahue, Karen Simonyan.
자연 이미지 합성을 위한 대규모 GAN 학습.
International Conference on Learning Representations, 2019.
[4] Tong Che, Ruixiang Zhang, Jascha Sohl-Dickstein, Hugo Larochelle, Liam Paull, Yuan Cao, Yoshua Bengio.
당신의 GAN은 사실 에너지 기반 모델이며, 판별자 기반 잠재 샘플링을 사용해야 한다.
arXiv preprint arXiv:2003.06060, 2020.
[5] Tian Qi Chen, Yulia Rubanova, Jesse Bettencourt, David K. Duvenaud.
신경 보통 미분방정식(Neural Ordinary Differential Equations).
Advances in Neural Information Processing Systems, 6571–6583, 2018.
[6] Xi Chen, Nikhil Mishra, Mostafa Rohaninejad, Pieter Abbeel.
PixelSNAIL: 향상된 자기회귀 생성 모델.
International Conference on Machine Learning, 863–871, 2018.
[7] Rewon Child, Scott Gray, Alec Radford, Ilya Sutskever.
희소 변환기(Sparse Transformers)를 이용한 긴 시퀀스 생성.
arXiv preprint arXiv:1904.10509, 2019.
[8] Yuntian Deng, Anton Bakhtin, Myle Ott, Arthur Szlam, Marc’Aurelio Ranzato.
잔여 에너지 기반 모델(Residual Energy-Based Models)을 이용한 텍스트 생성.
arXiv preprint arXiv:2004.11714, 2020.
[9] Laurent Dinh, David Krueger, Yoshua Bengio.
NICE: 비선형 독립 성분 추정(Non-linear Independent Components Estimation).
arXiv preprint arXiv:1410.8516, 2014.
[10] Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio.
Real NVP를 이용한 밀도 추정(Density Estimation Using Real NVP).
arXiv preprint arXiv:1605.08803, 2016.
[11] Yilun Du, Igor Mordatch.
에너지 기반 모델을 이용한 암시적 생성 및 모델링.
Advances in Neural Information Processing Systems, 3603–3613, 2019.
[12] Ruiqi Gao, Yang Lu, Junpei Zhou, Song-Chun Zhu, Ying Nian Wu.
다중 격자 모델링을 통한 생성적 ConvNets 학습.
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 9155–9164, 2018.
[13] Ruiqi Gao, Erik Nijkamp, Diederik P. Kingma, Zhen Xu, Andrew M. Dai, Ying Nian Wu.
플로우 기반 에너지 모델(Flow-Based Energy-Based Models) 학습.
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 7518–7528, 2020.
[14] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio.
생성적 적대 신경망(Generative Adversarial Nets).
Advances in Neural Information Processing Systems, 2672–2680, 2014.
[15] Anirudh Goyal, Nan Rosemary Ke, Surya Ganguli, Yoshua Bengio.
변분적 워크백(Variational Walkback): 확률적 순환 네트워크로서의 전이 연산자 학습.
Advances in Neural Information Processing Systems, 4392–4402, 2017.
[16] Will Grathwohl, Ricky T. Q. Chen, Jesse Bettencourt, David Duvenaud.
FJORD: 자유형 연속 역학을 통한 가역 생성 모델.
International Conference on Learning Representations, 2019.
[17] Will Grathwohl, Kuan-Chieh Wang, Joern-Henrik Jacobsen, David Duvenaud, Mohammad Norouzi, Kevin Swersky.
분류기를 에너지 기반 모델로 간주해야 한다.
International Conference on Learning Representations, 2020.
[18] Karol Gregor, Frederic Besse, Danilo Jimenez Rezende, Ivo Danihelka, Daan Wierstra.
개념적 압축(Towards Conceptual Compression).
Advances in Neural Information Processing Systems, 3549–3557, 2016.
[19] Prahladh Harsha, Rahul Jain, David McAllester, Jaikumar Radhakrishnan.
상관성의 복잡도(The Communication Complexity of Correlation).
Twenty-Second Annual IEEE Conference on Computational Complexity (CCC’07), 10–23, IEEE, 2007.
[20] Marton Havasi, Robert Peharz, José Miguel Hernández-Lobato.
압축된 모델 파라미터로부터의 정보 회복(Minimal Random Code Learning).
International Conference on Learning Representations, 2019.
[21] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, Sepp Hochreiter.
GAN의 안정적 학습을 위한 두 단계 규칙 업데이트: 로컬 내시 균형(Local Nash Equilibrium)에 수렴.
Advances in Neural Information Processing Systems, 6626–6637, 2017.
[22] Irina Higgins, Loïc Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, Alexander Lerchner.
Beta-VAE: 제약된 변분 프레임워크에서 기본 시각 개념 학습.
International Conference on Learning Representations, 2017.
[23] Jonathan Ho, Xi Chen, Aravind Srinivas, Yan Duan, Pieter Abbeel.
Flow++: 플로우 기반 생성 모델의 분산화 및 구조 설계 개선.
International Conference on Machine Learning, 2019.
[24] Sicong Huang, Alireza Makhzani, Yanshuai Cao, Roger Grosse.
딥 생성 모델의 손실 압축률 평가.
International Conference on Machine Learning, 2020.
[25] Nal Kalchbrenner, Aaron van den Oord, Karen Simonyan, Ivo Danihelka, Oriol Vinyals, Alex Graves, Koray Kavukcuoglu.
비디오 픽셀 네트워크(Video Pixel Networks).
International Conference on Machine Learning, 1771–1779, 2017.
[26] Nal Kalchbrenner, Erich Elsen, Karen Simonyan, Seb Noury, Norman Casagrande, Edward Lockhart, Florian Stimberg, Aaron van den Oord, Sander Dieleman, Koray Kavukcuoglu.
효율적인 자연 오디오 합성(Efficient Natural Audio Synthesis).
International Conference on Machine Learning, 2410–2419, 2018.
[27] Tero Karras, Timo Aila, Samuli Laine, Jaakko Lehtinen.
향상된 GAN을 위한 점진적 학습: 품질, 안정성, 다양성.
International Conference on Learning Representations, 2018.
[28] Tero Karras, Samuli Laine, Timo Aila.
StyleGAN: 스타일 기반 생성기 아키텍처를 이용한 생성적 적대 신경망.
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 4401–4410, 2019.
[29] Tero Karras, Miika Aittala, Janne Hellsten, Samuli Laine, Jaakko Lehtinen, Timo Aila.
제한된 데이터로 생성적 적대 신경망 학습.
arXiv preprint arXiv:2006.06676v1, 2020.
[30] Tero Karras, Samuli Laine, Miika Aittala, Janne Hellsten, Jaakko Lehtinen, Timo Aila.
StyleGAN 이미지 품질 향상: 분석 및 개선.
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8110–8119, 2020.
[31] Diederik P. Kingma, Jimmy Ba.
Adam: 확률적 최적화를 위한 방법.
International Conference on Learning Representations, 2015.
[32] Diederik P. Kingma, Prafulla Dhariwal.
Glow: 가역 1×1 합성곱을 사용하는 생성적 플로우.
Advances in Neural Information Processing Systems, 10215–10224, 2018.
[33] Diederik P. Kingma, Max Welling.
변분 오토인코딩 변분 베이즈(Auto-Encoding Variational Bayes).
arXiv preprint arXiv:1312.6114, 2013.
[34] Diederik P. Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, Max Welling.
자기회귀 플로우를 이용한 향상된 변분 추론.
Advances in Neural Information Processing Systems, 4743–4751, 2016.
[35] John Lawson, George Tucker, Bo Dai, Rajesh Ranganath.
샘플러 유도 분포를 학습하는 에너지 영감 모델(Energy-Inspired Models).
Advances in Neural Information Processing Systems, 8501–8513, 2019.
[36] Daniel Levy, Matt D. Hoffman, Jascha Sohl-Dickstein.
해밀토니안 몬테카를로를 신경망으로 일반화.
International Conference on Learning Representations, 2018.
[37] Lars Maaløe, Marco Fraccaro, Valentin Liévin, Ole Winther.
BIVA: 변분 모델의 매우 깊은 잠재 계층 구조.
Advances in Neural Information Processing Systems, 6548–6558, 2019.
[38] Jacob Menick, Nal Kalchbrenner.
서브스케일 픽셀 네트워크를 이용한 고해상도 이미지 생성.
International Conference on Learning Representations, 2019.
[39] Takeru Miyato, Toshiki Kataoka, Masanori Koyama, Yuichi Yoshida.
에너지 기반 모델 학습을 위한 스펙트럼 정규화(Spectral Normalization).
International Conference on Learning Representations, 2018.
[40] Alex Nichol.
VQ-DRAW: 순차적 분산 VAE.
arXiv preprint arXiv:2003.01599, 2020.
[41] Erik Nijkamp, Mitch Hill, Tian Han, Song-Chun Zhu, Ying Nian Wu.
에너지 기반 모델의 최대우도 해석에 대한 연구.
arXiv preprint arXiv:1903.12370, 2019.
[42] Erik Nijkamp, Mitch Hill, Song-Chun Zhu, Ying Nian Wu.
비수렴 MCMC를 활용한 에너지 기반 학습.
Advances in Neural Information Processing Systems, 5233–5243, 2019.
[43] Georg Ostrovski, Will Dabney, Rémi Munos.
자기회귀 모델링을 위한 오토레그레시브 분위수 네트워크.
International Conference on Machine Learning, 3936–3945, 2018.
[44] Ryan Prenger, Rafael Valle, Bryan Catanzaro.
WaveGlow: 음성 합성을 위한 플로우 기반 생성 네트워크.
ICASSP 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 3617–3621, IEEE, 2019.
[45] Ali Razavi, Aaron van den Oord, Oriol Vinyals.
VQ-VAE-2: 다양한 고해상도 이미지를 생성하는 모델.
Advances in Neural Information Processing Systems, 14837–14847, 2019.
[46] Danilo Rezende, Shakir Mohamed.
정규화 플로우를 이용한 변분 추론.
International Conference on Machine Learning, 1530–1538, 2015.
[47] Danilo Jimenez Rezende, Shakir Mohamed, Daan Wierstra.
근사 추론을 위한 확률적 역전파(Stochastic Backpropagation).
International Conference on Machine Learning, 1278–1286, 2014.
[48] Olaf Ronneberger, Philipp Fischer, Thomas Brox.
U-Net: 의료 영상 세분화를 위한 합성곱 신경망.
International Conference on Medical Image Computing and Computer-Assisted Intervention, 234–241, Springer, 2015.
[49] Tim Salimans, Durk P. Kingma.
가중 정규화(Weight Normalization): 심층 신경망 학습을 가속화하는 단순 재매개변수화.
Advances in Neural Information Processing Systems, 901–909, 2016.
[50] Tim Salimans, Diederik Kingma, Max Welling.
마르코프 체인 몬테카를로와 변분 추론의 결합.
International Conference on Machine Learning, 1218–1226, 2015.
[51] Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, Xi Chen.
GAN 학습 개선 기법.
Advances in Neural Information Processing Systems, 2234–2242, 2016.
[52] Tim Salimans, Andrej Karpathy, Xi Chen, Diederik P. Kingma.
PixelCNN++: 픽셀CNN의 개량 및 혼합 우도 수정.
International Conference on Learning Representations, 2017.
[53] Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, Surya Ganguli.
비평형 열역학 학습을 위한 심층 비지도 학습.
International Conference on Machine Learning, 2256–2265, 2015.
[54] Jiaming Song, Shengjia Zhao, Stefano Ermon.
A-NICE-MC: MCMC를 위한 적대적 학습.
Advances in Neural Information Processing Systems, 5140–5150, 2017.
[55] Yang Song, Stefano Ermon.
분포 기울기 추정을 통한 생성 모델 학습.
Advances in Neural Information Processing Systems, 11895–11907, 2019.
[56] Yang Song, Stefano Ermon.
점수 기반 생성 모델 학습 개선 기법.
arXiv preprint arXiv:2006.09011, 2020.
[57] Aaron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, Koray Kavukcuoglu.
WaveNet: 원시 오디오 생성을 위한 생성 모델.
arXiv preprint arXiv:1609.03499, 2016.
[58] Aaron van den Oord, Nal Kalchbrenner, Koray Kavukcuoglu.
픽셀 순환 신경망(Pixel Recurrent Neural Networks).
International Conference on Machine Learning, 2016.
[59] Aaron van den Oord, Nal Kalchbrenner, Oriol Vinyals, Lasse Espeholt, Alex Graves, Koray Kavukcuoglu.
PixelCNN 디코더를 이용한 조건부 이미지 생성.
Advances in Neural Information Processing Systems, 4790–4798, 2016.
[60] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, Illia Polosukhin.
Attention is All You Need.
Advances in Neural Information Processing Systems, 5998–6008, 2017.
[61] Pascal Vincent.
점수 매칭과 잡음 제거 오토인코더 간의 연결.
Neural Computation, 23(7):1661–1674, 2011.
[62] Sheng-Yu Wang, Oliver Wang, Richard Zhang, Andrew Owens, Alexei A. Efros.
CNN이 생성한 이미지는 놀랍도록 쉽게 탐지된다.
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020.
[63] Xiaolong Wang, Ross Girshick, Abhinav Gupta, Kaiming He.
비지역적 신경망(Non-local Neural Networks).
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7794–7803, 2018.
[64] Auke J. Wiggers, Emiel Hoogeboom.
자기회귀 모델을 위한 예측 샘플링(Predictive Sampling).
arXiv preprint arXiv:2002.09928, 2020.
[65] Hao Wu, Jonas Köhler, Frank Noé.
확률적 정규화 플로우(Stochastic Normalizing Flows).
arXiv preprint arXiv:2002.06707, 2020.
[66] Yuxin Wu, Kaiming He.
그룹 정규화(Group Normalization).
Proceedings of the European Conference on Computer Vision (ECCV), 3–19, 2018.
[67] Jianwen Xie, Yang Lu, Song-Chun Zhu, Ying Nian Wu.
생성적 합성곱 신경망의 이론(A Theory of Generative ConvNet).
International Conference on Machine Learning, 2635–2644, 2016.
[68] Jianwen Xie, Song-Chun Zhu, Ying Nian Wu.
공간-시간 생성 합성곱 신경망을 이용한 동적 패턴 합성(Synthesizing Dynamic Patterns by Spatial-Temporal Generative ConvNet).
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7093–7101, 2017.
[69] Jianwen Xie, Zilong Zheng, Ruiqi Gao, Wenguan Wang, Song-Chun Zhu, Ying Nian Wu.
3차원 형태 합성과 분석을 위한 디스크립터 네트워크 학습(Learning Descriptor Networks for 3D Shape Synthesis and Analysis).
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 8629–8638, 2018.
[70] Jianwen Xie, Song-Chun Zhu, Ying Nian Wu.
동적 패턴을 위한 에너지 기반 공간-시간 생성 합성곱 신경망 학습(Learning Energy-Based Spatial-Temporal Generative ConvNets for Dynamic Patterns).
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019.
[71] Fisher Yu, Yinda Zhang, Shuran Song, Ari Seff, Jianxiong Xiao.
LSUN: 인간의 검증 피드백을 이용한 대규모 이미지 데이터셋 구축.
arXiv preprint arXiv:1506.03365, 2015.
[72] Sergey Zagoruyko, Nikos Komodakis.
와이드 잔차 네트워크(Wide Residual Networks).
arXiv preprint arXiv:1605.07146, 2016.
추가 정보 (Extra information)
LSUN
LSUN 데이터셋의 FID 점수들은 표 3에 포함되어 있다.
별표(∗)로 표시된 점수들은 StyleGAN2에서 기준선으로 보고된 것이며,
다른 점수들은 각 저자들에 의해 보고되었다.
표 3: LSUN 256×256 데이터셋에 대한 FID 점수들
점진적 압축 (Progressive compression)
섹션 4.3에서 제시한 우리의 손실 압축(lossy compression) 논증은
개념 증명(proof of concept)에 불과하다.
그 이유는 알고리즘 3과 4가
고차원 데이터에 대해서는 계산이 불가능한(not tractable)
(minimal random coding [20]과 같은) 절차에 의존하기 때문이다.
이 알고리즘들은 Sohl-Dickstein 등 [53]의
변분 하한식(식 5)에 대한 압축 해석(compression interpretation)으로서의 의미를 가지며,
아직 실용적인 압축 시스템으로 사용될 수 있는 것은 아니다.
표 4: 비조건부(unconditional) CIFAR10 테스트 세트의 속도-왜곡(rate-distortion) 값들 (그림 5에 대응됨)
A 확장된 전개 (Extended derivations)
아래는 식 (5)의 유도이다.
이는 확산 모델(diffusion models)에 대한 분산 감소 변분 하한(reduced variance variational bound)이다.
이 내용은 Sohl-Dickstein 등 [53]의 자료에서 가져온 것으로, 완전성을 위해 여기에 포함하였다.
다음은 $L$의 또 다른 형태이다.
이는 계산이 가능하지는 않지만, 섹션 4.3의 논의를 위해 유용하다.
\[\begin{align} L &= \mathbb{E}_q \left[ - \log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_t \mid \mathbf{x}_{t-1})} \right] \tag{23} \\[8pt] &= \mathbb{E}_q \left[ - \log p(\mathbf{x}_T) - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} \cdot \frac{q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)} \right] \tag{24} \\[8pt] &= \mathbb{E}_q \left[ - \log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_T)} - \sum_{t \ge 1} \log \frac{p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} {q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)} - \log q(\mathbf{x}_0) \right] \tag{25} \\[8pt] &= D_{\mathrm{KL}}\bigl(q(\mathbf{x}_T) \,\|\, p(\mathbf{x}_T)\bigr) + \mathbb{E}_q \left[ \sum_{t \ge 1} D_{\mathrm{KL}}\bigl(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t) \,\|\, p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\bigr) \right] + H(\mathbf{x}_0) \tag{26} \end{align}\]B 실험 세부 사항 (Experimental details)
우리의 신경망 아키텍처는 PixelCNN++ [52]의 백본을 따르며,
Wide ResNet [72]에 기반한 U-Net [48]이다.
우리는 구현을 단순화하기 위해 가중치 정규화(weight normalization) [49]를
그룹 정규화(group normalization) [66]로 대체하였다.
우리의 32×32 모델은 네 단계의 특징 맵 해상도(32×32에서 4×4까지)를 사용하며,
256×256 모델은 여섯 단계를 사용한다.
모든 모델은 해상도 수준당 두 개의 합성곱 잔차 블록(convolutional residual blocks)과
16×16 해상도 수준에서 셀프-어텐션(self-attention) 블록을 포함한다 [6].
확산 시간 t는 Transformer의 사인파 위치 임베딩(sinusoidal position embedding) [60]을
각 잔차 블록에 추가하여 지정된다.
우리의 CIFAR10 모델은 35.7M(백만) 개의 파라미터를 가지며,
LSUN 및 CelebA-HQ 모델은 114M 파라미터를 가진다.
또한 LSUN Bedroom 모델의 필터 개수를 늘려 약 256M 파라미터를 가진 더 큰 변형 모델도 학습시켰다.
우리는 모든 실험에 TPU v3-8(8개의 V100 GPU와 유사한 성능)을 사용하였다.
CIFAR 모델은 초당 21 스텝, 배치 크기 128에서
800k 스텝 학습을 완료하는 데 약 10.6시간이 걸린다.
256개의 이미지 배치를 샘플링하는 데는 17초가 소요된다.
CelebA-HQ/LSUN(256²) 모델은 초당 2.2 스텝, 배치 크기 64에서
128개의 이미지를 샘플링하는 데 300초가 걸린다.
우리는 CelebA-HQ를 0.5M 스텝,
LSUN Bedroom을 2.4M 스텝,
LSUN Cat을 1.8M 스텝,
LSUN Church를 1.2M 스텝 동안 학습시켰다.
더 큰 LSUN Bedroom 모델은 1.15M 스텝 동안 학습되었다.
초기에는 메모리 제약 내에서 네트워크 크기가 맞도록 하기 위해
일부 하이퍼파라미터를 수동으로 설정하였으며,
이후 대부분의 하이퍼파라미터 탐색은 CIFAR10 샘플 품질을 최적화하는 방향으로 수행한 뒤,
그 결과를 다른 데이터셋에 적용하였다.
우리는 $\beta_{t}$ 스케줄을 상수, 선형, 이차 함수 중에서 선택하였으며,
$L_T \approx 0$이 되도록 제약하였다.
$T = 1000$으로 설정하고 스윕 없이 선형 스케줄을 사용하였으며,
$\beta_1 = 10^{-4}$, $\beta_T = 0.02$로 두었다.여기서 “스윕(sweep) 없이”란,
하이퍼파라미터 탐색(hyperparameter sweep) 과정을 수행하지 않고
단일 값만 고정하여 사용하는 것을 의미한다.
즉, 여러 후보 값을 실험적으로 비교·검증하지 않고
드롭아웃 값을 0으로 정해 그대로 사용했다는 뜻이다.CIFAR10의 드롭아웃 비율은 $\lbrace 0.1, 0.2, 0.3, 0.4 \rbrace$ 범위를 스윕하여 0.1로 설정하였다.
드롭아웃을 제거하면 정규화되지 않은 PixelCNN++ [52]의 과적합 아티팩트(artifact)와 유사한
품질 저하가 발생하였다.
다른 데이터셋에서는 스윕(sweep) 없이 드롭아웃을 0으로 설정하였다.“아티팩트(artifact)”란,
모델이 학습 과정에서 과적합(overfitting)으로 인해 만들어내는
비자연적이거나 왜곡된 시각적 패턴을 의미한다.
예를 들어, 이미지 생성 모델의 경우
실제 데이터에는 존재하지 않는 반복 무늬, 경계 노이즈, 또는 인위적인 질감 등이
아티팩트로 나타난다.따라서 여기서 말하는 “과적합 아티팩트”는
모델이 훈련 데이터에 지나치게 적합되어
새로운 입력에 대해 일반화하지 못하고
비정상적인 시각적 흔적을 만들어내는 현상을 가리킨다.우리는 CIFAR10 학습 중에 무작위 수평 반전(random horizontal flips)을 사용하였다.
수평 반전을 적용한 경우와 적용하지 않은 경우 모두 학습을 시도했으며,
수평 반전을 사용하면 샘플 품질이 약간 향상됨을 발견하였다.
또한 LSUN Bedroom을 제외한 모든 다른 데이터셋에서도
무작위 수평 반전을 사용하였다.우리는 실험 초기 단계에서 Adam [31]과 RMSProp을 모두 사용해 보았으며,
그중 전자를 선택하였다.
하이퍼파라미터는 표준(default) 값으로 그대로 두었다.
학습률(learning rate)은 스윕(sweeping) 없이 $2 \times 10^{-4}$로 설정하였으며,
$256 \times 256$ 해상도의 이미지의 경우에는
더 큰 학습률에서 학습이 불안정해 보였기 때문에
$2 \times 10^{-5}$로 낮추었다.CIFAR10의 배치 크기는 128로, 더 큰 이미지에서는 64로 설정하였다.
이 값들에 대해서는 스윕을 수행하지 않았다.모델 파라미터에 대해 EMA(지수 이동 평균)를 적용하였으며,
감쇠 계수(decay factor)는 0.9999로 설정하였다.
이 값 역시 스윕하지 않았다.EMA(Exponential Moving Average, 지수 이동 평균)은
학습 중 모델 파라미터의 진동(oscillation)과 불안정을 줄이기 위해
최근 파라미터 값에 더 높은 가중치를 두고
과거 파라미터의 정보를 점진적으로 반영하는 기법이다.즉, 현재 파라미터 $\theta_t$ 에 대해
\[\theta_{\text{EMA}} \leftarrow 0.9999 \, \theta_{\text{EMA}} + (1 - 0.9999) \, \theta_t\]
EMA 파라미터 $\theta_{\text{EMA}}$ 는 다음과 같이 갱신된다:여기서 감쇠 계수(decay factor) 0.9999는
과거 파라미터를 거의 완전히 유지하면서
최근 변화만 아주 미세하게 반영하도록 설정된 값이다.
이로 인해 모델은 학습 후반부에서 더 부드럽고
안정적인 파라미터를 가지게 된다.또한 이 계수는 실험적으로 스윕(sweep, 여러 후보 값을 탐색하는 과정) 없이
고정된 값으로 사용되었다.
최종 실험은 한 번만 학습되었으며,
학습 과정 전반에 걸쳐 샘플 품질(sample quality)을 평가하였다.
샘플 품질 점수와 로그 가능도(log likelihood)는
학습 과정 중 최소 FID 값에서의 결과로 보고된다.
CIFAR10의 경우,
OpenAI [51] 및 TTUR [21] 저장소의 원본 코드를 각각 사용하여
5만 개의 샘플에 대해 Inception 점수와 FID 점수를 계산하였다.
LSUN의 경우,
StyleGAN2 [30] 저장소의 코드를 사용하여
5만 개의 샘플에 대해 FID 점수를 계산하였다.
CIFAR10과 CelebA-HQ 데이터셋은
TensorFlow Datasets (https://www.tensorflow.org/datasets)에서
제공된 그대로 불러왔으며,
LSUN은 StyleGAN의 코드를 사용하여 준비하였다.
데이터셋의 분할(splits) — 혹은 분할이 없는 경우 — 은
생성 모델링(context of generative modeling)에서
각 데이터셋을 처음 사용한 논문에서 정의된 표준 설정을 따랐다.
모든 세부 사항은 소스 코드 공개본에서 확인할 수 있다.
C 관련 연구에 대한 논의 (Discussion on related work)
우리의 모델 아키텍처, 순방향 과정(forward process)의 정의, 그리고 prior는
NCSN [55, 56]과 미묘하지만 중요한 방식으로 다르며,
이러한 차이점들은 샘플 품질을 향상시킨다.
NCSN(Noise Conditional Score Network)은
점수 기반 생성 모델(score-based generative model)의 초기 형태로,
서로 다른 잡음 수준(noise scale)에 조건화된 점수 함수
$\nabla_{\mathbf{x}} \log p_\sigma(\mathbf{x})$ 를 학습하여
데이터를 복원(denoise)하거나 샘플링하는 모델이다.즉, 각 단계마다 다른 표준편차 $\sigma$의 잡음이 추가된 데이터를 입력받아
그 데이터의 로그 확률의 그래디언트(점수 함수)를 예측하도록 학습된다.
학습 후에는 랑주뱅 동역학(Langevin dynamics)으로 샘플을 점진적으로 복원함으로써
새로운 데이터를 생성할 수 있다.
특히, 우리는 샘플러를 학습 이후(post-hoc)에 추가하는 대신,
잠재 변수(latent variable) 모델로서 직접 학습시킨다는 점이 다르다.
자세히 설명하면 다음과 같다:
우리는 셀프-어텐션(self-attention)을 포함한 U-Net을 사용한다.
NCSN은 팽창 합성곱(dilated convolution)을 사용하는 RefineNet을 사용한다.
우리는 정규화(normalization) 레이어(NCSNv1)에서만 또는 출력(v2)에서만 추가하는 대신,
Transformer의 사인파 위치 임베딩(sinusoidal position embedding)을 추가하여
모든 레이어를 시간 $t$에 대해 조건화(condition)한다.확산(diffusion) 모델은 각 순방향 단계에서 데이터를
$\sqrt{1 - \beta_t}$ 배율로 축소(scaling down)한다.
이렇게 함으로써 노이즈를 추가할 때 분산이 증가하지 않으며,
신경망의 역방향 과정(reverse process)에 일관된 스케일의 입력을 제공한다.
반면 NCSN은 이러한 스케일링 요인을 생략한다.NCSN과 달리, 우리의 순방향 과정은 신호를 완전히 소거한다
($D_{\mathrm{KL}}(q(\mathbf{x}_T \mid \mathbf{x}_0) \,|\, \mathcal{N}(0, \mathbf{I})) \approx 0$),
이는 $\mathbf{x}_T$의 prior와 집계 사후분포(aggregate posterior)가
매우 잘 일치하도록 보장한다.
또한 NCSN과 달리, 우리의 $\beta_t$ 값은 매우 작기 때문에
순방향 과정이 조건부 가우시안 체인(conditional Gaussian Markov chain)에 의해
가역적(reversible)임을 보장한다.
이러한 두 요인은 샘플링 과정에서 분포의 이동(distribution shift)을 방지한다.우리의 랑주뱅(Langevin) 유사 샘플러는
순방향 과정에서의 $\beta_t$로부터 학습률(learning rate), 잡음 크기(noise scale) 등의
계수를 엄밀하게 도출한다.
따라서 우리의 학습 절차는 $T$단계 이후 데이터 분포에 맞추기 위해
샘플러를 직접 학습시키는 것이다.
즉, 변분 추론(variational inference)을 사용하여
샘플러를 잠재 변수(latent variable) 모델로 학습시킨다.
대조적으로, NCSN의 샘플러 계수들은 사후(post-hoc)에 수동으로 설정되며,
그들의 학습 절차는 샘플러의 품질 지표를 직접적으로 최적화한다는 보장이 없다.
D 샘플 (Samples)
추가 샘플 (Additional samples)
그림 11, 13, 16, 17, 18, 그리고 19는
CelebA-HQ, CIFAR10, 그리고 LSUN 데이터셋에서 학습된
확산(diffusion) 모델의 비선별된(uncurated) 샘플들을 보여준다.
잠재 구조와 역방향 과정의 확률성 (Latent structure and reverse process stochasticity)
샘플링 동안, prior인 $\mathbf{x}_T \sim \mathcal{N}(0, \mathbf{I})$ 와
랑주뱅(Langevin) 동역학은 확률적이다.
두 번째 잡음의 원천이 가지는 중요성을 이해하기 위해,
CelebA 256×256 데이터셋의 동일한 중간 잠재 변수(latent)에 대해
조건화된 여러 이미지를 샘플링하였다.
그림 7은
$t \in \lbrace 1000, 750, 500, 250 \rbrace$ 에 대해
동일한 잠재 변수 \(\mathbf{x}_t\) 를 공유하는
역방향 과정 \(\mathbf{x}_0 \sim p_\theta(\mathbf{x}_0 \mid \mathbf{x}_t)\)
으로부터의 여러 샘플을 보여준다.
이를 수행하기 위해, 우리는 prior에서 초기 샘플을 추출한 뒤
단일 역방향 체인(reverse chain)을 실행하였다.
중간 시점에서 이 체인은 여러 이미지를 샘플링하기 위해 분기된다(split).
체인이 $\mathbf{x}_{T=1000}$ 에서 분기될 경우,
샘플들은 서로 크게 다르다.
그러나 더 많은 단계 후에 체인을 분기할 경우,
샘플들은 성별(gender), 머리색(hair color), 안경 착용(eyewear),
채도(saturation), 자세(pose), 얼굴 표정(facial expression) 등의
고수준 속성을 공유한다.
이는 $\mathbf{x}_{750}$ 과 같은 중간 잠재 변수들이
비록 직접적으로 인식하기 어렵더라도
이러한 속성들을 인코딩하고 있음을 나타낸다.
거칠게에서 세밀하게 보간(Coarse-to-fine interpolation)
그림 9는 CelebA 256×256 이미지 쌍 사이의 보간(interpolation)을 보여주며,
이는 잠재 공간(latent space) 보간 이전에 수행된 확산 단계(diffusion step)의 수를 변화시키면서 얻어진 것이다.
확산 단계의 수를 늘리면 원본 이미지의 구조가 더 많이 파괴되며,
이 구조는 역방향 과정(reverse process) 동안 모델에 의해 복원된다.
이는 모델이 세밀한(fine) 수준과 거친(coarse) 수준 모두에서 보간을 수행할 수 있게 한다.
극한의 경우, 확산 단계를 0으로 설정하면 보간은
픽셀 공간(pixel space)에서의 원본 이미지 혼합을 의미한다.
반면, 1000개의 확산 단계를 거친 경우에는
원본 정보가 사라지고, 보간 결과는 새로운 샘플이 된다.
그림 9: 잠재 혼합(latent mixing) 이전의 확산 단계 수를 변화시킨
거칠게에서 세밀하게(coarse-to-fine) 보간(interpolation).
그림 10: 시간에 따른 비조건부(unconditional) CIFAR10의
점진적 샘플링(progressive sampling) 품질.
그림 11: CelebA-HQ 256×256 생성 샘플들.