[논문] NICE: NON-LINEAR INDEPENDENT COMPONENTS ESTIMATION
논문 출처
Laurent Dinh, David Krueger, Yoshua Bengio.
NICE: Non-linear Independent Components Estimation.
Université de Montréal, Département d’informatique et de recherche opérationnelle.
🔗 원문 링크 (arXiv: 1410.8516)
저자
- Laurent Dinh
- David Krueger
- Yoshua Bengio*
(Université de Montréal, Département d’informatique et de recherche opérationnelle)
*Yoshua Bengio는 CIFAR 선임 연구원(Senior Fellow)이다.
초록 (Abstract)
우리는 Non-linear Independent Component Estimation(NICE)이라 불리는
복잡한 고차원 밀도들을 모델링하기 위한 딥러닝 프레임워크를 제안한다.
이 접근법은, 좋은 표현(representation)이란
데이터가 모델링하기 쉬운 분포를 갖는 것이라는 아이디어에 기반한다.
이 목적을 위해
데이터의 비선형 결정적 변환(non-linear deterministic transformation)을 학습하여
이를 잠재 공간(latent space)으로 사상(mapping)함으로써,
변환된 데이터가 분리된(factorized) 분포에 부합하도록 만들며,
즉 독립적인 잠재 변수들(independent latent variables)로 이루어지도록 한다.
우리는 이 변환을 파라미터화하여
야코비안(Jacobian)과 역야코비안(inverse Jacobian)의
행렬식(determinant)을 계산하는 것을 쉽게(trivial) 만든다.
그럼에도 우리는, 각각이 심층 신경망에 기반한 단순한 구성 요소들을 조합함으로써,
복잡한 비선형 변환을 학습하는 능력을 유지한다.
훈련 기준은 단순히 정확한 로그-우도(log-likelihood)이며,
이는 계산 가능하다(tractable).
편향되지 않은(unbiased) 조상 샘플링(ancestral sampling) 또한 쉽다.
편향되지 않은(unbiased) 조상 샘플링(ancestral sampling)은
확률 그래프 모델에서
변수들을 부모(조상) 변수부터 차례대로 샘플링하는 방식으로,
상위(latent) 변수를 먼저 생성하고
그 값을 조건으로 하위 변수를 생성하는
순차적(top-down) 생성 과정을 의미한다.여기서 “편향되지 않은”이라는 말은
이 생성 과정이 모델이 정의한 확률 분포를 그대로 따르며,
추가적인 근사나 왜곡이 개입하지 않는다는 뜻이다.
즉, 모델이 표현한 구조적 의존성에 따라
정확한 조건부 분포를 순차적으로 적용해
원래 모델 분포로부터 그대로 샘플을 얻을 수 있다.이러한 조상 샘플링은
변분 오토인코더(VAE),
normalizing flow 기반 모델 등을 포함한
다양한 생성 모델에서
잠재 변수 분포로부터 데이터를 생성할 때
흔히 사용되는 방식이다.
우리는 이러한 접근 방식이 네 개의 이미지 데이터셋에서 우수한 생성 모델을 만들어내며,
인페인팅에도 사용할 수 있음을 보인다.
인페인팅(inpainting)이란
이미지의 일부가 가려지거나 손상된 경우,
주변 맥락(context)을 바탕으로
누락된 영역을 자연스럽게 복원하는 기법을 의미한다.
예를 들어 지워진 얼굴 일부를 채우거나,
가려진 배경을 원래 모습처럼 재구성하는 작업이 이에 해당한다.
1 서론 (Introduction)
비지도 학습에서 중심적인 질문들 중 하나는
알려지지 않은 구조를 가진 복잡한 데이터 분포를
어떻게 포착할 것인가 하는 것이다.
딥러닝 접근법들(Bengio, 2009)은
데이터의 가장 중요한 변화 요인들을 포착할 수 있는
데이터의 표현(representation)을 학습하는 것에 의존한다.
이는 다음과 같은 질문을 제기한다:
좋은 표현(representation)이란 무엇인가?
최근의 연구들
(Kingma and Welling, 2014; Rezende et al., 2014; Ozair and Bengio, 2014)과 마찬가지로,
우리는 좋은 표현(representation)이란
데이터의 분포가 모델링하기 쉬운 분포가 되는 것이라는
관점을 취한다.
이 논문에서 우리는 특별한 경우를 고려하는데,
그 경우란 학습자에게
데이터를 새로운 공간으로 변환하는
$h = f(x)$ 라는 변환을 찾도록 요구하는 것이다.
그리하여 결과로 얻어진 분포가 분리되도록,
즉 구성 요소들 $h_d$가 독립적이 되도록 하는 것이다.
제안된 훈련 기준은 로그-우도(log-likelihood)로부터 직접적으로 유도된다.
더 구체적으로, 우리는 $h = f(x)$ 라는 변수 변경(change of variables)을 고려하는데,
이는 $f$가 가역적(invertible)이며
$h$의 차원이 $x$의 차원과 동일하다고 가정하여
분포 $p_H$에 맞추기 위한 것이다.
변수 변경 공식(change of variable rule)은 우리에게 다음을 준다:
\[p_X(x) = p_H(f(x)) \left| \det \frac{\partial f(x)}{\partial x} \right|. \tag{1}\]여기에서 $\frac{\partial f(x)}{\partial x}$는 함수 $f$의 $x$에서의 야코비안(Jacobian) 행렬이다.
(1) 식은 변수 변환 시의 밀도 보존 원리로부터 직접적으로 도출된다.
원래 변수 $x$ 와 변환된 변수 $h = f(x)$ 사이의 관계는
확률 질량(probability mass)이 변환 전후 동일한 부피 요소(volume element)에 대해
동일하게 유지되어야 한다는 원리에 기반한다.즉, 다음이 성립해야 한다:
\[p_X(x)\, dx = p_H(h)\, dh.\](1-1) 기본 관계 $h = f(x)$ 를 미소 변화 관점에서 해석하면
\[dh = \frac{\partial f(x)}{\partial x}\, dx.\]
미소 부피 요소는 야코비안(Jacobian)으로 연결된다:(1-2) 따라서 부피 요소의 크기는 야코비안의 행렬식으로 변환된다:
\[|dh| = \left|\det \frac{\partial f(x)}{\partial x}\right|\, |dx|.\](2) 이를 확률 질량 보존 식에 대입하면 다음을 얻는다:
\[p_X(x)\, dx = p_H(f(x))\, |dh| = p_H(f(x))\left|\det \frac{\partial f(x)}{\partial x}\right| dx.\](3) 양변에서 $dx$ 를 약분하면 변수 변환에 따른 밀도 변환 공식이 얻어진다:
\[p_X(x) = p_H(f(x))\left|\det \frac{\partial f(x)}{\partial x}\right|.\]
이 논문에서 우리는
야코비안의 행렬식을 쉽게(trivially) 얻을 수 있도록
$f$를 선택한다.
더 나아가, 그 역함수 $f^{-1}$ 또한
마찬가지로 쉽게(trivially) 얻을 수 있어,
다음과 같이 $p_X(x)$ 로부터 쉽게 샘플링할 수 있게 해준다:
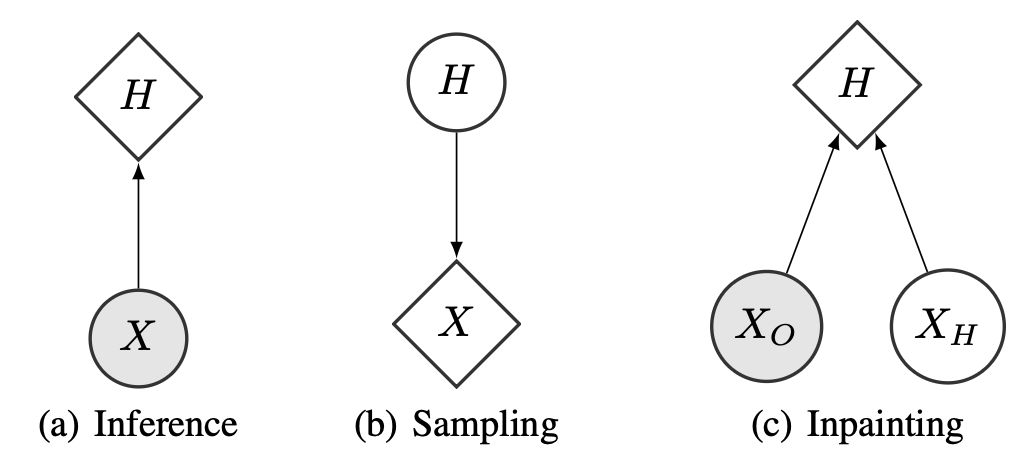
그림 1: 확률 모델의 계산 그래프. 다음의 공식들을 사용한다.
(a) 추론(Inference):
\[\log(p_X(x)) = \log(p_H(f(x))) + \log\left(|\det(\frac{\partial f(x)}{\partial x})|\right)\](b) 샘플링(Sampling):
\[h \sim p_H(h), \quad x = f^{-1}(h)\](c) 인페인팅(Inpainting):
\[\max_{x_H} \log(p_X((x_O, x_H))) = \max_{x_H} \log(p_H(f((x_O, x_H)))) + \log\left(|\det(\frac{\partial f((x_O, x_H))}{\partial x})|\right)\](a) 추론(Inference):
목적은 주어진 관측값 $x$ 의 로그 확률 $\log p_X(x)$ 를 계산하는 것이다.
NICE에서는 $x$ 를 잠재 변수 공간(latent space)로 변환하는
$h = f(x)$ 를 사용하여 확률을 계산한다.잠재 공간에서는 분포가 분리(factorized)되어 있으므로
\[\log(p_X(x)) = \log(p_H(f(x))) + \log \mid \det(\partial f(x)/\partial x) \mid\]
$p_H(h)$ 를 계산하기 쉽고,
실제 데이터 공간의 밀도는 변수변환 공식에 따라로 나타난다.
그림의 구조에서 $X$ → $H$ 로 화살표가 향하는 이유는
$x$ 를 $h=f(x)$ 로 변환하여 확률을 계산하기 때문이다.(b) 샘플링(Sampling):
데이터 생성 과정은 잠재 공간에서 시작된다.
NICE는 $p_H(h)$ 가 독립 분포이므로
샘플링이 매우 쉽다.1) 먼저 $h \sim p_H(h)$ 를 샘플링한다.
2) 그런 다음 역변환 $x = f^{-1}(h)$ 로 실제 데이터 공간의 샘플을 생성한다.이는 그림에서 $H$ → $X$ 로 화살표가 향하는 구조로 표현되어 있으며,
잠재 변수가 데이터의 원인(cause)이 되어
$x$ 를 생성하는 generative direction을 나타낸다.(c) 인페인팅(Inpainting):
인페인팅에서는 데이터 $(x_O, x_H)$ 중
일부 관측되지 않은 부분 $x_H$ 를 복원해야 한다.목표는 관측된 $x_O$ 를 조건으로 하여
\[\max_{x_H} \log(p_X((x_O, x_H)))\]
전체 데이터의 로그 확률 $\log p_X((x_O, x_H))$ 를
$x_H$ 에 대해 최대화하는 것이다:변수변환을 적용하면 다음과 같이 바뀐다:
\[\max_{x_H}\log(p_H(f((x_O, x_H)))) + \log \mid \det(\partial f((x_O, x_H))/\partial x) \mid\]즉, 미지수 $x_H$ 를 적절히 조절하여
잠재 공간에서 높은 확률을 갖는 방향으로
복원된 이미지를 찾는 것이다.그림에서는 $H$가 $X_O$와 $X_H$ 두 가지 입력으로부터 영향을 받는 구조로 나타나며,
부분 관측된 데이터를 잠재 공간으로 보내
숨겨진 부분($x_H$)을 조정하는 과정을 표현한다.
이 논문의 주요한 새로운 점은 야코비안의 행렬식을
“쉽게 계산할 수 있음(easy determinant of the Jacobian)”과
“역함수가 쉽게 계산될 수 있음(easy inverse)”이라는
이 두 가지 특성을 가지는 변환 $f$ 를 설계하는 것이다.
그러면서도 복잡한 변환을 학습하기 위해
필요한 만큼의 용량(capacity)을 가질 수 있도록 허용한다.
이 접근법의 핵심 아이디어는 $x$ 를 두 개의 블록 $(x_1, x_2)$로 나누고,
이를 이용하여 다음 형태의 $(x_1, x_2)$에서 $(y_1, y_2)$로의 변환을
빌딩 블록(building block)으로 적용할 수 있다는 것이다:
여기에서 $m$ 은 임의의 복잡한 함수이다.
(우리의 실험에서는 ReLU MLP)
이 빌딩 블록은 어떤 $m$에 대해서도
야코비안 행렬식이 1이 되고, 아래와 같이 쉽게 역함수(invertible)를 구할 수 있다:
세부 내용, 관련 논의, 그리고 실험 결과는 아래에서 전개된다.
변환은 다음과 같다:
\[y_1 = x_1\] \[y_2 = x_2 + m(x_1)\]여기서 $m(x_1)$은 $x_1$에만 의존하는 임의의 함수이다.
야코비안 행렬 $J$는 각 $y_i$ 를 $x_j$ 에 대해 편미분한 값으로 구성된다:
\[J = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{bmatrix}\]이를 각 항에 대해 계산하면:
\[\frac{\partial y_1}{\partial x_1} = 1\] \[\frac{\partial y_1}{\partial x_2} = 0\] \[\frac{\partial y_2}{\partial x_1} = m'(x_1)\] \[\frac{\partial y_2}{\partial x_2} = 1\]따라서 야코비안 행렬은 다음과 같은 상삼각 행렬이 된다:
\[J = \begin{bmatrix} 1 & 0 \\ m'(x_1) & 1 \end{bmatrix}\]상삼각 행렬의 행렬식은 대각 성분의 곱이다.
\[\det(J) = 1 \times 1 = 1\]즉, $m(x_1)$이 어떤 복잡한 함수이든
대각 항은 항상 1이므로 행렬식은 1로 고정된다.이 빌딩 블록은
- $m(x_1)$의 형태와 복잡성과 무관하게
- 야코비안 행렬식이 항상 $1$이며
- 따라서 volume-preserving(부피 보존) 변환이다.
2 연속 확률들의 전단사(bijective) 변환 학습
우리는 유한한 데이터셋 $\mathcal{D}$ 의 $N$ 개 예시(example) 각각이
공간 $\mathcal{X}$ 에 존재한다고 할 때 (보통 $\mathcal{X} = \mathbb{R}^D$),
밀도들의 매개변수적 집합(a parametric family of densities) $\lbrace p_\theta, \theta \in \Theta \rbrace$ 로부터
확률 밀도를 학습하는 문제를 고려한다.
핵심 관점: 무엇을 구하는 문제인가?
이 문장이 말하는 바는, 데이터가 존재하는 공간 $\mathcal{X}$ 위에서 정의된
확률 밀도 함수 $p_\theta(x)$의 파라미터 $\theta$를 학습하는 것이다.데이터셋의 역할
우리는 유한한 데이터셋 $\mathcal{D} = {x_1, \ldots, x_N}$ 을 가지고 있고,
각 예제 $x_i$ 는 공간 $\mathcal{X}$ 안에 존재한다.
보통 $\mathcal{X} = \mathbb{R}^D$ 이다.목표
우리의 목표는, $\mathcal{X}$ 공간에서 데이터가 어떻게 분포되어 있는지를 표현하는
확률 밀도 함수 $p_\theta(x)$의 최적 파라미터 $\theta$를 찾는 것이다.왜 ‘밀도의 매개변수적 집합’인가?
$p_\theta(x)$ 는 하나의 고정된 함수가 아니라
파라미터 $\theta$ 값에 따라 모양이 달라지는
확률 밀도 함수들의 집합이다.즉, $\theta$를 조정함으로써 다양한 분포 형태를 표현할 수 있다.
해결해야 하는 문제의 정확한 형태
관측된 $N$개의 데이터가 가장 높은 가능도로
발생하도록 만드는 방향으로
$\theta$를 최적화하여 $p_\theta(x)$를 학습하는 것이다.요약
결국 이 문장은, $\mathcal{X}$ 공간에서 정의된 확률 밀도 $p_\theta(x)$를
데이터셋 $\mathcal{D}$를 통해 학습하여
그 파라미터 $\theta$를 찾는 문제를 다룬다
라는 의미이다.
우리의 특정한 접근법은, 다음의 변수 변경 공식(change of variables formula)을 사용하여
데이터 분포를 더 단순한 분포로 변환하는
연속적이고 거의 모든 곳에서 미분 가능한 비선형 변환 $f$를
최대우도(maximum likelihood)를 통해 학습하는 것으로 구성된다.
여기에서 사전 분포(prior distribution)인 $p_H(h)$는
예를 들어 표준 등방성 가우시안과 같은 미리 정의된 밀도 함수1가 될 것이다.
1 이 사전분포(prior distribution)는 반드시 고정될 필요가 없으며,
또한 학습될 수도 있다는 점에 유의하라.
만약 사전분포가 분리된(factorial) (즉, 차원들이 독립적인) 분포라면,
우리는 다음의 비선형 독립 성분 추정
(non-linear independent components estimation, NICE) 기준을 얻게 되며,
분리된(factorial) 분포의 결정적 변환으로서의,
데이터에 대한 우리의 생성 모델 아래에서 단순히 최대우도에 해당한다:
여기에서 $f(x) = (f_d(x))_{d \leq D}$ 이다.
우리는 NICE를 데이터셋의 가역적인(invertible) 전처리 변환을 학습하는 것으로 볼 수 있다.
가역적 전처리를 사용하면 데이터를 수축(contracting)시키는 것만으로도
우도(likelihood)를 임의로 크게 만들 수 있다.
우리는 변수변환 공식(식 1)을 사용하여 이 현상을 정확히 상쇄(counteract)하고,
사전분포(prior) $p_H$ 의 분리된 구조를 이용해
모델이 데이터 안의 의미 있는 구조들을 발견하도록 장려한다.
이 공식에서, 변환 $f$ 의 야코비안(Jacobian) 행렬의 행렬식(determinant)은
수축을 패널티(penalize)하고
밀도가 높은 영역(예: 데이터 포인트들)에서는 확장을 장려하는 역할을 한다.
왜 수축하면 우도가 커지는가?
수축(contracting)을 하면, 입력 공간의 점들이
더 좁은 영역에 모이게 된다.그러면 동일한 데이터 샘플들이
더 작은 부피 안에 밀집하게 되고,
밀집된 영역에서는 밀도(density)가 자연스럽게 커진다.밀도란 “단위 부피당 데이터가 얼마나 모여 있는가”이므로,
부피를 줄이기만 해도 밀도 값은 원하는 만큼 크게 만들 수 있다.즉, 데이터를 수축시키면
분포가 더 뾰족해지고 집중되기 때문에
우도(likelihood) 역시 임의로 크게 만들 수 있다.그러나 전체 식을 보면,
우도는 두 항으로 구성되어 있다:1) 사전분포 항
\[\sum_{d=1}^{D} \log\left( p_{H_d}( f_d(x) ) \right)\]→ 수축하면 $h=f(x)$가 밀집되어 이 항은 커진다.
2) 야코비안 항
\[\log\left( \left| \det\left( \frac{\partial f(x)}{\partial x} \right) \right| \right)\]→ 수축하면 야코비안 행렬식이 1보다 작아지고,
로그를 취하면 음수가 되어 우도를 감소시키는 방향으로 작용한다.
→ 반대로, 필요하다면 확장(det > 1)을 통해
로그(det)를 양수로 만들어 우도를 보완하거나 증가시킬 수 있다.따라서 수축이 가져오는 “우도 증가 효과”는
야코비안 항의 “우도 감소 효과”에 의해
정확히 상쇄(counteract)된다.
또한 Jacobian 항은 상황에 따라
확장을 허용하여 우도를 유지하거나 높일 수 있는 여지도 제공한다.이것이 바로 변수변환 공식을 이용하는 이유다.
단순 수축으로 인한 인위적 우도 증가를 막고,
사전분포(prior) $p_H$ 의 분리된 구조를 통해
모델이 실제 데이터 내부의 의미 있는 구조를
올바르게 학습하도록 유도한다.
Bengio et al. (2013)에서 논의된 바와 같이, 표현 학습(representation learning)은
입력의 “더 흥미로운(interesting)” 영역들 (예: 비지도 학습의 경우 밀도가 높은 영역)에
연관된 표현 공간의 부피를 확장시키는 경향이 있다.
오토인코더들에 대한 이전 연구들,
특히 변분 오토인코더 (Kingma and Welling, 2014; Rezende et al., 2014;
Mnih and Gregor, 2014; Gregor et al., 2014)과 일치하게,
우리는 $f$ 를 인코더(encoder)라 부르고 그 역함수 $f^{-1}$ 를 디코더(decoder)라 부른다.
$f^{-1}$ 이 주어졌을 때, 모델로부터의 샘플링은
유향 그래프 모델 $H \rightarrow X$ 에서의 조상 샘플링(ancestral sampling)을 통해
매우 쉽게 수행될 수 있으며, 이는 식 2에서 기술된 바와 같다.
3 아키텍처 (Architecture)
3.1 삼각 구조(Triangular structure)
모델의 아키텍처는 야코비안(Jacobian) 행렬식이 계산 가능하고(tractable),
그 계산이 순방향(인코더 $f$)과 역방향(디코더 $f^{-1}$) 모두에서
직접적으로 이루어질 수 있는 전단사(bijection) 함수들의 계열을 얻기 위해 아주 중요하다.
여기에서 전단사(bijection)를 사용해야 하는 이유는
NICE 모델이 가역적 변환(invertible transform) 을 필요로 하기 때문이다.
만약 우리가 계층적(layered) 또는 합성된(composed) 변환
$f = f_L \circ \ldots \circ f_2 \circ f_1$ 을 사용한다면,
순방향 및 역방향 계산은 (적절한 순서로) 각 계층의 계산들을 구성한 것이 되며,
야코비안 행렬식은 그 계층들의 야코비안 행렬식들의 곱이 된다.
따라서 우리는 먼저 이 기본적인 구성 요소들을 정의하는 것을 목표로 한다.
먼저 우리는 아핀 변환(affine transformations)을 고려한다.
아핀 변환(affine transformation)이란,
선형 변환(linear transformation)에
평행 이동(translation)을 더한 형태의 변환을 뜻한다.즉, $y = Ax + b$ 와 같은 형태로 표현되며,
회전, 확대·축소, 반사, 전단(shear), 이동 등을
하나의 통합된 방식으로 다룰 수 있는 매우 일반적인 변환이다.
(Rezende et al., 2014)와 (Kingma and Welling, 2014)는
대각 행렬(diagonal matrices)이나 랭크-1 보정(rank-1 correction)을 가진 대각 행렬들을
변환 행렬(transformation matrices)로 사용할 때
역행렬(inverse)과 행렬식(determinant)에 대한 공식을 제공한다.
랭크-1 보정(rank-1 correction)이란
기본 행렬(예: 대각 행렬)에
랭크(rank)가 1인 행렬을 더해 보정(correction)하는 방식을 의미한다.랭크(rank)는 행렬의 독립적인 열(또는 행)의 개수를 의미하므로,
랭크-1 보정 행렬은$u v^\top$
형태처럼 두 벡터의 외적(outer product) 으로 표현될 수 있다.
이런 행렬을
대각 행렬 + $u v^\top$
같이 더해주면
기본 대각 행렬에는 없는 특정 방향으로의 변형(perturbation) 을 가할 수 있어
변환의 유연성을 높이면서도
역행렬과 행렬식을 계산 가능하고(tracable) 한 형태로 유지할 수 있다.NICE에서 언급되는 이유는
이런 랭크-1 보정이
야코비안 행렬식(det)을 효율적으로 계산할 수 있게 해주는
구조적 제약을 유지하는 동시에
보다 복잡한 변환을 표현할 수 있게 해주기 때문이다.
또 다른 계산 가능한(tracable) 행렬식들을 가진 행렬 계열은 삼각 행렬(triangular matrices)인데,
이들의 행렬식은 단순히 대각 원소(diagonal elements)들의 곱이다.
테스트 시점에서 삼각 행렬을 역변환(inverting)하는 것은 계산 면에서 합리적이다.
많은 정방 행렬(square matrices) $M$ 은
상삼각 행렬과 하삼각 행렬의 곱 $M = LU$ 로도 표현될 수 있다.
이러한 변환들은 서로 합성될 수 있으므로,
그 합성을 구성하는 유용한 요소들로는
야코비안이 대각 행렬(diagonal), 하삼각 행렬(lower triangular),
또는 상삼각 행렬(upper triangular) 형태가 되는 것들이 포함된다.
이러한 관찰을 이용하는 한 가지 방법은
삼각형 형태의 가중치 행렬과 전단사(bijective) 활성화 함수들을 가진
신경망을 구성하는 것이겠지만,
이는 아키텍처를 크게 제약하며,
깊이(depth)와 비선형성(non-linearities)의 선택을 제한한다.
대안적으로, 우리는
야코비안(Jacobian)이 삼각형(triangular)인 함수들의 계열을 고려할 수 있다.
야코비안의 대각 원소(diagonal elements)를 쉽게 계산할 수 있도록 보장함으로써,
야코비안의 행렬식(determinant) 또한 쉽게 계산될 수 있게 된다.
3.2 결합 층(Coupling Layer)
이 절(subsection)에서는
야코비안이 삼각 행렬(triangular)이 되어 야코비안 행렬식을 계산하기 쉬운
전단사(bijective) 변환들의 한 계열을 설명한다.
이는 변환 $f$ 를 위한 빌딩 블록 역할을 하게 될 것이다.
일반적 결합 층(General coupling layer)
$x \in \mathcal{X}$ 이고, $I_1, I_2$ 가 ⟦1, D⟧ 의 분할(partition)이며
$d = |I_1|$ 이라고 하자.
그리고 $m$ 이 $\mathbb{R}^d$ 위에서 정의된 함수라고 하자.
우리는 $y = (y_{I_1}, y_{I_2})$ 를 다음과 같이 정의할 수 있다:
\[\begin{aligned} y_{I_1} &= x_{I_1}, \\ y_{I_2} &= g(x_{I_2} \,;\, m(x_{I_1})). \end{aligned}\]여기서 $g : \mathbb{R}^{D-d} \times m(\mathbb{R}^d) \rightarrow \mathbb{R}^{D-d}$는 결합 법칙(coupling law)이며,
두 번째 인자가 주어졌을 때 첫 번째 인자에 대한 가역적인(invertible) 사상이다.
여기에서 함수 $g$는 결합(coupling) 역할을 하는 핵심 변환이다.
먼저 입력 벡터 $x$를 두 부분 $x_{I_1}$, $x_{I_2}$로 나눈다.
이때 $x_{I_1}$은 그대로 유지하고,
$x_{I_2}$만 변환하여 새로운 $y_{I_2}$를 만든다.이 변환을 담당하는 것이 바로 $g$이다.
$g$는 두 개의 입력을 받는다:1) 변환될 부분 $x_{I_2}$
2) 변환을 조절하는 조건(condition) 역할을 하는 $m(x_{I_1})$즉, $g$는 “$x_{I_1}$의 정보”를 이용해
“$x_{I_2}$를 어떻게 변화시킬지” 결정하는 함수이다.중요한 점은, $m(x_{I_1})$가 주어졌을 때
$g(\cdot ; m(x_{I_1}))$는
$x_{I_2}$에 대해 가역적(invertible)이어야 한다는 것이다.
그렇기 때문에 전체 변환도 전단사(bijection)를 유지할 수 있다.정리하면,
$g$는 $x_{I_2}$를 변형하되,
그 변형 방식은 $x_{I_1}$을 통해 조건부로 결정되는
조건부 가역적 변환(conditional invertible mapping)이다.
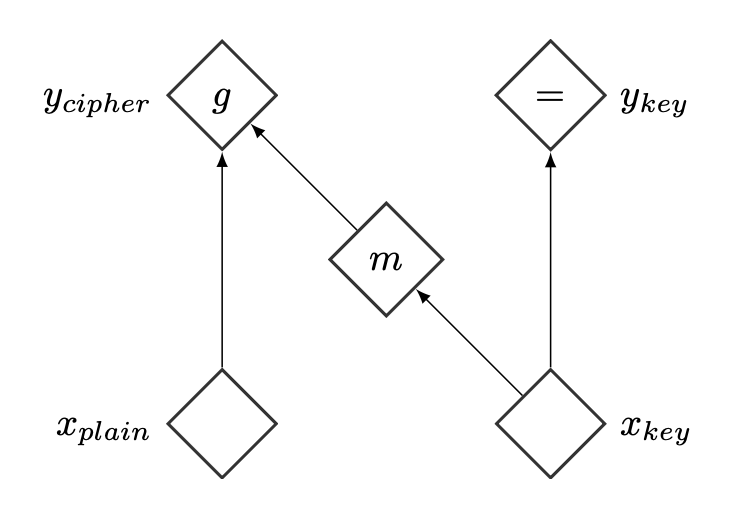
이에 대응하는 계산 그래프는 그림 2에 나타나 있다.
그림 2: 결합 층(coupling layer)의 계산 그래프
$I_1 = ⟦1, d⟧$, $I_2 = ⟦d, D⟧$ 이라고 하면,
이 함수의 야코비안(Jacobian)은 다음과 같다:
왜 야코비안이 이런 block-triangular 형태가 되는가?
결합 층(coupling layer)은 변수 집합을 두 부분으로 나누어
$I_1$ 부분은 그대로 전달(copy) 하고,
$I_2$ 부분만 $I_1$을 이용해 변환(transform) 한다.즉, \(y_{I_1} = x_{I_1}\) 이므로
$y_{I_1}$ 은 오직 $x_{I_1}$ 에만 의존하고,
$x_{I_2}$ 와는 아무런 관계가 없다.따라서 다음 미분이 0이 된다:
\[\frac{\partial y_{I_1}}{\partial x_{I_2}} = 0\]반면, $y_{I_2}$ 는
\[y_{I_2} = g(x_{I_2}; m(x_{I_1}))\]처럼 두 부분 모두에 의존하므로
\[\frac{\partial y_{I_2}}{\partial x_{I_1}}, \qquad \frac{\partial y_{I_2}}{\partial x_{I_2}}\]
아래 두 항은 일반적으로 0이 아니다:결국 야코비안은 다음 블록 구조를 갖는다:
- 왼쪽 위: 항등행렬 $I_d$
- 오른쪽 위: 0
- 왼쪽 아래: 일반적인 값
- 오른쪽 아래: 일반적인 값
여기서 $I_d$ 는 크기 $d$ 의 항등 행렬이다.
따라서 다음이 성립한다:
또한, 이 사상은 다음과 같이 역변환할 수 있다:
\[\begin{aligned} x_{I_1} &= y_{I_1}, \\ x_{I_2} &= g^{-1}(y_{I_2} \,;\, m(y_{I_1})). \end{aligned}\]우리는 이러한 변환을
결합 함수(coupling function) $m$ 을 가지는 결합 층(coupling layer)이라고 부른다.
가법 결합 층(Additive coupling layer)
단순함을 위해, 우리는 결합 법칙(coupling law)으로
\[g(a; b) = a + b\]를 선택한다. 따라서
\[a = x_{I_2}, \qquad b = m(x_{I_1})\]로 두면 다음과 같다:
\[y_{I_2} = x_{I_2} + m(x_{I_1})\] \[x_{I_2} = y_{I_2} - m(y_{I_1})\]그리고 이 변환의 역변환을 계산하는 것은
변환 자체를 계산하는 것과 동일한 정도로만 비용이 든다.
우리는 결합 함수 $m$ 의 선택에 어떤 제약도 없음을 강조한다
(올바른 정의역(domain)과 공역(codomain)을 갖는다는 것 외에는).
예를 들어, $m$ 은 $d$ 개의 입력 유닛과 $D - d$ 개의 출력 유닛을 가진 신경망이 될 수 있다.
더욱이 $\det \frac{\partial y_{I_2}}{\partial x_{I_2}} = 1$이므로, 가법 결합 층 변환은 자명한 역변환과 더불어
야코비안 행렬식이 1인(unit Jacobian determinant) 성질을 가진다.
또한, 다음과 같은 다른 종류의 결합(coupling)을 선택할 수도 있다.
예를 들어, 곱셈 결합 법칙(multiplicative coupling law)
\[g(a; b) = a \odot b, \qquad b \neq 0\]또는 아핀 결합 법칙(affine coupling law)
\[g(a; b) = a \odot b_1 + b_2, \qquad b_1 \neq 0\]단, $m : \mathbb{R}^d \rightarrow \mathbb{R}^{D-d} \times \mathbb{R}^{D-d}$ 인 경우이다.
왜 함수 $m$이 $\mathbb{R}^{D-d} \times \mathbb{R}^{D-d}$ 값을 반환해야 하는가?
곱셈 결합이나 아핀 결합은
변환될 벡터 $a \in \mathbb{R}^{D-d}$에 대해
원소별(element-wise) 연산을 수행하는 형태이다.예를 들어,
- 곱셈 결합: $g(a; b) = a \odot b$
- 아핀 결합: $g(a; b) = a \odot b_1 + b_2$
이 두 경우 모두
$a$와 동일한 차원($D-d$)의 벡터들이 필요하다.곱셈 결합에서는
$a$의 각 성분에 곱해줄 스케일(scale) 벡터 $b$가 필요하고,아핀 결합에서는
- 스케일 벡터 $b_1 \in \mathbb{R}^{D-d}$
- 이동(translation) 벡터 $b_2 \in \mathbb{R}^{D-d}$
두 개가 필요하다.따라서 $m(x_{I_1})$는
변환을 조절하는 매개변수로서
$D-d$ 차원짜리 벡터 두 개를 생성해야 한다.즉, $m$은 다음과 같은 형태여야 한다:
\[m : \mathbb{R}^{d} \rightarrow \mathbb{R}^{D-d} \times \mathbb{R}^{D-d}\]여기에서 “$\times$”는 곱셈이 아니라
두 벡터를 묶은 데카르트 곱(Cartesian product)을 의미하며,
이는 곧 $D-d$ 차원 벡터 두 개로 이루어진 튜플을 반환한다는 뜻이다.그래야 $g$가 $a \in \mathbb{R}^{D-d}$ 위에서
올바르게 작동하며,
전체 변환이 가역성을 유지할 수 있다.
우리는 수치적 안정성(numerical stability)의 이유로 가법 결합 층을 선택했다.
왜냐하면 결합 함수(coupling function) $m$ 이
렐루 신경망(rectified neural network)일 때,
이 변환이 구간별(piece-wise) 선형이 되기 때문이다.
왜 렐루(ReLU)와 구간별(piece-wise) 선형성이
수치적 안정성(numerical stability)에 기여하는가?먼저, 렐루(ReLU) 활성화 함수를 사용하는 신경망은
입력 공간을 여러 구간으로 나누고,
각 구간에서는 완전한 선형 변환만 수행한다.즉, 렐루 네트워크는 본질적으로
구간별(piece-wise) 선형 함수이다.이러한 성질은 다음과 같은 이유로
수치적 안정성에 큰 이점을 제공한다.1) 선형 함수는 야코비안(Jacobian) 계산이 매우 간단하다.
구간 내에서는 완전히 선형이므로
미분값이 일정하고, 큰 변동이 없어
역전파(backprop) 시 수치 폭주(exploding)나
수치 소실(vanishing)이 일어나기 어렵다.2) 비선형성이 “렐루의 꺾이는 지점”으로만 제한된다.
이는 변환 전체가
부드럽지 않을 수는 있지만,
미분이 존재하는 영역에서는 안정적이다.
특히 coupling layer에서는
Jacobian determinant를 다뤄야 하므로
예측 가능한 구조가 필요하다.3) 구간별 선형성은 역변환(inversion)을 쉽게 만든다.
coupling layer에서 $y_{I_2} = x_{I_2} + m(x_{I_1})$
같은 가법 구조를 사용하면
역변환이 단순한 뺄셈으로 이루어지며
수치적으로 매우 안정적이다.요약하면,
렐루 기반의 구간별 선형 구조는
① 계산 단순성, ② 미분 안정성, ③ 역변환 안정성
세 측면에서 coupling 층의 수치적 안정성을 크게 높여 준다.
결합 층 결합하기(Combining coupling layers)
우리는 여러 결합 층들을 합성(composition)하여 더 복잡한 계층적(layered) 변환을 얻을 수 있다.
결합 층은 입력의 일부를 변하지 않은 채로 남겨두기 때문에,
두 부분집합(subset)이 번갈아 가며 교환되도록 각 층에서 분할의 역할을 바꿔야 한다.
그러면 두 개의 결합 층의 합성만으로도 모든 차원을 수정(modify)할 수 있게 된다.
야코비안(Jacobian)을 조사해 보면,
우리는 적어도 세 개의 결합 층은 필요하며,
그래야 모든 차원들이 서로에게 영향을 미칠 수 있음을 관찰한다.
우리는 일반적으로 네 개를 사용한다.
3.3 리스케일링 허용(Allowing rescaling)
각 가법(additive) 결합 층은
단위(unit) 야코비안 행렬식(즉, 부피를 보존한다)을 가지므로,
그들의 합성 또한 필연적으로 단위 야코비안 행렬식을 갖게 된다.
이 문제를 다루기 위해,
우리는 대각 스케일링 행렬 $S$ 를 최상위(top) 층으로 포함시키는데,
이 행렬은 $i$번째 출력 값을 $S_{ii}$ 로 곱한다:
결합(coupling) 층들은 모두 “부피 보존(volume preserving)” 변환이라서
야코비안 행렬식이 항상 1이 된다.
즉, 어떤 차원도 늘어나거나 줄어들지 않고
데이터 공간의 ‘스케일(scale)’을 바꾸지 못한다.하지만 실제 데이터 분포는
어떤 차원에서는 변화량이 크고(스케일이 크고),
어떤 차원에서는 변화량이 작은 등
차원별 스케일이 다를 수 있다.
부피 보존만으로는 이런 변동성을 표현하기 어렵다.따라서 모델이 차원별로 스케일을 조정(rescaling) 하도록
마지막 단계에 대각 행렬 $S$ 를 추가한다.
$S$ 의 대각 원소 $S_{ii}$ 를 곱함으로써
$i$번째 차원의 출력만 확대/축소하며,
이는 전체 야코비안 행렬식에
$\prod_i S_{ii}$ 를 기여하게 되어
부피를 조절할 수 있게 한다(= 더 이상 단위 행렬식이 아님).요약하면, 이 스케일링 단계는
“모델이 어떤 차원은 더 크게 강조하고,
어떤 차원은 덜 강조하도록
학습 가능하게 만들어 주는 장치”이다.
이렇게 하면 학습자(learner)가
일부 차원에서는 더 많은 가중치를 주고(즉, 더 많은 변동을 모델링)
다른 차원에서는 더 적은 가중치를 주도록 할 수 있다.
$S_{ii}$ 가 어떤 $i$ 에 대해 $+\infty$ 로 가는 극한에서,
데이터의 유효 차원(effective dimensionality)은
1만큼 감소한 것으로 된다.
스케일링은 다음과 같이 표현된다: \(x'_i = S_{ii} x_i\)
만약 어떤 $S_{ii}$ 가 무한대로 증가한다고 가정하면,
매우 작은 $x_i$ 의 변화도
$x’_i$ 공간에서 무한히 크게 확대된다.
이는 기하학적으로 데이터 공간의 한 축이
매우 길고(flat) 의미 없는 방향으로 늘어나는 것과 동일하다.야코비안 행렬식은
\[\det(S) = \prod_{j=1}^D S_{jj}\]이므로,
\[\log|S_{ii}| \to +\infty\]
$S_{ii}$ 가 커지면 로그 야코비안 항은로 발산한다.
겉으로 보기엔 이 항 때문에 로그-우도가
$+\infty$ 로 갈 것 같지만 실제로는 그렇지 않다.왜냐하면 잠재 공간의 prior(대개 가우시안)가
훨씬 더 빠르게 $-\infty$ 로 발산하기 때문이다.스케일링 후 잠재변수는
\[h_i = f_i(x) = S_{ii} x_i\]이고, 가우시안 prior의 로그 확률은
\[\log p_H(h_i) = -\frac{1}{2} h_i^2 + C = -\frac{1}{2} S_{ii}^2 x_i^2 + C\]와 같이 제곱 속도로 $-\infty$ 로 발산한다.
전체 로그-우도는
\[\log p_X(x) = -\frac{1}{2} S_{ii}^2 x_i^2 + \log|S_{ii}| + C\]와 같은 형태를 갖게 되는데,
첫 번째 항의 발산 속도
\[-\frac{1}{2} S_{ii}^2 x_i^2\]가 두 번째 항
\[\log|S_{ii}|\]보다 훨씬 더 빠르다.
따라서 $S_{ii} \to +\infty$ 의 극한에서
\[\log p_X(x) \to -\infty\]
전체 로그-우도는로 수렴한다.
즉, 스케일을 무한대로 키우는 것은
우도를 올리는 방식이 아니라
우도를 최악으로 만드는 방식이며,
학습 중에는 절대로 이런 방향으로 가지 않는다.논문에서 말하는 “유효 차원(effective dimensionality)이 1 감소한다”는 표현은
실제 학습에서 $S_{ii}$ 가 무한대로 발산함을 의미하는 것이 아니라,
수학적 극한을 통해 해석한 ‘이론적 현상’을 설명한 것이다.즉, $S_{ii}$ 가 매우 커지면 해당 차원은
변동성을 잃고, 모델이 실질적으로 사용하지 않는 차원처럼 되기 때문에
데이터가 차원 $D$ 에 있음에도
모델이 효과적으로는 $D-1$ 차원만 사용한다는 의미이다.그러나 실제 학습에서는
$S_{ii}$ 를 크게 키우는 방향이
전체 우도를 떨어뜨리므로( $-\infty$ 로 감 )
그 차원으로는 전혀 이동하지 않는다.
이는 변환 $f$ 가 데이터 포인트 주변에서 가역성을 유지하는 한 가능하다.
“이는 변환 $f$ 가 데이터 포인트 주변에서 가역성을 유지하는 한 가능하다”의 의미는
스케일링을 매우 크게 하더라도,
그 변환 $f$ 자체가 여전히 역함수 $f^{-1}$ 를 가질 수 있어야 한다는 조건을 말한다.가역성(invertibility)이 유지된다는 말은
$f$ 가 데이터 근처에서
\(f : x \mapsto h = f(x)\) 를 1:1로 대응시키며,
작은 변화에 대해
\(x \leftrightarrow h\) 사이의 대응이 무너지지 않는다는 뜻이다.다시 말해,
스케일이 매우 커져도
\(\det\!\left(\frac{\partial f}{\partial x}\right) \neq 0\) 이고,
$f$ 가 국소적으로(local) 전단사(bijection)를 유지해야
변환된 값 $h$ 로부터
다시 원래 데이터 $x$ 를 복원할 수 있다.만약 스케일링이 너무 극단적이어서
어떤 차원에서 $f$ 의 야코비안이 0이 되거나
두 입력이 하나의 출력에 매핑되는(non-injective) 상황이 오면
더 이상 $f^{-1}$ 이 존재하지 않게 되며,
그 어떤 이론적 해석(유효 차원 감소 등)도 의미를 잃게 된다.따라서 논문이 말하는 “유효 차원 감소”는
수학적 극한에서 일어나는 현상을 설명한 것이고,
실제로 그 상태가 논리적으로 성립하려면
변환 $f$ 는 여전히
데이터 주변 부근에서 가역성 조건을 만족해야 한다는 점을 강조하는 것이다.
이와 같이 스케일된 대각 행렬을 마지막 단계로 두고,
나머지 단계들에서는 하삼각(lower triangular) 또는 상삼각(upper triangular) 구조를 사용한다면
(대각선에는 항등행렬을 둔 상태로),
NICE 기준(NICE criterion)은 다음과 같은 형태를 갖는다:
왜 위 식에는 야코비안 항이 별도로 등장하지 않는가?
NICE 구조에서 대부분의 결합(coupling) 변환은
\[y_{I_2} = x_{I_2} + m(x_{I_1})\]
가법 형태를 사용한다. 예를 들어,와 같은 형태이다.
이 가법 결합의 핵심 특징은
\[\det\left( \frac{\partial y}{\partial x} \right) = 1\]
야코비안이 항등행렬이 된다는 점이다. 즉,따라서
\[\log|\det(J)| = \log 1 = 0\]이 되어 야코비안 항은 우도 식에서 완전히 사라진다.
즉, NICE 변환의 대부분의 단계에서는
야코비안 항이 0이므로 우도에 영향을 주지 않는다.반면 마지막 단계로 추가되는 스케일 변환은
\[\det(S) = \prod_i S_{ii}\]
대각 행렬 $S$ 를 사용하므로 야코비안 행렬식이가 되고, 로그를 취하면
\[\sum_i \log |S_{ii}|\]만 남게 된다.
따라서 최종 NICE 기준식에서는
가법 coupling 층의 야코비안 항은 모두 0이기 때문에 나타나지 않으며,
오직 스케일 행렬의 대각 성분만 야코비안 항에 기여하게 된다.
우리는 이러한 스케일링 요인들을
PCA의 고유스펙트럼(eigenspectrum)에 관련지을 수 있는데,
이는 각 잠재 차원(latent dimension)에 얼마나 많은 변동성이 존재하는지를 보여준다.
($S_{ii}$ 가 클수록, 차원 $i$ 는 덜 중요한 것이다)
스펙트럼의 중요한 차원들은 알고리즘에 의해 학습된 매니폴드(manifold)로 볼 수 있다.
스펙트럼의 중요한 차원들이 매니폴드로 해석될 수 있는 이유는,
데이터가 실제로는 고차원 공간 전체를 채우지 않고
알고리즘이 발견한 저차원의 구조적 흐름 위에
대부분의 변동성이 집중되기 때문이다.
즉, 모델이 학습한 중요한 차원들은
데이터가 놓여 있는 의미 있는 저차원 곡면,
즉 매니폴드를 형성한다고 볼 수 있다.
사전(prior) 항은 $S_{ii}$ 를 작게 유지하도록 장려하는 반면,
행렬식(determinant) 항인 $\log S_{ii}$ 는 $S_{ii}$ 가 0에 도달하는 것을 방지한다.
왜 사전 항은 $S_{ii}$ 를 작게 만들고,
왜 $\log S_{ii}$ 항은 $S_{ii}$ 가 0에 가까워지는 것을 막는가?사전(prior) 항은
$f(x)$ 가 사전분포 $p_H$ 에서 높은 확률값을 갖도록 만들려 한다.
스케일 $S_{ii}$ 가 작아지면
$h = f(x)$ 가 더 압축되어 밀도가 높아지므로
사전 항의 값이 커져 우도를 증가시킨다.
따라서 사전 항은 $S_{ii}$ 를 작게 만드는 방향으로 작용한다.반면에 야코비안 항에서 등장하는
\[\log S_{ii} \rightarrow -\infty\]
$\log S_{ii}$ 는 $S_{ii} \rightarrow 0$ 이 되면로 발산해 우도를 크게 감소시킨다.
즉, $S_{ii}$ 가 0에 가까워지지 못하게
강하게 제약을 걸어준다.결과적으로
사전 항은 $S_{ii}$ 를 작게 만들고,
$\log S_{ii}$ 항은 $S_{ii}$ 가 0으로 붕괴되는 것을 막아
두 항의 상호작용을 통해
안정적인 최적값을 찾게 된다.
3.4 사전 분포(Prior distribution)
앞서 언급한 바와 같이, 우리는 사전 분포를 팩토리얼(factorial) 형태로 선택한다.
즉:
우리는 일반적으로 이 분포를 표준적인 분포 계열에서 선택한다.
예를 들어 가우시안 분포:
\[\log(p_{H_d}) = -\frac{1}{2} ( h_d^2 + \log(2\pi) )\]또는 로지스틱 분포(logistic distribution):
\[\log(p_{H_d}) = - \log(1 + \exp(h_d)) - \log(1 + \exp(-h_d))\]우리는 로지스틱 분포를 사용하는 경향이 있는데,
이는 더 잘 동작하는(more well-behaved) 그래디언트를 제공하는
경향이 있기 때문이다.
먼저 사전 분포 $p_H(h)$ 를 팩토리얼 형태로 두었기 때문에
각 차원 $h_d$ 의 분포 $p_{H_d}(h_d)$ 는 서로 독립이며,
로그를 취하면 차원별 로그-밀도의 합으로 쓸 수 있다.
NICE 논문에서는 각 $h_d$ 에 대해 “표준 가우스” 또는 “표준 로지스틱”을 사용하며,
아래 식들은 각각의 표준 분포의 로그-밀도(log-density) 를 전개한 것이다.(1) 가우시안 분포의 경우
표준 정규분포 $\mathcal{N}(0,1)$ 의 밀도는
\[p_{H_d}(h_d) = \frac{1}{\sqrt{2\pi}} \exp\!\left( -\frac{1}{2} h_d^2 \right)\]양변에 로그를 취하면
\[\log p_{H_d}(h_d) = \log\!\left( \frac{1}{\sqrt{2\pi}} \right) - \frac{1}{2} h_d^2\]그리고
\[\log\!\left( \frac{1}{\sqrt{2\pi}} \right) = -\log(\sqrt{2\pi}) = -\frac{1}{2}\log(2\pi)\]따라서 정리하면
\[\log p_{H_d}(h_d) = -\frac{1}{2} h_d^2 - \frac{1}{2}\log(2\pi) = -\frac{1}{2}\bigl(h_d^2 + \log(2\pi)\bigr)\](2) 로지스틱 분포의 경우
표준 로지스틱 분포의 CDF는
\[F(h_d) = \frac{1}{1 + \exp(-h_d)}\]PDF는 CDF의 미분:
\[p_{H_d}(h_d) = F'(h_d) = \frac{\exp(-h_d)}{(1 + \exp(-h_d))^2}\]이 식을 다음과 같이 재정리할 수 있다:
\[p_{H_d}(h_d) = \frac{1}{1 + \exp(h_d)} \cdot \frac{1}{1 + \exp(-h_d)}\]이제 로그를 취하면
\[\log p_{H_d}(h_d) = -\log(1 + \exp(h_d)) -\log(1 + \exp(-h_d))\]
4 관련된 방법들 (Related Methods)
생성 모델들에서 중요한 발전이 이루어져 왔다.
비유향 그래프 모델(undirected graphical models)인
딥 볼츠만 머신(DBM) (Salakhdinov and Hinton, 2009)은 매우 성공적이었으며,
효율적인 근사 추론과 학습 기법 덕분에 이 모델들은 연구의 강렬한 주제가 되었다.
그러나 이러한 모델들은 훈련과 샘플링을 위해
마르코프 연쇄 몬테카를로(MCMC) 샘플링 절차를 필요로 하며,
타깃 분포가 뾰족한 모드를 가질 때
이러한 연쇄들은 일반적으로 느리게 섞인다(slowly mixing).
또한, 로그-우도(log-likelihood)는 계산이 불가능하고(intractable),
가장 잘 알려진 추정 절차인 어닐링 중요도 샘플링(AIS) (Salakhutdinov and Murray, 2008)은
지나치게 낙관적인 평가를 초래할 수 있다 (Grosse et al., 2013).
어닐링 중요도 샘플링(AIS, Annealed Importance Sampling)이란?
AIS는 복잡한 확률분포의 정규화 상수(또는 로그-우도)를 추정하기 위해
여러 개의 중간 분포(intermediate distributions)를 사용하여
완만하게(annealing) 목표 분포로 이동하는 중요도 샘플링 기법이다.일반적인 중요도 샘플링(IS)은
한 번에 목표 분포로 샘플링하려 하기 때문에 분산이 매우 커질 수 있지만,
AIS는
$p_0 \rightarrow p_1 \rightarrow \dots \rightarrow p_T = p_{\text{target}}$
과 같이 점진적으로 난이도를 높여가며
분포 간 이동을 수행한다.각 단계에서 마르코프 전이(MCMC transition)를 적용하여
샘플이 목표 분포와 점점 더 유사해지도록 만들며,
각 전이 단계에서 중요도 가중치를 누적하여
최종적으로 정규화상수를 추정한다.왜 지나치게 낙관적이 될 수 있는가?
- MCMC 전이가 충분히 섞이지 않으면(slow mixing),
중간 분포의 샘플이 실제 분포를 제대로 반영하지 못한다.- 이 경우 중요도 가중치가 편향되어
목표 분포의 확률을 실제보다 과대평가(overestimate) 하는 경향이 있다.- 특히 고차원, 복잡한 에너지 모델(예: DBM)에서는
잘못된 모드에 갇히는 문제가 발생해
결과적으로 우도가 실제보다 크게 나타나는 지나친 낙관적 평가가 된다.
유향 그래프 모델(directed graphical models)은
DBM들이 효율적인 추론을 가능하게 하는 조건부 독립성 구조를 갖고 있지 않다.
그러나 최근 변분 오토인코더(VAE) (Kingma and Welling, 2014; Rezende et al., 2014;
Mnih and Gregor, 2014; Gregor et al., 2014) 의 개발로 인해
훈련 동안의 효율적인 근사 추론이 가능해졌다.
NICE 모델과는 대조적으로, 이러한 접근법들은
확률적 인코더 $q(h \mid x)$ 와 불완전한(imperfect) 디코더 $p(x \mid h)$ 를 사용하며,
이를 위해 재구성 항(reconstruction term)을 비용 함수에 포함시켜
디코더가 인코더를 근사적으로 역변환하도록 만든다.
이 과정은 오토인코더 루프에 노이즈를 주입하는데,
그 이유는 $h$ 가 참된 사후분포 $p(h \mid x)$ 에 대한
변분적 근사(variational approximation)인 $q(h \mid x)$ 로부터 샘플링되기 때문이다.
결과적으로 훈련 기준(training criterion)은
데이터 로그-우도에 대한 변분적 하한(variational lower bound)이 된다.
일반적으로 빠른 조상적 샘플링(ancestral sampling) 기법을
유향 그래프 모델이 제공한다는 점은 이러한 모델들을 매력적으로 만든다.
또한 로그-우도에 대한
중요도 샘플링 중요도 추정치(importance sampling estimator)는
기대값 관점에서 결코 지나치게 낙관적이 되지 않음을 보장한다.
여기서 말하는 “로그-우도에 대한 중요도 샘플링 추정치가
기대값 관점에서 결코 지나치게 낙관적이지 않다”는 뜻은
이 추정치의 기댓값이 항상 진짜 로그-우도보다 작거나 같다는 것을 의미한다.왜 이런 성질이 생기는지를 이해하려면
중요도 샘플링(IS)의 구조를 먼저 살펴봐야 한다.1) 주변우도 $p(x)$는 직접 계산 불가능하다
\[p(x)=\int p(x,h)\,dh\]고차원 적분이라 계산이 불가능(intractable)하다.
2) 이를 중요도 분포 $q(h \mid x)$로 재표현할 수 있다
\[p(x) =\int \frac{p(x,h)}{q(h\mid x)}\, q(h\mid x)\, dh\]즉, $q(h\mid x)$ 를 통해 기대값 형태로 다시 쓸 수 있다.
3) 이제 샘플링으로 근사할 수 있다
\[h^{(k)} \sim q(h \mid x)\]이렇게 뽑은 샘플들로
\[\hat{p}(x) = \frac{1}{K}\sum_{k=1}^K \frac{p(x, h^{(k)})}{q(h^{(k)} \mid x)}\]를 계산하면,
$\hat p(x)$ 는 우도 $p(x)$ 의 편향 없는(unbiased) 추정량이 된다.4) 하지만 우리가 실제로 필요로 하는 것은 $log p(x)$
\[\log \hat{p}(x)\]
그래서 보통을 로그-우도의 추정치로 사용한다.
5) 문제는 $log$가 오목(concave) 함수라는 점이다
\[\mathbb{E}[\log \hat{p}(x)] \le \log \mathbb{E}[\hat{p}(x)] = \log p(x)\]
Jensens 부등식에 의해가 항상 성립한다.
즉,
- $\hat p(x)$ 는 $p(x)$ 를 공평하게(unbiased) 추정하지만
- $\log \hat p(x)$ 는 오목성 때문에 항상 실제 로그 p(x)보다 작다.
이 말은 다시 말해,
샘플링을 많이 반복해서 평균을 내도
로그-우도 추정치가 실제 성능보다 높게 나오는 일(과대평가)은 절대 없다
는 뜻이다.그래서 논문에서는
“중요도 샘플링 기반의 로그-우도 추정치는
기대값 기준에서 결코 낙관적이지 않다”
라고 표현한 것이다.
그러나 하한 기준(lower bound criterion)을 사용하는 것은
진정한 로그-우도에 비해 차선(suboptimal)의 해를 얻을 수 있다.
여기서 말하는 “하한 기준(lower bound criterion)”은
VAE에서 사용하는 변분 하한(ELBO, Evidence Lower Bound) 를 의미한다.ELBO는
\[\log p(x) \ge \text{ELBO}\]와 같이 진짜 로그-우도보다 항상 낮은 값이며,
우리는 이 하한(ELBO)을 최대화함으로써 모델을 학습한다.하지만 ELBO가 진짜 로그-우도와 완전히 같지 않기 때문에,
ELBO를 최대로 만드는 해가
반드시 진짜 로그-우도를 최대로 만드는 해와 같다고는 보장할 수 없다.즉,
- 우리는 실제 목표인 $\log p(x)$ 를 직접 최적화하지 못하고
- 대신 더 쉬운 대체 목적 함수인 ELBO를 최적화하는데,
- 이 대체 함수는 본래 목표의 완전한 대체물이 아니다.
그 결과, 모델이 찾게 되는 파라미터는
정확히 최적(optimal)한 해가 아니라
진짜 로그-우도 관점에서 보면 차선(suboptimal)일 수 있다.이것이 “하한 기준을 사용하면
진짜 로그-우도에 비해 최적이 아닌 해를 얻게 된다”는 의미이다.
예를 들어, 그러한 차선의 해는
생성 과정에서 구조화되지 않은(unstructured) 상당한 양의 노이즈를 주입하여
부자연스러운 샘플을 만들 수 있다.
여기서 말하는 “차선의 해(suboptimal solution)”란
ELBO(변분 하한)를 최대화하는 과정에서
진짜 로그-우도 기준에서는 좋지 않은 파라미터가 선택되는 경우를 의미한다.VAE의 ELBO는
- 재구성 항(reconstruction term)
- KL 항(사후분포를 사전 분포에 가깝게 만드는 항)
의 두 요소로 구성되는데,
KL 항이 너무 강하게 작용하면
잠재 변수 $h$ 가 사전 분포에 과도하게 끌려가서
정보량이 부족해지는 문제가 발생한다.그 결과, 생성 단계에서
$p(x \mid h)$ 는 충분한 정보를 받지 못하여
잉여적이며 구조화되지 않은 노이즈(unstructured noise) 를
출력에 섞어 넣음으로써
데이터의 세부적인 구조나 패턴을 제대로 복원하지 못한다.이것이
“차선의 해는 생성 과정에서 불필요한 노이즈를 주입하여
부자연스러운 샘플을 만든다”
라는 문장이 의미하는 바이다.즉,
- ELBO를 맞추기 위해 잠재 공간의 표현력이 희생되고
- 디코더가 충분한 정보를 받지 못해
- 결과적으로 부드럽고 뭉개진(blurry), 혹은 노이즈가 섞인 이상한 샘플이 생성될 수 있다.
실제로는, 우리는 $p(x \mid h)$ 의 통계값—
예를 들면 기댓값이나 중앙값(median)—을 실제 샘플 대신 출력할 수 있다.
결정적 디코더(deterministic decoder)의 사용은
낮은 수준의 노이즈(low-level noise)를 제거하려는 목적에 의해 정당화될 수 있는데,
이 노이즈는 VAE 및 볼츠만 머신(Boltzmann machines)과 같은 모델에서
생성의 마지막 단계에서 자동으로 추가되기 때문이다
(숨겨진 변수 $h$ 가 주어졌을 때 관측변수는 독립적이라고 간주됨).
여기서 말하는 내용은 다음과 같다.
VAE나 볼츠만 머신 같은 생성 모델에서는
\[x = \mu(h) + \epsilon, \qquad \epsilon \sim \mathcal{N}(0, \sigma^2 I)\]
마지막 생성 단계에서 자동으로 노이즈가 섞인다.
예를 들어 VAE에서는
$p(x \mid h)$ 를 가우시안 분포로 두기 때문에
최종 출력 $x$ 는와 같은 확률적 샘플링 과정으로 만들어진다.
즉, 디코더가 아무리 잘 만들어도
마지막 단계에서 노이즈가 반드시 들어가게 된다.또한 볼츠만 머신에서도
관측변수들은 숨겨진 변수 $h$ 가 주어졌을 때
서로 독립이며,
각각을 샘플링으로 생성하므로
역시 노이즈가 포함된다.따라서 이미 생성 과정의 끝에서
노이즈가 한 번 추가되기 때문에,
디코더 자체를 확률적으로 만들 필요가 없으며
결정적(decoder) 함수로 두어도 충분하다는 의미다.즉,
디코더는 노이즈 없는 깨끗한 출력 값을 생성하고,
마지막 확률적 샘플링 단계에서 들어오는
필연적인 노이즈가 전체 모델의 불확실성을 담당하므로
결정적 디코더를 사용하는 것이 정당화된다는 뜻이다.
NICE 기준은 변분 오토인코더의 기준과 매우 유사하다.
좀 더 구체적으로 말하면,
변환과 그 역변환은 완전한 오토인코더 쌍으로 볼 수 있으므로 (Bengio, 2014),
재구성 항은 무시될 수 있는 상수이다.
NICE에서는 변환 $f$ 와 그 역변환 $f^{-1}$ 이 완전한 오토인코더 쌍(perfect auto-encoder pair)처럼 동작한다.
\[f^{-1}(f(x)) = x\]
즉,이 항상 정확히 성립한다.
변분 오토인코더(VAE)에서 재구성항은
\[\log p(x \mid h)\]와 같이 디코더가 입력을 얼마나 잘 복원하는지를 측정하는 항이다.
하지만 NICE에서는
디코더가 확률 모델이 아니라 정확한 역변환 $f^{-1}$ 자체이다.따라서
\[\hat{x} = f^{-1}(h) = f^{-1}(f(x)) = x\]이 항상 성립하므로,
재구성 오차(reconstruction error)는
\(0\) 이며,
재구성 로그-우도
\(\log p(x \mid h)\)
는 $x$ 와 무관한 상수 값이 된다.다시 말해,
NICE 구조에서는 “복원 실패”가 전혀 발생하지 않기 때문에
재구성항은 파라미터 학습에 어떤 영향도 주지 않는다.
따라서 학습 목적 함수에서 상수항이므로 제거(무시)할 수 있다.
이는 변분 기준(variational criterion)의 Kullback–Leibler 발산 항을 남기는데,
\[\log\!\big(p_H(f(x))\big)\]는 사전 분포(prior distribution)에 대한 항으로 볼 수 있으며,
이는 코드 \(h = f(x)\) 가 사전 분포에 대해 높은 우도를 가지도록 (to be likely with) 강제한다.
그리고
\[\log\left( \left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| \right)\]는 엔트로피 항으로 볼 수 있다.
우리가 다루는 기본 로그-우도 식은 다음과 같다:
\[\log\big(p_X(x)\big) = \log\!\big(p_H(f(x))\big) + \log\!\left( \left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| \right)\]이 식에서 첫 번째 항
\[\log\!\big(p_H(f(x))\big)\]은 변분 기준(variational criterion)의 사전 분포(prior distribution) 항으로 볼 수 있다.
\[h = f(x)\]
즉, 입력 $x$ 를 변환한 코드가 사전 분포 $p_H(h)$ 에서 “가능성이 높은 값”이 되도록 강제하는 역할을 한다.
(VAE에서의 KL 항이 $q(h\mid x)$ 를 $p(h)$ 쪽으로 끌어당기는 것과 같은 역할이다.)반면 두 번째 항
\[\log\!\left( \left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| \right)\]은 엔트로피(부피 변화) 항으로 해석된다.
\[\left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right|\]
여기서은 “$x$ 주변의 아주 작은 부피 요소가
변환 $f$ 를 거친 뒤 $h$ 공간에서 얼마나 커지거나(팽창) 작아지는지(수축)” 를 나타내는 값이다.
만약
\[\left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| > 1\]이면, $x$ 근처의 작은 상자(volume)가 $h$ 공간에서 팽창한 것이고,
$\log(\cdot)$ 가 양수가 되어 로그-우도에 양의 기여를 한다.반대로
\[\left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| < 1\]이면, 그 부피가 수축한 것이고,
로그 값이 음수가 되어 로그-우도에 음의 기여를 한다.따라서 이 야코비안 항은
변환 $f$ 가 데이터 분포를 잠재 공간으로 보낼 때
그 분포의 “퍼짐 정도(엔트로피)”를
얼마나 키우거나 줄이는지를 직접 반영한다.결론적으로, 전체 식은
사전 분포에 맞도록 코드 $h$ 를 유도하는 항
\[\log\big(p_H(f(x))\big)\]변환의 지역적 부피 변화(엔트로피 역할)를 나타내는 항
\[\log\left( \left| \det\!\left( \frac{\partial f(x)}{\partial x} \right) \right| \right)\]이렇게 두 부분으로 구성되어 있다.
이는 변분 기준(variational criterion)에서 등장하는 KL 발산의 구조와 직접적으로 대응된다.
변분 추정에서 KL 발산
\[\mathrm{KL}(q(z\mid x)\,\|\,p(z)) = -\mathbb{E}_{q}\big[\log p(z)\big] \;+\; \mathbb{E}_{q}\big[\log q(z\mid x)\big]\]는
1) 사전 항 $-\log p(z)$
2) 엔트로피(또는 volume) 항 $\log q(z\mid x)$두 가지로 구성되며,
NICE의 우도 식도
\[\log(p_H(f(x))) \quad+\quad \log\left|\det\left(\frac{\partial f}{\partial x}\right)\right|\]로 동일한 두 성분(사전 항 + 엔트로피/부피 항)을 명시적으로 포함한다.
따라서 NICE의 로그-우도 표현은
변분 기준의 KL 구조를 식 단위로 직접 보여주는 형태라고 볼 수 있다.
이 엔트로피 항은 데이터 주변(인코더에 대해)의 지역적 부피 확장을 반영하며,
이는 디코더 $f^{-1}$ 에서는 부피 수축으로 변환된다.
비슷한 방식으로, 변분 기준의 엔트로피 항은
근사 사후분포가 부피를 차지하도록 장려하며,
이 역시 디코더에서의 수축으로 변환된다.
핵심 아이디어는 다음과 같다:
어떤 변환이 공간을 확장하면(invertible mapping에서)
그 역변환은 정확히 그만큼 공간을 축소해야 한다.NICE에서는 $f$ 가 입력 공간 $x$ 를 잠재공간 $h = f(x)$ 로 보낼 때
야코비안이 나타내는 “부피 변화”가 발생한다.
- $f$ 가 데이터 근처에서 부피를 확장하면
역변환 $f^{-1}$ 은 같은 영역을 축소해야 한다.- 이는 완전한 전단사(bijection)이기 때문에 필연적이다.
변분 오토인코더(VAE)에서도 이 구조가 형식적으로 동일한 역할을 한다.
VAE의 인코더 $q(h \mid x)$ 는 데이터 주변에서 ‘부피를 확보’해야 한다.
VAE의 엔트로피(entropy) 항은
$q(h \mid x)$ 가 어느 정도 분산을 갖도록 장려한다.
즉, $h$ 공간에서 “어느 정도 넓은 영역(부피)”을 차지하도록 만드는 역할을 한다.이것은 NICE에서 $f$ 가 데이터 주변에서 부피를 확장하는 역할과 유사하다.
하지만 디코더 $p(x \mid h)$ 는 그 넓은 영역의 $h$ 를
다시 좁은 영역의 $x$ 로 ‘압축’해야 한다.
$h$ 의 작은 변화가 $x$ 에 큰 영향을 주지 않도록,
즉 $p(x \mid h)$ 가 안정적으로 $x$ 를 재구성하도록 만들기 위해
디코더는 자연스럽게 “수축(mapping contraction)”을 수행하게 된다.이는 NICE에서 $f^{-1}$ 이 부피를 축소하는 것과 일대일로 대응된다.
즉,
- 인코더는 부피 확장(또는 엔트로피 증가)
- 디코더는 부피 축소(또는 정보 압축)
를 수행하는 구조가
NICE와 VAE 모두에서 자연스럽게 나타난다.NICE에서는 이 과정이 역함수의 야코비안을 통해 직접적으로 수학적으로 표현되고,
VAE에서는 KL 항(인코더 엔트로피 증가) + 디코더 조건부 분포(부피 축소)
로 간접적으로 나타난다는 차이가 있을 뿐,
인코더–디코더의 공간 변화 구조는 본질적으로 유사하다.
완전한 재구성이 가능하다는 것은
상위 수준인 $h$ 에 존재하는 노이즈 역시
우리가 직접 모델링해야 한다는 결과를 낳는다.
반면, 다른 유향 그래프 모델에서는
이 노이즈가 일반적으로 조건부 분포 $p(x \mid h)$ 에 의해 처리된다.
여기서 말하는 핵심은 다음과 같다.
NICE에서는 변환 $f$ 와 역변환 $f^{-1}$ 이 완전한 오토인코더 쌍이므로
\[f^{-1}(f(x)) = x\]가 항상 정확히 성립한다.
즉, 디코더가 확률적이지 않고 완전히 결정적(deterministic) 이다.이러한 구조에서는
$x$ 를 생성할 때 어떤 랜덤 노이즈도 디코더에서 추가되지 않는다.
따라서 “생성 과정에서 필요한 모든 노이즈”는
오직 최상위 레벨 잠재 변수 $h$ 에서만 모델링되어야 한다.
즉,
- $h$ 가 랜덤(확률적)이어야 하고
- $h$ 안에 데이터의 모든 불확실성을 담아두어야 한다는 뜻이다.
반면, VAE나 다른 유향 그래프 모델에서는 구조가 다르다.
\[p(x \mid h)\]
이들 모델은 잠재 변수 $h$ 를 뽑은 뒤
조건부 분포에서 $x$ 를 샘플링한다.
이 조건부 분포 $p(x \mid h)$ 자체가 가우시안 등 확률적 형태를 가지므로
생성 과정에서 필요한 노이즈는 디코더 쪽에서 자동으로 추가된다.즉,
- NICE: 노이즈는 전부 $h$ 에서만 모델링됨 (디코더는 완전 결정적)
- 다른 그래프 모델(VAE 등): 노이즈는 주로 $p(x \mid h)$ 에서 생성 과정의 마지막 단계에서 추가됨
따라서 NICE에서는
“완전 재구성(perfect reconstruction)” 구조 때문에
노이즈까지도 전부 최상위 잠재 변수 $h$ 에 포함해서 모델링해야 한다”는 의미가 되는 것이다.
우리는 또한, 변분 기준을 재매개변수화 기법과 결합함으로써
(Kingma and Welling, 2014)가 사실상
보조 노이즈 변수인 $\epsilon$ 을 포함한 쌍 $(x, \epsilon)$ 의
결합 로그우도(joint log-likelihood)를 최대화하고 있음을 관찰한다.
이는 두 개의 아핀 결합 층을 갖는 NICE 모델과
가우시안 사전 분포(prior)를 사용하는 경우에 해당하며,
자세한 내용은 부록 C를 보라.
여기서 말하는 핵심은
VAE(변분 오토인코더)의 ELBO(변분 하한) 가
재매개변수화 기법을 사용하면
사실상 NICE와 같은 흐름 기반 모델(flow-based model)의
로그-우도를 최대화하는 형태로 해석될 수 있다는 점이다.특히,
VAE의 잠재 변수 샘플링
\[h = \mu(x) + \sigma(x) \odot \epsilon, \qquad \epsilon \sim \mathcal{N}(0, I)\]은
흐름의 입력을 잡음 $\epsilon$과 결합시켜
$h=f(x)$ 의 형태로 만들기 때문에
흐름 모델의 결합 변환(coupling transform)처럼 동작한다.두 개의 아핀 결합층을 가진 NICE는
잠재 변수와 노이즈 변수를 묶어 $(x, \epsilon)$
쌍의 로그-우도를 최대화한다.문장이 말하고자 하는 바는
VAE의 ELBO 최적화가 사실상
NICE와 같은 모델의 확률적 변환을 학습하는 것과
거의 동일한 목적을 가지게 된다는 점이다.즉,
“VAE + 재매개변수화 기법”의 수학적 구조가
“NICE + 아핀 결합층 + 가우시안 사전 분포”의 구조와
본질적으로 등가적임을 관찰했다는 뜻이다.
확률 밀도 함수에 대한 변수변환 공식(change of variable formula)은
역변환 샘플링(inverse transform sampling)에서 두드러지게 사용되며
(이는 여기서 샘플링에 사용된 절차와 사실상 동일하다).
독립 성분 분석(ICA) (Hyvärinen and Oja, 2000)은,
보다 구체적으로는 그 최대우도(maximum likelihood) 공식화(formulation)는,
데이터의 직교 변환(orthogonal transformation)을 학습하며,
매개변수 업데이트 사이에
비용이 많이 드는 직교화(orthogonalization) 절차를 요구한다.
ICA(Independent Component Analysis) 는
관측된 여러 신호가
서로 독립적인 숨겨진 원신호들의
선형 혼합(linear mixture) 으로 구성되어 있다고 가정하고,
그 독립적인 원성분들을 분리해내는 기법이다.예를 들어,
여러 개의 마이크가 서로 다른 위치에서 녹음한
여러 사람의 목소리(혼합 신호)로부터
각 사람의 목소리(독립 성분)를 분리해내는 문제에 쓰인다.ICA의 최대우도(maximum likelihood) 공식화에서는
이러한 독립 성분들을 찾기 위해
직교 행렬(orthogonal matrix) 에 가까운 변환을 학습하게 된다.하지만 이 과정에서는
변환 행렬을 반복적으로 “직교화(orthogonalization)” 해야 하며,
이는 SVD, QR 분해 등
계산 비용이 매우 큰 선형대수 연산을 포함한다.따라서 ICA는 이론적으로는 명확하고 강력하지만,
학습 중에 발생하는 고비용 직교화 단계 때문에
실질적으로 계산이 많이 들고
대규모 학습에 비효율적이라는 한계가 있다.
(Bengio, 1991)에서는 더 풍부한 변환들의 계열을 학습하는 것이 제안되었으나,
제안된 변환들의 계열인 신경망은
일반적으로 추론과 최적화를 실용적으로 만들기 위한
구조를 결여(lack)하고 있다.
(Chen and Gopinath, 2000)는
계층적 변환(layered transformation)을
가우시안 분포로 학습하지만,
탐욕적 방식(greedy fashion)으로 수행되며
실용적으로 다룰 수 있는(tracable)
샘플링 절차를 제공하는 데 실패한다.
(Rippel and Adams, 2013)은 이러한 변환들을 학습하는 아이디어를 재도입하지만,
전단사(bijectivity) 제약의 부재로 인해
로그-우도 최대화의 대리(proxy)로서
정규화된 오토인코더 설정으로 강제된다.
(Rippel and Adams, 2013)은
비전단사(non-bijective) 신경망 변환을 이용해
데이터를 더 단순한 잠재 분포로 매핑하려는 접근을 제안했는데,
즉 “일반적인 신경망으로도 복잡한 분포를 단순한 분포로 변환하는 것을 배울 수 있다”는
아이디어를 다시 도입하였다.하지만 이 접근은 변환이 전단사(bijective)라는 보장이 없기 때문에,
정확한 밀도 계산(즉 로그-우도 계산)과
정규화(normalizing) 기반 학습을 수행할 수 없다.그래서 논문에서는
전단사 제약을 만족하지 못하는 이 구조가
로그-우도 최대화의 대리(proxy) 로서
정규화된 오토인코더(regularized auto-encoder) 설정으로
강제로 해석된다고 설명한다.여기서 핵심은 전단사(bijective) 조건이 없으면
역변환이 항상 존재하지 않기 때문에
정상적인 의미의 로그-우도(log-likelihood)를 직접 최대화할 수 없다는 점이다.로그-우도 최대화가 가능하려면
데이터에서 잠재 공간으로 가는 변환이
1:1 대응이어야 하고(전단사),
야코비안 행렬식(det Jacobian)이 계산 가능해야 한다.그러나 (Rippel & Adams, 2013)의 접근은
변환이 전단사라는 보장이 없으므로
입력을 잠재 변수로 정확히 되돌릴 수 없고,
확률 밀도도 계산할 수 없다.따라서 논문에서는
“진짜 로그-우도”를 사용할 수 없어서
대신 정규화된 오토인코더 형태의
대리 목적함수(proxy objective) 를 사용해
간접적으로 학습할 수밖에 없다고 지적한다.즉,
- 전단사가 아니므로 normalizing flow처럼
정확한 확률 계산 자체가 불가능- 그래서 로그-우도 최대화를 사용할 수 없고
autoencoder-류 손실을 흉내 낸 대리 손실로 학습함- 이 때문에 접근 전체가
확률 모델링 관점에서는 근본적 한계를 가진다는 의미이다.
로그-우도의 더욱 원칙적인(principled) 대리(proxy)인
변분 하한(variational lower bound)은
비선형 독립 성분 분석(nonlinear independent components analysis)
(Hyvärinen and Pajunen, 1999)에서
앙상블 학습(ensemble learning)
(Roberts and Everson, 2001; Lappalainen et al., 2000)을 통해
더 성공적으로 사용되었으며,
(Helmholtz machine의 한 종류를 사용하는)
(Kingma and Welling, 2014; Rezende et al., 2014)에서도
사용되었다 (Dayan et al., 1995).
생성적 적대 신경망(GAN) (Goodfellow et al., 2014) 또한
단순한(예: 팩토리얼) 분포를
데이터 분포로 변환하는 생성 모델을 학습하지만,
반대 방향으로 가는 인코더를 요구하지 않는다.
GAN은, GAN 샘플과 실제 데이터를 구분하는
보조적인 이차 deep 네트워크를 학습함으로써
추론의 어려움을 우회한다(sidesteps).
이 분류기(classifier) 네트워크는
GAN 생성 모델에 대한 학습 신호(training signal)를 제공하여,
그 출력이 실제 훈련 데이터와
구분하기 어렵게 만드는 방법을 알려준다.
변분 오토인코더와 마찬가지로,
NICE 모델은 추론(inference)의 어려움을 피하기 위해
인코더를 사용하지만, 그 인코딩은 결정적(deterministic)이다.
로그-우도(log-likelihood)는 계산 가능하며,
학습 절차는 (데이터를 양자화하는 작업을 제외하면)
어떠한 샘플링도 요구하지 않는다.
NICE에서 계산 가능한(tractable) 특성을 확보하기 위해 사용되는
이 삼각 구조(triangular structure)는,
또 다른 계열의 계산 가능한(tractable) 밀도 모델인
신경 자기회귀 네트워크(neural autoregressive networks)
(Bengio and Bengio, 2000)에도 존재한다.
그리고 그 중 최근의 성공적인 예로는
신경 자기회귀 밀도 추정기(neural autoregressive density estimator, NADE)
(Larochelle and Murray, 2011)이 있다.
실제로, NADE 유향 그래프 모델에서의
인접 행렬(adjacency matrix)은 엄격하게 삼각형(triangular)이다.
그러나 요소별(element-by-element) 자기회귀 방식은
조상 샘플링(ancestral sampling) 절차를 계산적으로 매우 비싸게 만들고,
이미지 데이터와 같은 고차원 데이터의 생성 작업에서는
병렬 처리가 불가능하게 만든다.
하나의 결합 층(coupling layer)을 사용하는 NICE 모델은
두 개의 블록을 가진 NADE의 블록 버전으로 볼 수 있다.
NADE는 데이터를 한 요소씩 순차적으로 생성하는
자기회귀 구조를 갖는다.
예를 들어
$x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow \cdots$
와 같이 한 항목씩 조건부 확률을 모델링한다.반면 NICE의 결합층(coupling layer)은
입력을 두 부분으로 나누어
- 한쪽 블록은 그대로 복사하고
- 다른 쪽 블록은 첫 블록을 조건으로 변환
하는 방식으로 작동한다.따라서 한 결합층을 사용한 NICE는
NADE처럼 “한 부분을 다른 부분의 조건으로 변환한다”는 구조를 가지지만,
그 단위가 단일 변수(single variable)가 아니라
두 개의 큰 블록(blocks) 로 묶여 있다는 점에서
“블록 버전 NADE”로 해석될 수 있다.즉,
- NADE는 변수 단위(variable-wise) 자기회귀
- NICE 결합층은 블록 단위(block-wise) 자기회귀
로 볼 수 있으며,
NICE는 NADE의 더 큰 단위(block-wise) 구조적 변형으로 이해할 수 있다는 의미이다.
5 실험 (Experiments)
5.1 로그-우도(log-likelihood)와 생성(generation)
우리는 NICE를
MNIST(LeCun and Cortes, 1998),
Toronto Face Dataset(TFD)2(Susskind et al., 2010),
Street View House Numbers(SVHN)(Netzer et al., 2011),
그리고 CIFAR-10(Krizhevsky, 2010)에 대해 학습한다.
2우리는 이 데이터셋에 대해 라벨이 없는(unlabeled) 데이터로 학습한다.
(Uria et al., 2013)에서 규정한 바와 같이,
우리는 데이터의 비양자화(dequantized) 버전을 사용한다.
즉, 데이터에 $1/256$ 의 균일 노이즈(uniform noise)를 추가하고
비양자화 이후 데이터를 $[0, 1]^D$ 범위로 재스케일한다.
CIFAR-10의 경우에는
$1/128$ 의 균일 노이즈를 추가한 뒤
데이터를 $[-1, 1]^D$ 범위로 재스케일한다.
비양자화(dequantization)는
원래 정수 형태(예: 0~255)로 양자화된 픽셀 값을
연속적인 실수 공간으로 확장하기 위한 과정이다.이미지 데이터는 보통 8비트 정수로 저장되므로
본질적으로 이산적(discrete)이다.
하지만 NICE나 VAE처럼 연속 확률 밀도 함수를 다루는 모델은
이산 데이터에 직접 로그-우도를 정의할 수 없다.그래서 각 픽셀에 작은 균일 노이즈(예: $1/256$, $1/128$)를 더해
원래의 정수 격자(grid)를 부드럽게 풀어주고,
데이터를 $[0,1]^D$ 또는 $[-1,1]^D$ 범위로 재스케일하여
연속 확률 모델링이 가능하도록 변환하는 것이다.요약하면, 비양자화는
“픽셀을 연속값으로 바꿔서
모델이 제대로 된 확률 밀도 함수를 학습할 수 있게 하는 과정”이라고 이해할 수 있다.
우리가 사용하는 아키텍처는
지수적으로 매개변수화된(diagonally positive scaling parametrized exponentially)
대각 양의 스케일링 (diagonal positive scaling) $ \exp(s) $ 을 마지막 단계에 두고,
네 개의 결합 층(coupling layers)을 쌓은(stack) 구조이다.
여기서 말하는 “대각 양의 스케일링(diagonal positive scaling) $\exp(s)$” 은
마지막 단계에서 출력 벡터의 각 차원마다
양수 스케일 값만 적용되도록 강제하는 스케일링 변환을 의미한다.일반적인 스케일링 파라미터를 그대로 쓰면
음수가 될 수도 있고 0에 가까워질 수도 있어
역변환 시 안정성 문제가 생긴다.이를 방지하기 위해 스케일 파라미터 $s$ 를 직접 사용하지 않고
$ \exp(s) $ 형태로 변환하여 항상 양수 스케일이 되도록 보장하는 것이다.또한 스케일링 행렬이 대각(diagonal) 형태이므로
각 차원은 서로 영향을 주지 않고 독립적으로 스케일된다.마지막 단계에 이 스케일링을 두는 이유는
이전의 결합 층(coupling layers)들은 보통
Jacobian 행렬식이 1인 구조(additive coupling)를 사용해
부피 변화가 없기 때문에,
최종적으로 전체 변환의 부피(야코비안)를 제어하려면
마지막에 별도의 스케일링 층이 필요하기 때문이다.요약하면,
- $\exp(s)$ 덕분에 스케일은 항상 양수
- 대각 형태라 계산이 단순
- 마지막 단계에서 전체 변환의 부피 조절 역할
이 세 가지를 만족하도록 설계된 구조라는 의미이다.
그리고 TFD에는 근사적인 백색화(approximate whitening)를,
SVHN과 CIFAR-10에는 정확한 ZCA를 사용한다.
“TFD에는 근사적인 백색화(approximate whitening)를 사용하고,
SVHN과 CIFAR-10에는 정확한 ZCA를 사용한다”는 말은
데이터 전처리 단계에서 서로 다른 종류의 whitening 기법을 적용한다는 의미이다.whitening은 입력 데이터의 공분산을 정규화하여
상관성을 제거하고 분산을 1로 맞추는 과정이다.
이는 흐름 모델(flow model)에서 특히 중요하다.이유는 다음과 같다:
1) NICE의 첫 번째 결합층(coupling layer)은 입력을 두 부분으로 나누는데,
whitening이 제대로 되어 있지 않으면
어떤 부분은 정보가 과하게 몰리고
어떤 부분은 거의 변화가 없어
모델 학습이 어려워질 수 있다.2) TFD는 데이터 크기나 샘플 수가 상대적으로 제한적이기 때문에
공분산을 정확하게 추정하기 어렵다.
그래서 “근사적인(approximate)” whitening 방법을 사용해
무리하게 전체 공분산 역행렬을 계산하지 않고
안정적인 변환만 수행한다.3) 반면 SVHN과 CIFAR-10은
데이터가 매우 크고 다양하므로 공분산 추정이 안정적이다.
따라서 더 정확하고 계산 비용이 큰
ZCA(Zero-phase Component Analysis) whitening을 적용할 수 있다.따라서 이 문장은,
데이터셋마다 특성(규모, 노이즈, 구조)에 따라
적절한 수준의 whitening을 선택적으로 적용한다는 의미이다.
우리는 입력 공간(input space)을
홀수(odd) 성분 $ I_1 $ 과
짝수(even) 성분 $ I_2 $ 로 분할(partition)한다.
그 결과 식은 다음과 같다:
\[\begin{aligned} h^{(1)}_{I_1} &= x_{I_1} \\ h^{(1)}_{I_2} &= x_{I_2} + m^{(1)}(x_{I_1}) \end{aligned}\] \[\begin{aligned} h^{(2)}_{I_2} &= h^{(1)}_{I_2} \\ h^{(2)}_{I_1} &= h^{(1)}_{I_1} + m^{(2)}(x_{I_2}) \end{aligned}\] \[\begin{aligned} h^{(3)}_{I_1} &= h^{(2)}_{I_1} \\ h^{(3)}_{I_2} &= h^{(2)}_{I_2} + m^{(3)}(x_{I_1}) \end{aligned}\] \[\begin{aligned} h^{(4)}_{I_2} &= h^{(3)}_{I_2} \\ h^{(4)}_{I_1} &= h^{(3)}_{I_1} + m^{(4)}(x_{I_2}) \end{aligned}\] \[h = \exp(s) \odot h^{(4)}\]결합(coupling) 계층에 사용되는 결합(coupling) 함수 $m^{(1)}$, $m^{(2)}$, $m^{(3)}$, $m^{(4)}$ 는
모두 ReLU 기반의 심층 신경망 (deep rectified networks) 이며,
출력층은 선형(linear)으로 구성되어 있다.
각 결합 함수에는 동일한 네트워크 구조를 사용한다.
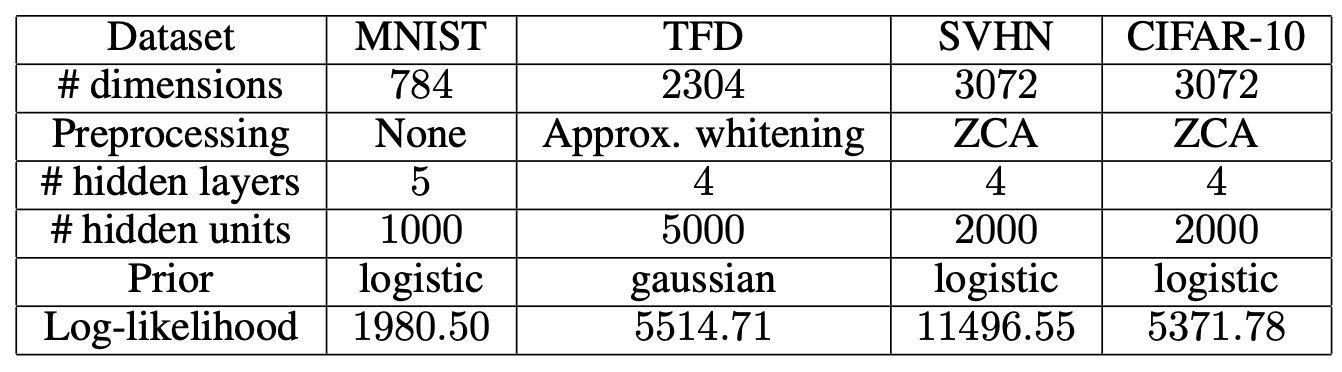
MNIST에는 1000 유닛을 가진 5개의 은닉층을,
TFD에는 5000 유닛의 4개 은닉층을,
SVHN과 CIFAR-10에는 2000 유닛의 4개 은닉층을 사용한다.
MNIST, SVHN, CIFAR-10에는
표준 로지스틱 분포가 prior로 사용된다.
TFD에는
표준 정규분포가 prior로 사용된다.
모델들은
로그-우도 $\log(p_H(h)) + \sum_{i=1}^{D} s_i$ 를
최대화하도록 AdaM(Kingma and Ba, 2014)으로 학습된다.
학습률은 $10^{-3}$,
모멘텀은 $0.9$,
$\beta_2 = 0.01$,
$\lambda = 1$,
$\epsilon = 10^{-4}$ 를 사용한다.
1500 에폭 후
검증 로그-우도(validation log-likelihood)를 기준으로
최적의 모델을 선택한다.
우리는 MNIST에서 1980.50,
TFD에서 5514.71,
SVHN에서 11496.55,
CIFAR-10에서 5371.78의
테스트 로그-우도를 얻었다.
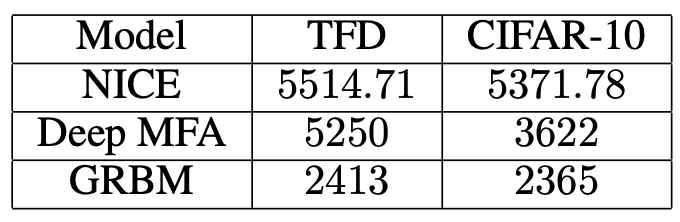
이는 로그-우도 관점에서 우리가 알고 있는 최상의 결과와 비교된다.
즉, TFD에서 5250, CIFAR-10에서 3622의 결과가
심층 요인분석기 혼합(deep mixtures of factor analysers)으로부터 보고되었다
(Tang et al., 2012).
(비록 여전히 하한 값이긴 하지만)
자세한 내용은 표 4(Table 4)를 보라.
연속적 MNIST에 대한 생성 모델들은
일반적으로 파르젠 윈도우 추정(Parzen window estimation)으로 평가되므로
공정한 비교는 불가능하다.
연속적 MNIST(continuous MNIST)는 픽셀 값을 이산값이 아닌 연속값으로 다루기 때문에
모델의 로그-우도를 직접적으로 계산하거나 공정하게 비교하기 어렵다.
그래서 과거 연구들은 파르젠 윈도우 추정(Parzen window estimation)을 사용해
우도를 근사적으로 계산했으나, 이 방법은
모델마다 최적의 커널 폭(sigma)이 달라지고
샘플 수에 따라 성능이 민감하게 변하는 등
비교 기준으로서 신뢰도가 낮다는 문제가 있다.따라서 서로 다른 생성 모델이 연속적 MNIST에서 보고한 수치를
동일한 기준으로 공정하게 비교하는 것은 불가능하다는 의미다.[파르젠 윈도우 추정(Parzen window estimation)이란?]
파르젠 윈도우는 ‘커널 밀도 추정(Kernel Density Estimation)’의 한 형태로,
데이터 포인트 하나하나에 폭이 정해진 커널(보통 가우시안)을 얹어
전체 확률밀도함수(PDF)를 근사하는 방법이다.즉, 여러 생성 모델이 만든 샘플을 모아
각 샘플 주변에 가우시안 커널을 놓고
이를 모두 더한 뒤 평균을 냄으로써
“해당 모델이 만든 데이터의 분포가 실제 데이터에 얼마나 가까운지”
간접적으로 평가하는 방식이다.하지만 커널 폭(sigma) 선택에 따라
점수가 크게 달라지며
모델 간 비교에서 일관성을 보장하기 어렵다는 단점이 있다.
학습된 모델이 생성한 샘플들은
그림 5(Fig. 5)에 제시되어 있다.
그림 3: 아키텍처와 결과들.
‘# hidden units’ 는 각 은닉층(hidden layer)당 유닛(unit)의 수를 의미한다.
그림 4: TFD와 CIFAR-10에 대한 로그-우도 결과들.
Deep MFA 수치는 (Tang et al., 2012)에서 얻어진 최상의 결과들에 해당하지만,
실제로는 변분 하한(variational lower bound)이다.
그림 5: 학습된 NICE 모델로부터 얻은 편향 없는 샘플들.
우리는 $h \sim p_H(h)$ 를 샘플링하고,
$x = f^{-1}(h)$ 를 출력한다.
5.2 인페인팅(Inpainting)
여기에서는 학습된 생성 모델들을 이용하여 인페인팅을 구현하기 위한
단순한 반복적 절차를 고려한다.
인페인팅을 위해 우리는 관측된 차원들 $x_O$ 을 해당 값에 고정(clamp)하고,
숨겨진 차원들 $X_H$ 에 대해 로그-우도를 최대화한다.
이는 투영된 그래디언트 상승(projected gradient ascent)을 사용하여 수행되며
(입력을 원래 값의 구간 내에 유지하기 위해),
스텝 크기 $\alpha_i = \frac{10}{100 + i}$ 로 가우시안 잡음과 함께 진행된다.
여기서 $i$ 는 반복(iteration)이다.
다음의 확률적 그래디언트 업데이트를 따른다:
\[x_{H,i+1} = x_{H,i} + \alpha_i \left( \frac{\partial \log(p_X((x_O, x_{H,i})))}{\partial x_{H,i}} + \epsilon \right)\] \[\epsilon \sim \mathcal{N}(0, I)\]여기서 $x_{H,i}$ 는 반복 $i$ 에서의 숨겨진 차원 값이다.
이 업데이트 식은 숨겨진 차원 $x_{H,i}$ 를
“로그-우도를 증가시키는 방향”으로 조금씩 이동시키는 과정이다.먼저,
\[\frac{\partial \log(p_X((x_O, x_{H,i})))}{\partial x_{H,i}}\]항은
관측된 부분 $x_O$ 를 고정한 상태에서
숨겨진 부분 $x_{H,i}$ 에 대해
“현재 모델이 얼마나 그럴듯한지”를 나타내는
로그-우도의 기울기(gradient)이다.즉, 이 기울기는
$x_{H,i}$ 를 어떻게 바꿔야
모델이 해당 데이터를 더 높은 확률로 설명하게 되는지를 알려준다.하지만 단순한 기울기 상승만 사용하면
지역 최적(local optimum)에 갇힐 수 있으므로,
추가적으로 $\epsilon \sim \mathcal{N}(0, I)$ 와 같은
가우시안 잡음을 더해 탐색성을 높인다.$\alpha_i = \frac{10}{100+i}$ 는
반복이 진행될수록 스텝 크기를 점점 줄이는 계획으로,
초기에는 크게 움직여 다양한 값을 탐색하고
후반에는 안정적으로 수렴시키는 역할을 한다.결과적으로 이 식은
“로그-우도 상승 + 무작위 탐색”을 결합한
확률적 그래디언트 업데이트이며,
숨겨진 차원 $x_{H,i}$ 를 점진적으로 복원(inpainting)하도록 유도한다.
결과는 MNIST 테스트 예시들에 대해 그림 6(Fig. 6)에 제시되어 있다.
비록 모델이 이 작업을 위해 훈련된 것은 아니지만,
이 인페인팅 절차는 비교적 타당한 정성적 성능을 보이는 것으로 보인다.
그러나 가끔씩 잘못된(spurious) 모드가 나타나는 것에 유의하라.
그림 6: MNIST에서의 인페인팅.
우리는 위의 가운데 그림에서 각 줄마다 마스킹된 이미지 부분의 유형을
위에서 아래로 다음과 같이 나열한다:
상단 행, 하단 행, 홀수 픽셀, 짝수 픽셀, 왼쪽 부분, 오른쪽 부분,
가운데 수직 방향, 가운데 수평 방향, 무작위 75%, 무작위 90%.
우리는 마스킹되지 않은 픽셀들은
그들의 실제 값(ground truth value)에 고정(clamp)하고,
마스킹된 픽셀들의 상태를
우도(likelihood)에 대한 투영된 그래디언트 상승(projected gradient ascent)을 통해 추론한다.
가운데 마스크의 경우,
숫자(digit)에 대한 정보가 거의 존재하지 않는다는 점에 유의하라.
6 결론 (Conclusion)
이 연구에서 우리는 학습 데이터를
그 분포가 분리되는(factorized) 공간으로 매핑하는
높이 비선형적인 전단사 변환(bijective transformation)을
학습하기 위한 새로운 유연한 아키텍처를 제시하였고,
이를 직접적으로 로그-우도를 최대화함으로써 달성하기 위한
프레임워크를 제시하였다.
NICE 모델은 효율적인 편향 없는 조상 샘플링(ancestral sampling)을 제공하며,
로그-우도 측면에서 경쟁력 있는 결과를 달성한다.
또한 우리의 모델 아키텍처는
그 장점을 활용할 수 있는 다른 귀납적(inductive) 원리로도
훈련될 수 있음을 유의하라.
예를 들어, toroidal subspace analysis(TSA) (Cohen and Welling, 2014)와 같은 방법이 있다.
저자들은 NICE 구조가 단순히 “로그-우도 최대화”라는 학습 방식에만 국한되지 않고,
다른 inductive principle(귀납적 학습 원리)을 적용해서도
훈련될 수 있다고 말하고 있다.즉, NICE의 구조 자체가 가지는 수학적/표현적 장점은
다른 목표 함수나 다른 학습 기준을 적용할 때도 여전히 유효하다는 뜻이다.여기서 예로 든 toroidal subspace analysis(TSA)는
데이터가 토러스(torus, 도넛 형태의 위상 공간) 같은
주기적 구조를 가진 잠재 공간(subspace)에 놓여 있다고 가정하는
대안적 학습 원리이다.따라서 NICE는 단지 “정확한 우도 계산이 가능한 생성 모델”일 뿐만 아니라,
상황에 따라 다른 귀납적 편향(inductive bias)을 부여하는
다양한 학습 방법에도 적용 가능한 유연한 구조라는 점을 강조하는 문장이다.
우리는 또한 변분 오토인코더(variational auto-encoder)와의 연결을 간단히 만들었다.
또한 NICE는 해당 모델들에서 더 복잡한 형태의
근사 사후분포(approximate posterior distribution) 또는
더 풍부한 사전분포(prior) 계열을 가능하게 함으로써
더 강력한 근사 추론을 가능하게 한다는 점을 지적한다.
감사의 말(Acknowledgements)
우리는 Yann Dauphin, Vincent Dumoulin, Aaron Courville, Kyle Kastner,
Dustin Webb, Li Yao, 그리고 Aaron Van den Oord에게
토론과 피드백에 대해 감사를 표한다.
Vincent Dumoulin은 시각화를 위한 코드를 제공하였다.
우리는 Theano 개발자들
(Bergstra et al., 2011; Bastien et al., 2012)과
Pylearn2 (Goodfellow et al., 2013) 개발자들에게도
감사를 표한다.
또한 Compute Canada와 Calcul Québec이 제공한
컴퓨팅 자원에 감사드리며,
NSERC, CIFAR, Canada Research Chairs가 제공한
연구 자금 지원에도 감사드린다.
참고문헌 (References)
Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard, N., and Bengio, Y. (2012). Theano: new features and speed improvements. Deep Learning and Unsupervised Feature Learning NIPS 2012 Workshop.
Bengio, Y. (1991). Artificial Neural Networks and their Application to Sequence Recognition. PhD thesis, McGill University, (Computer Science), Montreal, Canada.
Bengio, Y. (2009). Learning deep architectures for AI. Now Publishers.
Bengio, Y. (2014). How auto-encoders could provide credit assignment in deep networks via target propagation. Technical report, arXiv:1407.7906.
Bengio, Y. and Bengio, S. (2000). Modeling high-dimensional discrete data with multi-layer neural networks. In Solla, S., Leen, T., and Müller, K.-R., editors, Advances in Neural Information Processing Systems 12 (NIPS’99), pages 400–406. MIT Press.
Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013). Better mixing via deep representations. In Proceedings of the 30th International Conference on Machine Learning (ICML’13). ACM.
Bergstra, J., Bastien, F., Breuleux, O., Lamblin, P., Pascanu, R., Delalleau, O., Desjardins, G., Warde-Farley, D., Goodfellow, I. J., Bergeron, A., and Bengio, Y. (2011). Theano: Deep learning on gpus with python. In Big Learn workshop, NIPS’11.
Chen, S. S. and Gopinath, R. A. (2000). Gaussianization.
Cohen, T. and Welling, M. (2014). Learning the irreducible representations of commutative lie groups. arXiv:1402.4437.
Dayan, P., Hinton, G. E., Neal, R., and Zemel, R. (1995). The Helmholtz machine. Neural Computation, 7:889–904.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014). Generative adversarial networks. Technical Report arXiv:1406.2661, arxiv.
Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F., and Bengio, Y. (2013). Pylearn2: a machine learning research library. arXiv preprint arXiv:1308.4214.
Gregor, K., Danihelka, I., Mnih, A., Blundell, C., and Wierstra, D. (2014). Deep autoregressive networks. In International Conference on Machine Learning (ICML’2014).
Grosse, R., Maddison, C., and Salakhutdinov, R. (2013). Annealing between distributions by averaging moments. In ICML’2013.
Hyvärinen, A. and Oja, E. (2000). Independent component analysis: algorithms and applications. Neural networks, 13(4):411–430.
Hyvärinen, A. and Pajunen, P. (1999). Nonlinear independent component analysis: Existence and uniqueness results. Neural Networks, 12(3):429–439.
Kingma, D. and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
Kingma, D. P. and Welling, M. (2014). Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (ICLR).
Krizhevsky, A. (2010). Convolutional deep belief networks on CIFAR-10. Technical report, University of Toronto. Unpublished Manuscript.
Lappalainen, H., Giannakopoulos, X., Honkela, A., and Karhunen, J. (2000). Nonlinear independent component analysis using ensemble learning: Experiments and discussion. In Proc. ICA. Citeseer.
Larochelle, H. and Murray, I. (2011). The Neural Autoregressive Distribution Estimator. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS’2011), volume 15 of JMLR: W&CP.
LeCun, Y. and Cortes, C. (1998). The mnist database of handwritten digits.
Mnih, A. and Gregor, K. (2014). Neural variational inference and learning in belief networks. In ICML’2014.
Netzer, Y., Wang, T., Coates, A., Bissacco, A., Wu, B., and Ng, A. Y. (2011). Reading digits in natural images with unsupervised feature learning. Deep Learning and Unsupervised Feature Learning Workshop, NIPS.
Ozair, S. and Bengio, Y. (2014). Deep directed generative autoencoders. Technical report, U. Montreal, arXiv:1410.0630.
Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. Technical report, arXiv:1401.4082.
Rippel, O. and Adams, R. P. (2013). High-dimensional probability estimation with deep density models. arXiv:1302.5125.
Roberts, S. and Everson, R. (2001). Independent component analysis: principles and practice. Cambridge University Press.
Salakhutdinov, R. and Hinton, G. (2009). Deep Boltzmann machines. In Proceedings of the International Conference on Artificial Intelligence and Statistics, volume 5, pages 448–455.
Salakhutdinov, R. and Murray, I. (2008). On the quantitative analysis of deep belief networks. In Cohen, W. W., McCallum, A., and Roweis, S. T., editors, Proceedings of the Twenty-fifth International Conference on Machine Learning (ICML’08), volume 25, pages 872–879. ACM.
Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
Tang, Y., Salakhutdinov, R., and Hinton, G. (2012). Deep mixtures of factor analysers. arXiv preprint arXiv:1206.4635.
Uria, B., Murray, I., and Larochelle, H. (2013). Rnade: The real-valued neural autoregressive density-estimator. In NIPS’2013.
A 추가 시각화(Further Visualizations)
A.1 매니폴드 시각화(Manifold Visualization)
학습된 매니폴드를 설명하기 위해, 우리는 잠재 공간에서
3차원 구 $S$ 의 임의의 회전 $R$ 을 취하고 이를 데이터 공간으로 변환한다.
그 결과 $f^{-1}(R(S))$ 는 그림 7(Fig 7)에 제시되어 있다.
그림 7: 잠재 공간(latent space)에서의 구(sphere).
이 그림들은 모델이 학습한 매니폴드 구조의 일부를 보여준다.
이 그림은 잠재 공간(latent space)의 특정 곡면—여기서는 3차원 구(Sphere)의 임의 회전 $R(S)$—을
데이터 공간으로 역변환한 결과 $f^{-1}(R(S))$ 를 시각화한 것이다.즉, 모델이 학습한 매니폴드 구조가 실제로 어떤 형태를 갖고 있는지를
잠재 공간에서의 구 표면을 따라 이동하면서 생성된 샘플들로 보여주는 예시이다.(a) MNIST로 학습된 모델의 경우
잠재 공간에서 구 상의 위치가 조금씩 달라지면서
숫자 ‘9’의 형태가 부드럽게 변화하는 모습을 볼 수 있다.
이는 모델이 숫자 ‘9’에 대한 매니폴드를 연속적이고 일관되게 학습했다는 것을 의미한다.(b) TFD(Toronto Face Dataset)로 학습된 모델의 경우
얼굴의 윤곽, 조명, 표정 등이 구 표면을 따라
점진적으로 변하는 모습을 볼 수 있다.
이는 모델이 얼굴 데이터의 고차원 구조를
잠재 공간의 매니폴드로 잘 포착했음을 보여준다.전체적으로, 이 그림들은
NICE 모델이 학습한 잠재 매니폴드가 연속적이며
데이터의 중요한 변화를 부드럽게 반영하고 있음을 시각적으로 증명하는 자료이다.
A.2 스펙트럼(Spectrum)
우리는 마지막 대각 스케일링 계층을 조사하였고
그 계수들 \((S_{dd})_{d \leq D}\) 를 살펴보았다.
사전(prior) 분포와 대각 스케일링 계층을 함께 고려하면
$\sigma_d = S_{dd}^{-1}$ 는 각 독립 성분의 스케일 파라미터로 간주될 수 있다.
왜 $\sigma_d$ 가 $S_{dd}^{-1}$ 이 되는가?
NICE 모델의 마지막 층은 대각 스케일링 계층이며, 출력에 대해 다음 변환을 적용한다:
\[h_d = S_{dd} \, z_d\]여기서
- $z_d$ : 스케일링 계층의 입력
- $h_d$ : 스케일링 후의 출력
- $S_{dd}$ : d번째 축의 스케일 계수
모델은 최종 출력 $h$ 가 $p_H(h) = \mathcal{N}(0, I)$ 와 같은 표준 분포를 따른다고 가정한다.
(1) 역변환 관점
\[z_d = S_{dd}^{-1} h_d\]
스케일링을 역으로 적용하면:따라서 $z_d$ 는 스케일 계수의 역수만큼 조정된다.
(2) 확률밀도 관점
\[h_d \sim \mathcal{N}(0, 1)\]
만약 $h_d$ 가 표준 정규분포를 따른다면:역변환을 대입하면:
\[z_d = S_{dd}^{-1} h_d \sim \mathcal{N}(0, S_{dd}^{-2})\]즉, $z_d$ 의 분산은
\[\text{Var}(z_d) = S_{dd}^{-2}\]이고, 표준편차는
\[\sigma_d = |S_{dd}|^{-1}\]이 된다.
이는 $S_{dd}$ 가 클수록 해당 축의 분포가 더 압축되고,
$S_{dd}$ 가 작을수록 분포가 더 퍼진다는 것을 의미한다.따라서 실제 스케일 파라미터는
\[\sigma_d = S_{dd}^{-1}\]로 정의되며, 이는 각 축이 데이터에서 나타내는 변동의 크기와 중요도를 반영한다.
이는 모델이 각 성분에 부여한 중요성과
모델이 매니폴드를 학습하는 데 얼마나 성공적이었는지를 보여준다.
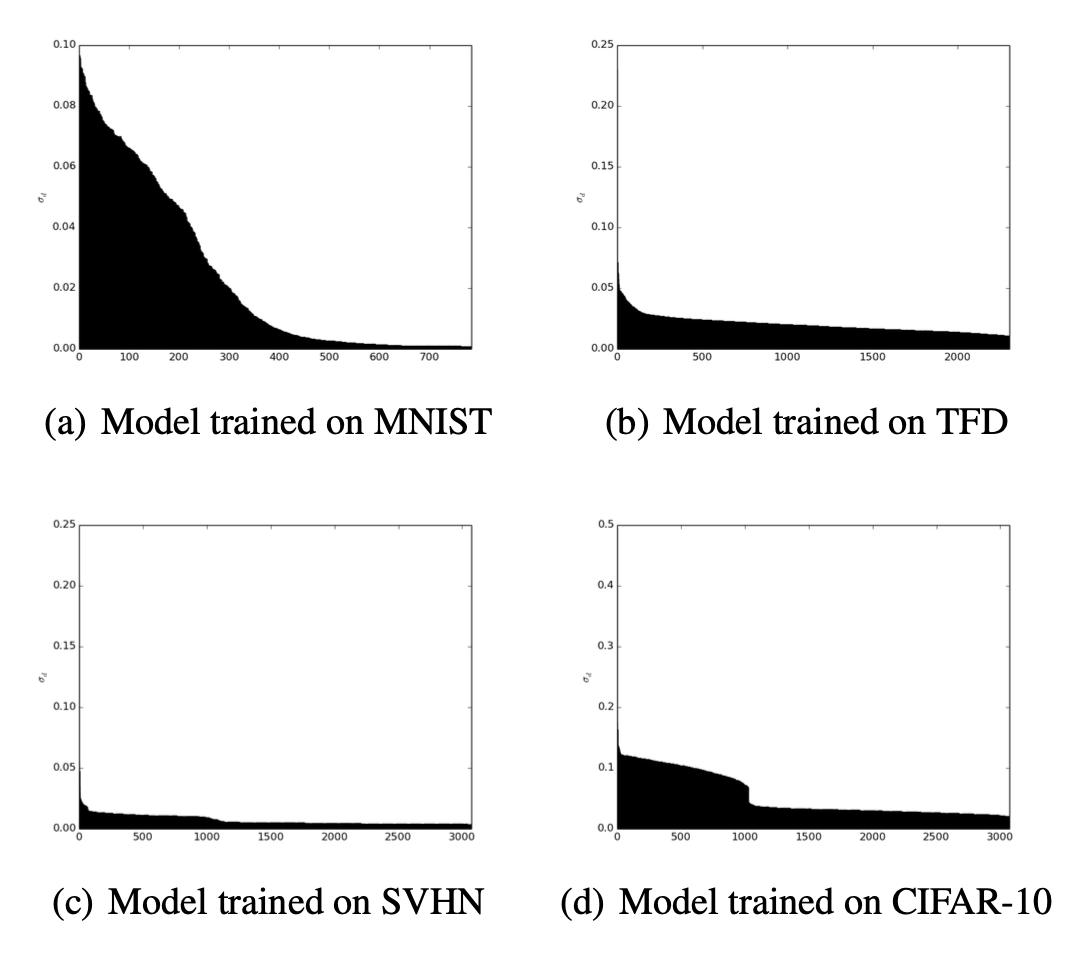
우리는 $(\sigma_d)_{d \leq D}$ 를 정렬하여 그림 8(Fig 8)에 나타냈다.
그림 8: $\sigma_d = S_{dd}^{-1}$ 의 감소(decay).
큰 값들은 모델이 더 큰 변동을 갖도록 선택한 차원들에 해당하며,
이로써 데이터로부터 학습된 매니폴드 구조가 강조된다.
이는 PCA의 경우 고유스펙트럼(eigenspectrum)에 해당하는 비선형적 대응물이다.
x축에는 구성요소 $d$ 가 있고,
y축에는 $\sigma_d$ 로 정렬된 값들이 있다.
이 그림은 스케일 파라미터 $\sigma_d = S_{dd}^{-1}$ 값을 큰 것부터 작은 것까지 정렬하여
각 데이터셋(MNIST, TFD, SVHN, CIFAR-10)에 대해 시각화한 것이다.$\sigma_d$ 값이 크다는 것은 해당 잠재 차원에서 변동성이 크고,
모델이 그 방향을 더 중요하게 사용했다는 의미이다.
반대로 $\sigma_d$ 값이 급격히 감소하는 형태는
많은 차원들이 상대적으로 덜 중요한 방향임을 보여준다.즉, 그래프의 기울기와 감소 패턴은
모델이 학습한 매니폴드의 “유효 차원 수(effective dimensionality)”를 직관적으로 나타낸다.
꼭 필요한 방향에서는 큰 $\sigma_d$ 를 유지하고,
중요하지 않은 방향에서는 매우 작은 값으로 수렴하는 모습을 확인할 수 있다.MNIST의 경우 상대적으로 적은 차원에서 큰 변동을 가지며,
CIFAR-10처럼 복잡한 데이터셋일수록 더 많은 차원에서
의미 있는 변동(큰 $\sigma_d$)이 유지되는 것으로 나타난다.이러한 패턴은 PCA의 고유값 스펙트럼(eigenvalue spectrum)과 유사하지만,
PCA가 선형 모델인 것과 달리
NICE는 비선형 변환을 통해 얻은 매니폴드 구조를 반영한다는 점에서 차이가 있다.
B 근사적 화이트닝(Approximate Whitening)
근사적 화이트닝을 학습하는 절차는 NICE 프레임워크를 사용하며,
아핀 함수와 표준 가우시안 prior 를 사용한다. 우리는 다음을 갖는다:
여기서 $L$ 은 하삼각 행렬(lower triangular)이며
$b$ 는 바이어스 벡터이다.
이는 가우시안 분포를 학습하는 것과 동일하다.
최적화 절차는 NICE와 동일하며: RMSProp을 사용하고
early stopping과 momentum을 적용한다.
화이트닝(whitening)은 데이터의 공분산을 제거하여
각 변수들이 상관관계 없이 동일한 분산을 갖도록 만드는 변환을 의미한다.예를 들어, 원본 데이터 $x$ 는 일반적으로 서로 상관된 특징을 가지고 있으며
공분산 행렬도 대각 행렬이 아닌 복잡한 형태를 갖는다.
화이트닝을 적용하면
\(z = Wx\)
형태의 적절한 선형 변환 $W$ 를 통해
$z$ 의 공분산을
\(\text{Cov}(z) = I\)
로 만들 수 있다.이런 변환이 필요한 이유는 다음과 같다:
(1) 많은 확률 모델은 표준 가우시안 분포나 분리된(factorized) 분포를 prior 로 사용한다.
(2) 하지만 실제 데이터는 상관구조를 갖기 때문에 바로 prior 에 맞지 않는다.
(3) 따라서 모델이 더 단순한 분포(prior)에 데이터를 맞추어 학습하려면
입력을 decorrelation(비상관화)하고 scale을 맞춰주는 과정이 필요하다.NICE 모델에서도 동일한 문제가 존재한다.
NICE는 최종 출력 $h$ 가
\(p_H(h) = \mathcal{N}(0, I)\)
와 같은 단순한 prior 를 따르도록 학습하지만,
데이터의 상관구조를 제거하지 않으면
매니폴드를 정확히 학습하거나 잠재공간 구조를 해석하기 어렵다.그래서 근사적 화이트닝 절에서는
NICE 프레임워크를 그대로 활용하면서
데이터를 표준 가우시안에 가깝게 만드는 선형 변환을 학습한다.그 변환이 다음 식이다:
\[z = Lx + b\]여기서
- $L$ 은 하삼각 행렬(lower triangular)
- $b$ 는 바이어스 벡터
하삼각 행렬을 사용하는 이유는
Jacobian $\frac{\partial z}{\partial x}$ 가 삼각 행렬이 되어
\(\log|\det(L)|\)
을 쉽게 계산할 수 있고,
또한 데이터의 공분산을 충분히 표현할 수 있기 때문이다.이 변환은 데이터를 표준 가우시안 분포로 보내기 위한
whitening transform 에 해당하며,
이 과정을 학습하는 것은 곧
“데이터가 가진 공분산 구조를 추정하는 것”
또는
“가우시안 분포를 학습하는 것”
과 동일하다.학습 방식은 NICE 전체와 동일하다.
RMSProp을 사용하고,
early stopping과 momentum을 적용하여
안정적 수렴을 유도한다.요약하자면,
이 절의 핵심은 NICE 모델의 마지막 스케일링 계층을
더 일반화한 형태의 화이트닝 변환으로 확장하여
데이터를 prior 에 더 잘 맞도록 만드는 과정이다.
C 변분 오토인코더(VAE)로서의 NICE (VARIATIONAL AUTO-ENCODER AS NICE)
우리는 확률적 그래디언트 변분 베이즈(SGVB) 알고리즘이
쌍 $(x, \epsilon)$ 에 대한 로그-우도를 최대화한다고 주장한다.
(Kingma and Welling, 2014)는 다음과 같은 인식 네트워크(recognition network)를 정의한다:
\[z = g_{\phi}(\epsilon \mid x),\quad \epsilon \sim \mathcal{N}(0, I)\]표준 가우시안 prior $p(z)$ 와 조건부 분포 $p(x \mid z)$ 에 대해, 우리는 다음을 정의할 수 있다:
\[\xi = \frac{x - f_{\theta}(z)}{\sigma}\]아래 식
\[\xi = \frac{x - f_{\theta}(z)}{\sigma}\]은 디코더가
\[x = f_{\theta}(z) + \sigma\,\xi\]와 같은 확률적 생성 방식을 따른다는 점을
\[x \sim \mathcal{N}(f_{\theta}(z),\, \sigma^{2} I)\]
명확히 드러내기 위해 도입된 보조 변수이다.
디코더의 조건부 분포가형태라면,
$x$ 는 평균 $f_\theta(z)$ 주변에서 표준편차 $\sigma$ 를 갖는 잡음 구조를 가진다.
이 잡음을 $\xi$ 로 정규화하면
$\xi \sim \mathcal{N}(0,I)$ 를 만족하게 되어
확률적 디코더를 표준 가우시안 잡음으로 재표현할 수 있다.변환
\[x = f_\theta(z) + \sigma\xi\]은 $\xi$ 를 $\sigma$ 배 만큼 스케일링한 후 평행 이동한 형태이다.
확률변수의 변환 규칙에 따르면
스케일링이 적용되면 확률밀도는 Jacobian의 역수를 곱해 보정된다.이때 Jacobian은
\[\frac{\partial x}{\partial \xi} = \sigma I\]이므로 determinant 는
\[\det(\sigma I) = \sigma^{D_X}.\]여기서 $D_X = dim(X)$ 이다.
따라서 $x$ 의 확률밀도는
\[p(x\mid z) = p_\xi(\xi)\, \sigma^{-D_X}.\]
다음과 같이 보정된 형태를 갖는다:여기서 $\sigma^{-D_X}$ 항은
$\xi$ 공간에서의 밀도를 $x$ 공간으로 옮길 때 필요한 스케일 보정이며,
스케일이 커질수록 밀도가 넓게 퍼지고
스케일이 작아질수록 밀도가 더 집중되는 효과를 반영한다.
만약 우리가 $h = (z, \xi)$ 에 표준 가우시안 prior 를 정의하면,
결과 비용 함수는 다음과 같다:
여기서 $D_X = dim(X)$ 이다.
이 식은 관측 쌍 $(x,\epsilon)$ 의 joint likelihood 를
세 가지 요인으로 분해한 것이다.1) prior 항 $\log(p_H(h))$
$h = (z,\xi)$ 로 두고,
\[\log(p_H(h))\]
$h$ 가 표준 가우시안 prior $p_H(h)$ 를 따른다고 가정한다.
그러면 관측된 $(x,\epsilon)$ 이 실제로 어떤 $(z,\xi)$ 로부터
생성되었는지에 대한 prior 확률이
likelihood 에 그대로 반영되어항이 등장한다.
2) 디코더 쪽 스케일 변환 보정 $-D_X \log(\sigma)$
디코더는
\[x = f_\theta(z) + \sigma \xi\]로 표현되며,
\[\frac{\partial x}{\partial \xi} = \sigma I \quad\Rightarrow\quad \det(\sigma I) = \sigma^{D_X},\]
이를 $\xi = \frac{x - f_\theta(z)}{\sigma}$ 로 바꾸어 쓰면
$x$ 대신 $\xi$ 를 사용하는 확률변수 변환이 된다.
이때 Jacobian 은이므로, density 변환 공식에 의해
\[p(x\mid z) = p_\xi(\xi)\,\sigma^{-D_X}\]형태가 된다.
로그를 취하면 $-D_X\log(\sigma)$ 항이 joint likelihood 에 더해진다.
즉, 이 항은 “$x$ 를 $\xi$ 로 바꾸어 표현하는 데 따른 스케일 보정”을 의미한다.3) 인식 네트워크의 Jacobian 보정
$\log\big|\det \frac{\partial g_\phi}{\partial \epsilon}(\epsilon;x)\big|$SGVB에서는 잠재변수 $z$ 를 직접 샘플링하지 않고
\[z = g_\phi(\epsilon \mid x), \quad \epsilon \sim \mathcal{N}(0,I)\]로 재매개변수화한다.
\[\log\Big(\big|\det \tfrac{\partial g_\phi}{\partial \epsilon}(\epsilon;x)\big|\Big)\]
따라서 $\epsilon$ 공간에서 정의된 밀도를
$z$ 공간으로 옮길 때, 변수변환 공식에 따라
Jacobian 의 determinant 가 likelihood 에 곱해지며,
로그에서항으로 나타난다.
이는 “$\epsilon$ 을 통해 $z$ 를 표현함으로써 생기는 density 보정”이다.한편, 표준 가우시안 잡음 $\epsilon$ 의 밀도 $p_\epsilon(\epsilon)$ 는
$\theta,\phi$ 와 무관한 상수 항이므로
최적화 관점에서 비용 함수에 추가적인 영향을 주지 않는다.
그래서 책 본문에서는
$-\log(p_\epsilon(\epsilon))$ 항을 포함시키지 않고
위와 같이 세 개의 항만 남긴 형태로 정리한 것이다.정리하면, 위 식은
① $(z,\xi)$ 에 대한 prior,
② 디코더의 스케일 보정,
③ 인식 네트워크의 Jacobian 보정
세 가지 요인으로 $(x,\epsilon)$ 의 joint likelihood 를 분해한 결과라고 볼 수 있다.
이는 다음과 동등하다(=로 정렬):
\[\begin{aligned} \log(p_{(x,\epsilon),(\theta,\phi)}(x,\epsilon)) - \log(p_{\epsilon}(\epsilon)) &= \log(p_H(h)) - D_X \log(\sigma) + \log\left(\left|\det \frac{\partial g_{\phi}}{\partial \epsilon}(\epsilon; x)\right|\right) - \log(p_{\epsilon}(\epsilon)) \\[6pt] &= \log(p_H(h)) - D_X \log(\sigma) - \log(q_{Z \mid X;\phi}(z)) \\[6pt] &= \log(p_{\xi}(\xi)p_Z(z)) - D_X \log(\sigma) - \log(q_{Z \mid X;\phi}(z)) \\[6pt] &= \log(p_{\xi}(\xi)) + \log(p_Z(z)) - D_X \log(\sigma) - \log(q_{Z \mid X;\phi}(z)) \\[6pt] &= \log(p_{\xi}(\xi)) - D_X \log(\sigma) + \log(p_Z(z)) - \log(q_{Z \mid X;\phi}(z)) \\[6pt] &= \log(p_{X \mid Z}(x \mid z)) + \log(p_Z(z)) - \log(q_{Z \mid X;\phi}(z)) \end{aligned}\]이것은 (Kingma and Welling, 2014)에서 제안된
SGVB 비용 함수의 몬테카를로 근사(Monte Carlo estimate)이다.
첫 줄은 단순히 양변에서 동일하게
$-\log(p_{\epsilon}(\epsilon))$
항을 빼서 정리한 형태이다.
SGVB에서 $\epsilon$ 은 표준 가우시안에서 샘플링된 외생 변수이며,
이 항은 최적화와 직접적으로 관련 없는 상수 역할을 한다.
따라서 이후 전개 과정에서 이 항을 분리해 두고 정리하기 위한 첫 단계이다.두 번째 줄 전개:
\[\log(p_H(h)) - D_X \log(\sigma) + \log\left|\det \tfrac{\partial g_\phi}{\partial\epsilon}(\epsilon;x)\right| - \log(p_{\epsilon}(\epsilon)) = \log(p_H(h)) - D_X \log(\sigma) - \log(q_{Z\mid X;\phi}(z))\]여기서는 다음 관계를 사용한다:
\[q_{Z\mid X;\phi}(z) = p_{\epsilon}(\epsilon)\, \left|\det \tfrac{\partial g_\phi}{\partial\epsilon}(\epsilon;x)\right|^{-1}\]즉, 인식 네트워크의 재매개변수화
$z = g_\phi(\epsilon\mid x)$
에 의해 Jacobian 보정과 noise density 가 합쳐져
변분 posterior $q(z\mid x)$ 로 단일화된다.
그 결과 두 항이 하나의 $-\log(q_{Z\mid X;\phi}(z))$ 로 묶인다.세 번째 줄 전개:
\[\log(p_H(h)) = \log(p_{\xi}(\xi)p_Z(z))\]이는 prior 를
\[p_H(h) = p_Z(z)\, p_\xi(\xi)\]
$h = (z,\xi)$ 로 분해했기 때문이다.
$h$ 전체가 표준 가우시안을 따른다고 했으므로가 성립한다.
따라서 prior 가 두 독립 확률변수의 곱으로 분해된다.네 번째 줄 전개:
\[\log(p_{\xi}(\xi)p_Z(z)) = \log(p_{\xi}(\xi)) + \log(p_Z(z))\]로그에서 곱은 합으로 분리된다.
이는 단순한 로그 성질을 사용한 변환이다.다섯 번째 줄은 단순한 항 재정렬이다:
\[\log(p_{\xi}(\xi)) + \log(p_Z(z)) - D_X \log(\sigma) = \log(p_{\xi}(\xi)) - D_X \log(\sigma) + \log(p_Z(z))\]항의 순서를 바꿔 표현하여
$p_\xi(\xi)$ 와 스케일 보정 항을 먼저 모은 형태이다.마지막 전개:
\[\log(p_{\xi}(\xi)) - D_X \log(\sigma) = \log(p_{X\mid Z}(x\mid z))\]이 부분이 가장 핵심이다.
디코더 모델
\[p_{X\mid Z}(x\mid z) = p_\xi(\xi)\,\sigma^{-D_X}\]
\(x = f_\theta(z) + \sigma \xi\)
에서 $\xi$ 는 표준 가우시안이므로
$x$ 의 조건부 확률은 변수변환 공식에 따라이 된다.
\[\log(p_\xi(\xi)) - D_X\log(\sigma)\]
로그를 취하면이므로, 위 항 전체가 바로
$\log(p_{X\mid Z}(x\mid z))$
로 치환된다.즉, 디코더의 확률모델을 $(z,\xi)$ 대신 $(x,z)$ 로 다시 표현한 것이다.
따라서 마지막 줄
\[\log(p_{X\mid Z}(x\mid z)) + \log(p_Z(z)) - \log(q_{Z\mid X;\phi}(z))\]는 SGVB(또는 VAE)의 ELBO 형태
\[\log p(x) \ge \mathbb{E}_{q(z\mid x)}[\log p(x\mid z)] - \text{KL}(q(z\mid x)\,\|\,p(z))\]와 동일한 구조이며,
SGVB 비용함수의 몬테카를로 근사 형태가 바로 이 결과로부터 얻어진다.