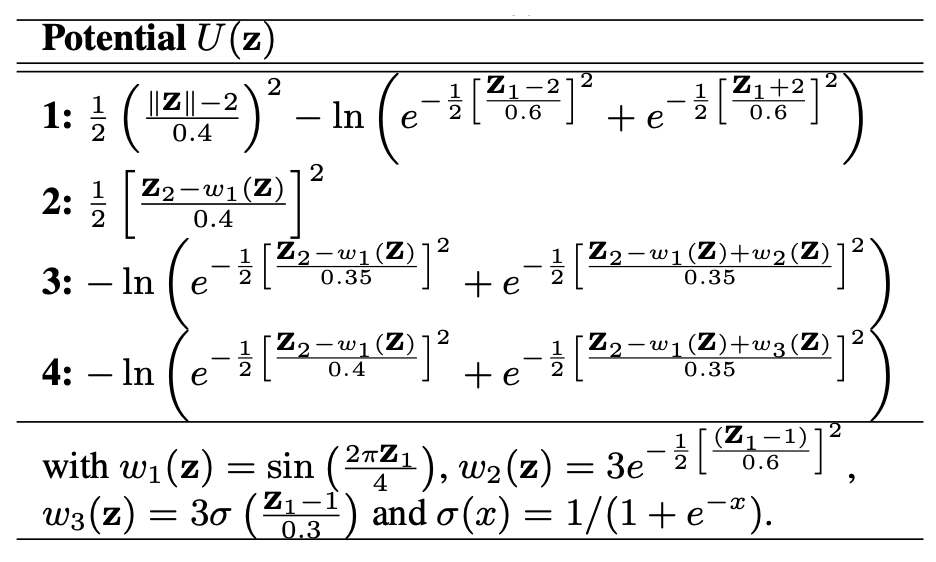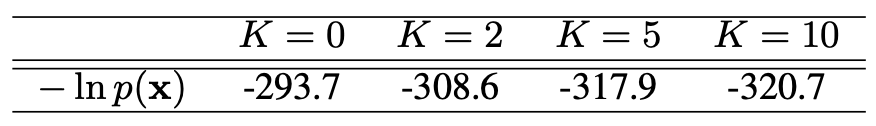[논문] Variational Inference with Normalizing Flows

게시 2025/11/02 업데이트 2025/11/14

By 김성진

134 분읽는 시간

논문 출처
Rezende, D. J., & Mohamed, S.
Variational Inference with Normalizing Flows.
Proceedings of the 32nd International Conference on Machine Learning (ICML), 2015.
🔗 원문 링크 (arXiv: 1505.05770)

저자

Danilo Jimenez Rezende: DANILOR@GOOGLE.COM
Shakir Mohamed: SHAKIR@GOOGLE.COM
Google DeepMind, London

제32회 국제 머신러닝 학술대회(International Conference on Machine Learning, ICML)
프랑스 릴(Lille)에서 2015년에 개최.
JMLR: 워크숍 및 컨퍼런스 절차집(Workshop and Conference Proceedings) 제37권 수록.
저작권 © 2015, 저자 소유.

초록 (Abstract)

변분 추론(variational inference)에서
근사 사후분포(approximate posterior distribution)를 선택하는 것은
핵심적인 문제 중 하나이다.

대부분의 변분 추론 응용에서는
효율적인 추론을 위해 평균장(mean-field) 또는
기타 단순한 구조적 근사를 사용하는
단순한 형태의 사후분포 근사를 채택한다.
하지만 이러한 제약은 변분 추론의 정확도와 표현력에
심각한 한계를 초래한다.

본 논문에서는 유연하고, 임의로 복잡하며,
확장 가능한 근사 사후분포를 정의하기 위한
새로운 접근법을 제시한다.

우리의 근사는 정규화 흐름(normalizing flow)을 통해 구성된 분포로,
단순한 초기 밀도(initial density)를 일련의 가역 변환(invertible transformations)에
순차적으로 적용함으로써 점차 복잡한 분포로 변환한다.
이 과정을 통해 원하는 수준의 복잡성을 달성할 수 있다.

이러한 관점에서 정규화 흐름을 이용하여
유한(normalizing flow of finite length) 및
무한(infinitesimal flow) 변환의 범주를 발전시키고,
풍부한 사후분포 근사를 구성하기 위한
통합된 접근법을 제시한다.

또한, 진짜 사후분포에 더 잘 부합하는 사후분포를 가지는 이론적 이점과,
상각(amortized) 변분 추론 접근법의 확장성(scalability)을 결합함으로써,
변분 추론의 성능과 적용 가능성 모두에서
뚜렷한 향상을 달성함을 보여준다.

전통적인 변분 추론에서는
각 데이터 포인트마다 고유한 변분 파라미터를 학습해야 하므로
계산 비용이 매우 크다.
반면, 상각(amortized) 변분 추론은
공유된 추론 네트워크(inference network) 또는 인코더(encoder)를 사용하여
관측값 $x$ 로부터 변분 파라미터(예: $\mu(x), \sigma(x)$)를 직접 예측한다.
즉, 모든 데이터에 대해 별도의 최적화를 수행하는 대신,
하나의 신경망을 학습시켜 추론 비용을 전체 데이터에 걸쳐 ‘상각(amortize)’시키는 방식이다.
이 접근법은 변분 추론의 효율성을 크게 향상시키며,
특히 변분 오토인코더(VAE) 와 같은 모델의 핵심 구성요소로 사용된다.

1. 서론 (Introduction)

변분 추론(variational inference)은
확률적 모델링(probabilistic modeling)을 대규모 데이터셋에 맞게 확장(scaling)하기 위한 수단으로서
최근 다시 큰 관심을 받고 있다.

변분 추론은 이제 대규모 텍스트 주제 모델(large-scale topic models of text)의 핵심에 있으며
(Hoffman et al., 2013),
준지도 분류(semi-supervised classification)에서
최첨단 성능(state-of-the-art)을 제공하고
(Kingma et al., 2014),
현재 가장 사실적인 이미지 생성 모델(generative models of images)을 구동하는
모델들의 기반이 되고 있다
(Gregor et al., 2014; 2015; Rezende et al., 2014; Kingma & Welling, 2014).

또한 변분 추론은
다양한 물리적 및 화학적 시스템(physical and chemical systems)을 이해하기 위한
기본 도구(default tool)로 자리 잡았다.

이러한 성공과 지속적인 발전에도 불구하고,
변분 방법(variational methods)에는 그 성능을 제한하고
통계적 추론(statistical inference)의 기본 방법으로서
더 널리 채택되는 것을 방해하는 여러 단점(disadvantages)이 존재한다.

이 논문에서 우리가 다루는 것은
그러한 한계들 중 하나인
사후분포 근사의 선택 문제이다.

변분 추론(variational inference)은
계산 불가능한(intractable) 사후분포(posterior distribution)를
알려진 확률분포(known probability distributions)의 한 계열(class)로
근사(approximate)할 것을 요구하며,
그 계열 내에서 우리는 진짜 사후분포(true posterior)에
가장 잘 근사하는 분포를 탐색한다.

사용되는 근사 분포의 계열(class of approximations)은
종종 제한적이며, 예를 들어 평균장(mean-field) 근사와 같은 형태가 있다.
이것은 어떤 해(solution)도 진짜 사후분포를 닮을 수 없다는 것을 의미한다.

이 점은 변분 방법(variational methods)에 대해
널리 제기되어 온 비판(widely raised objection) 중 하나로,
다른 추론 방법들 — 예를 들어 MCMC(Markov Chain Monte Carlo) — 과는 달리,
변분 추론에서는 비록 점근적(asymptotic) 상황에 이르더라도
진짜 사후분포를 복원(recover)할 수 없다는 것이다.

더 풍부하고(richer), 더 충실한(more faithful) 사후분포 근사가
더 나은 성능을 가져온다는 것은 많은 증거들에 의해 뒷받침된다.

예를 들어, 평균장(mean-field) 근사를 사용하는 시그모이드 신념망(sigmoid belief networks)과 비교할 때,
심층 자기회귀 신경망(deep auto-regressive networks)은
자기회귀적 종속 구조(autoregressive dependency structure)를 가진
사후분포 근사를 사용함으로써 성능이 명확히 향상됨을 보인다 (Mnih & Gregor, 2014).

또한 제한된 사후분포 근사가 초래하는
부정적 영향(detrimental effect)을 설명하는 많은 연구 결과들도 존재한다.
Turner & Sahani (2011)은 일반적으로 발생하는 두 가지 문제를 설명한다.

첫째는, 사후분포의 분산(variance)이 과소추정(under-estimation)되는
널리 관찰된 문제로, 이는 선택된 사후분포 근사에 기반한
부정확한 예측(poor predictions)과 신뢰할 수 없는 결정(unreliable decisions)으로 이어질 수 있다.

둘째는, 사후분포 근사의 제한된 표현력(limited capacity)이
모델 파라미터의 MAP(Maximum A Posteriori) 추정치에 편향(bias)을 유발할 수 있다는 것이다.
(이는 예를 들어 시계열 모델(time-series models)에서도 흔히 발생하는 현상이다.)

풍부한(rich) 사후분포 근사를 위한
여러 제안들이 탐구되어 왔으며,
이들은 일반적으로 근사 사후분포 내에서
어떤 기본적인 형태의 종속성(dependency)을 포함하는
구조적 평균장(structured mean-field) 근사에 기반하고 있다.

또 다른 잠재적으로 강력한 대안(alternative)은
근사 사후분포를 혼합모형(mixture model)으로 정의하는 것으로,
이는 Jaakkola & Jordan (1998); Jordan et al. (1999); Gershman et al. (2012)
에 의해 제안된 방법들과 유사하다.

그러나 혼합모형 접근법은 변분 추론의
잠재적인 확장성(scalability)을 제한한다.
그 이유는 각 혼합 구성요소(mixture component)마다
파라미터가 갱신될 때마다
로그 가능도(log-likelihood)와 그 그래디언트(gradient)를
평가해야 하기 때문이다.
이는 일반적으로 계산 비용이 많이 드는(computationally expensive) 작업이다.

이 논문은 변분 추론(variational inference)을 위한
근사 사후분포(approximate posterior distributions)를
정의하기 위한 새로운 접근법을 제시한다.

우리는 먼저 상각 변분 추론(amortized variational inference)과
효율적인 몬테카를로(Monte Carlo) 그래디언트 추정을 기반으로 하는
일반적인 유향 그래프 모델(directed graphical models)에서의
현재 최선의 추론 방법을 검토하며(section 2),
그 후 다음과 같은 공헌(contributions)을 제시한다.

우리는 정규화 흐름(normalizing flows) 을 사용하여
근사 사후분포를 정의하는 방법을 제안한다.
정규화 흐름은 일련의 가역적 변환(invertible mappings)을 통해
확률밀도(probability density)를 변환함으로써
복잡한 분포(complex distributions)를 구성하는 도구이다(section 3).
정규화 흐름을 이용한 추론은
추가적인 항들을 포함하는 더 조밀하고(tighter) 수정된 변분 하한(modified variational lower bound)을 제공하며,
이러한 추가 항들은 선형 시간 복잡도(linear time complexity)만을 가진다(section 4).
우리는 정규화 흐름(normalizing flows)이
무한소 흐름(infinitesimal flows)을 포함한다는 것을 보인다.
이 무한소 흐름은 점근적(asymptotic) 영역에서
진짜 사후분포(true posterior distribution)를 복원할 수 있는
사후분포 근사의 한 계열(class)을
정의할 수 있도록 해준다.
이는 변분 추론(variational inference)의
자주 인용되는 한계(one oft-quoted limitation)를 극복한다.
우리는 개선된 사후분포 근사를 위한 관련 접근법들을
특수한 형태의 정규화 흐름(normalizing flows)의 적용으로 통합적으로 바라보는
통일된 관점(unified view)을 제시한다(section 5).
우리는 실험적으로 일반적인 정규화 흐름(general normalizing flows)의 사용이
다른 경쟁적인 사후분포 근사 방법들보다
체계적으로 더 우수한 성능을 낸다는 것을 보인다.

2. 상각 변분 추론 (Amortized Variational Inference)

추론(inference)을 수행하기 위해서는
확률적 모델(probabilistic model)의 주변가능도(marginal likelihood)를 이용하는 것으로 충분하며,
이는 모델 내에서 누락되었거나(latent) 잠재(latent)된 변수들에 대한 적분(marginalization)을 요구한다.

이 적분은 일반적으로 계산 불가능(intractable)하므로,
대신 우리는 주변가능도에 대한 하한(lower bound)을 최적화한다.

관측값 $\mathbf{x}$, 적분해야 하는(latent) 잠재 변수 $\mathbf{z}$,
그리고 모델 파라미터 $\boldsymbol{\theta}$를 가진
일반적인 확률적 모델(probabilistic model)을 고려하라.

우리는 잠재 변수들에 대한 근사 사후분포 $q_\phi(\mathbf{z} \mid \mathbf{x})$를 도입하고,
Jordan et al. (1999)이 제시한 변분 원리(variational principle)를 따름으로써
주변가능도에 대한 하한(bound)을 얻을 수 있다.

\[\begin{align} \log p_\theta(\mathbf{x}) &= \log \int p_\theta(\mathbf{x}\mid\mathbf{z})\,p(\mathbf{z})\,d\mathbf{z} \tag{1}\\[6pt] &= \log \int \frac{q_\phi(\mathbf{z}\mid\mathbf{x})}{q_\phi(\mathbf{z}\mid\mathbf{x})}\, p_\theta(\mathbf{x}\mid\mathbf{z})\,p(\mathbf{z})\,d\mathbf{z} \tag{2}\\[6pt] &\ge - D_{\mathrm{KL}}\!\big[q_\phi(\mathbf{z}\mid\mathbf{x}) \,\|\, p(\mathbf{z})\big] + \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})}\!\big[\log p_\theta(\mathbf{x}\mid\mathbf{z})\big] = -\mathcal{F}(\mathbf{x}) \tag{3} \end{align}\]

여기서 Jensen 부등식(Jensen’s inequality)을 이용하여
마지막 식을 얻었다.

Jensen 부등식은 볼록(convex) 함수의 기댓값은 함수에 기댓값을 적용한 값보다 크거나 같다는 성질을 나타낸다.
수학적으로는 다음과 같이 표현된다.
\[f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)]\]
만약 $f$가 오목(concave) 함수라면 부등호의 방향이 반대가 된다.
변분 추론에서는 로그 함수가 오목함수이므로,
Jensen 부등식을 적용하여
\[\log \mathbb{E}[X] \geq \mathbb{E}[\log X]\]
형태의 부등식을 사용한다.
이 부등식을 통해 로그 가능도(log-likelihood)의 하한(lower bound) 을 유도할 수 있으며,
바로 그 결과가 ELBO (Evidence Lower Bound) 이다.

$p_\theta(\mathbf{x} \mid \mathbf{z})$ 는 가능도 함수(likelihood function)이고,
$p(\mathbf{z})$ 는 잠재 변수들에 대한 사전분포이다.

이 식은 파라미터 $\boldsymbol{\theta}$에 대한 사후 추론(posterior inference)으로도 쉽게 확장할 수 있지만,
여기서는 잠재 변수(latent variables)에 대한 추론에만 집중한다.

이 하한(bound)은 종종 음의 자유 에너지(negative free energy)
또는 증거 하한(Evidence Lower Bound, ELBO) 으로 불린다.

이 식은 두 항으로 구성된다.
첫 번째 항은 근사 사후분포(approximate posterior)와
사전분포(prior distribution) 간의 KL 발산(KL divergence)으로,
정규화 항(regularizer) 역할을 한다.
두 번째 항은 재구성 오차(reconstruction error)이다.

이 하한 식 (3)은 모델의 파라미터 $\boldsymbol{\theta}$와
변분 근사의 파라미터 $\boldsymbol{\phi}$ 모두를 최적화하기 위한
통합된(unified) 목적함수(objective function)를 제공한다.

변분 추론(variational inference)의 현재 최선의 구현(current best practice)은
미니배치(mini-batch)와 확률적 경사하강법(stochastic gradient descent)을 사용하여
이 최적화(optimization)를 수행하는 것이다.

이 접근법이 바로 변분 추론이
매우 큰 데이터셋을 가진 문제들로 확장될 수 있도록 해주는 이유이다.

변분 접근법(variational approach)을 성공적으로 사용하기 위해
해결해야 하는 두 가지 문제가 있다.

(1) 기대 로그 가능도(expected log-likelihood)
$\nabla_\phi \mathbb{E}_{q_\phi(\mathbf{z})}[\log p_\theta(\mathbf{x} \mid \mathbf{z})]$ 의
도함수를 효율적으로 계산하는 문제,

그리고 (2) 계산적으로 가능한(computationally-feasible) 범위 내에서
가장 풍부한(richest) 근사 사후분포(approximate posterior distribution)
$q(\cdot)$ 를 선택하는 문제이다.

두 번째 문제가 바로 본 논문의 핵심 주제이다.

첫 번째 문제를 다루기 위해,
우리는 두 가지 도구를 사용한다:
몬테카를로 그래디언트 추정(Monte Carlo gradient estimation)과
추론 네트워크(inference networks)이다.

이 두 가지를 함께 사용할 때,
우리는 이를 상각 변분 추론(amortized variational inference) 이라고 부른다.

2.1 확률적 역전파 (Stochastic Backpropagation)

지난 수년간 변분 추론(variational inference)에 관한 연구의 대부분은
기대 로그 가능도(expected log-likelihood)의 그래디언트(gradient)
$\nabla_\phi \mathbb{E}_{q_\phi(\mathbf{z})}[\log p_\theta(\mathbf{x} \mid \mathbf{z})]$를 계산하는 방법에 초점을 맞추어 왔다.

이전에 우리는 지역 변분 방법(local variational methods)
(Bishop, 2006)에 의존했을 것이지만,
일반적으로 이제 우리는 그러한 기댓값(expectations)을
몬테카를로 근사(Monte Carlo approximations)를 사용하여 항상 계산한다.
(이는 KL 항(KL term)이 분석적으로 알려져 있지 않은 경우,
하한(bound)에 포함되는 경우를 포함한다.)

지역 변분 방법은 전체 데이터셋에 대한 전역(global) 근사 대신,
각 데이터 포인트나 개별 변수에 대해 지역적으로(local)
변분 파라미터를 최적화하는 접근법이다.
이러한 방법은 계산량이 많고 확장성이 떨어지기 때문에,
현재는 몬테카를로 근사 기반의 확률적 추론(stochastic inference) 으로 대체되고 있다.

이 접근법은 적절하게 이름 붙여진
이중 확률 추정(doubly-stochastic estimation) 을 형성한다
(Titsias & Lazaro-Gredilla, 2014).

이는 우리가 미니배치(mini-batch)에서 오는
첫 번째 확률성(stochasticity) 원천과,
기댓값의 몬테카를로 근사(Monte Carlo approximation)에서 오는
두 번째 확률성 원천을 모두 가지고 있기 때문이다.

우리는 연속적인 잠재 변수(continuous latent variables)를 가진 모델들에 초점을 맞춘다.
이 접근법에서 필요한 그래디언트(gradients)는
비중심(non-centered) 재매개변수화(reparameterization)된 기댓값(expectation)의 형태로 계산되며
(Papaspiliopoulos et al., 2003; Williams, 1992),
몬테카를로 근사(Monte Carlo approximation)와 결합된다.
이 방법은 확률적 역전파(stochastic backpropagation) (Rezende et al., 2014)라 불린다.

이 접근법은 또한 확률적 그래디언트 변분 베이즈(stochastic gradient variational Bayes, SGVB)
(Kingma & Welling, 2014) 또는
아핀 변분 추론(affine variational inference) (Challis & Barber, 2012)이라 불리기도 한다.

확률적 역전파(stochastic backpropagation)는 두 단계로 이루어진다.

재매개변수화 (Reparameterization)
우리는 알려진 기본 분포(base distribution)와
미분 가능한 변환(differentiable transformation, 예: 위치-스케일(location-scale) 변환
또는 누적 분포 함수(cumulative distribution function))을 이용하여
잠재 변수(latent variable)를 재매개변수화한다.
예를 들어, 만약 $q_\phi(\mathbf{z})$ 가
$\mathcal{N}(\mathbf{z} \mid \mu, \sigma^2)$ 인 가우시안 분포(Gaussian distribution)이고
$\phi = \lbrace \mu, \sigma^2\rbrace$ 라면,
위치-스케일(location-scale) 변환은 다음과 같다:
\[\mathbf{z} \sim \mathcal{N}(\mathbf{z} \mid \mu, \sigma^2) \quad \Leftrightarrow \quad \mathbf{z} = \mu + \sigma \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(0, 1)\]
몬테카를로를 이용한 역전파 (Backpropagation with Monte Carlo)
이제 우리는 기본 분포(base distribution)로부터의 샘플(draws)을 사용한
몬테카를로 근사(Monte Carlo approximation)를 통해,
변분 분포(variational distribution)의 파라미터 $\phi$ 에 대해
미분(역전파, backpropagation)을 수행할 수 있다:
즉,
\[\nabla_\phi \mathbb{E}_{q_\phi(\mathbf{z})}[f_\theta(\mathbf{z})] \quad \Leftrightarrow \quad \mathbb{E}_{\mathcal{N}(\epsilon \mid 0,1)} \big[\nabla_\phi f_\theta(\mu + \sigma \epsilon)\big]\]
으로 표현된다.

몬테카를로 제어 변수(Monte Carlo control variate, MCCV) 추정량(estimator)에 기반한
여러 범용(general purpose) 접근법들이
확률적 역전파(stochastic backpropagation)의 대안으로 존재하며,
연속적이거나(discrete) 불연속적인(latent variables that may be continuous or discrete)
잠재 변수들에 대한 그래디언트 계산을 가능하게 한다
(Williams, 1992; Mnih & Gregor, 2014; Ranganath et al., 2013; Wingate & Weber, 2013).

확률적 역전파의 중요한 장점 중 하나는,
연속적인 잠재 변수를 가진 모델의 경우,
경쟁하는 다른 추정량들 중에서 분산(variance)이 가장 낮다는 것이다.

2.2 추론 네트워크 (Inference Networks)

두 번째로 중요한 구현 사항은,
근사 사후분포(approximate posterior distribution) $q_\phi(\cdot)$ 가
인식 모델(recognition model) 또는 추론 네트워크(inference network)를 사용하여
표현된다는 것이다 (Rezende et al., 2014; Dayan, 2000; Gershman & Goodman, 2014; Kingma & Welling, 2014).

추론 네트워크란 관측값(observations)으로부터 잠재 변수(latent variables)로의
역함수(inverse map)를 학습하는 모델이다.

추론 네트워크를 사용함으로써,
각 데이터 포인트마다 개별적인 변분 파라미터(variational parameters)를
계산할 필요가 없게 되며,
대신 학습(training)과 테스트(test) 모두에서 유효한
글로벌 변분 파라미터(global variational parameters) $\phi$ 의 집합을 계산할 수 있다.

이 접근법은 추론 네트워크의 파라미터를 통해
모든 잠재 변수들에 대한 사후분포 추정(posterior estimates)을 일반화함으로써,
추론(inference)의 비용을 상각(amortize)할 수 있도록 해준다.

우리가 사용할 수 있는 가장 단순한 추론 모델은
대각 가우시안 분포(diagonal Gaussian densities)이다.

\[q_\phi(\mathbf{z} \mid \mathbf{x}) = \mathcal{N}\!\big(\mathbf{z} \mid \mu_\phi(\mathbf{x}), \mathrm{diag}(\sigma_\phi^2(\mathbf{x}))\big)\]

여기서 평균(mean) 함수 $\mu_\phi(\mathbf{x})$ 와
표준편차(standard deviation) 함수 $\sigma_\phi(\mathbf{x})$ 는
심층 신경망(deep neural networks)을 이용하여 정의된다.

2.3 심층 잠재 가우시안 모델 (Deep Latent Gaussian Models)

이 논문에서는 심층 잠재 가우시안 모델(Deep Latent Gaussian Models, DLGM)을 연구한다.
DLGM은 심층 유향 그래프 모델(deep directed graphical models)의 일반적인 범주로,
가우시안 잠재 변수(Gaussian latent variables)의 $L$ 개 층(layer)으로 이루어진
계층적 구조(hierarchy)로 구성되어 있다.
각 층 $l$ 에는 잠재 변수 $\mathbf{z}_l$ 이 존재한다.

각 계층의 잠재 변수는 그 위 계층의 변수에 비선형적으로(non-linearly) 의존하며,
DLGM의 경우 이러한 비선형 의존성은 심층 신경망(deep neural networks)에 의해 정의된다.

결합 확률 모델(joint probability model)은 다음과 같다:

\[p(\mathbf{x}, \mathbf{z}_1, \ldots, \mathbf{z}_L) = p(\mathbf{x} \mid f_0(\mathbf{z}_1)) \prod_{l=1}^{L} p(\mathbf{z}_l \mid f_l(\mathbf{z}_{l+1})) \tag{4}\]

식 (4)는 심층 잠재 가우시안 모델(DLGM)의 결합 확률 구조를 나타낸다.
이를 풀어 쓰면 다음과 같다.
\[p(\mathbf{x}, \mathbf{z}_1, \ldots, \mathbf{z}_L) = p(\mathbf{x} \mid f_0(\mathbf{z}_1)) \cdot p(\mathbf{z}_1 \mid f_1(\mathbf{z}_2)) \cdot \ldots \cdot p(\mathbf{z}_{L-1} \mid f_{L-1}(\mathbf{z}_L)) \cdot p(\mathbf{z}_L)\]
즉, 최상위 계층의 잠재 변수 $\mathbf{z}_L$ 은 사전분포 $p(\mathbf{z}_L)$ 로부터 샘플링되며,
각 하위 계층의 잠재 변수 $\mathbf{z}_l$ 은
상위 계층의 잠재 변수 $\mathbf{z}_{l+1}$ 의 비선형 변환 $f_l(\mathbf{z}_{l+1})$ 에 조건부로 생성된다.
마지막으로 관측 데이터 $\mathbf{x}$ 는
가장 하위 잠재 변수 $\mathbf{z}_1$ 의 변환 $f_0(\mathbf{z}_1)$ 에 의해 생성된다.

여기서 $L$번째 가우시안 분포는 다른 어떤 확률 변수에도 의존하지 않는다.
잠재 변수에 대한 사전분포(prior)는 단위 가우시안(unit Gaussian)으로,
$p(\mathbf{z}_l) = \mathcal{N}(0, \mathbf{I})$ 이다.
관측값에 대한 우도함수(likelihood) $p_\theta(\mathbf{x} \mid \mathbf{z})$ 는
$\mathbf{z}_1$ 에 조건부로 주어지며(conditioned on $\mathbf{z}_1$),
심층 신경망에 의해 파라미터화(parameterized)된다 (그림 2).

이 모델 클래스(model class)는 매우 일반적이며,
요인 분석(factor analysis)과 주성분 분석(PCA),
비선형 요인 분석(non-linear factor analysis),
그리고 비선형 가우시안 신념망(non-linear Gaussian belief networks)
등을 특수한 경우로 포함한다 (Rezende et al., 2014).

DLGM은 잠재 변수 $\mathbf{z}$ 를 이용해 관측 데이터 $\mathbf{x}$ 를 생성하는
유향 확률 모델(directed probabilistic model) 의 한 형태이다.
PCA(주성분 분석)나 요인 분석(Factor Analysis)은
모두 잠재 변수 모델(latent variable model) 로,
선형 변환(linear transformation)을 통해
$\mathbf{x}$ 와 $\mathbf{z}$ 사이의 관계를 모델링한다.
예를 들어,
\[\mathbf{x} = \mathbf{Wz} + \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(0, \sigma^2 \mathbf{I})\]
와 같은 형태가 PCA/FA의 기본 구조이다.
반면, DLGM에서는 이 선형 변환을 비선형 함수 $f_l(\cdot)$ (예: 신경망)으로 일반화하고,
여러 계층(layer)의 잠재 변수를 포함하여
복잡한 데이터 분포를 모델링할 수 있다.
따라서 DLGM은
선형 함수를 사용하는 PCA, 요인 분석(FA)
비선형 함수를 사용하는 비선형 요인 분석(NLFA), 가우시안 신념망(GBN)
을 모두 하위 특수한 경우(special cases) 로 포함하는
보다 일반적인(latent hierarchical & nonlinear) 모델이다.

DLGM은 연속적인 잠재 변수(continuous latent variables)를 사용하며,
식 (3)에서 제시된 하한(lower bound)과 확률적 역전파(stochastic backpropagation)를 활용한
빠른 상각 변분 추론(amortized variational inference)에 완벽하게 적합한 모델 클래스이다.

DLGM과 추론 네트워크(inference network)의 종단 간(end-to-end) 시스템은
인코더-디코더(encoder-decoder) 아키텍처로 볼 수 있으며,
이것이 바로 Kingma & Welling (2014)이 취한 관점이다.
그들은 이러한 모델과 추론 전략의 결합을 변분 오토인코더(variational auto-encoder, VAE) 로 제시하였다.

Kingma & Welling (2014) 및 Rezende et al. (2014)에서 사용된 추론 네트워크는
단순한 대각선(diagonal) 또는 ‘대각선 + 저랭크(diagonal-plus-low-rank)’
가우시안 분포(Gaussian distributions)를 사용한다.

진짜 사후분포(true posterior distribution)는
이러한 가정이 허용하는 것보다 더 복잡할 것이며,
다봉형(multimodal)이고 제약된(constrained)
사후 근사(posterior approximations)를
확장 가능한(scalable) 방식으로 정의하는 것은
변분 추론(variational inference)에서 여전히 중요한 미해결 문제로 남아 있다.

3. 정규화 흐름 (Normalizing Flows)

식 (3)의 하한(bound)을 살펴보면,
$\mathbb{D}_{\mathrm{KL}}[q \parallel p] = 0$ 을 만족하는
최적의 변분 분포(optimal variational distribution)는
$q_\phi(\mathbf{z} \mid \mathbf{x}) = p_\theta(\mathbf{z} \mid \mathbf{x})$ 인 경우,
즉 $q$ 가 진짜 사후분포(true posterior distribution)와 일치하는 경우임을 알 수 있다.

그러나 이는 일반적으로 사용되는
$q(\cdot)$ 분포 — 예를 들어, 독립 가우시안(independent Gaussians)이나
기타 평균장(mean-field) 근사 — 에서는
명백히 실현 불가능한(possibility not realizable) 일이다.

실제로, 변분 방법론(variational methodology)의 한계 중 하나는
근사 가능한 분포 계열(approximating families)의 선택지가 제한되어 있기 때문에,
점근적(asymptotic) 상황에서도
진짜 사후분포(true posterior)를 얻을 수 없다는 점이다.

따라서 이상적인(ideal) 변분 분포 계열 $q_\phi(\mathbf{z} \mid \mathbf{x})$ 은
매우 유연하며(highly flexible),
가능하다면 진짜 사후분포를 하나의 해(solution)로 포함할 만큼
충분히 유연해야 한다.

이러한 이상적인 형태로 나아가는 하나의 경로는
정규화 흐름(normalizing flows) 의 원리에 기반한다
(Tabak & Turner, 2013; Tabak & Vanden-Eijnden, 2010).

정규화 흐름(normalizing flow)은
일련의 가역적 변환(invertible mappings)을 통해
확률 밀도(probability density)를 변환하는 과정을 설명한다.

변수 변경(change of variables)의 규칙을 반복적으로 적용함으로써,
초기 밀도(initial density)는
이 가역적 변환들의 연속을 따라 ‘흐르게(flow)’ 된다.

이러한 변환의 순서가 끝나면
우리는 유효한(valid) 확률 분포(probability distribution)를 얻게 되며,
따라서 이러한 형태의 흐름을 정규화 흐름(normalizing flow) 이라고 부른다.

3.1 유한 흐름 (Finite Flows)

밀도의 변환에 대한 기본 규칙은
역함수(inverse)가 존재하는 가역적(invertible)이고
매끄러운(smooth) 사상(mapping)
$f : \mathbb{R}^d \rightarrow \mathbb{R}^d$ 을 고려한다.
이때 그 역함수는 $f^{-1} = g$ 이며,
즉 합성함수 $g \circ f(\mathbf{z}) = \mathbf{z}$ 가 성립한다.

이 사상을 사용하여
분포 $q(\mathbf{z})$ 를 따르는 임의 변수(random variable) $\mathbf{z}$ 를 변환하면,
그 결과로 얻어지는 임의 변수 $\mathbf{z}’ = f(\mathbf{z})$ 는
다음과 같은 분포를 가진다.

\[q(\mathbf{z}') = q(\mathbf{z}) \left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right| = q(\mathbf{z}) \left| \det \frac{\partial f}{\partial \mathbf{z}} \right|^{-1} \tag{5}\]

마지막 등호는 연쇄 법칙(chain rule, 역함수 정리)에 의해 얻을 수 있으며,
이는 가역적 함수의 야코비안(Jacobian)의 성질이다.

(1) 밀도 보존 원리에서 시작한다.
변환된 변수 $\mathbf{z}’$ 가 주어졌을 때,
확률 질량(probability mass)은
변환 전후 동일한 부피 요소(volume element)에 대해
동일하게 유지되어야 한다.
따라서 밀도 보존은 다음과 같이 표현된다.
\[q(\mathbf{z})\, d\mathbf{z} = q(\mathbf{z}')\, d\mathbf{z}'\]
이는 변환 전과 후에 대응하는 부피 영역이
동일한 확률 질량을 가져야 한다는 의미이다.
(1-1) 먼저 변수 사이의 기본 관계는 다음과 같다.
\[\mathbf{z} = f^{-1}(\mathbf{z}')\]
이 식은 변환된 변수 $\mathbf{z}’$ 에 대해
원래 변수 $\mathbf{z}$ 가 역함수 $f^{-1}$을 통해 결정됨을 의미한다.
이제 이 관계를 미소 변화 관점에서 해석하면,
$\mathbf{z}’$ 가 아주 조금 변할 때 $\mathbf{z}$ 는 얼마나 변하는지를
역함수의 미분을 통해 얻을 수 있다.
즉, 양변을 미분하면 아래와 같은 식이 성립한다.
\[d\mathbf{z} = \frac{\partial f^{-1}}{\partial \mathbf{z}'}\, d\mathbf{z}'\]
(1-2) 따라서, 부피 요소의 크기 변화율은
야코비안 행렬의 행렬식(determinant)의 절댓값으로 주어진다.
\[\lvert d\mathbf{z} \rvert = \left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right| \lvert d\mathbf{z}' \rvert\]
(2) 이를 (1)의 확률 질량 보존 식에 대입하면,
\[q(\mathbf{z}) \left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right| d\mathbf{z}' = q(\mathbf{z}')\,d\mathbf{z}'\]
(3) 따라서 밀도 $q(\mathbf{z}’)$는 다음과 같이 정리된다.
\[q(\mathbf{z}') = q(\mathbf{z}) \left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right|\]
(4) 역함수 정리(inverse function theorem)에 따르면,
야코비안의 관계는 다음과 같다.
\[\left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right| = \left| \det \frac{\partial f}{\partial \mathbf{z}} \right|^{-1}\]
(5) 이를 식 (3)에 대입하면 식 (5)가 도출된다.
\[q(\mathbf{z}') = q(\mathbf{z}) \left| \det \frac{\partial f^{-1}}{\partial \mathbf{z}'} \right| = q(\mathbf{z}) \left| \det \frac{\partial f}{\partial \mathbf{z}} \right|^{-1}\]

여러 개의 단순한 사상(simple maps)을 합성(composing)하고
식 (5)를 연속적으로(successively) 적용함으로써,
임의로 복잡한(arbitrarily complex) 밀도(densities)를 구성할 수 있다.

분포 $q_0$ 를 갖는 임의의 변수 $\mathbf{z}_0$ 를
$K$ 개의 변환 $f_k$ 를 연속적으로 적용하여 변환함으로써 얻은
밀도 $q_K(\mathbf{z})$ 는 다음과 같다.

\[\mathbf{z}_K = f_K \circ \ldots \circ f_2 \circ f_1(\mathbf{z}_0) \tag{6}\] \[\ln q_K(\mathbf{z}_K) = \ln q_0(\mathbf{z}_0) - \sum_{k=1}^{K} \ln \left| \det \frac{\partial f_k}{\partial \mathbf{z}_{k-1}} \right| \tag{7}\]

(1) 먼저 식 (5)에 따라, 단일 변환 $f_k : \mathbf{z}_{k-1} \rightarrow \mathbf{z}_k$ 에 대해
밀도의 관계는 다음과 같다.
\[q_k(\mathbf{z}_k) = q_{k-1}(\mathbf{z}_{k-1}) \left| \det \frac{\partial f_k}{\partial \mathbf{z}_{k-1}} \right|^{-1}\]
(2) 로그를 취하면 곱셈 관계가 덧셈 형태로 바뀐다.
\[\ln q_k(\mathbf{z}_k) = \ln q_{k-1}(\mathbf{z}_{k-1}) - \ln \left| \det \frac{\partial f_k}{\partial \mathbf{z}_{k-1}} \right|\]
(3) 이제 이 변환을 $k=1$ 부터 $K$ 단계까지 순차적으로 적용하면,
각 단계에서 로그 항들이 누적되어 다음과 같은 합으로 표현된다.
\[\ln q_K(\mathbf{z}_K) = \ln q_0(\mathbf{z}_0) - \sum_{k=1}^{K} \ln \left| \det \frac{\partial f_k}{\partial \mathbf{z}_{k-1}} \right|\]

식 (6)은 본 논문 전체에서
합성 함수(composition) 표기 $f_K(f_{K-1}(\ldots f_1(x)))$ 를
간단히 나타내기 위한 약어로 사용된다.

초기 분포 $q_0(\mathbf{z}_0)$ 로부터 시작하여
$\mathbf{z}_k = f_k(\mathbf{z}_{k-1})$ 를 따라 이동하는 경로(path)는
‘흐름(flow)’이라고 불리며,
각 단계의 분포 $q_k$ 들이 형성하는 경로는 정규화 흐름(normalizing flow) 이라고 한다.

이러한 변환의 한 성질은,
종종 무의식 통계학자의 법칙(LOTUS, Law of the Unconscious Statistician) 이라고 불리는데,
변환된 밀도 $q_K$ 에 대한 기댓값(expectation)은
$q_K$ 를 명시적으로 계산하지 않고도 구할 수 있다는 것이다.

LOTUS는 “확률 변수의 변환에 대해, 변환된 확률밀도를 직접 구하지 않아도
기댓값을 계산할 수 있다”는 원리를 의미한다.
예를 들어, $\mathbf{z}’ = f(\mathbf{z})$ 이고 $\mathbf{z} \sim q(\mathbf{z})$ 라면,
변환된 변수의 기댓값은 다음과 같이 표현할 수 있다.
\[\mathbb{E}_{q_{f}}[h(\mathbf{z}')] = \int h(\mathbf{z}')\, q_{f}(\mathbf{z}')\, d\mathbf{z}' = \int h(f(\mathbf{z}))\, q(\mathbf{z})\, d\mathbf{z}\]
즉, 변환 후의 밀도 $q_f(\mathbf{z}’)$ 를 명시적으로 계산하지 않아도,
원래의 분포 $q(\mathbf{z})$ 와 변환 함수 $f$ 만 알면
기대값을 직접 계산할 수 있다는 뜻이다.
이 성질 덕분에 정규화 흐름(normalizing flow)에서는
복잡한 변환 뒤의 밀도를 일일이 계산하지 않고도
효율적으로 기대값이나 손실 함수를 평가할 수 있다.

임의의 함수 $h(\mathbf{z})$ 에 대한 기댓값은 다음과 같이 표현할 수 있다.

\[\mathbb{E}_{q_K}[h(\mathbf{z})] = \mathbb{E}_{q_0}\left[ h(f_K \circ f_{K-1} \circ \ldots \circ f_1(\mathbf{z}_0)) \right] \tag{8}\]

이는 $h(\mathbf{z})$ 가 $q_K$ 에 의존하지 않는 한,
로그-야코비안(log-determinant Jacobian) 항을
계산할 필요가 없음을 의미한다.

우리는 가역적 흐름(invertible flows)의 효과를
초기 밀도(initial density)에 대한 팽창(expansion) 또는 수축(contraction)의
연속적인 과정으로 이해할 수 있다.

팽창의 경우, 사상(mapping) $\mathbf{z}’ = f(\mathbf{z})$ 는
$\mathbb{R}^d$ 내의 어떤 영역(region)으로부터
점(point) $\mathbf{z}$ 들을 바깥으로 끌어내며,
그 영역 내의 밀도(density)를 감소시키는 동시에
그 영역 밖의 밀도를 증가시킨다.

반대로 수축의 경우, 사상은 점들을
영역의 내부로 밀어 넣으며,
그 내부의 밀도를 증가시키는 동시에
영역 밖의 밀도를 감소시킨다.

정규화 흐름(normalizing flows)의 형식(formalism)은
이제 변분 추론(variational inference)에 필요한
근사 사후분포(approximate posterior distributions) $q(\mathbf{z} \mid \mathbf{x})$ 를
체계적으로(specifically) 명시하는 방법을 제공한다.

적절한 변환 $f_K$ 를 선택하면,
처음에는 독립 가우시안(independent Gaussian)과 같은
단순한 분리된(factorized) 분포를 사용할 수 있으며,
그 후 서로 다른 길이의 정규화 흐름(normalizing flows)을 적용하여
점점 더 복잡하고 다봉(multi-modal) 분포들을
얻을 수 있다.

3.2 무한소 흐름 (Infinitesimal Flows)

정규화 흐름(normalizing flow)의 길이가
무한대로 발산하는(infinity로 향하는) 경우를 고려하는 것은 자연스럽다.

이 경우, 우리는 무한소 흐름(infinitesimal flow) 을 얻게 된다.
이는 유한한(finite) 개수의 변환 시퀀스 — 즉, 유한 흐름(finite flow) — 으로 표현되지 않고,
다음과 같은 편미분 방정식(partial differential equation)으로 표현된다.

이 방정식은 초기 밀도(initial density) $q_0(\mathbf{z})$ 가
‘시간(time)’에 따라 어떻게 변화하는지를 나타낸다.

\[\frac{\partial}{\partial t} q_t(\mathbf{z}) = \mathcal{T}_t[q_t(\mathbf{z})]\]

여기서 $\mathcal{T}$ 는 연속 시간(dynamic continuous-time) 상의
변화 과정을 기술(describes)한다.

“무한소 흐름(infinitesimal flow)” 은
유한한(finite) 단계의 변환을 하나씩 거치는 대신,
변환의 단계 수가 무한히 많아지면서 각 단계의 변화가 극도로 작아진 연속적인 흐름을 의미한다.
즉, 유한 흐름(finite flow)은
$K$ 번의 변환 $f_1, f_2, \ldots, f_K$ 를 거쳐
$q_0 \to q_K$ 로 바꾸는 과정이라면,
무한소 흐름은 $K \to \infty$ 로 가면서
시간 $t$ 에 따라 밀도 $q_t(\mathbf{z})$ 가 부드럽게 변하는 연속적 과정을 다루는 것이다.
따라서 개별적인 변환 함수들이 아닌,
“시간에 따른 변화율(derivative)”로 밀도의 변화를 기술하게 되며
그 결과가 편미분 방정식(Partial Differential Equation, PDE)으로 표현된다.
이때 연산자 $\mathcal{T}_t$ 는
주어진 시점 $t$ 에서 밀도 $q_t(\mathbf{z})$ 가
어떻게 ‘흐름(flow)’을 따라 이동하거나 변형되는지를 나타내는
연속 시간 상의 동역학(continuous-time dynamics) 을 의미한다.

랑주뱅 흐름 (Langevin Flow)

흐름의 한 중요한 부류(one important family of flows)는
랑주뱅 확률 미분 방정식(Langevin stochastic differential equation, SDE)에 의해 주어진다.

\[d\mathbf{z}(t) = \mathbf{F}(\mathbf{z}(t), t)\,dt + \mathbf{G}(\mathbf{z}(t), t)\,d\boldsymbol{\xi}(t), \tag{9}\]

여기서 $d\boldsymbol{\xi}(t)$ 는 Wiener 과정이며,
$\mathbb{E}[\xi_i(t)] = 0$ 이고
$\mathbb{E}[\xi_i(t)\xi_j(t’)] = \delta_{i,j}\delta(t - t’)$ 를 만족한다.

$\mathbf{F}$ 는 drift 벡터,
$\mathbf{D} = \mathbf{G}\mathbf{G}^{\top}$ 는 확산 행렬(diffusion matrix) 이다.

식 (9)는 랑주뱅 확률 미분 방정식(Langevin SDE) 의 일반적인 형태를 나타낸다.
이는 시간에 따라 확률적으로 변화하는 변수 $\mathbf{z}(t)$ 의
연속적인 진화를 수학적으로 기술하는 방정식이다.
첫 번째 항 $\mathbf{F}(\mathbf{z}(t), t)\,dt$ 는
결정론적(deterministic) 변화, 즉 시스템이 시간에 따라 평균적으로
어떤 방향으로 이동하는지를 나타내는 drift 항이다.
두 번째 항 $\mathbf{G}(\mathbf{z}(t), t)\,d\boldsymbol{\xi}(t)$ 는
확률적(stochastic) 변화, 즉 무작위 요인에 의한 변동을 반영하는 확산 항(diffusion term) 이다.
여기서 $d\boldsymbol{\xi}(t)$ 는 평균이 0이고,
공분산이 $\mathbb{E}[\xi_i(t)\xi_j(t’)] = \delta_{i,j}\delta(t - t’)$ 인
Wiener 과정(Brownian motion) 을 따른다.
따라서 $\mathbf{F}$ 는 시스템의 ‘평균적인 이동 방향’을 결정하고,
$\mathbf{G}$ 는 확률적 변동의 ‘크기와 방향’을 조절한다.
$\mathbf{D} = \mathbf{G}\mathbf{G}^{\top}$ 는 이러한 확산의 공분산을 나타내는 확산 행렬(diffusion matrix) 로,
시스템 내의 불확실성이 각 차원 간에 어떻게 퍼지는지를 수량적으로 기술한다.

초기 밀도 $q_0(\mathbf{z})$ 를 갖는 임의 변수(random variable) $\mathbf{z}$ 를
랑주뱅 흐름을 통해 변환하면,
밀도의 변환 규칙은 포커-플랑크(Fokker–Planck) 방정식
(또는 확률 이론에서의 Kolmogorov 방정식)에 의해 주어진다.

시간 $t$ 에서의 변환된 샘플들의 밀도 $q_t(\mathbf{z})$ 는 다음과 같이 변화한다.

\[\frac{\partial}{\partial t} q_t(\mathbf{z}) = -\sum_i \frac{\partial}{\partial z_i} [F_i(\mathbf{z}, t) q_t] + \frac{1}{2} \sum_{i,j} \frac{\partial^2}{\partial z_i \partial z_j} [D_{ij}(\mathbf{z}, t) q_t].\]

머신러닝에서, 우리는 주로
다음과 같은 형태의 랑주뱅 흐름을 사용한다.

\[\mathbf{F}(\mathbf{z}, t) = -\nabla_{\mathbf{z}} \mathcal{L}(\mathbf{z}), \quad \mathbf{G}(\mathbf{z}, t) = \sqrt{2}\,\delta_{ij},\]

여기서 $\mathcal{L}(\mathbf{z})$ 는 모델의 비정규화된 로그 밀도(unnormalised log-density) 이다.

특히 이 경우, $q_t(\mathbf{z})$ 의 정상 해(stationary solution)는
볼츠만 분포(Boltzmann distribution)로 주어지며 다음과 같다.

\[q_{\infty}(\mathbf{z}) \propto e^{-\mathcal{L}(\mathbf{z})}.\]

즉, 초기 밀도 $q_0(\mathbf{z})$ 로부터 시작하여
랑주뱅 확률 미분 방정식(SDE)을 통해 샘플 $\mathbf{z}_0$ 를 진화시키면,
결과 점 $\mathbf{z}_\infty$ 들은
$q_{\infty}(\mathbf{z}) \propto e^{-\mathcal{L}(\mathbf{z})}$ 를 따른다.

이는 진정한 사후분포(true posterior) 에 해당한다.

위 식은 포커–플랑크(Fokker–Planck) 방정식으로,
랑주뱅 확률 미분 방정식(Langevin SDE)에 의해
확률 밀도 $q_t(\mathbf{z})$ 가 시간에 따라 어떻게 변하는지를 기술한다.
이 방정식은 개별 샘플의 움직임이 아닌,
확률 분포 전체의 시간적 진화를 묘사한다는 점에서 의미가 있다.
첫 번째 항
\[-\sum_i \frac{\partial}{\partial z_i} [F_i(\mathbf{z}, t) q_t]\]
은 drift 항으로, 확률 질량이 평균적인 이동 방향 $\mathbf{F}$ 에 따라 이동하는 효과를 나타낸다.
두 번째 항
\[\frac{1}{2} \sum_{i,j} \frac{\partial^2}{\partial z_i \partial z_j} [D_{ij}(\mathbf{z}, t) q_t]\]
은 diffusion 항으로, 확률적 요인(잡음)에 의해 확률 질량이 퍼져나가는 현상을 나타낸다.
머신러닝에서 사용하는 단순화된 형태
\[\mathbf{F}(\mathbf{z}, t) = -\nabla_{\mathbf{z}} \mathcal{L}(\mathbf{z}), \quad \mathbf{G}(\mathbf{z}, t) = \sqrt{2}\,\delta_{ij},\]
는 확률적 그래디언트 하강(Stochastic Gradient Descent, SGD) 과 유사한 구조를 가진다.
이때 $\mathcal{L}(\mathbf{z})$ 는 에너지 함수(energy function) 역할을 하며,
$-\nabla_{\mathbf{z}} \mathcal{L}(\mathbf{z})$ 가 에너지를 최소화하는 방향으로 샘플을 이동시키고,
$\sqrt{2}\,\delta_{ij}$ 항이 확률적 변동을 더한다.
시간이 충분히 경과하면 시스템은 정상 상태(stationary state) 에 도달하며,
이때의 분포는 다음과 같은 볼츠만 분포(Boltzmann distribution) 로 수렴한다.
\[q_{\infty}(\mathbf{z}) \propto e^{-\mathcal{L}(\mathbf{z})}.\]
즉, 초기 분포 $q_0(\mathbf{z})$ 를
랑주뱅 동역학(Langevin dynamics)을 통해 점진적으로 진화시키면,
최종적으로 진정한 사후분포(true posterior) 에 해당하는 분포를 얻을 수 있다.

이 접근법은 복잡한 밀도에서의 샘플링(sampling)을 위해
Welling & Teh (2011), Ahn et al. (2012), Suykens et al. (1998) 등에 의해 탐구되었다.

해밀토니안 흐름(Hamiltonian Flow).

해밀토니안 몬테카를로(Hamiltonian Monte Carlo, HMC)는
확장된(augmented) 공간 $\tilde{\mathbf{z}} = (\mathbf{z}, \boldsymbol{\omega})$ 상의 정규화 흐름(normalizing flow)으로도 기술될 수 있으며,
그 동역학(dynamics)은 해밀토니안(Hamiltonian)

\[\mathcal{H}(\mathbf{z}, \boldsymbol{\omega}) = -\mathcal{L}(\mathbf{z}) - \tfrac{1}{2} \boldsymbol{\omega}^{\top}\mathbf{M}\boldsymbol{\omega}\]

으로부터 유도된다.

HMC는 머신러닝에서도 널리 사용되며 (예: Neal, 2011),
본 논문에서는 해밀토니안 흐름을 사용하여
Salimans 등(2015)이 최근에 제안한
해밀토니안 변분 접근법(Hamiltonian variational approach)과의 연관성을
섹션 5에서 다룬다.

해밀토니안 흐름(Hamiltonian flow)은 물리학의 에너지 보존 원리를
확률적 샘플링(sampling) 문제에 적용한 개념이다.
여기서 $\mathbf{z}$ 는 ‘위치(position)’에 해당하고,
$\boldsymbol{\omega}$ 는 ‘운동량(momentum)’에 해당한다.
두 변수를 합친 확장 공간 $\tilde{\mathbf{z}} = (\mathbf{z}, \boldsymbol{\omega})$ 에서
확률 분포의 움직임을 물리적 시스템의 운동처럼 기술할 수 있다.
해밀토니안 함수 $\mathcal{H}(\mathbf{z}, \boldsymbol{\omega})$ 는
시스템의 전체 에너지(total energy) 를 의미하며,
여기서 $-\mathcal{L}(\mathbf{z})$ 는 잠재 공간의 ‘위치 에너지(potential energy)’이고,
$\tfrac{1}{2}\boldsymbol{\omega}^\top \mathbf{M} \boldsymbol{\omega}$ 는
‘운동 에너지(kinetic energy)’를 나타낸다.
HMC(Hamiltonian Monte Carlo)는
이 에너지 보존 법칙을 이용해 샘플을 “물리적으로” 이동시킴으로써
사후분포의 고차원 공간을 효율적으로 탐색한다.
즉, 확률적 움직임에 의존하는 단순한 랜덤 워크가 아니라,
물리 법칙에 따라 연속적으로 샘플을 이동시키기 때문에
더 빠르고 효율적인 탐색이 가능하다.
이러한 원리를 정규화 흐름(normalizing flow)의 틀에서 해석하면,
해밀토니안 흐름은 에너지 보존을 만족하는 특수한 형태의 invertible flow 로 이해할 수 있다.

4. 정규화 흐름을 이용한 추론 (Inference with Normalizing Flows)

유한한 정규화 흐름(finite normalizing flows)을 사용하여
확장 가능한 추론(scalable inference)을 가능하게 하려면,
사용할 수 있는 가역 변환(invertible transformations)의 한 종류(class)를 명시하고,
야코비안(Jacobian)의 행렬식(determinant)을 계산하기 위한
효율적인 메커니즘을 마련해야 한다.

식 (5)에 사용할 수 있는 가역적인 매개변수 함수(invertible parametric functions)를
구성하는 것은 비교적 간단하다.
예를 들어, 가역 신경망(invertible neural networks) (Baird et al., 2005; Rippel & Adams, 2013) 등이 있다.
그러나 이러한 접근 방식은 일반적으로
야코비안 행렬식의 계산 복잡도가 $O(LD^3)$ 로 증가한다.
여기서 $D$ 는 은닉층(hidden layer)의 차원 수이고,
$L$ 은 사용된 은닉층의 개수이다.

또한, 야코비안 행렬식의 그래디언트를 계산하는 과정에서도
$O(LD^3)$ 에 해당하는 여러 추가 연산이 필요하며,
이때 행렬의 역행렬(matrix inverse)이 포함되므로
수치적으로 불안정(numerically unstable)할 수 있다.

따라서 우리는
행렬식의 계산 비용이 낮거나,
야코비안을 전혀 계산할 필요가 없는 정규화 흐름(normalizing flows) 이 필요하다.

4.1. 가역적인 선형 시간 변환 (Invertible Linear-time Transformations)

다음 형태의 변환들의 집합(family)을 고려한다:

\[f(\mathbf{z}) = \mathbf{z} + \mathbf{u} h(\mathbf{w}^\top \mathbf{z} + b), \tag{10}\]

여기서
$\lambda = \lbrace \mathbf{w} \in \mathbb{R}^D, \mathbf{u} \in \mathbb{R}^D, b \in \mathbb{R} \rbrace$ 는
자유 매개변수(free parameters)이며,
$h(\cdot)$ 는 매끄러운(smooth) 원소별 비선형 함수(element-wise non-linearity)로서,
그 도함수(derivative)는 $h’(\cdot)$ 로 표시된다.

이러한 사상(mapping)에 대해,
행렬식 보조정리(matrix determinant lemma)를 이용하면
로그-야코비안(logdet-Jacobian) 항을 $O(D)$ 시간 안에 계산할 수 있다.

\[\boldsymbol{\psi}(\mathbf{z}) = h'(\mathbf{w}^\top \mathbf{z} + b)\mathbf{w} \tag{11}\] \[\left| \det \frac{\partial f}{\partial \mathbf{z}} \right| = \left| \det(\mathbf{I} + \mathbf{u}\boldsymbol{\psi}(\mathbf{z})^\top) \right| = \left| 1 + \mathbf{u}^\top \boldsymbol{\psi}(\mathbf{z}) \right|. \tag{12}\]

먼저, 식 (10)의 변환
\[f(\mathbf{z}) = \mathbf{z} + \mathbf{u}h(\mathbf{w}^\top \mathbf{z} + b)\]
를 $\mathbf{z}$ 에 대해 미분하면 다음과 같다.
\[\frac{\partial f}{\partial \mathbf{z}} = \mathbf{I} + \mathbf{u} \frac{\partial h(\mathbf{w}^\top \mathbf{z} + b)}{\partial \mathbf{z}}\]
여기서 체인 룰(chain rule)을 적용하면
\[\frac{\partial h(\mathbf{w}^\top \mathbf{z} + b)}{\partial \mathbf{z}} = h'(\mathbf{w}^\top \mathbf{z} + b)\mathbf{w}^\top\]
이므로,
\[\frac{\partial f}{\partial \mathbf{z}} = \mathbf{I} + \mathbf{u}\mathbf{w}^\top h'(\mathbf{w}^\top \mathbf{z} + b)\]
이제 이를 간단히 표기하기 위해
\[\boldsymbol{\psi}(\mathbf{z}) = h'(\mathbf{w}^\top \mathbf{z} + b)\mathbf{w}\]
로 정의한다.
따라서,
\[\frac{\partial f}{\partial \mathbf{z}} = \mathbf{I} + \mathbf{u}\boldsymbol{\psi}(\mathbf{z})^\top\]
행렬식 보조정리(Matrix Determinant Lemma)에 따르면,
임의의 벡터 $\mathbf{u}$, $\mathbf{v}$ 에 대해
\[\det(\mathbf{I} + \mathbf{u}\mathbf{v}^\top) = 1 + \mathbf{v}^\top \mathbf{u}\]
가 성립하므로, 본 식의 야코비안 행렬식은
\[\left| \det \frac{\partial f}{\partial \mathbf{z}} \right| = \left| 1 + \mathbf{u}^\top \boldsymbol{\psi}(\mathbf{z}) \right|\]
로 계산된다.
이때 계산 복잡도는 벡터 내적(inner product) 연산만 포함하므로
$O(D)$ 시간에 효율적으로 계산할 수 있다.

식 (7)로부터,
임의의 초기 밀도(initial density) $q_0(\mathbf{z})$ 가
식 (10) 형태의 일련의 사상 $f_k$ 를 통해 변환될 때
얻어지는 밀도 $q_K(\mathbf{z})$ 는 다음과 같이 암묵적으로 표현된다:

\[\mathbf{z}_K = f_K \circ f_{K-1} \circ \ldots \circ f_1(\mathbf{z})\] \[\ln q_K(\mathbf{z}_K) = \ln q_0(\mathbf{z}_0) - \sum_{k=1}^{K} \ln \left| 1 + \mathbf{u}_k^\top \boldsymbol{\psi}_k(\mathbf{z}_{k-1}) \right|. \tag{13}\]

식 (13)에 의해 정의된 흐름(flow)은
초기 밀도(initial density) $q_0$ 를 수정하는데,
이는 초평면(hyperplane) $\mathbf{w}^\top \mathbf{z} + b = 0$ 에
수직(perpendicular)한 방향으로 수축(contraction)과 팽창(expansion)의
일련의 변환을 적용함으로써 이루어진다.
따라서 이러한 사상(mapping)을 평면 흐름(planar flows) 이라고 부른다.

식 (10)의 변환
\[f(\mathbf{z}) = \mathbf{z} + \mathbf{u}h(\mathbf{w}^\top \mathbf{z} + b)\]
는
입력 벡터 $\mathbf{z}$ 가 초평면 $\mathbf{w}^\top \mathbf{z} + b = 0$ 을 기준으로
이동하는 방식의 변환을 정의한다.
여기서 $h(\mathbf{w}^\top \mathbf{z} + b)$ 는
점 $\mathbf{z}$ 가 초평면으로부터 얼마나 떨어져 있는지를 나타내는 스칼라 함수로,
그 값이 클수록 더 많이, 작을수록 덜 이동하게 만든다.
초평면의 방정식 $\mathbf{w}^\top \mathbf{z} + b = 0$ 은
벡터 $\mathbf{w}$ 를 법선(normal) 방향으로 가지므로,
$\mathbf{w}^\top \mathbf{z} + b$ 의 부호와 크기는
점 $\mathbf{z}$ 가 초평면에 대해 어느 쪽에,
얼마나 떨어져 있는지를 결정한다.
따라서,
$\mathbf{w}^\top \mathbf{z} + b > 0$ 인 점들은 초평면의 한쪽 영역에 있고,
$\mathbf{w}^\top \mathbf{z} + b < 0$ 인 점들은 반대쪽 영역에 위치한다.
함수 $h(\cdot)$ 의 값이 이러한 거리(또는 방향)에 따라 변하므로,
각 점은 $\mathbf{u}$ 방향으로 이동하는데,
이 이동의 크기는 초평면에 대한 거리 $\mathbf{w}^\top \mathbf{z} + b$ 에 의해 조절된다.
특히, $\mathbf{u}$ 가 $\mathbf{w}$ 방향과 같거나 반대 방향으로 설정되면,
점들의 이동은 초평면에 대해 정확히 수직 방향으로 이루어진다.
이 경우 초평면은 움직임의 기준면이 되어
한쪽에서는 팽창(expansion), 다른 쪽에서는 수축(contraction) 이 발생한다.
따라서 이 변환은 초평면을 기준으로,
각 점을 그 면에 수직한 방향으로 밀거나 끌어당기는 변환이라 할 수 있으며,
이러한 이유로 평면 흐름(planar flow) 이라 부른다.

대안으로, 기준점(reference point) $\mathbf{z}_0$ 주변의
초기 밀도 $q_0$ 를 수정하는 변환 집합(family of transformations)을 고려할 수 있다.
이 변환 집합은 다음과 같다:

\[f(\mathbf{z}) = \mathbf{z} + \beta h(\alpha, r)(\mathbf{z} - \mathbf{z}_0), \tag{14}\] \[\left| \det \frac{\partial f}{\partial \mathbf{z}} \right| = [1 + \beta h(\alpha, r)]^{d-1} [1 + \beta h(\alpha, r) + \beta h'(\alpha, r)r],\]

여기서 $r = \lVert \mathbf{z} - \mathbf{z}_0 \rVert$,
$h(\alpha, r) = 1 / (\alpha + r)$ 이며,
사상의 매개변수(parameters)는
$\lambda = \lbrace \mathbf{z}_0 \in \mathbb{R}^D, \alpha \in \mathbb{R}^+, \beta \in \mathbb{R} \rbrace$ 이다.

이 집합 역시 행렬식(determinant)을 선형 시간(linear-time) 내에 계산할 수 있다.
이는 기준점 $\mathbf{z}_0$ 주변에서의
방사형 수축(radial contraction) 과
방사형 팽창(radial expansion) 을 적용하므로,
이러한 변환을 방사형 흐름(radial flows) 이라고 부른다.

식 (14)는 방사형 흐름(radial flow) 을 정의하는 식으로,
기준점 $\mathbf{z}_0$ 를 중심으로 주변 점들을
방사형(radial) 방향, 즉 중심에서 바깥쪽 혹은 안쪽으로
이동시키는 변환을 나타낸다.
구체적으로, 각 점 $\mathbf{z}$ 는
중심점 $\mathbf{z}_0$ 로부터의 거리 $r = \lVert \mathbf{z} - \mathbf{z}_0 \rVert$ 에 따라
이동 정도가 달라진다.
함수 $h(\alpha, r) = 1/(\alpha + r)$ 는
거리 $r$ 이 커질수록 작아지므로,
중심에 가까운 점일수록 더 크게 이동하고
멀리 있는 점일수록 거의 움직이지 않게 된다.
계수 $\beta$ 는 이동의 방향과 강도를 조절하는 파라미터로,
$\beta > 0$이면 점들이 중심에서 멀어지며 팽창(expansion) 하고,
$\beta < 0$이면 점들이 중심으로 끌려들어가며 수축(contraction) 한다.
따라서 이 변환은
초평면을 기준으로 한 평면 흐름(planar flow)과 달리,
기준점 $\mathbf{z}_0$ 을 중심으로 한 구형(spherical) 변형을 수행한다.
야코비안 행렬식의 항
$\left| \det \frac{\partial f}{\partial \mathbf{z}} \right|$
은
변환에 따라 확률 밀도가 얼마나 늘어나거나 줄어드는지를 나타낸다.

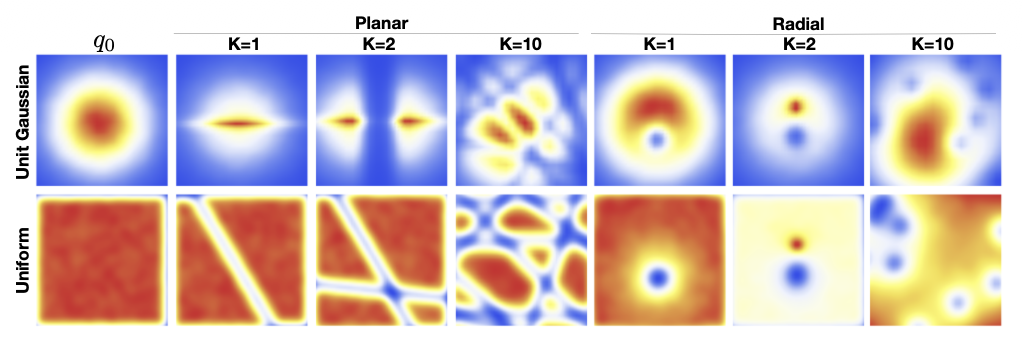
그림 1에서는 흐름 (10)과 (14)를 사용하여
균등 분포(uniform)와 가우시안(Gaussian) 초기 밀도에
팽창과 수축을 적용한 결과를 시각화하였다.
이 시각화는 두 번의 연속적인 변환을 적용함으로써
구형 가우시안 분포(spherical Gaussian distribution)를
쌍봉(bimodal) 분포로 변환할 수 있음을 보여준다.

그림 1. 두 분포에 대한 정규화 흐름(normalizing flow)의 효과.

식 (10) 또는 (14) 형태의 모든 함수가
가역적(invertible)인 것은 아니다.
부록(appendix)에서는 이러한 함수들이
가역성을 만족시키는 조건과,
이를 수치적으로 안정적인 방식으로 구현하는 방법을 논의한다.

4.2. 흐름(Flow)을 기반으로 한 자유 에너지 경계 (Flow-Based Free Energy Bound)

길이 $K$ 의 흐름(flow)을 갖는 근사 사후분포(approximate posterior distribution)
$q_\phi(\mathbf{z} \mid \mathbf{x}) := q_K(\mathbf{z}_K)$ 로 매개변수를 설정하면,
자유 에너지(free energy)는 초기 분포 $q_0(\mathbf{z})$ 에 대한 기댓값(expectation)으로 다음과 같이 쓸 수 있다:

\[\begin{align} \mathcal{F}(\mathbf{x}) &= \mathbb{E}_{q_\phi(\mathbf{z}\mid \mathbf{x})} [\log q_\phi(\mathbf{z}\mid \mathbf{x}) - \log p(\mathbf{x}, \mathbf{z})]\\[6pt] &= \mathbb{E}_{q_0(\mathbf{z}_0)} [\log q_K(\mathbf{z}_K) - \log p(\mathbf{x}, \mathbf{z}_K)]\\[6pt] &= \mathbb{E}_{q_0(\mathbf{z}_0)}[\log q_0(\mathbf{z}_0)] - \mathbb{E}_{q_0(\mathbf{z}_0)}[\log p(\mathbf{x}, \mathbf{z}_K)] \notag\\[4pt] &\quad - \mathbb{E}_{q_0(\mathbf{z}_0)}\!\left[ \sum_{k=1}^{K}\ln\!\left|1 + \mathbf{u}_k^{\top}\boldsymbol{\psi}_k(\mathbf{z}_{k-1})\right| \right]. \tag{15} \end{align}\]

첫 번째 식은 자유 에너지 $\mathcal{F}(\mathbf{x})$ 의 정의식으로,
근사 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 와 결합분포 $p(\mathbf{x}, \mathbf{z})$ 간의
로그 확률 차이에 대한 기댓값으로 표현된다.
이는 변분 추론(variational inference)에서 사용하는 기본 형태이다.
두 번째 식에서는 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
길이 $K$ 의 정규화 흐름(normalizing flow) $q_K(\mathbf{z}_K)$ 로 표현된다는 점을 이용한다.
즉, 잠재 변수 $\mathbf{z}$ 는 초기 샘플 $\mathbf{z}_0$ 로부터
일련의 가역 변환들 $f_1, f_2, \ldots, f_K$ 을 통해
$\mathbf{z}_K = f_K \circ f_{K-1} \circ \cdots \circ f_1(\mathbf{z}_0)$ 로 매핑된다.
따라서 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대한 기댓값은
동일한 확률 질량을 보존하는 $q_0(\mathbf{z}_0)$ 에 대한 기대값으로 바뀔 수 있다.
또한, $\log p(\mathbf{x}, \mathbf{z})$ 항의 $\mathbf{z}$ 역시
흐름을 통해 변환된 변수 $\mathbf{z}_K$ 로 대체된다.
이는 모델이 실제로 샘플링하는 잠재 변수의 최종 형태가 $\mathbf{z}_K$ 이기 때문이다.
따라서 결합분포의 평가 지점도 자연스럽게 $\mathbf{z}_K$ 로 바뀐다.
세 번째 식은 식 (7)에서의 흐름 변환 관계를 대입하여
$\log q_K(\mathbf{z}_K)$ 를 $\log q_0(\mathbf{z}_0)$ 와
야코비안의 로그 행렬식(log-determinant Jacobian) 항으로 분리한 결과이다.
\[\log q_K(\mathbf{z}_K) = \log q_0(\mathbf{z}_0) - \sum_{k=1}^{K}\ln\!\left|\det \frac{\partial f_k}{\partial \mathbf{z}_{k-1}}\right|.\]
여기서 각 야코비안 항은 식 (12)의 결과에 따라
\[\ln|1 + \mathbf{u}_k^{\top}\boldsymbol{\psi}_k(\mathbf{z}_{k-1})|\]
로 단순화된다.
따라서 전체 자유 에너지는
(1) 초기 밀도의 로그 항,
(2) 관측 데이터에 대한 결합 확률 로그 항,
(3) 흐름의 야코비안 기여 항
세 부분으로 분리되어 표현된다.

정규화 흐름(normalizing flow)과 이 자유 에너지 경계(free energy bound)는
일반화된 변분 EM을 포함한 어떠한 변분 최적화 기법(variational optimization scheme)과도 함께 사용할 수 있다.

상각 변분 추론(amortized variational inference)을 위해,
심층 신경망(deep neural network)을 사용하여
관찰값 $\mathbf{x}$ 로부터 초기 밀도 $q_0 = \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma})$ ($\boldsymbol{\mu} \in \mathbb{R}^D$, $\boldsymbol{\sigma} \in \mathbb{R}^D$)의 매개변수와
흐름(flow)의 매개변수 $\boldsymbol{\lambda}$ 로의 사상(mapping)을 구성한다.

4.3 알고리즘 요약 및 복잡도 (Algorithm Summary and Complexity)

결과적으로 얻어지는 알고리즘은
Kingma & Welling (2014), Rezende et al. (2014) 에서 기술된
DLGM에 대한 분할 상환 추론(amortized inference) 알고리즘의
단순한 수정 버전이다.
이 알고리즘을 알고리즘 1에서 요약한다.

알고리즘 1
정규화 흐름(Normalizing Flows)을 이용한 변분 추론 (Variational Inference with Normalizing Flows)

파라미터:
$\phi$ — 변분 파라미터 (variational),
$\theta$ — 생성 파라미터 (generative)

while 수렴하지 않을 때까지 do

$\mathbf{x} \leftarrow$ {미니배치 가져오기 (Get mini-batch)}

$\mathbf{z}_0 \sim q_0(\cdot \mid \mathbf{x})$

$\mathbf{z}_K \leftarrow f_K \circ f_{K-1} \circ \ldots \circ f_1(\mathbf{z})$

$\mathcal{F}(\mathbf{x}) \approx \mathcal{F}(\mathbf{x}, \mathbf{z}_K)$

$\Delta\boldsymbol{\theta} \propto -\nabla_{\boldsymbol{\theta}}\mathcal{F}(\mathbf{x})$

$\Delta\boldsymbol{\phi} \propto -\nabla_{\boldsymbol{\phi}}\mathcal{F}(\mathbf{x})$

end while

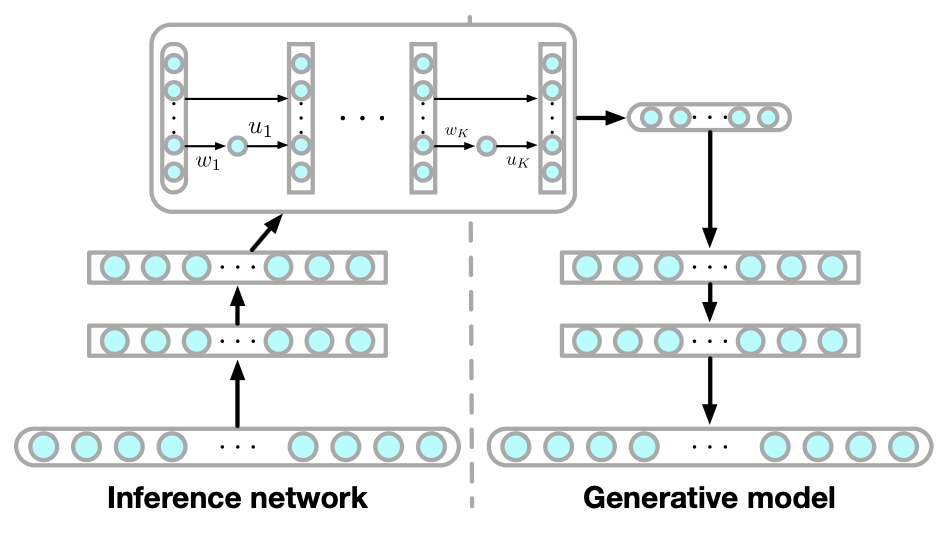
그림 2. 추론 모델(inference model)과 생성 모델(generative model).
왼쪽: 추론 네트워크(inference network)는 관측값(observations)을
흐름(flow)의 파라미터로 매핑한다.
오른쪽: 생성 모델은 학습 시(training time)
추론 네트워크로부터 사후분포 샘플(posterior samples)을 입력받는다.

원형 컨테이너(round containers)는 확률적 변수층(stochastic variable layers)을,
사각형 컨테이너(square containers)는 결정론적 층(deterministic layers)을 나타낸다.

정규화 흐름(Normalizing Flow)은
단순한 분포(예: 가우시안 분포)로부터 복잡한 분포를 생성하기 위해
일련의 가역적(invertible) 변환 $f_1, f_2, \dots, f_K$ 을 적용하는 방식이다.
각 변환 $f_k$ 는 야코비안 행렬(Jacobian)을 통해
밀도의 변화(density transformation)를 계산할 수 있도록 정의된다.
즉, 단순한 분포에서 샘플링한 $\mathbf{z}_0 \sim q_0(\mathbf{z})$ 를
여러 번의 변환을 거쳐 $\mathbf{z}_K = f_K \circ \dots \circ f_1(\mathbf{z}_0)$ 로 변환하면,
최종 분포 $q_K(\mathbf{z}_K)$ 는 훨씬 복잡하고 유연한 형태의 분포가 된다.
그림 2와 같이, 추론 네트워크(inference network)와
생성 모델(generative model)은 다음과 같은 역할을 수행한다.
(1) 인코더(Encoder, 추론 네트워크)
입력 $\mathbf{x}$ 로부터 초기 잠재 변수 $\mathbf{z}_0$ 의 분포 $q_0(\mathbf{z}_0 \mid \mathbf{x})$ 를 예측한다.
즉, 단순한 분포(예: $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma})$)의 평균과 분산을 추정하여
잠재 공간(latent space) 상의 출발점을 정의한다.
이 네트워크는 동시에 정규화 흐름의 파라미터 $\boldsymbol{\lambda}$
(예: 각 변환의 $\mathbf{u}, \mathbf{w}, b$) 도 출력한다.
즉, 그림 2의 왼쪽에서처럼 관측값을 흐름의 파라미터로 매핑하는 역할을 한다.
인코더의 출력 분포 $q_0(\mathbf{z}_0 \mid \mathbf{x})$ 로부터
실제 샘플링이 한 번 발생한다.
이는 reparameterization trick을 사용하여
$\mathbf{z}_0 = \boldsymbol{\mu}_\phi(\mathbf{x}) + \boldsymbol{\sigma}_\phi(\mathbf{x}) \odot \boldsymbol{\epsilon}$,
$\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$
의 형태로 표현된다.
따라서 모델 내에서 확률적 샘플링은 이 구간에서만 수행된다.
(2) 정규화 흐름(Flow)
인코더가 예측한 초기 잠재 변수 $\mathbf{z}_0$ 와 파라미터 $\boldsymbol{\lambda}$ 를 이용해
$K$ 번의 가역적 변환을 수행한다.
이 과정은 완전히 결정론적(deterministic) 변환이며,
각 단계는 $\mathbf{z}_k = f_k(\mathbf{z}_{k-1}; \boldsymbol{\lambda}_k)$ 의 형태로 정의된다.
하지만 입력 $\mathbf{z}_0$ 가 확률 변수이므로,
변환 결과 $\mathbf{z}_K$ 또한 확률적 성질을 유지한다.
즉, Flow는 확률 변수를 결정론적으로 변환하되,
확률성이 입력으로부터 전파(propagate)된다.
이 과정을 통해 단순한 분포 $q_0$ 가 점차 복잡한 분포 $q_K$ 로 바뀌게 된다.
흐름의 파라미터 $\boldsymbol{\lambda}$ 는 인코더의 일부로 간주되어
인코더 파라미터 $\boldsymbol{\phi}$ 와 함께 역전파를 통해 학습된다.
(3) 디코더(Decoder, 생성 모델)
학습 과정에서 추론 네트워크로부터 전달된 사후분포 샘플 $\mathbf{z}_K$ 를 입력으로 받아,
관측값 $\mathbf{x}$ 의 복원 확률 $p_\theta(\mathbf{x} \mid \mathbf{z}_K)$ 를 예측한다.
디코더는 결정론적 신경망으로 구성되어 있지만,
입력 $\mathbf{z}_K$ 가 확률 변수이므로
전체적으로 확률적 생성 모델로 작동한다.
즉, 잠재 표현으로부터 데이터를 복원하거나 새로운 샘플을 생성하는 역할을 한다.
파라미터들의 역할 요약
$\boldsymbol{\phi}$: 인코더(추론 네트워크)의 파라미터
$\mathbf{x}$ 로부터 $q_0(\mathbf{z}_0 \mid \mathbf{x})$ 와 $\boldsymbol{\lambda}$ 를 예측한다.
$\boldsymbol{\mu}(\mathbf{x}), \boldsymbol{\sigma}(\mathbf{x})$ 및 흐름 파라미터의 초기값을 학습한다.
$\boldsymbol{\lambda}$: 정규화 흐름(Flow)의 파라미터
각 단계의 변환 $f_k$ 를 정의하는 가중치들 (예: $\mathbf{u}, \mathbf{w}, b$).
인코더로부터 입력받아 매 스텝의 변환을 조절하며,
인코더 파라미터 $\boldsymbol{\phi}$ 와 함께 업데이트된다.
$\boldsymbol{\theta}$: 디코더(생성 모델)의 파라미터
최종 잠재 변수 $\mathbf{z}_K$ 로부터 $p_\theta(\mathbf{x} \mid \mathbf{z}_K)$ 를 추정한다.
데이터 복원 및 생성 과정을 담당한다.
요약하면,
인코더($\boldsymbol{\phi}$)는 관측값으로부터 초기 분포와 흐름 파라미터를 추정하고,
정규화 흐름($\boldsymbol{\lambda}$)은 그 분포를 결정론적으로 변형하며,
디코더($\boldsymbol{\theta}$)는 변환된 잠재 표현으로부터 입력을 재구성한다.
샘플링은 인코더의 출력인 $\mathbf{z}_0$ 단계에서 한 번만 일어나며,
이후 정규화 흐름은 결정론적으로 확률성을 전달한다.
따라서 전체 과정은 하나의 연산 그래프 내에서
$\boldsymbol{\theta}, \boldsymbol{\phi}, \boldsymbol{\lambda}$ 가 동시에 학습되면서,
확률적 추론과 결정론적 변환이 결합된 형태로 작동한다.

이 추론 네트워크를 사용함으로써,
하나의 계산 그래프(computational graph)를 구성할 수 있으며,
이를 통해 추론 네트워크(inference network)와
생성 모델(generative model)의 모든 파라미터에 대한
기울기(gradient)를 손쉽게 계산할 수 있다.

추정된 기울기들은
RMSprop 또는 AdaGrad(Duchi et al., 2010)와 같은
사전조건화(preconditioned) 확률적 경사 기반 최적화 방법과 결합되어 사용된다.
여기서 파라미터 갱신은 다음과 같은 형태를 따른다:

\[(\boldsymbol{\theta}^{t+1}, \boldsymbol{\phi}^{t+1}) \leftarrow (\boldsymbol{\theta}^{t}, \boldsymbol{\phi}^{t}) + \boldsymbol{\Gamma}^{t}(\mathbf{g}_{\boldsymbol{\theta}}^{t}, \mathbf{g}_{\boldsymbol{\phi}}^{t}),\]

여기서 $\boldsymbol{\Gamma}$ 는 대각 사전조건화 행렬(diagonal preconditioning matrix) 로,
기울기를 적응적으로 스케일링하여 수렴을 빠르게 한다.

모델 파라미터 $\boldsymbol{\theta}$ 와 $\boldsymbol{\phi}$ 를 동시에 업데이트하는
일반적인 확률적 경사 하강법(SGD) 형태를 나타낸다.
$(\mathbf{g}_{\boldsymbol{\theta}}^{t}, \mathbf{g}_{\boldsymbol{\phi}}^{t})$ 는
시점 $t$ 에서의 기울기(gradient)를 의미하며,
$\boldsymbol{\Gamma}^{t}$ 는 학습률(learning rate)과 유사한 역할을 하는
사전조건화 행렬(preconditioning matrix) 이다.
사전조건화(preconditioning) 란,
최적화 과정에서 기울기의 방향과 크기를 조정하여 학습 효율을 높이는 기법이다.
즉, 파라미터 공간에서 경사면이 가파르거나 비등방적(anisotropic)일 때
이를 적절히 “정규화(normalize)”하여,
경사 하강이 더 균형 잡히고 빠르게 수렴하도록 만든다.
사전조건화 행렬 $\boldsymbol{\Gamma}^{t}$ 는
각 파라미터의 스케일(scale)이나 변화량을 반영해
학습률을 자동으로 조정(adaptive scaling)한다.
그 결과, 경사가 큰 축에서는 보폭을 줄이고,
경사가 완만한 축에서는 보폭을 늘려
안정적이고 효율적인 수렴(stable and efficient convergence) 을 유도한다.
RMSprop, AdaGrad 등은 이러한 사전조건화 기법을
실제로 구현한 대표적인 알고리즘이다.

추론 모델의 로그-야코비안(log-det-Jacobian) 항을
공동으로 샘플링하고 계산하는 알고리즘 복잡도는
$O(LN^2) + O(KD)$ 로 스케일된다.

여기서 $L$ 은 데이터를 흐름(flow)의 파라미터로
매핑하는 데 사용되는 결정론적(deterministic) 계층의 수이고,
$N$ 은 평균 은닉층 크기(average hidden layer size),
$K$ 는 흐름의 길이(flow-length),
그리고 $D$ 는 잠재 변수(latent variables)의 차원이다.

$L$ 은 추론 네트워크(inference network) 내부의
결정론적(deterministic) 계층의 개수를 의미한다.
이는 입력 데이터 $\mathbf{x}$ 를 받아
정규화 흐름(normalizing flow)의 파라미터(예: $\mathbf{u}, \mathbf{w}, b$ 등)로
매핑(mapping)하는 데 필요한 층(layer)의 수를 나타낸다.

$N$ 은 각 은닉층(hidden layer)의 평균 크기로,
각 층이 가지는 뉴런(또는 노드)의 개수를 의미한다.
따라서 $L$ 개의 계층이 있고 각 층이 평균적으로 $N$ 개의 노드를 가지면,
네트워크의 연산 복잡도는 대략 $O(LN^2)$ 로 증가한다.

$K$ 는 정규화 흐름의 길이(flow-length)로,
즉 연속적으로 적용되는 변환(transformation) $f_1, f_2, \dots, f_K$ 의 개수를 뜻한다.
흐름이 길수록 더 정교한 분포 근사가 가능하지만,
계산 비용 또한 선형적으로 증가한다.

$D$ 는 잠재 변수(latent variable) $\mathbf{z}$ 의 차원(dimension)으로,
모델이 표현할 수 있는 잠재 공간(latent space)의 크기를 의미한다.
이 값이 커질수록 야코비안 계산과 샘플링의 비용이 함께 커진다.

따라서 전체 알고리즘은 많아야 이차적(quadratic) 복잡도를 가지며,
이는 전체 접근 방식이 실제로 사용되는 다른 대규모 시스템들과
경쟁 가능한 수준의 효율성을 가짐을 의미한다.

5. 대안적인 흐름 기반 사후분포 (Alternative Flow-based Posteriors)

정규화 흐름(normalizing flow)의 틀을 사용하면
보다 유연한 사후분포 근사(posterior approximation)를 설계하기 위한
최근의 다양한 제안들을 통합된 관점에서 볼 수 있다.

우선, 야코비안(Jacobian)을 어떻게 처리하는지에 따라
두 가지 종류의 흐름 메커니즘(flow mechanism)을 구분할 수 있다.

이 논문에서는 일반 정규화 흐름(general normalizing flows) 을 다루며,
야코비안을 선형 시간(linear time) 내에 계산할 수 있는 방법을 제시한다.

이에 반해 부피 보존 흐름(volume-preserving flows) 은
야코비안 행렬식(determinant)이 항상 1이 되도록 설계되며,
그럼에도 불구하고 복잡한 사후분포를 표현할 수 있다.

이 두 범주 모두 유한하거나(infinitesimal)
무한소 단위로 구성될 수 있는 흐름을 허용한다.

비선형 독립 성분 추정(Non-linear Independent Components Estimation, NICE)
은 Dinh 등(2014)에 의해 개발된 부피 보존 흐름의 한 예이다.

이 변환에서 사용되는 함수 $f(\cdot)$ 는
역변환 $g(\cdot)$ 을 쉽게 계산할 수 있는 신경망(neural network)으로 정의된다:

\[f(\mathbf{z}) = (\mathbf{z}_A, \mathbf{z}_B + h_\lambda(\mathbf{z}_A)), \tag{16}\] \[g(\mathbf{z}') = (\mathbf{z}'_A, \mathbf{z}'_B - h_\lambda(\mathbf{z}'_A)), \tag{17}\]

여기서 $\mathbf{z} = (\mathbf{z}_A, \mathbf{z}_B)$ 는
벡터 $\mathbf{z}$ 의 임의의 분할(partition)이며,
$h_\lambda$ 는 파라미터 $\lambda$ 를 가진 신경망이다.

이 형태는 상삼각 부분이 0인 야코비안 행렬을 만들며,
따라서 행렬식은 1이 된다.

초기 확률변수 $\mathbf{z}_0$ 의 모든 성분을 혼합할 수 있는
변환을 구성하기 위해서는,
이러한 흐름은 서로 다른 분할 $\mathbf{z}_k$ 들 사이를
번갈아 적용해야 한다.

순방향 및 역방향 변환을 사용하여 얻어지는
결과 밀도(resulting density)는 다음과 같다:

\[\ln q_K(f_K \circ f_{K-1} \circ \dots \circ f_1(\mathbf{z}_0)) = \ln q_0(\mathbf{z}_0), \tag{18}\] \[\ln q_K(\mathbf{z}') = q_0(g_1 \circ g_2 \circ \dots \circ g_K(\mathbf{z}')). \tag{19}\]

순방향 변환(forward transformation)이란
단순한 초기 확률변수 $\mathbf{z}_0$ 를
연속적인 변환 $f_1, f_2, \dots, f_K$ 을 통해
점점 더 복잡한 확률변수 $\mathbf{z}_K$ 로 바꾸는 과정을 의미한다.
즉, $f_K \circ f_{K-1} \circ \dots \circ f_1(\mathbf{z}_0)$ 의 형태로
순차적으로 변환이 적용되며,
각 단계의 변환은 밀도의 형태를 점점 유연하게 만들어
복잡한 분포를 생성(generation)할 수 있게 한다.
수식 (18)은 이러한 순방향 변환을 모두 적용했을 때의
최종 밀도 $\ln q_K$ 가
초기 밀도 $\ln q_0$ 와 같음을 보여준다.
이는 부피 보존 흐름(volume-preserving flow)의 특성상
야코비안의 행렬식이 1이므로
변환 과정에서 전체 확률 질량이 보존됨을 의미한다.
역방향 변환(inverse transformation)이란
순방향 변환의 반대 방향으로
복잡한 확률변수 $\mathbf{z}’$ 로부터
원래의 단순한 확률변수 $\mathbf{z}_0$ 를 복원하는 과정을 뜻한다.
각 단계에서 $f_k$ 의 역함수 $g_k$ 를 사용하며,
전체 변환은 $g_1 \circ g_2 \circ \dots \circ g_K$ 의 형태로 이루어진다.
역방향 변환은 단순히 순방향의 반대 과정이 아니라,
밀도 계산(density evaluation) 을 위해 꼭 필요하다.
정규화 흐름(normalizing flow)은
단순한 분포(예: 가우시안)로부터 복잡한 분포를 생성하지만,
실제로는 새로운 데이터 $\mathbf{z}’$ 가 주어졌을 때
그 데이터가 모델이 학습한 복잡한 분포 $q_K(\mathbf{z}’)$ 상에서
얼마나 가능성 있는지, 즉 확률 밀도(probability density) 를
계산해야 하는 경우가 많다.
이를 위해 $\mathbf{z}’$ 로부터 역방향 변환을 적용하여
단순한 초기 변수 $\mathbf{z}_0$ 로 되돌린 후,
이미 알고 있는 단순 분포 $q_0(\mathbf{z}_0)$ 로부터
밀도를 계산한다.
수식 (19)는 이러한 원리를 보여준다.
역방향 변환을 통해 복잡한 분포의 확률 밀도를
단순한 분포에서 효율적으로 추정할 수 있으며,
따라서 순방향 변환이 표현(생성) 을 위한 과정이라면,
역방향 변환은 밀도 계산(추정) 을 위한 과정이라고 할 수 있다.

우리는 NICE를 2.1절에서 설명된 일반적인 변환 접근법과 비교할 것이다.

Dinh et al. (2014)은 분할이 다음과 같은 형태라고 가정한다:

$\mathbf{z} = [\mathbf{z}_A = \mathbf{z}_{1:d}, \mathbf{z}_B = \mathbf{z}_{d+1:D}]$.

흐름(flow) 내에서 성분들의 혼합(mixing)을 강화하기 위해,
분리된 하위 그룹 $\mathbf{z}_A$ 와 $\mathbf{z}_B$ 로 나누기 전에
$\mathbf{z}$ 의 성분들을 혼합하기 위한 두 가지 메커니즘을 도입한다.

첫 번째 메커니즘은 임의의 순열(random permutation)을 적용하는 것으로
이를 NICE-perm이라 하며,
두 번째 메커니즘은 임의의 직교 변환(random orthogonal transformation)을 적용하며
이를 NICE-orth¹라 한다.

¹ 임의의 직교 변환(random orthogonal transformation)은
서로 독립적인 단위 가우시안 항목들을 갖는 행렬 $A_{i,j} \sim \mathcal{N}(0, I)$ 을
샘플링한 후, QR 분해(QR-factorization)를 수행함으로써 생성될 수 있다.
그 결과로 얻어지는 Q-행렬은 임의의 직교 행렬(random orthogonal matrix)이 된다 (Genz, 1998).

해밀토니안 변분 근사(Hamiltonian variational approximation, HVI)는
Salimans et al. (2015)에 의해 개발되었으며,
이는 무한소(infinitesimal) 부피 보존 흐름(volume-preserving flow)의 한 예이다.

HVI에서는 추가적인 보조 변수(auxiliary variable) $\boldsymbol{\omega}$ 를 사용하는
사후분포 근사 $q(\mathbf{z}, \boldsymbol{\omega} \mid \mathbf{x})$ 를 고려한다.

잠재 변수(latent variable) $\mathbf{z}$ 는 보조 변수 $\boldsymbol{\omega}$ 와 독립이며,
변수 변경 공식(change of variables rule)을 사용하면
결과적인 분포는 다음과 같이 주어진다:

\[q(\mathbf{z}', \boldsymbol{\omega}') = |\mathbf{J}| q(\mathbf{z}) q(\boldsymbol{\omega})\]

여기서 $\mathbf{z}’, \boldsymbol{\omega}’ = f(\mathbf{z}, \boldsymbol{\omega})$ 이며, $f$ 는 변환 함수(transformation)이다.

Salimans et al. (2015)는
MCMC 문헌에서 사용되는 이러한 전이 연산자(transition operator),
특히 Langevin 방법과 Hybrid Monte Carlo 방법을 활용함으로써
부피 보존(volume-preserving) 가역 변환(invertible transformation)을 얻는다.

이 접근법은 매우 우아한 방법으로,
전이 함수의 반복(iteration) 횟수가 무한대로 증가함에 따라
분포 $q(\mathbf{z}’)$ 가 참된 분포 $p(\mathbf{z} \mid \mathbf{x})$ 에
수렴하게 된다는 것을 보여준다.

이는 3.2절에서 설명된 해밀토니안 무한소 흐름(Hamiltonian infinitesimal flow)을
활용하는 또 다른 대안적 방법이다.

Langevin 흐름 또는 해밀토니안 흐름을 사용하는 단점은,
학습 단계와 테스트 단계 모두에서
각 반복(iteration)마다 가능도(likelihood)와 그 그래디언트(gradient)를
하나 이상 평가해야 한다는 점이다.
이는 리프프로그(leapfrog) 단계의 수에 따라 달라진다.

리프프로그(leapfrog) 단계란
해밀토니안 역학(Hamiltonian dynamics) 을 수치적으로 근사하기 위해
사용되는 시간적 이산화(time discretization) 방법 중 하나이다.
해밀토니안 흐름(Hamiltonian flow)은
연속적인 미분방정식 형태로 표현되므로
실제 계산에서는 이를 직접 해석적으로 풀 수 없고,
시간 단위로 나누어 근사적으로 계산해야 한다.
리프프로그 방법은 이러한 근사 계산을 수행할 때,
위치(position) 변수와 운동량(momentum) 변수를
번갈아가며 갱신(update)하는 특징을 가진다.
이 과정이 ‘한 번은 위치를, 한 번은 운동량을 건너뛴다(leapfrog)’는
의미에서 이름이 붙었다.
각 리프프로그 단계(leapfrog step)는
(1) 운동량을 절반만큼 업데이트 →
(2) 위치를 한 번 전체 업데이트 →
(3) 다시 운동량을 절반만큼 업데이트
의 순서로 진행된다.
이러한 구조 덕분에 리프프로그 방법은
수치적 안정성이 높고,
에너지 보존 특성을 잘 유지하면서도
역변환(invertibility)을 보장할 수 있어
해밀토니안 몬테카를로(HMC)나 변분 추론(VI)에서
매우 널리 사용된다.

6. 결과 (Results)

이 절 전반에 걸쳐 우리는 심층 잠재 가우시안 모델(Deep Latent Gaussian Models, DLGM) 에서의 추론을 위해
정규화 흐름 기반 사후분포 근사(normalizing flow–based posterior approximations)를
사용하는 효과를 평가한다.

학습은 자유 에너지의 어닐링(annealed, 점진적으로 온도를 변화시키며 안정화를 유도하는 기법) 버전 (식 20)의
그래디언트에 대한 몬테카를로 추정치를 따르는 방식으로 수행되었으며,
모델 파라미터 $\theta$ 와 변분 파라미터 $\phi$ 에 대해
확률적 역전파(stochastic backpropagation)를 사용하였다.

몬테카를로 추정치는 매개변수 업데이트마다 데이터 포인트당
잠재 변수의 단일 샘플을 사용하여 계산된다.

더 나은 결과를 제공하는 것으로 밝혀졌기 때문에,
자유 에너지의 단순한 어닐링(annealed, 점진적 온도 조절) 버전을 사용한다.
수정된 경계는 다음과 같다:

\[\begin{align} \mathbf{z}_K &= f_K \circ f_{K-1} \circ \dots \circ f_1(\mathbf{z}) \\[8pt] \mathcal{F}^{\beta_t}(\mathbf{x}) &= \mathbb{E}_{q_0(\mathbf{z}_0)}\!\big[\ln p^{K}(\mathbf{z}_K) - \log p(\mathbf{x}, \mathbf{z}_K)\big] \\[8pt] &= \mathbb{E}_{q_0(\mathbf{z}_0)}[\ln q_0(\mathbf{z}_0)] - \beta_t\, \mathbb{E}_{q_0(\mathbf{z}_0)}[\log p(\mathbf{x}, \mathbf{z}_K)] \\[6pt] &\quad - \mathbb{E}_{q_0(\mathbf{z}_0)}\!\left[ \sum_{k=1}^{K}\ln\big|1 + \mathbf{u}_k^{\top}\boldsymbol{\psi}_k(\mathbf{z}_{k-1})\big| \right] \tag{20} \end{align}\]

여기서 $\beta_t \in [0,1]$ 는 역온도(inverse temperature) 로,
훈련 과정에서 점진적으로 증가하는 값이다.
스케줄(schedule)은 다음과 같이 정의된다:

\[\beta_t = \min(1,\; 0.01 + t/10000)\]

즉, 10,000회의 반복(iteration)을 거치면서
0.01에서 1까지 점진적으로 증가하며
모델이 점차 안정적인 상태로 수렴하도록 유도한다.

기존 자유 에너지 식 (15)과 어닐링(annealed) 버전 식 (20)의 차이는
두 번째 항, 즉 로그 결합 확률(log joint probability) 항의 가중치에
어닐링 계수 $\beta_t$ 가 곱해졌다는 점이다.
두 식을 비교하면 다음과 같다:
기존 자유 에너지 (식 15):
\[\mathcal{F}(\mathbf{x}) = \mathbb{E}_{q_0(\mathbf{z}_0)}[\log q_0(\mathbf{z}_0)] - \mathbb{E}_{q_0(\mathbf{z}_0)}[\log p(\mathbf{x}, \mathbf{z}_K)] - \mathbb{E}_{q_0(\mathbf{z}_0)}\!\left[ \sum_{k=1}^{K}\ln\!\left|1 + \mathbf{u}_k^{\top}\boldsymbol{\psi}_k(\mathbf{z}_{k-1})\right| \right].\]
어닐링 버전 자유 에너지 (식 20):
\[\mathcal{F}^{\beta_t}(\mathbf{x}) = \mathbb{E}_{q_0(\mathbf{z}_0)}[\log q_0(\mathbf{z}_0)] - \beta_t\,\mathbb{E}_{q_0(\mathbf{z}_0)}[\log p(\mathbf{x}, \mathbf{z}_K)] - \mathbb{E}_{q_0(\mathbf{z}_0)}\!\left[ \sum_{k=1}^{K}\ln\!\left|1 + \mathbf{u}_k^{\top}\boldsymbol{\psi}_k(\mathbf{z}_{k-1})\right| \right].\]
즉, $\beta_t \in [0,1]$ 이 새롭게 추가되어
데이터 우도(likelihood) 항의 기여도를 조절한다.
$\beta_t$ 가 작을 때 (예: 0.01):
모델은 주로 재구성(reconstruction) 에 집중하며 안정적으로 학습 시작.
$\beta_t$ 가 커질 때 (→ 1):
점차 KL 발산(KL divergence) 항의 영향을 강화하여
사후분포 정규화를 유도.
따라서, 어닐링 버전의 자유 에너지는
학습 초기에 모델이 너무 강한 정규화로 수렴하지 않도록 완화시켜
점진적 안정 학습(gradual stabilization) 을 가능하게 한다.

무작위 변수들 간의 조건부 확률을 형성하는 심층 신경망은
400개의 은닉 유닛(hidden units)을 갖는 결정론적 층(deterministic layer)들로 구성되며,
4개의 변수에 대한 윈도우(window)를 사용하는
Maxout 비선형성(Maxout non-linearity)을 적용한다 (Goodfellow et al., 2013).

간단히 말해, 윈도우 크기 $\Delta$ 를 갖는 Maxout 비선형성은
입력 벡터 $\mathbf{x} \in \mathbb{R}^d$ 를 받아 다음과 같이 계산한다:

\[\text{Maxout}(\mathbf{x})_k = \max_{i \in \{\Delta_k, \Delta_{(k+1)}\}} \mathbf{x}_i \quad \text{for} \; k = 0, \dots, d / \Delta.\]

우리는 100개의 데이터 포인트로 구성된 미니배치(mini-batch)와
RMSprop 최적화 방법(learning rate = $1 \times 10^{-5}$, momentum = 0.9)을 사용하였다
(Kingma & Welling, 2014; Rezende et al., 2014).

결과는 500,000번의 파라미터 업데이트 후에 수집되었다.
각 실험은 서로 다른 난수 시드(random seed)를 사용하여 100회 반복되었으며,
평균 점수와 표준 오차(standard error)를 보고하였다.

진짜 주변 가능도(true marginal likelihood)는
추론 네트워크(inference network)에서
200개의 샘플을 사용한 중요도 샘플링(importance sampling)을 통해 추정되었다
(Rezende et al., 2014, 부록 E).

6.1. 정규화 흐름의 표현력 (Representative Power of Normalizing Flows)

정규화 흐름(normalizing flow)을 기반으로 한 밀도 근사(density approximation)의
표현력(representative power)에 대한 통찰을 제공하기 위해,
정규화되지 않은(unormalized) 2차원 밀도 $p(\mathbf{z}) \propto \exp[-U(\mathbf{z})]$ 의 집합을
매개변수화(parameterize)하였다.
이들은 표 1에 나열되어 있다.

표 1. 테스트 에너지 함수 (Test energy functions)

표 1의 네 가지 잠재 함수 $U(\mathbf{z})$ 는
정규화 흐름(normalizing flow)의 표현력(representative power),
즉 “얼마나 복잡한 분포를 근사할 수 있는가”를 평가하기 위한
테스트용 에너지 함수(potential energy functions) 들이다.
여기서 $p(\mathbf{z}) \propto \exp[-U(\mathbf{z})]$ 이므로,
$U(\mathbf{z})$ 의 형태가 복잡할수록 결과적으로 더 복잡한 확률 분포가 생성된다.
각 함수는 서로 다른 구조적 특징을 가진 2차원 밀도를 만들도록 설계되었다.
1번: 원형 링(ring) 형태의 분포.
$|\mathbf{z}|$ 항을 사용하여 중심에서 떨어진 반지름 방향의 밀도를 제어하고,
$\log$ 항을 통해 두 개의 봉우리(두 개의 모드, bimodal)를 만든다.
$\Rightarrow$ “이중 링(bimodal ring)” 구조의 밀도.
2번: 사인 함수 형태의 경로를 따라 분포가 형성되는 구조.
$w_1(\mathbf{z}) = \sin(2\pi z_1 / 4)$ 를 사용하여
$z_1$ 방향으로 움직일 때 $z_2$ 방향의 평균이 사인 곡선을 그리도록 한다.
$\Rightarrow$ “비선형 곡선(S-curve)” 형태의 밀도.
3번: 두 개의 좁은 띠(band)가 나란히 존재하는 형태.
첫 번째 띠는 $w_1(\mathbf{z})$ 에 의해,
두 번째 띠는 $w_1(\mathbf{z}) + w_2(\mathbf{z})$ 에 의해 만들어진다.
여기서 $w_2(\mathbf{z})$ 는 $z_1 \approx 1$ 근처에서만 활성화되므로,
두 띠가 특정 위치에서 가까워졌다 멀어지는 복잡한 구조를 생성한다.
$\Rightarrow$ “이중 곡선(double S-curve)” 형태의 밀도.
4번: 3번과 유사하지만 $w_3(\mathbf{z})$ 가 sigmoid 함수로 정의되어
$z_1$ 이 커질수록 점진적으로 변형되는 분포를 만든다.
즉, $z_1$ 방향으로 이동할수록 한쪽 띠가 천천히 다른 쪽으로 수렴한다.
$\Rightarrow$ “비대칭적인 이중 곡선(asymmetric double S-curve)” 형태의 밀도.
따라서, 이 네 가지 $U(\mathbf{z})$ 는
단순한 단봉 분포에서 다봉/비선형 구조까지 다양하게 포함하며,
정규화 흐름이 이러한 복잡한 구조를 얼마나 잘 근사할 수 있는지를
실험적으로 평가하기 위한 표현력 테스트 세트(representative test set) 역할을 한다.

그림 3(a)에서는 네 가지 경우에 대한 실제 분포(true distribution)를 보여준다.
이 분포들은 다중 모달리티(multimodality)와 주기성(periodicity)과 같은 특성을 가지며,
이는 일반적으로 사용되는 사후분포 근사(posterior approximations)로는 포착할 수 없는 특징들이다.

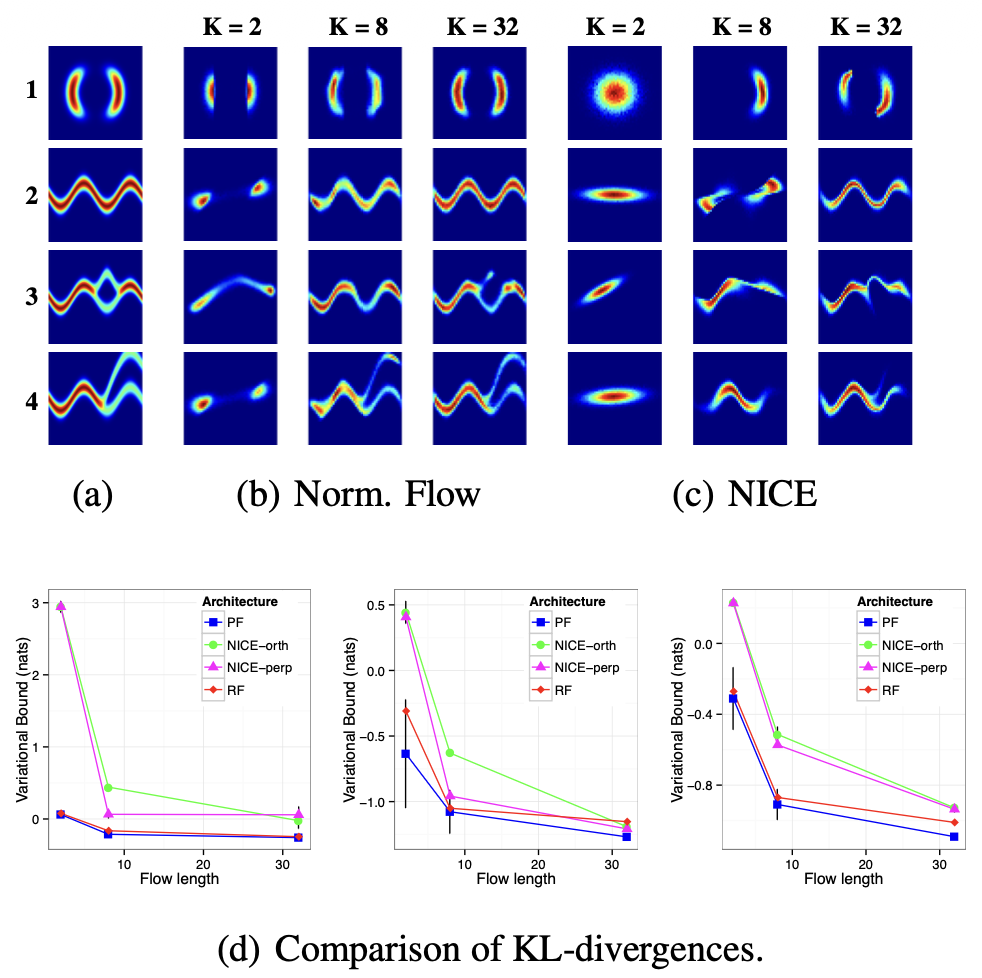
그림 3. 네 가지 비가우시안(non-Gaussian) 2차원 분포의 근사.
이미지들은 표 1에 제시된 각 에너지 함수에 대한
범위 $(-4, 4)^2$ 내의 밀도를 나타낸다.
(a) 실제 사후분포(true posterior);
(b) 정규화 흐름(식 13)을 사용한 근사 사후분포(approximate posterior);
(c) NICE(식 19)를 사용한 근사 사후분포;
(d) 첫 세 가지 경우에 대해,
실제 밀도와 근사된 밀도 간의 KL 발산(KL-divergence)을 비교한 요약 결과(summary results).

그림 3(b)는 이러한 밀도들에 대해
2, 8, 그리고 32개의 변환으로 구성된
정규화 흐름 근사(normalizing flow approximation)의 성능을 보여준다.

식 (10)에서 정의된 비선형 함수 $h(\mathbf{z}) = \tanh(\mathbf{z})$ 가 매핑에 사용되었고,
초기 분포는 대각 가우시안(diagonal Gaussian) $q_0(\mathbf{z}) = \mathcal{N}(\mathbf{z} \mid \boldsymbol{\mu}, \sigma^2 \mathbf{I})$ 로 설정되었다.
흐름의 길이를 늘릴수록 근사 품질이 현저히 향상되는 것을 확인할 수 있다.

그림 3(c)는 동일한 수의 변환을 사용하되,
NICE (Dinh et al., 2014)에서 사용된 부피 보존 변환(volume-preserving transformation)을 적용한 근사를 보여준다.

그림 3(d)에서는 평면 흐름(planar flow) (식 13)과 NICE (식 18)에 대해,
무작위 직교 행렬(random orthogonal matrices)과
무작위 순열 행렬(random permutation matrices)을 사용한
요약 통계(summary statistics)를 보여준다.

NICE와 평면 흐름(planar flow) (식 13)은
흐름 길이가 증가함에 따라 동일한 점근적 성능(asymptotic performance)에 도달할 수 있으나,
평면 흐름(식 13)은 훨씬 더 적은 수의 파라미터만을 필요로 한다는 것을 발견하였다.

이는 평면 흐름의 모든 파라미터가 학습되는 반면,
NICE는 구성 요소 간 혼합을 위해 학습되지 않은
무작위 초기화(random initialization)된 추가적인 메커니즘이 필요하기 때문으로 보인다.

또한 NICE 내에서 무작위 직교 행렬을 사용하는 경우와
무작위 순열 행렬을 사용하는 경우 사이에
유의미한 차이는 관찰되지 않았다.

6.2. MNIST와 CIFAR-10 이미지

MNIST 숫자 데이터셋 (LeCun & Cortes, 1998)은
0부터 9까지의 열 개의 손글씨 숫자에 대한
60,000개의 학습 이미지와 10,000개의 테스트 이미지를 포함한다.
각 숫자는 $28 \times 28$ 픽셀 크기이다.

우리는 Uria et al. (2014)에서 사용된 것과 동일한 이진화된(binarized) 데이터셋을 사용하였다.

40개의 잠재 변수(latent variable)를 갖는
서로 다른 심층 잠재 가우시안 모델(DLGM)을
500,000번의 파라미터 업데이트 동안 학습시켰다.

평면(planar) 정규화 흐름(normalizing flow) (DLGM+NF) 근사를 사용하는 DLGM의 성능은,
서로 다른 흐름 길이(flow-length) $K$ 에 대해
정확히 동일한 모델에서 부피 보존(volume-preserving) 접근법인
NICE (DLGM+NICE)를 사용한 경우와 비교되었으며,
그 성능은 그림 4에 요약되어 있다.

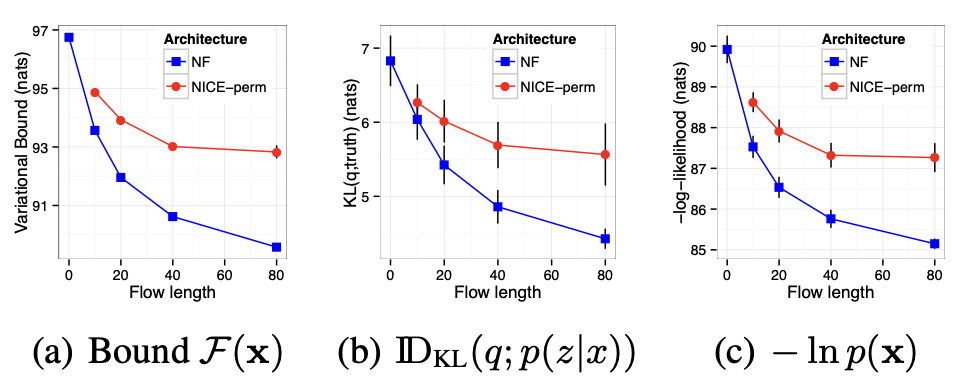
그림 4. MNIST에서의 흐름 길이(flow-length)의 영향.

이 그래프는 흐름 길이 $K$가 증가할수록
그림 4(a)에 보인 것처럼 경계(bound) $\mathcal{F}$ 가 체계적으로 향상되고,
근사 사후분포 $q(\mathbf{z} \mid \mathbf{x})$ 와
진짜 사후분포 $p(\mathbf{z} \mid \mathbf{x})$ 간의
KL 발산(KL-divergence)이 감소함을 보여준다 (그림 4(b)).

또한, 일반적인 정규화 흐름(normalizing flow)을 사용하는 접근법이
NICE보다 더 우수한 성능을 보인다는 것도 알 수 있다.

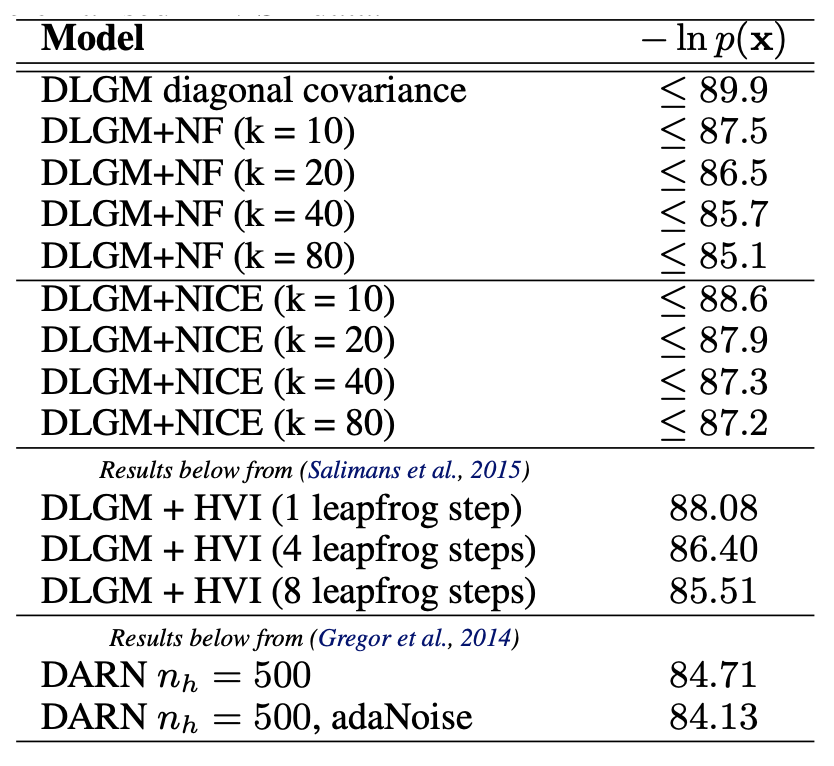
표 2에는 보다 넓은 비교 결과를 함께 제시하였다.

결과에는 해밀토니안 변분 접근법(Hamiltonian variational approach)도 포함되어 있으나,
이 모델의 명세(specification)는 다르기 때문에
이 데이터셋에서의 해당 접근법의 달성 가능한 성능 범위에 대한
참고 지표로만 제시되었다.

표 2. 이진화된(binarised) MNIST 데이터의 테스트 세트에서
음의 로그 확률(negative log-probabilities)의 비교.

CIFAR-10 자연 이미지 데이터셋 (Krizhevsky & Hinton, 2010)은
$3 \times 32 \times 32$ 픽셀 크기의 RGB 이미지로 구성되어 있으며,
50,000개의 학습 이미지와 10,000개의 테스트 이미지를 포함한다.
이로부터 $3 \times 8 \times 8$ 크기의 무작위 패치(random patches)를 추출하였다.

색상 범위는 $\epsilon = 0.0001$인 경우,
$[\epsilon, 1 - \epsilon]$ 구간으로 변환되었다.

이 실험에서는 MNIST 실험에서 사용한 것과 동일한 DLGM 구조를 사용하였지만,
잠재 변수의 수는 30개로 설정하였다.

이 데이터가 이진(binary) 형태가 아니므로,
우리는 로그-정규 관찰 가능도(logit-normal observation likelihood)를 사용하였다:

\[p(\mathbf{x} \mid \boldsymbol{\mu}, \boldsymbol{\alpha}) = \prod_i \frac{ \mathcal{N}_{(logit(\mathbf{x}_i) \mid \mu_i, \alpha_i)} }{ \mathbf{x}_i (1 - \mathbf{x}_i) }, \quad \text{where} \quad logit(x) = \log \frac{x}{1 - x}.\]

표 3에 결과를 요약하였다.
흐름 길이 $K$가 증가할수록
테스트 로그 가능도(test log-likelihood)가 체계적으로 향상되어,
더 나은 사후분포 근사(posterior approximation)를 산출함을 보여준다.

표 3. CIFAR-10 데이터의 테스트 세트 성능.

7. 결론 및 논의 (Conclusion and Discussion)

이 연구에서 우리는 단순한 밀도를 정규화 흐름(normalizing flow)을 통해
더 복잡한 밀도로 변환(transform)함으로써,
고도로 비가우시안(non-Gaussian)인 사후 밀도(posterior density)를 학습하기 위한
간단한 접근법을 개발하였다.

추론 네트워크(inference network)를 사용한 변분 추론(variational inference) 접근법과
효율적인 몬테카를로(Monte Carlo) 기울기(gradient) 추정 방식을 결합함으로써,
다양한 문제에서 단순한 근사 방법에 비해
명확한 성능 향상을 보여줄 수 있었다.

정규화 흐름에 대한 이러한 관점을 통해,
유연한 사후 추정(flexible posterior estimation)을 위한
다른 관련된 여러 방법들을 하나의 통합적 관점에서 조망할 수 있었으며,
이는 서로 다른 통계적 및 계산적 절충(trade-off)을 가진
더 강력한 사후 근사(posterior approximation)를 설계하기 위한
다양한 접근법들의 폭넓은 스펙트럼을 제시한다.

3장에서의 논의로부터 중요한 결론은,
정규화 흐름의 여러 종류(class)가 존재하며
이를 통해 변분 추론을 위한
매우 풍부한 사후 근사(posterior approximation)를 생성할 수 있다는 점이다.

정규화 흐름을 사용함으로써,
점근적(asymptotic) 상태에서
해(solution)의 공간이 실제 사후 분포(true posterior distribution)를
포함할 만큼 충분히 풍부함을 보여줄 수 있었다.

만약 이를 특정 잠재 변수 모델(latent variable model)들에서의
최대우도추정(maximum likelihood estimation)에 대한
국소 수렴(local convergence) 및 일관성(consistency) 결과와 결합한다면
(Wang & Titterington, 2004),

변분 추론을 경쟁력 있는(statistically competitive)
통계적 추론(statistical inference)의 기본 접근법(default approach)으로
사용하는 데 제기되던 반대(opposition)를
극복할 수 있게 되었음을 알 수 있다.

이러한 주장을 엄밀하게(rigorous) 입증하는 것은
향후 연구에서 중요한 과제가 될 것이다.

정규화 흐름은 단순히 흐름의 길이(flow length)를 늘림으로써
실행 시간(run-time) 중에 사후 분포의 복잡도를
제어할 수 있게 해준다.

본 연구에서 제안한 접근법은
식 (10)과 (14) 형태의 단순한 변환(simple transformation)을 기반으로 한
정규화 흐름을 고려하였다.

이들은 사용 가능한 수많은 변환(map) 중 단 두 가지 예시일 뿐이며,
사후 근사에서 제한된 지지집합(restricted support) 등
다른 제약 조건이 필요한 경우
대체 변환(alternative transform)을 설계할 수도 있다.

향후 연구의 중요한 방향은,
사후 분포의 다양한 특성을 허용하면서도
효율적이고 선형 시간(linear-time) 계산이 가능한
변환 클래스(transformation class)를 기술(describe)하는 데 있다.

감사의 글 (Acknowledgements):

우리는 Charles Blundell, Theophane Weber, Daan Wierstra에게
유익한 논의를 제공해준 것에 대해 감사를 표한다.

참고문헌 (References)

Ahn, S., Korattikara, A., and Welling, M.
Bayesian posterior sampling via stochastic gradient Fisher scoring.
In ICML, 2012.

Baird, L., Smalenberger, D., and Ingkiwiang, S.
One-step neural network inversion with PDF learning and emulation.
In IJCNN, volume 2, pp. 966–971. IEEE, 2005.

Bishop, C. M.
Pattern recognition and machine learning.
Springer, New York, 2006.

Challis, E. and Barber, D.
Affine independent variational inference.
In NIPS, 2012.

Dayan, P.
Helmholtz machines and wake-sleep learning.
Handbook of Brain Theory and Neural Network. MIT Press, Cambridge, MA, 44(0), 2000.

Dinh, L., Krueger, D., and Bengio, Y.
NICE: Non-linear independent components estimation.
arXiv preprint arXiv:1410.8516, 2014.

Duchi, J., Hazan, E., and Singer, Y.
Adaptive subgradient methods for online learning and stochastic optimization.
JMLR, 12:2121–2159, 2010.

Genz, A.
Methods for generating random orthogonal matrices.
Monte Carlo and Quasi-Monte Carlo Methods, 1998.

Gershman, S., Hoffman, M., and Blei, D.
Nonparametric variational inference.
In ICML, 2012.

Gershman, S. J. and Goodman, N. D.
Amortized inference in probabilistic reasoning.
In Annual Conference of the Cognitive Science Society, 2014.

Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y.
Maxout networks.
ICML, 2013.

Gregor, K., Danihelka, I., Mnih, A., Blundell, C., and Wierstra, D.
Deep autoregressive networks.
In ICML, 2014.

Gregor, Karol, Danihelka, Ivo, Graves, Alex, Jimenez Rezende, Danilo, and Wierstra, Daan.
DRAW: A recurrent neural network for image generation.
In ICML, 2015.

Hoffman, M. D., Blei, D. M., Wang, C., and Paisley, J.
Stochastic variational inference.
JMLR, 14(1):1303–1347, 2013.

Jaakkola, T. S. and Jordan, M. I.
Improving the mean field approximation via the use of mixture distributions.
In Learning in graphical models, pp. 163–173. 1998.

Jordan, M. I., Ghahramani, Z., Jaakkola, T. S., and Saul, L. K.
An introduction to variational methods for graphical models.
Machine learning, 37(2):183–233, 1999.

Kingma, D. P. and Welling, M.
Auto-encoding variational Bayes.
In ICLR, 2014.

Kingma, D. P., Mohamed, S., Rezende, D. J., and Welling, M.
Semi-supervised learning with deep generative models.
In NIPS, pp. 3581–3589, 2014.

Krizhevsky, A. and Hinton, G.
Convolutional deep belief networks on CIFAR-10.
Unpublished manuscript, 2010.

LeCun, Y. and Cortes, C.
The MNIST database of handwritten digits, 1998.

Mnih, A. and Gregor, K.
Neural variational inference and learning in belief networks.
In ICML, 2014.

Neal, R. M.
MCMC using hamiltonian dynamics.
Handbook of Markov Chain Monte Carlo, 2011.

Papaspiliopoulos, O., Roberts, G. O., and Sköld, M.
Non-centered parameterisations for hierarchical models and data augmentation.
In Bayesian Statistics 7, 2003.

Ranganath, R., Gerrish, S., and Blei, D. M.
Black box variational inference.
In AISTATS, 2013.

Rezende, D. J., Mohamed, S., and Wierstra, D.
Stochastic backpropagation and approximate inference in deep generative models.
In ICML, 2014.

Rippel, O. and Adams, R. P.
High-dimensional probability estimation with deep density models.
arXiv:1302.5125, 2013.

Salimans, T., Kingma, D. P., and Welling, M.
Markov chain Monte Carlo and variational inference: Bridging the gap.
In ICML, 2015.

Suykens, J. A. K., Verrelst, H., and Vandewalle, J.
Online learning Fokker-Planck machine.
Neural processing letters, 7(2):81–89, 1998.

Tabak, E. G. and Turner, C. V.
A family of nonparametric density estimation algorithms.
Communications on Pure and Applied Mathematics, 66(2):145–164, 2013.

Tabak, E. G. and Vanden-Eijnden, E.
Density estimation by dual ascent of the log-likelihood.
Communications in Mathematical Sciences, 8(1):217–233, 2010.

Titsias, M. and Lázaro-Gredilla, M.
Doubly stochastic variational Bayes for non-conjugate inference.
In ICML, 2014.

Turner, R. E. and Sahani, M.
Two problems with variational expectation maximisation for time-series models.
In Barber, D., Cemgil, T., and Chiappa, S. (eds.),
Bayesian Time Series Models, chapter 5, pp. 109–130.
Cambridge University Press, 2011.

Uria, B., Murray, I., and Larochelle, H.
A deep and tractable density estimator.
In ICML, 2014.

Wang, B. and Titterington, D. M.
Convergence and asymptotic normality of variational Bayesian approximations for exponential family models with missing values.
In UAI, 2004.

Welling, M. and Teh, Y. W.
Bayesian learning via stochastic gradient Langevin dynamics.
In ICML, 2011.

Williams, Ronald J.
Simple statistical gradient-following algorithms for connectionist reinforcement learning.
Machine learning, 8(3-4):229–256, 1992.

Wingate, D. and Weber, T.
Automated variational inference in probabilistic programming.
In NIPS Workshop on Probabilistic Programming, 2013.

A. 가역성 조건 (Invertibility conditions)

이 절에서는 3장에서 설명된 평면 정규화 흐름(planar normalizing flows)과
방사형 정규화 흐름(radial normalizing flows)에 대해
가역적인(invertible) 사상(map)을 갖기 위해 필요한 제약 조건을 기술한다.

A.1. 평면 흐름 (Planar flows)

식 (10) 형태의 함수들은 비선형성과 선택된 매개변수들에 따라
항상 가역적인 것은 아니다.
$h(x) = \tanh(x)$ 일 때,
$f(\mathbf{z})$ 가 가역적이기 위한 충분조건은
$\mathbf{w}^\top \mathbf{u} \ge -1$ 이다.

이것은 벡터 $\mathbf{z}$ 를 $\mathbf{w}$ 에 수직인 성분 $\mathbf{z}_\perp$ 과
$\mathbf{w}$ 에 평행한 성분 $\mathbf{z}_\parallel$ 의 합으로 분할하여
$\mathbf{z} = \mathbf{z}_\perp + \mathbf{z}_\parallel$ 로 쓸 수 있음을 통해 확인할 수 있다.
이를 식 (10)에 대입하면 다음과 같다.

\[f(\mathbf{z}) = \mathbf{z}_\perp + \mathbf{z}_\parallel + \mathbf{u}h(\mathbf{w}^\top \mathbf{z}_\parallel + b). \tag{21}\]

식 (10)은
\[f(\mathbf{z}) = \mathbf{z} + \mathbf{u} h(\mathbf{w}^\top \mathbf{z} + b), \tag{10}\]
식 (21)에서는 $h(\mathbf{w}^\top \mathbf{z}_\parallel + b)$ 형태로만 나타나 있으며
$\mathbf{z}_\perp$ 가 괄호 안에 등장하지 않는다.
이는 $\mathbf{z}_\perp$ 가 $\mathbf{w}$ 에 수직(orthogonal) 이기 때문에
$\mathbf{w}^\top \mathbf{z}_\perp = 0$ 이 되기 때문이다.
따라서 $\mathbf{w}^\top \mathbf{z} = \mathbf{w}^\top (\mathbf{z}_\perp + \mathbf{z}_\parallel) = \mathbf{w}^\top \mathbf{z}_\parallel$ 이다.

이 방정식은 $\mathbf{z}_\parallel$ 이 주어졌을 때 $\mathbf{z}_\perp$ 에 대해,
$\mathbf{y} = f(\mathbf{z})$ 로부터 유일하게 풀 수 있다.

\[\mathbf{z}_\perp = \mathbf{y} - \mathbf{z}_\parallel - \mathbf{u}h(\mathbf{w}^\top \mathbf{z}_\parallel + b). \tag{22}\]

평행 성분(parallel component)은

\[\mathbf{z}_\parallel = \alpha \frac{\mathbf{w}}{\|\mathbf{w}\|^2}\]

로 더 확장될 수 있다.
여기서 $\alpha \in \mathbb{R}$ 이다.

벡터 $\mathbf{z}_\parallel$ 은 $\mathbf{w}$ 와 같은 방향을 가지므로,
그 크기를 나타내는 스칼라 계수 $\alpha$ 를 곱해 표현할 수 있다.
$\mathbf{w}$ 의 크기를 보정하기 위해 $|\mathbf{w}|^2$ 로 나누어
$\mathbf{z}_\parallel$ 이 정확히 $\mathbf{w}$ 방향의 성분만을 나타내도록 한 것이다.

$\alpha$ 를 풀기 위한 방정식은 (21)에 $\mathbf{w}$ 와의 내적(dot product)을 취하면 얻어진다.

\[\mathbf{w}^\top f(\mathbf{z}) = \alpha + \mathbf{w}^\top \mathbf{u}h(\alpha + b). \tag{23}\]

$\alpha$ 는 $\mathbf{z}$ 의 $\mathbf{w}$ 방향 성분의 크기를 나타내는 스칼라이므로,
$\mathbf{w}$ 와의 내적을 취하면 $\mathbf{w}$ 방향으로의 투영(projection) 값만 남게 된다.
따라서 식 (21)에 $\mathbf{w}^\top$ 을 곱하면
$\mathbf{z}$ 의 평행 성분 크기 $\alpha$ 와 그에 대응하는 항들만 남아,
$\alpha$ 를 직접적으로 포함한 1차원 방정식을 얻을 수 있다.

식 (23)이 $\alpha$ 에 대해 가역적이기 위한 충분조건은,
오른쪽 항 $ \alpha + \mathbf{w}^\top \mathbf{u}h(\alpha + b)$ 가
단조 증가 함수(non-decreasing function)가 되는 것이다.
이 조건은

\[1 + \mathbf{w}^\top \mathbf{u} h'(\alpha + b) \ge 0 \equiv \mathbf{w}^\top \mathbf{u} \ge -\frac{1}{h'(\alpha+b)}\]

로 표현된다.
$\tanh’(x) \le 1$ 이므로,
$\mathbf{w}^\top \mathbf{u} \ge -1$ 이면 충분하다.

이 제약 조건은 임의의 벡터 $\mathbf{u}$ 를 취한 뒤,
그 벡터의 $\mathbf{w}$ 에 평행한 성분을 수정하여
$\mathbf{w}^\top \hat{\mathbf{u}} > -1$ 을 만족하는
새로운 벡터 $\hat{\mathbf{u}}$ 를 생성함으로써 강제된다.

수정된 벡터는 다음과 같이 간결히 표현된다.

\[\hat{\mathbf{u}}(\mathbf{w}, \mathbf{u}) = \mathbf{u} + [m(\mathbf{w}^\top \mathbf{u}) - (\mathbf{w}^\top \mathbf{u})] \frac{\mathbf{w}}{\|\mathbf{w}\|^2},\]

여기서 스칼라 함수 $m(x)$ 는 $m(x) = -1 + \log(1 + e^x)$ 로 정의된다.

앞서 가역성을 보장하기 위한 충분조건이 $\mathbf{w}^\top \mathbf{u} \ge -1$ 이었는데,
모든 학습 과정에서 이 조건을 직접 강제하기 어렵다.
따라서 이 식에서는 벡터 $\mathbf{u}$ 의 $\mathbf{w}$ 방향 성분만 수정하여
항상 $\mathbf{w}^\top \hat{\mathbf{u}} > -1$ 이 되도록 재매개변수화(reparameterization)한다.
수정식에서
\[[m(\mathbf{w}^\top \mathbf{u}) - (\mathbf{w}^\top \mathbf{u})] \frac{\mathbf{w}}{\|\mathbf{w}\|^2}\]
항은 $\mathbf{u}$ 의 $\mathbf{w}$ 방향 성분을 보정하는 역할을 한다.
여기서 $m(x) = -1 + \log(1 + e^x)$ 는 항상 $m(x) > -1$ 을 만족하는
스무스한(smooth) 함수이므로,
이 함수를 사용하면 학습 과정 전체에서
$\mathbf{w}^\top \hat{\mathbf{u}} > -1$ 조건이 자동으로 유지된다.

A.2. 방사형 흐름 (Radial flows)

식 (14) 형태의 함수들도
$\alpha$ 와 $\beta$ 의 값에 따라 항상 가역적인 것은 아니다.
이를 보기 위해,
벡터 $\mathbf{z}$ 를 $\mathbf{z}_0$ 에서의 거리 $r = |\mathbf{z} - \mathbf{z}_0|$ 와 방향 $\hat{\mathbf{r}} = \frac{\mathbf{z} - \mathbf{z}_0}{r}$ 로 분할하자.
이를 식 (14)에 대입하면 다음과 같다.

\[f(\mathbf{z}) = \mathbf{z}_0 + \hat{\mathbf{r}}\,\frac{r}{\alpha + r}\,(\alpha + \beta r). \tag{24}\]

식 (14)는
\[f(\mathbf{z}) = \mathbf{z} + \beta h(\alpha, r)(\mathbf{z} - \mathbf{z}_0), \tag{14}\]
먼저 식 (14)에 $\mathbf{z} - \mathbf{z}_0 = r \hat{\mathbf{r}}$ 를 대입하면 다음과 같다.
\[f(\mathbf{z}) = \mathbf{z} + \beta h(\alpha, r)(\mathbf{z} - \mathbf{z}_0) = (\mathbf{z}_0 + r\hat{\mathbf{r}}) + \beta h(\alpha, r)(r\hat{\mathbf{r}})\]
정리하면,
\[f(\mathbf{z}) = \mathbf{z}_0 + r\hat{\mathbf{r}} + \beta r h(\alpha, r)\hat{\mathbf{r}}.\]
$\hat{\mathbf{r}}$ 을 묶어내면,
\[f(\mathbf{z}) = \mathbf{z}_0 + \hat{\mathbf{r}}\, r \big[1 + \beta h(\alpha, r)\big].\]
이제 $h(\alpha, r) = \frac{1}{\alpha + r}$ 를 대입하면,
\[f(\mathbf{z}) = \mathbf{z}_0 + \hat{\mathbf{r}}\, r \left(1 + \frac{\beta}{\alpha + r}\right).\]
이 항을 통분하여 정리하면,
통분 과정을 단계별로 살펴보면,
\[1 + \frac{\beta}{\alpha + r} = \frac{\alpha + r}{\alpha + r} + \frac{\beta}{\alpha + r} = \frac{\alpha + r + \beta}{\alpha + r}.\]
여기서 $\beta$ 항은 단순한 상수가 아니라,
거리 $r$ 에 따라 변환의 세기를 조절하는 계수이므로
실제로는 $\beta$ 가 $r$ 에 선형적으로 작용해야 한다.
따라서 $\beta$ 항을 $r$ 에 비례하도록 확장하면
변환 비율이 거리 $r$ 에 따라 점진적으로 변하는 형태가 되고,
최종적으로 다음과 같이 정리된다.
\[1 + \frac{\beta}{\alpha + r} = \frac{\alpha + \beta r}{\alpha + r}.\]
이 항은 $r$ 이 커질수록 점점 $\beta$ 의 영향이 커지는 방사형(radial) 스케일링을 표현하며,
결과적으로 식 (24)의 형태로 단순화된다.
\[f(\mathbf{z}) = \mathbf{z}_0 + \hat{\mathbf{r}}\,\frac{r}{\alpha + r}(\alpha + \beta r),\]

이 방정식은 $r$ 과 $\mathbf{y} = f(\mathbf{z})$ 가 주어졌을 때
$\hat{\mathbf{z}}$ 에 대해 유일하게 풀 수 있다.

\[\hat{\mathbf{z}} = \frac{\mathbf{y} - \mathbf{z}_0}{r\left(1 + \frac{\beta}{\alpha + r}\right)}. \tag{25}\]

식 (24)에서 $\mathbf{y} = f(\mathbf{z}) = \mathbf{z}_0 + \hat{\mathbf{r}}\, r\left(1 + \frac{\beta}{\alpha + r}\right)$ 이므로,
$\mathbf{z}$ 를 복원하기 위해서는 $\hat{\mathbf{r}}$ 을 다시 표현해야 한다.
$\hat{\mathbf{r}} = \frac{\mathbf{z} - \mathbf{z}_0}{r}$ 이므로 이를 식에 대입하면,
\[\mathbf{y} - \mathbf{z}_0 = \frac{\mathbf{z} - \mathbf{z}_0}{r}\,r\left(1 + \frac{\beta}{\alpha + r}\right)\]
양변을 정리하면,
\[\mathbf{z} - \mathbf{z}_0 = \frac{\mathbf{y} - \mathbf{z}_0}{1 + \frac{\beta}{\alpha + r}}.\]
그리고 $\hat{\mathbf{z}} = \frac{\mathbf{z} - \mathbf{z}_0}{r}$ 이므로,
이를 위 식에 대입하면 식 (25)가 얻어진다.

스칼라 방정식을 얻기 위해 양변의 노름(norm)을 취하면 다음이 된다.

\[|\mathbf{y} - \mathbf{z}_0| = r\left(1 + \frac{\beta}{\alpha + r}\right). \tag{26}\]

$\hat{\mathbf{z}}$ 는 $\mathbf{z}$ 의 방향만을 나타내는 단위 벡터(unit vector)로 정의되어 있다.
정의에 따라
\[\hat{\mathbf{z}} = \frac{\mathbf{z} - \mathbf{z}_0}{r}, \quad \text{where } r = \|\mathbf{z} - \mathbf{z}_0\|.\]
이때 $\mathbf{z} - \mathbf{z}_0$ 는 기준점 $\mathbf{z}_0$ 로부터의 방향 벡터,
$r$ 은 그 길이(크기)이므로,
두 값을 나누면 길이가 1인 방향 벡터가 된다.
즉,
\[\|\hat{\mathbf{z}}\| = \frac{\|\mathbf{z} - \mathbf{z}_0\|}{r} = \frac{r}{r} = 1.\]
따라서 식 (25)의
\[\hat{\mathbf{z}} = \frac{\mathbf{y} - \mathbf{z}_0}{r\left(1 + \frac{\beta}{\alpha + r}\right)}\]
양변에 노름(norm)을 취하면,
$|\hat{\mathbf{z}}| = 1$ 이므로
\[1 = \frac{|\mathbf{y} - \mathbf{z}_0|}{r\left(1 + \frac{\beta}{\alpha + r}\right)}.\]
이를 정리하면
\[|\mathbf{y} - \mathbf{z}_0| = r\left(1 + \frac{\beta}{\alpha + r}\right)\]
이 된다.
즉, $\hat{\mathbf{z}}$ 가 단위 방향 벡터이기 때문에
벡터 방정식이 절댓값(거리) 형태의 스칼라 방정식으로 단순화될 수 있는 것이다.

식 (26)이 가역적이기 위한 충분조건은
오른쪽 항 $r\left(1 + \frac{\beta}{\alpha + r}\right)$ 이
단조 증가 함수(non-decreasing function)가 되는 것이다.
이는 $\beta \ge -\alpha$ 를 의미한다.
$r \ge 0$ 이므로, $\beta \ge -\alpha$ 를 impose하면 충분하다.
이 제약은 $\beta$ 를
$\beta = -\alpha + m(\beta)$ 로 재매개변수화(reparameterization)하여
만족시킬 수 있다.
여기서 $m(x) = \log(1 + e^x)$ 이다.

논문