[확률과 통계] 13주차
p2. Motivation
강의 내용
지난 주에 GAN 모델을 공부했었는데
이어서 Normalizing Flow라는 새로운 종류의 생성 모델을 공부하도록 하겠습니다.GAN 같은 경우에는
generator와 discriminator가
서로 속이는 게임을 한다.그래서 zero-sum, 게임이론에 의거해서 훈련을 했었고
그것에 따라 파티클들이 점점 샘플 퀄리티에 가깝게 되면서 진화를 하고
최종적으로 원하는 데이터 distribution에 근접하는 결과를 낸다.이런 것들을 공부했었는데
오늘은 조금 다른 관점으로 갈 것 같습니다.generator도 그렇고 VAE도 그렇고
뉴럴 네트워크가 어떤 데이터를 인풋으로 받고
아웃풋을 한 번에 출력하는 그런 모델들을 공부했었잖아요.Normalizing Flow는 조금 다릅니다.
데이터를 처리하기 위해서
GAN 같은 경우에는 generator에
latent code, latent gaussian distribution을
input으로 넣으면
output으로 데이터가 생성되는 샘플들이 나왔었는데수학이나 확률통계에서는 이를 variational하게 한다고 표현하는데
Normalizing Flow는 그 단계를 여러 단계로 구성합니다.즉, 뉴럴 네트워크에서 여러 번 feed-forward를 하면서
여러 스텝을 통해
가우시안 디스트리뷰션으로부터 점진적으로 샘플이 구성되게 합니다.GAN에서의 트레이닝은
네트워크에 입력과 출력은 한 번씩이지만
discriminator와 generator가 번갈아가면서
여러 번 학습을 하게 되죠.Normalizing Flow는 그런 관점이 아니라
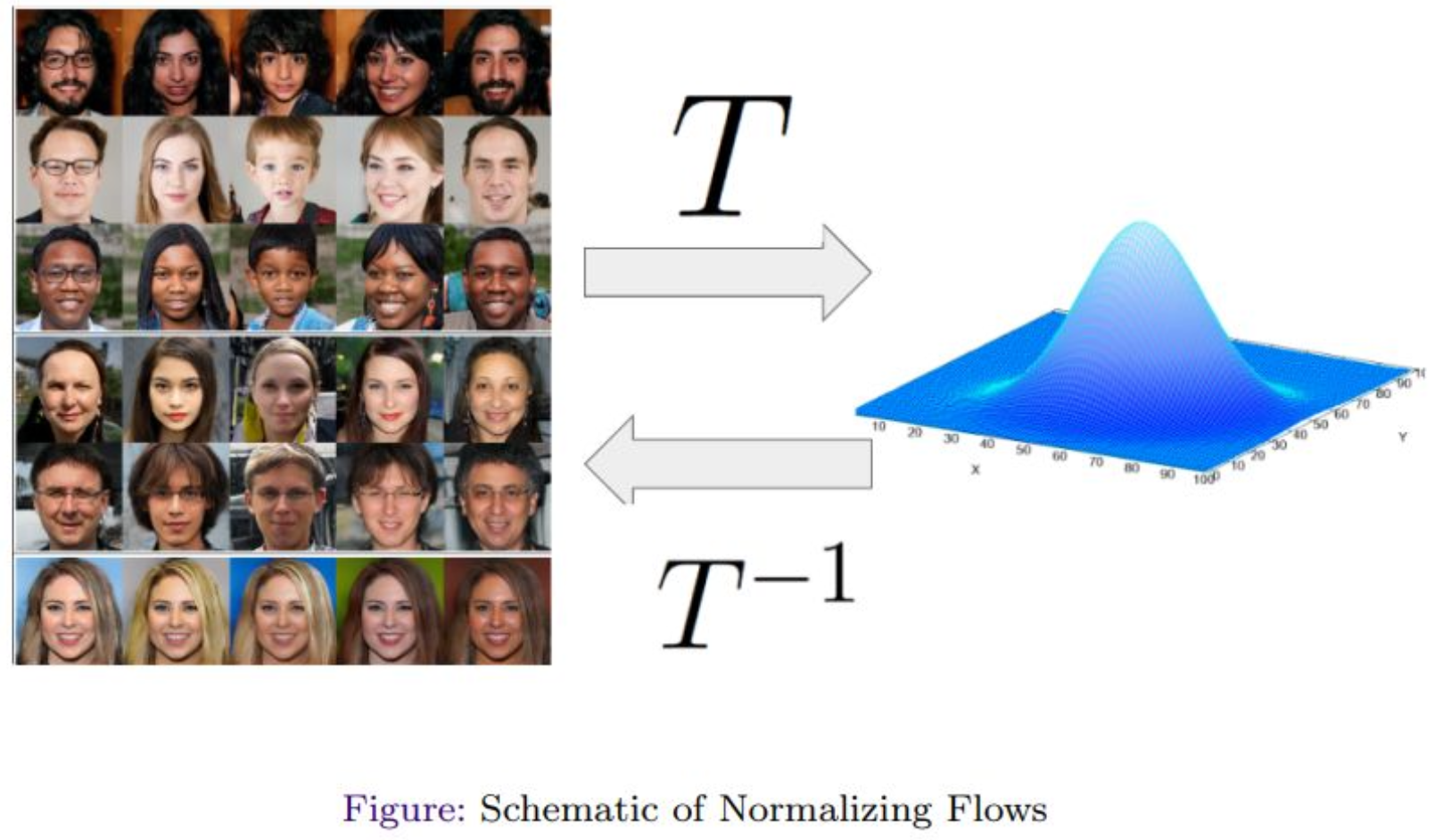
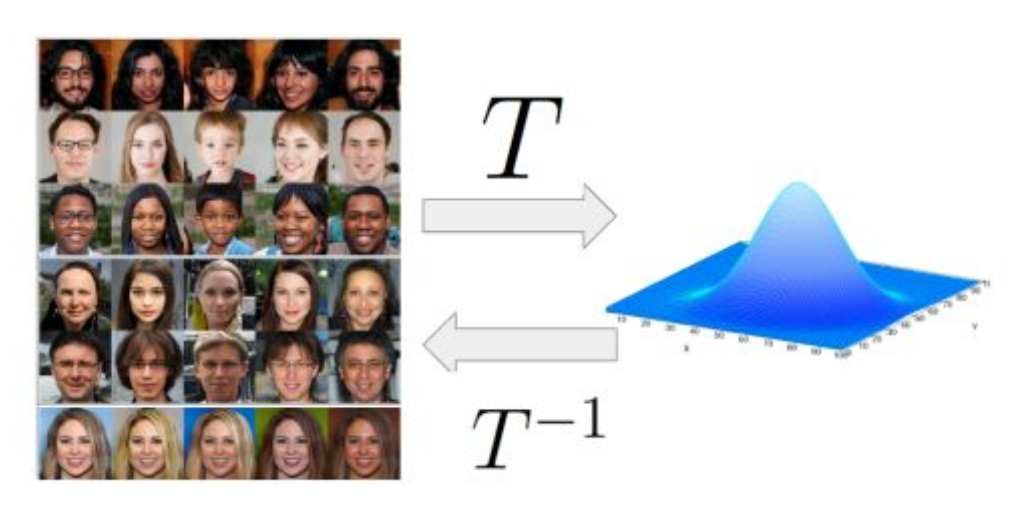
$T^{-1}$이라는 변환을 통해
가우시안으로부터 점점 샘플에 가깝게
순차적이고 절차적으로 생성을 하는 것이 목적이라고 생각하면 될 것 같습니다.그래서 Normalizing Flow에는 큰 공리가 있습니다.
데이터 디스트리뷰션이 있다고 가정할 때
가우시안 디스트리뷰션으로 가는 어떤 맵핑 $T$가 존재한다.
그리고 $T$는 역함수가 있어야 한다.여러분들이 역함수의 개념은 알고 계실 것이라고 생각해요.
역함수가 있다는 것은 사실 굉장한 제약이며,
수학에서는 특정한 함수들만 역함수가 존재합니다.예를 들어 일반적인 뉴럴 네트워크에
역함수가 존재하느냐고 묻는다면
일반적으로 존재하지 않습니다.그렇기 때문에 뉴럴 네트워크를 이용해
이 $T$ 혹은 $T^{-1}$을 모델링해야 하는데
뉴럴 네트워크는 일반적으로 역함수가 없으므로
어떤 수학적 처리를 통해 이를 가능하게 해야 합니다.이것이 Normalizing Flow의 핵심 포인트라고 생각하시면 됩니다.
앞에서 우리가 중간고사 보기 전에 배웠던 내용부터
이야기를 이어가 보겠습니다.
p3. Motivation
강의 내용
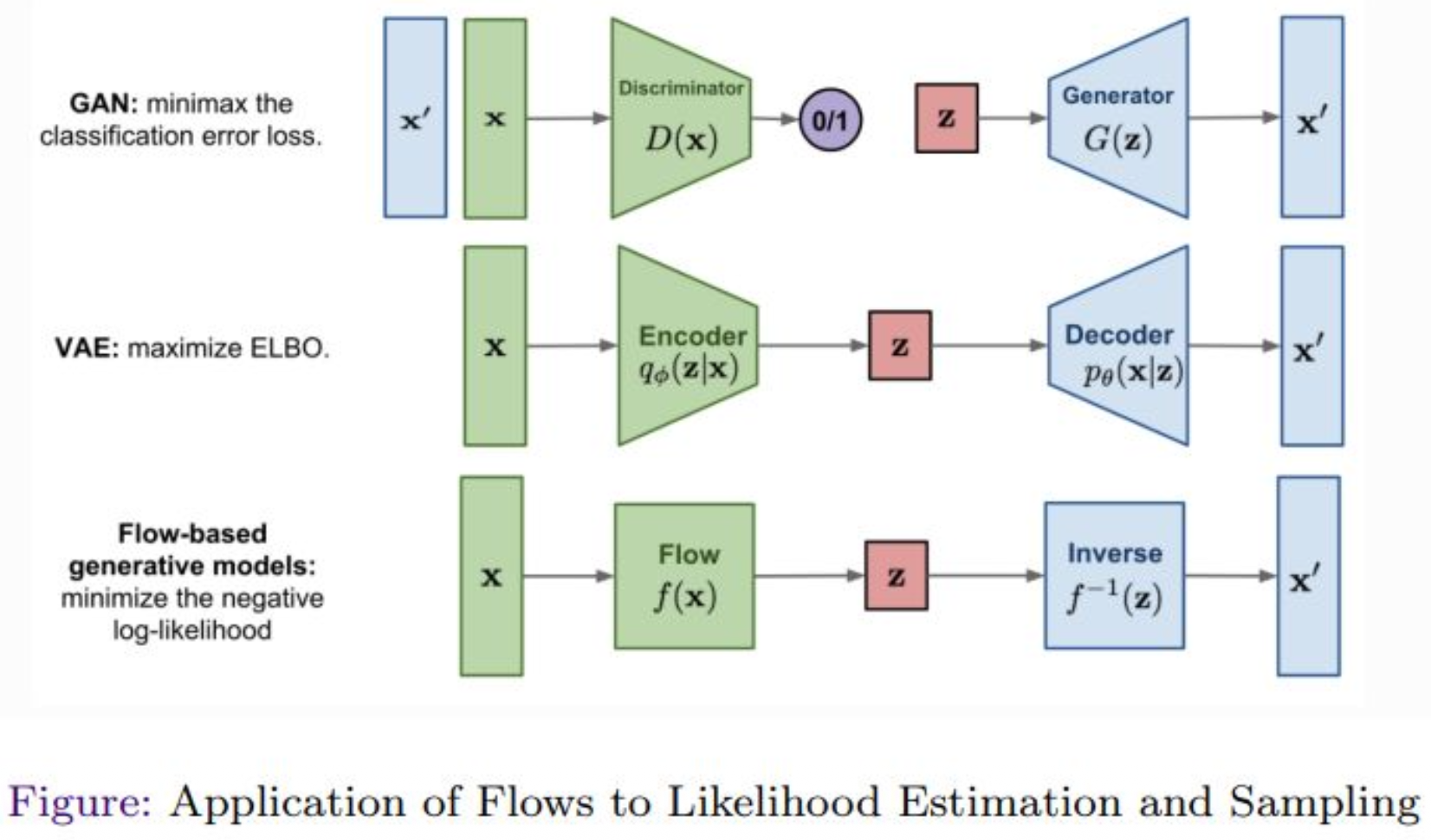
VAE를 배웠었고
GAN은 VAE처럼 파이프라인으로 표현할 수 있었는데
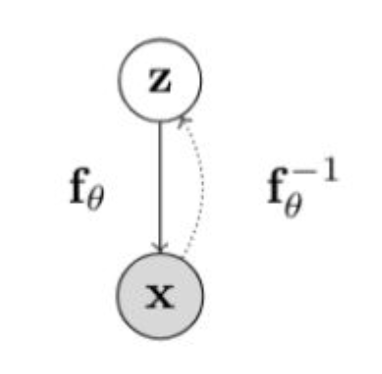
Flow-based 모델은 아래와 같이 표현할 수 있습니다.$T$라는 function이 있고, $T^{-1}$이 있는데
그걸 그냥 $f$라고 하겠습니다.
notation은 계속 변해도 되니까요.그래서 $x$라는 것이 존재하고
Flow라는 function $f$를 통해
$z$까지 맵핑을 합니다.그림에서는 한 번에 결과가 나오는 것으로 보이지만
이는 개략적인 표현이고
실제로는 순차적으로 $x$에서 $z$를 만들어 냅니다.이렇게 순차적으로 만들었으면
inverse function이 다시 이미지를 복원해야 합니다.그래서 inverse function을 통해
순차적으로 역연산을 수행하여
원래의 $x’$을 만듭니다.이때 우리가 원하는 것은
$x$와 $x’$이 최대한 닮도록 만드는 것입니다.Normalizing Flow는
뒤에 나올 Diffusion 모델에서 사용되는 여러 테크닉의
새로운 철학적 출발점이라고 볼 수 있습니다.
순차적 생성이라는 관점에서요.그래서 GAN과 VAE가 이런 방식으로 고려되었고
Likelihood Estimation도 유사하게 적용되며모든 생성 모델과 마찬가지로
결국에는 KL-divergence Minimization을 수행하게 됩니다.그런 과정을 조금 다른 형태로,
다양한 모습으로 확인할 수 있습니다.
p4. Change of Variables
변수 변경 (1차원 경우):
\[p_X(x) = p_Z(h(x))\, \mid h'(x) \mid\]
만약 $X = f(Z)$ 이고 $f(\cdot)$ 가 단조이며 역함수 $Z = f^{-1}(X) = h(X)$ 가 존재하면:이전 예시:
$X = f(Z) = 4Z$, $Z \sim \mathcal{U}[0,2]$ 일 때 $p_X(4)$ 는 무엇인가?- $h(X) = X/4$
- $p_X(4) = p_Z(1)\, h’(4) = \frac{1}{2} \times \mid 1/4 \mid = \frac{1}{8}$
더 흥미로운 예시:
$X = f(Z) = \exp(Z)$, $Z \sim \mathcal{U}[0,2]$ 일 때 $p_X(x)$ 는 무엇인가?- $h(X) = \ln(X)$
- $p_X(x) = p_Z(\ln(x))\, \mid h’(x) \mid = \frac{1}{2x}$ for $x \in [\exp(0), \exp(2)]$
$p_X(x)$ 의 “모양(shape)” 은 prior $p_Z(z)$ 보다 더 복잡할 수 있음에 유의하자.
강의 내용
본격적인 내용에 들어가기 앞서
중요한 수학적 개념을 알아야 합니다.바로 change of variables라는 개념입니다.
이에 대해 설명을 드려보겠습니다.학부 때도 배우셨을 것이고,
중간고사 이전에도 간략히 언급했었는데,
확률 변수를 변환할 때 사용하는
매우 중요하고 일반적이며 널리 알려진 결과라고 보시면 됩니다.$f$라는 function이 존재한다고 할 때
최종적으로는 이를 neural network로 표현하고자 합니다.$Z$라는 random variable이 있을 때
$Z$는 보통 Gaussian, 즉 latent information이었죠.이때 $f(Z)$를 $X$라고 표현하면
$f$에 대해 monotone이라는 개념이 등장합니다.
이것은 새롭게 등장하는 중요한 개념입니다.$f$가 monotone이라고 가정하면
$f$의 inverse, 즉 $X$를 inverse하여 매핑했을 때 나오는 값을 $Z$라고 두고
이 inverse function을 $h$라고 부르겠습니다.그러면 다음과 같은 관계가 성립합니다.
$P_X$는 $X$에 대한 PDF, 즉 probability density function입니다.
그런데 $P_Z$의 입력에 $h(X)$를 넣고,
그 뒤에 $h$를 미분한 값의 absolute value를 곱하면
다음과 같은 등식이 성립하는데,
이것이 change of variables theorem의 핵심입니다.즉,
$X$와 $Z$는 random variable이며,
random variable에는 항상 대응되는 PDF가 존재합니다.$X$가 있으면 $P_X(X)$가 있고
$Z$가 있으면 $P_Z(Z)$가 있습니다.
여기서는 보통 $Z$를 Gaussian distribution으로 가정하죠.random variable의 값이 변환되었을 때
해당 PDF가 어떻게 변해야 하는지를 기술하는 것이
change of variables의 목적입니다.이 직관을 잘 이해하는 것이 매우 중요합니다.
$P_Z(Z)$의 입력에는 원래 $Z$가 들어가야 하지만
역함수인 $h(x)$가 들어가 있으며,
그 뒤에는 $h$의 도함수의 absolute value가 곱해집니다.이는 계산 과정에서 자연스럽게 등장하는 항이며
이런 구조가 존재한다는 정도로 이해하시면 됩니다.$P_Z(Z)$는 scalar이고,
$h$는 univariate function이므로
$h$를 미분해도 scalar이며,
absolute value를 취해도 여전히 scalar입니다.따라서 전체 수식의 모든 항은
scalar dimension의 값이라고 생각하시면 됩니다.예제에서 보았듯이
change of variables는 random variable의 변환에 따라
PDF가 어떻게 변하는지를 알려주는 유용한 theorem입니다.여기서 중요한 개념이 하나 있습니다.
바로 monotone입니다.monotone은
monotone increasing, monotone decreasing
두 가지로 나눌 수 있습니다.monotone increasing은
입력이 증가할수록 값이 증가하거나 같음을 의미하고
monotone decreasing은 그 반대입니다.두 경우 모두 strict한 ordering을 유지하기 때문에
one-to-one correspondence가 성립합니다.예를 들어,
$x^2 = y$는 monotone이 아닙니다.
한쪽에서는 decreasing, 다른 쪽에서는 increasing이기 때문입니다.즉,
change of variables를 사용하고 싶다면
뉴럴 네트워크의 $f$라는 함수가
monotone한 성질을 따라야 합니다.왜냐하면
normalizing flow의 핵심 철학 중 하나가
$T$와 $T^{-1}$을 모두 정의하는 것이고,
monotone function은 inverse function을 가지기 때문입니다.monotone이 아니면 inverse가 존재하지 않거나
well-defined하지 않습니다.이런 이유로
normalizing flow에서는 모노톤한 구조의 함수를 사용합니다.간단한 예제를 봅시다.
$Z$라는 latent variable이 있고
$\mathcal{U}$는 uniform distribution입니다.실수값을 다루므로
예를 들어 $Z$가 $0$과 $2$ 사이의 uniform distribution이라고 하면
$4Z$는 단순히 $0$에서 $8$ 사이의 uniform distribution이 됩니다.그래서 $P_X(4)$를 계산하면
간단히 다음과 같은 결과가 나옵니다.마찬가지로 exponential 함수에 대해서도
동일한 방식으로 계산할 수 있습니다.이 정도는 직관적으로 이해하실 수 있을 것입니다.
보충 자료
수식 도출 과정
1단계. 확률은 동일 — 변수만 다르다
변수변환의 출발점은 매우 단순하다.
$X$가 어떤 작은 구간에 있을 확률 = $Z$가 그 구간으로 변환된 구간에 있을 확률
즉,
\[P(X \in [x, x+dx]) = P(Z \in [z, z+dz])\]여기서
\[z = h(x)\]2단계. 양쪽을 확률밀도로 표현
왼쪽(X 쪽):
\[P(X \in [x, x+dx]) = p_X(x)\, dx\]오른쪽(Z 쪽):
\[P(Z \in [z, z+dz]) = p_Z(z)\, dz\]두 확률이 같으므로:
\[p_X(x)\, dx = p_Z(z)\, dz\]3단계. $Z = h(X)$ 를 미분하여 $dz$와 $dx$ 관계 구하기
\[z = h(x)\]양변 미분하면:
\[dz = h'(x)\, dx\]4단계. $dz = h’(x)\, dx$ 를 확률식에 대입
확률식:
\[p_X(x)\, dx = p_Z(z)\, dz\]여기에 $z = h(x)$, $dz = h’(x)\, dx$를 대입하면:
\[p_X(x)\, dx = p_Z(h(x))\, h'(x)\, dx\]양변에서 $dx$ 제거:
\[p_X(x) = p_Z(h(x))\, h'(x)\]5단계. 왜 절댓값이 필요한가?
단조 감소일 때:
\[h'(x) < 0\]그러면
\[p_Z(h(x))\, h'(x)\]이 음수가 되어버린다 → 확률밀도는 음수가 될 수 없음.
또한 변수 변환에서 필요한 것은
방향이 아니라 “길이의 변화량(스케일)”
이며, 이는 항상 양수여야 한다.
따라서 절댓값을 붙여주면:
\[p_X(x) = p_Z(h(x))\, |h'(x)|\]
p5. Change of Variables
- $Z$를 $[0,1]^n$ 구간에의 균등(uniform) 확률벡터라고 하자.
- $X = A Z$ 이고, $A$는 역행렬 $W = A^{-1}$을 갖는 정방행렬이라고 하자.
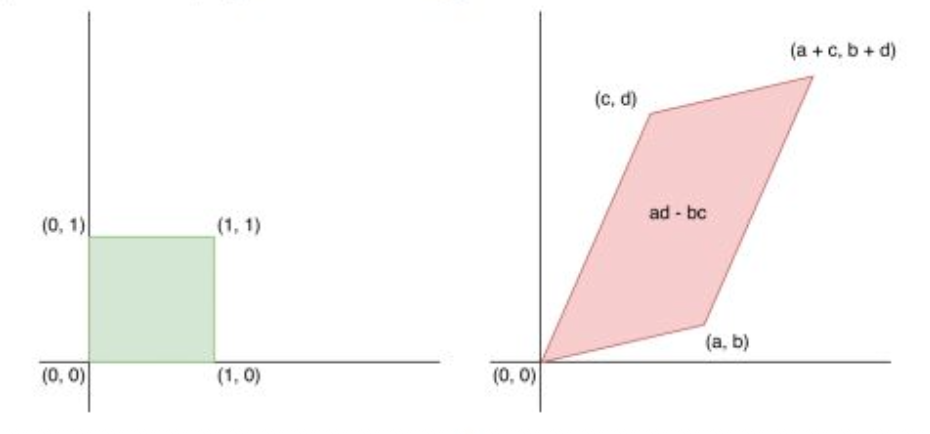
이때 $X$는 어떻게 분포하는가? - 기하학적으로, 행렬 $A$는 단위 하이퍼큐브 $[0,1]^n$을 하나의 parallelotope(평행다포체)로 사상한다.
- 하이퍼큐브와 parallelotope는 정사각형/정육면체와 평행사변형/평행육면체를 고차원으로 일반화한 개념이다.
그림: 행렬 \(A = \begin{pmatrix} a & c \\ b & d \end{pmatrix}\) 는 단위 정사각형을 평행사변형으로 사상한다.
강의 내용
1-dimensional 예시는 직관을 위해 사용한 것이고,
실제로는 n-dimensional로 확장해야 합니다.
우리가 다루는 이미지 등 대부분의 데이터는
고차원 공간에 존재하기 때문입니다.이를 위해 다음과 같은 상황을 생각해 봅시다.
$Z$가 $[0,1]^n$에 균등 분포된 random variable이라고 하겠습니다.
이는 unit cube라고 부르며,
$n=1$이면 구간 $[0,1]$,
$n=2$이면 정사각형 $[0,1]\times[0,1]$,
$n=3$이면 3차원 큐브를 의미합니다.이제 $X = AZ$라고 두고,
$A$는 invertible matrix,
$W$는 $A^{-1}$이라고 가정합시다.이때 $X$가 어떻게 분포되는지 알고 싶은 것입니다.
앞에서 보았던 change of variable을 적용하면 되지만,
이 페이지에서는 직관을 제공하기 위해 기하적 예시를 사용합니다.왼쪽 아래 초록색 박스는 $n=2$일 때 unit cube이고,
invertible matrix $A$를 곱하면
초록색 영역이 오른쪽의 빨간색 영역처럼 변형됩니다.
즉, unit cube가 평행사변형 형태 등으로 변형되는 것입니다.여기서 핵심은 다음과 같습니다.
초록색에서 빨간색으로 옮기는 연산 $AZ$ 역시
$f(Z)$라는 함수로 볼 수 있으며,
이는 normalizing flow에서 등장하는 기본 구조입니다.또한 빨간색 결과에 대해
또 다른 matrix $B$를 사용하여
부드럽게 또 다른 형태로 변환할 수 있고,
이러한 변환을 반복할 수 있습니다.여러 번 반복하면 우리의 믿음은 다음과 같습니다.
반복된 변환을 통해
최종적으로 데이터 distribution과 동일하거나 매우 가까운 형태의
support 영역에 수렴하게 된다.이것이 normalizing flow의 핵심 아이디어입니다.
실제로는 $A$가 뉴럴 네트워크로 표현되므로
박스가 nonlinear하게 비틀리고
매우 복잡한 표현력으로 변환될 수 있습니다.이런 변환을 여러 번 체이닝하면
원하는 데이터 분포에 도달하도록 만들 수 있습니다.
이것이 normalizing flow의 전체 철학이며,
이 아이디어를 이해하면 핵심을 이해한 것입니다.수학적으로 조금 더 말하자면,
invertible matrix $A$는 2D에서
정사각형을 사다리꼴이나 평행사변형으로 변형하는 역할을 합니다.이 직관을 가지고 normalizing flow를 이해하면 훨씬 재밌습니다.
이제 첫 번째 질문을 해봅시다.
한 번에 맵핑하면 되지 않습니까?
왜 여러 개의 function을 체이닝해야 합니까?두 번째 질문은,
체이닝을 해야 한다면 몇 번 해야 합니까?
이는 뉴럴 네트워크의 복잡성에 따라 달라집니다.첫 번째 질문에 답하자면,
normalizing flow에서는 변환이 invertible해야 합니다.matrix $A$는 invertible하므로 문제가 없지만
이를 뉴럴 네트워크로 일반화하면
invertible하다는 조건을 유지하기 어렵습니다.이를 만족시키기 위해 monotone이라는 성질을 부여하지만
monotone function 하나만으로는
네트워크 파라미터가 아무리 많아도
복잡한 분포를 충분히 표현할 수 없다는 것이
이론적으로 알려져 있습니다.즉, 표현력에 한계가 있습니다.
그래서 학계에서는 divide and conquer 방식의 아이디어를 사용했습니다.
하나의 monotone function으로 전체를 모델링하지 않고,
여러 개의 monotone function을 나누어
각각을 체이닝하여 조합하면
훨씬 더 강력한 표현력을 가진다는 사실이 밝혀졌습니다.이러한 연구는 2015년부터 2018년 사이에 활발히 진행되었습니다.
따라서 normalizing flow의 목표는
monotone하면서 invertible한 함수들의 체이닝을 통해
데이터를 점점 데이터 분포에 가깝게 변화시키는 것입니다.수식으로 표현하면
$X$라는 distribution이
여러 개의 함수 합성, 즉 function composition을 통해
$Z$라는 distribution과 연결되는 구조가 됩니다.
p6. Change of Variables
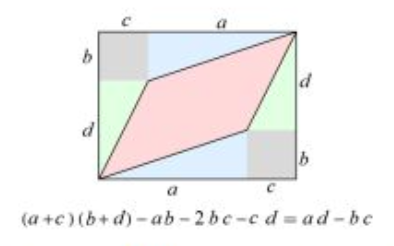
parallelotope의 부피(volume)는 행렬 $A$의 행렬식(determinant)의 절댓값과 동일하다.
\[\det(A) = \det \begin{pmatrix} a & c \\ b & d \end{pmatrix} = ad - bc\]$X = A Z$라고 하자. 여기서 $A$는 정방의 가역 행렬이며, 그 역행렬은 $W = A^{-1}$이다.
\[p_X(x) = p_Z(Wx)\,/\,|\det(A)|\] \[= p_Z(Wx)\,|\det(W)|\]
$X$는 면적이 $|\det(A)|$인 parallelotope 상에서 균일하게 분포한다.
따라서 다음을 얻는다:왜냐하면 $W = A^{-1}$이면
\[\det(W) = \frac{1}{\det(A)}\]1차원 경우의 공식과의 유사성에 주목하라.
강의 내용
앞의 예제를 다시 보자면,
determinant 자체는 이 단계에서는 크게 신경 쓰지 않아도 됩니다.우리가 $X = AZ$,
즉 $X = f(Z)$라고 가정했을 때,
이 케이스에서는 $X$라는 random variable에 대한 distribution이
아래의 수식처럼 표현되며,
이를 통해 최종적으로 확률적 정보가 어떻게 바뀌는지를
이해할 수 있습니다.즉, 선형 변환 $A$를 적용했을 때
random variable의 PDF가 어떻게 변하는지를 보여주는 예제이며,
change of variable의 개념을 직관적으로 이해하는 데 도움이 됩니다.
보충 자료
1차원 공식과의 유사성 설명
다변량 선형변환에서도 밀도변환 공식의 핵심 구조는
“원래 밀도를 역변환한 지점에서 평가하고, 스케일 변화량의 절댓값으로 나눈다”는 점에서
1차원 변수변환 공식과 완전히 동일하다.1차원에서는
\(p_X(x) = p_Z(h(x))\,|h'(x)|\) 로서 스케일 변화량이 도함수 $h’(x)$ 하나였다.다변량에서는
\(p_X(x) = p_Z(Wx)\,|\det(W)|,\) 여기서 스케일 변화량이 Jacobian의 절댓값 = $\det(W)$ 로 일반화되었을 뿐이다.즉,
1D: 길이(scale) 변화 → $|h’(x)|$
nD: 부피(volume) 변화 → $|\det(W)|$따라서 다변량 공식은 1차원 변수변환의 자연스러운 확장(extension)이다.
p7. Change of Variables
$A$를 통한 선형변환의 경우, 부피의 변화는 행렬 $A$의 행렬식(determinant)로 주어진다.
비선형 변환 $f(\cdot)$의 경우, 선형화된(linearized) 부피 변화는
$f(\cdot)$의 Jacobian의 행렬식(determinant)으로 주어진다.변수변환(일반 경우):
\[p_X(x) = p_Z\!\bigl(f^{-1}(x)\bigr) \left| \det\!\left( \frac{\partial f^{-1}(x)}{\partial x} \right) \right|\]
$f : \mathbb{R}^n \to \mathbb{R}^n$ 이 $X = f(Z)$ 와 $Z = f^{-1}(X)$ 를 만족하도록 가역일 때,
$Z$와 $X$의 대응(mapping)은 다음과 같다:Note 0:
이는 이전 1차원 경우
$p_X(x) = p_Z(h(x))\,|h’(x)|$
를 일반화한 것이다.Note 1:
VAE와 달리, $x, z$는 연속적이어야 하며 같은 차원을 가져야 한다.
예를 들어, $x \in \mathbb{R}^n$ 이면 $z \in \mathbb{R}^n$ 이다.Note 2:
어떤 가역행렬 $A$에 대해서도
$\det(A^{-1}) = \det(A)^{-1}$ 이다.따라서,
\[p_X(x) = p_Z(z) \left| \det\!\left( \frac{\partial f(z)}{\partial z} \right) \right|^{-1}\]
강의 내용
이제 좀 더 본격적인 경우를 살펴보겠습니다.
앞에서는 $A$라는 매트릭스를 통한 리니어 트랜스폼을 다뤘지만,
이번에는 논리니어 트랜스폼, 즉 뉴럴 네트워크와 유사한 형태의 변환을 고려해보자는 것입니다.이 페이지에서는 change of variable의 일반적 형태를 다루고 있는데,
여기서 특히 중요한 점은
$f$가 입력과 출력의 차원을 바꾸면 안 된다는 것입니다.
입력이 $n$차원이라면 출력도 반드시 $n$차원이어야 합니다.이 $f$를 우리는 뉴럴 네트워크로 설계할 것이며,
따라서 이 조건은 네트워크 디자인의 주요 제약 조건이 됩니다.GAN이나 VAE에서는 이런 제약이 존재했나요?
인코더와 디코더를 합쳐놓으면 전체 구조의 차원은 맞아야 하지만,
개별 인코더만 보면 입력과 출력의 차원이 다르고,
디코더도 마찬가지로 차원이 다릅니다.즉, 일반적 생성 모델의 뉴럴 네트워크 구조는
입력과 출력의 차원이 동일하지 않아도 문제가 되지 않습니다.
그러나 normalizing flow에서는 차원 유지가 필수입니다.
이 지점에서부터 모델 구조가 달라져야 한다는 점을 이해해야 합니다.뒤에 다룰 디퓨전 모델에서도
U-Net이라는 구조가 널리 사용되는데,
나노바나나 등 최신 모델에도 이 구조가 변형된 형태로 포함되어 있습니다.
핵심 아이디어는 그대로 유지한 채,
여러 구성 요소를 하이퍼파라미터화하여 최적화한 U-Net의 변형들을 사용합니다.이런 구조가 왜 필요한지는
나중에 네트워크 파이프라인을 보면 자연스럽게 이해될 것입니다.요약하자면,
단순한 수학적 제약이
모델의 구조적 사양(specification)까지 달라지게 만들고,
그에 따라 U-Net 같은 구조가 사용된다는 점을 이해하면 됩니다.아래에 보이는 식은
앞에서 예제를 보고 와서 어느 정도 익숙하게 느껴지지만,
처음 보면 쉽지 않은 내용들입니다.
예를 들어 $f$의 inverse를 미분한다는 표현도
처음에는 다소 생소할 수 있습니다.
이 부분은 뒤에서 단계적으로 설명될 예정입니다.우리가 다루는 핵심은
정보를 어떻게 변형시키는지에 대한 수학적 룰이며,
생성 모델의 발전사는
이 룰을 점점 더 정교하게 만드는 과정이라고 이해할 수 있습니다.
change of variable은
GAN과 VAE 이후 진화한 한 형태의 접근이라고 생각하면 됩니다.다만 이 형태는 매우 constrained된 구조입니다.
예를 들어 determinant는 고차원에서 계산 비용이 매우 높은 연산입니다.이미지 차원이 1000이라면 그리 큰 편이 아닌데도,
$1000 \times 1000$ 차원 매트릭스의 determinant를 계산하는 데
이미 상당한 비용이 듭니다.
여기에 inverse function까지 구해야 하고,
이를 다시 미분해야 하며,
그 결과로 나오는 $\partial f^{-1}(x) / \partial x $ 도 Jacobian matrix로
역시 $n \times n$ 형태가 됩니다.데이터 차원이 10만이라면
$10^5 \times 10^5$ 크기의 매트릭스가 나타나고,
determinant 연산의 계산 복잡도는 전통적으로 $O(N^3)$입니다.즉, $n^2$ 규모의 행렬을 구한 뒤
$n^3$ 연산을 해야 하므로
현실적으로는 절대 그대로 사용할 수 없습니다.따라서 이 수식을 실전 모델링에서 그대로 적용하는 것은 불가능하며,
반드시 엔지니어링적 테크닉이 필요합니다.그러나 이 페이지의 핵심은
앞에서 본 1D 예제에서 느꼈던 직관이
그대로 고차원에서도 유지된다는 점입니다.
나머지는 모두 구현 단계에서 해결해야 하는 테크니컬한 문제들입니다.
p8. Example: Two-dimensional Change of Variables
$Z_1$과 $Z_2$를 결합밀도 $p_{Z_1,Z_2}$를 갖는 연속 확률변수라고 하자.
$u : \mathbb{R}^2 \to \mathbb{R}^2$ 를 가역변환이라고 하자.
두 입력과 두 출력으로 이루어져 있으며, 이를 $u = (u_1, u_2)$로 표기한다.$v = (v_1, v_2)$ 를 그 역변환이라고 하자.
$X_1 = u_1(Z_1, Z_2)$ 이고 $X_2 = u_2(Z_1, Z_2)$ 라고 하자.
\[p_{X_1,X_2}(x_1,x_2)\] \[= p_{Z_1,Z_2}\bigl(v_1(x_1,x_2),\, v_2(x_1,x_2)\bigr) \left| \det \begin{pmatrix} \dfrac{\partial v_1(x_1,x_2)}{\partial x_1} & \dfrac{\partial v_1(x_1,x_2)}{\partial x_2} \\[6pt] \dfrac{\partial v_2(x_1,x_2)}{\partial x_1} & \dfrac{\partial v_2(x_1,x_2)}{\partial x_2} \end{pmatrix} \right| \quad \text{(inverse)}\] \[= p_{Z_1,Z_2}(z_1,z_2) \left| \det \begin{pmatrix} \dfrac{\partial u_1(z_1,z_2)}{\partial z_1} & \dfrac{\partial u_1(z_1,z_2)}{\partial z_2} \\[6pt] \dfrac{\partial u_2(z_1,z_2)}{\partial z_1} & \dfrac{\partial u_2(z_1,z_2)}{\partial z_2} \end{pmatrix} \right|^{-1} \quad \text{(forward)}\]
그러면 $Z_1 = v_1(X_1, X_2)$ 이고 $Z_2 = v_2(X_1, X_2)$ 이다.
강의 내용
그래서 이것은 하나의 예제가 될 수 있습니다.
2차원에서 $u$라는 어떤 invertible한,
즉 nonlinear transformation이 존재한다고 가정할 때
이러한 형태로 표현된다고 설명드렸습니다.앞에서 말씀드렸던 $f^{-1}$를 $x$에 대해 미분하는 연산은
여기에서 $2 \times 2$ 매트릭스로 표현되어 있습니다.
차원이 2이기 때문에 결과가 $2 \times 2$ 매트릭스로 나타나는 것입니다.이러한 규칙을 따르게 되며,
세부적인 수학적 내용은 직접 살펴보시면 좋을 것 같습니다.
개념 자체는 straightforward하며
다만 표기(Notation)가 복잡해질 뿐입니다.
보충 자료
inverse의 의미
inverse는 역변환 Jacobian을 사용했다는 뜻이다.
즉, $x \mapsto z$ 로 가는 역함수 $v(x)$를 미분하여
$ \frac{\partial v(x)}{\partial x} $ 의 Jacobian determinant를 쓰는 방식이다.
이는
\(p_X(x) = p_Z(v(x))\,\left|\det\!\left(\frac{\partial v(x)}{\partial x}\right)\right|\)
형태로 표현된다.forward의 의미
forward는 정방향 변환 Jacobian을 사용했다는 뜻이다.
즉, $z \mapsto x$ 로 가는 원래 함수 $u(z)$를 미분하여
$ \frac{\partial u(z)}{\partial z} $ 의 Jacobian determinant를 쓰고,
그 역수를 취하는 방식이다.
이는
\(p_X(x) = p_Z(z)\, \left| \det\!\left(\frac{\partial u(z)}{\partial z}\right) \right|^{-1}\)
형태로 표현된다.두 방식의 관계
역함수 정리(inverse function theorem)에 의해
\(\det\!\left(\frac{\partial v(x)}{\partial x}\right) = \left[\det\!\left(\frac{\partial u(z)}{\partial z}\right)\right]^{-1}\)
이므로, inverse 방식과 forward 방식은 완전히 동일한 결과를 준다.
p9. Motivation: Normalizing Flows
관측 변수 $X$와 잠재 변수 $Z$ 위의
유향(directed) 잠재변수(latent-variable) 모델을 고려하자.normalizing flow 모델에서,
$f_\theta : \mathbb{R}^n \to \mathbb{R}^n$ 로 주어지는 $Z$와 $X$ 사이의 사상(mapping)은
결정적(deterministic)이며 가역적(invertible)이다.
따라서
\(X = f_\theta(Z), \quad Z = f_\theta^{-1}(X)\)변수변환(change of variables)를 사용하면, 주변우도(marginal likelihood) $p(x)$는 다음과 같이 주어진다:
\[p_X(x;\theta) = p_Z\!\left(f_\theta^{-1}(x)\right) \left| \det\!\left( \frac{\partial f_\theta^{-1}(x)}{\partial x} \right) \right|\]참고: $x, z$는 연속적이어야 하며 동일한 차원을 가져야 한다.
강의 내용
네.
이제 normalizing flow로 정의를 하겠습니다.
normalizing flow라는 것은
Z라는 latent variable과 X라는 data variable이 존재할 때
주어진 $f_{\theta}$라는 neural network가 있어서
이를 기반으로 정의되는 모델을 의미합니다.이때 해당 neural network는 반드시 deterministic해야 합니다.
random component가 들어가면 안 됩니다.
뒤에서 다룰 diffusion 모델은 deterministic하지 않기 때문에
stochastic한 방식으로 동작하지만,
normalizing flow에서는 random이 아닌
deterministic한 neural network가 존재해야 하며
동일한 차원의 input을 받아 동일한 차원의 output을 내야 합니다.또한 이 함수는 invertible해야 하고
또는 monotone해야 합니다.이런 조건하에서 $f_{\theta}(z)$는 $x$를 생성하고
$f_{\theta}^{-1}(x)$는 $z$를 복원하도록
구성된 모델을 normalizing flow라고 부릅니다.다만 flow라는 용어는 사실 이 정의와 완전히 일치하지 않습니다.
flow는 본래 “흐름”이라는 의미이며
수학에서는 vector field 등을 다룰 때
여러 변환이 연속적으로 중첩된 상태를 flow라고 부르기 때문에
정확한 용어라고 보기는 어렵지만
편의상 이렇게 부르고 있는 것입니다.앞에서 다뤘던
general case의 change of variable 공식에 등장하던 $f$들이
여기서는 $f_{\theta}$로 바뀐 형태라고 이해하면 됩니다.이렇게 구성했을 때 우리는 X에 대한 distribution을 구할 수 있었고
그러면 자연스럽게 이렇게 묻고 싶어집니다.양변에 로그를 씌우고 싶지 않나요?
저만 그런가요?실제로 양변에 로그를 취해서 계산합니다.
왜냐하면 $log P_X$를 기반으로 하는
negative log-likelihood를 평가해야 하기 때문입니다.로그를 취하면 $log(AB) = log A + log B$가 되므로
식이 쉽게 분해(decomposition)되고
훨씬 다루기 쉬운 형태가 됩니다.
p10. Flow of Transformations
Normalizing:
가역 변환을 적용한 후, 변수변환(change of variables)은 정규화된(normalized) 밀도를 제공한다.
Flow:
가역 변환들은 서로 합성될 수 있다.
- $z_0$에 대해 단순한(simple) 분포로 시작한다 (예: 가우시안).
- 최종적으로 $x = z_M$ 을 얻기 위해, $M$개의 가역 변환을 순차적으로 적용한다.
변수변환 공식에 의해,
\[p_X(x;\theta) = p_Z\!\left(f_\theta^{-1}(x)\right) \prod_{m=1}^{M} \left| \det \left( \frac{\partial (f_\theta^{m})^{-1}(z_m)} {\partial z_m} \right) \right|\](참고: 행렬곱의 determinant 는 determinant 들의 곱과 동일하다)
강의 내용
이 페이지에서는 Flow라는 개념이 왜 필요한지를
설명하고자 합니다.먼저 $f^{1}$부터 $f^{m}$까지 총 $m$개의 Neural Network를 준비하고,
이 함수들은 각각 N-dimensional vector를 입력받아 출력하는 구조라고 봅니다.$z_{0}$은 쉽게 말해
Gaussian distribution이나 Uniform distribution에서
샘플링된 random variable이라고 생각할 수 있으며,
이러한 일련의 변환 과정을 Chaining이라고 부릅니다.수학적·정식 용어로는 Composition이라고 해야 하지만,
Learning Theory나 Machine Learning 분야에서는
Neural Network나 일반적인 Function을
여러 층으로 중첩해 변환시키는 과정을
Chaining되어 있다, Chaining한다라고 표현합니다.
말 그대로 사슬(Chain)처럼 이어진 구조라는 의미입니다.이렇게 $m$개의 Neural Network가 Composition 형태로
$f_{\theta}$의 Chaining 구조를 이루고,
이를 통해 $z_{m}$을 만들어 내는 방식이
Flow라는 이름이 붙게 된 이유입니다.이 가정에 따라 Change of Variable 공식을
그대로 적용하게 되며,
여러 개의 함수가 중첩되었기 때문에
최종 식은 아래와 같은 형태가 됩니다.큰 파이 기호는 곱(product)을 의미하며,
$m$이 $1$부터 $m$까지 변할 때
각 단계마다 determinant의 absolute 값을 취한
총 $m$개의 항을 모두 곱한 구조입니다.또한 $Z$의 distribution과 $X$의 distribution은
중간 과정과 무관하게 그대로 동일하게 유지됩니다.그래서 전체 형태가 곱셈만으로
매우 깔끔하게 정리된 형태로 표현되는 것이고,
이는 다음 성질을 이용한 결과입니다.Determinant of product = Product of determinants.
즉, $det(AB) = det(A) det(B)$라는 성질 때문에
원래 내부에 있어야 할 곱셈 항이
바깥으로 깔끔하게 빠져나올 수 있었던 것입니다.매우 중요한 성질이므로
이 프로퍼티만 기억해 두면 충분할 것 같습니다.
p11. Maximum Likelihood Estimation
- 데이터셋 $\mathcal{D}$ 위에서 maximum likelihood를 이용한 학습:
inverse 변환 $x \mapsto z$ 와 변수변환 공식(change of variables)을 통한
정확한 우도 계산(exact likelihood evaluation)forward 변환 $z \mapsto x$ 를 통한 샘플링(sampling)
- inverse 변환을 통해 잠재 표현(latent representations) 추론
(inference network가 필요 없음!)
강의 내용
이 페이지에서는 앞서 언급한 것처럼
$log$를 취하고 싶다는 내용을 실제로 반영한 식을 설명하고 있습니다.먼저 $X$라는 Random Variable과 $Z$라는 Random Variable이 있을 때
양변에 $log$를 취하여 표현을 정리한 형태이며,
여기에는 체이닝으로 인한 product 표기가 생략되어 있습니다.원래는 log 내부에 파이(∏) 기호로 표시된
product 항이 포함되어야 하고
log 적용 후에는 summation 형태가 되어야 하지만
이해를 돕기 위해 단순화하여 표현한 것입니다.즉, $f$가 여러 개의 함수로 체이닝되어 있다고 가정하고
큰 function 관점에서 하나의 $f$로 간주해 정리한 식입니다.이어서 summation 아래에 있는 $x \in D$에서
$D$는 training data이며 test data가 아닙니다.이 summation 구조는 무엇을 의미하냐면,
우리가 중간고사 이전에 배웠던 estimator 개념입니다.즉, iid인 $n$개의 sample에 대해
likelihood를 합산(summation)하여
true likelihood를 근사하는 estimator를 구성하는 과정입니다.따라서 이것은 estimator이며,
이 estimator를 최대화(maximization)하도록
neural network parameter $\theta$를 찾는 것이 목표입니다.이를 위해 우리는 gradient descent의 반대 방향,
즉 gradient ascent를 사용해
maximum log-likelihood가 되도록 학습을 진행합니다.이렇게 maximum log-likelihood 학습이 완료되면
어떤 결과가 나오느냐 하면,$x$를 $f_{\theta}$에 입력하면
최종적으로 $z$를 생성할 수 있으며,
반대로 $z$를 inverse function에 넣으면
$x$를 얻을 수 있게 됩니다.즉, 학습이 잘 되었다면
forward와 inverse mapping 모두를
실제로 관찰 가능하게 되는 것입니다.그렇게 훈련이 끝나면
이제 샘플링을 어떻게 하느냐를 살펴볼 수 있습니다.VAE나 GAN에서는 neural network가 두 개 필요했죠.
GAN은 discriminator와 generator,
VAE는 encoder와 decoder를 사용했습니다.그런데 normalizing flow는 흥미롭게도
$f$와 $f^{-1}$이라는 추상적 개념은 두 개지만
실제 구현은 하나의 neural network로 해결됩니다.inverse는 별도의 네트워크가 아니라
같은 네트워크에 특정한 operation을 적용하여 구현하기 때문입니다.따라서 normalizing flow에서는
neural network을 하나만 사용합니다.이것은 매우 큰 차이이며,
샘플링과 inference(test time)에서
불필요한 네트워크가 제거된다는 이점이 있습니다.예를 들어 VAE에서는 encoder를 버렸고
GAN에서는 discriminator를 버렸습니다.하지만 normalizing flow는 버려지는 것이 없습니다.
이는 모델이 variational한 formulation을 기반으로 하고
데이터가 어떻게 변해야 하는지에 대한
수학적 규칙을 명확히 정의하기 때문에
neural network 사용 방식이 brute force가 아니라
매우 효율적으로 구성되기 때문입니다.encoder와 decoder가 mirrored 구조로
거의 동일한 parameter 규모를 갖고 있었음을 떠올려보면
normalizing flow에서는
동일한 역할을 하나의 network로 수행하기 때문에
parameter가 절반, 비용도 절반,
필요한 인프라도 절반으로 줄어듭니다.이러한 이유 때문에
현대 generative AI에서는 GAN이 더 이상 주력 모델이 아닙니다.디퓨전 모델이 더 stable하고 expressive하지만
GAN은 무엇보다 인프라가 2배로 든다는 치명적인 단점이 있었습니다.실례로 H100 GPU 2,000대로 1년 학습하는 비용이 엄청난데
네트워크 두 개를 사용하면 4,000대가 필요하게 되어
사실상 감당할 수 없는 수준이 됩니다.이런 맥락 속에서 디퓨전 모델 시대가 열렸고
상업적 활용이 가능해졌다고 판단할 수 있습니다.생성 모델을 오랫동안 연구한 입장에서 보면
최근의 디퓨전 모델은 이전 세대보다
훨씬 모델다운 모델로 발전한 지점이라고 할 수 있습니다.아직 디퓨전 모델도 끝이 아니며
앞으로 훨씬 많은 발전이 필요하지만
이미 매우 빠르게 개량되고 있는 상황입니다.이러한 흐름 전체를 이해하는 것이 중요합니다.
강의에서는 생성 모델의 발전사를
실제 시간 순서대로 따라가며 설명하고 있으며,
VAE → GAN → Normalizing Flow → Diffusion으로 이어지는
큰 흐름 속에서 각각의 역할과 한계를
자연스럽게 이해할 수 있도록 구성되어 있습니다.다시 본문의 내용으로 돌아오면,
샘플링은 결국 $f_{\theta}$의 체이닝 구조를 따라
$z = z_{0}$에서 시작하여
neural network를 연속적으로 input–output 시키며
for-loop처럼 반복 적용하는 방식입니다.여기서 중요한 점은 divide and conquer의 함정입니다.
문제를 잘게 나누는 것은 좋지만
호출 횟수가 크게 늘어난다는 단점이 있습니다.즉, 총 인프라 규모는 줄었어도
동일한 neural network를 N번 호출해야 하므로
시간 복잡도는 증가합니다.디퓨전 모델도 동일하게
같은 네트워크를 수천 번 호출해야 하므로
이미지 한 장 생성하는 데 시간이 오래 걸립니다.예를 들어 나노바나 모델로 이미지 생성 시
내부적으로 neural network를
5,000번 정도 호출하는 경우도 존재합니다.GAN은 단 한 번 호출로 끝나지만
학습 시 불안정성과 높은 인프라 비용이라는 단점이 있었습니다.따라서 생성 모델 전체에는
항상 여러 trade-off가 존재하며
완벽한 마법 같은 도구는 없다는 점을 기억해야 합니다.이런 맥락을 이해한 상태에서 보면,
flow 기반 샘플링과 inversion은 매우 자연스럽습니다.inverse mapping을 사용하는 encoding 과정에서도
동일하게 체이닝을 반복 적용하면
$x \rightarrow z$ 변환을 수행할 수 있습니다.결국 normalizing flow는
encoder와 decoder라는 두 네트워크의 쌍에서 벗어나
하나의 network만으로 양방향 변환을 수행한다는 점이
가장 큰 핵심 메시지라고 할 수 있습니다.
p12. Flow of Transformations
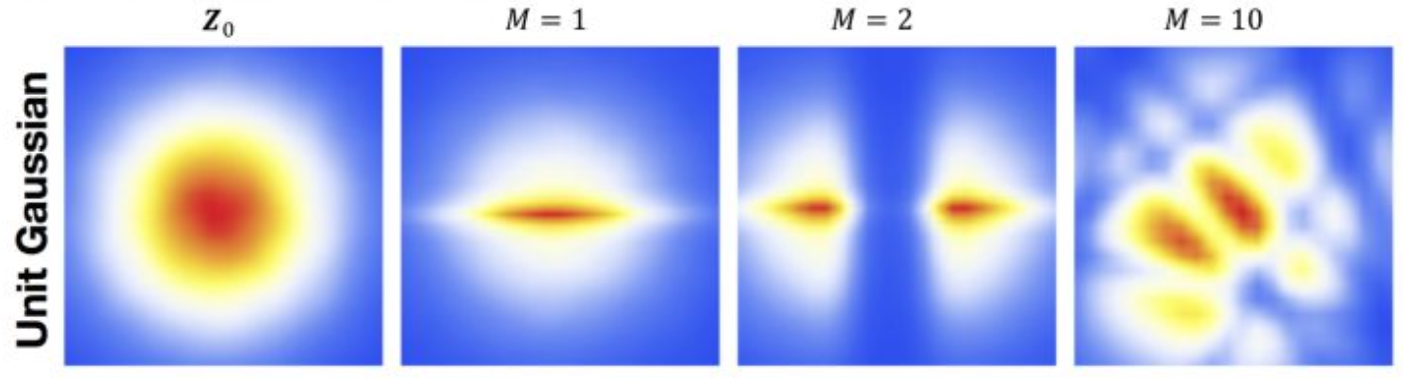
기본 분포(base distribution): Gaussian
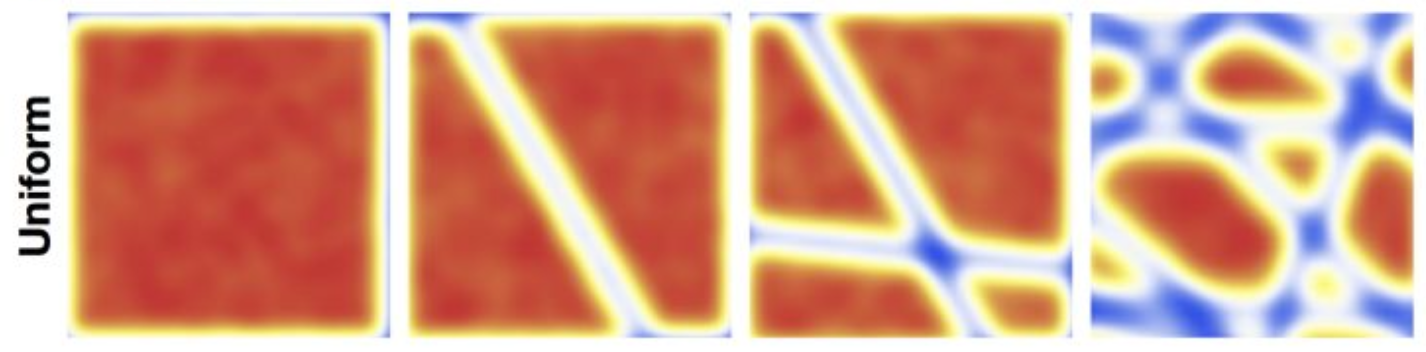
기본 분포(base distribution): Uniform
10개의 planar(평면) 변환은 단순한 분포들을 더 복잡한 분포로 변환할 수 있다.
강의 내용
앞에서 A라는 매트릭스를 이용해 모양을 순차적으로 변형시키는 과정을 설명했었고,
그 변형이 반복되면서 최종적으로 우리가 원하는 형태에 도달하는 것이
현재 살펴보고 있는 모델의 특징이라고 말씀드렸습니다.
이제 이를 그림을 통해 다시 이해해보자는 내용입니다.우선 Z라는 latent variable을
Gaussian, 특히 unit Gaussian(standard Gaussian)이라고 가정해봅시다.
그러면 그림의 맨 왼쪽에 있는 초기 분포에서 출발하게 됩니다.그리고 또 하나의 가정으로,
모노톤한 neural network가 존재하고
그 네트워크가 충분히 훈련되었다고 가정해보겠습니다.이때 그림에서 M이라고 표시된 값이
앞에서 언급했던 체이닝(chaining)의 횟수입니다.
즉, flow를 몇 번 적용했는지를 의미합니다.체이닝을 진행할 때는
각 단계에서 분포의 형태가 어떻게 바뀌는지를 계속 관찰하게 됩니다.처음에는 Gaussian distribution이었던 것이
한 번 transformation을 거치면 약간 눌린 형태가 되고,
두 번 transformation을 거치면 분포가 둘로 쪼개지는 등
점점 더 복잡한 형태로 변화하게 됩니다.그리고 예를 들어 10번 정도 체이닝을 반복하면
매우 복잡한 프로파일까지 표현할 수 있는 분포로 변형됩니다.두 번째 예시에서는
초기 분포를 Uniform distribution이라고 가정합니다.Uniform distribution 역시 transformation 한 번에 반으로 쪼개지고,
두 번 하면 또 다른 방식으로 쪼개지고,
이런 식으로 여러 단계의 propagation을 거치면서
마찬가지로 10번 정도 반복하면
매우 복잡한 분포 형태를 만들 수 있게 됩니다.다만 이것은 단순한 예시일 뿐이며,
“한 번에 이렇게 쪼개지고, 두 번에 이렇게 쪼개진다”라는 규칙이
항상 정해져 있는 것은 아닙니다.
실제 형태는 neural network의 구조에 따라 달라집니다.여기서 핵심 가정은
planar transformation, 즉 $aX + b$ 형태의 linear 함수로는
위와 같은 복잡한 모양을 만들 수 없다는 점입니다.$aX + b$는 완전히 linear한 변환이기 때문에
한 번의 절단(하이퍼플레인으로 한 번 나누는 정도)만 가능하며
복잡한 분포 구조를 만들 수 없습니다.
(서포트 벡터 머신의 결정 경계 개념을 떠올리면 이해가 쉽습니다.)따라서 affine transformation 수준에서는
위에서 본 것과 같은 복잡한 분포로의 변화가 불가능하고,
오직 nonlinear neural network 기반의 flow 구조가
이와 같은 고차원적·복잡한 분포 변형을 가능하게 한다는 점을
이해하시면 되겠습니다.
p13. Flow of Transformations
효율적인 샘플링과 계산 가능한(tractable) 우도 평가(likelihood evaluation)를
가능하게 하는 단순한 prior $p_Z(z)$.
예: 등방성 가우시안(isotropic Gaussian)- 계산 가능한 평가를 갖는 가역 변환들:
- 우도 계산(likelihood evaluation)은
$x \mapsto z$ 매핑을 효율적으로 계산할 수 있어야 한다. - 샘플링은
$z \mapsto x$ 매핑을 효율적으로 계산할 수 있어야 한다.
- 우도 계산(likelihood evaluation)은
- 우도를 계산하는 것은 또한
$n \times n$ Jacobian 행렬들의 행렬식(determinant) 계산을 필요로 한다.
여기서 $n$은 데이터의 차원이다.- $n \times n$ 행렬의 행렬식(determinant) 계산은 $O(n^3)$으로,
학습 루프 내에서 사용하기에는 지나치게 비싸다.
- $n \times n$ 행렬의 행렬식(determinant) 계산은 $O(n^3)$으로,
- 핵심 아이디어(Key idea):
Jacobian 행렬이 특별한 구조를 갖도록 변환을 선택한다.
예를 들어, 삼각행렬(triangular matrix)의 행렬식(determinant)은
대각 원소들의 곱이며, 이는 $O(n)$ 연산이다.
강의 내용
여기서는 개요를 다시 정리하는 맥락에서,
앞에서 언급했듯이
$n \times n$ 매트릭스의 디터미넌트(determinant)를 계산하려면
일반적으로 계산 비용이 $n^{3}$ 규모로 든다는 것이
우리가 알고 있는 정석적·표준적 사실입니다.그런데 실제 모델에서 이렇게 $n^{3}$의 비용을 그대로 감수하는 것은
거의 불가능합니다.
따라서 디터미넌트를 보다 효율적으로 계산할 수 있는
구조나 방법을 반드시 찾아야 합니다.즉, 디터미넌트를 그대로 계산하는 방식은 실용적이지 않으며
이를 대체할 적절한 수학적·구조적 접근이 필요하다는 의미입니다.세부적인 수학적 내용은 여기서는 생략하고,
시간이 남으면 뒤에서 더 다루도록 하겠습니다.
p14. Triangular Jacobian
\[\mathbf{x} = (x_1, \ldots, x_n) = f(\mathbf{z}) = (f_1(\mathbf{z}), \ldots, f_n(\mathbf{z}))\] \[J = \frac{\partial f}{\partial \mathbf{z}} = \begin{pmatrix} \frac{\partial f_1}{\partial z_1} & \cdots & \frac{\partial f_1}{\partial z_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial z_1} & \cdots & \frac{\partial f_n}{\partial z_n} \end{pmatrix}\]$x_i = f_i(\mathbf{z})$가 $\mathbf{z}_{\le i}$에만 의존한다고 하자. 그러면
\[J = \frac{\partial f}{\partial \mathbf{z}} = \begin{pmatrix} \frac{\partial f_1}{\partial z_1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial z_1} & \cdots & \frac{\partial f_n}{\partial z_n} \end{pmatrix}\]는 하삼각(lower triangular) 구조를 갖는다.
행렬식(determinant)은 선형 시간(linear time) 안에 계산될 수 있다.
마찬가지로, $x_i$가 $\mathbf{z}_{\ge i}$에만 의존하는 경우
Jacobian은 상삼각(upper triangular)이다.
p15. Normalizing Flows: Theoretical Side
표기(conventions)
$\mu$와 $\nu$를 $\mathbb{R}^d$ 위의 확률측도(probability measures)라고 하고,
각각 르베그(Lebesgue) 밀도 $p$와 $q$를 갖는다고 하자.우리는 $\mu$와 $p$를 목표(target) 측도/밀도라고 부르고,
$\nu$와 $q$를 기준(reference) 측도/밀도라고 부른다.
그림: $\mu$는 왼쪽, $\nu$는 오른쪽
보충 자료
르베그 밀도(Lebesgue density)란?
르베그 밀도는 $\mathbb{R}^d$ 공간에서 정의된 확률측도가
르베그 측도(일반적인 유클리드 공간의 길이·면적·부피 개념) 에 대해
절대연속일 때 존재하는 확률밀도 함수이다.즉, 확률측도 $\mu$가 르베그 측도 $\lambda$에 대해 절대연속이면
\[d\mu(x) = p(x)\, d\lambda(x)\]
라돈-니코딤 정리에 의해 다음을 만족하는 함수 $p(x)$가 존재한다:여기서의 $p(x)$가 바로 르베그 밀도(Lebesgue density) 이다.
직관적으로 말하면,
“일반적인 연속 공간에서의 확률밀도 함수(pdf)”가
바로 르베그 밀도라고 이해할 수 있다.
p16. Normalizing Flows: Theoretical Side
normalizing flow는
$p$에서 $q$로 가는 사상(mapping) $T : \mathbb{R}^d \to \mathbb{R}^d$로서,
다음 조건들을 만족한다:
(i) $T$는 거의 모든 곳에서(a.e.) 미분 가능하며,
거의 모든 $z$에 대해 $\det J_T(z) \neq 0$ 이다.
(ii) \(T_{\#}\mu = \nu\), 혹은 밀도 관점에서 쓰면 다음과 같다:
\[q(y) = \frac{p\!\left(T^{-1}(y)\right)} {\left|\det J_T\!\left(T^{-1}(y)\right)\right|} \qquad \Longleftrightarrow \qquad p(x) = q(T(x)) \,\left|\det J_T(x)\right|\]여기서 $J_T$는 $T$의 Jacobian이다.
이 식을 다음과 같이 쓸 수도 있다:
\(q = T_{\#}p\).
식 (1)에 나타난 양의 로그(log)를 자주 고려하게 된다:
\[\log p(x) = \log q \circ T(x) + \log\!\left|\det J_T(x)\right|\]p17. Normalizing Flows: Theoretical Side
$T_1, T_2, \ldots, T_n$이 normalizing flow라고 하고,
$T = T_n \circ T_{n-1} \circ \cdots \circ T_1$이 $q$에서 $p$로 가는 normalizing flow라고 하자.
그러면,
\[\log p(x) = \log(q \circ T(x)) + \log\left|\det J_T(x)\right|\]또는,
\[\log p(x) = \log(q \circ T(x)) + \sum_{j=1}^{n} \log\left|\det J_{T_j}(z_{j-1})\right|\]여기서
$z_0 = x$,
$z_1 = T_1(z_0)$,
$z_2 = T_2(z_1)$,
$\ldots,$
$z_{n-1} = T_{n-1}(z_{n-2})$ 이다.
p18. Recap : KL divergence
KL-발산의 성질은 Jensen 부등식으로부터 얻어진다:
\[\begin{aligned} - D_{\mathrm{KL}}(\pi_1 \mid \pi_2) &= - \mathbb{E}_{\pi_1}\!\left( \log \frac{\pi_1}{\pi_2} \right) \\[6pt] &= \mathbb{E}_{\pi_1}\!\left( \log \frac{\pi_2}{\pi_1} \right) \\[6pt] &\le \log\!\left( \mathbb{E}_{\pi_1}\!\left( \frac{\pi_2}{\pi_1} \right) \right) \qquad\qquad\qquad\text{since log is concave} \\[6pt] &= \log\!\left( \int_{\{\pi_1(x) > 0\}} \pi_1(x)\, \frac{\pi_2(x)}{\pi_1(x)}\, dx \right) \\[6pt] &\le \log(1) \qquad\qquad\qquad\quad\quad\quad\quad\quad\text{as log increasing} \\[6pt] &= 0. \end{aligned}\]보충 자료
왜 ‘since log is concave’가 등장하는가?
Jensen 부등식에 따르면, 어떤 함수가 concave(오목) 하면
\(\mathbb{E}[f(X)] \le f(\mathbb{E}[X])\)
이 성립한다.
여기서 로그 함수 $\log(\cdot)$는 concave이므로
\(\mathbb{E}_{\pi_1}\!\left( \log \frac{\pi_2}{\pi_1} \right) \le \log\!\left( \mathbb{E}_{\pi_1}\!\left( \frac{\pi_2}{\pi_1} \right) \right)\)
이 부등식이 바로 Jensen 부등식의 직접적인 적용이다.왜 ‘as log increasing’이 등장하는가?
로그 함수 $\log(\cdot)$는 증가함수(increasing function) 이고,
\(\int \pi_1(x)\, \frac{\pi_2(x)}{\pi_1(x)} dx = 1\)
이므로
\(\log\!\left(\int \cdots \right) \le \log(1)\)
이 성립한다.
즉, 내부 값이 1 이하라면 $\log$를 취해도 그 관계가 유지되며,
결국 최종적으로 $0$ 이하가 되고 KL 발산의 음수 형태가 0 이하임을 보여준다.
p19. Maximum Likelihood Estimation
최적화 기반 $T$ 학습(Learning $T$ via Optimization)
\[\min D_{\mathrm{KL}}(T_{\#}p \mid q) \quad\text{s.t.}\quad \det \nabla T > 0 \;\;\text{and}\;\; T \in \mathcal{F}.\]\(D_{\mathrm{KL}}(T_{\#}p \mid q) = D_{\mathrm{KL}}(p \mid T_{\#}^{-1} q)\) 이므로,
${x_i}_{i=1}^n$이 $\mu$로부터의 i.i.d. 표본일 때, 표본 평균 근사는 다음과 같다:
강의 내용
네.
그래서 여기까지가 전체적인 개요라고 보시면 되고요.
시간이 남으면 이론적인 내용을 조금 다뤄보겠다고 했었는데
조금만 더 이야기하고 마무리하도록 하겠습니다.우리가 optimization 이야기를 살짝 했었는데,
그러면 optimization 관점에서 maximum likelihood와
normalizing flow를 연결해서 한번 생각해봅시다.제가 앞에서 말씀드렸듯이
결국 우리가 하는 일은 여기서도 마찬가지로
$KL$ divergence를 줄이는 과정입니다.여기서 $T_{\sharp}$이라는 표기는
$p$가 확률분포이고 $q$도 확률분포일 때,
$p$를 어떤 방식으로 옮겨주는 push-forward 연산을 의미합니다.
(설명 과정에서 $p$가 Gaussian distribution이라고 말했지만
실제로는 $q$가 Gaussian distribution임)그래서 $T$라는 변환을 통해
Gaussian distribution을 데이터 분포로 보내는 과정에서
두 분포 사이의 $KL$ divergence가 최소화되어야 한다는 의미입니다.그런데 이 과정에서 중요한 가정조건이 등장합니다.
바로
$\det \nabla T > 0$
이라는 조건입니다.이것이 의미하는 바는
앞에서 이야기했던 convex, monotone 등의 조건들이
모두 맞아떨어져야 inverse function이 존재할 수 있다는 점입니다.매우 중요한 내용인데,
이런 가정조건을 두는 이유는
앞에서 언급했던 형태로 $KL$ divergence를 전개하면
아래와 같은 형태가 되기 때문입니다.그리고 이 형태는
우리가 목표로 삼았던 objective function과 일치하는 구조를 갖습니다.따라서 $T$를 planar flow,
혹은 input convex neural network와 같은 형태로 선택하면
이러한 수학적 제약조건을 모두 만족하고
결과적으로 데이터를 잘 생성할 수 있게 됩니다.이렇게 이해하시면 충분합니다.
보충 자료
우리는 변환 $T$ 를 학습하고 싶다.
즉, 복잡한 데이터 분포($x$ 의 분포 = $p$)를 단순한 기준 분포($z$ 의 분포 = $q$)로
최대한 잘 밀어(push) 넣도록 하는 변환 $T$ 를 찾는다는 뜻이다.\(T_{\#}p\) 는 푸시포워드(pushforward) 분포로,
“$x$-공간의 분포 $p$를 변환 $T$에 통과시켜
$z$-공간의 분포로 옮겼을 때 얻어지는 분포”를 의미한다.
즉,
$x \sim p$ 이면
\(z = T(x)\) 의 분포가 바로 \(T_{\#}p\) 이다.
그리고 $x \mapsto T(x) = z$ 이다.제한식 $\det \nabla T > 0$ 은
$T$ 가 거의 어디서나 가역이며 Jacobian의 행렬식이 0이 되지 않도록 보장한다는 뜻이다.조건 $T \in \mathcal{F}$ 는
$T$ 가 미리 정한 함수 클래스(예: 특정 신경망 구조) 안에 있어야 한다는 뜻이다.항등식
\[D_{\mathrm{KL}}(T_{\#}p \mid q) = D_{\mathrm{KL}}(p \mid T_{\#}^{-1} q)\]는 KL 발산이 변수변환 아래에서 형태를 유지한다는 뜻이다.
KL 발산은 확률밀도에 대한 적분 형태로 정의되는데,
변수변환(예: $x \mapsto T(x)$ 또는 $z \mapsto T^{-1}(z)$)을 적용해도
Jacobian 항이 나타나면서 양쪽 식이 서로 정확히 보정된다.즉,
분포를 $T$ 로 밀어(push) 옮기느냐,
혹은 $T^{-1}$ 로 끌어오느냐의 표현만 달라질 뿐
“두 분포 사이의 정보 차이” 자체는 동일하게 유지되기 때문에
위 항등식이 성립한다는 뜻이다.표본 ${x_i}_{i=1}^n$ 을 이용해 기대값을
표본 평균으로 근사할 수 있다는 뜻이다.최종 최적화식
\[\min -\frac{1}{n} \sum_{i=1}^{n} \left[ \log(q(T(x_i))) + \log \left| \det \nabla T(x_i) \right| \right]\]는 normalizing flow에서 사용되는 로그-우도의 최대화와 동등하다는 뜻이다.
p20. Maximum Likelihood Estimation
강의 내용
그래서 굉장히 복잡합니다.
그리고 논문을 쓰기 위해 이런 계산을 매일 하게 됩니다.이렇게 사라지는 항들이 존재하고,
$KL$ divergence가 어떻게 유도되는지 등을
직접 계산을 통해 확인할 수 있습니다.
보충 자료
(1) 첫 번째 줄
\[D_{\mathrm{KL}}(T_{\#}p \,\|\, q) = \int_{\mathbb{R}^d} (T_{\#}p)(y)\,\log\frac{(T_{\#}p)(y)}{q(y)}\,dy\]KL 발산의 정의를 그대로 쓴 것이다.
(2) 두 번째 줄 — pushforward 밀도 \((T_{\#}p)(y)\) 를 전개한 단계
\[\int_{\mathbb{R}^d} p(T^{-1}(y))\,\det\nabla T^{-1}(y)\, \log \frac{ p(T^{-1}(y))\,\det\nabla T^{-1}(y) }{ q(y) } dy\]이유: pushforward 밀도는 정의상
\[(T_{\#}p)(y) = p(T^{-1}(y))\, \left|\det\nabla T^{-1}(y)\right|\]KL 식 안의 모든 \((T_{\#}p)(y)\) 를 이 정의로 치환했기 때문에 이렇게 바뀐다.
(3) 세 번째 줄
아래 줄은 앞 단계의 적분을
\[\int_{\mathbb{R}^d} p(x)\, \log \frac{ p(x) }{ q(T(x))\,\det\nabla T(x) } dx\]
변수변환 $y = T(x)$ 로 바꾸고 난 뒤의 결과이다:(a) 먼저, 치환을 적용한다: $y = T(x)$
이제 적분 변수는 $y$ 대신 $x$ 가 된다.
이때 항등적으로
\(T^{-1}(y) = x\) 이므로, 기존 적분에 나타났던
$p(T^{-1}(y))$ 는 단순히
\(p(x)\)
로 바뀐다.(b) 미분 형식 변화: $dy = \mid \det\nabla T(x) \mid \,dx$
적분에서 변수 치환을 하면
$dy$ 를 $dx$ 로 바꿔야 하는데,
이때 “부피 변화율”이 Jacobian determinant 이다.즉, \(dy = \left|\det\nabla T(x)\right|\,dx.\)
따라서 이전 적분에 있던 $dy$ 자리는
\(\left|\det\nabla T(x)\right|\,dx\)
로 바뀐다.(c) 역함수 Jacobian 관계를 적용한다
inverse function theorem 에 의해,
\[\det\nabla T^{-1}(y) = \frac{1}{\det\nabla T(x)}.\]이것이 아주 중요하다.
왜냐하면 이전 단계의 integrand 에는 $p(T^{-1}(y))\det\nabla T^{-1}(y)$
그리고 measure $dy$ 안에는 $|\det\nabla T(x)|$
라는 두 개의 Jacobian 이 곱 형태로 등장하기 때문이다.(d) Jacobian 항들이 정확히 상쇄되는 과정
치환 전 integrand 의 Jacobian 파트:
\[\det\nabla T^{-1}(y)\]치환으로 생긴 measure 변화: \(dy = (\det\nabla T(x))\,dx\)
둘을 곱하면:
\[\det\nabla T^{-1}(y)\; \det\nabla T(x) = \frac{1}{\det\nabla T(x)}\; \det\nabla T(x) = 1.\]즉, 완전히 사라진다.
(e) log 안에서 일어나는 변화
기존 식에서는
\[\log\frac{ p(T^{-1}(y))\,\det\nabla T^{-1}(y) }{ q(y) }\]이제 각각을 $x$ 기준으로 바꾸면:
- $p(T^{-1}(y)) \rightarrow p(x)$
- $q(y) \rightarrow q(T(x))$
- $\det\nabla T^{-1}(y) \rightarrow 1/\det\nabla T(x)$
따라서 log 내부는:
\[\log\frac{ p(x) }{ q(T(x))\,\det\nabla T(x) }.\](f) 최종 정리
적분 변수는 전부 $x$ 기준, Jacobian 은 log 안과 measure 에서 정확히 정리되고, 전체 결과는 다음과 같이 깔끔해진다:
\[\int_{\mathbb{R}^d} p(x)\, \log \frac{ p(x) }{ q(T(x))\,\det\nabla T(x) } dx\](4) 네 번째 줄 — 로그 분리 및 적분 분리
\[\log \frac{p(x)}{q(T(x))\,\det\nabla T(x)} = \log p(x) - \log q(T(x)) - \log \det\nabla T(x)\]로그 성질 적용:
적분의 선형성 때문에 세 항을 분리 가능:
\[= \int_{\mathbb{R}^d} p(x)\log p(x)\,dx - \int_{\mathbb{R}^d} p(x)\log q(T(x))\,dx - \int_{\mathbb{R}^d} p(x)\log\det\nabla T(x)\,dx\]
p21. Maximum Likelihood Estimation
p22. Normalizing Flows의 예시
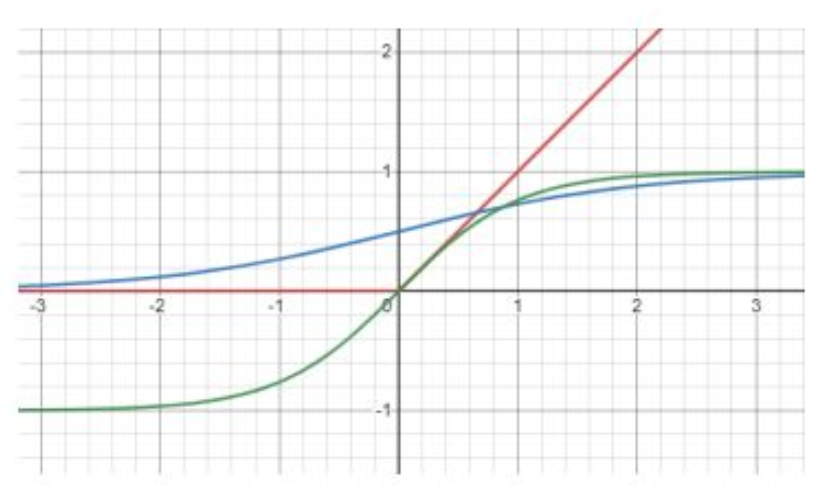
비선형성 함수 $h : \mathbb{R} \to \mathbb{R}$
Jacobian 계산에는 “행렬 행렬식 보조정리(matrix determinant lemma)”가 필요하다:
\[\det(A + u v^{T}) = \left( 1 + v^{T} A^{-1} u \right)\det(A)\]그림: $h$의 예시들
보충 자료
행렬 행렬식 보조정리(matrix determinant lemma)란?
이 보조정리는
\[\det(A + u v^{T}) = \left( 1 + v^{T} A^{-1} u \right)\det(A)\]
행렬 $A$ 에 랭크 1(rank-1) 행렬 $u v^{T}$ 를 더한 행렬
$A + u v^{T}$ 의 행렬식을형태로 매우 간단하게 계산할 수 있게 해주는 정리이다.
즉,
큰 행렬의 행렬식을 직접 계산하지 않고,
$A^{-1}$과 $u, v$의 내적만으로
새로운 행렬의 행렬식을 얻을 수 있게 해주는 도구이다.이 성질은 normalizing flow에서 Jacobian 행렬이
“기본 행렬 + rank-1 보정” 형태로 나올 때
연산을 크게 줄여주는 핵심 트릭이다.그림의 의미 (Examples of $h$)
그림은 normalizing flow에서 사용되는
비선형성 함수 $h$ 의 여러 예시를 보여준다.
- 파란색: 완만한 S-curve 형태의 비선형 함수
- 빨간색: 단순 선형 함수
- 초록색: sigmoid-like 형태의 비선형 함수
이러한 $h$들은 flow 모델에서
복잡한 분포를 만들기 위한 비선형 변형의 기본 요소로 사용된다.즉,
간단한 분포(z)를 복잡한 분포(x)로 만들기 위해
어떤 모양의 비선형 함수를 사용할 수 있는지 시각적으로 보여주는 그림이다.
p23. Planar Flows (Single Layer SVM)
$u, w \in \mathbb{R}^d$, $b \in \mathbb{R}$, 그리고 비선형성 $h : \mathbb{R} \to \mathbb{R}$가 주어졌을 때,
\[T_{pf}(z) = z + u\, h(w^{T} z + b).\]
planar flow $T_{pf} : \mathbb{R}^d \to \mathbb{R}^d$ 를 다음과 같이 정의한다:우리는 다음을 계산한다:
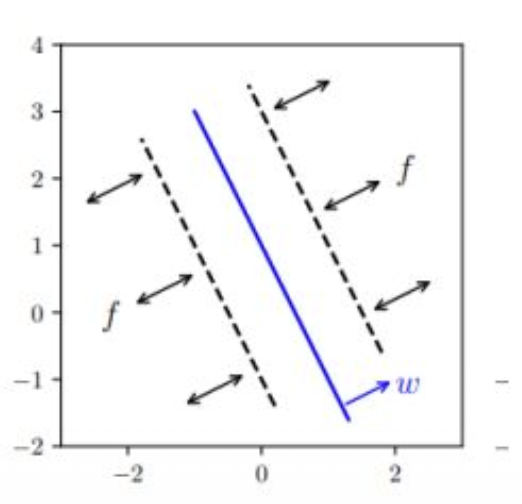
\[J_{T_{pf}}(z) = I_d + (u w^{T})\, h'(w^{T} z + b) \;\;\Longrightarrow\;\; \det J_{T_{pf}}(z) = 1 + w^{T} u\, h'(w^{T} z + b).\]그림: Planar flow에서의 변형 예시
강의 내용
그게 아니라, 그러면 우리가 어떻게 해야 하느냐.
디터미넌트를 $n^{3}$의 뉴머리컬 알고리즘으로 구하게 되면
에너지가 많이 들고 오래 걸리기 때문에
함수를 미리 정해놓는 방식으로 접근합니다.어떤 함수를 정하느냐 하면,
첫 번째는 디터미넌트가 명확하게 알려져 있는 함수 패밀리,
두 번째는 앞에서 말했듯이 모노톤하고 인버스 펑션이 존재하는
그런 형태의 함수를 선택합니다.이 PPT에서는 플레이너 플로우를 예로 들고 있는데
$z$가 인풋으로 들어왔을 때
$w$, $b$, $u$가 파라미터이며
$z$는 입력, $h$는 논리니어리티(보통 $\tanh$나 ReLU 등을 사용)를 의미합니다.이 플레이너 플로우는 무엇이냐 하면,
형태를 보면 완전히 리니어한, 즉 fully connected layer와 동일합니다.
그래서 그 구조를 그대로 한 플로우 형태로 표현한 것입니다.이렇게 fully connected layer 형태의 플로우를 사용하면
자코비안을 구할 수 있고
자코비안의 디터미넌트 역시 계산할 수 있기 때문에
change of variable을 적용하기 위한 모든 준비가
이미 갖추어진 형태가 됩니다.뉴럴 네트워크 관점에서는
파이토치의 nn.Parameter 같은 것으로
$w, u, b$를 파라미터로 두고 학습하게 됩니다.그런데 상식적으로 보면
이 구조는 굉장히 단순해 보입니다.
그래서 플로우를 여러 번 적용하는 것이 의미가 생깁니다.수학적 제약 때문에
단일 플로우 함수 자체는 매우 단순할 수밖에 없지만
이를 여러 번 중첩시키면
파라미터의 수가 증가하고
각 함수가 가진 표현력이 누적되기 때문에
만약 이런 플로우가 10만 개, 100만 개 쌓여 있다면
충분히 강력한 표현력을 가질 수 있을 것이라는
기대가 생기게 됩니다.이런 이유로 이러한 함수들을
체이닝한다는 관점으로 이해하시면 될 것 같습니다.
보충 자료
(1) 변환 정의식
\[T_{pf}(z) = z + u\,h(w^{T}z + b)\]
- 기본 입력 $z$ 에 작은 변화량을 더해 주는 구조이다.
- 이 변화량은 스칼라 값 $h(w^{T}z + b)$ 를 계산한 뒤,
이를 벡터 $u$ 방향으로 늘려주어 적용하는 형태이다.- 즉, “$z$ 를 $u$ 방향으로 밀어주는(push) 비선형 변형”이라고 볼 수 있다.
- $w^{T}z + b$ 는 하이퍼플레인(평면)을 정의하며, $h(\cdot)$ 는 그 평면을 기준으로
어느 정도 변형을 줄지 결정한다.(2) Jacobian 계산식
\[J_{T_{pf}}(z) = I_d + (u w^{T})\, h'(w^{T}z + b)\]
- $T_{pf}$ 는 항등변환(identity) $I_d$ 에
랭크-1(rank-1) 행렬 $u w^{T}$ 를 더한 구조이다.- $h’(w^{T}z + b)$ 는 스칼라이므로, 전체로는 “랭크-1 업데이트(Jacobian)”가 된다.
- 이 구조 덕분에 행렬식(det)을 매우 효율적으로 계산할 수 있다.
(3) 행렬식(det) 계산식
\[\det J_{T_{pf}}(z) = 1 + w^{T}u\, h'(w^{T} z + b)\]
- 이는 matrix determinant lemma
$\det(A + uv^{T}) = (1 + v^{T} A^{-1} u)\det(A)$
를 그대로 적용한 결과이다.- 여기서는 $A = I_d$ 이므로 $\det(I_d)=1$, $A^{-1} = I_d$ 가 되어
계산이 매우 단순해진다.- 따라서 planar flow는 “가벼운 비용으로” Jacobian determinant 를
계산할 수 있게 설계된 구조이다.(4) 그림의 의미
- 그림의 파란 직선은 벡터 $w$ 가 정의하는 하이퍼플레인(직선) 을 나타낸다.
- 이 직선에 수직 방향이 $w$ 의 방향이며,
planar flow는 이 평면 주변에서만 변형이 세게 일어난다.- 점선으로 표시된 두 개의 선은 $w^{T} z + b = \text{constant}$ 형태의 레벨셋(level set)이며,
flow가 해당 영역 근처에서 공간을 뒤틀고(push) 있다는 것을 보여준다.- 화살표들은 실제로 입력 공간이 planar flow에 의해
“어떤 방향으로 변형되는지” 시각적으로 표현한 것이다.- 요약하면,
planar flow는 어떤 하나의 평면에 기반하여 데이터를 u 방향으로 비선형적으로 밀어서
분포를 더 복잡하게 만드는 변환이다.
p24. Radial Flows (Physically-informed NN)
\(a \in \mathbb{R}_{>0}\), \(b \in \mathbb{R}\), 그리고 \(z_0 \in \mathbb{R}^d\) 가 주어졌을 때,
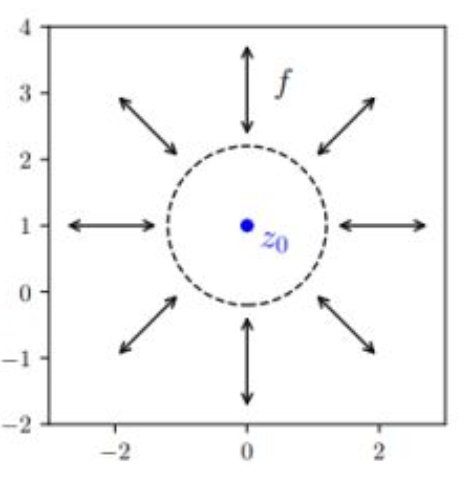
\[T_{rf}(z) = z + \frac{b}{\,a + \|z - z_0\|_2\,} (z - z_0).\]
우리는 radial flow \(T_{rf} : \mathbb{R}^d \rightarrow \mathbb{R}^d\)를 다음과 같이 정의한다:
강의 내용
그리고 이것은 physical informed neural net이라고 불리는 분야와도 관련이 있습니다.
요즘은 physical AI라는 표현도 많이 사용하는데,
과학자들이 이러한 형태의 플로우 모델들을 활용하여
유체 해석, 단백질 동역학 등의 문제를 모델링할 때
radial flow 같은 구조를 많이 사용해 왔습니다.여기에 수학적인 이유도 존재하며,
단순히 직관적인 이유만으로 선택된 것은 아닙니다.따라서 이러한 형태의, 모양이 독특하게 생긴 구조들도
flow로 표현하여 다룰 수 있습니다.
p25. Sylvester Flows (Single Layer MLP)
양의 정수 $m < d$,
\[T_{\text{syl}}(z) = z + A\,h(B^T z + b).\]
$A \in \mathbb{R}^{d \times m}$,
$B \in \mathbb{R}^{d \times m}$,
$b \in \mathbb{R}^m$,
$h : \mathbb{R} \rightarrow \mathbb{R}$ 가 주어졌을 때,
Sylvester flow $T_{\text{syl}} : \mathbb{R}^d \rightarrow \mathbb{R}^d$ 를 다음과 같이 정의한다:계산하면,
\[J_{T_{\text{syl}}}(z) = I_d + A\,\mathrm{diag}\!\big(h'(B^T z + b)\big)\,B^T.\]Sylvester의 determinant 항등식(Kobyzev et al. (2020))에 의해, 다음을 얻는다:
\[\det J_{T_{\text{syl}}}(z) = \det\!\left( I_d + A\,\mathrm{diag}\!\big(h'(B^T z + b)\big)\,B^T \right)\] \[= \det\!\left( I_m + \mathrm{diag}\!\big(h'(B^T z + b)\big)\,B^T A \right).\]참고 문헌:
Kobyzev, I., Prince, S. J., and Brubaker, M. A. (2020).
Normalizing flows: An introduction and review of current methods.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(11):3964–3979.
강의 내용
네, 그래서 앞에서 planar flow에서는 벡터 형태의 파라미터들을 사용했는데,
이 벡터를 그대로 두는 대신
전체 구조를 유지한 채 matrix 형태로 확장할 수 있지 않을까
라는 아이디어에서 나온 것이 바로 실베스터 플로우라는 개념입니다.여기서 기본적인 구조는 그대로이고
단지 사용하던 벡터가 matrix 형태로 바뀐 것입니다.벡터가 $n$ dimensional일 때,
이를 matrix화하면 $n \times n$이 되므로
파라미터 수는 $n$에서 $n^{2}$로 크게 증가하게 됩니다.파라미터가 많아지면
flow에서 필요한 함수(레이어)의 개수를 줄일 수도 있다고 볼 수 있고,
실제로 앞에서 언급한 내용은 예시 설명을 위한 것이었고
affine transform의 성질을 갖는 함수를 고려한다고 하면
보통 실베스터 플로우의 single-layer MLP 형태를 가진
이런 function을 사용하게 됩니다.그리고 이런 구조는 flow 모델을 공부하면 항상 보게 되는 현상인데,
제가 시퀀셜 모델들을 연구할 때도 비슷한 패턴이 많았습니다.
예를 들어 mamba 같은 모델을 들어보셨나요?state space 모델들을 보면 관점이 조금 다르지만,
시간에 따라 정보를 흐르게 한다는 철학을 기반으로
타임 시리즈를 모델링하는 구조들이 존재하죠.사실 여기서도 비슷한 관점이 적용됩니다.
기본적으로는 MLP이고
이걸 여러 번 concatenation 시키면 그 자체가 neural network가 됩니다.MLP 블록이 8개 있으면 8층짜리 neural network가 되는 것처럼,
실베스터 플로우도 이런 단순한 구조를 반복적으로 쌓아
정보 흐름을 만드는 방식입니다.mamba도 마찬가지입니다.
아주 간단한 구조를 가진 function을 가정한 뒤
그것을 반복적으로 concatenation하여
타임 시리즈 데이터를 처리하는 neural network를 구성하죠.결국 이러한 모델들은
정보를 흐르게 하는 작은 component들을 반복적으로 쌓아
전체 network를 구성한다는 점에서
관점이 서로 많이 닮아 있습니다.뒤에서 시간이 되면
이러한 모델들이 mamba 같은 구조에
어떤 영향을 주었는지도 설명드릴 수 있을 것 같습니다.말을 길게 했지만,
사실 이 구조는 neural network를 여러 개 합쳐놓은 것과 거의 동일하다고
이해하시면 됩니다.
여러 개의 function을 체이닝한다고 가정하면 되는 것이죠.그래서 이 부분에서는
특정한 수학적 조건들을 이미 만족하도록 설계된
함수 구조를 기반으로 모델을 구성하고 있는 것입니다.
보충 자료
Sylvester flow는 다층 퍼셉트론(MLP)의 단일 레이어 형태를 이용해
입력 벡터 $z \in \mathbb{R}^d$ 를 변환하는 normalizing flow의 한 종류이다.먼저, $m < d$ 인 양의 정수와
행렬 $A \in \mathbb{R}^{d \times m}$, $B \in \mathbb{R}^{d \times m}$,
그리고 편향 $b \in \mathbb{R}^m$,
비선형 함수 $h : \mathbb{R} \to \mathbb{R}$ 를 정의한다.그런 다음 변환
\[T_{\text{syl}}(z) = z + A\,h(B^T z + b)\]를 사용해 입력 $z$ 를 변형한다.
이는 선형 변환 $B^T z + b$에 비선형 $h$를 취하고,
이를 다시 행렬 $A$ 를 통해 원래 공간 $\mathbb{R}^d$로 올려서
잔차 형태(residual form)로 더해주는 구조이다.Jacobian은
\[J_{T_{\text{syl}}}(z) = I_d + A\,\mathrm{diag}(h'(B^T z + b))\,B^T\]와 같이 계산된다.
여기에서 $\mathrm{diag}(h’(\cdot))$ 는 비선형 함수의 도함수를
각 성분에 대해 대각행렬로 만든 것이다.그러나 일반적으로 $d \times d$ Jacobian의 행렬식을 직접 계산하는 것은 어렵다.
따라서 Sylvester의 행렬식 항등식을 이용해 계산을 크게 단순화한다.Sylvester의 항등식에 따르면
\[\det(I_d + A D B^T) = \det(I_m + D B^T A)\]로 바꿀 수 있다. (여기에서 $D = \mathrm{diag}(h’(B^T z + b))$)
즉, $d \times d$ 행렬식을
더 작은 크기인 $m \times m$ 행렬식으로 변환할 수 있다.
($m < d$ 이므로 계산량이 매우 감소한다.)따라서 최종적으로
\[\det J_{T_{\text{syl}}}(z) = \det\!\big( I_m + \mathrm{diag}(h'(B^T z + b))\,B^T A \big)\]와 같이 계산된다.
이 구조 덕분에 Sylvester flow는
표현력은 충분히 유지하면서도 Jacobian 행렬식 계산을 효율적으로 수행할 수 있어
normalizing flow 모델에서 매우 유용하게 쓰인다.
p26. Generic Neural Networks
정규화 흐름(normalizing flows)의 결합 레이어(coupling layers)는
신경망(neural networks)을 사용하여 모델링될 수 있다.일반적으로, 신경망은 가역(invertible)이 아니다.
그러나, 가역성은 종종 네트워크가 전단사(bijective)임을 보임으로써 보장된다.
Lemma (보조정리)
만약 $NN(\cdot) : \mathbb{R} \rightarrow \mathbb{R}$이,
다층 퍼셉트론(multilayer perceptron)이고,
모든 가중치가 양수이며,
모든 활성화 함수가 엄격히 단조(strictly monotone)라면,
$NN(\cdot)$ 은 엄격히 단조 함수이다.
가역성을 강제로 만족시키는 다른 방법들:
$NN(\cdot) : \mathbb{R} \rightarrow \mathbb{R}_{>0}$이 되도록 강제하고
그것을 적분(integrate)한다.$NN(\cdot) : \mathbb{R} \rightarrow \mathbb{R}$이 볼록(convex)이 되도록 강제하고
그것을 미분(differentiate)한다
(입력에 대해 볼록한 신경망 - input convex neural networks).
강의 내용
그래서 generic한 neural network을 한 번 생각해보자는 겁니다.
약간 이론적인 내용이긴 한데,
만약 일반적인 neural network을 이용해서 체이닝을 하고 싶다면
아래 두 가지 조건을 만족해야 합니다.첫 번째는 어떤 force,
즉 convex하다는 개념을 추가적인 mathematical constraint로 고려하는 것입니다.앞에서는 monotone하기만 하면 inverse function을 만들 수 있었는데
여기서는 convex하다는 조건을 다시 요구합니다.우리가 최종적으로 달성하고 싶은 상위 개념은
함수가 invertible하다는 것이고,
이를 위해 앞에서는 monotone function을 찾았던 것이죠.그런데 monotone 조건보다 더 강하고,
만족시키기 어려운 조건이 convex입니다.모든 convex function은 invertible하게 만들 수 있고,
모든 monotone function도 invertible하게 만들 수 있습니다.따라서 이러한 집합 관계 속에서
일반적인 neural network이 특정한 form으로 제한되지 않더라도
flow model을 구성할 수 있도록 연구가 많이 이루어졌습니다.앞에서 예로 든 $x^{2}$ 같은 경우는
convex라는 개념과는 조금 다르지만
이 부분을 깊게 다루면 내용이 어려워지므로
핵심 개념만 이해하시면 됩니다.즉, 이런 convex 조건을 만족하도록 설계된 neural network을
input convex neural network라고 부릅니다.
convex 조건을 만족하기 때문에
이런 구조는 invertible한 함수로 사용할 수 있습니다.
보충 자료
첫 번째 방법:
$NN(\cdot) : \mathbb{R} \rightarrow \mathbb{R}_{>0}$ 이 되도록 강제하고, 그것을 적분한다.핵심 아이디어:
NN의 출력이 항상 양수라는 것은 NN이 “입력이 증가하면 기울기가 절대로 음수가 되지 않는”
형태의 함수를 만들 수 있다는 뜻이다.NN(x) > 0 이므로, 다음과 같은 함수를 정의할 수 있다:
\[F(x) = \int NN(t)\, dt\]이때 F(x)는 입력이 증가할수록 항상 증가하는 단조 증가(strictly monotone) 함수가 된다.
단조 증가 함수는 서로 다른 입력이 같은 출력을 만들 수 없으므로 가역적이다.
즉,
양수 출력 NN → 적분 → 단조 증가 함수 → 가역성 확보.두 번째 방법:
$NN(\cdot) : \mathbb{R} \rightarrow \mathbb{R}$ 이 볼록(convex)이 되도록 강제하고, 그것을 미분한다.핵심 아이디어:
볼록 함수 $\phi(x)$ 는 미분했을 때 $\phi’(x)$ 가 항상 단조 증가한다.
즉, 입력 x가 증가하면 기울기 또한 절대로 감소하지 않는다.그래서 NN을 “입력에 대해 볼록한 신경망(input convex neural network)”으로 만들었을 때,
\[\phi'(x)\]
NN을 $\phi(x)$ 라고 보고,
그 도함수를 사용하면 자동으로 단조 증가하는 함수가 된다.
단조 증가 함수는 가역성을 만족한다.
즉, 볼록 NN → 미분 → 단조 증가 함수 → 가역성 확보.
p27. Input Convex Neural Network
PICNN \(f(x, y; \theta)\)는 두 개의 은닉층 집합 \(\{u_i\}_{i=1}^k\)와 \(\{z_i\}_{i=1}^k\)에 의해
기술되며, 각각 $x$-경로(x-path)와 $y$-경로(y-path)에 대응한다.$K$-층 PICNN의 구조는 다음과 같은 반복되는 은닉 유닛들에 의해 주어진다:
\[\begin{aligned} u_{i+1} &= \tilde{g}_i\!\left(\tilde{W}_i u_i + \tilde{b}_i\right) \\[10pt] z_{i+1} &= g_i\Big( W_i^{(z)} \big( z_i \circ [ W_i^{(zu)} u_i + b_i^{(zu)} ] \big) + W_i^{(y)} \big( y \circ [ W_i^{(yu)} u_i + b_i^{(yu)} ] \big) + W_i^{(u)} u_i + b_i \Big) \end{aligned}\]여기서 $\tilde{g}_i$ 와 $g_i$ 는 비선형 활성화 함수들이다.
\[f(x, y; \theta) = z_K\]
PICNN의 최종 스칼라 값 출력은이다.
강의 내용
그래서 여러 가지 방식으로 고려할 수 있는데,
예를 들어 이러한 표현 형태가 존재할 수 있습니다.
디테일한 내용은 여기서는 생략하도록 하겠습니다.
보충 자료
PICNN이 $x$에 대해 볼록(convex)이 되는 핵심 이유는
네트워크 구조 전체가 “볼록성을 보존하는 연산들”로만 구성되기 때문이다.첫 번째로, $u$-경로는
\(u_{i+1} = \tilde{g}_i(\tilde{W}_i u_i + \tilde{b}_i)\)
의 형태인데, 여기서 \(\tilde{W}_i\) 는 비음수(nonnegative) 행렬로 제한된다.
비음수 행렬과 단조 증가 활성화 함수 \(\tilde{g}_i\) 는
볼록성을 깨지 않는 연산이다.또한 매우 중요한 점은, 비록 위 식이 $u_i$만을 포함하는 것처럼 보이지만
실제로는 \(u_0 = x\) 에서 시작해
\(u_1 = \tilde{g}_0(\tilde{W}_0 x + \tilde{b}_0), \quad u_2 = \tilde{g}_1(\tilde{W}_1 u_1 + \tilde{b}_1)\)
와 같이 모든 $u_i$ 가 본질적으로 $x$의 함수라는 것이다.
즉, $u_i = u_i(x)$ 이므로 $u$-경로는 $x$와 직접적 관계가 있으며,
그 업데이트 규칙이 볼록성을 보존하는 구조이기 때문에
$u_{i+1}$ 역시 $x$에 대해 볼록이 된다.
이는
“볼록 함수에 비음수 조합 + 단조 활성화 = 여전히 볼록”
이라는 볼록성 보존 법칙에서 비롯된다.두 번째로, $z$-경로는
\(z_{i+1} = g_i\!\Big( W_i^{(z)}(z_i \circ [ W_i^{(zu)}u_i + b_i^{(zu)} ]) + W_i^{(y)}(y \circ [ W_i^{(yu)}u_i + b_i^{(yu)} ]) + W_i^{(u)}u_i + b_i \Big)\)
와 같은 구조를 갖는다.여기서 중요한 점은 $W_i^{(u)}$, $W_i^{(zu)}$, $W_i^{(yu)}$ 등이
모두 비음수 행렬로 제한된다는 사실이다.
비음수 조합은 볼록성을 보존하며,
$u_i$ 자체가 이미 $x$에 대해 볼록이므로
$u_i$ 를 포함하는 모든 항들이 여전히 $x$에 대해 볼록이다.또한 Hadamard 곱(원소별 곱) $a \circ b$ 는
두 항 중 하나가 비음수일 경우 볼록성을 보존하는 연산이며,
이 조건 또한 네트워크 설계에서 보장된다.
따라서
$z_i \circ [ W_i^{(zu)} u_i + b_i^{(zu)} ]$
역시 볼록성을 유지한다.세 번째로, 마지막에는 단조 증가 활성화 함수 $g_i$ 를 적용한다.
단조 증가 함수는 볼록함수의 볼록성을 절대 깨지 않는다.
즉, $g_i(\cdot)$ 의 출력도 볼록이다.이런 식으로 각 계층에서
“볼록성 보존 → 볼록성 보존 → 볼록성 보존”
구조가 반복되므로,
$z_K$ 는 $x$에 대해 확실하게 볼록(convex)하게 된다.PICNN이 본질적으로 convexity를 강제할 수 있는 이유는
모든 경로가 볼록성을 파괴할 수 있는 연산(음수 가중치, 비단조 활성화 등)을 제거하고,
볼록성을 보존하는 연산만으로 전체 네트워크를 구성했기 때문이다.요약하면:
- 비음수 가중치 → 볼록 조합
- 단조 증가 활성화 → 볼록성 유지
- Hadamard 곱의 구조적 제약 → 볼록성 유지
- $u$ 경로가 실제로는 $x$로부터 시작하는 연쇄 구조 → $x$에 대한 볼록성 유지
- $z$ 경로 역시 볼록성을 보존하는 연산으로 구성
결과적으로
\(f(x, y; \theta) = z_K\)
는 $x$에 대해 볼록함수(convex function)가 된다.
p28. Input Convex Neural Network
명제(Proposition) 1, Amos et al. (2017)
모든 ${ W_i^{(z)} }_{i=1}^{k-1}$ 이 비음수(non-negative)이고,
모든 함수 $\tilde{g}_i$ 가 볼록(convex)이며
단조 증가(non-decreasing)일 때,
함수 $f$ 는 $y$ 에 대해 볼록(convex)이다.증명은
볼록 함수들의 볼록 조합(convex combinations) 과
볼록 함수들의 합성(compositions) 역시 볼록이라는
단순한 아이디어를 따른다.$f^j$ 가 $x_j$ 에 대한 볼록 함수가 되도록 보장하려면,
$W^{(z)}$ 의 모든 항목이 비음수(non-negative)가 되도록 제약해야 한다.학습 과정은 (3)번 식의 $KL(\theta)$가 최소화되도록
파라미터 $\theta$ 를 최적화한다.정규화 항(regularization term)은
\[-\frac{1}{n} \sum_{i=1}^{n} \Bigg( \log g \circ T(\theta)(x_i) + \sum_{j=1}^{d} \log(\nabla T(\theta))_j(x_i) \Bigg) + \lambda \sum_{j=1}^{d} \sum_{k=1}^{K} \left\| \max\!\big(-(W_j^{(z)})_k,\, 0\big) \right\|_{F}^{2}.\]
모든 층(layer)의 모든 $W^{(z)}$ 가중치 행렬 항목이
양수(positive)가 되도록 보장하기 위해 추가되며,
다음과 같은 식을 갖는다:
강의 내용
마찬가지로 디테일은 생략하지만, 내용은 매우 복잡해집니다.
예를 들어, $w_i$가 neural network의 parameter라고 할 때
이 값이 non-negative 해야 하고,
그렇게 되면 convex하고 non-declining 하도록 만들어서
monotonity를 만족시키고,
그 상태에서 다시 invertible해야 하므로
전체 구조가 상당히 복잡해집니다.하여튼 우리가 function 패밀리를 크게 잡으면 잡을수록
요구되는 수학적 가정 조건이 더 정밀해지고 복잡해지는
최신 연구들이 존재한다고 이해하시면 될 것 같습니다.그러한 조건들을 통해
log likelihood를 maximize하는
loss function이 아래와 같은 형태로 표현됩니다.이 식을 굳이 외우거나 모두 이해할 필요는 없지만,
전체 구조가 매우 복잡해진다는 점만
이해하면 충분합니다.
보충 자료
위 식은 두 부분으로 구성되어 있다.
첫 번째 부분
\(-\frac{1}{n}\sum_{i=1}^{n}\Big(\log g\!\circ\!T(\theta)(x_i)+\sum_{j=1}^{d}\log(\nabla T(\theta))_j(x_i)\Big)\)
는 normalizing flow 학습에서 사용하는 기본 로그-우도(log-likelihood) 최대화 항이다.
이는 변환 $T(\theta)$ 를 적용한 뒤 얻어지는 분포가
데이터에 잘 맞도록 만드는 역할을 한다.두 번째 부분
\(\lambda\sum_{j=1}^{d}\sum_{k=1}^{K}\left\|\max(-(W_j^{(z)})_k,0)\right\|_F^2\)
는 정규화 항(regularization term) 으로,
$W^{(z)}$ 의 항목이 음수가 되지 않도록 강제하는 역할을 한다.여기서 $\max(-(W_j^{(z)})_k, 0)$ 는
$W^{(z)}$ 의 요소가 음수일 경우 그 절댓값을 반환하고,
양수일 경우 0을 반환한다.
따라서 이 항을 제곱해 패널티로 더하면
음수 가중치가 등장할 때에만 비용이 증가하게 된다.즉, 이 항은
“$W^{(z)}$ 의 모든 요소가 비음수(non-negative)가 되도록 만드는 페널티”
로 작동하며, 이것이 PICNN의 볼록성(convexity) 보장을 위한 핵심 제약이다.최종적으로 이 정규화 항을 포함시키면
학습 과정 동안 $W^{(z)}$ 의 값이 음수가 되지 않도록 유지되어
네트워크의 볼록성과 가역성(invertibility) 조건을 지속적으로 만족하게 된다.
강의 마무리
여기까지가 오늘 전체적인 내용이라고 보시면 될 것 같고요.
그 직관은 전달되었다고 생각합니다.
디퓨전 모델이 사실 더 어렵거든요. 이것보다.
더 어렵고 지금 이 normalizing flow에서의 직관을 많이 전달드리려고 하고
메시지를 많이 전달드리려고 했는데
그런 관점에서 좀 이해를 잘 하셔야 될 것 같아요.
그래야 다음 이제 마지막 저희 그 컨텐츠인 디퓨젼 모델 DDPM에 대해서
더 잘 이해를 하실 수 있을 것 같습니다.
거기서는 수학적인 얘기도 많이 나오거든요.
그때는 이런 직관을 다 갖고 있다고 가정을 하고
수학적인 것도 다 다루겠습니다.
디퓨젼 모델이 제일 중요한 것이기 때문에.이 앞에서 모델들은
제가 말씀드렸었던 것처럼 flow based model 같은 경우는
어떤 특별한 purpose들이 있는데, 쓰는 경우들.
optimal test, AI process 이런 것들에서 잠깐 쓰는데
GAN이랑 VAE는 머신러닝에서 없다고 생각하시면 됩니다. 안 씁니다.그럼에도 우리가 역사를 알아야 할 때에도 그런 걸 하는 건데
디퓨젼 모델이 완전 뉴노멀이고
완전한 이제 이것도 그룹 간의 헤게모니 싸움에서 또 졌어요. 학문에서도.
그래서 완전히 이쪽으로 다 치우쳐져 있기 때문에
코드 저희가 이제 공부를 하잖아요.다음 주에 GAN이랑 normalizing flow 코드 실습을 할 텐데
그다음에 이제 디퓨젼 모델은 여러분들이 완벽하게 이해를 하신다고 가정을 하고
에너지를 많이 써서 공부를 하신다고 봐주시면 될 것 같아요.네.
오늘은 이 정도까지가 메인 콘텐츠이고 질문 있으시면.(질문)
15페이지에서 보면 $\mu$하고 $p$가 왼쪽이라고 되어 있거든요.
그런데 아까 $p$가 가우시안이라는 설명하셨는데
그 $p$하고 여기 $p$하고 서로 다른 $p$일까요?(답변)
제가 거꾸로 말씀드린 것 같아요.
$\mu$랑 $p$가 데이터.
$\nu$랑 $q$가 레퍼런스니까.(질문)
그러니까 $T^{\sharp}$은 그 데이터 샘플 스페이스에서
가우시안으로 옮기는 거죠.(답변)
네. 맞습니다.
제가 거꾸로 말했습니다.
질문 감사합니다.또 질문 사항 있으실까요?
네. 감사합니다.
1분만 더 있다가 강의 마무리하도록 하겠습니다.(질문)
아까 잘 못 들었는데 23페이지에서 … (멀어서 잘 안 들림)(답변)
여기 어떤 뜻이냐면 정확하게는
이거에 벡터로 표현이 되어 있을 때
이게 매트릭스화로 되어 있는 게 실베스터 플로우고
얘가 싱글레이어 MLP라고 되어 있는데
여기 MLP 구조랑 똑같이 생긴 거예요. 실제로.$B^Tz + b$ 되어 있는 게
우리가 뉴럴 네트워크 파이토치 같은 코드를 열어보다 보면
이렇게 생겼습니다. 실제로.그리고 $h$는 우리가 앞에서 CNN 공부할 때도
레이어를 통과한 뒤에 relu 같은 걸 적용하잖아요.
그 relu 같은 역할을 $h$라고 보시면 될 것 같아요.그다음에 이게 왜 레이어가 하나 더 있는 거냐라고 하면
그 아웃풋에 $a$를 곱한 다음에 또 $z$를 더했습니다.
그러니까 또 한 번 변환을 한 거거든요.
그래서 이걸 싱글레이어 MLP라고 표현한 거죠.(질문)
지금 이게 $T$랑 $T^{-1}$을 찾는 거라고 저는 이해를 했는데
어떻게 보면 인코더가 $T$고 디코더가 $T$의 역함수
인코더의 역함수라고 생각할 수 있을 것 같은데
인코더와 디코더를 넣는 것은 성립하지 않나요?(답변)
인코더, 디코더는 추상적 역할로 보면 비슷하지만
이 mathematical constraint가 만족되는지가 핵심입니다.결국 우리가 change of variable을 해야 하는데
이를 위해 실제 계산을 해보면
일반 인코더/디코더 구조는 아무것도 성립하지 않습니다.예를 들어 인코더/디코더 구조를
$f$와 $f^{-1}$로 놓고 change of variable을 적용하면
수학적 조건이 전혀 만족되지 않습니다.즉, VAE의 objective는
change of variable과 호환되는 형태가 아니기 때문에
단순히 대체할 수 없습니다.
목표는 비슷하지만, 수학적 구조가 완전히 다르기 때문입니다.(질문)
인코더와 디코더가 모노톤하지 않아서 그런가요?(답변)
그것도 있고, 그뿐만이 아닙니다.
인코더와 디코더는 애초에 inverse function의 개념이 아니고
단지 미러 구조일 뿐입니다.(질문)
그러면 VAE는 인코더·디코더가 별도의 파라미터고
normalizing flow는 한 개의 파라미터가
$T$ 역할도 하고 $T^{-1}$ 역할도 한다,
이렇게 보면 될까요?(답변)
네, 그렇게 생각하시면 됩니다.
되게 오묘한 개념이지만 핵심은
normalizing flow는 하나의 네트워크가
$T$와 $T^{-1}$을 모두 수행할 수 있도록
수학적으로 설계되어 있다는 점입니다.
단순히 인코더·디코더를 넣는다고 되는 구조가 아닙니다.