[확률과 통계] 2주차

게시 2025/09/23 업데이트 2025/12/12

By 김성진

73 분읽는 시간

[확률과 통계] 2주차

p2. (연속) 확률변수

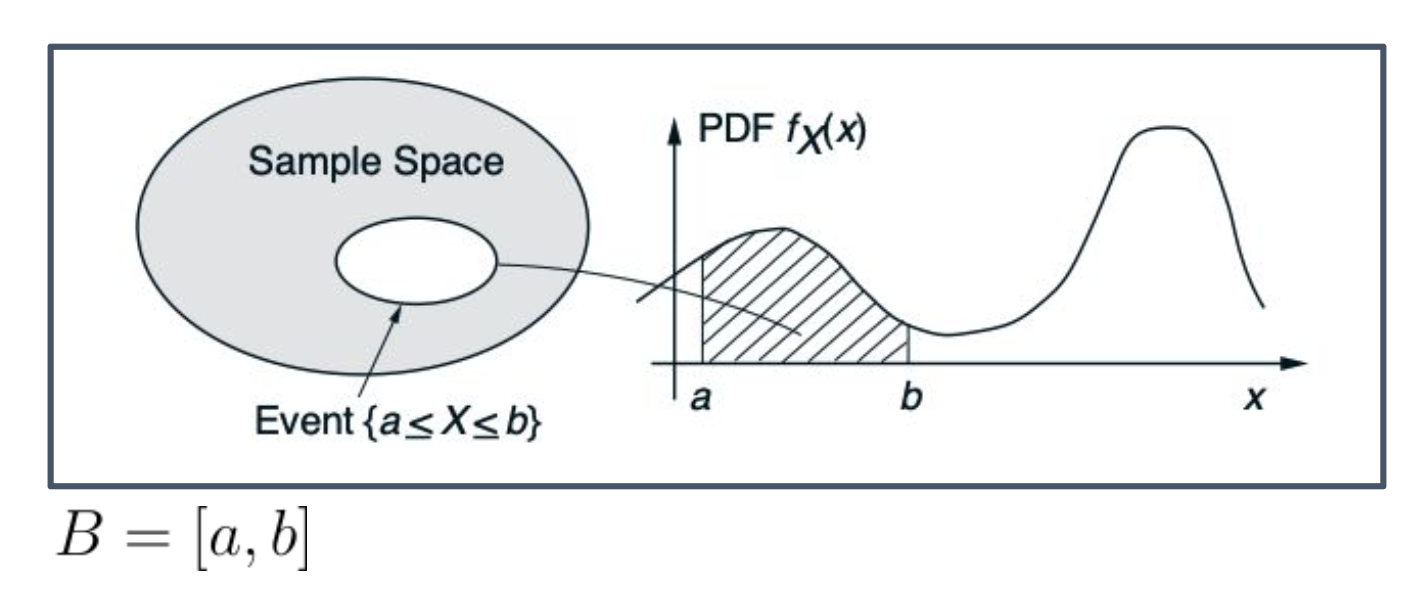
확률변수(Random Variable) 는 데이터 공간의 임의의 부분집합 $B$에 대해 그 확률 법칙(Probability law) 이 음이 아닌 함수, 즉 확률밀도함수(PDF, Probability Density Function)(= 확률분포)로 표현될 수 있을 때 연속형 확률변수 라고 한다.

\[P(X \in B) = \int_B f_X(x)\, dx,\] \[P(a \leq X \leq b) = \int_a^b f_X(x)\, dx,\]

이는 확률밀도함수 그래프 아래의 적분된 면적으로 해석될 수 있다.

1. 확률변수란 무엇인가?
확률변수(Random Variable)는 확률적 사건을 숫자로 대응시키는 함수이다.
예: 동전을 던졌을 때, 앞면이 나오면 1, 뒷면이 나오면 0으로 대응시키면
\[X = \begin{cases} 1, & \text{앞면} \\ 0, & \text{뒷면} \end{cases}\]
즉, 불확실한 결과를 수학적으로 다룰 수 있는 숫자 값으로 바꿔주는 도구이다.
확률변수는 주로 $X$ 라는 문자로 표기한다.
2. 출발점: 확률은 본질적으로 집합에 정의됨
확률이란 확률공간의 사건(=부분집합)에 대해 정의된다.
따라서 “확률변수 $X$가 어떤 값을 가진다”는 것도 사실은 ${X \in B}$라는 사건에 확률을 주는 것이다.
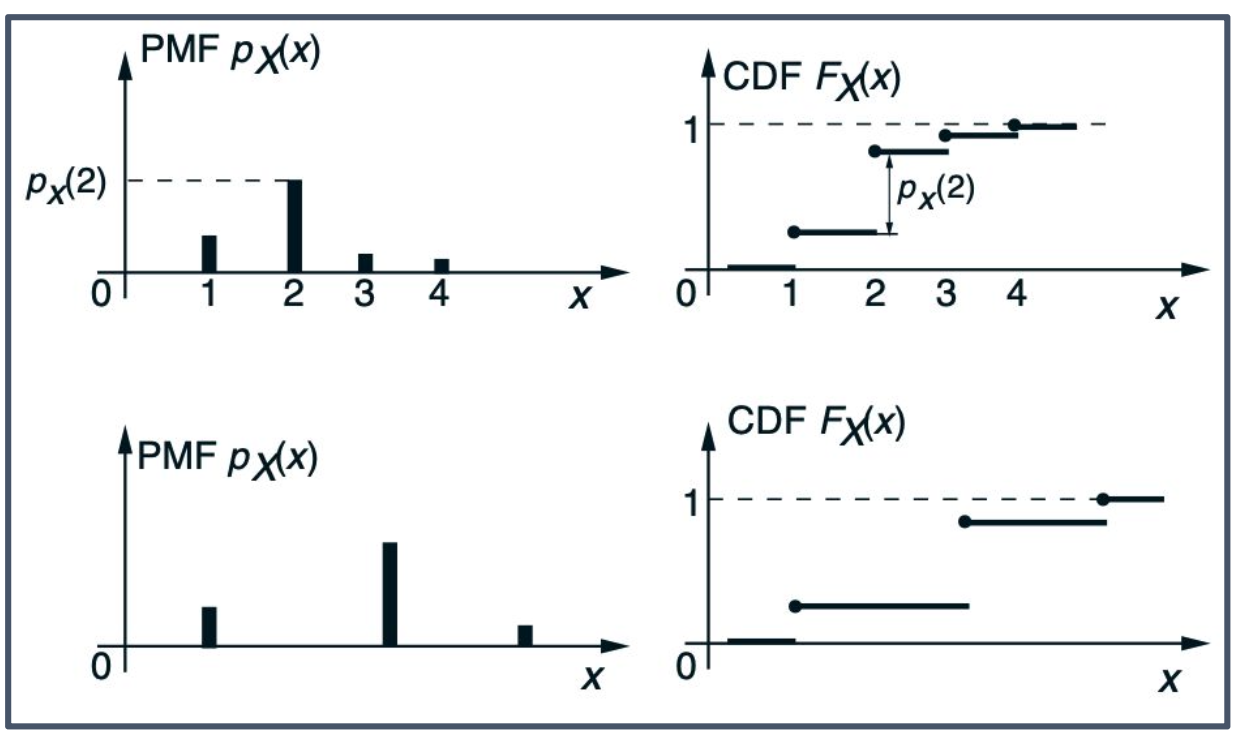
3. 이산형 변수와 연속형 변수의 차이
이산형: 개별 점 단위로 확률을 줄 수 있다.
예: $P(X=2)=1/6$.
연속형: 개별 점의 확률은 0이다.
예: $P(X=170)=0$.
따라서 반드시 구간이나 부분집합 단위로 확률을 정의해야 한다.
4. PDF를 통한 부분집합 확률 정의
연속형 확률변수 $X$는 확률밀도함수 $f_X(x)$를 통해
\[P(X \in B) = \int_B f_X(x)\, dx\]
로 정의된다.
여기서 $B$는 단순한 구간일 수도, 더 복잡한 영역일 수도 있다.
5. 왜 부분집합 단위가 필수적인가
점 확률은 모두 0이므로, 집합 단위가 아니면 확률을 정의할 수 없다.
예: 과녁 중심에서 정확히 1cm 떨어진 한 점에 맞출 확률은 0.
그러나 중심에서 10~12cm의 범위(면적)로 정의하면 확률 계산이 가능하다.
확률은 합집합, 교집합, 여집합 등 집합 연산 성질을 만족해야 하므로 처음부터 임의의 부분집합 $B$에 확률을 주는 방식이 가장 자연스럽다.
6. 확률 법칙(Probability law)이란?
확률 법칙은 확률변수 $X$가 어떤 값들을 얼마나 큰 확률로 취하는지를 기술한 규칙이다.
이산형:
확률질량함수(PMF) $p_X(x)=P(X=x)$ 로 표현된다.
연속형:
확률밀도함수(PDF) $f_X(x)$ 로 표현되고
\[P(X \in B) = \int_B f_X(x)\, dx\]
로 사건의 확률을 정한다.
즉, 확률 법칙은 확률변수의 분포(distribution)를 의미하며, PMF나 PDF가 그 구체적 표현이다.
예: 균등분포, 지수분포, 가우시안 분포 등

p3. (연속) 확률변수

하나의 값 $a$에 대해서는 사건의 확률이 0이 된다. 즉, 다음을 얻을 수 있다.

\[P(X = a) = \int_a^a f_X(x)\, dx = 0\]

이러한 이유로, 구간의 양 끝점을 포함하거나 포함하지 않는 것은 확률에 영향을 주지 않는다.

\[P(a \leq X \leq b)\] \[= P(a < X < b)\] \[= P(a \leq X < b)\] \[= P(a < X \leq b)\]

확률밀도함수(PDF)는 모든 입력에 대해 음이 아니어야 하며, 또한 정규화 조건을 만족해야 한다.

\[\int_{-\infty}^{\infty} f_X(x)\, dx = P(-\infty < X < \infty) = 1\]

p4. (연속) 확률변수

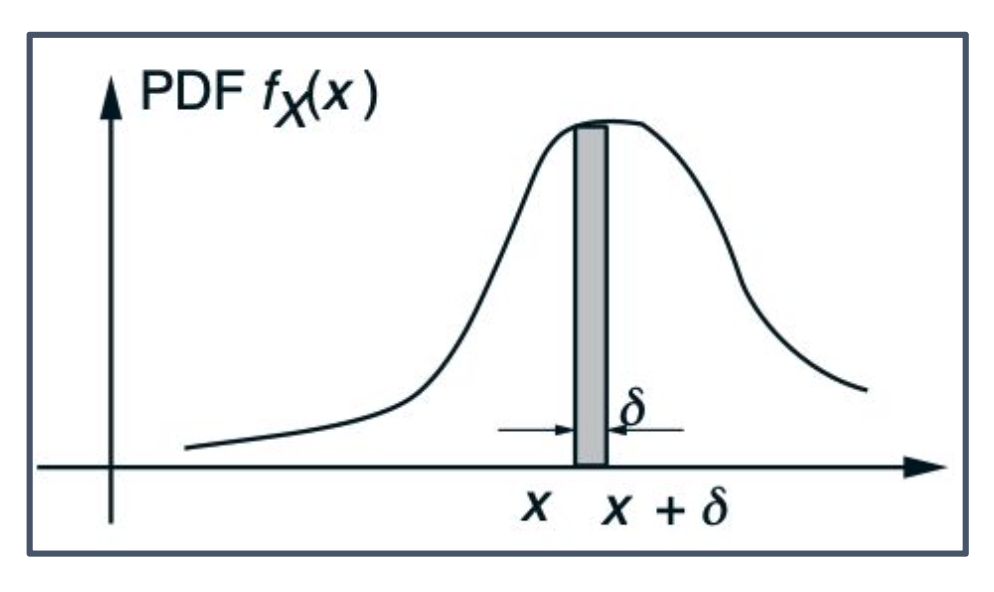
PDF를 해석하기 위해, 길이가 매우 작은 구간에 대해 다음과 같은 근사식을 얻을 수 있다.

\[P([x, x+\delta]) = \int_x^{x+\delta} f_X(t)\, dt \approx f_X(x) \cdot \delta\]

여기서 $f_X(x)$는 단위 길이당 확률 질량 (probability mass per unit length) 을 의미한다.

p5. 예시 : 균등 분포

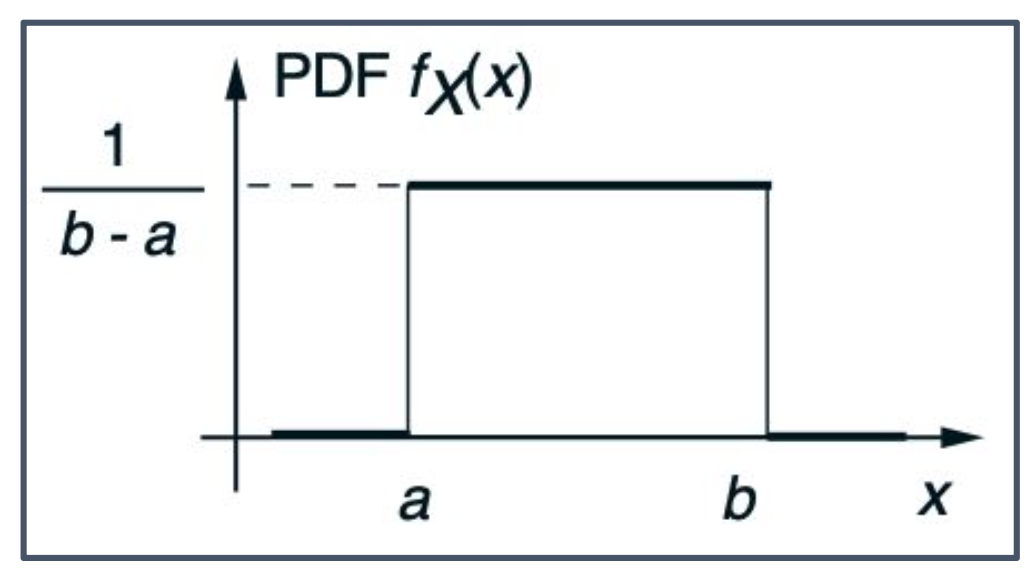
동일한 길이의 모든 부분구간(subintervals)이 똑같이 발생할 가능성이 있다고 가정하자. 이 경우 이러한 확률변수를 균일(uniform) 또는 균일분포(uniformly distributed) 라고 한다.

이때 확률밀도함수(PDF)는 다음과 같은 형태를 가진다.

\[f_X(x) = \begin{cases} c & \text{if } a \leq x \leq b, \\ 0 & \text{otherwise}, \end{cases} \quad c = \frac{1}{b-a}.\]

상수 $c$ 값은 정규화 조건(normalization equation)을 만족시키기 위해 $\frac{1}{b-a}$로 정해진다.
구간의 양 끝점 $a, b$에서는 불연속(discontinuous)이 발생할 수 있다.
미분이 불가능하다는 특징 때문에 머신러닝에서는 자주 사용되지 않는다.

p6. 예시 : 균등 분포

집합 $I$ 안에서 값을 가질 확률은 다음과 같이 계산할 수 있다.

\[P(X \in I) = \int_{[a,b]\cap I} \frac{1}{b-a} \, dx = \frac{1}{b-a} \int_{[a,b]\cap I} dx = \frac{\text{length of } [a,b] \cap I}{\text{length of } [a,b]}.\]

p7. (연속) 확률변수

PDF 성질의 요약

$X$가 확률밀도함수 $f_X$를 갖는 연속형 확률변수라고 하자.

모든 $x$에 대해 $f_X(x) \geq 0$이다.
$\int_{-\infty}^{\infty} f_X(x)\, dx = 1$이다.
$\delta$가 매우 작을 때, $P((x,[x+\delta]) \approx f_X(x) \cdot \delta$이다.
실수 집합 위의 임의의 부분집합 $B$에 대해,

\[P(X \in B) = \int_B f_X(x)\, dx.\]

p8. 기대값

확률변수의 기대값(기댓값, 평균)

확률변수의 기대값은 확률밀도함수(PDF)를 이용하여 다음과 같이 정의된다.

\[\mathbb{E}[X] = \int_{-\infty}^{\infty} x f_X(x)\, dx\]

확률변수의 평균은 확률분포의 “무게중심(center of gravity)” 으로 해석할 수 있다.

임의의 연속 함수 (g(x))에 대해서도 다음의 기대값 공식(expected value rule)이 성립한다.

\[\mathbb{E}[g(X)] = \int_{-\infty}^{\infty} g(x) f_X(x)\, dx\]

여기서 $x$는 확률변수 $X$의 실현값(value)을 의미한다.
확률변수 $X$는 확률적 객체이고, $x$는 그것이 취할 수 있는 구체적인 값을 나타낸다.
$f_X(x)$는 확률변수 $X$의 확률밀도함수(PDF)이다.
입력: $x$ (확률변수의 값)
출력: 그 값에서의 밀도(density)
따라서 기대값 정의는 다음과 같다.
\[\mathbb{E}[X] = \int_{-\infty}^{\infty} x f_X(x)\, dx\]
적분 변수 $x$: 확률변수 $X$가 가질 수 있는 값
$f_X(x)$: 그 값이 나올 가능성의 밀도
$x f_X(x)$: 값 × 그 값이 나올 가능성
즉, $x f_X(x)$를 전 구간에서 적분하면 확률변수 $X$의 평균(기대값)이 된다.
기대값은 PDF에서 가장 중요한 값이다.
$\mathbb{E}[X]$는 분포의 수학적 무게중심(center of math gravity)을 의미한다.
$\mathbb{E}[g(X)]$는 $X$에 대한 새로운 렌즈로 바라본 기대값이며, 확률변수를 함수로 치환하여 평균을 구하는 방식이다.

p9. 분산

확률변수의 분산

분산(Variance)은 확률변수와 그 평균의 차이를 제곱한 값의 기대값으로 정의된다.

\[\mathrm{var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \int_{-\infty}^{\infty} (x - \mathbb{E}[X])^2 f_X(x)\, dx\]

다음이 성립한다:

\[0 \leq \mathrm{var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\]

$Y = aX + b$일 때, ($a, b$는 주어진 상수)

\[\mathbb{E}[Y] = a\mathbb{E}[X] + b, \quad \mathrm{var}(Y) = a^2 \mathrm{var}(X)\]

이 단축식은 제곱 전개와 기대값의 선형성을 이용해 유도된다.
\[\begin{aligned} \mathrm{var}(X) &= \mathbb{E}[(X - \mathbb{E}[X])^2] \\ &= \mathbb{E}[X^2 - 2X\mathbb{E}[X] + (\mathbb{E}[X])^2] \\ &= \mathbb{E}[X^2] - 2\mathbb{E}[X]\mathbb{E}[X] + (\mathbb{E}[X])^2 \\ &= \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \end{aligned}\]
즉, 분산은 제곱의 기대값에서 기대값의 제곱을 뺀 값으로 단순화된다.
분산은 확률변수가 얼마나 퍼져 있는지를 나타낸다.
$(x - \mathbb{E}[X])$는 평균으로부터의 distance이다.
기대값 공식(expected value rule)에서 $g(x)$를 $(x - \mathbb{E}[X])^2$로 치환하면 분산 공식이 된다.
$\mathbb{E}[Y] = a\mathbb{E}[X] + b$는 Expectation의 선형성(linearity)을 나타낸다.
$\mathrm{var}(Y) = a^2 \mathrm{var}(X)$에서 $b$는 사라지고, $a$는 제곱되어 분산의 크기를 조정한다.

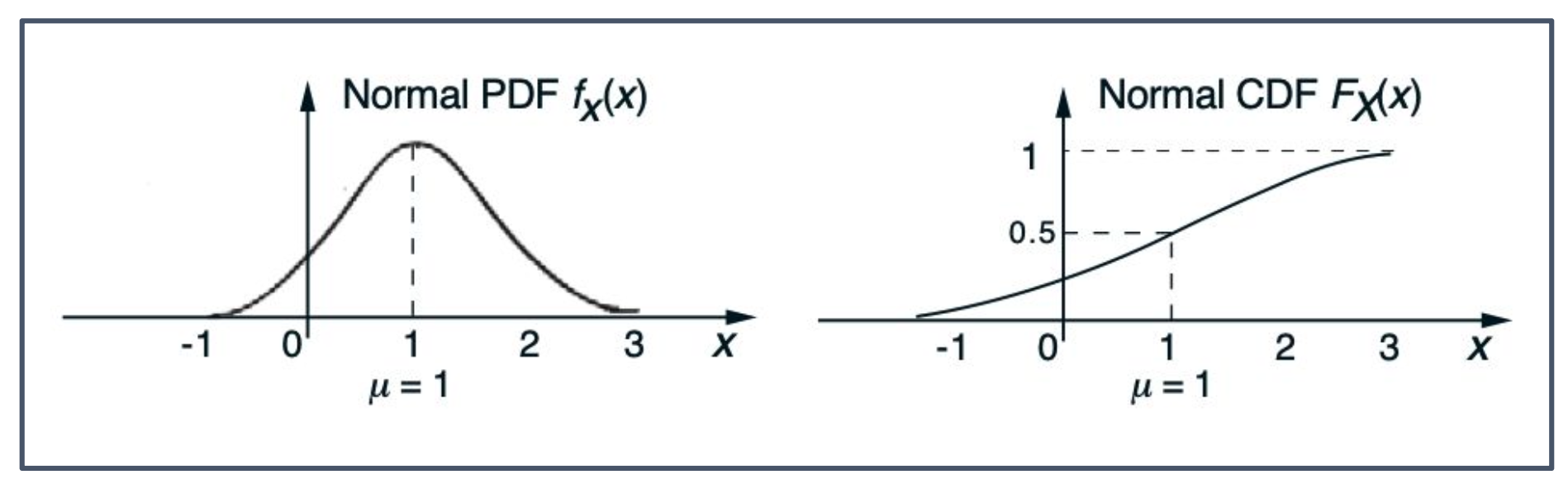
p10. 누적분포함수

확률변수의 누적분포함수

누적분포함수(CDF, Cumulative Distribution Function)는 어떤 값까지의 누적 확률(accumulated probability)을 나타낸다.

\[F_X(x) = P(X \leq x) = \begin{cases} \sum_{k \leq x} p_X(k), & X: discrete, \\ \int_{-\infty}^{x} f_X(t)\, dt, & X: continuous. \end{cases}\]

$F_X$는 단조 증가(monotonically nondecreasing)한다.
즉, $x \leq y$이면 $F_X(x) \leq F_X(y)$이다.
$x \to -\infty$일 때 $F_X(x) \to 0$,
$x \to \infty$일 때 $F_X(x) \to 1$이다.

CDF는 현재 시점까지 누적된 확률을 의미한다.
불연속(discrete)인 경우는 합(Σ), 연속(continuous)인 경우는 적분(∫) 으로 정의된다.
$F_X$는 항상 단조 증가한다.
$F_X(x)$의 값은 음의 무한대로 갈 때 0, 양의 무한대로 갈 때 1에 수렴한다.
CDF는 보통 대문자 F로 표기한다.

p11. 누적분포함수

PDF와 CDF의 관계

$X$가 연속형(continuous) 확률변수일 경우, PDF(확률밀도함수)와 CDF(누적분포함수)는 적분(integration) 또는 미분(differentiation) 을 통해 서로 구할 수 있다.

\[F_X(x) = \int_{-\infty}^{x} f_X(t)\, dt,\] \[f_X(x) = \frac{dF_X(x)}{dx}.\]

이는 미적분학의 기본정리(Fundamental of Calculus) 에 해당한다.

p12. 가우시안 확률변수

연속형 확률변수는 확률밀도함수(PDF)가 다음과 같은 형태일 때 가우시안(Gaussian) 또는 정규(normal)라고 한다.

\[f_X(x) = \frac{1}{\sqrt{2\pi}\sigma} \, e^{-\frac{(x - \mu)^2}{2\sigma^2}}\]

$\mu$: 평균(mean)
$\sigma^2$: 분산(variance)
White noise는 가우시안 분포를 따른다고 가정한다.

p13. 가우시안 확률변수

여기서 두 매개변수 $(\mu, \sigma)$는 PDF의 평균(mean)과 표준편차(standard deviation)를 나타내는데, 이는 다음 성질을 만족하기 때문이다.

\[\mathbb{E}[X] = \int_{-\infty}^{\infty} x p_X(x)\, dx\] \[= \int_{-\infty}^{\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\, dx\]

치환 $y = \frac{x-\mu}{\sigma}$

\[= \int_{-\infty}^{\infty} (\mu + \sigma y) \cdot \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right)\, dy\] \[= \mu \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right)\, dy+ \sigma \int_{-\infty}^{\infty} y \cdot \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right)\, dy\] \[= \mu \cdot 1 + \sigma \cdot 0\] \[= \mu\]

1. 왜 치환 후 분모에 있던 $\sigma$가 없어졌는가?
$y = \frac{x - \mu}{\sigma}$ 로 치환하면 $dy = \frac{dx}{\sigma}$가 된다.
따라서 $dx = \sigma \, dy$ 로 바뀌고, 적분식에 있던 분모의 $\sigma$와 곱해지면서 서로 소거된다.
2. 왜 적분이 1과 0인가? — 두 가지 설명
1) 직관적·확률론적 설명 (가우시안의 성질)
첫 번째 적분
\[\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right) dy = 1\]
이는 표준정규분포 $N(0,1)$의 확률밀도함수 $\phi(y)$가 전 구간에서 1이 되기 때문이다.
두 번째 적분
\[\int_{-\infty}^{\infty} y \cdot \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right) dy = 0\]
적분함수 $y \phi(y)$는 홀함수이며, 대칭구간 $(-\infty,\infty)$에서 값이 서로 상쇄되어 0이 된다.
2) 엄밀한 적분 계산
(a)
\[\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} \, dy = 1\]
$I = \int_{-\infty}^{\infty} e^{-y^2/2} dy$ 라 두면
\[I^2 = \int_{\mathbb{R}^2} e^{-(x^2 + y^2)/2} dx dy\]
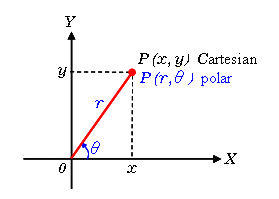
극좌표로 변환하면 면적 요소가 $dx dy = r \, dr \, d\theta$가 된다.
(참고) 직교좌표와 극좌표
직교좌표에서 미소면적은 $dx \cdot dy$로,
극좌표에서는 밑변 $dr$ 과 호 길이 $r\, d\theta$ 로 이루어진
직사각형 모양의 면적으로 $r \, dr \, d\theta$가 된다.
따라서
\[I^2 = \int_0^{2\pi} \int_0^\infty e^{-r^2/2} r \, dr \, d\theta = 2\pi \int_0^\infty e^{-r^2/2} r \, dr\]
치환 $u = r^2/2$ (따라서 $du = r dr$):
\[I^2 = 2\pi \int_0^\infty e^{-u} du = 2\pi [ -e^{-u} ]_0^\infty = 2\pi(0 - (-1)) = 2\pi\]
따라서 $I = \sqrt{2\pi}$.
표준정규 pdf 를 곱하면
\[\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy = \frac{1}{\sqrt{2\pi}} \cdot \sqrt{2\pi} = 1\]
(b)
\[\int_{-\infty}^{\infty} y \cdot \frac{1}{\sqrt{2\pi}} e^{-y^2/2}\, dy = 0\]
$g(y) = e^{-y^2/2}$ 라 하면 $g’(y) = -y e^{-y^2/2}$.
따라서
\[\int_{-\infty}^{\infty} y e^{-y^2/2} \, dy = -\int_{-\infty}^{\infty} g'(y) \, dy = -[g(y)]_{-\infty}^{\infty} = -(1 - 1) = 0\]
정규화 상수 $\frac{1}{\sqrt{2\pi}}$를 곱해도 0이다.
또는 홀함수의 대칭성을 이용해 즉시 0임을 알 수 있다.

p14. 가우시안 확률변수

여기서 두 매개변수 $(\mu, \sigma)$는 PDF의 평균(mean)과 표준편차(standard deviation)를 나타내는데, 이는 다음 성질을 만족하기 때문이다.

\[\mathrm{Var}(X) = \int_{-\infty}^{\infty} (x-\mu)^2 p_X(x)\, dx\] \[= \int_{-\infty}^{\infty} (x-\mu)^2 \cdot \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\, dx\]

치환 $y = \frac{x-\mu}{\sigma}$

\[= \int_{-\infty}^{\infty} (\sigma y)^2 \cdot \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right)\, dy\] \[= \sigma^2 \int_{-\infty}^{\infty} y^2 \cdot \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right)\, dy\] \[= \sigma^2 \cdot 1\] \[= \sigma^2\]

왜 적분이 1이 되는가? — 두 가지 설명
1) 직관적·확률론적 설명 (가우시안의 성질)
\[\int_{-\infty}^{\infty} y^2 \cdot \frac{1}{\sqrt{2\pi}} e^{-y^2/2}\, dy\]
이 적분은 표준정규분포 $N(0,1)$의 분산 정의와 동일하다.
따라서 그 값은 1이 된다.
2) 엄밀한 적분 계산
표준정규 pdf 를 $\phi(y)=\frac{1}{\sqrt{2\pi}} e^{-y^2/2}$ 라 두면
\[\int_{-\infty}^{\infty} y^2 \phi(y)\, dy = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} y^2 e^{-y^2/2}\, dy\]
부분적분 설정
$u = y,\quad dv = y e^{-y^2/2} dy$
$du = dy,\quad v = -e^{-y^2/2}$
검산: $v$를 미분하면 $dv = y e^{-y^2/2}dy$가 되어 정확하다.
부분적분 공식 $\int u\, dv = uv - \int v\, du$ 적용
\[\int_{-\infty}^{\infty} y^2 e^{-y^2/2}\, dy = [-y e^{-y^2/2}]_{-\infty}^{\infty} + \int_{-\infty}^{\infty} e^{-y^2/2}\, dy\]
첫 번째 항은 $y \to \pm\infty$ 에서 0이므로 사라진다.
남는 적분은 잘 알려진 가우시안 적분
\[\int_{-\infty}^{\infty} e^{-y^2/2}\, dy = \sqrt{2\pi}\]
따라서
\[\int_{-\infty}^{\infty} y^2 e^{-y^2/2}\, dy = \sqrt{2\pi}\]
정규화 상수 $\frac{1}{\sqrt{2\pi}}$를 곱하면
\[\int_{-\infty}^{\infty} y^2 \phi(y)\, dy = \frac{1}{\sqrt{2\pi}} \cdot \sqrt{2\pi} = 1\]

p15. 가우시안 확률변수의 선형변환

선형변환에 의해 정규성이 보존됨

만약 $X$가 평균 $\mu$와 분산 $\sigma^2$을 가진 정규 확률변수이고, $a, b$가 상수라면,

\[Y = aX + b\]

역시 정규분포를 따르며, 그 평균과 분산은 다음과 같다:

\[\mathbb{E}[Y] = a\mu + b, \quad \mathrm{Var}(Y) = a^2\sigma^2\]

선형변환을 적용해도 정규분포의 성질(normality) 은 유지된다.
$\mathbb{E}[Y] = a\mu + b$는 평균의 선형성(linearity of expectation) 을 반영한다.
$\mathrm{Var}(Y) = a^2\sigma^2$에서 $b$는 사라지고, $a$는 제곱되어 분산에 반영된다.
따라서 새로운 확률변수 $Y$도 정규분포(Gaussian)를 따른다.

p16. 가우시안 확률변수의 선형변환

다음의 간단한 계산을 통해, 가우시안 확률변수의 평균과 분산이 선형변환에 의해 어떻게 변하는지 확인할 수 있다.

\[\mathbb{E}[Y] = \mathbb{E}[aX + b]\] \[= \int_{-\infty}^{\infty} (ax + b) p_X(x)\, dx\] \[= a \int_{-\infty}^{\infty} x p_X(x)\, dx + b \int_{-\infty}^{\infty} p_X(x)\, dx\] \[= a \mathbb{E}[X] + b \cdot 1\] \[= a \mathbb{E}[X] + b\]

\[\mathrm{Var}(Y) = \mathbb{E}[(Y - \mathbb{E}[Y])^2]\] \[= \mathbb{E}[(aX + b - (a\mathbb{E}[X] + b))^2]\] \[= \mathbb{E}[(a(X - \mathbb{E}[X]))^2]\] \[= a^2 \mathbb{E}[(X - \mathbb{E}[X])^2]\] \[= a^2 \mathrm{Var}(X)\]

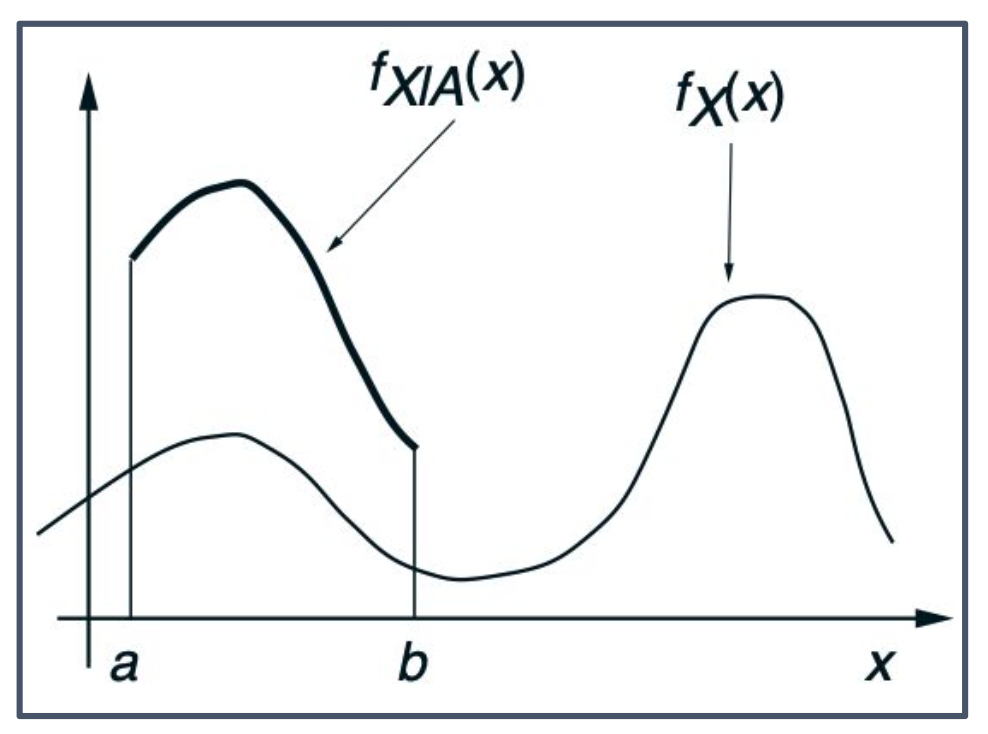
p17. 조건부 확률밀도함수

조건부 확률밀도함수(Conditional PDF)

특정 사건을 조건으로 한 확률변수의 조건부 확률밀도함수(Conditional PDF)는 다음을 만족하는 함수이다:

\[P(X \in B \mid A) = \int_B f_{X \mid A}(x)\, dx\]

또한,

\[P(X \in B \mid X \in A) = \frac{P(X \in B \text{ and } X \in A)}{P(X \in A)} = \frac{\int_{A \cap B} f_X(x)\, dx}{P(X \in A)}\]

따라서 조건부 PDF는 다음과 같이 정의된다:

\[f_{X \mid A}(x \mid A) = \begin{cases} \frac{f_X(x)}{P(X \in A)} & \text{if } x \in A, \\ 0 & \text{otherwise}. \end{cases}\]

1. 표본구간 축소
조건부 확률밀도함수 $f_{X \mid A}(x)$는 원래의 확률밀도함수 $f_X(x)$를 사건 $A$라는 구간에 제한하여 정의한다.
즉, 표본공간이 전체가 아니라 $A$로 줄어들기 때문에 그 안에서의 확률의 합(적분값)이 1이 되도록 확률밀도를 다시 조정해야 한다.
이 과정에서 원래 함수 $f_X(x)$보다 값이 커지는 효과가 나타날 수 있다.
이는 전체 확률을 $P(X \in A)$로 나누는 과정에서 발생한다.
2. 표기법
\[f_{X \mid A}(x) \quad vs \quad f_{X \mid A}(x \mid A)\]
$f_{X \mid A}(x)$ : 사건 $A$가 주어졌을 때의 조건부 확률밀도함수 전체를 의미한다.
$f_{X \mid A}(x \mid A)$ : 같은 의미이지만 “조건 $A$”를 명확히 강조하기 위해 적는 표기다.
수학적으로는 $f_{X \mid A}(x)$와 완전히 동일하며, 단지 강조 방식의 차이일 뿐이다.
“given A”는 조건부 사건을 의미한다.
그림에서 $f_X(x)$보다 $f_{X \mid A}(x)$가 더 높아지는 이유는 정규화(normalization) 때문이다.
이 개념은 멀티모달 모델이나 텍스트-이미지 생성에서 conditioning을 설명할 때도 활용된다.

p18. 조건부 확률밀도함수와 기대값

조건부 확률밀도함수(Conditional PDF)와 기대값

확률변수 $X$가 연속형이고, 사건 $A$에 대해 $P(A) > 0$일 때 조건부 확률밀도함수 $f_{X \mid A}$는 다음을 만족한다.

\[P(X \in B \mid A) = \int_B f_{X|A}(x)\, dx\]

만약 $A$가 $P(X \in A) > 0$인 실수직선의 부분집합이라면,

\[f_{X|A}(x) = \begin{cases} \dfrac{f_X(x)}{P(X \in A)} & \text{if } x \in A, \\ 0 & \text{otherwise}, \end{cases}\]

그리고 임의의 집합 $B$에 대해,

\[P(X \in B \mid X \in A) = \int_B f_{X|A}(x)\, dx\]

여기서 $B$는 임의의 집합으로 둘 수 있다. 그러나 조건부 확률의 정의
\[P(X \in B \mid X \in A) = \frac{P(X \in A \cap B)}{P(X \in A)}\]
에 따르면 실제 계산에서는 $A \cap B$가 등장한다.
따라서 $B$가 $A$에 포함되지 않아도 식은 항상 성립하지만,
$B$ 중에서 $A$ 밖에 있는 부분은 모두 확률 계산에서 제거된다.
결론적으로, 해석할 때는 $B$를 “$A$ 내부에 있는 부분으로 제한된 집합”처럼 생각하는 것이 자연스럽다.

p19. 조건부 기댓값

조건부 기대값은 다음과 같이 정의된다.

\[\mathbb{E}[X \mid A] = \int_{-\infty}^{\infty} x f_{X \mid A}(x)\, dx\]

또한 기대값 공식(expected value rule)은 조건부 상황에서도 성립한다.

\[\mathbb{E}[g(X) \mid A] = \int_{-\infty}^{\infty} g(x) f_{X \mid A}(x)\, dx\]

위 수식의 $X$는 아래 수식의 $g(X)$로 일반화된다.
적분 내의 $x$도 $g(x)$로 확장된다.
따라서 조건부 기대값은 단순 변수 $X$뿐 아니라 임의의 함수 $g(X)$에도 동일하게 적용된다.

p20. 다변량 확률변수

두 개의 확률변수가 동일한 실험에 의해 정의되고, 함께 연속형이라고 할 때, 그들의 결합 확률밀도함수(joint PDF) 는 다음 조건을 만족한다:

\[P\big((X,Y) \in B\big) = \iint_{(x,y) \in B} f_{X,Y}(x,y)\, dx\, dy\]

\[P(a \leq X \leq b, \; c \leq Y \leq d) = \int_c^d \int_a^b f_{X,Y}(x,y)\, dx\, dy\]

\[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_{X,Y}(x,y)\, dx\, dy = 1\]

단위 면적당 확률밀도 (probability per unit area):

\[P(a \leq X \leq a+\delta, \; c \leq Y \leq c+\delta) = \int_c^{c+\delta} \int_a^{a+\delta} f_{X,Y}(x,y)\, dx\, dy \approx f_{X,Y}(a,c)\, \delta^2\]

적분 기호 위/아래 $a, b, c, d$는 각각 $X, Y$의 범위를 지정한다.
마지막 근사식은 작은 사각형 영역에서의 확률이 $f_{X,Y}(a,c)$ 값과 넓이 $\delta^2$의 곱으로 표현된다는 의미이다.

p21. 다변량 확률변수

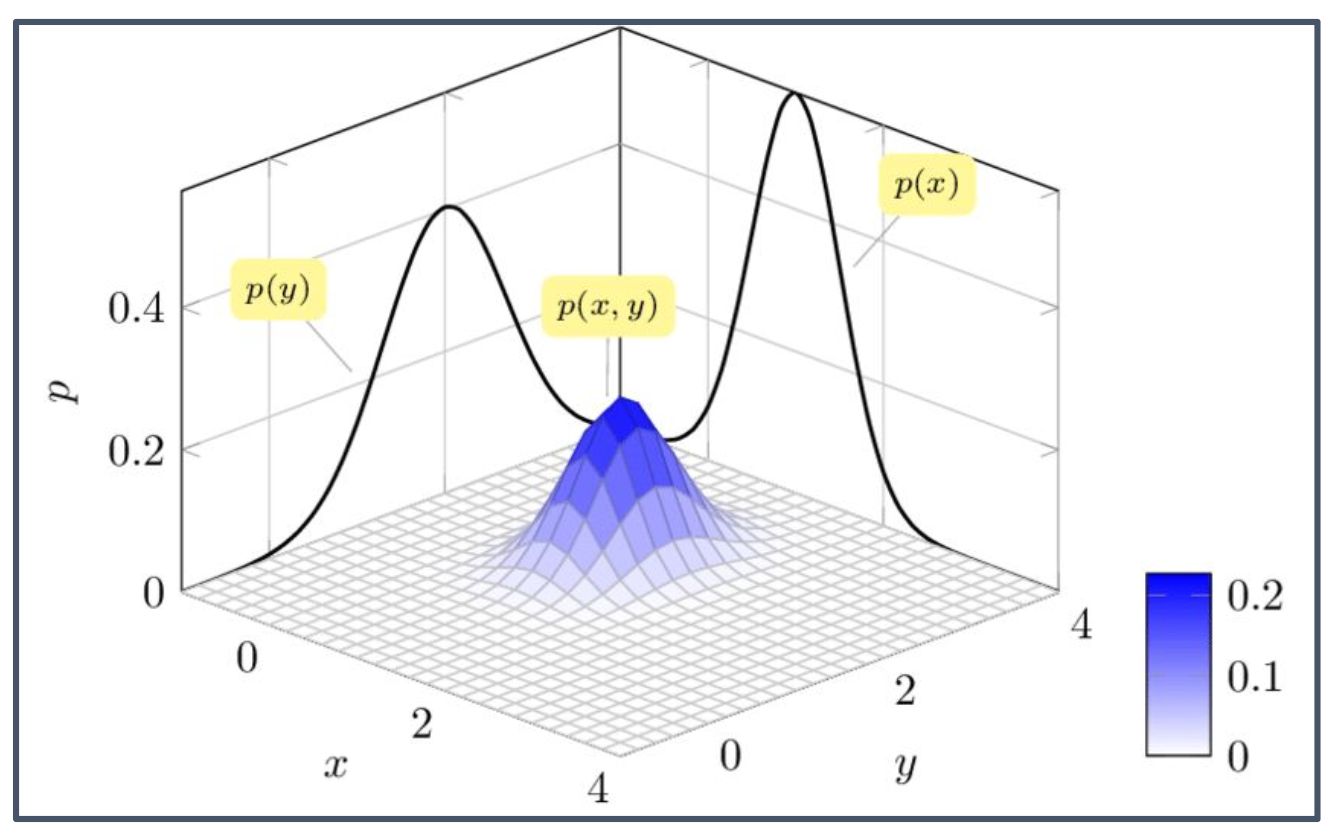
특수한 경우로, 결합 확률밀도함수(joint PDF)는 하나의 확률변수만 관련된 사건의 확률을 계산하는 데 사용할 수 있다. 특정 축을 적분해 제거하는 과정을 marginalization이라 한다.

\[P(X \in A) = P(X \in A \;\text{and}\; Y \in (-\infty, \infty)) = \int_A \int_{-\infty}^{\infty} f_{X,Y}(x,y)\, dy\, dx\]

⬇️ Marginalization (주변화) ⬇️

\[f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x,y)\, dy\] \[f_Y(y) = \int_{-\infty}^{\infty} f_{X,Y}(x,y)\, dx\]

Marginalization: 결합 확률밀도함수에서 특정 변수를 적분해 제거하여 다른 변수의 확률밀도를 얻는 과정이다.
실제 적용 상황에서는 $X$는 이미지(image), $Y$는 랭귀지(language)가 될 수 있다.

p22. 조건부 다변량 확률변수

고정된 조건 변수에 대해, 조건부 확률밀도함수와 조건부 사건의 확률은 다음과 같이 계산된다.

\[f_{X|Y}(x \mid y) = \frac{f_{X,Y}(x,y)}{f_Y(y)}\] \[\int_{-\infty}^{\infty} f_{X|Y}(x \mid y)\, dx = 1\] \[P(X \in A \mid Y = y) = \int_A f_{X|Y}(x \mid y)\, dx\]

두 확률변수가 독립(independent) 이라고 하는 것은, 이들의 결합확률밀도함수(joint PDF)가 주변확률밀도함수(marginal PDF)의 곱으로 표현될 수 있을 때이다.

\[f_{X,Y}(x,y) = f_X(x) f_Y(y), \quad \text{for all } x,y\] \[f_{X|Y}(x \mid y) = f_X(x)\] \[\mathbb{E}[g(X)h(Y)] = \mathbb{E}[g(X)] \, \mathbb{E}[h(Y)]\] \[P(X \in A \text{ and } Y \in B) = \int_{x \in A} \int_{y \in B} f_{X,Y}(x,y)\, dy\, dx\] \[= \int_{x \in A} \int_{y \in B} f_X(x) f_Y(y)\, dy\, dx\] \[= \int_{x \in A} f_X(x)\, dx \int_{y \in B} f_Y(y)\, dy\] \[= P(X \in A) \, P(Y \in B)\]

independence : 연관 관계 없는 상태 — 예시) 각각 랜덤하게 크롤링한 텍스트와 이미지 등

p23. 다변량 가우시안 확률변수

d차원 확률변수 $X = (X_1, \dots, X_d)^\top$의 다변량 가우시안 분포는 다음과 같이 표현된다.

\[X \sim \mathcal{N}(\mu, \Sigma)\]

고차원 다변량 상황에서, 가우시안의 모수는 평균 벡터(mean vector) 와 공분산 행렬(covariance matrix) 로 나타낸다:

\[\mu = \mathbb{E}[X] = (\mathbb{E}[X_1], \mathbb{E}[X_2], \dots, \mathbb{E}[X_d])^\top\] \[\Sigma_{i,j} = \mathbb{E}[(X_i - \mu_i)(X_j - \mu_j)] = \mathrm{Cov}[X_i, X_j]\]

1. 기댓값 벡터를 전치하는 이유
$(\mathbb{E}[X_1], \dots, \mathbb{E}[X_d])$는 기본적으로 행벡터(row vector)로 표현된다.
그러나 다변량 확률변수 $X$는 열벡터(column vector)로 정의하는 것이 일반적이다.
따라서 평균 벡터도 같은 형식을 맞추기 위해 transpose를 취해 열벡터 형태로 쓴다.
2. 공분산 행렬의 구조
예를 들어, $X = (X_1, X_2, X_3)^\top$라면
\[\Sigma = \begin{bmatrix} \mathrm{Var}(X_1) & \mathrm{Cov}(X_1, X_2) & \mathrm{Cov}(X_1, X_3) \\ \mathrm{Cov}(X_2, X_1) & \mathrm{Var}(X_2) & \mathrm{Cov}(X_2, X_3) \\ \mathrm{Cov}(X_3, X_1) & \mathrm{Cov}(X_3, X_2) & \mathrm{Var}(X_3) \end{bmatrix}\]
대각선 원소는 각 변수의 분산이다.
비대각선 원소는 서로 다른 변수 간의 공분산이다.
3. “투영(projection)”의 의미
다변량 확률분포의 투영은 고차원 분포를 저차원으로 사영(projection)하는 것을 의미한다.
예: 2차원 분포 $p(x,y)$에서 $x$축으로의 투영은 $y$를 적분으로 제거하여 주변분포 $p(x)$를 얻는 것이다.
\[p(x) = \int_{-\infty}^{\infty} p(x,y)\,dy\]
다변량 가우시안은 이러한 주변화(marginalization)를 해도 여전히 가우시안 형태를 유지한다.
따라서 “가우시안을 투영하면 다시 가우시안이 된다”는 것은 주변화를 해도 분포 형태가 변하지 않는다는 의미이다.
다변량 가우시안의 투영은 주변화(marginalization)를 의미하며, 결과는 언제나 가우시안이다.
평균 벡터는 각 변수의 기댓값들을 연결하여 만든다.
공분산 행렬 $\Sigma$는 항상 대칭이다.
분산(variance)은 공분산(covariance)의 특수한 경우이다.
예: 키, 몸무게, 나이 변수를 고려할 때 키와 몸무게의 상관관계가 공분산에 반영된다.

p24. 다변량 가우시안 확률변수

d차원 다변량 정규분포의 확률밀도함수(PDF):

\[f_X(x) = \frac{1}{(2\pi)^{d/2}\,|\Sigma|^{1/2}} \exp\!\left(-\frac{1}{2}\,(x-\mu)^\top \Sigma^{-1}(x-\mu)\right)\]

2차원(상관계수 $\rho$)의 경우:

\[f(x,y) = \frac{1}{2\pi\,\sigma_X \sigma_Y \sqrt{1-\rho^2}} \exp\!\left( -\frac{1}{2(1-\rho^2)}\!\left[ \left(\frac{x-\mu_X}{\sigma_X}\right)^2 -2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right) +\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2 \right]\right)\]

평균 벡터와 공분산 행렬:

\[\mu=\begin{pmatrix}\mu_X\\ \mu_Y\end{pmatrix},\qquad \Sigma=\begin{pmatrix} \sigma_X^2 & \rho \sigma_X \sigma_Y\\ \rho \sigma_X \sigma_Y & \sigma_Y^2 \end{pmatrix}\]

1. 단변량와의 비교
단변량에서는 분산을 계산할 때 $\mathrm{Var}(X)=\mathbb{E}[(X-\mu)^2]$ 공식을 사용한다.
즉, 평균으로부터 떨어진 정도를 제곱하여 거리로 본다.
다변량에서는 각 변수의 분산뿐 아니라 변수들 간의 공분산도 반영해야 하므로 단순 제곱거리 대신 공분산 행렬 $\Sigma$와 그 역행렬 $\Sigma^{-1}$을 사용한다.
2. 마할라노비스 거리와 정규화 상수의 역할
지수항 $(x-\mu)^\top \Sigma^{-1}(x-\mu)$는 마할라노비스 거리이다.
$\Sigma^{-1}$은 각 방향의 스케일을 조정한다.
분산이 큰 방향 → 작은 가중치가 곱해져 거리가 줄어든다.
분산이 작은 방향 → 큰 가중치가 곱해져 거리가 커진다.
분포 앞의 정규화 상수 $\tfrac{1}{(2\pi)^{d/2} \mid \Sigma \mid ^{1/2}}$는 전체 확률이 1이 되도록 보정한다.
$ \mid \Sigma \mid $는 공분산 행렬의 행렬식으로, 분포가 차지하는 부피(퍼짐 정도)를 의미한다.
$ \mid \Sigma \mid ^{1/2}$는 그 부피의 제곱근이며, 확률밀도가 데이터의 퍼짐 정도에 맞게 조정되도록 한다.
3. 2차원(2D) 식의 유도 요약
평균과 공분산 행렬은 $\mu=(\mu_X,\mu_Y)^\top,\ \Sigma=\begin{pmatrix}\sigma_X^2 & \rho\sigma_X\sigma_Y\ \rho\sigma_X\sigma_Y & \sigma_Y^2\end{pmatrix}$.
행렬식은 $|\Sigma|=\sigma_X^2\sigma_Y^2(1-\rho^2)$
역행렬은 $\Sigma^{-1} =\frac{1}{\sigma_X^2\sigma_Y^2(1-\rho^2)} \begin{pmatrix} \sigma_Y^2 & -\rho\sigma_X\sigma_Y\\ -\rho\sigma_X\sigma_Y & \sigma_X^2 \end{pmatrix}$
지수항 전개는 $(x-\mu)^\top\Sigma^{-1}(x-\mu) =\frac{1}{1-\rho^2}\left[ \left(\frac{x-\mu_X}{\sigma_X}\right)^2 -2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right) +\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2 \right]$
정규화 상수는 $\frac{1}{2\pi\sigma_X\sigma_Y\sqrt{1-\rho^2}}$
평균 벡터는 각 축의 기대값을 쌓은 열벡터이고, 공분산 행렬은 대각에 분산, 비대각에 공분산이 온다.

p25. 다변량 가우시안 확률변수

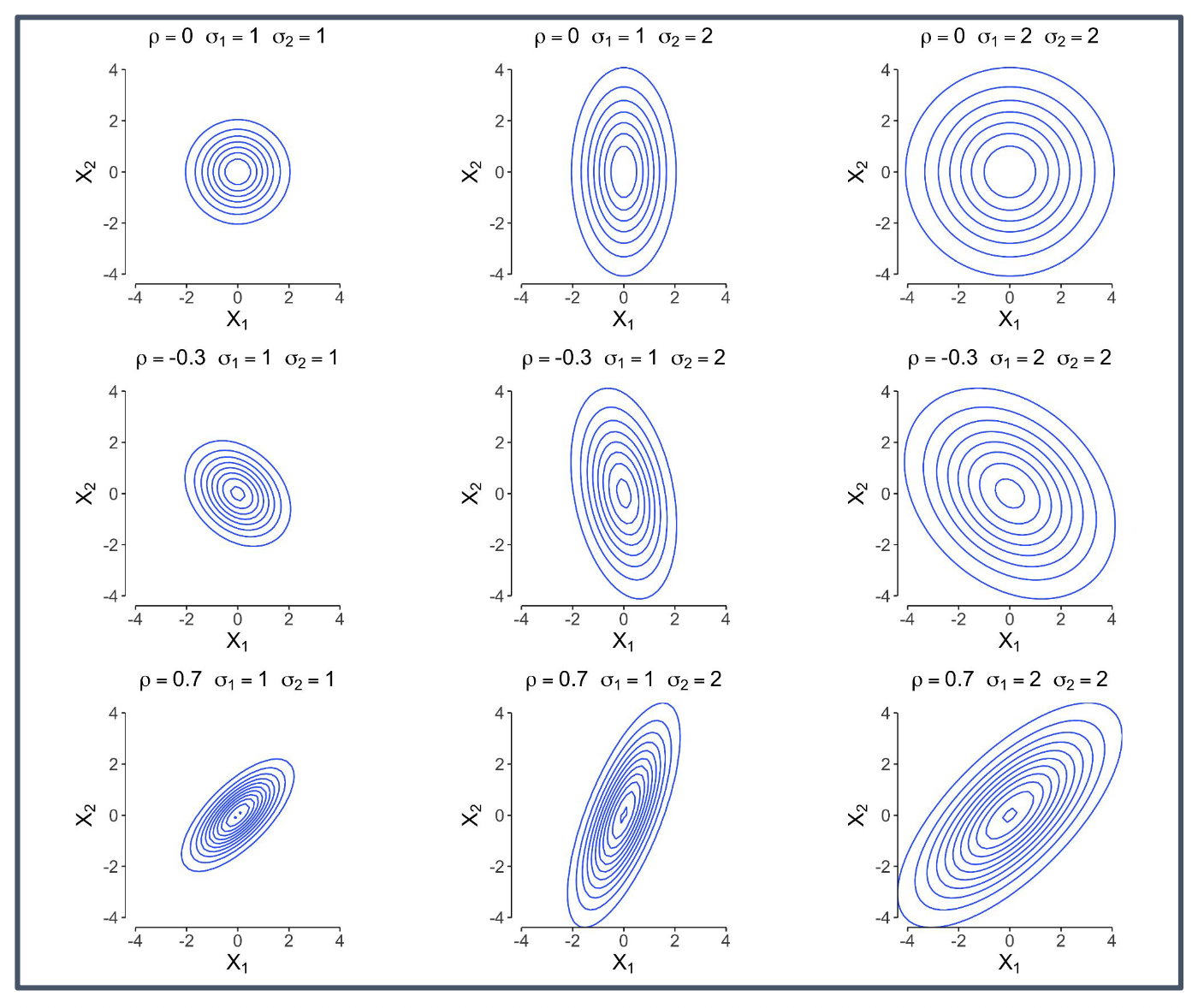
위 그림은 2차원 가우시안 분포에서 상관계수 $\rho$와 각 축의 표준편차 $\sigma_1, \sigma_2$ 값에 따라
등고선(등밀도 곡선)의 모양이 어떻게 달라지는지를 보여준다.
$\rho = 0$일 때는 두 변수가 독립이므로 등고선은 원형 또는 축에 평행한 타원 형태를 가진다.
$\rho < 0$이면 음의 상관관계가 나타나며, 타원이 왼쪽 위 ↔ 오른쪽 아래 방향으로 기울어진다.
$\rho > 0$이면 양의 상관관계가 나타나며, 타원이 왼쪽 아래 ↔ 오른쪽 위 방향으로 기울어진다.
각 변수의 분산 $\sigma_1^2, \sigma_2^2$가 커질수록 해당 축 방향으로 더 넓어지며,
이는 그 방향으로의 데이터 분포가 더 크게 퍼져 있음을 의미한다.

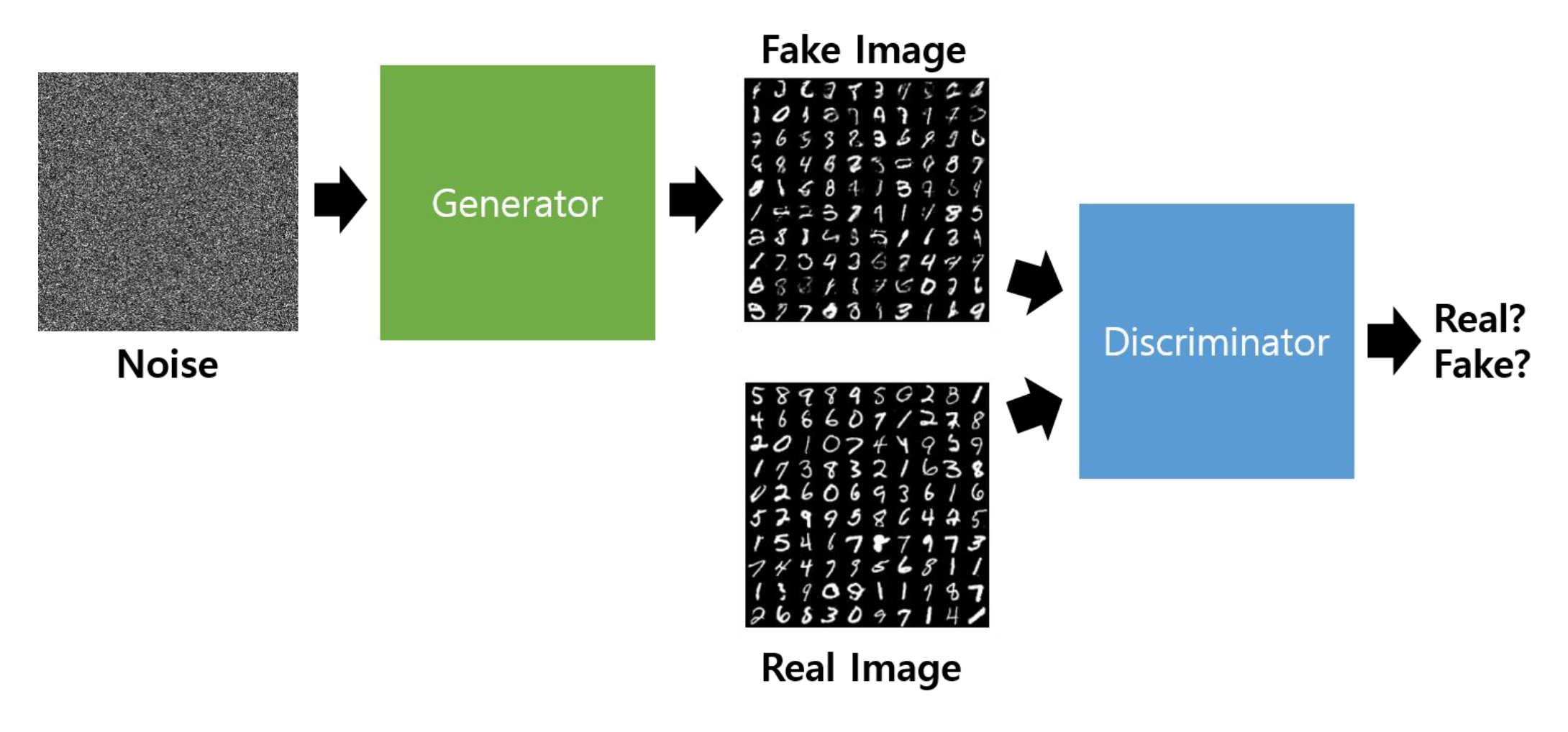
p26. 왜 다변량 가우시안 확률변수인가?

위 그림은 GAN(Generative Adversarial Network)의 구조를 단순화하여 보여준다.
왼쪽의 Noise(잡음)는 고차원 확률공간에서 뽑은 벡터이며, 일반적으로 다변량 가우시안 분포에서 샘플링한다.
Generator(생성기)는 이 잡음을 입력받아 가짜 이미지를 생성한다.
Discriminator(판별기)는 진짜 이미지와 가짜 이미지를 입력받아 둘을 구분하는 역할을 한다.
다변량 가우시안을 사용하는 이유는 고차원에서의 잡음을 효율적으로 모델링하고, 생성기가 이를 다양한 데이터(예: 손글씨 이미지)로 변환할 수 있도록 하는 데 적합하기 때문이다.

p27. 퀴즈 (15 ~ 30분)

경제학 이론에서 폰 노이만-모겐슈테른 효용 함수(Von Neumann-Morgenstern Utility Function)를 생각해 보자.

폰 노이만(John von Neumann)과 오스카 모겐슈테른(Oskar Morgenstern)은
1944년 『Theory of Games and Economic Behavior』(게임 이론과 경제행동)를 공동 집필하였다.
이 책에서 정의된 효용 함수(Utility Function)는 불확실성 상황에서 합리적 의사결정을 수학적으로 표현하기 위한 핵심 개념이다.
기대효용(Expected Utility) 개념이 도입되어 사람들이 위험(risk)이나 불확실성 하에서 선택을 어떻게 하는지를 설명할 수 있게 되었다.
오늘날에도 이 함수는 게임이론, 의사결정 이론, 행동경제학, 인공지능(특히 강화학습) 등 다양한 분야에서 중요한 이론적 기초가 된다.

p28. 퀴즈 (15 ~ 30분)

구체적으로 폰 노이만-모겐슈테른 효용 함수(Von Neumann-Morgenstern Utility Function) 라고 불리는 다음의 누적분포함수(CDF) 들과 확률밀도함수(PDF) 들을 고려한다:

\[F_{X,Y}(x,y) = F_X(x)F_Y(y)\big[1 + \theta(1 - F_X(x))(1 - F_Y(y))\big], x > 0, y > 0\] \[F_X(x) = 1 - e^{-\lambda x}, \quad f_X(x) = \lambda e^{-\lambda x},\] \[F_Y(y) = 1 - e^{-\mu y}, \quad f_Y(y) = \mu e^{-\mu y}\]

\[f_{X,Y}(x,y) = f_X(x)f_Y(y)\big[1 + \theta(1 - 2F_X(x))(1 - 2F_Y(y))\big]\] \[= \lambda \mu e^{-\lambda x - \mu y}\big[1 + \theta(-1 + 2e^{-\lambda x})(-1 + 2e^{-\mu y})\big]\]

다음의 확률 표현들에 대해 closed-form solution 을 구하라:

$f_{X \mid Y}(x \mid y)$
$\mathbb{E}[X \mid Y = y]$

조건: $x$와 $y$ 이외의 다른 변수들은 모두 상수(environment variables) 로 고정된다.

p29. 퀴즈 (15 ~ 30분)

구체적으로 폰 노이만-모겐슈테른 효용 함수 (Von Neumann-Morgenstern Utility Function) 라고 불리는 다음의 누적분포함수(CDF) 들과 확률밀도함수(PDF) 들을 고려한다:

기대값(Expectation) 공식들

단일 확률변수 $X$:

\[\mathbb{E}[g(X)] = \int g(x) f_X(x)\, dx\]

결합 확률변수 $(X,Y)$:

\[\mathbb{E}[g(X,Y)] = \iint g(x,y) f_{X,Y}(x,y)\, dx\, dy\]

조건부 기대값 (주어진 $Y=y$):

\[\mathbb{E}[g(X)\mid Y=y] = \int g(x) f_{X|Y}(x|y)\, dx\]

조건부 기대값 (함수 $g(X,Y)$에 대하여):

\[\mathbb{E}[g(X,Y)\mid Y=y] = \int g(x,y) f_{X|Y}(x|y)\, dx\]

힌트: 위의 공식을 활용하라.

문제 풀이

구해야 할 것:

1) $f_{X \mid Y}(x \mid y)$
2) $\mathbb{E}[X \mid Y=y]$

1. 조건부 밀도 $f_{X \mid Y}(x \mid y)$

\[f_{X \mid Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_Y(y)}\] \[= \frac{f_X(x) f_Y(y)\Big[1+\theta(1-2F_X(x))(1->2F_Y(y))\Big]}{f_Y(y)}\] \[= f_X(x)\Big[1+\theta(1-2F_X(x))(1-2F_Y(y))\Big]\]

여기서

\[f_X(x)=\lambda e^{-\lambda x},\quad F_X(x)=1-e^{-\lambda x},\quad F_Y(y)=1-e^{-\mu y}\] \[f_{X \mid Y}(x \mid y)=\lambda e^{-\lambda x}\Big[1+\theta(-1+2e^{-\lambda x})(-1+2e^{-\mu y})\Big],\quad x>0\]

2. 조건부 기댓값 $\mathbb{E}[X\mid Y=y]$

\[\mathbb{E}[X\mid Y=y] = \int_0^\infty x f_{X \mid Y}(x \mid y)\, dx\] \[= \int_0^\infty x \lambda e^{-\lambda x}\Big[1+\theta(-1+2e^{-\lambda x})(-1+2e^{-\mu y})\Big] dx\] \[= \int_0^\infty x\lambda e^{-\lambda x} dx + \theta(-1+2e^{-\mu y}) \int_0^\infty x\lambda e^{-\lambda x}(-1+2e^{-\lambda x}) dx\]

첫 번째 항:

\[\int_0^\infty x\lambda e^{-\lambda x} dx = \frac{1}{\lambda}\]

두 번째 항:

\[-\frac{1}{\lambda} + 2\cdot \frac{1}{4\lambda} = -\frac{1}{2\lambda}\]

따라서

\[\mathbb{E}[X\mid Y=y] = \frac{1}{\lambda} + \theta(-1+2e^{-\mu y})\Big(-\frac{1}{2\lambda}\Big)\] \[= \frac{1}{\lambda}\Big[1+\theta\Big(\tfrac{1}{2}-e^{-\mu y}\Big)\Big]\]

왜 $\int_0^\infty x\lambda e^{-\lambda x}\, dx = \tfrac{1}{\lambda}$ 가 되는가?
부분적분을 사용한다.
\[u = x,\quad dv = \lambda e^{-\lambda x} dx\] \[du = dx,\quad v = -e^{-\lambda x}\]
따라서
\[\int_0^\infty x\lambda e^{-\lambda x}\, dx = [uv]_0^\infty - \int_0^\infty v\,du\]
첫 번째 항:
\[uv = -x e^{-\lambda x},\quad [uv]_0^\infty = 0\]
두 번째 항:
\[-\int_0^\infty v\,du = \int_0^\infty e^{-\lambda x}\, dx\]
이 적분은
\[\int_0^\infty e^{-\lambda x}\, dx = \left[-\frac{1}{\lambda}e^{-\lambda x}\right]_0^\infty = \frac{1}{\lambda}\]
따라서
\[\int_0^\infty x\lambda e^{-\lambda x}\, dx = \frac{1}{\lambda}\]

p30. LLN & CLT

$X, X_1, X_2, \ldots, X_n$ 은 i.i.d. 확률변수이고,
$\mu = \mathbb{E}[X]$, $\sigma^2 = \mathbb{V}[X]$ 라 하자.

대수의 법칙 (Law of Large Numbers, weak and strong):

\[\overline{X}_n := \frac{1}{n} \sum_{i=1}^n X_i \quad \xrightarrow[n\to\infty]{P,\, a.s.} \quad \mu\]

중심극한정리 (Central Limit Theorem):

\[\frac{\sqrt{n}(\overline{X}_n - \mu)}{\sigma} \xrightarrow[n\to\infty]{(d)} \mathcal{N}(0,1)\]

(동치적으로, Equivalently):

\[\sqrt{n}(\overline{X}_n - \mu) \xrightarrow[n\to\infty]{(d)} \mathcal{N}(0,\sigma^2)\]

1. i.i.d. (independent and identically distributed)
independent(독립): 하나의 확률변수 결과가 다른 변수에 영향을 주지 않는다.
identically distributed(동일 분포): 모두 같은 분포에서 뽑힌다.
즉, i.i.d.는 서로 독립이고 동일한 분포를 따르는 확률변수들이다.
2. $P$, a.s. 수렴
$\xrightarrow{P}$: 확률수렴. $n$이 커질수록 표본평균 $\overline{X}_n$이 모평균 $\mu$ 근처에 있을 확률이 커진다.
$\xrightarrow{a.s.}$: 거의 확실수렴. 확률 0의 경우를 제외하고 대부분의 경우에 $\overline{X}_n$이 $\mu$로 수렴한다.
3. $\tfrac{\sqrt{n}(\overline{X}_n - \mu)}{\sigma}$ 식이 나오는 이유
각 표본을 표준화하면
\[Z_i = \frac{X_i - \mu}{\sigma}\]
표준화된 표본평균은
\[\overline{Z}_n = \frac{1}{n}\sum_{i=1}^n Z_i = \frac{\overline{X}_n - \mu}{\sigma}.\]
평균 계산:
\[\mathbb{E}[\overline{Z}_n] = \frac{\mathbb{E}[\overline{X}_n] - \mu}{\sigma} = 0\]
분산 계산:
\[\mathrm{Var}(\overline{Z}_n) = \frac{1}{\sigma^2}\mathrm{Var}(\overline{X}_n) = \frac{1}{\sigma^2}\cdot \frac{\sigma^2}{n} = \frac{1}{n}\]
분산을 1로 맞추기 위해 $\sqrt{n}$을 곱하면
\[\sqrt{n}\,\overline{Z}_n = \frac{\sqrt{n}(\overline{X}_n - \mu)}{\sigma}.\]
평균: 0, 분산: 1이 된다.
4. $d$ 수렴
$\xrightarrow{d}$는 분포수렴을 의미한다.
이는 확률변수 자체가 아니라 그 확률분포의 모양이 $N(0,1)$과 같아진다는 의미이다.
5. 왜 동치가 되는가?
중심극한정리에 따르면
\[\frac{\sqrt{n}(\overline{X}_n - \mu)}{\sigma} \xrightarrow{d} \mathcal{N}(0,1)\]
양변에 $\sigma$를 곱하면
\[\sqrt{n}(\overline{X}_n - \mu) \xrightarrow{d} \sigma \cdot \mathcal{N}(0,1)\]
상수 $c$를 곱하면 평균은 $c$, 분산은 $c^2$ 배가 되므로
\[\sigma\cdot \mathcal{N}(0,1) = \mathcal{N}(0,\sigma^2)\]
따라서
\[\sqrt{n}(\overline{X}_n - \mu) \xrightarrow{d} \mathcal{N}(0,\sigma^2)\]
위의 두 표현은 동치이다.
평균이 0, 분산이 1인 $N(0,1)$은 표본이 어떤 분포에서 왔는지와 관계없이 표본평균이 가지는 공통적 성질만 남은 것이다.
중심극한정리의 핵심은 “원래 분포가 무엇이든, 표본을 많이 모아 평균을 내면 정규분포로 간다”는 점이다.

p31. 수렴의 유형 (1 / 2)

$(T_n)_{n \ge 1}$ 을 확률변수의 수열이라 하고, $T$를 하나의 확률변수라 하자.
($T$는 결정적일 수도 있다.)

거의 확실한 (almost surely, a.s.) 수렴:

\[T_n \xrightarrow[n \to \infty]{a.s.} T \quad \text{iff} \quad \mathbb{P}\Big(\big\{\omega : T_n(\omega) \xrightarrow[n \to \infty]{} T(\omega)\big\}\Big) = 1\]

확률적 수렴 (convergence in probability):

\[T_n \xrightarrow[n \to \infty]{P} T \quad \text{iff} \quad \mathbb{P}\big(|T_n - T| \ge \varepsilon\big) \xrightarrow[n \to \infty]{} 0, \quad \forall \varepsilon > 0\]

1. iff (if and only if)
약어: if and only if
한국어: “~일 때 그리고 그때에 한해서”, “필요충분조건”
어떤 조건이 성립하기 위한 필요조건이자 충분조건임을 동시에 나타낸다.
2. a.s. (almost surely) 수렴
확률론의 기본 구조
표본공간 $\Omega$: 가능한 모든 결과들의 집합
원소 $\omega \in \Omega$: 실제로 발생한 하나의 결과
확률변수 $T_n(\omega)$: 결과 $\omega$가 주어졌을 때 $n$번째 시행 이후의 표본평균
예시: 주사위 1000번 던지기
표본공간: $6^{1000}$
원소: 실제 관측된 수열 (예: $(3,5,1,6,\dots)$)
$T_n(\omega)$와 $T(\omega)$
$T_n(\omega)=\frac{1}{n}\sum_{i=1}^n X_i(\omega)$
$T(\omega)$는 수렴 대상. 대수의 법칙에서는 $T(\omega)=\mu$
수식의 의미
\[T_n \xrightarrow[n\to\infty]{a.s.} T \quad\iff\quad \mathbb{P}\big(\{\omega : T_n(\omega)\to T(\omega)\}\big)=1\]
즉, 확률 0의 경우를 제외한 대부분의 경우에서
$T_n(\omega)\to T(\omega)$가 성립한다.
주사위 예시
모평균: $\mu=\frac{1+2+3+4+5+6}{6}=3.5$
대부분의 시나리오 $\omega$에서 $T_n(\omega)\to 3.5$
예외적 시나리오(예: 무한히 1만 나오는 경우)는 확률 0
직관적 설명
무한히 반복하면 표본평균이 거의 항상 모평균 3.5로 모인다.
이를 a.s. 수렴이라 부른다.
3. 확률적 수렴 (convergence in probability, $\xrightarrow{P}$)
정의:
\[\lim_{n\to\infty}\mathbb{P}\big(|T_n-T|>\varepsilon\big)=0\]
의미
$n$이 커질수록 $T_n$이 $T$ 근처에 있을 확률이 커진다.
모든 시나리오에서 반드시 수렴한다고 보장하지는 않는다. a.s.보다 약함.
예시: 동전 던지기
$T_n$: 앞면 비율
$T=0.5$
\[T_n \xrightarrow{P} 0.5\]
즉, $n$이 증가할수록 $T_n$이 0.5 근처에 있을 확률이 1에 가까워진다.

p32. 수렴의 유형 (2/2)

3. $L^p$ 수렴 (Convergence in $L^p$, $p \ge 1$)

\[T_n \xrightarrow[n\to\infty]{L^p} T \quad \text{iff} \quad \mathbb{E}\!\left[\,|T_n - T|^{p}\,\right] \xrightarrow[n\to\infty]{} 0\]

4. 분포 수렴 (Convergence in distribution, d)

조건: 확률변수 $T$의 누적분포함수(CDF)가 연속인 모든 실수 $x \in \mathbb{R}$에 대해

\[T_n \xrightarrow[n\to\infty]{(d)} T \quad \text{iff} \quad \mathbb{P}\!\left[T_n \le x\right] \xrightarrow[n\to\infty]{} \mathbb{P}\!\left[T \le x\right]\]

1. $L^p$ 수렴
정의
확률변수의 수열 $(T_n)$이 확률변수 $T$에 대해 $L^p$ 수렴한다는 것은
\[T_n \xrightarrow[n\to\infty]{L^p} T \quad\iff\quad \mathbb{E}[|T_n - T|^p] \to 0\]
의미
두 확률변수의 차이를 $p$제곱한 값의 평균이 0으로 수렴한다는 뜻이다.
$p=2$일 때는 평균제곱오차(MSE) 기준에서 수렴하는 의미가 된다.
값의 오차가 평균적으로 작아지는 것에 초점이 맞추어진 수렴 개념이다.
예시
$T_n$: 표본평균
$T$: 모평균
$p=2$이면 $\mathbb{E}[(T_n - T)^2] \to 0$, 즉 평균제곱오차가 0으로 수렴한다.
2. 분포 수렴
정의
확률변수의 수열 $(T_n)$이 확률변수 $T$에 분포 수렴한다는 것은
확률변수 $T$의 누적분포함수(CDF)가 연속인 모든 실수 $x$에 대해
\[T_n \xrightarrow[n\to\infty]{d} T \quad\iff\quad \mathbb{P}(T_n \le x) \to \mathbb{P}(T \le x)\]
의미
개별 값의 수렴이 아니라, 확률변수들의 분포 함수(CDF) 자체가 수렴하는 개념이다.
즉, 실제 값이 같아지는 것이 아니라 분포의 모양이 같아진다는 의미이다.
예시
중심극한정리(CLT): 적절히 표준화된 표본평균의 분포는 원래 분포와 무관하게
표준정규분포 $N(0,1)$에 가까워진다.
이 경우 $T_n$이 실제 값에서 $T$로 수렴한다는 보장은 없지만
분포는 점점 $N(0,1)$과 동일해진다.

p33. 확률적 (약한) 수렴

확률변수 수열의 분포가 극한의 분포에 접근할 때,
우리는 그 확률변수 수열이 극한에 약하게 수렴한다(converges weakly) 고 말한다.

\[T_n \xrightarrow[n \to \infty]{(d)} T\]
연속이고 유계(bounded) 인 모든 함수 $f$에 대해

\[\mathbb{E}[f(T_n)] \;\longrightarrow\; \mathbb{E}[f(T)], \quad n \to \infty\]

1. 유계 (bounded)
함수의 값이 어떤 고정된 상수 범위 안에 머무른다는 뜻이다.
예: $f(x)=\tfrac{1}{1+x^2}$ 는 모든 실수 $x$에서 값이 0과 1 사이에 있으므로 bounded.
반면 $f(x)=x$ 는 $x\to\infty$일 때 값이 무한대로 커지므로 bounded가 아니다.
2. 모든 $f$에 대해 성립해야 함
분포 수렴의 정의에서 “연속이고 유계인 모든 함수 $f$”에 대해
\[\mathbb{E}[f(T_n)] \to \mathbb{E}[f(T)]\]
가 성립해야 한다.
이는 일부 함수에만 성립하는 것이 아니라 가능한 모든 연속·유계 함수에서 해당 조건이 충족되어야 함을 의미한다.
이렇게 해야 분포의 전체 형태가 수렴함을 보장할 수 있다.
3. Weak convergence와 GAN의 관계
데이터 분포: 현실 세계에서 관측되는 데이터가 따른다고 보는 분포
(예: 실제 고양이 사진 전체가 따른다고 보는 분포)
생성 분포: 생성기(Generator)가 만들어내는 데이터가 따른다고 보는 분포
(예: GAN이 생성한 고양이 이미지들의 분포)
GAN의 목표는 생성 분포가 데이터 분포와 거의 동일해지도록 만드는 것이다.
두 분포가 같아졌는지 확인하는 방법 중 하나가 weak convergence(분포 수렴) 개념이다.
즉, 모든 연속·유계 함수 $f$에 대해
\[\mathbb{E}_{X \sim P_G}[f(X)] \;\to\; \mathbb{E}_{X \sim P_{\text{data}}}[f(X)]\]
가 성립하면 생성 분포 $P_G$는 데이터 분포 $P_{\text{data}}$에 수렴했다고 말할 수 있다.
GAN에서는 “모든 함수 $f$”를 직접 다루지 않고, 판별기(discriminator) 가 이 역할을 근사한다.
따라서 GAN이 성공적으로 학습되었다는 것은
생성된 데이터의 분포가 실제 데이터의 분포에 약하게 수렴한다 (weak convergence) 는 의미로 해석할 수 있다.

p34. 지수분포

$T_1$의 밀도:

\[f(t) = \lambda e^{-\lambda t}, \quad \forall t \ge 0\]

기댓값:

\[\mathbb{E}[T_1] = \frac{1}{\lambda}\]

따라서, $\tfrac{1}{\lambda}$의 자연스러운 추정량은

\[\overline{T}_n = \frac{1}{n} \sum_{i=1}^n T_i\]

$\lambda$의 자연스러운 추정량은

\[\hat{\lambda} = \frac{1}{\overline{T}_n}\]

평균과 분산:

\[\mu = \frac{1}{\lambda}, \quad \sigma^2 = \frac{1}{\lambda^2}\]

1. 왜 $\lambda$를 추정하려고 하는가?
지수분포의 모양을 결정하는 핵심 매개변수가 $\lambda$이다.
$\lambda$가 커지면 사건이 더 빨리 일어나고, $\lambda$가 작아지면 사건이 더 느리게 발생한다.
예: “부품이 고장 날 때까지 걸리는 시간”이 지수분포를 따른다면 평균 수명은 $1/\lambda$이므로, $\lambda$를 알아야 전체 수명을 이해할 수 있다.
2. 왜 표본평균이 $1/\lambda$의 추정량인가?
지수분포에서
\[\mathbb{E}[T_1] = \frac{1}{\lambda}\]
표본평균
\[\overline{T}_n = \frac{1}{n} \sum_{i=1}^n T_i\]
는 대수의 법칙에 의해 $1/\lambda$에 수렴한다.
따라서 $\overline{T}_n$은 자연스럽게 $1/\lambda$의 추정량이 된다.
3. 왜 $\hat{\lambda} = 1/\overline{T}_n$인가?
우리가 구하고자 하는 값은 $1/\lambda$가 아니라 $\lambda$이다.
$\overline{T}_n \approx 1/\lambda$이므로 양변의 역수를 취하면
\[\hat{\lambda} = \frac{1}{\overline{T}_n}\]
따라서 $\hat{\lambda}$는 $\lambda$의 자연스러운 추정량(estimator)이 된다.
지수분포는 평균과 표준편차가 모두 $1/\lambda$가 되는 특성을 가진다.
즉, 하나의 매개변수 $\lambda$만으로 분포의 중심과 퍼짐을 동시에 설명할 수 있다.
이는 다른 분포와 비교했을 때 지수분포가 가지는 단순하면서도 강력한 특징이다.

p35. 지수분포

대수의 법칙 (LLN)에 의해
\[\overline{T}_n \xrightarrow[n \to \infty]{a.s./P} \frac{1}{\lambda}\]
따라서
\[\hat{\lambda} = \frac{1}{\overline{T}_n} \xrightarrow[n \to \infty]{a.s./P} \lambda\]
중심극한정리 (CLT)에 의해
\[\sqrt{n}\left(\overline{T}_n - \frac{1}{\lambda}\right) \xrightarrow[n \to \infty]{d} \mathcal{N}(0, \lambda^{-2})\]

1. 표본평균의 의미와 추정량의 직관
지수분포 $Exp(\lambda)$에서 $T_1,\dots,T_n$의 표본평균 $\overline{T}_n$은 사건 사이의 평균 대기시간을 의미한다.
평균 대기시간의 역수가 곧 발생률(rate)이므로, $\hat{\lambda}=1/\overline{T}_n$은 자연스럽고 직관적인 추정량이 된다.
즉, 대기시간이 짧을수록(평균 간격이 작을수록) $\lambda$가 커지는 지수분포의 성질을 그대로 반영한 형태이다.
2. CLT의 적용
30페이지의 CLT 공식
\[\sqrt{n}\left(\overline{X}_n - \mu\right) \xrightarrow[n\to\infty]{d} \mathcal{N}(0,\sigma^2)\]
지수분포의 경우 평균과 분산은 $\mu=\tfrac{1}{\lambda},\ \sigma^2=\tfrac{1}{\lambda^2}$ 이므로 대입하면
\[\sqrt{n}\left(\overline{T}_n - \frac{1}{\lambda}\right) \xrightarrow[n\to\infty]{d} \mathcal{N}\!\left(0,\frac{1}{\lambda^2}\right)\]
이는 LLN이 말해주는 단순한 수렴( $\overline{T}_n \to 1/\lambda$ )을 넘어, 수렴 과정에서 표본평균이 어떤 분포를 따르는지를 정규분포 형태로 정확히 알려주는 결과이다.

p36. 통계적 모델 : 정의

통계적 실험의 관측 결과가 표본 $X_1, \dots, X_n$이라고 하자.
$X_1, \dots, X_n$은 어떤 측도공간(measurable space) $E$ (보통 $E \subseteq \mathbb{R}$) 위의 $n$개의 i.i.d. 확률변수들이며, 이들의 공통 분포를 $\mathbb{P}$라고 표기한다.

그 통계적 실험에 연관된 통계적 모델(statistical model)은 다음의 쌍이다.

\[(E, (\mathbb{P}_\theta)_{\theta \in \Theta})\]

여기에서:

$E$는 표본공간(sample space)이다.
$\left(P_{\theta} \right)_{\theta \in \Theta}$는 $E$ 위의 확률측도(probability measures)들의 모임이다.
$\Theta$는 임의의 집합(any set)으로, 모수공간(parameter set)이라고 부른다.

1. 측도론의 3요소
확률은 측도론(measure theory)의 틀에서 정의된다.
기본 구조는 다음 세 가지로 이루어진다.
측도공간 (measurable space): $(E, F)$
$E$: 표본공간(sample space), 가능한 모든 결과들의 집합
$F$: 시그마-대수(σ-algebra), $E$의 부분집합 중에서 “확률을 매길 수 있는 집합”들의 모임
측도(measure): 확률 $P$, $F$에 속하는 집합에 대해 확률을 부여하는 함수
예시:
동전 던지기: $E={\text{앞, 뒤}}$, $F=E$의 모든 부분집합
주사위: $E={1,\dots,6}$
연속값: $E=\mathbb{R}$, $F$는 보렐 집합들
2. 비탈리 집합(Vitali set)
[0,1] 구간의 실수들을 “차이가 유리수이면 같은 그룹”으로 묶는다.
예: 0.1과 0.4는 차이가 0.3 → 같은 그룹
예: 0.1과 $\pi/10$은 차이가 무리수 → 다른 그룹
각 그룹에서 대표자 하나씩만 뽑아 만든 집합이 비탈리 집합이다.
비탈리 집합은 확률을 정의할 수 없는 대표적 반례(counterexample)이다.
이유:
유리수만큼 평행이동한 모든 복사본들이 서로 겹치지 않고 [0,1] 전체를 덮는다.
만약 비탈리 집합에 확률을 부여하면:
확률이 0이면 전체가 0
양수이면 무한대
어느 쪽도 전체 확률 1 조건과 모순
결론: 확률론은 모든 부분집합을 다루지 않고, “측정 가능한 집합”들만 모은 σ-대수를 사용한다.
3. 보렐 시그마-대수(Borel σ-algebra)
비탈리 집합 같은 문제 때문에, 확률을 정의할 수 있는 집합들을 모아둔 것이 보렐 σ-대수이다.
정의:
실수선에서 열린 구간 $(a,b)$들을 시작으로
이들에 대해 σ-대수 연산(합집합, 교집합, 여집합)을 무한히 적용해 얻은 집합들의 모임
특징:
구간, 닫힌구간, 반구간, 유한한 구간들의 합집합 등이 모두 포함된다.
가우시안 분포 같은 확률분포는 보렐 σ-대수 위에서 정의된다.
예:
$N(0,1)$ 분포는 $E=\mathbb{R}$, $F=$ 보렐 σ-대수 위에서 확률 $P$를 정의한다.
4. 통계모델 (Statistical Model)
구성요소:
측도공간 $(E,F)$
확률측도들의 집합 ${P_\theta:\theta\in\Theta}$
각 $P_\theta$는 $(E,F)$ 위에서 정의된 확률측도이며, 매개변수 $\theta$ 값에 따라 달라진다.
통계모델은
\[(E,\{P_\theta\}_{\theta\in\Theta})\]
로 표현된다.
직관:
표본공간 $E$는 고정
그 위에 올릴 “가능한 분포들”이 $\theta$에 따라 달라지는 구조
즉 하나의 공간 위에 여러 후보 분포를 모아놓은 틀이 통계모델이다.
5. 통계모델과 머신러닝 모델의 관계
통계모델:
$(E,{P_\theta})$ 형태
즉, 하나의 공간 위에 매개변수 $\theta$에 의해 정의되는 확률분포들의 집합
예: 정규분포족 ${N(\mu,\sigma^2)}$
머신러닝 모델:
신경망, 결정트리, 로지스틱 회귀 등 “학습 가능한 구조”라고 부른다.
그러나 수학적으로는 이들도 특정 $\theta$가 주어지면 하나의 확률분포를 정의한다.
예: 로지스틱 회귀
$\theta$가 주어지면 $P_\theta(Y=1 \mid X)=\sigma(\theta^\top X)$라는 분포가 된다.
가능한 모든 $\theta$에 대응하는 분포들의 집합이 곧 로지스틱 회귀 모델이다.
정리:
통계모델과 머신러닝 모델은 표현은 다르지만 모두 “가능한 분포들의 집합”이라는 공통된 뿌리를 가진다.
차이점은 통계학에서는 이론적으로 모델링하고, 머신러닝에서는 데이터를 통해 $\theta$를 학습한다는 점이다.
측도공간(measurable space)은 공간을 임의로 잘게 잘라 놓아도 그 부분집합들에 확률을 부여할 수 있도록 설계된다.
통계모델(statistical model)은 하나의 분포가 아니라 가능한 모든 분포들의 집합이며, 머신러닝에서 “모델 = 분포 집합”이라는 관점과 자연스럽게 연결된다.

p37. 통계모델 예시

베르누이 시행 (Bernoulli trials)
- $X_1, \dots, X_n \sim \text{Ber}(p), \; p \in (0,1)$
- 통계모델:
  $\big( \{0,1\}, \; (\text{Ber}(p))_{p \in (0,1)} \big)$
지수분포 (Exponential distribution)
- $X_1, \dots, X_n \overset{iid}{\sim} \text{Exp}(\lambda), \; \lambda > 0$
- 통계모델:
  $\big( \mathbb{R}^+, \; (\text{Exp}(\lambda))_{\lambda > 0} \big)$
포아송 분포 (Poisson distribution)
- $X_1, \dots, X_n \overset{iid}{\sim} \text{Poiss}(\lambda), \; \lambda > 0$
- 통계모델:
  $\big( \mathbb{N}, \; (\text{Poiss}(\lambda))_{\lambda > 0} \big)$
정규분포 (Normal distribution)
- $X_1, \dots, X_n \overset{iid}{\sim} \mathcal{N}(\mu, \sigma^2), \; \mu \in \mathbb{R}, \; \sigma^2 > 0$
- 통계모델:
  $\big( \mathbb{R}, \; (\mathcal{N}(\mu, \sigma^2))_{(\mu, \sigma^2) \in \mathbb{R} \times \mathbb{R}^*_+} \big)$

1. 표본공간과 측도공간의 차이
표본공간(sample space, $E$): 관찰되는 데이터가 가질 수 있는 모든 값들의 집합
예: 베르누이 시행 → $E={0,1}$
예: 정규분포 → $E=\mathbb{R}$
측도공간(measurable space, $(E,\mathcal{F})$):
표본공간 $E$와, 그 위에서 확률을 부여할 수 있는 부분집합들의 모임(σ-대수) $\mathcal{F}$를 함께 고려한 구조
즉, (데이터의 가능한 값들) + (확률을 정의할 수 있는 사건들의 모음)
왜 혼동되는가?
교재에서는 단순화를 위해 $E$만 표기하는 경우가 많아 보이지만
정확히는 $(E,\mathcal{F})$ 전체를 의미하는 축약 표현이다.
정리: 슬라이드의 왼쪽 항은 “표본공간”처럼 보이나 실제로는 측도공간 전체를 축약한 표현이다.
2. 베르누이 시행 (Bernoulli trials)
표본공간: $E={0,1}$
매개변수: 성공확률 $p$ ($0\le p\le1$)
통계모델: ${\text{Ber}(p): p\in[0,1]}$
3. 지수분포 (Exponential distribution)
표본공간: $E=\mathbb{R}^+$
매개변수: $\lambda>0$ (발생률, rate)
통계모델: ${\text{Exp}(\lambda): \lambda>0}$
4. 포아송 분포 (Poisson distribution)
표본공간: $E=\mathbb{N}$
매개변수: $\lambda>0$ (단위 시간/구간당 평균 발생 횟수)
통계모델: ${\text{Poiss}(\lambda): \lambda>0}$
5. 정규분포 (Normal distribution)
표본공간: $E=\mathbb{R}$
매개변수: $\mu\in\mathbb{R}$, $\sigma^2>0$
통계모델: ${\mathcal{N}(\mu,\sigma^2): \mu\in\mathbb{R},\ \sigma^2>0}$

p38. 통계적 추정

아이디어

표본 $X_{1}, \dots, X_{n}$ 과 통계모델 $(E, (P_{\theta})_{\theta \in \Theta})$ 가 주어졌을 때,
관심 있는 것은 모수 $\theta$를 추정하는 것이다.

정의

통계량 (Statistic):
표본으로부터 정의되는 임의의 측정가능한 함수.
예: $\overline{X}_{n}, \max_{i} X_{i}, X_{1} + \log(1 + |X_{n}|),$ 표본분산 등
$\theta$의 추정량(Estimator):
그 표현식(expression)이 모수 $\theta$에 의존하지 않는 임의의 통계량
모수 $\theta$에 대한 약한(weak) 또는 강한(strong) 일치(consistent)의 필요충분조건은 다음과 같다.
\[\hat{\theta}_{n} \xrightarrow[n \to \infty]{P \, (\text{resp. a.s.})} \theta \quad \text{(with respect to } P_{\theta}\text{)}\]

1. 표현식이 $\theta$에 의존하지 않는 임의의 통계량
통계량은 표본 $(X_1,\dots,X_n)$의 함수로 정의된다.
“$\theta$에 의존하지 않는다”는 것은 그 표현식 안에 모수 $\theta$가 직접 등장하지 않는다는 의미이다.
예:
표본평균 $\overline{X}_n = \frac{1}{n}\sum_{i=1}^n X_i$
표본분산 $S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X}_n)^2$
정리하면, 추정량 $\hat{\theta}_n$은 “표본을 입력으로 하는 함수”로서 모수 $\theta$를 직접 포함하지 않는 통계량이다.
2. 수식에서 $P\,(\text{resp. a.s.})$의 의미
resp.는 respectively의 줄임말로 “각각에 대해”라는 의미이다.
다음 식은 두 가지 경우를 동시에 표현한다:
\[\hat{\theta}_n \xrightarrow[n\to\infty]{P\,(\text{resp. a.s.})} \theta\]
1) 확률수렴 (약한 일치성) $\hat{\theta}_n \xrightarrow[n\to\infty]{P} \theta$
2) 거의 확실한 수렴 (강한 일치성) $\hat{\theta}_n \xrightarrow[n\to\infty]{\text{a.s.}} \theta$
3. “with respect to $P_\theta$”의 의미
다음 식에서
\[\hat{\theta}_n \xrightarrow[n\to\infty]{P\,(\text{resp. a.s.})} \theta \quad (\text{w.r.t. } P_\theta)\]
“with respect to $P_\theta$”는 수렴이 확률분포 $P_\theta$ 하에서 성립한다는 뜻이다.
통계모델은 $(E,(P_\theta)_{\theta\in\Theta})$로 주어지고, 실제 표본 $(X_1,\dots,X_n)$은 특정 모수값 $\theta$에 대응하는 분포 $P_\theta$에 따라 생성된다.
따라서 일치성은 항상 해당 모수 $\theta$에서의 분포 $P_\theta$ 아래에서 정의된다.
만약 표본이 $P_{\theta’}$에서 생성되었다면 ($\theta’\neq\theta$), “$\theta$에 대한 일치성”이라는 명제 자체가 성립할 수 없다.

p39. 통계적 추정

추정량 $\hat{\theta}_{n}$의 편향 (Bias):

\[\text{Bias}(\hat{\theta}_{n}) = \mathbb{E}[\hat{\theta}_{n}] - \theta\]

추정량 $\hat{\theta}_{n}$의 위험 (Risk, 또는 제곱위험 Quadratic Risk):

\[R(\hat{\theta}_{n}) = \mathbb{E}\big[\,|\hat{\theta}_{n} - \theta|^{2}\,\big]\]

주석
만약 모수 공간이 $\Theta \subseteq \mathbb{R}$ 이라면,

\[\text{Quadratic risk} = (\text{Bias})^{2} + \text{Variance}\]

1. 편향(Bias)과 위험(Risk)의 해석
편향은 추정량의 평균이 실제 모수 $\theta$에서 얼마나 체계적으로 벗어나 있는지를 나타낸다.
위험(제곱위험)은 제곱손실 기준에서 추정량이 모수 $\theta$와 얼마나 차이가 나는지를 평균적으로 측정한 값이다.
위험은 단일 표본이 아니라 추정량의 평균적 성능을 반영한다.
2. Bias–Variance 분해의 도출 과정(스칼라 모수, 제곱손실)
모수 공간이 $\Theta \subseteq \mathbb{R}$이고 $\mathbb{E}[\hat{\theta}_n^{2}]<\infty$라고 하자.
표기를 단순하게 하기 위해 $\hat{\theta}\equiv\hat{\theta}_n$, $\mu\equiv\mathbb{E}[\hat{\theta}]$로 둔다.
위험의 정의:
\[R(\hat{\theta})=\mathbb{E}[(\hat{\theta}-\theta)^2].\]
평균 $\mu$를 기준으로 더하고 빼면:
\[\hat{\theta}-\theta =(\hat{\theta}-\mu)+(\mu-\theta).\]
제곱 전개 후 기댓값을 취하면:
\[\begin{aligned} R(\hat{\theta}) &=\mathbb{E}\!\left[(\hat{\theta}-\mu+\mu-\theta)^2\right] \\ &=\mathbb{E}\!\left[(\hat{\theta}-\mu)^2\right] +2(\mu-\theta)\mathbb{E}[\hat{\theta}-\mu] +(\mu-\theta)^2. \end{aligned}\]
$\mathbb{E}[\hat{\theta}-\mu]=0$ 이므로 가운데 항은 사라지고:
\[R(\hat{\theta}) =\mathbb{E}[(\hat{\theta}-\mu)^2]+(\mu-\theta)^2 =\mathrm{Var}(\hat{\theta})+\mathrm{Bias}(\hat{\theta})^2.\]
정리: 제곱손실 하에서 스칼라 모수의 위험은 분산과 편향의 제곱의 합으로 분해된다.
3. 편향–분산 상충의 의미
편향을 줄이면 분산이 커지고, 분산을 줄이면 편향이 커지는 상충(trade-off)이 존재한다.
모델 선택(규제 강도, 차원 축소 정도 등)이나 하이퍼파라미터 조정은 이 상충을 조절하여 위험을 최소화하는 과정이다.

대학원 수업, 확률과 통계