[확률과 통계] 3주차
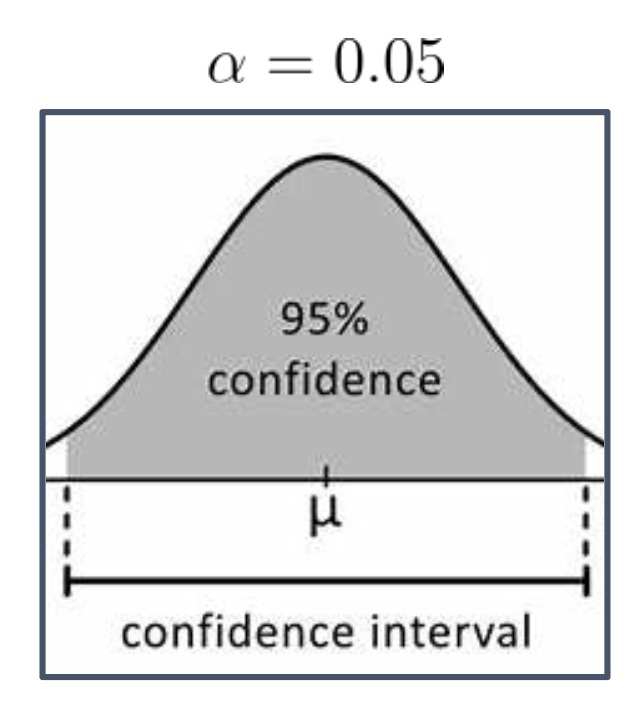
p2. 신뢰구간(CI)
\((E, \left( P_{\theta} \right)_{\theta \in \Theta})\)는 관측치 $X_{1}, \dots, X_{n}$에 기반한 통계모델이라 하고, 모수 공간 $\Theta$는 $\mathbb{R}$의 부분집합이라고 가정하자.
정의
$\alpha \in (0,1)$이라고 하자.
모수 $\theta$에 대한 신뢰수준 $1-\alpha$의 신뢰구간 (Confidence Interval, C.I. of level $1-\alpha$ for $\theta$):
\[\mathbb{P}_{\theta}[\theta \in \mathcal{I}] \geq 1 - \alpha, \quad \forall \theta \in \Theta\]
경계가 $\theta$에 의존하지 않고 (예: $X_{1}, \dots, X_{n}$ 등에 의존하는), 다음을 만족하는 임의의 구간 $\mathcal{I}$:모수 $\theta$에 대한 점근적 신뢰수준 $1-\alpha$의 신뢰구간 (C.I. of asymptotic level $1-\alpha$ for $\theta$):
\[\lim_{n \to \infty} \mathbb{P}_{\theta}[\theta \in \mathcal{I}] \geq 1 - \alpha, \quad \forall \theta \in \Theta\]
경계가 $\theta$에 의존하지 않고, 다음을 만족하는 임의의 구간 $\mathcal{I}$:
1. 경계가 $\theta$에 의존하지 않는다는 의미
- 신뢰구간의 경계(boundary)는 표본 $(X_1,\dots,X_n)$의 함수로 정의된다.
- “$\theta$에 의존하지 않는다”는 것은 그 표현식 안에 모수 $\theta$가 명시적으로 등장하지 않는다는 뜻이다.
예:
\[\mathcal{I} = \left[ \overline{X}_n - 1.96\cdot\frac{S}{\sqrt{n}},\; \overline{X}_n + 1.96\cdot\frac{S}{\sqrt{n}} \right]\]여기서 신뢰구간의 양 끝점은 $\overline{X}_n$과 $S$에만 의존하고, 모수 $\theta$는 경계에 직접 나타나지 않는다.
- 정리하면, 신뢰구간의 경계는 “표본만을 입력으로 하는 함수”이므로 $\theta$에 직접적으로 의존하지 않는다.
2. 점근적 신뢰수준의 의미
첫 번째 정의: 모든 유한한 표본 크기 $n$에서
신뢰구간이 모수 $\theta$를 포함할 확률이 항상 $1-\alpha$ 이상이어야 한다.
→ 엄밀한 신뢰구간(exact confidence interval).두 번째 정의: $n\to\infty$일 때
신뢰구간이 모수 $\theta$를 포함할 확률이 $1-\alpha$ 이상으로 수렴하면 충분하다.
→ 점근적 신뢰구간(asymptotic confidence interval).- 예:
- 유한 표본 신뢰구간: 모든 $n$에서 정확히 $1-\alpha$ 보장
- 점근적 신뢰구간: 유한 $n$에서는 $1-\alpha$에서 벗어날 수 있으나
$n$이 커지면 포함확률이 $1-\alpha$에 수렴- 정리:
첫 번째는 “유한 표본에서의 엄밀한 신뢰구간”,
두 번째는 “$n\to\infty$에서 성립하는 점근적 신뢰구간”을 의미하며,
‘점근적(asymptotic)’이란 표본 크기를 무한대로 보냈을 때 드러나는 성질을 나타낸다.
p3. 총분산거리(TV)
\((E, (P_{\theta})_{\theta \in \Theta})\)를 i.i.d.인 확률변수 $X_{1}, \dots, X_{n}$의 표본과 연관된 통계모형이라고 하자.
\(X_{1} \sim P_{\theta^{*}}\)인 \(\theta^{*} \in \Theta\)가 존재한다고 가정하자:
이때 $\theta^{*}$는 참(true) 모수이다.
통계학자의 목표:
\(X_{1}, \dots, X_{n}\)가 주어졌을 때,
참 모수 \(\theta^{*}\)에 대해 \(P_{\hat{\theta}}\)가 \(P_{\theta^{*}}\)에 근접하도록 하는 추정량 $\hat{\theta} = \hat{\theta}(X_{1}, \dots, X_{n})$을 찾는 것.
이는 곧, 모든 $A \subset E$에 대해
\[|P_{\hat{\theta}}(A) - P_{\theta^{*}}(A)|\]가 작다는 것을 의미한다.
정의
두 확률측도 $P_{\theta}, P_{\theta’}$ 사이의 총분산거리 (Total Variation Distance)는 다음과 같이 정의된다.
(한 꼭지 요약) 총분산거리(Total Variation, TV)의 의미와 직관
- 총분산거리는 두 확률분포가 서로 얼마나 다른지를 측정하는 가장 직접적이고 해석적인 거리 척도이다.
정의의 직관:
\[TV(P_\theta, P_{\theta'}) = \max_{A} |P_\theta(A) - P_{\theta'}(A)|\]이는 “두 분포가 가장 다르게 확률을 할당하는 사건 $A$에서의 차이”를 의미한다. 즉, 실제 관측 결과에 대해 두 분포가 얼마나 다르게 예측하는지를 수치화한 값이다.
- 그래프적 해석: 밀도 $f_\theta(x)$와 $f_{\theta’}(x)$의 그래프 아래 면적이 얼마나 겹치지 않는지 나타낸다. 완전히 같으면 $TV=0$, 전혀 겹치지 않으면 $TV=1$이다.
- 해석 포인트: TV가 작다는 것은 “두 분포를 실제 데이터로 구분하기 어렵다”는 의미이며, 추정된 확률모형이 참 분포를 잘 근사하고 있음을 뜻한다.
- 활용 예시:
- 모형 적합도 평가: $P_{\hat{\theta}}$가 $P_{\theta^*}$에 얼마나 가까운지 측정
- 통계적 수렴 기준: 분포 추정이 참 분포에 수렴할 때 $TV \to 0$
- 이론적 비교 기준: KL, Wasserstein 등 다른 거리 척도의 기준 지표로 사용
- 요약 한 줄: “총분산거리는 두 분포가 같은 사건에 대해 내리는 판단이 얼마나 다른지를 나타내는, 확률적 차이를 가장 직접적으로 표현한 거리 척도이다.”
왜 max가 필요한가?
$A \subseteq E$는 무수히 많으며, 각 사건마다
\[|P_\theta(A) - P_{\theta'}(A)|\]값이 달라진다.
- 이 무한한 값들 중에서 “두 분포가 가장 다르게 행동하는 사건”을 선택해야, 분포 간 차이를 하나의 수치로 요약할 수 있다.
- 따라서 총분산거리의 정의에는 최대값(max)이 필수적이다.
정리
\[TV(P_\theta, P_{\theta'}) = \max_{A \subseteq E} |P_\theta(A) - P_{\theta'}(A)|\]
이는 두 분포가 어떤 사건에 대해 줄 수 있는 최대 확률 차이를 의미한다.
- $\theta^{*}$는 optimal 모수로, 참 모수(true parameter)와 동일하게 취급한다.
- $X \sim P_\theta$는 “distributed as”를 뜻한다.
- $\hat{\theta}$는 표본으로부터 모수를 추정하는 추정량(estimator)이다.
- $A \subset E$ 전체를 고려하는 정의는 수학적으로는 잘 정의되지만, 실제로는 고차원에서 모든 사건을 비교하는 것이 불가능할 수 있다.
- 결국 우리가 평가하는 것은, 확률측도 $P$ 위에서 추정량 $\hat{\theta}$가 최적 모수 $\theta^*$에 얼마나 가까운지를 측정하는 것이다.
p4. 총분산거리(TV)
$E$가 연속형 공간이라고 가정하자. (예: Gaussian, Exponential 등)
$X$가 모든 $A \subset E$에 대해 밀도 $P_{\theta}(X \in A) = \int_{A} f_{\theta}(x)\, dx$ 를 가진다고 가정하자.
\[f_{\theta}(x) \geq 0, \quad \int_{E} f_{\theta}(x)\, dx = 1\]두 확률측도 $P_{\theta}$와 $P_{\theta’}$ 사이의 총분산거리 (Total Variation Distance)는
밀도함수 $f_{\theta}, f_{\theta’}$의 단순한 함수이다.
3페이지와 4페이지의 총분산거리 정의가 동치임을 보이는 과정
1. 출발점: 3페이지의 정의
\[TV(P_{\theta},P_{\theta'})=\max_{A\subset E}\,|P_{\theta}(A)-P_{\theta'}(A)|\]이는 두 분포가 같은 사건 $A$에 대해 얼마나 다른 확률을 부여하는지를 측정한다.
2. 밀도를 이용한 표현 두 분포가 밀도 $f_{\theta}$, $f_{\theta’}$를 가진다면 임의의 사건 $A$에 대해
\[P_{\theta}(A)-P_{\theta'}(A)=\int_A(f_{\theta}(x)-f_{\theta'}(x))\,dx\]$g(x)=f_{\theta}(x)-f_{\theta’}(x)$라 두면
\[|P_{\theta}(A)-P_{\theta'}(A)|=\left|\int_A g(x)\,dx\right|\]3. $g$의 적분값이 0임 밀도의 적분은 1이므로
\[\int_E g(x)\,dx = \int_E f_{\theta}(x)\,dx - \int_E f_{\theta'}(x)\,dx = 1-1=0\]즉, $g$의 양의 부분 적분과 음의 부분 적분의 크기가 서로 같다.
4. 최댓값을 주는 사건 $A$의 선택
\[\max_A\left|\int_A g(x)\,dx\right|=\int_{\{g>0\}} g(x)\,dx\]
- $A={x:g(x)>0}$로 택하면 $\int_A g(x)\,dx$는 양수 방향에서 최대가 된다.
- $A={x:g(x)<0}$도 절댓값 기준으로 같은 크기를 준다. 따라서
5. 양·음 부분의 균형 관계 $g$의 양수 영역 적분과 음수 영역 적분은 크기가 동일하므로
\[\int_{\{g>0\}} g(x)\,dx =\tfrac{1}{2}\int_E |g(x)|\,dx\]6. 최종 결론 위 관계를 대입하면
\[TV(P_{\theta},P_{\theta'}) =\tfrac{1}{2}\int_E |f_{\theta}(x)-f_{\theta'}(x)|\,dx\]요약
- 3페이지 정의: “사건별 확률 차이 중 최댓값”
- 4페이지 정의: “밀도 차이의 절댓값 적분의 절반”
밀도가 존재할 때 두 정의는 완전히 동치
- 3페이지 수식의 형식을 4페이지 형식으로 단순히 변환한 것이며,
이 두 표현은 본질적으로 동일한 내용을 담고 있다.
p5. 총분산거리(TV)
총분산거리(Total Variance Distance)의 성질
대칭성 (Symmetry):
\[TV(P_{\theta}, P_{\theta'}) = TV(P_{\theta'}, P_{\theta})\]비음수성 (Non-negativity):
\[TV(P_{\theta}, P_{\theta'}) \geq 0\]확정성 (Definiteness):
\[TV(P_{\theta}, P_{\theta'}) = 0 \quad \Rightarrow \quad P_{\theta} = P_{\theta'}\]삼각 부등식 (Triangle inequality):
\[TV(P_{\theta}, P_{\theta'}) \leq TV(P_{\theta}, P_{\theta''}) + TV(P_{\theta''}, P_{\theta'})\]
이것은 총분산거리(Total Variation Distance)가 확률분포들 사이의 하나의 거리(distance) 라는 것을 의미한다.
1. 확정성(Definiteness)
총분산거리 $TV(P_{\theta},P_{\theta’})=0$ 이라는 것은
\[\max_{A\subset E}\,|P_{\theta}(A)-P_{\theta'}(A)|=0\]를 의미한다.
즉, 모든 사건 $A$에 대해
\[P_{\theta}(A)=P_{\theta'}(A)\]가 성립해야 한다.
- 두 분포가 조금이라도 다르다면 어떤 사건에서는 반드시 확률이 다르게 할당되므로, 최대 차이가 0이 되는 일은 없다.
따라서
\[TV(P_{\theta},P_{\theta'})=0 \;\Leftrightarrow\; P_{\theta}=P_{\theta'}\]총분산거리는 두 분포가 동일할 때에만 0이 되는 “거리(metric)”의 확정성 조건을 만족한다.
2. 삼각부등식(Triangle inequality)
임의의 세 분포 $P_{\theta},P_{\theta’},P_{\theta’’}$에 대해
\[TV(P_{\theta},P_{\theta'})\;\le\; TV(P_{\theta},P_{\theta''})+TV(P_{\theta''},P_{\theta'})\]가 성립한다.
- 이는 “분포 간의 직접 거리”가 “중간 분포를 경유했을 때의 경로 길이”보다 항상 크지 않다는 뜻이다.
- 유클리드 공간에서 세 점이 이루는 삼각형에서
한 변의 길이가 다른 두 변의 합보다 작거나 같은 것과 동일한 구조이다.- 삼각부등식이 성립함으로써 총분산거리는 단순한 유사도 척도를 넘어
수학적으로 타당한 거리(metric)로 기능할 수 있다.
p6. 총분산거리(TV): 예시(1/2)
두 정규분포와 정의
\[f_{\theta} = \mathcal{N}(\mu_{1}, \sigma^{2})\] \[f_{\theta'} = \mathcal{N}(\mu_{2}, \sigma^{2})\]평균 차이와 기준점
\[\Delta = |\mu_{1} - \mu_{2}|\] \[m = \frac{(\mu_{1} + \mu_{2})}{2}\]수식 전개 과정
\[TV(P_{\theta}, P_{\theta'}) = \frac{1}{2} \int_{-\infty}^{\infty} | f_{\mu_{1}}(x) - f_{\mu_{2}}(x) | \, dx\] \[= \frac{1}{2} \left( \int_{-\infty}^{m} (f_{\mu_{2}}(x) - f_{\mu_{1}}(x)) dx + \int_{m}^{\infty} (f_{\mu_{1}}(x) - f_{\mu_{2}}(x)) dx \right)\] \[= \int_{-\infty}^{m} f_{\mu_{1}}(x) dx - \int_{-\infty}^{m} f_{\mu_{2}}(x) dx\] \[= \frac{1}{\sqrt{2\pi}\sigma} \left[ \int_{-\infty}^{m} \exp\left(-\frac{(x-\mu_{1})^{2}}{2\sigma^{2}}\right) dx - \int_{-\infty}^{m} \exp\left(-\frac{(x-\mu_{2})^{2}}{2\sigma^{2}}\right) dx \right]\] \[= \frac{1}{\sqrt{2\pi}} \left[ \int_{-\infty}^{\frac{m-\mu_{1}}{\sigma}} e^{-t^{2}/2} dt - \int_{-\infty}^{\frac{m-\mu_{2}}{\sigma}} e^{-t^{2}/2} dt \right]\] \[= \frac{1}{\sqrt{2\pi}} \left[ \int_{-\Delta/(2\sigma)}^{0} e^{-t^{2}/2} dt - \int_{-\infty}^{-\Delta/(2\sigma)} e^{-t^{2}/2} dt \right]\] \[= \frac{1}{\sqrt{2\pi}} \int_{-\Delta/(2\sigma)}^{\Delta/(2\sigma)} e^{-t^{2}/2} dt\] \[= \frac{2}{\sqrt{2\pi}} \int_{0}^{\Delta/(2\sigma)} e^{-t^{2}/2} dt\]1. 두 분포의 가정
같은 분산을 갖는 두 정규분포:
\[f_{\theta}=\mathcal{N}(\mu_1,\sigma^2),\qquad f_{\theta'}=\mathcal{N}(\mu_2,\sigma^2)\]기호 정리:
\[\Delta=\mu_1-\mu_2>0,\qquad m=\frac{\mu_1+\mu_2}{2}\]즉, 두 분포는 모양(분산)은 같고 중심(평균)만 다르다.
2. 적분 구간 나누기 (절댓값 처리)
총분산거리:
\[TV(P_{\theta},P_{\theta'}) =\tfrac12\int_{-\infty}^{\infty}|f_{\mu_1}(x)-f_{\mu_2}(x)|\,dx\]교차점 $m$을 기준으로 절댓값 제거:
\[=\tfrac12\left[ \int_{-\infty}^{m}(f_{\mu_1}-f_{\mu_2})\,dx + \int_{m}^{\infty}(f_{\mu_2}-f_{\mu_1})\,dx \right]\]$m$보다 작은 구간에서는 $f_{\mu_1}\ge f_{\mu_2}$, 큰 구간에서는 그 반대이므로 절댓값이 제거된다.
3. CDF 성질을 이용한 중간 정리
pdf의 적분은 항상 1:
\[\int_{m}^{\infty}f_{\mu_i}(x)\,dx =1-\int_{-\infty}^{m}f_{\mu_i}(x)\,dx\]이를 이용해 정리하면:
\[TV =\int_{m}^{\infty}f_{\mu_1}(x)\,dx -\int_{m}^{\infty}f_{\mu_2}(x)\,dx\]4. 정규분포 밀도 대입
\[TV =\frac{1}{\sqrt{2\pi}\sigma}\left[ \int_{m}^{\infty}\exp\!\Big(-\tfrac{(x-\mu_{1})^{2}}{2\sigma^{2}}\Big)\,dx - \int_{m}^{\infty}\exp\!\Big(-\tfrac{(x-\mu_{2})^{2}}{2\sigma^{2}}\Big)\,dx \right]\]5. 변수 치환을 통한 표준화(및 σ 약분)
치환: $t=\frac{x-\mu_i}{\sigma}$, $dx=\sigma\,dt$
\[\frac{1}{\sqrt{2\pi}}\int_{\frac{m-\mu_i}{\sigma}}^{\infty}e^{-t^2/2}\,dt\]따라서:
\[TV =\frac{1}{\sqrt{2\pi}}\left[ \int_{\frac{m-\mu_{1}}{\sigma}}^{\infty}e^{-t^{2}/2}\,dt - \int_{\frac{m-\mu_{2}}{\sigma}}^{\infty}e^{-t^{2}/2}\,dt \right]\]6. 적분 구간 변환
항등식:
\[\int_{a}^{\infty}g(t)\,dt-\int_{b}^{\infty}g(t)\,dt =\int_{a}^{b}g(t)\,dt\]적용:
\[TV =\frac{1}{\sqrt{2\pi}} \int_{\frac{m-\mu_{1}}{\sigma}}^{\frac{m-\mu_{2}}{\sigma}} e^{-t^{2}/2}\,dt\]7. 중점 치환 ($\mu_1>\mu_2$)
계산:
\[m-\mu_1=-\frac{\Delta}{2},\qquad m-\mu_2=\frac{\Delta}{2}\]따라서:
\[TV =\frac{1}{\sqrt{2\pi}} \int_{-\Delta/(2\sigma)}^{\Delta/(2\sigma)}e^{-t^{2}/2}\,dt\]8. 최종 간단화(짝함수 이용)
\[TV(P_{\theta},P_{\theta'}) =\frac{2}{\sqrt{2\pi}} \int_{0}^{\Delta/(2\sigma)}e^{-t^{2}/2}\,dt\]
p7. 총분산거리(TV): 예시(2/2)
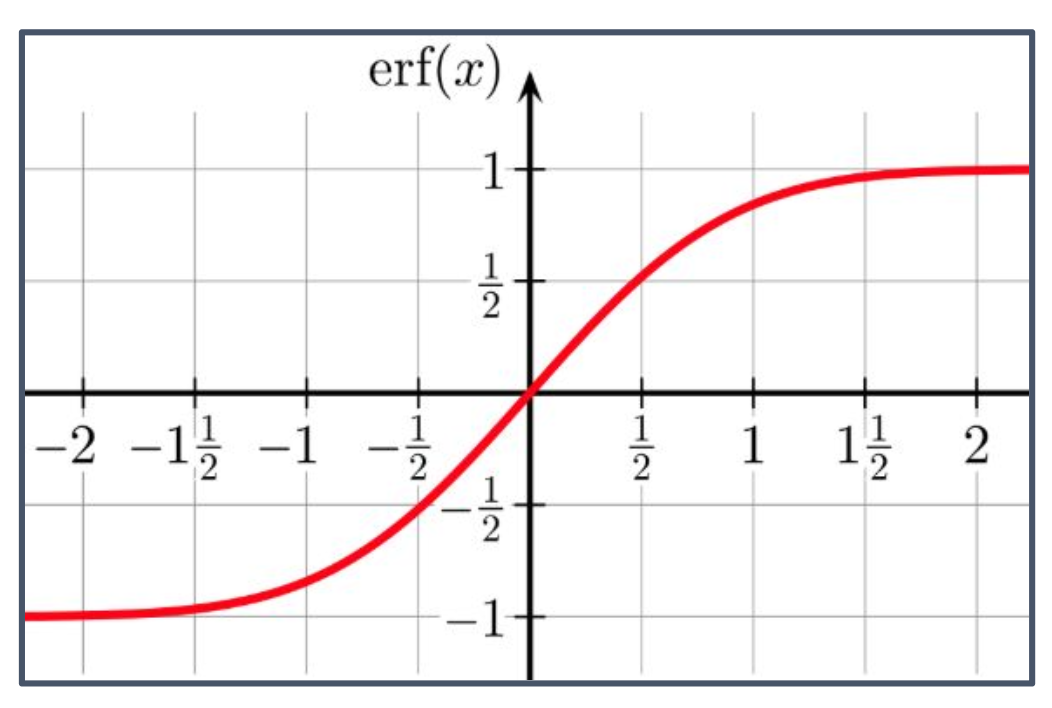
\[TV(P_{\theta}, P_{\theta'}) = \frac{2}{\sqrt{2\pi}} \int_{0}^{\Delta/(2\sigma)} e^{-t^{2}/2}\, dt\] \[= \frac{2}{\sqrt{2\pi}} \sqrt{2} \int_{0}^{\Delta/(2\sqrt{2}\sigma)} e^{-u^{2}}\, du\] \[= \frac{2}{\sqrt{\pi}} \int_{0}^{\Delta/(2\sqrt{2}\,\sigma)} e^{-u^{2}}\, du\] \[= \operatorname{erf}\!\left(\frac{\Delta}{2\sqrt{2}\,\sigma}\right)\]\[\operatorname{erf}(x) = \frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-t^{2}}\, dt\] \[\operatorname{erfc}(x) = 1 - \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} e^{-t^{2}}\, dt.\]
1. 수식 전개 내역 (p7)
정의
\[TV(P_{\theta},P_{\theta'})=\frac{2}{\sqrt{2\pi}}\int_{0}^{\Delta/(2\sigma)} e^{-t^{2}/2}\,dt\]\[u=\frac{t}{\sqrt{2}},\quad t=\sqrt{2}\,u,\quad dt=\sqrt{2}\,du,\] \[t=0\Rightarrow u=0,\;\; t=\frac{\Delta}{2\sigma}\Rightarrow u=\frac{\Delta}{2\sqrt{2}\,\sigma}.\]
- 지수를 $e^{-u^{2}}$ 꼴로 만들기 위해 스케일 치환을 한다.
\[\begin{aligned} TV &=\frac{2}{\sqrt{2\pi}}\int_{0}^{\Delta/(2\sigma)} e^{-t^{2}/2}\,dt \\ &=\frac{2}{\sqrt{2\pi}}\int_{0}^{\Delta/(2\sqrt{2}\sigma)} e^{-(\sqrt{2}u)^{2}/2}\,(\sqrt{2}\,du) \\ &=\frac{2}{\sqrt{2\pi}}\sqrt{2}\int_{0}^{\Delta/(2\sqrt{2}\sigma)} e^{-u^{2}}\,du \\ &=\frac{2}{\sqrt{\pi}}\int_{0}^{\Delta/(2\sqrt{2}\sigma)} e^{-u^{2}}\,du. \end{aligned}\]
- 전개
예시
\[\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-t^{2}}\,dt \quad\Rightarrow\quad TV=\operatorname{erf}\!\Big(\frac{\Delta}{2\sqrt{2}\,\sigma}\Big).\]정리
\[TV(P_{\theta},P_{\theta'})=\operatorname{erf}\!\Big(\frac{\Delta}{2\sqrt{2}\,\sigma}\Big),\]
- 즉 $TV$는 $\Delta/\sigma$만의 함수이며 단조 증가한다.
2. $\operatorname{erf}$의 홀함수 성질
정의
\[\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-t^{2}}\,dt.\]
- 적분함수 $e^{-t^{2}}$는 양수·짝함수지만, 적분 한계가 $0 \to x$이므로 전체 함수는 홀함수가 된다.
정리
\[\begin{aligned} \operatorname{erf}(-x) &=\frac{2}{\sqrt{\pi}}\int_{0}^{-x} e^{-t^{2}}\,dt \quad(t=-u,\,dt=-du) \\ &= -\frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-u^{2}}\,du = -\operatorname{erf}(x). \end{aligned}\]
- 따라서 $x<0\Rightarrow \operatorname{erf}(x)<0$, $\operatorname{erf}(0)=0$, $x>0\Rightarrow \operatorname{erf}(x)>0$
p8. KL 발산
쿨백–라이블러(Kullback–Leibler, KL) 발산
확률측도 사이의 거리는 여러 가지가 있다. 총분산거리(total variation)를 대체할 수 있는 것들 중에서, 여기서는 다루기 더 편한 하나를 선택한다.
정의
두 확률측도 \(\mathbb{P}_\theta\)와 \(\mathbb{P}_{\theta'}\) 사이의 KL 발산은 다음과 같이 정의한다.
$E$가 이산(discrete)인 경우
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) \;=\; \sum_{x\in E} p_\theta(x)\, \log\!\left(\frac{p_\theta(x)}{p_{\theta'}(x)}\right)\]$E$가 연속(continuous)인 경우
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) \;=\; \int_E f_\theta(x)\, \log\!\left(\frac{f_\theta(x)}{f_{\theta'}(x)}\right)\,dx\]
(한 꼭지 요약) KL 발산의 의미와 직관적 이해
KL 발산은 두 확률분포가 얼마나 다른지, 즉 정보적으로 얼마나 멀리 떨어져 있는지를 재는 척도이다.
직관
한 분포 P를 근사 분포 Q로 대신 사용했을 때 평균적으로 얼마만큼의 정보 손실이 발생하는지를 나타낸다.
따라서 Q가 P를 잘 설명할수록 KL 값은 작아지고, 다를수록 커진다.비대칭성
$ \mathrm{KL}(P|Q) \neq \mathrm{KL}(Q|P) $ 이므로 대칭적 의미의 거리는 아니지만,
한 방향에서의 정보 손실량을 나타내는 지표로 사용된다.그래프 비유
P(x)와 Q(x)의 곡선이 겹칠수록 KL은 0에 가까워지고,
차이가 커질수록 로그 비율 항이 커져 KL 값이 증가한다.- 활용 예시
- 최대우도추정(MLE): 참 분포 P와 모델 분포 $Q_\theta$ 의 KL을 최소화하는 $\theta$가 최대우도해이다.
- 머신러닝·딥러닝: 변분추론, VAE, GAN 등에서 모델 분포가 실제 데이터 분포에 근접하도록 KL을 최소화한다.
- 정보이론: 한 분포를 다른 분포로 잘못 인코딩했을 때 필요한 추가 비트 수(정보 손실)로 해석된다.
- 요약
KL 발산은 한 분포를 다른 분포로 대체할 때 발생하는 평균적 정보 손실량을 수치로 보여주는 척도이다.
p9. KL 발산
KL 발산의 성질 (Properties)
비대칭성 (Asymmetry)
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) \neq \mathrm{KL}(\mathbb{P}_{\theta'},\mathbb{P}_\theta) \quad \text{(일반적으로)}\]음이 아닌 값 (Non-negativity)
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) \ge 0\]정확성/정부호성 (Definiteness)
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) = 0 \;\Rightarrow\; \mathbb{P}_\theta=\mathbb{P}_{\theta'}\]삼각부등식 불성립 (No triangle inequality)
\[\mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta'}) \not\le \mathrm{KL}(\mathbb{P}_\theta,\mathbb{P}_{\theta''}) + \mathrm{KL}(\mathbb{P}_{\theta''},\mathbb{P}_{\theta'}) \quad \text{(일반적으로)}\]
그래서 거리가 아니라 발산이라고 불림
비대칭성은 우리가 추정할 수 있는 능력의 핵심이다.
1. 비대칭성: 등호가 성립하지 않는 이유
\[\mathrm{KL}(P\|Q)=\int p(x)\log\frac{p(x)}{q(x)}\,dx\] \[\mathrm{KL}(Q\|P)=\int q(x)\log\frac{q(x)}{p(x)}\,dx\]
- 서로 다른 분포로 가중(평균)을 취하므로 일반적으로 $\mathrm{KL}(P|Q)\neq \mathrm{KL}(Q|P)$ 이다.
- 등호가 성립하려면 보통 $p=q$ (a.e.) 같은 특수한 경우여야 한다.
a.e.는 almost everywhere 라는 뜻임
2. 비음수성(Non-negativity)
\[\phi(u)=u-1-\log u \quad (u>0)\]
- 기브스 부등식 증명
\[\phi'(u)=1-\frac{1}{u}\]
- 1차 미분:
\[\phi''(u)=\frac{1}{u^2}>0\]
- 2차 미분:
\[\log u \le u-1 \quad (\text{등호는 } u=1 \text{에서만})\]
$\phi’‘(u)>0$이면 그래프는 아래로 볼록(convex)이며, 기울기 $\phi’(u)$는 계속 증가한다.
따라서 $\phi’(u)=0$이 되는 $u=1$에서 최솟값을 갖고, $\phi(1)=0$이므로 $\phi(u)\ge 0$ (등호는 $u=1$에서만).
곧,
\[\log\frac{q(x)}{p(x)} \le \frac{q(x)}{p(x)} - 1\]
비음수성 증명(부호 반전 단계 추가)
위 부등식에 $u=\frac{q(x)}{p(x)}$를 대입하면
\[-\log\frac{q(x)}{p(x)} \ge 1 - \frac{q(x)}{p(x)} \quad\Longleftrightarrow\quad \log\frac{p(x)}{q(x)} \ge 1 - \frac{q(x)}{p(x)}\]
- 양변에 -1을 곱하면 부호가 바뀌어
\[\int p(x)\log\frac{p(x)}{q(x)}\,dx \ge \int (p(x)-q(x))\,dx\]
- 이제 양변에 $p(x)$를 곱해 적분하면
\[\int (p(x)-q(x))\,dx = \int p(x)\,dx - \int q(x)\,dx = 1-1 = 0\]
- 오른쪽은 확률밀도의 총질량이 1이므로
\[\mathrm{KL}(P\|Q)=\int p(x)\log\frac{p(x)}{q(x)}\,dx \ge 0,\]
- 따라서
- 등호는 거의 어디서나(a.e.) $p(x)=q(x)$일 때만 성립한다.
3. 정확성/정부호성(Definiteness)
- $\mathrm{KL}(P|Q)=0 \Longleftrightarrow p(x)=q(x)$ (a.e.).
- 위 기브스 부등식의 등호 조건이 $u\equiv 1$일 때뿐이므로 $q/p\equiv 1 \Rightarrow p=q$ (거의 어디서나).
4. 삼각부등식 불성립(No triangle inequality)
- KL은 한쪽 분포로 가중된 비대칭 발산이라 일반적으로
$\mathrm{KL}(P|R)\le \mathrm{KL}(P|Q)+\mathrm{KL}(Q|R)$ 가 성립하지 않는다.5. 결론: 거리(distance)가 아니라 발산(divergence)
- KL은 (i) 비음수, (ii) $=0\Rightarrow P=Q$ 는 만족하지만 (iii) 대칭이 아니고
(iv) 삼각부등식도 불성립한다.- 따라서 수학적 의미의 거리(metric)가 아니라 발산(divergence)이다.
p10. KL 발산: 예시(1/2)
두 정규분포와 가정
\[f_{\theta} = \mathcal{N}(\mu_{1}, \sigma^{2})\] \[f_{\theta'} = \mathcal{N}(\mu_{2}, \sigma^{2})\]평균 차이와 기준점
\[\Delta = |\mu_{1} - \mu_{2}|\] \[m = \frac{\mu_{1} + \mu_{2}}{2}\]수식 전개 과정
\[\mathrm{KL}(\mathbb{P}_{\theta}\,\|\,\mathbb{P}_{\theta'}) = \int_{\mathbb{R}} \log\!\left(\frac{d\mathbb{P}_{\theta}}{d\mathbb{P}_{\theta'}}(x)\right)\, d\mathbb{P}_{\theta}(x)\] \[= \int_{\mathbb{R}} f_{\theta}(x)\, \log\!\left(\frac{f_{\theta}(x)}{f_{\theta'}(x)}\right)\, dx\] \[= \int_{\mathbb{R}} f_{\theta}(x)\, \frac{(x-\mu_{2})^{2} - (x-\mu_{1})^{2}}{2\sigma^{2}}\, dx\] \[= \frac{1}{2\sigma^{2}} \int_{\mathbb{R}} f_{\theta}(x)\, \big[(x-\mu_{2})^{2} - (x-\mu_{1})^{2}\big]\, dx\]1. 두 분포의 가정
\[f_{\theta}=\mathcal{N}(\mu_{1},\sigma^{2}),\qquad f_{\theta'}=\mathcal{N}(\mu_{2},\sigma^{2})\]
- 정의
같은 분산을 갖는 두 정규분포:\[\Delta=\mu_{1}-\mu_{2},\qquad m=\frac{\mu_{1}+\mu_{2}}{2}\]
- 표현식
2. KL 정의 → 밀도형식으로 바꾸기
\[\mathrm{KL}(\mathbb{P}_{\theta}\,\|\,\mathbb{P}_{\theta'}) = \int \log\!\left(\frac{d\mathbb{P}_{\theta}}{d\mathbb{P}_{\theta'}}(x)\right)\, d\mathbb{P}_{\theta}(x)\] \[= \int f_{\theta}(x)\,\log\frac{f_{\theta}(x)}{f_{\theta'}(x)}\,dx.\]
- 표현식
- 설명
연속형에서 $d\mathbb{P}(x)=f(x)\,dx$ 로 쓸 수 있어 밀도비(log-density ratio) 형태로 정리된다.3. 정규 pdf 대입 & 상수 소거
\[f_{\mu}(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\!\left(-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right),\] \[\log f_{\mu}(x)= -\frac{1}{2}\log(2\pi\sigma^{2})-\frac{(x-\mu)^{2}}{2\sigma^{2}}.\]
- 대입
\[\log\frac{f_{\mu_{1}}(x)}{f_{\mu_{2}}(x)} = \frac{(x-\mu_{2})^{2}-(x-\mu_{1})^{2}}{2\sigma^{2}}.\]
- 같은 $\sigma$ 이므로 정규화상수는 소거되어
4. KL 전개 연결
\[\mathrm{KL}(\mathbb{P}_{\theta}\,\|\,\mathbb{P}_{\theta'}) = \int f_{\theta}(x)\,\log\frac{f_{\theta}(x)}{f_{\theta'}(x)}\,dx\] \[= \int f_{\theta}(x)\,\frac{(x-\mu_{2})^{2}-(x-\mu_{1})^{2}}{2\sigma^{2}}\,dx\] \[= \frac{1}{2\sigma^{2}}\!\int f_{\theta}(x)\,\big[(x-\mu_{2})^{2}-(x-\mu_{1})^{2}\big]\,dx.\]
- 표현식
- 자연 현상은 최대엔트로피 원리와 확산·열 등 미분방정식의 해 때문에 지수꼴 분포가 자주 나타난다.
- KL에서 로그를 사용하면 곱이 합으로 바뀌고 밀도비의 정규화상수가 소거되어 계산이 단순해진다.
- 두 가우시안의 KL에서는 지수항이 사라져 이차식 차이만 남고 평균 성질을 이용해 쉽게 적분된다.
- 동일 분산인 경우 KL은 평균 차이의 제곱에 비례하는 단순한 닫힌형식이 되어 실전 계산이 수월하다.
p11. KL 발산: 예시(2/2)
\[\mathrm{KL}(\mathbb{P}_{\theta}\,\|\,\mathbb{P}_{\theta'}) = \frac{1}{2\sigma^{2}} \int_{\mathbb{R}} f_{\theta}(x)\,\big[2(\mu_{1}-\mu_{2})x+\mu_{2}^{2}-\mu_{1}^{2}\big]\,dx\] \[= \frac{1}{2\sigma^{2}} \left[ 2(\mu_{1}-\mu_{2})\int_{\mathbb{R}} x\,f_{\theta}(x)\,dx \;+\; (\mu_{2}^{2}-\mu_{1}^{2})\int_{\mathbb{R}} f_{\theta}(x)\,dx \right]\] \[= \frac{1}{2\sigma^{2}}\big[\,2(\mu_{1}-\mu_{2})\mu_{1}+(\mu_{2}^{2}-\mu_{1}^{2})\,\big]\] \[= \frac{(\mu_{1}-\mu_{2})^{2}}{2\sigma^{2}} = \frac{\Delta^{2}}{2\sigma^{2}}\]1. 제곱 전개
\[\log\frac{f_{\mu_1}(x)}{f_{\mu_2}(x)} = \frac{(x-\mu_2)^2-(x-\mu_1)^2}{2\sigma^2}.\]
- 출발식
\[(x-\mu_2)^2-(x-\mu_1)^2\] \[= (x^2-2\mu_2 x+\mu_2^2)-(x^2-2\mu_1 x+\mu_1^2)\] \[= 2(\mu_1-\mu_2)x+(\mu_2^2-\mu_1^2).\]
- 전개(직접 전개)
2. KL에 대입
\[\mathrm{KL}(\mathbb{P}_{\theta}\|\mathbb{P}_{\theta'}) = \int_{\mathbb{R}} f_{\theta}(x)\, \log\frac{f_{\mu_1}(x)}{f_{\mu_2}(x)}\,dx\] \[= \frac{1}{2\sigma^{2}} \int_{\mathbb{R}} f_{\theta}(x)\, \big[2(\mu_{1}-\mu_{2})x+\mu_{2}^{2}-\mu_{1}^{2}\big]\,dx.\]
- 표현식
3. 적분의 선형성(상수 인출, 항별 분리)
\[= \frac{1}{2\sigma^{2}} \left\{ 2(\mu_{1}-\mu_{2})\!\int_{\mathbb{R}} x\,f_{\theta}(x)\,dx + (\mu_{2}^{2}-\mu_{1}^{2})\!\int_{\mathbb{R}} f_{\theta}(x)\,dx \right\}.\]4. 평균과 전체질량 사용
\[\int_{\mathbb{R}} f_{\theta}(x)\,dx = 1,\qquad \int_{\mathbb{R}} x\,f_{\theta}(x)\,dx = \mu_{1}\]
- 사실 $f_{\theta}=\mathcal{N}(\mu_1,\sigma^2)$ 이므로
\[= \frac{1}{2\sigma^{2}} \Big[\,2(\mu_{1}-\mu_{2})\mu_{1}+(\mu_{2}^{2}-\mu_{1}^{2})\,\Big]\]
- 대입
5. 대수 정리(단순화)
\[2(\mu_{1}-\mu_{2})\mu_{1}+(\mu_{2}^{2}-\mu_{1}^{2})\] \[= \mu_1^2-2\mu_1\mu_2+\mu_2^2 = (\mu_1-\mu_2)^2\]6. 최종식
\[\mathrm{KL}(\mathbb{P}_{\theta}\|\mathbb{P}_{\theta'}) = \frac{(\mu_{1}-\mu_{2})^{2}}{2\sigma^{2}} = \frac{\Delta^{2}}{2\sigma^{2}},\qquad \Delta=|\mu_{1}-\mu_{2}|\]
p12. MLE
Maximum Likelihood Estimation
\[\mathrm{KL}(\mathbb{P}_{\theta^\ast}, \mathbb{P}_\theta) = \mathbb{E}_{\theta^\ast}\!\left[\log \frac{p_{\theta^\ast}(X)}{p_\theta(X)}\right]\] \[= \mathbb{E}_{\theta^\ast}[\log p_{\theta^\ast}(X)] \;-\; \mathbb{E}_{\theta^\ast}[\log p_\theta(X)]\]따라서 함수 \(\theta \mapsto \mathrm{KL}(\mathbb{P}_{\theta^\ast}, \mathbb{P}_\theta)\)는 다음 형태이다:
\[\text{“constant”} \;-\; \mathbb{E}_{\theta^\ast}[\log p_\theta(X)]\]대수의 법칙(LLN)에 의해 다음과 같이 추정할 수 있다.
\[\mathbb{E}_{\theta^\ast}[h(X)] \;\sim\; \frac{1}{n}\sum_{i=1}^{n} h(X_i)\] \[\widehat{\mathrm{KL}}(\mathbb{P}_{\theta^\ast}, \mathbb{P}_\theta) = \text{“constant”} \;-\; \frac{1}{n}\sum_{i=1}^{n}\log p_\theta(X_i)\]1. 왜 $\mathbb{E}_{\theta^\ast}[\cdot]$ 인가? (KL의 가중 분포)
\[\mathrm{KL}(P\|Q) = \int \log\left(\frac{dP}{dQ}\right)\, dP\]
- 정의
KL 발산은 첫 번째 분포로 가중한 평균이다.즉, 괄호 안의 로그 비율 함수를 P에 대한 기대값(평균)으로 본다.
\[\mathrm{KL}(\mathbb{P}_{\theta^\ast}\,\|\,\mathbb{P}_{\theta}) = \int p_{\theta^\ast}(x)\,\log\frac{p_{\theta^\ast}(x)}{p_\theta(x)}\,dx = \mathbb{E}_{\theta^\ast}\!\left[\log\frac{p_{\theta^\ast}(X)}{p_\theta(X)}\right]\]
- 밀도함수 표현
만약 $P_\theta$가 밀도 $p_\theta(x)$를 가진다면,따라서 KL은 “참 분포” $\mathbb{P}_{\theta^\ast}$ 에 따라 표본이 생성되고, 그 표본을 기준으로 로그 비율을 평균낸 값이다.
2. \(\mathbb{E}_{\theta^\ast}[\log p_{\theta^\ast}(X)]\) 는 상수인 이유
- 항 \(\mathbb{E}_{\theta^\ast}[\log p_{\theta^\ast}(X)]\) 은
\(\theta^\ast\) 로 고정된 분포에서 계산되므로
최적화 변수 $\theta$ 에 의존하지 않는다.
따라서 $\theta$ 에 대해 상수항이다.3. 대수의 법칙(LLN)에 따른 기대값의 근사
\[\mathbb{E}_{\theta^\ast}[h(X)] \approx \frac{1}{n}\sum_{i=1}^n h(X_i)\]
- 일반적으로 분포의 기대값은 직접 계산하기 어렵기 때문에
샘플 $X_1,\dots,X_n$ 으로 다음과 같이 근사한다.
KL 분해식의 경우
\(h(X) = \log p_\theta(X)\) 이 되어, 로그우도의 평균을 계산하는 과정이 된다.이를 KL 분해식에 적용하면
두 번째 항 \(\mathbb{E}_{\theta^\ast}[\log p_\theta(X)]\) 를
표본 평균으로 대체할 수 있다.4. $\widehat{\mathrm{KL}}$ 의 의미 (추정량의 역할)
\[\frac{1}{n}\sum_{i=1}^{n}\log p_\theta(X_i)\]
실제 데이터에서는 참분포 \(\mathbb{P}_{\theta^\ast}\) 를 알 수 없으므로
\(\mathbb{E}_{\theta^\ast}[\log p_\theta(X)]\) 를 직접 계산할 수 없다.따라서 관측된 표본을 이용한 경험적 평균
으로 대체하여 KL을 근사한다.
\[\widehat{\mathrm{KL}}(\mathbb{P}_{\theta^\ast}, \mathbb{P}_\theta) = \text{constant} - \frac{1}{n}\sum_{i=1}^{n}\log p_\theta(X_i)\]
- 이렇게 얻은 값이
이며, 이를 최소화하는 것이 최대우도추정(MLE)이다.
- 즉, KL 발산을 직접 구하기 어려울 때
로그우도의 표본 평균을 통해 KL을 추정하는 방식이
MLE의 핵심 아이디어이다.
p13. 함수의 최대화/최소화
다음 동치가 성립한다.
\[\min_{\theta\in\Theta}\big(-h(\theta)\big)\;\Longleftrightarrow\;\max_{\theta\in\Theta} h(\theta).\] \[\Downarrow\]이 수업에서는 최대화에 초점을 맞춘다.
\[\arg\min_{\theta\in\Theta}\!\left(\,-\sum_{i=1}^{n}\log p_{\theta}(x_i)\right) \;\Longleftrightarrow\; \arg\max_{\theta\in\Theta}\sum_{i=1}^{n}\log p_{\theta}(x_i).\]
- 수학에서는 음의 부호가 붙은 최소화 문제를 동치인 최대화 문제로 바꾸어 다루는 편이 더 단순해 선호된다.
- 학습은 목적함수를 최대화하여 최적의 매개변수 $\theta$를 찾는 과정이다.
p14. 단변수 함수의 최대화/최소화
정의
두 번 미분 가능한 함수 $h:\Theta\subset\mathbb{R}\to\mathbb{R}$가 다음을 만족하면 concave (오목) 라고 한다:
\[h''(\theta)\le 0,\quad \forall\,\theta\in\Theta.\]부등식이 엄격하면 strictly concave (엄격히 오목) 라고 한다:
\[h''(\theta)<0.\]또한 $-h$가 (strictly) concave이면 $h$를 (strictly) convex라 하며, 이는 곧.
\[h''(\theta)\ge 0\ \big(h''(\theta)>0\big).\]예시
- $\Theta=\mathbb{R},\quad h(\theta)=-\theta^{2}$
- $\Theta=(0,\infty),\quad h(\theta)=\sqrt{\theta}$
- $\Theta=(0,\infty),\quad h(\theta)=\log\theta$
- $\Theta=[0,\pi],\quad h(\theta)=\sin\theta$
- $\Theta=\mathbb{R},\quad h(\theta)=2\theta-3$
1. concave(오목)의 정의와 직관
- 두 번 미분 가능한 함수 $h:\Theta\to\mathbb{R}$ 가 $h’’(\theta)\le 0$ 를 만족하면 concave라 한다.
- $h’’(\theta)<0$ 이면 strictly concave라 한다.
- 직관적으로, 임의의 점에서의 접선은 그래프 위쪽에 있고, 두 점을 이은 현은 그래프 아래에 놓인다.
2. 판별법(실무용)
- 정의역 $\Theta$ 에서 $h’’(\theta)$ 를 계산하여 $\le 0$(또는 $<0$)인지 확인한다.
- 선형함수는 $h’’(\theta)=0$ 이므로 concave이면서 convex이기도 하다.
3. 최적화와의 관계
- concave 함수에서 임계점 $h’(\theta)=0$ 은 전역 최댓값이 된다.
- strictly concave이면 그 전역 최댓값은 유일하다.
4. 예시 확인
$h(\theta)=-\theta^2$ (정의역 $\mathbb{R}$): $h’’(\theta)=-2<0$ 이므로 strictly concave.
$h(\theta)=\sqrt{\theta}$ (정의역 $(0,\infty)$): $h’’(\theta)=-\tfrac{1}{4}\theta^{-3/2}<0$ 이므로 strictly concave.
$h(\theta)=\log\theta$ (정의역 $(0,\infty)$): $h’’(\theta)=-\theta^{-2}<0$ 이므로 strictly concave.
$h(\theta)=\sin\theta$ (정의역 $[0,\pi]$): $h’’(\theta)=-\sin\theta\le 0$ 이므로 concave(열린 구간에서는 strictly).
$h(\theta)=2\theta-3$ (정의역 $\mathbb{R}$): $h’’(\theta)=0$ 이므로 선형이며 concave이면서 convex.
5. 정의역 주의
- concavity는 정의역에 따라 달라질 수 있다. 예: $\sin\theta$ 는 $[0,\pi]$ 에서는 concave이지만 다른 구간에서는 그렇지 않을 수 있다.
목적함수가 (strictly) convex이면 모든 국소 최소점이 전역 최소점이며, strictly convex일 때 전역 최소해는 유일하다.
적절한 조건에서 gradient descent는 그 전역 최소해로 수렴한다.$h’’(\theta)<0$ 이면 concave(∩ 모양),
$h’’(\theta)>0$ 이면 convex(∪ 모양)이다.실제 문제에서는 $h(\theta)$ 의 이차 미분이 복잡하거나 존재하지 않을 수 있다. 이때는 1차 정보(기울기)만 쓰는 방법, 서브그래디언트,
또는 알려진 볼록/오목 성질을 활용하는 편이 실용적이다.
p15. 다변수 함수의 최대화/최소화
더 일반적으로 다변수 함수에 대해:
$h:\Theta\subset\mathbb{R}^{d}\to\mathbb{R}$, $d\ge 2$ 에 대하여 다음을 정의한다.
그래디언트 벡터 (gradient vector)
\[\nabla h(\theta)= \begin{pmatrix} \dfrac{\partial h}{\partial \theta_{1}}(\theta)\\[2pt] \vdots\\[2pt] \dfrac{\partial h}{\partial \theta_{d}}(\theta) \end{pmatrix} \in \mathbb{R}^{d}\]헤시안 행렬 (Hessian matrix)
\[\nabla^{2}h(\theta)= \begin{pmatrix} \dfrac{\partial^{2}h}{\partial \theta_{1}\partial \theta_{1}}(\theta) & \cdots & \dfrac{\partial^{2}h}{\partial \theta_{1}\partial \theta_{d}}(\theta)\\ \vdots & \ddots & \vdots\\ \dfrac{\partial^{2}h}{\partial \theta_{d}\partial \theta_{1}}(\theta) & \cdots & \dfrac{\partial^{2}h}{\partial \theta_{d}\partial \theta_{d}}(\theta) \end{pmatrix} \in \mathbb{R}^{d\times d}\]
concave/strictly concave의 조건
\[h\ \text{is concave}\ \Longleftrightarrow\ x^{\top}\!\nabla^{2}h(\theta)\,x \le 0,\quad \forall x\in\mathbb{R}^{d},\ \theta\in\Theta.\] \[h\ \text{is strictly concave}\ \Longleftrightarrow\ x^{\top}\!\nabla^{2}h(\theta)\,x < 0,\quad \forall x\in\mathbb{R}^{d},\ \theta\in\Theta.\]예시
- $\Theta=\mathbb{R}^{2},\; h(\theta)=-\theta_{1}^{2}-2\theta_{2}^{2}$ 또는 $h(\theta)=-(\theta_{1}-\theta_{2})^{2}$
- $\Theta=(0,\infty),\; h(\theta)=\log(\theta_{1}+\theta_{2})$
1. 그래디언트·헤시안과 방향 도함수
\[g(t) = h(\theta + t x)\]
준비: 변수와 방향
우리는 스칼라 값을 출력하는 다변수 함수 $h:\mathbb{R}^d \to \mathbb{R}$ 를 생각한다.
입력은 $d$-차원 벡터 $\theta=(\theta_1,\dots,\theta_d)$ 이다.
방향 벡터 $x=(x_1,\dots,x_d)$ 를 잡고, “점 $\theta$ 에서 방향 $x$ 로 움직일 때 함수 값은 어떻게 변하는가?”를 본다.방향 미분을 왜 하는가?
다변수 함수는 모든 방향에서 변화하므로 특정 방향 $x$ 를 골라 1변수 함수처럼 절단해 이해한다.
이것이 방향 도함수이다.방향 함수 정의
\[g'(t) = \frac{d}{dt}h(\theta+tx) = \sum_{i=1}^d \frac{\partial h}{\partial \theta_i}(\theta+tx)\, x_i = \nabla h(\theta+tx)\cdot x\]
- 1차 미분: 방향 기울기
\[\nabla h(\theta)= \begin{bmatrix} \frac{\partial h}{\partial \theta_1} \\ \vdots \\ \frac{\partial h}{\partial \theta_d} \end{bmatrix}\]
- 그래디언트
내적 $\nabla h(\theta)\cdot x$ 는 “방향 $x$ 로 본 순간 기울기”이다.
\[g''(t) = \frac{d}{dt}\big(\nabla h(\theta+tx)\cdot x\big)\] \[= \sum_{i=1}^d \sum_{j=1}^d \frac{\partial^2 h}{\partial \theta_j \partial \theta_i}(\theta+tx)\, x_i x_j\]
- 2차 미분: 방향 곡률
\[\nabla^2 h(\theta)= \begin{bmatrix} \frac{\partial^2 h}{\partial \theta_1^2} & \cdots & \frac{\partial^2 h}{\partial \theta_1\partial\theta_d} \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 h}{\partial \theta_d\partial\theta_1} & \cdots & \frac{\partial^2 h}{\partial \theta_d^2} \end{bmatrix}\]
- 헤시안 정의
\[g''(t) = x^\top \nabla^2 h(\theta+tx)\, x,\qquad g''(0)=x^\top \nabla^2 h(\theta)x\]
- 따라서
- 요약
$\nabla h$: 축 방향 기울기
$\nabla h\cdot x$: 방향 기울기
$\nabla^2 h$: 축·쌍방향 곡률
$x^\top\nabla^2h\,x$: 방향 $x$ 의 곡률2. concave / strictly concave와 방향 2차 도함수의 관계
\[x^\top \nabla^2 h(\theta)x \le 0 \quad\Rightarrow\quad \text{concave}\] \[x^\top \nabla^2 h(\theta)x < 0 \quad\Rightarrow\quad \text{strictly concave}\]
- 정의
의미
$x^\top\nabla^2 h(\theta)x$ 는 방향 $x$ 로 본 단면의 곡률.
concave는 모든 방향에서 곡률이 0 이하.정리
strictly concave이면 항상 음의 곡률이며 극댓값이 유일.3. 예시 해석
\[h(\theta)=-\theta_1^2 - 2\theta_2^2\] \[\nabla^2 h= \begin{bmatrix} -2 & 0 \\ 0 & -4 \end{bmatrix}\] \[x^\top \nabla^2 h x = -2x_1^2 - 4x_2^2 < 0\]
- 예시 1
strictly concave.
\[h(\theta)=-(\theta_1-\theta_2)^2\] \[\nabla^2 h= \begin{bmatrix} -2 & 2 \\ 2 & -2 \end{bmatrix}\] \[x^\top\nabla^2 h x = -2(x_1-x_2)^2 \le 0\]
- 예시 2
$x_1=x_2$ 에서는 0 → concave but not strictly.
\[h(\theta)=\log(\theta_1+\theta_2)\] \[\nabla^2 h= -\frac{1}{(\theta_1+\theta_2)^2} \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}\] \[x^\top \nabla^2 h x = -\frac{(x_1+x_2)^2}{(\theta_1+\theta_2)^2} \le 0\]
- 예시 3
concave, but not strictly (일부 방향에서 0).
4. 왜 $t=0$에서의 방향 2차 도함수로 concavity를 판단하는가?
\[g(t)=h(\theta+tx),\qquad g''(0)=x^\top\nabla^2 h(\theta)x\]
- 방향 함수
\[f''(x)\le 0 \iff \text{concave}\]
이유
concavity는 “모든 점에서 모든 방향”의 곡률이 0 이하인지 확인하는 개념이므로
기준점 $\theta$ 에서의 $g’‘(0)$ 만 보면 충분하다.1변수의 확장
\[x^\top \nabla^2 h(\theta)x \le 0\]
- 정리
이면 점 $\theta$ 에서의 concavity 조건이 성립한다.
p16. Convex / Concave 함수 예시
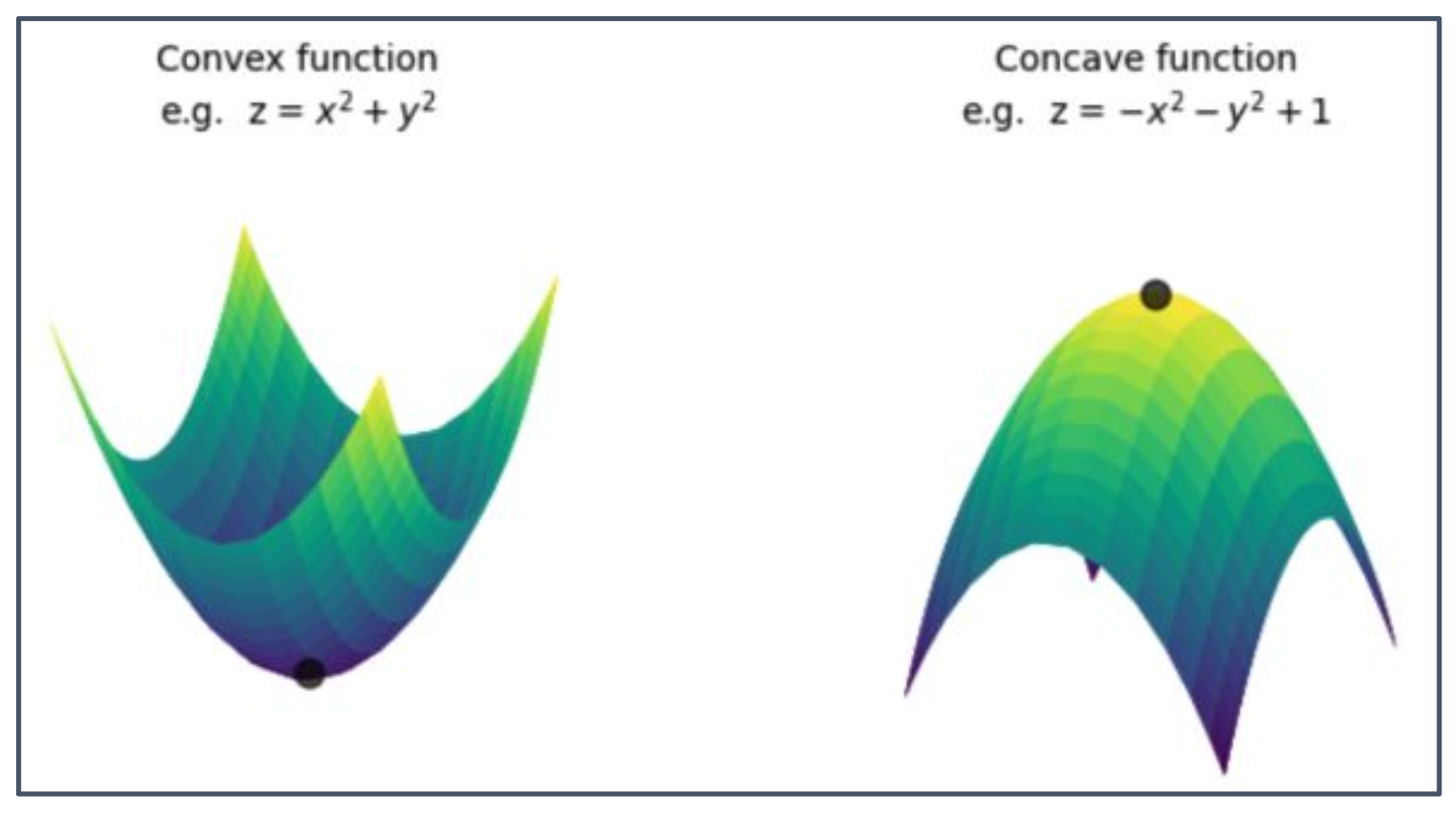
왼쪽 그림은 Convex 함수의 예시로 $z = x^{2} + y^{2}$,
오른쪽 그림은 Concave 함수의 예시로 $z = -x^{2} - y^{2} + 1$을 나타낸다.
Convex function (볼록 함수)
그래프가 위로 열린 그릇 모양이며, 어떤 두 점을 잡아도 그 사이를 잇는 직선이 함수 위에 놓인다.
헤시안 행렬은 양의 정부호(positive definite)이고, 모든 방향 2차 도함수 $x^\top \nabla^2 h(\theta)x \ge 0$ 이다.
따라서 최소점을 가지며, 그림에서 바닥의 검은 점이 극솟값을 나타낸다.Concave function (오목 함수)
그래프가 뒤집힌 그릇 모양이며, 어떤 두 점을 잡아도 그 사이를 잇는 직선이 함수 아래에 놓인다.
헤시안 행렬은 음의 정부호(negative definite)이고, 모든 방향 2차 도함수 $x^\top \nabla^2 h(\theta)x \le 0$ 이다.
따라서 최대점을 가지며, 그림에서 꼭대기의 검은 점이 극댓값을 나타낸다.정리
Convex 함수는 최적화 문제에서 최소화 성질을 설명할 때,
Concave 함수는 최대화 성질을 설명할 때 중요한 예시가 된다.
p17. 함수의 최대화/최소화
strictly concave 함수는 최대화하기 쉽다. 최대값이 존재한다면 그것은 유일(unique)하다.
이는 다음 조건의 유일한 해로 주어진다.
- 1차원 함수의 경우:
- 다변수 함수의 경우:
수치적으로 해를 찾기 위한 알고리즘이 많이 존재하며, 이는 convex optimization 이론에 속한다.
이번 수업에서는 최대값이 닫힌 형태(closed form formula)로 표현되는 경우가 자주 등장한다.
위 조건은 그래디언트가 0인 점(= stationary point)을 찾는 것이며, 이때 헤시안의 부호가 그 점이 최대값인지 최소값인지를 판별한다.
헤시안이 음의 정부호(negative definite) → 해당 점은 최대값.
헤시안이 양의 정부호(positive definite) → 해당 점은 최소값.따라서 strictly concave 함수에서는 stationary point가 존재하면 그것이 곧 유일한 최대값이 된다.
p18. 통계모델의 우도
\((E, (\mathbb{P}_\theta)_{\theta \in \Theta})\)를 i.i.d.인 확률변수 \(X_{1}, \dots, X_{n}\)의 표본과 연관된 통계모델이라고 하자.
$E$는 이산(discrete) 집합(유한 혹은 가산)이라고 가정한다.
정의
모델의 우도(likelihood)는 다음과 같이 정의된 사상(map) $L_{n}$ (또는 간단히 $L$) 이다.
\[\begin{array}{rcl} L_{n} & : & \;\;\;\;\;\;\;\;\; E^{n} \times \Theta \;\to\; \mathbb{R} \\ & & (x_{1}, \dots, x_{n}, \theta) \;\mapsto\; \mathbb{P}_{\theta}[X_{1} = x_{1}, \dots, X_{n} = x_{n}] \end{array}\]
위 식은 i.i.d. 표본 $(X_{1}, \dots, X_{n})$ 이 실제로 특정 값 $(x_{1}, \dots, x_{n})$ 을 관측했을 때,
그 사건이 모수 $\theta$ 하에서 일어날 확률을 함수로 나타낸 것이다.즉, $L_{n}$ 은 입력으로 표본 데이터 $(x_{1}, \dots, x_{n})$ 와 모수 $\theta$ 를 받고,
출력으로 해당 표본이 $\theta$ 하에서 관측될 확률
\(\mathbb{P}_{\theta}[X_{1}=x_{1}, \dots, X_{n}=x_{n}]\)
을 돌려준다.확률분포의 관점에서 보면 $L_{n}$ 은 $\theta$ 의 함수가 아니라 데이터 $(x_{1}, \dots, x_{n})$ 의 함수처럼 보이지만,
통계학에서는 표본을 고정된 값으로 보고 $\theta$ 를 변수로 취급한다.
이때 $L_{n}(\theta)$ 를 우도(likelihood) 라고 부른다.따라서 우도함수는
“어떤 모수 $\theta$ 가 주어졌을 때, 실제 관측된 데이터가 나올 가능성이 얼마나 높은가”를
정량화한 함수이다.
p19. 가우시안 모델의 우도
예제 1 (가우시안 모델):
만약 $X_{1}, \dots, X_{n} \overset{iid}{\sim} \mathcal{N}(\mu, \sigma^{2})$, some $\mu \in \mathbb{R}, \ \sigma^{2} > 0$라 하자.
- $E = \mathbb{R}$
- $\Theta = \mathbb{R} \times (0, \infty)$
$\forall (x_{1}, \dots, x_{n}) \in \mathbb{R}^{n}, \ \forall (\mu, \sigma^{2}) \in \mathbb{R} \times (0, \infty)$,
\[L(x_{1}, \dots, x_{n}, \mu, \sigma^{2}) = \frac{1}{(\sigma \sqrt{2\pi})^{n}} \exp \left( -\frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (x_{i} - \mu)^{2} \right).\]
\[f(x \mid \mu, \sigma^{2}) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left( -\frac{(x-\mu)^{2}}{2\sigma^{2}} \right)\]
$X_{1}, \dots, X_{n} \overset{iid}{\sim} \mathcal{N}(\mu, \sigma^{2})$ 라는 것은
각 표본 $X_{i}$ 가 평균 $\mu$, 분산 $\sigma^{2}$ 인 정규분포를 따르며
서로 독립이고 동일한 분포(i.i.d.)임을 의미한다.확률 공간은 $E=\mathbb{R}$, 모수 공간은 $\Theta=\mathbb{R}\times(0,\infty)$ 이다.
여기서 $\mu \in \mathbb{R}$, $\sigma^{2} \in (0,\infty)$ 로 주어진다.정규분포의 확률밀도함수(pdf)는
\[L(x_{1},\dots,x_{n},\mu,\sigma^{2}) = \prod_{i=1}^{n} f(x_{i} \mid \mu,\sigma^{2})\]
- 독립성을 가정하면 $n$개의 관측치에 대한 결합확률은 곱으로 표현된다:
\[L(x_{1},\dots,x_{n},\mu,\sigma^{2}) = \frac{1}{(\sigma \sqrt{2\pi})^{n}} \exp\left( -\frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (x_{i}-\mu)^{2} \right)\]
- 지수함수의 성질에 의해 곱이 합으로 바뀌어 다음과 같이 정리된다:
p20. 포아송 모델의 우도
예제 2 (포아송 모델):
만약 $X_{1}, \dots, X_{n} \overset{iid}{\sim} \text{Poiss}(\lambda)$ for some $\lambda > 0$라 하자.
- $E = \mathbb{N}$
- $\Theta = (0, \infty)$
$\forall (x_{1}, \dots, x_{n}) \in \mathbb{N}^{n}, \ \forall \lambda > 0$,
\[\begin{aligned} L(x_{1}, \dots, x_{n}, \lambda) &= \prod_{i=1}^{n} \mathbb{P}_{\lambda}[X_{i} = x_{i}] \\ &= \prod_{i=1}^{n} \frac{e^{-\lambda} \lambda^{x_{i}}}{x_{i}!} \\ &= e^{-n\lambda} \frac{\lambda^{\sum_{i=1}^{n} x_{i}}}{x_{1}!\cdots x_{n}!}. \end{aligned}\]
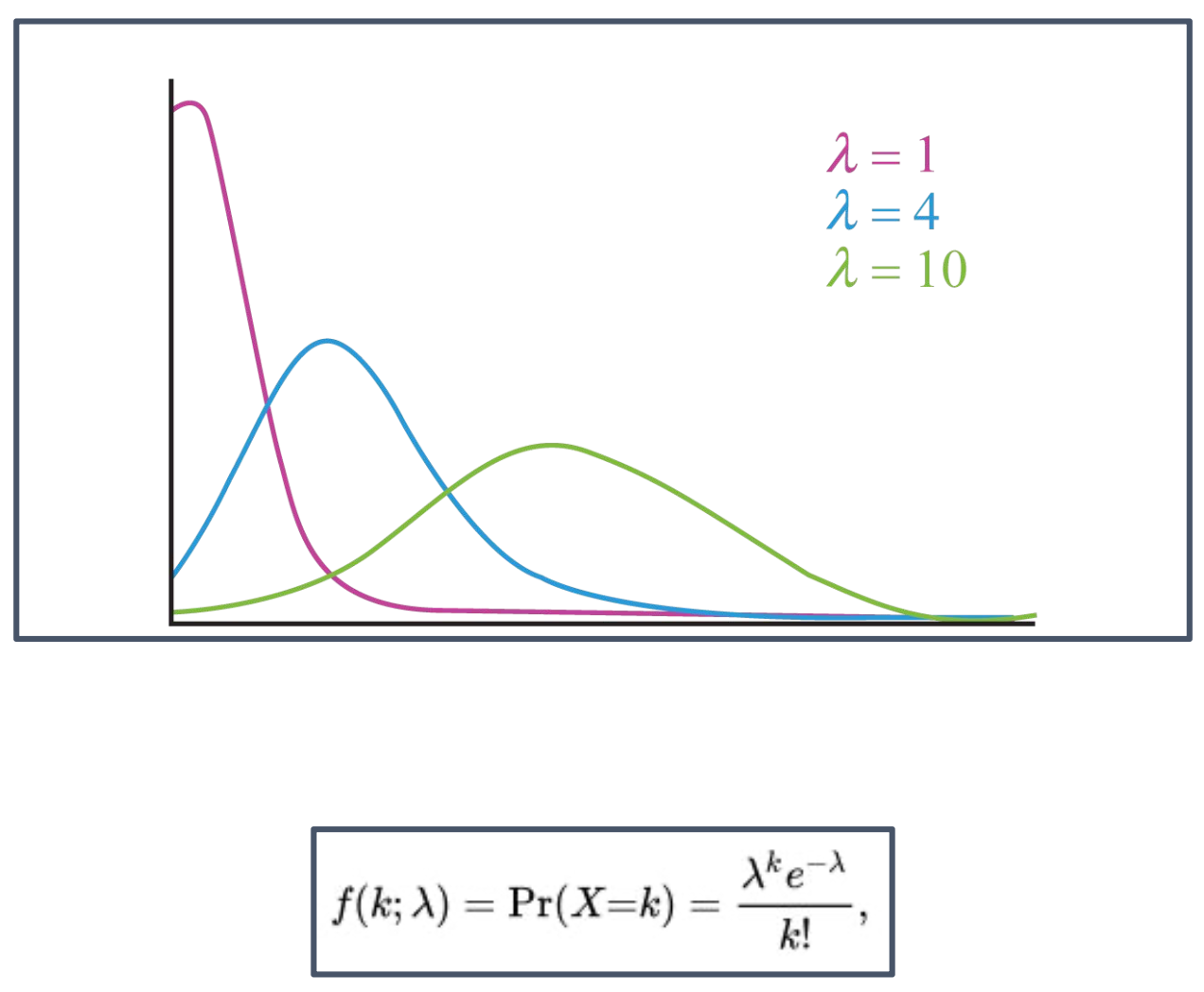
\[f(x \mid \lambda) = \mathbb{P}_{\lambda}[X=x] = \frac{e^{-\lambda} \lambda^{x}}{x!}, \quad x \in \mathbb{N}.\]
$X_{1}, \dots, X_{n} \overset{iid}{\sim} \text{Poiss}(\lambda)$ 라는 것은
각 표본 $X_{i}$ 가 모수 $\lambda>0$ 인 포아송 분포를 따르며
서로 독립이고 동일한 분포임을 의미한다.확률 공간은 $E=\mathbb{N}$, 모수 공간은 $\Theta=(0,\infty)$ 이다.
포아송 분포의 확률질량함수(pmf)는
\[L(x_{1},\dots,x_{n},\lambda) = \prod_{i=1}^{n} \frac{e^{-\lambda}\lambda^{x_{i}}}{x_{i}!}.\]
- $n$ 개의 관측치에 대한 결합확률은 독립성 때문에 곱으로 표현된다:
\[L(x_{1},\dots,x_{n},\lambda) = e^{-n\lambda} \frac{\lambda^{\sum_{i=1}^{n} x_{i}}}{x_{1}!\cdots x_{n}!}.\]
- 지수항 $e^{-\lambda}$ 는 곱해지면 $e^{-n\lambda}$ 로,
$\lambda^{x_{i}}$ 항은 지수 합으로 묶여 다음과 같이 단순화된다:
- 따라서 우도 함수는
표본의 합 $\sum_{i=1}^{n} x_{i}$ 와
표본 각각의 팩토리얼에 의해 결정된다.
p21. 최대우도추정량
Maximum Likelihood Estimator
$X_{1}, \dots, X_{n}$는 통계모델 $(E, (P_{\theta})_{\theta \in \Theta})$와 연관된 i.i.d. 표본이라 하고, 이에 대응하는 우도를 $L$이라 하자.
정의
$\theta$의 최대우도추정량(MLE)은 다음과 같이 정의된다:
단, 존재한다고 가정한다.
비고 (로그우도추정량)
실제 계산에서는 로그우도를 사용한다:
MLE의 직관
최대우도추정량(Maximum Likelihood Estimator, MLE)은
주어진 표본이 실제로 관측될 가능성을 가장 크게 만드는 모수값을 선택하는 방법이다.
즉, 우도함수 $L(X_{1},\dots,X_{n},\theta)$ 를 최대로 만드는 $\theta$ 를 추정치로 삼는다.로그우도의 사용 이유
\[\log \prod_{i=1}^{n} f(x_{i} \mid \theta) = \sum_{i=1}^{n} \log f(x_{i} \mid \theta)\]
곱으로 이루어진 우도함수는 $n$ 이 커질수록 수치적으로 계산하기 어렵다.
로그를 취하면 곱이 합으로 변하여 계산이 단순해지고
미분을 이용한 최적화도 훨씬 쉬워진다.
예:추정량의 성질
적절한 정규성 조건하에서 MLE는
일치성(consistency), 점근적 정규성(asymptotic normality), 효율성(efficiency)
등의 좋은 성질을 가진다.
따라서 통계학과 머신러닝의 수많은 모델에서 기본적인 추정 방법으로 사용된다.
p22. 피셔 정보
정의: 피셔 정보(Fisher information)
한 관측치에 대한 로그우도를 다음과 같이 정의한다:
\[\ell(\theta) = \log L_{1}(X, \theta), \quad \theta \in \Theta \subset \mathbb{R}^{d}\]$\ell$이 거의 모든 경우(a.s.)에서 두 번 미분 가능하다고 가정하자.
일정한 정규성 조건하에서 (Under some regularity conditions), 통계모델의 피셔 정보는 다음과 같이 정의된다:
만약 $\Theta \subset \mathbb{R}$이면,
\[I(\theta) = \mathrm{var}\!\big[\ell'(\theta)\big] = -\mathbb{E}[\ell''(\theta)].\](한 꼭지 요약) 피셔 정보의 직관과 활용성
\[\mathrm{Var}(\hat{\theta}) \ge \frac{1}{n\,I(\theta)}\]
의미(직관): 피셔 정보 $I(\theta)$ 는 “데이터가 모수 $\theta$ 를 얼마나 선명하게 식별하는가”를 나타내는 척도이다.
로그우도 곡선의 곡률이 클수록 작은 모수 변화에도 우도가 크게 변하므로 정보가 많다.
반대로 곡선이 평평하면 여러 $\theta$ 가 비슷한 우도를 가져 정보가 적고 불확실성이 크다.분산 하한(Cramér–Rao Bound):
정보가 많을수록($I(\theta)$ 큼) 추정의 분산은 작아진다.
우도 곡선이 뾰족할수록 정확한 추정이 가능하며, 평평할수록 흔들림이 크다.\[\hat{\theta}_{\mathrm{MLE}} \approx \mathcal{N}(\theta,\,[n\,I(\theta)]^{-1})\]
- MLE의 근사 분포:
피셔 정보의 역수가 추정량의 불확실도(표준오차)를 결정한다.
실무적 활용:
① 신뢰구간·표준오차 계산: $[n\,I(\hat{\theta})]^{-1/2}$
② 실험 설계: 정보가 커지도록 샘플링 조정
③ 모델 비교: 동일 데이터에서 더 큰 정보를 주는 모델이 더 정밀함요약 한 줄:
피셔 정보는 “우도의 곡률 = 모수 식별력 = 추정 정확도의 한계(분산 하한)”을 보여주는 핵심 척도이다.1. 왜 a.s.라는 표현이 붙는가?
- 로그우도 $\ell(\theta)$ 가 항상 두 번 미분 가능한 것은 아니다.
드물게 미분 불가능한 표본이 있으나 그 확률은 0이다.
따라서 “거의 확실히(a.s.) 두 번 미분 가능”이라는 표현을 쓴다.2. 일정한 정규성 조건의 의미
\[\mathbb{E}\!\left[\frac{\partial}{\partial\theta}\ell(\theta)\right] = \frac{\partial}{\partial\theta}\mathbb{E}[\ell(\theta)]\]
- 미분과 기댓값을 교환하는 과정이 필요하다:
- 위와 같은 식이 자연스럽게 성립하도록 보장하는 가정을 “정규성 조건”이라 한다.
3. 수식 전개 과정
\[\mathrm{Var}(X)=\mathbb{E}\big[(X-\mathbb{E}[X])^{2}\big]\]
- 스칼라 분산:
\[\mathrm{Var}(U)=\mathbb{E}[(U-\mathbb{E}[U])\,(U-\mathbb{E}[U])^{\top}]\]
- 벡터 분산 → 공분산 행렬:
\[\mathbb{E}[(U_i-\mathbb{E}[U_i])(U_j-\mathbb{E}[U_j])]\]
- 외적을 쓰는 이유:
$(U-\mathbb{E}[U])(U-\mathbb{E}[U])^{\top}$ 의 $(i,j)$ 성분이즉 공분산이기 때문이다.
\[U(\theta)=\nabla\ell(\theta)=\frac{\partial}{\partial\theta}\log L_{1}(X,\theta)\]
- 점수 함수:
\[I(\theta)=\mathrm{Var}[U(\theta)]\]
- 피셔 정보:
\[\mathrm{Var}[U]=\mathbb{E}[UU^{\top}] - \mathbb{E}[U]\mathbb{E}[U]^{\top}\]
- 분산 전개(외적 전개 후 기대값):
\[I(\theta)=\mathbb{E}[U(\theta)U(\theta)^{\top}]\]
- 정규성 조건하에서 $\mathbb{E}[U(\theta)]=0$ 이므로:
4. 피셔 정보의 두 표현이 같아지는 이유
\[I(\theta)=\mathbb{E}[U(\theta)U(\theta)^{\top}] = -\mathbb{E}[\nabla^{2}\ell(\theta)]\]
- 로그우도 $\ell(\theta)=\log p_\theta(X)$ 의 2차 미분 전개를 통해:
\[\mathbb{E}[U_i(\theta)U_j(\theta)] = -\mathbb{E}\!\left[\frac{\partial^2}{\partial\theta_i\partial\theta_j}\ell(\theta)\right]\]
- 성분별로는:
- 첫 번째 항 $\int \partial^2 p_\theta/\partial\theta_i\partial\theta_j \, dx = 0$ 이므로 소거되고
점수 함수 항만 남는다.5. 스칼라 모수의 경우
\[U(\theta)=\ell'(\theta)\]
- 점수 함수:
\[I(\theta)=\mathrm{Var}[\ell'(\theta)]\]
- 피셔 정보:
\[I(\theta)=-\mathbb{E}[\ell''(\theta)]\]
- 로그우도 2차 도함수 표현:
- 스칼라일 때는 행렬이 아닌 단일 값으로 주어지며
위 두 표현이 동일한 피셔 정보를 나타낸다.
p23. 최대우도추정량(MLE)의 성질
정리 (Theorem)
$\theta^{\ast} \in \Theta$ (참 모수, true parameter)라 하자. 다음을 가정한다:
- 모델이 식별 가능하다 (The model is identified).
- 모든 $\theta \in \Theta$에 대해, 분포 $P_\theta$의 지지집합(support)은 $\theta$에 의존하지 않는다.
- $\theta^{\ast}$는 $\Theta$의 경계(boundary)에 있지 않다.
- $I(\theta)$는 $\theta^{\ast}$ 근방에서 가역적(invertible)이다.
- 그 외 몇 가지 기술적인 조건들이 성립한다.
그렇다면, $\hat{\theta}_n^{MLE}$는 다음을 만족한다:
일치성(Consistency):
\[\hat{\theta}_n^{MLE} \;\;\xrightarrow{P}\;\; \theta^{\ast}, \quad n \to \infty, \quad \text{w.r.t. } \mathbb{P}_{\theta^{\ast}}.\]점근정규성(Asymptotic Normality):
\[\sqrt{n}\,(\hat{\theta}_n^{MLE} - \theta^{\ast}) \;\;\xrightarrow{d}\;\; \mathcal{N}\!\big(0,\, I(\theta^{\ast})^{-1}\big), \quad n \to \infty, \quad \text{w.r.t. } \mathbb{P}_{\theta^{\ast}}.\]
(한 꼭지 요약) MLE의 의미와 직관적 요약
최대우도추정량(MLE)은 여러 정규성 조건 아래에서 가장 정보가 많은 방향으로 수렴하는 추정량이다.
(1) 모델 식별성은 서로 다른 모수가 서로 다른 분포를 만들어야 MLE의 수렴 목표가 정의된다는 뜻이다.
(2) 지지집합의 불변성은 모수가 달라져도 확률변수가 가질 수 있는 값의 범위가 변하지 않아야 미분·적분 교환이 안정적으로 가능함을 의미한다.
(3) 경계 외부의 모수는 추정이 비정상적인 경계값(예: 분산=0)에서 멈추지 않도록 하여 점근정규성을 보장한다.
(4) 피셔 정보의 가역성은 추정량의 분산이 유한하고 정규근사가 성립함을 의미한다.
(5) 기술적 조건들은 미분·적분 교환, 연속성, CLT 적용 등 수학적 조작을 정당화한다.
결국 MLE는
“모델이 잘 정의되고, 충분히 매끄럽고, 정보가 잘 분리되는 환경에서
표본이 커질수록 참값으로 수렴하고, 그 주변에서 정규분포 형태로 퍼지는 추정량” 이다.1. 모델이 식별 가능하다는 의미
서로 다른 모수 $\theta_1\neq\theta_2$ 가 서로 다른 분포 $P_{\theta_1}\neq P_{\theta_2}$ 를 만든다는 뜻이다.
데이터를 통해 모수를 유일하게 식별할 수 있어야 하며, 그렇지 않으면 추정량이 어디로 수렴해야 하는지 정의되지 않는다.2. 지지집합(support)이 $\theta$ 에 의존하지 않는다는 의미. 지지집합은 $p_\theta(x)>0$ 인 $x$ 의 집합이다.
“$\theta$ 에 의존하지 않는다”는 것은 모수가 달라져도 확률변수가 가질 수 있는 값의 범위가 변하지 않는다는 뜻이다.
예: 정규분포 $N(\mu,\sigma^2)$ 의 지지집합은 항상 $\mathbb{R}$ 이므로 $\mu,\sigma$ 와 무관하다.3. $\theta^{\ast}$ 가 경계(boundary)에 있지 않다는 의미. 참 모수 $\theta^{\ast}$ 는 모수공간 $\Theta$ 의 내부에 존재해야 한다.
예: 분산이 0에 가까우면 미분 가능성이 깨지거나 점근정규성이 무너질 수 있다.4. $I(\theta)$ 가 가역적(invertible)이라는 의미. 피셔 정보행렬이 양의 정부호이면 역행렬이 존재한다.
역행렬이 없으면 MLE의 점근올바른 분산을 계산할 수 없고,
점근정규분포도 특이(singular)해져 신뢰구간·검정이 불가능해진다.5. 그 외 기술적 조건들. 로그우도의 적분·미분 교환을 보장하는 정규성 조건,
모수공간의 연속성·매끄러움(smoothness),
CLT 적용을 위한 제한 조건(균등적분 가능성 등) 등이 포함된다.
이들은 수학적 조작(미분, 적분, 기댓값, 극한)의 정당화를 위한 조건이다.6. 결론 (첫 번째 항목: 일치성)
\[\hat{\theta}_n^{MLE} \xrightarrow{P} \theta^{\ast}\]표본 크기가 커지면 최대우도추정량이 참 모수에 확률적으로 수렴하며,
MLE는 일치추정량(consistent estimator)이다.7. 결론 (두 번째 항목: 점근정규성)
\[\sqrt{n}\,(\hat{\theta}_n^{MLE} - \theta^{\ast}) \xrightarrow{d} \mathcal{N}\big(0,\, I(\theta^{\ast})^{-1}\big)\]MLE는 참 모수 주변에서 정규분포를 따르게 되며,
$n$ 이 클수록 평균 $\theta^\ast$, 공분산 $I(\theta^\ast)^{-1}$ 인 정규분포로 근사된다.
이를 이용해 신뢰구간을 만들고 가설검정을 수행할 수 있다.