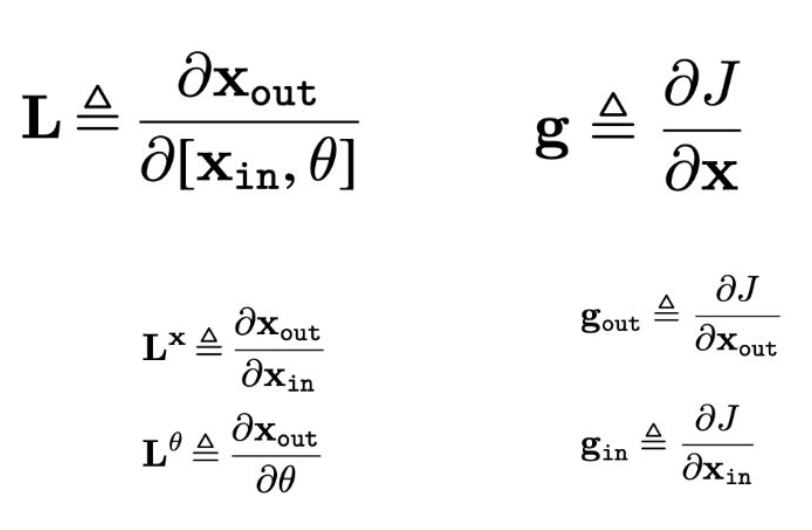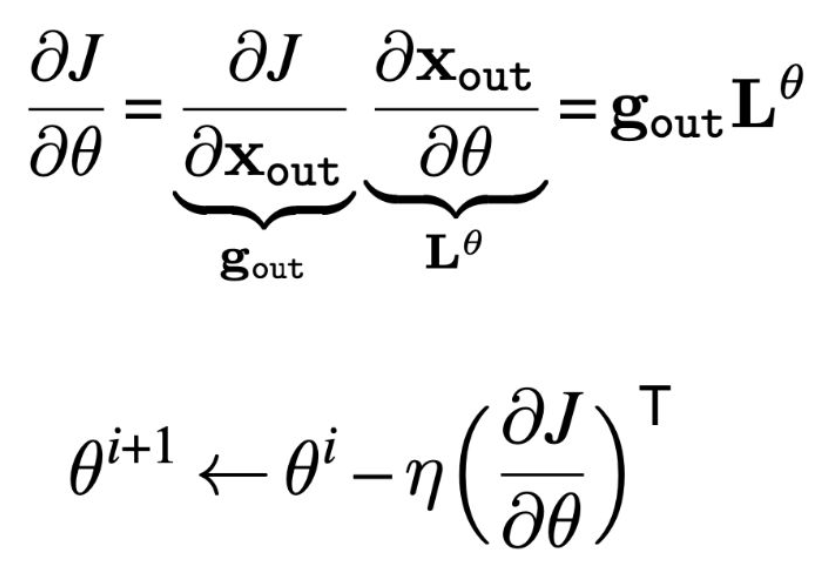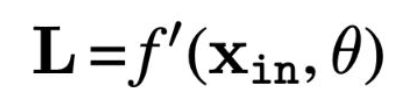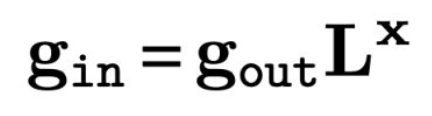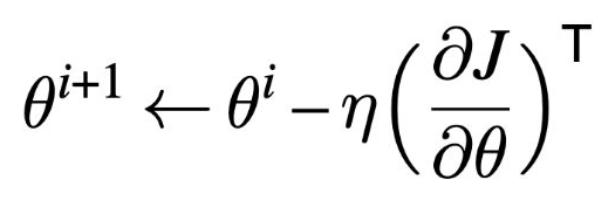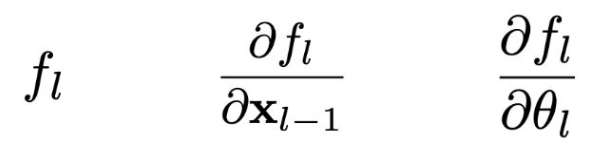[확률과 통계] 4주차

게시 2025/09/28 업데이트 2025/12/12

By 김성진

81 분읽는 시간

[확률과 통계] 4주차

p2. 신경망을 학습시키는 방법?

경사하강법(gradient descent), 확률적 경사하강법(SGD) 복습
계산 그래프(computation graphs)
사슬 구조를 통한 역전파(backprop through chains)
다층 퍼셉트론(MLPs)을 통한 역전파(backprop through MLPs)
유향 비순환 그래프(DAGs)를 통한 역전파(backprop through DAGs)
미분 가능한 프로그래밍(differentiable programming)

p3. 기본 원리? (Basic rationale?)

1. 기본 원리
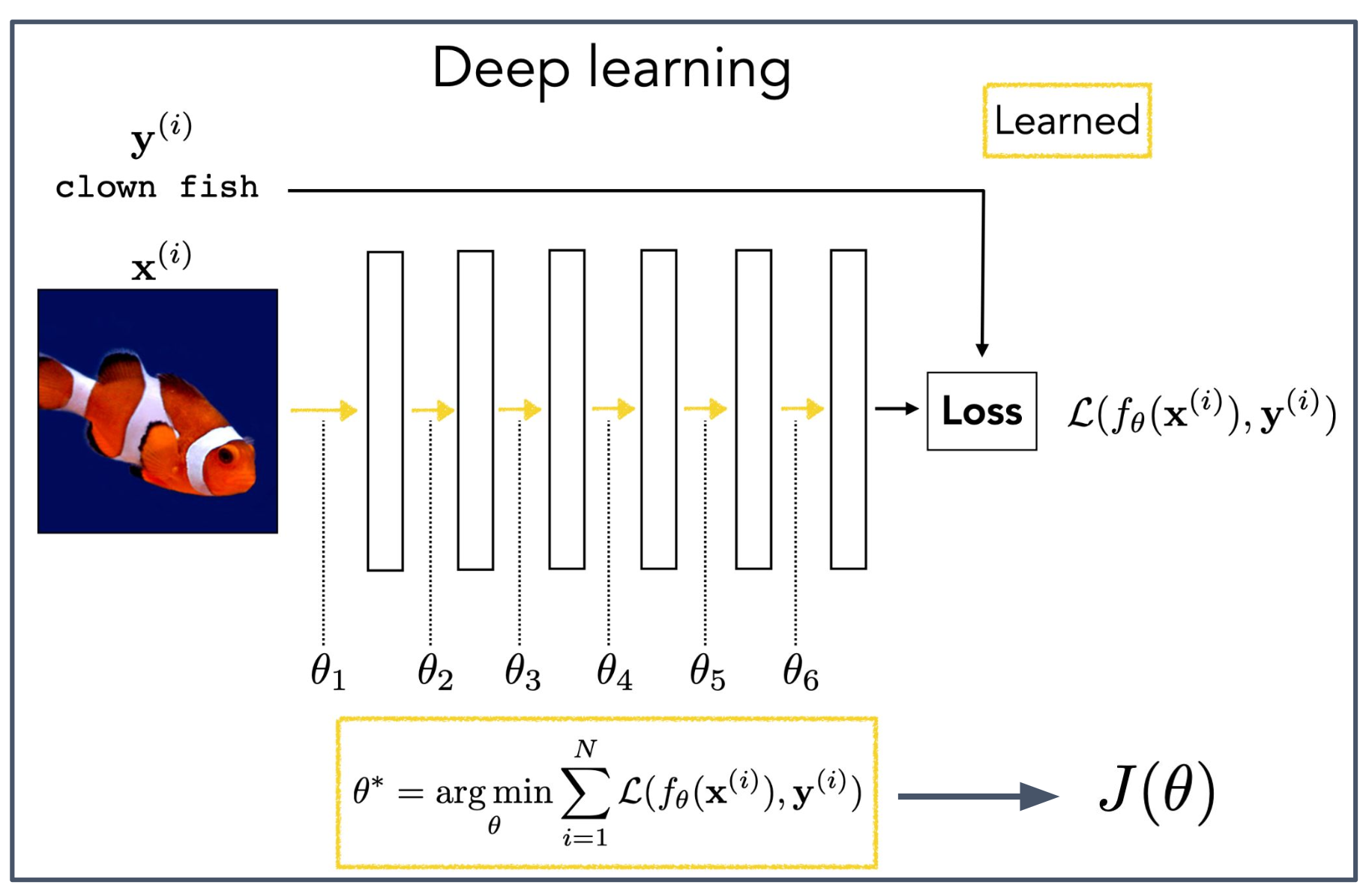
딥러닝의 목적은 데이터 인스턴스 $x^{(i)}$ 를 입력받아 올바른 분류 레이블 $y^{(i)}$ 를 출력하도록 모델 $f_\theta$ 를 학습하는 것이다.
이를 위해 손실 함수(loss) $\mathcal{L}(f_\theta(x^{(i)}), y^{(i)})$ 를 정의하여, 예측과 실제 정답 사이의 차이를 수치로 측정한다.
손실 함수는 보통 거리 기반 함수로 정의되며, 어떻게 정의하느냐가 모델 학습 성능에 큰 영향을 준다.
2. 모델 파라미터와 학습 과정
각 레이어는 $\theta_1, \theta_2, \dots, \theta_6$ 등 파라미터 집합을 가진다.
학습의 목표는 모든 데이터 인스턴스에 대해 손실의 합을 최소화하는 파라미터 $\theta^\ast$ 를 찾는 것이다.
\[\theta^\ast = \arg\min_{\theta} \sum_{i=1}^N \mathcal{L}\big(f_\theta(x^{(i)}), y^{(i)}\big)\]
이 과정을 통해 모델은 데이터에 가장 잘 맞는 매개변수를 학습한다.
3. 손실 함수(Loss function)와 목적 함수(Objective function)의 관계
손실 함수(Loss function): 개별 데이터 인스턴스 $(x^{(i)}, y^{(i)})$ 에 대한 오차를 측정한다.
\[\mathcal{L}(f_\theta(x^{(i)}), y^{(i)})\]
목적 함수(Objective function): 전체 데이터셋에 대해 손실을 합산/평균한 값으로, 실제로 최소화해야 하는 대상이다.
\[J(\theta) = \frac{1}{N}\sum_{i=1}^N \mathcal{L}(f_\theta(x^{(i)}), y^{(i)})\]
따라서 학습은 결국 목적 함수 $J(\theta)$ 를 최소화하는 최적화 문제로 귀결된다.
손실 함수는 그 목적 함수를 구성하는 기본 단위라고 볼 수 있다.

p4. 최적화 (Optimization)

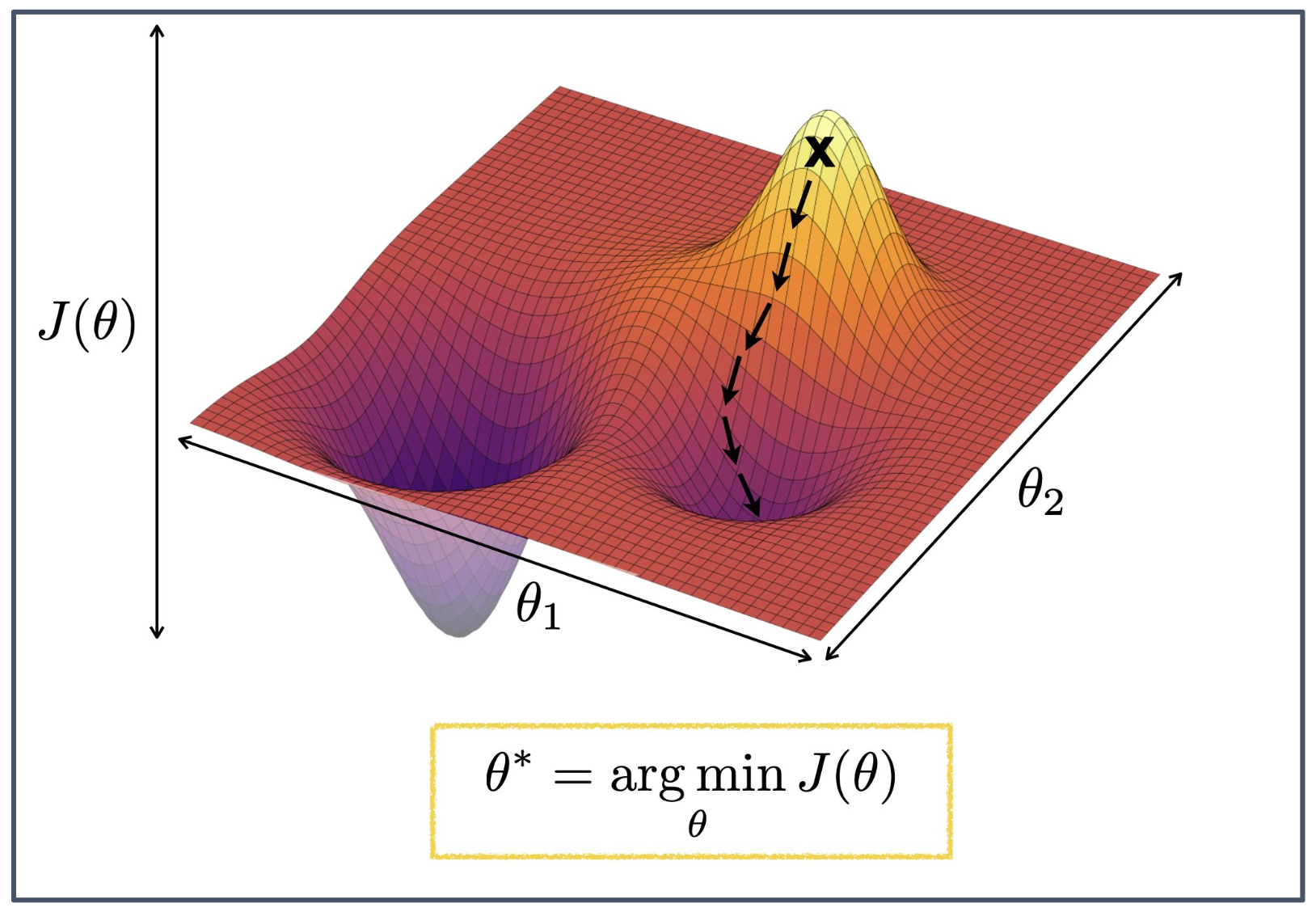
\[\theta^\ast = \arg\min_{\theta} J(\theta)\]

우리가 $J$에 대해 알고 있는 지식은 무엇인가?

우리는 $J(\theta)$ 를 계산할 수 있다.
→ Black box optimization
우리는 $J(\theta)$ 와 $\nabla_\theta J(\theta)$ 를 계산할 수 있다. ($\nabla_\theta$는 Gradient)
→ First order optimization
우리는 $J(\theta)$, $\nabla_\theta J(\theta)$, 그리고 $H_\theta(J(\theta))$ 를 계산할 수 있다. ($H_\theta$는 Hessian)
→ Second order optimization

1. 블랙박스 최적화
내부 구조를 알지 못한 채 단순히 함수값 $J(\theta)$ 만을 이용하여 최소화를 시도하는 방식이다.
신경망을 처음 보면 내부 계산 과정을 명확히 알 수 없다는 점에서 black box optimization 으로 이해할 수 있다.
2. 1차 최적화 (First-order optimization)
함수값과 함께 기울기(gradient) $\nabla_\theta J(\theta)$ 를 사용할 수 있다.
경사하강법(gradient descent), 확률적 경사하강법(SGD) 등이 이 범주에 속한다.
3. 2차 최적화 (Second-order optimization)
함수값과 기울기뿐 아니라, 헤시안(Hessian) $H_\theta(J(\theta))$ 까지 활용한다.
곡률 정보를 이용해 더 정밀한 최적화가 가능하지만, 계산량이 매우 크다는 단점이 있다.

p5. 경사하강법 (Gradient Descent)

1. 경사하강법의 기본 개념
목적 함수 $J(\theta)$ 를 최소화하기 위해 파라미터 $\theta$ 를 반복적으로 갱신하는 방법이다.
현재 위치에서 기울기(gradient)의 반대 방향으로 이동하여 $J(\theta)$ 값을 줄인다.
2. 지역 최소값(Local minima)과 전역 최소값(Global minimum)
최적화 곡면은 여러 개의 골짜기를 가질 수 있다.
이 중 일부는 지역 최소값으로, 더 낮은 값이 존재하더라도 그 안에 머무를 수 있다.
반면 가장 낮은 지점은 전역 최소값으로, 이론적으로는 도달해야 하는 목표점이다.
실제로는 지역 최소값에 도달하는 경우가 대부분이며, 흔히 “local minima에 빠지는 게 99.9% 이상”이라고 말할 정도로 전역 최소값에 도달하는 것은 힘들다.
3. 파라미터 공간과 양자화(Quantization)
실제 학습에서 사용하는 파라미터 공간은 전체 범위를 다 활용하지 못하고, 비효율적으로 사용되는 경우가 많다.
이런 상황에서 quantization 기법을 적용하면 파라미터를 압축해 표현할 수 있으며, 계산 및 저장 효율을 크게 높일 수 있다.
4. 양자화(Quantization)의 의미
양자화란 연속적인 값(실수 값)을 이산적인 값(정해진 단계의 값)으로 근사하는 과정이다.
예: 실수형 파라미터를 32비트(float32)로 저장하는 대신 8비트 정수(int8)로 변환하여 저장하는 것.
이를 통해 메모리 사용량 감소, 연산 속도 향상, 에너지 절약 효과를 얻을 수 있다.
단, 값의 표현력이 줄어들기 때문에 모델 정확도가 약간 떨어질 수 있으나, 최근에는 이를 보완하는 기법들이 활발히 연구되고 있다.

p6. 확률적 경사하강법 (Stochastic Gradient Descent, SGD)

전체 손실 함수 $J$ (각 샘플별 개별 손실의 합)를 최소화하고자 한다.
확률적 경사하강법에서는 데이터의 부분집합(batch)에 대해 그래디언트를 계산한다.
- 배치 크기(batchsize)=1인 경우, 각 샘플마다 $\theta$ 가 갱신된다.
- 배치 크기(batchsize)=N (전체 집합)인 경우, 이는 표준 경사하강법(standard gradient descent)이 된다.
그래디언트 방향은 모든 샘플에 대해 평균을 취한 경우(표준 경사하강법)에 비해 노이즈가 많다(noisy).
장점
- 더 빠르다: 작은 샘플로 전체 그래디언트를 근사한다.
- 암묵적인 정규화 효과(implicit regularizer)가 있다.
단점
- 분산이 크고(high variance), 갱신이 불안정하다(unstable updates).

1. 확률적(Stochastic)이라는 명칭의 이유
확률적 경사하강법(SGD)은 전체 데이터를 한 번에 학습하는 대신, 데이터를 작은 덩어리(chunk, mini-batch)로 나누어 학습한다.
이때 어떤 chunk(샘플 집합)를 사용할지는 확률적으로(random) 선택된다.
따라서 학습 과정에서 매번 다른 부분 집합을 기반으로 파라미터가 갱신되며, 이러한 무작위성이 반영되어 “Stochastic”이라는 이름이 붙는다.
2. 암묵적인 정규화 효과(Implicit Regularization)
SGD는 전체 데이터에 대해 정확한 그래디언트를 계산하지 않고, 무작위로 선택된 작은 샘플 집합으로 근사한다.
이 과정에서 갱신 방향에 노이즈가 섞이게 되는데, 이런 노이즈가 모델이 특정 데이터에 과적합(overfitting)되는 것을 방지하는 역할을 한다.
즉, 명시적으로 정규화 항을 추가하지 않아도, 확률적 샘플링으로 인한 변동성이 일종의 규제(regularization)로 작용하여 일반화 성능을 높여준다.

p7. 모멘텀 (Momentum)

언덕을 굴러 내려가는 무거운 공이 속도를 얻는 것과 같다.
그래디언트 스텝은 이전 업데이트 방향을 계속 따르는 쪽으로 편향된다.

\[\theta^{t+1} \leftarrow \theta^t - \eta \nabla f(\theta^t) - \alpha \cdot m^t\]

도움을 줄 수도 있고, 방해가 될 수도 있다.
모멘텀의 강도(strength of momentum)는 하이퍼파라미터(hyperparameter) 이다.

1. 모멘텀에 대한 직관적인 설명
단순한 경사하강법은 현재 기울기에만 의존해 파라미터를 이동시킨다.
모멘텀을 적용하면 이전 단계의 이동 방향이 누적되어, 마치 공이 굴러가며 가속도를 얻는 것처럼 파라미터 갱신에 관성이 붙는다.
이로 인해 지역 최소값(local minima)에 갇히지 않고 벗어날 수 있는 가능성이 커진다.
2. 수식 해석
$\eta$ : 학습률(learning rate), 업데이트 크기를 조절한다.
$\nabla f(\theta^t)$ : 현재 시점에서의 그래디언트.
$\alpha \cdot m^t$ : 이전 업데이트에서 온 관성(모멘텀 항), $\alpha$ 가 클수록 더 큰 영향을 준다.
결과적으로 이동 방향은 현재 그래디언트와 과거의 업데이트가 결합된 형태가 된다.
3. 모멘텀의 효과
장점: 진동(oscillation)을 줄이고, 평평한 지역을 빠르게 통과하며, 지역 최소값에서 빠져나오는 데 도움을 준다.
단점: 하이퍼파라미터 $\eta$ 와 $\alpha$ 를 적절히 조정하지 않으면 오히려 발산하거나 최적점 근처에서 크게 진동할 수 있다.
4. 하이퍼파라미터로서의 $\alpha$의 의미
모멘텀의 강도 $\alpha$ 는 문제와 데이터셋에 따라 달라지는 값이며, 반드시 실험적으로 조정해야 한다.
$\alpha$는 학습률 $\eta$ 와 함께 모델의 수렴 속도와 안정성을 좌우하는 핵심 요소다.

p8. 예시: SGD의 동작

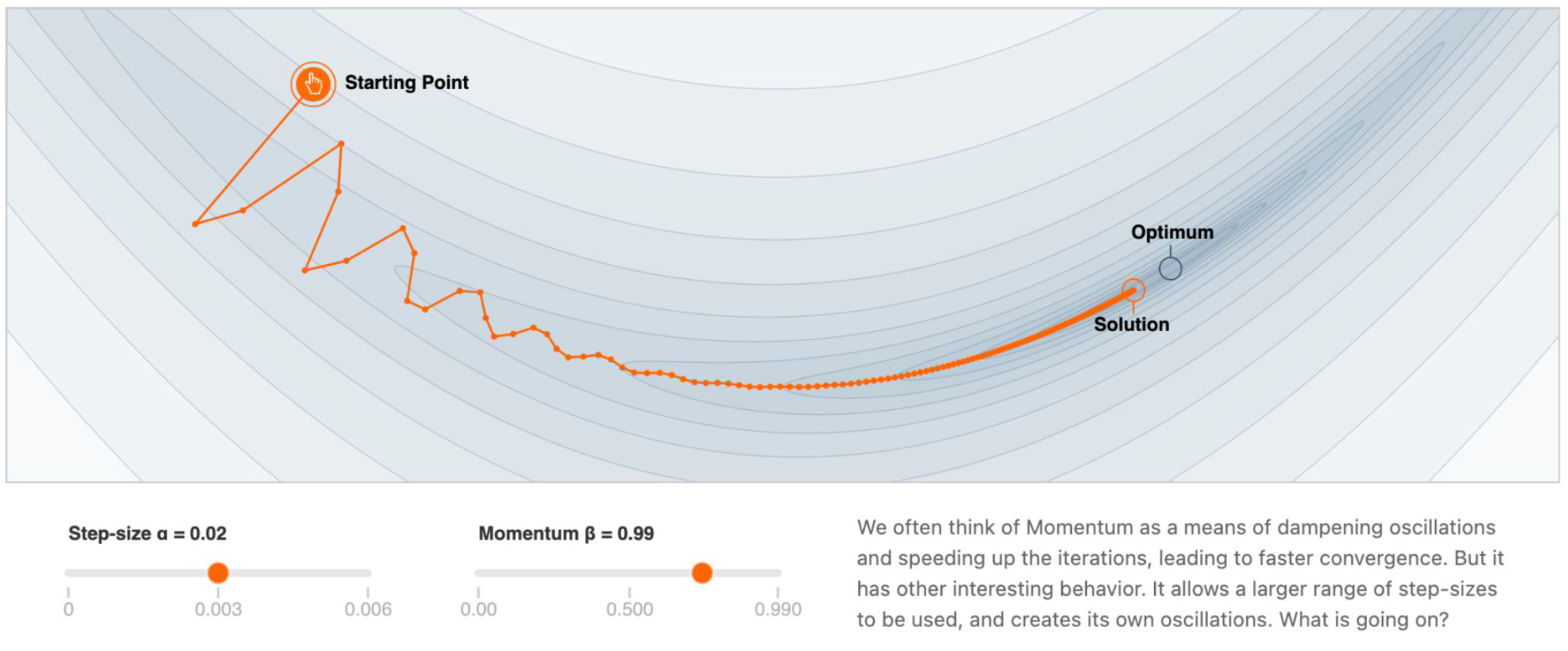
스텝 크기 $\alpha = 0.02$
모멘텀 $\beta = 0.99$

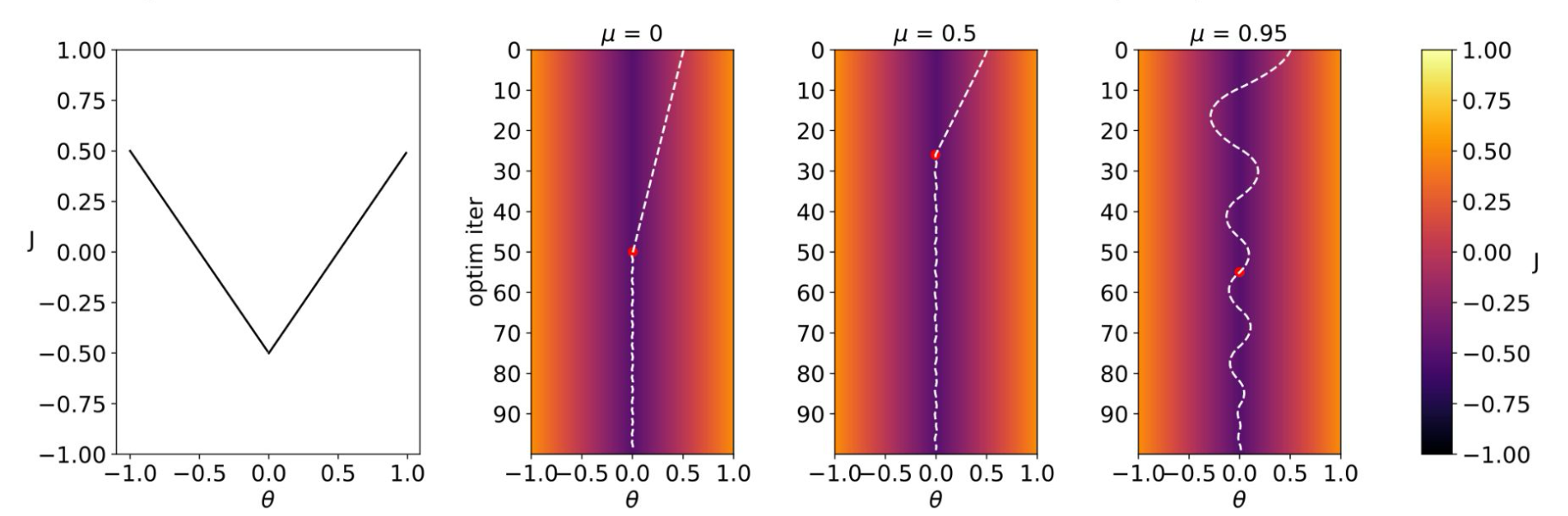
모멘텀은 보통 진동을 억제하고 반복(iteration)의 속도를 높여 더 빠른 수렴을 가능하게 하는 수단으로 이해된다.
하지만 모멘텀은 또 다른 흥미로운 동작을 보인다.
더 넓은 범위의 스텝 크기를 사용할 수 있게 하고, 동시에 자체적인 진동을 만들어내기도 한다.
그렇다면 어떤 일이 일어나고 있는 것일까?

[참고 링크: https://distill.pub/2017/momentum/]

1. SGD의 이동 경로
그림에서 주황색 궤적은 확률적 경사하강법(SGD)이 출발점에서 해(solution)로 이동하는 과정을 나타낸다.
단순 경사하강법은 불안정하거나 수렴이 느릴 수 있는데, 모멘텀을 적용하면 궤적이 달라진다.
2. 모멘텀의 영향
모멘텀은 진동을 줄이고 더 빠른 방향으로 이동하게 만든다.
그러나 동시에, 스텝 크기와 결합될 때 새로운 진동을 만들어낼 수도 있다.
따라서 모멘텀은 단순히 학습 속도를 높이는 요소를 넘어서, 최적화 경로 자체를 바꾸는 요인이 된다.
3. 스텝 크기와 모멘텀의 조합
학습률(스텝 크기, $\alpha$)과 모멘텀($\beta$)은 서로 긴밀히 상호작용한다.
$\alpha$가 지나치게 크면 발산할 수 있고, $\beta$가 너무 크면 진동이 심해진다.
적절한 조합을 선택하면 빠른 수렴과 안정성을 동시에 얻을 수 있다.

p9. 목적 함수의 예시 (손실 함수)

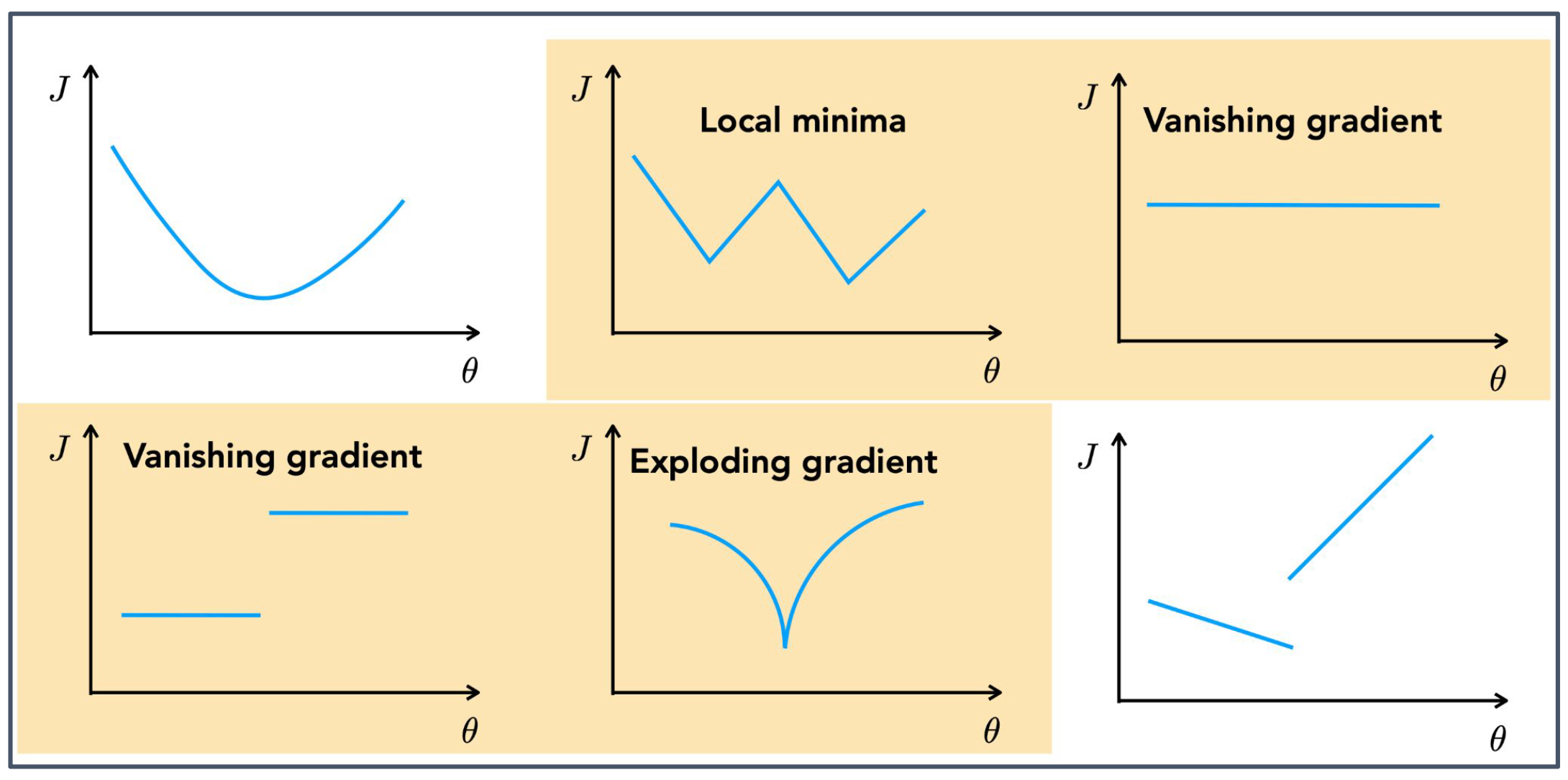
1. (상단의 첫 번째 그림)
목적 함수 $J(\theta)$ 가 매끄럽고 단일한 곡선 형태를 보이는 경우이다.
전역 최소값(global minimum)을 안정적으로 찾을 수 있으며, 학습이 빠르고 안정적으로 수렴한다.
2. (상단의 두 번째 그림) Local minima
여러 개의 골짜기를 가지는 경우, 전역 최소값이 아닌 지역 최소값(local minima)에 머무를 수 있다.
이런 경우 더 좋은 해를 찾지 못하고 학습 성능이 제한될 수 있다.
3. (상단의 세 번째 그림) Vanishing gradient
그래프가 상수 함수 형태를 보인다.
상수 함수 $J(\theta) = c$ 를 미분하면
\[\nabla_\theta J(\theta) = 0\]
따라서 파라미터 업데이트가 전혀 일어나지 않아 학습이 멈춘다.
4. (하단의 첫 번째 그림) Vanishing gradient (단계적)
계단 함수 형태의 그래프에서는 특정 구간에서 기울기가 0이 된다.
이런 경우에도 $\nabla_\theta J(\theta) = 0$ 이 되어 학습이 정체된다.
5. (하단의 두 번째 그림) Exploding gradient
그래프 모양은 두 곡선이 아래쪽에서 만나면서 원점 근처에서 값이 급격히 커지는 형태이다.
예를 들어 다음과 같은 함수가 있다:
\[J(\theta) = \frac{1}{|\theta|}\]
이때 그래디언트는
\[\nabla_\theta J(\theta) = \frac{d}{d\theta}\left(\frac{1}{|\theta|}\right) = -\frac{\text{sgn}(\theta)}{\theta^2}\]
$\theta \to 0$ 으로 다가가면 분모 $\theta^2$ 가 0에 수렴하므로 그래디언트가 폭발적으로 커진다.
이로 인해 파라미터 업데이트가 매우 불안정해지고, 학습이 발산하거나 최적점을 지나칠 수 있다.
6. (하단의 세 번째 그림)
불연속적이거나 급격한 변화가 있는 그래프의 경우, 그래디언트 방향이 일관성을 가지지 못한다.
이런 상황에서는 최적화가 불안정해지고, 수렴하기 어려워진다.

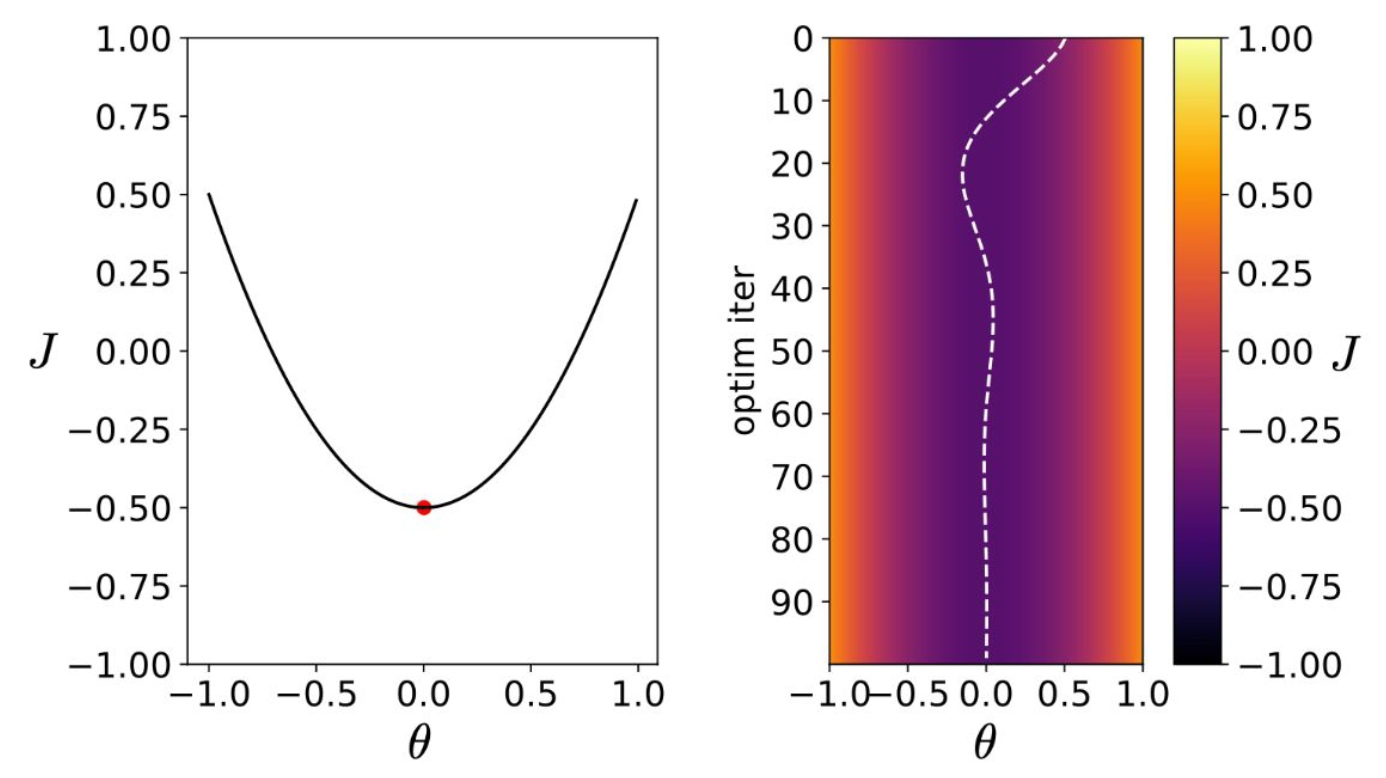
p10. 볼록 함수 (Convex function)

단순한 케이스:

볼록(convex)
단일 최소값(single minimum)
모든 지점에서 그래디언트는 최소값을 향한다
최소값에 가까워질수록 그래디언트가 점진적으로 0에 수렴한다

1. 볼록 함수의 특징
볼록 함수는 전체 영역에서 오직 하나의 최소값만 존재한다.
따라서 최적화 과정에서 여러 지역 최소값(local minima)에 갇히는 문제가 발생하지 않는다.
2. 그래디언트의 방향성
함수의 어느 지점에서나 그래디언트는 항상 최소값 쪽을 가리킨다.
이 성질 덕분에 경사하강법은 단순하면서도 안정적으로 전역 최소값에 도달할 수 있다.
3. 그래디언트의 크기 변화
최소값 근처에 접근할수록 그래디언트의 크기가 점차 줄어든다.
이는 학습이 급격하게 요동치지 않고, 점진적으로 수렴하게 만드는 중요한 성질이다.

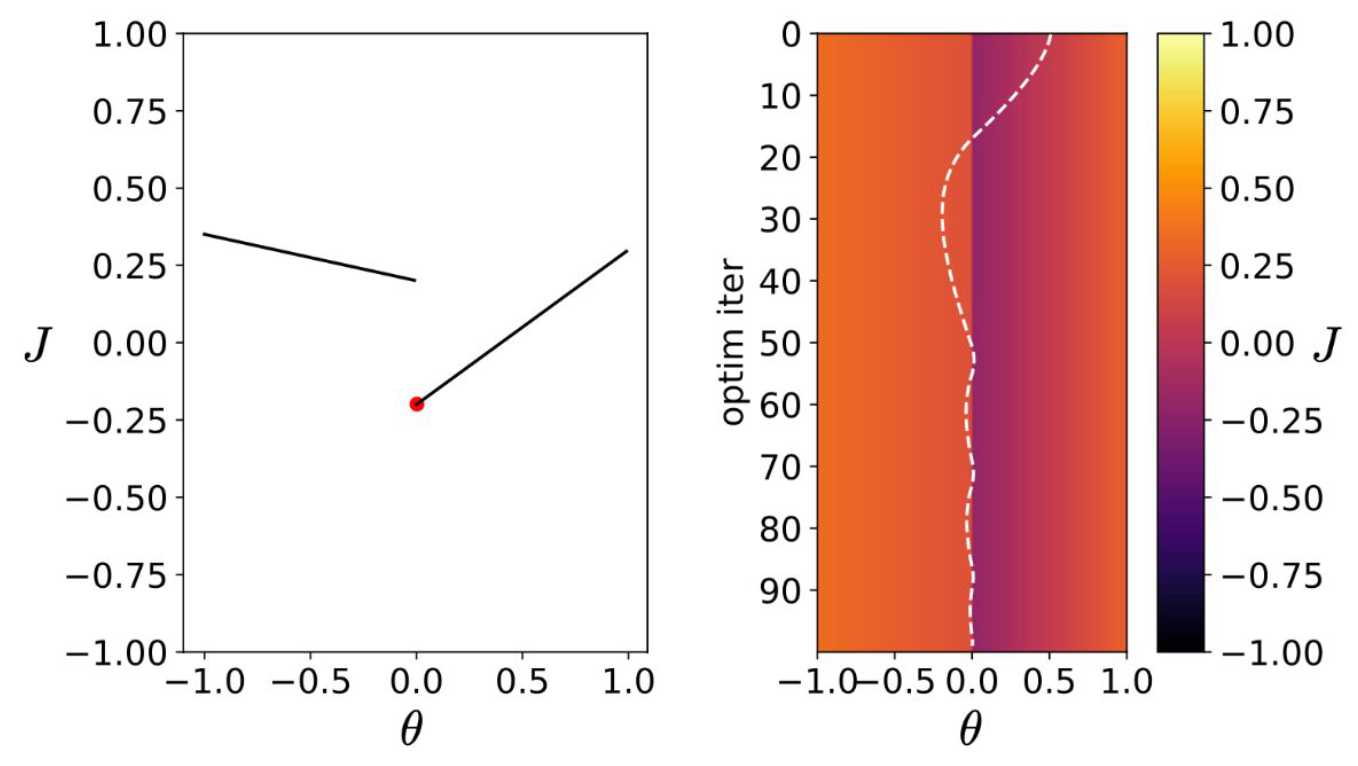
p11. 선형 불연속(구간별 선형) 함수 : Linear discontinuous(Piecewise linear) function

불연속적(discontinuous):

하지만 한쪽에서 정의된 편도 도함수(one-sided derivatives)가 존재한다.
PyTorch에서는 문제가 되지 않는다.

1. 구간별 선형 함수의 특징
구간별 선형 함수(piecewise linear function)는 여러 구간에서 서로 다른 직선으로 정의된다.
이 때문에 특정 지점에서는 미분이 불연속적(discontinuous)일 수 있다.
예시: ReLU 함수 $f(x)=\max(0,x)$ 는 $x=0$에서 기울기가 왼쪽은 $0$, 오른쪽은 $1$로 달라진다.
2. 편도 도함수(one-sided derivative)의 정의 가능성
불연속 지점에서도 왼쪽 미분(left derivative)과 오른쪽 미분(right derivative)을 따로 정의할 수 있다.
따라서 최적화 알고리즘은 어느 방향으로 업데이트할지를 결정할 수 있다.
3. PyTorch와 같은 자동 미분 프레임워크의 처리 방식
PyTorch는 이러한 구간별 정의를 고려하여 편도 도함수(one-sided derivative)를 자동으로 선택한다.
예를 들어 ReLU의 $x=0$에서는 관습적으로 오른쪽 미분(gradient = 1)을 적용하거나, 상황에 따라 0을 선택한다.
덕분에 함수가 불연속적인 모양을 가지더라도 학습 과정(gradient descent)에서는 문제가 되지 않는다.

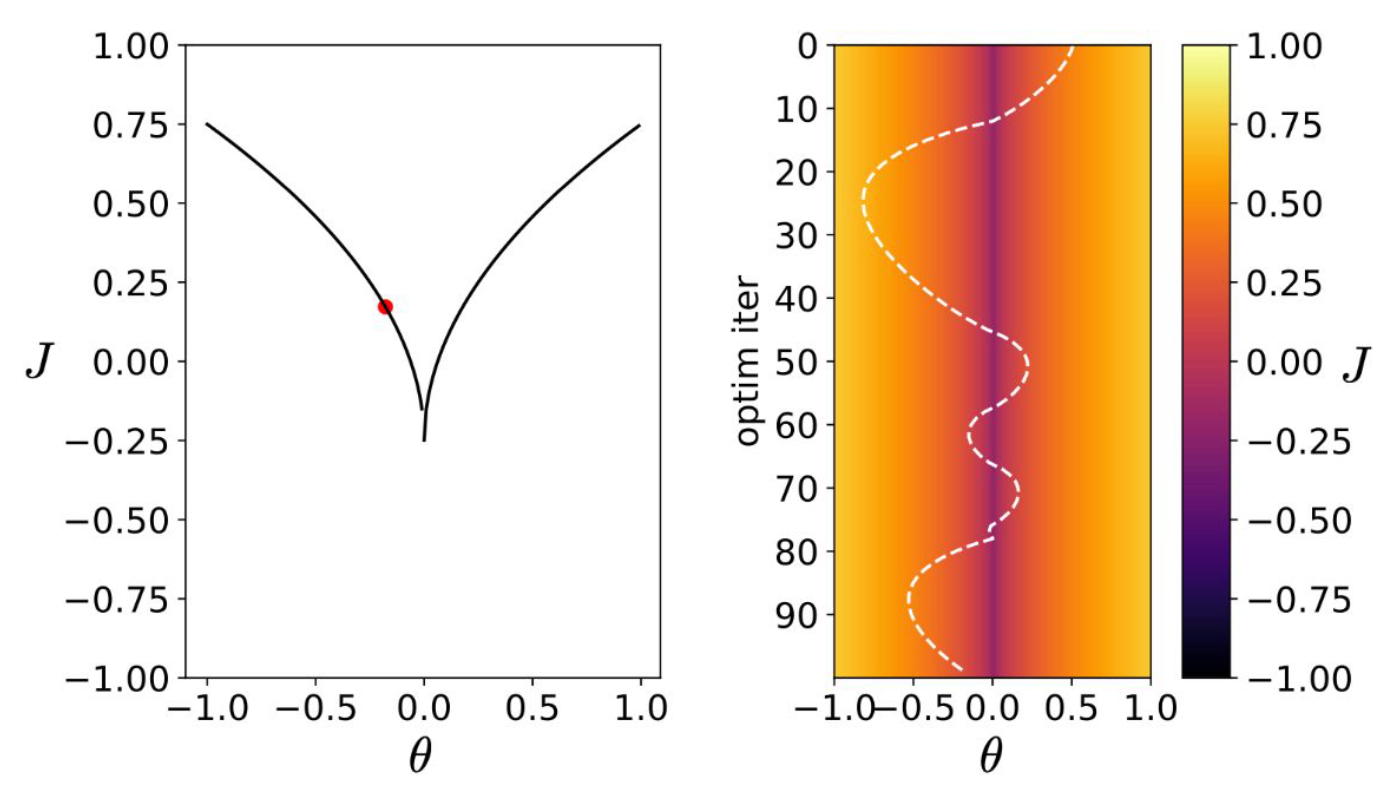
p12. 그래디언트 폭발 (Exploding Gradient)

그래디언트 폭발(Exploding gradient):

최소점(minimizer)에 가까워질수록 그래디언트가 무한대로 발산한다.
불안정한 업데이트와 overshoot(최적점을 지나쳐 버림)이 발생한다.

함수 $1/x$ 의 원점에서의 도함수는 무엇인가?

1. 그래프의 형태
$J(\theta)$ 가 두 곡선이 아래에서 만나면서 $\theta=0$ 근처에서 매우 가파르게 꺾인다.
이 지점에서 그래디언트가 급격히 커지며 발산하는 것이 특징이다.
2. 수학적 해석
예를 들어 $J(\theta)=\frac{1}{\theta}$ 라고 하면,
\[\nabla_\theta J(\theta) = -\frac{1}{\theta^2}\]
$\theta \to 0$ 에 가까워지면 분모가 0에 수렴하므로 그래디언트가 무한대로 커진다.
이로 인해 학습 과정에서 파라미터가 큰 폭으로 갱신되면서 발산하거나 최적점을 지나쳐 버리는 문제가 생긴다.
3. 학습 과정에서의 영향
그래디언트 폭발은 특히 심층 신경망에서 층(layer)의 곱이 누적되면서 발생할 수 있다.
파라미터 업데이트가 지나치게 커져 네트워크가 안정적으로 학습하지 못하게 된다.
이를 막기 위해 그래디언트 클리핑(gradient clipping), 정규화, 적절한 가중치 초기화와 같은 기법이 사용된다. ㄴ

p13. 손실 함수(loss function)에 중요한 것은 무엇인가?

어디에서나 연속적(continuous) 일 것
어디에서나 미분 가능(differentiable) 할 것
어디에서나 매끄럽(smooth) 게 변할 것

이러한 성질들을 가진 “가능한 최선의” 비선형성을 우리는 어떻게 모델링할 수 있을까?

p14. 손실 함수(loss function)에 중요한 것은 무엇인가?

어디에서나 연속적(continuous) ✔️
어디에서나 미분 가능(differentiable) ✔️
어디에서나 매끄럽다(smooth) ✔️

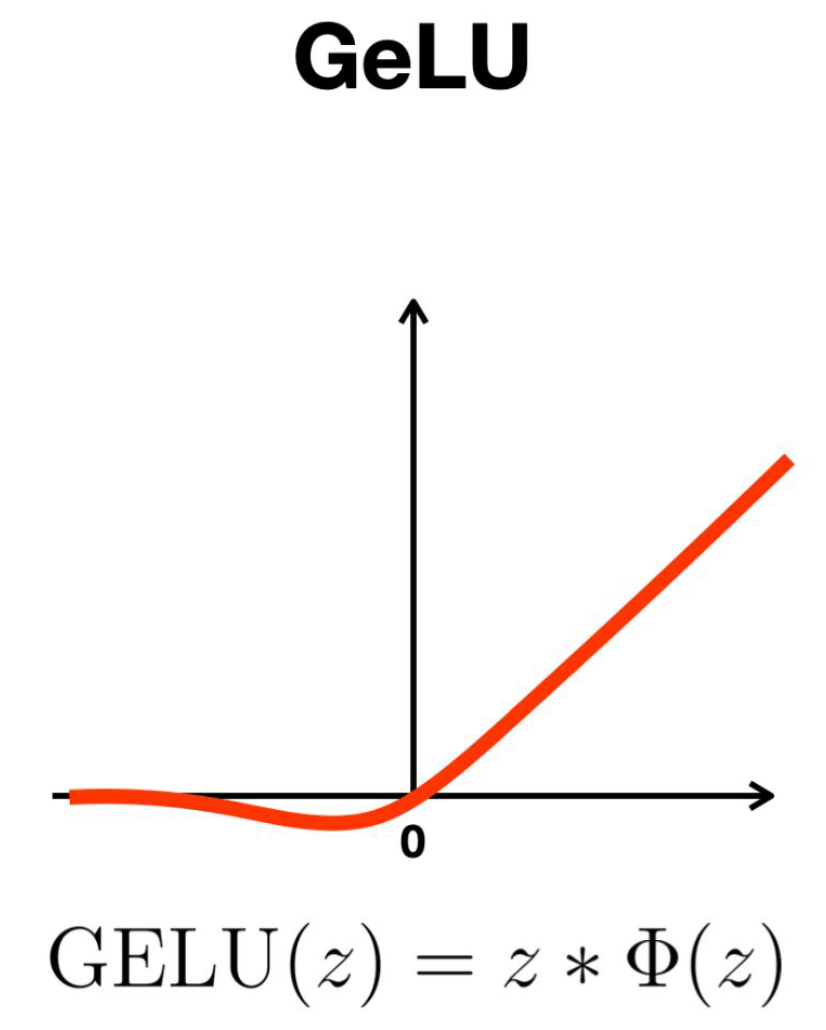
$\Phi$ 는 임의의 매끄러운 함수(smoothing function)이다.

1. GeLU의 정의
GeLU(Gaussian Error Linear Unit)는 활성화 함수의 한 종류로, 입력 $x$에 확률적 매끄러움(smoothing)을 적용한 형태이다.
기본 정의는 다음과 같다:
\[\text{GeLU}(z) = z \cdot \Phi(z)\]
여기서 $\Phi(z)$ 는 표준 정규분포의 누적분포함수(CDF)이다.
2. 정규분포 CDF 형태
$\Phi(z)$ 는 표준 정규분포 확률밀도함수(pdf) $\phi(t)$를 적분해 얻는다.
\[\Phi(z) = \int_{-\infty}^z \phi(t)\, dt, \qquad \phi(t) = \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}}\]
3. 근사 표현 (Practical Approximation)
실제 계산에서는 효율을 위해 $\tanh$ 를 사용한 근사식이 널리 사용된다:
\[\text{GeLU}(z) \approx 0.5z \left( 1 + \tanh \Big( \sqrt{\tfrac{2}{\pi}} \left( z + 0.044715 z^3 \right) \Big) \right)\]
4. 연속성, 미분 가능성, 매끄러움
GeLU는 모든 구간에서 연속적이며 미분 가능하다.
곡선이 부드럽게 연결되는 형태라 매끄러운(smooth) 특성을 가진다.
5. 반복 적용 시의 안정성
연속성, 미분 가능성, 매끄러움의 세 성질이 유지되므로, 여러 층(layer)에 걸쳐 반복적으로 적용해도 학습이 안정적이다.
이러한 특성 덕분에 Transformer, BERT 등 최신 모델에서도 널리 사용된다.

p15. 계산 그래프(Computation Graphs)

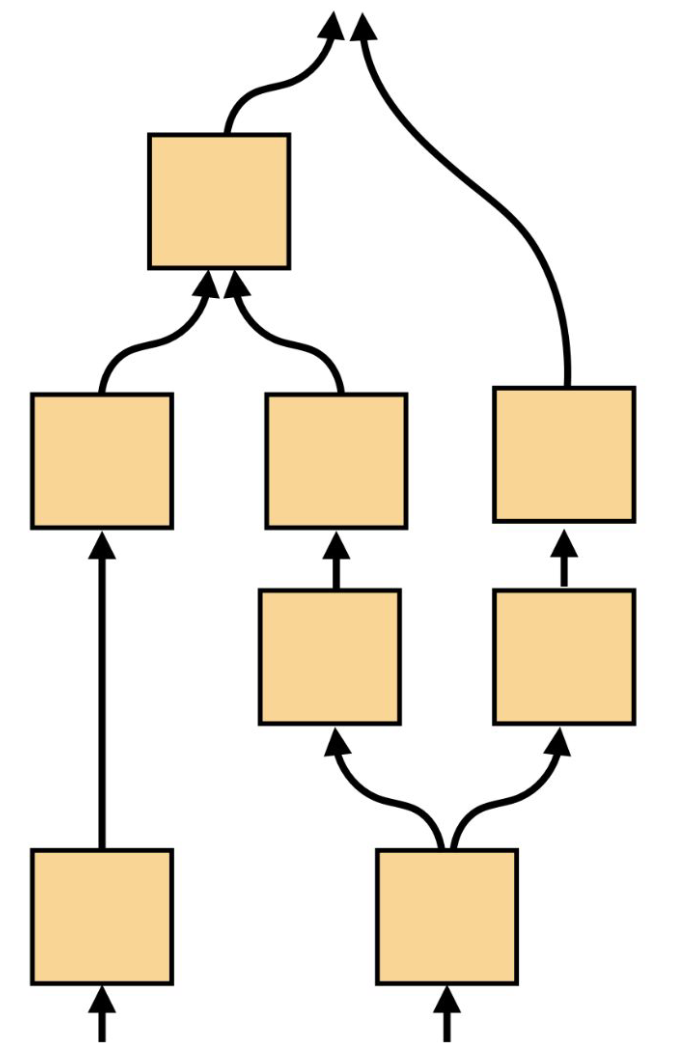
함수적 변환들의 그래프, 즉 노드로 이루어져 있으며, 이들이 연결되면 유용한 계산을 수행한다.
딥러닝은 주로 유향 비순환 그래프(directed acyclic graphs, DAGs) 형태의 계산 그래프를 다루며, 각 노드는 미분 가능하다.

1. 계산 그래프의 개념
계산 그래프는 입력 데이터(예: 텐서)가 여러 연산을 거쳐 출력으로 변환되는 과정을 구조적으로 표현한 것이다.
각 노드는 덧셈, 곱셈, 활성화 함수 등 특정 연산을 나타낸다.
2. DAG 구조의 특징
사이클이 없는 방향 그래프(DAG)이므로 연산의 흐름이 입력에서 출력으로 일방향으로 진행된다.
이 구조 덕분에 순전파(forward pass)와 역전파(backpropagation)를 체계적으로 수행할 수 있다.
3. 프레임워크에서의 활용
PyTorch, TensorFlow 같은 딥러닝 프레임워크는 모델을 정의하면 내부적으로 자동으로 계산 그래프를 생성한다.
이를 통해 복잡한 미분 과정을 자동 미분(autograd)으로 처리할 수 있으며, 사용자는 직접 도함수를 계산할 필요가 없다.

p16. 계산 그래프 (Computation Graph)

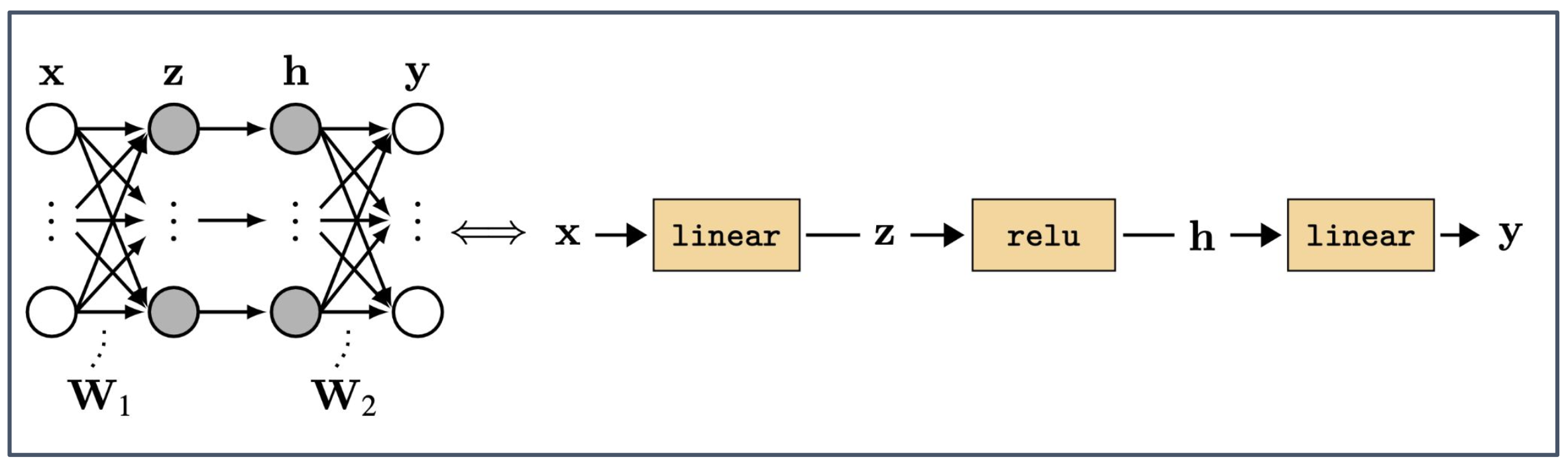
입력 $x$ 가 가중치 $W_1$ 과 결합되어 선형 변환을 거친 후 $z$ 가 된다.
$z$ 는 활성화 함수(ReLU)를 거쳐 은닉 표현 $h$ 가 된다.
$h$ 는 다시 가중치 $W_2$ 와 결합된 선형 변환을 거쳐 출력 $y$ 로 이어진다.

1. 중간 노드(Intermediate node) $z$
$z$ 는 입력 $x$ 와 가중치 $W_1$ 를 곱하고 편향을 더해 얻는 중간 결과물이다.
계산 그래프에서는 이러한 중간 노드가 이후 연산의 입력이 되며, 역전파 시 그래디언트 전파에도 중요한 역할을 한다.
2. 계산 흐름의 구조
선형 변환(linear)과 비선형 활성화 함수(ReLU)가 번갈아 적용되며 모델의 표현력이 강화된다.
계산 그래프는 이 흐름을 순차적으로 나타내어 입력에서 출력으로 이어지는 과정을 직관적으로 이해할 수 있게 한다.
3. 계산 그래프의 해석
신경망의 복잡한 연산을 노드와 엣지의 조합으로 단순화하여 표현할 수 있다.
이는 모델 구조를 분석하거나 자동 미분을 수행할 때 핵심적인 틀이 된다.

p17. 순전파 (Forward pass)

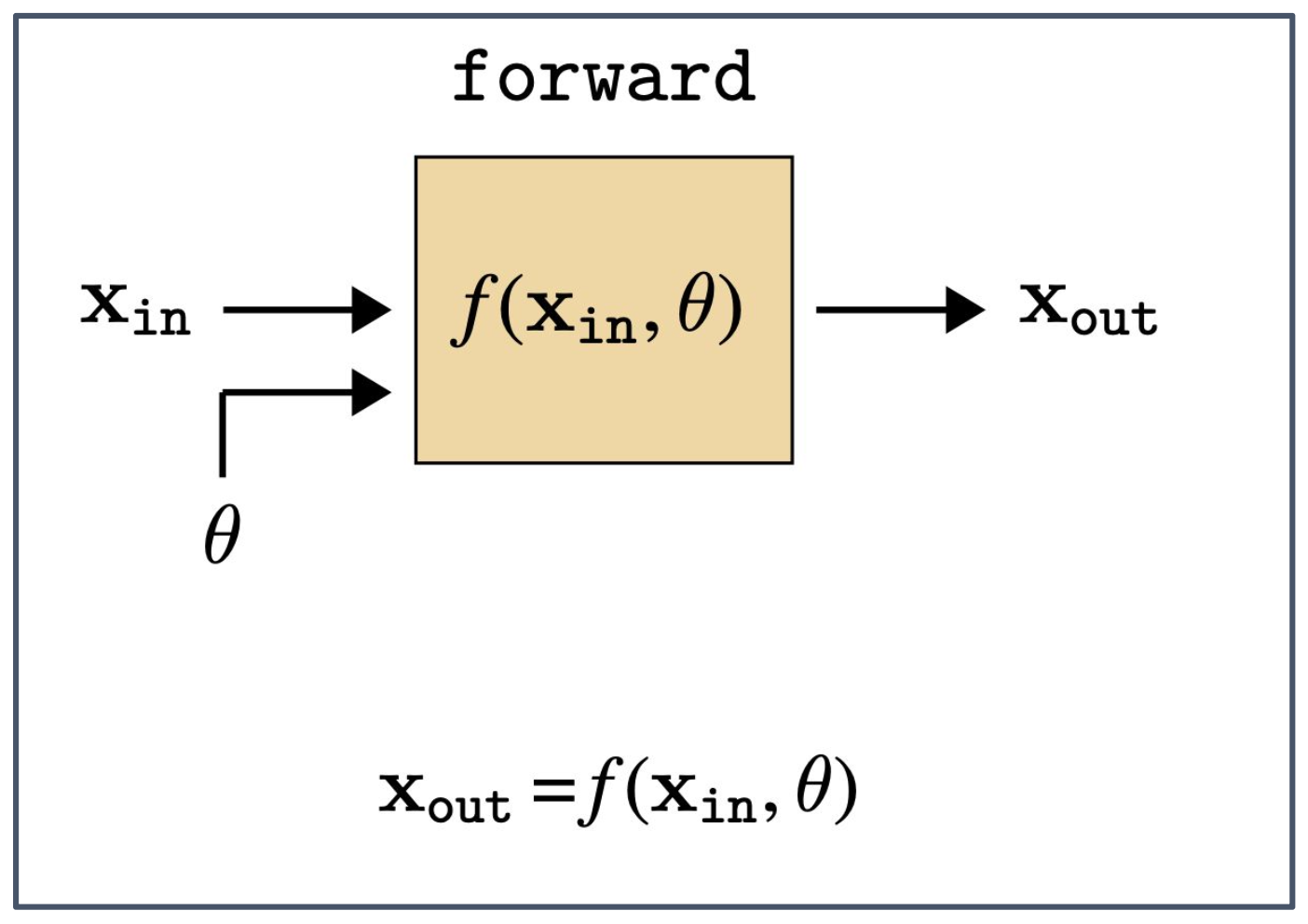
1. 순전파의 정의
순전파(forward pass)는 입력 데이터 $x_{\text{in}}$ 과 모델의 매개변수 $\theta$ 를 함수 $f$ 에 적용하여 출력 $x_{\text{out}}$ 을 얻는 과정이다.
이는 신경망에서 예측을 생성하는 단계에 해당한다.
2. 함수 $f$ 의 역할
$f$ 는 선형 변환, 비선형 활성화 함수, 합성곱(convolution) 연산 등 다양한 연산으로 구성될 수 있다.
계산 그래프 상에서는 이러한 연산들이 일련의 노드와 에지로 표현된다.
3. 학습과의 연계성
순전파에서 얻은 $x_{\text{out}}$ 은 손실 함수(loss function)에 입력되어 모델의 성능을 측정한다.
이후 역전파(backpropagation)를 통해 $\theta$ 에 대한 그래디언트가 계산되고, 파라미터 업데이트로 이어진다.

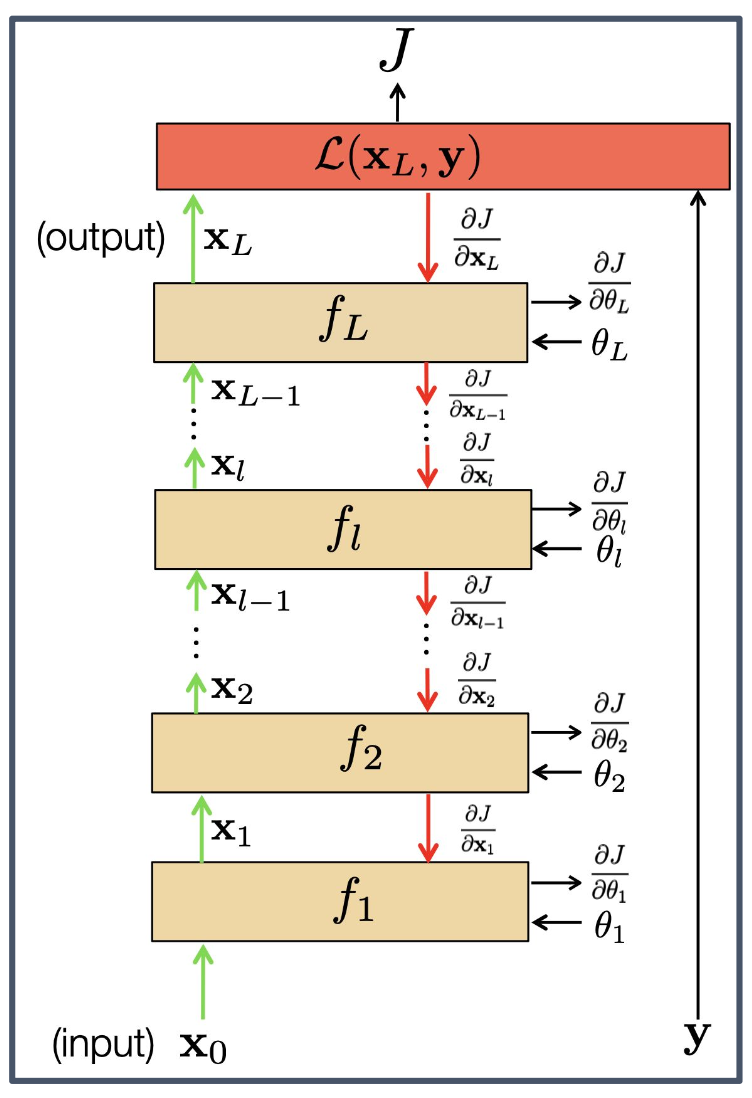
p18. 순전파: 다층 구조 (Forward Path : Multiple Layers)

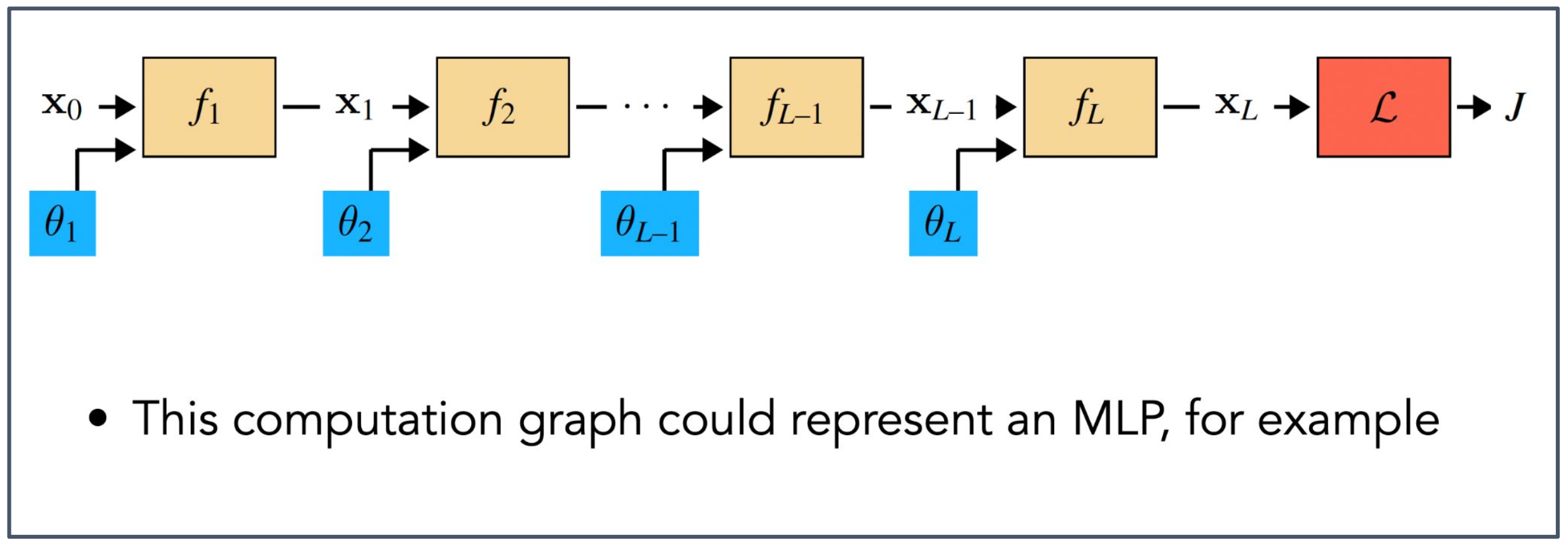
예를 들어, 이 계산 그래프(computation graph)는 다층 퍼셉트론(Multi-Layer Perceptron, MLP)을 나타낼 수 있다.

주어진 계산 그래프 MLP는 “통계적 모델(statistical model)”의 좋은 예시이다.

1. 순전파의 다층 구조
입력 $x_0$ 가 첫 번째 함수 $f_1$ 과 매개변수 $\theta_1$ 에 의해 변환되어 $x_1$ 이 된다.
이후 $x_1$ 은 $f_2$ 와 $\theta_2$ 를 거쳐 $x_2$ 로 변환되고, 이러한 과정이 $L$ 개의 층(layer)에 걸쳐 반복된다.
마지막 층의 출력 $x_L$ 은 손실 함수 $\mathcal{L}$ 에 입력되어 최종 목적 함수 $J$ 가 계산된다.
2. 계산 그래프의 해석
각 함수 $f_i$ 는 선형 변환이나 비선형 활성화 함수를 포함할 수 있고, $\theta_i$ 는 해당 층의 학습 가능한 매개변수이다.
계산 그래프는 입력에서 출력, 그리고 손실 함수에 이르는 전체 흐름을 구조적으로 보여준다.
3. MLP와 통계적 모델
다층 퍼셉트론(MLP)은 계산 그래프 구조를 대표적으로 보여주는 신경망 모델이다.
여러 층을 통해 특징을 변환하며, 확률적 또는 통계적 관점에서 해석 가능한 모델로 확장된다.

p19. 다층 신경망 학습 (Training Multi-layer Neural Networks)

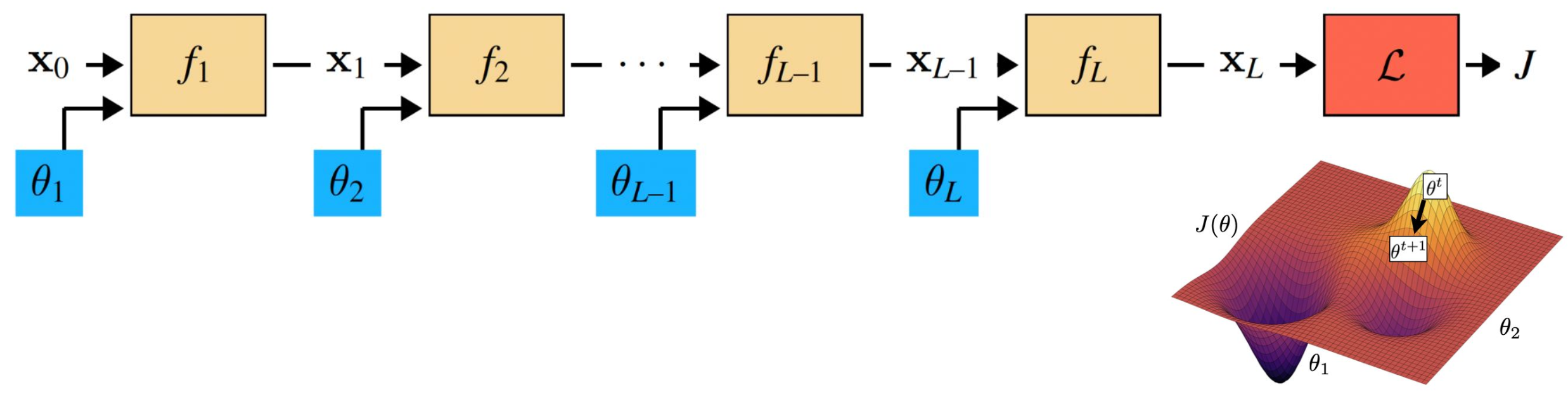
우리는 비용 함수 $J$ 의 그래디언트를 모델 매개변수(model parameters) 에 대해 계산해야 한다.
설계상, 각 층은 자신의 입력(데이터와 매개변수)에 대해 미분 가능하도록 구성된다.

1. 그래디언트의 전파
최종 출력 $J$ (비용 함수)에서 그래디언트가 계산되고, 연쇄법칙(chain rule)에 의해 역전파된다.
이 과정에서 각 층 $f_1, f_2, \dots, f_L$ 에 대응하는 매개변수 $\theta_1, \theta_2, \dots, \theta_L$ 에 대한 그래디언트가 계산된다.
2. 비용 함수 표면에서의 최적화
오른쪽 그림은 비용 함수 $J(\theta)$ 의 표면을 나타내며, 매개변수 $\theta$ 가 반복(iteration)을 거치며 업데이트되는 과정을 보여준다.
그래디언트는 현재 지점에서의 기울기를 바탕으로 파라미터가 이동할 방향과 크기를 결정한다.

p20. 벡터(행렬) 미적분학 요약

x: 크기가 $[n \times 1]$인 열 벡터(column vector)

\[\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\]

벡터 x에 대한 함수를 정의한다:

\[\mathbf{y} = f(\mathbf{x})\]

$y$가 스칼라인 경우

\[\frac{\partial y}{\partial \mathbf{x}} = \left( \frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2}, \dots, \frac{\partial y}{\partial x_n} \right)\]

→ 이때 도함수는 크기가 $[1 \times n]$인 행 벡터(row vector) 가 된다.
$\mathbf{y}$가 $[m \times 1]$ 벡터인 경우 (야코비안, Jacobian 표현식)

\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n} \end{pmatrix}\]

→ 이때 도함수는 크기가 $[m \times n]$인 행렬(matrix) 이 된다.
(행의 개수는 $m$, 열의 개수는 $n$)

p21. 벡터(행렬) 미적분학 요약

$y$가 스칼라(scalar)이고, X가 크기 $[n \times m]$인 행렬(matrix)이라면

\[\frac{\partial y}{\partial \mathbf{X}} = \begin{pmatrix} \frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{21}} & \cdots & \frac{\partial y}{\partial x_{n1}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y}{\partial x_{1m}} & \frac{\partial y}{\partial x_{2m}} & \cdots & \frac{\partial y}{\partial x_{nm}} \end{pmatrix}\]

결과는 크기가 $[m \times n]$인 행렬(matrix)이다.

p22. 벡터(행렬) 미적분학 요약

연쇄 법칙(Chain rule):
함수 $h(\mathbf{x}) = f(g(\mathbf{x}))$ 에 대하여,
그 도함수는 다음과 같다:
\[h'(\mathbf{x}) = f'(g(\mathbf{x})) g'(\mathbf{x})\]
$\mathbf{z} = f(\mathbf{u}), \ \mathbf{u} = g(\mathbf{x})$ 로 두면:
\[\left.\frac{\partial \mathbf{z}}{\partial \mathbf{x}}\right|_{\mathbf{x}=a} = \left.\frac{\partial \mathbf{z}}{\partial \mathbf{u}}\right|_{\mathbf{u}=g(a)} \cdot \left.\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\right|_{\mathbf{x}=a}\]
- $\frac{\partial \mathbf{z}}{\partial \mathbf{x}} \in \mathbb{R}^{m \times n}$
- $\frac{\partial \mathbf{z}}{\partial \mathbf{u}} \in \mathbb{R}^{m \times p}$
- $\frac{\partial \mathbf{u}}{\partial \mathbf{x}} \in \mathbb{R}^{p \times n}$
여기서 $p =$ 벡터 $\mathbf{u}$의 길이($\mid \mathbf{u} \mid$),
$m = \mid \mathbf{z} \mid$, $n = \mid \mathbf{x} \mid$.
예시:
$\mid \mathbf{z} \mid = 1$, $\mid \mathbf{u} \mid = 2$, $\mid \mathbf{x} \mid = 4$ 라면

p23. 연쇄 법칙(Chain Rule)에 의한 동적 프로그래밍

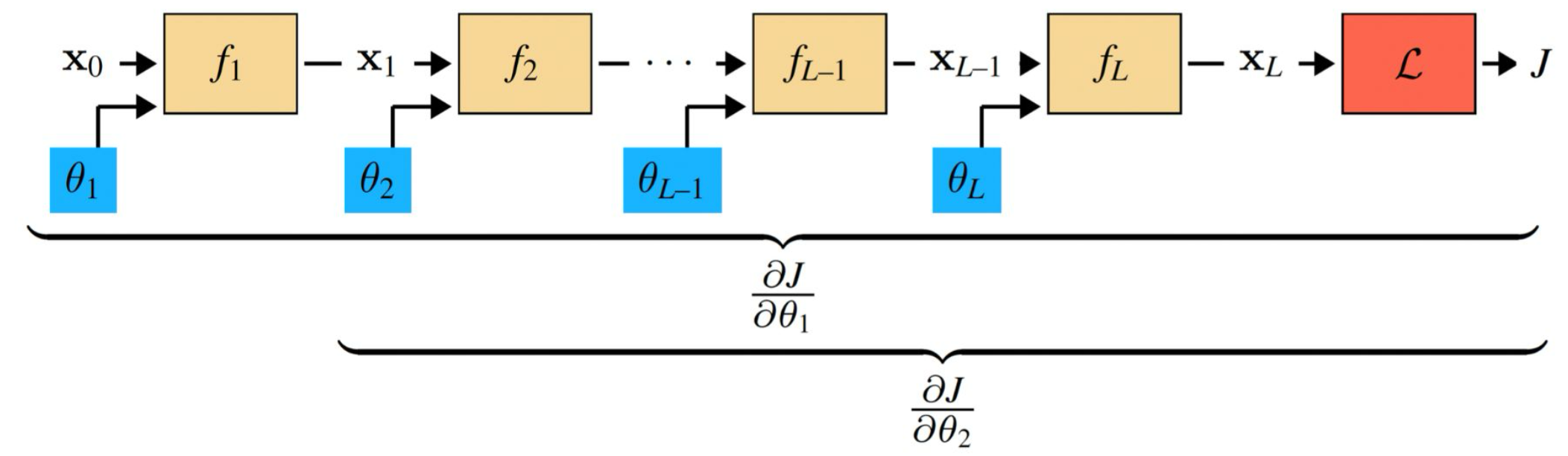
우리는 연쇄 법칙을 사용하여 모든 도함수를 개별적으로 계산할 수 있다.
그러나 회색 박스 안의 항들은 공유된다. 따라서 이 값은 한 번만 계산하면 된다.
역전파(Backpropagation) 는 계산 그래프 전체에서 공유되는 항들을 전파(propagating)하는 알고리즘이다.

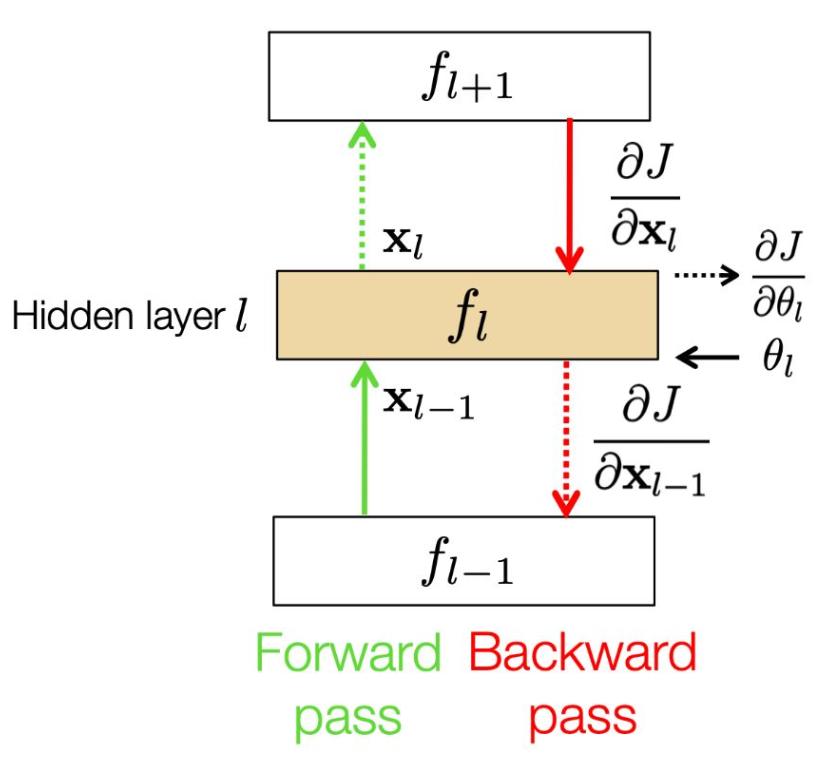
p24. 정보의 순방향 / 역방향 (Forward / Backward direction of information)

Forward pass

네트워크를 통해 데이터를 순방향으로 전달하며, 출력을 계산하고 손실(loss)을 계산한다.

Backward pass

출력과 손실로부터의 오차 신호(그래디언트)를 네트워크를 통해 역방향으로 전달하여, 입력과 매개변수로 되돌려 준다.

p25. 일반적인 층(Generic Layer)의 역전파

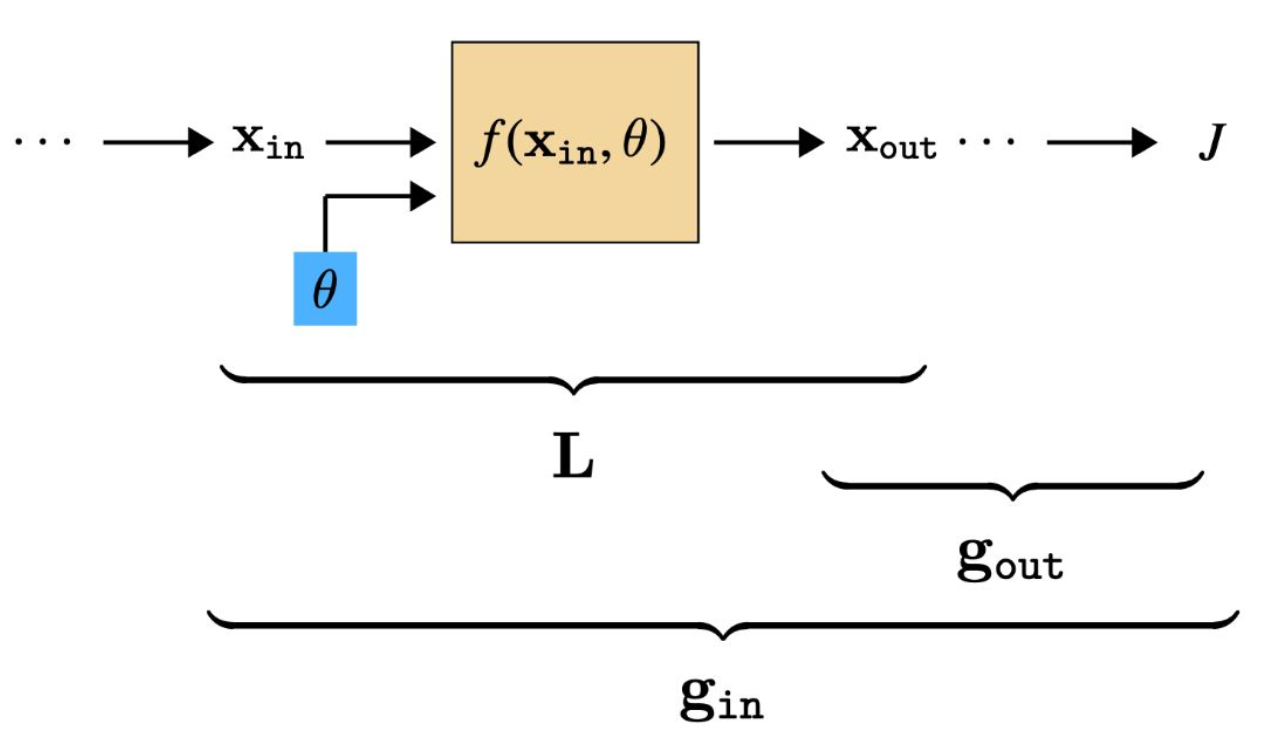
우리는 두 종류의 편도함수 배열을 추적할 것이다:
- L : 층 입력에 대한 층 출력의 그래디언트 (행렬)
- g : 활성화(activation)에 대한 비용(cost)의 그래디언트 (행 벡터)

p26. 일반적인 층(Generic Layer)의 역전파 (계속)

한 층에 대해 L 과 g 를 알고 있다면, 매개변수 업데이트(parameter update) 는 간단하다.

p27. 일반적인 층(Generic Layer)의 역전파 (계속)

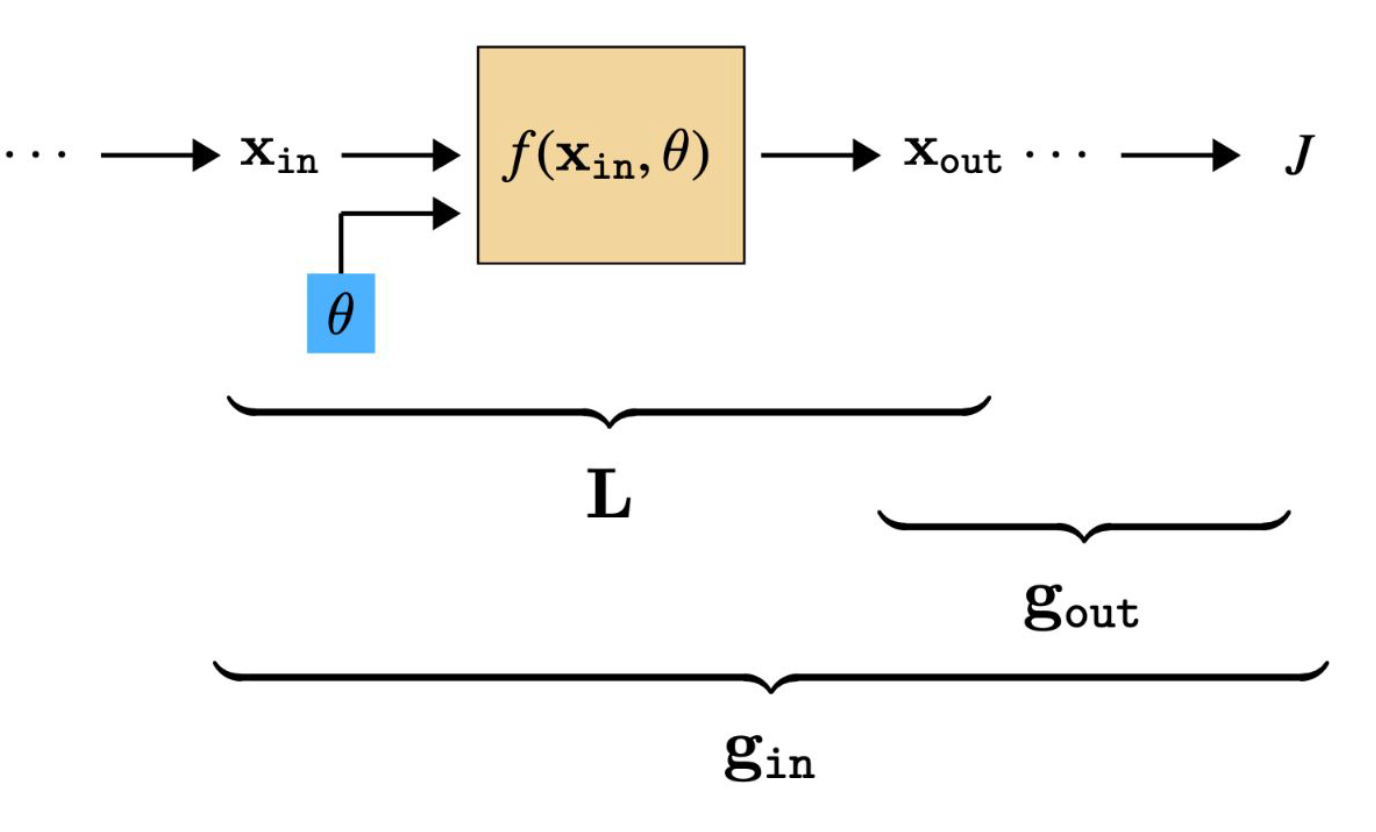
그런데, 각 층에 대해 $L$ 과 $g$ 는 어떻게 구할 수 있을까?
L 은 해당 층의 도함수 함수 $f’$ 로부터 얻어진다 (주어진다고 가정함):

g 는 다음의 점화식을 통해 반복적으로 계산될 수 있다:

오차 신호의 역전파(backpropagation of error signals)를 통해 그래디언트가 전달된다.

p28. 일반적인 층(Generic Layer)의 역전파

이 모든 과정은 매개변수 갱신 방향(parameter update directions) 을 계산하기 위한 것이다.

p29. 모든 것을 종합하기 (Putting it all together)

Forward

데이터를 네트워크를 따라 순방향으로 전달하여 출력과 손실(loss)을 계산한다.

Backward

출력과 손실로부터 발생한 오차 신호(그래디언트) 를 네트워크를 통해 역방향으로 전달한다.

Update:

매개변수 갱신

그리고 이 과정을 반복한다.

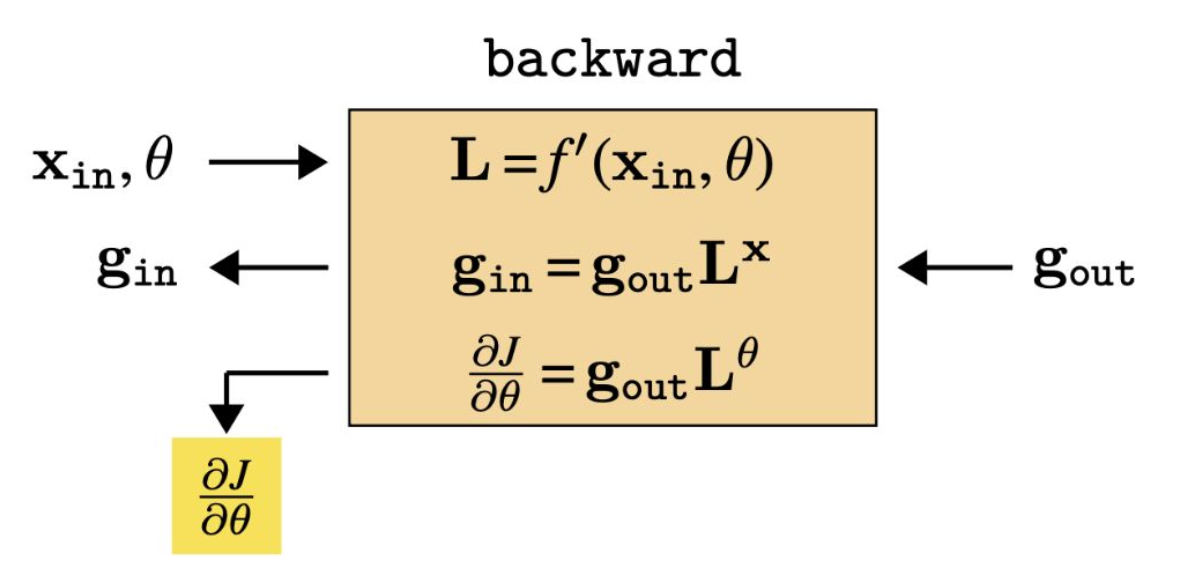
p30. 일반적인 층(Generic Layer)에 대한 역전파

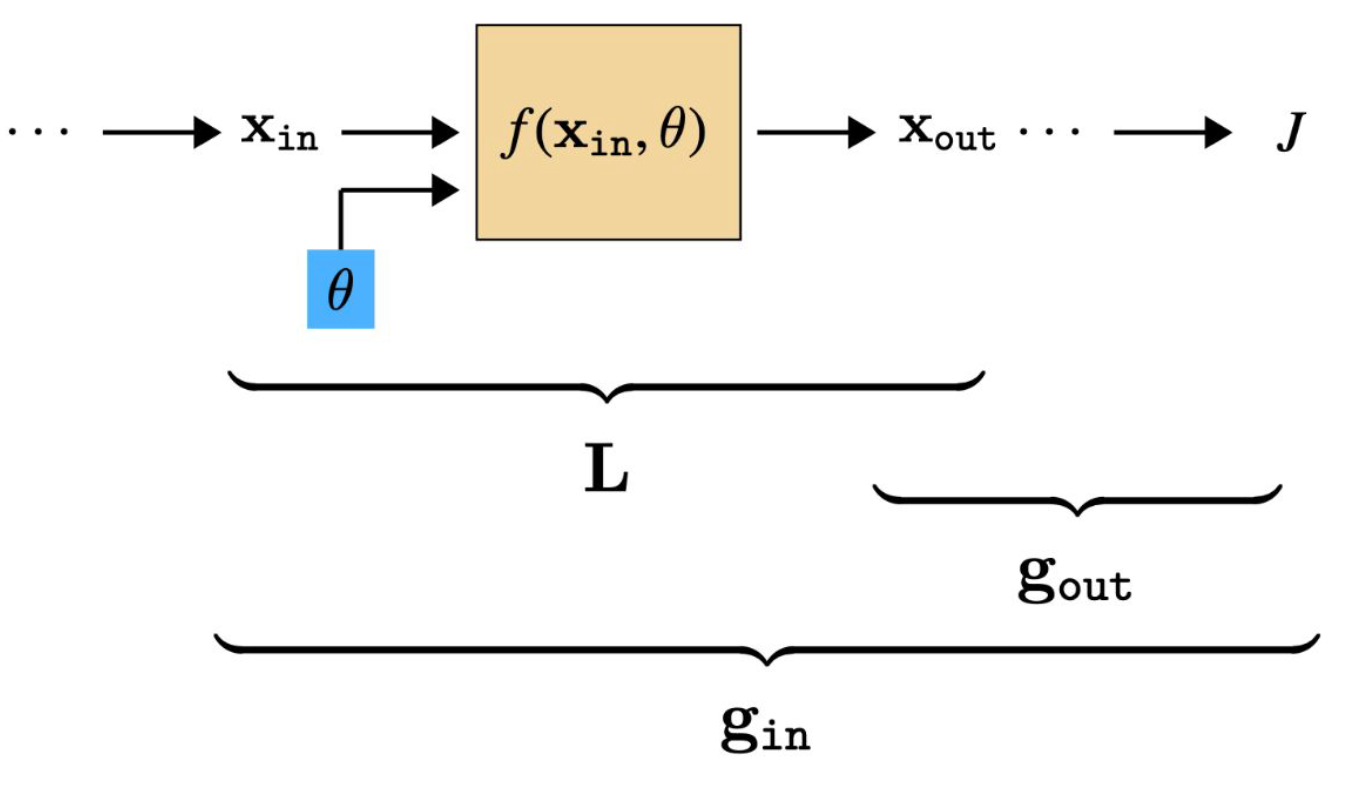
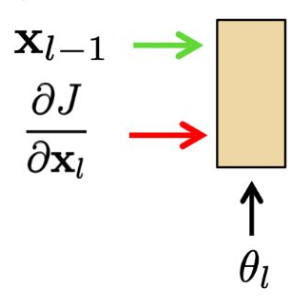
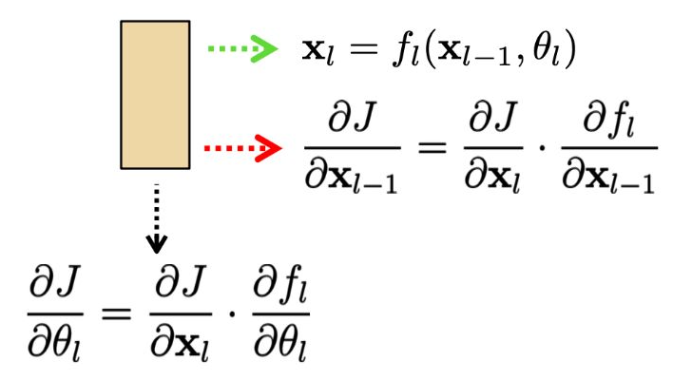
학습하는 도중 층(layer) $l$은 세 개의 입력을 가진다:

그리고 세 개의 출력을 가진다:

주어진 입력이 있을 때, 우리는 다음을 계산하면 된다:

p31. 요약 (Summary)

Forward pass: 각 학습 예제에 대해, 모든 층의 출력을 계산한다.

\[x_l = f_l(x_{l-1}, \theta_l)\]

Backward pass: 위에서부터 아래로 순차적으로 손실 함수의 도함수를 계산한다.

\[\frac{\partial J}{\partial x_{l-1}} = \frac{\partial J}{\partial x_l} \cdot \frac{\partial f_l}{\partial x_{l-1}}\]

Parameter update: 가중치에 대한 그래디언트를 계산하고, 가중치를 갱신한다.

\[\frac{\partial J}{\partial \theta_l} = \frac{\partial J}{\partial x_l} \cdot \frac{\partial f_l}{\partial \theta_l}\]

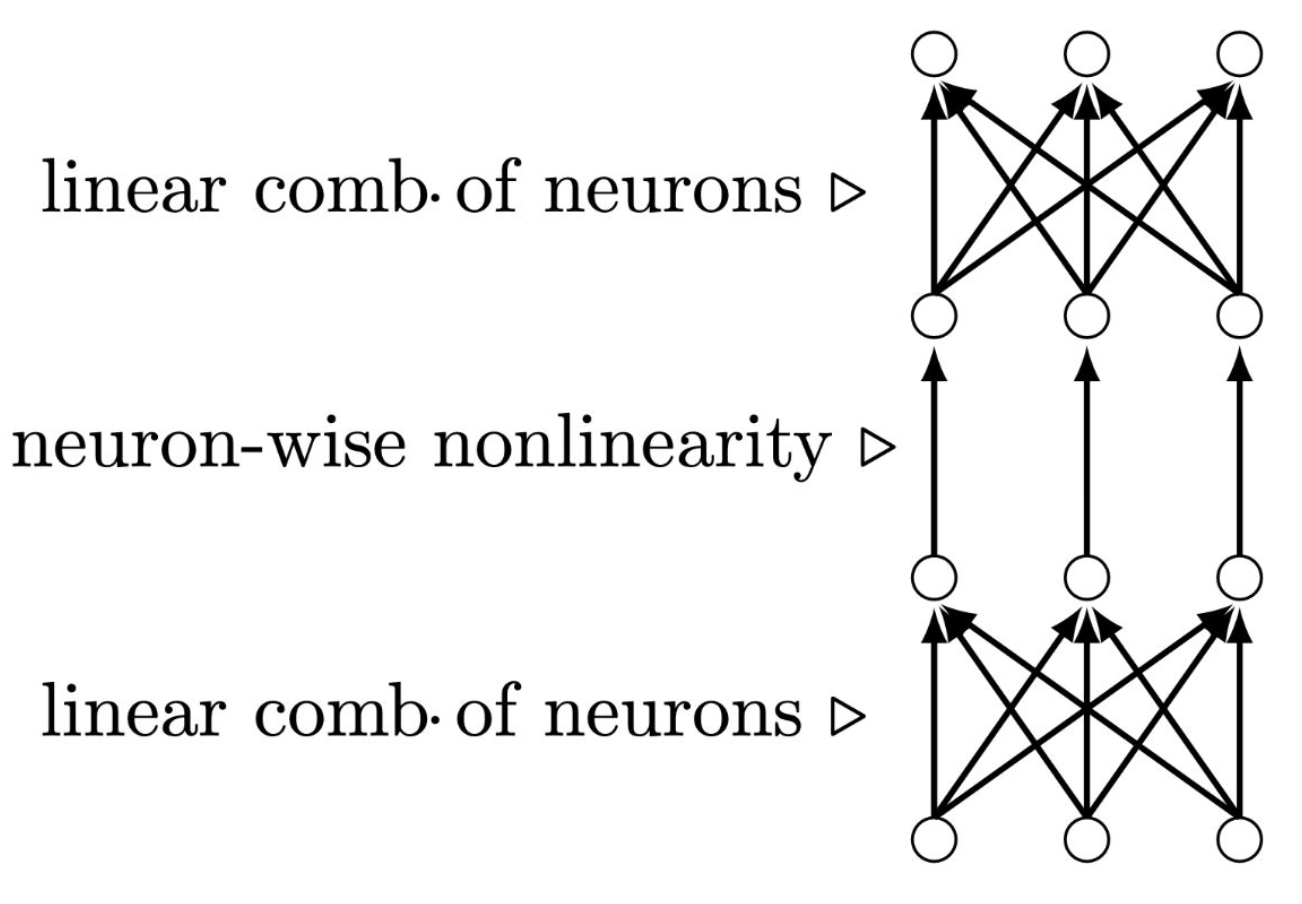
p32. 다층 퍼셉트론(MLP)? 장점과 단점

장점

보편성 (Universal)
단순함, 우아한 이론 (Simple, elegant theory)
병렬화가 매우 쉬움 (Embarrassingly parallel)

단점

약한 귀납적 편향 (Weak inductive biases)
샘플 비효율적, 데이터 많이 필요 (Sample inefficient / data hungry)
밀집된(fully-connected) 선형 계층은 많은 계산 자원을 소모함

약한 귀납적 편향(Weak Inductive Bias)의 의미
귀납적 편향(Inductive bias)은 모델이 학습할 때 데이터로부터 일반화(generalization)를 가능하게 만드는 사전적 가정(prior assumption)을 의미한다.
예: CNN은 인접한 픽셀이 관련 있다는 지역성(locality), 특징이 위치와 상관없이 나타난다는 평행이동 불변성(translation invariance)을 가진다.
예: RNN은 순서(sequence)가 있는 데이터라는 시간적 의존성(temporal dependency)을 가정한다.
반면 MLP(다층 퍼셉트론)는 모든 입력 노드가 모든 출력 노드에 연결되는 완전연결 구조를 사용하므로
입력의 공간적·시간적 구조에 대한 사전 가정이 거의 없다.
즉, 모델이 모든 패턴을 처음부터 스스로 학습해야 하므로 귀납적 편향이 약하다.
결과적으로, 약한 귀납적 편향의 특징은 다음과 같다.
표현력(expressivity)은 높다.
그러나 데이터 효율성(data efficiency)은 낮아, 많은 데이터와 계산 자원이 요구된다.
요약:
MLP는 사전 구조 가정이 거의 없어 어떤 패턴도 표현할 수 있지만,
대신 모든 규칙을 직접 학습해야 해서 데이터가 많이 필요하고 일반화가 어렵다.

p33. 왜 다른 아키텍처(architecture)를 사용해야 하는가?

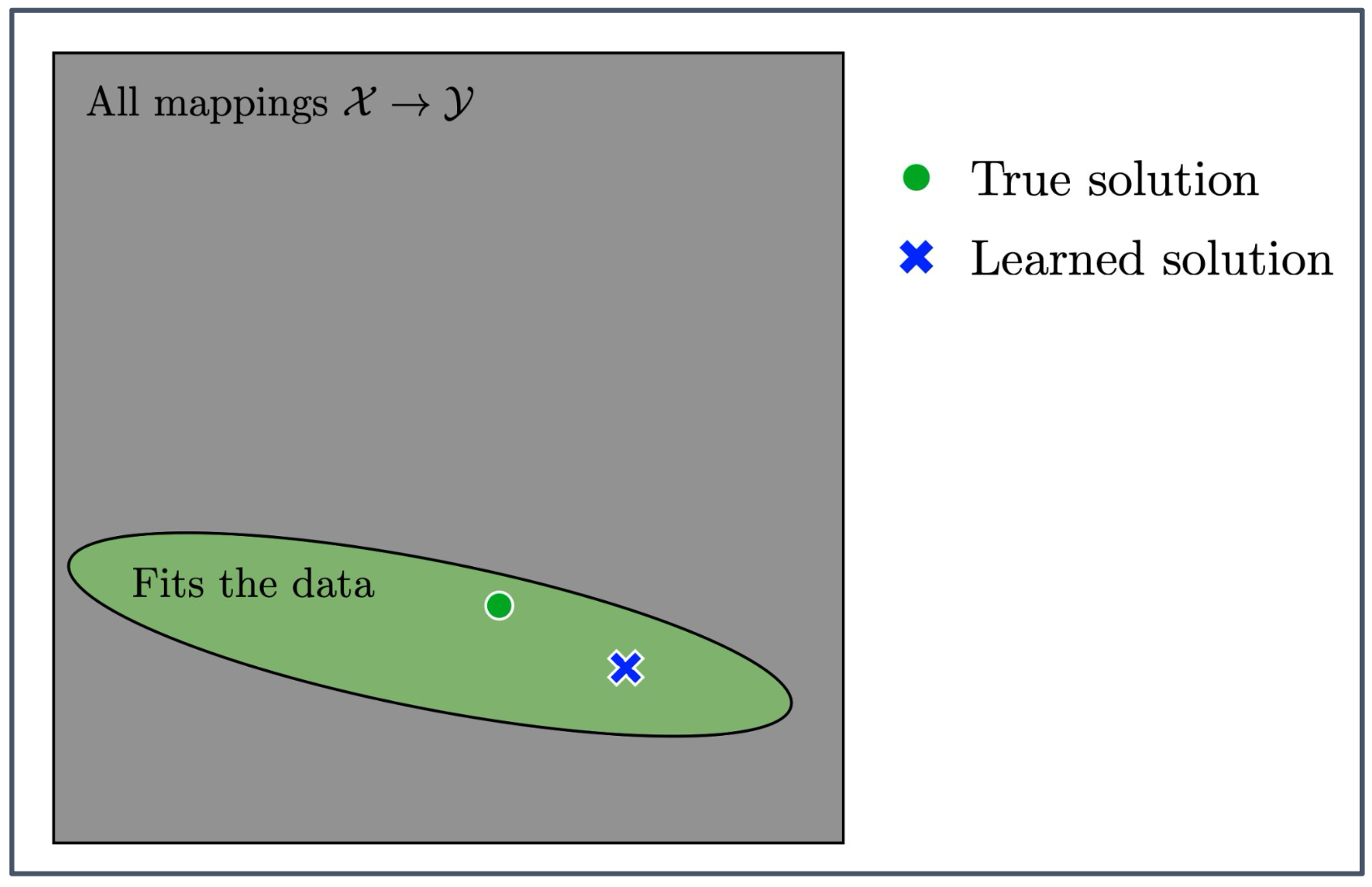
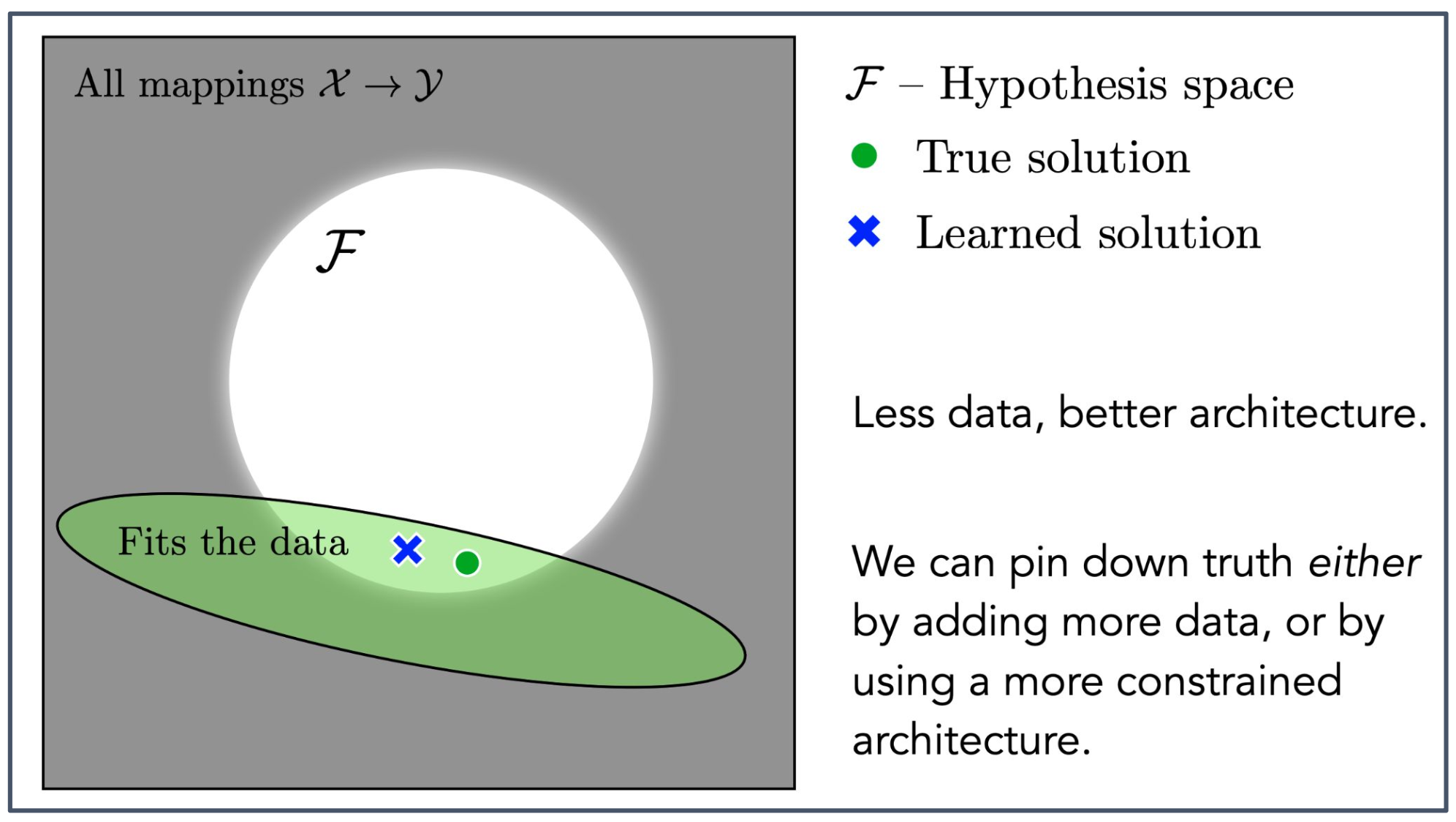
전체 회색 사각형의 의미
입력 공간 $\mathcal{X}$ 에서 출력 공간 $\mathcal{Y}$ 로 가는 모든 가능한 함수들의 집합을 의미한다.
즉, 이 안에는 우리가 상상할 수 있는 모든 입력–출력 매핑이 포함되어 있다.
초록색 타원의 의미
주어진 데이터를 설명할 수 있는 함수들의 집합을 나타낸다.
이 영역 안의 함수들은 최소한 관찰된 데이터에는 들어맞는 함수들이다.
위 그림의 종합적인 의미
실제로는 모든 가능한 함수(회색 영역)를 다 고려하는 것이 아니라,
데이터에 맞는 함수(초록색 영역) 중에서 학습 알고리즘이 하나의 해답(파란색 X)을 선택한다는 것을 보여준다.
하지만 선택된 해답이 참 해답(초록색 원)과 항상 일치하는 것은 아니다.

p34. 왜 다른 아키텍처(architecture)를 사용해야 하는가?

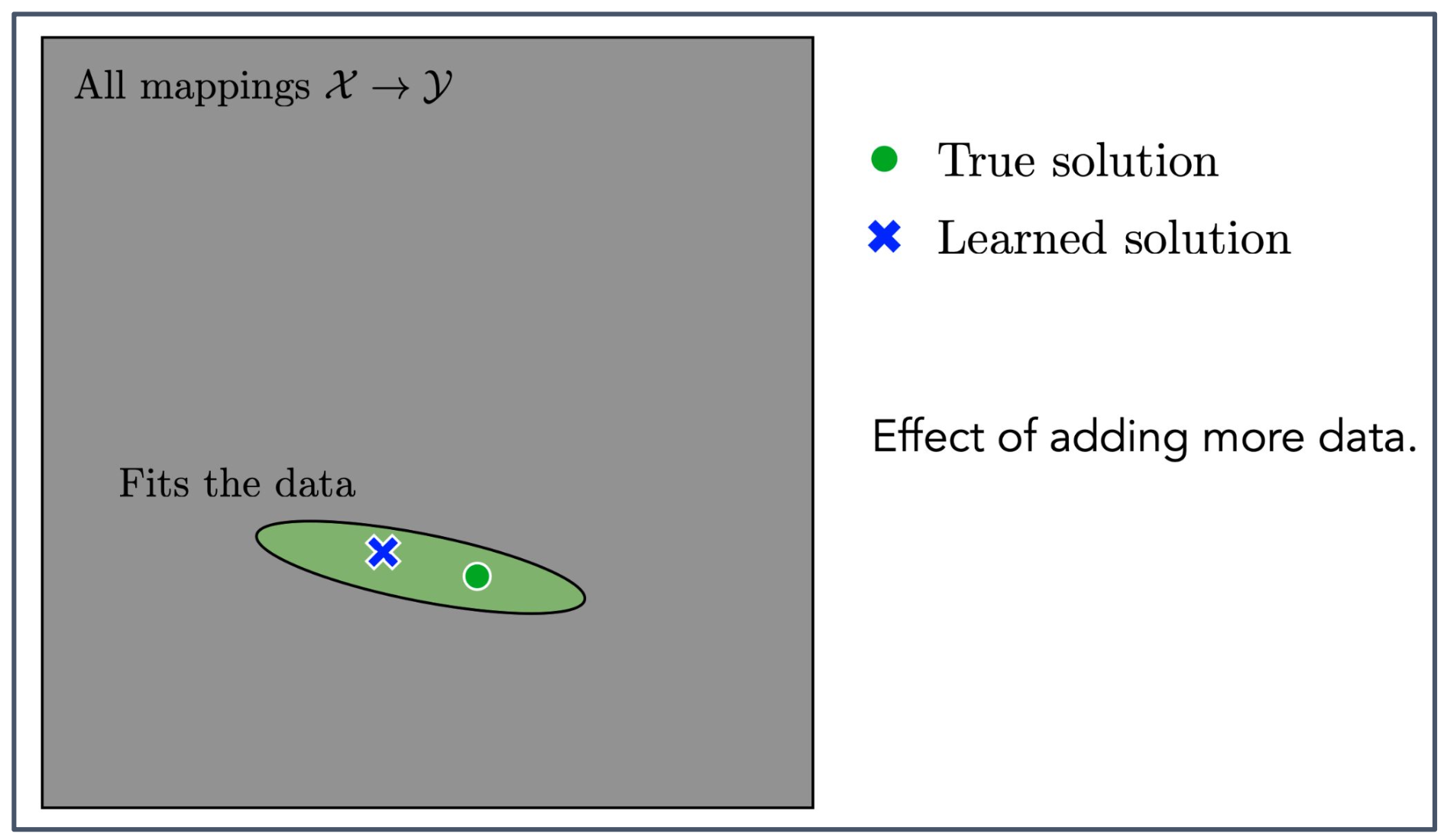
데이터의 역할
학습에 사용되는 데이터가 많아질수록, 주어진 데이터와 잘 맞는 해답의 범위가 점점 좁아진다.
그림의 의미
33페이지에서 보여준 초록색 영역(Fits the data)이 더 작은 타원으로 표현된다.
이는 모델이 찾을 수 있는 해답의 불확실성이 줄어드는 과정을 의미한다.

p35. 왜 다른 아키텍처(architecture)를 사용해야 하는가?

데이터가 적을수록, 더 나은 아키텍처가 필요하다.

우리는 참 해답에 더 가까워질 수 있다.

방법 1: 더 많은 데이터를 추가하는 것
방법 2: 더 제한적인 아키텍처를 사용하는 것

가설 공간(hypothesis space)은 모델이 만들 수 있는 함수들의 전체 집합을 의미한다.
초록색 타원은 주어진 데이터와 일치하는 함수들의 집합이며,
흰색 원 $\mathcal{F}$ 는 현재 모델 구조(architecture)로 표현 가능한 함수들의 범위이다.
두 영역이 겹친다는 것은
데이터와 맞는 함수들 중에서 모델이 실제로 표현할 수 있는 후보가 존재한다는 뜻이다.
더 제한적인 아키텍처란 모델이 표현할 수 있는 함수의 범위를 인위적으로 줄이는 것을 의미한다.
예: 모든 복잡한 함수를 허용하는 대신
CNN의 합성곱 구조나 RNN의 순차 구조처럼 특정 형태를 강제로 사용하는 것.
이러한 구조적 제한은 학습된 해답(파란 X)이 불필요하게 넓은 함수 공간에 퍼지지 않도록 하고,
참 해답(초록 O)에 더 가깝도록 후보 영역을 좁혀주는 효과를 가진다.

p36. 일반화(Generalization)와 아키텍처(Architectures)

— 참 해답 (True solution)
— 학습된 해답 (Learned solution)
● 훈련 데이터 (Training data)

1. 일반화의 의미
일반화(generalization)는 훈련 데이터(●)에만 맞추는 것이 아니라, 새로운 입력 구간에서도 참 해답(— True solution)에 가깝게 예측하는 능력을 의미한다.
학습된 해답(— Learned solution)이 초록색 참 해답과 얼마나 잘 일치하는지가 핵심이다.
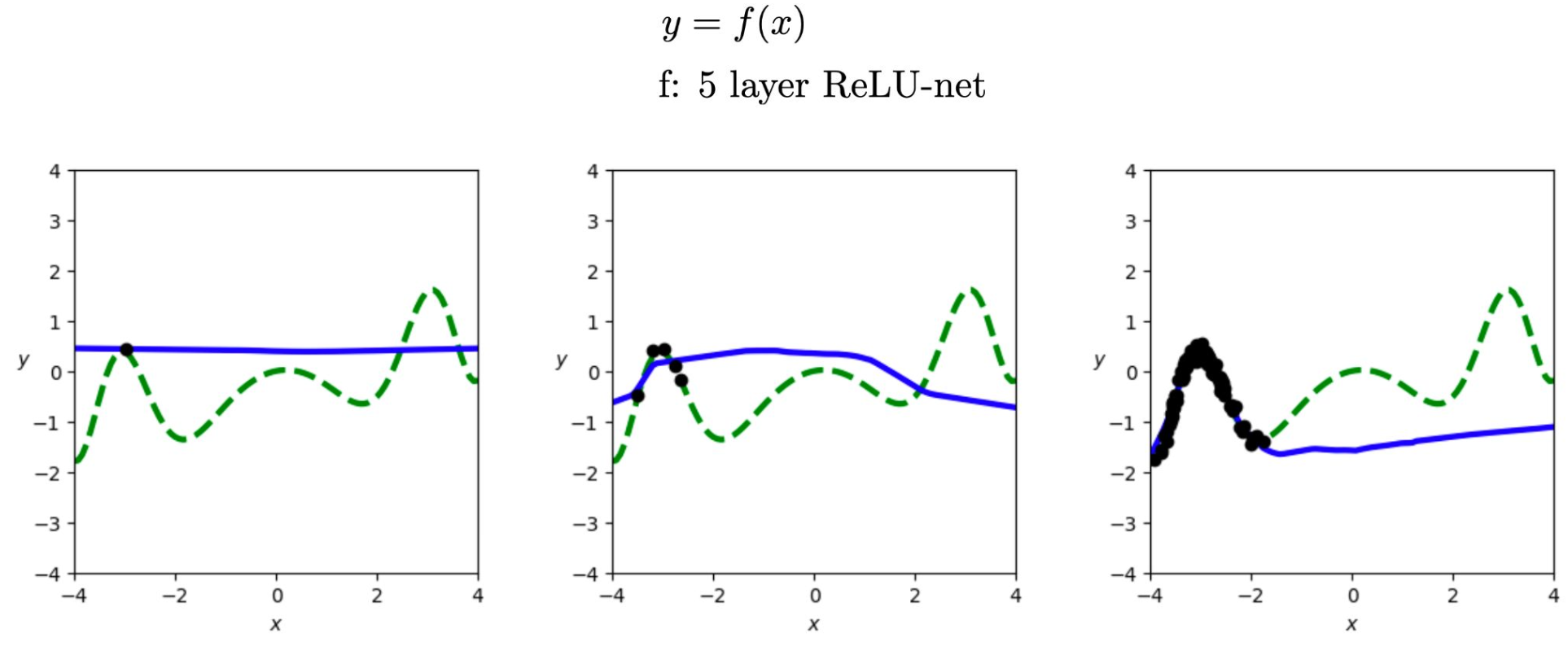
2. 데이터 양의 영향
왼쪽 그래프: 데이터가 매우 적을 때는 모델이 단순한 직선 형태로 해답을 내며, 참 해답과 큰 차이가 난다.
가운데 그래프: 데이터가 조금 늘어나면 훈련 구간 근처에서는 참 해답과 비슷해지지만, 그 외 구간에서는 여전히 단순한 곡선 형태에 머무른다.
오른쪽 그래프: 데이터가 충분해지면 훈련 데이터 구간에서는 참 해답과 거의 일치하지만, 구간 밖에서는 여전히 직선 형태로 벗어난다.
3. 아키텍처의 한계
5층 ReLU 네트워크는 데이터가 늘어날수록 훈련 구간 안에서는 참 해답에 가까워지지만, 훈련 구간 밖에서는 일반화하지 못한다.
이는 데이터 양만 늘린다고 완전한 일반화를 얻을 수 없으며, 아키텍처 설계가 매우 중요함을 보여준다.

p37. 일반화(Generalization)와 아키텍처(Architecture)

— 참 해답 (True solution)
— 학습된 해답 (Learned solution)
● 훈련 데이터 (Training data)

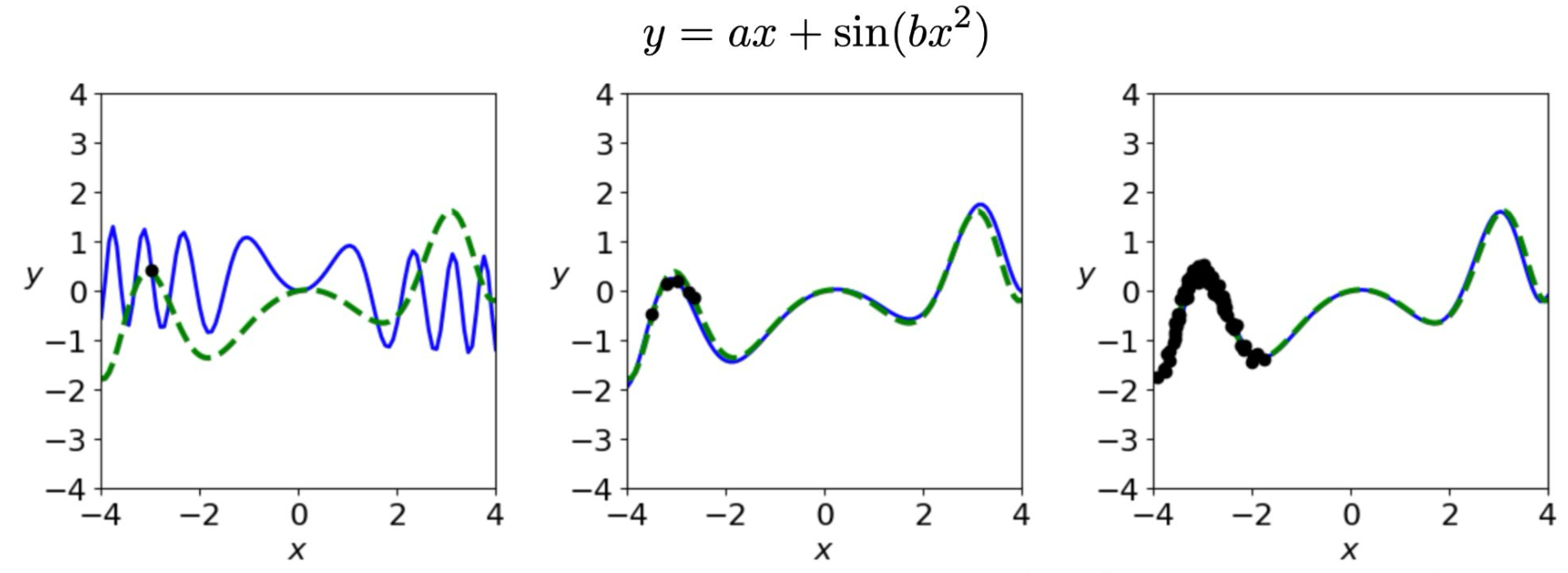
아키텍처(Architecture)는 우리가 훈련 데이터 분포 밖(outside the training distribution)에서도 일반화(generalize)할 수 있도록 도와준다.

좋은 아키텍처(good architecture)는

참 함수를 잘 표현할 수 있어야 하고,
불필요하게 복잡하지 않아야 하며,
경사 기반 학습(gradient-based learning)에 의해 탐색이 용이해야 하고,
병렬화(parallelization)에 적합하고, GPU에서 빠르게 동작할 수 있어야 한다.

1. 36페이지와의 차이점
36페이지에서는 데이터가 많아지면 훈련 구간에서는 참 해답과 일치했지만, 훈련 데이터 밖에서는 단순 직선으로 크게 빗나갔다.
이는 아키텍처가 주어진 데이터 범위에만 맞추는 데 그친 결과이다.
2. 이번 페이지(37p)의 특징
이번 그림에서는 학습 데이터 외 구간에서도 학습된 해답(파란색)이 참 해답(초록색)과 거의 완벽히 일치한다.
즉, 아키텍처를 적절히 선택했기 때문에 데이터가 없는 구간에서도 올바른 함수 형태를 일반화할 수 있었다.
3. 종합적 의미
충분한 데이터만으로는 일반화가 보장되지 않는다.
좋은 아키텍처 선택이 일반화 성능을 크게 좌우한다는 점을 시각적으로 보여준다.

p38. 일반화(Generalization)와 아키텍처(Architecture)

— 참 해답 (True solution)
— 학습된 해답 (Learned solution)
● 훈련 데이터 (Training data)

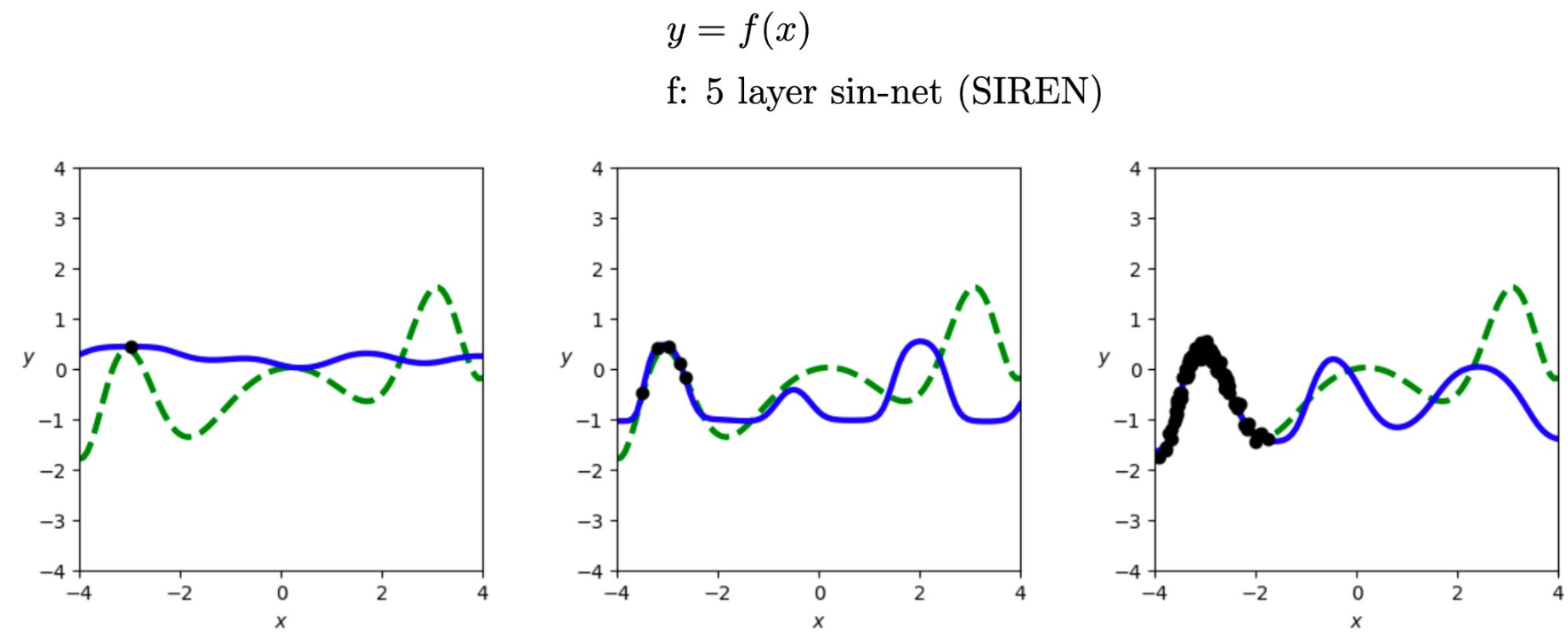
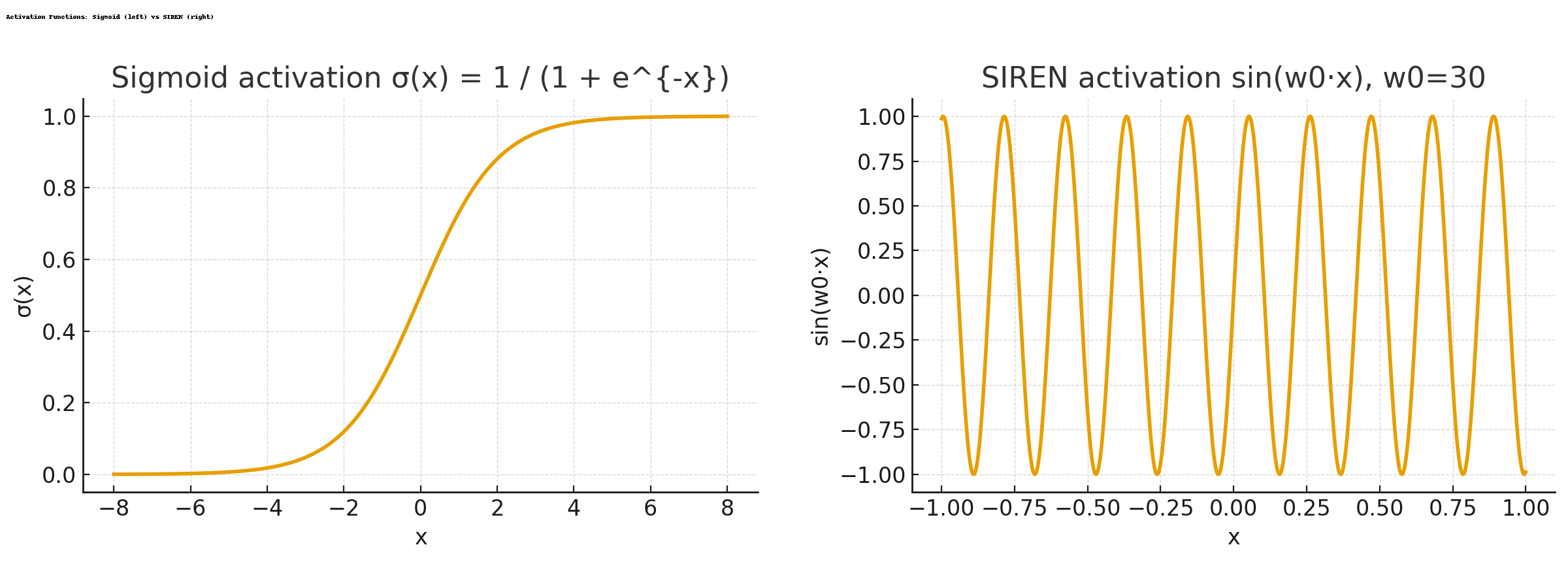
1. SIREN의 핵심 수식(사인 활성화 함수)
일반 MLP: $h^{(\ell)} = \sigma \left(W^{(\ell)}h^{(\ell-1)} + b^{(\ell)}\right)$
SIREN: $h^{(\ell)} = \sin \left(W^{(\ell)}h^{(\ell-1)} + b^{(\ell)}\right)$
실무에서는 첫 층에 주파수 스케일 $\omega_0$를 곱해 고주파 표현력을 높인다:
\[h^{(1)} = \sin\!\left(\omega_0 W^{(1)}x + b^{(1)}\right), \qquad h^{(\ell)} = \sin\!\left(W^{(\ell)}h^{(\ell-1)} + b^{(\ell)}\right), \quad (\ell \ge 2)\]
사인 함수는 연속이고 무한히 미분 가능하며
$\frac{d}{dz}\sin z = \cos z$ 이므로
미분 기반 최적화와 역전파에서 안정적인 신호를 제공한다.
2. 왜 사인을 쓰나?
주기적·진동적 패턴과 세밀한 연속 변화를 자연스럽게 표현할 수 있다.
ReLU(조각별 선형)는 부드럽게 진동하는 참 함수를 근사하기 어려워, 이러한 경우 SIREN이 더 유리하다.
3. 그래프 해석(이 페이지)
데이터가 늘어날수록 학습된 해답(파란색)은 참 해답(초록색)의 주기적 형태를 점진적으로 포착한다.
그러나 모든 구간에서 완전히 일치하지는 않으며, 일부 영역에서는 차이가 남는다.
4. 비교 요약
ReLU 기반(36p)보다 SIREN이 이번 데이터의 구조를 더 잘 반영한다.
하지만 37p의 아키텍처만큼 이 데이터에 완벽히 적합한 최적의 선택은 아니다.

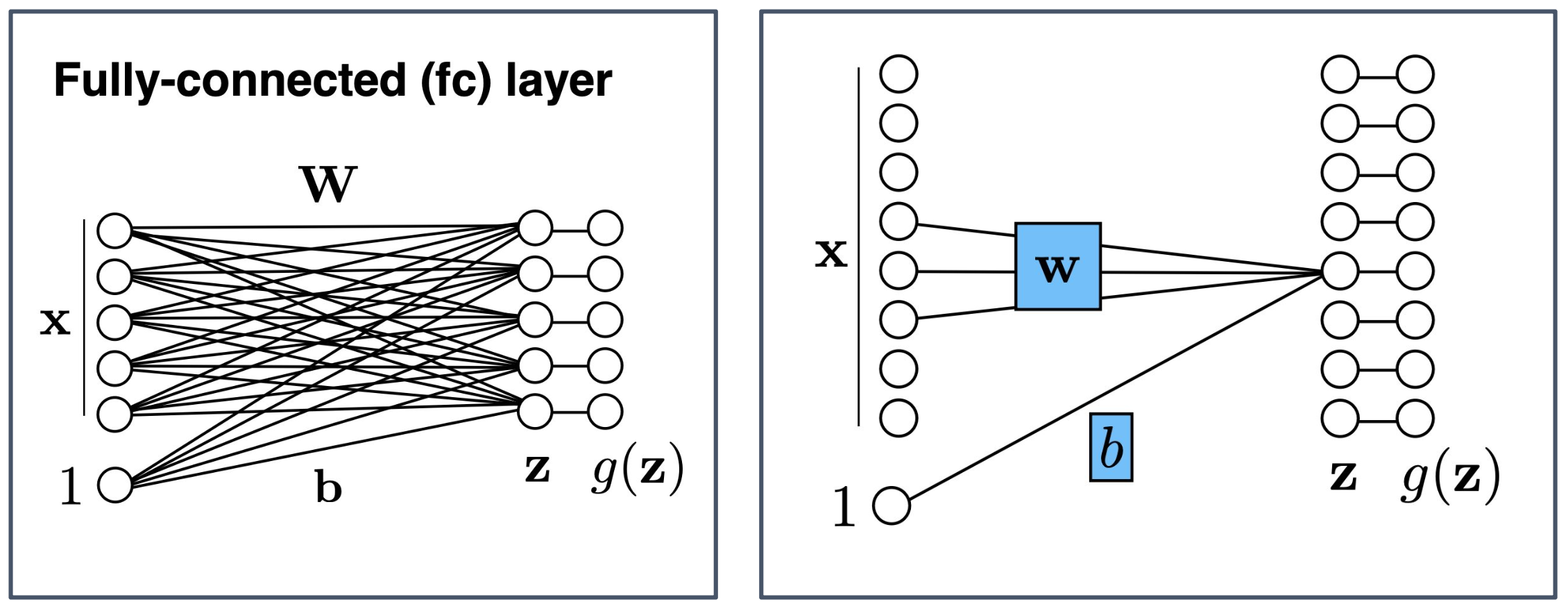
p39. 완전 연결 계층(Fully-connected Layer) vs 지역 연결 계층(Locally-connected Layer)

완전 연결 계층 (Fully-connected layer, fc layer)
- 입력 $x$의 모든 요소가 가중치 행렬 $W$를 통해 모든 출력 노드와 연결된다.
- 편향 $b$가 더해져 중간 값 $z$가 계산되고, 이후 활성화 함수 $g(\cdot)$를 거쳐 최종 출력 $g(z)$를 얻는다.
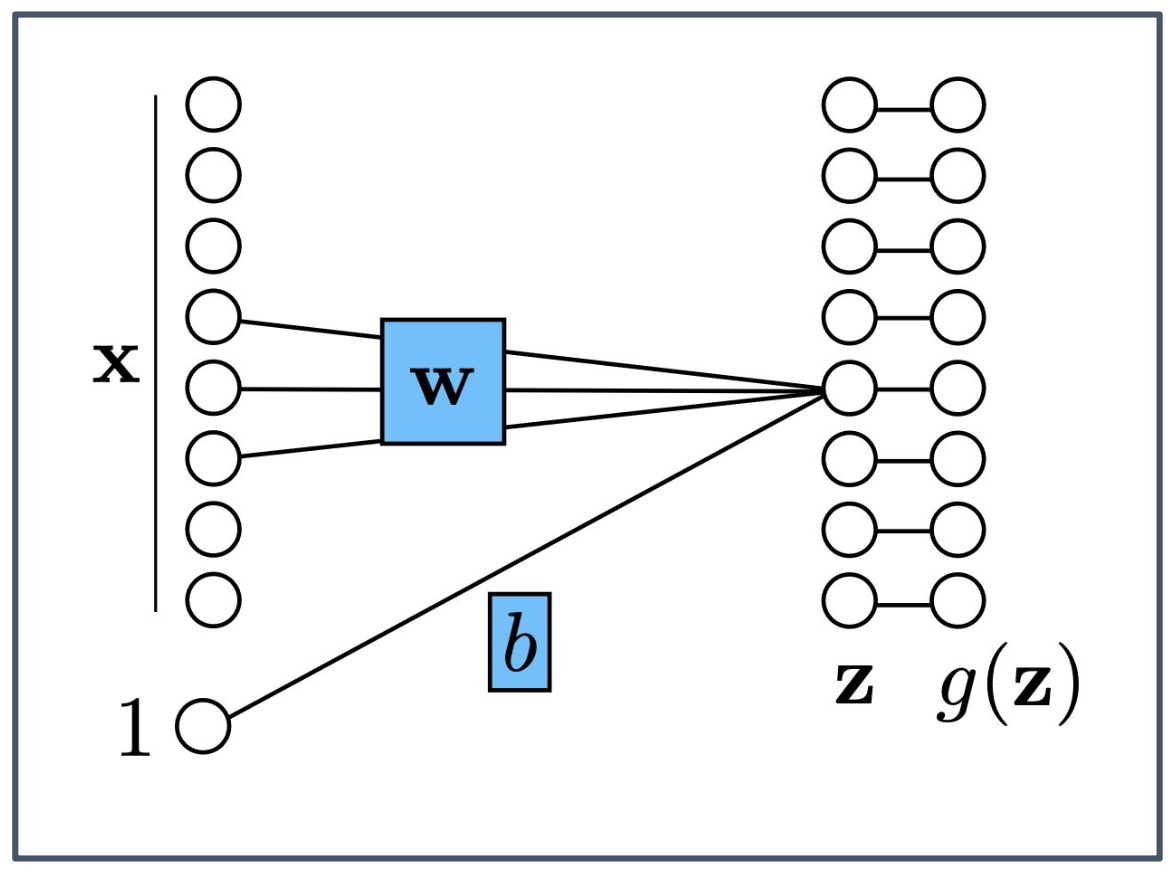
지역 연결 계층 (Locally-connected layer)
- 입력 $x$의 일부 지역(local region)만 가중치 $w$와 연결된다.
- 동일한 가중치를 전체 입력에 공유하지 않고, 위치마다 다른 가중치를 사용한다.
- 편향 $b$가 더해져 $z$가 계산되고, 활성화 함수 $g(\cdot)$를 거쳐 출력 $g(z)$가 얻어진다.

1. 완전 연결 계층의 특징 (Fully-connected layer)
모든 입력이 모든 출력과 연결되므로 표현력(representational power)이 크다.
그러나 매개변수(parameter) 수가 매우 많아 계산량이 증가하고, 과적합(overfitting) 위험이 커진다.
2. 지역 연결 계층의 특징 (Locally-connected layer)
입력의 특정 위치 정보에 따라 연결이 제한되므로 지역적 특성(local feature)을 반영할 수 있다.
합성곱 계층(convolution layer)과 달리 가중치 공유(weight sharing)를 하지 않는다.
위치마다 서로 다른 패턴을 학습할 수 있다는 장점이 있지만,
파라미터 수는 합성곱 계층보다 더 많아질 수 있다.

p40. 완전 연결 계층(Fully-connected Layer) vs 지역 연결 계층(Locally-connected Layer)

우리는 종종 출력(output)이 입력(input)의 지역적(local) 함수라고 가정한다.
동일한 가중치(weights)를 사용하여 각 지역 함수(local function)를 계산한다면, 이를 가중치 공유(weight sharing) 라고 부른다.
가중치 공유를 적용한 지역 연결 계층은 합성곱 신경망(Convolutional Neural Network, CNN) 이 된다.

1. 지역적 함수(Local function)의 의미
지역 연결 계층은 입력 전체를 보지 않고, 일부 구간(local region)의 값만 활용해 출력을 계산한다.
예를 들어 이미지에서는 특정 픽셀 주변 값들만 사용하여 지역적 특징을 추출하는 방식과 같다.
2. 가중치 공유(Weight sharing)의 역할
동일한 가중치 집합(weight set)을 입력 전체의 여러 위치에 반복 적용한다.
이를 통해 파라미터 수가 크게 줄어들고, 위치와 무관하게 동일한 패턴을 인식할 수 있게 된다.
3. CNN과의 관계
지역 연결(Local connectivity)과 가중치 공유(Weight sharing)를 결합하면 합성곱 신경망(CNN)이 된다.
CNN은 이미지나 시계열처럼 공간적·시간적 구조(spatial/temporal structure)를 가진 데이터를 처리하는 데 매우 효과적이다.

p41. 합성곱 신경망(Convolutional Neural Network)

선형, 평행 이동 불변 변환(Linear, shift-invariant transformation)

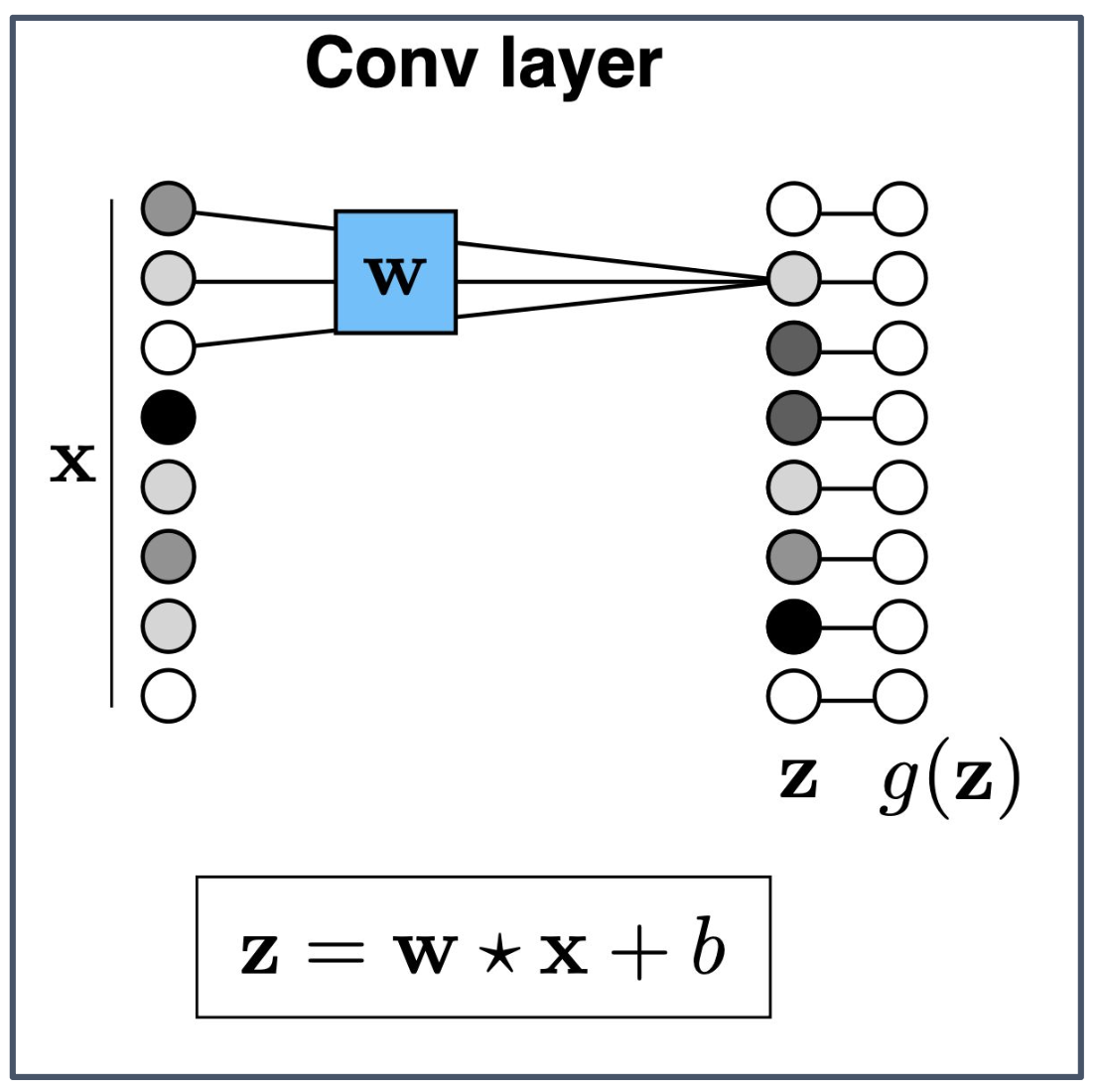
1. 합성곱(Convolution)과 합성곱 계층(Conv layer)
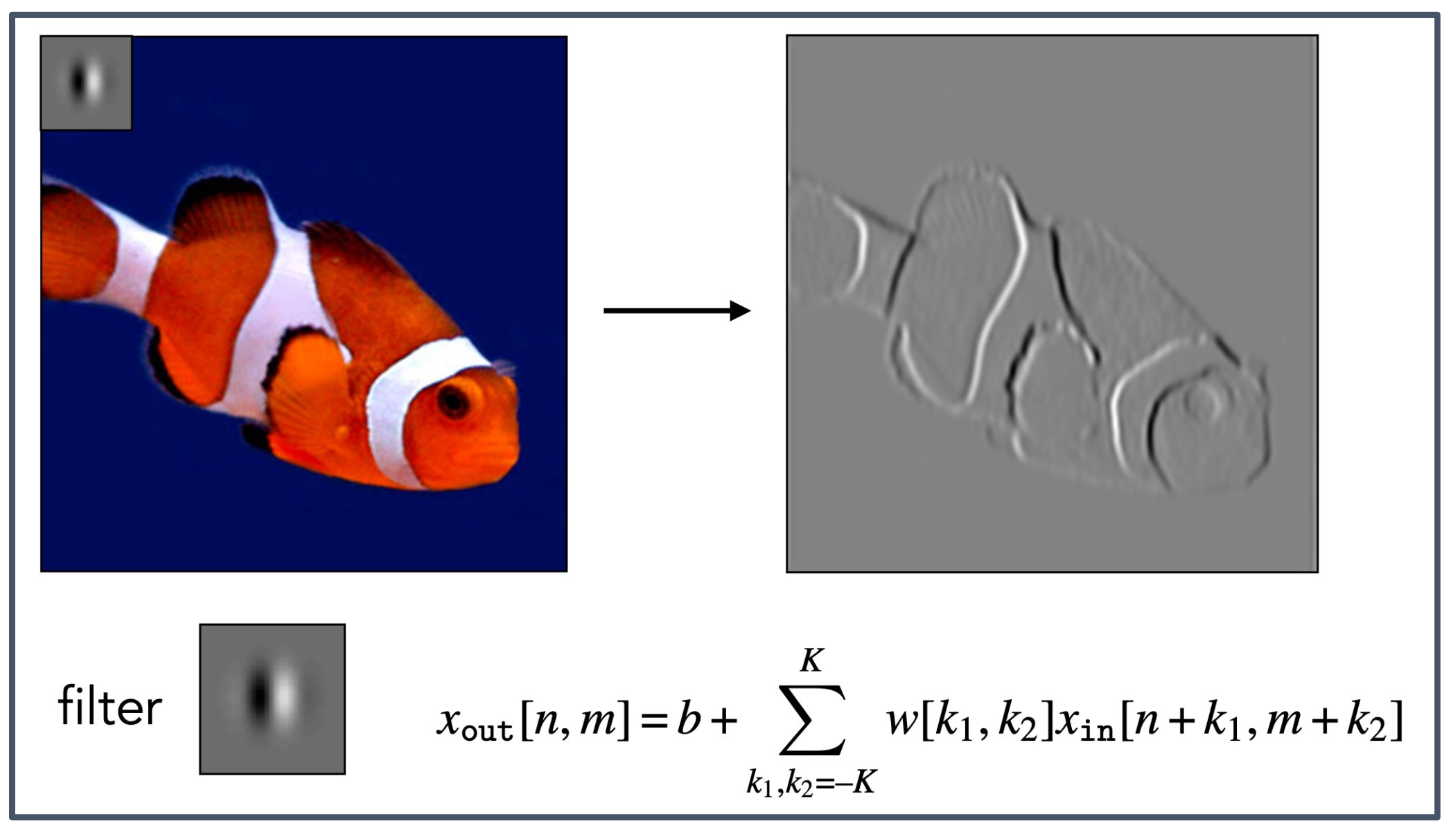
합성곱 계층은 입력 $x$ 에 필터(filter) $w$ 를 적용하여 합성곱(convolution)을 수행한다.
수식 $z = w \star x + b$ 에서 $\star$ 는 합성곱 연산을 의미한다.
2. 선형, 평행 이동 불변 변환(Linear, shift-invariant transformation)
합성곱은 선형(linear) 변환이며, 입력이 평행 이동(shift)하더라도 동일한 방식으로 처리된다.
따라서 물체나 패턴이 위치만 달라져도 같은 패턴으로 인식된다.
3. 출력 수식(Output formula)
$x_{\text{out}}[n,m]$ 은 입력 $x_{\text{in}}$ 과 필터 $w$ 의 합성곱 결과에 편향 $b$ 를 더해 계산된다.
4. 필터(Filter)의 의미
필터는 입력 데이터에서 특정 지역적 패턴(local pattern) 을 추출한다.
예: 에지(edge), 모서리(corner), 질감(texture) 등 특정 특징(feature)을 검출하는 역할을 한다.
5. 물고기 그림의 의미
왼쪽의 컬러 물고기 이미지는 원본 입력을 의미한다.
작은 회색 사각형은 적용된 필터(filter) 를 나타낸다.
오른쪽의 회색 영상은 필터가 입력과 합성곱되어 생성된 결과이며, 물고기의 윤곽선(edge) 이 강조되어 보인다.
이는 합성곱 계층이 특정 특징을 학습하고 추출하는 과정을 시각적으로 보여주는 예시이다.

p42. 완전 연결 계층(Fully-Connected Layer)

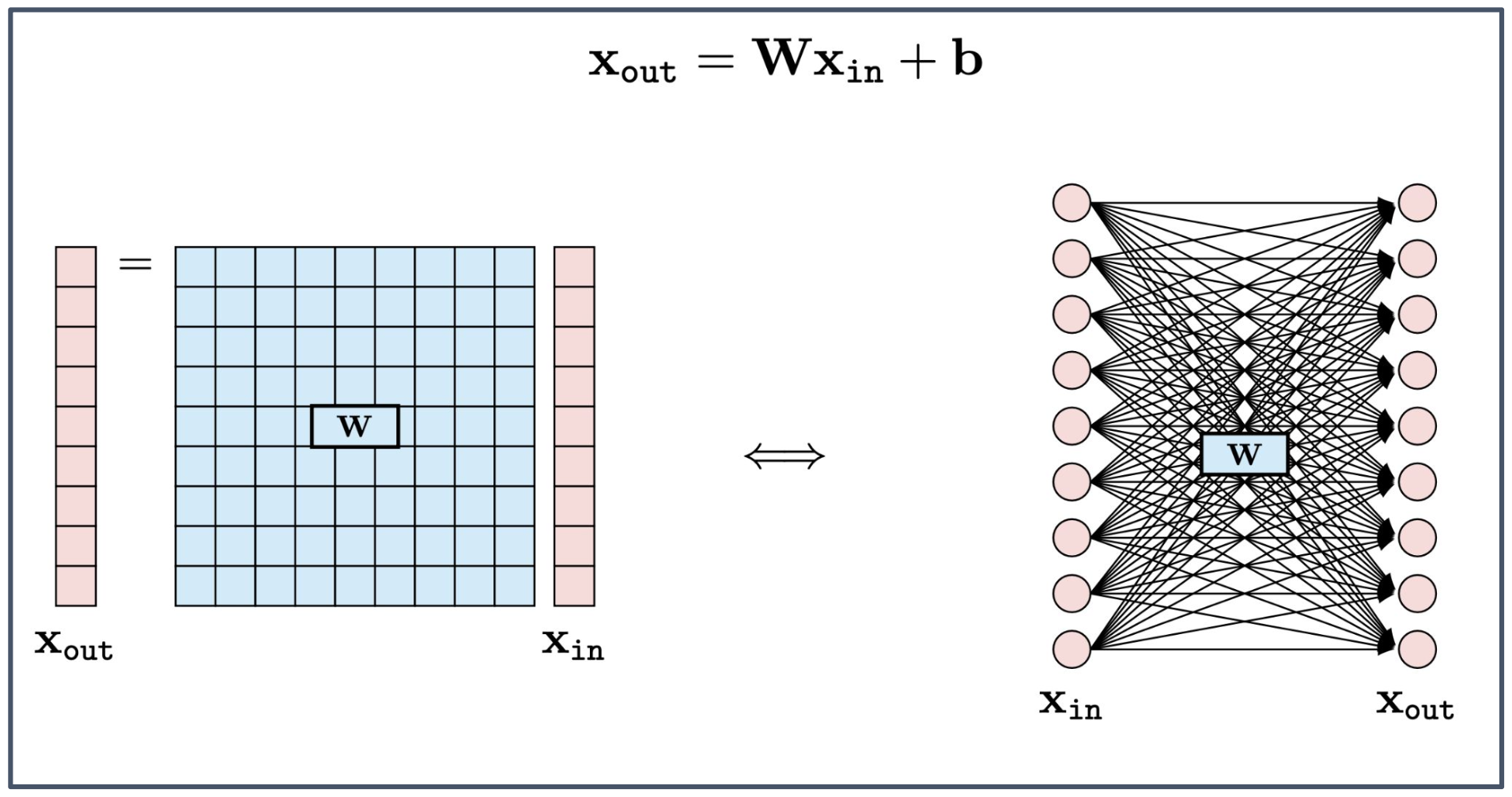
$x_{\text{out}} = W x_{\text{in}} + b$
$x_{\text{in}}$: 입력 벡터 (input vector)
$x_{\text{out}}$: 출력 벡터 (output vector)
$W$: 가중치 행렬 (weight matrix)
$b$: 편향 (bias)

1. 행렬 연산으로서의 완전 연결 계층
완전 연결 계층은 입력 $x_{\text{in}}$ 과 가중치 행렬 $W$ 를 곱하고 편향 $b$ 를 더해 출력 $x_{\text{out}}$ 을 계산한다.
즉, 여러 입력 노드와 출력 노드 사이의 모든 연결을 하나의 선형 변환(linear transformation)으로 표현한 것이다.
2. 그래프 표현과 행렬 표현의 대응
오른쪽 그림은 모든 입력 노드와 출력 노드가 완전히 연결된 구조를 시각적으로 나타낸다.
왼쪽의 행렬 표현은 동일한 계산을 보다 간결하게 표현한 것이며, 실제 구현에서는 행렬 곱을 통해 효율적으로 계산된다.

p43. 합성곱 계층(Convolutional Layer)

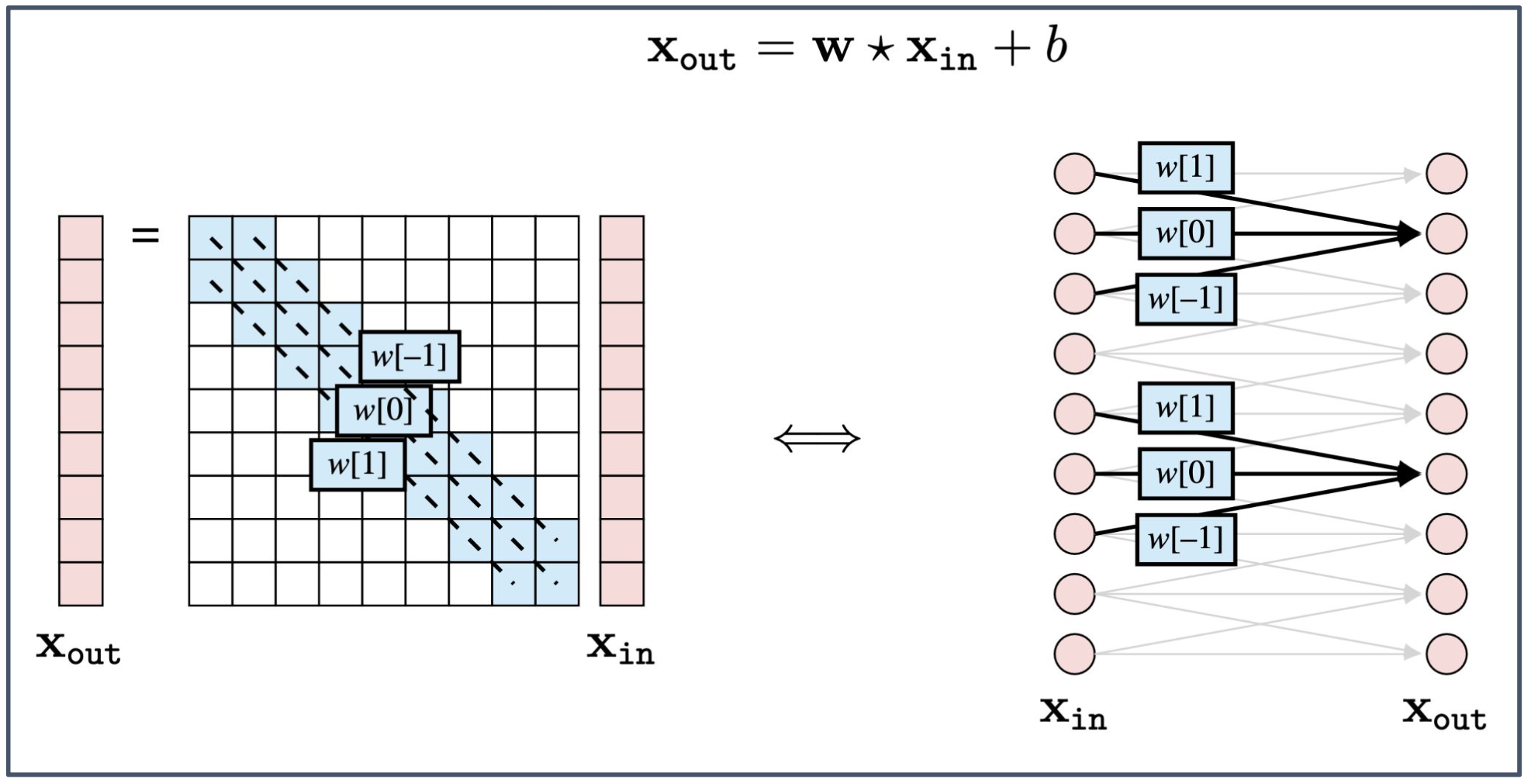
$x_{\text{out}} = w \star x_{\text{in}} + b$
$x_{\text{in}}$: 입력 벡터 (input vector)
$x_{\text{out}}$: 출력 벡터 (output vector)
$w[-1], w[0], w[1]$: 합성곱 필터 계수(convolution filter coefficients)
$b$: 편향 (bias)

1. 합성곱(Convolution)과 합성곱 계층(Conv layer)
합성곱 계층은 입력 $x_{\text{in}}$ 의 지역 구간(local region) 에 필터 $w$ 를 적용하여 출력을 계산한다.
수식 $x_{\text{out}} = w \star x_{\text{in}} + b$ 에서 $\star$ 는 합성곱(convolution) 연산을 의미한다.
2. 가중치 공유(Weight sharing)
동일한 필터 계수 $w[-1], w[0], w[1]$ 이 입력 전체에 반복 적용된다.
덕분에 파라미터 수가 줄어들고, 입력이 어디에 위치하든 동일한 패턴을 인식할 수 있게 된다.
3. 행렬 표현과 그래프 표현
왼쪽의 행렬 표현은 합성곱이 입력에 대해 대각선 방향으로 동일한 필터가 적용된다는 점을 보여준다.
오른쪽의 신경망 그림은 동일한 가중치 집합이 여러 입력 구간에 적용되어 출력 노드로 연결되는 구조를 나타낸다.

p44. 합성곱 계층(Convolutional Layer)

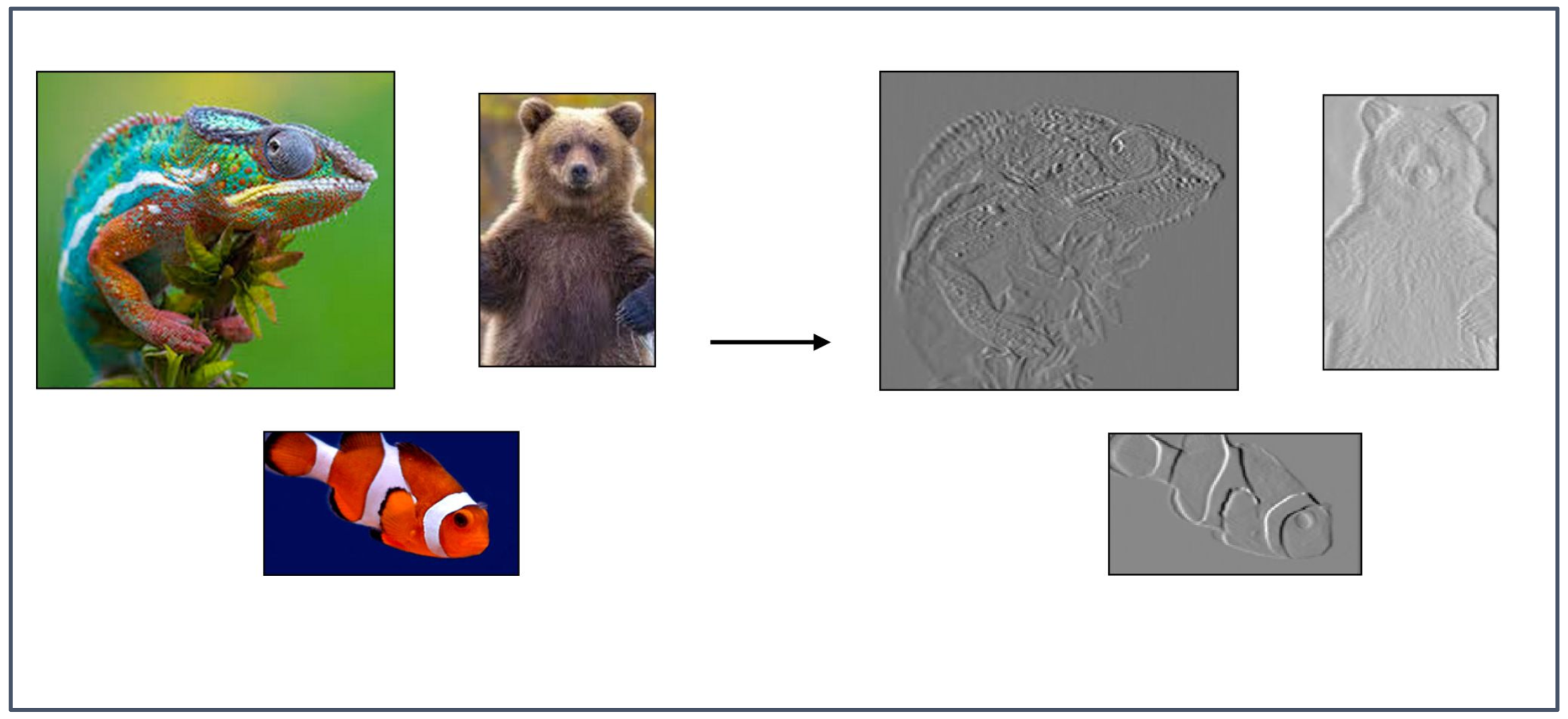
1. 필터(Filter)의 역할
필터는 입력 이미지에서 경계(edge), 윤곽선(outline), 질감(texture)과 같은 지역적 패턴(local pattern)을 검출하는 역할을 한다.
동일한 필터가 전체 이미지에 적용되므로, 특정 시각적 특징을 위치와 무관하게 찾아낼 수 있다.
2. 그림의 의미
왼쪽의 컬러 이미지는 원본 입력이며, 오른쪽의 회색 이미지는 합성곱 계층을 거쳐 얻어진 특징 맵(feature map)이다.
카멜레온, 곰, 물고기의 윤곽선과 경계가 강조된 모습은 합성곱 계층이 이러한 패턴을 추출하는 과정을 시각적으로 보여준다.

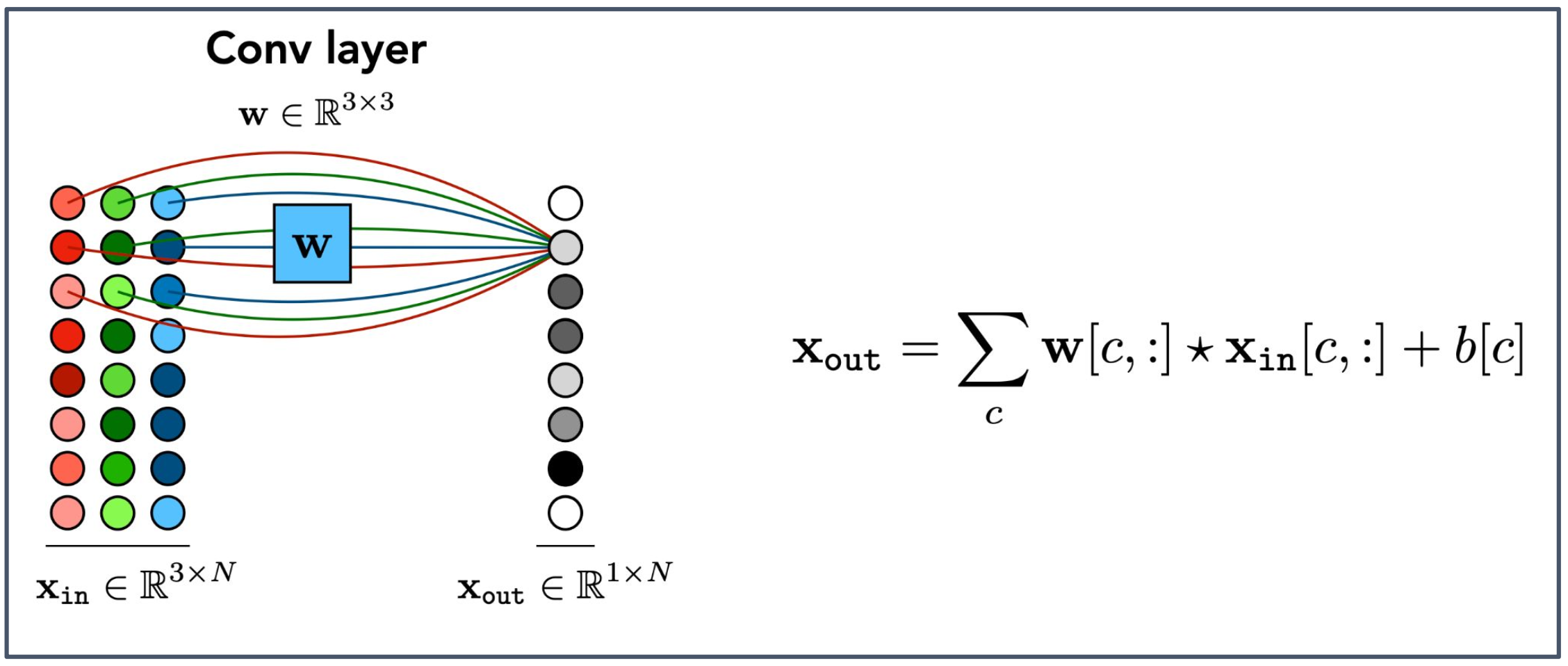
p45. 합성곱 계층: 다채널(Convolutional Layer : Multichannel)

1. 다채널 입력(Multichannel input)
입력 $x_{\text{in}}$ 은 RGB 이미지처럼 여러 채널(channel)로 구성된다.
예: $x_{\text{in}} \in \mathbb{R}^{3 \times N}$ 은 3채널(R, G, B)이 각각 $N$차원 데이터를 갖는 입력을 의미한다.
2. 채널별 합성곱(Convolution per channel)
각 채널 $c$ 마다 동일한 크기의 필터 $w[c, :]$ 를 적용하여 부분 출력을 계산한다.
이렇게 얻은 채널별 출력을 모두 합(sum)하여 최종 출력 $x_{\text{out}}$ 을 만든다.
3. 그림의 의미
왼쪽 그림은 3채널(R, G, B) 입력이 필터 $W$ 를 통해 개별적으로 처리되는 과정을 나타낸다.
오른쪽의 $x_{\text{out}}$ 은 각 채널별 합성곱 결과가 더해져 생성된 단일 출력 맵(single output map)이다.

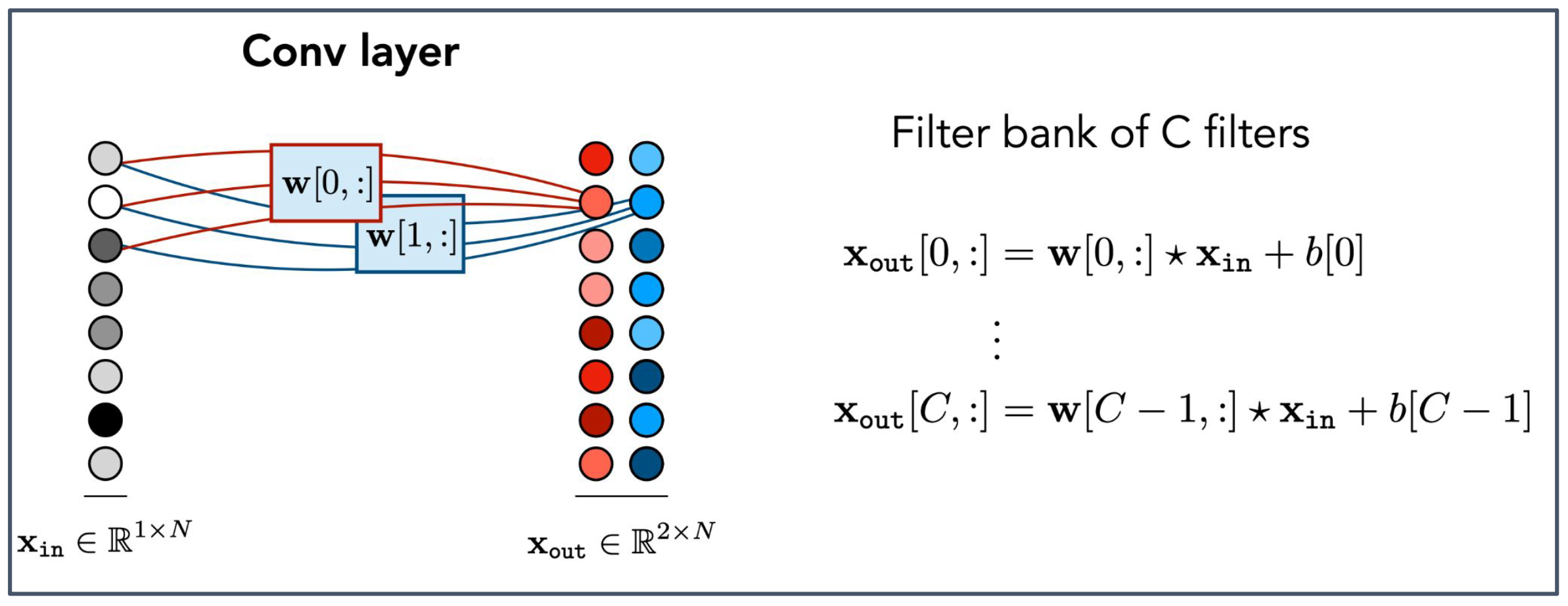
p46. 합성곱 계층: 다채널(Convolutional Layer : Multichannel)

1. 다중 필터(Multiple filters)
다채널 합성곱 계층은 입력 $x_{\text{in}}$ 에 대해 여러 개의 필터(filter bank)를 동시에 적용한다.
각 필터 $w[i, :]$ 는 입력에서 서로 다른 특징(feature)을 추출한다.
2. 출력 구조(Output structure)
각 필터는 하나의 출력 채널(output channel)을 생성한다.
따라서 $C$ 개의 필터가 있으면 출력은 $C$ 개의 채널이 쌓인 형태가 되어
$x_{\text{out}} \in \mathbb{R}^{C \times N}$ 이 된다.
3. 그림의 의미
왼쪽 그림은 단일 입력 $x_{\text{in}}$ 이 여러 필터($w[0,:],\, w[1,:]$ 등)를 통해 병렬적으로 처리되는 과정을 보여준다.
오른쪽의 $x_{\text{out}}$ 은 각 필터가 만들어낸 서로 다른 특징 맵(feature map)이 채널 방향으로 쌓인 결과이다.

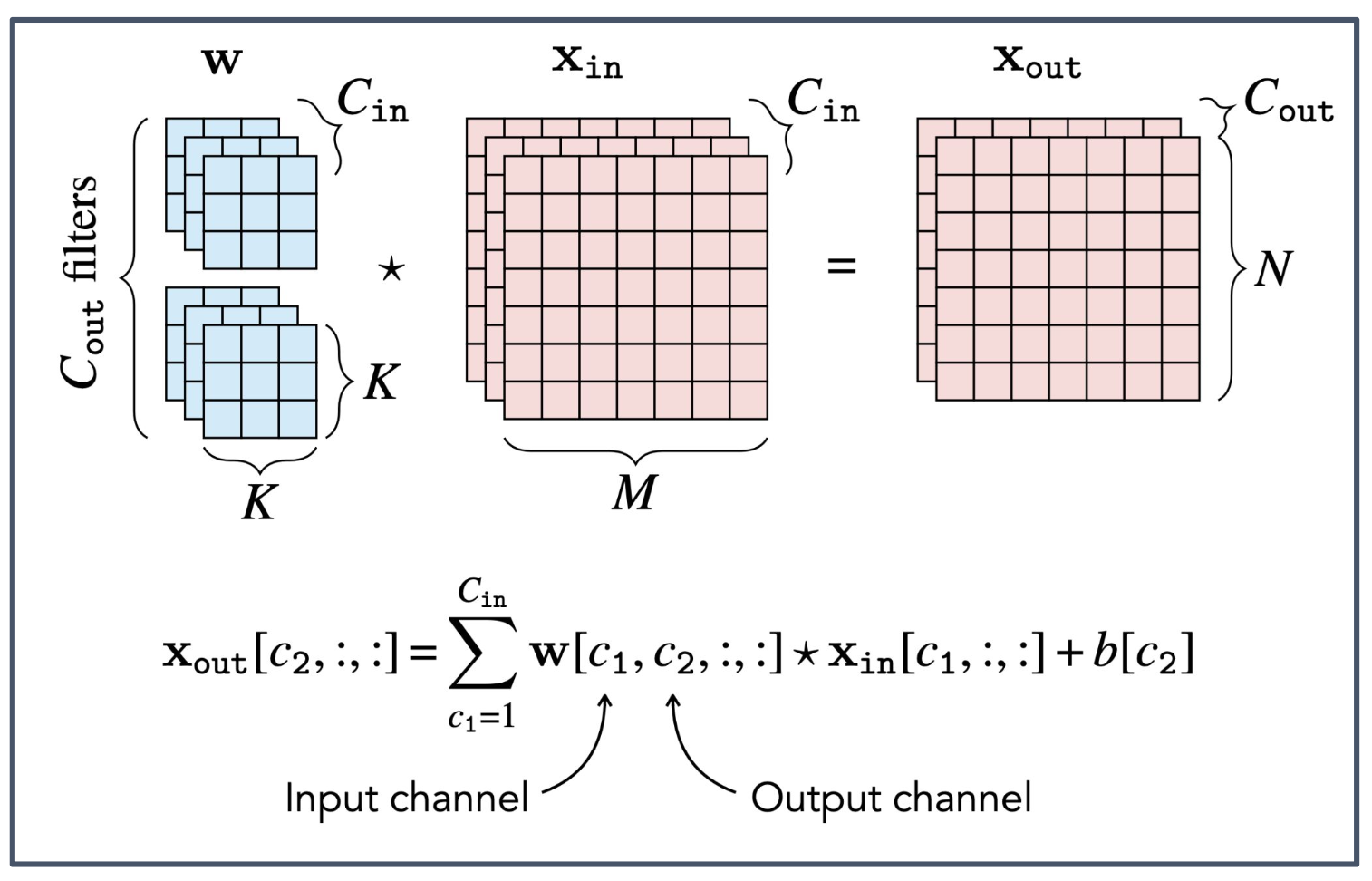
p47. 일반 합성곱 계층: 다중 입출력(General Convolutional Layer : Multi - I/O)

참고 (Reference):
- Pytorch 2.8 Document: Conv2D
  - https://docs.pytorch.org/docs/stable/generated/torch.nn.Conv2d.html
  - https://github.com/pytorch/pytorch/blob/v2.8.0/torch/nn/modules/conv.py#L374

1. 다중 입력 채널(Multi-input channels)
입력 $x_{\text{in}}$ 은 여러 개의 채널 $C_{\text{in}}$ 로 구성된다.
예: RGB 이미지는 $C_{\text{in}} = 3$ 인 다채널 입력이다.
2. 다중 출력 채널(Multi-output channels)
합성곱 계층은 여러 개의 필터 $C_{\text{out}}$ 을 사용하여 다중 출력 채널을 생성한다.
각 출력 채널은 입력의 모든 채널에 대해 합성곱을 수행하고, 그 결과를 합하여 만들어진다.
3. 그림의 의미
왼쪽의 $w$ 는 각 출력 채널과 여러 입력 채널이 연결된 필터 집합을 나타낸다.
가운데의 $x_{\text{in}}$ 은 다중 채널 입력 텐서를 의미한다.
오른쪽의 $x_{\text{out}}$ 은 각 필터가 생성한 다중 출력 채널이 쌓여 구성된 출력 텐서이다.

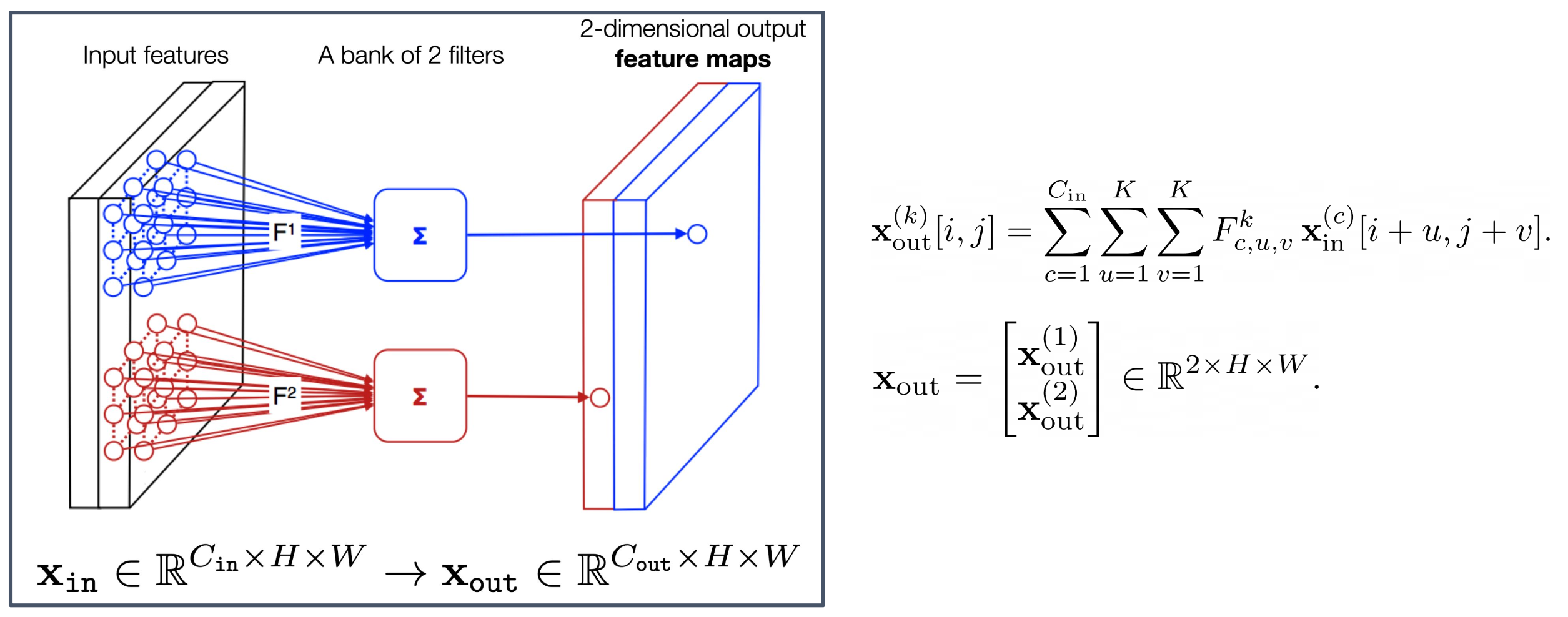
p48. 합성곱 계층(Convolutional Layer)

1. 다중 필터(Multiple filters)와 출력 특징 맵(Output feature maps)
입력 $x_{\text{in}}$ 에 여러 개의 필터가 적용되면, 각 필터는 하나의 출력 특징 맵(feature map)을 생성한다.
따라서 필터가 2개라면 $x_{\text{out}}$ 은 두 개의 채널(channel)로 이루어진 출력 텐서가 된다.
2. 그림의 의미
왼쪽: 입력 특징(input features).
가운데: 두 개의 필터 집합(a bank of 2 filters)이 각각 합성곱을 수행하는 과정.
오른쪽: 두 개의 출력 특징 맵이 채널 방향으로 쌓여 2차원 형태로 표현된 결과.

p49. 특징 맵(Feature maps)

conv1 (첫 번째 합성곱 계층 이후, after first conv layer)
conv2 (두 번째 합성곱 계층 이후, after second conv layer)
각 계층(layer)은 $C$ 개의 특징 맵(feature maps) 집합, 즉 채널(channels)로 생각할 수 있다.
각 특징 맵(feature map)은 $N \times M$ 크기의 이미지이다.

1. 특징 맵(Feature map)의 의미
합성곱 계층의 출력은 입력 이미지의 특정 특징(feature)을 강조한 특징 맵(feature map) 으로 표현된다.
각 특징 맵은 하나의 필터가 입력 전체에 적용된 결과이며, 에지(edge), 질감(texture) 등의 패턴을 나타낸다.
2. 계층에 따른 특징 맵 변화
conv1 단계: 에지, 윤곽선 등 비교적 단순한 로컬 패턴이 드러난다.
conv2 단계: 구조적 형태나 부분적 질감 등 더 복잡하고 추상화된 패턴이 나타난다.
3. 채널(Channels)과 이미지 표현
각 특징 맵은 $N \times M$ 형태의 2차원 이미지이며, 여러 개의 특징 맵이 쌓여 채널을 이룬다.
따라서 합성곱 신경망의 한 계층의 출력은 다채널 이미지(tensor)로 이해할 수 있다.

p50. 퀴즈 (점수 없음, Quiz no credit..)

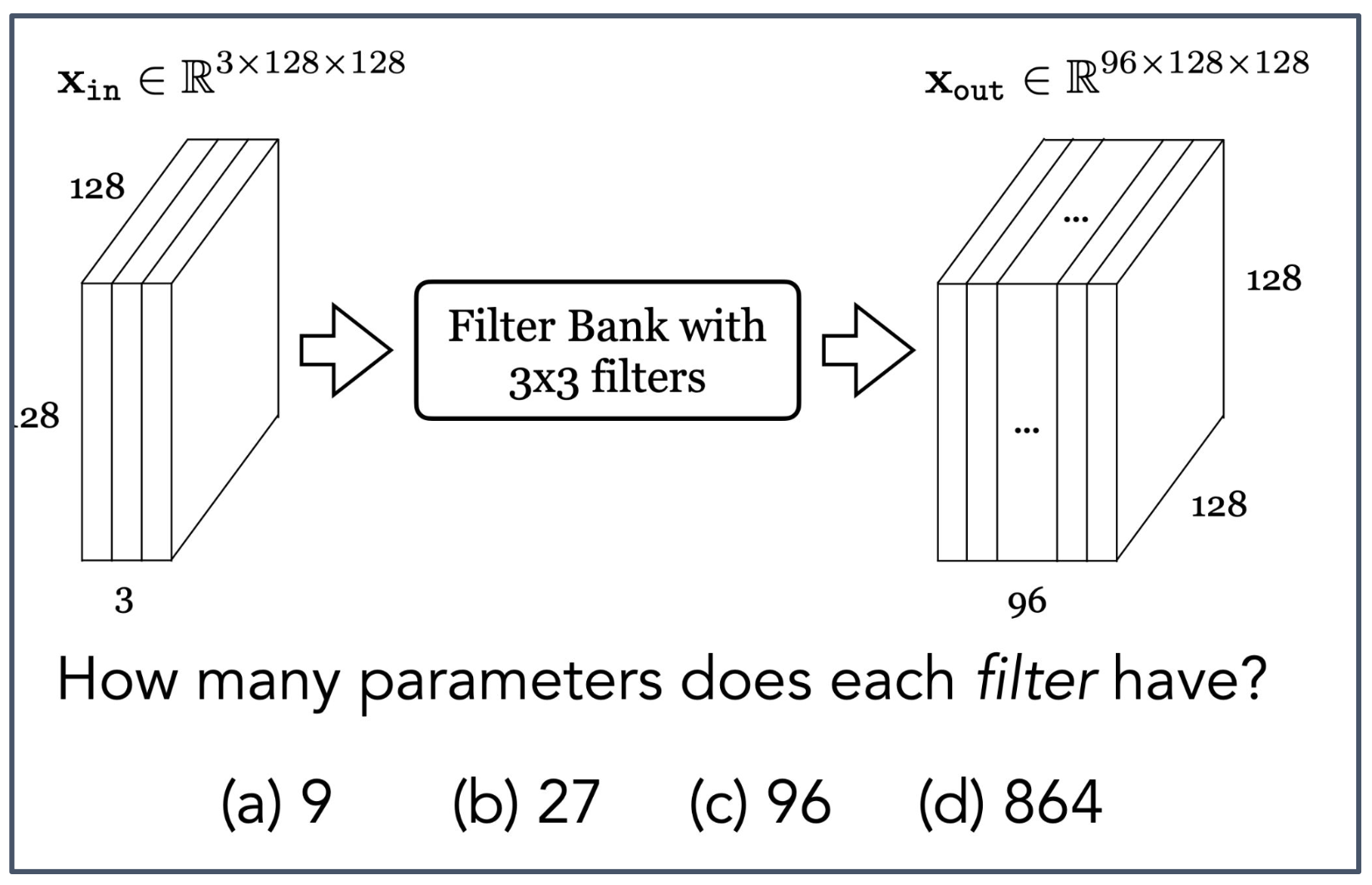
입력: $x_{\text{in}} \in \mathbb{R}^{3 \times 128 \times 128}$
출력: $x_{\text{out}} \in \mathbb{R}^{96 \times 128 \times 128}$
필터 뱅크(Filter Bank) with $3 \times 3$ filters

질문: 각 필터(filter)는 몇 개의 파라미터(parameters)를 가지는가?

(a) 9 (b) 27 (c) 96 (d) 864

1. 필터의 크기와 입력 채널
필터의 공간적 크기는 $3 \times 3$ 이다.
입력 텐서는 3개의 채널(R, G, B와 동일한 구조)을 가지므로, 필터는 모든 입력 채널에 대해 가중치를 포함해야 한다.
2. 파라미터 수 계산
한 채널당 파라미터 수: $3 \times 3 = 9$
입력 채널 수: $3$
따라서 각 필터의 총 파라미터 수는
\[9 \times 3 = 27\]
3. 정답
(b) 27

p51. 퀴즈 (점수 없음, Quiz no credit..)

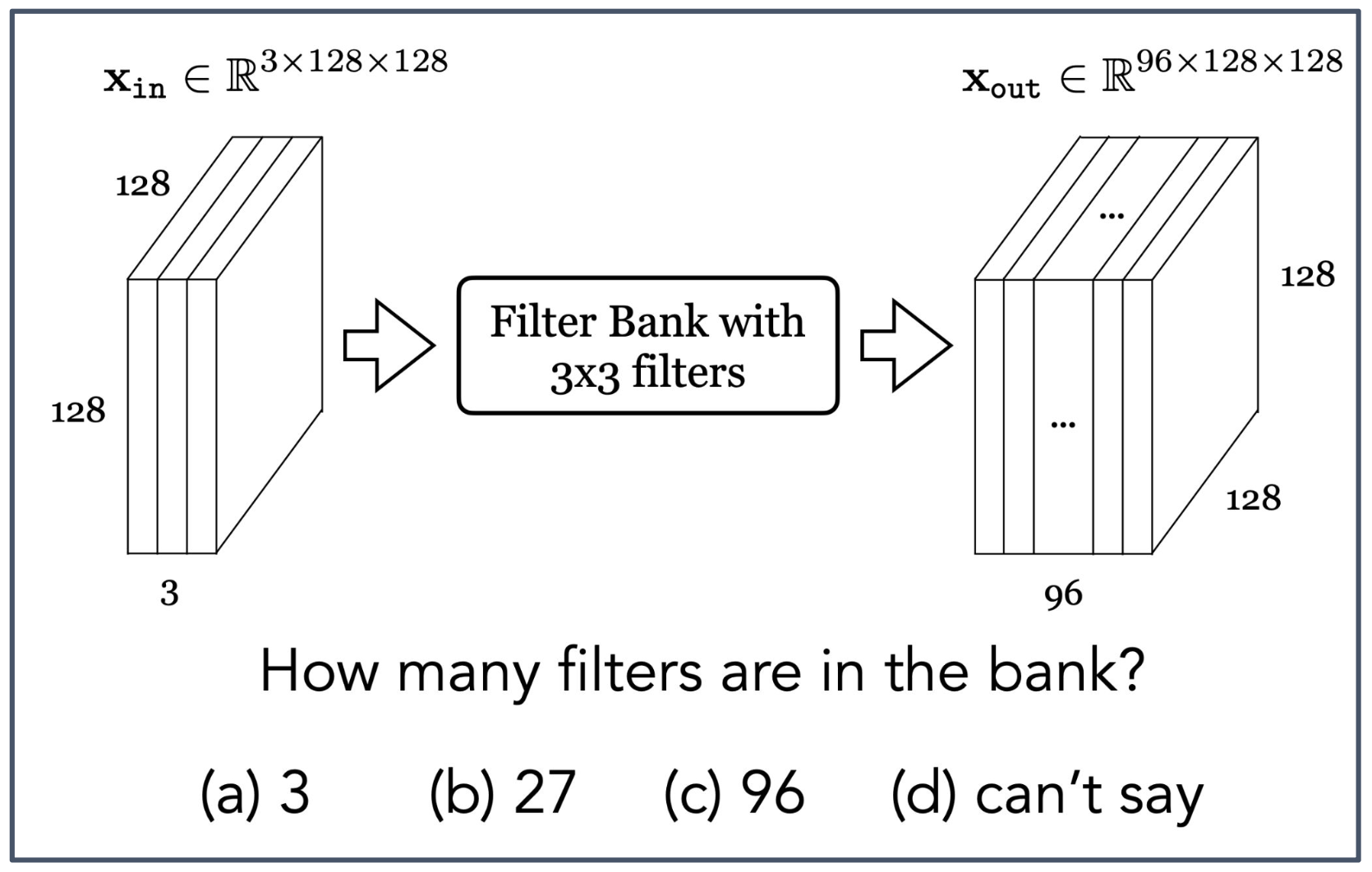
입력: $x_{\text{in}} \in \mathbb{R}^{3 \times 128 \times 128}$
출력: $x_{\text{out}} \in \mathbb{R}^{96 \times 128 \times 128}$
필터 뱅크(Filter Bank) with $3 \times 3$ filters

질문: 필터 뱅크에 몇 개의 필터(filters)가 있는가?

(a) 3 (b) 27 (c) 96 (d) 알 수 없다(can’t say)

1. 출력 채널 수와 필터 수의 관계
합성곱 계층에서 출력 채널(output channels)의 개수는 필터 개수와 동일하다.
각 필터는 입력 전체(3채널)에 대해 합성곱을 수행하고, 그 결과 하나의 출력 채널을 생성한다.
2. 문제 조건 해석
출력 텐서 $x_{\text{out}}$ 의 크기가 $96 \times 128 \times 128$ 로 주어졌다.
따라서 출력 채널 수는 96이다.
3. 정답
필터의 개수 = 출력 채널 수 = 96
정답: (c) 96

p52. 풀링(Pooling)

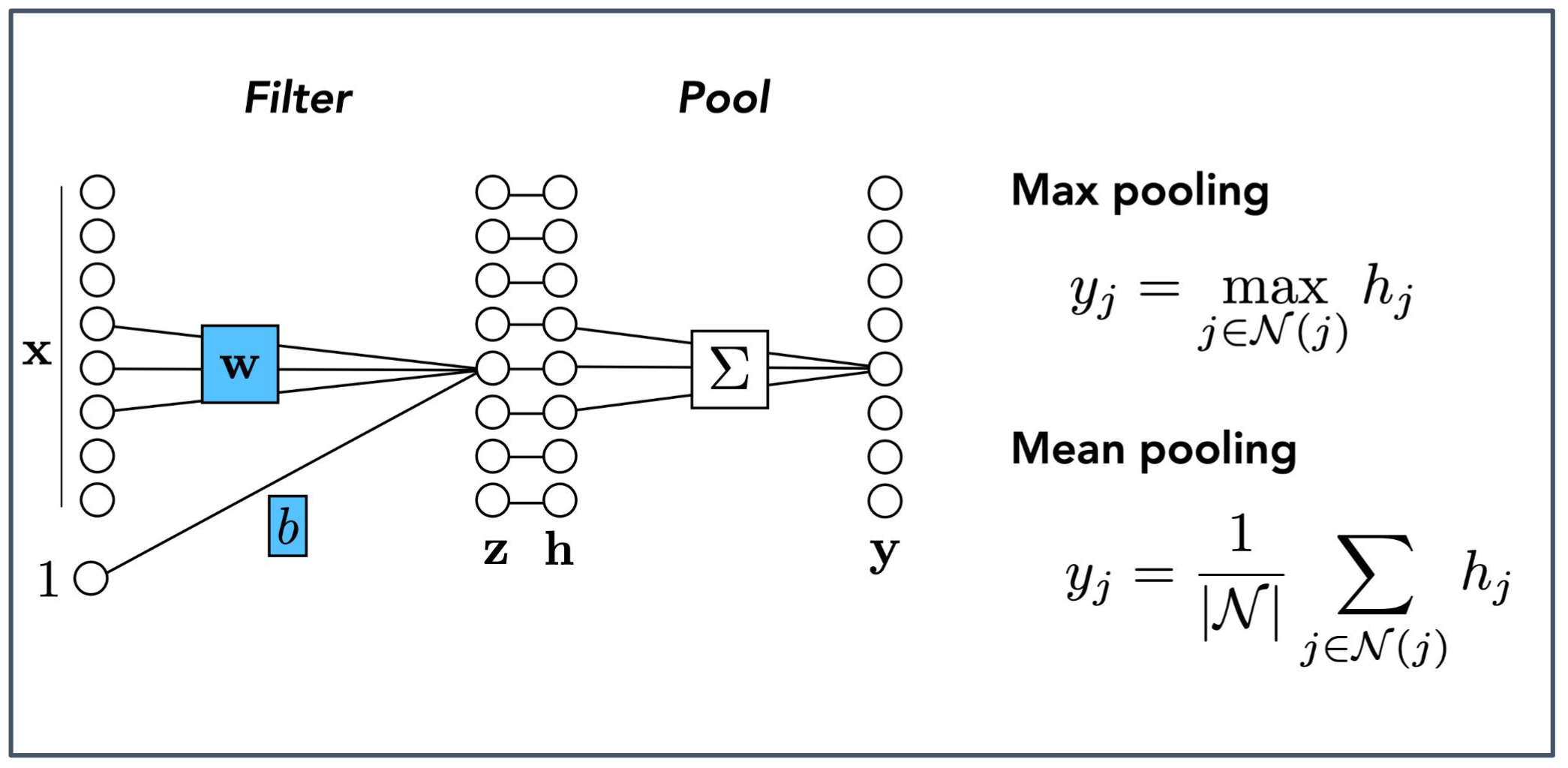
1. 풀링(Pooling)의 개념
풀링은 합성곱 계층 뒤에 적용되어 출력 특징 맵(feature map)의 공간 크기를 줄이는 연산이다.
주요 목적은 계산량을 줄이고, 불필요한 세부 정보를 제거하면서 중요한 특징을 보존하는 것이다.
2. 최대 풀링(Max pooling)
이웃 영역(neighborhood) $\mathcal{N}(j)$ 에서 가장 큰 값을 선택한다.
가장 두드러진 특징(가장 강한 에지나 패턴)을 보존하는 효과가 있다.
3. 평균 풀링(Mean pooling)
이웃 영역 $\mathcal{N}(j)$ 에 속한 값들의 평균을 계산한다.
전체적인 평균 정보를 반영하여 출력이 부드럽게(smoothing) 표현되는 효과가 있다.

p53. 풀링(Pooling)?

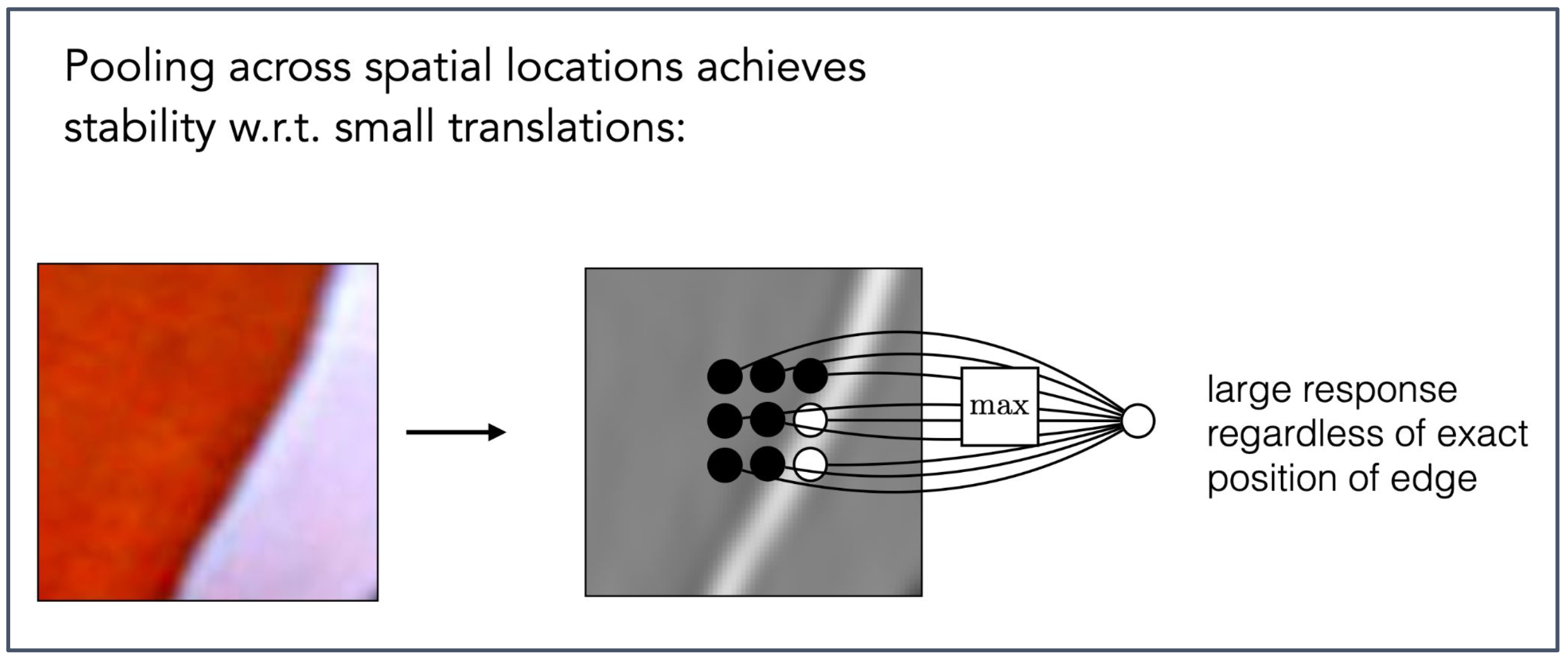
Pooling across spatial locations achieves stability w.r.t. small translations:
공간적 위치(spatial locations)에 걸친 풀링은 작은 평행 이동(small translations)에 대해 안정성(stability)을 달성한다.
large response regardless of exact position of edge
에지(edge)의 정확한 위치와 관계없이 큰 반응(large response)을 얻는다.

1. 풀링의 목적
풀링(pooling)은 입력 특징 맵(feature map)에서 작은 이동(translation)에 대한 불변성(invariance) 을 제공한다.
즉, 물체나 패턴이 약간 이동하더라도 동일한 특징으로 인식될 수 있도록 한다.
2. 에지(edge) 검출에서의 효과
작은 위치 변화가 있더라도 최대 풀링(max pooling)은 해당 영역에 강한 에지 신호가 존재하는지를 안정적으로 포착한다.
이로 인해 에지의 정확한 위치보다 존재 여부에 더 강하게 반응할 수 있다.

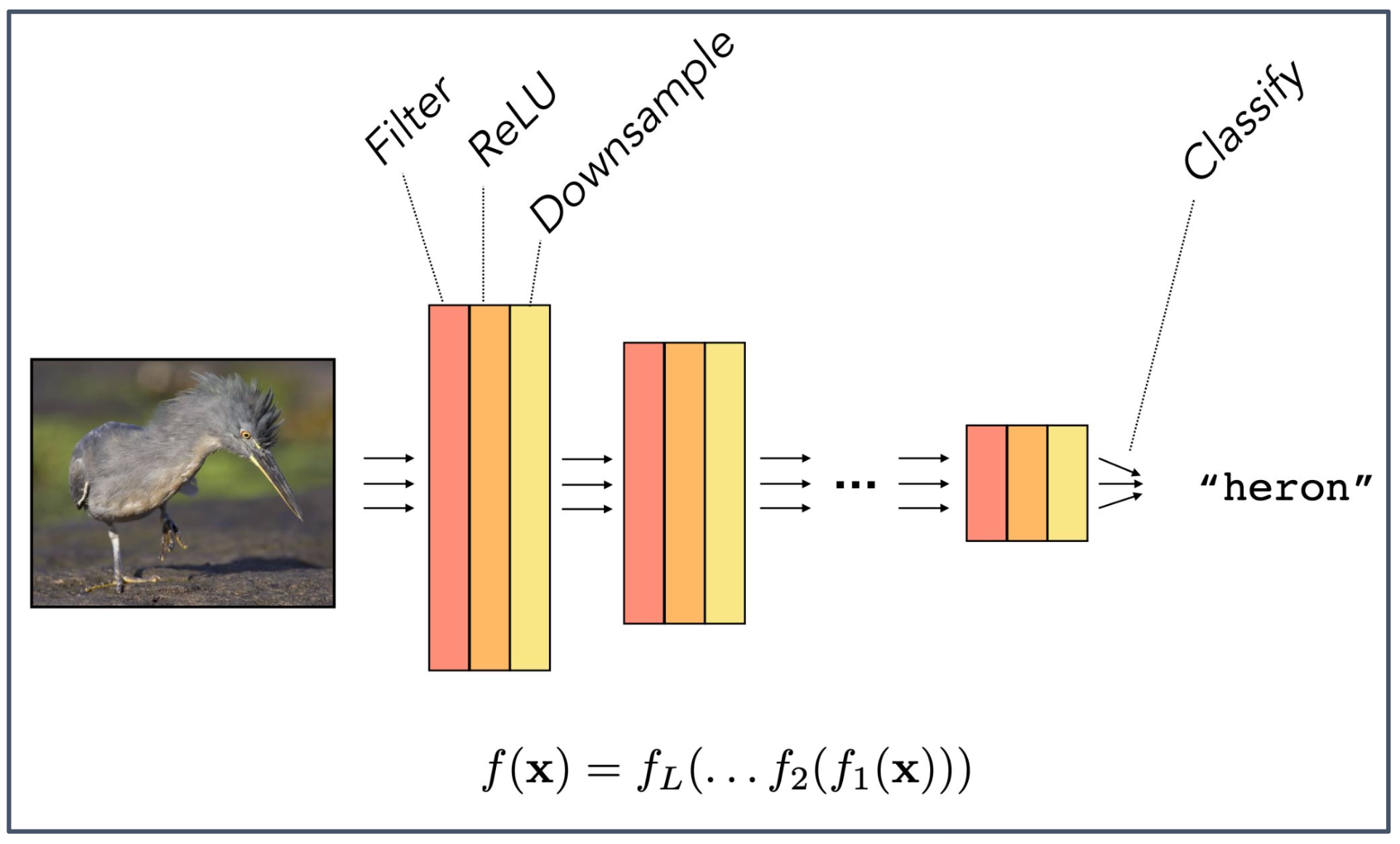
p54. 분류를 위한 합성곱 신경망(CNNs for Classification)

Filter → ReLU → Downsample → Classify

\[f(\mathbf{x}) = f_L(\dots f_2(f_1(\mathbf{x})))\]

최종 출력: "heron" (왜가리)

1. CNN의 기본 흐름
입력 이미지는 합성곱 계층(conv layer)에서 필터(filter) 를 통해 지역적 특징을 추출한다.
활성화 함수 ReLU 가 비선형성을 부여하여 더 복잡한 패턴을 학습할 수 있게 한다.
다운샘플링(Downsample, pooling) 을 통해 특징 맵의 공간 크기를 줄여 계산 효율성을 높이고, 작은 이동에 대한 불변성(translation invariance)을 확보한다.
마지막으로 완전연결계층(fully-connected layer) 또는 소프트맥스 분류기를 통해 특정 클래스(예: “heron”)로 분류한다.
2. 함수 합성 관점
CNN 전체는 일련의 함수들의 합성으로 표현될 수 있다.
\[f(\mathbf{x}) = f_L(\dots f_2(f_1(\mathbf{x})))\]
여기서 $f_1, f_2, \dots, f_L$ 은 각각 합성곱, 활성화, 풀링, 분류기 등을 의미하며,
입력 이미지가 단계적으로 처리되어 최종 출력에 도달하는 전체 구조를 나타낸다.

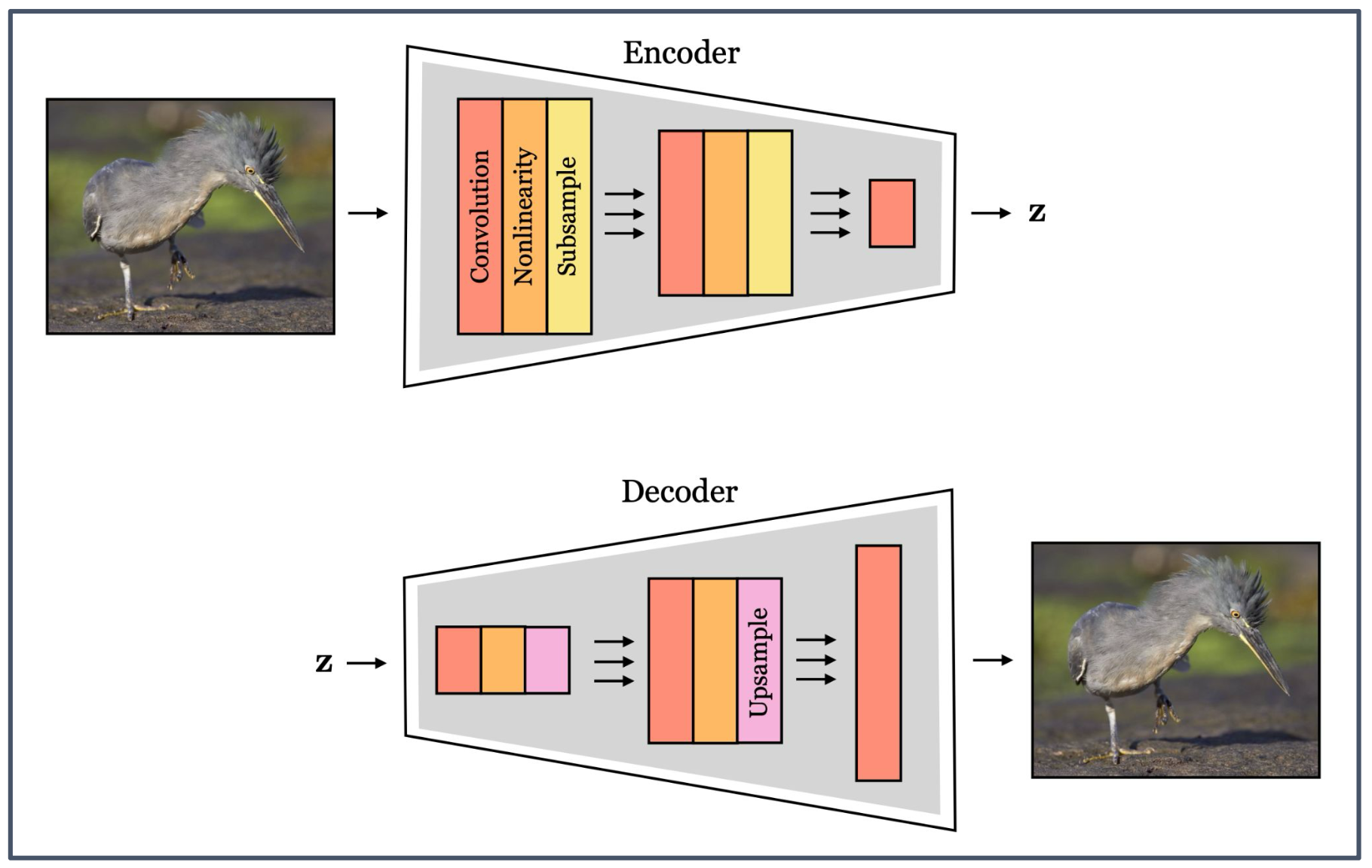
p55. 일반적인 인코더-디코더 합성곱 신경망(Generic Encoder-Decoder CNNs)

Encoder
- Convolution
- Nonlinearity (비선형성)
- Subsample (하위 샘플링)
- 출력: 잠재 벡터(latent vector) $z$
Decoder
- Upsample (업샘플링)
- 원래 입력과 유사한 출력 복원

1. 인코더(Encoder)
입력 이미지를 점차 축소(subsample)하면서 핵심 특징을 추출한다.
합성곱(convolution)과 비선형성(nonlinearity)을 거쳐 고차원 이미지를 저차원 잠재 표현(latent representation) $z$ 로 변환한다.
2. 디코더(Decoder)
잠재 벡터 $z$ 를 업샘플링(upsample)하여 다시 원래와 유사한 형태로 복원한다.
이 과정에서 입력 이미지의 구조적 특징이 유지된 형태로 출력이 생성된다.

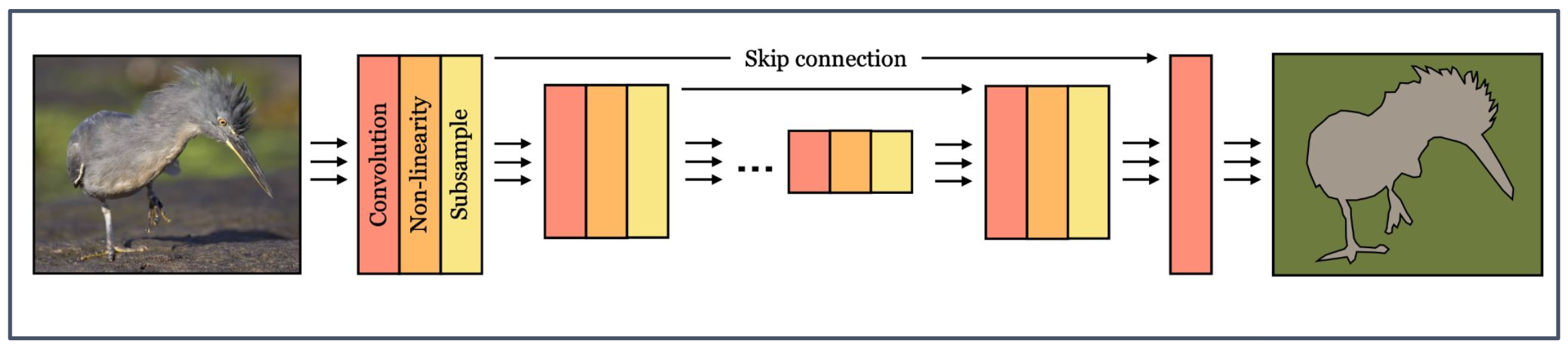
p56. U-Net

Convolution (합성곱)
Non-linearity (비선형성)
Subsample (하위 샘플링)
Skip connection (스킵 연결)

1. U-Net 구조
인코더(Encoder): 합성곱(convolution), 비선형성(non-linearity), 하위 샘플링(subsample)을 통해 입력 이미지를 점차 축소하며 특징을 추출한다.
디코더(Decoder): 인코더에서 추출된 특징을 업샘플링하여 점차 복원하며, 원래 이미지와 유사한 크기의 출력을 생성한다.
2. 스킵 연결(Skip connection)
인코더 단계의 중간 출력을 디코더 단계로 직접 연결해 전달한다.
이를 통해 세부 정보가 보존되며, 복원 과정에서 더 정밀한 출력을 얻을 수 있다.

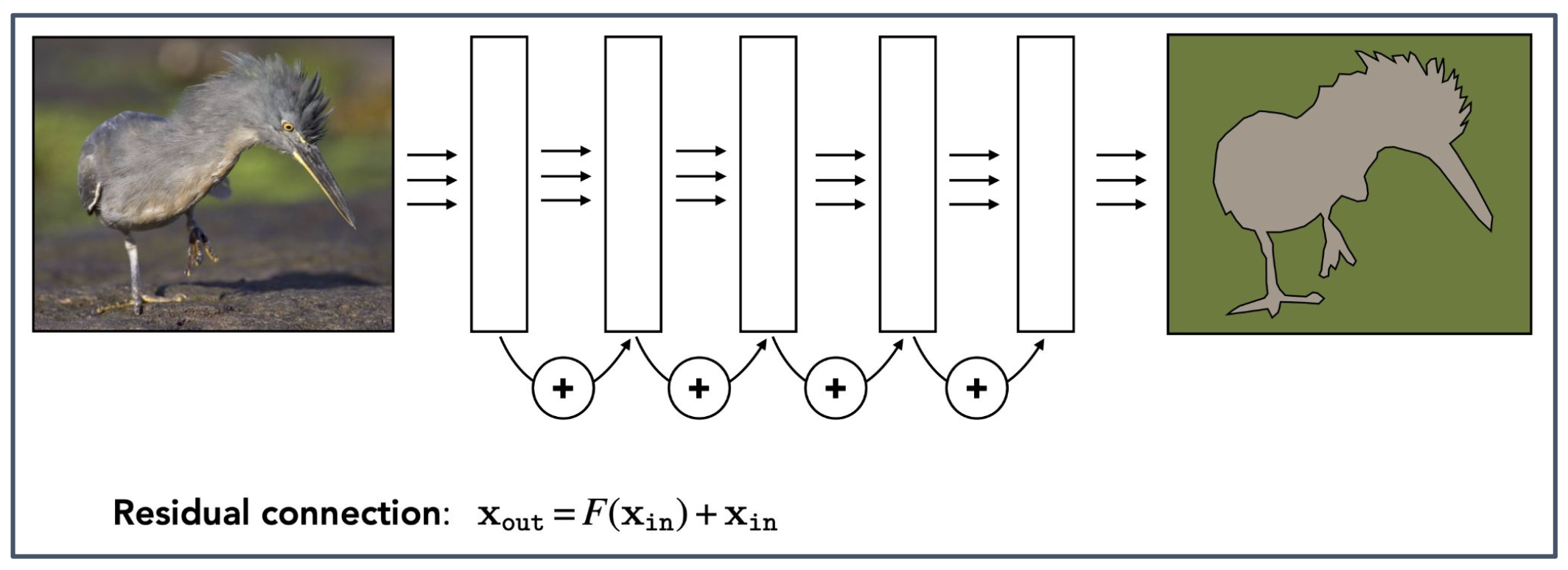
p57. ResNet

Residual connection (잔차 연결):
$x_{\text{out}} = F(x_{\text{in}}) + x_{\text{in}}$
Pytorch Torchvision Document: ResNet
- https://docs.pytorch.org/vision/main/_modules/torchvision/models/resnet.html

1. ResNet의 핵심 아이디어
딥러닝 네트워크가 깊어질수록 기울기 소실(vanishing gradient) 문제가 발생하여 학습이 어려워진다.
이를 해결하기 위해 잔차 연결(residual connection) 을 도입하여, 입력 $x_{\text{in}}$ 을 출력에 직접 더해준다.
2. 잔차 연결의 효과
네트워크가 학습해야 할 목표를 $F(x)$ 라는 잔차(residual) 로 단순화한다.
그 결과 깊은 네트워크에서도 기울기 흐름이 원활하게 유지되며, 학습 안정성이 크게 향상된다.

대학원 수업, 확률과 통계