[확률과 통계] 5주차

p2. 단변량 가우시안 분포 (Univariate Gaussian distribution)

---

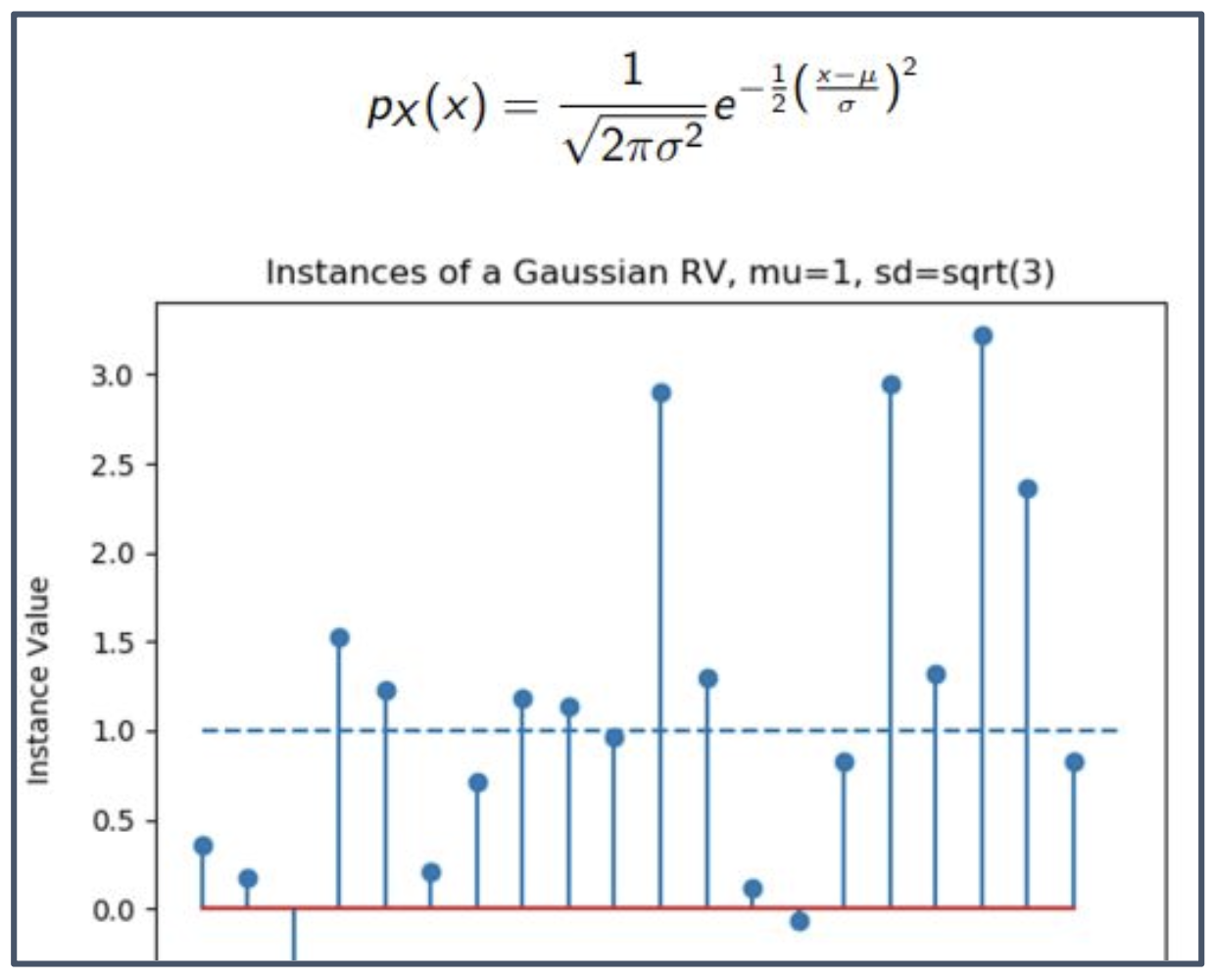
그래프 해석

• 세로축: 표본 값(instance value).
• 이 그래프는 평균이 $\mu = 1$, 표준편차가 $\sqrt{3}$ 인 단변량 가우시안 확률변수(univariate Gaussian RV)에서 생성된 여러 표본(instance)들을 보여준다.
• 표본들은 평균 주변에 밀집하는 경향을 가지며, 표준편차가 클수록 더 넓게 퍼져 분포한다.

---

p3. 다변량 가우시안 분포 (Multivariate Gaussian distribution)

---

1. 수식 해석

• 다변량 가우시안 분포는 평균 벡터 $\vec{\mu}$ 와 공분산 행렬 $\Sigma$ 로 정의된다.
• 확률밀도함수는 다음과 같다.

\[p_{\vec{X}}(\vec{x}) = \frac{1}{(2\pi)^{D/2}\,|\Sigma|^{1/2}} \exp\!\left( -\tfrac{1}{2}(\vec{x}-\vec{\mu})^T \Sigma^{-1} (\vec{x}-\vec{\mu}) \right)\]

2. 가우시안 랜덤 벡터(Gaussian random vector)

• $\vec{x}$ 는 $D$차원의 확률변수이며, 각 성분은 $x_0, x_1, \dots, x_{D-1}$ 로 구성된다.
• 평균 벡터 $\vec{\mu} = E[\vec{x}]$ 는 각 차원별 평균 $\mu_0, \mu_1, \dots, \mu_{D-1}$ 로 이루어진다.

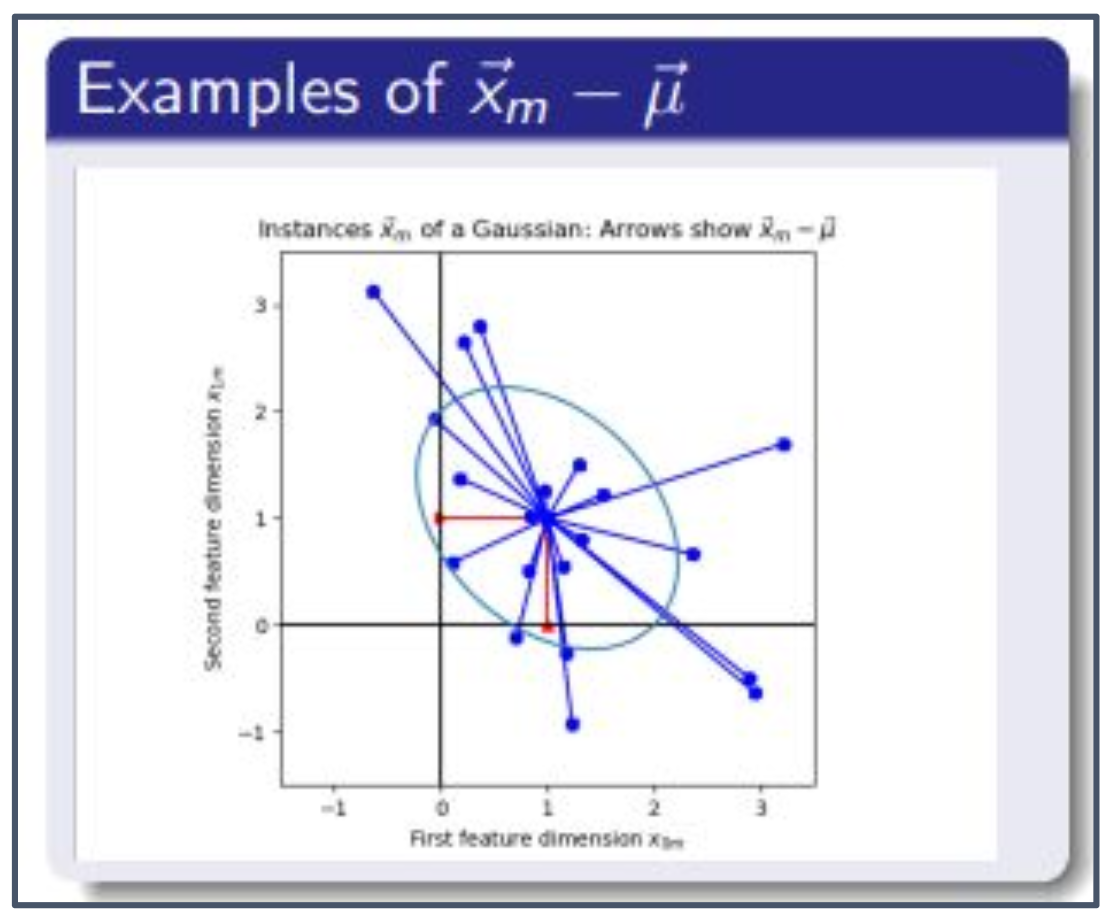
3. 그림 해석

• 왼쪽의 파란 점들은 평균이 $\mu = [1,1]$ 인 2차원 가우시안 분포에서 생성된 표본(instance)들이다.
• 빨간 십자가는 평균 벡터 $\mu$ 를 나타내며, 표본들이 그 주변에 퍼져 있다.
• 점들이 퍼지는 방향과 범위는 공분산 행렬 $\Sigma$ 에 의해 결정된다.

---

p4. 다변량 가우시안 분포 (Multivariate Gaussian distribution)

---

1. 그림 해석

• 왼쪽 그림의 파란 점들은 평균이 $\mu = [1,1]$ 인 2차원 가우시안 분포에서 추출된 표본(instance)들이다.
• 빨간 십자가는 평균 벡터 $\mu$ 를 나타내며, 점들이 그 주변에 퍼져 분포한다.

2. 공분산 행렬 $\Sigma$

• $\Sigma$ 는 각 차원의 분산과, 서로 다른 차원 간의 공분산을 포함하는 행렬이다.
• 대각 원소 $\sigma_i^2$ 는 차원 $x_i$ 의 분산을 의미한다.
• 비대각 원소 $\rho_{ij}$ 는 $x_i$ 와 $x_j$ 사이의 공분산을 의미한다.

3. 수식의 의미

• $\rho_{ij} = E[(x_i - \mu_i)(x_j - \mu_j)]$ : 두 변수 $x_i, x_j$ 사이의 공분산을 정의한다.
• $\sigma_i^2 = E[(x_i - \mu_i)^2]$ : 각 변수 $x_i$ 의 분산을 정의한다.

---

p5. 최대우도추정 (Maximum Likelihood Estimation, MLE)

최대우도 매개변수 추정 (Maximum Likelihood Parameter Estimation)

• 실제 세계에서는 우리는 $\vec{\mu}$ 와 $\Sigma$를 알지 못한다.
• 만약 학습 데이터베이스 \(D = \{\vec{x}_0, \dots, \vec{x}_{M-1}\}\) 가 있다면,
  $\vec{\mu}$ 와 $\Sigma$를 다음과 같이 추정할 수 있다.

\[\{\hat{\mu}_{ML}, \hat{\Sigma}_{ML}\} = \arg\max \prod_{m=0}^{M-1} p(\vec{x}_m | \vec{\mu}, \Sigma)\] \[= \arg\max \sum_{m=0}^{M-1} \ln p(\vec{x}_m | \vec{\mu}, \Sigma)\]

---

---

1. 수식의 의미

• 위 수식은 주어진 데이터 집합 $D$ 가 발생할 가능성을 최대로 하는 평균 $\vec{\mu}$ 와 공분산 $\Sigma$ 를 찾는 문제를 나타낸다.
• 첫 번째 식은 모든 표본 확률의 곱(우도, likelihood)을 최대로 만드는 파라미터를 구한다는 의미이다.
• 두 번째 식은 우도에 로그를 취해 계산을 단순화한 형태로, 로그-우도(log-likelihood) 를 최대로 하는 파라미터를 찾는 것을 의미한다.

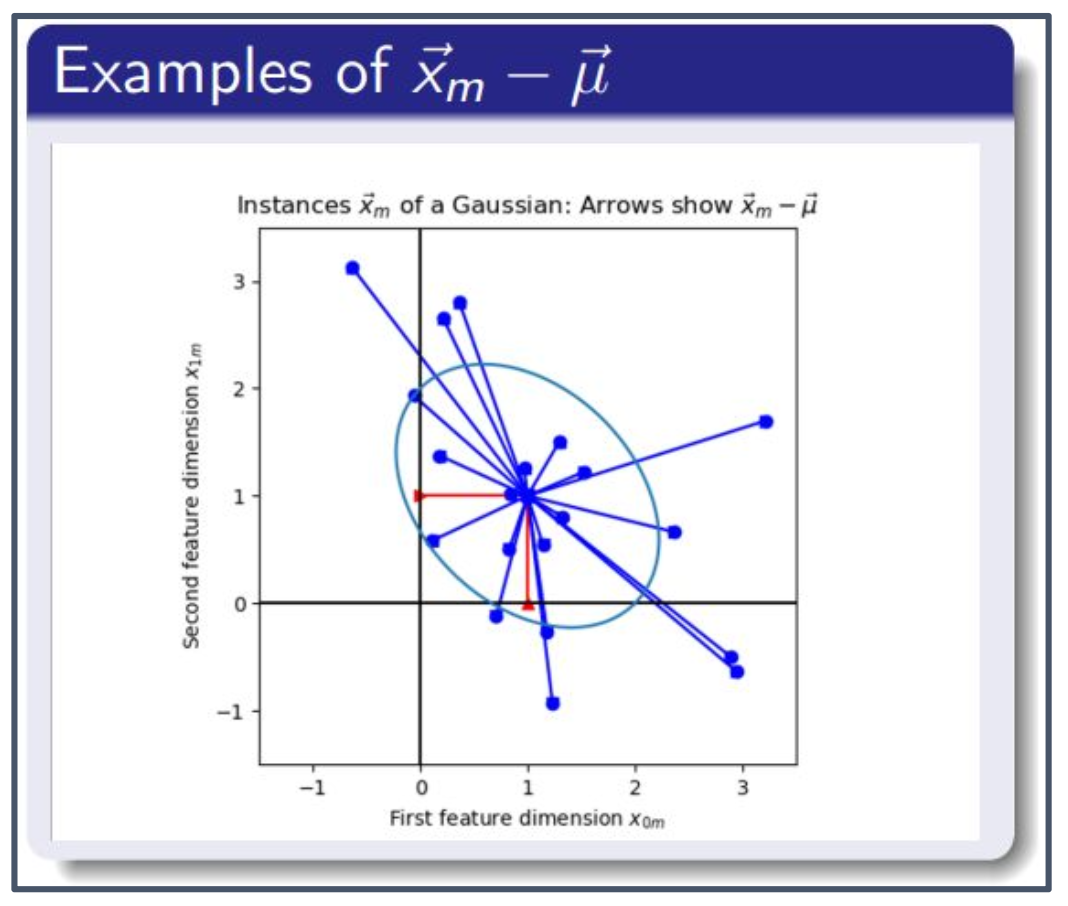
2. 그림 해석

• 오른쪽 그림에서 파란 점들은 표본(instance) $\vec{x}_m$ 을 나타낸다.
• 각 화살표는 $\vec{x}_m - \vec{\mu}$ 로, 표본과 평균 벡터 사이의 차이 벡터를 의미한다.
• MLE는 이 차이 벡터들의 분포를 가장 잘 설명할 수 있는 평균 $\vec{\mu}$ 와 공분산 $\Sigma$ 를 찾는다.
• 즉, 화살표들이 모여 있는 중심이 평균 $\vec{\mu}$ 이고, 화살표들의 퍼짐과 방향성은 공분산 $\Sigma$ 에 반영된다.

---

p6. 대수의 법칙 / 통계적 추정량 (LLN / Statistical Estimator)

최대우도 매개변수 추정 (Maximum Likelihood Parameter Estimation)

• 이전 슬라이드의 오른쪽 항(RHS)을 미분하고 이를 0으로 두면,
  최대우도 해는 다음과 같이 된다.

\[\hat{\mu}_{ML} = \frac{1}{M} \sum_{m=0}^{M-1} \vec{x}_m\] \[\hat{\Sigma}_{ML} = \frac{1}{M} \sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\]

---

---

1. 로그-우도(log-likelihood)의 전개

• $M$개의 표본 \(\{\vec{x}_m\}_{m=0}^{M-1}\) 이 다변량 정규분포 \(\mathcal{N}(\vec{\mu},\Sigma)\) 에서 독립적으로 추출되었다고 하자.
• 한 표본의 확률밀도는 다음과 같다.

\[p(\vec{x}_m|\vec{\mu},\Sigma) = \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}} \exp\!\left(-\tfrac{1}{2}(\vec{x}_m-\vec{\mu})^T\Sigma^{-1}(\vec{x}_m-\vec{\mu})\right).\]

• 전체 데이터셋의 우도(likelihood)는

\[L(\vec{\mu},\Sigma) = \prod_{m=0}^{M-1}p(\vec{x}_m|\vec{\mu},\Sigma).\]

• 로그를 취하면 곱이 합으로 바뀌어 계산이 단순해진다.

\[\ell(\vec{\mu},\Sigma) = -\frac{M}{2}\ln|2\pi\Sigma| -\frac{1}{2}\sum_{m=0}^{M-1}(\vec{x}_m-\vec{\mu})^T\Sigma^{-1}(\vec{x}_m-\vec{\mu}).\]

• 여기서 $-\tfrac{MD}{2}\ln(2\pi)$ 항은 상수이므로 const 로 묶는다.

\[\ell(\vec{\mu},\Sigma) = -\frac{M}{2}\ln|\Sigma| -\frac{1}{2}\sum_{m=0}^{M-1}(\vec{x}_m-\vec{\mu})^T\Sigma^{-1}(\vec{x}_m-\vec{\mu}) + \text{const}.\]

2. 평균 추정치의 도출

• $\vec{\mu}$ 에 대해 미분하면

\[\frac{\partial \ell}{\partial \vec{\mu}} = \Sigma^{-1}\!\left(\sum_{m=0}^{M-1}\vec{x}_m - M\vec{\mu}\right).\]

• 이를 0으로 두면

\[\hat{\mu}_{ML} = \frac{1}{M}\sum_{m=0}^{M-1}\vec{x}_m.\]

3. 공분산 추정치의 도출

• 산포행렬을 $S = \sum_{m=0}^{M-1}(\vec{x}_m-\vec{\mu})(\vec{x}_m-\vec{\mu})^T$ 로 두면

\[\ell(\vec{\mu},\Sigma) = -\frac{M}{2}\ln|\Sigma| -\frac{1}{2}\operatorname{tr}(\Sigma^{-1} S) +\text{const}.\]

• $\Sigma$ 에 대해 미분해 0으로 두면

\[S = M\Sigma \quad\Rightarrow\quad \hat{\Sigma}_{ML} = \frac{1}{M}\sum_{m=0}^{M-1}(\vec{x}_m-\hat{\mu}_{ML})(\vec{x}_m-\hat{\mu}_{ML})^T.\]

4. 그림 해석 (MLE와의 관련성)

• 그림에서 파란 점들은 표본 \(\vec{x}_m\) 이고, 빨간 점은 평균 추정치 \(\hat{\mu}_{ML}\) 이다.
• 각 화살표 \((\vec{x}_m - \hat{\mu}_{ML})\) 는 표본과 평균 간의 차이를 나타낸다.
• MLE는 이 차이 벡터들의 분포를 가장 잘 설명하는 평균과 공분산을 찾는 과정이다.
  • 평균 $\hat{\mu}_{ML}$ 은 모든 화살표의 총합이 0이 되는 중심점이다.
  • 공분산 $\hat{\Sigma}_{ML}$ 은 화살표들의 퍼짐 방향과 크기를 반영하여 분포의 타원 모양을 결정한다.
• 따라서 그림에서 빨간 점이 중심으로 잡히고, 화살표들의 퍼짐이 $\hat{\Sigma}_{ML}$ 로 표현되는 것이 바로 MLE의 의미이다.

---

p7. 대수의 법칙 / 통계적 추정량 (LLN / Statistical Estimator)

표본평균 (Sample Mean), 표본공분산 (Sample Covariance)

• $\Sigma$의 최대우도추정(MLE)은 보통 실제보다 작게 나온다.
• 따라서 이를 약간 조정하는 것이 더 낫다.
• 다음은 $\vec{\mu}$ 와 $\Sigma$의 불편추정량(unbiased estimators) 으로,
  각각 표본평균(sample mean) 과 표본공분산(sample covariance) 이라고 부른다.

\[\vec{\mu} = \frac{1}{M} \sum_{m=0}^{M-1} \vec{x}_m\] \[\Sigma = \frac{1}{M-1} \sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\]

---

---

1. 왜 분모가 M−1 이어야 하는가?

• MLE 방식의 표본분산은

  \[s^2_{MLE}=\frac{1}{M}\sum_{i=1}^M (x_i-\bar{x})^2\]

  이고, 이를 전개하면

  \[\sum_{i=1}^M (x_i-\bar{x})^2 =\sum_{i=1}^M (x_i-\mu)^2 - M(\bar{x}-\mu)^2.\]

  따라서

  \[s^2_{MLE} =\frac{1}{M}\Big(\sum_{i=1}^M (x_i-\mu)^2 - M(\bar{x}-\mu)^2\Big).\]

  기대값을 취하면

  \[E[s^2_{MLE}] =\frac{1}{M}\Big(\sum_{i=1}^M E[(x_i-\mu)^2] - M E[(\bar{x}-\mu)^2]\Big).\]

  여기서 $E[(x_i-\mu)^2]=\sigma^2$ 이므로 핵심은 $E[(\bar{x}-\mu)^2]$ 의 계산이다.

왜 $E[(\bar{x}-\mu)^2]=\sigma^2/M$ 인가?

• 표본평균의 정의

  \[\bar{x}=\frac{1}{M}\sum_{i=1}^M x_i\]
• 분산의 성질
  • $\mathrm{Var}(aX)=a^2\mathrm{Var}(X)$
  • 독립이면 $\mathrm{Var}(X+Y)=\mathrm{Var}(X)+\mathrm{Var}(Y)$

• 표본평균의 분산

  \[\mathrm{Var}(\bar{x}) =\frac{1}{M^2}(M\sigma^2) =\frac{\sigma^2}{M}.\]

  따라서

  \[E[(\bar{x}-\mu)^2]=\mathrm{Var}(\bar{x})=\frac{\sigma^2}{M}.\]

결론:

• 이를 대입하면

  \[E[s^2_{MLE}] =\frac{M-1}{M}\sigma^2,\]

  즉 실제 분산보다 작다(biased).

• 이를 보정하기 위해 $M$ 대신 $M-1$ 로 나누면

  \[s^2=\frac{1}{M-1}\sum_{i=1}^M (x_i-\bar{x})^2\]

  이 되고,

  \[E[s^2]=\sigma^2\]

  이므로 불편(unbiased) 추정량이 된다.

2. 그림 해석

• 파란 점: 표본(instance) $\vec{x}_m$
• 빨간 점: 표본평균 $\vec{\mu}$
• 화살표: 차이 벡터 $(\vec{x}_m-\vec{\mu})$

• 이 벡터를 외적하면

  \[(\vec{x}_m-\vec{\mu})(\vec{x}_m-\vec{\mu})^T\]

  이 되고, 이는 단일 표본이 공분산에 기여하는 행렬이다.

  • 대각 원소: 각 축 방향의 분산
  • 비대각 원소: 축 간 공분산

• 모든 표본에 대해 평균을 내면

  \[\Sigma =\frac{1}{M-1}\sum_{m=0}^{M-1}(\vec{x}_m-\vec{\mu})(\vec{x}_m-\vec{\mu})^T\]

  로, 이것이 표본공분산 행렬이다.

• 즉, 그림 속 화살표들의 퍼짐과 방향성을 집계한 결과가 $\Sigma$ 로 나타난다.

---

p8. 대수의 법칙 / 통계적 추정량 (LLN / Statistical Estimator)

표본평균 (Sample Mean), 표본공분산 (Sample Covariance)

\[\vec{\mu} = \frac{1}{M}\sum_{m=0}^{M-1} \vec{x}_m\] \[\Sigma = \frac{1}{M-1}\sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\]

• 표본평균과 표본공분산은 실제 평균(real mean)과 실제 공분산(real covariance)과 동일하지 않다.
• 그러나 특별히 구분할 필요가 없는 경우, 같은 기호 $\vec{\mu}, \Sigma$ 를 사용한다.

---

---

1. 표본 추정량과 모집단 모수의 차이

• $\vec{\mu}$ 와 $\Sigma$ 는 실제 모집단의 모수(parameter)가 아니라, 주어진 표본을 기반으로 계산된 추정치(estimator) 이다.
• 표본 수 $M$ 이 커질수록, 즉 $M \to \infty$ 일 때 표본평균과 표본공분산은 실제 평균과 공분산에 점점 더 가까워진다(일치성, consistency).

2. 그림 해석

• 파란 점들은 표본(instance)을 나타내고, 빨간 점은 표본평균 $\vec{\mu}$ 이다.
• 각 화살표는 표본과 평균의 차이 벡터 $(\vec{x}_m - \vec{\mu})$ 이며,
  이 차이 벡터들의 외적을 평균한 값이 표본공분산 $\Sigma$ 를 이룬다.

---

p9. 고유벡터와 고유값 (Eigenvector and Eigenvalue)

• $D \times D$ 정방행렬 $A$의 오른쪽 고유벡터(right eigenvector) $\vec{v}$ 는 다음을 만족하는 벡터이다.

\[A \vec{v} = \lambda \vec{v} \tag{1}\]

• 이때 $\lambda$ 를 고유값(eigenvalue) 이라고 한다.
• 식 (1)이 해(solution)를 가지기 위한 필요충분조건은

\[|A - \lambda I| = 0 \tag{2}\]

이다.

---

1. 고유값 방정식의 의미

• $A\vec{v}=\lambda\vec{v}$ 는 행렬 $A$ 가 벡터 $\vec{v}$ 의 방향은 그대로 유지한 채 크기만 $\lambda$ 배로 변환한다는 의미이다.
• 즉, $\vec{v}$ 는 행렬 $A$ 의 선형변환에 대해 방향이 변하지 않는 불변 벡터(eigenvector) 이다.

2. 행렬식 조건

• 식 $(A-\lambda I)\vec{v}=0$ 이 영벡터가 아닌 해(비자명 해) 를 가지려면,
  $(A-\lambda I)$ 가 가역(invertible)하지 않아야 한다.
• 따라서 행렬식이 다음을 만족해야 한다.

\[|A-\lambda I|=0\]

• 이 식을 특성방정식(characteristic equation) 이라 하며, 이를 풀어 고유값 $\lambda$ 를 구하게 된다.

---

p10. 고유벡터와 고유값 (Eigenvector and Eigenvalue)

• 지금까지 우리는 오른쪽 고유벡터(right eigenvector)와 오른쪽 고유값(right eigenvalue)을 다루어 왔다.

\[A \vec{v}_d = \lambda_d \vec{v}_d\]

• 또한 왼쪽 고유벡터(left eigenvector)도 존재할 수 있는데, 이는 행벡터(row vector) $\vec{u}_d$ 이며, 그에 대응하는 왼쪽 고유값(left eigenvalue) $\kappa_d$ 는 다음을 만족한다.

\[\vec{u}_d^T A = \kappa_d \vec{u}_d^T\]

---

1. 열 관점 (오른쪽 고유벡터)

• 행렬 $A$ 와 열벡터 $\vec{x}$ 의 곱 $A\vec{x}$ 는,
  $A$ 의 각 열(column) 이 $\vec{x}$ 의 성분에 의해 가중합된 표현이다.

  예:

  \[A=\begin{bmatrix}2 & 1\\0 & 3\end{bmatrix},\quad \vec{x}=\begin{bmatrix}x_1\\x_2\end{bmatrix}\] \[A\vec{x} =x_1\begin{bmatrix}2\\0\end{bmatrix} +x_2\begin{bmatrix}1\\3\end{bmatrix}\]

• 따라서 $A\vec{v}=\lambda\vec{v}$ 를 만족하는 오른쪽 고유벡터 $\vec{v}$ 는
  “$A$ 의 열들의 조합이 $\lambda\vec{v}$ 로 정확히 떨어지는 방향”을 의미한다.

2. 행 관점 (왼쪽 고유벡터)

• 행벡터 $\vec{u}^T$ 와 행렬 $A$ 의 곱 $\vec{u}^T A$ 는
  $A$ 의 행(row) 들이 $\vec{u}$ 의 성분으로 가중합된 결과이다.

  예:

  \[\vec{u}^T A =u_1\begin{bmatrix}2 & 1\end{bmatrix} +u_2\begin{bmatrix}0 & 3\end{bmatrix}\]

  계산하면

  \[\vec{u}^T A=\begin{bmatrix}2u_1,\;u_1+3u_2\end{bmatrix}\]

• $\vec{u}^T A=\kappa \vec{u}^T$ 를 만족하는 왼쪽 고유벡터 $\vec{u}^T$ 는
  “$A$ 의 행들의 조합이 자기 자신 방향(배율 $\kappa$)을 유지하는 경우”를 의미한다.

3. 종합

• 오른쪽 고유벡터 $\vec{v}$:
  • $A\vec{v}=\lambda\vec{v}$
  • $A$ 가 데이터를 곱해 변환하는 방향(열 공간) 을 설명한다.
• 왼쪽 고유벡터 $\vec{u}^T$:
  • $\vec{u}^T A=\kappa\vec{u}^T$
  • $A$ 의 행들이 데이터를 관찰·결합하는 방향(행 공간) 을 설명한다.
• 즉,
  • 오른쪽 고유벡터는 “$A$ 가 입력을 변화시키는 방향”,
  • 왼쪽 고유벡터는 “$A$ 의 행이 입력을 바라보는 방향”
    을 각각 표현한다.

---

p11. 고유벡터와 고유값 (Eigenvector and Eigenvalue)

행렬을 고유벡터와 곱할 때, 앞뒤로 동시에 곱하면 흥미로운 결과를 얻을 수 있다:

\[\vec{u}_i^T (A\vec{v}_j) = \vec{u}_i^T (\lambda_j \vec{v}_j) = \lambda_j \vec{u}_i^T \vec{v}_j\]

하지만,

\[(\vec{u}_i^T A)\vec{v}_j = (\kappa_i \vec{u}_i^T)\vec{v}_j = \kappa_i \vec{u}_i^T \vec{v}_j\]

두 식이 동시에 참이려면 가능한 경우는 두 가지뿐이다:

• $\kappa_i = \lambda_j$
• 또는 $\vec{u}_i^T \vec{v}_j = 0$

---

1. 왼쪽 고유벡터와 오른쪽 고유벡터의 관계

• 오른쪽 고유벡터 $\vec{v}_j$ 는 $A\vec{v}_j = \lambda_j \vec{v}_j$ 를 만족한다.
• 왼쪽 고유벡터 $\vec{u}_i^T$ 는 $\vec{u}_i^T A = \kappa_i \vec{u}_i^T$ 를 만족한다.
• 따라서 $A$를 앞뒤로 곱한 식을 비교하면, 고유값이 같거나 두 벡터가 직교해야만 모순이 생기지 않는다.

2. 의미

• 서로 다른 고유값을 갖는 경우, $\vec{u}_i^T \vec{v}_j = 0$ 이어야 한다. 즉, 왼쪽·오른쪽 고유벡터 쌍은 서로 직교한다.
• 고유값이 같은 경우에는 직교 조건 없이도 두 식이 동시에 성립한다.

---

p12. 고유벡터와 고유값 (Eigenvector and Eigenvalue)

두 식이 동시에 참이려면 가능한 경우는 단 두 가지뿐이다:

• $\kappa_i = \lambda_j$
• 또는 $\vec{u}_i^T \vec{v}_j = 0$

즉, 고유값들이 서로 다를 경우(distinct), 각 $\kappa_i$와 같아질 수 있는 $\lambda_j$ 는 많아야 하나(at most one) 뿐이라는 의미이다:

\[\begin{cases} i \neq j \quad \Rightarrow \quad \vec{u}_i^T \vec{v}_j = 0 \\ i = j \quad \Rightarrow \quad \kappa_i = \lambda_i \end{cases}\]

---

1. 직교 조건

• 서로 다른 고유값을 가지는 경우($i \neq j$), 왼쪽 고유벡터 $\vec{u}_i$ 와 오른쪽 고유벡터 $\vec{v}_j$ 는 직교한다.
• 즉, $\vec{u}_i^T \vec{v}_j = 0$ 이 성립한다.

2. 동일한 고유값의 경우

• 만약 $i = j$ 라면, 대응하는 왼쪽·오른쪽 고유벡터 쌍은 동일한 고유값을 공유한다.
• 즉, $\kappa_i = \lambda_i$ 가 된다.

---

p13. 고유벡터와 고유값 (Eigenvector and Eigenvalue)

만약 $A$가 대칭행렬($A = A^T$)이라면, 왼쪽 고유벡터(left eigenvector)와 오른쪽 고유벡터(right eigenvector), 그리고 고유값(eigenvalue)은 동일하다. 왜냐하면

\[\lambda_i \vec{u}_i^T = \vec{u}_i^T A = (A^T \vec{u}_i)^T = (A \vec{u}_i)^T\]

이고, 마지막 항은 $\lambda_i \vec{u}_i^T$ 와 같아지는데, 이는 오직 $\vec{u}_i = \vec{v}_i$ 일 때만 성립한다.

---

1. 왼쪽 고유벡터 정의
왼쪽 고유벡터 $\vec{u}_i^T$에 대해

\[\vec{u}_i^T A = \lambda_i \vec{u}_i^T\]

가 성립한다고 한다.

---

2. 전치(Transpose) 취하기
양변을 전치하면,

\[(\vec{u}_i^T A)^T = (\lambda_i \vec{u}_i^T)^T\]

즉,

\[A^T \vec{u}_i = \lambda_i \vec{u}_i\]

가 된다.

---

3. 대칭행렬 조건 사용
$A$가 대칭행렬이라면 $A^T = A$ 이므로,

\[A \vec{u}_i = \lambda_i \vec{u}_i\]

---

4. 결론
이는 $\vec{u}_i$가 $A$의 오른쪽 고유벡터 조건을 만족함을 뜻한다.
따라서 대칭행렬의 경우, 왼쪽 고유벡터와 오른쪽 고유벡터는 동일하다:

\[\vec{u}_i = \vec{v}_i\]

---

p14. 대칭행렬: 고유벡터들은 직교정규(Orthonormal)이다

다음 사실들을 종합해보자:

• $\vec{u}_i^T \vec{v}_j = 0 \quad (i \neq j)$
  → 서로 다른 고유값(distinct eigenvalues)을 가진 임의의 정방행렬(square matrix)에 대해 성립한다.

• $\vec{u}_i = \vec{v}_i$
  → 대칭행렬(symmetric matrix)의 경우 왼쪽 고유벡터와 오른쪽 고유벡터가 동일하다.

• $\vec{v}_i^T \vec{v}_i = 1$
  → 임의의 행렬에 대해 고유벡터를 표준적으로 정규화(normalization)하면,
  즉 $|\vec{v}_i| = 1$ 이 된다.

---

이 모든 사실을 종합하면,

\[\vec{v}_i^T \vec{v}_j = \begin{cases} 1 & i = j \\ 0 & i \neq j \end{cases}\]

---

1. 서로 다른 고유값의 경우 직교한다

• 만약 $i \neq j$라면, $\vec{u}_i^T \vec{v}_j = 0$ 이 성립한다.
• 즉, 고유값이 다르면 대응하는 고유벡터들은 서로 직교한다는 사실이다.

---

2. 대칭행렬에서는 왼쪽과 오른쪽 고유벡터가 같다

• $\vec{u}_i = \vec{v}_i$ 이므로, $\vec{u}_i^T \vec{v}_j$ 는 곧 $\vec{v}_i^T \vec{v}_j$ 로 쓸 수 있다.
• 따라서 “고유값이 다르면 직교한다”는 성질을 오른쪽 고유벡터들끼리의 관계로 바로 옮길 수 있다.

---

3. 정규화의 효과

• 고유벡터는 스칼라 배를 곱해도 여전히 고유벡터이므로, 크기를 1로 맞춰주는 정규화(normalization)를 할 수 있다.
• 정규화하면 $\vec{v}_i^T \vec{v}_i = |\vec{v}_i|^2 = 1$ 이 된다.

---

4. 종합하기

• $i \neq j$일 때: 위 1번 성질에 의해 $\vec{v}_i^T \vec{v}_j = 0$.
• $i = j$일 때: 정규화했으므로 $\vec{v}_i^T \vec{v}_i = 1$.

\[\vec{v}_i^T \vec{v}_j = \begin{cases} 1 & i = j \\ 0 & i \neq j \end{cases}\]

즉, 대칭행렬의 고유벡터들은 직교정규(orthonormal) 집합을 이룬다.

---

p15. 대칭행렬: 고유벡터는 직교정규(Orthonormal)이다

만약 $A$가 대칭행렬(symmetric matrix)이고, 서로 다른 고유값(distinct eigenvalues)을 가진다면,
그 고유벡터들은 직교정규(orthonormal) 하다:

\[\vec{v}_i^T \vec{v}_j = \begin{cases} 1 & i = j \\ 0 & i \neq j \end{cases}\]

이를 다음과 같이 쓸 수 있다:

\[V^T V = I\]

여기서,

\[V = [\vec{v}_0, \dots, \vec{v}_{D-1}]\]

---

1. 직교(orthogonal)와 정규화(normalization)의 결합

• $i \neq j$일 때 $\vec{v}_i^T \vec{v}_j = 0$ 이므로 서로 직교한다.
• $i = j$일 때 $\vec{v}_i^T \vec{v}_i = 1$ 이므로 각 고유벡터는 길이가 1로 정규화된다.
• 따라서 고유벡터 집합은 서로 직교하고 동시에 정규화되어 있어 직교정규 집합(orthonormal set)을 이룬다.

2. 행렬 $V$의 의미

• $V$는 $A$의 고유벡터들을 열(column)로 모은 행렬이다.
• $V^T V = I$라는 식은 $V$가 직교행렬(orthogonal matrix)임을 뜻한다.
• 즉, $V$의 역행렬은 $V^T$로 주어지며, 이 성질은 고유분해(Eigendecomposition)와 주성분분석(PCA)에서 핵심적인 역할을 한다.

---

p16. 대칭행렬: 고유벡터는 직교정규 (Orthonormal)

이미 우리가 $V^T V = I$ 임을 보였다.

그리고 또한 다음이 성립함을 알 수 있다:

\[V V^T = I\]

증명:

\[V V^T = V I V^T = V (V^T V) V^T = (V V^T)^2\]

그런데 $V V^T = (V V^T)^2$ 를 만족하는 유일한 행렬은

\[V V^T = I\]

이다.

---

1. $V^T V = I$와 $V V^T = I$의 차이

• $V^T V = I$는 $V$의 열 벡터들(column vectors)이 서로 직교정규(orthonormal)임을 의미한다.
• $V V^T = I$는 $V$의 행 벡터들(row vectors)도 서로 직교정규임을 뜻한다.

2. 직교행렬(Orthogonal matrix)의 정의

• 어떤 행렬 $V$가 $V^T V = I$와 $V V^T = I$를 동시에 만족하면 $V$는 직교행렬(orthogonal matrix)이라고 한다.
• 직교행렬은 역행렬이 전치행렬과 같아서 $V^{-1} = V^T$가 된다.

3. 직관적 의미

• 고유벡터들이 직교정규라는 것은, 이 벡터들이 서로 수직이고 길이가 1인 새로운 좌표축 역할을 한다는 뜻이다.
• 따라서 $V$는 좌표계를 바꾸는 회전(rotation)이나 반사(reflection)를 나타내는 변환행렬로 이해할 수 있다.

---

p17. 대칭행렬: 고유벡터는 직교정규 (Orthonormal)

이제 $A$가 대칭(symmetric)이라고 가정하자:

\[\vec{v}_i^T A \vec{v}_j = \vec{v}_i^T (\lambda_j \vec{v}_j) = \lambda_j \vec{v}_i^T \vec{v}_j = \begin{cases} \lambda_j, & i = j \\ 0, & i \neq j \end{cases}\]

즉, 대칭행렬이 $D$개의 서로 다른 고유값(distinct eigenvalues)을 가진다면,
그 고유벡터들은 $A$를 직교화(orthogonalize)한다:

\[V^T A V = \Lambda\]

여기서 $\Lambda$는 대각행렬(diagonal matrix)이고,

\[\Lambda = \begin{bmatrix} \lambda_0 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \lambda_{D-1} \end{bmatrix}\]

이다.

---

1. 고유값과의 직접 연결

• $i = j$일 때 $\vec{v}_i^T A \vec{v}_i = \lambda_i$ 가 된다.
• 이는 고유벡터 $\vec{v}_i$가 $A$의 고유값 $\lambda_i$와 직접 연결됨을 보여준다.

2. 서로 다른 고유벡터의 직교성

• $i \neq j$일 때 $\vec{v}_i^T A \vec{v}_j = 0$ 이므로 서로 다른 고유벡터들은 직교(orthogonal) 관계를 갖는다.

3. 대각화의 의미

• $V^T A V = \Lambda$라는 식은 대각화(diagonalization)를 의미한다.
• 대칭행렬 $A$는 직교행렬 $V$에 의해 대각화될 수 있으며, 그 대각 원소들은 $A$의 고유값이 된다.

---

추가 설명: 대각화란 무엇인가?

• 대각화(diagonalization)는 행렬 $A$를 고유벡터 행렬 $V$와 고유값 대각행렬 $\Lambda$로 표현하는 과정이다.

\[A = V \Lambda V^T\]

• 원래 행렬 $A$는 다양한 원소가 얽혀 있지만, $\Lambda$는 대각선에 고유값만 남고 나머지는 0이어서 계산이 매우 단순해진다.

• 예를 들어, $A^k$를 계산하고자 할 때

\[A^k = (V \Lambda V^T)^k = V \Lambda^k V^T\]

• 즉, 대각화는 복잡한 행렬 연산을 단순한 고유값 연산으로 바꾸어주는 강력한 도구이다.

---

p18. 대칭행렬: 고유벡터는 직교정규 (Orthonormal)

한 가지 더, 다음을 주목하자:

\[A = V V^T A V V^T = V \Lambda V^T\]

마지막 항은 다음과 같다:

\[[\vec{v}_0, \ldots, \vec{v}_{D-1}] \begin{bmatrix} \lambda_0 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \lambda_{D-1} \end{bmatrix} \begin{bmatrix} \vec{v}_0^T \\ \vdots \\ \vec{v}_{D-1}^T \end{bmatrix} = \sum_{d=0}^{D-1} \lambda_d \vec{v}_d \vec{v}_d^T\]

---

1. 고유값·고유벡터 조합으로서의 행렬 표현

• 위 전개는 행렬 $A$가 고유값 $\lambda_d$와 고유벡터 $\vec{v}_d$의 조합으로 표현될 수 있음을 보여준다.
• 즉, $A$는 단일 수식이 아니라 여러 고유벡터 방향에서의 작용을 종합한 형태로 이해할 수 있다.

2. 외적 $\vec{v}_d \vec{v}_d^T$의 의미

• $\vec{v}_d \vec{v}_d^T$는 벡터 $\vec{v}_d$의 외적(outer product)으로, 임의의 벡터를 $\vec{v}_d$ 방향으로 투영(projection)하는 연산이다.

• 임의의 벡터 $\vec{x}$에 대해

  \[\vec{v}_d \vec{v}_d^T \vec{x}\]

  를 계산하면 먼저 $\vec{v}_d^T \vec{x}$가 계산되고, 이는 $\vec{x}$가 $\vec{v}_d$ 방향으로 얼마나 들어맞는지를 나타내는 스칼라이다.

• 따라서

  \[\vec{v}_d \vec{v}_d^T \vec{x} = (\vec{v}_d^T \vec{x}) \vec{v}_d\]

  가 되어, $\vec{x}$를 $\vec{v}_d$ 방향으로 사영한 벡터가 된다.

• 즉, $\vec{v}_d \vec{v}_d^T$는 “$\vec{v}_d$ 방향 성분만 남기고 나머지는 제거하는 행렬”이다.

3. 각 항 $\lambda_d \vec{v}_d \vec{v}_d^T$의 역할

• 각 항은 벡터를 먼저 $\vec{v}_d$ 방향으로 투영한 뒤, 고유값 $\lambda_d$만큼 스케일링하는 역할을 한다.
• 따라서 행렬 $A$는 모든 고유벡터 방향에 대해 ‘투영 후 스케일링’을 수행하고, 그 결과들을 합친 것과 같다.

4. 스펙트럴 분해(Spectral decomposition)

• 이 표현은 스펙트럴 분해라고 하며, 대칭행렬은 각 고유벡터의 투영 행렬을 고유값으로 가중합한 것과 같다는 사실을 보여준다.

---

p19. 대칭행렬: 고유벡터는 직교정규성을 가진다 (Symmetric matrices: eigenvectors are orthonormal)

만약 $A$가 $D$개의 고유벡터(eigenvectors)를 가지고,
또한 $D$개의 서로 다른 고유값(distinct eigenvalues)을 가진 대칭행렬이라면,

\[A = V \Lambda V^T\] \[\Lambda = V^T A V\] \[V V^T = V^T V = I\]

---

1. 고유벡터 행렬 $V$의 정의

• \(V = [\vec{v}_0, \dots, \vec{v}_{D-1}]\)
  는 $A$의 고유벡터들을 모아 만든 행렬이다.

2. $V^T A V = \Lambda$의 의미

• 이 식은 $A$를 고유벡터 기저로 표현하면 단순히 고유값만 곱하는 대각행렬이 된다는 뜻이다.

3. 좌표계 관점에서의 해석

• 원래 좌표계에서는 $A$가 벡터의 방향과 크기를 함께 변화시키지만,
  고유벡터 좌표계에서는 각 좌표 성분을 $\lambda_i$만큼 스케일링할 뿐이다.

---

p20. 최근접 이웃 분류기 (Nearest-Neighbors Classifier)

가정해보자. 우리가 하나의 테스트 이미지 $\vec{x}_{test}$를 가지고 있다고 하자.
우리는 이 사람이 누구인지 알아내고 싶다.

---

p21. 최근접 이웃 분류기 (Nearest-Neighbors Classifier)

테스트 이미지를 분류하기 위해서는, 일부 훈련 데이터가 필요하다.
예를 들어, 우리가 훈련 데이터로 다음 네 개의 이미지를 가지고 있다고 하자.
각 이미지 $\vec{x}_m$ 은 라벨 $y_m$ 과 함께 주어지며, 여기서 $y_m$ 은 단순히 그 개인의 이름을 나타내는 문자열이다.

---

p22. 아이겐페이스 (Eigenface)

• Original Image : 원본 얼굴 이미지
• $r = 25, 50, 100, 200, 400, 800, 1600$ : 아이겐페이스(eigenface) 성분의 개수 $r$를 다르게 하여 복원한 얼굴 이미지

$r$이 커질수록, 즉 더 많은 아이겐페이스를 사용하면 원본 이미지와 유사한 얼굴로 점점 더 정확히 복원된다.

---

1. 아이겐페이스(Eigenface)의 개념

• PCA(주성분 분석)를 얼굴 이미지 데이터에 적용하면, 얼굴 데이터의 주요 변화를 설명하는 축(고유벡터)이 생성된다.
• 이 고유벡터를 얼굴 이미지 형태로 시각화한 것이 아이겐페이스이다.

2. 얼굴 복원 과정

• 임의의 얼굴 이미지는 여러 개의 아이겐페이스들의 선형 결합으로 근사할 수 있다.
• 사용할 아이겐페이스의 수 $r$이 증가할수록 더 많은 세부 정보를 반영할 수 있다.

3. 해석

• $r$이 작을 때는 흐릿하고 추상적인 얼굴 형태만 표현된다.
• $r$이 충분히 커지면 눈, 코, 입, 윤곽 등 개별 얼굴 특징이 뚜렷하게 복원된다.

---

p23. 최근접 이웃 분류기 (Nearest-Neighbors Classifier)

“최근접 이웃 분류기(nearest neighbors classifier)”는 다음과 같이 추정한다:
테스트 벡터는 가장 가까운 학습 벡터와 동일한 사람의 이미지라고 가정한다.

\[\hat{y}_{test} = y_{m^\ast}, \quad m^\ast = \arg\min_{m=0}^{M-1} \|\vec{x}_m - \vec{x}_{test}\|\]

여기서 “가장 가깝다(closest)”의 의미는 유클리드 거리(Euclidean distance) 이다:

\[\|\vec{x}_m - \vec{x}_{test}\| = \sqrt{ \sum_{d=0}^{D-1} (x_{md} - x_{test,d})^2 }\]

---

1. 유클리드 거리의 의미

• 두 벡터 \(\vec{x}_m\)과 \(\vec{x}_{test}\)의 차이를 각 좌표별로 제곱해 더한 뒤 제곱근을 취한 값이다.
• 이는 두 점 사이의 직선 거리로 해석된다.

2. 최근접 이웃 분류의 원리

• 테스트 이미지와 모든 학습 이미지 간의 거리를 계산한다.
• 가장 거리가 작은 학습 이미지를 찾고, 그 이미지의 라벨을 테스트 이미지의 예측값으로 한다.

3. 특징

• 직관적이고 단순한 분류 방법이다.
• 하지만 학습 데이터가 많아질수록 계산 비용이 커지고, 고차원 공간에서는 성능이 떨어질 수 있다.

---

p24. 최근접 이웃 분류기의 한계와 개선 (Nearest-Neighbors Classifier)

• 최근접 이웃 분류기의 문제는 한 이미지를 다른 이미지에서 픽셀 단위로 빼면, 그 결과가 노이즈(noise)에 의해 지배되는 측정값이 된다는 점이다.

• 따라서 우리는 더 나은 측정 방법이 필요하다.

• 해결책은 하나의 신호 표현(signal representation) $\vec{y}_m$을 찾는 것이다.
  이렇게 하면 $\vec{y}_m$은 이미지 $\vec{x}_m$이 다른 얼굴들과 어떻게 다른지를 요약(summarize)하게 된다.

• 만약 $\vec{y}_m$을 주성분 분석(Principal Components Analysis, PCA) 을 이용해 찾는다면,
  이 $\vec{y}_m$은 아이겐페이스(Eigenface) 표현이라고 불린다.

---

1. 노이즈의 문제

• 픽셀 단위로 이미지를 비교하면 조명, 작은 위치 변화, 배경의 잡음 등으로 인해 실제 인물과 무관한 차이가 크게 측정될 수 있다.
• 즉, 얼굴의 본질적인 차이가 아니라 주변 환경 요인에 의해 거리가 왜곡될 수 있다.

2. 아이겐페이스(Eigenface)의 아이디어

• PCA를 통해 얼굴 이미지 데이터에서 가장 변동이 큰 방향(주성분)을 찾아낸다.
• 이 주성분들을 새로운 좌표축으로 삼아 얼굴 이미지를 요약된 벡터 $\vec{y}_m$로 표현하면, 불필요한 픽셀 단위의 잡음이 줄어든다.

3. 장점

• 얼굴 이미지를 저차원 특징 공간으로 변환하므로 노이즈의 영향을 완화할 수 있다.
• 또한 계산 효율성이 좋아지고, 얼굴 인식에서 중요한 패턴만을 강조할 수 있다.

---

p25. 주성분 분석 (PCA, Principal Component Analysis)

표본 공분산(Sample covariance)

\[\Sigma = \frac{1}{M-1} \sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\] \[= \frac{1}{M-1} X^T X\]

여기서 $X$는 중심화(centered)된 데이터 행렬이다:

\[X = \begin{bmatrix} (\vec{x}_0 - \vec{\mu})^T \\ \vdots \\ (\vec{x}_{M-1} - \vec{\mu})^T \end{bmatrix}\]

---

예시 (Examples of $\vec{x}_m - \vec{\mu}$)

• 오른쪽 그림: 가우시안 분포의 샘플 $\vec{x}_m$ 들이 점으로 표시되어 있으며,
  화살표는 각 $\vec{x}_m - \vec{\mu}$ 를 나타낸다.

---

1. 공분산 행렬의 의미

• 공분산 행렬 $\Sigma$는 데이터의 분산(흩어짐)과 변수 간 상관관계를 요약한다.
• 얼굴 이미지의 경우, 픽셀 간의 상관성과 변동 패턴을 반영한다.

2. 중심화(centered data)

• 각 데이터 $\vec{x}_m$에서 평균 $\vec{\mu}$를 뺀 값이 중심화 데이터이다.
• 이를 통해 데이터의 중심을 원점으로 맞추어 분산과 상관관계를 분석하기 쉽게 만든다.

3. PCA와의 연결

• PCA는 공분산 행렬 $\Sigma$의 고유벡터를 찾아 데이터의 주요 변동 방향을 결정한다.
• 고유값의 크기는 해당 방향에서의 분산 크기를 나타낸다.

---

p26. 주성분 분석 (PCA, Principal Component Analysis)

표본 공분산(Sample covariance)

\[\Sigma = \frac{1}{M-1} X^T X\]

행렬 $X^T X$는 제곱합 행렬(sum-of-squares, SS matrix) 이라고 불린다.
이 행렬은 스칼라 배수 $(M-1)$에 의해 표본 공분산 행렬(sample covariance matrix) 과 관련된다.

---

예시 (Examples of $\vec{x}_m - \vec{\mu}$)

• 오른쪽 그림: 가우시안 분포의 샘플 $\vec{x}_m$ 들이 점으로 표시되어 있으며,
  화살표는 각 $\vec{x}_m - \vec{\mu}$ 를 나타낸다.

---

1. 제곱합 행렬(SS matrix)의 의미

• $X^T X$는 각 데이터의 분산과 공분산이 모두 합산된 형태를 담고 있다.
• 이는 데이터가 전체적으로 얼마나 퍼져 있는지를 나타내는 기초적인 척도이다.

2. 공분산 행렬과의 관계

• 표본 공분산 행렬은 $X^T X$를 단순히 $(M-1)$로 나누어 얻는다.
• 즉, 공분산 행렬은 SS 행렬을 표준화(normalization)한 결과라고 볼 수 있다.

3. PCA와의 연결

• PCA는 이 공분산 행렬을 고유분해하여 주성분(Principal Components)을 찾는다.
• 주성분은 데이터가 가장 크게 퍼져 있는 방향을 나타내며, 차원 축소와 잡음 제거에 활용된다.

---

p27. 주성분 분석 (PCA, Principal Component Analysis)

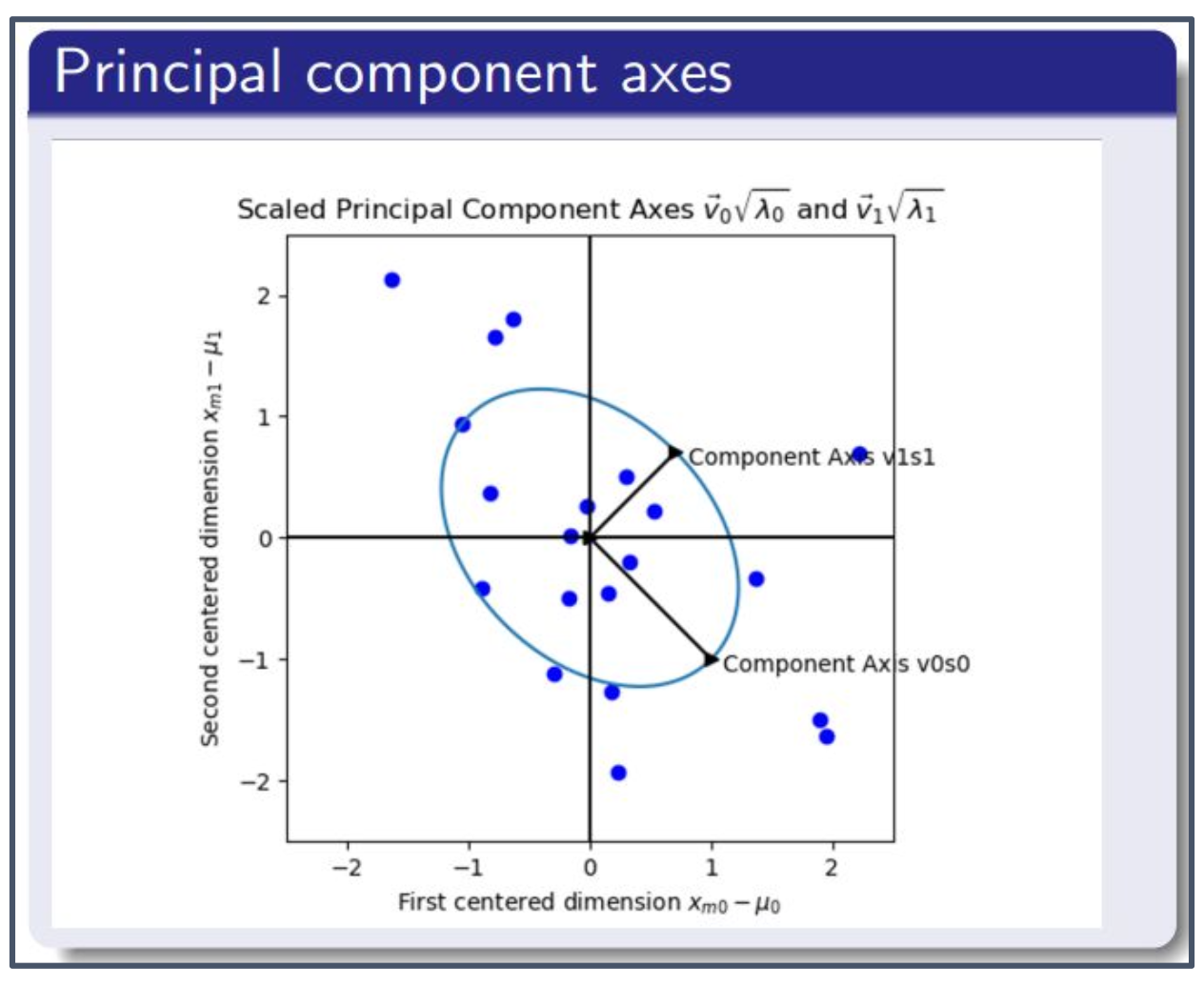
주성분 축(Principal component axes)

$X^T X$ 는 대칭행렬(symmetric)이다!
따라서,

\[X^T X = V \Lambda V^T\]

여기서,

\[V = [\vec{v}_0, \ldots, \vec{v}_{D-1}]\]

는 $X^T X$의 고유벡터들(eigenvectors)로 이루어진 행렬이다.
이 고유벡터들은 주성분 축(principal component axes) 또는 주성분 방향(principal component directions) 이라고 불린다.

---

예시 (Principal component axes)

• 오른쪽 그림: 데이터 분포에서 주성분 축이 가장 큰 분산을 설명하는 방향으로 나타나며,
  이는 데이터의 주요 패턴을 잡아내는 축 역할을 한다.

---

1. 왜 $X^T X$가 대칭행렬인가?

• 임의의 행렬 $X$에 대해

  \[(X^T X)^T = X^T (X^T)^T = X^T X\]

  가 성립한다.

• 따라서 $X^T X$는 항상 대칭행렬이다.

2. 대칭행렬의 고유벡터 성질

• $X^T X$가 대칭행렬이므로, 고유벡터들은 서로 직교할 수 있다.

• 또한 각 고유벡터는 정규화(normalization)를 통해

  \[\vec{v}_i^T \vec{v}_j = \begin{cases} 1 & i=j \\ 0 & i \neq j \end{cases}\]

  의 조건을 만족하게 할 수 있다.

3. PCA와 연결

• $X^T X$의 고유벡터들이 주성분 축(principal component axes)을 이룬다.
• 즉, 데이터는 이 직교정규 기저 위에서 새로운 좌표계로 표현될 수 있다.

---

p28. 주성분 분석 (Principal Component Analysis, PCA)

\[\Sigma = \frac{1}{M-1} X^T X, \quad \text{따라서} \quad \Sigma = V \left( \frac{1}{M-1} \Lambda \right) V^T\]

\(V = [\vec{v}_0, \dots, \vec{v}_{D-1}]\) 는
합제곱행렬(sum-of-squares matrix) 과
공분산행렬(covariance matrix) 의 고유벡터들이다.

$\Lambda$ 는 합제곱행렬의 고유값들이며,
이는 공분산행렬의 고유값에 $(M-1)$을 곱한 것과 같다.

---

1. 합제곱행렬 (Sum-of-Squares matrix)

\[S = X^T X = \sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\]

2. 공분산행렬 (Covariance matrix)

\[\Sigma = \frac{1}{M-1} X^T X = \frac{1}{M-1} \sum_{m=0}^{M-1} (\vec{x}_m - \vec{\mu})(\vec{x}_m - \vec{\mu})^T\]

→ 따라서, $\Sigma = \dfrac{1}{M-1} S$ 이다.

3. 고유값 관계

• 합제곱행렬의 고유값 $\lambda^{(S)}$ 와
  공분산행렬의 고유값 $\lambda^{(\Sigma)}$ 는 다음 관계를 가진다:

  \[\lambda^{(S)} = (M-1) \lambda^{(\Sigma)}\]

• 고유벡터는 두 행렬에서 동일하다.

---

p29. 주성분 분석 (Principal Component Analysis, PCA)

행렬의 고유벡터(eigenvectors)는 그것을 대각화(diagonalize)한다는 것을 기억하라.
따라서 $V$가 $X^T X$의 고유벡터들이라면,

\[V^T X^T X V = \Lambda\] \[\vec{v}_i^T X^T X \vec{v}_j = \begin{cases} \lambda_j & \lambda_i = \lambda_j \\ 0 & \lambda_i \neq \lambda_j \end{cases}\]

또한 $X$의 행은 $(\vec{x}_m - \vec{\mu})^T$ 이므로, 다음과 같이 정의하면

\[(\vec{x}_m - \vec{\mu})^T V = \vec{y}_m^T, \quad Y = \begin{bmatrix} \vec{y}_0^T \\ \vdots \\ \vec{y}_{M-1}^T \end{bmatrix}\]

우리는 다음을 얻는다:

\[Y^T Y = \Lambda\]

즉, $\vec{y}$ 벡터들의 공분산행렬은 대각행렬(diagonal matrix)이다!

---

1. 행렬 $X$의 정의

• $X$는 평균 중심화(mean-centered)된 데이터 행렬이다.

• 각 행은 한 데이터 포인트에서 평균을 뺀 벡터로 이루어진다:

  \[X = \begin{bmatrix} (\vec{x}_0 - \vec{\mu})^T \\ (\vec{x}_1 - \vec{\mu})^T \\ \vdots \\ (\vec{x}_{M-1} - \vec{\mu})^T \end{bmatrix}\]
• 따라서 $X$는 $M \times D$ 크기의 행렬이며, $M$개의 샘플이 $D$차원 공간에 존재할 때 사용할 수 있다.

2. 고유벡터에 의한 대각화

• $X^T X$는 대칭행렬이므로 직교 고유벡터 집합 $V$로 대각화할 수 있다.

  \[V^T X^T X V = \Lambda\]
• $\Lambda$는 고유값들을 대각선에 가진 행렬이다.
• 직교성 때문에 서로 다른 고유벡터 방향은 직교하고, 같은 방향에서는 고유값 $\lambda_j$만큼 스케일된다.

3. 기저변환(좌표계 변환)의 의미

• 데이터를 고유벡터(Principal Components)로 이루어진 새로운 기저

  \[V = [\vec{v}_0, \dots, \vec{v}_{D-1}]\]

  위에 표현하는 것이 PCA 좌표계로의 변환이다.

• 한 데이터 벡터에 대해

  \[(\vec{x}_m - \vec{\mu})^T V = \vec{y}_m^T\]

  로 나타나며, $\vec{y}_m$은 고유벡터 기저에서의 좌표(주성분 표현)이다.

4. 모든 데이터의 변환

• 같은 변환을 모든 샘플에 적용하면 새로운 행렬 $Y$를 얻는다:

  \[Y = X V\] \[Y = \begin{bmatrix} \vec{y}_0^T \\ \vdots \\ \vec{y}_{M-1}^T \end{bmatrix}\]

• $Y$의 각 행은 해당 데이터가 PCA 기저로 표현된 새로운 좌표를 의미한다.

5. 새로운 좌표계에서의 공분산

• $Y^T Y = \Lambda$가 성립한다는 사실은
  변환된 좌표계(주성분 좌표계)에서 축들끼리 상관되지 않고 독립적임을 의미한다.
• 따라서 $\vec{y}$ 벡터들의 공분산행렬은 대각행렬이 된다.

---

p30. 주성분 분석 (Principal Component Analysis, PCA)

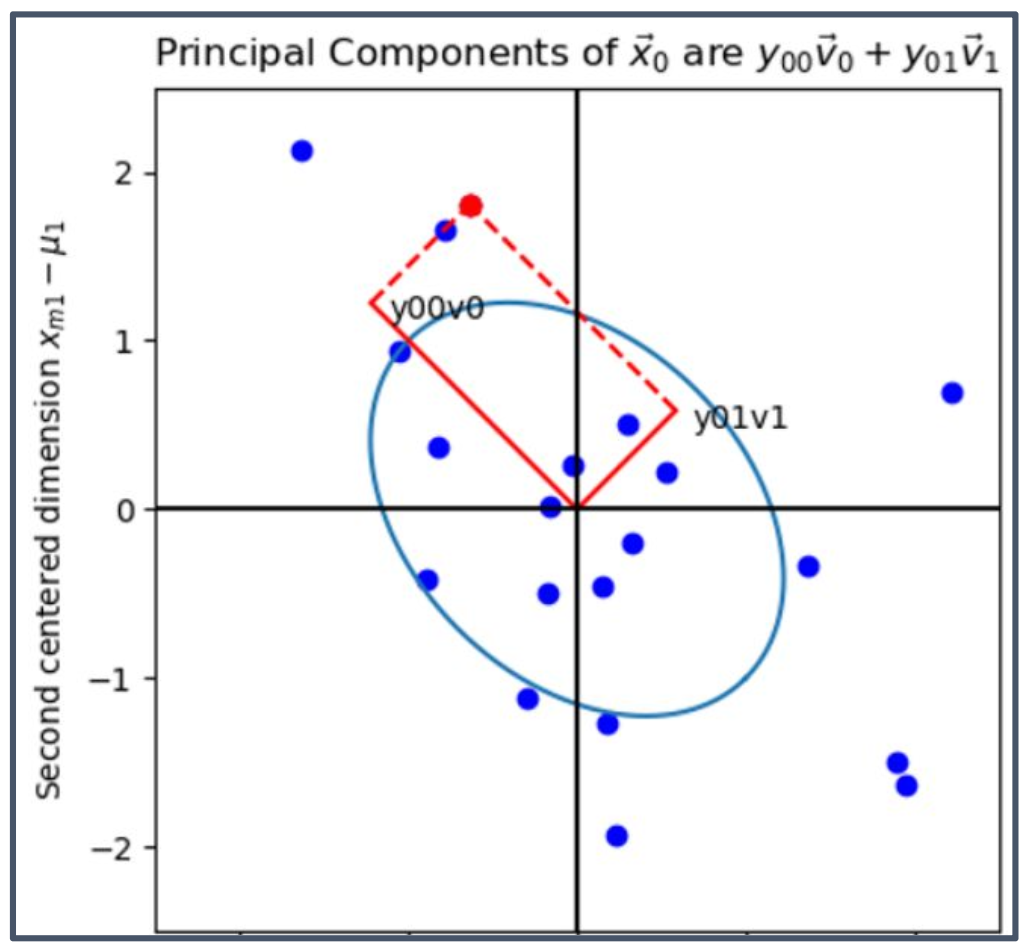
\[\vec{y}_m = V^T (\vec{x}_m - \vec{\mu})\]

---

1. 식의 의미

• $\vec{y}_m$은 데이터 $\vec{x}_m$을 평균 중심화한 뒤, 고유벡터 기저 $V$ 위로 투영한 좌표이다.
• 즉, 원래 데이터가 PCA 기저에서 어떤 좌표값으로 표현되는지를 나타낸다.

2. 그림의 의미

• 그림에서 $\vec{x}_0 - \vec{\mu}$는 빨간색 화살표로 표현된 벡터이다.
• 이 벡터는 PCA의 첫 번째 주성분 $\vec{v}_0$과 두 번째 주성분 $\vec{v}_1$ 방향으로 분해된다.

• 각 방향에 대한 투영 성분은

  \[y_{00}\vec{v}_0 \quad\text{(첫 번째 주성분 축 성분)},\] \[y_{01}\vec{v}_1 \quad\text{(두 번째 주성분 축 성분)}\]

  으로 나타난다.

• 따라서 원래 벡터는 이 두 성분의 합으로 복원된다.

3. 직관적 해석

• PCA는 데이터를 서로 직교하는 주성분 벡터들의 선형결합으로 표현한다.
• 이는 데이터를 “새로운 좌표계”로 옮겨서, 데이터의 분산을 가장 잘 설명하는 축 위로 나누어 표현하는 과정이다.

---

p31. 주성분 분석 (Principal Component Analysis, PCA)

$Y = XV$ 라고 쓰자, 그리고 $Y^T = V^T X^T$ 이다.
즉,

\[(\vec{x}_m - \vec{\mu})^T V = \vec{y}_m^T\] \[XV = Y\] \[V^T X^T X V = Y^T Y = \Lambda\]

여기서

\[\vec{y}_m = [y_{m,0}, \dots, y_{m,D-1}]^T\]

는 $\vec{x}_m$의 주성분 벡터이다.

공식 $Y^T Y = \Lambda$를 전개하면, PCA가 데이터셋을 직교화(orthogonalize)함을 알 수 있다:

\[\sum_{m=0}^{M-1} y_{im} y_{jm} = \begin{cases} \lambda_i & i = j \\ 0 & i \neq j \end{cases}\]

---

1. 식의 의미

• $Y = X V$는 데이터를 고유벡터 기저 $V$ 위에 투영하여 얻은 주성분 좌표행렬이다.
• $Y^T Y = \Lambda$는 변환된 좌표계에서 공분산 행렬이 대각화됨을 의미한다.
• 즉, 서로 다른 주성분 축들은 상관되지 않고 독립적이다.

2. 직교화의 의미

• $\sum_{m=0}^{M-1} y_{im} y_{jm}$은 $i$번째와 $j$번째 주성분 성분들 간의 내적이다.
• $i = j$일 때는 고유값 $\lambda_i$가 되고, $i \neq j$일 때는 $0$이 된다.
• 따라서 주성분 축들이 서로 직교하며, 데이터의 분산이 각 축으로 분리되어 설명된다.

3. 직관적 해석

• PCA는 데이터를 새로운 직교 좌표계로 옮겨 각 축마다 독립적으로 분산을 측정할 수 있게 한다.
• 그 결과 데이터의 상관된 성분이 제거되고, 큰 고유값을 가지는 방향 중심으로 차원 축소가 가능하다.

---

p32. 주성분 분석 (Principal Component Analysis, PCA)

데이터셋 전체의 에너지(total dataset energy)는 $i$번째 주성분 방향에서 다음과 같다:

\[\sum_{m=0}^{M-1} y_{mi}^2 = \lambda_i\]

하지만 $V^T V = I$임을 기억하라. 따라서 데이터셋 전체의 에너지는 원래 이미지 공간에서 계산하든, PCA 영역에서 계산하든 동일하다:

\[\sum_{m=0}^{M-1} \sum_{d=0}^{D-1} (x_{md} - \mu_d)^2 = \sum_{m=0}^{M-1} \sum_{i=0}^{D-1} y_{mi}^2 = \sum_{i=0}^{D-1} \lambda_i\]

---

1. 식의 의미

• $\sum_{m=0}^{M-1} y_{mi}^2 = \lambda_i$는 $i$번째 주성분 축에서의 총 분산(에너지)이 곧 그 축의 고유값 $\lambda_i$임을 의미한다.
• 즉, 각 고유값은 해당 축이 설명하는 데이터 분산의 크기를 나타낸다.

2. 전체 에너지 보존

• $V^T V = I$는 PCA 변환이 직교 변환(orthogonal transformation)임을 의미한다.

• 직교 변환에서는 데이터의 길이(에너지)가 보존된다.

  \[\| \vec{x} \|^2 = \| V^T \vec{x} \|^2\]
• 따라서 원래 좌표계에서의 분산 합과 PCA 좌표계에서의 분산 합은 동일하다.

3. 직관적 해석

• 데이터의 총 에너지는 원래 공간에서 계산하든 PCA로 변환한 뒤 계산하든 변하지 않는다.
• PCA는 데이터를 각 주성분 축으로 “분해”하여 분산을 나누어 설명하는 과정이다.
• 고유값 $\lambda_i$가 클수록 해당 주성분 축이 데이터의 구조를 잘 설명하는 방향임을 의미한다.

---

p33. 주성분 분석 (Principal Component Analysis, PCA)

• Gram 행렬 (Gram Matrix)

• $X^T X$는 보통 합제곱행렬(sum-of-squares matrix)이라고 불린다.

• $\tfrac{1}{M-1} X^T X$는 표본 공분산(sample covariance)이다.

• $G = X X^T$는 Gram 행렬이라고 불린다.
• Gram 행렬의 $(i,j)$번째 원소는 $i$번째 데이터 샘플과 $j$번째 데이터 샘플의 내적(dot product)이다:

\[g_{ij} = (\vec{x}_i - \vec{\mu})^T (\vec{x}_j - \vec{\mu})\]

---

1. Gram 행렬의 의미

• Gram 행렬은 모든 샘플 벡터 쌍 사이의 내적을 모아 놓은 행렬이다.

• $G = X X^T$이며, 원소 $g_{ij}$는 $i$번째 샘플과 $j$번째 샘플 벡터의 내적이다:

  \[g_{ij} = (\vec{x}_i - \vec{\mu})^T (\vec{x}_j - \vec{\mu})\]
• Gram 행렬은 데이터 간의 유사성을 측정하는 핵심 도구이며, 특히 커널 방법(kernel methods)에서 중심적으로 사용된다.

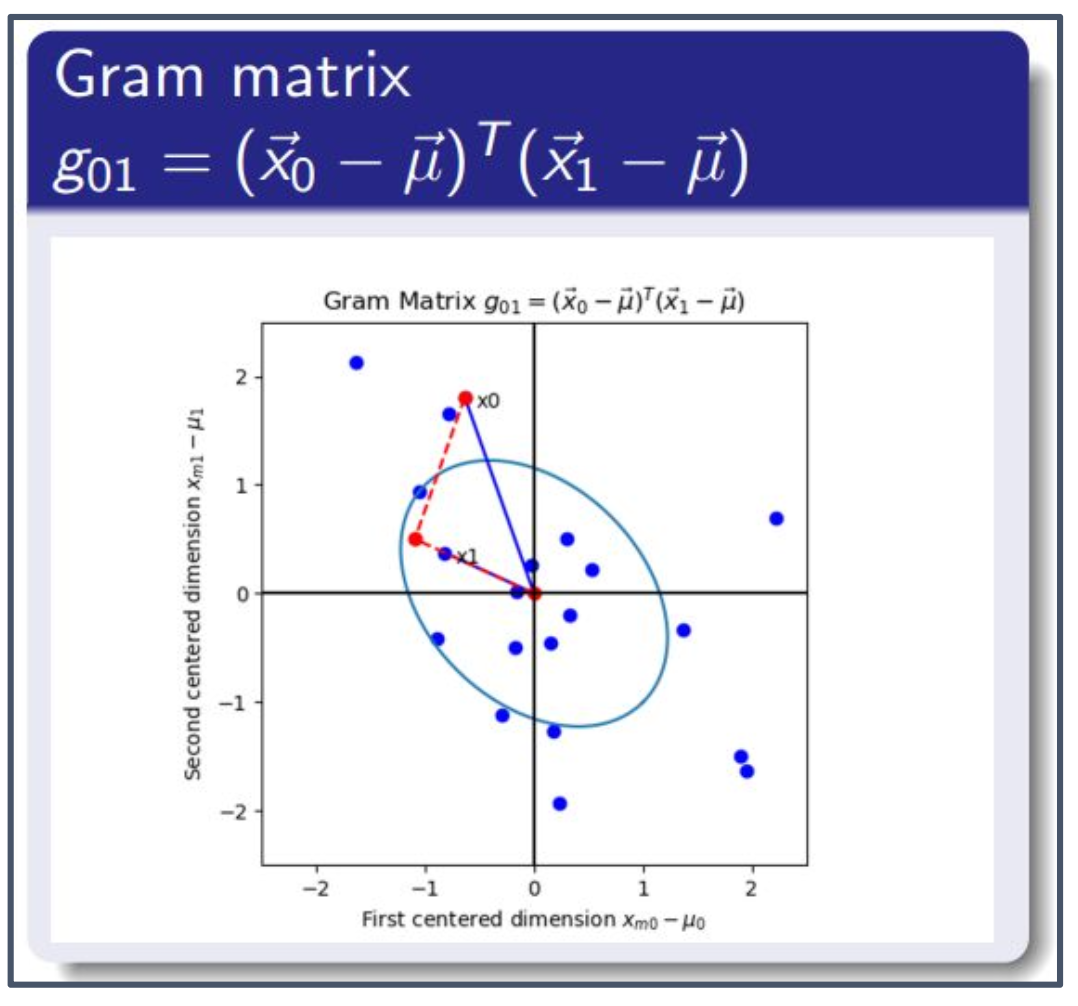
2. 그림의 의미 (구성 요소별 설명)

• 빨간색 화살표: $\vec{x}_0 - \vec{\mu}$와 $\vec{x}_1 - \vec{\mu}$를 나타내는 벡터
• 파란 점들: 모든 데이터 샘플을 2차원으로 투영한 점들
• 내적 $g_{01}$: 두 빨간 벡터의 내적
  • 방향이 유사할수록 값이 크다.
  • 직교하면 $0$
  • 반대 방향이면 음수
• 타원(파란색 타원): 데이터의 공분산 구조를 나타내며, PCA의 주성분 축과 관련된다.
• 좌표축(검은색 십자선): 평균이 0인 중심화 좌표계

3. 직관적 해석

• Gram 행렬은 “샘플-샘플 유사도 행렬”이다.
• $g_{ij}$가 클수록 $i$번째와 $j$번째 샘플이 서로 유사하다.
• PCA뿐 아니라 SVM, Kernel PCA 등 여러 머신러닝 알고리즘에서 중요한 역할을 한다.

---

p34. 주성분 분석 (Principal Component Analysis, PCA)

Gram 행렬의 고유벡터 (Eigenvectors of the Gram matrix)

• $XX^T$ 또한 대칭 행렬(symmetric)이므로, 직교 정규(orthonormal) 고유벡터를 가진다:

\[XX^T = U \Lambda U^T\] \[UU^T = U^T U = I\]

• 놀라운 사실(Surprising Fact):
  $X^T X$와 $XX^T$는 동일한 고유값($\Lambda$)을 갖지만, 서로 다른 고유벡터를 가진다.
  • $X^T X$의 고유벡터는 $V$
  • $XX^T$의 고유벡터는 $U$

---

1. $X^T X$와 $X X^T$의 관계

• $X^T X$와 $X X^T$는 차원은 다르지만 동일한 고유값을 공유한다.
• PCA에서는 이 성질을 활용해, 샘플 수 $M$이 특성 차원 $D$보다 작은 경우 계산을 크게 단순화할 수 있다.
• 예: 얼굴 인식에서는 한 장의 이미지가 수천 픽셀($D$)이지만 학습 샘플 수($M$)는 수백 장 정도이므로, $M \times M$인 $X X^T$를 사용하는 것이 훨씬 효율적이다.

2. 특성 공간 vs 샘플 공간

• $X$의 크기를 $M \times D$라 하면
  • $M$: 샘플 개수
  • $D$: 특성 차원(예: 픽셀 수)
• $X^T X$
  • 크기: $D \times D$
  • 각 성분은 특성(feature) 간 공분산
  • 고유벡터 $V$는 특성 공간(feature space) 에서 정의
  • 해석: 데이터가 어떤 특성 축 방향으로 가장 많이 퍼지는지(분산이 큰 방향)
• $X X^T$
  • 크기: $M \times M$
  • 각 성분은 샘플 간 내적(유사도)
  • 고유벡터 $U$는 샘플 공간(sample space)에서 정의
  • 해석: 어떤 샘플들이 서로 유사하게 분포하는지

3. 정리

• $X^T X$는 특성 차원 $D$가 매우 클 때 직접 계산하기 어려울 수 있다.
• 하지만 $X X^T$를 사용하면 같은 고유값을 얻고, 필요하면 고유벡터 $V$로 변환해 사용할 수 있다.
• 즉, 특성 공간 고유벡터($V$)와 샘플 공간 고유벡터($U$)는 서로 다른 공간에서 정의되지만 PCA 결과(고유값)는 동일하다.

---

p35. 주성분 분석 (Principal Component Analysis, PCA)

이미지 한 장당 $D \sim 240000$ 픽셀이라고 가정하고,
서로 다른 이미지가 $M \sim 240$ 장 있다고 하자.

그렇다면 고유값 분석(eigenvalue analysis)을 수행하기 위해:

\[X^T X = V \Lambda V^T\]

을 계산하는 것은, 차수가 $240000$인 다항식
($|X^T X - \lambda I| = 0$)을 인수분해해야 하고,
각 고유벡터 $\vec{v}_d$를 구하기 위해 $240000$개의 미지수를 가진
$240000$개의 연립방정식을 풀어야 함을 의미한다:

\[X^T X \vec{v}_d = \lambda_d \vec{v}_d\]

만약 이를 np.linalg.eig 같은 함수로 풀려고 한다면,
PC가 하루 종일 계산만 하게 될 것이다.

반면에,

\[XX^T = U \Lambda U^T\]

를 사용하면, $240$개의 미지수를 가진 $240$개의 방정식만 풀면 된다.

즉,
\(240^2 \ll 240000^2\)
임은 전문가라면 모두 동의할 것이다.

---

1. 계산 복잡도의 차이

• $X^T X$는 크기가 $D \times D$ ($240000 \times 240000$)이므로 직접 고유분해를 수행하면 연산량이 매우 크다.
• 반면 $X X^T$는 $M \times M$ ($240 \times 240$) 크기이므로 연산량이 작아 실제로 계산이 가능하다.

2. 고유값의 공유

• $X^T X$와 $X X^T$는 동일한 고유값을 공유한다.
• 따라서 작은 차원의 행렬 $X X^T$에서 고유값과 고유벡터를 구한 뒤, 이를 변환하여 $X^T X$의 고유벡터로 얻을 수 있다.

3. 실제 활용

• 얼굴 인식(Eigenface)과 같은 고차원 문제에서는 항상 $X X^T$ 방식(샘플 공간 고유분해)을 사용한다.
• 이를 통해 수십만 차원의 벡터를 직접 다루지 않고도 PCA를 효율적으로 계산할 수 있다.

---

p36. 특이값 (Singular Values)

• $X^T X$와 $X X^T$는 모두 양의 준정부호(positive semi-definite) 행렬이므로,
  그 고유값들은 음이 아닌 값을 가진다. 즉, $\lambda_d \geq 0$.

• $X$의 특이값(singular values) 은 $X^T X$ 또는 $X X^T$의 고유값의 제곱근으로 정의된다:

\[S = \begin{bmatrix} s_0 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & s_{D-1} \end{bmatrix}, \quad \Lambda = S^2 = \begin{bmatrix} s_0^2 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & s_{D-1}^2 \end{bmatrix}\]

---

1. 양의 준정부호(PSD)의 정의

• 어떤 대칭행렬 $A$가 양의 준정부호(PSD)라면, 모든 벡터 $\vec{z}$에 대해

  \[\vec{z}^T A \vec{z} \ge 0\]

  가 성립해야 한다.

• 이러한 표현을 이차형식(quadratic form) 이라고 부른다.

2. 예시: 이차형식

• 예를 들어

  \[A= \begin{bmatrix} 2 & 0\\ 0 & 3 \end{bmatrix}, \qquad \vec{z}= \begin{bmatrix} z_1\\ z_2 \end{bmatrix}\]

  라면

  \[\vec{z}^T A \vec{z} = 2 z_1^2 + 3 z_2^2 \ge 0\]

  가 항상 성립하므로 $A$는 PSD 행렬이다.

3. $X^T X$가 PSD임을 보이는 방법

• \[\vec{z}^T (X^T X)\vec{z} = (X\vec{z})^T (X\vec{z}) = \|X\vec{z}\|^2 \ge 0\]

  이므로 $X^T X$는 PSD이다.

• 동일한 방식으로 $X X^T$도 PSD임을 보일 수 있다.

4. PSD와 고유값의 관계

• 고유벡터 $\vec{v}$에 대해

  \[(X^T X)\vec{v} = \lambda \vec{v}\]

  의 양변에 $\vec{v}^T$를 곱하면

  \[\vec{v}^T (X^T X)\vec{v} = \lambda \|\vec{v}\|^2\]

  이 된다.

• 왼쪽은 $|X\vec{v}|^2 \ge 0$이므로

  \[\lambda \ge 0\]

  이 반드시 성립한다.

• 즉, PSD 행렬의 고유값은 항상 0 이상이다.

5. 특이값과 고유값의 관계

• $X$의 특이값 $s_d$는 고유값 $\lambda_d$의 제곱근이다:

  \[s_d = \sqrt{\lambda_d}\]

• 따라서 특이값은 항상 실수이며 0 이상이다.

6. 직관적 해석

• 선형변환 $X$는 벡터를 특정 방향으로 늘리거나 줄인다.
• 고유값 $\lambda$는 “변환된 길이의 제곱”을 의미하고,
  특이값 $s=\sqrt{\lambda}$는 실제 “길이의 비율”을 나타낸다.
• PSD 성질 덕분에 길이(에너지)는 음수가 될 수 없으며, 이는 PCA 결과가 안정적인 이유가 된다.

---

p37. 특이값 분해 (Singular Value Decomposition)

PCA 분해 공식에서 $\Lambda = SS$라는 식을 사용해 보자:

\[X^T X = V \Lambda V^T = V S S V^T = V S I S V^T\]

… 여기서 마지막 식은 단순히 항등행렬(identity matrix) $I$를 삽입한 것이다.
하지만 $U$가 직교정규(orthonormal)하다는 점을 기억하면, $I = U^T U$로 쓸 수 있고, 따라서

\[X^T X = V S U^T U S V^T = (U S V^T)^T (U S V^T)\]

---

1. 식의 의미

• $X^T X = V \Lambda V^T$는 PCA에서의 고유값 분해(eigendecomposition)이다.
• $\Lambda = S^2$이므로 $\Lambda$를 $S S$로 치환해 표현할 수 있다.
• 항등행렬 $I$를 삽입한 이유는 곱셈 구조를 재배열하여 SVD 형태를 드러내기 위함이다.

2. $U$의 역할

• $U$는 $X X^T$의 고유벡터 행렬이며 직교정규 행렬이다.
• 따라서 $I = U^T U$가 성립하고, 이를 $\Lambda = S I S$에 대입하면 SVD 형태로 변환된다.

3. 최종 SVD 형태

• 위 전개로부터

  \[X^T X = (U S V^T)^T (U S V^T)\]

  가 성립한다.

• 이는 결국 $X = U S V^T$라는 특이값 분해(SVD) 공식을 자연스럽게 도출하는 과정이다.

4. 직관적 해석

• PCA가 고유값 분해를 통해 데이터의 분산이 큰 방향(주성분)을 찾는 과정이라면,
  SVD는 이를 더 일반화한 분해 방식으로 $X$를 직교행렬 $U, V$와 대각행렬 $S$의 곱으로 분해한다.
• 즉, PCA와 SVD는 본질적으로 밀접하게 연결되어 있으며, PCA는 SVD의 특수한 경우로 이해할 수 있다.

---

p38. 특이값 분해 (Singular Value Decomposition)

이번에는 동일한 과정을 Gram 행렬에서 시작해 보자: 공식은 다음과 같다.

\[XX^T = U \Lambda U^T = U S S U^T = U S I S U^T = U S V^T V S U^T = (USV^T)(USV^T)^T\]

---

1. 식의 전개 과정

• $X X^T$를 고유값 분해하면 $X X^T = U \Lambda U^T$로 표현된다.
• $\Lambda = S^2$이므로 이를 $S S$로 치환해 전개할 수 있다.
• 항등행렬 $I$를 삽입하면 $U S I S U^T$가 되며,
  $I = V^T V$를 대입하면 $U S V^T V S U^T$로 쓸 수 있다.
• 최종적으로 이는 $(U S V^T)(U S V^T)^T$ 형태가 된다.

2. PCA와의 연결

• 이전에는 $X^T X$에서 출발하여 $(U S V^T)^T (U S V^T)$ 형태를 얻었다.
• 이번에는 $X X^T$에서 출발하여 $(U S V^T)(U S V^T)^T$ 형태를 얻는다.
• 두 전개 모두 결국 $X = U S V^T$라는 특이값 분해(SVD) 구조를 자연스럽게 드러낸다.

3. 직관적 의미

• $X^T X$는 특성 공간(feature space)의 분산 구조를 반영한다.
• $X X^T$는 샘플 공간(sample space)의 유사도 구조를 반영한다.
• 두 행렬은 동일한 특이값 $S$를 공유하므로,
  SVD는 데이터의 두 공간을 동시에 연결해 주는 분해 방식이다.

---

p39. 특이값 분해 (Singular Value Decomposition)

임의의 $M \times D$ 행렬 $X$는 다음과 같이 쓸 수 있다:

\[X = U S V^T\]

• \(U = [\vec{u}_0, \dots, \vec{u}_{M-1}]\) 는 $XX^T$의 고유벡터들이다.
• \(V = [\vec{v}_0, \dots, \vec{v}_{D-1}]\) 는 $X^T X$의 고유벡터들이다.
• $S$는 특이값(singular values)을 대각 성분으로 가지는 행렬이다:

\[S = \begin{bmatrix} s_0 & 0 & 0 & 0 & 0 \\ 0 & \ddots & 0 & 0 & 0 \\ 0 & 0 & s_{\min(D, M)-1} & 0 & 0 \\ \end{bmatrix}\]

$M > D$이면 $S$는 모두 0인 열(all-zero columns)을 일부 가지고,
$M < D$이면 모두 0인 행(all-zero rows)을 일부 가진다.

---

1. $U$, $V$, $S$의 의미

• $U$: 데이터 샘플 공간(sample space)의 직교 기저를 형성한다.
• $V$: 데이터 특성 공간(feature space)의 직교 기저를 형성한다.
• $S$: 각 축 방향으로의 스케일(크기)을 나타내며, 데이터의 분산 크기와 직접 연결된다.

2. SVD의 일반성

• SVD는 임의의 행렬에 대해 항상 존재하는 분해 방식이다.
• PCA가 공분산 행렬의 고유분해(eigendecomposition)에 기반한다면,
  SVD는 이를 더 일반화하여 어떤 직사각형 행렬에도 적용 가능하다.

3. 행/열 크기 조건의 해석

• $M > D$: 샘플 수가 특성 차원보다 많을 때, 필요 이상의 축이 존재하여 $S$에 0인 열이 생긴다.
• $M < D$: 특성 차원이 샘플 수보다 많을 때, $S$에 0인 행이 생긴다.
• 이러한 현상은 데이터의 랭크(rank)와 직접적인 관련이 있으며,
  SVD에서 0인 특이값의 개수는 랭크 부족(rank deficiency)을 의미한다.

---

p40. 특이값 분해 (Singular Value Decomposition)

먼저, np.linalg.svd는 $X^T X$의 고유벡터를 찾을지 $X X^T$의 고유벡터를 찾을지 결정한다.
이는 단순히 $M > D$ 인지 $M < D$ 인지를 확인하는 것이다.

만약 $M < D$ 라고 판정되면:

1. $X X^T = U \Lambda U^T$ 를 계산하고, $S = \sqrt{\Lambda}$ 로 둔다.
   이제 우리는 $U$와 $S$를 얻었으므로, $V$만 찾으면 된다.

2. $X^T = V S U^T$ 이므로, 단순히 곱셈을 통해 $V$를 얻을 수 있다:

\[\tilde{V} = X^T U\]

여기서 $\tilde{V} = V S$ 는 정확히 $V$와 동일하지만, 각 열이 서로 다른 특이값(singular value)로 스케일된 형태이다.
따라서 우리는 단순히 정규화(normalization)만 해주면 된다:

\[\|\vec{v}_i\| = 1, \quad v_{i0} > 0\]

---

1. $M < D$일 때의 의미

• 샘플 수 $M$보다 특성 차원 $D$가 더 큰 경우, $X^T X$의 크기는 $D \times D$가 되어 계산이 매우 비효율적이다.
• 이때는 $M \times M$ 크기의 $X X^T$를 사용해 먼저 $U$와 $S$를 구한 뒤, 이를 이용해 $V$를 유도하는 방식이 훨씬 효율적이다.

2. $V$의 유도 과정

• $X^T U$를 계산하면 $V$의 각 열이 특이값 $S$로 스케일된 형태로 얻어진다.
• 따라서 각 열을 정규화(normalization)하여 단위 길이가 되도록 만들면 $V$를 얻을 수 있다.

3. 정규화 조건

• $|\vec{v}_i| = 1$: 모든 고유벡터는 단위 벡터(norm 1)이어야 한다.
• $v_{i0} > 0$: 부호(orientation)를 일관되게 하기 위해 첫 번째 원소가 양수가 되도록 방향을 정한다.

---

p41. 특이값 분해 (Singular Value Decomposition)

• 공분산 행렬 방법 (covariance matrix method):
  $X^T X$의 고유벡터 분석은 올바른 결과를 주지만, 매우 오랜 시간이 걸린다.

• Gram 행렬 방법 (gram matrix method):
  훨씬 빠르다. $X X^T$로부터 $U$를 얻기 위해 np.linalg.eig를 적용하고,
  $\tilde{V} = X^T U$ 를 계산한다.
  주의할 점: 정규화하여 \(\|\vec{v}_k\| = 1, \; v_{k,1} \geq 0\) 이 되도록 한다.

• SVD 방법:
  np.linalg.svd(X)를 직접 적용한다.
  속도는 $\min(\text{covariance 방법의 속도}, \; \text{gram 방법의 속도})$ 로 주어진다.
  주의할 점: $\lambda_m = s_m^2$ 이다.

무엇을 하든, 고유값들은 반드시 크기 순으로 정렬해야 한다:

\[|\lambda_k| \geq |\lambda_{k+1}|\]

---

1. 세 가지 방법 비교

• 공분산 행렬 기반 접근: 이론적으로 단순하지만, $D$가 매우 클 경우 계산량이 급격히 증가한다.
• Gram 행렬 기반 접근: $M \ll D$일 때 특히 유리하며, SVD로 자연스럽게 연결된다.
• 직접 SVD 접근: np.linalg.svd와 같은 라이브러리 함수로 가장 안정적이고 효율적이다.

2. 정규화의 필요성

• Gram 행렬을 사용할 경우 $\tilde{V} = V S$ 형태로 얻기 때문에 $V$ 자체를 바로 얻지 못한다.
• 따라서 각 열 벡터를 정규화(normalization)하여 진짜 직교 기저 $V$를 복원해야 한다.

3. 고유값 정렬의 의미

• 고유값은 데이터가 각 주성분 방향으로 얼마나 퍼져 있는지를 나타낸다(분산 크기).
• 고유값을 내림차순으로 정렬하면, 가장 많은 분산을 설명하는 주성분부터 순서대로 사용할 수 있다.