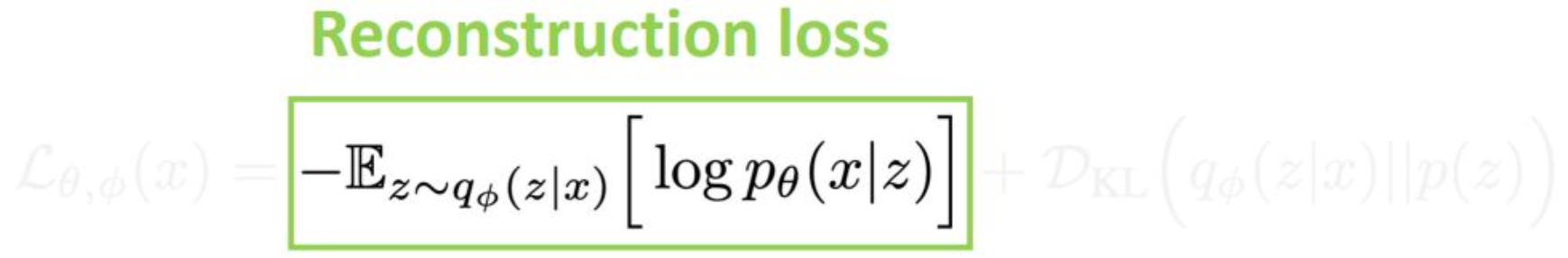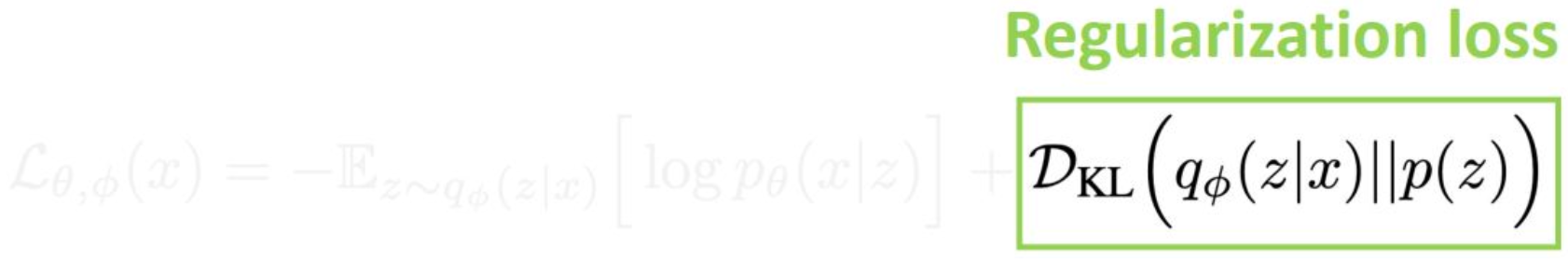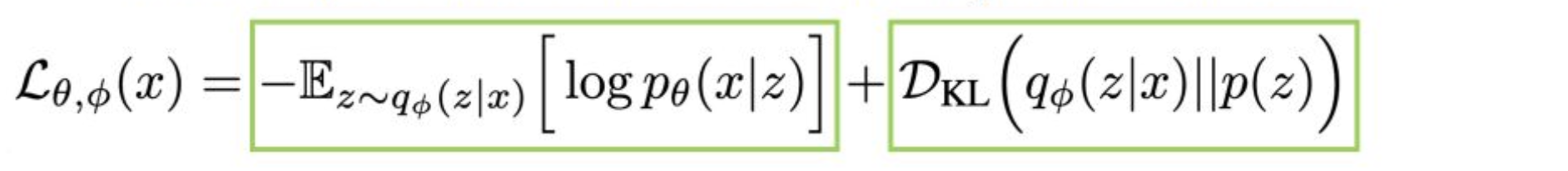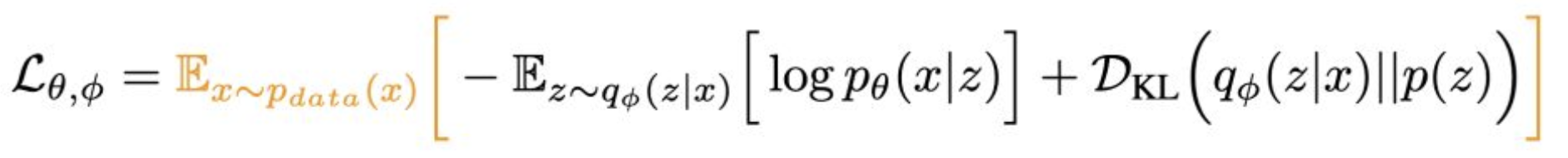[확률과 통계] 9주차

게시 2025/10/28 업데이트 2025/12/12

By 김성진

125 분읽는 시간

[확률과 통계] 9주차

p2. 생성 모델의 일반 개념 (General Concept of Generative Models)

강의 내용
생성 모델이 무엇인지 먼저 생각해보는 것이 좋을 것 같습니다.
예를 들어
텍스트가 주어지고 해당 텍스트에 대응하는
어떤 형태(shape)나 이미지를 생성하는
AI 모델을 떠올려보면,
이는 제너레이티브 모델, 즉 생성 모델입니다.
따라서 생성하는 역할을 담당하는 생성자(generator)가 필요합니다.
그래서 이러한 생성자를 제너레이터라고 부릅니다.
제너레이티브 모델이기 때문입니다.
제너레이터에는 크게 두 가지 입력이 존재합니다.
첫 번째 입력은 condition input입니다.
텍스트 기반 이미지 생성이라고 한다면
텍스트 청크들, 토큰 시퀀스,
혹은 원-핫 벡터 등으로 표현된
어떤 개념적(condition) 정보가
첫 번째 입력으로 들어갑니다.
두 번째 입력은 랜덤성입니다.
제너레이티브 모델은 확률론과 통계학적으로
매우 잘 정의된 학문적 기반을 갖고 있는데
가장 중요한 점은
입력으로 random variable이 반드시 포함되어야 한다는 것입니다.
이 랜덤성이 무엇을 표현하느냐 하면
random variable(예: 주사위처럼 표현되는 랜덤성)이 입력되었을 때
출력 분포, 즉 이미지 분포의 다양한 surface를
표현할 수 있도록 해준다는 것입니다.
예를 들어
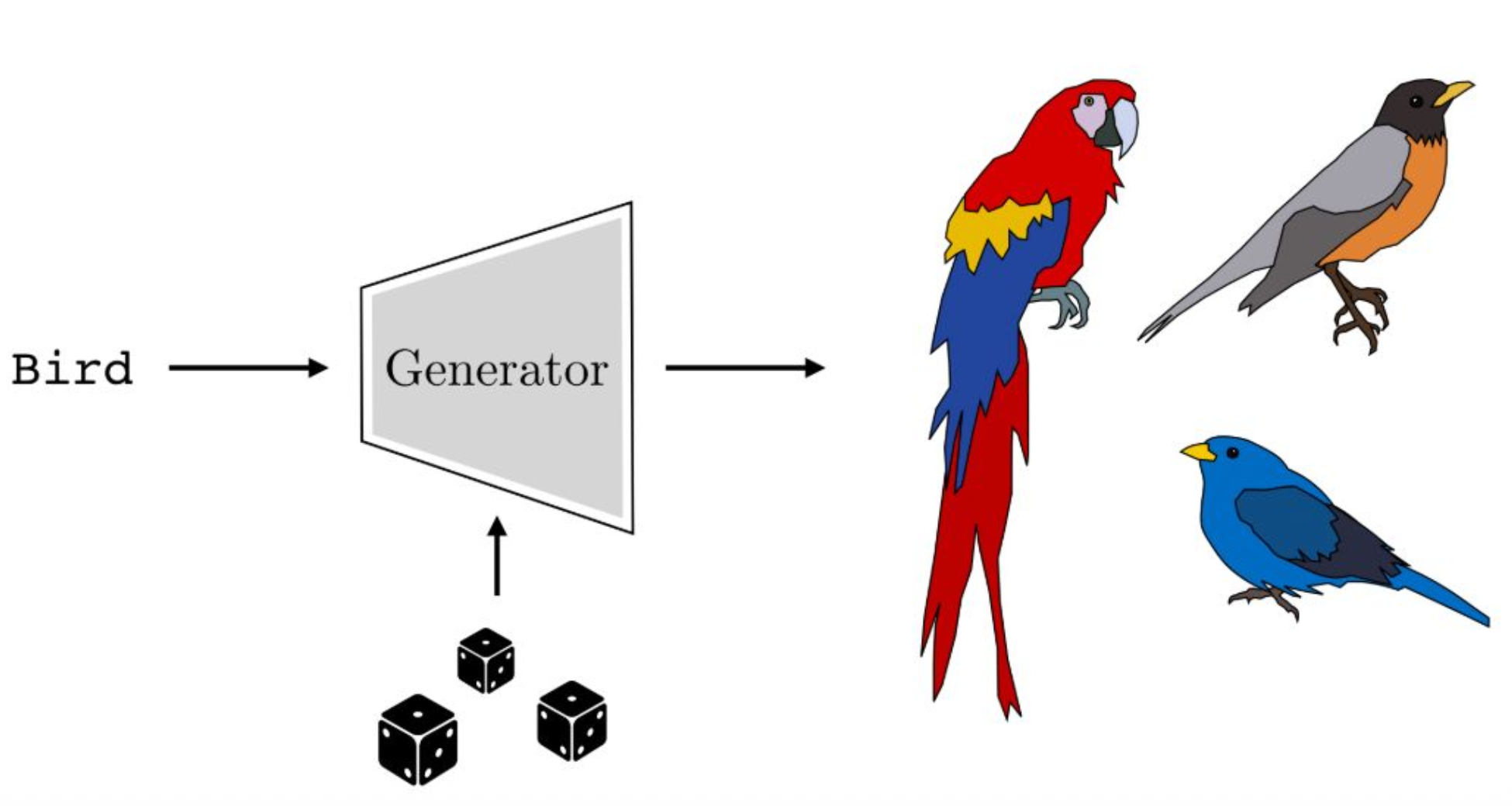
입력 텍스트가 Bird라고 했을 때
항상 동일한 이미지만 생성되면 안 됩니다.
Bird에 대한 다양한 variation이 생성되어야 하고
이러한 다양성을 표현해주는 요소가
바로 random variable입니다.
현대의 생성 모델들은
대부분 이러한 구조적 파이프라인을 따릅니다.
매우 개념적이고 단순화된 형태로 설명했지만
큰 틀에서 보면 생성 모델은 이러한 방식으로 작동합니다.

p3. 생성 모델의 확률적 표현 (Probabilistic Representation of Generative Models)

강의 내용
그러면 이런 것을 한번 생각해보겠습니다.
Bird라는 텍스트가 주어졌을 때
Bird의 어떤 latent information을 통해
새의 다양한 모양들을 표현할 수 있을까?
이런 부분이 핵심적인 질문입니다.
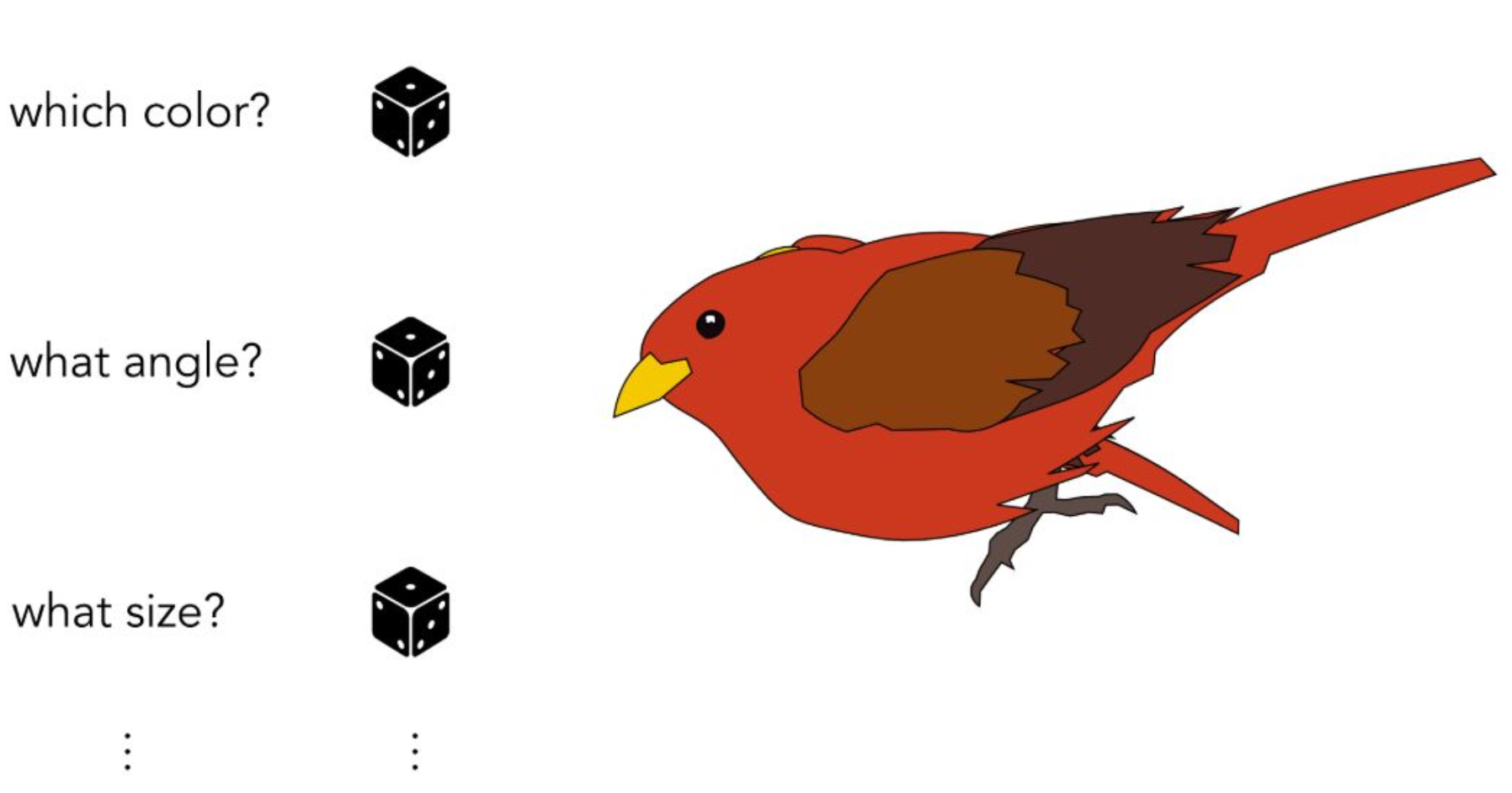
여러 개의 주사위가 그려져 있는 것은
각각의 랜덤성이 어떤 역할을 하는지 설명하기 위한 예시입니다.
즉, 랜덤성의 각 feature가
생성되는 이미지의 어떤 요소를 결정하는가를
생각해볼 수 있습니다.
예를 들어
첫 번째 주사위는 색(color),
두 번째 주사위는 구성 요소의 결합 방식이나 각도(angle),
또 다른 주사위는 새의 크기(size) 등을 결정한다고 할 수 있습니다.
이렇게 랜덤 변수들이
생성될 이미지의 다양한 속성을
통계적으로 결정하게 됩니다.
여기서 표현하려는 핵심은
high-dimensional한 랜덤 변수가 입력된다는 점입니다.
앞에서 배웠듯이
보통 multivariate Gaussian 랜덤 변수가
이러한 랜덤성의 근원이 됩니다.
흥미로운 점은
multivariate Gaussian distribution 자체에는
아무런 semantic이 없다는 것입니다.
즉, 각 축이
색이나 각도를 표현하라고 지정되어 있지 않습니다.
그런데 생성 모델을 학습시키면
명확하게 첫 번째 축은 색, 두 번째 축은 각도처럼
고정적으로 매핑되는 것은 아니지만
학습 과정에서 자연스럽게 semantic한 구조가 형성되기 시작합니다.
실습을 통해 보시겠지만
latent space의 특정 방향이
semantic feature와 연관되는 현상이 나타납니다.
그래서 이러한 특징은
generative 모델의 매우 중요한 특성 중 하나입니다.
우리가 feature를 직접 설계하지 않아도
학습 이후에는 high-dimensional한 random variable의
특정 방향(차원)이
semantic한 feature와 association을 형성하게 된다는 점입니다.
이런 부분은 매우 흥미롭고
실습을 통해 더 자세히 살펴보도록 하겠습니다.

p4. 데이터 생성기의 분류 (Categorization of Data Generators)

두 가지 접근 방식이 있다.

직접 접근(Direct approach): 데이터를 직접 생성하는 함수를 학습한다.
(혼동스럽게도, 때때로 “암묵적 생성 모델(implicit generative model)”이라고도 불린다.)
\[G : \mathcal{Z} \rightarrow \mathcal{X}\]
간접 접근(Indirect approach): 데이터를 평가(score)하는 함수를 학습하고,
이 함수 아래에서 점수가 높은 지점을 찾아 데이터를 생성한다.
\[E : \mathcal{X} \rightarrow \mathbb{R}\]

강의 내용
Data Generator에는 크게 두 가지 접근 방식이 있습니다.
먼저 Direct Approach가 있습니다.
앞에서 설명했던 GAN이
Direct Approach를 사용하는 대표적인 모델 중 하나입니다.
Direct Approach란
random variable을 입력으로 받아
출력 데이터를 직접적으로 생성하는 모델들을 의미합니다.
반면 Indirect Approach가 있습니다.
대표적인 예로 Diffusion 모델이
Indirect Approach에 속합니다.
이러한 경우에는
Neural Network input에 random variable을 넣고
바로 output 데이터를 생성하는 방식이 아니라
추가적인 파이프라인이 하나 더 존재합니다.
그 파이프라인의 한 구성 요소로
Neural Network가 동작하며
보통 energy function이나 score function으로 표현되는
함수를 학습하여
데이터가 얼마나 잘 생성되었는지를 판단합니다.
이 score 또는 energy를
Neural Network로 모델링하여
생성 과정을 진행하는 방식입니다.
앞서 언급했던 Diffusion 모델과
Normalizing Flow 모델들이
이러한 Indirect Approach에 포함됩니다.
오늘 다룰 VAE는
Direct Approach와 Indirect Approach의
중간 정도에 위치한 모델이라고 볼 수 있습니다.
다만 전체적으로는
Direct Approach에 더 가깝다고 이해하는 것이 좋습니다.

p5. 직접 접근(Direct Approach)의 학습과 샘플링 과정

강의 내용
이제 데이터 생성 파이프라인을
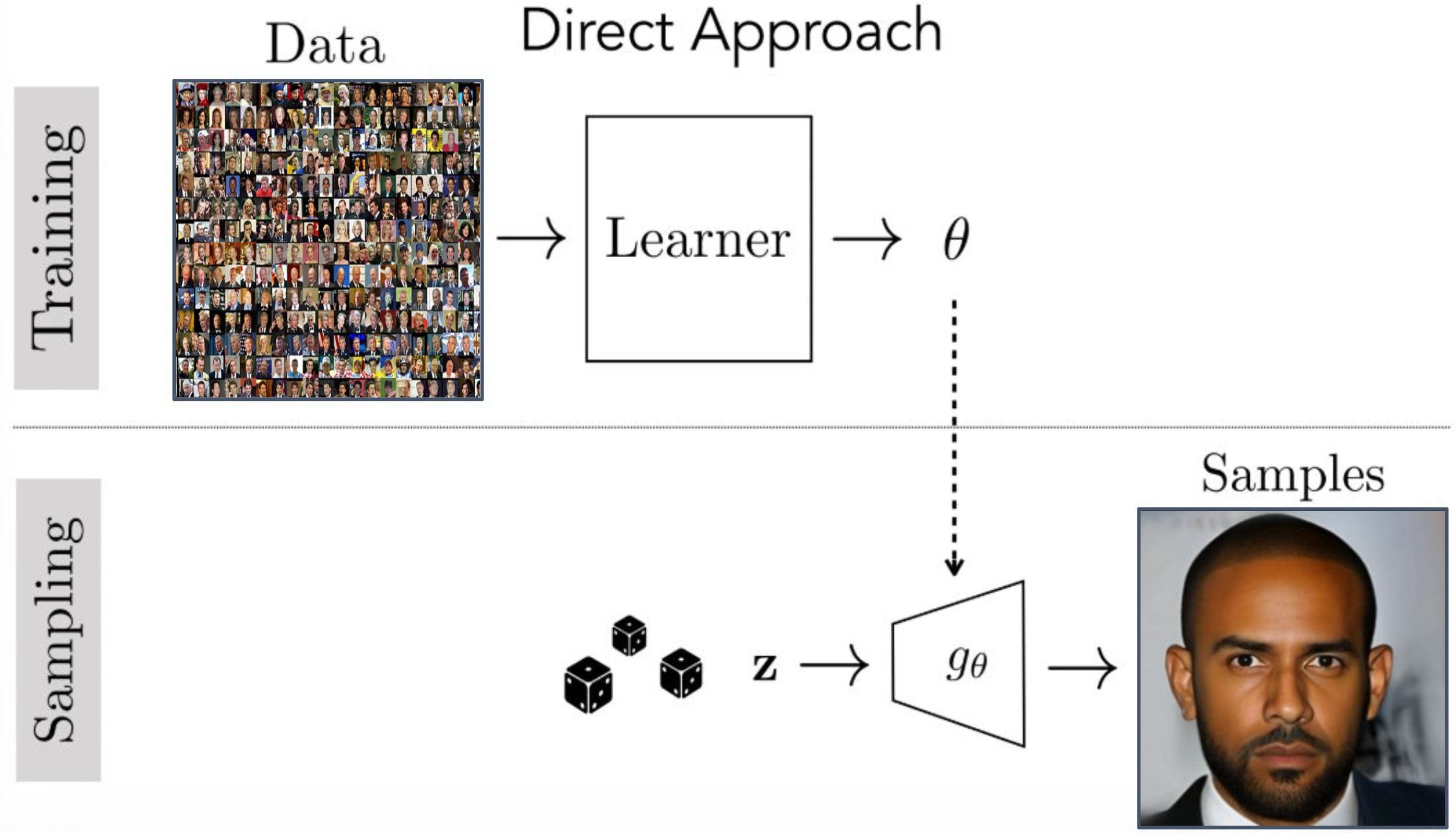
이렇게 생각해볼 수 있습니다.
예를 들어 사람 얼굴을 생성한다고 해봅시다.
왼쪽과 같은 사람 얼굴 이미지들을 많이 모아 둔 데이터셋이 있고
learner가 그 데이터셋을 기반으로
optimal한 파라미터를 찾습니다.
그렇게 학습된 파라미터는
Neural Network, 즉 generator의 파라미터로 사용됩니다.
이것이 트레이닝 과정입니다.
반면 샘플링할 때,
test time 또는 inference time이라고도 부르는 단계에서는
Gaussian random variable을 generator에 입력하면
우리가 원하는 이미지가 출력되기를 기대합니다.
대부분의 생성 모델들은
이렇게 training time과 test time이 명확히 구분된 구조를 갖습니다.
하지만 앞에서 잠깐 살펴본
classification 모델은 이러한 scheme을 따르지 않습니다.
classification 모델은
input과 output의 형태가 동일하고
데이터 모양만 다를 뿐
트레이닝 단계와 샘플링 단계가 같은 파이프라인을 사용합니다.
반면 생성 모델은
트레이닝 과정과 샘플링 과정의 파이프라인이
이처럼 분리되어 있다는 특징이 있습니다.
따라서 생성 모델은
기존의 잘 알려진 딥러닝 Neural Network 기반 문제들과
파이프라인 구조가 다르다는 점을
이해하고 있어야 합니다.

p6. 간접 접근 (Indirect Approach)

강의 내용
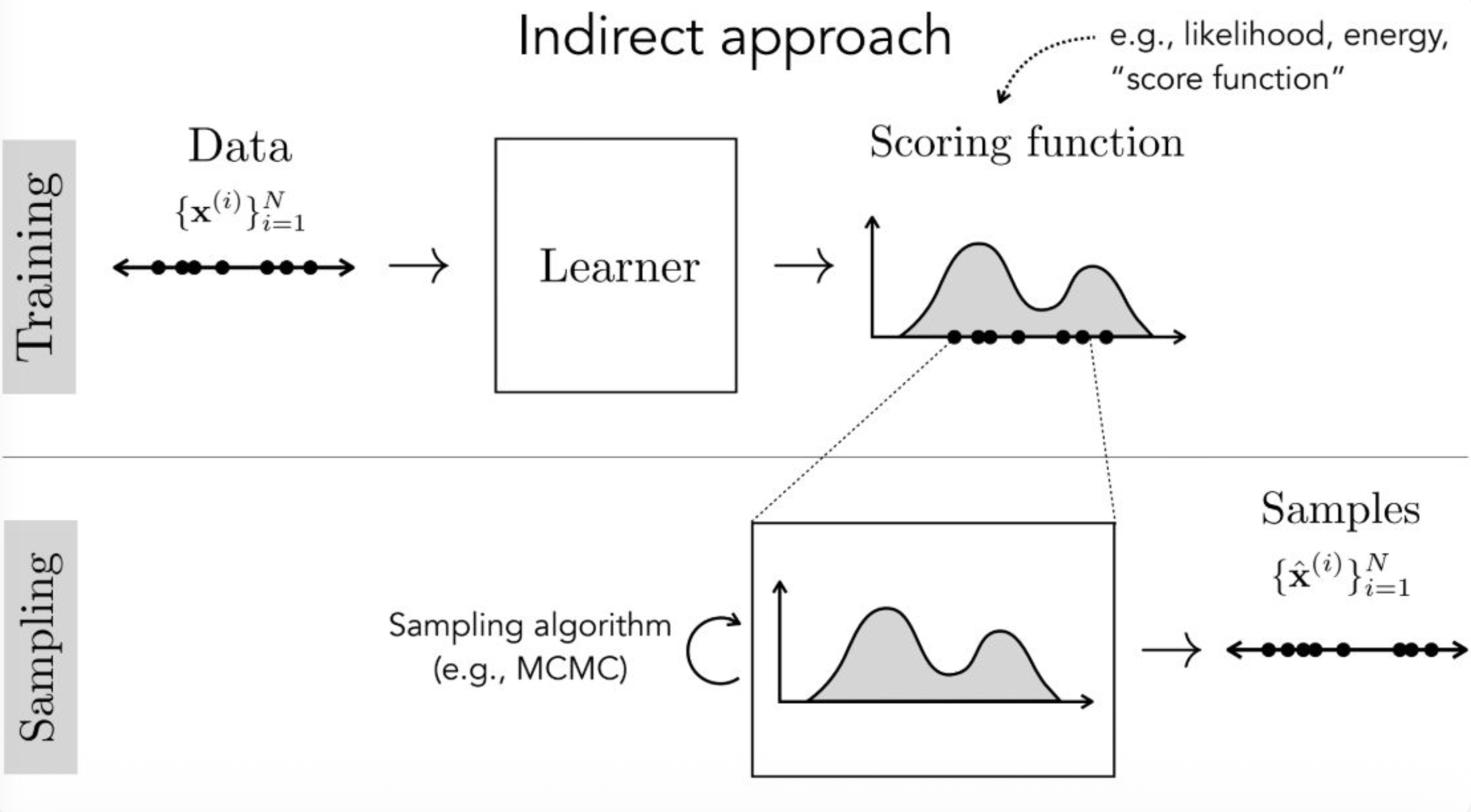
이제 Indirect Approach를 잠깐 살펴보겠습니다.
데이터가 존재하고 그 데이터를 학습하는 러너(learner)가 존재합니다.
앞에서 언급했듯이
score function이라는 것이 등장하는데
이는 energy, likelihood와 같은 개념을
점수(score)로 표현하는 함수입니다.
트레이닝 methodology가 존재하여
score function의 값을 높이거나 낮추는 방식으로
간접적으로 스코어링을 수행하게 됩니다.
이렇게 스코어링된,
즉 score가 최적으로 된 위치들이
샘플링 시 생성되는 데이터의 위치라고 볼 수 있습니다.
여기에서도 트레이닝과 샘플링은 분리되어 있습니다.
트레이닝 단계에서는
score function의 값을 조정하는 과정이 이루어지고
샘플링 단계에서는
그렇게 학습된 러너의 파라미터를 이용하여
MCMC 등의 알고리즘을 통해
실제 샘플을 생성합니다.
현재 이 파이프라인만 보면
이해하기 어려울 수 있습니다.
하지만 뒤에서 배우게 될
normalizing flow와 diffusion model을 이해하게 되면
이 구조가 무엇을 의미하는지
명확하게 이해할 수 있을 것입니다.
다만 오늘 강의는
이 부분에 초점을 맞춘 것은 아니며
강의를 계속 진행하다 보면
자연스럽게 다시 등장하게 될 것입니다.

p7. 생성 모델 (Generative Models)

목표는 학습 데이터를 그대로 복제하는 것이 아니라,
새로운(new) 데이터를 만드는 것이다.
그 데이터는 현실적인(realistic) 데이터여야 하며,
실제 데이터의 본질적인 속성(essential properties)을 포착해야 한다.

이것을 정량화하는 한 가지 방법은
모델 하에서의 테스트 데이터의 가능도(likelihood)를 이용하는 것이다.
(학습 데이터를 기억하는 모델은,
분류기(classifier)가 과적합(overfit)되는 것과
정확히 같은 의미에서 과적합된 것이다.)

\[\{x_{\text{test}}^{(i)}\}_{i=1}^{N}, \quad x_{\text{test}}^{(i)} \sim p_{\text{data}}\] \[\text{generalization error} = \sum_i \log p_\theta (x_{\text{test}}^{(i)})\]

강의 내용
생성 모델의 목표가 무엇인지에 대해
여러분들이 헷갈릴 수 있을 것 같아
이 부분을 명확하게 짚고 넘어가야 할 것 같습니다.
우리는 트레이닝 데이터를 가지고
그 데이터를 완벽하게 그대로 재현하는 것을 목표로 하지 않습니다.
특정 트레이닝 데이터가 만들어내는 distribution이 있다고 할 때
그 distribution과 유사한 데이터를 생성하는 것이 목표입니다.
만약 트레이닝 데이터를 완벽하게 복제하는 것이 목표라면
GPT 같은 생성 모델도
생성할 때마다 데이터셋과 완전히 동일한 문장을
그대로 재현하게 될 것입니다.
하지만 새로운 가치를 만들어내는 능력, 즉 extrapolation은
현대 generative AI 모델의 핵심 특징 중 하나입니다.
생성 모델은 새로운 정보를 창출합니다.
물론 그 창출된 정보가
현실의 physical knowledge를 위반할 경우
이를 hallucination이라고 부릅니다.
이처럼 extrapolation과 hallucination 사이의 균형이 존재합니다.
결국 생성 모델의 목표는
트레이닝 데이터를 완벽하게 복사하는 것이 아니라
현실적이고
world knowledge를 잘 반영하는
새로운 데이터를 만들어내는 것입니다.
그렇다면 이를 어떻게 정량화할까요?
language 모델의 evaluation 개념과도
철학적으로 연결되는 부분입니다.
이제 test data를 고려해봅시다.
여기에서 등장하는 $\log p_\theta$는
앞에서 다뤘던 log-likelihood 개념에서 나온 notation입니다.
$p_\theta$는 statistical model을 의미합니다.
트레이닝이 끝난 후 test data에 대해
우리가 학습한 statistical model의
likelihood estimation을 수행했을 때
얼마나 많은 에러가 발생하는가를 측정합니다.
이것이 바로 generalization error입니다.
generalization error가 크면 클수록
앞에서 말한 extrapolation과 hallucination 사이에서
어떤 현상이 벌어지고 있는지를 나타낸다고 볼 수 있습니다.
generalization error가 크다고 해서
무조건 나쁜 것은 아니며
generalization error가 0이라는 것은
test data가 트레이닝 데이터와 완전히 동일하다는 의미인데
이것 또한 좋은 경우만은 아닙니다.
요즘에는 extrapolation의 철학적 정의,
새로운 정보 생성의 정의를 두고
활발한 논의가 이어지고 있습니다.
language model을 평가하기 위한
최적의 metric이 무엇인가에 대한 논의도
이러한 철학적 배경에서 비롯된 것입니다.

p8. 밀도 기반 모델 (Density-based Models)

강의 내용
이제 density based model에 대해 생각해보겠습니다.
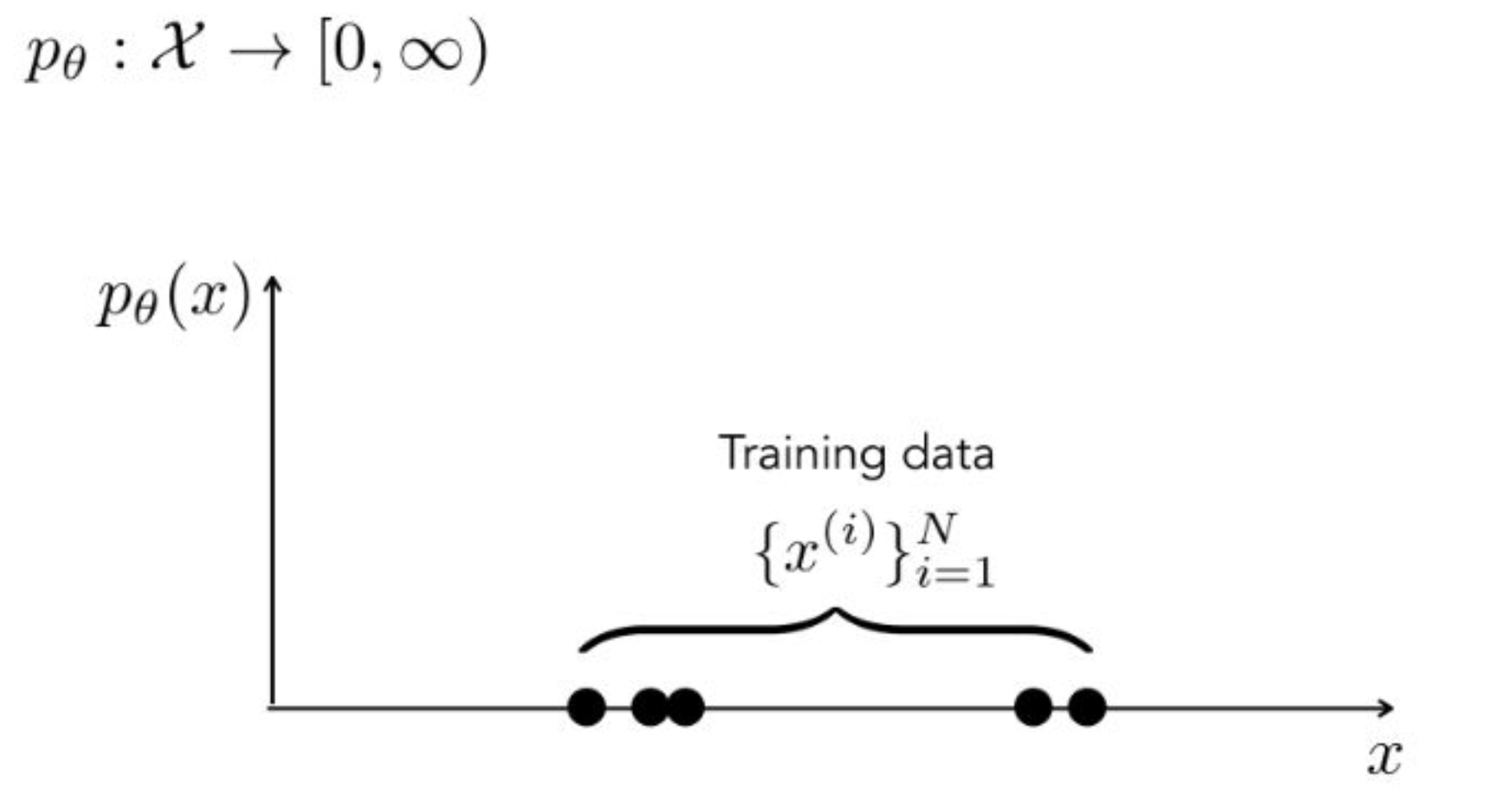
트레이닝 데이터가 $N$개 주어졌다고 할 때
probability density의 중요한 특징은
전체를 적분(또는 합)했을 때 값이 $1$이 된다는 점입니다.
이는 normalization equation에 의해 보장됩니다.

p9. 밀도 기반 모델 (Density-based Models)

강의 내용
트레이닝 데이터가 존재한다고 할 때
discrete한 경우에는 봉 형태의 분포가 나타날 것입니다.
이때 트레이닝 데이터 각각에 대응하는
$y$축 값들을 모두 summation 했을 때
그 합이 $1$이 되어야 한다는 조건을
떠올릴 수 있습니다.

p10. 밀도 기반 모델 (Density-based Models)

강의 내용
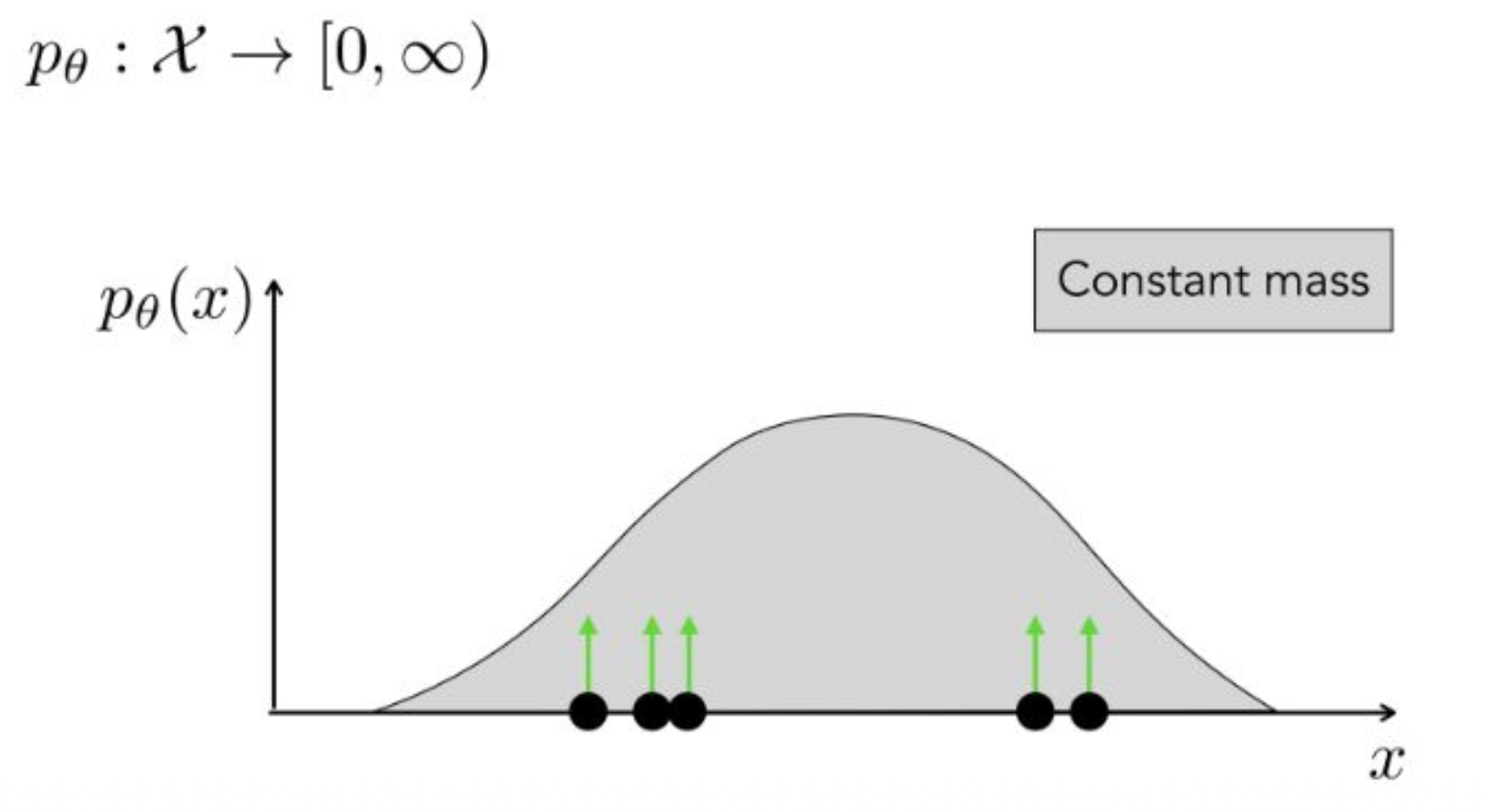
그래서 데이터가 존재하는 위치에서는
mass가 충분히 표현되어야 합니다.
즉, 데이터가 있는 지점에서는 높이가 높게 평가되고
데이터가 없는 지점에서는 높이가 낮게 평가되어야 합니다.
이러한 특성 때문에
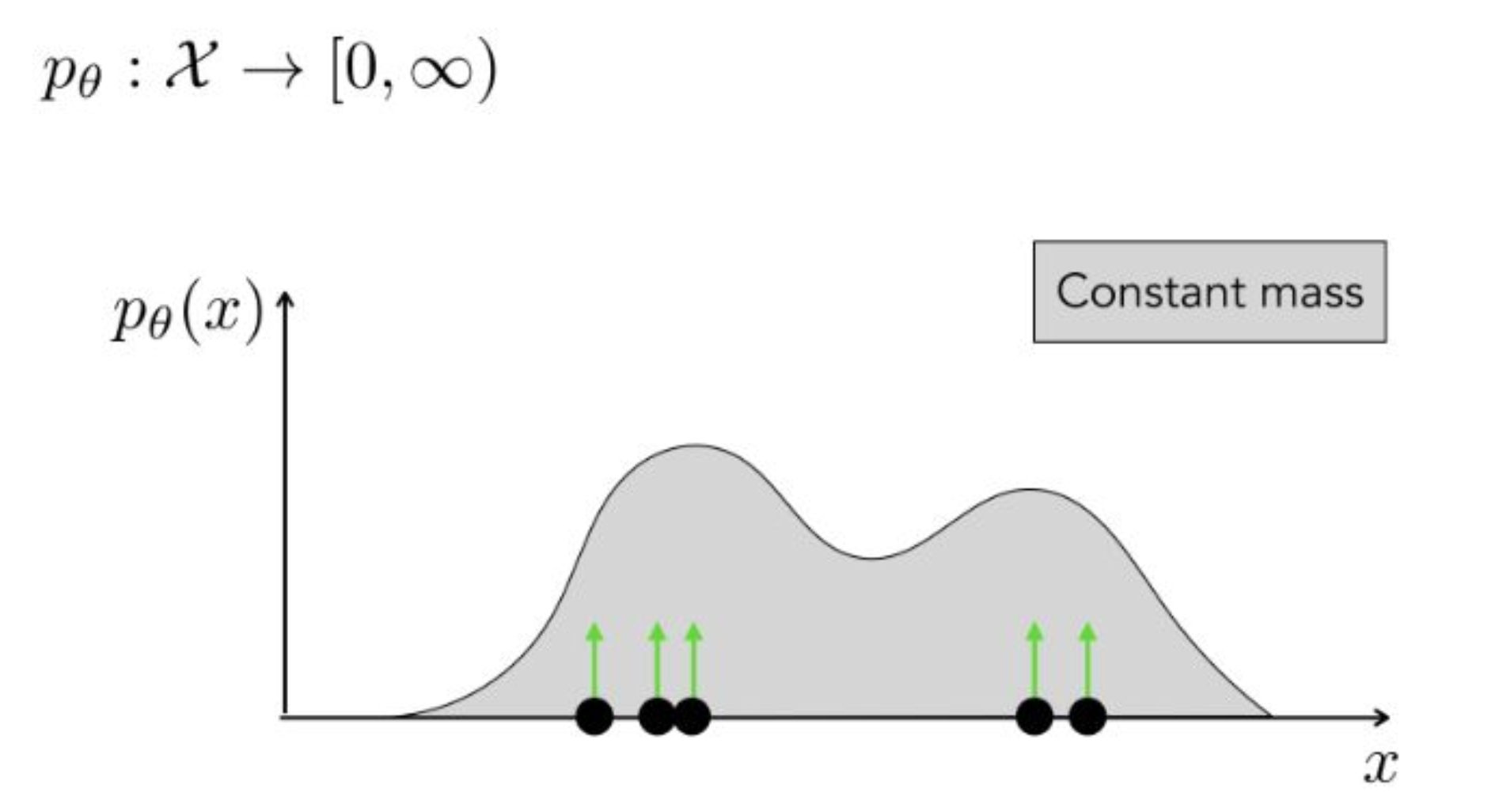
density based model들, 예를 들어 energy model이나 diffusion model은
학습 후 density estimation을 해보면
이러한 형태의 분포가 많이 나타납니다.
이러한 모양이 제대로 나오면
전문가가 보았을 때
트레이닝이 잘 이루어졌다고 판단하는 경우가 많습니다.

p11. 밀도 기반 모델 (Density-based Models)

\[\begin{aligned} p_\theta^* &= \arg \min_{p_\theta} \text{KL}(p_{\text{data}}, p_\theta) \\ &= \arg \min_{p_\theta} \mathbb{E}_{x \sim p_{\text{data}}} \left[- \log \frac{p_\theta(x)}{p_{\text{data}}(x)} \right] \\ &= \arg \max_{p_\theta} \mathbb{E}_{x \sim p_{\text{data}}} [ \log p_\theta(x) ] - \mathbb{E}_{x \sim p_{\text{data}}} [ \log p_{\text{data}}(x) ] \quad\quad\quad \text{(max likelihood)} \\ &= \arg \max_{p_\theta} \mathbb{E}_{x \sim p_{\text{data}}} [ \log p_\theta(x) ] \quad\quad\quad \text{(두 번째 항은 } p_\theta \text{에 의존하지 않기 때문에 생략)} \\ &\approx \arg \max_{p_\theta} \frac{1}{N} \sum_{i=1}^{N} \log p_\theta(x^{(i)}) \end{aligned}\]

강의 내용
이 내용을 보고 처음 보는 개념이라고 생각하면 안 됩니다.
시험에도 나왔고, 앞에서 충분히 다뤘던 내용입니다.
maximum likelihood estimation,
즉 $p_\theta^*$를 구하는 과정에서
최적의 probability distribution은
KL divergence를 최소화하는 것이었습니다.
계산 과정을 따라가 보면
constant 항이 등장하고,
$p_{\text{data}}$와 $p_\theta$의 관계,
그리고 $log$ 함수를 통한 분해(decompose)를 거치면
마지막에는
$\arg\max \log p_\theta$
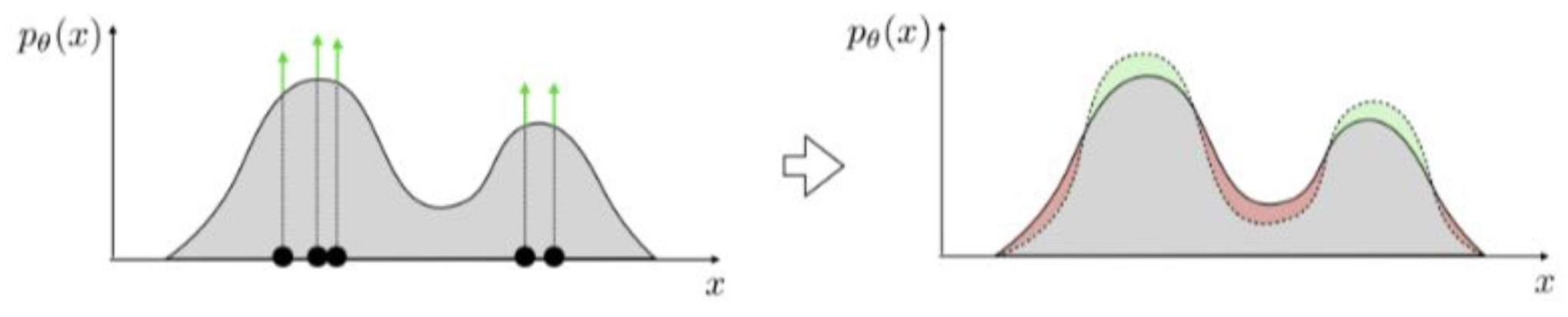
를 수행하는 형태가 됩니다.
물리적인 관점에서 보면
그림에서 표현된 것처럼
데이터가 있는 영역에서는 확률을 높이고
데이터가 없는 영역에서는 확률을 낮추는 방식으로
분포가 조정됩니다.
앞에서는 이를 수학적으로만 배웠지만
실제로는 이러한 물리적 성질을 이용하여
maximum likelihood가 정의되고
생성 모델의 학습 방식이 결정됩니다.
이렇게 이해하시면 됩니다.
(질문)
회색 실선이 $p_\theta$이고
점들이 $p_{\text{data}}$라고 보면 될까요?
점 위의 녹색 화살표가 $p_{\text{data}}$를 의미하는 것처럼 보이는데요.
(답변)
왼쪽 그림을 말씀하시는 거죠?
알고리즘에서 maximization을 수행하면
예를 들어 왼쪽에 회색 분포가 하나 있었다고 할 때
maximization 과정은 한 번에 끝나는 것이 아니라
시간이 지나며 iterative하게 진행됩니다.
그 과정에서
mass가 존재하는 지점은 초록색처럼 확률이 점점 높아지고
mass가 없는 지점은 빨간색처럼 확률이 점점 낮아지는 형태로
분포가 업데이트됩니다.
(질문)
그럼 오른쪽 그림에서는
회색이 $p_\theta$이고
녹색·빨간색 영역이 $p_{\text{data}}$인가요?
(답변)
그 영역은 업데이트된 $p_\theta$입니다.
$p_{\text{data}}$는 x축에 위치해 있습니다.
그렇게 이해하시면 됩니다.

p12. 변분 오토인코더 (Variational Autoencoder)

데이터 생성 과정을 다음과 같이 가정한다.

$z$: 잠재 변수(latent variables)
$x$: 관측 변수(observed variables)

강의 내용
여기까지가 개요입니다.
오늘의 교육 내용은 강의 길이가 꽤 길기 때문에
아마 다음 주까지 코드 실습과 함께 이어질 수 있습니다.
이제 variational auto encoder, 즉 VAE에 대해
살펴보도록 하겠습니다.
앞에서 제가 VAE가
direct approach에 더 가깝다고 말씀드렸는데
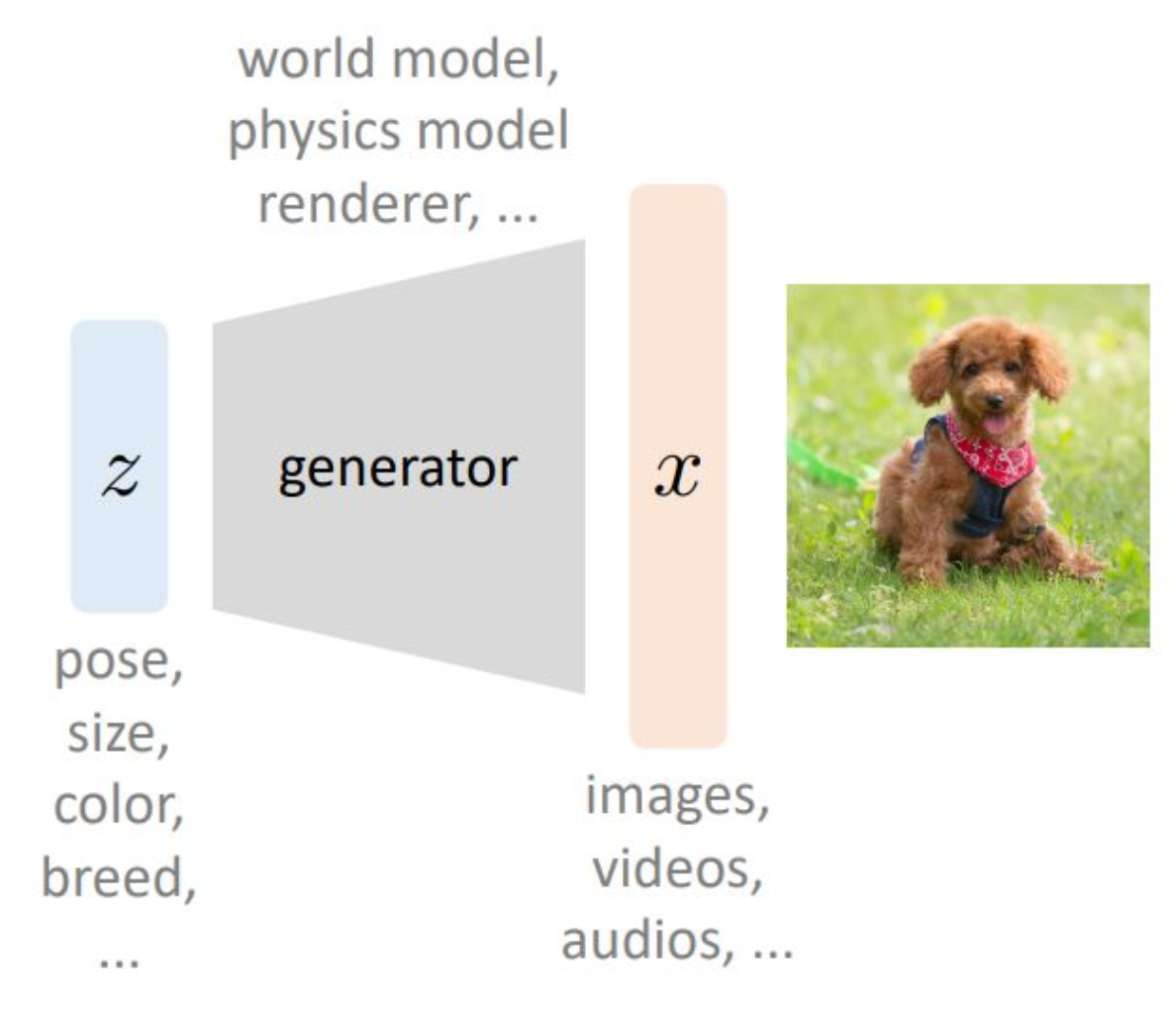
먼저 그림을 보며 이런 구조를 생각해보겠습니다.
$z$라는 latent variable,
즉 Gaussian random variable이 존재합니다.
앞에서 설명했던 것처럼
size, color, breed 등의 다양한 feature에 대해
인간이 직접 정의한 것은 아니지만
모델을 학습시키다 보면
이러한 feature들이 latent space에서
자연스럽게 mapping되는 역할을 하게 됩니다.
generator는
이 $z$를 받아서 실제 데이터를 생성하는
mapping 함수라고 볼 수 있습니다.
여기서 notation을 명확하게 정리해보겠습니다.
$z$는 latent variable,
$x$는 observed variable,
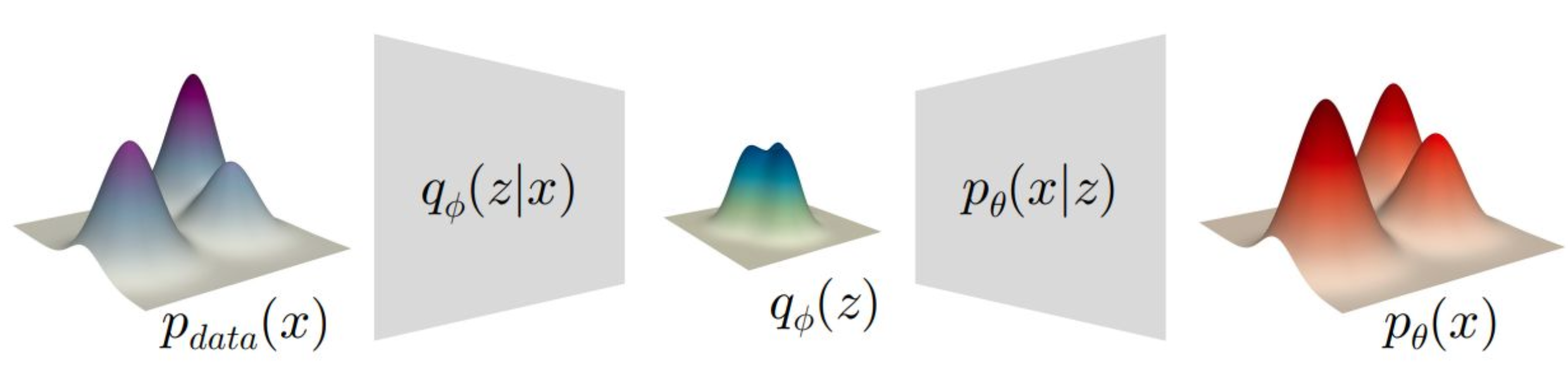
즉 데이터셋 안에 실제로 존재하는 데이터입니다.
그림과 텍스트에서 보이는 것처럼
world model, physical model, renderer, image, videos, audio 등
현대의 모든 생성 모델은
이와 같은 프레임을 기반으로 표현할 수 있습니다.
예를 들어
Yann LeCun이 말한 world model 구조나
요즘 3D 비디오를 인터랙티브하게 생성하는 모델들도
모두 이러한 기본 구조를 따릅니다.
실제로 pipeline을 뜯어보고
모델 아키텍처를 분석해보면
결국 이러한 방식으로 데이터를 생성합니다.
개념적으로 이러한 구조를 이해하고 있는 것이
매우 중요합니다.

보충 자료
world model이라 함은, 인공지능이 외부 세계의 구조를 스스로 학습하여
환경의 규칙과 변화를 내부적으로 표현하려는 개념이라 한다.
여기에서는 에이전트가 모든 정보를 직접 관찰하지 못하더라도
세계가 어떻게 움직이는지 예측할 수 있는 능력을 갖추는 것을 목표로 한다.
다시 말해, world model은 단순한 입력–출력 함수가 아니라
환경의 인과관계와 시간적 동역학을 내재적으로 담아내는
일종의 내부 시뮬레이터라 할 수 있다.
이러한 모델이 구성되면,
“어떤 행동을 취하면 세계가 어떻게 변할 것인가”를
에이전트가 스스로 추론할 수 있게 되며,
이는 보다 고차원적인 reasoning과 지능을 구현하는 데
핵심적 역할을 수행한다.

p13. 변분 오토인코더 (Variational Autoencoder)

데이터 생성 과정을 다음과 같이 가정한다.

$z$: 잠재 변수(latent variables)
$x$: 관측 변수(observed variables)

잠재 변수는 사전 분포(prior distribution)로부터 샘플링된다.

\[z \sim p(z)\]

그리고 생성기(generator)는 잠재 변수 $z$를 입력으로 받아
관측 변수 $x$의 분포(distribution)를 생성한다.

강의 내용
이제 조금 더 distributional한 관점에서 이야기해보겠습니다.
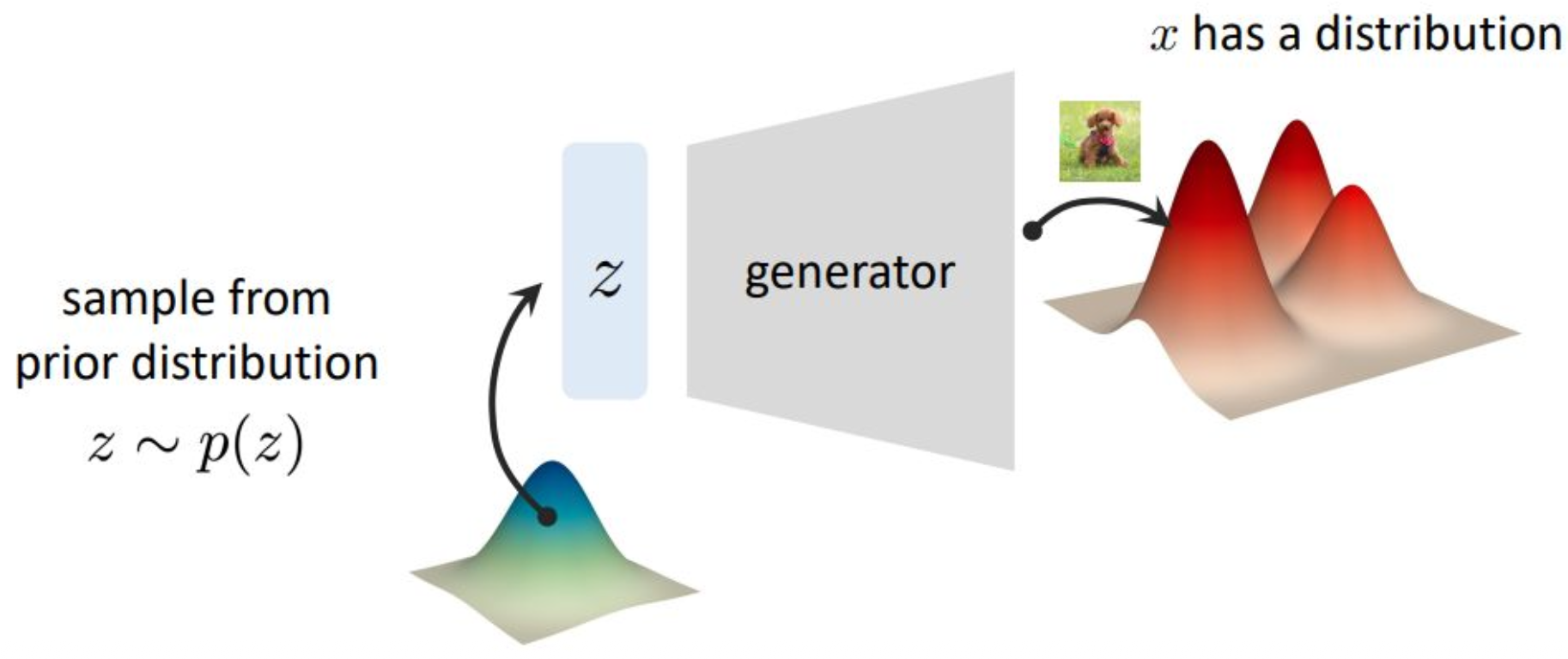
latent variable을 샘플링한다고 하면
$p(z)$라는 probability density로부터
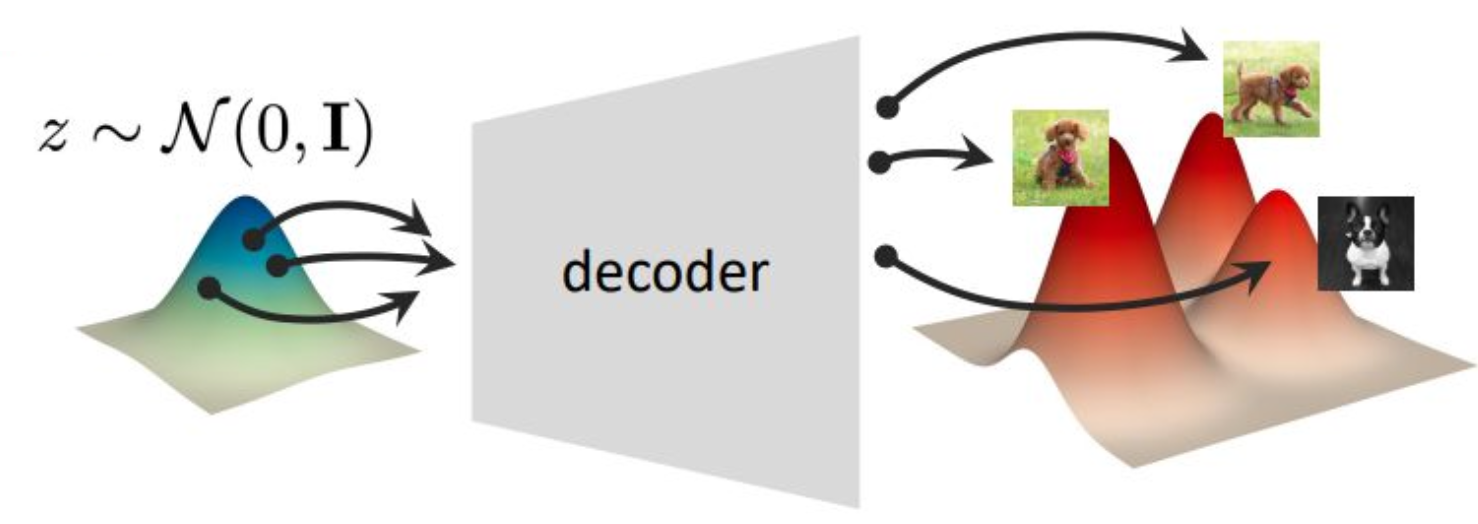
$z$라는 random sample, 즉 latent variable을 뽑는다는 의미입니다.
지금 그림을 보면
우리가 논의하는 대상이
distribution에서 distribution으로 가는 mapping 구조로 확장된 것을 볼 수 있습니다.
파란색 distribution은 매우 단순한 형태입니다.
정보가 거의 없습니다.
앞에서 예시로 들었던 것처럼
보통 Gaussian 형태의 간단한 분포를 의미합니다.
여기서는 1-dimensional 데이터를 예로 들었지만
실제 데이터는 high-dimensional하기 때문에
density를 단순히 $z$축의 봉우리처럼 표현하기는 어렵습니다.
그러나 개념적으로는
오른쪽과 같은 multi-modal density,
즉 로컬 미니멈과 로컬 맥시멈이 많은
매우 복잡한 분포로
단순한 분포를 mapping하는 것이
제네레이터의 역할이라고 볼 수 있습니다.
앞에서 단순히 언어적으로 설명했던
pose, size 등의 feature들도
이러한 관점에서 보면
수학적으로는
쉬운 분포를 어려운 분포로 보내는 mapping으로 해석할 수 있습니다.
제네레이터 모델은
간단한 분포에서 복잡한 분포로
데이터를 변환하는 역할을 수행한다는 점을
이렇게 이해하시면 좋습니다.
이 개념은 사실 매우 심오한 이론들과 연결되며
이후 차분히 더 다루도록 하겠습니다.

p14. 변분 오토인코더 (Variational Autoencoder)

신경망(Neural Network)을 이용하여 확률 분포(distribution)를 표현한다.

$ \theta $ : 학습 가능한 파라미터(learnable parameters)
표현되는 함수:
\[p_\theta(x \mid z)\]

강의 내용
그래서 제네레이터가 무엇인가를
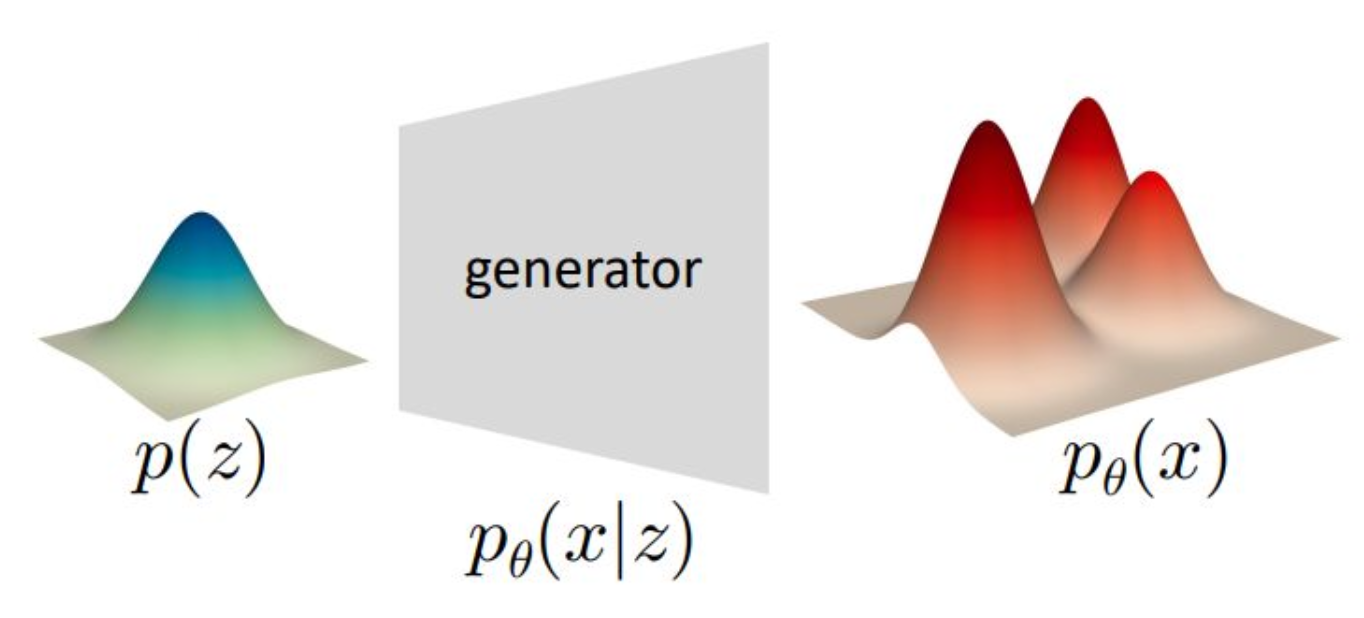
수학적으로 조금 더 깊게 생각해보겠습니다.
$p(z)$는 latent variable에 대한 distribution입니다.
$p_\theta(x)$는
제네레이터가 $\theta$라는 파라미터로 parameterization되어 있기 때문에
그 파라미터를 통해 생성된 결과물의 distribution을 의미하며
그래서 $p_\theta(x)$라고 표현합니다.
이제 제네레이터는
conditional probability 관점에서
확률적으로 해석할 수 있습니다.
앞에서 conditioning, marginalization 등을 공부했었는데
이를 적용해보면 다음과 같습니다.
랜덤 변수 $z$가 주어졌을 때
그 조건 하에서 생성되는 데이터 $x$의 모양은
어떤 분포를 따르는가라는 질문을 할 수 있습니다.
즉, 제네레이터는
$p_\theta(x \mid z)$라는
수학적 객체로 표현할 수 있습니다.
여기서부터 확률론에서 학습했던
다소 재미없게 느껴졌던 도구들이
생성 모델을 다루기 위한 중요한 도구로 재해석됩니다.
예를 들어
marginalization은
이러한 분포들의 평균적인 움직임을 계산하는 과정이며
latent variable이 하나일 때뿐 아니라
여러 개의 latent variable이 존재할 때
정보량이 어떻게 연결되고 흘러가는지
앞에서 수식으로 배웠던 내용들이
바로 이 영역에서 사용됩니다.
이러한 개념들이
뒤에서 생성 모델을 학습하기 위한
수학적 기반이 됩니다.
따라서 앞에서 배운 내용을 떠올리며
지금 다루는 개념들이
어떻게 이어지는지 보시면 도움이 될 것입니다.

p15. 최대우도추정 (Maximum Likelihood Estimation)

Kullback–Leibler (KL) 발산 최소화:

\[\min_{\theta} \, D_{\mathrm{KL}}(p_{\text{data}} \, \| \, p_{\theta})\]

KL발산 외에 고려할 수 있는 다른 기준은?

즉, 우도 최대화(Maximize likelihood):

\[\max_{\theta} \, \mathbb{E}_{x \sim p_{\text{data}}} [\log p_{\theta}(x)]\]

전개 과정:

\[\begin{aligned} \arg \min_{\theta} D_{\mathrm{KL}}(p_{\text{data}} \, \| \, p_{\theta}) &= \arg \min_{\theta} \sum_{x} p_{\text{data}}(x) \log \frac{p_{\text{data}}(x)}{p_{\theta}(x)} \\ &= \arg \min_{\theta} \left[- \sum_{x} p_{\text{data}}(x) \log p_{\theta}(x) + \text{const}\right] \\ &= \arg \max_{\theta} \sum_{x} p_{\text{data}}(x) \log p_{\theta}(x) \\ &= \arg \max_{\theta} \mathbb{E}_{x \sim p_{\text{data}}} [\log p_{\theta}(x)] \end{aligned}\]

강의 내용
우리가 KL Divergence를 공부했고
Total variance도 다뤘지만
생성 모델에서는 KL Divergence를 주로 사용한다고 했습니다.
제가 그때 말했듯이
거의 모든 생성 모델은 KL Divergence와 밀접하게 연결되어 있습니다.
그래서 여기에서도 KL Divergence를 줄이는 것이
우리의 주요 목표가 됩니다.
그런데 이 minimization 관점에서 생각해보면
데이터가 매우 크고 복잡한 경우
파라미터 $\theta$가 아무리 커도
KL Divergence를 일정 이하로만 줄일 수 있을 뿐
0으로 만드는 것은 불가능합니다.
데이터가 가진 복잡도는 매우 높은데
모델이 표현할 수 있는 파라미터 용량은 제한되어 있기 때문입니다.
즉 KL Divergence를 최소화하되
이는 어디까지나 로컬 미니멈 수준의 최소화이며
뉴럴 네트워크라는 비선형 구조에서는
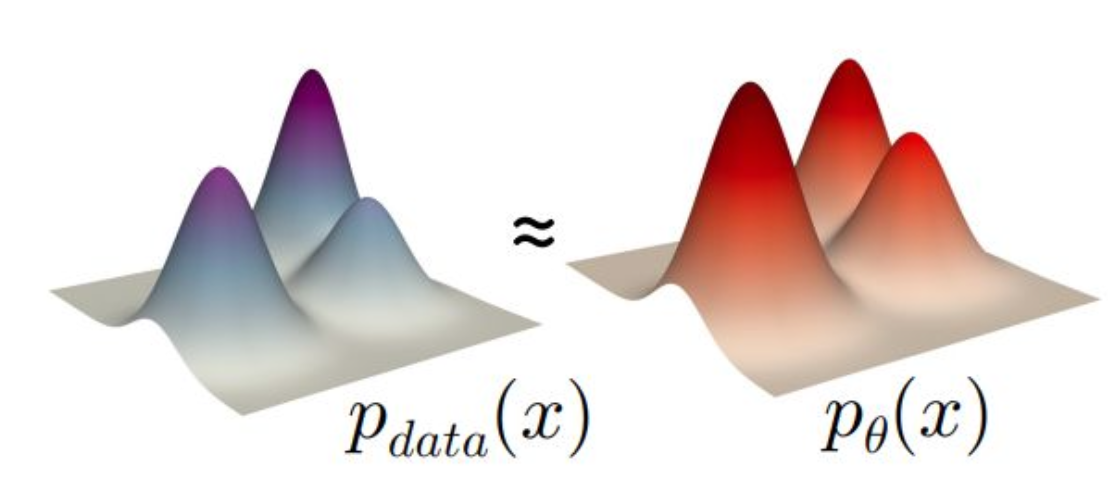
글로벌 미니멈을 찾는 것은 거의 불가능합니다.
KL Divergence의 의미를 다시 떠올려보면
두 분포 간의 차이를 측정하는 functional입니다.
즉 데이터의 distribution $p_{\text{data}}$와
모델이 생성한 distribution $p_\theta(x)$가 있을 때
이 둘의 차이를 최대한 줄이는 것이 목적입니다.
KL Divergence가 충분히 작은 값이라면
다음과 같은 기대를 할 수 있습니다.
$p_\theta(x)$가 $p_{\text{data}}$를 잘 모방했으므로
모델이 샘플링하여 생성한 이미지들이
실제 데이터셋에 존재하는 이미지들과
닮아 있을 것이라는 기대를 가지는 것입니다.
이것이 input과 output에 대한 철학적 관점이라면
이제는 훈련 방법론의 철학으로 넘어갑니다.
classification 모델은 어떠했습니까?
classification에서는
하나의 이미지와
그 이미지에 대응하는 하나의 레이블이 존재하여
one-to-one 매칭 구조를 갖습니다.
그러나 생성 모델에서는 그렇지 않습니다.
여기서는 probability distribution을 매칭하기 때문에
다대다 매칭 구조가 됩니다.
$p_{\text{data}}$에는 매우 많은 데이터가 존재하고
$p_\theta$ 또한 무수히 많은 데이터를 생성할 수 있습니다.
따라서 이들 사이에는
직접적인 페어링이 존재하지 않습니다.
그래서 distribution 단위로 비교를 수행합니다.
이것이 철학적 차이점이며
우리가 KL Divergence를 공부했던 이유이기도 합니다.
분포 간 다대다 매칭을 위해 필요한 도구이기 때문입니다.
다대다 매칭의 의미를 다시 생각해보면
첫 번째 슬라이드에서 본 것처럼
랜덤 변수를 샘플링할 때마다
다른 데이터가 생성되도록 하는 파이프라인이
이러한 훈련 방법론에서 비롯된 것입니다.
랜덤 변수가 계속 달라지는데
생성 결과가 항상 똑같다면
그것은 잘못된 모델입니다.
랜덤 변수를 동일하게 주더라도
샘플링 과정에서는 다양한 이미지가 생성될 수 있습니다.
매우 흥미로운 현상이지만
이 또한 분포 기반 학습 철학의 일부입니다.
따라서 우리는 KL Divergence와
maximum likelihood estimation의 연결을 배웠고
KL Divergence를 minimization하는 과정이
maximum likelihood와 등가임을 확인했으며
생성 모델을 학습하는 방법은
이러한 원리 위에서 전개된다는 것을 배웠습니다.

p16. 최대우도추정 (Maximum Likelihood Estimation)

우리는 다음 식을 최대화하고자 한다.

\[\mathbb{E}_{x \sim p_{\text{data}}} [\log p_\theta(x)]\]

여기서 $p_\theta(x)$는 다음과 같이 표현된다.

\[p_\theta(x) = \int_z p_\theta(x \mid z) \, p(z) \, dz\]

이때 두 가지 미지항(unknowns)이 존재한다.

최적화 대상: $\theta$ — 학습 가능한 파라미터
제어 불가능한 요소: “진짜” 사전 분포 $p(z)$

따라서 다음과 같은 아이디어가 제시된다.
→ “제어 가능한(controllable)” 분포 $q(z)$를 도입한다.

강의 내용
조금 더 디테일하게 살펴보겠습니다.
$\log p_\theta$는
생성된 데이터가 따르는 distribution이라고 설명했었고
$\theta$는 뉴럴 네트워크의 파라미터입니다.
이제 $p_\theta(x)$를
앞에서 배웠던 marginalization과 conditioning의 룰을 사용하여
적분 형태로 분해해보겠습니다.
이 표현은
conditional probability의 정의에 따라
정확하게 등식으로 성립합니다.
여기서 $p(z)$는 Gaussian Random Variable에 대한 분포이고
$p_\theta(x \mid z)$는 제네레이터입니다.
따라서
$p_\theta(x)$, 즉 데이터 생성에 대한 분포는
이러한 방식으로 연결됩니다.
앞에서 그린 파이프라인에서는
모델에 데이터를 넣고
랜덤 변수를 넣고
latent variable을 넣는다,
라는 식으로 설명했지만
이제 이것을 수학적으로 명확하게 정리한 것입니다.
informal한 설명을
formal한 수학적 단계로 바꿔 표현한 것이죠.
그래서 이러한 적분 형태로 표현하는 것이
제네레이터를 나타내는 하나의 방법입니다.
그런데 여기서 문제가 생깁니다.
$\theta$를
즉, 제네레이터의 파라미터를
이러한 conditional한 구조 속에서
어떻게 optimization할 것인가.
이것이 바로 핵심적인 어려움이 됩니다.

보충 자료
최대우도추정(MLE)은 실제 데이터 분포 $p_{\text{data}}$에 대해
모델 분포 $p_\theta(x)$의 로그 가능도 $\log p_\theta(x)$를 최대화하는 것을 목표로 한다.
그런데 $p_\theta(x)$는 단순한 형태가 아니라
잠재 변수 $z$에 대한 적분 형태로 표현된다. 조건부 확률의 정의를 이용하면 다음과 같다.
\[p_\theta(x) = \int_z p_\theta(x \mid z)\, p(z)\, dz\]
여기서
$p(z)$는 잠재 변수의 사전 분포(prior distribution)이며 보통 가우시안으로 가정한다.
$p_\theta(x \mid z)$는 생성기(generator)로, “$z$가 주어졌을 때 $x$가 생성될 확률”을 나타낸다.
이 적분식은 우리가 앞서 직관적으로 이해했던
“잠재 변수 $z$를 입력받아 데이터를 생성한다”는 개념을
수학적으로 공식화한 표현이다.
하지만 이 식을 직접 최적화하는 것은 매우 어렵다. 그 이유는 다음과 같다.
1) $p_\theta(x)$는 $z$에 대한 적분이므로 폐형식(closed form)으로 계산이 불가능하다.
2) $p(z)$는 우리가 직접 제어할 수 없는 고정된 분포이다.
따라서 실제 학습에서는
직접적인 사전 분포 $p(z)$ 대신
제어 가능한(controllable) 근사 분포 $q(z)$를 도입하여
계산과 최적화를 가능하게 만든다.
이 발상이 바로 변분 오토인코더(VAE)의 핵심 동기이다.
즉, $p_\theta(x)$를 직접 계산하는 대신
잠재 공간의 “근사 posterior”인 $q(z)$를 활용하여
효율적으로 로그 가능도를 최대화할 수 있는 구조를 만든다.
다시 말해, VAE는
잠재 변수 적분 때문에 계산 불가능한 MLE 문제를
변분 근사(variational approximation)를 이용해 해결하려는 방법이다.

p17. 잠재 변수 모델 (Latent Variable Model)

강의 내용
제가 정말 강조하고 싶었던 부분이 바로 이 페이지입니다.
이것이 오늘 배우는 VAE 구조의 모든 핵심을
하나의 식으로 압축해 표현한 것이라고 생각하시면 됩니다.
겉으로 보기에는 어려워 보일 수 있지만
실제로는 구조를 잘 따라가면 그렇게 어렵지 않습니다.
이 수식을 완전히 이해하면
VAE가 수학적으로 어떤 의미를 가지는지
명확하게 파악할 수 있습니다.
이런 형태의 수식 전개를
Latent Variable Model이라고 부르며
확률론과 통계학, 특히 Bayesian 통계에서
매우 널리 사용되는 방식입니다.
이제 $\log p_\theta(x)$를
여러 개의 해석 가능한 항으로 분해하는 과정이
어떻게 이루어지는지 살펴보겠습니다.
먼저 우리의 목표는
$\log p_\theta(x)$를 maximization하는 것이었습니다.
다음 줄을 보면
$\int q(z)\,\log p_\theta(x)\,dz$
라는 형태로 표현됩니다.
이 적분이 등식으로 성립하는 이유는 다음과 같습니다.
$\log p_\theta(x)$는 $z$와 무관하기 때문에
적분 밖으로 꺼낼 수 있고,
그러면 $\int q(z)\,dz$가 남습니다.
모든 확률분포는 적분하면 1이므로
이 등식이 성립합니다.
이제 conditioning을 꺼내기 위해
Bayes rule을 사용합니다.
$p_\theta(x)$는 다음처럼 쪼개집니다.
$p_\theta(x) = \dfrac{p_\theta(x \mid z)\,p_\theta(z)}{p_\theta(z \mid x)}$
여기서 조건부의 방향이 뒤집힌 것을 확인할 수 있습니다.
이제 양변에 $q(z)/q(z)$를 곱합니다.
이는 1을 곱하는 것과 동일하므로 식을 바꾸지 않습니다.
그리고 로그의 성질
$\log(ab) = \log a + \log b$
를 사용하여 항들을 분리합니다.
이렇게 항들을 정리하면
최종적으로 VAE의 기본 구조를 이루는
세 가지 주요 term이 등장합니다.
이 세 항을 Neural Network로 구현한 것이
바로 VAE입니다.
이제 각 항의 의미를 하나씩 살펴봅시다.
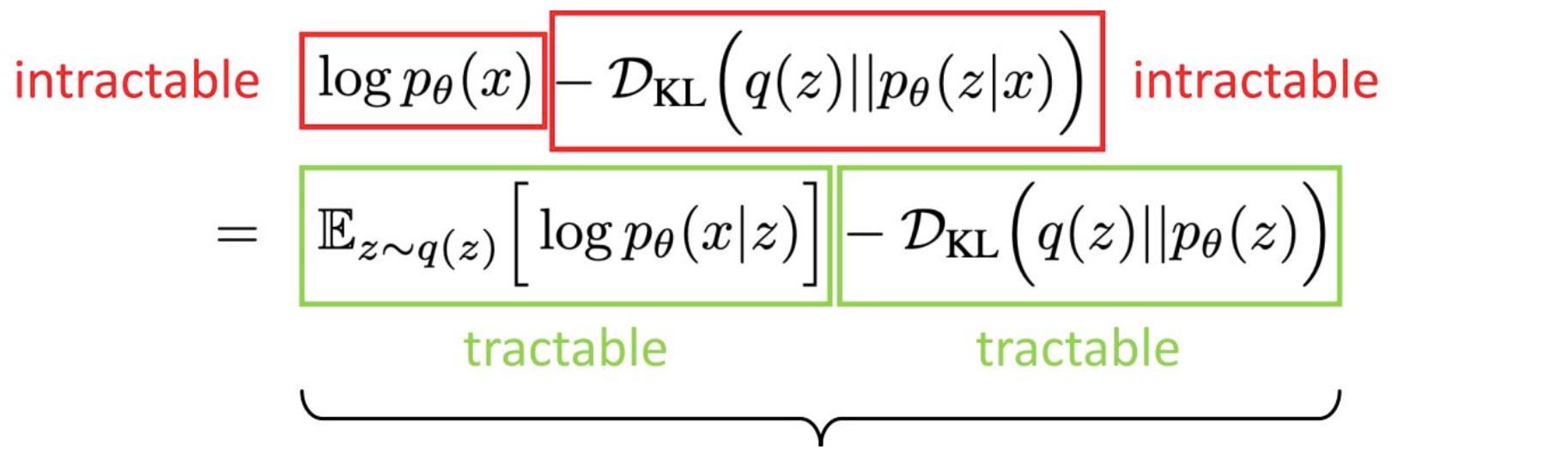
먼저 intractable term인
$p_\theta(x)$는
수학적으로 직접 계산할 수 없습니다.
그 이유는 다음과 같습니다.
실세계 데이터($x$)는
이미지, 음성, 언어처럼
매우 복잡하고 high-dimensional한 공간에 존재한다.
이러한 데이터 분포는
특별한 경우가 아니면
수학적으로 표현하거나 적분할 수 없다.
따라서 직접 다루는 것이 불가능하기 때문에
위와 같은 방식으로 표현을 바꾸어
tractable한 형태로 재구성하는 것입니다.

보충 자료
목표는 $\log p_\theta(x)$를 최대화하는 것이다.
이를 다루기 위해, 임의의 보조 분포 $q(z)$를 곱해 적분 형태로 변환하면
$z$에 무관한 상수항인 $\log p_\theta(x)$를 적분 내부로 옮길 수 있다.
베이즈 규칙
\[p_\theta(z \mid x)=\frac{p_\theta(x\mid z)\,p_\theta(z)}{p_\theta(x)}\]
을 대입하고,
$q(z)$를 곱하고 나누어(즉, 1을 곱한 것과 동일)
로그의 성질 $\log a - \log b$를 사용해 각 항을 분리한다.

p18. 계산 불가능한 식에서 계산 가능한 형태로 (From Intractable to Tractable Formulation)

강의 내용
우리가 $\log p_\theta(x)$ 수식을 전개하면서
맨 마지막 항을 남겨두었는데,
여기서 tractable하다는 것은
우리가 직접 계산할 수 있다는 의미이고
intractable하다는 것은
계산이 불가능하다는 뜻입니다.
그렇다면 계산할 수 없는 항이 존재하는데
왜 이런 모델이 필요한가라는 의문이 생길 수 있습니다.
컴퓨터 공학 하시는 분들은
(저는 수학을 깊게 공부한 입장이라 좀 답답하긴 하지만)
intractable한 항을 과감하게 무시합니다.
KL divergence를 계산하면
항상 양수 혹은 특정한 제약된 값을 가지게 되는데
그렇기 때문에 마지막 항을 제어하지 않더라도
앞의 두 항만 잘 제어하면
최종적으로 $\log p_\theta(x)$를
충분히 control할 수 있다는 철학을 따릅니다.
그래서 intractable한
마지막 term은 그냥 무시해도 된다는 결론이 나옵니다.
물론 이 항까지 완전히 control할 수 있는
새로운 방법이 등장한다면
$\log p_\theta(x)$를 더욱 정확하게 묘사할 수 있을 것입니다.
하지만 현실적으로는
이 항을 무시해도
모델이 꽤 잘 동작하는 경우가 많습니다.

보충 자료
우리가 다루는 $\log p_\theta(x)$는 직접 계산이 불가능(intractable) 하다.
그 이유는 잠재변수 $z$에 대해
$p_\theta(x)=\int p_\theta(x\mid z)p_\theta(z)\,dz$
와 같은 고차원 적분을 닫힌 형태(closed-form)로 계산하기 어렵기 때문이다.
이를 우회하기 위해, $\log p_\theta(x)$를
$\mathbb{E}_{z\sim q(z)}[\log p_\theta(x\mid z)] \;-\; D_{\mathrm{KL}}(q(z)\,\|\,p_\theta(z)) \;+\; D_{\mathrm{KL}}(q(z)\,\|\,p_\theta(z\mid x))$
와 같이 세 항으로 분해한다.
초록색의 두 항(앞의 두 항)은 ‘원래는’ 계산이 불가능(intractable) 하지만,
아래 두 가지 이유로 실제 학습 과정에서는 계산 가능(tractable) 하다:
① 첫 번째 항 $\mathbb{E}_{z\sim q(z)}[\log p_\theta(x\mid z)]$는
몬테카를로 샘플링(Monte-Carlo estimation) 을 이용하면
충분히 정확하게 추정할 수 있기 때문이다.
즉, $z\sim q(z)$ 를 샘플링한 후
$\log p_\theta(x\mid z)$ 값을 평균 내면 된다.
② 두 번째 항 $D_{\mathrm{KL}}(q(z)\,|\,p_\theta(z))$는
q(z)와 p(z)가 모두 가우시안인 경우(표준 VAE의 기본 설정)
해석적(analytic) 닫힌형 해(closed-form solution) 이 존재한다.
따라서 이 항은 직접 계산이 가능해진다.
반면 마지막 항
$D_{\mathrm{KL}}(q(z)\,\|\,p_\theta(z\mid x))$
은 여전히 계산 불가능(intractable) 하다.
이유는 $p_\theta(z\mid x)$ 를 구하려면
\[p_\theta(z\mid x)=\frac{p_\theta(x\mid z)p_\theta(z)}{p_\theta(x)}\]
이 되는데, 여기서 또다시 계산 불가능한 $\log p_\theta(x)$가 등장하기 때문이다.
하지만 이 항은 항상 0 이상이며,
우리는 이를 직접 계산하지 않아도
앞의 두 항(ELBO)의 합을 최대화하는 것만으로
원래 목적 함수 $\log p_\theta(x)$를 간접적으로 최대화할 수 있다.
이것이 바로 변분추론(VI)의 핵심 아이디어이다.
계산 불가능한 목적을 직접 최적화하지 않고,
계산 가능한 하한(ELBO) 을 최대화함으로써
$\log p_\theta(x)$에 최대한 가까운 값을 찾는다.

p19. 증거 하한 (Evidence Lower Bound, ELBO)

이것을 Evidence Lower Bound (ELBO) 라고 부른다.
이는 $\log p_\theta(x)$의 하한(lower bound)이다.
이 식은 임의의 분포 $q(z)$ 에 대해서도 성립한다.

강의 내용
이제 좌변과 우변을 정리해보면 다음과 같은 구조가 됩니다.
intractable한 항 두 개는 왼쪽에,
tractable한 항 두 개는 오른쪽에 배치합니다.
이렇게 조합하면
evidence lower bound(ELBO)라는
매우 중요한 개념이 도출됩니다.
lower bound와 upper bound를
단순한 함수 예시로 생각해 보면,
$f(x) = -x^2 + c$라는 함수에서
upper bound는 $c$입니다.
어떤 값이 변화하더라도
그 함수가 도달할 수 있는 최대값이
upper bound가 되는 것이죠.
lower bound는 이와 반대되는 개념입니다.
여기서도 동일하게,
intractable한 항을 무시하고 왼쪽으로 넘긴 뒤
나머지를 양수 형태로 계산하고
equality를 inequality로 바꾸면
자연스럽게 lower bound가 등장합니다.
그래서 이를 evidence lower bound라고 부릅니다.
evidence라는 표현을 사용하는 이유는
tractable한 항들만으로
모델을 판단하고 최적화할 수 있기 때문입니다.
(질문)
가장 오른쪽 항이 intractable한 이유가
given $x$인데
$x$가 intractable하므로
마지막 항도 intractable한 것인가요?
(답변)
그렇지 않습니다.
문제는 $z \mid x$를 알 수 없다는 데 있습니다.
slide의 마지막 항을 말씀하시는 것이죠?
(질문)
네.
그렇다면 첫 번째 $x \mid z$는 왜 tractable한가요?
(답변)
그것은 generator이기 때문입니다.
$z$를 입력했을 때
generator가 어떻게 작동하는지는
우리가 모델링하고 있기 때문에
그 conditional probability는 tractable합니다.
하지만 $z \mid x$는 다릅니다.
$x$는 정보가 매우 많은 실제 데이터이고
$z$는 latent variable로 정보가 거의 없습니다.
즉 정보가 많은 것을 input으로 넣어
정보가 없는 latent variable을 추정해야 하는데
이러한 mapping은 본질적으로 매우 어렵고
tractable한 모델이 존재하지 않습니다.
그래서 이 항은 intractable한 것입니다.
의미적으로 보면
이것은 Bayes rule에서 온 구조이며
사전 확률과 사후 확률의 개념을 알고 있다면
더 직관적으로 이해될 것입니다.
지금 강의에서 Bayes의 철학까지는 다루지 않기 때문에
앞에서 설명한 요지 정도로 이해하면 충분합니다.
중요한 점은
$p_\theta(z \mid x)$는 직접 모델링하기 어렵기 때문에
새로운 분포 $q(z)$를 도입해
이를 대체하고 근사한다는 것입니다.
그리고 이 $q(z)$가
뒤에서 핵심적으로 다루게 될 중요한 개념입니다.

p20. 매개변수화(Parameterization)

이것은 Evidence Lower Bound (ELBO) 라고 불린다.
이는 $\log p_\theta(x)$ 의 하한(lower bound)이다.
이 식은 임의의 분포 $q(z)$ 에 대해서도 성립한다.
이제 $q(z)$를 직접 다루기 어려우므로,
이를 매개변수화(parameterize) 하여
$q_\phi(z \mid x)$ 로 표현한다.
여기서 $\phi$ 는 추론 네트워크(inference network) 의
학습 가능한 파라미터이다.
반면, $p_\theta(z)$ 는 단순하고 알려진 사전분포(prior) 로 둔다.

강의 내용
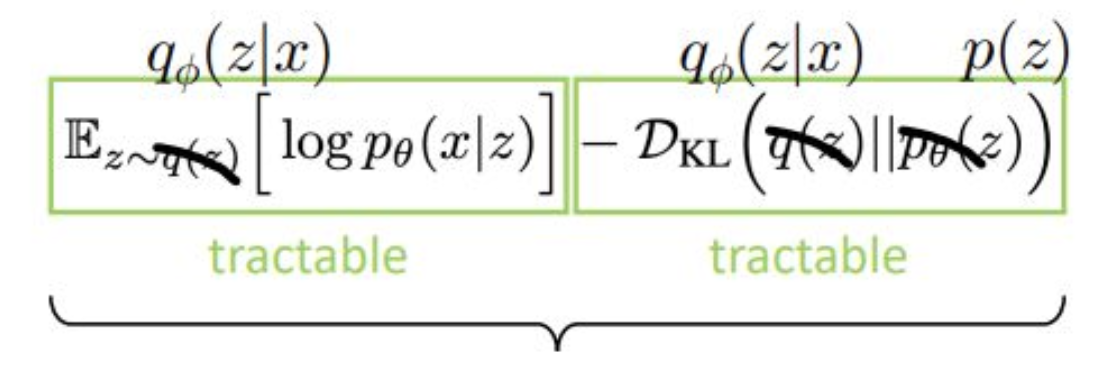
$q(z)$를 직접 다루기 어렵기 때문에
이제 $q$를 $\phi$라는 파라미터로
파라미터라이즈합니다.
즉, 뉴럴 네트워크 구조를 사용해
$q(z)$를 모델링하겠다는 의미입니다.
그래서 $q(z)$를
$q_{\phi}(z \mid x)$로 바꾸어 표현합니다.
한편 $p_{\theta}(z)$는
prior knowledge가 반영된
이미 알고 있는 분포인 $p(z)$로 대체할 수 있습니다.
이것은 단순히 사용하는 테크닉이라고
이해하시면 될 것 같습니다.

보충 자료
실제로 $q(z)$는 임의의 형태를 가질 수 있지만,
그 분포를 명시하거나 직접 계산하는 것은 불가능하다.
따라서 이를 신경망으로 근사(parameterize) 하여
$q_\phi(z \mid x)$ 형태로 표현한다.
이때 $\phi$는 인코더(추론 네트워크)의 학습 가능한 파라미터이다.
인코더 $q_\phi(z \mid x)$는 입력 데이터 $x$로부터 잠재변수 $z$를 추정하고,
디코더 $p_\theta(x \mid z)$는 잠재변수 $z$로부터 데이터를 복원 또는 생성한다.
이렇게 두 확률 모델이 짝을 이루어 작동한다.
사전분포 $p_\theta(z)$는 보통 표준정규분포 $\mathcal{N}(0, I)$ 로 설정한다.
이는 계산을 단순하게 하고, 잠재공간의 구조를 일정하게 유지시킨다.
결국 인코더와 디코더의 파라미터 $\phi, \theta$를 조정하여
ELBO를 최대화하는 것이 VAE의 학습 과정이다.
이는 곧 잠재변수 분포 추정과 데이터 생성 과정 학습을
동시에 수행하는 절차이다.

p21. 변분 오토인코더(Variational Autoencoder)

강의 내용
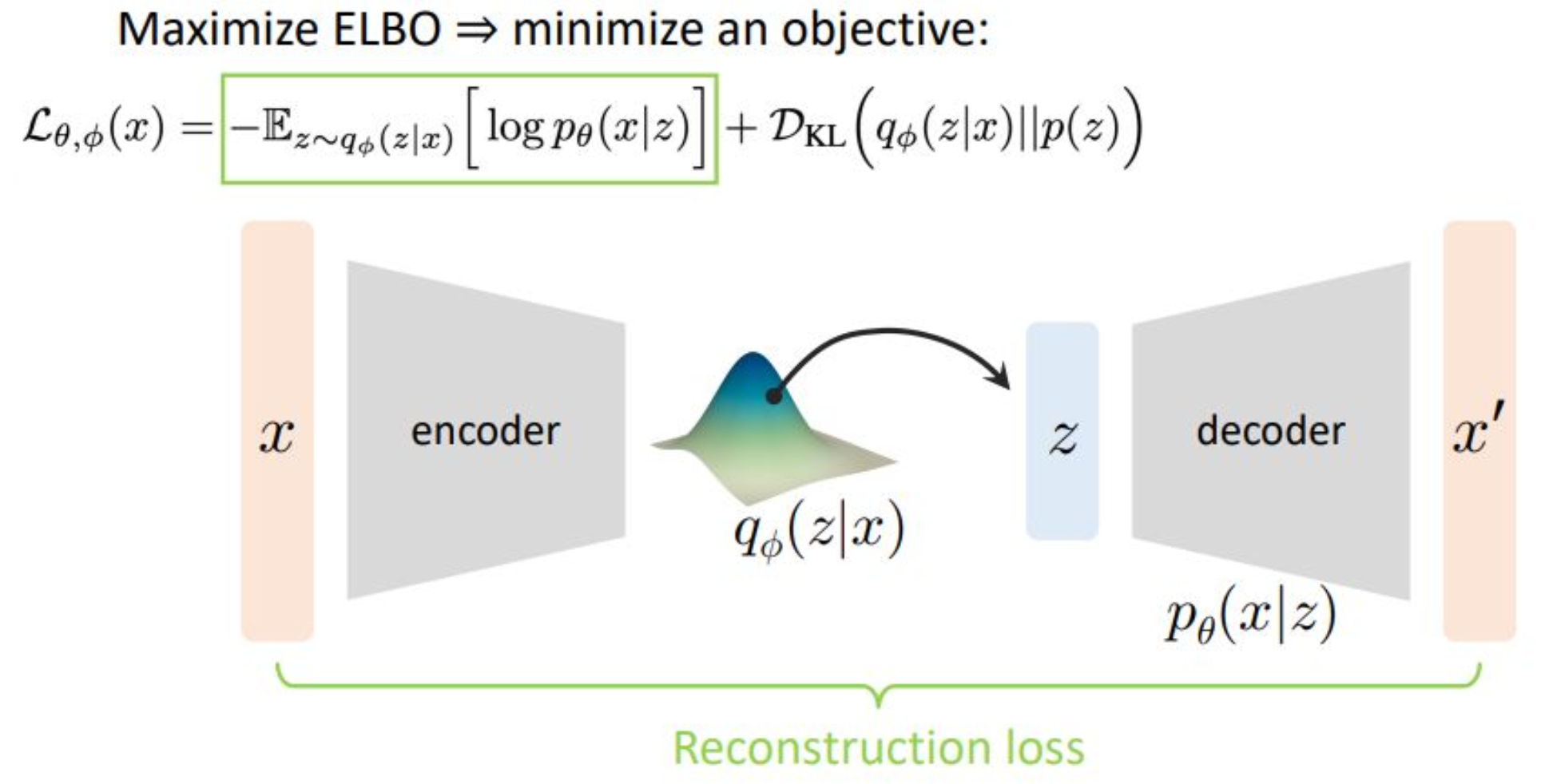
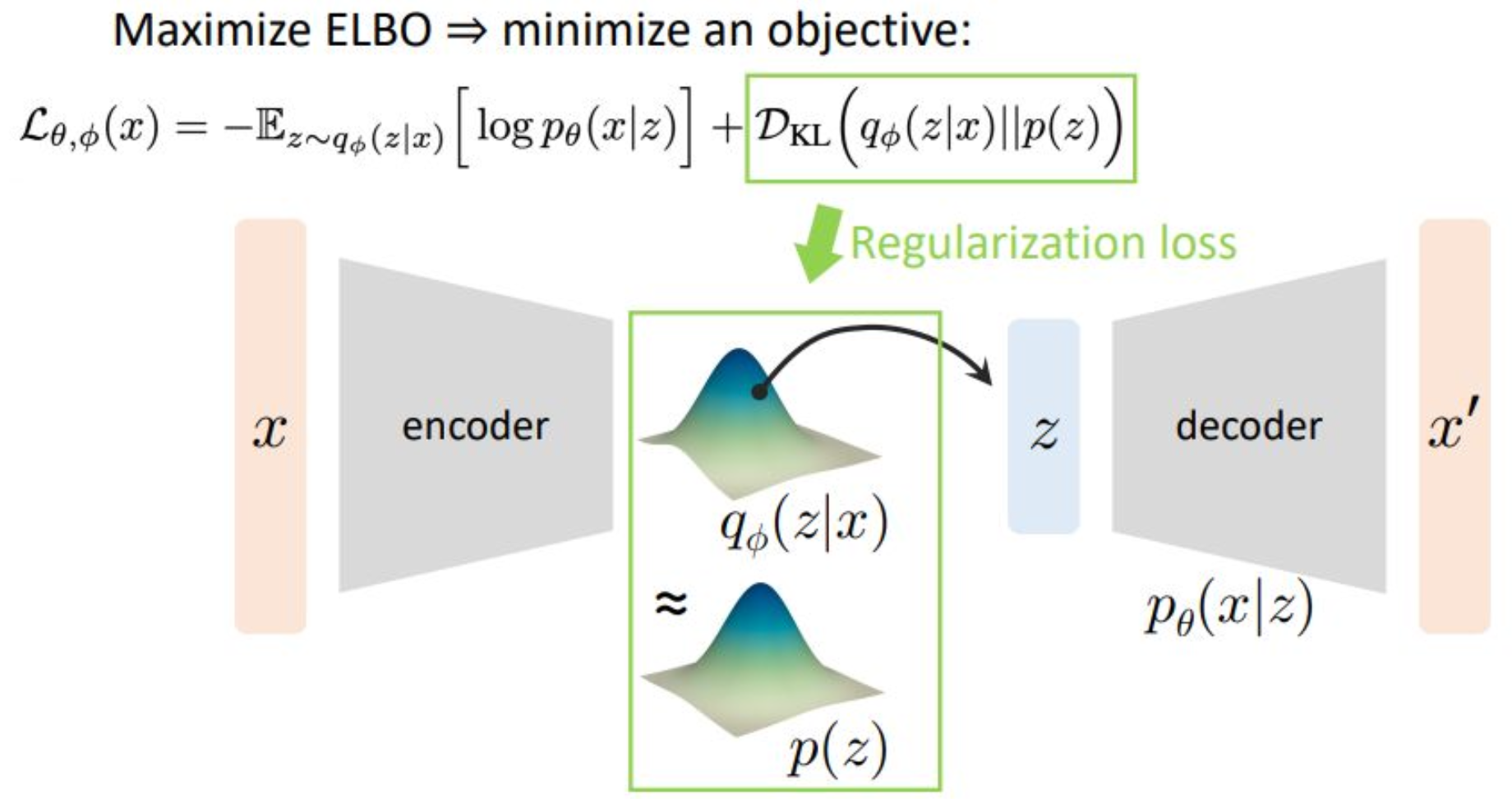
이렇게 여러 테크닉을 적용해 식을 가공하면
ELBO의 변형된 동치 형태가 나오게 됩니다.
이를 해석하기 위해서는
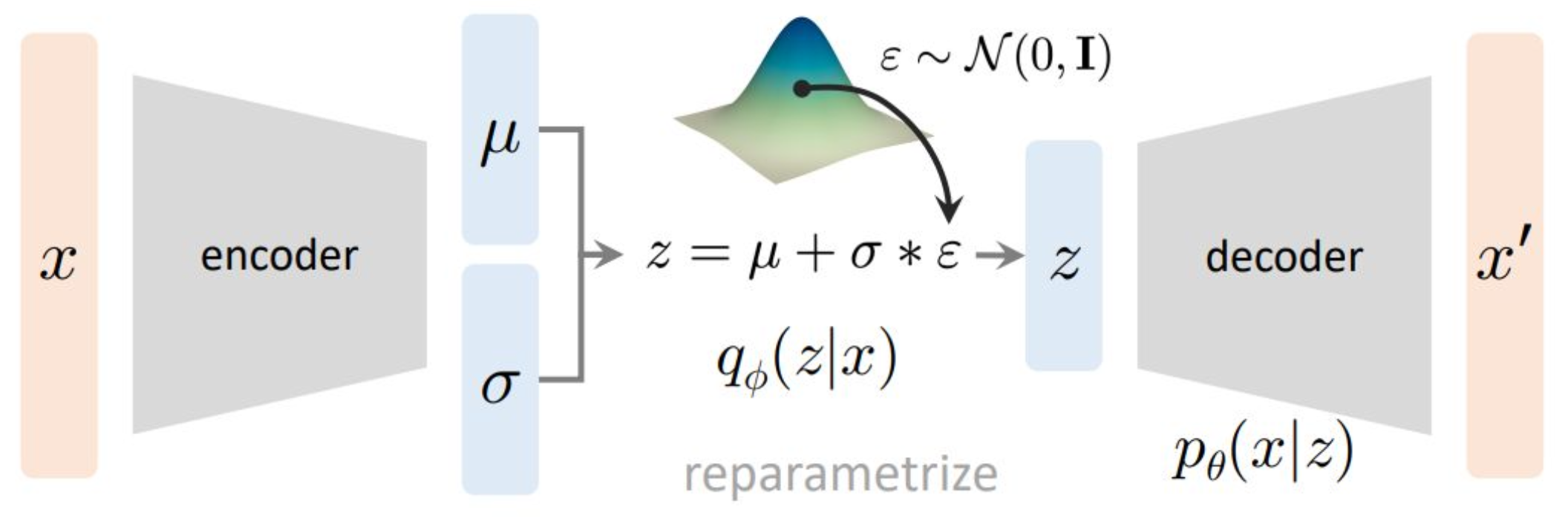
아래 파이프라인을 함께 보아야 합니다.
이것이 바로 VAE의 전체 파이프라인이라고 생각하시면 됩니다.
뒤쪽에 표시된 $z$, 디코더, 그리고 $x’$은
앞에서 제네레이터로 설명했던 파이프라인의 뒷부분에 해당합니다.
즉, 이것은 전체 구조의 반쪽입니다.
VAE가 독특한 이유는
여기에 앞부분의 반쪽, 즉 인코더가 추가된다는 점입니다.
이제 수학적 내용을 잠시 뒤로 미루고
동작 원리에 대해 먼저 살펴보겠습니다.
VAE는 $x$를 인코더 구조를 통해
중간의 분포 $q_{\phi}(z \mid x)$에 매핑시킵니다.
이것이 인코딩 과정입니다.
인코딩은 정보를 압축하는 과정이며
디코딩은 그 정보를 다시 복원하는 과정입니다.
이러한 인코더-디코더 구조는
통신 이론에서도 근본적인 개념이며
VAE에서도 같은 철학을 공유합니다.
따라서 원본 이미지 $x$를
인코더를 거쳐
파라미터화된 분포 $q_{\phi}(z \mid x)$로 매핑하고
(뒤에서 보겠지만 보통 Gaussian 분포입니다)
그 분포로부터 $z$라는 latent variable을 샘플링합니다.
이 $z$가
앞에서 생성 모델 파이프라인에서 보았던
제네레이터의 입력 $z$가 됩니다.
여기서 $p_{\theta}$를 $p$로 바꾼다는 의미도
바로 이것과 연결됩니다.
이렇게 샘플링된 $z$를
디코더에 입력하여
$x’$이라는 재구성된 데이터를 출력하게 됩니다.
그러면 원본 데이터 $x$가
인코더와 디코더를 거쳐
$x’$이라는 새로운 형태로 다시 생성되는데
이 둘의 차이를 줄이는 것이 매우 중요합니다.
그래서 $x$와 $x’$의 모양을
최대한 같게 만들기 위한
reconstruction loss를 정의합니다.
이것이 VAE에서 첫 번째로 중요한 항이며
초록색 박스로 표시된 영역이
바로 reconstruction loss의 rationale을 설명하는 부분입니다.
수식을 보면
$x$가 입력되어
$q_{\phi}(z \mid x)$가 $z$를 출력하고
다시 그 $z$가
$\log p_{\theta}(x \mid z)$를 통해
$x’$로 복원됩니다.
즉 이 파이프라인은
인코딩과 디코딩을 연결하는
수학적 구조를 그대로 반영하고 있습니다.

보충 자료
인코더 $q_\phi(z \mid x)$는 입력 데이터 $x$를 받아
잠재변수 $z$의 분포를 추정하는 역할을 한다.
일반적으로 이 분포는 가우시안(정규분포) 형태로 가정된다.
디코더 $p_\theta(x \mid z)$는 샘플링된 $z$로부터
원래의 입력 $x$를 재구성하도록 학습된다.
즉, 인코더가 정보를 요약하고,
디코더가 그 정보를 바탕으로 데이터를 복원하는 구조이다.
전체 손실 함수는 두 부분으로 구성된다.
(1) $-\mathbb{E}_{z \sim q_\phi(z \mid x)}[\log p_\theta(x \mid z)]$
재구성 손실로서, 입력 $x$와 복원된 $x’$의 차이를 최소화한다.
(2) $D_{\mathrm{KL}}(q_\phi(z \mid x)\,|\,p_\theta(z))$
정칙화 항으로서, 인코더가 추정한 분포가
사전분포 $p_\theta(z)$(보통 $\mathcal{N}(0, I)$)와
유사하도록 만드는 역할을 한다.
이 두 항의 균형을 조정함으로써
VAE는 잠재공간을 구조적으로 유지하면서
새로운 데이터를 생성할 수 있는 능력을 갖추게 된다.
이러한 구조는 생성 모델로서뿐 아니라
이상치 탐지(Anomaly Detection)와 같은 응용에서도 널리 활용된다.
학습된 모델은 정상 데이터의 잠재공간을 학습하므로,
재구성 오차가 큰 데이터는 이상치로 판별된다.

p22. 변분 오토인코더(Variational Autoencoder)

강의 내용
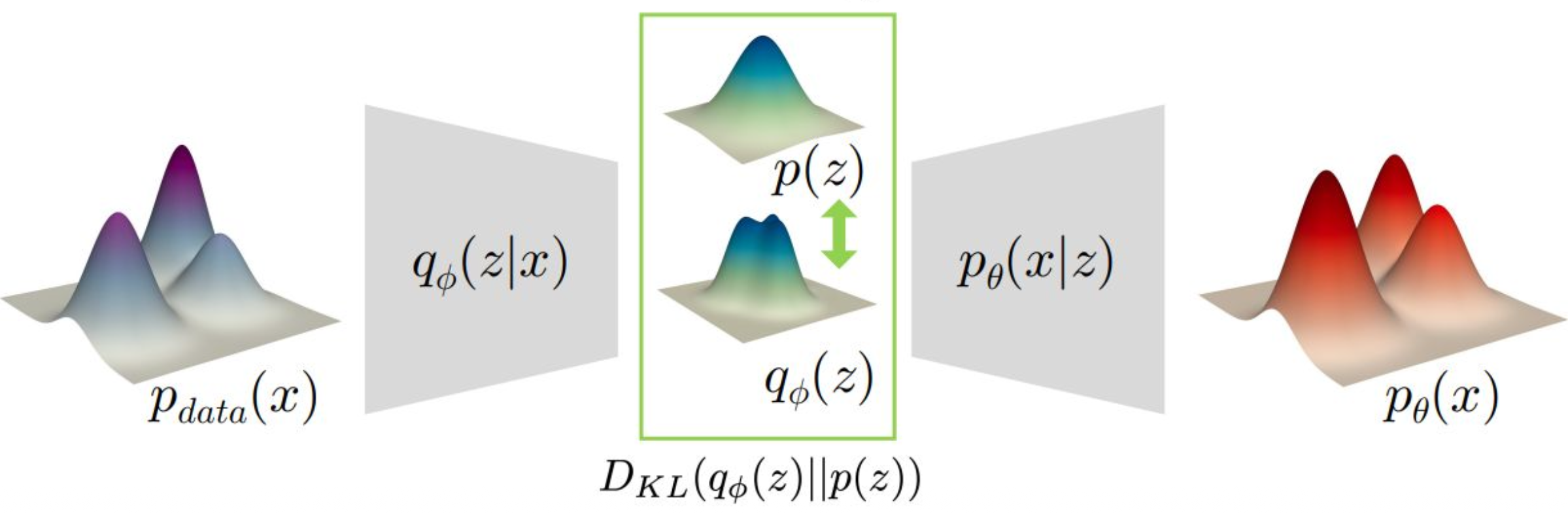
이제 두 번째 term은
regularization loss입니다.
우리가 $q_{\phi}$를
뉴럴 네트워크로 파라미터라이즈하여 모델링한다고 했는데
이 분포의 모양이 제대로 컨트롤되지 않으면
$z$를 안정적으로 샘플링할 수 없습니다.
하지만 $z$를 샘플링해야만
인코더–디코더 구조를 통해
$x’$을 생성할 수 있기 때문에
$p(z)$는 Gaussian 분포처럼
알고 있는 간단한 분포로 설정하고
KL divergence를 통해
$q_{\phi}(z \mid x)$와 $p(z)$의 거리를
줄이도록 학습합니다.
이 KL divergence가 0에 가까워지면
$q_{\phi}(z \mid x)$가
Gaussian Random Variable과 거의 동일해지므로
단순히 Gaussian에서 샘플링하면
제네레이터가 잘 동작하게 됩니다.
이런 의미에서
$q_{\phi}$의 모양을 컨트롤하기 위한 term이
regularization loss이며
이것이 두 번째 loss 항입니다.
결국 첫 번째 loss(재구성 손실)와
두 번째 loss(정규화 손실)를
함께 고려해 학습하는 것이
VAE 전체의 학습 파이프라인입니다.
이 모든 구조는
latent variable 모델링에서 비롯된 것입니다.
이 흐름을 보면
VAE가 직관적으로 조금 더 이해될 것입니다.
$\log p_{\theta}(x)$를 직접 계산할 수 없기 때문에
여러 단계의 우회적인 방법을 사용했지만
결국 이러한 구조를 통해
그 목표를 달성하려는 것이
VAE의 철학입니다.
Diffusion Model, Latent Variable Model,
Normalizing Flow Model도
모두 비슷한 철학을 공유하지만
접근 방식은 서로 다릅니다.
따라서 이 큰 파이프라인을
반드시 이해하고 넘어가는 것이 중요합니다.
(수학적 디테일을 모두 몰라도 괜찮습니다.)
$x$가 인코더를 통해
latent variable로 매핑되고
다시 디코더를 통해 복원되는 구조,
이 흐름을 이해하고 있어야
실제 코드를 볼 때
“아, 이 부분이 인코더였구나”
“이 부분이 디코더였구나” 하고
바로 연결 지을 수 있습니다.
이런 구조적 이해는
앞으로 직접 코딩을 진행하면서
자연스럽게 더 깊게 이해될 것입니다.

보충 자료
위 식은 ELBO를 최대화하는 대신, 동등하게 손실을 최소화하는 형태로 표현된 것이다.
왼쪽 항은 재구성 손실(reconstruction loss),
오른쪽 항은 정칙화 손실(regularization loss)에 대응한다.
인코더 $q_\phi(z \mid x)$는 입력 데이터 $x$를
잠재공간(latent space) 상의 확률분포로 압축하여 표현한다.
여기서 $\phi$는 인코더의 학습 파라미터이며,
인코더는 $q_\phi(z \mid x)$가 사전분포(prior) $p(z)$에
가깝도록 학습된다.
사전분포 $p(z)$는 일반적으로
가우시안 분포 $\mathcal{N}(0, I)$로 설정된다.
이렇게 단순한 분포를 prior로 두는 이유는
잠재공간이 구조적으로 안정적이고,
샘플링이 쉬운 공간이 되도록 만들기 위함이다.
정칙화 항 $D_{\mathrm{KL}}(q_\phi(z \mid x)\,|\,p(z))$은
인코더가 만든 분포 $q_\phi(z \mid x)$가
$\mathcal{N}(0, I)$와 멀어지지 않도록 제한하는 제약 조건이다.
이 값이 작아질수록 잠재분포는
표준정규분포에 더 잘 정렬된다.
디코더 $p_\theta(x \mid z)$는 잠재변수 $z$로부터
원래 입력 $x$를 재구성하는 역할을 한다.
여기서 $\theta$는 디코더의 학습 파라미터이며,
학습의 목표는 입력 $x$와 재구성된 $x’$의 차이를
최소화하는 것이다.
결국 VAE의 학습 과정은
(1) 데이터를 잘 재구성하는 능력과
(2) 잠재공간의 확률적 구조를 유지하는 능력
두 가지를 동시에 최적화하는 과정이라고 볼 수 있다.

p23. 첫 번째 항: 재구성 손실 (Reconstruction Loss)

예시: L2 손실 (L2 loss)

1단계 몬테카를로(Monte Carlo) 샘플링:
$z \sim q_\phi(z \mid x)$
디코더 네트워크에 의한 매핑:
$g_\theta(z) \rightarrow x’$
(network estimates distribution’s parameters)
가우시안 분포로 모델링:
$p_\theta(x \mid z) = \mathcal{N}(x \mid x’, \sigma_0^2 I)$
(assume fixed std)
음의 로그우도(negative log-likelihood):
\[-\log p_\theta(x \mid z) = \frac{1}{2\sigma_0^2}\|x - x'\|^2 + \text{const}\]
L2 손실은 데이터 포인트 $x$ 주변의
가우시안 근방(Gaussian neighborhood)을 의미함

강의 내용
Reconstruction Loss에 대해
디테일한 수식 설명은 생략하겠지만
핵심 개념만 정리해보겠습니다.
Reconstruction이라는 것은
구조적으로 입력과 출력이
최대한 같게 만들어지는 것을 의미합니다.
이를 위해 가장 널리 사용되는 메트릭이
L2 Loss, 즉 유클리디언 거리입니다.
Negative Log-likelihood를 전개해보면
결국 입력 $x$와
디코더에서 생성된 출력 $x’$ 사이의
유클리디언 거리를 취하고
이를 $\sigma_0$라는 스케일 파라미터를 통해
조절하는 형태로 표현됩니다.
즉, Reconstruction Loss란
입력 $x$와
인코더·디코더 파이프라인을 거쳐
찰흙처럼 빚어진 출력 $x’$ 사이의 거리입니다.
이 값이 0이라면
입력과 출력의 모양이 완전히 동일하다는 의미가 됩니다.
이것이 Reconstruction Loss의 기본 구조이며
이 항을 먼저 정의한 뒤
그 다음에 Regularization 항을 결합하여
전체 VAE objective를 구성하게 됩니다.

보충 자료
1. 몬테카를로 샘플링 (Monte Carlo Sampling)
기댓값
\[\mathbb{E}_{z \sim q_\phi(z \mid x)}[\log p_\theta(x \mid z)]\]
은 잠재변수 $z$ 에 대한 적분 형태로 표현되며 해석적으로 계산하기 어렵다.
따라서 $q_\phi(z \mid x)$ 에서 샘플링한 $z$ 들을 이용해
$\log p_\theta(x \mid z)$ 값을 평균하여 근사한다.
이를 몬테카를로 근사(Monte Carlo approximation) 라고 한다.
샘플링 과정은 재매개변수화 기법(Reparameterization trick) 으로
미분 가능하게 만들어, 인코더와 디코더 모두를 역전파로 학습할 수 있다.
2. 디코더 매핑 $g_\theta(z) \rightarrow x’$
디코더 $g_\theta$ 는 잠재변수 $z$ 를 입력받아 생성 데이터의 평균값 $x’$ 을 출력한다.
디코더는 단순 복원 함수가 아니라
확률분포 $p_\theta(x \mid z)$ 의 모수(parameter)를 추정하는 함수 로 해석된다.
가장 단순한 경우 디코더는 평균만 출력한다고 두며,
\[x'=\mu_\theta(z)\]
분산은 고정 상수 $\sigma_0^2$ 로 둔다.
즉, 디코더는 “데이터가 존재할 법한 중심(mean)”을 학습한다.
따라서 디코더는 확률적 생성 모델의 평균 함수(mean function) 이다.
3. 가우시안 분포로 모델링하는 이유
실제 데이터는 노이즈와 불확실성을 포함하므로 $x$ 와 $x’$ 를 완전히 일치시키기보다
$x$ 가 $x’$ 주변에서 나올 확률을 모델링하는 것이 타당하다.
VAE는 다음과 같이 가정한다.
\[p_\theta(x \mid z) = \mathcal{N}(x \mid x', \sigma_0^2 I)\]
여기서
$x’=g_\theta(z)$ : 평균
$\sigma_0^2 I$ : 분산
$x$ : 관측값
이는 “데이터는 평균 $x’$ 를 중심으로 정규분포 형태에 따라 생성된다”는
확률적 가정을 의미한다.
이 가정 덕분에 모델은 불확실성을 표현할 수 있고,
로그우도(log-likelihood)가 닫힌형(closed form) 으로 계산 가능해진다.
4. 재구성 손실이 L2 손실이 되는 이유
가우시안 가정하에서 로그 가능도는
\[\log p_\theta(x \mid z) = -\frac{1}{2\sigma_0^2}\|x-x'\|^2 -\frac{d}{2}\log(2\pi\sigma_0^2)\]
로 전개된다.
따라서 음의 로그 가능도는
\[-\log p_\theta(x \mid z) = \frac{1}{2\sigma_0^2}\|x-x'\|^2 + \text{const}\]
이 되며, 이는 L2 손실(Mean Squared Error) 과 동일한 형태이다.
즉, 디코더가 출력하는 평균 $x’$ 을 기준으로 데이터 $x$ 를 설명하는 과정이
곧 L2 거리 최소화와 같다.
5. 전체적 관계 요약
$x$: 관측 데이터
$z$: 인코더가 샘플링한 잠재변수
$x’=g_\theta(z)$: 디코더가 추정한 평균
\[p_\theta(x \mid z) = \mathcal{N}(x \mid x', \sigma_0^2 I)\]
: 관측 $x$ 는 평균 $x’$ 중심의 정규분포에서 샘플링된 것으로 해석
재구성 손실 최소화는
“실제 데이터 $x$” 와 “디코더 평균 $x’$” 사이의 거리를 줄이는 것과 같다.

p24. 두 번째 항: 정규화 손실 (Regularization Loss)

예시: 가우시안 사전분포 (Gaussian prior)

$p(z) = \mathcal{N}(z \mid 0, I)$ 로 둔다.
$q_\phi(z \mid x)$ 를 가우시안으로 모델링한다:
$q_\phi(z \mid x) = \mathcal{N}(z \mid \mu, \sigma)$
인코더 네트워크에 의한 매핑:
$f_\phi(x) \rightarrow (\mu, \sigma)$
(network estimates distribution’s parameters)
손실을 분석적으로 계산한다:
\[D_{\mathrm{KL}}\big(\mathcal{N}(z \mid \mu, \sigma)\,\|\,\mathcal{N}(z \mid 0, I)\big)\]
공분산을 고정한 경우:
fixed covariance → $\mu$ 에 대한 L2 손실

강의 내용
Regularization 항도 디테일한 전개는 생략하고
핵심만 정리해보겠습니다.
Neural Network는
$q_{\phi}$의 분포 파라미터인
$\mu$와 $\sigma$를 출력하게 됩니다.
$q_{\phi}$는 Gaussian Distribution이라고 가정하며
그 파라미터가 뉴럴 네트워크에서 생성되는 구조입니다.
반면 $p(z)$는
앞에서 설명한 것처럼
Standard Gaussian Distribution으로 설정합니다.
이렇게 서로 다른 Gaussian 분포 간의
KL Divergence를 계산하면
closed-form(명시적) 해가 존재합니다.
실제로 계산해보면
L2 형태와 유사한 구조가 나타나는데
이러한 형태는
이후 코드 실습에서 직접 확인할 수 있을 것입니다.

보충 자료
1. 정규화 항의 역할
정규화 손실 $D_{\mathrm{KL}}(q_\phi(z \mid x)\,|\,p(z))$ 은
인코더가 학습한 잠재 분포 $q_\phi(z \mid x)$ 이
사전 분포 $p(z)$ (보통 표준 정규분포 $\mathcal{N}(0, I)$) 와
얼마나 다른지를 측정한다.
이 항은 잠재공간이 지나치게 왜곡되지 않도록 제약을 주며,
특정 데이터에 과도하게 맞춰진 잠재표현을 방지하여
일관된 잠재 구조를 유지하게 만든다.
2. KL 발산의 계산 방식
두 가우시안 분포 사이의 KL 발산은 닫힌형(closed-form)으로 계산된다.
\[D_{\mathrm{KL}}\!\big(\mathcal{N}(\mu,\sigma^2)\,\|\,\mathcal{N}(0,1)\big) =\frac{1}{2}(\mu^2+\sigma^2-\log\sigma^2-1)\]
이 표현은 VAE 학습에서 매우 효율적으로 사용되며,
손실을 직접 계산해 최적화할 수 있게 한다.
3. 공분산 고정 시 L2 손실과의 관계
공분산 $\sigma^2$ 를 고정하면 KL 항은
$\mu^2$ 에 비례하는 형태가 된다.
\[D_{\mathrm{KL}} \propto \|\mu\|^2\]
즉, KL 항은 잠재변수 평균 $\mu$ 에 대한
L2 정규화(L2 penalty) 처럼 동작한다.
이는 잠재벡터가 사전분포의 중심(0 근처)에 있도록
압박하는 효과를 낸다.
4. 직관적 해석
인코더는 입력 $x$ 에 따라 $\mu$ 와 $\sigma$ 를 출력한다.
KL 항은 “너무 특이한” 잠재벡터를 생성하지 않도록 억제하며,
전체 잠재공간이 사전분포 $p(z)$ 와 유사한 모양을 유지하게 만든다.
그 결과, 학습이 끝난 후 임의의 $z \sim p(z)$ 를 샘플링해도
자연스럽고 일관된 생성 결과를 얻을 수 있게 된다.

p25. 역전파는 어떻게 이루어질까? (Backpropagation?)

보충 자료
1. 인코더와 샘플링의 관계
인코더는 입력 $x$ 로부터 잠재 변수의 분포 $q_\phi(z \mid x)$ 를 학습한다.
평균 $\mu_\phi(x)$ 와 표준편차 $\sigma_\phi(x)$ 를 추정하여 확률적으로 $z$ 를 샘플링하고,
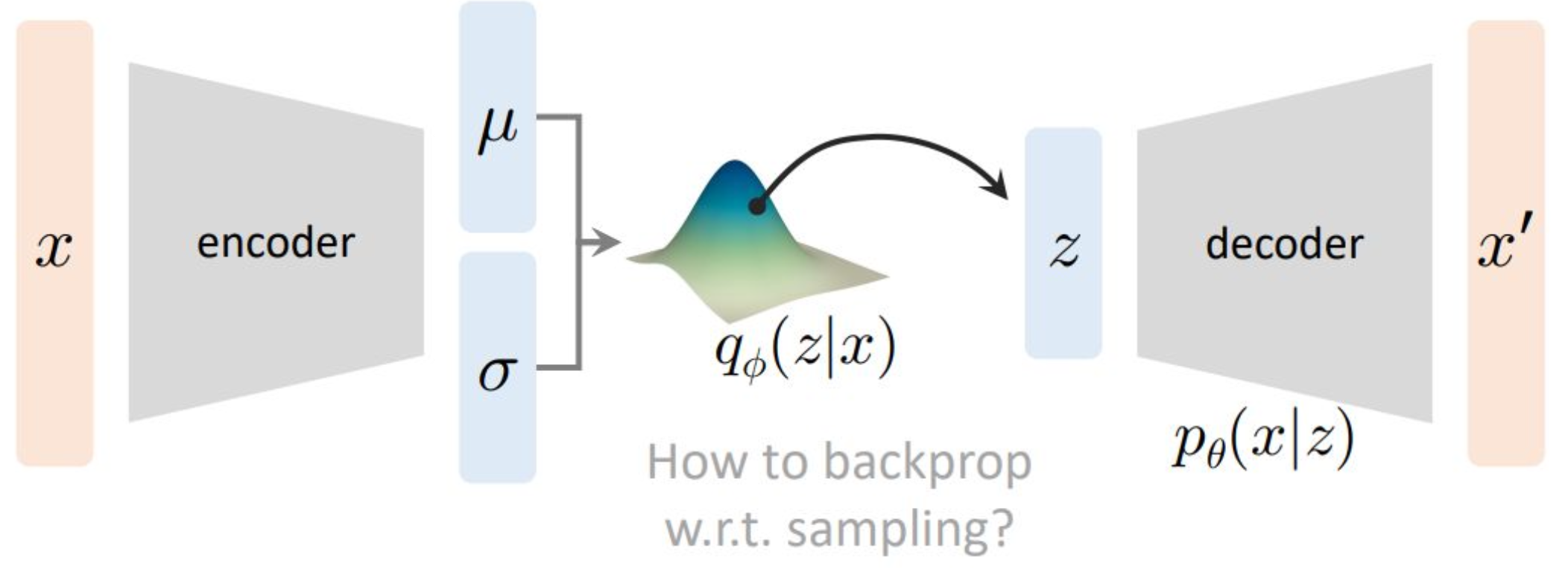
샘플링된 $z$ 는 디코더 $p_\theta(x \mid z)$ 로 전달되어 재구성된 출력 $x’$ 를 생성한다.
2. 역전파의 문제점
샘플링 과정은 확률적이므로
\[z \sim q_\phi(z \mid x)\]
와 같이 난수에 의해 결정된다.
이 연산은 비결정적이며 미분 불가능하므로,
역전파는 $z$ 에서 인코더 파라미터 $\phi$ 로 기울기를 전달할 수 없다.
즉, 샘플링 순간에 역전파 경로가 끊긴다.
3. 직관적 비유
인코더는 분포의 모양(평균·분산)을 제시하고,
샘플링은 그 분포에서 주사위를 던지는 과정이다.
주사위의 결과값 $z$ 에 대해 $\mu$ 또는 $\sigma$ 로 직접 미분할 수 없기 때문에
일반적인 역전파 규칙을 적용할 수 없다.
4. 해결책의 방향
이를 해결하기 위해 재매개변수화 기법(Reparameterization Trick)을 사용한다.
이 방법은 확률적 샘플링 과정을 결정적 함수 형태로 다시 표현하여
미분이 가능하도록 만들어, 끊겼던 역전파 경로를 복원해 준다.

p26. 재매개변수화 (Reparameterization)

가우시안 매개변수들은 신경망의 출력값에 의해 매개변수화되어(parameterized),
중간 조건부 분포들(intermediate conditional distributions)을 근사하기 위해 사용된다!

보충 자료
1. 재매개변수화의 핵심 아이디어
확률적 샘플링 $z \sim q_\phi(z \mid x)$ 은 미분 불가능하여 역전파가 단절된다.
재매개변수화 기법(Reparameterization Trick)은 이 확률적 과정을
결정적(deterministic) 함수로 변환하여 미분 가능하게 만든다.
즉, 잠재 변수 $z$ 를 직접 샘플링하지 않고,
표준 정규분포에서 샘플링한 잡음 $\varepsilon$ 을 이용해 다음과 같이 계산한다:
\[z = \mu_\phi(x) + \sigma_\phi(x)\,\varepsilon, \qquad \varepsilon \sim \mathcal{N}(0, I)\]
2. 수식의 의미
$\varepsilon$ 은 고정된 분포 $\mathcal{N}(0, I)$ 에서만 샘플링되므로
랜덤성은 $\varepsilon$ 에만 존재한다.
반면 $\mu_\phi(x)$, $\sigma_\phi(x)$ 는 결정적 함수이므로
$z$ 는 $\phi$ 에 대해 미분 가능한 형태가 된다.
따라서 역전파를 통해 인코더 파라미터 $\phi$ 까지 기울기가 전달된다.
이로써 샘플링 단계가 신경망의 연산 그래프에 포함된다.
3. 직관적 이해
원래는 “분포로부터 직접 샘플링”했지만,
이제는 “고정된 분포에서 노이즈를 샘플링하고
그 노이즈를 평균과 분산으로 변환하는 과정”으로 바뀐 것이다.
즉, 확률적 샘플링을
노이즈를 입력으로 받는 결정적 함수로 바꾸어
학습 가능한 형태로 만든다.
4. 전체 구조의 연결
인코더는 입력 $x$ 로부터 $(\mu, \sigma)$ 를 출력하고,
표준 가우시안 잡음 $\varepsilon$ 을 사용해
$z = \mu + \sigma \varepsilon$ 을 계산한다.
디코더는 이 $z$ 를 입력받아 $p_\theta(x \mid z)$ 를 통해 데이터를 재구성한다.
이 구조를 통해 확률적 생성 모델이
전부 미분 가능한 신경망 형태로 구현된다.

p27. 변분 오토인코더 (Variational Autoencoder)

지금까지는 하나의 $x$ 에 대한 목적함수를 논의해왔다:

전체 손실(overall loss)은
데이터 분포에 대한 기대값으로 표현된다:

보충 자료
1. 단일 데이터 샘플 $x$ 에 대한 손실
위의 첫 번째 식은 단일 입력 샘플 $x$ 에 대한 손실 함수 $\mathcal{L}_{\theta,\phi}(x)$ 를 정의한 것이다.
첫 번째 항
\[-\mathbb{E}_{z \sim q_\phi(z \mid x)}[\log p_\theta(x \mid z)]\]
은 재구성 손실(Reconstruction Loss)로, 디코더가 입력 $x$ 를 얼마나 잘 복원하는지 측정한다.
두 번째 항 $D_{\mathrm{KL}}(q_\phi(z \mid x)\,|\,p(z))$ 은 정규화 손실(Regularization Loss)로,
인코더가 생성한 잠재공간 분포 $q_\phi(z \mid x)$ 가 사전분포 $p(z)$ 와 얼마나 다른지를 측정한다.
2. 전체 데이터셋에 대한 손실
실제 학습에서는 한 개의 샘플이 아니라 데이터셋 전체에 대해 평균 손실을 계산한다.
손실 함수는 데이터 분포 $p_{\text{data}}(x)$ 에 대한 기대값으로 확장되며
\[\mathbb{E}_{x \sim p_{\text{data}}(x)}[\mathcal{L}_{\theta,\phi}(x)]\]
으로 표현된다.
이 기대값은 실질적으로는 미니배치 평균(mini-batch mean)으로 근사되어 학습 중에 최적화된다.
3. 전체 목적함수의 의미
최종 손실 $\mathcal{L}_{\theta,\phi}$ 는
데이터 복원 성능과 잠재공간의 규칙성 사이의 균형을 조절하는 역할을 한다.
즉, 인코더가 잠재공간에서 의미 있는 구조를 학습하도록 하면서
디코더가 입력을 잘 복원할 수 있도록 두 항을 함께 최소화하는 것이 VAE 학습의 핵심이다.

p28. 추론 (Inference)

추론 (생성):

잠재 변수 $z$ 를 다음 분포에서 샘플링함:
\[z \sim \mathcal{N}(0, I)\]
디코더 네트워크에 의해 $z$ 를 매핑함:
\[g_\theta(z)\]

디코더(Decoder)는 한 분포에서 다른 분포로의 결정적 매핑(deterministic mapping)이다.

보충 자료
1. 추론(생성)의 단계
학습이 완료된 후에는 인코더는 사용하지 않는다.
잠재공간에서 직접 $z \sim \mathcal{N}(0, I)$ 를 샘플링한다.
이는 학습 과정의 KL 발산 항이 $q_\phi(z \mid x)$ 를 $p(z)$ 와 유사하게 만들도록
인코더를 학습시켰기 때문에 가능하다.
따라서 학습이 끝난 뒤 $p(z)$ 에서 샘플링하는 것은
실제 데이터 공간에서 의미 있는 위치를 선택하는 것과 같다.
이렇게 얻은 $z$ 를 디코더 $g_\theta(z)$ 에 입력하면
새로운 샘플을 생성할 수 있다.
2. 학습 전과 학습 후의 차이
학습 전에는 $\mathcal{N}(0, I)$ 가 단순한 랜덤 노이즈일 뿐이며
그 안의 점들은 의미가 없다.
학습 후에는 인코더 $q_\phi(z \mid x)$ 가 데이터를 잠재공간으로
의미 있게 매핑하고, KL 발산 항이 이 공간을 정규분포 형태로 정렬한다.
그 결과 $\mathcal{N}(0, I)$ 상의 점들은 실제 데이터의
의미적 표현을 반영하는 좌표가 된다.
즉, 학습 전에는 의미 없던 점들이
학습 후에는 데이터 구조를 보존하는 의미 있는 코드가 된다.
3. 디코더의 역할
디코더는 결정적 함수로, $z$ 를 입력받아
$p_\theta(x \mid z)$ 혹은 그 평균을 생성한다.
같은 $z$ 에 대해 같은 출력이 생성되지만,
$z$ 자체가 확률적으로 샘플링되므로
전체 모델은 확률적 생성 모델 성격을 유지한다.
4. 요약
학습 중에는 인코더·디코더가 함께 작동하여
데이터 구조를 정규분포 형태의 잠재공간으로 매핑한다.
학습이 끝난 뒤에는 $\mathcal{N}(0,I)$ 자체가 의미 있는 잠재공간이 되므로
인코더 없이 디코더만으로 새로운 샘플을 생성할 수 있다.

p29. 개요 (Overview)

인코더(encoder): 데이터 분포를 잠재 분포로 매핑함
디코더(decoder): 잠재 분포를 데이터 분포로 매핑함

강의 내용
지금 보면 Neural Network가 두 개 존재합니다.
하나는 $\theta$라는 파라미터를 가진 Neural Network,
즉 디코더이고,
다른 하나는 $\phi$라는 파라미터를 가진
인코더 Neural Network입니다.
디코더($\theta$)는
$z$라는 Random Variable을 입력받아
원본 데이터를 복원하는 역할을 합니다.
인코더($\phi$)는
$p(z)$를 근사하기 위해
Gaussian 분포의 파라미터를 생성하는
Neural Network입니다.
이렇게 두 개의 Neural Network를 구성해
동시에 학습시키는 것이
VAE의 기본 학습 과정입니다.
그런데 GAN과 마찬가지로
VAE에도 치명적인 단점이 존재합니다.
Neural Network가 두 개라는 점에서
“왜 굳이 두 개여야 할까?”
라는 질문이 생길 수 있습니다.
비즈니스 관점, 산업 관점에서 보면
모델이 하나일 때와 두 개일 때의
시스템 규모는 크게 달라집니다.
모델이 두 개라는 것은
Complexity가 두 배가 된다는 말이며
인프라도 두 배의 비용이 요구된다는 의미입니다.
즉 같은 양의 데이터를 처리하는 데
두 배의 자원이 필요하게 되고
이는 실무적으로 비효율적입니다.
이러한 이유 때문에
VAE는 현대의 생성 모델 분야에서
잘 사용되지 않는 편입니다.
게다가 파라미터 수도 많고
두 개의 네트워크를 동시에 학습시켜야 하지만
그럼에도 GAN이나 Diffusion 모델 대비
출력 품질이 크게 우수하지 않습니다.
그러나 VAE가 가진 장점도 존재합니다.
GAN은 latent space $z$나
$q_\phi$와 같은 분포 자체를 설계하거나
다루기가 매우 어렵습니다.
반면 VAE는 분포 구조가 명확하고
이를 활용해 anomaly detection에
매우 효과적으로 사용할 수 있습니다.
이를 예로 설명해 보면,
입력이 $x$가 아니라 새로운 $y$라고 가정합니다.
$y$를 인코더에 넣어
latent space로 매핑한 뒤
디코더를 통과시키면
$y’$가 생성됩니다.
이제 $y$와 $y’$의 distortion(차이)을 측정하면
해당 데이터가
훈련 데이터 분포에 속하는지,
즉 정상인지 비정상인지 판단할 수 있습니다.
수학적으로도 이유가 명확합니다.
우리는 학습 과정에서
$x$와 $x’$의 거리가 0에 가까워지도록
reconstruction loss를 최소화했습니다.
그러나 학습 데이터에 없는
새로운 데이터 $y$가 들어오면
$y’$이 $y$와 비슷하게 복원된다는
보장은 없습니다.
이 “차이”가 anomaly를 나타내는 것입니다.
그래서 제조업·품질 검사·센서 기반 모니터링 등
여러 실무 환경에서
VAE 구조가 anomaly detection에
널리 응용됩니다.
반면 inference 단계에서는
두 개의 Neural Network가 모두 필요한 것이 아닙니다.
학습 시에는 인코더와 디코더가 모두 필요하지만
실제로 샘플링할 때는
디코더 $p_\theta$만 사용합니다.
인코더 파트는
학습 후에는 통째로 버려지는 구조입니다.
즉 inference 단계에서는
Gaussian Random Variable을 샘플링하여
디코더에만 넣어주면 됩니다.
이러한 점도
VAE의 비효율적인 구조를 보여주는 부분입니다.
그렇지만 VAE는
latent space가 잘 정리되어 있다는 장점 때문에
many-to-many 매칭이 가능해지고
KL divergence 기반 매핑을 통해
다양한 데이터 구조를 표현할 수 있습니다.
마지막으로 전체 구조를
다시 수학적으로 정리해보면 다음과 같습니다.
$p_{\text{data}}(x)$라는
실제 데이터의 분포가 존재하고,
$x$는 인코더 $q_\phi(z \mid x)$를 통해
latent 분포 $q_\phi(z)$로 매핑되며
이는 Gaussian Random Variable로 모델링됩니다.
디코더 $p_\theta(x \mid z)$는
$z$를 입력받아
다시 원본 데이터 $x$를 복원하려고 합니다.
$p_\theta$에서 생성된 $x’$와
원본 $x$가
reconstruction loss를 통해
최대한 가깝도록 학습됩니다.
이것이 바로 VAE의 전체 흐름이며
오늘 강의의 주요 내용입니다.
인코더와 디코더가 어떤 역할을 하고
어떤 철학적 배경을 가지며
어디에 응용될 수 있는지
이런 부분들을 기억해두면
앞으로 코드를 보거나 모델을 설계할 때
큰 도움이 될 것입니다.

보충 자료
1. 전체 구조의 흐름
입력 데이터 $x$ 는 인코더 $q_\phi(z \mid x)$ 를 거쳐 잠재 변수 $z$ 의 확률분포로 변환된다.
이 분포는 데이터의 내재된 구조나 의미적 특성을 요약한 표현이다.
인코더를 통해 얻은 $z$ 는 잠재 공간에서의 점이며,
이 공간 전체가 표준 정규분포 $\mathcal{N}(0, I)$ 형태로 정렬되도록 학습된다.
이후 디코더 $p_\theta(x \mid z)$ 는 이 $z$ 로부터 원래 데이터 분포를 복원하여
$x’$ 를 생성하는 과정을 학습한다.
2. 인코더와 디코더의 관계
인코더는 데이터 분포 $p_{\text{data}}(x)$ 를 잠재 분포 $q_\phi(z)$ 로 압축하는 역할을 한다.
이는 고차원 데이터(이미지, 음성, 언어 등)를 의미적으로 요약된 표현으로 변환하는 과정이다.
디코더는 이 잠재 분포를 다시 데이터 분포 $p_\theta(x)$ 로 확장하여
원본 데이터에 가까운 샘플을 생성한다.
이 과정이 VAE가 생성 모델로 기능하는 핵심이다.
3. 학습의 목표
학습 과정에서 인코더와 디코더는 상호 보완적으로 최적화된다.
인코더는 $x \rightarrow z$, 디코더는 $z \rightarrow x’$ 를 수행하며
두 네트워크는 $p_{\text{data}}(x)$ 와 모델 분포 $p_\theta(x)$ 가
최대한 유사해지도록 동시에 학습된다.
4. 요약적 해석
인코더는 데이터 공간에서 잠재 공간으로의 압축(encoding)을 담당하고,
디코더는 잠재 공간에서 데이터 공간으로의 복원(decoding)을 담당한다.
결국 VAE는
데이터 ↔ 잠재 표현 ↔ 데이터
로 이어지는 양방향 확률적 매핑을 학습하는 모델이다.

p30. 변분 오토인코더 (Variational Autoencoder)

인코딩된 잠재 분포(encoded latent distribution):
\[q_\phi(z) = \int_x q_\phi(z \mid x) \, p_{\text{data}}(x) \, dx\]

보충 자료
1. 인코딩된 잠재 분포의 의미
$q_\phi(z)$ 는 전체 데이터 분포 $p_{\text{data}}(x)$ 에 대해
인코더가 생성한 잠재 변수 분포들의 평균적 형태를 나타낸다.
즉, 각 데이터 $x$ 가 인코더를 거쳐 $z$ 로 변환될 때
그 모든 $z$ 들이 형성하는 전역적 분포 구조를 의미한다.
이 관계는
\[q_\phi(z)=\mathbb{E}_{x \sim p_{\text{data}}(x)}[\,q_\phi(z \mid x)\,]\]
으로 표현되며, 인코더가 전체 데이터셋을 통해 형성한
잠재공간의 전역 구조를 나타낸다.
2. $p(z)$ 와 $q_\phi(z)$ 의 관계
$p(z)$ 는 사전에 정의한 단순한 분포(prior)로 보통 $\mathcal{N}(0, I)$ 이다.
이는 학습의 기준점 역할을 한다.
반면 $q_\phi(z)$ 는 실제 데이터에서 인코더가 추정한 복잡한 잠재 분포이다.
KL 발산 항 $D_{KL}(q_\phi(z)\,|\,p(z))$ 이 이를 최소화하도록 유도하여
학습이 진행될수록 $q_\phi(z)$ 가 $p(z)$ 와 유사해지도록 만든다.
따라서 이 KL 항은 잠재공간을 정규화하는 정규화 제약이다.
3. 전체 흐름의 의미
1) 데이터 분포 $p_{\text{data}}(x)$ 에서 샘플된 $x$ 가
인코더를 통해 $q_\phi(z \mid x)$ 로 변환된다.
2) 이를 모든 $x$ 에 대해 통합하면 전체 잠재 분포 $q_\phi(z)$ 가 형성된다.
3) KL 발산 항은 $q_\phi(z)$ 가 $p(z)$ 와 유사해지도록 학습을 유도한다.
4) 디코더 $p_\theta(x \mid z)$ 는 잠재 변수로부터 데이터 분포를 복원한다.
4. 직관적 해석
인코더는 실제 데이터 분포를 잠재 변수 분포 $q_\phi(z)$ 로 변환하고,
KL 발산 항은 이를 정규분포 $p(z)$ 에 정렬한다.
이 과정 덕분에 복잡한 데이터의 구조가 단순하고 해석 가능한 잠재공간으로 매핑된다.
결국 VAE는
“데이터 분포 → 인코더 → 잠재공간 정규화 → 디코더 → 복원된 데이터 분포”
로 이어지는 완전한 확률적 경로를 학습한다.

p31. 예시 그림 (Example Illustration)

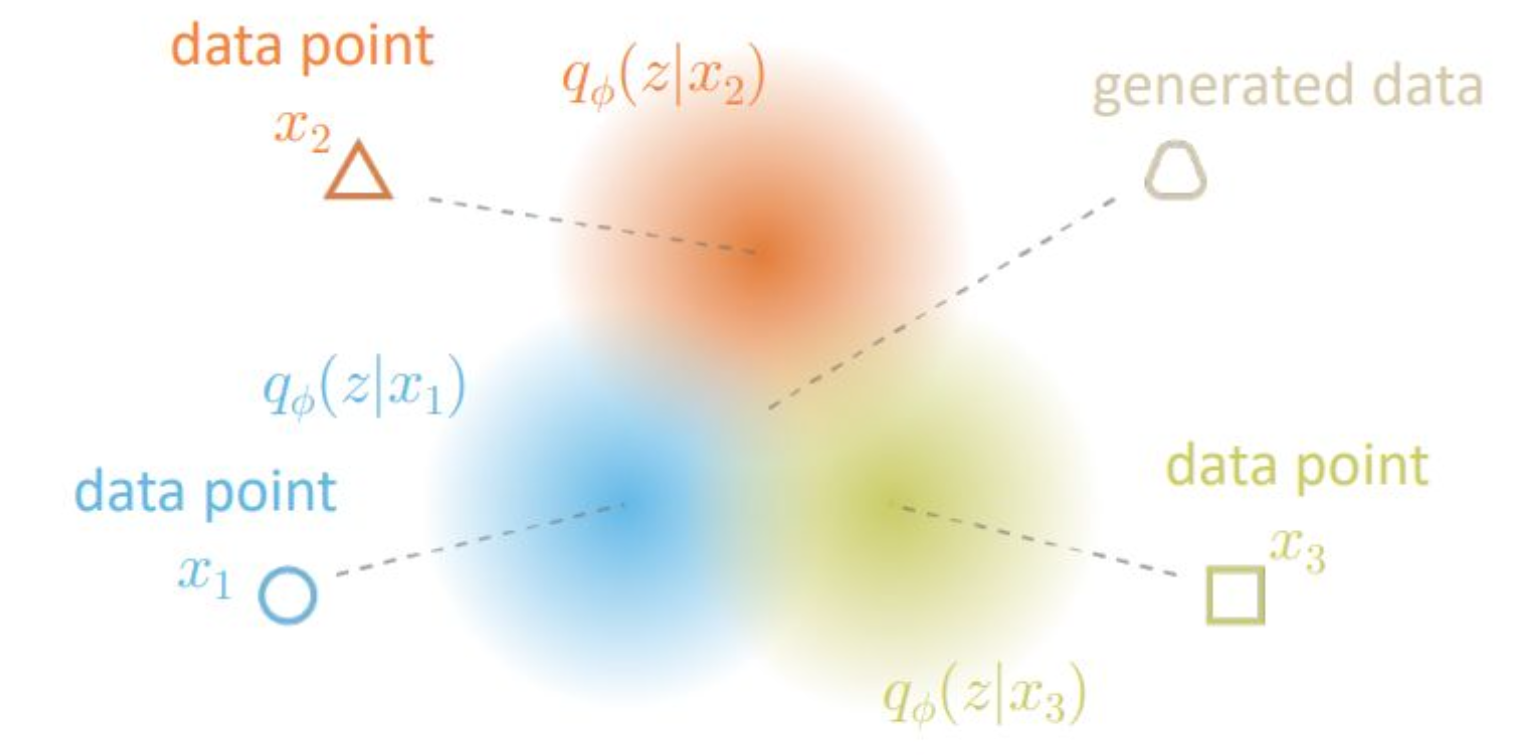
각 데이터 포인트 $x_1$, $x_2$, $x_3$ 는
인코더 $q_\phi(z \mid x)$ 를 통해
잠재공간(latent space)의 분포 $q_\phi(z \mid x_i)$ 로 매핑된다.
각 분포 $q_\phi(z \mid x_i)$ 는
잠재공간 내에서 서로 다른 위치에
데이터의 의미적 특징을 반영하여 분포하게 된다.
디코더는 각 $z$ 로부터 대응되는
재구성된 데이터(generated data) 를 복원한다.

보충 자료
1. 데이터 포인트와 잠재 분포의 대응 관계
원래의 데이터 포인트 $x_i$ 들은 인코더를 통과하면서 각각 잠재 분포 $q_\phi(z \mid x_i)$ 로 표현된다.
이 분포들은 데이터의 고유한 특성을 반영하며, 비슷한 데이터일수록 잠재공간에서 가까운 위치를 갖는다.
예를 들어 $x_1, x_2, x_3$ 가 유사한 클래스에 속하면,
이들의 잠재 분포 $q_\phi(z \mid x_i)$ 는 잠재공간에서 서로 겹치거나 인접한 영역에 위치하게 된다.
2. 생성 과정의 시각적 의미
각 $q_\phi(z \mid x_i)$ 에서 샘플링된 $z$ 는 디코더 $p_\theta(x \mid z)$ 를 통해
재구성된 데이터 $\hat{x}_i$ 를 생성한다.
이 과정 전체가 “입력 데이터 → 잠재공간 표현 → 데이터 복원”이라는
확률적 생성 경로를 학습하는 것이다.
3. 이상치 탐지(Anomaly Detection)와의 연관
VAE는 정상 데이터의 분포를 학습하므로 정상 데이터는 잠재공간에서 $p(z)$ 근처에 정렬된다.
반면 이상치는 학습된 $q_\phi(z)$ 와 잘 맞지 않아 낮은 복원 확률을 가지게 된다.
따라서 VAE는 복원 오차나 잠재 확률을 기반으로 이상치를 탐지하는 데 활용될 수 있다.
4. 데이터 정화(Purification) 관점
입력 데이터가 노이즈를 포함하거나 왜곡되었더라도,
인코더를 거쳐 잠재공간으로 투영되고 디코더를 통해 복원되는 과정에서
학습된 데이터 분포에 맞춰 정제된 형태로 출력될 수 있다.
즉, VAE는 생성 모델임과 동시에 데이터 복원 및 정화 모델로도 작동할 수 있다.

p32. MNIST의 2차원 잠재공간 (2D Latent Space on MNIST)

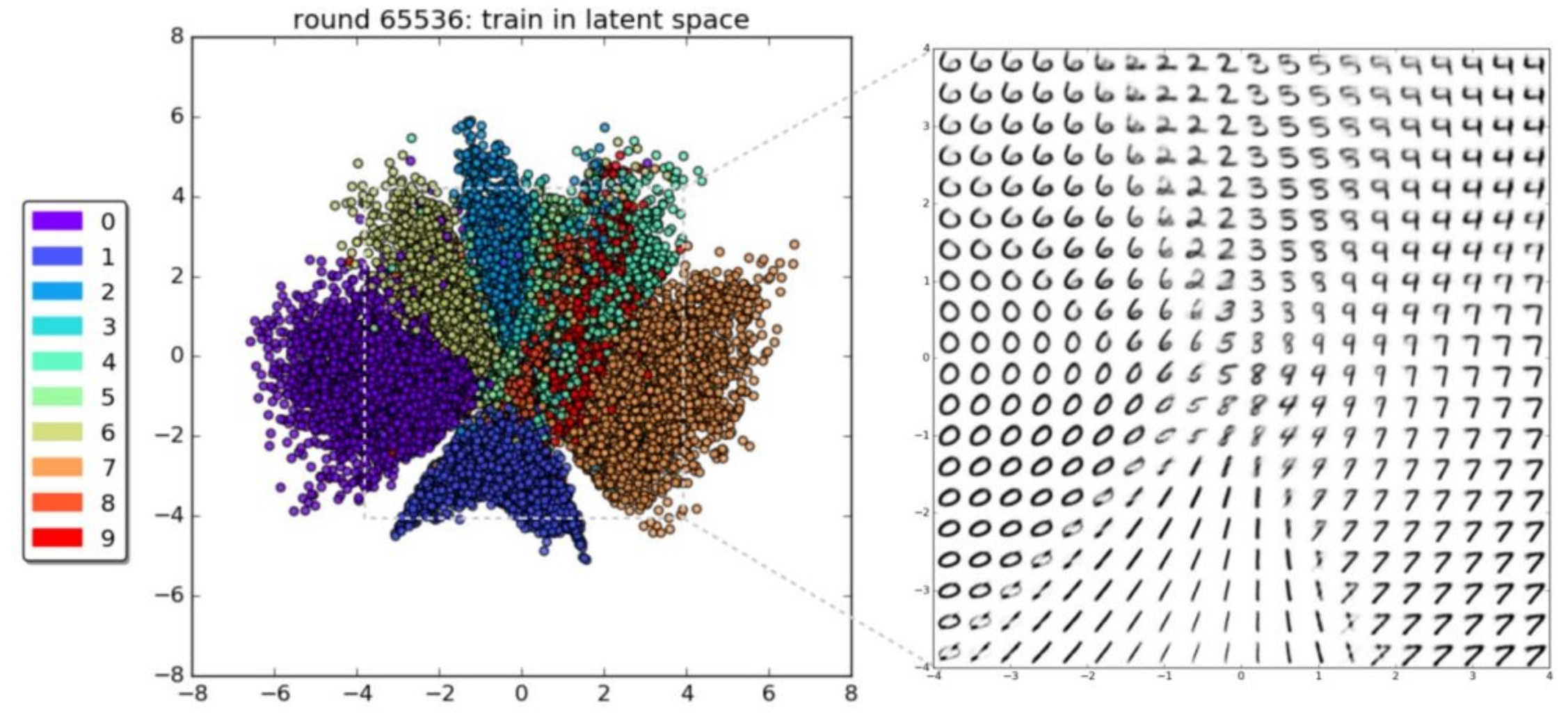
왼쪽: 각 숫자 클래스(0~9)가 인코딩된 잠재변수 공간의 분포
오른쪽: 잠재공간 상의 위치에 따라 디코더가 생성한 숫자 이미지

강의 내용
재미있는 예제를 보고 마무리하겠습니다.
VAE는 latent space, 즉 latent information을
조작(manipulation)하는 데에 많은 장점을 가지고 있습니다.
마지막 장의 예제를 보면 그 특징이 잘 드러납니다.
왼쪽 그림은 high-dimensional latent space를
256차원으로 설정한 뒤
각 숫자(label)에 해당하는 latent vector들을 시각화한 것입니다.
레이블을 주고 학습한 것도 아니고,
conditional 학습도 하지 않았는데
완전히 unconditional하게 학습했음에도 불구하고
숫자 0에 대한 latent variable,
숫자 1에 대한 latent variable 등
서로 모양이 비슷한 것들이
자연스럽게 뭉쳐서 클러스터링되는 현상이 나타납니다.
이는 매우 흥미로운 특성입니다.
이러한 특성 덕분에
latent space 위에서 interpolation을 하면
예를 들어 시작점이 숫자 6, 끝점이 숫자 4라고 할 때
$z$ 공간에서 직선을 따라 이동하며 interpolation을 하면
디코더를 통해 생성되는 이미지가
6에서 4로 스무스하게 변화하는 모습을 볼 수 있습니다.
latent space에서 정보가 알아서 클러스터링되며
interpolation이 자연스럽게 되는 현상을
linearized effect라고 부릅니다.
이러한 현상은 생성 모델의 중요한 철학적 기반이며,
실제로 여러분이 많이 본
“지브리 풍으로 바꾸는 모델” 같은 것도
바로 이 아이디어 위에서 동작한다고 보면 됩니다.
즉, 하나의 모달리티에서 다른 모달리티로 변환하는 기술의 배경에
이러한 latent space 구조가 자리 잡고 있다는 뜻입니다.
이 그림이 처음 나온 뒤 실제 이미지 변환 모델들이 등장하기까지
약 6년이 걸렸습니다.
따라서 이러한 기본 원리를 이해해 두는 것은
향후 등장할 새로운 생성 모델들을 이해하는 데 매우 큰 도움이 됩니다.
(질문)
마지막 그림에서 특정 방향(예: 한시 방향)으로는
분포가 많이 섞여 보이는데,
차원을 늘리면 더 잘 분리되나요?
(답변)
단순히 차원을 늘리면 표현력이 떨어질 수 있어
오히려 어려워지기도 합니다.
더 정확하게 말하면
인코더·디코더의 파라미터 수를 늘리고
학습이 잘 되도록 구조를 개선하면
분리가 잘 이루어지게 됩니다.
(질문)
아니면 단지 시각화를 2D로 했기 때문에
섞여 보이는 것일까요?
3D나 더 높은 차원으로 시각화하면
더 잘 구분되지는 않을까요?
(답변)
네, 그 설명도 정확합니다.
차원을 낮춰 시각화하면
구조가 섞여 보일 수 있습니다.
하지만 가장 중요한 것은 파라미터의 수,
즉 인코더·디코더 Neural Network가 가진 용량(capacity)입니다.
학습력이 부족한 상태에서 VAE를 학습하면
separability가 떨어지고
결과적으로 “지브리 변환 같은 효과”가 잘 나오지 않습니다.
잘 분리된 latent 구조에서는
숫자 6, 9, 5, 2처럼 모양이 다른 클래스들이
명확히 분리되어 나타나지만,
학습이 충분하지 않으면 서로 헷갈립니다.
현대의 생성 모델에서는
어려운 영역과 쉬운 영역에 대해
서로 다른 가중치(distribution weight)를 주는 방식 등
더 정교한 학습 기법들이 존재하지만
이 강의에서는 다루지 않습니다.
(질문)
reparameterization trick을 아까 설명하셨나요?
이 수업에서 중요한 개념인가요?
(답변)
크게 중요하지는 않습니다.
개념만 간단히 이해하면 충분하며
깊게 설명할 필요는 없습니다.
핵심은 $q_\phi$라는 분포가
$\phi$라는 Neural Network로 parameterization될 때
$\mu, \sigma$를 어떻게 사용해
랜덤 변수를 만들 것인가 하는 기술적 문제일 뿐입니다.
(질문)
VAE가 anomaly detection에 강점이 있다고 하셨는데
생성 모델인데 어떻게 anomaly를 검출하나요?
잘 이해가 되지 않습니다.
(답변)
최대한 간단히 설명해보겠습니다.
anomaly detection 문제에서는
두 종류의 데이터셋이 존재합니다.
전문가가 정상이라고 판단한, 매우 깨끗한 훈련 데이터
실제 온라인 환경에서 들어오는, 정상인지 이상인지 모르는 데이터
훈련 단계에서는
전문가가 깨끗하다고 분류한 데이터만 사용하여
VAE를 학습시킵니다.
따라서 $x$와 $x’$의 거리가 매우 작아지도록
reconstruction loss가 최소화됩니다.
그런데 온라인 환경에서 들어오는 새로운 샘플 $y$는
defect가 있을 수도, 없을 수도 있습니다.
이 $y$를 인코더·디코더 구조에 통과시켜
$y’$를 얻으면
$y$가 정상이라면 $y$와 $y’$의 거리는 작고
$y$가 defect(이상)를 포함하면 $y$와 $y’$의 거리는 크게 튀어오릅니다.
이 거리를 기준으로 스코어링하여
예를 들어 threshold를 100으로 잡으면
거리 > 100 → anomaly
거리 < 100 → 정상
이런 방식으로 anomaly detection이 가능합니다.
VAE는 이 구조 덕분에
anomaly detection의 표준적 접근 방식으로
지금도 많이 사용됩니다.
(질문)
그런데 inference 때는 인코더는 안 쓰고
디코더만 사용한다고 하지 않았나요?
(답변)
맞습니다.
VAE의 본래 목적이 “생성”일 때는
inference에서 디코더만 사용합니다.
하지만 anomaly detection에서는
생성 목적이 아니라
“입력이 재구성되는가?”를 측정하는 것이 핵심이므로
인코더와 디코더를 모두 활용합니다.
즉 VAE는 생성 모델로 태어났지만
구조가 anomaly detection에 유용하여
그렇게 재활용되는 것입니다.

보충 자료
1. 잠재공간의 구조
이 그림은 MNIST 데이터셋으로 VAE를 학습한 뒤 잠재공간(latent space)을 2차원으로 시각화한 결과이다.
각 점은 인코더 $q_\phi(z \mid x)$ 를 통해 얻어진 잠재벡터 $z$ 를 나타내며,
점의 색깔은 해당 데이터의 실제 숫자 레이블(0~9)에 대응된다.
서로 유사한 숫자들은 잠재공간에서 인접한 영역에 분포하며,
클래스 간 경계도 매끄럽게 이어진다.
2. 연속적(latent-continuous)인 공간의 특징
잠재공간이 2차원으로 제한되어 있음에도 각 숫자 클래스는 클러스터 형태로 잘 구분된다.
또한 그 사이 영역에서도 연속적인 변형이 가능하다.
잠재공간의 한 점에서 인접한 점으로 이동하면
디코더가 생성하는 숫자의 형태가 점진적으로 변화하며,
“6 → 0”, “4 → 9” 등 자연스러운 전이가 나타난다.
이러한 연속성은 라벨을 사용하지 않는 unconditional VAE에서도
잠재공간이 구조적으로 정렬되도록 학습되었음을 의미한다.
3. 잠재공간이 의미를 갖게 되는 이유
학습 전의 $z \sim \mathcal{N}(0,I)$ 샘플들은 단순한 무작위 가우시안이다.
그러나 학습이 진행되면 인코더 $q_\phi(z \mid x)$ 가 데이터 구조를 반영하여
$p(z)$ 공간에 의미 있는 좌표계를 형성하게 된다.
그 결과 잠재공간의 각 영역은 특정 숫자 형태나 패턴을 나타내는
의미적 지역(semantic region)으로 변환된다.
4. 응용: 이상치 탐지 및 데이터 보간
잠재공간이 구조적으로 정렬되어 있으므로
이상치 탐지(anomaly detection)나 데이터 보간(interpolation)이 가능하다.
학습된 분포 영역 바깥의 $z$ 에서 생성된 샘플은
비정상적이거나 왜곡된 형태를 띠므로,
이는 VAE가 학습 데이터 분포를 벗어난 입력을 탐지하는 근거가 된다.

대학원 수업, 확률과 통계