[확률과 통계] 주피터 노트북 실습

주성분 분석(Principal Component Analysis, PCA): 그림으로 보는 소개

이 노트북은 시각화를 곁들여 주성분 분석(PCA) 을 간단하고 예제 중심으로 소개한다.
합성된 2차원 데이터셋에서 시작하여 고차원 예제로 확장하고, NumPy/SVD 기반 구현과 표준 라이브러리 구현을 비교한다.

학습 목표

• PCA를 단위 노름 제약 조건 하에서 투영된 분산을 최대로 하는 직교 선형 변환으로 이해한다.
• 특잇값 분해(SVD)와 공분산 행렬의 고유분해를 통해 PCA를 계산한다.
• 주성분 축, 설명된 분산, 저차원 투영, 그리고 복원(reconstruction)을 시각화한다.

수학적 공식화 (formulation)

중심화된 데이터 행렬 $X \in \mathbb{R}^{n \times d}$ 가 주어졌을 때,
PCA는 다음을 만족하는 직교 단위 벡터 집합 $\lbrace w_k \rbrace_{k=1}^d$ 를 찾는다.

\[\max_{\|w\|_2=1} \operatorname{Var}(Xw) = \frac{1}{n}\|Xw\|_2^2,\]

여기서 연속된 벡터들은 서로 직교하도록 제약된다.
동등하게, $\Sigma = \tfrac{1}{n}X^\top X$ 라 하면 $w_k$ 는 고유값이 큰 순서대로 정렬된 $\Sigma$의 고유벡터들이다.

또한 $X = U S V^\top$ 가 thin SVD라면, 주성분 방향은 (V)의 열벡터들이고, 설명된 분산은 $S^2/n$ 이다.

순위-$r$ PCA 근사는 다음과 같이 정의된다.

\[X_r = Z_r W_r^\top, \quad Z_r = X W_r, \quad W_r = [w_1, \dots, w_r], \quad r \le d,\]

이 근사는 모든 순위-$r$ 선형 복원 중에서 프로베니우스 오차(Frobenius error)를 최소화한다.

---

이 식은 PCA의 핵심 아이디어를 수학적으로 정리한 것이다.
한 줄로 말하면,
“데이터를 가장 잘 설명하는 직교 축(방향)을 찾아서 그 축을 기준으로 데이터를 단순화(차원 축소)한다”는 내용이다.

1. 데이터와 분산의 개념

• $X \in \mathbb{R}^{n\times d}$는 평균이 0으로 중심화된 데이터 행렬이다.
• 각 행은 하나의 데이터 샘플, 각 열은 하나의 특성(feature)을 의미한다.

• PCA는 임의의 방향 $w$에서 데이터가 얼마나 퍼져 있는지를

  \[\operatorname{Var}(Xw)=\frac{1}{n}\|Xw\|_2^2\]

  로 측정하며, 이 값을 최대화하는 방향이 첫 번째 주성분이다.

2. 공분산 행렬과 고유벡터

• 데이터의 공분산 행렬은

  \[\Sigma=\frac{1}{n}X^\top X\]

  로 주어진다.

• $\Sigma$의 고유벡터는 데이터가 실제로 퍼진 방향을 나타내고,
  고유값은 그 방향에서의 분산 크기를 뜻한다.
• 따라서 가장 큰 고유값에 대응하는 고유벡터가 데이터가 가장 퍼져 있는 방향이며, 이것이 첫 번째 주성분이다.

3. SVD로 계산하는 이유

• 공분산을 직접 고유분해하지 않고 SVD로

  \[X = U S V^\top\]

  를 계산할 수 있다.

• 이때 $V$의 열벡터는 주성분 방향이며, $S^2/n$은 각 주성분의 분산(고유값)에 해당한다.
• 따라서 SVD 한 번으로 PCA의 모든 결과를 얻을 수 있다.

4. 랭크-$r$ 근사(차원 축소의 의미)

• 상위 $r$개의 주성분만 선택하면 저차원 근사 $X_r$은

  \[X_r = Z_r W_r^\top,\quad Z_r = X W_r\]

  로 표현된다.

• 이는 가능한 모든 $r$차원 복원 중 오차가 가장 작은 근사이다.
• 즉, 중요 정보를 최대한 유지하면서 차원을 줄이는 방식이다.

한 줄 요약

• PCA는 데이터를 가장 많이 설명하는 축을 찾아 그 축 방향으로 데이터를 압축하여
  정보 손실을 최소화하는 차원 축소 방법이다.

---

# 필요한 라이브러리 불러오기
import numpy as np                  # 수치 계산을 위한 라이브러리
import matplotlib.pyplot as plt     # 시각화를 위한 라이브러리
from pathlib import Path            # 파일 및 디렉토리 경로 처리를 위한 라이브러리

# 난수 생성기를 초기화 (seed=7로 고정하여 재현 가능하게 함)
rng = np.random.default_rng(7)

1. 상관된 방향을 가진 합성 2차원 데이터

비등방성 공분산을 가진 2차원 가우시안 분포의 점 구름(cloud)을 생성하고, 산점도를 시각화한 뒤,
SVD 기반 PCA로 계산된 주성분 축을 함께 표시한다.

# ------------------------------------------
# PCA (주성분 분석, Principal Component Analysis)
# 2차원 데이터 예제 - 주성분 축 시각화
# ------------------------------------------

n = 300                                # 샘플 개수 (데이터 점 300개 생성)
mu = np.array([0.0, 0.0])              # 데이터의 평균 벡터 (중심은 원점)
A = np.array([[2.0, 1.2], [0.0, 0.4]]) # 공분산 구조를 만드는 변환 행렬

# 표준 정규분포에서 난수 샘플 생성 (n x 2 행렬)
# np.random.standard_normal()로 만든 난수를 선형변환 A.T로 비틀어서
# 서로 상관된 2차원 데이터(X2)를 만든다.
X2 = rng.standard_normal((n, 2)) @ A.T + mu

# 데이터 중심화 (mean-centered)
# 각 열(특성)의 평균을 빼서 평균이 0이 되도록 만든다.
Xc = X2 - X2.mean(axis=0, keepdims=True)

# 특이값 분해 (SVD)
# Xc = U S Vt 형태로 분해
U, S, Vt = np.linalg.svd(Xc, full_matrices=False)

# 주성분 방향(Principal components): V의 열벡터들
W = Vt.T

# 각 축의 설명된 분산 (eigenvalue)
# 특이값 S는 √(n * 분산) 에 해당하므로 S²/n = 분산
explained = (S**2) / Xc.shape[0]

# 각 주성분이 전체 분산 중 차지하는 비율
ratio = explained / np.sum(explained)

# ------------------------------------------
# 시각화 (데이터 + 주성분 축)
# ------------------------------------------
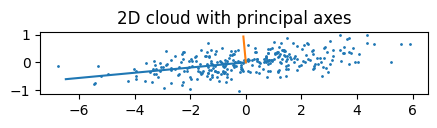
fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(111)

# 중심화된 데이터 산점도
ax.scatter(Xc[:, 0], Xc[:, 1], s=1)

# 원점 벡터 (주성분 축을 그릴 기준점)
origin = np.zeros(2)

# 두 개의 주성분 축(PC1, PC2)을 그림
for k in range(2):
    # 주성분 방향 벡터 길이를 분산 크기만큼 조정
    vec = W[:, k] * np.sqrt(explained[k]) * 3.0
    # 원점에서 주성분 방향으로 선을 그림
    ax.plot([origin[0], vec[0]], [origin[1], vec[1]])

# 축 비율을 동일하게 설정 (왜곡 방지)
ax.set_aspect("equal", adjustable="box")

# 그래프 제목
ax.set_title("2D cloud with principal axes")

plt.show()

# ------------------------------------------
# 📘 요약
# - 무작위 데이터를 만들고, SVD를 이용해 주성분 방향(V)을 구함
# - explained = 각 주성분이 설명하는 분산의 크기
# - ratio = 전체 분산 중 각 주성분이 차지하는 비율
# - 최종적으로 데이터의 ‘가장 많이 퍼진 방향(주성분 축)’을 시각적으로 표현
# ------------------------------------------

2. SVD로 처음부터 구현하는 PCA

PCA를 위한 가벼운 유틸리티를 구현한다: 중심화(centering), SVD, (r)개 성분으로의 투영, 복원(reconstruction), 그리고 설명된 분산 비율(explained-variance ratio).

# -------------------------------------------------------------
# ✅ PCA를 SVD로 직접 구현한 간단한 함수 (from scratch)
# -------------------------------------------------------------
# PCA는 데이터를 '가장 잘 설명하는 방향(주성분)'을 찾아
# 고차원 데이터를 저차원으로 압축하는 방법이다.
# 이 함수는 그 과정을 직접 코드로 구현한 것이다.
# -------------------------------------------------------------

def pca_svd(X, r=None):
    # 1️⃣ 평균 중심화 (Centering)
    #    각 열(특성)의 평균을 빼서 데이터의 중심을 원점(0)으로 맞춘다.
    #    이렇게 해야 PCA가 “분산의 방향”만 보고 판단할 수 있다.
    Xc = X - X.mean(axis=0, keepdims=True)

    # 2️⃣ SVD (Singular Value Decomposition, 특이값 분해)
    #    Xc = U * S * Vt 로 분해한다.
    #    - U: 샘플 방향의 벡터
    #    - S: 특이값 (데이터의 분산 크기를 나타냄)
    #    - Vt: 변수 방향의 벡터 (주성분 방향)
    U, S, Vt = np.linalg.svd(Xc, full_matrices=False)

    # 3️⃣ 사용할 주성분 개수 r 설정
    #    r이 주어지지 않으면 가능한 모든 주성분을 사용한다.
    if r is None:
        r = Vt.shape[0]

    # 4️⃣ 주성분 벡터(Principal components) 선택
    #    Vt의 앞부분 r개 행이 가장 큰 분산 방향이다.
    #    행렬 곱셈을 위해 전치(transpose)하여 사용한다.
    W = Vt[:r].T  # W: (d x r)

    # 5️⃣ 저차원 표현(Projection) 계산
    #    Xc를 주성분 방향 W에 투영 → 저차원 데이터 Z를 얻는다.
    Z = Xc @ W  # Z: (n x r)

    # 6️⃣ 각 주성분이 설명하는 분산 크기 계산
    #    S는 특이값(singular values)이므로, S**2가 분산 비율과 비례한다.
    explained = (S**2) / Xc.shape[0]

    # 7️⃣ 전체 분산 중 각 주성분이 차지하는 비율 (Explained variance ratio)
    ratio = explained / np.sum(explained)

    # 8️⃣ 결과 반환
    #    Z: 저차원 표현, W: 주성분 벡터, Xc: 중심화된 데이터
    #    explained: 각 주성분의 분산 크기, ratio: 그 비율
    return Z, W, Xc, explained, ratio


# -------------------------------------------------------------
# ✅ 복원 함수 (Reconstruction)
# -------------------------------------------------------------
# 저차원 표현 Z를 다시 원래 차원으로 복원하는 함수
# -------------------------------------------------------------
def reconstruct(Z, W, X_mean):
    # 1️⃣ Z @ W.T : 저차원 데이터를 다시 원래 축으로 되돌린다.
    # 2️⃣ X_mean : 중심화할 때 뺀 평균을 다시 더해 원래 위치로 복원.
    return Z @ W.T + X_mean

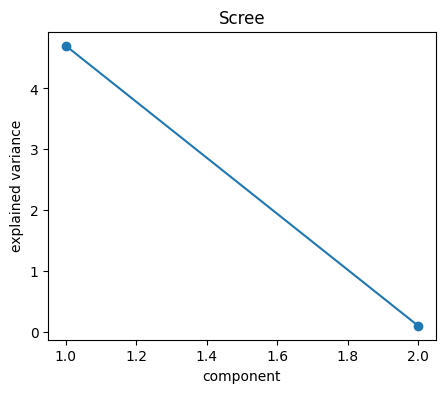
2.1 Scree plot (explained variance)

고유값의 크기와 누적 설명된 분산을 시각화한다.

---

1. Scree plot이란?

• ‘Scree’는 산 비탈 아래에 쌓인 자갈더미(rock debris)를 뜻한다.
• PCA에서 주성분의 고유값(eigenvalue) 또는 설명된 분산(explained variance)을 크기순으로 그리면
  그래프가 처음에는 급격히 떨어지다가 이후 완만해지는 형태가 된다.
• 이 모양이 산기슭의 자갈 경사면(scree slope)과 비슷해 Scree plot이라 부른다.

2. Scree plot의 축 해석

• x축: 주성분 번호(1번째, 2번째, …)
• y축: 각 주성분이 설명하는 분산(고유값 또는 explained variance)

3. 그래프가 의미하는 것

• 처음 몇 개 주성분은 데이터의 대부분 분산을 설명한다.
• 이후의 성분들은 작은 분산만 설명하며 주로 노이즈나 중복된 정보를 담는다.

4. ‘무릎(Knee)’ 또는 ‘엘보(Elbow)’ 지점의 의미

• 그래프에서 기울기가 급격히 완만해지는 지점이 중요하다.
• 그 지점까지의 주성분만 선택해도 데이터의 핵심 구조를 충분히 유지할 수 있다.
• 이는 “몇 개의 주성분을 남길지” 결정하는 실질적 기준이 된다.

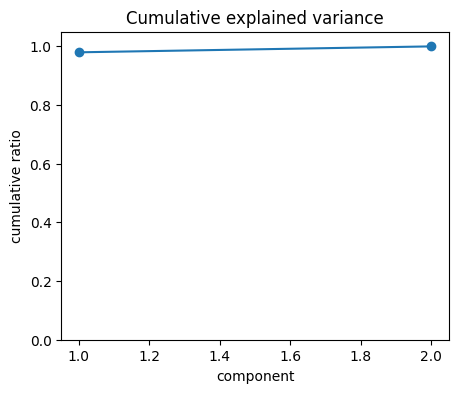
5. 누적 설명 분산(Cumulative explained variance)과 함께 사용

• Scree plot만으로는 판단이 모호할 수 있어 누적 비율 그래프와 함께 본다.
• 예를 들어 누적 설명 분산이 90% 이상이 되는 지점까지 주성분을 선택하면
  정보 손실을 최소화하면서 효율적으로 차원을 줄일 수 있다.

요약 한 줄

• Scree plot은 “데이터의 분산을 얼마나 잘 설명하는 주성분이 어디까지인지”를 시각적으로 보여주는 그래프이며,
  주성분 개수를 결정하는 가장 직관적인 도구이다.

---

# -------------------------------------------------------------
# ✅ 2.1 Scree Plot (설명된 분산 시각화)
# -------------------------------------------------------------
# PCA를 하면 각 주성분(component)이 데이터의 분산(정보)을
# 얼마나 잘 설명하는지를 수치로 얻을 수 있다.
# 여기서는 그것을 그래프로 시각화한다.
# -------------------------------------------------------------

# PCA 수행 (2차원 데이터 X2를 입력으로)
# - Z: 투영된 저차원 데이터
# - W: 주성분 벡터
# - Xc2: 중심화된 데이터
# - expl2: 각 주성분의 분산 크기 (고유값)
# - ratio2: 전체 분산 중 각 주성분이 차지하는 비율
Z, W, Xc2, expl2, ratio2 = pca_svd(X2, r=2)

# -------------------------------------------------------------
# 📈 (1) Scree Plot: 각 주성분이 설명하는 분산 크기
# -------------------------------------------------------------
fig = plt.figure(figsize=(5,4))
ax = fig.add_subplot(111)

# x축: 주성분 번호(1, 2)
# y축: 각 주성분이 설명하는 분산의 크기 (explained variance)
ax.plot(np.arange(1, 3), expl2, marker="o")

ax.set_xlabel("component")         # x축 이름
ax.set_ylabel("explained variance")# y축 이름
ax.set_title("Scree")              # 그래프 제목
plt.show()

# 🔍 해석:
# - 점이 높을수록 그 축이 데이터를 잘 설명함 (즉, 분산이 큼)
# - 분산이 급격히 줄어드는 지점 이후는 “정보가 적은 축”이므로
#   그 이후 주성분은 버려도 됨 (차원 축소의 기준!)

# -------------------------------------------------------------
# 📊 (2) 누적 설명 분산 (Cumulative Explained Variance)
# -------------------------------------------------------------
fig = plt.figure(figsize=(5,4))
ax = fig.add_subplot(111)

# 각 주성분 비율의 누적합을 그림
ax.plot(np.arange(1, 3), np.cumsum(ratio2), marker="o")

ax.set_xlabel("component")
ax.set_ylabel("cumulative ratio")  # 누적 비율
ax.set_ylim(0, 1.05)               # y축 범위를 0~1로 설정
ax.set_title("Cumulative explained variance")
plt.show()

# 🔍 해석:
# - 누적 비율이 0.9(90%) 이상이 되는 지점까지의 주성분만 써도
#   전체 데이터의 대부분 정보를 유지할 수 있다.
# - 즉, “어디까지의 주성분을 사용할지” 결정하는 데 쓰인다.

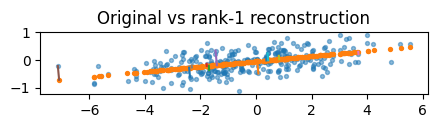
2.2 1차원 투영과 복원

첫 번째 성분에 데이터를 투영하고, 복원된 결과를 시각화한다.

# -------------------------------------------------------------
# ✅ 2.2 Projection to 1D and Reconstruction (1차원 투영과 복원)
# -------------------------------------------------------------
# 이번 단계는 “2D → (r=1) 1D → 2D” 흐름을 그림으로 보여준다.
# - 투영(Projection): 2차원 데이터 X2를 ‘첫 번째 주성분’(가장 분산이 큰 축)으로만 표현 → Z1 (n×1)
# - 복원(Reconstruction): Z1을 다시 원래 좌표계(2D)로 되돌리되, 주성분 1개만 써서 복원 → Xr1 (n×2)
#   ⚠️ r=1이므로 복원된 점들은 2차원 평면 안의 “한 직선(주성분 축)” 위에 모여 보인다.
#   (완전 복원이 아니라, rank-1 최적 선형 근사)
# -------------------------------------------------------------

# 1️⃣ PCA 수행 (r=1 → 첫 번째 주성분만 사용)
#    - Z1 : (n×1) 1차원으로 압축된 좌표 (주성분 축 위 위치)
#    - W1 : (2×1) 첫 번째 주성분 방향 벡터
#    - Xc2b : (n×2) 중심화된 데이터
#    - expl2b, ratio2b : 각 성분의 분산과 그 비율
Z1, W1, Xc2b, expl2b, ratio2b = pca_svd(X2, r=1)

# 2️⃣ 원본 데이터의 평균 (복원 시, 중심화했던 평균을 다시 더해 원래 위치로 되돌림)
Xmean = X2.mean(axis=0, keepdims=True)

# 3️⃣ 복원 (r=1이므로 2D 공간의 ‘한 직선’ 위로 복원됨)
#    Xr1[i] = Xmean + Z1[i] * W1  (평균점을 지나는 주성분-직선 위로 투영된 근사점)
Xr1 = reconstruct(Z1, W1, Xmean)

# 4️⃣ 그림 준비
fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(111)

# 5️⃣ 원본 데이터 산점도
#    (matplotlib 기본 색상 순서로 보통 첫 번째가 파란색)
ax.scatter(X2[:,0], X2[:,1], s=8, alpha=0.5)

# 6️⃣ 복원된 데이터 산점도
#    (보통 두 번째가 주황색) → 직선(주성분 축) 위에 일렬로 놓임
ax.scatter(Xr1[:,0], Xr1[:,1], s=8)

# 7️⃣ 원본 점 → 복원 점 연결선 (일부만)
#    이 짧은 선이 “원본 점이 주성분 축으로 투영되어 어디로 갔는지”를 보여줌
for i in range(0, X2.shape[0], 25):
    ax.plot([X2[i,0], Xr1[i,0]], [X2[i,1], Xr1[i,1]])

# 8️⃣ 축 비율 동일 (모양 왜곡 방지)
ax.set_aspect("equal", adjustable="box")

# 9️⃣ 제목
ax.set_title("Original vs rank-1 reconstruction")

# 10️⃣ 표시
plt.show()

# -------------------------------------------------------------
# 💡 해석 요약:
# - 파란 점(원본)과 주황 점(복원)을 비교하면,
#   복원된 점들이 ‘한 직선’ 위에 모여 있음 → r=1이라 1차원 정보만 유지했기 때문.
# - 연결선은 각 원본 점이 그 직선(첫 번째 주성분 축)으로 “직교 투영”되어
#   어디에 놓였는지(=복원 위치)를 시각적으로 보여준다.
# -------------------------------------------------------------

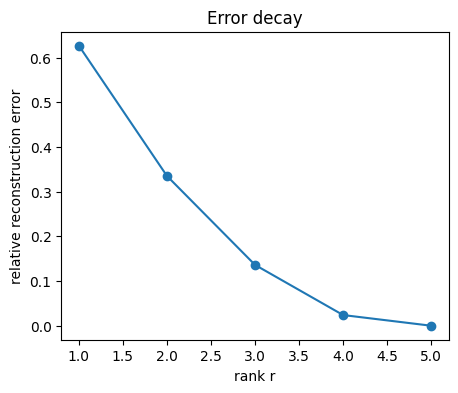
3. 차원에 따른 복원 오차

비등방성 5차원 데이터셋에서, 보존된 순위(rank)가 증가함에 따라 프로베니우스(Frobenius) 복원 오차가 어떻게 감소하는지 살펴본다.

# -------------------------------------------------------------
# ✅ 3. Reconstruction error vs dimension
# -------------------------------------------------------------
# 이번 실험은 “주성분 개수(r)”를 늘릴 때마다
# 복원 오차(reconstruction error)가 얼마나 줄어드는지를 관찰하는 것이다.
#
# 즉, “차원을 얼마나 남기느냐에 따라 데이터 복원 품질이 어떻게 변하는가?”
# 를 확인한다.
# -------------------------------------------------------------

# 1️⃣ 데이터 생성 (5차원, 비등방성 분포: anisotropic)
n = 800   # 표본 개수
d = 5     # 차원 수

# 무작위 직교행렬 Q (회전 행렬)
Q, _ = np.linalg.qr(rng.standard_normal((d, d)))

# 각 축의 분산(고유값)을 다르게 설정 → 일부 축은 크고, 일부는 작게
# 즉, 분산이 한쪽 방향으로 치우친(anisotropic) 데이터 생성
vals = np.linspace(3.0, 0.2, d)   # 고유값 크기 (큰 → 작은 순서)
C = Q @ np.diag(vals) @ Q.T       # 공분산 행렬 Σ = Q Λ Qᵀ

# 위 공분산을 따르는 5차원 정규분포 샘플 생성
X5 = rng.multivariate_normal(np.zeros(d), C, size=n)

# -------------------------------------------------------------
# ✅ 차원 r을 바꾸면서 복원 오차를 계산
# -------------------------------------------------------------

errs = []  # 각 r별 복원 오차를 저장할 리스트

# 전체 분산(기준 오차) 계산
# 중심화된 데이터의 제곱 노름을 기준으로 삼는다.
tot = np.linalg.norm(X5 - X5.mean(axis=0, keepdims=True))**2

# 1차원부터 5차원까지 차례로 실험
for r in range(1, d+1):
    # PCA 수행 (앞의 r개 주성분만 사용)
    Z, W, Xc, expl, ratio = pca_svd(X5, r=r)

    # 복원 (r차원 근사)
    Xr = reconstruct(Z, W, X5.mean(axis=0, keepdims=True))

    # Frobenius norm 기반 복원 오차 계산
    # → 원본과 복원된 데이터 간의 제곱거리 합
    e = np.linalg.norm(X5 - Xr)**2
    errs.append(e)

# -------------------------------------------------------------
# ✅ 시각화: 차원(r)에 따른 상대 복원 오차
# -------------------------------------------------------------

fig = plt.figure(figsize=(5,4))
ax = fig.add_subplot(111)

# 상대 오차 (e / tot): 전체 분산 대비 잔여 오차 비율
ax.plot(range(1, d+1), np.array(errs)/tot, marker="o")

ax.set_xlabel("rank r")                   # 남긴 주성분 개수
ax.set_ylabel("relative reconstruction error")  # 상대 복원 오차
ax.set_title("Error decay")               # 오차 감소 곡선
plt.show()

# -------------------------------------------------------------
# 💡 해석 요약:
# - rank r이 커질수록(즉, 더 많은 주성분을 사용할수록)
#   복원 오차가 점점 작아진다 → 더 많은 분산을 설명하게 됨.
# - 반대로, r이 작을수록 데이터의 중요한 축 일부만 남기므로
#   복원 오차가 커진다.
# - 이 곡선은 “차원을 줄였을 때 정보 손실이 얼마나 되는가”를
#   직관적으로 보여준다.
# -------------------------------------------------------------

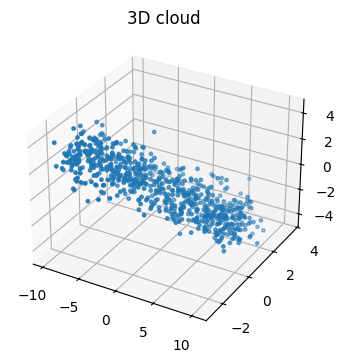
4. 3D 시각화

$ \mathbb{R}^3 $에서 거의 1차원에 가까운 필라멘트 형태의 데이터를 합성하고, 점구름을 시각화한 뒤, 2차원 PCA 투영 결과와 비교한다.

# -------------------------------------------------------------
# ✅ 4. 3D Visualization (3차원 데이터 시각화)
# -------------------------------------------------------------
# 이번 실험에서는 3차원 공간상의 "얇은 선 모양(거의 1차원 구조)" 데이터를 생성하고,
# PCA를 이용해 3D 데이터를 2D 평면에 투영했을 때 어떤 결과가 나오는지 시각적으로 확인한다.
# -------------------------------------------------------------

# 1️⃣ 샘플 개수
m = 700

# 2️⃣ 1차원 매개변수 t를 균일하게 생성 (-3 ~ 3)
t = rng.uniform(-3, 3, size=m)

# 3️⃣ t를 이용해 3차원 공간상의 선(필라멘트) 생성
#     - 실제로는 거의 1차원 구조지만 3D 공간 안에 놓여 있다.
#     - x, y, z 좌표가 t에 선형적으로 의존한다.
line = np.stack([3*t, 0.5*t, -t], axis=1)

# 4️⃣ 노이즈를 추가해서 실제 데이터처럼 만든다.
#     - 각 점이 선 주위에 조금씩 흩어지도록 한다.
noise = rng.normal(scale=0.7, size=(m, 3))
X3 = line + noise

# 5️⃣ PCA 수행 (2개의 주성분만 남김)
#     - 원래 3D → 2D로 축소
#     - 즉, 가장 분산이 큰 두 방향만 남긴다.
Z, W, Xc, expl, ratio = pca_svd(X3, r=2)

# 6️⃣ 3D 산점도: 원본 데이터
fig = plt.figure(figsize=(5, 4))
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X3[:,0], X3[:,1], X3[:,2], s=6)
ax.set_title("3D cloud")
plt.show()
# 💬 결과 해석:
#   - 데이터가 대체로 한 줄(거의 1차원 구조)을 따라 퍼져 있음.
#   - 노이즈로 인해 약간 퍼져 있지만, 주로 한 방향(주성분 축)을 따라 분산이 크다.

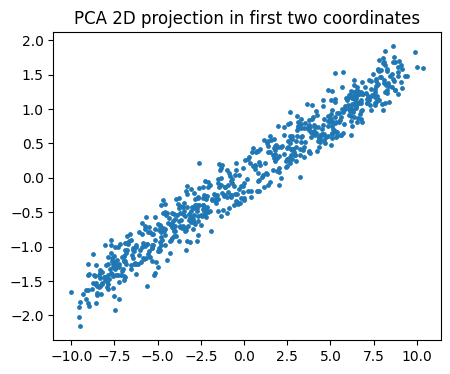
# 7️⃣ 2D 평면으로 투영
#     - PCA의 결과를 이용해 3D 데이터를 2D로 줄인다.
#     - Xproj는 2D로 축소된 데이터가 다시 원래 공간의 평균 위치 근처로 복원된 것.
Xproj = Z @ W.T + X3.mean(axis=0, keepdims=True)

# 8️⃣ 2D 산점도 (PCA 투영 결과)
fig = plt.figure(figsize=(5, 4))
ax = fig.add_subplot(111)
ax.scatter(Xproj[:,0], Xproj[:,1], s=6)
ax.set_title("PCA 2D projection in first two coordinates")
plt.show()
# 💬 결과 해석:
#   - 3D 데이터의 핵심 구조가 2D 평면 위에 거의 그대로 보존되어 있음.
#   - 즉, 데이터가 본질적으로 1차원 선분 형태였기 때문에,
#     3차원에서 2차원으로 줄여도 정보 손실이 거의 없다.
#   - 이렇게 PCA는 “불필요한 차원(노이즈 방향)”을 제거하고
#     데이터의 주요 패턴을 유지하는 차원 축소 방법임을 확인할 수 있다.
# -------------------------------------------------------------

5. 라이브러리 기반 PCA (옵션) — 고전 데이터셋

가능하다면 표준 구현을 사용하여 잘 알려진 데이터셋에 적용해 본다.

# -------------------------------------------------------------
# ✅ 5. Library PCA (optional) on classic datasets
# -------------------------------------------------------------
# 이번에는 우리가 직접 구현한 PCA 대신,
# scikit-learn의 PCA 클래스를 이용해
# 대표적인 데이터셋(iris, digits)에 PCA를 적용해본다.
# -------------------------------------------------------------

try:
    from sklearn.decomposition import PCA
    from sklearn import datasets

    # ---------------------------------------------------------
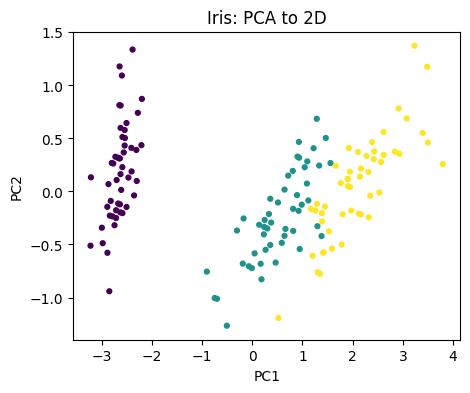
    # 🌸 (1) Iris dataset
    # ---------------------------------------------------------
    # - 꽃받침(sepal), 꽃잎(petal)의 길이·너비 등 4차원 데이터
    # - 3종류의 붓꽃(Setosa, Versicolor, Virginica)을 분류하는 문제
    iris = datasets.load_iris()
    X = iris.data   # 입력 특징 (4차원)
    y = iris.target # 꽃의 종류 (0, 1, 2)

    # PCA 수행: 4차원 → 2차원으로 축소
    pca = PCA(n_components=2, svd_solver="full")
    Xp = pca.fit_transform(X)

    # 시각화
    fig = plt.figure(figsize=(5,4))
    ax = fig.add_subplot(111)
    ax.scatter(Xp[:,0], Xp[:,1], s=12, c=y)
    ax.set_title("Iris: PCA to 2D")
    ax.set_xlabel("PC1")
    ax.set_ylabel("PC2")
    plt.show()

    # 💬 해석:
    # - 4차원 데이터를 2개의 주성분(PC1, PC2)으로 줄였음에도
    #   세 개의 품종이 어느 정도 분리되어 나타난다.
    # - PCA가 데이터의 주요 변동 방향(패턴)을 잘 포착했음을 보여준다.

    # ---------------------------------------------------------
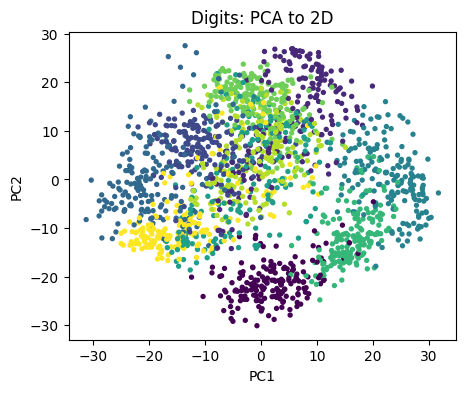
    # 🔢 (2) Digits dataset
    # ---------------------------------------------------------
    # - 손글씨 숫자(0~9)를 8x8 픽셀 → 64차원 벡터로 표현한 데이터
    # - 1797개의 샘플
    digits = datasets.load_digits()
    Xd = digits.data
    yd = digits.target

    # PCA 수행: 64차원 → 2차원 축소 (randomized solver로 빠르게 계산)
    pca2 = PCA(n_components=2, svd_solver="randomized", random_state=0)
    Xpd = pca2.fit_transform(Xd)

    # 시각화
    fig = plt.figure(figsize=(5,4))
    ax = fig.add_subplot(111)
    sc = ax.scatter(Xpd[:,0], Xpd[:,1], s=8, c=yd)
    ax.set_title("Digits: PCA to 2D")
    ax.set_xlabel("PC1")
    ax.set_ylabel("PC2")
    plt.show()

    # 💬 해석:
    # - 고차원(64D) 이미지 데이터를 2D로 줄였음에도,
    #   숫자별로 군집이 약하게 구분되는 모습을 볼 수 있다.
    # - PCA는 비지도 학습 방식으로도
    #   데이터의 “유사한 모양”을 가진 숫자들을 가까이 모아준다.
    # - 하지만 완벽한 분리(클래스별 경계)는 어렵기 때문에
    #   이런 경우 t-SNE, UMAP 같은 비선형 차원축소 기법이 더 효과적일 수 있다.

except Exception as e:
    # sklearn 모듈이 없는 환경일 경우 대체 출력
    fig = plt.figure(figsize=(5,2))
    ax = fig.add_subplot(111)
    ax.text(0.05, 0.5, "sklearn not available in this runtime", fontsize=12)
    ax.axis("off")
    plt.show()