[텍스트 마이닝] 12. Search 1 - Lexical Retrieval

게시 2025/11/23 업데이트 2025/12/12

By 김성진

38 분읽는 시간

p6. 검색: 우리가 정보를 얻는 방식의 핵심

우리가 “검색(search)”을 생각할 때, 우리는 종종
Google에 무언가를 입력하는 웹 검색(web search) 을 떠올린다.

하지만 실제로, 검색은 우리 주변 어디에나 있다.
- 몇 년 전의 오래된 이메일 스레드(old email thread) 이나 사진(photo) 을 찾는 것.
- 회의 요약을 위해 채팅 기록(chat history) 을 검색하는 것.
- 개인 기기에 저장된 로컬 파일(local files) 이나 개인 데이터(personal data) 를 찾아보는 것.
그리고 중요한 점은, 검색은 단순 검색 기능을 넘어 발전해 왔다는 점이다.
- 검색은 검색-증강 생성(Retrieval-Augmented Generation, RAG) 을 통해
  대규모 언어 모델(LLMs) 의 핵심 요소가 되었다.

p7. 검색: LLM의 핵심 요소

2025년 10월 20일 질의:
- “추천 시스템에서 PL ranking model의 역할은 무엇인가?”
ChatGPT 답변(직역):
- 추천 시스템에서 PL(pairwise learning-to-rank) 모델은
  후보 아이템들을 순위화(ranking) 하는 역할을 한다.
  이는 절대 점수를 예측하는 대신,
  아이템 쌍들 사이의 사용자 선호의 상대적 관계(relative user preferences) 를 학습하는 방식이다.
  아래는 그 역할과 중요성에 대한 분해(breakdown)이다.
PL ranking model은 Plackett–Luce 모델을 의미하며,
가장 근본적인 순위 매김 모델 중 하나이다.
관련 연구 설명(직역):
- “Plackett-Luce(PL) 모델(Plackett 1975; Luce 1959)은
  가장 근본적인 순위 매김 모델 중 하나이다.
  n개의 아이템으로 이루어진 공간에서,
  PL 모델은 아이템 i가 잠재적 효용(utility)을 가진다고 가정한다.”
- 출처:
  Nguyen et al., Efficient and Accurate Learning of Mixtures of Plackett-Luce Models, AAAI’23

p8. 검색: LLM의 핵심 요소

검색 시스템은 개별 사용자(individual users)를 이해하는 것과
특수화된 도메인(specialized domains)을 다루는 것에 어려움을 겪는다.
검색 시스템은 LLM 기반 생성(LLM-based generation)의 근본적인 병목(fundamental bottleneck) 이다.

왼쪽 그림 설명
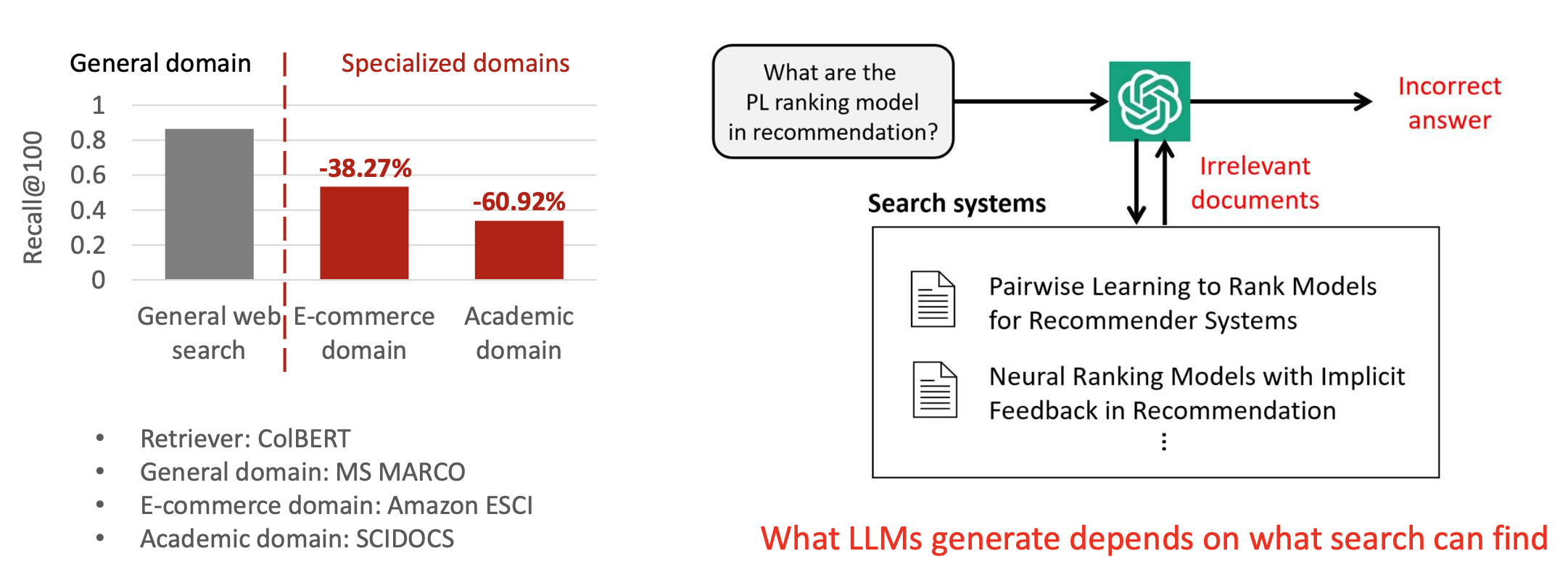
이 그래프는 검색 시스템의 성능이 도메인에 따라 크게 달라진다는 점을 보여준다.
일반 웹 검색에서는 높은 Recall@100 성능을 보이지만, 특수 도메인으로 갈수록 성능이 급격히 감소한다.
전자상거래 도메인에서는 –38.27%, 학술 도메인에서는 –60.92% 성능 하락이 나타난다.
이는 검색 시스템이 특수한 분야의 문서를 잘 찾지 못하는 구조적 한계를 의미한다.
사용된 데이터셋은 General: MS MARCO, E-commerce: Amazon ESCI, Academic: SCIDOCS이며, Retriever는 CoLBERT이다.
오른쪽 그림 설명
LLM이 생성하는 답변은 검색 시스템이 어떤 문서를 찾아주는가에 의해 결정된다.
예시 질문 “추천에서 PL ranking model이 무엇인가?”가 들어오면,
검색 시스템이 관련 문서를 검색해 LLM에 전달한다.
하지만 이 검색 과정에서 ‘관련 없는 문서’를 반환하면,
LLM은 그 문서를 근거로 잘못된 답변을 생성할 수밖에 없다.
따라서 검색 시스템은 LLM 기반 생성의 근본적인 병목이며,
LLM의 성능은 검색 시스템의 품질에 크게 의존한다.

p9. 검색: 개요

우리는 실제(real-world) 검색 엔진을 작동시키는 핵심 기술들을 배우게 된다.

어휘 기반 검색 (Lexical retrieval)
- 쿼리와 문서를 단어 개수 기반의 희소 벡터(sparse vectors)로 표현한다.
- 쿼리와 문서 사이의 정확한 단어 일치(exact word matching)에 초점을 맞춘다.
고밀도 임베딩 검색 (Dense retrieval)
- 쿼리와 문서를 연속적인 벡터 공간에서 표현하기 위해 고밀도 임베딩(dense embeddings)을 사용한다.
- 의미적 유사성(semantic similarity)을 포착하여 키워드가 겹치지 않는 경우에도 검색이 가능하게 한다.
LLM 기반 향상 검색 (LLM-enhanced retrieval)
- 대규모 언어 모델(LLMs)을 활용하여 검색 프로세스를 향상시킨다.

(왼쪽 그림 설명)
Sparse Retrieval: 쿼리를 희소 벡터로 변환하여 문서 코퍼스와 비교한다.
Dense Retrieval: 쿼리를 밀집 벡터로 변환하여 의미적으로 유사한 문서를 더 잘 잡아낸다.
(오른쪽 그림 설명)
LLM이 먼저 추론(reasoning)을 수행하며 쿼리를 확장한다(“Let’s augment this query.”).
그 후 확장된 쿼리를 기반으로 검색 단계를 수행한다(Search).
검색된 결과는 보상 계산(retrieval reward computation)에 사용된다.
보상은 LLM에게 다시 전달(update)되어, 더 나은 검색-생성 루프를 만든다.

p11. 작업: 애드혹 검색 (Task: ad-hoc search)

사용자가 쿼리(query) 를 제출하면,
시스템은 컬렉션(collection)에서 순위가 매겨진 문서 목록(ranked list of documents) 을 반환한다.
- Document: 웹페이지, 논문, 문단 등 어떠한 텍스트 단위도 문서(document)가 될 수 있다.
- Collection: 시스템이 검색할 수 있는 모든 문서들의 집합을 의미한다.
- Index: 효율적이고 효과적인 검색을 가능하게 하기 위해 구축된 데이터 구조이다.
- Query: 사용자의 정보 요구(information need)를 용어들의 집합으로 표현한 것이다.

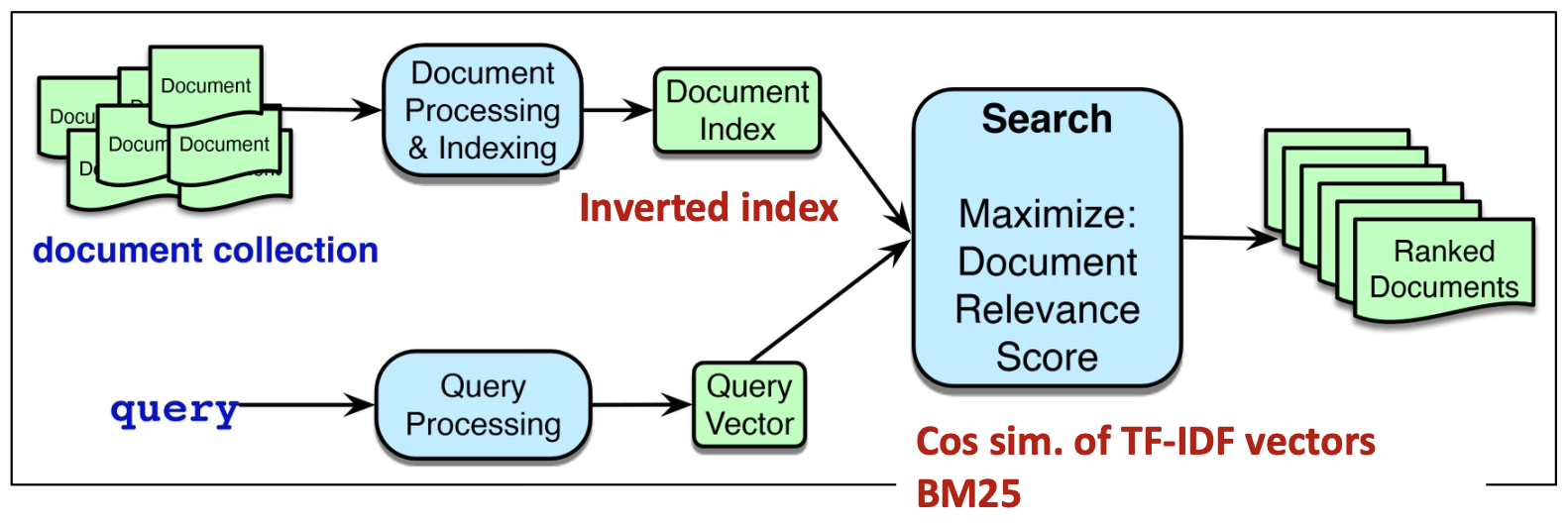
(아래 그림 설명)
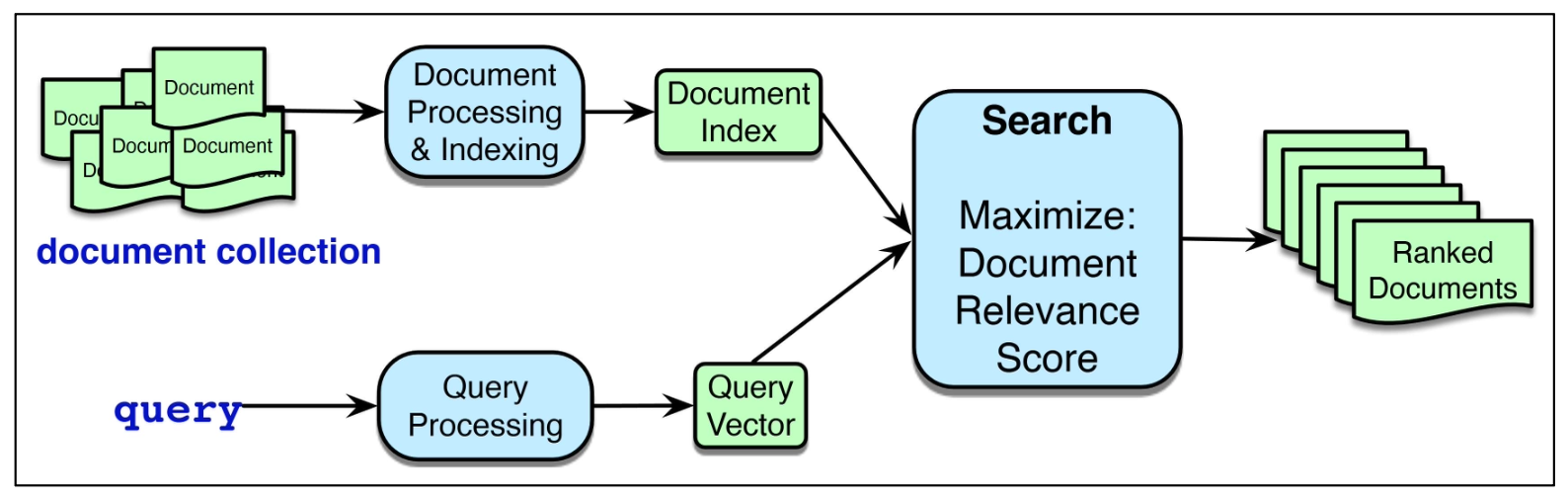
문서 컬렉션(document collection)은
문서 처리 및 색인(Document Processing & Indexing)을 거쳐 문서 인덱스(Document Index) 로 변환된다.
사용자의 쿼리는 쿼리 처리(Query Processing)를 통해 쿼리 벡터(Query Vector) 로 변환된다.
검색(Search)은 문서 인덱스와 쿼리 벡터를 결합하여
문서 관련성 점수(Document Relevance Score) 를 최대화하는 문서들을 찾는다.
최종적으로 시스템은 순위화된 문서들(Ranked Documents) 을 반환한다.

p12. 작업: 애드혹 검색 (Task: ad-hoc search)

시스템은 쿼리와의 관련성(relevance) 에 따라 문서들을 순위화(ranks) 한다.
- Relevance score: 사용자의 정보 요구를 충족하는지 여부에 대해 각 문서에 부여되는 점수이다.
그렇다면 이 “관련성(relevance)”은 어떻게 측정할까?
- 일반적으로 쿼리와 문서 사이의 텍스트 유사도(textual similarity) 를 이용해 이를 근사한다.

p13. 평가 지표: Precision@N, Recall@N

Top-N으로 순위화된 문서 목록이 주어졌을 때, 우리는 검색 결과의 품질을 평가한다.
두 가지 직관적인 평가 지표는 precision 과 recall 이며, 분류 작업과 유사하게 정의된다.

Precision@N:
\[\text{Precision@N} = \frac{\text{상위 N개 안의 관련 문서 수}}{N}\]
상위 N개의 검색 결과가 얼마나 관련 문서들로 구성되어 있는지를 나타낸다.
Recall@N:
\[\text{Recall@N} = \frac{\text{상위 N개 안의 관련 문서 수}}{\text{전체 관련 문서 수}}\]
코퍼스 전체의 관련 문서 중 얼마나 많이 검색되었는지를 나타낸다.

p14. 평가 지표: Precision@N, Recall@N

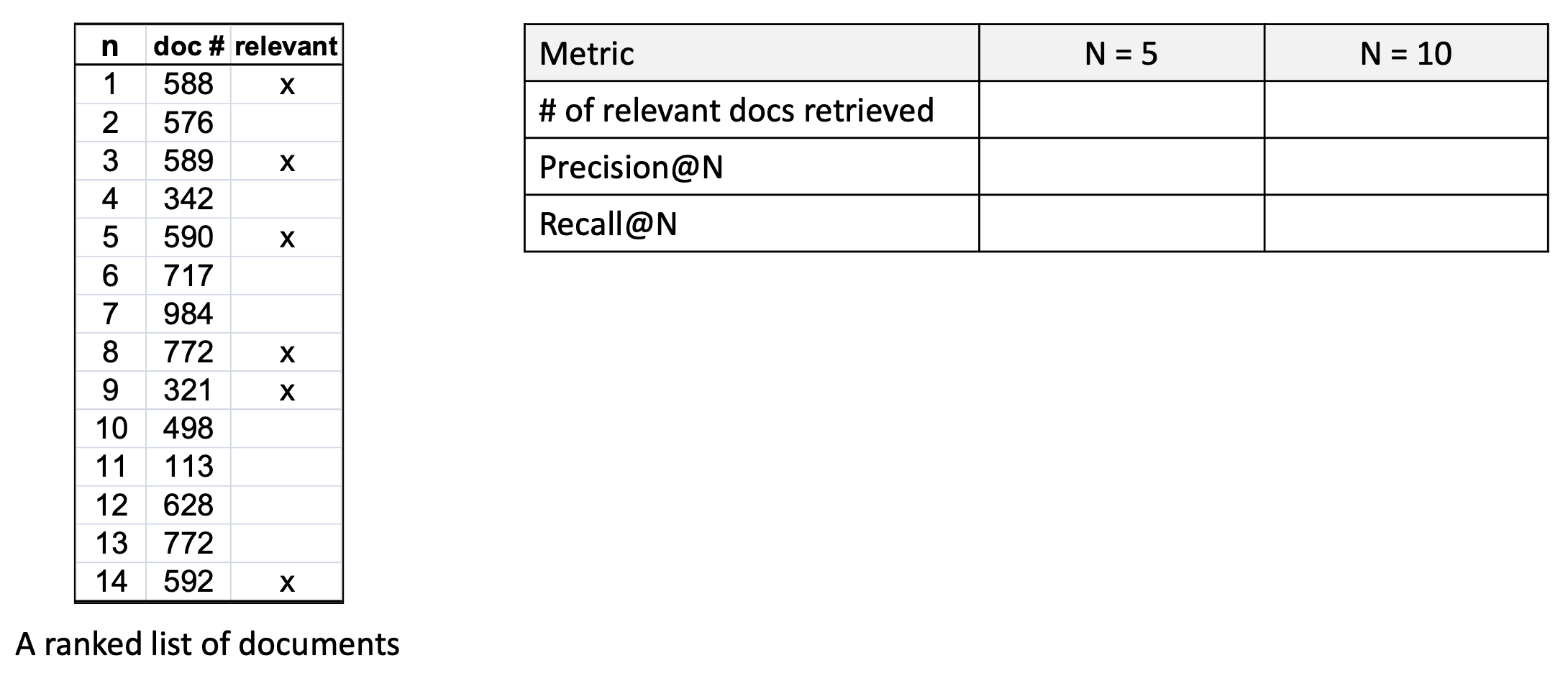
주어진 쿼리에 대해, 코퍼스 안에 6개의 관련 문서(six relevant documents) 가 있다고 가정하자.
- 아래의 순위화된 문서 목록을 사용해
  N = 5, N = 10 에 대해 Precision@N 과 Recall@N 을 계산한다.

p15. 평가 지표: NDCG@N

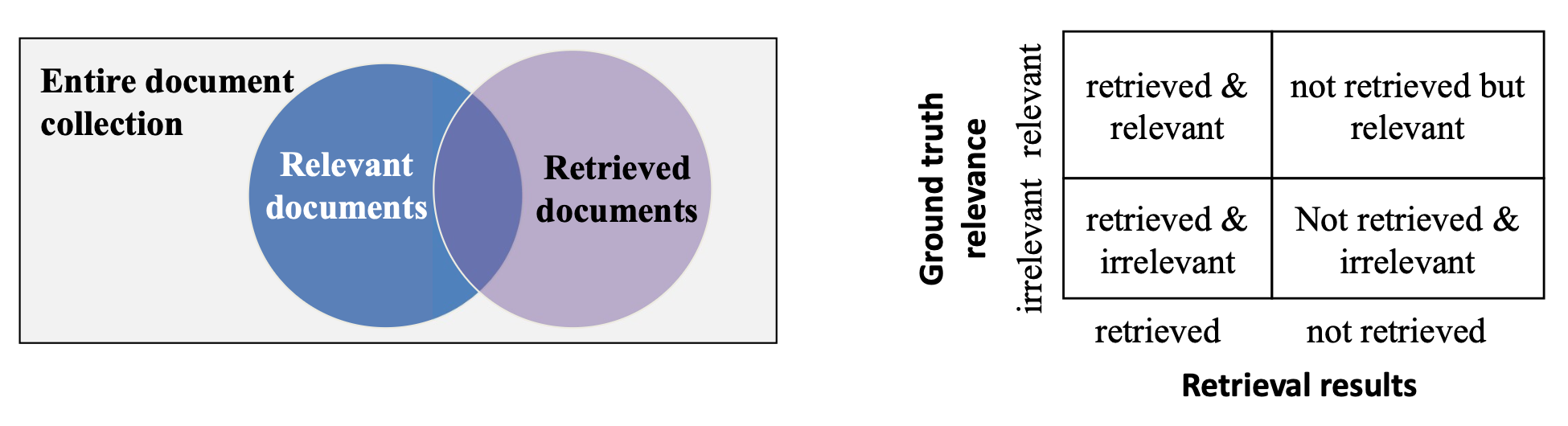
문서들은 쿼리에 대해 완전히 관련 있음(entirely relevant) 혹은
완전히 관련 없음(non-relevant) 인 경우가 거의 없다.
많은 경우, 우리는 단계적 관련성(graded relevance) 을 가진다.
(즉, 관련성 여부가 이진(binary)으로만 결정되지 않는다.)
- 예시: ESCI 데이터셋
  - Exact → 매우 관련 있음 (1.0)
  - Substitute → 어느 정도 관련 있음 (0.8)
  - Complement → 약하게 관련 있음 (0.2)
  - Irrelevant → 관련 없음 (0.0)
우리는 다양한 수준의 관련성(varying degrees of relevance) 을 반영할 수 있는
평가 지표가 필요하다.
- 이러한 지표는 다음을 만족해야 한다:
  - 더 높은 관련성을 가지며(ranked higher), 더 위에 위치한 문서들에
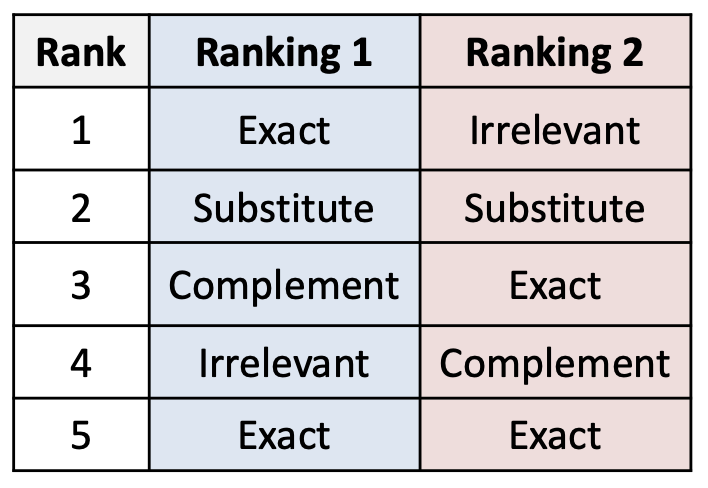
    더 큰 보상을 부여해야 한다.
    - 두 개의 순위(Ranking 1, Ranking 2)는
      모두 top-5 안에 동일한 수의 Exact 및 다른 관련(S, C) 문서들을 포함한다.
    - 그러나 Ranking 1이 더 좋다.
      그 이유는 더 관련성이 높은 문서들을 더 높은 위치에 배치하기 때문이다.

p16. 평가 지표: NDCG@N

가장 단순한 접근 방법으로, 단계적 관련성 판단(graded relevance judgments)을 사용하면
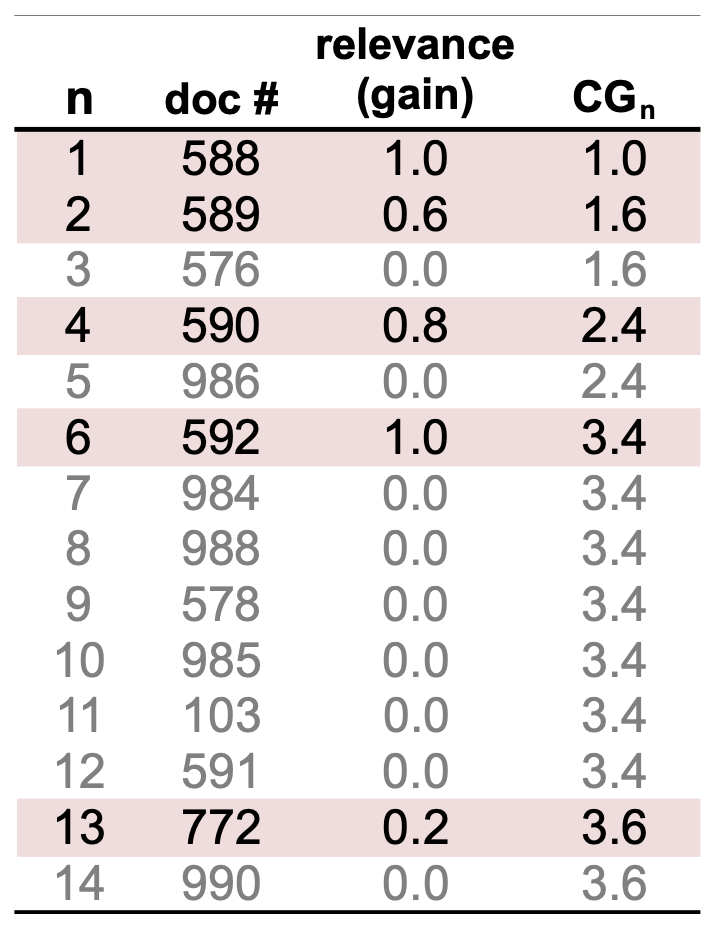
각 순위에서의 gain(획득량) 을 계산할 수 있다.
순위 $n$ 에서의 누적 획득량(Cumulative Gain, CG) 은
해당 순위까지의 총 누적 gain으로 정의된다:
\[CG_n = \sum_{i=1}^{n} rel_i\]
여기서 $rel_i$ 는 순위 $i$ 위치에 있는 문서의 단계적 관련성(graded relevance)이다.

p17. 평가 지표: NDCG@N

사용자는 더 높은 순위의 문서(higher-ranked documents) 를 더 중요하게 여긴다.
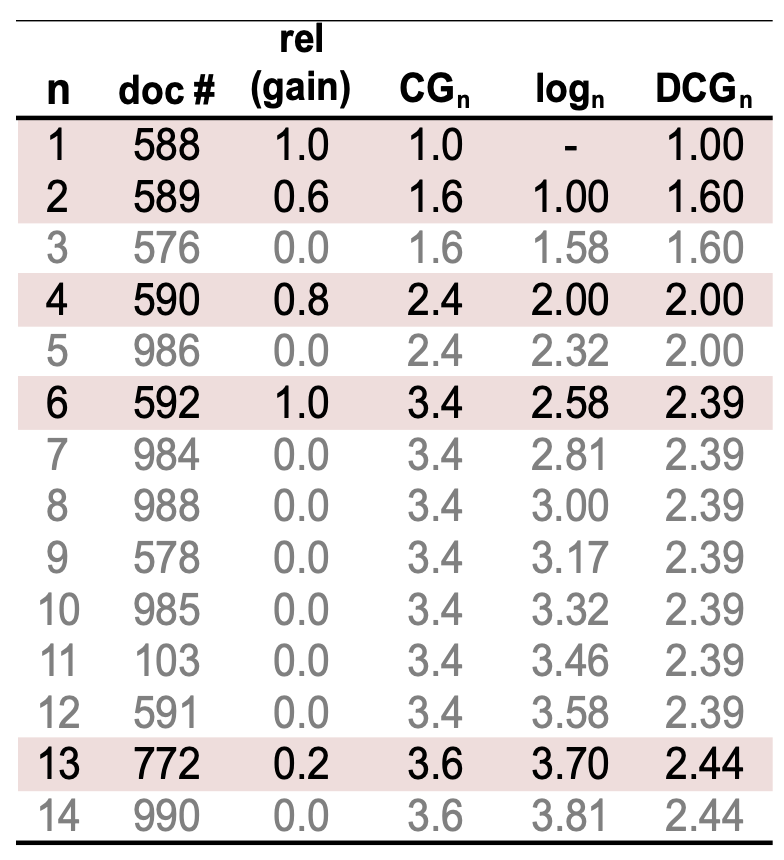
따라서 문서의 순위(position)에 따라 gain을 할인(discount)한다:
\[\frac{1}{\log_2(\text{rank})}\]
순위 $n$ 에서의 할인 누적 획득량(Discounted Cumulative Gain, DCG) 은 다음과 같이 정의된다:
\[DCG_n = rel_1 + \sum_{i=2}^{n} \frac{rel_i}{\log_2 i}\]
여기서 $rel_i$ 는 순위 $i$ 위치에 있는 문서의 단계적 관련성(graded relevance)이다.
이는 해당 순위까지의 총 누적 gain이며,
순위가 낮은 문서(lower-ranked documents) 는 더 적은 기여도를 갖는다.

p18. 평가 지표: NDCG@N

각 쿼리는 서로 다른 최대 가능한(different maximum possible) gain 을 가질 수 있다.
- 어떤 쿼리는 exact 매칭이 5개 있을 수 있지만,
  다른 쿼리는 단 1개만 있을 수도 있다.
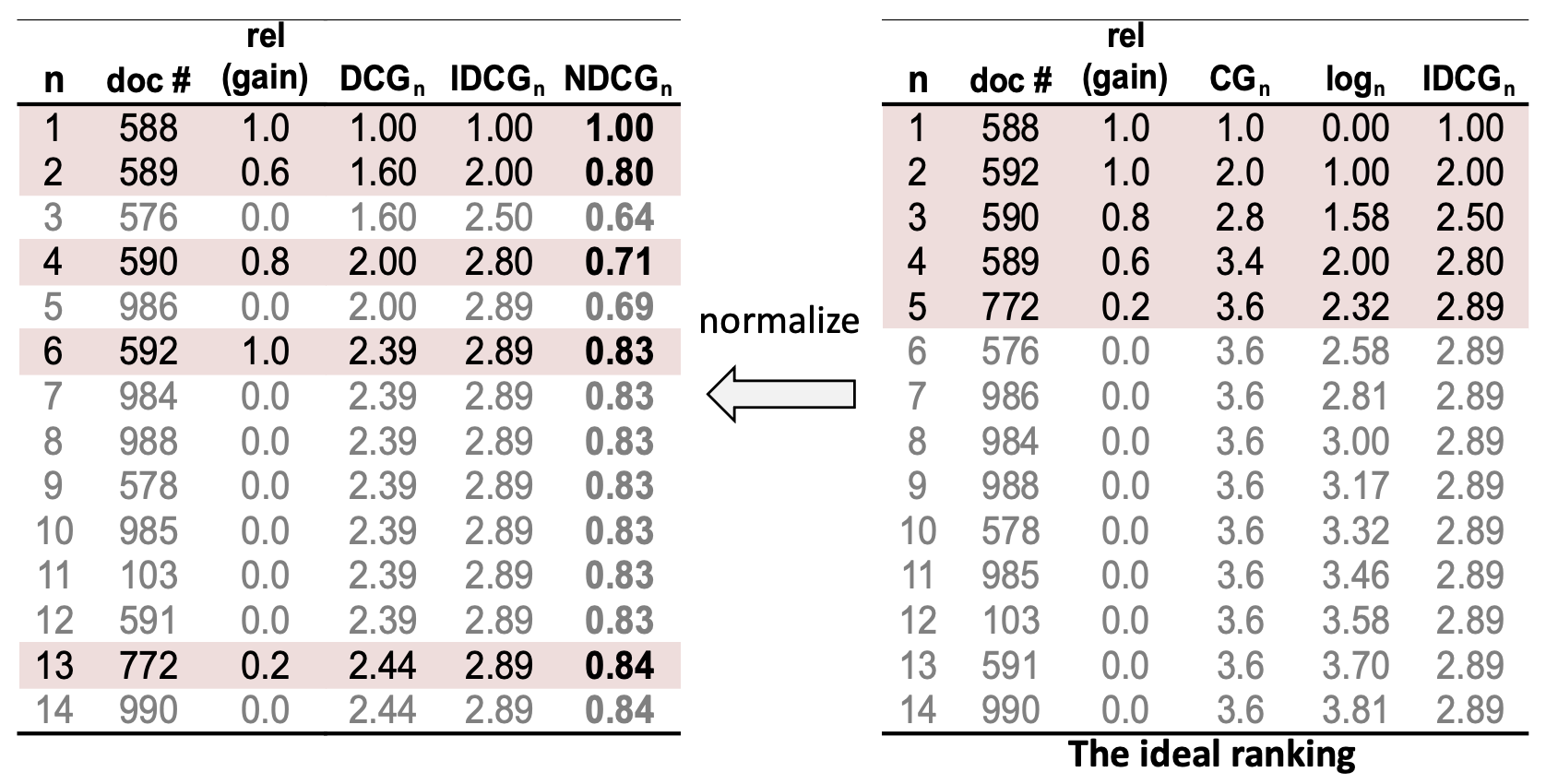
서로 다른 쿼리들 간에 DCG 값을 공정하게 비교하기 위해,
우리는 이를 정규화(normalize) 하여
이상적인 순위(ideal ranking) 가 1.0의 값을 갖도록 만든다.

p19. 평가 지표: NDCG@N

각 쿼리는 서로 다른 최대 가능한 gain 을 가질 수 있다!
- 어떤 쿼리는 exact 매칭이 5개 있을 수 있지만,
  다른 쿼리는 단 1개만 있을 수 있다.
쿼리들 간의 DCG 값을 공정하게 비교하기 위해,
우리는 DCG 값을 정규화(normalize) 한다.
이렇게 하면 이상적인 순위(ideal ranking) 가 1.0 의 값을 갖게 된다.

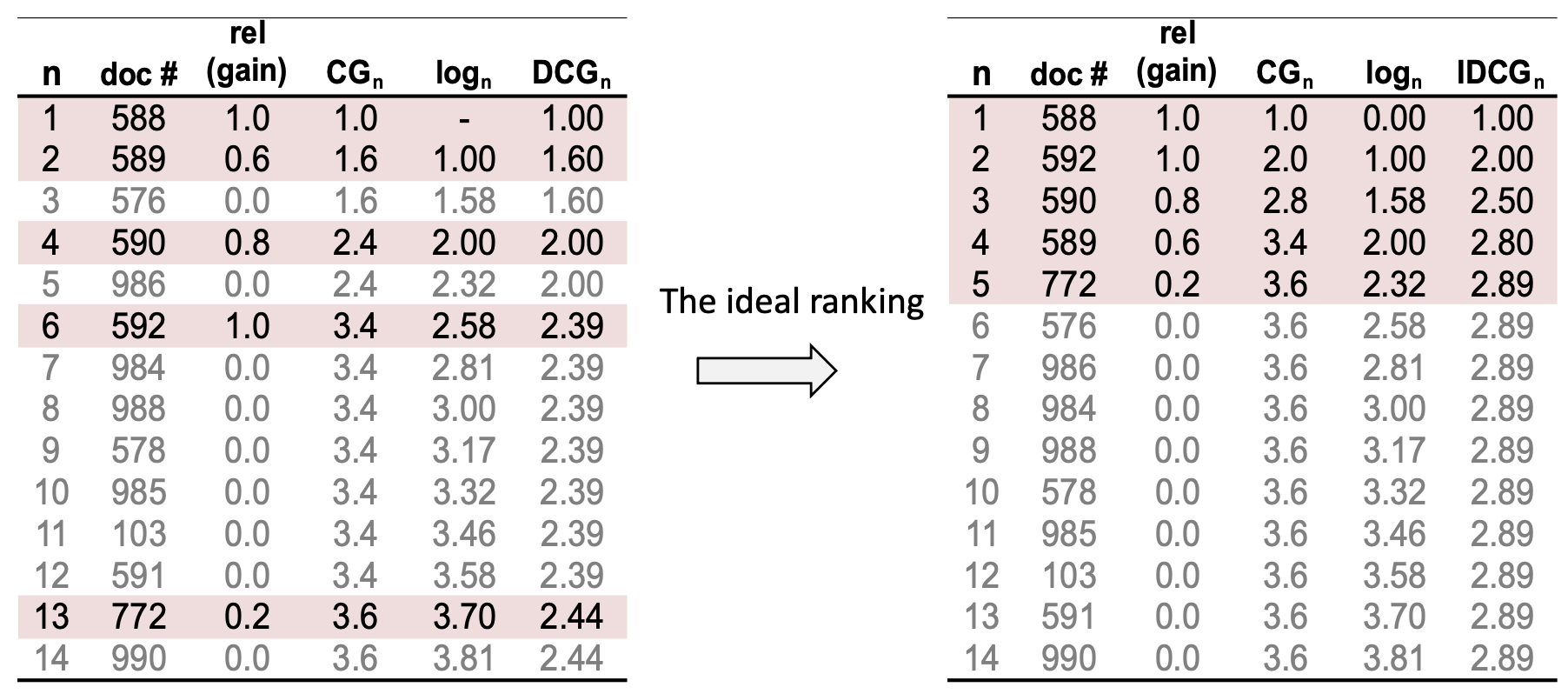
IDCG (Ideal Discounted Cumulative Gain)
이상적인 순위에서 얻을 수 있는 DCG 값.
Maximum achievable DCG
주어진 문서 집합에서 가능한 최댓값.
우리는 이 값을 정규화에 사용한다!

p20. 평가 지표: NDCG@N

정규화 할인 누적 이득(Normalized Discounted Cumulative Gain, NDCG) 은
이상적인 순위(ideal ranking)의 DCG 로 DCG 값을 나누어 정규화한다.
수식:
\[NDCG_n = \frac{DCG_n}{IDCG_n}\]

이 정규화(normalization)를 통해
서로 다른 쿼리들이 관련 문서의 개수가 다르더라도,
공정한 비교가 가능해진다.
시스템이 모든 관련 문서를 완벽하게 순위화할 경우,
NDCG = 1.0 이 된다.

p21. 평가 지표: 예시 (examples)

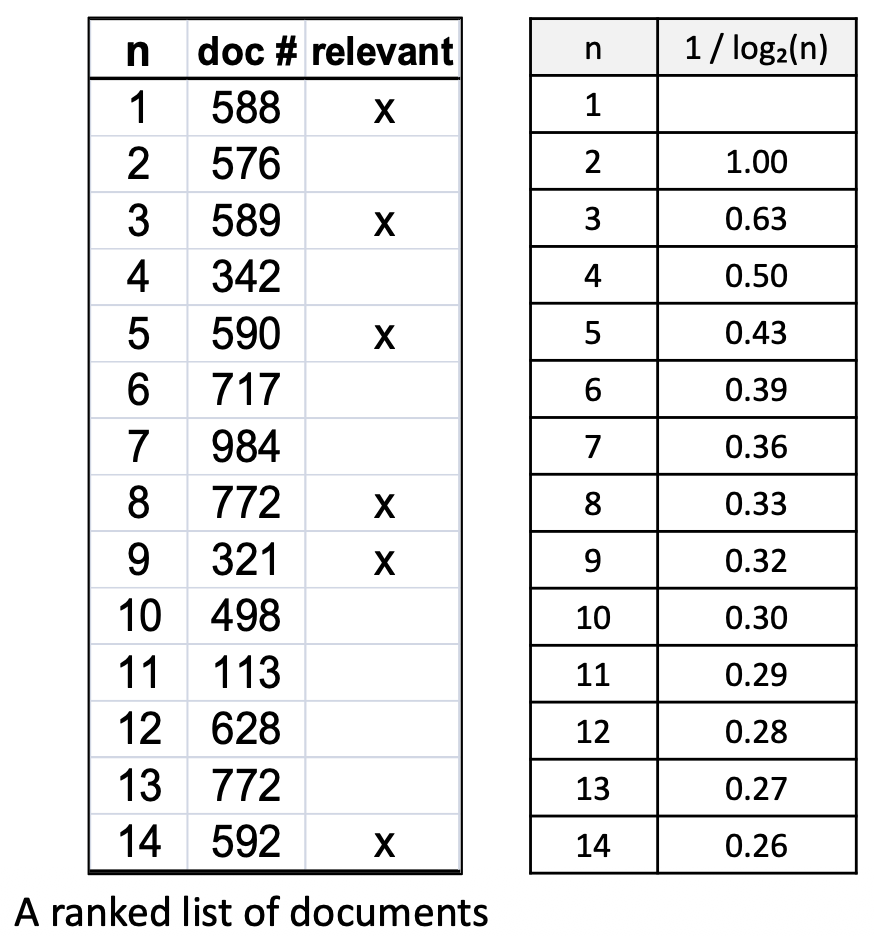
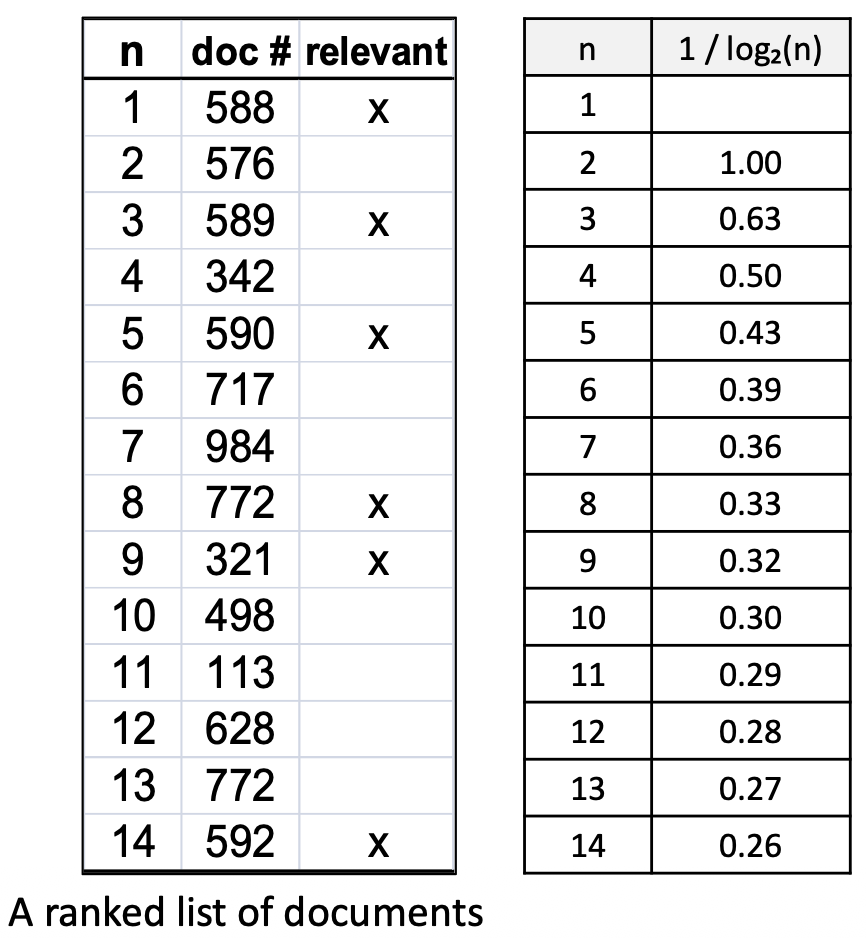
주어진 쿼리에 대해, 코퍼스 안에 6개의 관련 문서(six relevant documents) 가 있다고 가정하자.
- N = 5, N = 10 에 대해 NDCG@N 을 계산한다.
  (관련 문서: 1, 비관련 문서: 0)

p22. 평가 지표: 예시들 (Evaluation metrics: examples)

주어진 쿼리에 대해, 코퍼스 안에 6개의 관련 문서(six relevant documents) 가 있다고 가정하자.
- N = 5, N = 10 에 대해 NDCG@N 을 계산한다.
  (관련 문서: 1, 비관련 문서: 0)
\[DCG_n = rel_1 + \sum_{i=2}^{n} \frac{rel_i}{\log_2 i}\]

$DCG@5 = 1.0 + 0.63 + 0.43 = 2.06$

$DCG@10 = 1.0 + 0.63 + 0.43 + 0.33 + 0.32 = 2.71$

$IDCG@5 = 1.0 + 1.0 + 0.63 + 0.50 + 0.43 = 3.56$

$IDCG@10 = 1.0 + 1.0 + 0.63 + 0.50 + 0.43 + 0.39 = 3.95$

$NDCG@5 = \frac{2.06}{3.56} = 0.58$

$NDCG@10 = \frac{2.71}{3.95} = 0.69$

p24. 어휘 기반 검색 (Lexical retrieval)

어휘 기반 검색(Lexical retrieval) 은
쿼리(query)와 문서(document)를 단어 개수(word counts) 에 기반한
희소 벡터(sparse vectors) 로 표현하는 방식을 의미한다.
- 쿼리와 문서 사이의 정확한 단어 일치(exact word matching) 에 초점을 맞춘다.
다룰 내용:
- 역색인(inverted index) 이 어떻게 효율적인 어휘 기반 검색을 가능하게 하는가
- 어떻게 관련성 점수(relevance scores) 를 계산하는가
  (예: TF-IDF의 코사인 유사도, BM25)

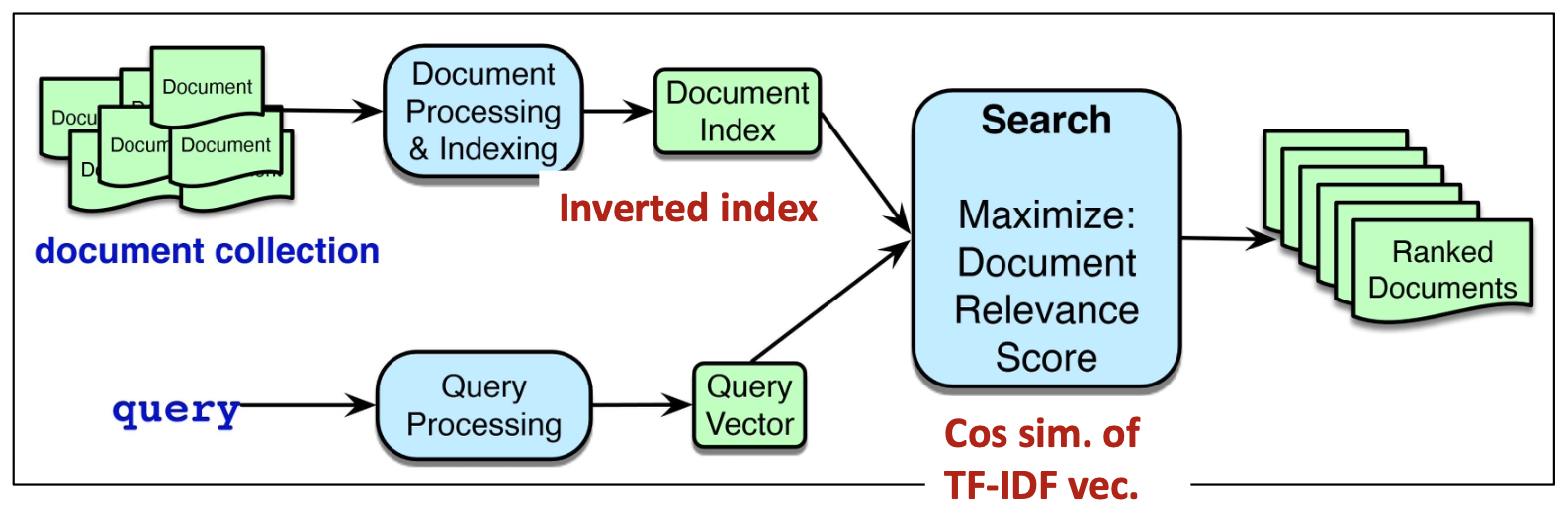
(아래 그림 설명)
문서 컬렉션(document collection)은
문서 처리 및 색인(Document Processing & Indexing)을 거쳐
문서 인덱스(Document Index) 로 변환된다.
이는 검색을 위한 핵심 구조인 역색인(inverted index) 을 형성한다.
사용자의 쿼리는 쿼리 처리(Query Processing)를 통해
쿼리 벡터(Query Vector) 로 변환된다.
검색(Search) 단계에서는
문서 인덱스와 쿼리 벡터를 비교하여
TF-IDF 벡터의 코사인 유사도(Cosine similarity) 및 BM25 점수 등을 사용해
문서 관련성 점수(Document Relevance Score) 를 계산한다.
최종적으로 시스템은 순위화된 문서들(Ranked Documents) 을 반환한다.

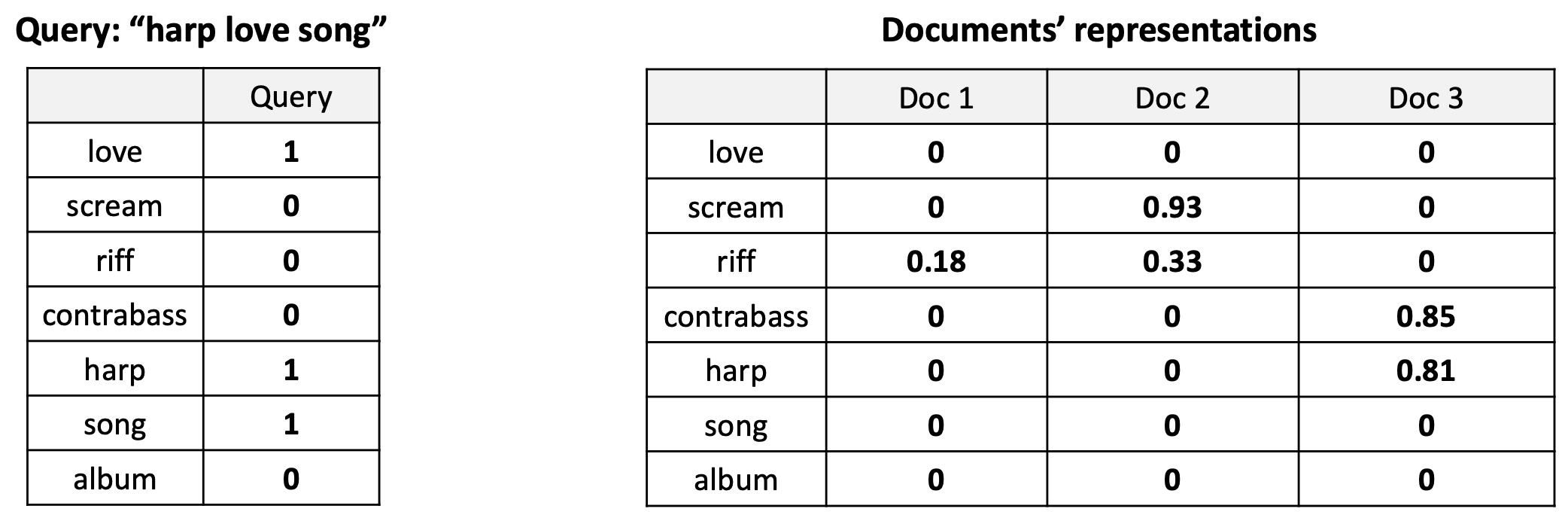
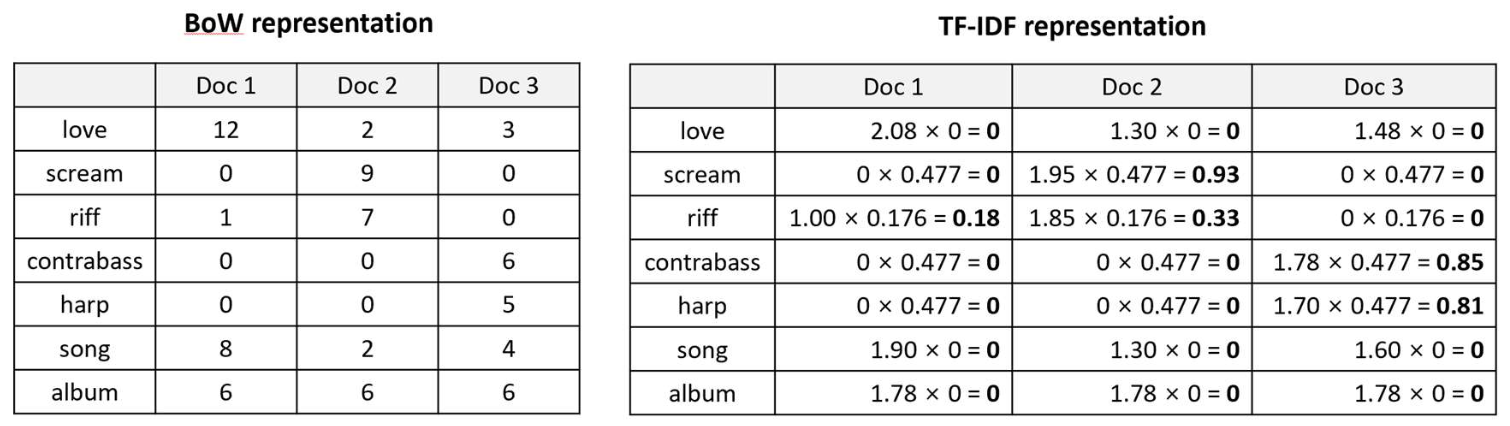
p31. 희소 벡터(TF-IDF)를 이용한 검색 (Retrieval with sparse vector, TF-IDF)

Relevance score (관련성 점수)

\[\cos(q, d_1) = \frac{(1 \times 0 + 1 \times 0 + 1 \times 0)}{(\sqrt{1^2 + 1^2 + 1^2}) \times \sqrt{0.18^2}} = \frac{0}{(1.732) \times (0.18)} = 0\] \[\cos(q, d_2) = \frac{(1 \times 0 + 1 \times 0 + 1 \times 0)}{(\sqrt{1^2 + 1^2 + 1^2}) \times \sqrt{0.93^2 + 0.33^2}} = \frac{0}{(1.732) \times (0.987)} = 0\] \[\cos(q, d_3) = \frac{(1 \times 0 + 1 \times 0.81 + 1 \times 0)}{(\sqrt{1^2 + 1^2 + 1^2}) \times \sqrt{0.85^2 + 0.81^2}} = \frac{0.81}{(1.732) \times (1.175)} = 0.40\]

Relevance ranking (관련성 순위)

Doc 3 > Doc 1 = Doc 2

p32. 희소 벡터(TF-IDF)를 이용한 검색 (Retrieval with sparse vector, TF-IDF)

모든 문서를 고려해야 할까?
- 아니다! 쿼리 단어를 전혀 포함하지 않은 문서는 무시할 수 있다.
  그런 문서들의 코사인 유사도는 0이 될 것이기 때문이다.
그렇다면, 어떻게 쿼리 용어를 포함하는 모든 문서를 효율적으로 찾을 수 있을까?
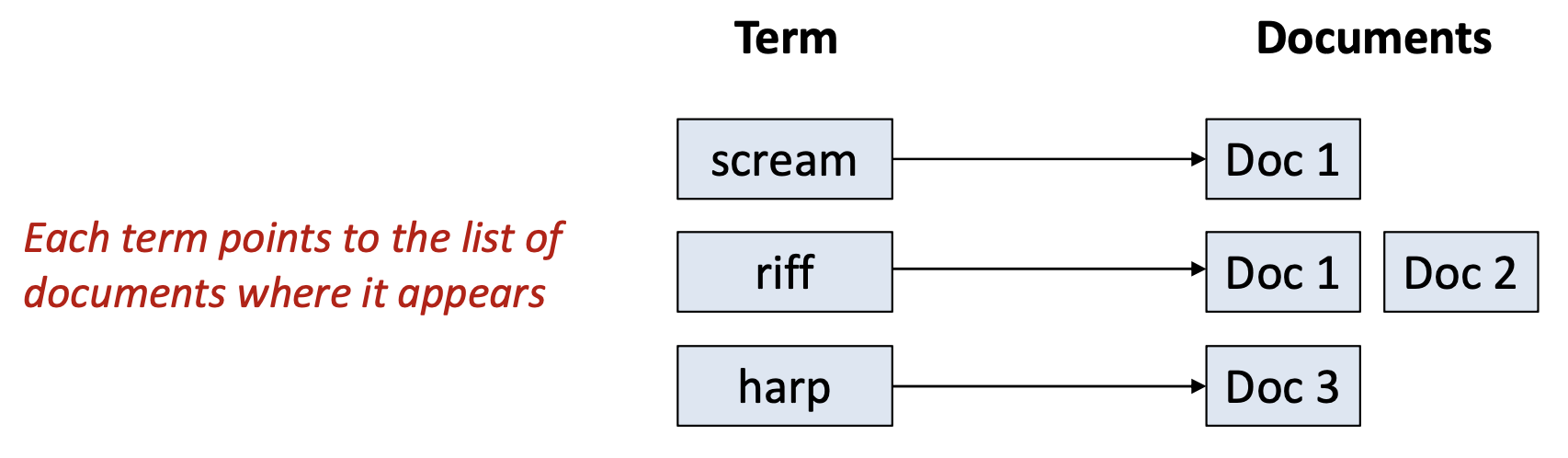
- 용어(terms)를 그 용어를 포함하는 문서(documents)에 매핑하는
  데이터 구조(data structure)가 필요하다.
- 이 구조를 역색인(inverted index) 이라고 부른다.

(각 용어는 해당 용어가 나타나는 문서들의 목록을 가리킨다)

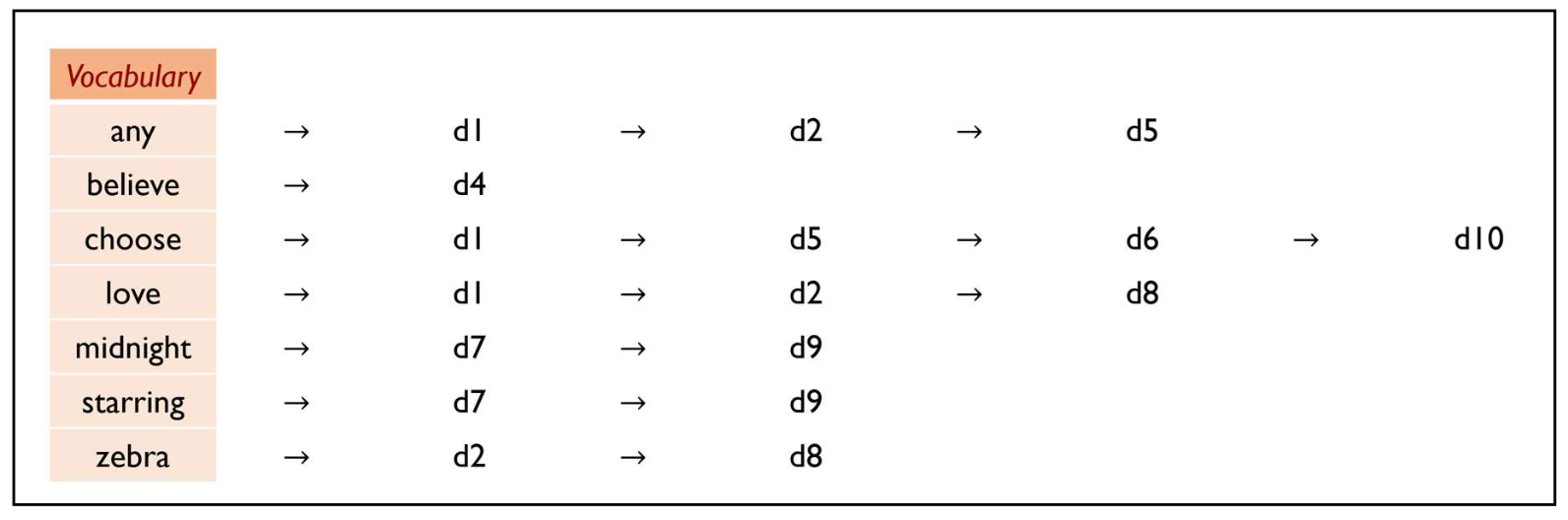
p33. 역색인 (Inverted index)

역색인(inverted index) 은
각 용어(term)를 그 용어를 포함하는 문서들의 목록(list of documents)과 매핑한다.
역색인은 두 부분으로 구성된다:
- 사전(Dictionary 또는 vocabulary):
  컬렉션에 존재하는 고유 용어(unique terms) 들의 집합
- 포스팅 리스트(Postings Lists):
  각 용어가 등장하는 문서들(documents) 의 목록
이는 주어진 쿼리에 대해
빠른 문서 조회(fast document lookup) 를 가능하게 한다.

p34. 역색인 구축 (Inverted index: construction)

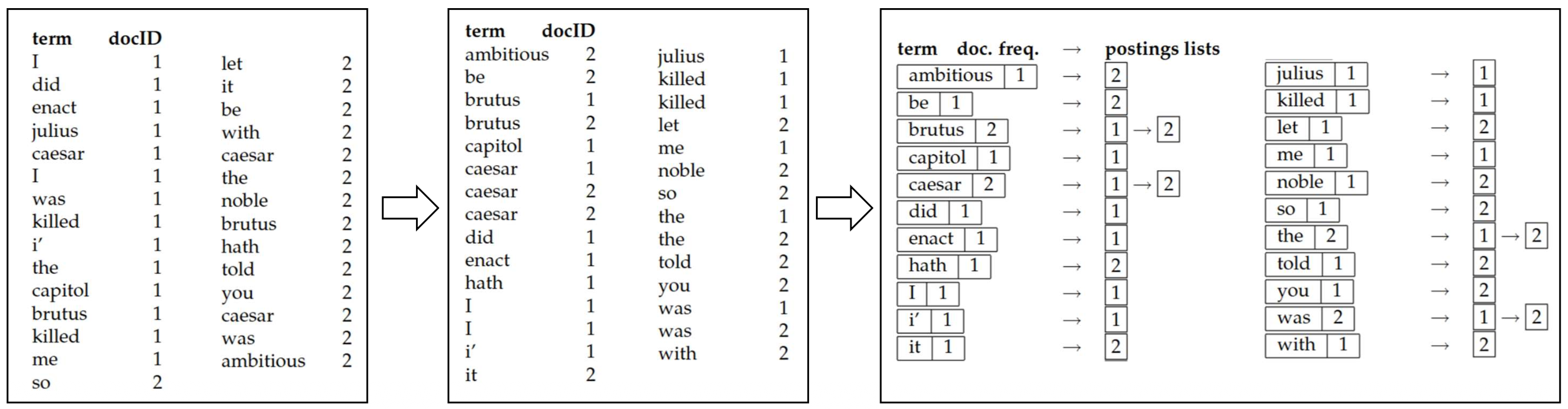
1. 모든 용어–문서 쌍(term–document pairs) 수집

각 문서를 단어들로 토큰화한다.
모든 토큰으로부터 (term, docID) 쌍을 생성한다.

2. 용어(그리고 문서 ID)에 따라 정렬

모든 쌍을 용어 기준으로 알파벳순으로 정렬하고, 그다음 docID로 정렬한다.

3. 포스팅 리스트(posting lists) 생성

동일한 용어에 대한 문서 ID들을 하나의 리스트로 병합한다.
선택적으로, 용어 통계 정보를 저장할 수 있다:
• df (document frequency)
• tf (term frequency per document)

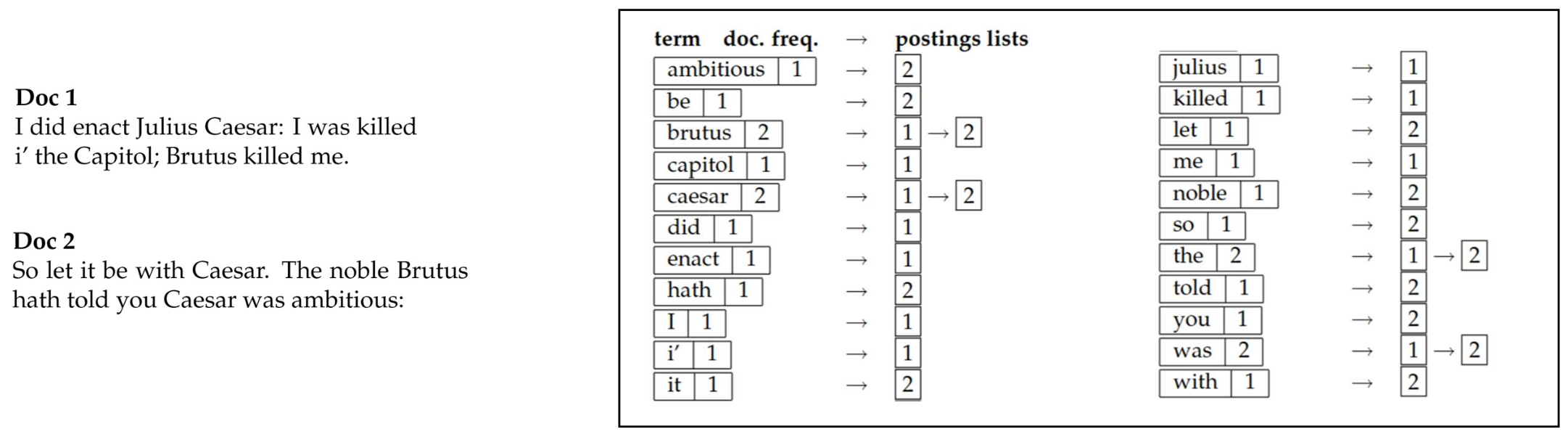
Doc 1
I did enact Julius Caesar: I was killed
i’ the Capitol; Brutus killed me.

Doc 2
So let it be with Caesar. The noble Brutus
hath told you Caesar was ambitious:

p35. 역색인(Inverted index)

역색인(inverted index)은 시스템이 관련 없는 모든 문서들을 건너뛸 수 있도록 해 준다.
전체 컬렉션을 읽는 대신, 우리는 쿼리 용어(query terms) 에 대한 포스팅(postings)만 조회한다.
이러한 리스트들의 합집합(union) 은 우리에게 랭킹을 위한 후보 집합(candidate set) 을 제공한다.
- 전통적인 불리언 검색(Boolean retrieval)에서는 교집합(intersection) 이 사용되었다.
- 현대 시스템들은 보통 랭킹 전에 후보들을 수집하기 위해 합집합(union) 을 사용한다.

Query: “zebra believe” → {d2, d4, d8}
Query: “zebra love” → {d1, d2, d8}

우리는 오직 이 후보들에 대해서만 관련성 점수를 계산한다!

p36. TF-IDF 기반 역색인(Inverted index) 요약

검색 과정(Search process)
1. 역색인(inverted index)을 사용하여,
  하나 이상의 쿼리 용어를 포함하는 문서들만 검색한다.
2. 각 후보 문서는 쿼리 벡터와의 코사인 유사도(cosine similarity)에 의해 순위가 매겨진다.
단순화된 점수 함수(a simplified scoring function)
\[\text{Score}(q, d) = \sum_{t \in q} \text{tfidf}_{t,d}\]
- 각 $\text{tfidf}_{t,d}$ 는 문서 d에 대한
  정규화된 TF-IDF 벡터(normalized TF-IDF vector)의 한 요소를 의미한다.
- 쿼리 벡터의 정규화(query vector normalization)는
  모든 문서에 대해 일정하므로 생략된다.

p38. 왜 1995년의 방법을 이야기하는가?

BM25는 현대 검색 시스템의 중추(backbone)로 남아 있다.
- BM25는 단순하지만 효과적인(simple yet effective) 관련성 확률 모델을 제공한다.
- 오래된 방법임에도 불구하고, 강건하고(robust), 해석 가능하며(interpretable), 계산 효율적(computationally efficient) 이다.
오늘날에도 여전히 널리 사용된다!
- 많은 검색 엔진들(예: Elasticsearch, Lucene, Solr)이 기본 랭킹 함수로 BM25를 사용한다.
- 딥러닝 기반 검색기(deep learning–based retrievers)를 평가할 때 기준선(baseline) 역할을 한다.
- 구현이 쉽고, 학습이 필요 없으며, GPU 지원에 의존하지 않는다.

p39. BM25

우리가 역색인(inverted index)을 사용하여 후보 문서 집합(candidate set) 을 가져오면,
이제 쿼리에 대한 문서의 관련성(relevance) 에 따라 문서를 순위화해야 한다.
BM25는 어휘 기반 검색(lexical retrieval)에서 가장 널리 사용되는 순위 함수(ranking function) 중 하나이다.
- BM = Best Match, 25 = 이 함수의 25번째 버전이라는 의미이다.
- BM25는 TF-IDF의 철학 — 즉, 단어 빈도(term frequency) 와 역문서빈도(inverse document frequency) 의 결합 — 을 따르지만, 여기에 몇 가지 수정 사항을 추가한다.

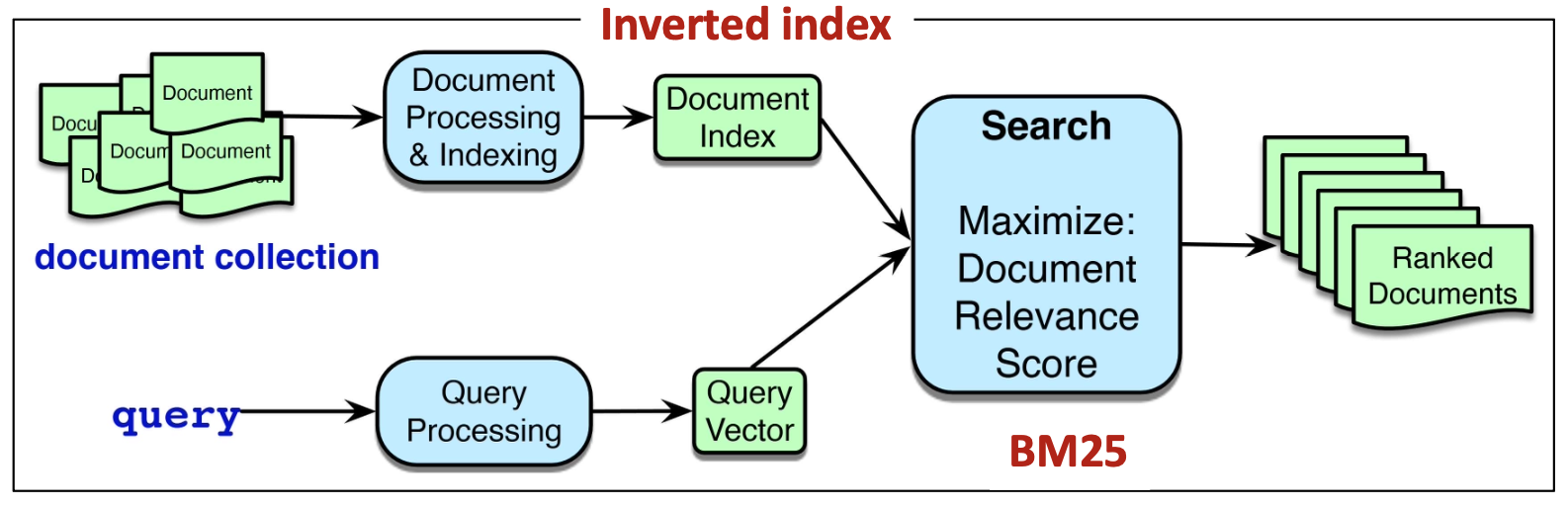
(아래 그림 설명 — 사용자가 직접 삽입)
문서 컬렉션(document collection)은 문서 처리 및 색인(Document Processing & Indexing)을 거쳐 문서 인덱스(Document Index) 로 변환된다.
쿼리는 쿼리 처리(Query Processing)를 거쳐 쿼리 벡터(Query Vector) 로 변환된다.
검색(Search)은 BM25를 사용하여 문서 관련성 점수(Document Relevance Score) 를 최대화하는 문서들을 찾는다.
최종적으로 시스템은 순위화된 문서들(Ranked Documents) 을 반환한다.

p40. BM25: 점수 함수

BM25는 TF-IDF의 철학 — 즉, 용어 빈도(term frequency) 와
역문서빈도(inverse document frequency) 의 결합 — 을 따르지만,
몇 가지 수정 사항을 도입한다.
점수 함수
- 파란색 부분: 역문서빈도(Inverse document frequency part)
  - $N$: 전체 문서 수
  - $n(t)$: 용어 $t$ 를 포함하는 문서 수 (문서 빈도)
- 빨간색 부분: 용어 빈도 부분(term frequency part)
  - $f(t,d)$: 문서 $d$ 내 용어 $t$의 등장 횟수
  - $\mid d \mid$: 문서 $d$의 전체 단어 수(문서 길이)
  - $\text{avgdl}$: 평균 문서 길이
TF와 IDF는 BM25에서 다르게 정의되며, 이에 대해서는 이후에 자세히 살펴본다.

p41. BM25 — 완화된 역문서빈도(smoothed inverse document frequency)

TF-IDF에서, 역문서빈도(IDF)는 한 용어가 얼마나 정보적인지를 정량화한다:
\[IDF(t) = \log\left(\frac{N}{n(t)}\right)\]
- $N$: 전체 문서 수
- $n(t)$: 용어 $t$를 포함하는 문서의 수 (document frequency)
제한점(Limitation):
- 이것은 희귀한 용어(rare terms)를 강화하고, 빈번한 용어(frequent terms)는 패널티를 준다, 그러나 극단적인 값(extreme values) 을 만들어낼 수 있다.
  - 희귀한 용어는 지나치게 큰 가중치를 얻고, 일반적인 용어는 너무 빠르게 0으로 떨어진다!

p42. BM25 — 스무딩된 역문서빈도 (smoothed inverse document frequency)

BM25에서, 역문서빈도(IDF)는 다음과 같다:
\[\text{IDF}(t) = \log\left(\frac{N - n(t) + 0.5}{n(t) + 0.5} + 1\right)\]
- $N$: 전체 문서의 개수
- $n(t)$: 용어 $t$를 포함하는 문서의 개수 (문서 빈도, document frequency)
여전히 희귀한 용어는 증가시키고, 자주 등장하는 용어는 감소시키지만, 극단적인 값을 방지하기 위해 스무딩을 도입한다.
확률적 모델(probabilistic model)의 영감에서, IDF는 한 용어가 존재하는 것보다 존재하지 않을 가능성이 얼마나 더 높은지를 나타낸다.

Symbol	Meaning
$N - n(t)$	용어가 없는 문서의 수 (부재 확률의 근사)
$n(t)$	용어가 존재하는 문서의 수 (존재 확률의 근사)
$+0.5$	스무딩 항 ( $n(t)=0$ 일 때 분모가 0이 되는 것을 방지 )

BM25 — 용어 빈도와 문서 길이 정규화 (term frequency and length normalization)

TF-IDF에서 용어 빈도(TF)는 다음과 같다:
\[TF(t, d)= \begin{cases} 1 + \log(f(t,d)), & \text{if } f(t,d) > 0 \\ 0, & \text{otherwise} \end{cases}\]
$f(t,d)$: 용어 (t)가 문서 (d)에서 등장한 원시(raw) 횟수
- 단순히 등장 횟수 (f(t,d))를 세는 것은 반복되는 용어를 과도하게 강조할 수 있다.
- 로그 스케일링(logarithmic scaling)은 증가 속도를 완화한다 — 등장 횟수가 두 배가 되어도 중요도가 두 배가 되지는 않는다.
제약(Limitation):
- TF 스케일링은 정적(static) 이다 — 문서 길이에 따라 조정되지 않는다!
  - 더 긴 문서들은 전체적으로 더 많은 단어들을 포함하고 있다는 이유만으로 TF 값이 더 높아지는 경향이 있다.
  - 더 짧은 문서들은 그 용어가 매우 집중되어 있음에도 불구하고 종종 과소평가(underweighted)된다.
- 즉, TF-IDF는 “긴 문서에서의 여러 번의 등장”과
  “짧은 문서에서의 소수의 집중된 등장”을 구분하지 못한다.

p44. BM25 — 용어 빈도(TF)와 길이 정규화(length normalization)

BM25에서 용어 빈도(TF)는 다음과 같다:
- $f(t, d)$ : 문서 $d$ 안에서 용어 $t$가 등장한 횟수(raw count)
- $\mid d \mid$ : 문서 $d$의 전체 길이(단어 수)
- $avgdl$ : 전체 문서의 평균 길이

	역할 Role	효과 및 예시 Effect & Example
$k_1$	TF 포화(saturation) 조절 용어 빈도의 영향이 얼마나 빨리 포화되는지를 제어함	- $k_1 = 0$이면: TF 효과가 사라짐 → 순수 IDF처럼 동작 - $k_1 = 2$이면: TF가 거의 선형적으로 증가함 (raw count처럼) → $k_1$이 클수록 TF 포화가 느리게 일어남
$b$	문서 길이 정규화(weight) 문서 길이가 점수에 얼마나 강하게 영향을 미치는지를 결정함	- $b = 0$이면: 길이 정규화 없음 → 긴 문서가 불리하지 않음 - $b = 1$이면: 완전한 길이 정규화 → 긴 문서는 길이에 비례하여 페널티를 받음

p45. BM25 — 용어 빈도와 길이 정규화

BM25에서 용어 빈도(TF)는 다음과 같다:
- $f(t,d)$ : 문서 $d$ 안에서 용어 $t$의 raw count
- $\mid d \mid$ : 문서 $d$의 전체 용어 수(길이)
- avgdl : 평균 문서 길이

단순화를 위해 먼저 $1 - b + b\cdot \frac{\mid d \mid}{avgdl}$ 항을 무시한다.
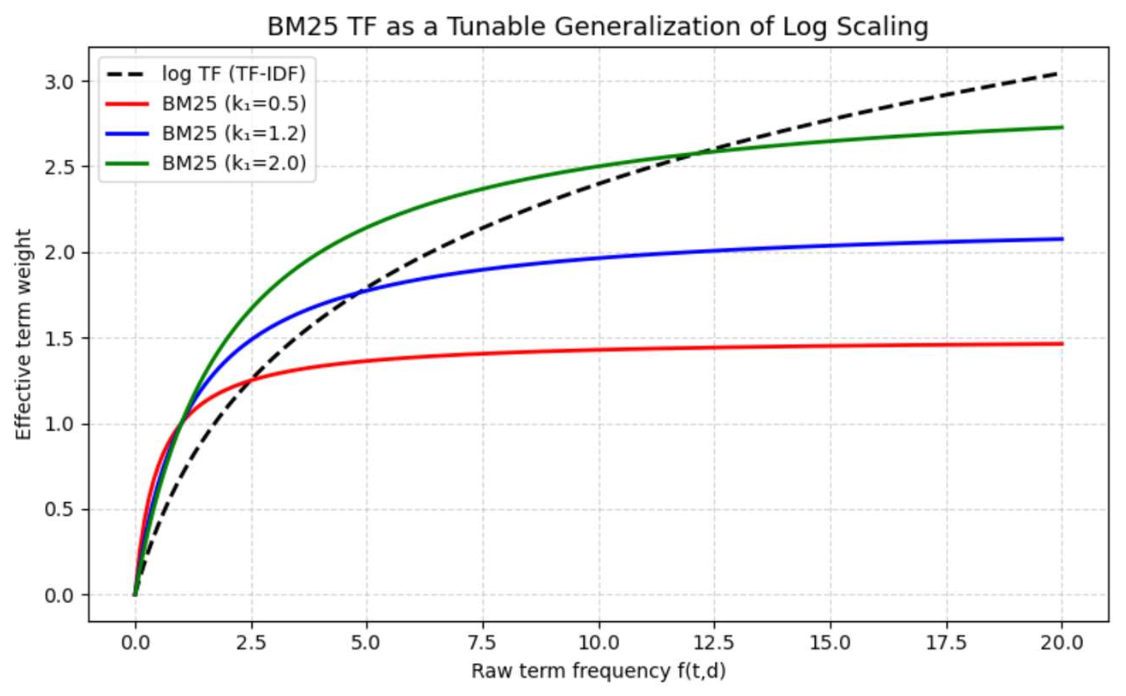
아래 함수는 로그 함수의 일반화된 형태로 볼 수 있으며,
$k_1$이 TF 기여도가 얼마나 빠르게 포화되는지를 조절한다.
\[TF(t,d)=\dfrac{f(t,d)\cdot (k_1+1)}{f(t,d)+k_1}\]
$k_1$은 일반적으로 1.2에서 2 사이로 설정된다.

p46. BM25 — 용어 빈도와 길이 정규화

BM25에서, 용어 빈도(TF)는 다음과 같다:
- $ f(t,d) $: 문서 $d$ 안에서 용어 $t$의 등장 횟수(raw count)
- $ \mid d \mid $: 문서 $d$의 전체 용어 수(길이)
- $ avgdl $: 평균 문서 길이
해석(Interpretation):
- $ B = 1 - b + b\cdot \dfrac{\mid d \mid}{avgdl} $ 라고 하자.
- 문서 $d$의 길이가 정확히 평균 문서 길이라면?
  - $ B = 1 - b + b = 1 $, 정규화할 필요 없음
- 문서 $d$가 평균보다 더 길다면 (예: $ \mid d \mid = 2\times avgdl $)?
  - $ B = 1 - b + 2b = 1 + b > 1 $
- 문서 $d$가 평균보다 짧다면 (예: $ \mid d \mid = 0.5\times avgdl $)?
  - $ B = 1 - b + 0.5b = 1 - 0.5b < 1 $
- $ b = 1 $: 완전한 문서 길이 정규화
- $ b = 0 $: 문서 길이 정규화 없음
- $ b $는 일반적으로 0.75로 설정됨

p47. BM25: 예시

$ N $: 전체 문서 수
$ n(t) $: 용어 $ t $가 포함된 문서의 개수(document frequency)
$ f(t,d) $: 문서 $ d $에서 용어 $ t $의 등장 횟수(raw count)
$ \mid d \mid $: 문서 $ d $의 전체 용어 수(길이)
$ avgdl $: 평균 문서 길이

예시:
- 쿼리 $q$: “any zebra”, 문서 $d$: “zebra any love any”
- 10,000개의 문서; “any”는 그중 1,000개의 문서에 등장; “zebra”는 10개의 문서에 등장
- $avgdl = 10,\; k_1 = 1.2,\; b = 0.75$
\[\begin{align} \text{BM25}(q,d) &= \log\!\left( \frac{10,000 - 1,000 + 0.5}{1,000 + 0.5} + 1 \right) \cdot \frac{2 \cdot (1.2 + 1)} {2 + 1.2\left(1 - 0.75 + 0.75 \cdot \frac{4}{10}\right)} \\[14pt] &\quad+\; \log\!\left( \frac{10,000 - 10 + 0.5}{10 + 0.5} + 1 \right) \cdot \frac{1 \cdot (1.2 + 1)} {1 + 1.2\left(1 - 0.75 + 0.75 \cdot \frac{4}{10}\right)} \end{align}\]

p48. 어휘 기반 검색: 요약

어휘 기반 검색(Lexical retrieval)
- 쿼리와 문서를 단어 일치 기반의 희소 벡터(sparse vectors) 로 표현한다 (TF-IDF, BM25).
- 큰 말뭉치 위에서 효율적인 검색을 가능하게 하는 역색인(inverted index) 을 사용한다.
장점(Pros):
- 대규모 검색에서도 단순하고 효율적이다.
- 투명함 — 설명하고 해석하기 쉽다.
- 학습 데이터가 필요 없다.
단점(Cons):
- 의미적 정보나 동의어(semantic meaning or synonyms) 를 포착하지 못한다.
  - 예: 쿼리 “car insurance” vs. 문서 “automobile insurance” (정확히 일치하지 않아 매칭 실패)
- 어휘 불일치(vocabulary mismatch) 에 민감하다.
  - 예: 쿼리 “AI job openings” vs. 문서 “machine learning engineer positions”
    (표현이 달라서 매칭 실패)

p49. 추천 읽기 (Recommended readings)

Books:
- Chapter 11: Information Retrieval and Retrieval-Augmented Generation, Speech and Language Processing

대학원 수업, 텍스트 마이닝