[텍스트 마이닝] 13. Search 2 - Dense Retrieval 1

게시 2025/12/01 업데이트 2025/12/12

By 김성진

14 분읽는 시간

p5. 검색: 개요

우리는 실제(real-world) 검색 엔진을 작동시키는 핵심 기술들을 배우게 된다.

어휘 기반 검색 (Lexical retrieval)
- 쿼리와 문서를 단어 개수 기반의 희소 벡터(sparse vectors)로 표현한다.
- 쿼리와 문서 사이의 정확한 단어 일치(exact word matching)에 초점을 맞춘다.
고밀도 임베딩 검색 (Dense retrieval)
- 쿼리와 문서를 연속적인 벡터 공간에서 표현하기 위해 고밀도 임베딩(dense embeddings)을 사용한다.
- 의미적 유사성(semantic similarity)을 포착하여 키워드가 겹치지 않는 경우에도 검색이 가능하게 한다.
LLM 기반 향상 검색 (LLM-enhanced retrieval)
- 대규모 언어 모델(LLMs)을 활용하여 검색 프로세스를 향상시킨다.

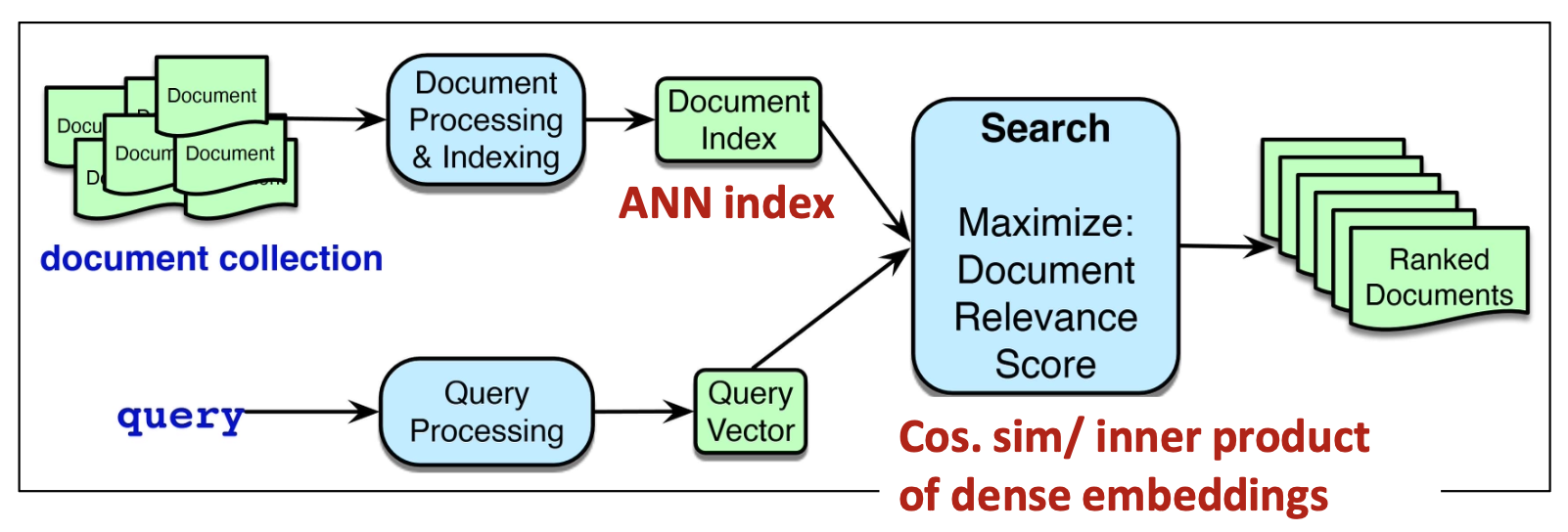
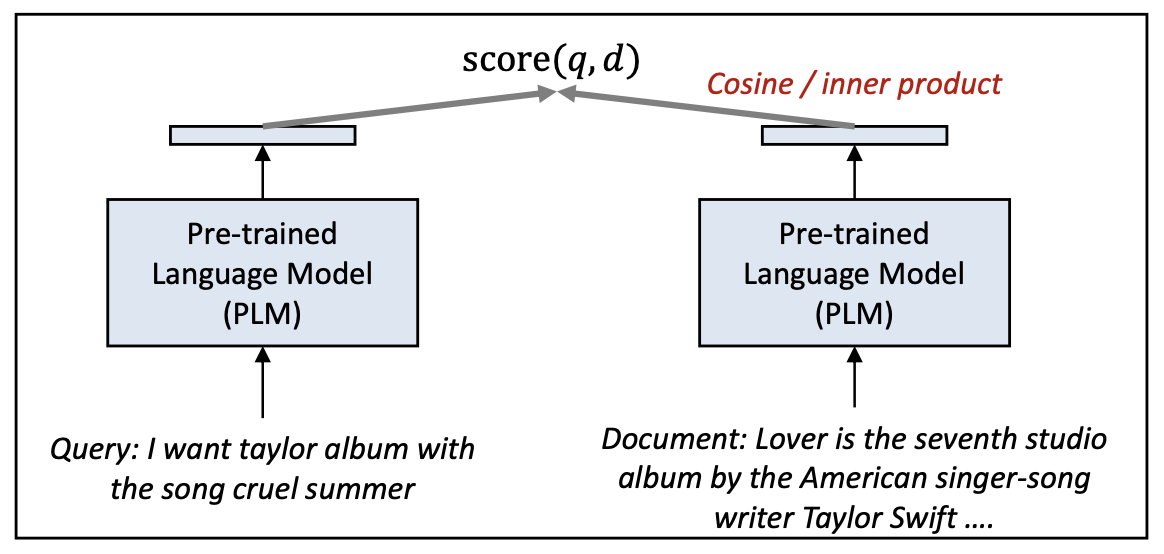
p7. 밀집 검색(Dense retrieval)

미리 학습된 모델들(예: BERT)로부터의 밀집 임베딩(dense embeddings)을 사용하여
쿼리와 문서를 표현한다.

1. 각 문서는 밀집 벡터(dense vector)로 인코딩되고 벡터 인덱스(vector index)에 저장된다
(이를 ANN index라고 부른다).

2. 쿼리 시점에는 입력 쿼리 또한 밀집 벡터로 인코딩되며,
시스템은 높은 임베딩 유사도(high embedding similarity)
(예: 코사인 유사도 또는 내적)을 가진 문서들을 검색한다.

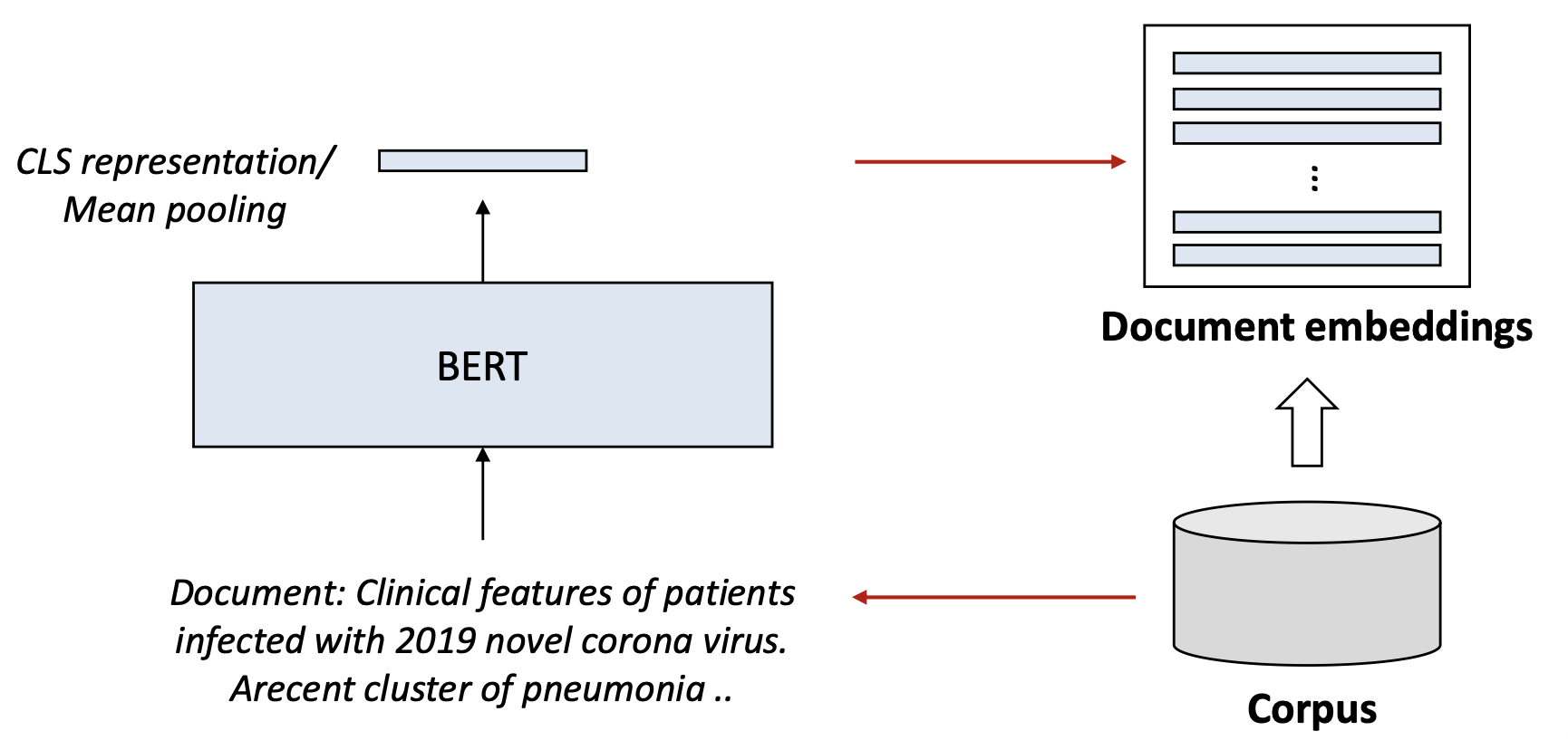
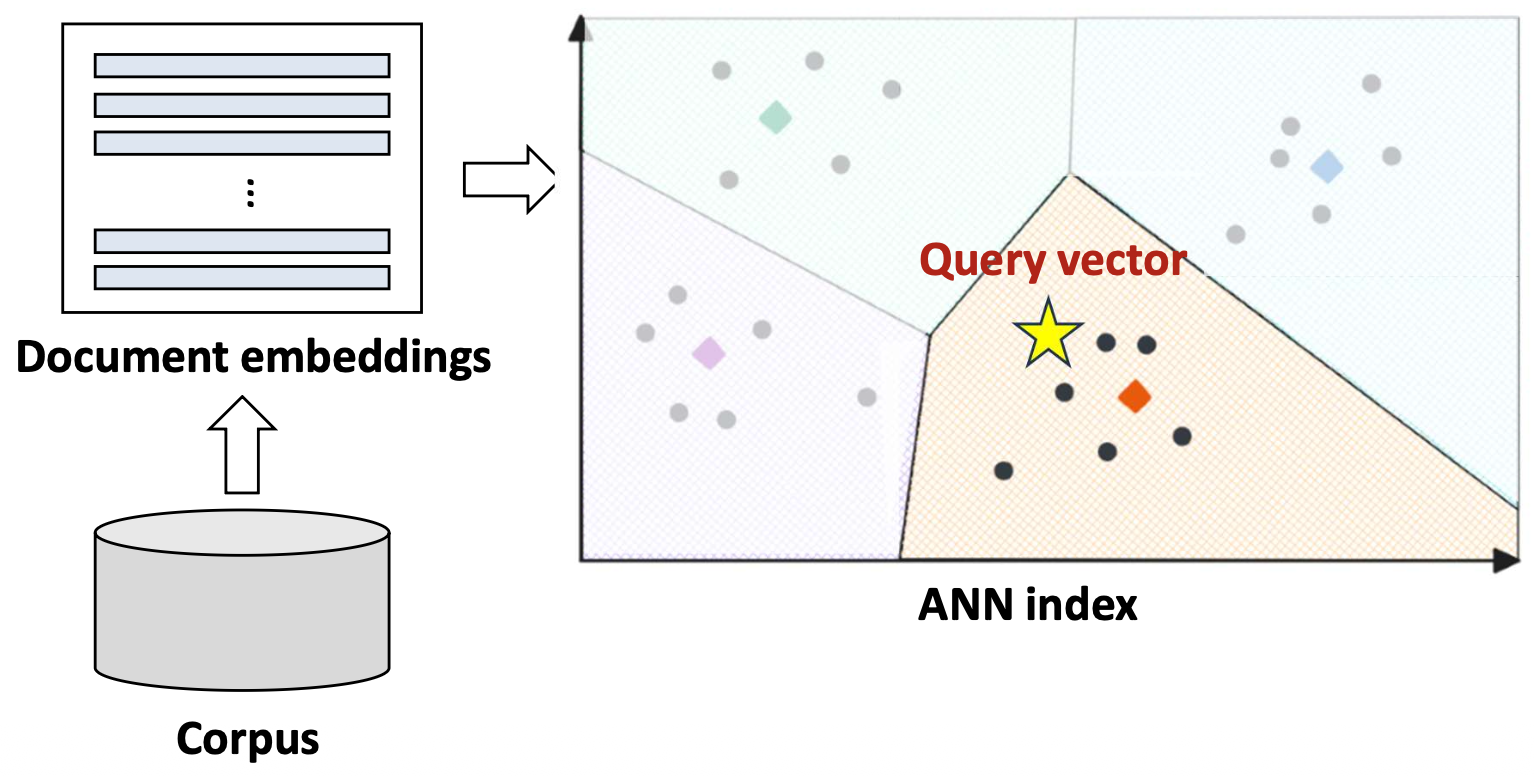
p8. 밀집 검색: 예시(Dense retrieval: illustration)

미리 학습된 모델들(예: BERT)로부터의 밀집 임베딩(dense embeddings)을 사용하여
쿼리와 문서를 표현한다.

1. 각 문서는 밀집 벡터(dense vector)로 인코딩되고 벡터 인덱스(vector index)에 저장된다
(이를 ANN index라고 부른다).

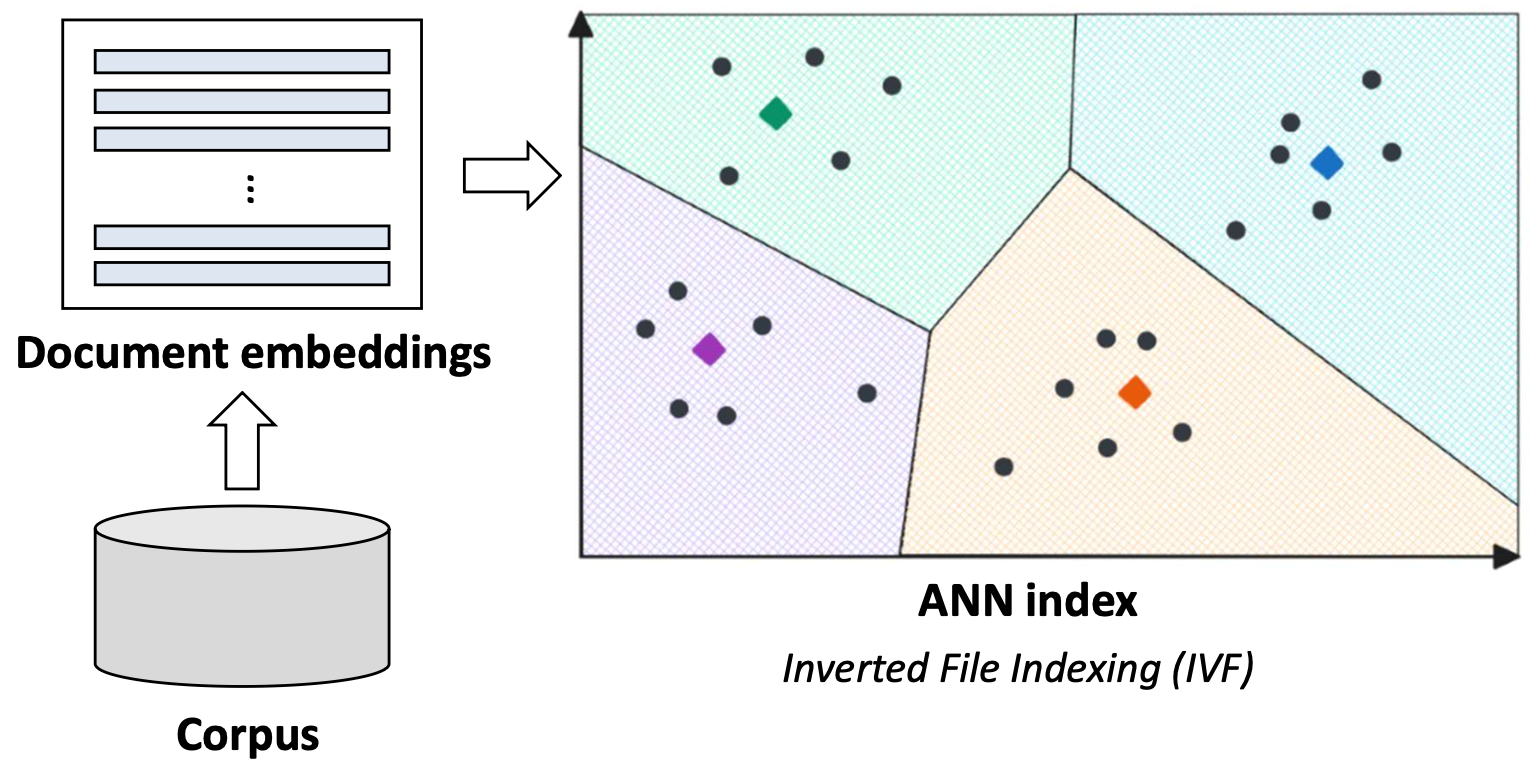
p9. 밀집 검색: 예시(Dense retrieval: illustration)

✓ ANN(Approximate Nearest Neighbor) 인덱스

쿼리를 모든 문서 벡터들과 비교하는 것은 계산적으로 매우 비용이 크다.
ANN 인덱스는 전체 비교를 수행하지 않고도
가장 유사한 문서 후보들을 빠르게 찾는 데 사용된다.
- ANN 인덱스를 구축하는 방법에는 여러 가지가 있으며,
  이는 이 수업의 범위를 벗어난다.

ANN 인덱스는 문서 벡터들을 클러스터들(색으로 구분된 영역들)로 조직한다.
각 영역(region)은 서로 의미적으로 유사한 문서들로 구성된다.
각 영역은 대표 벡터(centroid)로 표현되며,
이는 효율적인 최근접 이웃 검색에 사용된다.

p10. 밀집 검색: 예시(Dense retrieval: illustration)

미리 학습된 모델들(예: BERT)로부터의 밀집 임베딩(dense embeddings)을 사용하여
쿼리와 문서를 표현한다.

2. 쿼리 시점에는 입력 쿼리 또한 밀집 벡터(dense vector)로 인코딩되며,
시스템은 높은 임베딩 유사도(high embedding similarity)
(예: 코사인 유사도 또는 내적)을 가진 문서들을 검색한다.

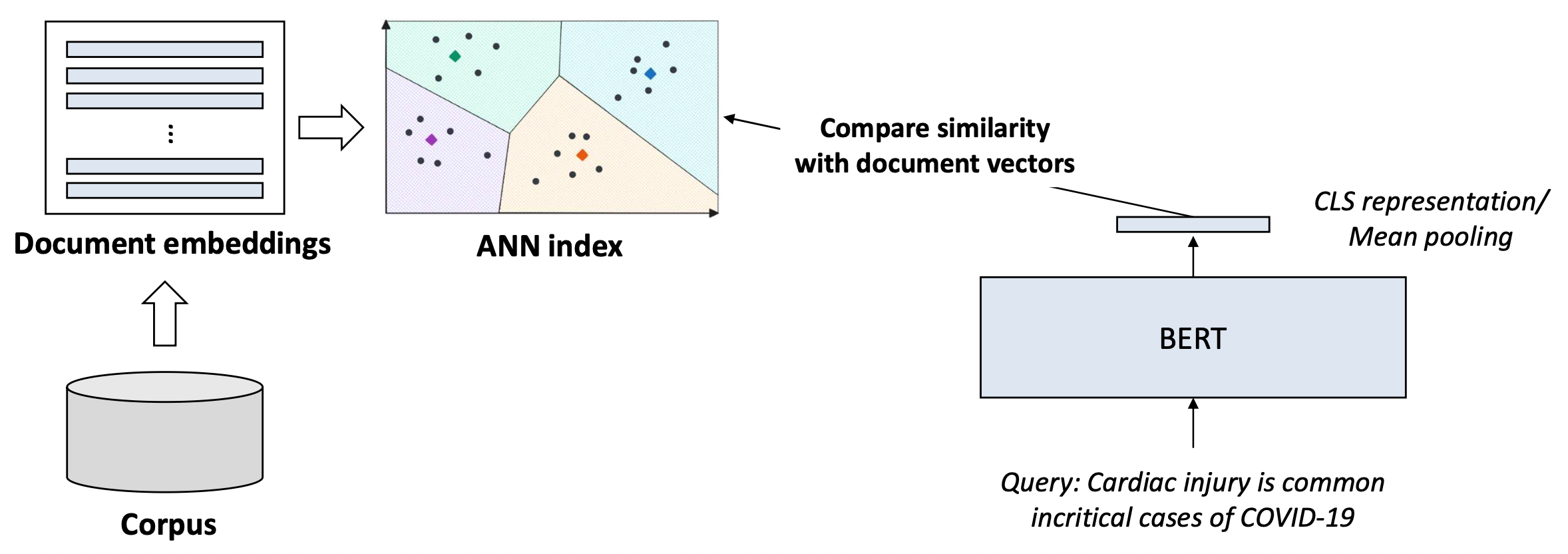
p11. 밀집 검색: 예시(Dense retrieval: illustration)

미리 학습된 모델들(예: BERT)로부터의 밀집 임베딩(dense embeddings)을 사용하여
쿼리와 문서를 표현한다.

시스템은 쿼리 벡터에 가장 가까운 센트로이드(centroid)를 찾아,
가장 가까운 클러스터(nearest cluster)를 식별한다.
이후, 그 클러스터 내부의 문서들에 대해서만 유사도(similarity)를 계산한다.

✓ 이러한 접근법은 최적(optimal)은 아니지만,
훨씬 빠르고(faster) 많은 경우에 충분히 정확(reasonably accurate)하다!

p14. 순위를 학습하기 (Learning to rank)

관련된 쿼리–문서 쌍의 데이터셋이 있다고 가정하자 $ \lbrace (q, d) \rbrace $
우리의 목표는 각 쿼리에 대해 관련된 문서를 더 높게(rank higher) 배치하도록
retriever를 파인튜닝하는 것이다.
- 순위 매기기(ranking)란 무엇인가?
  분류(classification)와는 어떻게 다른가?
  - 순위 매기기는 여러 후보들의 상대적 순서(relative order) 를 정하는 것이며,
    각 항목에 대해 독립적으로 예측하는 것이 아니다.

p15. 순위를 학습하기: 개요 (Learning to rank: overview)

순위 매기기(ranking) 작업을 위한 모델은 어떻게 학습시키는가?
어떤 종류의 손실 함수(loss function)가 필요한가?

Point-wise learning
- 각 쿼리–문서 쌍의 관련성을 독립적으로 예측한다.
Pair-wise learning
- 두 문서를 비교하여, 더 관련성이 높은 문서가 더 높은 점수를 갖도록 만든다.
List-wise learning
- 모든 후보 문서들에 대한 상대적 순위(relative ranking) 를
  전체적으로(jointly) 최적화한다.

p17. 순위를 학습하기: point-wise (Point-wise)

목표(Objective):
쿼리–문서 쌍 $(q, d)$ 이 관련(relevant) 있는지 여부를 예측한다 (이진 분류).
\[\hat{y}_{q,d} = p(\text{relevant} \mid q, d) = \sigma(\text{score}(q,d))\] \[\text{score}(q,d) = e_q^{\top} e_d\]
이진 교차 엔트로피(Binary cross-entropy, BCE) 손실:
\[\mathcal{L}_{\text{point}} = -y_{q,d}\log \hat{y}_{q,d} - (1 - y_{q,d})\log(1 - \hat{y}_{q,d})\]
- 만약 $q$ 와 $d$ 가 관련이 있다면 $y_{q,d} = 1$, 그렇지 않으면 $0$

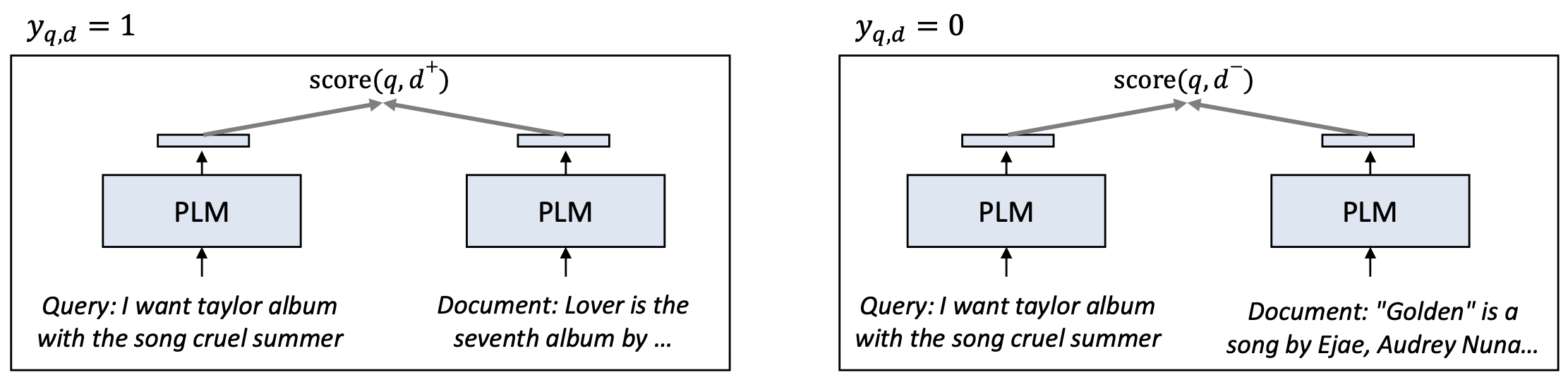
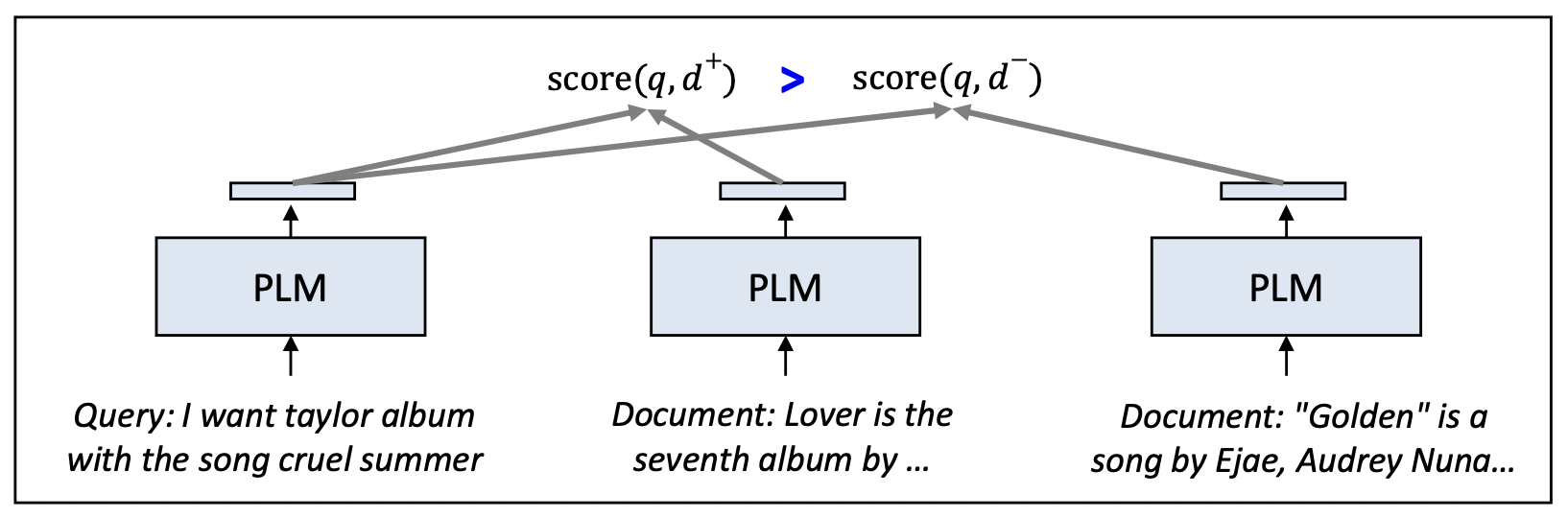
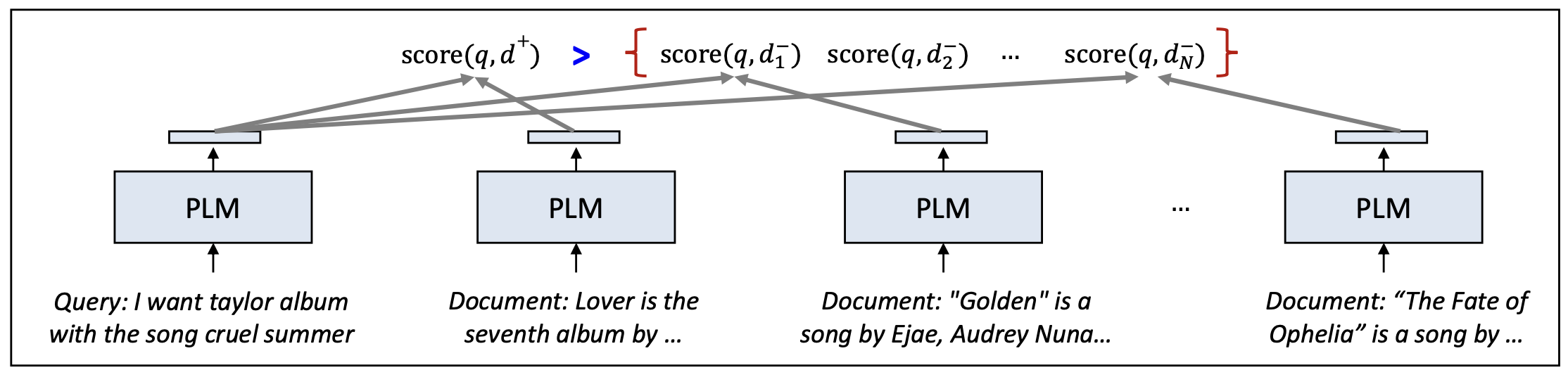
p19. 순위를 학습하기: pair-wise (Pair-wise)

목표(Objective):
쿼리 $q$ 가 주어졌을 때, 관련 문서 $d^{+}$ 가 비관련 문서 $d^{-}$ 보다 더 높은 점수를 갖도록 한다.
\[\sigma(\text{score}(q, d^{+}) - \text{score}(q, d^{-})) = \frac{\exp(\text{score}(q, d^{+}))}{\exp(\text{score}(q, d^{+})) + \exp(\text{score}(q, d^{-}))}\]
Pair-wise loss:
\[\mathcal{L}_{\text{pair}} = -\log \sigma\big(\text{score}(q, d^{+}) - \text{score}(q, d^{-})\big)\]
절대적인 관련도를 예측하는 것이 아니라,
pairwise 학습은 모델이 $d^{+}$ 를 $d^{-}$ 보다 선호(prefer) 하도록 가르친다.

p22. 순위를 학습하기: list-wise (binary)

목표(Objective):
쿼리 $q$ 와 문서 집합 $\lbrace d^{+}, d_1^{-}, d_2^{-}, \dots, d_N^{-} \rbrace$ 이 주어졌을 때,
모델은 관련 문서 $d^{+}$ 에 가장 높은 점수를 부여하도록 학습한다.
\[\mathcal{L}_{\text{list}} = -\log\left( \frac{\exp(\text{score}(q, d^{+}))} {\exp(\text{score}(q, d^{+})) + \sum_{i=1}^{N} \exp(\text{score}(q, d_i^{-}))} \right)\]
List-wise 학습은 단일 loss 안에서 여러 문서들의 상대적 관련도(relative relevance) 를 함께 고려한다.

p23. 순위를 학습하기: list-wise (binary)

이 접근법은 대조 학습 손실(contrastive learning loss) 로도 알려져 있다.
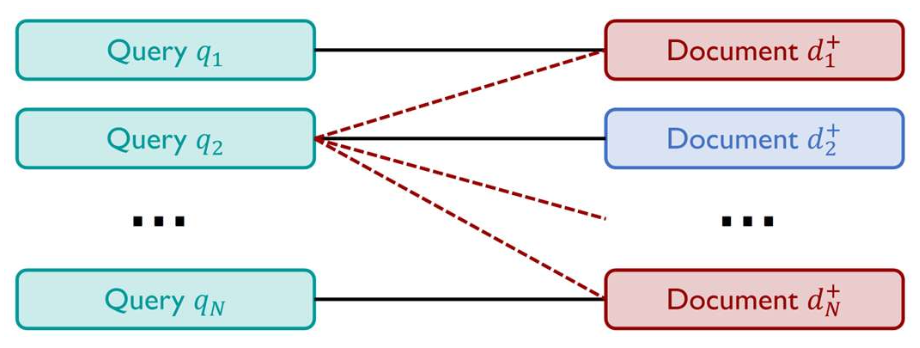
\[\mathcal{L}_{\text{list}} = -\log \frac{\exp(\text{score}(q, d^{+}))}{\exp(\text{score}(q, d^{+})) + \sum_{i=1}^{N-1}\exp(\text{score}(q, d^{-}_{i}))}\]
부정 문서들 $\lbrace d^{-}_{1}, d^{-}_{2}, \ldots, d^{-}_{N} \rbrace$ 을 얻는 방법은?
- 순진한 방법(Naïve way): 코퍼스에서 무작위로 부정 문서를 샘플링한다.
- 더 효율적인 방법: In-batch negative!

$N$개의 (쿼리, 긍정 문서) 쌍을 하나의 배치로 GPU에 넣는다.
같은 배치에 있는 다른 쿼리들의 긍정 문서들이
현재 쿼리의 부정 문서들(negatives) 로 사용된다.

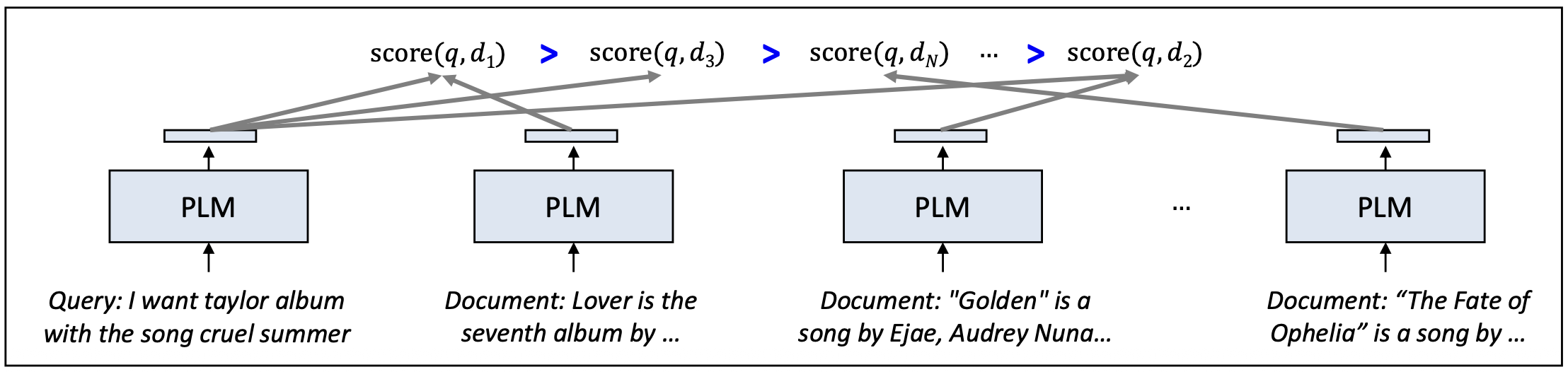
p24. 순위를 학습하기: list-wise (graded relevance)

이전 list-wise 손실은 모든 비관련 문서가 동일하게 비관련(irrelavant) 하다고 가정한다.
그렇다면 문서들 사이에 상대적 선호(graded relevance) 가 존재한다면 어떻게 할까?
특정 쿼리에 대해 $N$개의 문서와
그들의 상대적 중요도 순서 $\pi^{*}$ 가 다음과 같이 주어진다고 하자:
\[d_{1} > d_{3} > d_{N} > \cdots > d_{2}\]
우리는 모델이 예측에서 이 순위 구조를 보존하도록 만들고 싶다.
그렇다면 어떤 종류의 손실 함수를 사용해야 할까?

p25. 순위를 학습하기: list-wise (graded relevance)

Plackett–Luce 모델은 순위 배열(ranking permutation)을 확률 분포로 표현하기 위한 확률적 기반을 제공한다.
- 주어진 쿼리 $q$에 대해, 특정한 순위 배열 $\pi$가 관측될 확률은 다음과 같이 정의된다:
  \[P(\pi \mid q) \;=\; \prod_{i=1}^{N} \frac{\exp(\text{score}(q, d_{\pi_i}))} {\sum_{k=i}^{N} \exp(\text{score}(q, d_{\pi_k}))}\]
  여기서 $\pi_i$ 는 순위 배열 $\pi$에서 $i$번째로 선택된 문서를 의미한다.
예시:
네 개의 문서 $\lbrace d_{1}, d_{2}, d_{3}, d_{4} \rbrace$ 와
모델이 예측한 점수 $s_{1}, s_{2}, s_{3}, s_{4}$ 가 있다고 하자.
올바른 순위 배열이
$\pi = [d_{2}, d_{1}, d_{4}, d_{3}]$ 라고 하면,
이 순위 배열이 관측될 확률은 다음과 같다:
\[\frac{\exp(s_{2})} {\exp(s_{2}) + \exp(s_{1}) + \exp(s_{3}) + \exp(s_{4})} \cdot \frac{\exp(s_{1})} {\exp(s_{1}) + \exp(s_{3}) + \exp(s_{4})} \cdot \frac{\exp(s_{4})} {\exp(s_{4}) + \exp(s_{3})}\]
교체 없이 순차적으로 선택하는 과정 (Sequential selection process (w/o replacement))

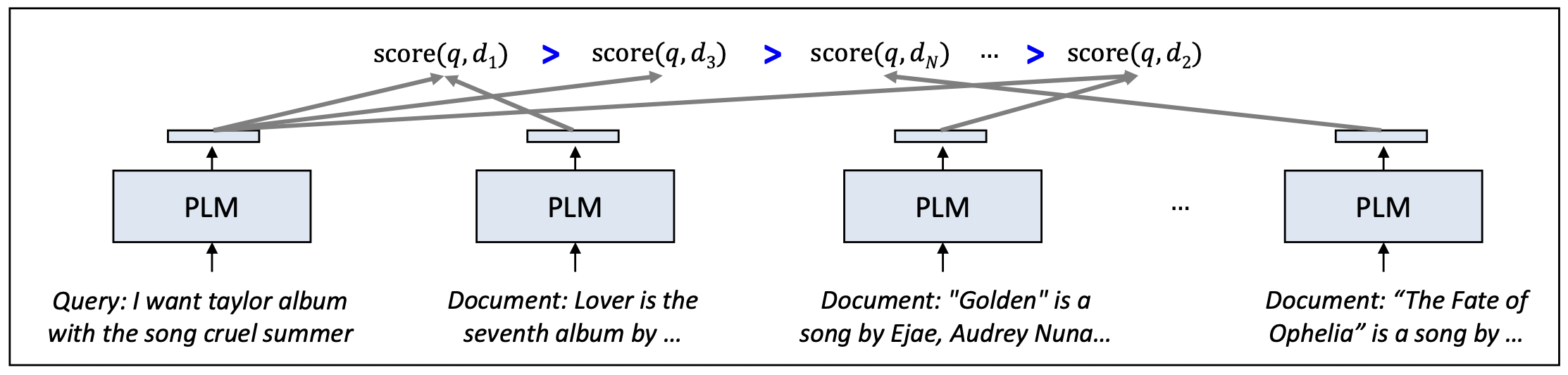
p27. 순위를 학습하기: list-wise (graded relevance)

주어진 쿼리 $q$에 대해, $N$개의 문서와
그 문서들의 상대적 관련도 순서 $\pi^{*}$가 주어졌다고 하자.
목표(Objective):
주어진 관련도 수준(graded relevance)에 따라
올바른 순위 순서를 유지하도록 모델을 학습한다.
\[\mathcal{L}_{\text{list}} = - \log P(\pi^{*} \mid q) = - \sum_{i=1}^{N} \log \frac{\exp(\text{score}(q, d_{\pi^{*}_i}))} {\sum_{k=i}^{N} \exp(\text{score}(q, d_{\pi^{*}_k}))}\]
이 손실은 binary list-wise loss(모든 비관련 문서를 동일하게 취급)와 달리,
세밀한 차이(fine-grained differences) 를 포착한다.
(예: “매우 관련” > “부분적으로 관련” > “비관련”)

p28. 요약: 순위를 학습하기 (learning to rank)

밀집 검색(Dense retrieval) 은
사전학습 언어모델(pre-trained language models, 예: BERT)의
밀집 표현(dense representations) 을 활용한다.
- 이러한 모델들은 검색을 위해 특별히 학습된 것이 아니므로,
  만족스러운 성능을 위해서는 파인튜닝(fine-tuning) 이 필요하다.
본 강의에서는 다음 네 가지 학습 목적을 다루었다:
1. Point-wise learning
  \[\mathcal{L}_{\text{point}} = - y_{q,d}\log \hat{y}_{q,d} - (1 - y_{q,d})\log (1 - \hat{y}_{q,d})\]
2. Pair-wise learning
  \[\mathcal{L}_{\text{pair}} = - \log \sigma\big(\text{score}(q, d^{+}) - \text{score}(q, d^{-})\big)\]
3. List-wise learning (binary)
  \[\mathcal{L}_{\text{list}} = - \log \frac{\exp(\text{score}(q, d^{+}))} {\exp(\text{score}(q, d^{+})) + \sum_{i=1}^{N-1}\exp(\text{score}(q, d^{-}_{i}))}\]
4. List-wise learning (graded)
  \[\mathcal{L}_{\text{list}} = - \log P(\pi^{*} \mid q) = - \sum_{i=1}^{N} \log \frac{\exp(\text{score}(q, d_{\pi^{*}_{i}}))} {\sum_{k=i}^{N}\exp(\text{score}(q, d_{\pi^{*}_{k}}))}\]
List-wise learning 은 일반적으로 가장 좋은 성능을 내지만,
계산 비용(computational cost) 이 더 크다는 단점이 있다.

p29. 추천 읽을거리 (Recommended readings)

도서:
- Chapter 11: Information Retrieval and Retrieval-Augmented Generation, Speech and Language Processing
  (11장: 정보 검색 및 검색-증강 생성, 음성 및 언어 처리)
기사:
- https://en.wikipedia.org/wiki/Learning_to_rank
  (Learning to Rank 개요 설명)
논문:
- Listwise Approach to Learning to Rank – Theory and Algorithm, ICML’08
  (리스트-기반 학습-to-rank 접근법: 이론 및 알고리즘)

대학원 수업, 텍스트 마이닝