[텍스트 마이닝] 2. Machine Learning 1
기본 개념
p4. 예측 태스크의 유형
- 회귀(Regression): 입력이 주어졌을 때 연속적인 출력값을 예측하는 것
p5. 예측 태스크의 유형
- 분류(Classification): 미리 정의된 범주 집합 $C$에서 이산적인 레이블을 예측하는 것
- 이진 분류 (Binary classification, $\mid C \mid = 2$)
- 다중 클래스 분류 (Multiclass classification, $\mid C \mid > 2$)
p6. 예측 태스크의 유형
- 랭킹(Ranking): 아이템 집합에서 관련성에 따라 최적의 순서 $\pi$ 를 예측하는 것
- $\Pi(X)$ : 가능한 모든 순열(permutations)의 집합
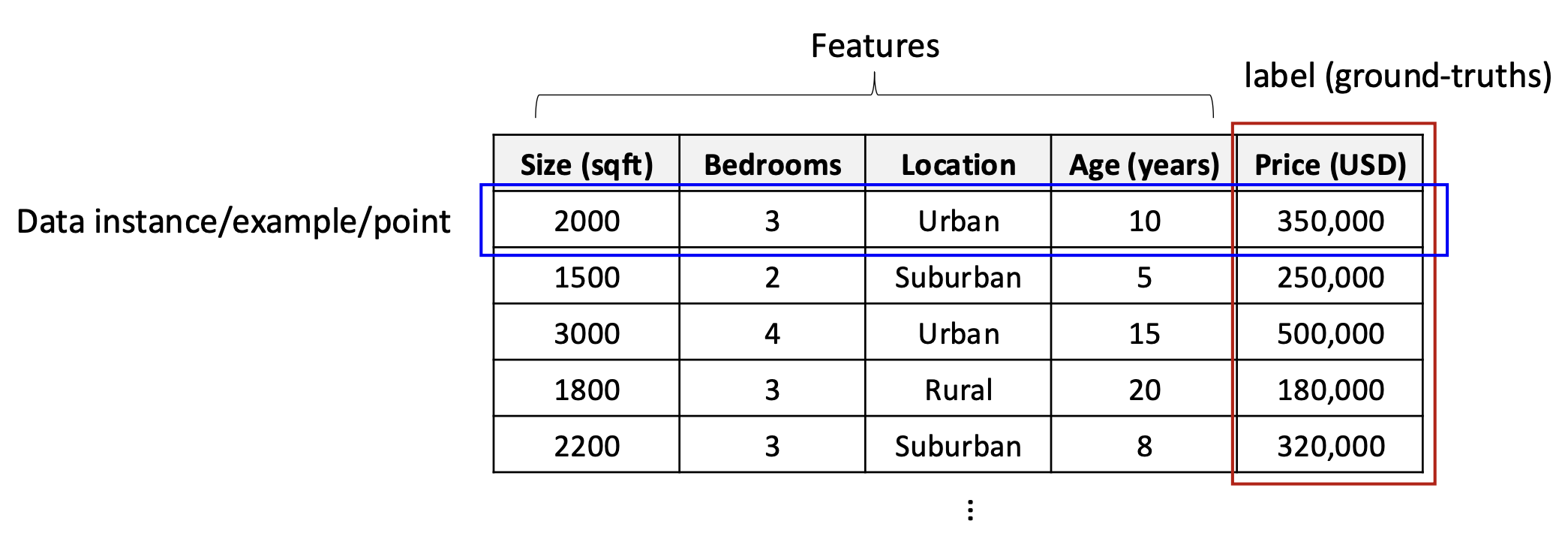
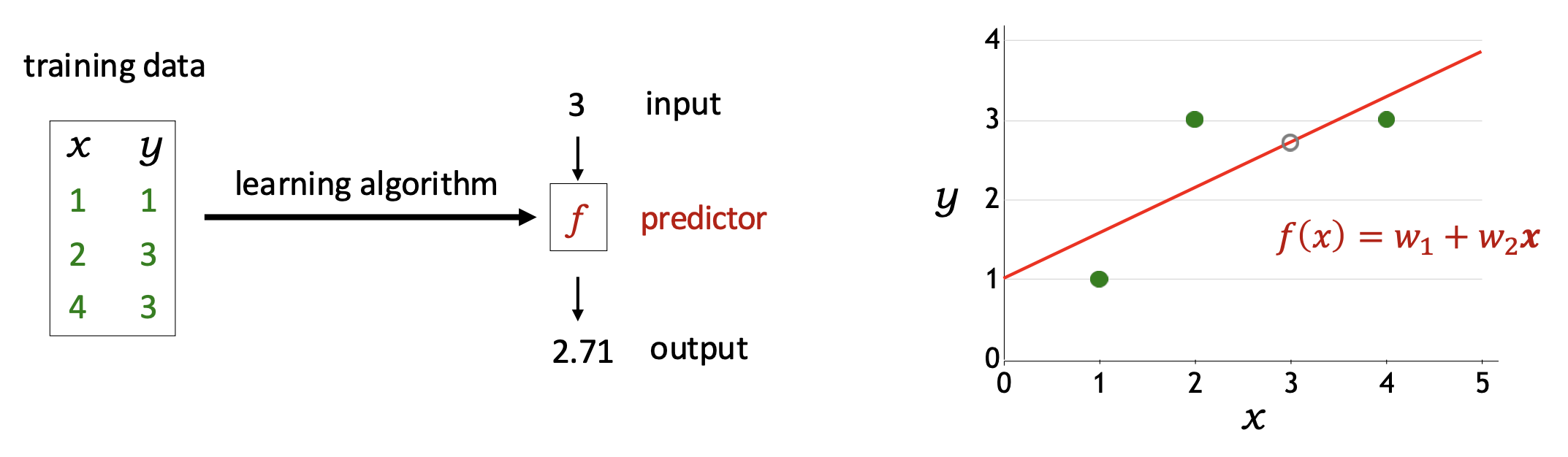
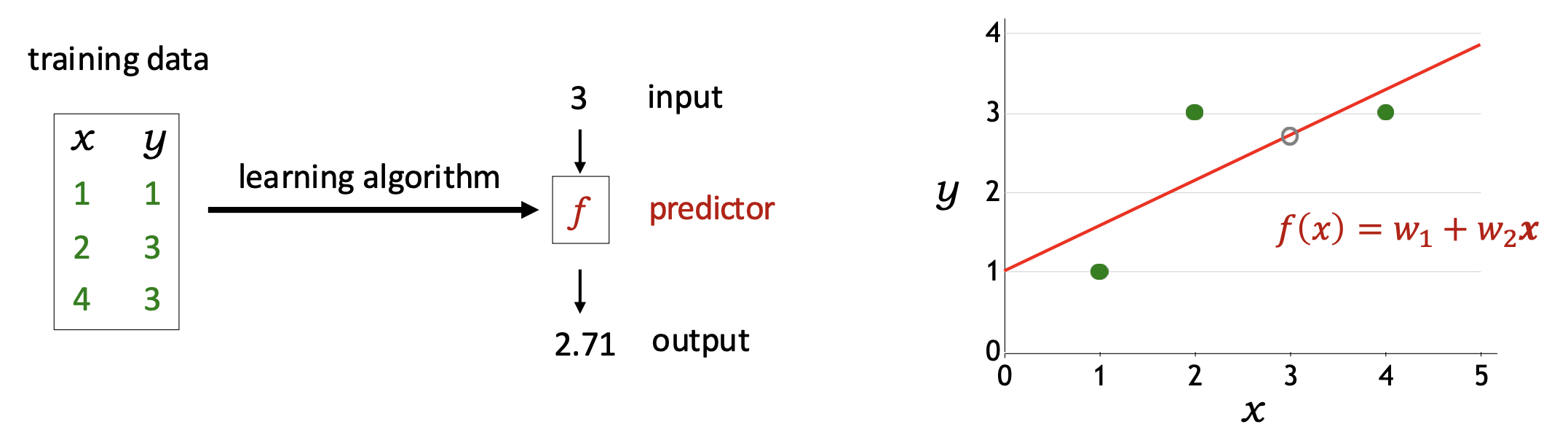
p7. 데이터 (지도학습, supervised learning)
데이터 인스턴스(Data instance): 입력–출력 쌍 $(x, y)$, 여기서 $y$는 $x$에 대한 레이블(정답 출력, ground-truth output)이다.
훈련 데이터(Training data): 인스턴스들의 집합
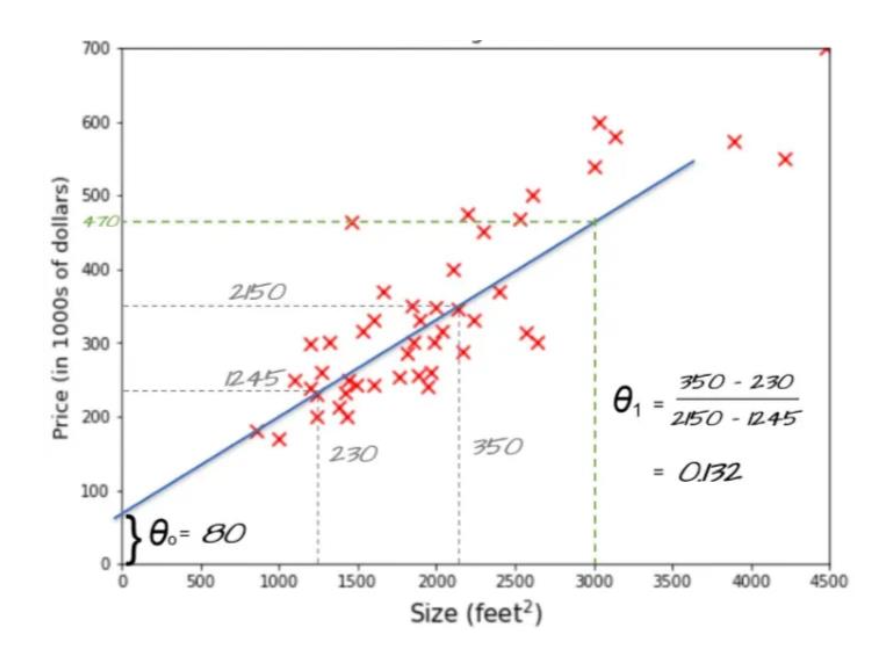
\(D_{train} = \{(x_1, y_1), \dots, (x_n, y_n)\}\)주택 가격 예측을 위한 데이터 예시
p8. 데이터로부터 학습
- 머신러닝은 데이터로부터 특징(feature)과 레이블(label) 사이의 패턴을 학습하는 것이다.
- 모델은 관측된 데이터(seen data)(즉, 훈련 데이터)로 학습된다.
- 그 모델은 관측되지 않은 데이터(unseen data)(즉, 테스트 데이터)에 대해 예측하는 데 사용된다.
- 일반화(Generalization): 모델이 관측되지 않은 데이터(unseen data)에서도 잘 작동하는 능력을 의미한다.
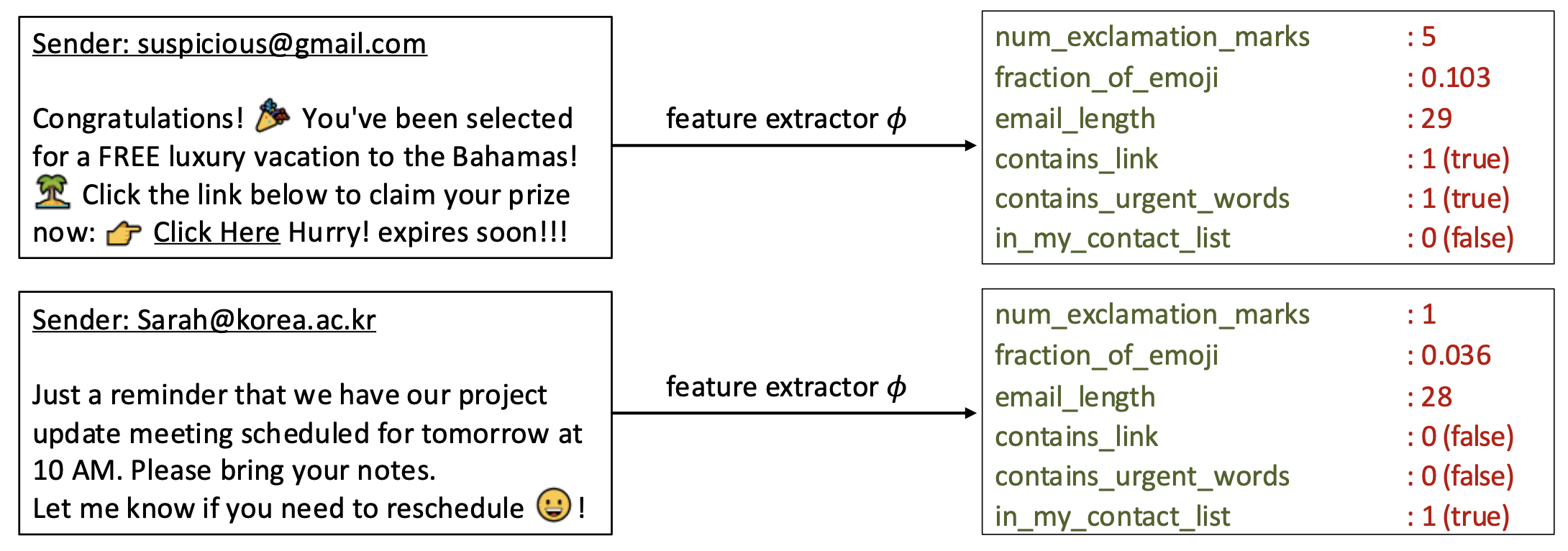
p9. 특성 추출 (Feature extraction)
실제 과제(real-world tasks)에서는 종종 원시 데이터(raw data)를 의미 있는 특성(meaningful features)으로 변환해야 한다.
→ 이렇게 해야 머신러닝 모델이 더 효과적으로 예측할 수 있다.특성 추출기(Feature extractor): 입력 $x$가 주어졌을 때, (특성 이름, 특성 값) 쌍들의 집합을 출력한다.
- 특성 추출기(Feature extractor)는 입력 데이터를 특성 벡터로 변환하는 함수이다.
- 보통 그리스 문자 φ(파이)로 표기한다.
- 즉, $x \;\;\xrightarrow{\;\;\varphi\;\;}\;\; (feature\ name,\ feature\ value)$ 와 같이 나타낼 수 있다.
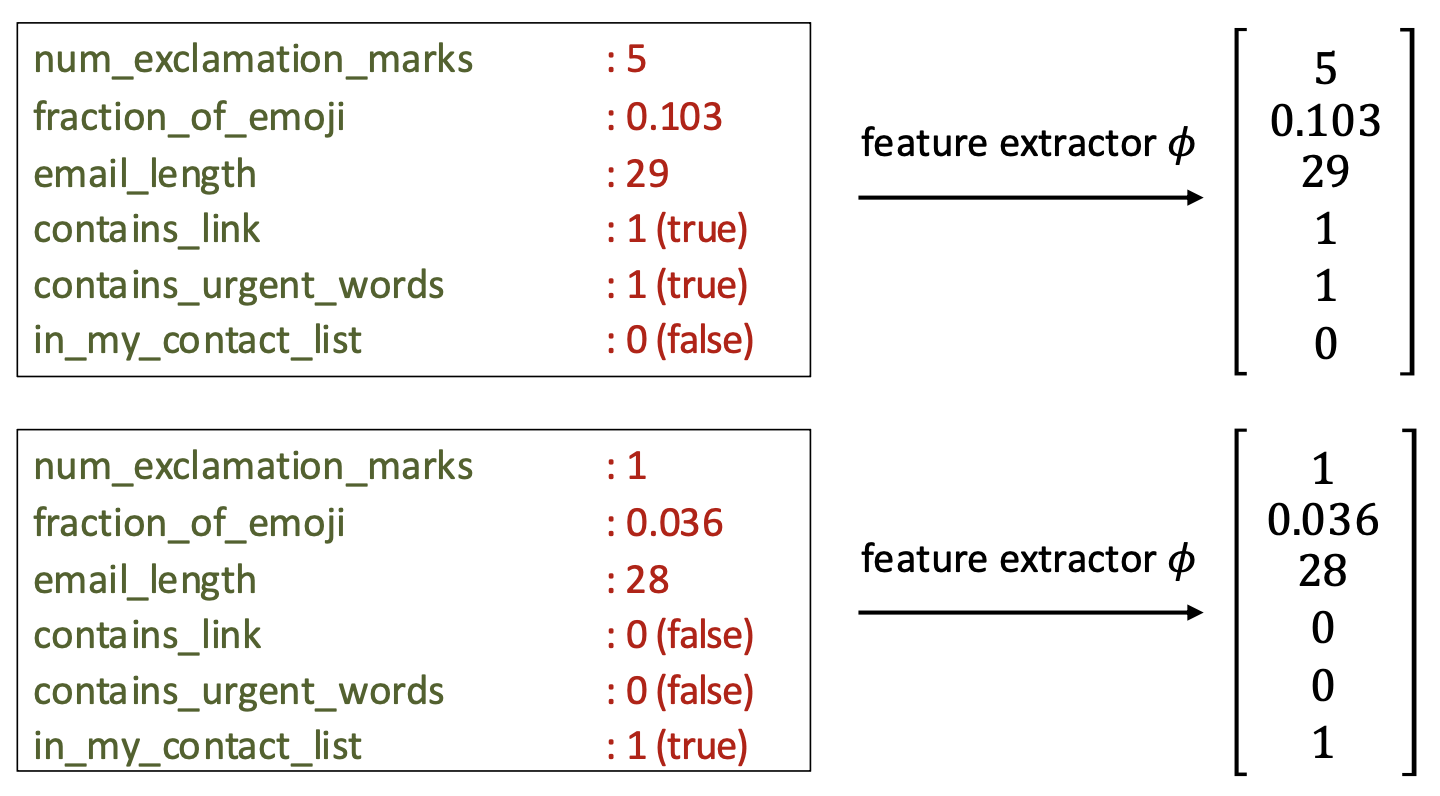
p10. 특성 벡터 (Feature vector)
각 입력 $x$는 특성 벡터(feature vector)
\[\varphi(x) = [\varphi_1(x), \dots, \varphi_d(x)]\]로 표현된다.
수학적으로, 특성 벡터는 반드시 특성 이름을 가질 필요는 없다.
$\varphi(x) \in \mathbb{R}^d$ 는 $d$차원 공간의 한 점(point)으로 생각할 수 있다.
p11. 가중치 벡터 (Weight vector)
가중치 벡터 $\mathbf{w} \in \mathbb{R}^d$ 는 각 특성이 예측에 기여하는 정도를 결정하는 실수 값 매개변수들로 구성된다.

가중치 벡터는 모델의 핵심 구성 요소이며, 모델 파라미터(model parameters)라고도 불린다.
이는 학습(최적화) 알고리즘에 의해 훈련 데이터 $D_{train}$ 으로부터 자동으로 학습된다.
p12. 선형 예측기 (Linear predictors)
선형 예측기는 입력 특성들의 가중치 합(weighted sum of input features)을 사용하여 예측을 수행한다.
점수(Score):
\[\mathbf{w} \cdot \varphi(x) = \sum_{j=1}^{d} w_j \varphi(x)_j\]예시:
\[(2.2 \times 5) + (5.9 \times 0.103) + (-1.2 \times 29) + (0.5 \times 1) + (0.75 \times 1) + (7.9 \times 0) = -21.9423\]
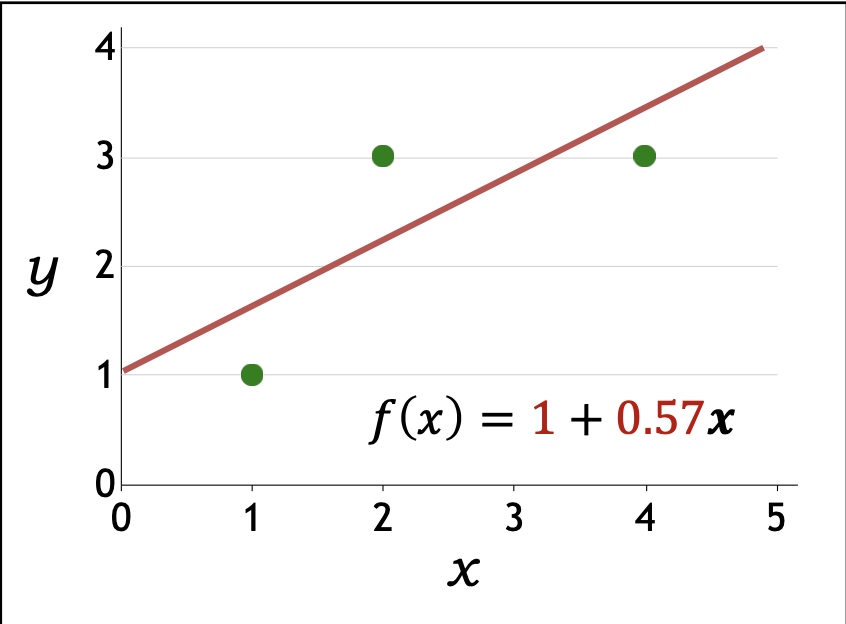
선형 회귀(Linear Regression)
p14. 선형 회귀
- 벡터 표기(Vector notation):
- 가중치 벡터: $\mathbf{w} = [w_1, w_2]$
- 특성 벡터: $\varphi(x) = [1, x]$
특성 벡터에 첫번째 항목 1이 없으면 $\mathbf{w} \cdot \varphi(x)$가 원점 밖에 지나지 못함
- 점수(Score):
- 가설 클래스(Hypothesis class):
- 고정된 $\varphi(x)$ 와 가변적인 $\mathbf{w}$ 에 따라 가능한 예측기들의 집합
p15. 선형 회귀: 예측기는 얼마나 좋은가?
- 손실 함수(Loss function):
- 손실 함수 $Loss(x, y, \mathbf{w})$는 정답 출력이 $y$일 때, $\mathbf{w}$를 사용하여 $x$에 대한 예측을 했을 때 얼마나 “불만족스러운지”를 수치화한다.
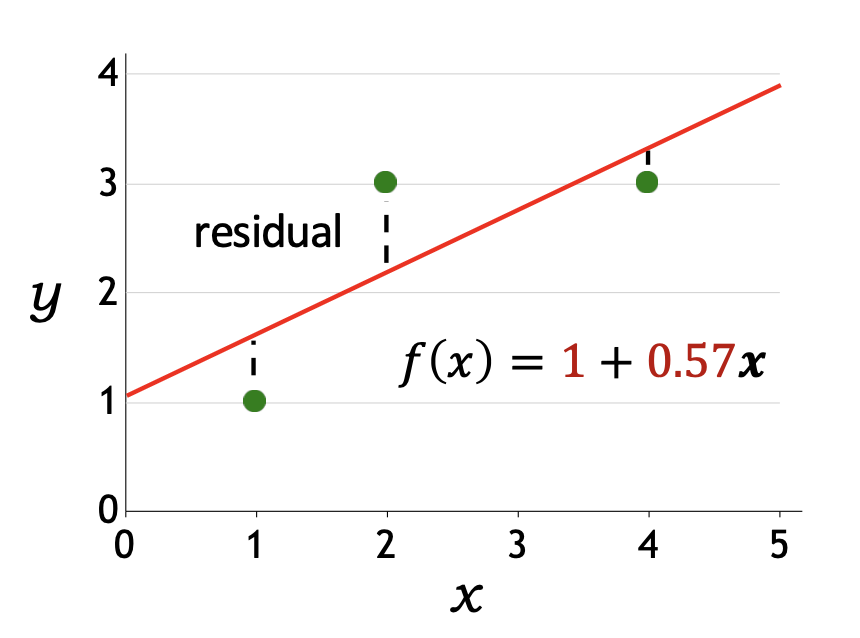
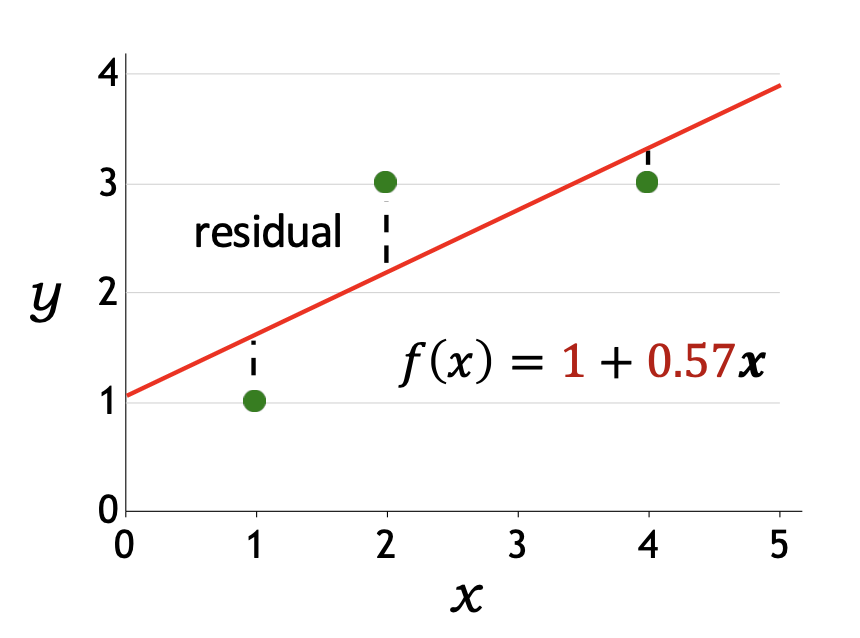
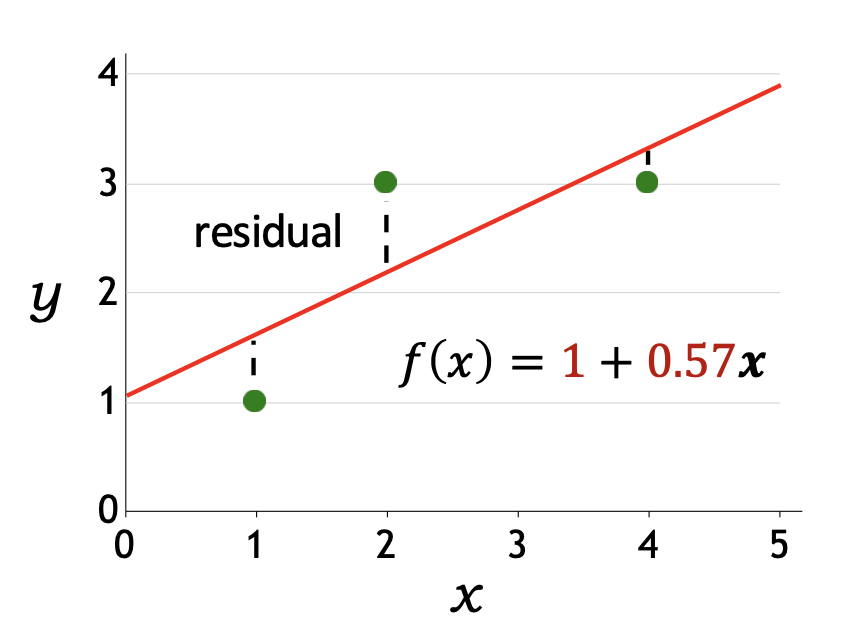
- 잔차(residual):
- 잔차는 $(\mathbf{w} \cdot \varphi(x)) - y$ 로 정의된다.
- 즉, 예측값 $f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x)$가 실제 목표값 $y$를 얼마나 초과(overshoot)했는지를 나타낸다.
p16. 선형 회귀: 예측기는 얼마나 좋은가?
- 손실 함수(Loss function):
- 손실 함수 $Loss(x, y, \mathbf{w})$는 정답 출력이 $y$일 때, $\mathbf{w}$를 사용하여 $x$에 대한 예측을 했을 때 얼마나 불만족스러운지를 수치화한다.
- 제곱 손실(Squared loss):
각 데이터 인스턴스에서 제곱 손실은 다음과 같이 정의된다.
\[Loss(x, y, \mathbf{w}) = (f_{\mathbf{w}}(x) - y)^2\]
예시:
\[Loss([1,1], [1,0.57]) = ([1,0.57] \cdot [1,1] - 1)^2\] \[Loss([2,3], [1,0.57]) = ([1,0.57] \cdot [1,2] - 3)^2\] \[Loss([4,3], [1,0.57]) = ([1,0.57] \cdot [1,4] - 3)^2\]
p17. 선형 회귀: 예측기는 얼마나 좋은가?
- 손실 함수(Loss function):
- 손실 함수 $Loss(x, y, \mathbf{w})$는 정답 출력이 $y$일 때, $\mathbf{w}$를 사용하여 $x$에 대해 예측을 했을 때 얼마나 불만족스러운지를 수치화한다.
- 제곱 손실(Squared loss):
각 데이터 인스턴스에서 제곱 손실은 다음과 같이 정의된다.
\[Loss(x, y, \mathbf{w}) = (f_{\mathbf{w}}(x) - y)^2\]
- 훈련 데이터 전체(whole training data)에 대한 손실 최소화:
목표는 훈련 데이터 전체에 대한 손실을 최소화하는 것이다.
\[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} Loss(x, y, \mathbf{w})\]
예시:
\[TrainLoss([1, 0.57]) = 0.38\]
p18. 선형 회귀: 예측기를 어떻게 최적화할까?
- 목표(Goal):
전체 훈련 데이터에서 손실을 최소화하는 $\mathbf{w}$를 찾는 것
\[\min_{\mathbf{w}} TrainLoss(\mathbf{w})\] \[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} Loss(x, y, \mathbf{w})\]
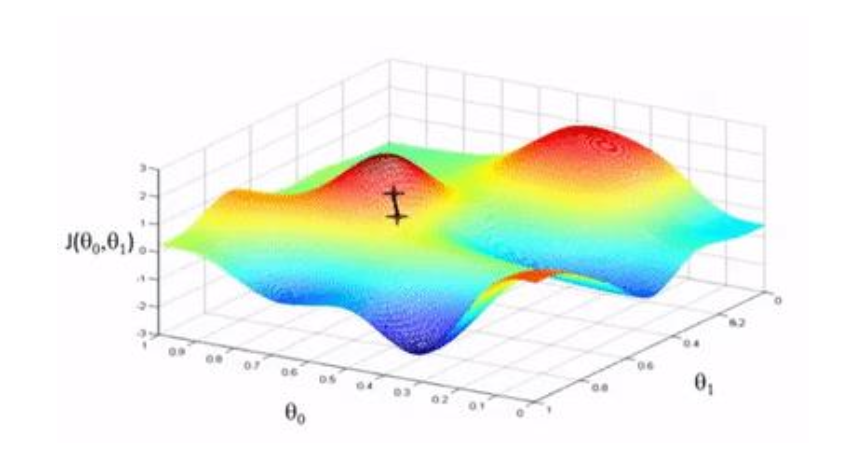
- 최적화 방법(How to optimize?): 경사하강법(gradient descent)
- 기울기 $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$는 훈련 손실을 가장 크게 증가시키는 방향을 의미한다.
💻 알고리즘 (Algorithm)
- $\mathbf{w}$를 무작위로 초기화
수렴할 때까지 반복:
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} TrainLoss(\mathbf{w})\]
- 여기서 $\eta$ (학습률, step size)는 하이퍼파라미터이다.
p20. 선형 회귀: 예측기를 어떻게 최적화할까?
- 경사하강법 예시(Gradient descent example):
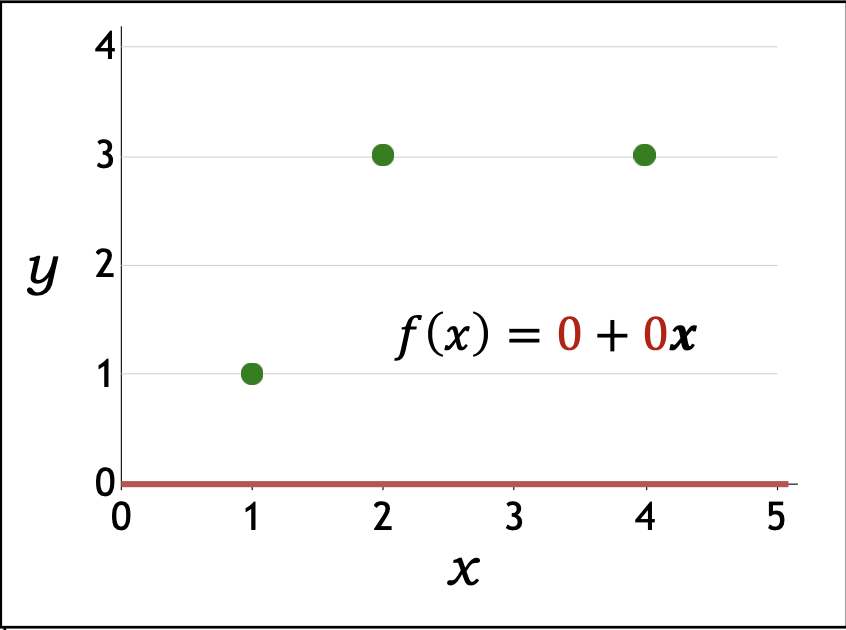
훈련 데이터:
\[D_{train} = \{(1,1), (2,3), (4,3)\}\]초기화:
\[\mathbf{w} \leftarrow [0,0]\]
훈련 손실(TrainLoss):
\[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} (\mathbf{w} \cdot \varphi(x) - y)^2\]기울기(Gradient):
\[\nabla_{\mathbf{w}} TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} 2(\mathbf{w} \cdot \varphi(x) - y)\varphi(x)\]업데이트 규칙(Update rule):
\[\mathbf{w} \leftarrow \mathbf{w} - 0.1 \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w}), \quad (\eta = 0.1)\]
- 반복(iteration) 과정:
| Iteration $t$ | Gradient $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$ | Updated parameter $\mathbf{w}$ |
|---|---|---|
p22. 선형 회귀: 예측기를 어떻게 최적화할까?
- 경사하강법 예시(Gradient descent example):
훈련 데이터:
\[D_{train} = \{(1,1), (2,3), (4,3)\}\]초기화:
\[\mathbf{w} \leftarrow [0,0]\]
훈련 손실(TrainLoss):
\[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} (\mathbf{w} \cdot \varphi(x) - y)^2\]기울기(Gradient):
\[\nabla_{\mathbf{w}} TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} 2(\mathbf{w} \cdot \varphi(x) - y)\varphi(x)\]업데이트 규칙(Update rule):
\[\mathbf{w} \leftarrow \mathbf{w} - 0.1 \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w}), \quad (\eta = 0.1)\]
- 반복(iteration) 과정:
| Iteration $t$ | Gradient $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$ | Updated parameter $\mathbf{w}$ |
|---|---|---|
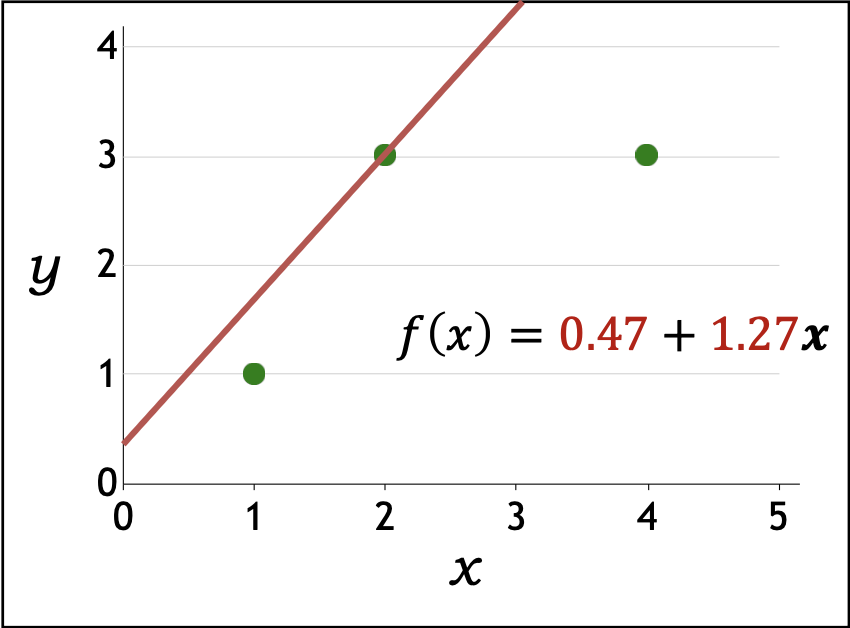
| 1 | $\tfrac{1}{3}(2([0,0]\cdot[1,1]-1)[1,1] + 2([0,0]\cdot[1,2]-3)[1,2]$ $+ 2([0,0]\cdot[1,4]-3)[1,4]) = [-4.67,\,-12.67]$ | $[0.47,\,1.27]$ |
p24. 선형 회귀: 예측기를 어떻게 최적화할까?
- 경사하강법 예시(Gradient descent example):
훈련 데이터:
\[D_{train} = \{(1,1), (2,3), (4,3)\}\]초기화:
\[\mathbf{w} \leftarrow [0,0]\]
훈련 손실(TrainLoss):
\[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} (\mathbf{w} \cdot \varphi(x) - y)^2\]기울기(Gradient):
\[\nabla_{\mathbf{w}} TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} 2(\mathbf{w} \cdot \varphi(x) - y)\varphi(x)\]업데이트 규칙(Update rule):
\[\mathbf{w} \leftarrow \mathbf{w} - 0.1 \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w}), \quad (\eta = 0.1)\]
- 반복(iteration) 과정:
| Iteration $t$ | Gradient $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$ | Updated parameter $\mathbf{w}$ |
|---|---|---|
| 1 | $\tfrac{1}{3}(2([0,0]\cdot[1,1]-1)[1,1] + 2([0,0]\cdot[1,2]-3)[1,2]$ $+ 2([0,0]\cdot[1,4]-3)[1,4]) = [-4.67,\,-12.67]$ | $[0.47,\,1.27]$ |
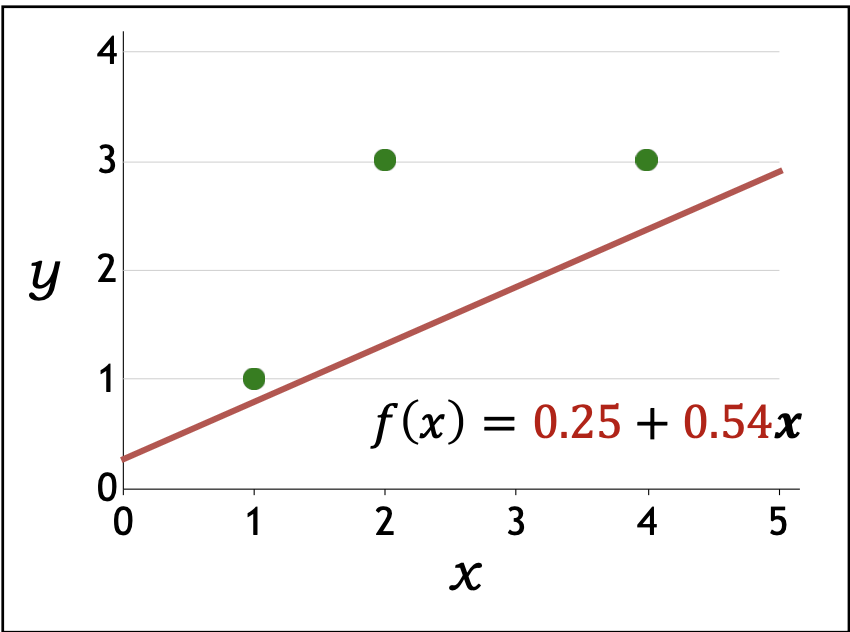
| 2 | $\tfrac{1}{3}(2([0.47,1.27]\cdot[1,1]-1)[1,1] + 2([0.47,1.27]\cdot[1,2]-3)[1,2]$ $+ 2([0.47,1.27]\cdot[1,4]-3)[1,4]) = [2.18,\,7.24]$ | $[0.25,\,0.54]$ |
p26. 선형 회귀: 예측기를 어떻게 최적화할까?
- 경사하강법 예시(Gradient descent example):
훈련 데이터:
\[D_{train} = \{(1,1), (2,3), (4,3)\}\]초기화:
\[\mathbf{w} \leftarrow [0,0]\]
훈련 손실(TrainLoss):
\[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} (\mathbf{w} \cdot \varphi(x) - y)^2\]기울기(Gradient):
\[\nabla_{\mathbf{w}} TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} 2(\mathbf{w} \cdot \varphi(x) - y)\varphi(x)\]업데이트 규칙(Update rule):
\[\mathbf{w} \leftarrow \mathbf{w} - 0.1 \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w}), \quad (\eta = 0.1)\]
- 반복(iteration) 과정:
| Iteration $t$ | Gradient $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$ | Updated parameter $\mathbf{w}$ |
|---|---|---|
| 1 | $\tfrac{1}{3}(2([0,0]\cdot[1,1]-1)[1,1] + 2([0,0]\cdot[1,2]-3)[1,2]$ $+ 2([0,0]\cdot[1,4]-3)[1,4]) = [-4.67,\,-12.67]$ | $[0.47,\,1.27]$ |
| 2 | $\tfrac{1}{3}(2([0.47,1.27]\cdot[1,1]-1)[1,1] + 2([0.47,1.27]\cdot[1,2]-3)[1,2]$ $+ 2([0.47,1.27]\cdot[1,4]-3)[1,4]) = [2.18,\,7.24]$ | $[0.25,\,0.54]$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 200 (수렴) | $\tfrac{1}{3}(2([1,0.57]\cdot[1,1]-1)[1,1] + 2([1,0.57]\cdot[1,2]-3)[1,2]$ $+ 2([1,0.57]\cdot[1,4]-3)[1,4]) = [0,\,0]$ | $[1,\,0.57]$ |
p27. 요약
- 어떤 예측기들이 가능한가?
가설 클래스(Hypothesis class):
\[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) \}\]
- 예측기가 얼마나 좋은가?
손실 함수(Loss function):
\[Loss(x,y,\mathbf{w}) = (f_{\mathbf{w}}(x) - y)^2\]
- 예측기를 어떻게 최적화할까?
경사하강법(Gradient descent):
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w})\]
선형 분류(Linear Classification)
p28. 선형 분류
분류기(classifier)는 서로 다른 클래스들을 가장 잘 구분하는 결정 경계(decision boundary)를 학습한다.
- 결정 경계(decision boundary)는 분류기의 예측이 한 클래스에서 다른 클래스로 전환(switches)되는 표면(surface)이다.
이 작업(task)에 대해 우리는 어떻게 분류기를 정의하고 최적화할 수 있을까?
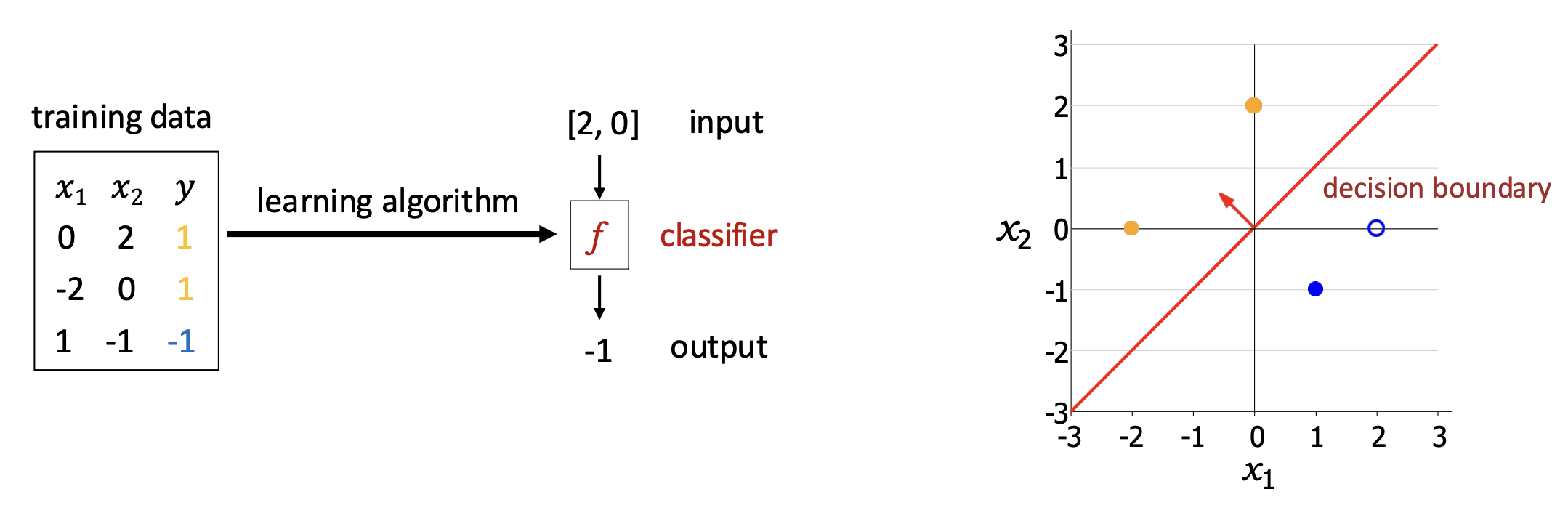
p29. 선형 (이진) 분류
벡터 표기:
가중치 벡터 $\mathbf{w} \in \mathbb{R}^d$, 특성 벡터 $\varphi(x) \in \mathbb{R}^d$
\[f_{\mathbf{w}}(x) = \text{sign}(\mathbf{w} \cdot \varphi(x)) = \begin{cases} +1 & \mathbf{w} \cdot \varphi(x) > 0 \\ -1 & \mathbf{w} \cdot \varphi(x) < 0 \end{cases}\]이진 분류기 $f_{\mathbf{w}}$는 법선 벡터 $\mathbf{w}$를 갖는 초평면을 정의한다.
예시:
$\mathbf{w} = [-0.6,\,0.6]$
\[f([0,2]) = \text{sign}([-0.6,0.6]\cdot[0,2]) = \text{sign}(1.2) = 1\] \[f([-2,0]) = \text{sign}([-0.6,0.6]\cdot[-2,0]) = \text{sign}(1.2) = 1\] \[f([1,-1]) = \text{sign}([-0.6,0.6]\cdot[1,-1]) = \text{sign}(-1.2) = -1\]
$\mathcal{F} = { f_{\mathbf{w}} : \mathbf{w} \in \mathbb{R}^2 }$
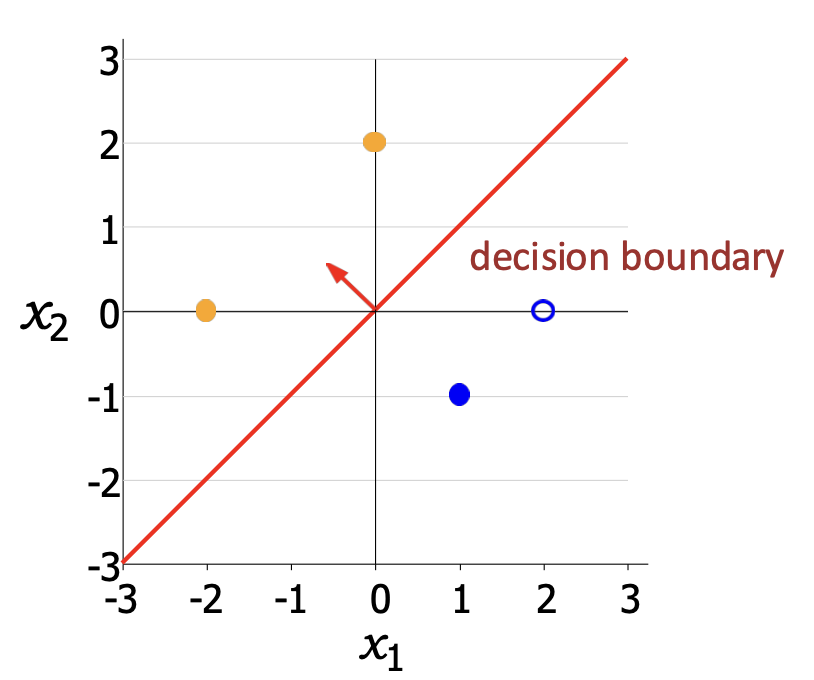
1. 결정 경계의 정의
\[\mathbf{w} \cdot \varphi(x) = 0\]
결정 경계는을 만족하는 점들의 집합이다.
즉, $\varphi(x)$ 가 $\mathbf{w}$ 와 내적했을 때 0이 되는 점들이 결정 경계이다.2. 내적과 수직성의 관계
\[\mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\|\|\mathbf{b}\|\cos\theta\]
벡터 내적은로 정의된다.
내적이 0이면 $\cos\theta = 0$ 이므로 두 벡터는 수직(orthogonal)이다.3. 법선 벡터로서의 $\mathbf{w}$
결정 경계를 이루는 모든 $\varphi(x)$ 는 $\mathbf{w}$ 와 내적했을 때 0이 된다.
따라서 결정 경계 위의 $\varphi(x)$ 는 항상 $\mathbf{w}$ 와 수직이며,
$\mathbf{w}$ 는 결정 경계에 수직인 법선 벡터이다.4. 예시 (2차원)
\[2x_1 + x_2 = 0 \quad \Rightarrow \quad x_2 = -2x_1\]
$\mathbf{w}=(2,1)$ 일 때 결정 경계는이다.
\[\frac{1}{2}\]
직선의 기울기는 $-2$ 이다.
벡터 $\mathbf{w}=(2,1)$ 의 기울기는이다.
\[(-2) \times \left(\tfrac{1}{2}\right) = -1\]
두 기울기를 곱하면이므로 직선과 $\mathbf{w}$ 는 서로 수직이다.
5. 정리
결정 경계: $\mathbf{w} \cdot \varphi(x) = 0$
경계 위의 $\varphi(x)$ 는 항상 $\mathbf{w}$ 와 직교
따라서 $\mathbf{w}$ 는 결정 경계의 법선 벡터이다.
p31. 선형 분류: 분류기는 얼마나 좋은가?
벡터 표기:
가중치 벡터 $\mathbf{w} \in \mathbb{R}^d$, 특성 벡터 $\varphi(x) \in \mathbb{R}^d$
\[f_{\mathbf{w}}(x) = \text{sign}(\mathbf{w} \cdot \varphi(x)) = \begin{cases} +1 & \mathbf{w} \cdot \varphi(x) > 0 \\ -1 & \mathbf{w} \cdot \varphi(x) < 0 \end{cases}\]- 예측된 레이블: $f_{\mathbf{w}}(x)$
- 타깃 레이블: $y$
점수(Score): 예시 $(x,y)$에서의 점수는 $\mathbf{w} \cdot \varphi(x)$이며, 이는 우리가 +1을 예측하는 데 얼마나 확신(confident) 하는지를 나타낸다.
마진(Margin): 예시 $(x,y)$에서의 마진은 $(\mathbf{w} \cdot \varphi(x))y$이며, 이는 우리가 얼마나 정확(correct) 한지를 나타낸다.
- 기하학적으로, $|\mathbf{w}| = 1$이라면 입력 $x$의 여유는 그 특성 벡터 $\varphi(x)$로부터 결정 경계까지의 정확한 거리이다.
1. 마진의 정의
\[\text{margin}(x,y) = (\mathbf{w} \cdot \varphi(x))y\]
어떤 데이터 인스턴스 $(x,y)$ 에 대해 마진은로 정의된다.
여기서 $y \in \lbrace +1, -1 \rbrace$ 이므로 부호는 올바른 분류 여부를 나타내고, 크기는 결정 경계에서 얼마나 떨어져 있는지를 반영한다.2. 결정 경계의 정의
\[\mathbf{w} \cdot \varphi(x) = 0\]
결정 경계는으로 정의된다.
3. 점과 초평면 사이의 거리
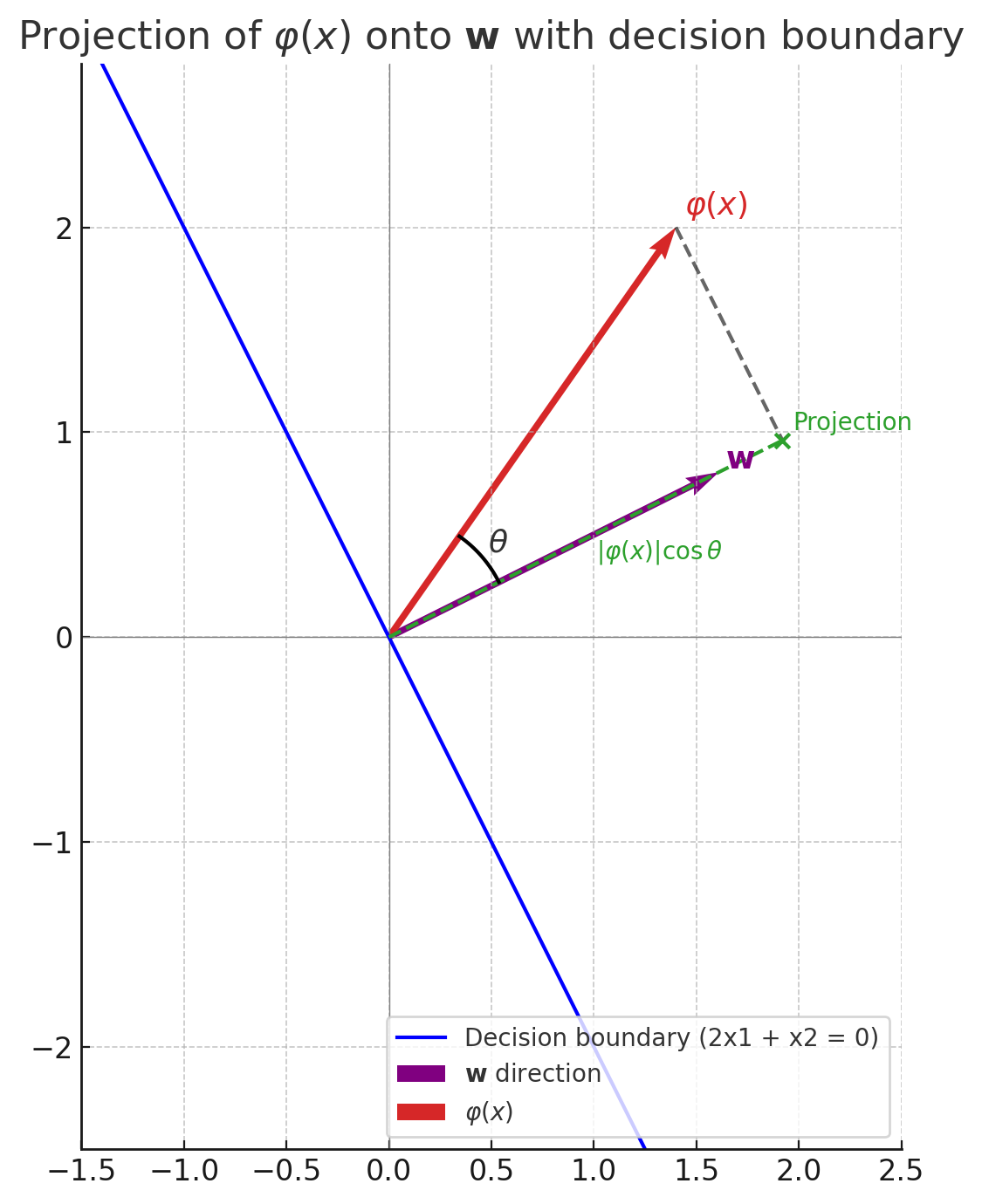
\[\frac{\mathbf{w} \cdot \varphi(x)}{\|\mathbf{w}\|}\]
$\mathbf{w}$ 는 초평면의 법선 벡터이므로, 초평면에 가장 가까운 경로는 항상 $\mathbf{w}$ 방향으로 수직인 직선이다.
따라서 점 $\varphi(x)$ 에서 초평면까지의 거리를 구하려면, $\varphi(x)$ 를 $\mathbf{w}$ 방향으로 투영해야 한다.
내적의 성질에 따르면, 벡터 $\varphi(x)$ 를 $\mathbf{w}$ 방향으로 투영한 길이는이다.
그림에서 파란선은 초평면이고, 보라색 $\mathbf{w}$ 는 초평면의 법선 벡터이다.
\[\mathbf{w}\cdot\varphi(x) = \|\mathbf{w}\|\,\|\varphi(x)\|\cos\theta\]
점 $\varphi(x)$ 에서 초평면까지의 최단 거리는 점 $\varphi(x)$ 의 $\mathbf{w}$ 방향 성분이다.
내적 공식은이므로, 투영 길이는
\[\frac{\mathbf{w}\cdot\varphi(x)}{\|\mathbf{w}\|}\]이 되고, $\mathbf{w}$ 가 단위 벡터일 때는 $|\varphi(x)|\cos\theta$ 와 같다.
하지만 거리는 음수가 될 수 없으므로 절댓값을 취해
\[\frac{|\mathbf{w} \cdot \varphi(x)|}{\|\mathbf{w}\|}\]라는 공식이 된다.
즉, $\mathbf{w}$ 와 $\varphi(x)$ 의 내적이 클수록 점은 초평면에서 멀리 있고, 0 에 가까울수록 초평면에 더 가깝다.4. $|\mathbf{w}| = 1$ 인 경우
\[|\mathbf{w} \cdot \varphi(x)|\]
$|\mathbf{w}| = 1$ 이면 위 식은로 단순해진다.
따라서 마진 $(\mathbf{w}\cdot\varphi(x))y$ 는 곧 데이터 인스턴스 $\varphi(x)$ 에서 결정 경계까지의 거리이다.5. 마진과 거리의 관계
올바른 분류( $y$ 와 $\mathbf{w}\cdot\varphi(x)$ 의 부호가 같음 )라면 마진은 양수이며, 이는 초평면과의 거리로서 얼마나 확신 있게 예측했는지를 나타낸다.
잘못된 분류(부호가 다름)라면 마진은 음수이며, 이는 초평면과의 거리로 얼마나 크게 잘못했는지를 나타낸다.
p32. 선형 분류: 분류기는 얼마나 좋은가?
선형 (이진) 분류기의 손실 함수 (Loss function)
우리가 찾고자 하는 $\mathbf{w}$는 다음을 만족해야 한다:
\[\begin{cases} \mathbf{w}\cdot \varphi(x) > 0 & \text{if } y = +1 \\ \mathbf{w}\cdot \varphi(x) < 0 & \text{if } y = -1 \end{cases} \quad \forall (x,y) \in \mathcal{D}\]이는 동일하게 표현할 수 있다:
\[(\mathbf{w}\cdot \varphi(x))y > 0, \quad \forall (x,y) \in \mathcal{D}\]따라서 손실 함수는 다음과 같이 정의된다:
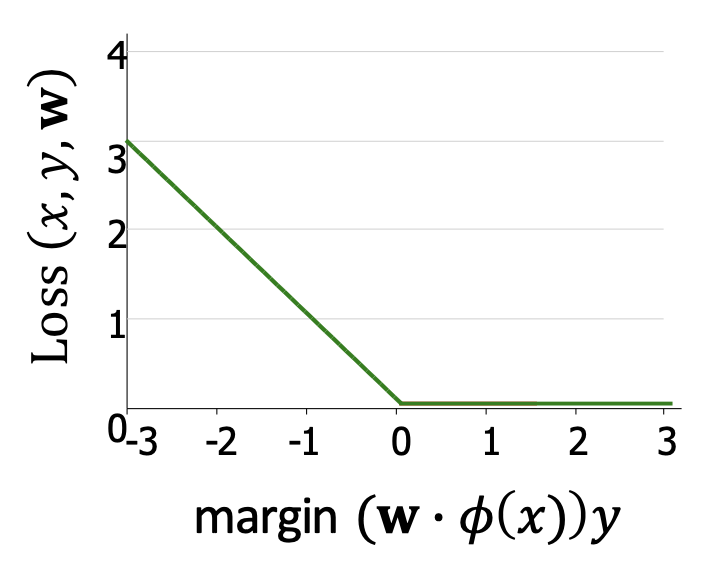
\[Loss(x,y,\mathbf{w}) = \max\{-(\mathbf{w}\cdot \varphi(x))y, \, 0\}\]
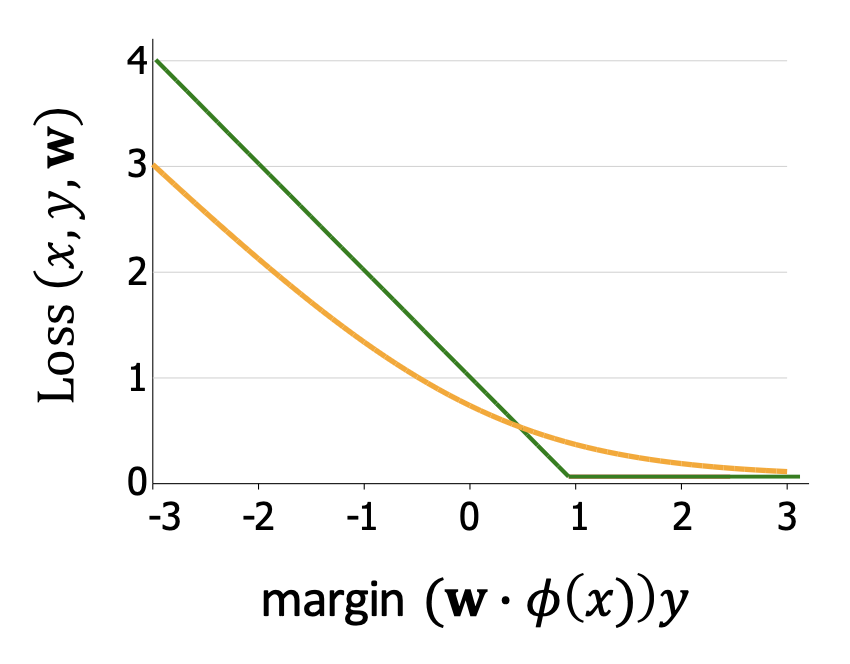
- 그림 설명
- x축: 마진 $(\mathbf{w}\cdot \varphi(x))y$
- y축: 손실 $Loss(x,y,\mathbf{w})$
- 마진이 0보다 크면 손실은 0이 되고, 마진이 음수일수록 손실이 커진다.
Loss 함수에서 margin에 음수를 붙이는 이유
- margin $(\mathbf{w}\cdot \varphi(x))y$ 자체는 클수록 올바르게 분류된 정도가 큰 지표이다.
- 하지만 Loss는 “나쁨”을 측정하는 지표이므로, margin이 클수록 Loss가 작아져야 한다.
- 이를 위해 margin에 마이너스(-) 를 붙여 $-(\mathbf{w}\cdot \varphi(x))y$ 형태로 정의한다.
- margin이 양수(= 올바른 분류)일 때는 음수가 되므로 $\max(\cdot,0)$에서 Loss = 0.
- margin이 음수(= 잘못된 분류)일 때는 양수가 되어 Loss 값이 커진다.
- 따라서 Loss는 margin의 “올바름 지표”를 “틀림의 지표”로 변환하여, 학습 과정에서 최소화해야 할 대상으로 만든다.
p33. 선형 분류: 분류기는 얼마나 좋은가?
- 손실 함수 (Loss function)
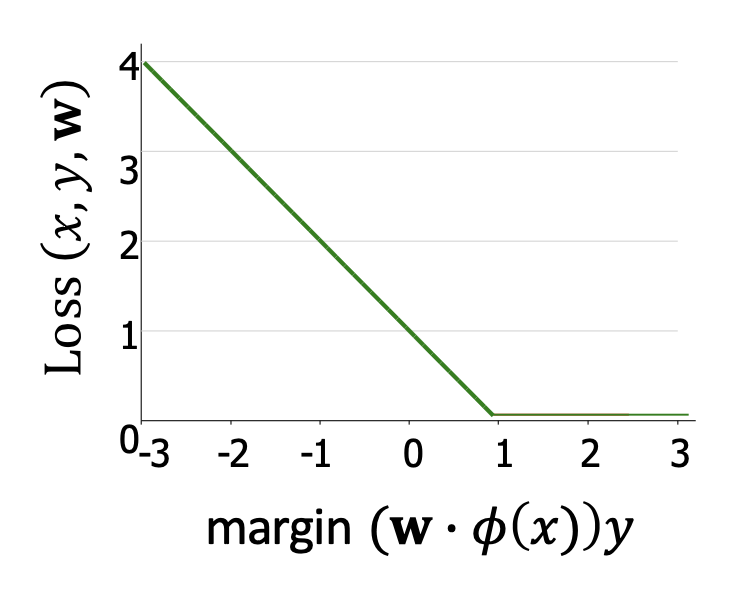
- 더 일반적인 형태: 힌지 손실 (hinge loss)
- 설명:
1은 여유(buffer) 를 주기 위한 것 → 힌지 손실은 분리 초평면을 찾되, 마진(margin)이 최소 1 이상 되도록 유도한다.- 마진이 위배되면(loss > 0) → 손실은 선형적으로 증가한다.
- 마진이 만족되면(loss = 0) → 손실은 0이 된다.
힌지 손실의 기울기 (gradient):
\[\nabla_{\mathbf{w}} Loss_{\text{hinge}}(x,y,\mathbf{w}) = -\varphi(x)y \cdot \mathbf{1}[(\mathbf{w}\cdot \varphi(x))y < 1]\]여기서
- $\mathbf{1}[\text{condition}] =$
- 조건이 참이면 1
- 거짓이면 0
- $\mathbf{1}[\text{condition}] =$
1. 왜 ‘힌지 손실(hinge loss)’이라고 부르는가?
힌지 손실의 그래프를 보면, 마진이 1 이상일 때는 손실이 0으로 유지되다가
마진이 1 미만으로 줄어들면 기울기 -1의 직선 형태로 증가한다.
이때 마치 문이 경첩(hinge)에서 꺾이는 것처럼, 마진 = 1 지점을 기준으로 꺾이는 형태를 가진다.
이러한 그래프 모양 때문에 ‘힌지(hinge)’라는 이름이 붙었다.2. 힌지 손실이 의미하는 것
힌지 손실은 분류 경계로부터의 여유(마진)를 얼마나 확보했는지를 측정한다.
마진이 충분히 크면 손실은 0이 되어 “잘 분류되었다”고 본다.
반대로 마진이 1보다 작아지면 손실이 선형적으로 커지면서
잘못 분류되었거나 경계에 너무 가까운 점에 대해 벌점을 준다.
따라서 힌지 손실은 “얼마나 안전하게 분리되었는가”를 수치로 나타내는 손실 함수이다.
p34. 선형 분류: 예측기를 어떻게 최적화할까?
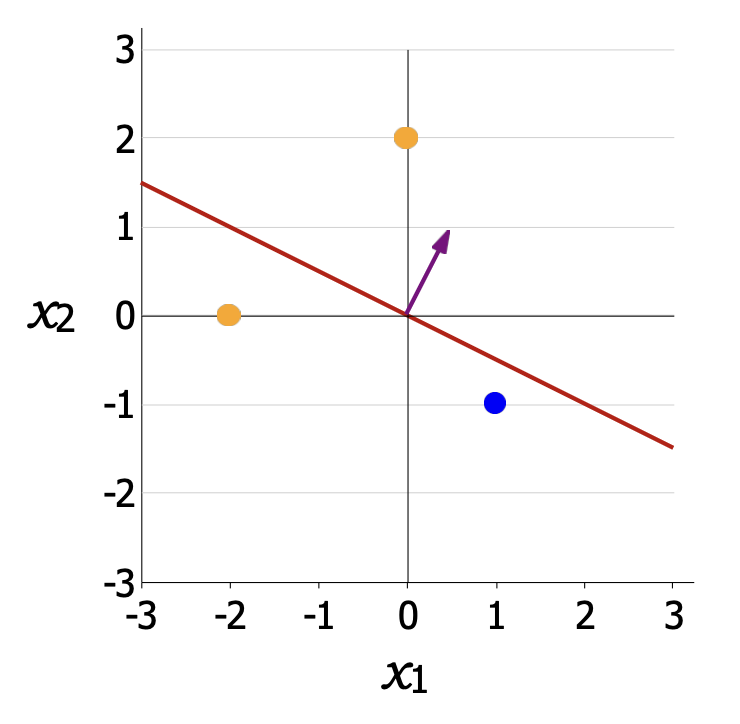
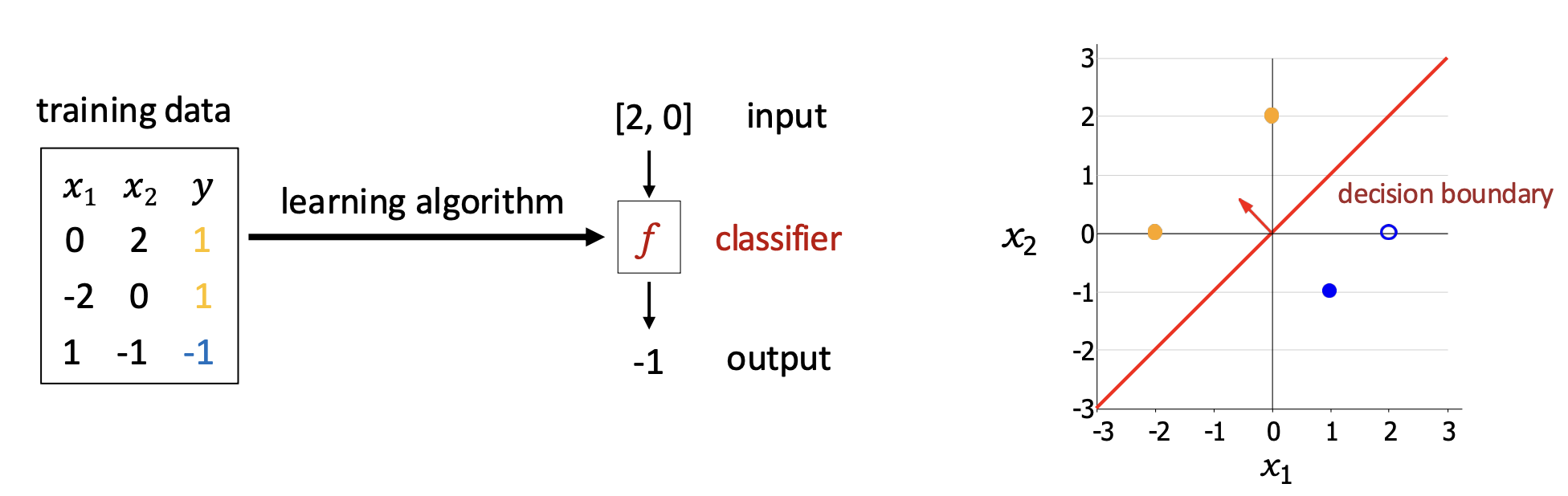
- 훈련 데이터 $D_{train}$
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 2 | 1 |
| -2 | 0 | 1 |
| 1 | -1 | -1 |
- 모델 정의
\(f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x)\) \(\mathbf{w} = [0.5,\,1]\) \(\varphi(x) = [x_1,\,x_2]\)
- 힌지 손실(hinge loss):
- $D_{train}$에 대한 손실(loss) 계산
- 그래디언트(gradient) 계산
1. 힌지 손실의 미분 규칙
\[Loss_{\text{hinge}}(x,y,\mathbf{w})=\max\{1-(\mathbf{w}\cdot\varphi(x))y,\;0\}\]
힌지 손실은로 정의된다.
만약 $1-(\mathbf{w}\cdot\varphi(x))y \le 0$이면 손실이 0이므로 기울기도 0이 된다.
반대로 $1-(\mathbf{w}\cdot\varphi(x))y > 0$이면 손실이 양수이며,
이때는 안쪽 항 $1-(\mathbf{w}\cdot\varphi(x))y$ 를 $\mathbf{w}$ 에 대해 미분한다.그래서
\[\nabla_{\mathbf{w}} Loss_{\text{hinge}}(x,y,\mathbf{w})= \begin{cases} -y\,\varphi(x), & (\mathbf{w}\cdot\varphi(x))y<1 \\ [0,0], & (\mathbf{w}\cdot\varphi(x))y\ge 1 \end{cases}\]2. 데이터 인스턴스별 계산 과정
(1) $(x,y)=([0,2],1)$
- $\mathbf{w}\cdot\varphi(x)=[0.5,1]\cdot[0,2]=2$
- $y(\mathbf{w}\cdot\varphi(x))=2$
- $2>1$ → 마진 만족 → 기울기 = $[0,0]$
(2) $(x,y)=([-2,0],1)$
- $\mathbf{w}\cdot\varphi(x)=-1$
- $y(\mathbf{w}\cdot\varphi(x))=-1$
- $-1<1$ → 마진 위반
- $\nabla Loss=-y\varphi(x)=-(1)[-2,0]=[2,0]$
(3) $(x,y)=([1,-1],-1)$
- $\mathbf{w}\cdot\varphi(x)=-0.5$
- $y(\mathbf{w}\cdot\varphi(x))=0.5$
- $0.5<1$ → 마진 위반
- $\nabla Loss=-y\varphi(x)=-(-1)[1,-1]=[1,-1]$
3. 평균 기울기 (Train Gradient)
\[\nabla TrainLoss([0.5,1])=\frac{[0,0]+[2,0]+[1,-1]}{3}=[1,\,-0.33].\]
세 인스턴스 기울기의 평균은
p35. 로지스틱 회귀: 로지스틱 손실 (logistic loss)
- 또 다른 인기 있는 손실 함수: 로지스틱 손실
예측이 아무리 정확하더라도, 손실은 항상 0이 아닌 값을 가진다.
→ 따라서 마진을 키우는 방향으로 손실을 줄이려는 유인이 계속 존재한다.
(다만 그 효과는 점점 감소한다.)로지스틱 손실을 선형 분류기에 적용하면, 그 모델을 로지스틱 회귀(logistic regression) 모델이라고 부른다.
- 그래프
- 초록색 선: 힌지 손실
- 주황색 곡선: 로지스틱 손실
- 차이점:
- 힌지 손실은 마진이 1 이상일 때 손실이 0이 된다.
- 로지스틱 손실은 마진이 커져도 손실이 0에 가까워질 뿐 완전히 0이 되지 않는다.
p36. 로지스틱 회귀 (Logistic regression)
로지스틱 회귀는 선형 이진 분류(linear binary classification) 알고리즘으로,
어떤 데이터 인스턴스가 특정 클래스에 속할 확률(probability)을 예측한다.이때 출력 확률을 만들기 위해 시그모이드 함수(sigmoid function)를 사용한다.
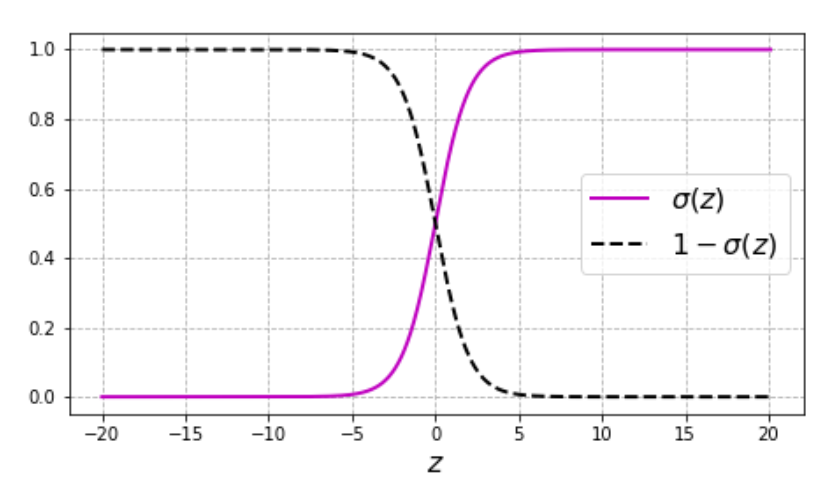
- 시그모이드 함수의 성질
- 입력 $z \in [-\infty, +\infty]$ → 이를 logit이라 부른다.
- $z \to -\infty$일 때 $\sigma(z) \to 0$
- $z \to +\infty$일 때 $\sigma(z) \to 1$
- $\sigma(-z) = 1 - \sigma(z)$
도함수:
\[\frac{d}{dz}\sigma(z) = \sigma(z)\sigma(-z) = \sigma(z)(1 - \sigma(z))\]
- 그래프 해석
- 분홍색 곡선: $\sigma(z)$ (출력 확률)
- 검정 점선: $1 - \sigma(z)$
- $z=0$에서 $\sigma(z)=0.5$ → 분류 경계 기준점이 됨.
시그모이드 도함수 도출 과정
1. 시그모이드 함수 정의:
\[\sigma(z) = \frac{1}{1 + e^{-z}}\]2. 분모를 $u = 1 + e^{-z}$ 라고 두면:
\[\sigma(z) = \frac{1}{u}\]3. $\frac{d}{dz}\sigma(z)$ 계산:
\[\frac{d}{dz}\sigma(z) = -\frac{1}{u^2} \cdot \frac{du}{dz}\]4. $u = 1 + e^{-z}$ 이므로:
\[\frac{du}{dz} = -e^{-z}\]5. 따라서:
\[\frac{d}{dz}\sigma(z) = -\frac{1}{(1+e^{-z})^2} \cdot (-e^{-z}) = \frac{e^{-z}}{(1+e^{-z})^2}\]6. 이를 $\sigma(z)$ 로 표현하면:
\[\sigma(z) = \frac{1}{1+e^{-z}}, \qquad 1-\sigma(z) = \frac{e^{-z}}{1+e^{-z}}\]7. 곱하면:
\[\sigma(z)(1-\sigma(z)) = \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}} = \frac{e^{-z}}{(1+e^{-z})^2}\]8. 최종 결과:
\[\frac{d}{dz}\sigma(z) = \sigma(z)(1-\sigma(z))\]
p37. 로지스틱 회귀: 확률적 관점
- 베르누이 분포 (Bernoulli distribution)
- 확률변수 $y$는 확률 $p$로 1이 되고, 확률 $1-p$로 0이 된다.
예:우도(likelyhood)
\[p(Y = \{1,0,1,0,0\}) = p(1-p)p(1-p)(1-p) = p^2(1-p)^3\]
로지스틱 회귀 (Logistic regression)
\[\mathbb{E}[y|x] = p(y=1|x) = \sigma(\mathbf{w} \cdot \varphi(x))\]
로지스틱 회귀는 입력과 출력을 조건부 베르누이 분포 (conditional Bernoulli distribution)로 모델링한다.주어진 훈련 데이터셋의 우도 (Likelihood)
\[\prod_{n=1}^N p(y_n=1|x_n)^{y_n}(1-p(y_n=1|x_n))^{1-y_n}\]
주어진 ${(x_n, y_n)}_{n=1}^N$에 대해, 우도는 다음과 같이 주어진다:이를 로지스틱 함수 $\sigma(z)$로 치환하면,
\[\prod_{n=1}^N \sigma(\mathbf{w}\cdot\varphi(x_n))^{y_n} \big(1-\sigma(\mathbf{w}\cdot\varphi(x_n))\big)^{1-y_n}\]이 된다.
이는 특정 가중치 벡터 $\mathbf{w}$가 주어졌을 때, 주어진 데이터셋이 관측될 확률을 나타낸다.
1. 베르누이 분포와 확률 모수
- $y \in {0,1}$ 인 이진 분류 문제는 베르누이 분포로 모델링된다.
- 이때 필요한 것은 $p = P(y=1 \mid x)$ 라는 하나의 확률 모수이다.
2. 선형 결합만으로는 부족함
- 만약 $p = \mathbf{w}\cdot \varphi(x)$ 라고 두면, $\mathbf{w}\cdot \varphi(x)$ 값은 음수나 1보다 큰 값도 가능하다.
- 그러나 확률은 $0 \le p \le 1$ 범위여야 하므로 직접 선형 결합을 확률로 사용할 수 없다.
3. 시그모이드 변환의 도입
- 실수 전체를 입력받아 (0,1) 범위의 값을 출력하는 시그모이드 함수(sigmoid)를 사용한다.
따라서 $p(y=1 \mid x)$ 를 다음과 같이 정의한다.
\[p(y=1|x) = \sigma(\mathbf{w}\cdot \varphi(x)), \qquad \sigma(z) = \frac{1}{1+e^{-z}}\]4. 직관적 해석
- $\mathbf{w}\cdot \varphi(x)$ 는 입력 $x$ 가 결정 경계로부터 얼마나 떨어져 있는지를 나타낸다.
- $\sigma(\cdot)$ 는 이 선형 값을 확률로 변환하여,
경계에서 멀수록 확률을 0 또는 1에 가깝게 만들고,
경계 주변에서는 0.5 부근의 불확실한 값을 출력한다.5. 정리
\[P(y=1|x) = \sigma(\mathbf{w}\cdot \varphi(x))\]
- 즉, 선형 모델과 시그모이드 변환을 결합하여
베르누이 확률 모수를 입력 $x$ 에 의존하도록 표현한 것이다.
p38. 로지스틱 회귀: 확률적 관점
주어진 ${(x_n, y_n) \mid n = 1, \ldots, N}$에 대해, 가능도(likelihood)는 다음과 같이 주어진다:
\[\prod_{n=1}^N p(y_n=1|x_n)^{y_n} (1 - p(y_n=1|x_n))^{1-y_n} = \prod_{n=1}^N \sigma(\mathbf{w}\cdot \varphi(x_n))^{y_n} (1 - \sigma(\mathbf{w}\cdot \varphi(x_n)))^{1-y_n}\]→ 이는 특정 가중치 벡터 $\mathbf{w}$가 주어졌을 때, 주어진 데이터셋이 관측될 확률을 의미한다.
우리는 모델을 학습할 때 로그-가능도(log-likelihood)를 극대화한다:
\[\mathcal{L} = \sum_{n=1}^N \log p(y_n|x_n) = \sum_{n=1}^N \{y_n \log \hat{y}_n + (1-y_n)\log(1-\hat{y}_n)\}\]여기서 $\hat{y}_n = \sigma(\mathbf{w}\cdot \varphi(x_n))$.
- 이는 수학적으로 로지스틱 손실(logistic loss) 을 최소화하는 것과 동등하다.
또한 (이진) 교차 엔트로피 손실(cross-entropy loss) 이라고도 불린다.
\[Loss_{\text{logistic}}(x,y,\mathbf{w}) = \log(1 + e^{-(\mathbf{w}\cdot \varphi(x))y})\]
1. 가능도의 의미
- 가능도(likelihood)는 “모델이 주어진 데이터를 얼마나 잘 설명하는가”를 나타내는 수치이다.
- 로지스틱 회귀에서는 각 데이터 $(x_n, y_n)$ 의 조건부 확률을 모두 곱해 전체 가능도를 정의한다.
2. 로그-가능도의 도입 이유
- 확률들을 곱하면 데이터 개수 $N$ 이 커질수록 값이 매우 작아져 계산이 어렵다.
- 로그를 취하면 곱셈이 덧셈으로 변해 계산 안정성이 높아지고, 미분을 통한 최적화도 쉬워진다.
3. 로지스틱 손실과의 관계
- 로그-가능도를 최대화하는 것은 로지스틱 손실(logistic loss)을 최소화하는 것과 수학적으로 동일하다.
- 즉, 가능도 최대화 관점과 손실 최소화 관점이 서로 연결된다.
4. 교차 엔트로피 손실의 의미
- 교차 엔트로피(cross-entropy)는 “실제 분포와 모델이 추정한 분포 사이의 차이”를 측정하는 척도이다.
- 따라서 이를 최소화하는 것은 모델의 예측 확률이 실제 레이블 분포에 가까워지도록 만드는 과정이다.
p39. 요약
- 어떤 예측기들이 가능한가?
가설 클래스(Hypothesis class):
\[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) \}\]
- 예측기가 얼마나 좋은가?
손실 함수(Loss function):
힌지 손실(Hinge loss):
\[Loss_{\text{hinge}}(x,y,\mathbf{w}) = \max\{1 - (\mathbf{w} \cdot \varphi(x))y,\,0\}\]로지스틱 손실(Logistic loss):
\[Loss_{\text{logistic}}(x,y,\mathbf{w}) = \log(1 + e^{-(\mathbf{w} \cdot \varphi(x))y})\]
- 예측기를 어떻게 최적화할까?
경사하강법(Gradient descent):
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \, \nabla_{\mathbf{w}} TrainLoss(\mathbf{w})\]
확률적 경사하강법(SGD)
p41. 경사하강법(Gradient Descent, GD) 요약
- 목표(Goal):
전체 훈련 데이터에서 손실을 최소화하는 $\mathbf{w}$를 찾는 것
\[\min_{\mathbf{w}} TrainLoss(\mathbf{w})\] \[TrainLoss(\mathbf{w}) = \frac{1}{|D_{train}|} \sum_{(x,y)\in D_{train}} Loss(x, y, \mathbf{w})\]
- 최적화 방법(How to optimize?): 경사하강법(Gradient descent)
- 기울기 $\nabla_{\mathbf{w}} TrainLoss(\mathbf{w})$는 훈련 손실을 가장 크게 증가시키는 방향을 의미한다.
- 따라서 그 반대 방향으로 $\mathbf{w}$를 갱신하여 손실을 줄인다.
💻 알고리즘 (Algorithm)
- $\mathbf{w}$를 무작위로 초기화
수렴할 때까지 반복:
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} TrainLoss(\mathbf{w})\]
- 여기서 $\eta$ (학습률, step size)는 하이퍼파라미터이다.
- 문제점(Problem):
- 경사하강법은 느리다!
- 그래디언트를 계산하려면 전체 훈련 데이터를 모두 사용해야 한다.
p42. 확률적 경사하강법 (SGD)
- 확률적 경사하강법(Stochastic gradient descent, SGD) 은 무작위로 선택된 하나의 데이터 포인트 를 사용하여 가중치를 업데이트한다.
💻 알고리즘 (Algorithm)
- w 를 무작위로 초기화한다.
- 수렴할 때까지 반복한다:
무작위로 선택된 $(x, y) \in D_{train}$ 에 대해
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} Loss(\mathbf{w})\]
- 장점 (Pros):
- 더 빠른 업데이트 가능
- 지역 최소값(local minima)에서 벗어날 수 있음
- (결정적(deterministic) vs. 확률적(stochastic))
- 단점 (Cons):
- 업데이트가 잡음(noisy) 이 섞여 매끄럽게 수렴하지 않을 수 있음
p43. 확률적 경사하강법 (SGD)
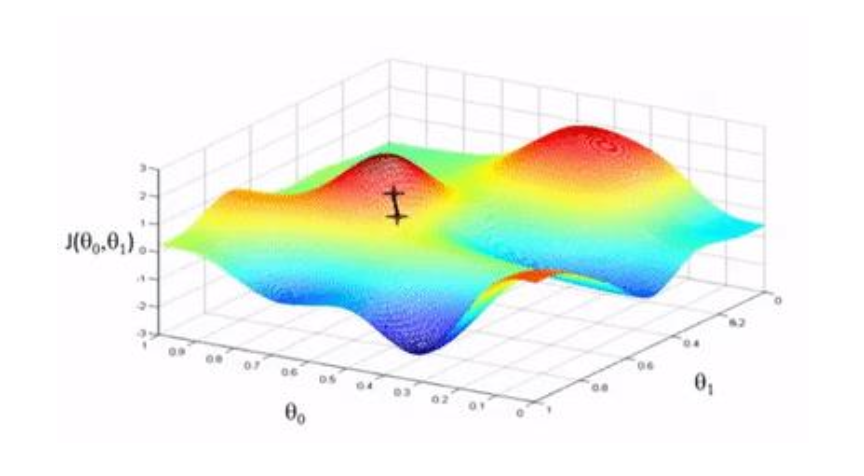
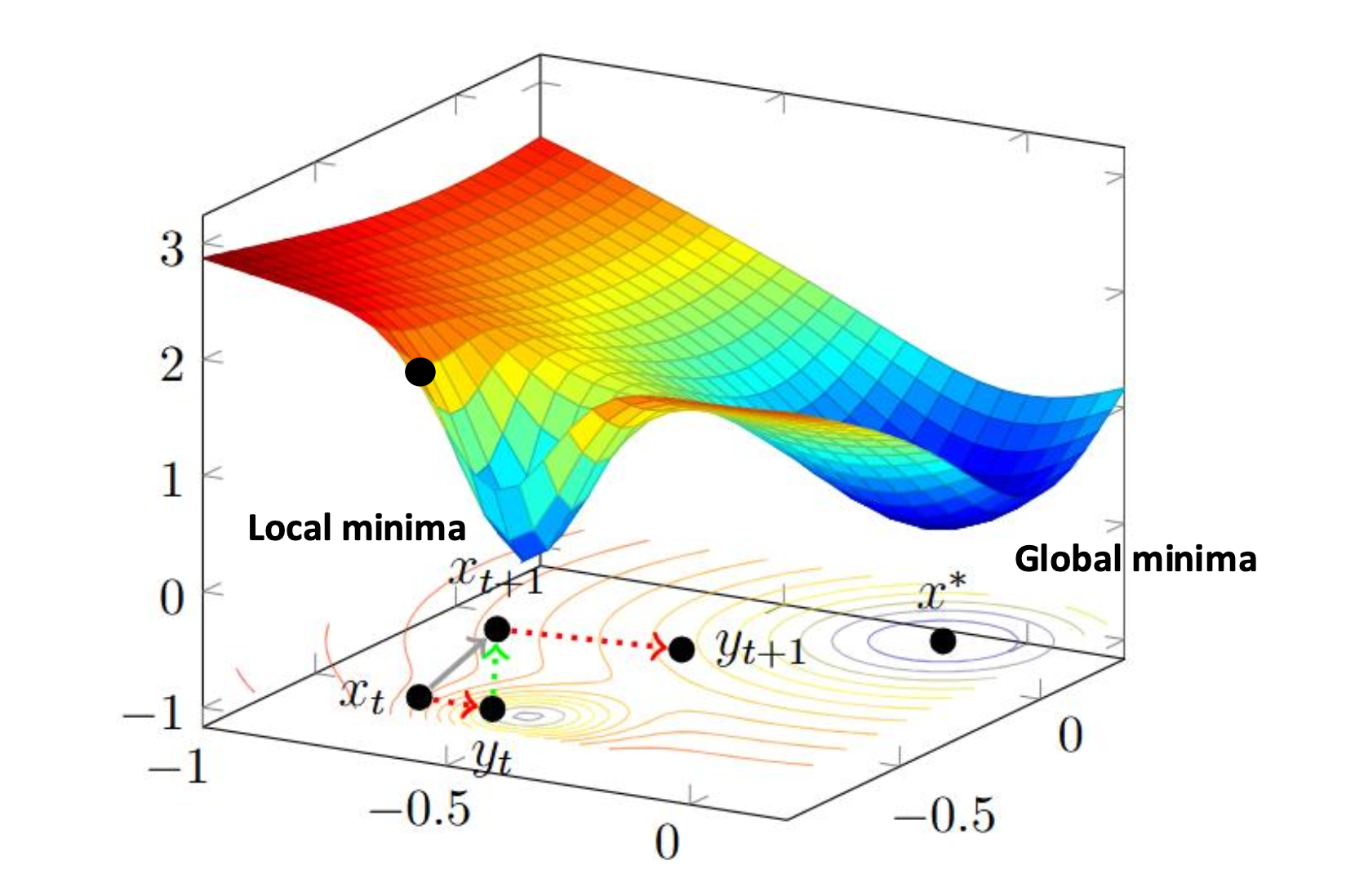
이 그림은 SGD(Stochastic Gradient Descent) 가 가지는 중요한 특징을 보여준다.
- 경사하강법(GD)은 결정적(deterministic) 방식으로 이동하므로, 한 번 지역 최소값(local minima) 에 빠지면 그 안에 머무르게 된다.
- 반면 SGD는 무작위성(stochasticity) 때문에 매 스텝마다 잡음(noise) 이 섞여 있어,
지역 최소값을 빠져나와 전역 최소값(global minima) 에 도달할 가능성이 생긴다.즉, SGD의 불안정해 보이는 진동이 단점처럼 보일 수 있지만,
복잡한 최적화 문제에서는 오히려 더 좋은 해를 찾는 데 도움이 된다.
p44. 확률적 경사하강법 (SGD)
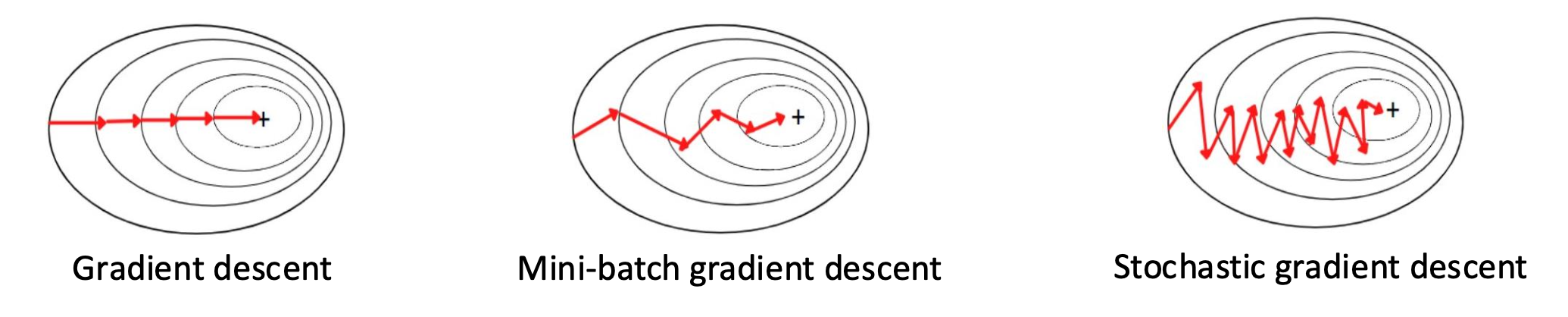
- 미니배치 경사하강법(mini-batch gradient descent) 은 작은 훈련 예시 집합을 사용하여 가중치를 갱신함으로써 GD와 SGD 사이의 균형을 잡는다.
💻 알고리즘 (Algorithm)
- $\mathbf{w}$를 무작위로 초기화
- 수렴할 때까지 반복:
각 배치 $\mathcal{B} \subset D_{train}$ 에 대해:
\[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} \frac{1}{|\mathcal{B}|} \sum_{i=1}^{|\mathcal{B}|} Loss(\mathbf{w})\]
- (미니)배치 $\mathcal{B}$ 는 $D_{train}$의 무작위 부분집합이고, 배치 크기 $\mid \mathcal{B} \mid$ 는 하이퍼파라미터이다.
- $\mid \mathcal{B} \mid = 1 \;\;\Rightarrow\;$ SGD
- $\mid \mathcal{B} \mid = \mid D_{train} \mid \;\;\Rightarrow\;$ GD
미니배치 경사하강법(mini-batch gradient descent) 은
전체 데이터를 한 번에 사용하는 배치 경사하강법(GD)과
한 개의 데이터만 사용하는 확률적 경사하강법(SGD) 사이의 중간 방식이다.
- 배치 크기 $|\mathcal{B}|$ 를 적절히 선택하면
계산 효율성과 수렴 안정성 사이에서 균형을 맞출 수 있다.장점
- 전체 데이터셋을 사용하는 것보다 훨씬 빠른 학습 가능
- SGD에 비해 노이즈가 줄어들어 더 안정적인 수렴 가능
단점
- 배치 크기를 잘못 선택하면 계산 낭비가 커지거나 학습이 불안정해질 수 있다.
실제 딥러닝에서는 대부분 미니배치 방식이 사용되며,
배치 크기(batch size) 는 매우 중요한 하이퍼파라미터로 취급된다.