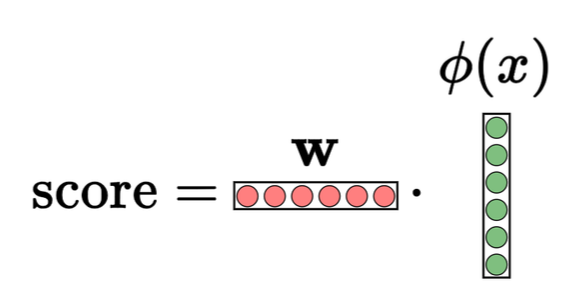[텍스트 마이닝] 3. Machine Learning 2

게시 2025/09/24 업데이트 2025/12/12

By 김성진

47 분읽는 시간

비선형 특성(Non-linear features)

p6. 선형 예측기와 비선형 특성

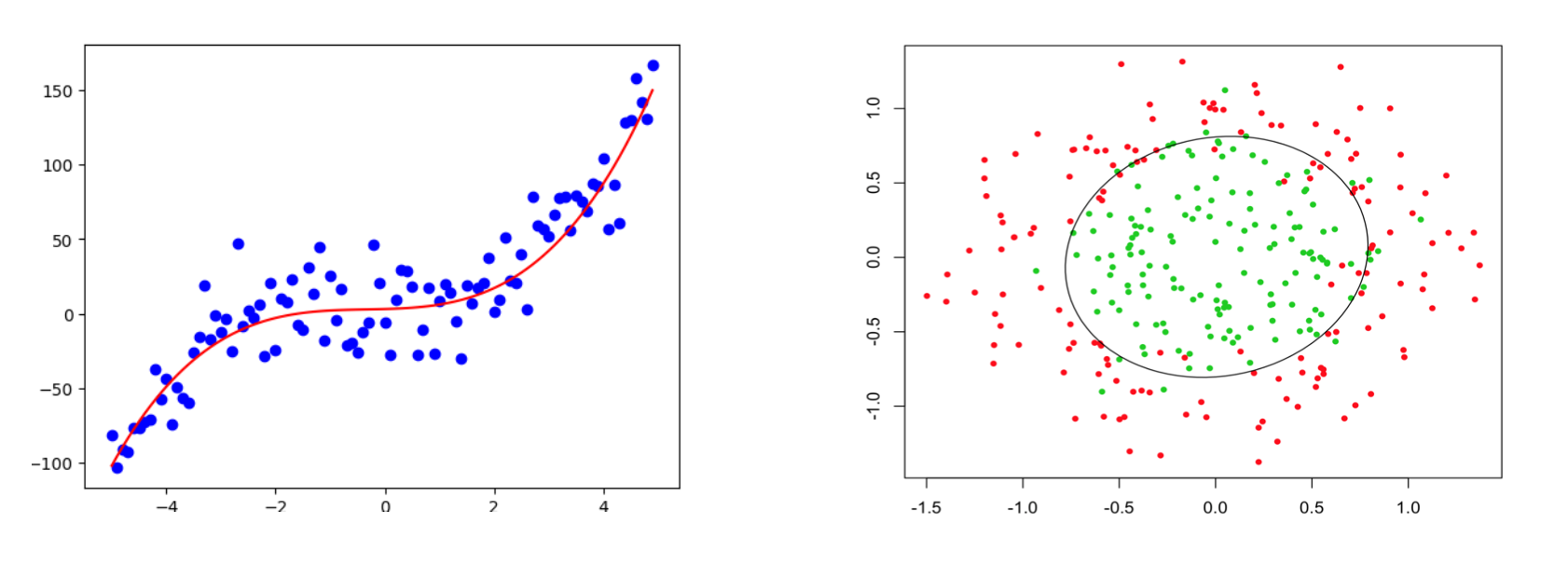
질문(Q): 선형 분류기를 사용하여 원형인 결정 경계를 얻을 수 있을까?
- 네! (Yes!)
- 주의: ‘선형(linear)’은 가중치 벡터와 예측값 사이의 관계를 의미한다. (입력 $x$가 아님)

p7. 선형 예측기에서의 특성

선형 모델의 경우, 가설 클래스는 특성 추출기(feature extractor) $\varphi(x)$의 선택에 의해 결정된다.

\[\mathbf{w} \cdot \varphi(x) = \sum_{j=1}^{d} w_j \varphi(x)_j\]

따라서, 특성 설계는 데이터에서 의미 있는 관계를 포착하는 데 매우 중요하다.
현실 세계 데이터에서의 비선형성(non-linearity)의 어려움:
1. 비단조성(non-monotonicity): 특성과 목표 변수 간의 관계는 항상 단조적으로 증가하거나 감소하지 않는다.
2. 포화(saturation): 일부 특성은 특정 지점을 넘어가면 효과가 줄어든다.
3. 특성 간 상호작용(interactions between features): 하나의 특성의 영향은 다른 특성의 존재에 따라 달라질 수 있으며, 이는 선형 모델이 자연스럽게 포착할 수 없다.

가설 클래스(hypothesis class)란
모델이 학습 과정에서 선택할 수 있는 함수들의 집합을 의미한다.
즉, “어떤 모양의 함수들 중에서 최적의 것을 찾을 것인가”를 미리 정해 놓은 틀이다.
예시:
선형 회귀:
\[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot x \}\]
입력 $x$ 에 대해 직선(또는 초평면) 형태의 함수만 고려한다.
비선형 특성 변환:
\[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) \}\]
$\varphi(x)$ 를 통해 다항식, 곡선, 원형 경계 등 더 복잡한 형태를 포함할 수 있다.
즉, 가설 클래스는
모델이 어떤 함수 형태를 학습할 수 있는가,
문제를 어떤 방식으로 수학적으로 표현할 것인가
를 결정하는 모델의 표현력 범위라 할 수 있다.

p8. 선형 예측기의 특징

예: 건강 예측하기
- 입력(Input): 환자 정보 $x$
- 출력(Output): 건강 $y \in \mathbb{R}$ (값이 클수록 더 좋음)
- 의료 진단을 위한 특징들: 키, 몸무게, 체온, 혈압 등
- 직접적인 접근법(straightforward approach) 은 이 특징들을 입력으로 직접 사용하는 것임:

\[\varphi(x) = [1, height(x), weight(x), temperature(x), blood\;pressure(x)]\] \[y = w_1 + w_2 \, height(x) + w_3 \, weight(x) + w_4 \, temperature(x) + w_5 \, blood\;pressure(x)\]

그러나, 이 접근법은 한계가 있으며, 우리는 다음에서 이를 살펴볼 것임.

p9. 비단조성(Non-monotonicity)

도전 과제: 특징들과 목표 변수 사이의 관계는 항상 단조적으로 증가하거나 감소하지 않는다.

직접적인 접근법:

\[\varphi(x) = [1, \; temperature(x)], \quad y = w_1 + w_2 \; temperature(x)\]

문제: 모델은 극단적인 값을 선호하지만, 실제 관계는 비단조적이다.

시도: 이차 특징(quadratic features) 도입

\[\varphi(x) = [1, \; (temperature(x) - 36.5)^2], \quad y = w_1 + w_2 \; (temperature(x) - 36.5)^2\]

단점: 이 접근법은 수동으로 도메인 특화(domain-specific) 변환을 정의해야 한다.

p10. 비단조성(Non-monotonicity)

더 나은 접근법:
결합할 수 있는 간단한 구성 요소(building blocks)로 특징을 설계한다.

\[\varphi(x) = [1, \; temperature(x), \; temperature(x)^2]\] \[y = w_1 + w_2 \; temperature(x) + w_3 \; temperature(x)^2\]

새로운 가설 클래스(hypothesis class)는 이전 것을 포괄하면서도 개념적으로 더 유연하다.

💡 여기서 $w_1, w_2, w_3$는 사용자가 직접 정하는 값이 아니라,
학습 과정(training) 을 통해 데이터로부터 자동으로 추정된다.

일반적인 규칙:
복잡한 특징을 직접 설계하는 대신, 먼저 원하는 함수 형태를 고려한 후
그것을 간단한 구성 요소(building blocks)로 분해한다.

p11. 포화(Saturation)

문제점: 일부 특징들은 일정 지점을 넘어서면 효과가 감소한다.
예시: 제품 추천
- 입력: 제품 정보 $x$
- 출력: 관련성 $y \in \mathbb{R}$
- 특징 $N(x)$: 제품 $x$를 구매한 사람 수
직접적인 접근법:

\[\varphi(x) = [1, N(x)], \quad y = w_1 + w_2 N(x)\]

문제: 1000명이 구매한 제품에 비해 10000명이 구매한 제품이 정말로 10배의 관련성을 갖는가?
- 그렇지 않다! 인기는 포화될 수 있으며, 추가적인 구매는 인지된 관련성에 덜 기여할 수 있다.

p12. 포화(Saturation)의 개선 방법

더 나은 접근법들:

로그 변환(Logarithmic transformation)
\[\varphi(x) = [1, \log N(x)], \quad y = w_1 + w_2 \log N(x)\]
- 값의 범위(dynamic range)가 매우 클 때 좋은 아이디어가 될 수 있다.
이산화(Discretization, binning)
\[\varphi(x) = [1, \; 1[0 < N(x) \leq 10], \; 1[10 < N(x) \leq 50], \; \dots, \; 1[500 < N(x) \leq 1000]]\] \[y = w_1 + w_2 \; 1[0 < N(x) \leq 10] + \cdots + w_6 \; 1[500 < N(x) \leq 1000]\]
- $N(x)$는 미리 정의된 구간(bin)으로 나누어진다.
- 각 구간마다 다른 가중치를 학습할 수 있어, 구간별로 상이한 영향을 반영할 수 있다.

p13. 특성들 간의 상호작용

예시: 건강 예측
- 입력: 환자 정보 $x$
- 출력: 건강 $y \in \mathbb{R}$ (높을수록 더 좋음)
- 두 특징을 고려: 키(height)와 몸무게(weight).
  건강한 몸무게 범위는 명확히 키에 의존한다.
직접적인 접근법: 이 관계를 포착할 수 없다.

\[\varphi(x) = [1, \; height(x), \; weight(x)], \quad y = w_1 + w_2 \; height(x) + w_3 \; weight(x)\]

더 나은 접근법: 여러 상호작용 항을 포함하는 특징들을 추가

\[\varphi(x) = [1, \; height(x), \; weight(x), \; height(x)weight(x), \; weight(x)/height(x)^2]\] \[y = w_1 + w_2 \; height(x) + w_3 \; weight(x) + w_4 \; height(x)weight(x) + w_5 \; weight(x)/height(x)^2\]

$BMI = \dfrac{weight(kg)}{height(m)^2}$
- 도메인 지식(domain knowledge)이 반영될 수 있다.

p14. 비선형 특성 설계: 회귀

이차 특성(Quadratic features)

\[\varphi(x) = [1, x, x^2]\] \[f(x) = [2, 1, -0.2] \cdot \varphi(x)\] \[f(x) = [4, -1, 0.1] \cdot \varphi(x)\] \[f(x) = [1, 1, 0] \cdot \varphi(x)\] \[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) : \mathbf{w} \in \mathbb{R}^3 \}\]

주기성 특성(Periodicity features)

\[\varphi(x) = [1, x, x^2, \cos(3x)]\] \[f(x) = [1, 1, -0.1, 1] \cdot \varphi(x)\] \[f(x) = [3, -1, 0.1, 0.5] \cdot \varphi(x)\] \[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) : \mathbf{w} \in \mathbb{R}^4 \}\]

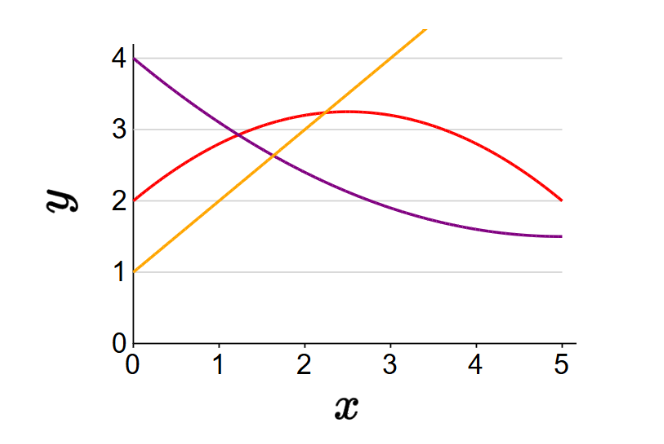
1. 이차 특성의 예시 전개
특성 벡터:
$\varphi(x) = [1, x, x^2]$
첫 번째 경우:
$f(x) = [2, 1, -0.2] \cdot [1, x, x^2] = 2 + x - 0.2x^2$
두 번째 경우:
$f(x) = [4, -1, 0.1] \cdot [1, x, x^2] = 4 - x + 0.1x^2$
세 번째 경우:
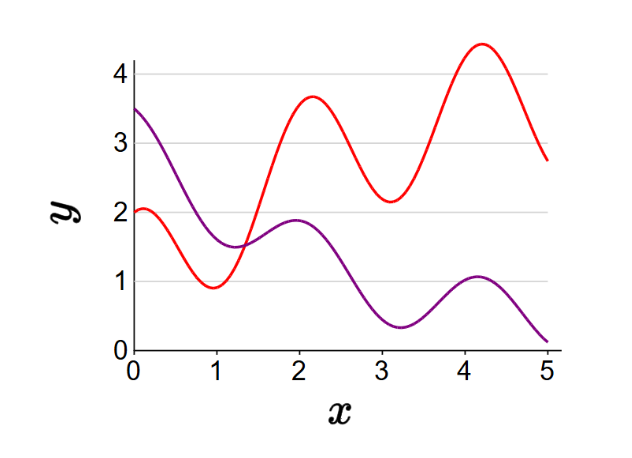
$f(x) = [1, 1, 0] \cdot [1, x, x^2] = 1 + x$
2. 주기성 특성의 예시 전개
특성 벡터:
$\varphi(x) = [1, x, x^2, \cos(3x)]$
첫 번째 경우:
$f(x) = [1, 1, -0.1, 1] \cdot [1, x, x^2, \cos(3x)] = 1 + x - 0.1x^2 + \cos(3x)$
두 번째 경우:
$f(x) = [3, -1, 0.1, 0.5] \cdot [1, x, x^2, \cos(3x)] = 3 - x + 0.1x^2 + 0.5\cos(3x)$

p15. 비선형 특성 설계: 분류

이차 특성(Quadratic features)

\[\varphi(x) = [x_1, x_2, x_1^2 + x_2^2]\] \[f(x) = \text{sign}([2, 2, -1] \cdot \varphi(x))\] \[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) : \mathbf{w} \in \mathbb{R}^3 \}\]

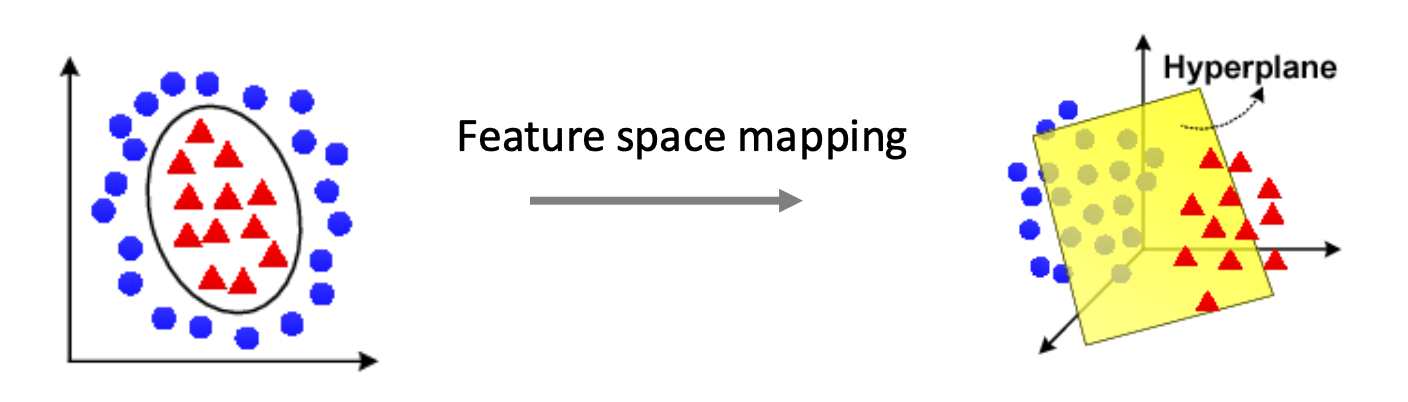
등가적 표현(Equivalently):

\[f(x) = \begin{cases} 1 & \text{if } (x_1 - 1)^2 + (x_2 - 1)^2 \leq 2 \\ -1 & \text{otherwise} \end{cases}\]

원래 입력 공간에서, 결정 경계(decision boundary)는 원(circle) 이다.
변환된 특성 공간에서는, 결정 경계가 초평면(hyperplane) 이 된다.

1. 원래 공간에서의 결정 경계
입력이 $(x_1, x_2)$일 때 결정 함수는
\[f(x) = 2x_1 + 2x_2 - (x_1^2 + x_2^2)\]
이다.
$f(x) = 0$ 으로 두면
\[(x_1 - 1)^2 + (x_2 - 1)^2 = 2\]
가 되어, 원래의 공간에서는 원의 형태가 결정 경계가 된다.
2. 변환된 공간에서의 표현
특성 벡터를
\[\varphi(x) = [x_1, x_2, x_1^2 + x_2^2]\]
로 정의한다.
새로운 좌표 $(z_1, z_2, z_3)$ 를
\[z_1 = x_1,\quad z_2 = x_2,\quad z_3 = x_1^2 + x_2^2\]
라고 두면, 결정 함수는
\[f(x) = [2, 2, -1] \cdot \varphi(x) = 2z_1 + 2z_2 - z_3\]
로 표현된다.
3. 초평면으로 단순화되는 이유
결정 경계 $f(x)=0$ 은
\[2z_1 + 2z_2 - z_3 = 0\]
의 형태가 된다.
이는 $(z_1, z_2, z_3)$ 공간에서의 평면 방정식이므로,
변환된 공간에서는 단순한 선형 초평면이 된다.

p16. 선형 예측기와 비선형 특성

무엇에 대해 선형인가?
- 예측은 점수(score)에 의해 결정된다: $\mathbf{w} \cdot \varphi(x) = \sum_{j=1}^d w_j \varphi(x)_j$
- $\mathbf{w}$에 대해 선형인가? → 예 (Yes)
- $\varphi(x)$에 대해 선형인가? → 예 (Yes)
- $x$에 대해 선형인가? → 아니오 (No!)
  ($x$는 반드시 벡터일 필요조차 없다)

요약 (Summary):

선형 예측기 $f_{\mathbf{w}}(x)$는 비선형 함수(non-linear functions)를 모델링할 수 있으며,
$x$에 대한 비선형 결정 경계(non-linear decision boundaries)를 만들 수 있다.
점수(score) $\mathbf{w} \cdot \varphi(x)$는
$\mathbf{w}$에 대한 선형 함수(linear function)이므로 효율적인 학습이 가능하다.
선형 예측기(linear predictors)는 도메인 지식(domain knowledge)에
기반한 잘 설계된 특성과 결합될 때 여전히 매우 효과적이다.

신경망(Neural networks)

p18. 비선형 예측기

선형 예측기

\[f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x), \quad \varphi(x) = [1, x]\]

비선형 특성을 가진 선형 예측기
- $\varphi(x)$를 바꾸어 비선형 함수를 모델링할 수 있다.

\[f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x), \quad \varphi(x) = [1, x, x^2]\]

비선형 신경망
- $\varphi(x)$를 사람이 직접 설계하는 대신, 신경망을 이용해 복잡한 변환(complex transformations)을 자동으로 학습할 수 있다.

\[f_{\mathbf{w}}(x) = \mathbf{w} \cdot \sigma(\mathbf{V}\varphi(x)), \quad \varphi(x) = [1, x]\]

최적의 transformation을 직접 디자인하는 것은 어려움
$\sigma(\mathbf{V}\varphi(x))$는 transformation을 자동으로 찾는 과정

p19. 동기 부여 예시

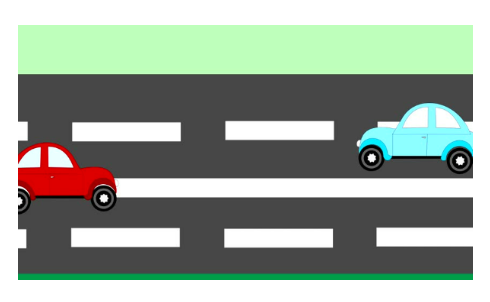
예시: 자동차 충돌 예측 (car collision prediction)
- 입력: 마주 오는 두 자동차의 위치
  \[x = [x_1, x_2]\]
- 출력: 안전(safe) 여부 또는 충돌(collide) 여부
  \[y = +1 \; \text{(안전)}, \quad y = -1 \; \text{(충돌)}\]

참 함수(true function)를 가정:
- 두 자동차가 충분히 멀리 떨어져 있으면(거리 ≥ 1) 안전하다.
\[y = \text{sign}(|x_1 - x_2| - 1)\]

p20. 문제를 분해하기

신경망을 이해하는 한 가지 방법은(뇌를 예로 들지 않고도) 문제 분해(problem decomposition) 이다.
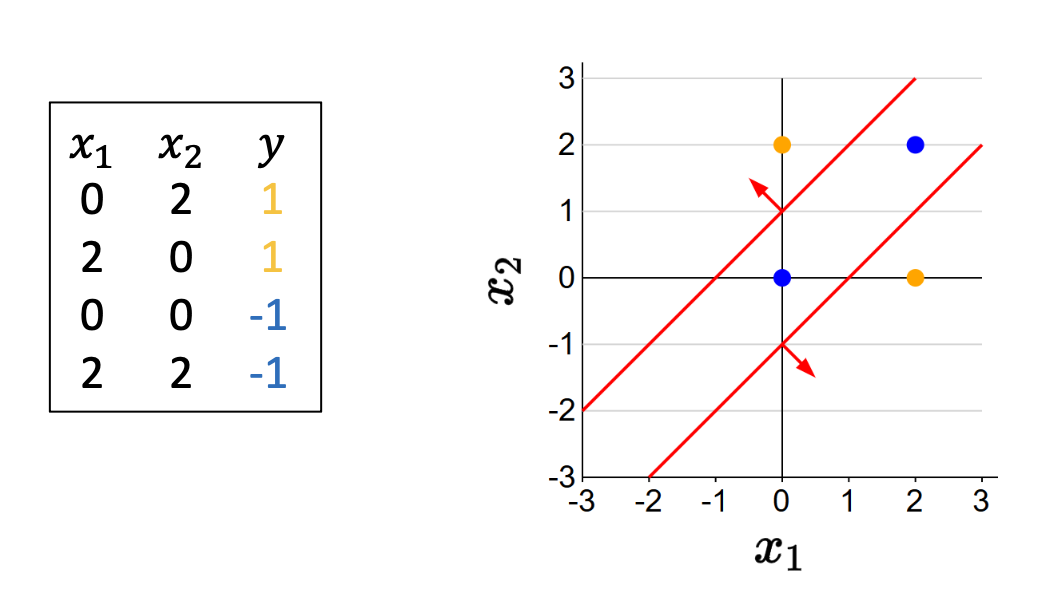
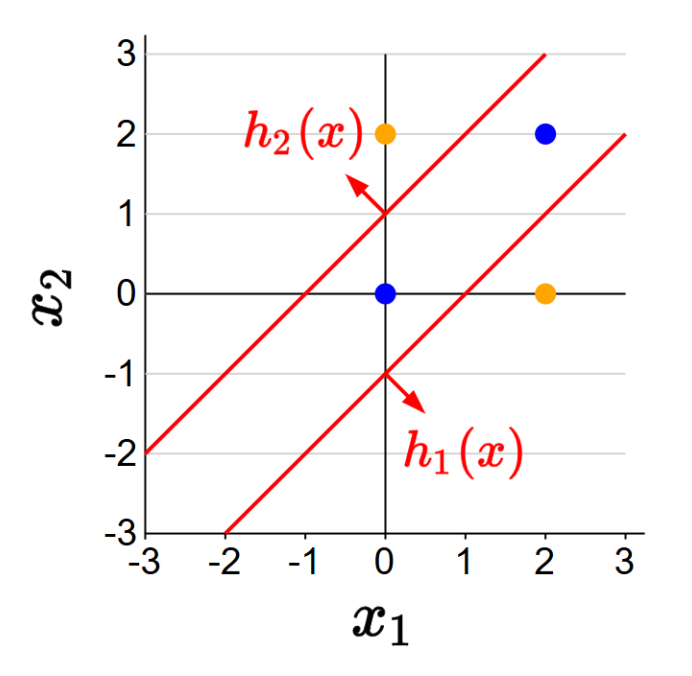
[하위 문제 1] 자동차 1이 자동차 2의 오른쪽에 충분히 멀리 있는지 확인:
\[h_1(x) = 1[x_1 - x_2 \geq 1]\]
[하위 문제 2] 자동차 2가 자동차 1의 오른쪽에 충분히 멀리 있는지 확인:
\[h_2(x) = 1[x_2 - x_1 \geq 1]\]

[예측] 둘 중 하나라도 참이면 안전(safe):
\[f(x) = \text{sign}(h_1(x) + h_2(x))\]

p21. 벡터 표기를 사용한 재작성

특성 벡터:
\[\varphi(x) = [1, x_1, x_2]\]
중간 하위 문제들:

\[h_1(x) = 1[x_1 - x_2 \geq 1] = 1[\mathbf{v}_1 \cdot \varphi(x) \geq 0], \quad \mathbf{v}_1 = [-1, +1, -1]\] \[h_2(x) = 1[x_2 - x_1 \geq 1] = 1[\mathbf{v}_2 \cdot \varphi(x) \geq 0], \quad \mathbf{v}_2 = [-1, -1, +1]\]

$1[\text{조건}]$ 는 조건이 참이면 1, 거짓이면 0을 반환하는 Indicator 함수이다.

최종 예측:

\[f_{\mathbf{v}, \mathbf{w}}(x) = \text{sign}(w_1 h_1(x) + w_2 h_2(x))\]

$\varphi(x)$가 주어졌을 때 우리의 목표는 아래 2개를 학습하는 것이다
1. 숨겨진 하위 문제들 $\mathbf{V} = (\mathbf{v}_1, \mathbf{v}_2)$
2. 결합 가중치 $\mathbf{w} = [w_1, w_2]$

p22. Zero 그래디언트 피하기

우리는 학습을 위해 경사하강법(gradient descent)을 사용하지만, 중요한 문제가 발생한다:
\[h(x) = 1[\mathbf{v} \cdot \varphi(x) \geq 0]\]
에서는 $\mathbf{v}$에 대한 $h(x)$의 그래디언트가 거의 모든 구간에서 0이 된다.
해결책:
- 0이 아닌 그래디언트를 보장하기 위해 매끄러운 활성화 함수(smooth activation function) $\sigma$로 대체한다.
\[h(x) = \sigma(\mathbf{v} \cdot \varphi(x))\]
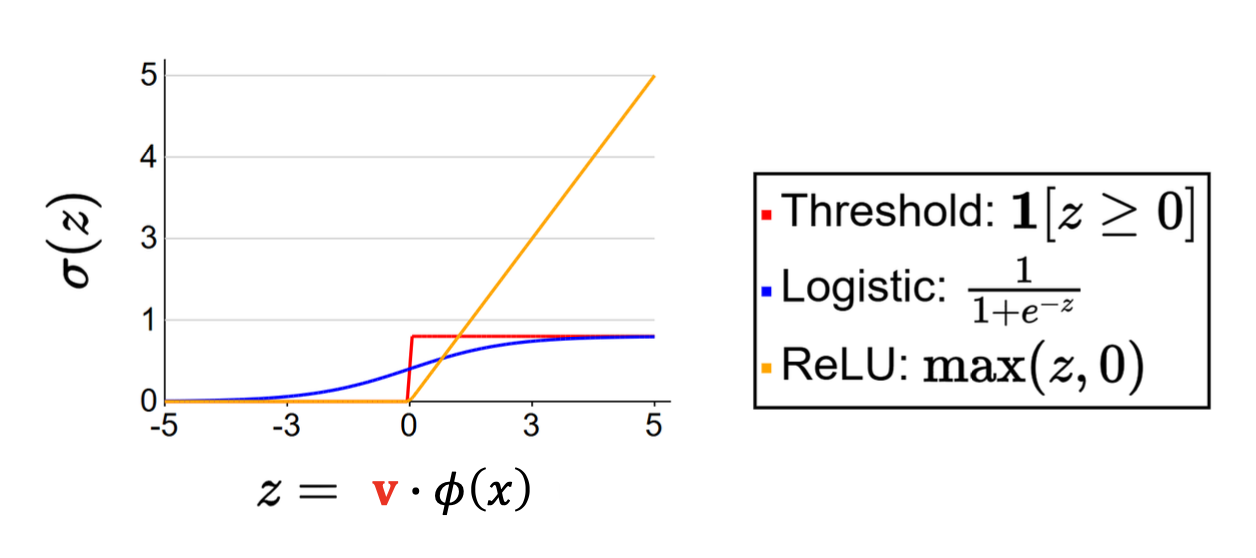
$\sigma$로 주로 활용되는 함수들
- Threshold:
  \[1[z \geq 0]\]
- Logistic (Sigmoid):
  \[\frac{1}{1+e^{-z}}\]
- ReLU (rectified linear unit):
  \[\max(z, 0)\]
- 기타 변형들: Leaky ReLU, ELU, SELU, GELU 등

1. Indicator 함수의 불연속성
함수 $h(x) = 1[\mathbf{v} \cdot \varphi(x) \ge 0]$ 은
$\mathbf{v} \cdot \varphi(x)$ 가 0을 기준으로 값이 갑자기 0에서 1로 바뀌는 불연속 함수이다.
대부분의 영역에서는 값이 일정하게 유지되고, 기준점에서만 점프(discontinuity)가 발생한다.
2. 거의 모든 구간에서 그래디언트가 0인 이유
함수 값이 일정한 구간에서는 변화율이 없으므로 그래디언트가 0이다.
오직 $\mathbf{v} \cdot \varphi(x) = 0$ 인 경계점에서만 값이 불연속적으로 변할 뿐,
그 외의 거의 모든 지점에서 그래디언트는 0이다.
3. 학습 과정에서의 문제
경사하강법은 그래디언트를 이용해 매개변수 $\mathbf{v}$ 를 갱신한다.
그러나 그래디언트가 0이면 매개변수가 더 이상 업데이트되지 않아 학습이 멈추게 된다.
따라서 매끄러운 활성화 함수(smooth activation function)를 사용하여
비제로(non-zero) 그래디언트를 확보하는 방식으로 문제를 해결한다.

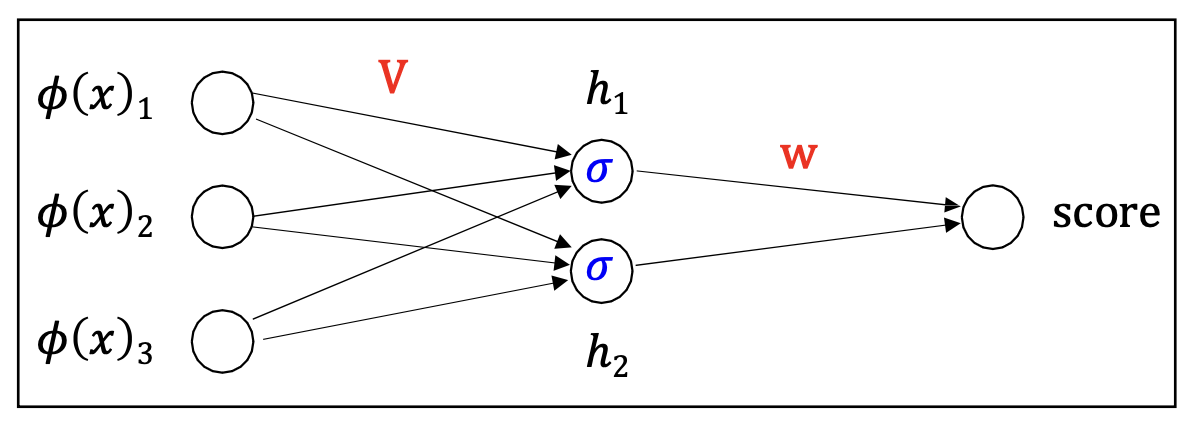
p23. 신경망 (Neural networks)

이제 우리는 2-계층(two-layer) 신경망을 정의할 준비가 되었다:

중간(hidden) 유닛들:
\[h_j = \sigma(\mathbf{v}_j \cdot \varphi(x))\]
출력(Output):
\[\text{score} = \mathbf{w} \cdot \mathbf{h}\]
표기
- $\mathbf{V}$ : 첫 번째 계층(first layer)의 가중치
- $\mathbf{w}$ : 두 번째 계층(second layer)의 가중치
Key insight:
- 중간(hidden) 유닛들은 선형 예측기(linear predictor) 의 학습된 특징(learned features)으로 작동한다.

1. 학습된 특징(learned features)의 의미
전통적인 선형 예측기는 사람이 직접 설계한 특성(feature design)에 의존한다.
그러나 신경망의 중간(hidden) 유닛들은 학습 과정에서 데이터로부터 유용한 패턴을 자동으로 추출한다.
따라서 이 유닛들은 스스로 학습된 특징(learned features) 로 해석될 수 있다.
2. 선형 예측기와의 관계
최종 출력은 여전히 선형 결합
\[\text{score} = \mathbf{w} \cdot \mathbf{h}\]
의 형태를 따른다.
하지만 입력 $x$ 자체가 아니라, 중간 유닛들이 생성한 변환된 표현 $\mathbf{h}$ 에 대해 선형 결합을 수행한다는 점에서
단순 선형 모델보다 훨씬 복잡한 관계를 표현할 수 있다.
3. 신경망에서의 입력 처리
신경망에서는 $\varphi(x)$ 와 같은 별도의 특성 설계를 하지 않고, 주어진 입력을 그대로 사용한다.
복잡한 특징 변환은 네트워크 내부의 계층과 활성화 함수에 의해 자동으로 이루어지며,
이는 사람이 일일이 feature design 을 하지 않아도 된다는 장점을 제공한다.

p24. 신경망에서의 특성 학습

중간(hidden) 유닛들은 선형 예측기의 학습된 특성으로 작동한다.
선형 모델:
- 점수(score)는 주어진 특성 $\varphi(x)$의 선형 결합으로 계산된다.
\[\text{score} = \mathbf{w} \cdot \varphi(x)\]
- 선형 예측기는 사람이 직접 지정한 특성 $\varphi(x)$에 적용된다.
신경망:
- 입력 $\varphi(x)$는 은닉층(hidden layer)을 거쳐 새로운 표현 $h(x)$로 변환된다.
- 점수(score)는 이 학습된 표현을 기반으로 계산된다.
\[\text{score} = \mathbf{w} \cdot \mathbf{h}\]
- 선형 예측기는 사람이 지정한 특성이 아니라, 자동으로 학습된 특성
  \[h(x) = [h_1(x), \dots, h_k(x)]\]
  에 적용된다.

p25. 심층 신경망

우리는 이러한 개념들을 확장하여 더 깊은 신경망을 구축할 수 있다.
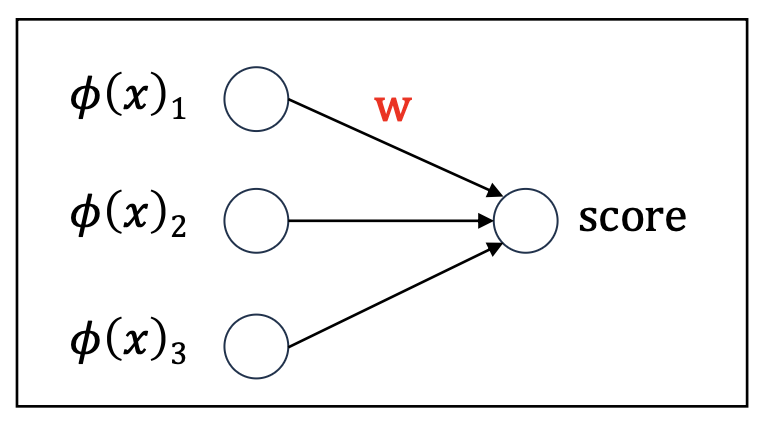
1-계층 신경망 (선형 예측기, linear predictor):
$\text{score} = \mathbf{w} \cdot \varphi(x)$
- 은닉층(hidden layer)의 수: 0
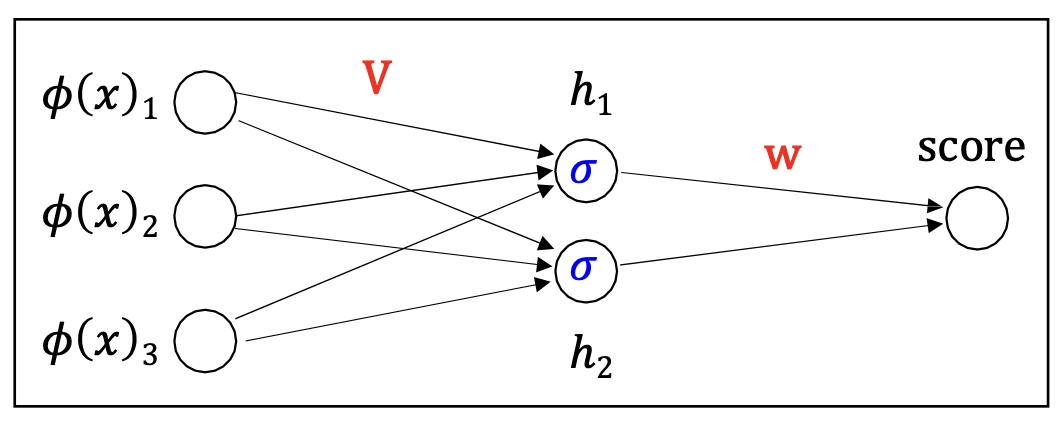
2-계층 신경망:
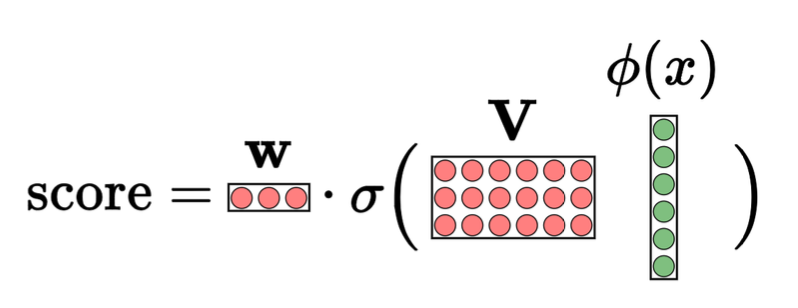
$\text{score} = \mathbf{w} \cdot \sigma(\mathbf{V} \varphi(x))$
- 은닉층의 수: 1
3-계층 신경망:
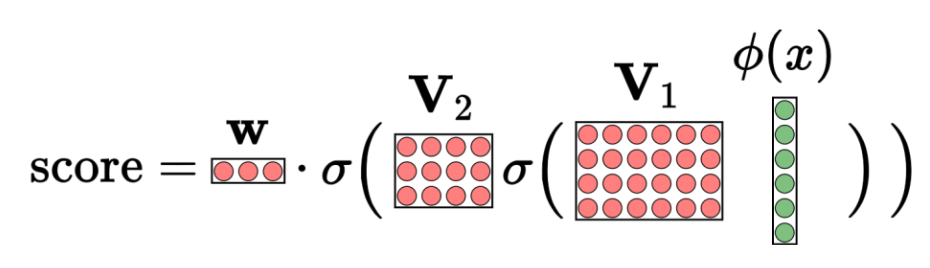
$\text{score} = \mathbf{w} \cdot \sigma(\mathbf{V}_2 \, \sigma(\mathbf{V}_1 \varphi(x)))$
- 은닉층의 수: 2

1-계층 신경망 (선형 예측기)
계산 과정:
$\text{score} = \mathbf{w} \cdot \varphi(x)$
의미:
입력 $\varphi(x)$ 를 가중치 벡터 $\mathbf{w}$ 와 단순히 선형 결합한 값이다.
은닉층이 없으므로 비선형 변환은 일어나지 않는다.
기본적인 선형 모델에 해당한다.
2. 2-계층 신경망
계산 과정:
은닉층 계산:
\[h = \sigma(\mathbf{V} \varphi(x))\]
$\mathbf{V}$ : 입력을 은닉 유닛으로 변환하는 가중치 행렬
$\sigma$ : 비선형 활성화 함수 (sigmoid, ReLU 등)
출력 계산:
\[\text{score} = \mathbf{w} \cdot h\]
의미:
$\mathbf{V}$ 와 $\sigma$ 에 의해 입력이 비선형적으로 변환된다.
변환된 표현 $h$ 는 사람이 설계하지 않은 학습된 특성으로 해석할 수 있다.
$\mathbf{w}$ 는 이 학습된 특성들을 다시 선형 결합하여 최종 출력을 만든다.
3. 3-계층 신경망
계산 과정:
첫 번째 은닉층:
\[h^{(1)} = \sigma(\mathbf{V}_1 \varphi(x))\]
두 번째 은닉층:
\[h^{(2)} = \sigma(\mathbf{V}_2 h^{(1)})\]
출력 계산:
\[\text{score} = \mathbf{w} \cdot h^{(2)}\]
의미:
입력 $\varphi(x)$ 가 여러 번의 비선형 변환을 거치며 점점 더 복잡한 특성으로 추출된다.
$\mathbf{V}_1, \mathbf{V}_2$ 는 각 층에서 입력을 새로운 표현으로 바꾸는 가중치 행렬이다.
$\sigma$ 는 각 층에 비선형성을 부여해 단순 선형 모델이 표현할 수 없는 복잡한 패턴을 학습하게 한다.
마지막에 $\mathbf{w}$ 가 이 최종 표현을 결합해 예측을 만든다.

p26. 왜 더 깊게 가는가?

더 깊은 신경망은 단순한 특성들의 조합을 더 복잡한 패턴으로 확장할 수 있으며,
이는 더 나은 일반화(generalization)로 이어질 수 있다.

원시 픽셀 (입력)
- 원시 입력은 픽셀 값들로 구성된다.

⬇️

1번째 계층
- 하위 계층은 단순한 패턴을 감지한다.
- 예: 에지(edges)

⬇️

2번째 계층
- 에지들의 조합이 곡선, 질감, 그리고 객체의 부분을 형성한다.
- 예: 눈, 코, 입

⬇️

3번째 계층
- 더 높은 계층에서는 뉴런이 전체 객체에 반응한다.
- 예: 얼굴 전체

점점 더 추상적이고 고수준의 특성을 표현할 수 있다

p27. 왜 더 깊게 가는가?

원칙적으로, 하나의 은닉층(one hidden layer) 을 가진 신경망은 어떤 함수도 근사할 수 있다.
✔ 보편 근사 정리(Universal approximation theorem) [1]
- $\mathbb{R}^d$ 위의 임의의 연속 함수는, 유한한 수의 노드와 비선형 활성화 함수를 포함하는 하나의 은닉층 신경망에 의해 임의의 정밀도로 근사될 수 있다.
그러나, 층의 크기(layer size) 가 비현실적으로 커져야 하므로 학습이 매우 느려진다.

더 깊은 신경망은 얕고 넓은 신경망과 동일한 함수들을 표현할 수 있다.
하지만 더 적은 매개변수(parameters) 로 가능하며, 이는 더 나은 일반화(generalization)로 이어질 수 있다.

1. 1개 은닉층 신경망 (총 75개 가중치)
입력 노드 = 4
은닉 노드 = 15
각 은닉 노드 = 입력 4개 + bias 1개 = 5
총 가중치 수 = $15 \times 5 = 75$
2. 3개 은닉층 신경망 (총 75개 가중치)
첫 번째 은닉층 (bias 포함)
입력 = 4
각 노드 = 입력 4개 + bias 1개 = 5
가중치 수 = $5 \times 5 = 25$
두 번째 은닉층 (bias 제외)
입력 = 첫 번째 은닉층 출력 5개
각 노드 = 입력 5개
가중치 수 = $5 \times 5 = 25$
세 번째 은닉층 (bias 제외)
입력 = 두 번째 은닉층 출력 5개
각 노드 = 입력 5개
가중치 수 = $5 \times 5 = 25$
총합 = $25 + 25 + 25 = 75$
3. 경로 수 비교 (입력 1개 기준)
1개 은닉층 신경망
입력 1개가 은닉층 15개 노드로 연결됨
각 노드에서 바로 출력으로 연결
경로 수 = $15$
3개 은닉층 신경망
입력 1개 → 첫 번째 은닉층 5개 노드
첫 번째 은닉층 5개 → 두 번째 은닉층 5개
두 번째 은닉층 5개 → 세 번째 은닉층 5개
최종적으로 출력과 연결
경로 수 = $5 \times 5 \times 5 = 125$
4. 의미
두 구조 모두 총 가중치 수는 $75$ 개이지만,
3층 구조는 더 많은 경로(125)를 가져
같은 가중치 수로도 더 복잡한 표현을 학습할 수 있다.

역전파(Backpropagation)

p29. 동기: 신경망을 이용한 손실 최소화

이제 다음 단계는 신경망을 학습(train) 하는 것이다.
예시로, 4계층 신경망(four-layer neural networks) 에서의 회귀 손실을 생각해보자:

\[\text{Loss}(x, y, \mathbf{V}_1, \mathbf{V}_2, \mathbf{V}_3, \mathbf{w}) = \Big( \mathbf{w} \cdot \sigma\big( \mathbf{V}_3 \, \sigma(\mathbf{V}_2 \, \sigma(\mathbf{V}_1 \varphi(x))) \big) - y \Big)^2\]

경사하강법(gradient descent)을 적용하기 위해서는, 각 학습 파라미터에 대한 그래디언트를 계산해야 한다.

\[\mathbf{V}_1 \leftarrow \mathbf{V}_1 - \eta \nabla_{\mathbf{V}_1} \, \text{Loss}(x, y, \mathbf{V}_1, \mathbf{V}_2, \mathbf{V}_3, \mathbf{w})\] \[\mathbf{V}_2 \leftarrow \mathbf{V}_2 - \eta \nabla_{\mathbf{V}_2} \, \text{Loss}(x, y, \mathbf{V}_1, \mathbf{V}_2, \mathbf{V}_3, \mathbf{w})\] \[\mathbf{V}_3 \leftarrow \mathbf{V}_3 - \eta \nabla_{\mathbf{V}_3} \, \text{Loss}(x, y, \mathbf{V}_1, \mathbf{V}_2, \mathbf{V}_3, \mathbf{w})\] \[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} \, \text{Loss}(x, y, \mathbf{V}_1, \mathbf{V}_2, \mathbf{V}_3, \mathbf{w})\]

이것은 가능하지만, 수작업 계산량(manual computation)이 너무 많다는 문제가 있다.

p30. 계산 그래프

계산 그래프(computation graph) 는 방향성이 있는 비순환 그래프(directed acyclic graph)로서,
루트 노드는 최종 수학적 표현을 나타내고, 각 내부 노드는 중간 부분식을 나타낸다.

\[\text{Loss}(x, y, \mathbf{V}, \mathbf{w}) = \left(\mathbf{w} \cdot \sigma(\mathbf{V}\varphi(x)) - y\right)^2\]

계산 그래프를 사용하면, 역전파 알고리즘(backpropagation algorithm) 을 통해
그래디언트를 효율적으로 계산할 수 있다.
PyTorch 같은 프레임워크는 이 과정을 자동으로 처리하지만,
어떻게 작동하는지를 이해하는 것은 중요하다.

p31. 계산 그래프: 모듈 박스로서의 함수

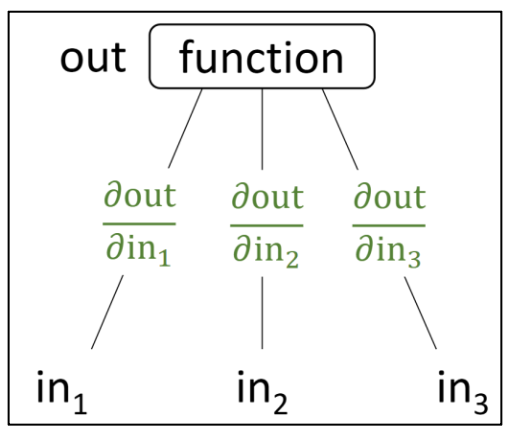
하나의 함수를 박스(box) 로 생각해 보자.
이 박스는 입력들의 집합을 받아서 출력을 계산한다.
편미분(partial derivative) 은 각 입력에서 출력으로 연결되는 엣지(edge) 위에 표시된다.

편미분(gradient) 은 출력이 각 입력의 변화에 얼마나 민감한지를 정량화한다.

예시 (Example):

\[out = 2in_1 + in_2 in_3\]

$in_2$ 에 $\epsilon$ 만큼 작은 변화를 주면:

\[\Rightarrow 2in_1 + (in_2 + \epsilon) in_3 = out + in_3 \epsilon\]

즉, 출력이 $in_3 \epsilon$ 만큼 변한다.
이는 다음 편미분에 해당한다:

\[\frac{\partial out}{\partial in_2}\]

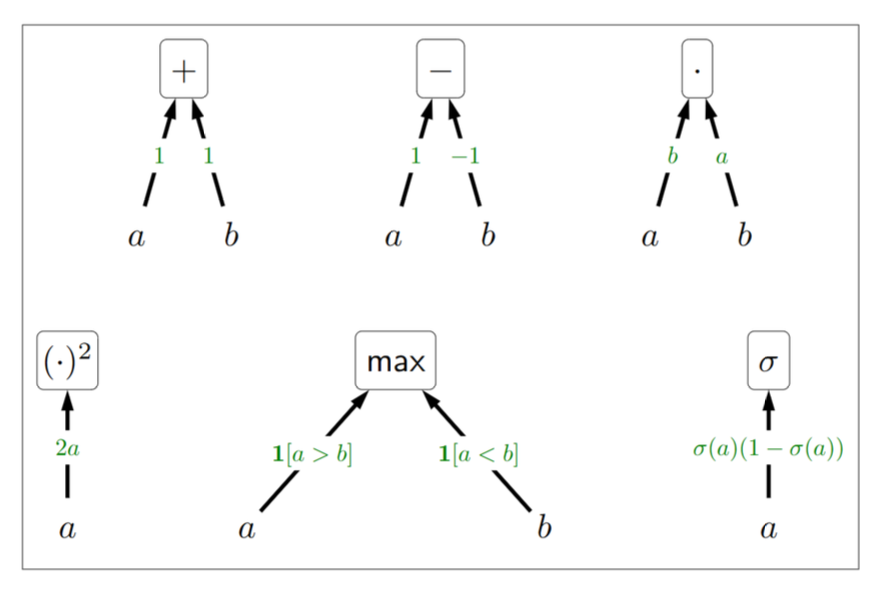
p32. 계산 그래프: 기본 빌딩 블록

다음은 간단한 함수 다섯 가지와 그 편미분(partial derivatives) 예시이다.

덧셈 ($a + b$)
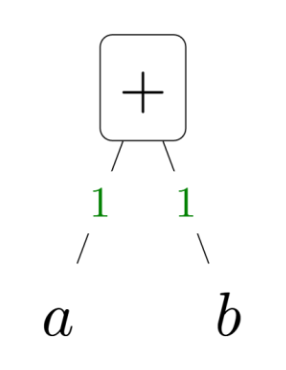
- 입력: a, b
- 출력: a + b
- 편미분:
  - $\frac{\partial}{\partial a}(a+b) = 1$
  - $\frac{\partial}{\partial b}(a+b) = 1$
뺄셈 ($a - b$)
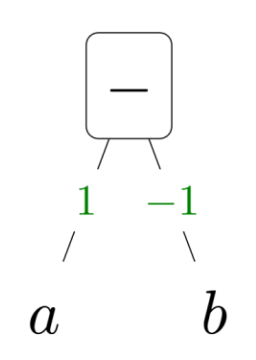
- 입력: a, b
- 출력: a - b
- 편미분:
  - $\frac{\partial}{\partial a}(a-b) = 1$
  - $\frac{\partial}{\partial b}(a-b) = -1$
곱셈 ($a \cdot b$)
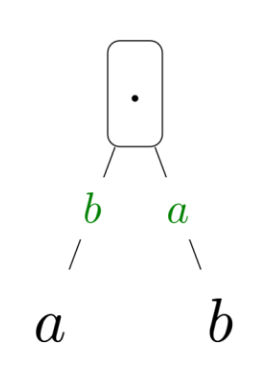
- 입력: a, b
- 출력: $a \cdot b$
- 편미분:
  - $\frac{\partial}{\partial a}(ab) = b$
  - $\frac{\partial}{\partial b}(ab) = a$
최대값 ($max(a, b)$)
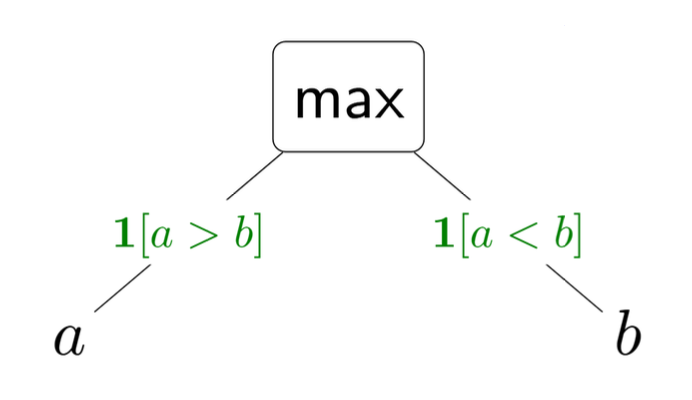
- 입력: a, b
- 출력: $\max(a, b)$
- 편미분:
  - $\frac{\partial}{\partial a}(\max(a, b)) = 1[a > b]$ (a가 b보다 클 때 1, 그렇지 않으면 0)
  - $\frac{\partial}{\partial b}(\max(a, b)) = 1[a < b]$ (b가 a보다 클 때 1, 그렇지 않으면 0)
시그모이드 함수 (Sigmoid function)
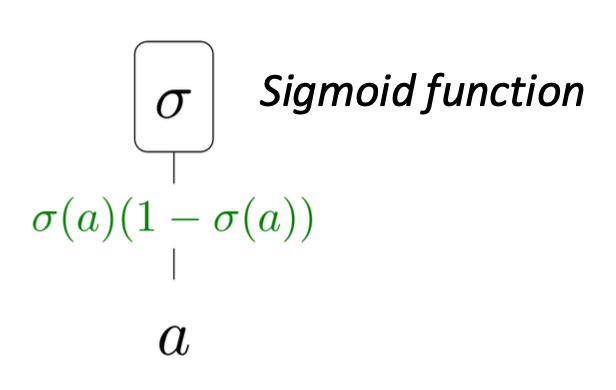
- 입력: a
- 출력: $\sigma(a)$
- 편미분:
  - $\frac{\partial}{\partial a}(\sigma(a)) = \sigma(a)(1 - \sigma(a))$

1. 시그모이드 정의
시그모이드는
\[\sigma(a)=\frac{1}{1+e^{-a}}\]
로 정의한다.
2. 분수 미분 공식으로 단계별 미분
분수 미분 공식(quotient rule):
\[\left(\frac{u}{v}\right)'=\frac{u'v-u\,v'}{v^2}\]
여기서 $u(a)=1,\; v(a)=1+e^{-a}$.
\[u'(a)=0,\qquad v'(a)=-e^{-a}\]
공식을 대입하면
\[\frac{d\sigma(a)}{da} =\frac{0\cdot(1+e^{-a})-1\cdot(-e^{-a})}{(1+e^{-a})^2} =\frac{e^{-a}}{(1+e^{-a})^2}.\]
3. 거듭제곱–연쇄 규칙으로도 같은 결과
$\sigma(a)=(1+e^{-a})^{-1}$ 로 보고 미분하면
\[\frac{d\sigma(a)}{da} =-1\cdot(1+e^{-a})^{-2}\cdot(-e^{-a}) =\frac{e^{-a}}{(1+e^{-a})^2}.\]
4. 최종 정리: $\sigma(a)(1-\sigma(a))$ 꼴로 변형
1)
\[\sigma(a)=\frac{1}{1+e^{-a}},\qquad 1-\sigma(a)=\frac{e^{-a}}{1+e^{-a}}\]
2)
\[\sigma(a)(1-\sigma(a)) =\frac{1}{1+e^{-a}}\cdot\frac{e^{-a}}{1+e^{-a}} =\frac{e^{-a}}{(1+e^{-a})^2}.\]
3) 위 결과가 $\dfrac{d\sigma(a)}{da}$ 와 동일하므로
\[\boxed{\frac{d\sigma(a)}{da}=\sigma(a)(1-\sigma(a))}\]

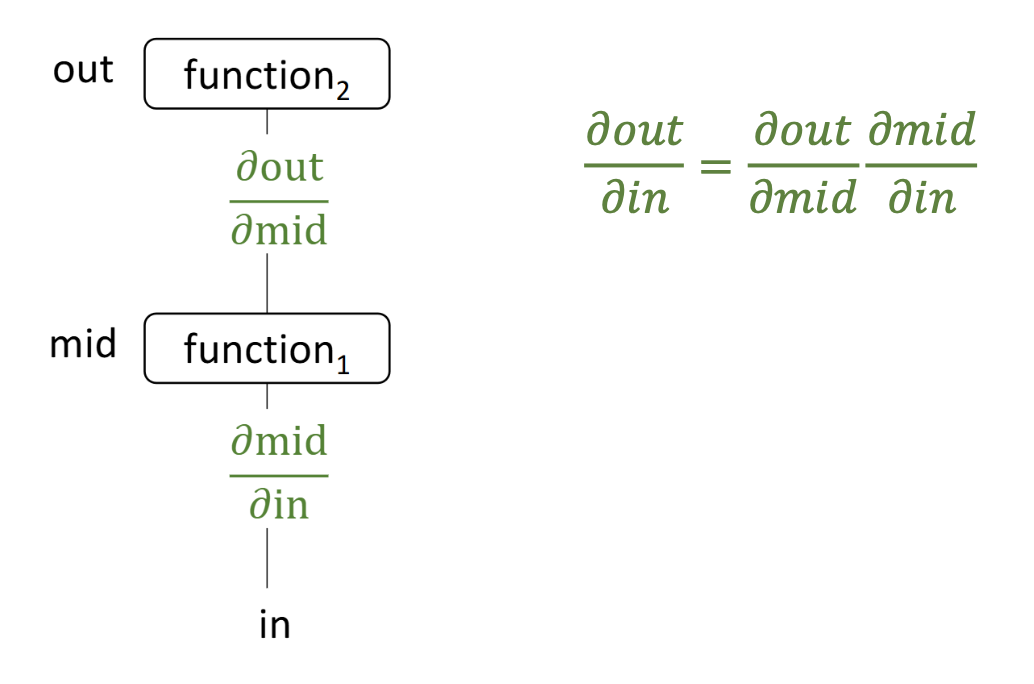
p33. 계산 그래프: 함수의 합성 (Composing functions)

이러한 기본 블록들을 사용하여, 연쇄 법칙(chain rule)을 통해 체계적으로 도함수(derivatives)를 계산하면서 더 복잡한 함수를 만들 수 있다.
연쇄 법칙(Chain rule):
출력(out)의 입력(in)에 대한 도함수는, 연산 그래프에서 경로를 따라 나타나는 중간 도함수들을 곱함으로써 얻어진다.

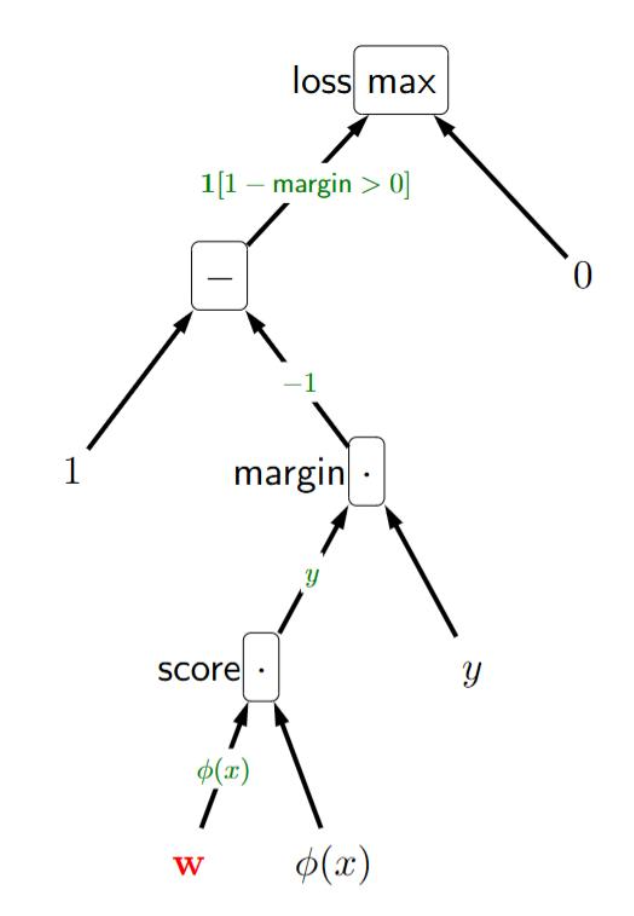
p34. 예시: 힌지 손실(Hinge loss)을 사용한 선형 분류

손실 함수는 다음과 같이 주어진다:
\[\text{Loss}(x, y, \mathbf{w}) = \max \{1 - (\mathbf{w} \cdot \varphi(x))y, \; 0 \}\]
연산 그래프(computation graph)는 다음과 같이 구성할 수 있다.

연쇄 법칙(chain rule)을 적용하면, 그래디언트는 다음과 같이 계산된다:
\[\nabla_{\mathbf{w}} \, \text{Loss}(x, y, \mathbf{w}) = (1[\text{margin} < 1])(-1)(y)(\varphi(x))\] \[= -\varphi(x) y \; 1[\text{margin} < 1]\]

1. 순전파 (Forward)
1) 점수 (score)
$s = \mathbf{w} \cdot \varphi(x)$
2) 마진 (margin)
$m = y \cdot s$
3) 잔차 (residual)
$r = 1 - m$
4) 손실 (loss)
$L = \max(r, 0)$
$r \le 0 \Rightarrow L = 0$ (마진 충분)
$r > 0 \Rightarrow L = r$ (마진 부족 또는 오분류)
2. 역전파 (Backward: 단계별 편미분)
① 손실 노드 $L = \max(r,0)$ 의 $r$에 대한 편미분
$r>0$ 일 때:
$\frac{\partial L}{\partial r} = 1$
$r \le 0$ 일 때:
$\frac{\partial L}{\partial r} = 0$
요약:
$\frac{\partial L}{\partial r} = 1[r>0]$
② 잔차 노드 $r = 1 - m$ 의 $m$에 대한 편미분
$\frac{\partial r}{\partial m} = -1$
③ 마진 노드 $m = y \cdot s$ 의 편미분
$s$ 에 대해:
$\frac{\partial m}{\partial s} = y$
$y$ 에 대해:
$\frac{\partial m}{\partial y} = s$
④ 점수 노드 $s = \mathbf{w} \cdot \varphi(x)$ 의 편미분
$\mathbf{w}$ 에 대해:
$\frac{\partial s}{\partial \mathbf{w}} = \varphi(x)$
$\varphi(x)$ 에 대해:
$\frac{\partial s}{\partial \varphi(x)} = \mathbf{w}$
3. 최종 그래디언트 (체인 룰 적용)
가중치 $\mathbf{w}$ 에 대한 그래디언트
\[\nabla_{\mathbf{w}} L = \frac{\partial L}{\partial r} \cdot \frac{\partial r}{\partial m} \cdot \frac{\partial m}{\partial s} \cdot \frac{\partial s}{\partial \mathbf{w}}\] \[= 1[r>0] \cdot (-1) \cdot y \cdot \varphi(x) = -\varphi(x)\, y \, 1[r>0]\]

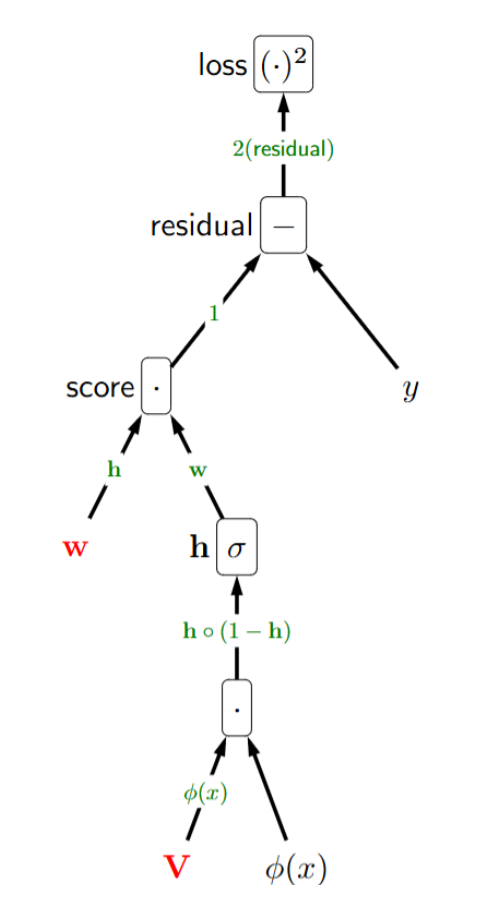
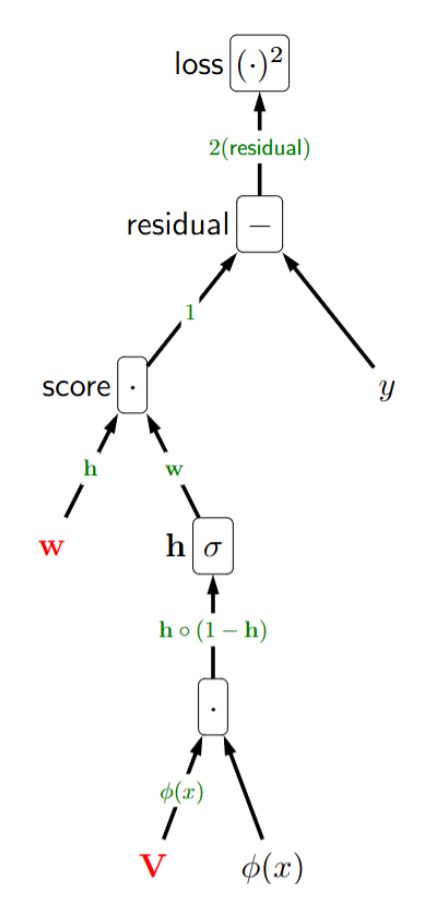
p35. 예시: 이층(two-layer) 신경망을 사용한 회귀

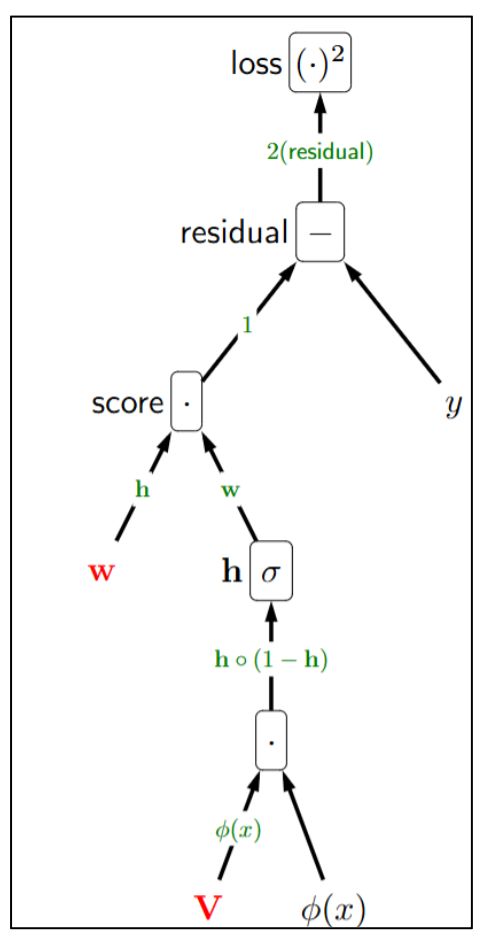
손실 함수는 다음과 같이 주어진다:

\[\text{Loss}(x, y, \mathbf{V}, \mathbf{w}) = \big(\mathbf{w} \cdot \sigma(\mathbf{V}\varphi(x)) - y\big)^2\]

계산 그래프(computation graph)는 다음과 같이 구성할 수 있다.

연쇄 법칙(chain rule)을 적용하면, 그래디언트는 다음과 같이 계산된다:

\[\nabla_{\mathbf{w}} \, \text{Loss}(x, y, \mathbf{V}, \mathbf{w}) = 2(\text{residual}) \, \mathbf{h}\] \[\nabla_{\mathbf{V}} \, \text{Loss}(x, y, \mathbf{V}, \mathbf{w}) = 2(\text{residual}) \, \mathbf{w} \circ \mathbf{h} \circ (1-\mathbf{h}) \varphi(x)^\top\]

주의:
$\circ$ 는 원소별(elementwise) 곱셈을 의미한다. 이는 활성화 함수(activation) 가 각 원소에 독립적으로 적용되기 때문에 필요하다.

Shape (행렬/벡터의 차원)

$\mathbf{w}$ : $k \times 1$
$\mathbf{h}$ : $k \times 1$
$\mathbf{V}$ : $k \times d$
$\varphi(x)$ : $d \times 1$
$\mathbf{w} \cdot \mathbf{h} = \mathbf{w}^\top \mathbf{h}$

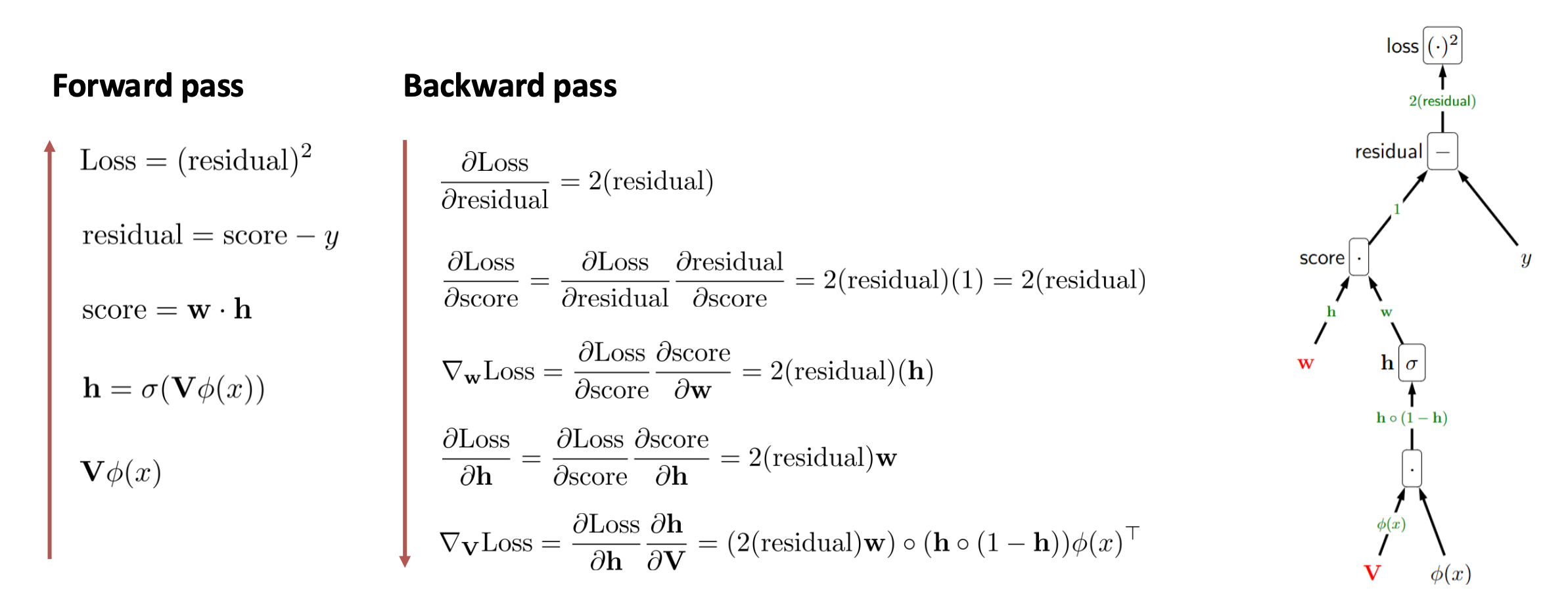
1. 순전파 (Forward)
1) 은닉층 입력
$z = \mathbf{V} \varphi(x)$
2) 은닉층 활성화
$\mathbf{h} = \sigma(z)$
3) 출력 (예측값)
$\hat{y} = \mathbf{w} \cdot \mathbf{h}$
4) 잔차 (residual)
$r = \hat{y} - y$
5) 손실 (loss)
$L = r^2 = (\hat{y} - y)^2$
2. 역전파 (Backward: 단계별 편미분)
① 손실 노드 $L = r^2$ 의 $r$에 대한 편미분
$\frac{\partial L}{\partial r} = 2r$
② 잔차 노드 $r = \hat{y} - y$
$\hat{y}$ 에 대해
$\frac{\partial r}{\partial \hat{y}} = 1$
$y$ 에 대해
$\frac{\partial r}{\partial y} = -1$
③ 출력 노드 $\hat{y} = \mathbf{w} \cdot \mathbf{h}$
$\mathbf{w}$ 에 대해
$\frac{\partial \hat{y}}{\partial \mathbf{w}} = \mathbf{h}$
$\mathbf{h}$ 에 대해
$\frac{\partial \hat{y}}{\partial \mathbf{h}} = \mathbf{w}$
④ 은닉층 노드 $\mathbf{h} = \sigma(z)$
$\frac{\partial \mathbf{h}}{\partial z} = \mathbf{h} \circ (1 - \mathbf{h})$
⑤ 은닉층 입력 $z = \mathbf{V}\varphi(x)$
$\mathbf{V}$ 에 대해
$\frac{\partial z}{\partial \mathbf{V}} = \varphi(x)^\top$
$\varphi(x)$ 에 대해
$\frac{\partial z}{\partial \varphi(x)} = \mathbf{V}$
3. 최종 그래디언트 (체인 룰 적용)
가중치 $\mathbf{w}$ 에 대한 그래디언트
$\nabla_{\mathbf{w}} L = (2r)\cdot(1)\cdot \mathbf{h} = 2r\,\mathbf{h}$
가중치 $\mathbf{V}$ 에 대한 그래디언트
$\nabla_{\mathbf{V}} L = (2r)\cdot(1)\cdot \mathbf{w}\cdot (\mathbf{h}\circ(1-\mathbf{h}))\cdot \varphi(x)^\top$
추가 보충 설명: 왜 미분하면 전치가 나타나는가?
1) 형상(Shape) 확인
$\mathbf{V}$ : $(k \times d)$
$\varphi(x)$ : $(d \times 1)$
따라서 $z=\mathbf{V}\varphi(x)\in\mathbb{R}^{k\times 1}$
2) $z$의 $i$번째 원소
\[z_i = \sum_{j=1}^d V_{ij}\,\varphi_j(x) = \mathbf{V}_{i,:}\cdot \varphi(x)\]
3) $i$행에 대한 미분
\[\frac{\partial z_i}{\partial \mathbf{V}_{i,:}} = [\varphi_1(x),\dots,\varphi_d(x)] = \varphi(x)^\top\]
→ 특정 행에 대한 그래디언트가 행벡터 = $\varphi(x)^\top$ 로 나타난다.
4) 전체 $\mathbf{V}$ 에 대한 미분
\[\frac{\partial z}{\partial \mathbf{V}} = \begin{bmatrix} \varphi(x)^\top \\ \varphi(x)^\top \\ \vdots \\ \varphi(x)^\top \end{bmatrix}_{k\times d}\]
즉, 모든 행이 동일하게 $\varphi(x)^\top$ 로 구성된 행렬이 된다.

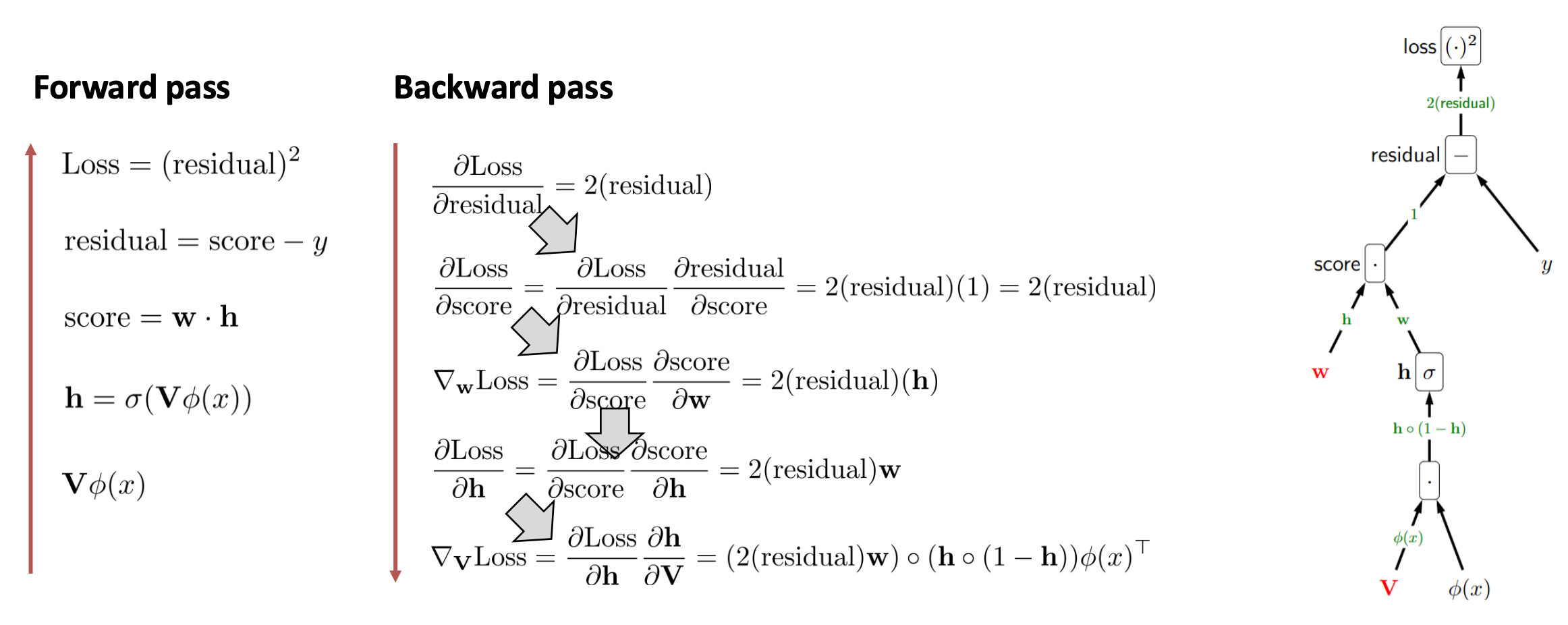
p36. 역전파를 통한 최적화

역전파는 그래디언트 계산 알고리즘으로,
출력층에서 발생한 오차 신호를 이전 층으로 거슬러 올라가며 전파한다.
이는 연쇄 법칙에 기반하여, 불필요한 중복 계산을 피할 수 있도록 한다.

💻 알고리즘

순전파:
- 각 노드에 대해 (리프 → 루트) 방향으로 순전파 값을 계산한다.
역전파:
- 각 노드에 대해 (루트 → 리프) 방향으로 역전파 값을 계산한다.

p37. 역전파를 통한 최적화

역전파(Backpropagation) 는 그래디언트 계산 알고리즘으로,
출력층에서 이전 층으로 오차 신호를 거꾸로 전파한다.
이는 연쇄 법칙(chain rule) 에 기반하며, 중복 계산을 피하기 위해 사용된다.

p38. 역전파를 통한 최적화

역전파(Backpropagation) 는 그래디언트 계산 알고리즘으로,
출력층에서 이전 층으로 오차 신호를 거꾸로 전파한다.
이는 연쇄 법칙(chain rule) 에 기반하며, 중복 계산을 피하기 위해 사용된다.

p39. 역전파를 통한 최적화

역전파를 사용하여 그래디언트를 계산하면,
경사하강법(gradient descent) 을 적용하여 모델 파라미터를 반복적으로 업데이트한다.
목표는 학습 데이터에서의 손실을 최소화하는 것이다:

💻 알고리즘 (Algorithm: SGD)

$\mathbf{w}, \mathbf{V}$ 를 무작위로 초기화한다.
수렴할 때까지 반복한다:
- 무작위로 선택된 $(x, y) \in D_{train}$ 에 대해
  \[\mathbf{w} \;\leftarrow\; \mathbf{w} - \eta \, (2 \cdot \text{residual}) \, \mathbf{h}\] \[\mathbf{V} \;\leftarrow\; \mathbf{V} - \eta \, (2 \cdot \text{residual}) \, \mathbf{w} \circ \mathbf{h} \circ (1-\mathbf{h}) \, \varphi(x)^\top\]

여기서 $\eta$ (학습률, learning rate)는 하이퍼파라미터(hyperparameter) 로, 한 번의 업데이트에서 이동하는 크기를 결정한다.

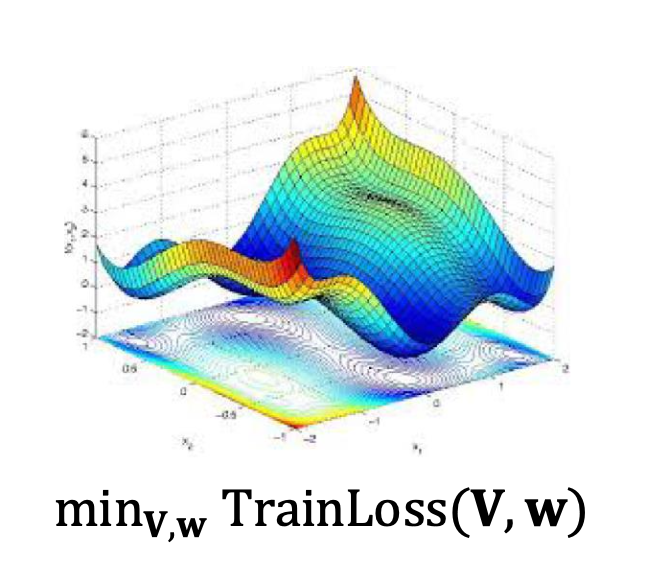
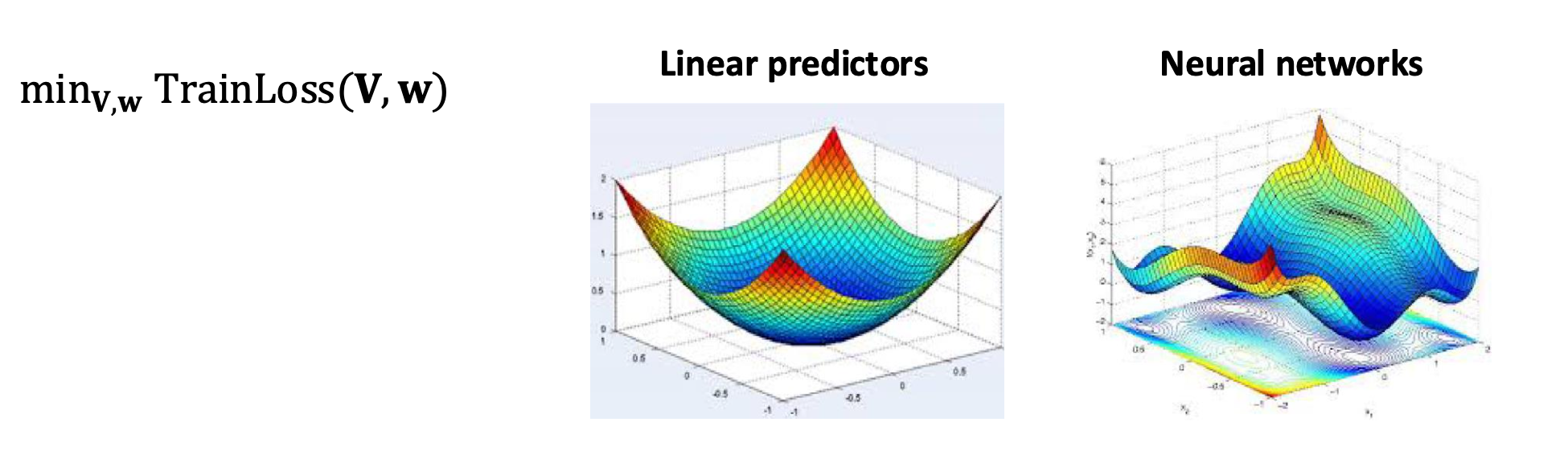
p40. 신경망 최적화는 어려울 수 있다

선형 예측기의 경우, 손실 함수는 볼록(convex)이다.
- 이는 단일 전역 최소값(global minimum)을 가진다는 의미이다.
- 따라서 적절하게 선택된 학습률(step size)을 사용하면 SGD가 최적해로 수렴한다.
신경망의 경우, 손실 함수는 비볼록(non-convex)이다.
- 이는 여러 개의 지역 최적해(local optima)가 존재한다는 의미이다.
- 그 결과 SGD는 차선의 해(suboptimal solution)에 수렴할 수 있으며, 성능은 초기화(initialization)와 학습률에 크게 의존한다.

1. 다층 구조로 인한 비선형성
선형 예측기는 입력과 출력 사이의 관계가 단일 선형 결합으로 표현된다.
반면 신경망은 여러 개의 은닉층을 거치며 각 층에서 새로운 표현을 만든다.
이 과정에서 입력이 여러 차례 비선형 변환을 거치므로 손실 함수의 형태는 단순한 볼록 함수가 아니라 복잡한 비볼록 함수가 된다.
2. 활성화 함수의 영향
시그모이드(sigmoid), ReLU 등의 활성화 함수는 모델에 비선형성을 부여한다.
이러한 함수의 곡선적 성질 때문에 매개변수 공간에서 손실 함수는 매끄럽지 않고 복잡한 지형을 갖는다.
그 결과, 여러 개의 지역 최적해나 안장점(saddle points)이 자연스럽게 나타난다.
3. 매개변수 공간의 고차원성
신경망은 수천, 수만 개 이상의 가중치와 편향을 포함하는 고차원 매개변수 공간을 가진다.
차원이 높아질수록 손실 함수의 표면은 더욱 복잡해지며, 직관적인 볼록성을 유지하기 어렵다.
이 때문에 최적화 과정에서 SGD 같은 기법이 전역 최소값보다 지역 최소값이나 평평한 구간에 머물 가능성이 크다.
4. 요약
신경망의 손실 함수가 복잡한 이유는
1) 다층 구조로 인한 반복적 비선형 변환,
2) 활성화 함수가 만들어내는 곡선적 특성,
3) 매개변수 공간의 높은 차원성
때문이다.
이 세 요소가 결합되면서 손실 함수는 자연스럽게 비볼록(non-convex) 형태를 띠게 된다.

p41. 요약 (Summary)

신경망 (Neural networks):
사람이 직접 $\varphi(x)$를 설계하는 대신, 복잡한 변환을 자동으로 학습한다.
계산 그래프 (Computation graphs):
그래디언트를 시각화하고 이해할 수 있게 한다.
역전파 (Backpropagation):
그래디언트를 계산하기 위한 범용 알고리즘으로 사용된다.

대학원 수업, 텍스트 마이닝