포스트

[텍스트 마이닝] 4. Machine Learning 3

게시 업데이트
By 김성진
30 분읽는 시간
[텍스트 마이닝] 4. Machine Learning 3

p2. 질문

  • 머신러닝의 진정한 목적은 무엇인가?
    1. 학습 세트(training set)에서의 오류를 최소화한다
    2. 보이지 않는 미래의 데이터(unseen future examples)에서 오류를 최소화한다
    3. 기계에 대해 배운다 (learn about machines)
    4. 경사하강법(gradient descent)을 통해 학습 손실을 최소화한다

일반화(Generalization)

p5. 과소적합과 과대적합

  • 모델의 크기와 깊이를 늘리면 항상 일반화(generalization)가 좋아질까?
    • 아니다! (No!)

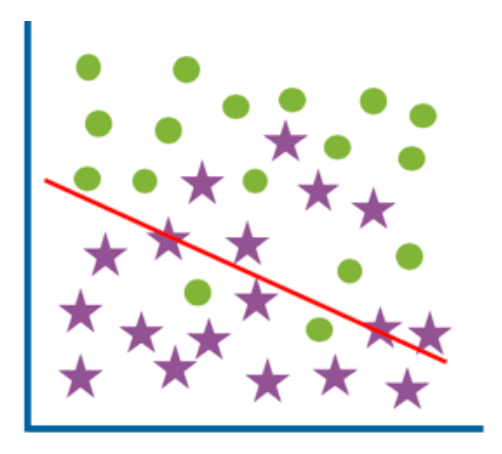
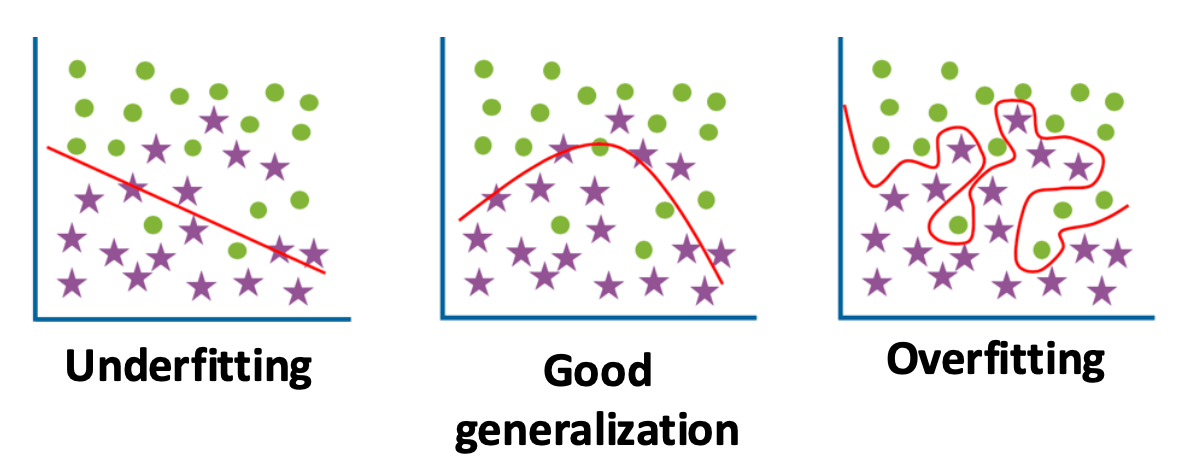
과소적합 (Underfitting)

  • 모델이 너무 단순해서 패턴을 포착하지 못한다.
  • 높은 학습 오류 (High training error)
  • 높은 테스트 오류 (High test error)

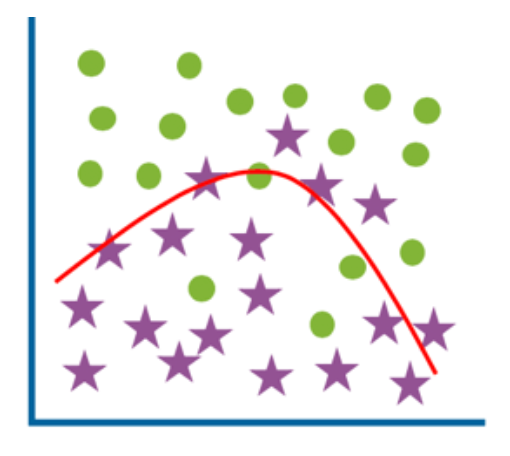
image

좋은 일반화 (Good generalization)

  • 낮은 학습 오류 (Low training error)
  • 낮은 테스트 오류 (Low test error)

image

과대적합 (Overfitting)

  • 모델이 학습 집합의 모든 잡음(noise) 을 외워버린다.
  • 낮은 학습 오류 (Low training error)
  • 높은 테스트 오류 (High test error)

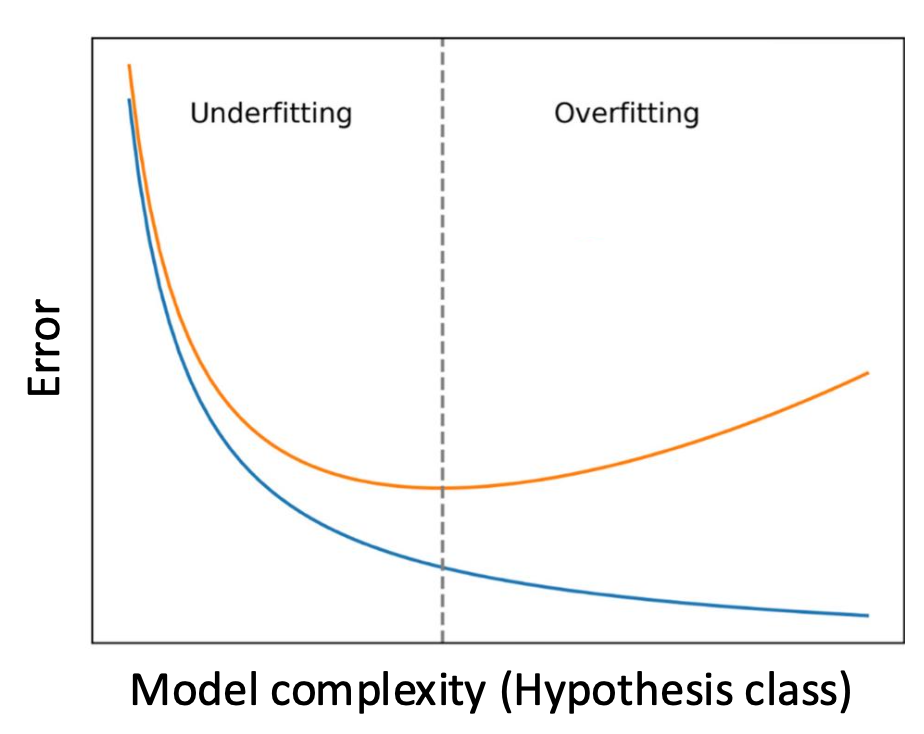
image

p6. 과소적합과 과대적합

  • 과소적합 은 모델이 데이터 속의 내재된 패턴(underlying patterns) 을 포착하기에 너무 단순할 때 발생한다.
  • 과대적합 은 모델이 일반화 가능한 패턴을 학습하지 않고, 학습 데이터를 외워버릴 때(memorizes the training data) 발생한다.

image

  • 파란색: 훈련 세트(Training set)
  • 주황색: 테스트 세트(Test set)
  • 가로축: 모델 복잡도(가설 클래스)
  • 세로축: 오류(Error)

참고: 가설 클래스(Hypothesis class)는 가능한 모든 예측기들의 집합이다.

image

p7. 학습(fitting)과 일반화(generalization) 이해하기

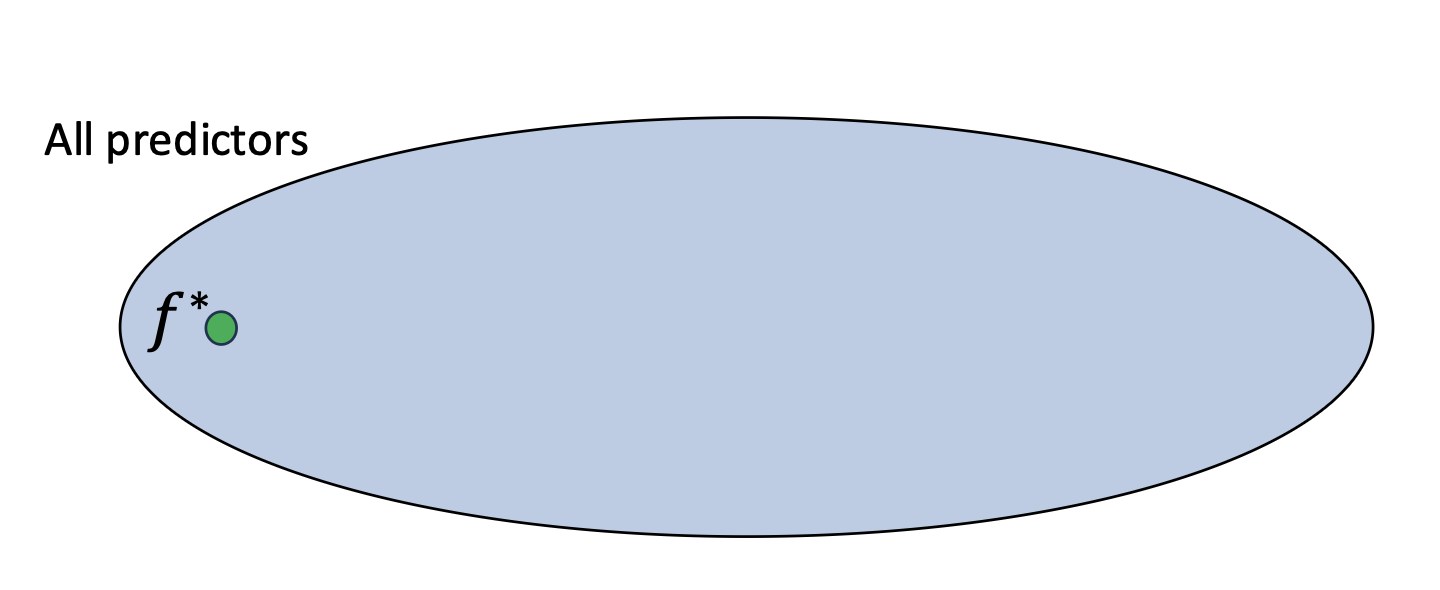
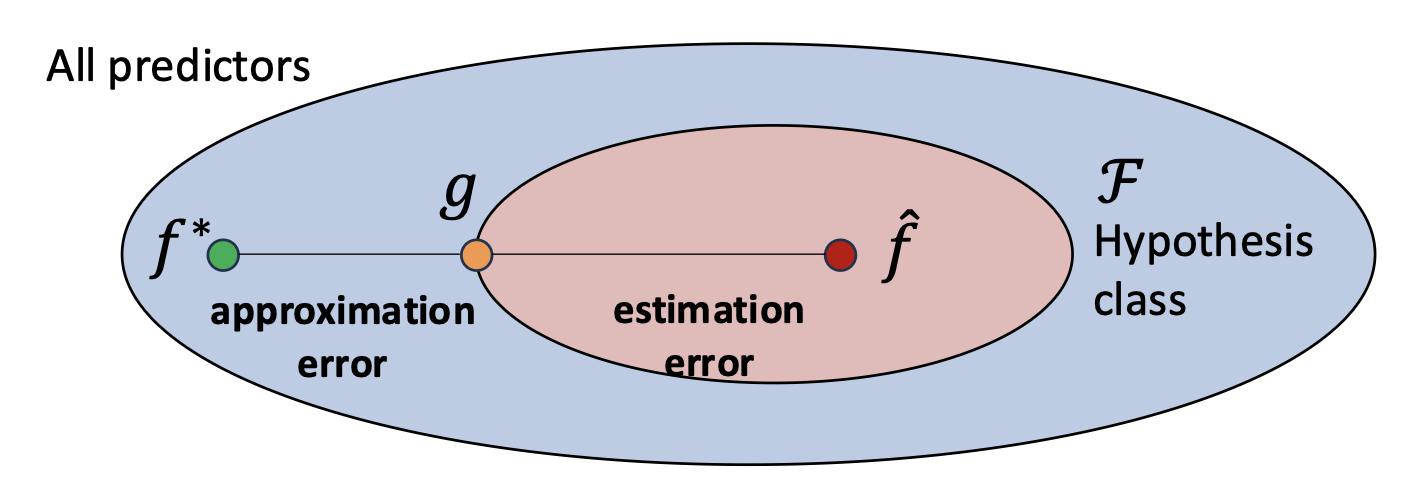
  • 가능한 모든 예측기(predictors)의 공간을 생각해보자.
    • 그 안에는 완벽하게 예측하는 최적 예측기(optimal predictor) $f^*$ 가 존재한다.
    • 물론, 이 예측기는 도달할 수 없는(unattainable) 것이다.
    • 그렇다면, 우리는 $f^*$ 로부터 얼마나 떨어져 있을까?

image

p8. 학습(fitting)과 일반화(generalization) 이해하기

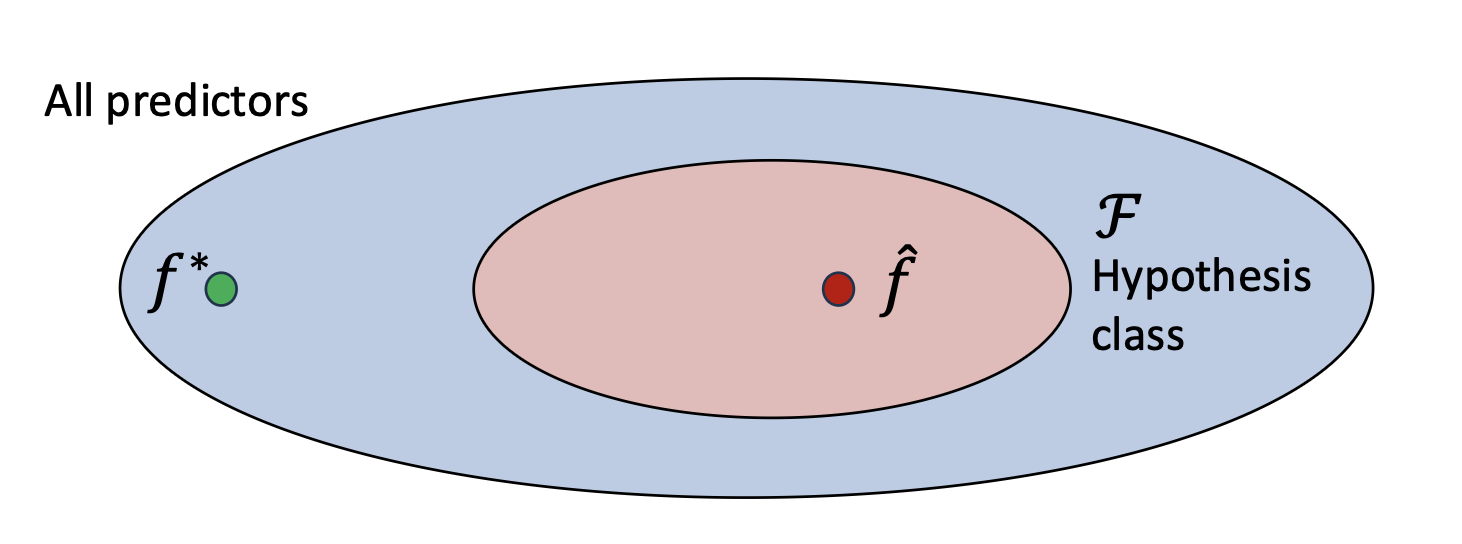
  • 실제로 우리는 가능한 모든 예측기(predictors)를 고려할 수 없다.
    • 대신, 가설 클래스(hypothesis class) $\mathcal{F}$ 를 정의하여, 공간을 관리 가능한 모델 집합으로 제한한다.
    • 학습이 끝난 후, 우리는 학습된 예측기(learned predictor) $\hat{f}$ 를 얻게 된다.

image

p9. 학습(fitting)과 일반화(generalization) 이해하기

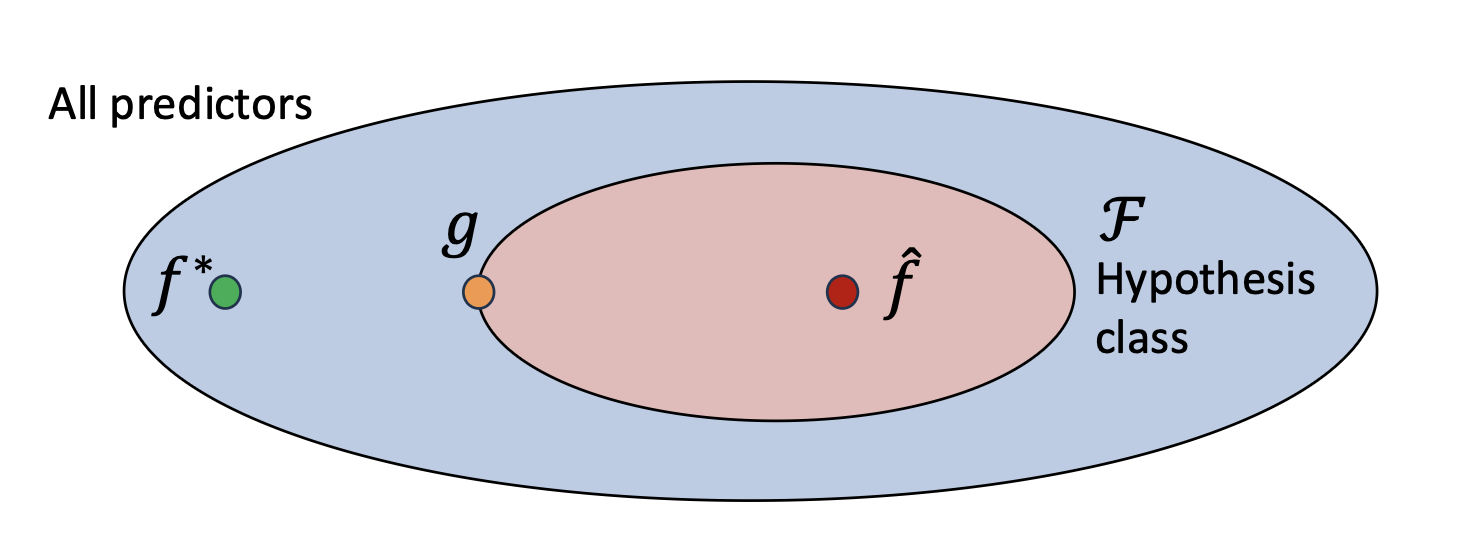
  • 실제로 우리는 가능한 모든 예측기(predictors)를 고려할 수 없다.
    • 대신, 가설 클래스(hypothesis class) $\mathcal{F}$ 를 정의하여, 공간을 관리 가능한 모델 집합으로 제한한다.
    • 또한, $\mathcal{F}$ 안에는 가능한 한 최선의 함수(the best possible function) $g$ 가 존재한다.

image

p10. 학습(fitting)과 일반화(generalization) 이해하기

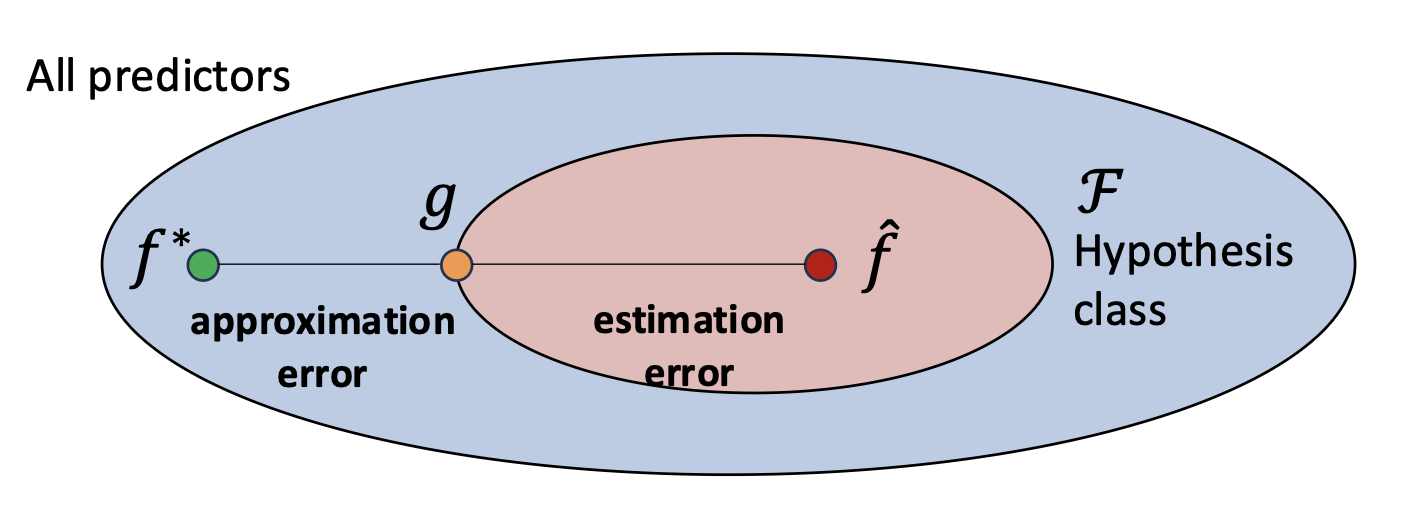
  • 우리는 $f^*$ 로부터 얼마나 떨어져 있는가?

image

\[\text{Err}(\hat{f}) - \text{Err}(f^*) = \underbrace{\text{Err}(\hat{f}) - \text{Err}(g)}_{\text{estimation error}} + \underbrace{\text{Err}(g) - \text{Err}(f^*)}_{\text{approximation error}}\]
  • 추정 오차(Estimation error) 는 제한된 데이터와 학습의 비효율성(limited data and learning inefficiencies) 으로부터 발생한다.
  • 근사 오차(Approximation error) 는 가설 클래스(hypothesis class)의 한계(limitations) 로부터 발생한다.

p13. 학습(fitting)과 일반화(generalization) 이해하기

  • 우리는 $f^*$ 로부터 얼마나 떨어져 있는가?

image

  • 가설 클래스(hypothesis class)의 크기가 커질수록 (예: 선형 모델에서 심층 신경망으로 갈수록):
    • 근사 오차(Approximation error) 는 감소한다.
      • 모델이 더 표현력이 풍부해져서 최적 함수에 더 가까워질 수 있기 때문이다.
    • 추정 오차(Estimation error) 는 증가한다.
      • 더 복잡한 가설 클래스는 효과적인 학습을 위해 더 많은 데이터가 필요하기 때문이다.
      • 데이터가 제한되어 있을 때, 표현력이 큰 모델은 일반화하지 못하고 학습 집합을 외워버리는(overfitting) 경향이 있다.
  • 목표는 두 오차를 모두 최소화하는 적절한 균형(right balance) 을 찾아내어, 최상의 일반화 성능을 얻는 것이다.

1. 데이터 제약과 모델 복잡도

  • 실제로는 데이터의 양이 제한되어 있기 때문에
    복잡한 모델을 학습시키더라도 최적함수 $f^*$ 에 도달하기 어렵다.
  • 모델이 복잡해질수록(예: 선형 → 다층 신경망) 더 많은 데이터가 필요하다.
  • 즉, 모델 복잡도와 데이터 양은 항상 균형을 이루어야 하며,
    데이터가 부족한 상황에서 지나치게 큰 모델을 사용하면
    일반화 성능이 오히려 나빠질 수 있다.

2. Feature selection의 역할

  • 사용할 입력 특징(feature)의 개수를 조절하는 것은
    모델 복잡도를 제어하는 또 다른 방법이다.
  • 예를 들어 1,000개의 변수 중 20개만 선택해 사용하면
    모델이 단순해지고 추정 오차(estimation error)를 줄일 수 있다.
  • 반대로 너무 많은 특징을 사용하면
    학습 데이터에 과도하게 맞추는 과적합(overfitting)이 발생할 수 있다.

3. 현대적 관점에서의 균형 찾기

  • 최근에는 GPU 성능 향상으로 모델의 크기를 키우는 것 자체는 큰 문제가 아니다.
  • 대신 feature selection, 정규화, 데이터 확장(data augmentation) 등
    다양한 방법을 통해 복잡한 모델 내부에서의 균형점을 찾는 접근이 선호된다.
  • 즉, 모델의 표현력을 유지하면서도
    불필요한 복잡성을 줄여
    근사 오차와 추정 오차 사이의 최적 균형 을 맞추는 것이 핵심이다.

p14. 어떻게 과대적합(overfitting)을 줄일 수 있을까?

  1. 특성 선택(Feature selection): 입력 차원 줄이기

    • 가능한 모든 특성(all possible features) 을 사용하는 대신,
      가장 관련 있는 특성들(only the most relevant ones) 만 선택하여 복잡성을 줄일 수 있다.

    • 왜 이것이 도움이 될까?

      • 더 많은 특성들은 모델 파라미터 수를 증가시킨다.
      • 특성 선택은 모델을 단순화하면서, 필요한 정보만 유지할 수 있도록 해준다.

p15. 어떻게 과대적합(overfitting)을 줄일 수 있을까?

  1. 특성 선택(Feature selection): 입력 차원 줄이기

    • 가능한 모든 특성(all possible features) 을 사용하는 대신,
      가장 관련 있는 특성들(only the most relevant ones) 만 선택하여 복잡성을 줄일 수 있다.

    • 왜 이것이 도움이 될까?
      • 더 많은 특성들은 모델 파라미터 수를 증가시킨다.
      • 특성 선택은 모델을 단순화하면서, 필요한 정보만 유지할 수 있도록 해준다.
    • 어떻게 수행되는가(How is this done)?
      • 이 부분은 본 강의 범위를 벗어난다.

image

  • 특성 선택은 현재 활발히 연구되는 주제(hot research topic)이다.
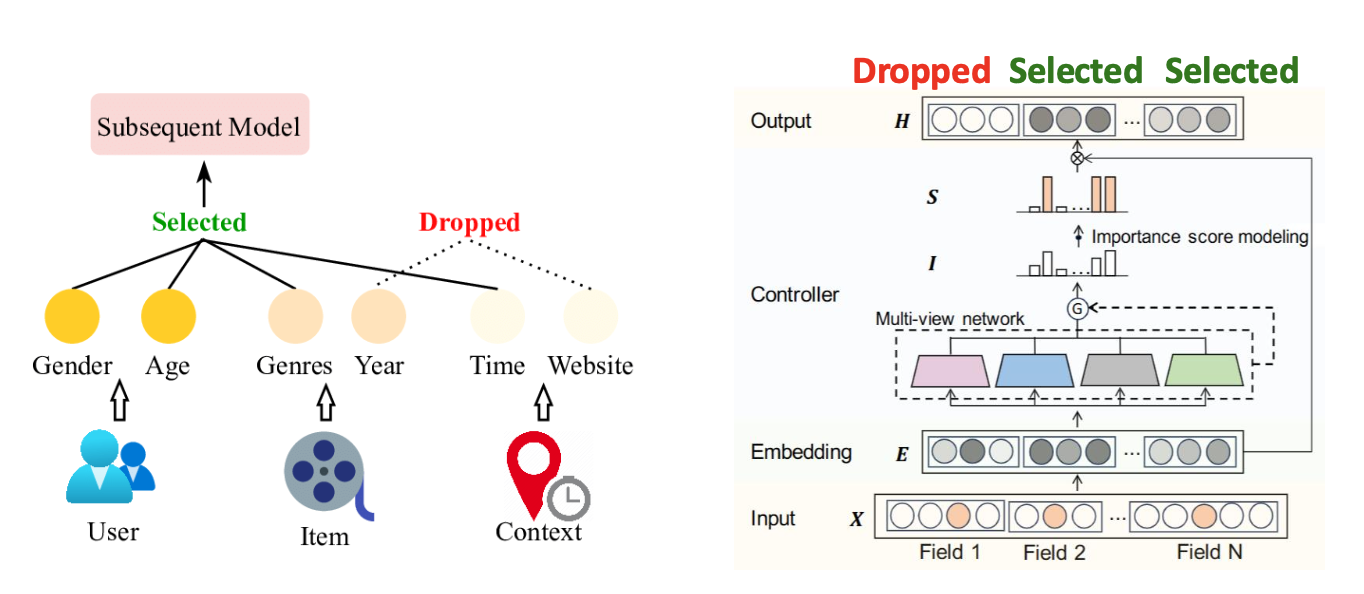
  • 최근 방법들은 가장 관련 있는 입력 특성들(the most relevant input features) 을 자동으로 찾아낸다.

(그림 출처: MvFS: Multi-view Feature Selection for Recommender System, ACM CIKM, 2023)

p17. 어떻게 과대적합(overfitting)을 줄일 수 있을까?

  1. 정규화(Regularization): 모델 복잡도 제어하기

  • 정규화는 모델 파라미터에 패널티(penalty) 를 추가하여 과도한 복잡성을 억제한다.

  • 왜 이것이 도움이 될까?

    • 정규화는 모델이 더 단순하고, 더 일반적인 패턴을 학습하도록 강제한다.

✔ L2 정규화(L2 regularization):

  • 모델 가중치의 L2 노름(norm)을 제한하여, 더 작은 가중치를 갖도록 유도한다.
\[\min_{\mathbf{w}} \; \text{TrainLoss}(\mathbf{w}) \;+\; \frac{\lambda}{2}\|\mathbf{w}\|^2\]
  • 여기서 $\lambda$ 는 정규화 강도(strength of regularization) 를 조절하는 하이퍼파라미터(hyperparameter) 이다.

💻 알고리즘 (Algorithm: 경사하강법 with L2 정규화)

  1. $\mathbf{w}$ 를 무작위로 초기화한다.

  2. 수렴할 때까지 반복한다:

    \[\mathbf{w} \;\leftarrow\; \mathbf{w} - \eta \, \big( \nabla_{\mathbf{w}} \text{TrainLoss}(\mathbf{w}) + \lambda \mathbf{w} \big)\]
  • 여기서 $\eta$ 는 학습률(learning rate)이다.

1. L2 정규화 목적식

  • 목표:

    \[\min_{\mathbf{w}}\; TrainLoss(\mathbf{w}) + \frac{\lambda}{2}\|\mathbf{w}\|^2\]

  • $\lambda$: 정규화 강도를 조절하는 하이퍼파라미터

2. 경사하강법에서의 수축(Weight Decay) 메커니즘

  • 업데이트 식:

    \[\mathbf{w} \leftarrow \mathbf{w} - \eta\bigl(\nabla_{\mathbf{w}}TrainLoss(\mathbf{w}) + \lambda \mathbf{w}\bigr)\]

  • 전개하면:

    \[\mathbf{w} \leftarrow (1-\eta\lambda)\,\mathbf{w}\;-\;\eta\,\nabla_{\mathbf{w}}TrainLoss(\mathbf{w})\]

  • 해석:

    • $(1-\eta\lambda)\mathbf{w}$ 항이 현재 가중치를 일정 비율로 직접 축소(weight decay) 한다.
    • 큰 가중치일수록 더 빠르게 줄어들며 과도한 복잡도를 억제한다.

3. 효과 요약

  • 가중치 크기를 억제하여 단순하고 일반화 성능이 좋은 모델을 만든다.
  • $\eta\lambda$가 너무 크면 underfitting(과소 적합),
    너무 작으면 정규화 효과가 약해진다.

p18. 어떻게 과대적합(overfitting)을 줄일 수 있을까?

  1. 정규화(Regularization): 모델 복잡도 제어하기
  • 정규화는 모델 파라미터에 패널티(penalty) 를 추가하여 과도한 복잡성을 억제한다.

✔ L2 정규화(L2 regularization):

  • 모델 가중치의 L2 노름(norm)을 제한하여, 더 작은 가중치를 갖도록 유도한다.

image

  • 참고(Note): L2 노름은 벡터가 원점으로부터 떨어진 유클리드 거리(Euclidean distance) 를 측정한다.

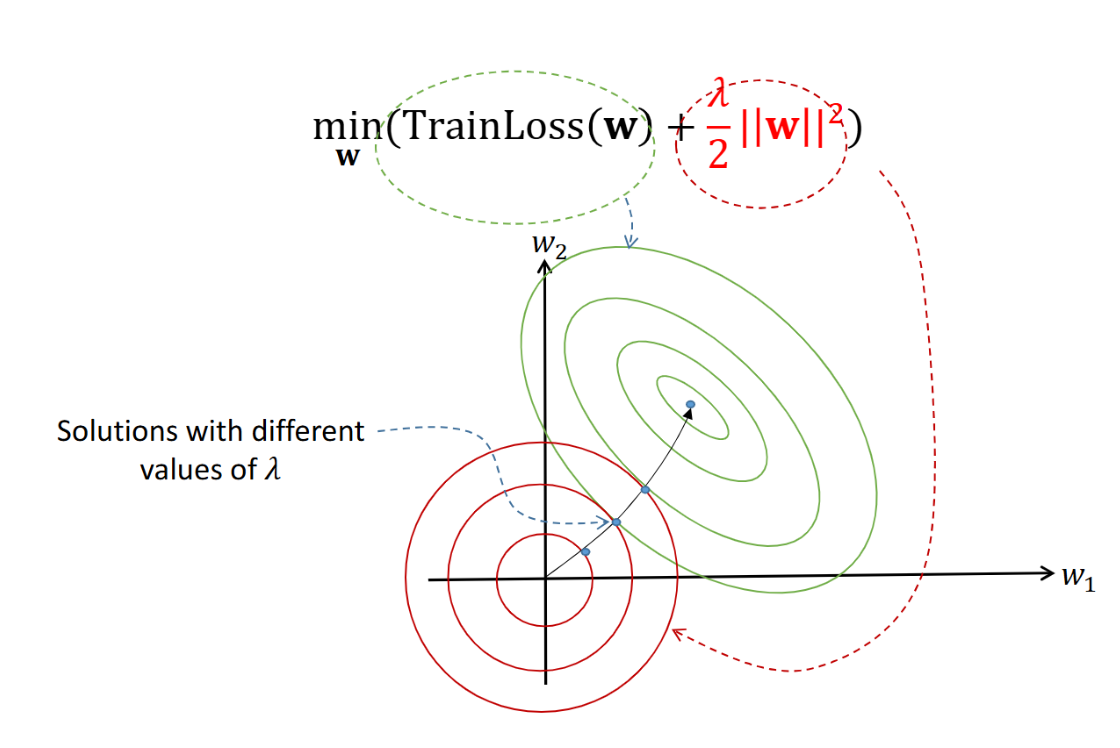
1. 등고선 그래프의 의미

  • 초록색 선은 훈련 손실(TrainLoss)의 등고선,
    빨간색 선은 L2 패널티 항의 등고선을 나타낸다.
  • 두 곡선이 만나는 지점이 정규화가 적용된 최적 해이다.
    즉, 손실을 최소화하면서 동시에 가중치의 크기를 제한하는 균형점이다.

2. λ(람다)의 크기에 따른 변화

  • λ가 작을 때 (예: 0.1)
    • L2 패널티의 영향이 약하다.
    • 최적점이 훈련 손실의 중심부 쪽에 더 가까워진다.
    • 가중치가 커질 수 있어 모델이 복잡해지고 과적합 위험이 증가한다.
  • λ가 클 때 (예: 100)
    • 패널티 항이 매우 강하게 작용한다.
    • 최적점이 원점(0,0)에 가까워진다.
    • 가중치가 거의 0 방향으로 수축되어 모델이 단순해진다.

3. 요약

  • λ의 크기에 따라 TrainLoss 중심과 원점 사이에서 타협점이 달라진다.
  • λ가 크면 수축 방향(원점 쪽),
    λ가 작으면 데이터 적합 방향(TrainLoss 중심 쪽).
  • 정규화는 이 두 힘 사이에서 적절한 균형점을 찾는 과정이다.

p19. 어떻게 과대적합(overfitting)을 줄일 수 있을까?

  1. 조기 종료(Early stopping): 과도한 학습 방지

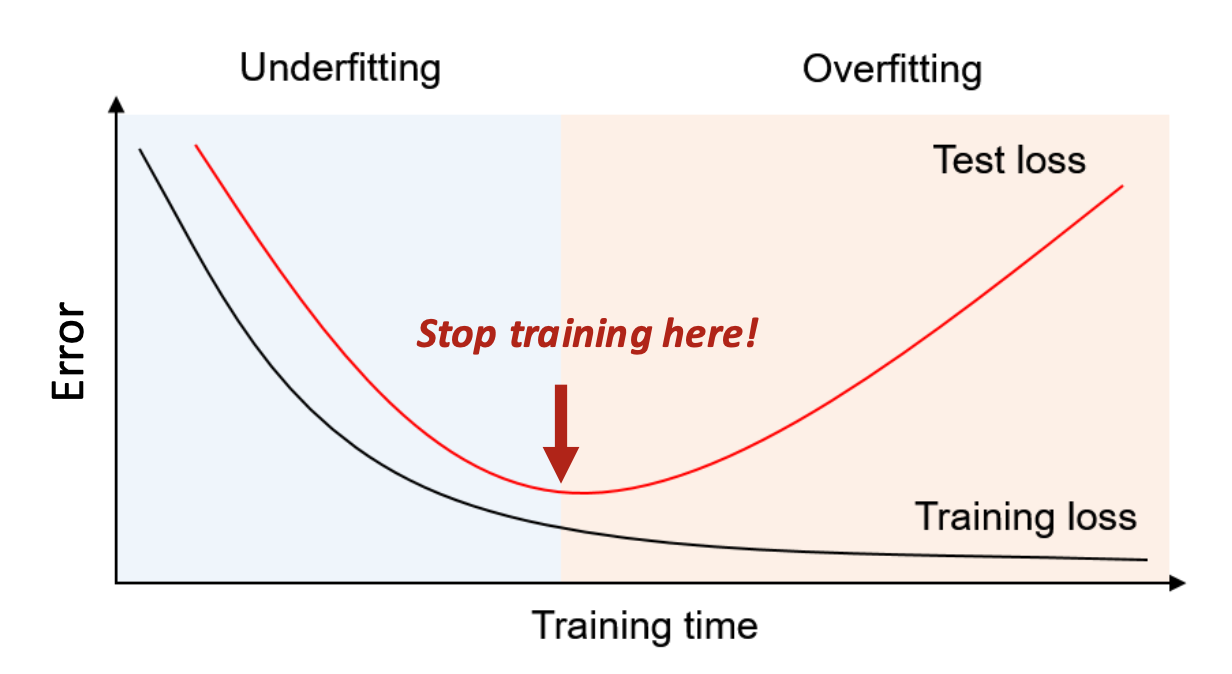
  • 조기 종료는, 추가적인 학습이 더 이상 일반화를 개선하지 않을 때 학습을 멈춤으로써
    모델이 잡음(noise)을 외워버리는 것을 막는다.

  • 그러나 테스트 데이터는 학습에 사용할 수 없다.

    • 따라서, 언제 학습을 멈출지를 어떻게 결정할까?

image

  • 왼쪽: 모델이 충분히 학습되지 않음
  • 오른쪽: 모델이 학습 데이터를 외우지만 일반화에는 실패함

과적합(overfitting)은 모델이 지나치게 복잡할 때뿐 아니라
하나의 모델 내에서 학습이 과도하게 진행될 때도 발생할 수 있다.

  • 학습이 너무 오래 지속되면, 모델이 데이터의 노이즈나 우연한 패턴까지 외워버려
    일반화 성능이 떨어질 수 있다.
  • Early stopping은 이런 현상을 방지하기 위해
    검증 손실(validation loss)이 더 이상 개선되지 않을 때
    학습을 조기에 종료하는 기법이다.

즉, 과적합의 원인은

  • 모델 복잡도 자체뿐 아니라
  • 학습을 오래 진행하는 행위 자체에서도 발생할 수 있다.

Early stopping은 이러한 ‘학습 진행 정도’를 조절해
과적합을 방지하는 핵심 기법이다.

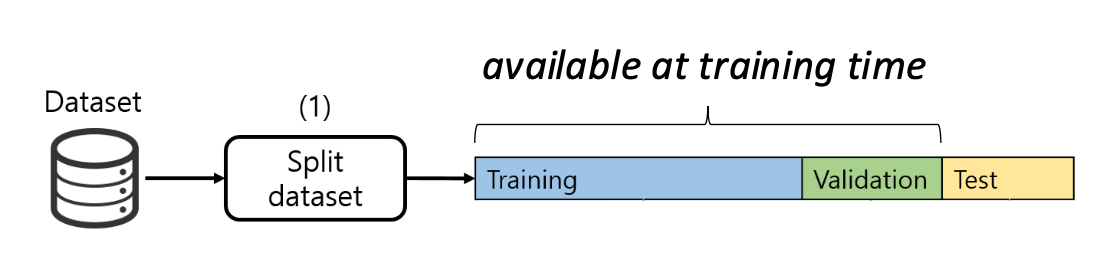
p20. 검증 세트(Validation set)

  • 검증 세트(validation set) 는 훈련 세트(training set) 의 일부를 따로 떼어놓은 부분(held-out subset)으로,
    테스트 세트(test set) 를 직접 사용하지 않고 모델의 성능을 평가하는 데 사용된다.

    • 검증 세트는 테스트 세트의 대리(proxy) 역할을 한다.
      즉, 아직 보지 못한 데이터(simulated unseen data) 를 시뮬레이션 한다.

    image

(그림 위치: 데이터 세트(dataset) → 훈련 세트 / 검증 세트 / 테스트 세트 분할 과정,
그리고 훈련 세트 / 검증 세트 / 테스트 세트 로봇 그림)

  • 훈련 세트(Training set): 라벨이 있는 데이터에서 패턴을 학습한다.
    image
  • 검증 세트(Validation set): 모델이 얼마나 잘 학습되고 있는지 주기적으로 확인한다.
    image
  • 테스트 세트(Test set): 라벨이 없는 데이터에 대해 모델이 최종적으로 예측을 수행한다.
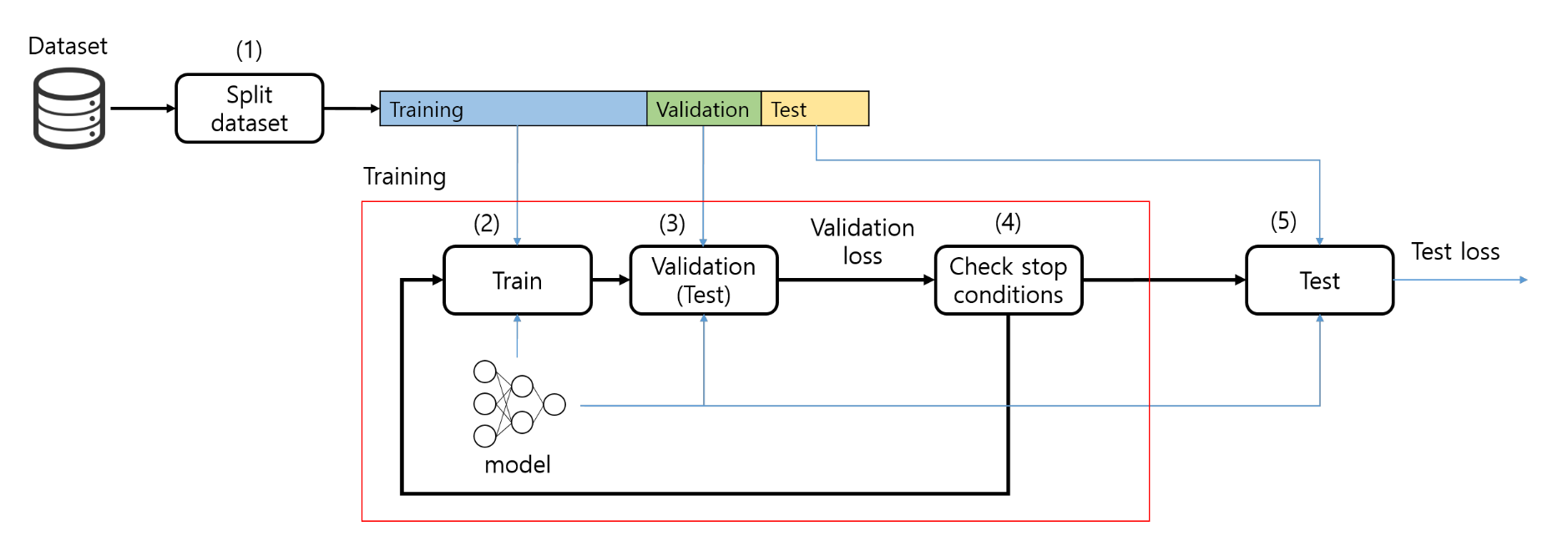
    image

p21. 전형적인 개발 사이클

A. 데이터 세트 분할
1) 데이터 세트를 훈련 세트, 검증 세트, 테스트 세트로 나눈다.

B. 훈련 (수렴할 때까지 반복)
2) 훈련 세트를 사용하여 모델을 업데이트한다.
3) 검증 세트를 사용하여 모델을 평가한다.
4) 중단 조건을 확인한다.

C. 테스트
5) 최종 모델을 테스트 세트에서 평가한다.

✔ 하이퍼파라미터 튜닝

  • 서로 다른 하이퍼파라미터 값으로 모델을 여러 번 훈련한다.
  • 검증 세트를 기준으로 값을 선택한다.

image

p22. 요약

적합(fitting)과 일반화(generalization)

  • 실제 목표가 아닌 것: 훈련 손실을 최소화하는 것 (이미 본 예시에서는 잘 동작함)
  • 실제 목표: 일반화 (앞으로 보지 못한 새로운 예시에서도 잘 동작함)
  • 일반 원칙: 훈련 오류를 최소화하면서 동시에 모델 복잡성을 제어해야 한다
    (가설 클래스(hypothesis class)를 작게 유지할 것!)

과적합(overfitting)을 방지하기 위한 최선의 방법들

  • 특성 선택(feature selection): 불필요한 입력을 줄여 모델을 단순화한다.
  • 정규화(regularization): 가중치에 패널티를 부여하여 과도한 복잡성을 억제한다.
  • 조기 종료(early stopping): 모델이 노이즈를 암기하기 전에 훈련을 중단한다.
  • 검증 세트(validation set): 보지 못한 데이터를 시뮬레이션하고, 따로 분리한 데이터 세트를 사용하여 모델을 조정한다.
  • 추가 데이터 수집: 더 다양하고(different) 많은 데이터를 수집한다 (예산이 허락한다면).

비지도 학습(Unsupervised learning)

p27. 지도 학습과 비지도 학습

지도 학습:

  • 데이터 인스턴스: 입력–출력 쌍 $(x, y)$, 여기서 $y$는 $x$에 대한 라벨이다.
  • 라벨링은 사람의 노력이 필요하므로 비용이 많이 든다.
    (예: 10,000개의 라벨이 달린 데이터를 얻는 것은 매우 비싸다.)

비지도 학습:

  • 데이터 인스턴스: 입력 $x$. 라벨이 없음!
  • 라벨이 없는 데이터는 대규모로 수집하기 쉽다.
    (예: 1억 개의 라벨 없는 데이터는 저렴하게 얻을 수 있다.)

p28. 비지도 학습 예시: 단어 클러스터링

입력:

  • 원시 텍스트 (뉴스 기사 1억 단어)

출력:

  • 클러스터 1: Friday Monday Thursday Wednesday Tuesday Saturday Sunday weekends Sundays Saturdays
  • 클러스터 2: June March July April January December October November September August
  • 클러스터 3: water gas coal liquid acid sand carbon steam shale iron
  • 클러스터 4: great big vast sudden mere sheer gigantic lifelong scant colossal
  • 클러스터 5: man woman boy girl lawyer doctor guy farmer teacher citizen
  • 클러스터 6: American Indian European Japanese German African Catholic Israeli Italian Arab
  • 클러스터 7: pressure temperature permeability density porosity stress velocity viscosity gravity tension
  • 클러스터 8: mother wife father son husband brother daughter sister boss uncle
  • …
  • 클러스터 14: had hadn’t hath would’ve could’ve should’ve must’ve might’ve
  • 클러스터 15: head body hands eyes voice arm seat eye hair mouth

p29. 비지도 학습은 무엇을 할 수 있는가?

  • 비지도 학습은 라벨이 없는 데이터에서 숨겨진 패턴과 구조를 발견하는 데 도움을 준다.

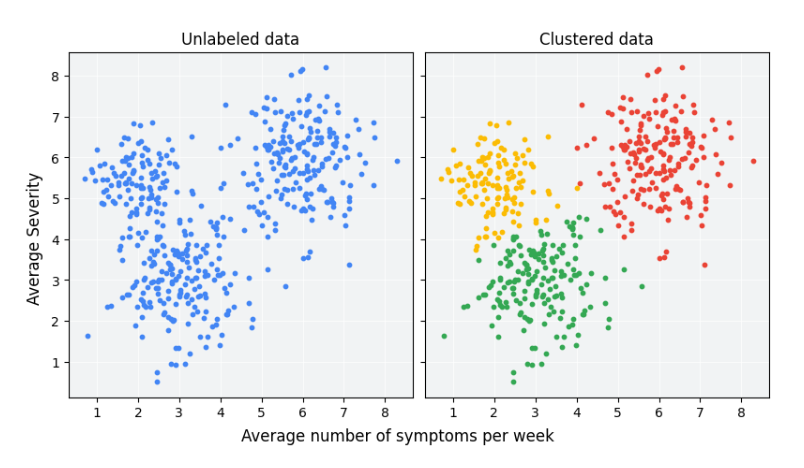
클러스터링 (Clustering)

  • 유사한 데이터 포인트들을 같은 클러스터로 묶는다.

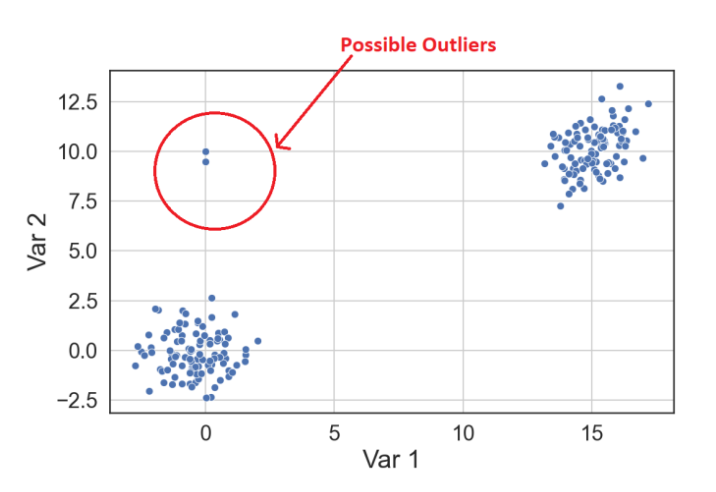
image

이상치/이상 탐지 (Outlier/anomaly detection)

  • 드물거나 비정상적인 데이터 포인트를 식별한다.

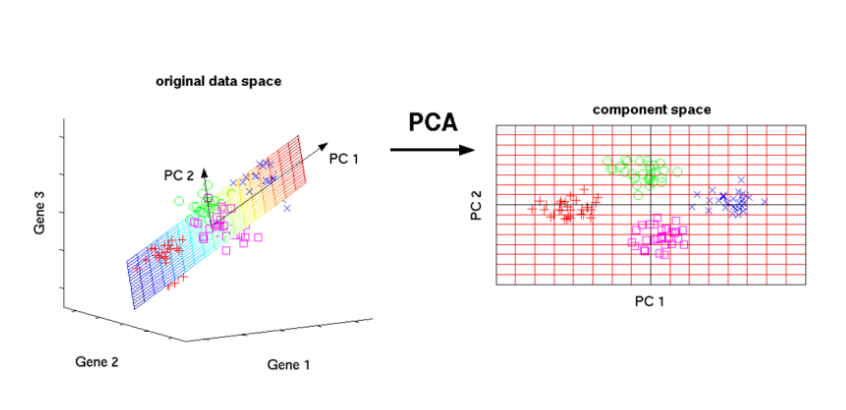
image

차원 축소 (Dimensionality reduction)

  • 중요한 정보를 보존하면서 데이터의 복잡성을 줄인다.

image

p30. 클러스터링 (Clustering)

  • 클러스터링이란 객체 집합을 그룹화하는 작업으로,
    같은 그룹(클러스터)에 속한 인스턴스(instance) 들은 서로 더 유사하고,
    다른 클러스터에 속한 것들과는 덜 유사하도록 하는 것이다.

  • 입력 (Input): 데이터 인스턴스

\[D_{train} = \{x_1, \ldots, x_n\}\]
  • 출력 (Output): 각 인스턴스를 클러스터에 할당
\[\mathbf{z} = [z_1, \ldots, z_n], \quad z_i \in \{1, \ldots, K\}\]

  • $K$ (클러스터의 개수) 는 하이퍼파라미터(hyperparameter)이다.

  • 중심점(centroid) $\mu_k$ 는 클러스터 $k$의 대표 벡터(representative vector) 이다.

image

p31. 클러스터링: K-평균 (K-means)

  • K-평균(K-means) 은 데이터를 $K$개의 클러스터(cluster)로 나누는 클러스터링 알고리즘이다.
    각 인스턴스는 가장 가까운 평균(centroid, 중심점) 을 가진 클러스터에 속한다.

  • 목표(Objectives):

    1. 각 데이터 포인트 $\phi(x_i)$ 를 가장 가까운 클러스터에 할당한다.
    2. 클러스터 중심점(centroids) $\mu_k$ 를 배치하여 클러스터 내부 분산(intra-cluster variance)을 최소화한다.
\[\min_{\mathbf{z}} \min_{\mu} \; \text{Loss}_{k\text{-means}}(\mathbf{z}, \mu)\] \[\text{Loss}_{k\text{-means}}(\mathbf{z}, \mu) \;=\; \sum_{i=1}^{n} \left\| \phi(x_i) - \mu_{z_i} \right\|^2\]
  • K-평균(K-means) 은 중심점(centroids) $\mu$ 와 클러스터 할당(cluster assignments) $\mathbf{z}$ 를 동시에 최적화(jointly optimize) 한다.

p32. 클러스터링: K-평균 (K-means)

  • 최적화(Optimization): 교대 최소화(alternating minimization)
    • 교대 최소화는 목적 함수(objective function)를 최적화하기 위해,
    • 다른 변수들은 고정한 상태로, 일부 변수 집합(subsets of variables)을
      반복적으로 업데이트하는 방식이다.
  • Step 1: $\mu$를 고정한 상태에서 $\mathbf{z}$를 최적화한다.
  • Step 2: $\mathbf{z}$를 고정한 상태에서 $\mu$를 최적화한다.

💻 알고리즘: K-평균 (K-means)

  1. 무작위로 중심점(centroids) $\mu = [\mu_1, \dots, \mu_K]$ 를 초기화한다.
  2. $t = 1, \dots, T$ 에 대해 반복한다:
    • Step 1: $\mu$가 주어졌을 때 $\mathbf{z}$ (클러스터 할당)를 설정한다.
      • 각 데이터 포인트 $i = 1, \dots, n$ 에 대해:
      \[z_i \;\leftarrow\; \arg\min_{k=1,\dots,K} \;\|\phi(x_i) - \mu_k\|^2\]
    • Step 2: $\mathbf{z}$가 주어졌을 때 중심점(centroids) $\mu$를 설정한다.
      • 각 클러스터 $k = 1, \dots, K$ 에 대해:
      \[\mu_k \;\leftarrow\; \frac{1}{|\{ i : z_i = k \}|} \sum_{i: z_i = k} \phi(x_i)\]

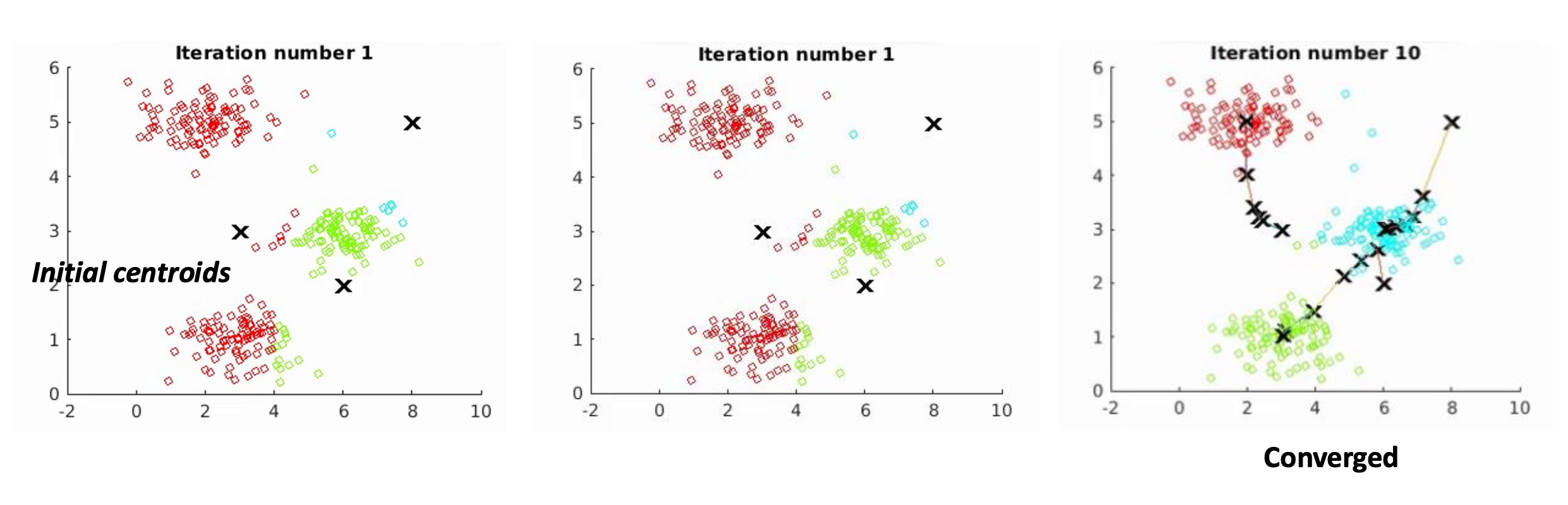
p33. K-평균 (K-means) 예시

  • 주어진 학습 데이터:
\[D_{train} = \{0, 2, 10, 12\}, \quad \mu = [0, 2]\]

image

※ 보라색 표시된 점이 중심점(centroids)

  • Iteration 1

    • Step 1:
      \(z_1 = 1, \quad z_2 = 2, \quad z_3 = 2, \quad z_4 = 2\)

    • Step 2:
      \(\mu_1 = 0, \quad \mu_2 = 8\)

image

  • Iteration 2

    • Step 1:
      \(z_1 = 1, \quad z_2 = 1, \quad z_3 = 2, \quad z_4 = 2\)

    • Step 2:
      \(\mu_1 = 1, \quad \mu_2 = 11\)

image

  • 수렴 (Converged)

1. 초기 설정

  • 데이터: $D_{train} = {0, 2, 10, 12}$
  • 초기 중심점: $\mu_1 = 0,\; \mu_2 = 2$
  • 목표: 가장 가까운 중심점으로 데이터 할당 → 중심점 갱신

2. Iteration 1
Assignment step

  • $0 \rightarrow \mu_1$ 에 더 가까움 → 클러스터 1
  • $2, 10, 12 \rightarrow \mu_2$ 에 더 가까움 → 클러스터 2
  • 결과:
    $z_1 = 1,\; z_2 = 2,\; z_3 = 2,\; z_4 = 2$

Update step

  • 클러스터 1: $0$ → $\mu_1 = 0$
  • 클러스터 2: $(2 + 10 + 12)/3 = 8$ → $\mu_2 = 8$

3. Iteration 2
Assignment step

  • $0, 2 \rightarrow \mu_1$ 에 더 가까움 → 클러스터 1
  • $10, 12 \rightarrow \mu_2$ 에 더 가까움 → 클러스터 2
  • 결과:
    $z_1 = 1,\; z_2 = 1,\; z_3 = 2,\; z_4 = 2$

Update step

  • 클러스터 1: $(0 + 2)/2 = 1$ → $\mu_1 = 1$
  • 클러스터 2: $(10 + 12)/2 = 11$ → $\mu_2 = 11$

4. 수렴 (Converged)

  • 다음 반복에서도 할당이 변하지 않음
  • 최종 중심점:
    \(\mu_1 = 1,\qquad \mu_2 = 11\)

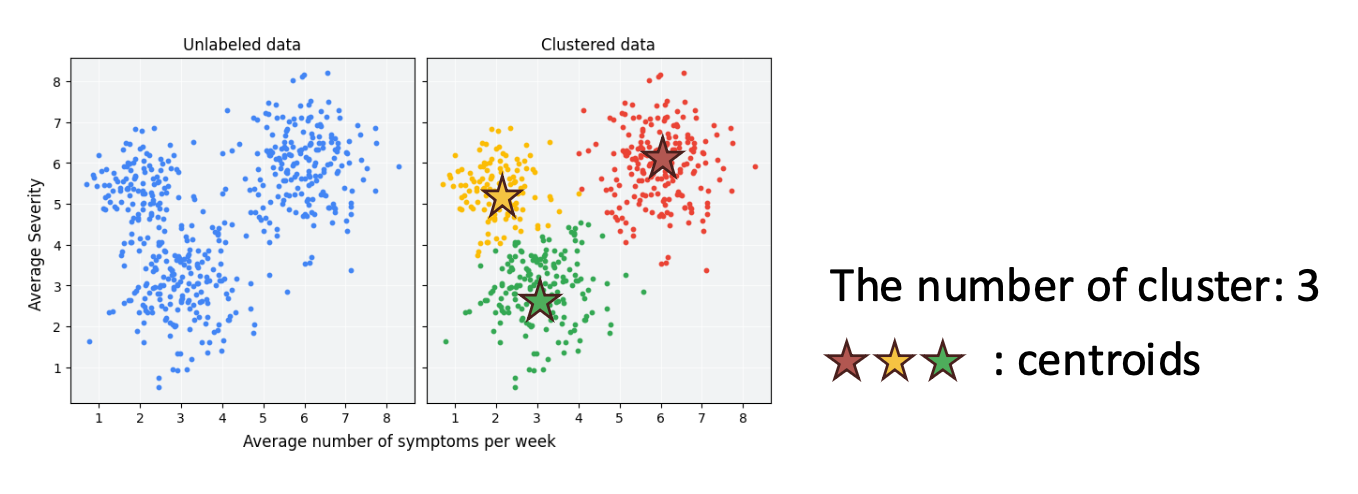
p34. K-평균 (K-means) 예시

  • 클러스터의 개수 ($K$): 3

image

p35. 요약: 기계 학습 (machine learning)

  • 특성 추출 (Feature extraction): 선형 & 비선형 특성, 가설 클래스(hypothesis class)
  • 예측 과제 (Prediction task): 회귀(regression), 분류(classification), 순위화(ranking), 군집(clustering)
  • 선형 및 비선형 모델 (Linear and nonlinear models): 선형 예측기(linear predictors), 신경망(neural networks)
  • 최적화 (Optimization): 경사 하강법(gradient descent), 역전파(backpropagation), 교대 최소화(alternating minimization)
  • 일반화 (Generalization): 과적합(overfitting), 과소적합(underfitting), 오류 분해(error decomposition), 개발 주기(development cycle)
대학원 수업, 텍스트 마이닝
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.