포스트

[텍스트 마이닝] 5. Representing Texts with Vectors 1

게시 업데이트
By 김성진
22 분읽는 시간
[텍스트 마이닝] 5. Representing Texts with Vectors 1

p7. 우리의 첫 번째 계획: 텍스트를 벡터로 표현하기

  • 왜 벡터인가?
    • 예를 들어, 우리 상점의 각 상품은 텍스트 설명을 가진다.
      (예: “Nike Air Force”, “Harry Potter book”)
    • 사용자는 자연어 질의를 이용해 검색한다.
      (예: “농구에 가장 좋은 신발”, “Harry Potter 첫 번째 책”)
    • 항목을 분류하거나 검색하기 위해, 시스템은 텍스트를 수학적으로 비교할 수 있는 방법이 필요하다.
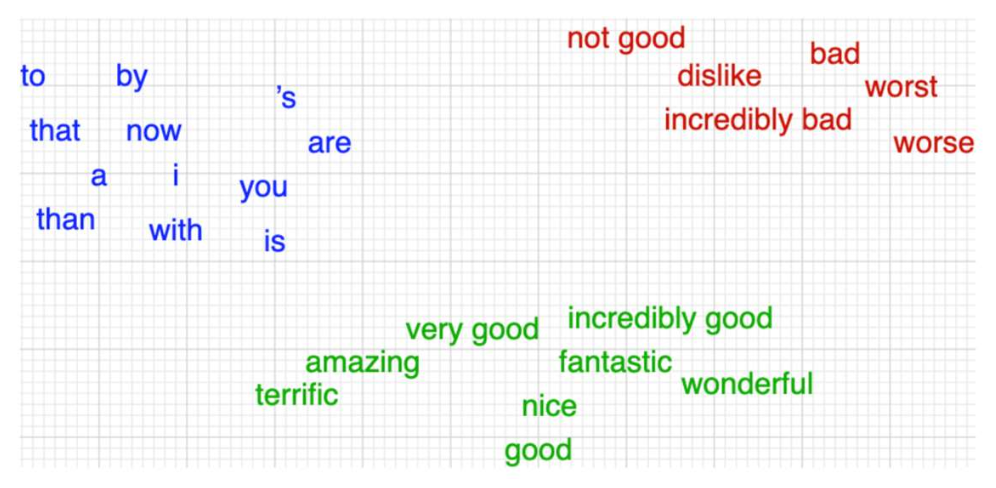
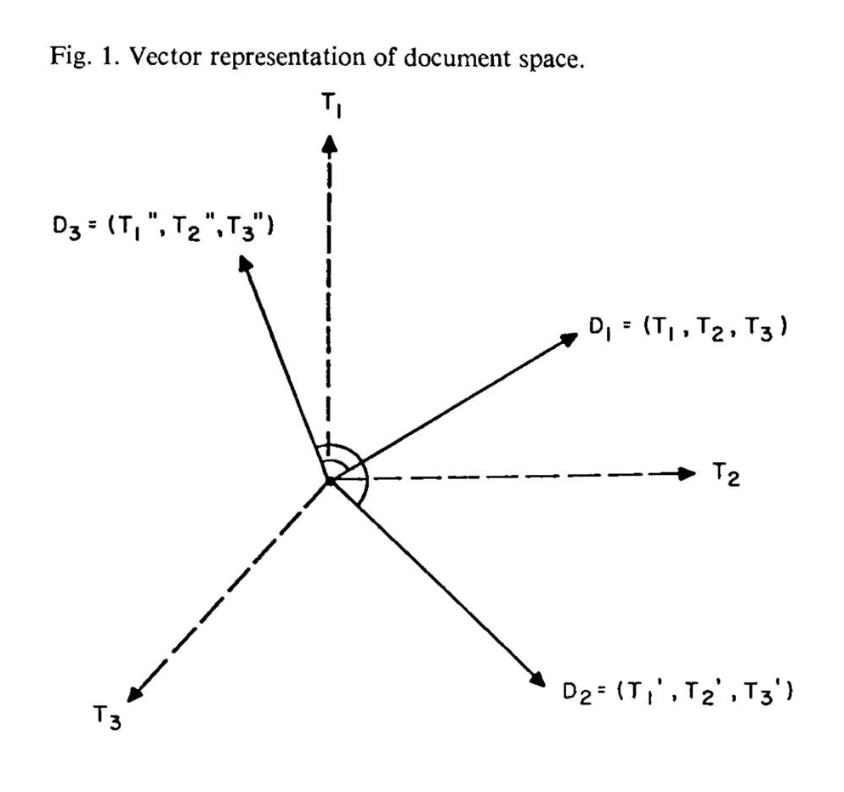
  • 우리는 텍스트를 고차원 공간(high-dimensional space) 의 벡터로 표현한다.
    이렇게 하면 그 의미(semantics)를 포착하고 비교할 수 있다.

image

p8. 우리의 첫 번째 계획: 텍스트를 벡터로 표현하기

  • 우리는 텍스트를 고차원 공간(high-dimensional space) 의 벡터로 표현한다.
    이렇게 하면 그 의미(semantics)를 포착하고 비교할 수 있다.

  • 예를 들어, 어떤 상품이 질의(query)와 더 관련성이 높은 경우는
    벡터 공간에서 서로 더 “유사(similar)” 할 때이다.
    • “similar”의 의미에 대해서는 나중에 논의할 것이다.

  • 축(axes)은 무엇인가?

  • 어휘집(vocabulary)의 각 단어를 하나의 차원으로 표현한다면 어떨까?

image

텍스트를 벡터로 표현하기: 희소 표현 (Sparse representation)

  • 단순화를 위해, 우리는 제품 설명(예: 제목, 특성)을 문서(documents)라고 부른다.

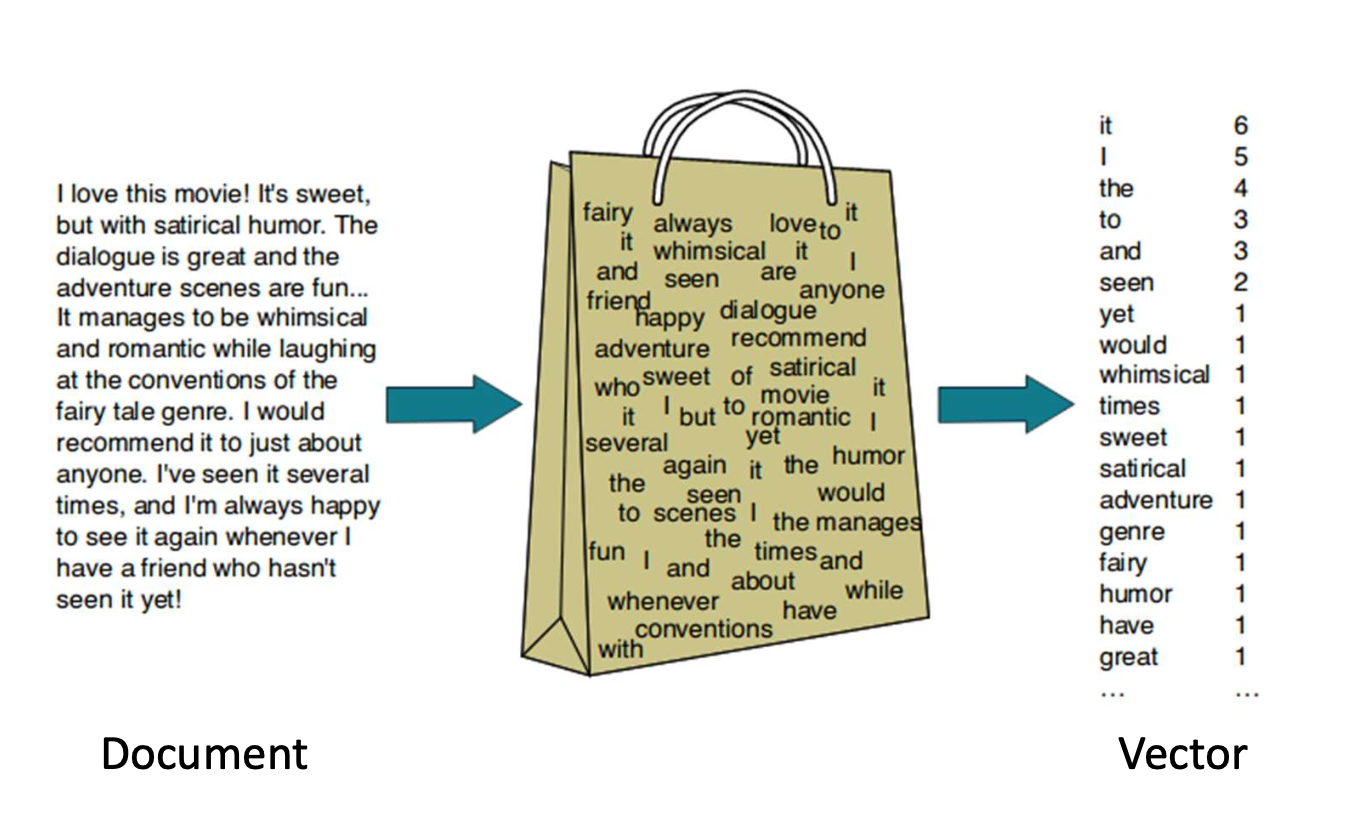
p10. 단어들의 집합 (Bag-of-words, BoW)

  • BoW 모델은 문서를 단어 개수(빈도, word counts / frequencies)의 벡터로 표현한다.
    • 어휘집(vocabulary)은 말뭉치(corpus) 전체에서의 고유한 단어들의 집합으로 미리 정의된다.
    • BoW는 단어의 순서와 문맥(context)을 무시하고, 각 단어가 몇 번 등장하는지만 집중한다.

image

p12. 단어들의 집합 (Bag-of-words, BoW)

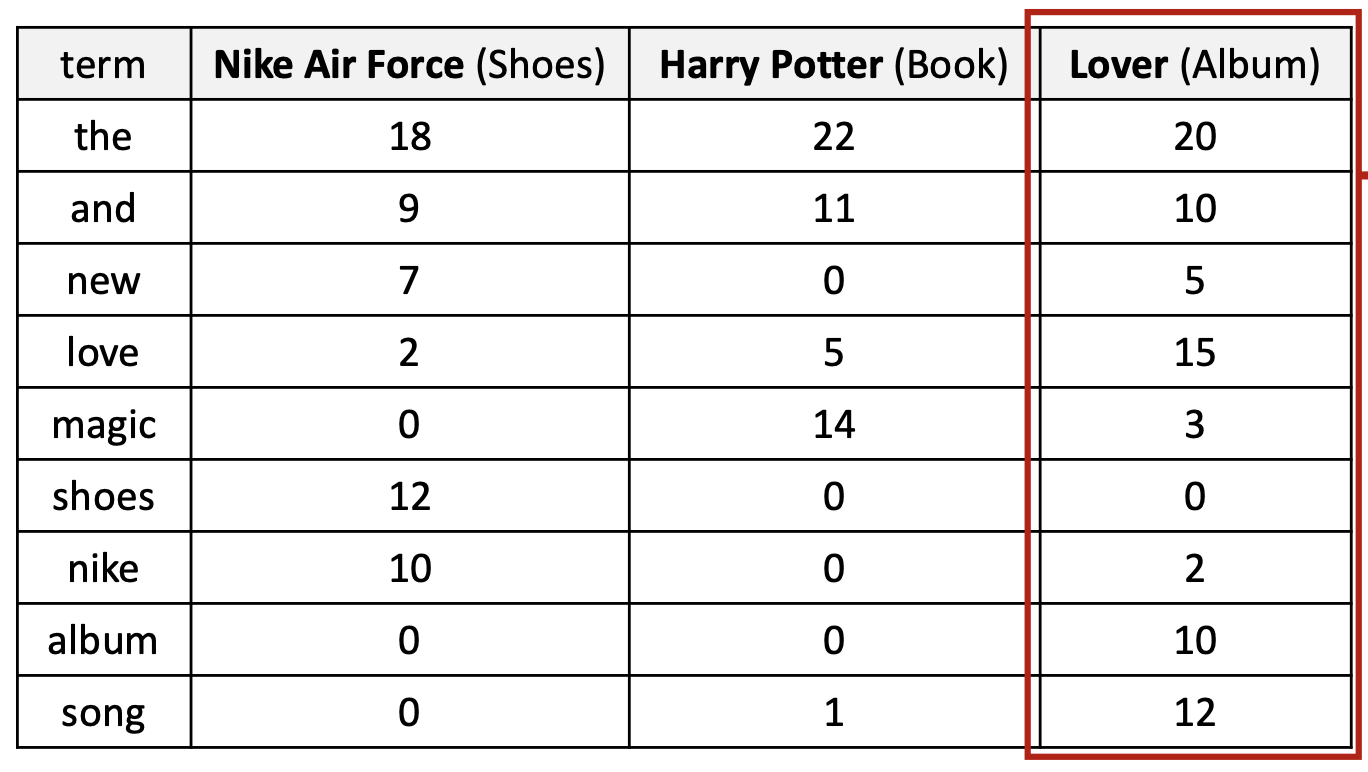
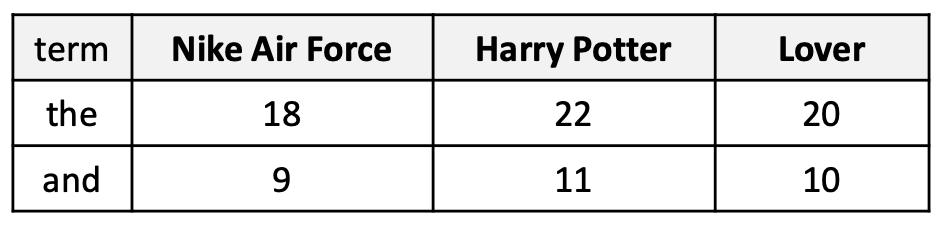
✔ 용어-문서 빈도 행렬 (Term-document count matrix)

  • 각 행(row) 은 하나의 용어(term) 에 대응한다.
  • 각 열(column) 은 하나의 문서(document) 에 대응한다.
  • 행렬의 값은 단순히 해당 문서에서 용어(term)가 등장한 횟수 를 의미한다.

image

  • 문서는 어휘(vocabulary) 크기에 기반한 카운트 벡터(count vectors) 로 변환된다.
  • 실제로는 어휘 크기가 매우 크기 때문에, 이 벡터들 안의 많은 항목들이 0이 된다.
    → 따라서 희소 벡터(sparse vectors) 가 된다.

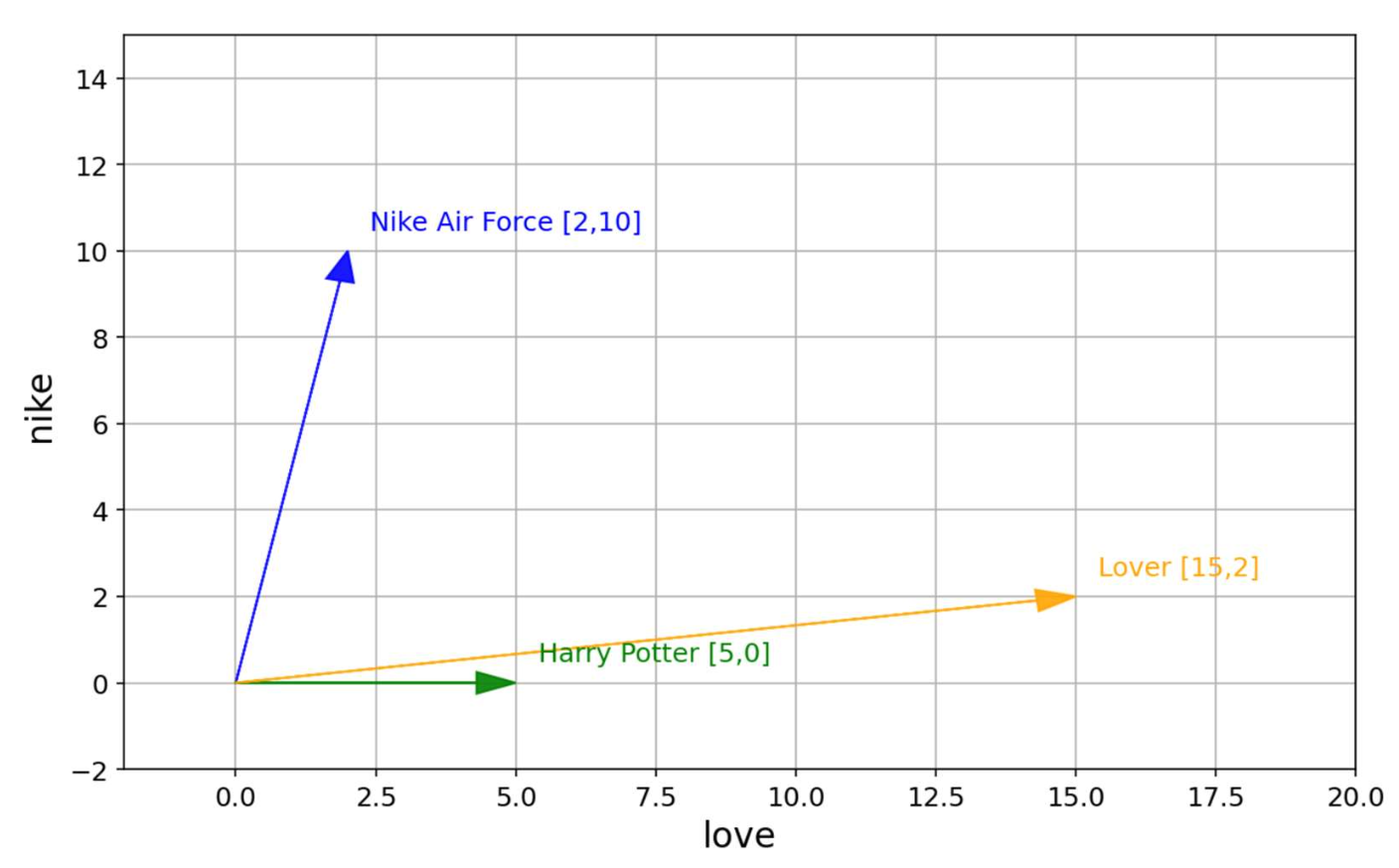
p13. 단어들의 집합 (Bag-of-words, BoW): 문서 벡터 시각화

  • 문서 벡터 시각화 (Visualizing document vectors)
    • 어휘(vocabulary): {nike, love}

image

  • 문서는 어휘 크기에 기반한 카운트 벡터(count vectors) 가 된다.
  • 이러한 벡터들은 문서 내 용어 분포(term distributions) 를 반영한다.

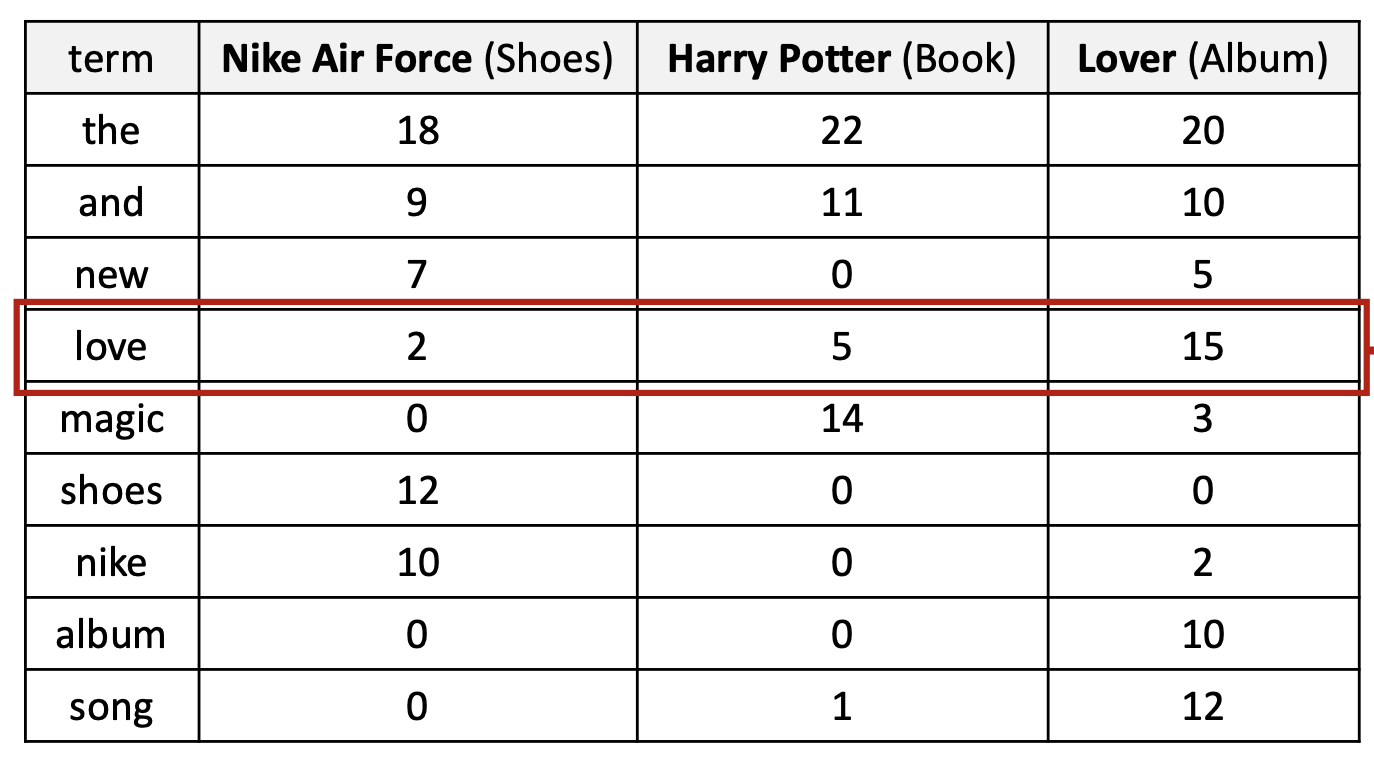
p14. 단어들의 집합 (Bag-of-words, BoW)

  • 용어-문서 카운트 행렬 (Term-document count matrix)
    • 각 행(row)은 용어(term) 에 대응하고, 각 열(column)은 문서(document) 에 대응한다.
    • 값(value)은 단순히 해당 문서에서 용어(term)가 등장한 횟수 를 의미한다.

image

  • 단어 또한 벡터로 표현될 수 있다
  • ‘love’ → 음악 앨범이나 로맨틱한 콘텐츠와 관련된 문서에서 자주 등장한다.
  • ‘shoes’ → 스니커즈 제품 설명에서 자주 등장한다.

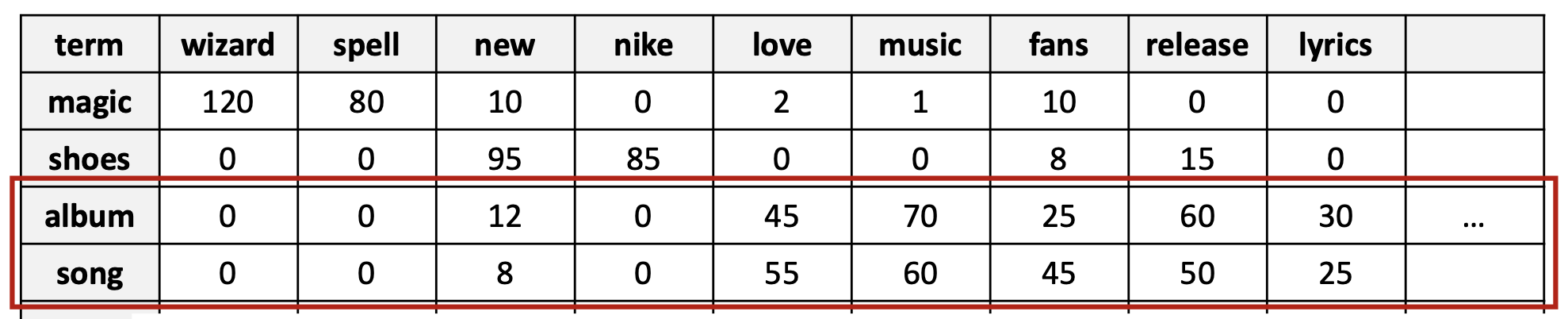
p16. 단어에 대한 더 일반적인 선택

  • 단어-단어 동시발생 행렬 (Word-word co-occurrence matrix)
    • ‘용어-맥락 행렬(term-context matrix)’이라고도 불린다.
    • 크기는 $V \times V$이며, 여기서 $V$는 어휘(vocabulary)의 크기이다.
    • 각 항목(entry)은 한 단어(행, row)가 다른 단어(열, column)와 컨텍스트 윈도우(context window) 안에서 얼마나 자주 함께 나타나는지를 센다.
  • 컨텍스트 윈도우(context window)은 몇 개의 이웃 단어들을 고려할지를 정의한다. image

image

  • 두 단어는, 만약 이들의 컨텍스트 벡터(context vectors) (행렬의 행)이 유사하다면, 서로 유사한 것으로 간주된다.

p18. Bag-of-words (BoW): 한계점

  • 문제: 단어 빈도(word frequency)가 항상 좋은 표현(representation)인 것은 아니다.

    • 빈도는 분명히 유용하다. 두 문서가 유사한 단어 빈도 분포를 가진다면, 의미적으로 유사할 가능성이 크다.
    • 그러나 매우 흔한 단어들 (예: the, it)은 문서의 실제 내용에 대한 정보를 거의 제공하지 않는다.
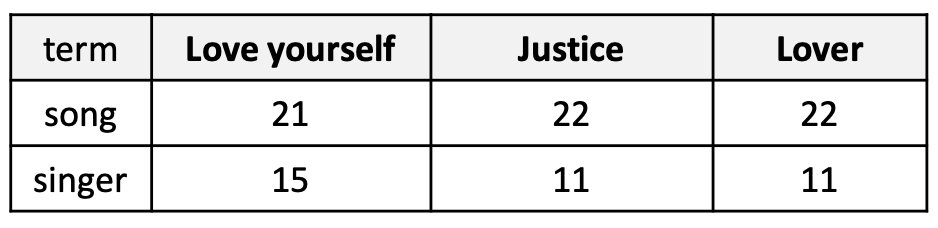
    • 또한, 유사한 주제(예: 앨범)를 가진 말뭉치(corpus) 에서는 특정 주제와 관련된 용어들 (예: song, singer)이 모든 문서에서 자주 등장할 수 있다.

image
image

  • 이것은 역설(paradox) 을 만든다!
    • 빈도는 유용하다. 그러나 지나치게 자주 등장하는 단어들은 오해를 불러일으킬 수 있다.
    • 그렇다면 우리는 이 두 상충되는 제약 조건을 어떻게 균형(balance) 잡을 수 있을까?

p20. TF-IDF 가중치

  • 한 문서 내의 특정 단어(term)는 다음의 경우 더 중요한 것으로 간주된다:
    (1) 해당 문서 안에서 자주 등장할 때 (TF, Term Frequency)
    (2) 다른 많은 문서들에는 잘 등장하지 않을 때 (IDF, Inverse Document Frequency)
  1. TF (단어 빈도, Term Frequency)
    • 단어가 한 문서 안에서 얼마나 자주 등장하는지를 측정한다.
    • 문서 내부에서의 중요성을 반영한다.
  2. IDF (역문서 빈도, Inverse Document Frequency)
    • 단어가 말뭉치(corpus) 전체에서 얼마나 드문지를 측정한다.
    • 흔한 단어의 가중치는 낮추고, 드문 단어의 가중치는 높인다.

image

p21. 단어 빈도 (TF, Term Frequency)

  • 단어 빈도 $tf_{t,d}$
    • TF는 단어 $t$가 문서 $d$에서 등장하는 횟수(number of times)로 정의된다.
    • 직관(Intuition): 단어가 더 자주 나타날수록, 해당 문서 안에서 더 중요하게 간주된다.
  • 원시(raw) 단어 빈도 자체는 우리가 원하는 것이 아니다.
    • 어떤 단어가 10번 더 많이 나타난다고 해서, 그 단어가 10배 더 중요하다는 뜻은 아니다.
    • 중요성은 빈도에 비례하여 증가하지 않는다.
  • 가장 흔히 쓰이는 형태는 로그 스케일 빈도(log-scaled frequency) 이다.
\[tf_{t,d} = \begin{cases} 1 + \log_{10}(\text{count}(t, d)), & \text{if } \text{count}(t, d) > 0 \\ 0, & \text{otherwise} \end{cases}\]
  • (+1은 값이 0이 되는 것을 방지한다.)

p22. 역문서 빈도 (IDF, Inverse Document Frequency)

  • 역문서 빈도 $idf_t$
    • IDF는 각 단어 $t$가 모든 문서에서 얼마나 드물게 등장하는지에 따라 점수를 매긴다.
    • 직관(Intuition): 어떤 단어가 전체 문서 집합(collection)에서 드물수록, 그 단어는 더 많은 정보를 담고 있다.

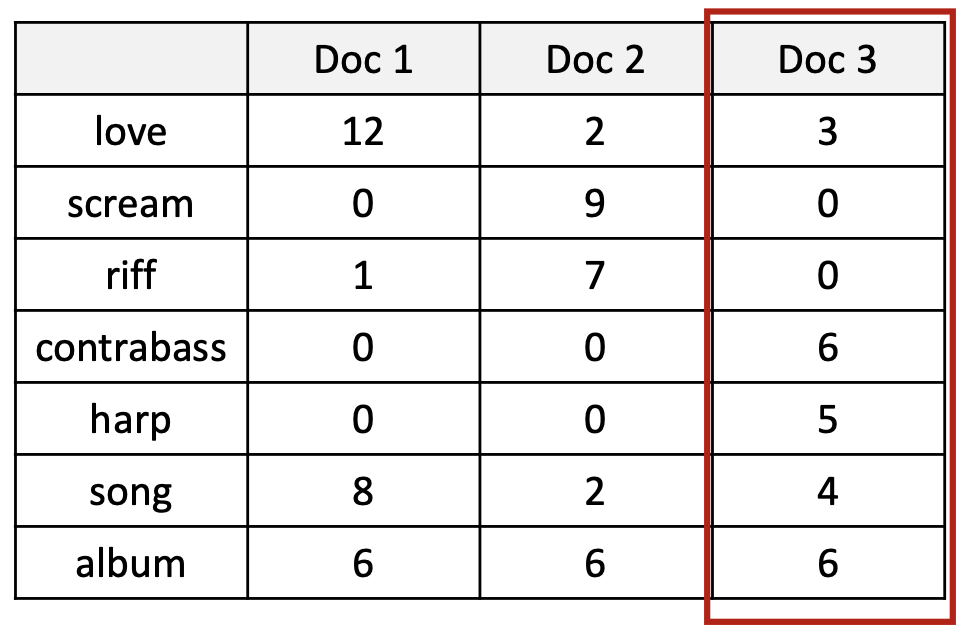
image

  • 비교: album과 singer에 비해, contrabass와 piano는 문서 3(Document 3)을 더 독특하게 나타낸다.
  • 이유는?

p23. 역문서 빈도 (IDF, Inverse Document Frequency)

✓ 역문서 빈도 $idf_t$

  • IDF는 각 단어 $t$가 모든 문서에서 얼마나 드물게 등장하는지에 따라 점수를 매긴다.
  • 가장 일반적인 형태는 로그 스케일(log-scaled) 이다:
\[idf_t = \log_{10}\left(\frac{N}{df_t}\right)\]
  • $N$ : 전체 문서의 개수 (total number of documents)

  • $df_t$ : 단어 $t$가 등장한 문서의 개수 (number of documents containing term $t$)

  • 예시 (Example):

    • 전체 문서 수 $N = 1,000$

    • 단어 “album” 은 300개 문서에 등장

      \[idf_{album} = \log_{10}\left(\frac{1000}{300}\right) = \log_{10}(3.33) \approx 0.52\]

    • 단어 “singer” 는 200개 문서에 등장

      \[idf_{singer} = \log_{10}\left(\frac{1000}{200}\right) = \log_{10}(5) \approx 0.70\]

    • 단어 “piano” 는 20개 문서에 등장

      \[idf_{piano} = \log_{10}\left(\frac{1000}{20}\right) = \log_{10}(50) \approx 1.70\]

    • 단어 “contrabass” 는 5개 문서에 등장

      \[idf_{contrabass} = \log_{10}\left(\frac{1000}{5}\right) = \log_{10}(200) \approx 2.30\]

p26. TF-IDF 가중치: 예시

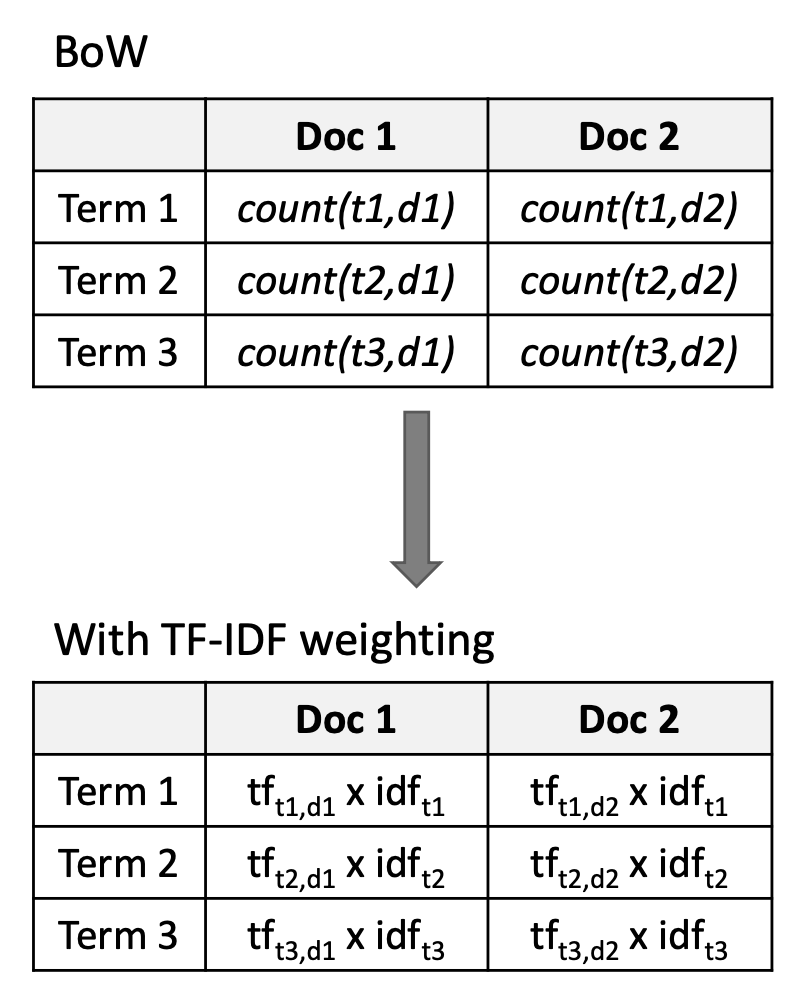
  • BoW 표현
    단어의 등장 횟수로만 문서를 표현한다.

    image

  • TF-IDF 표현
    단어의 등장 빈도(TF, Term Frequency)와 역문서빈도(IDF, Inverse Document Frequency)를 곱하여
    문서를 실수 값 벡터로 표현한다.

    image

  • 핵심 설명

    • 이제 각 문서는 TF-IDF 가중치로 이루어진 실수 벡터 $\in \mathbb{R}^{ \mid V \mid }$ 로 표현된다.
    • BoW와 달리, TF-IDF는 흔한 단어의 중요도를 낮추고, 문서를 구분하는 단어를 강조한다.

1. 각 단어의 $idf_t$ 계산

단어등장 문서 수 ($df_t$)$idf_t=\log_{10}(N/df_t)$결과
love3$\log_{10}(3/3)=0$0
scream1$\log_{10}(3/1)=0.477$0.477
riff2$\log_{10}(3/2)=0.176$0.176
contrabass1$\log_{10}(3/1)=0.477$0.477
harp1$\log_{10}(3/1)=0.477$0.477
song3$\log_{10}(3/3)=0$0
album3$\log_{10}(3/3)=0$0

→ love, song, album 은 모든 문서에 등장하므로 IDF = 0 → 중요도 0

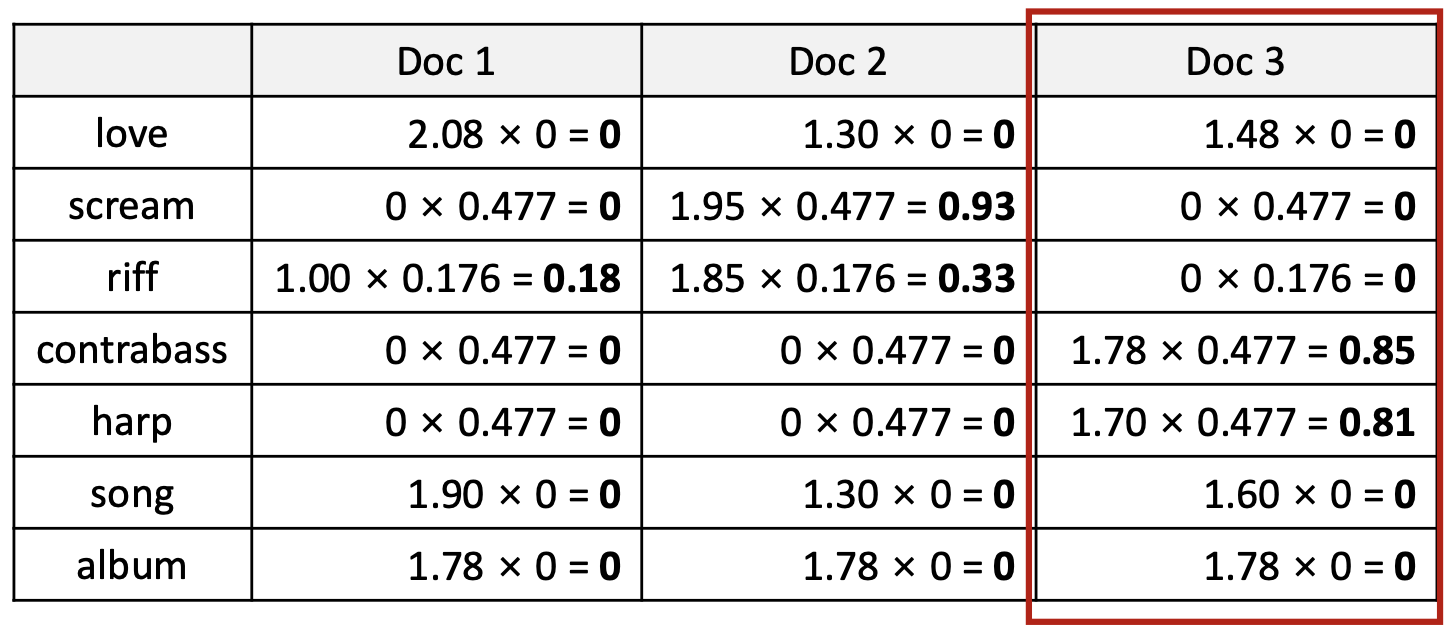
2. 각 단어의 $tf_{t,d}$ 계산

  • 예시:
    \(tf_{love,Doc1} = 1 + \log_{10}(12) = 1 + 1.08 = 2.08\)

  • 같은 방식으로 계산한 결과:

단어Doc1Doc2Doc3
love2.081.301.48
scream01.950
riff1.001.850
contrabass001.78
harp001.70
song1.901.301.60
album1.781.781.78

희소 표현(sparse representation)을 활용한 벡터 공간 모델(Vector Space Model)

image

p28. 희소 표현(sparse representation)의 유사성

  • 쿼리(query)와 문서(document)의 유사성 계산
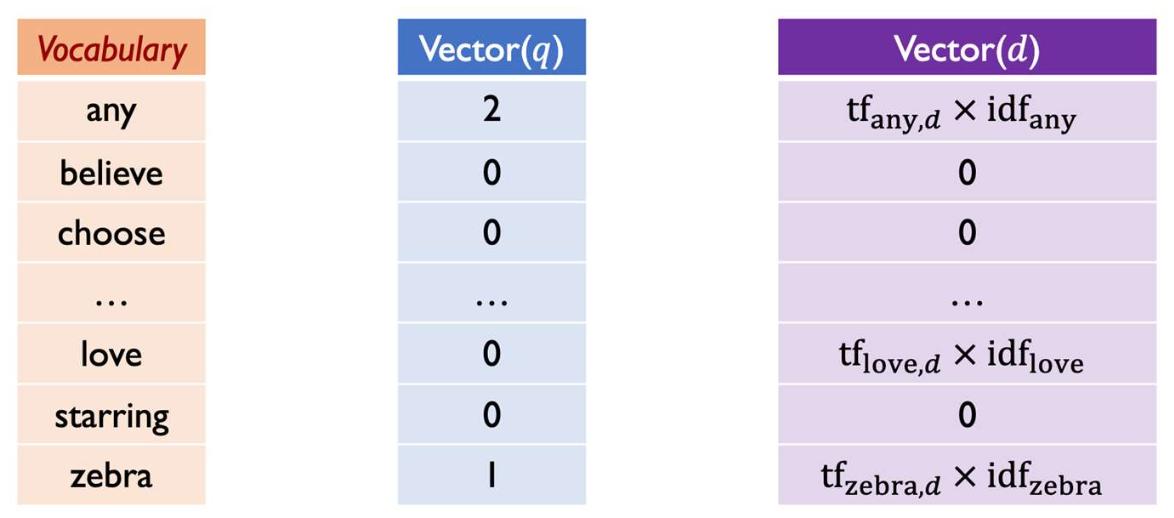
    쿼리 $q$와 문서 $d$가 주어졌을 때, 희소 표현(sparse representation)을 기반으로 유사성을 계산한다.

    • 쿼리 $q$: 단어 $t$의 각 항목은 $tf_{t,q}$
    • 문서 $d$: 단어 $t$의 각 항목은 $tf_{t,d} \times idf_t$
  • 주의 (Note)
    쿼리에 IDF를 적용하지 않는 것이 표준 관례이다.
    • 쿼리는 일반적으로 매우 짧으며, 소수의 단어만 포함한다.
    • IDF를 적용하면 이러한 단어들의 가중치가 과도하게 낮아져, 쿼리 표현의 효과성이 줄어든다.
  • 예시 (Example)
    • 쿼리 $q$: "any any zebra"
    • 문서 $d$: "zebra any love any zebra"

    image

단순화를 위해, 위 그림에서는 원시 빈도(raw counts)를 $tf$로 표시한다.

p29. 희소 표현(sparse representation)의 유사성

  • 예시 (Example)
    • 쿼리 $q$: "any any zebra"
    • 문서 $d$: "zebra any love any zebra"

    image

  • 문제 (Question)
    Vector($q$)와 Vector($d$)의 내적(inner product)은 무엇인가?

  • 계산 과정
\[\text{Vector}(q) \cdot \text{Vector}(d) = 2 \times tf_{any,d} \times idf_{any} + 1 \times tf_{zebra,d} \times idf_{zebra}\] \[= tf_{any,d} \times idf_{any} + tf_{any,d} \times idf_{any} + tf_{zebra,d} \times idf_{zebra}\] \[= \sum_{t \in q} (tf_{t,d} \times idf_t)\]

p30. 내적(inner product)의 문제점

  • 예시 (Example)
    • 쿼리 $q$: "any any zebra"
    • 문서 $d_1$: "zebra any love any zebra"
    • 문서 $d_2$: "zebra any love any zebra zebra any love any zebra" (2번 반복)

    image

  • 쿼리 $q$는 동일하지만, 문서 $d_2$는 단순히 $d_1$을 두 번 반복한 형태일 뿐이다.
  • 그러나 내적(inner product)은 단어 등장 횟수(tf)에 직접 비례하므로
    $d_2$의 벡터 값은 $d_1$의 벡터 값보다 정확히 2배가 된다.
  • 이 때문에 문서의 길이 차이(length difference) 로 인해
    실제 의미적 유사도와 상관없이 유사도가 왜곡될 수 있다.

p31. 내적(inner product)의 문제점

  • 예시 (Example)
    • 쿼리 $q$: "any any zebra"
    • 문서 $d_1$: "zebra any love any zebra"
    • 문서 $d_2$: "zebra any love any zebra zebra any love any zebra" (2회 반복)
    • 문서 $d_{100}$: "zebra any love any zebra zebra any love any zebra ..." (100회 반복)

    image

  • 문서 $d_{100}$ 은 단순히 $d_1$ 의 내용을 100번 반복한 것에 불과하다.
  • 그러나 내적(inner product)을 계산하면 $d_{100}$ 의 벡터는 $d_1$ 벡터의 모든 항이 100배로 증가한다.
  • 그 결과, 문서의 길이가 길어질수록 실제 내용적 차이가 없음에도
    쿼리와의 유사도가 과대평가된다.
  • 따라서 단순한 내적은 문서 길이에 매우 민감하게 반응한다는 문제가 있다.

p32. 내적(inner product)의 문제점

  • 예시 (Example)
    • 쿼리 $q$: "any any zebra"
    • 문서 $d_1$: "zebra any love any zebra"
    • 문서 $d_2$: "zebra any love any zebra zebra any love any zebra" (2회 반복)
    • 문서 $d_{100}$: "zebra any love any zebra zebra any love any zebra ..." (100회 반복)
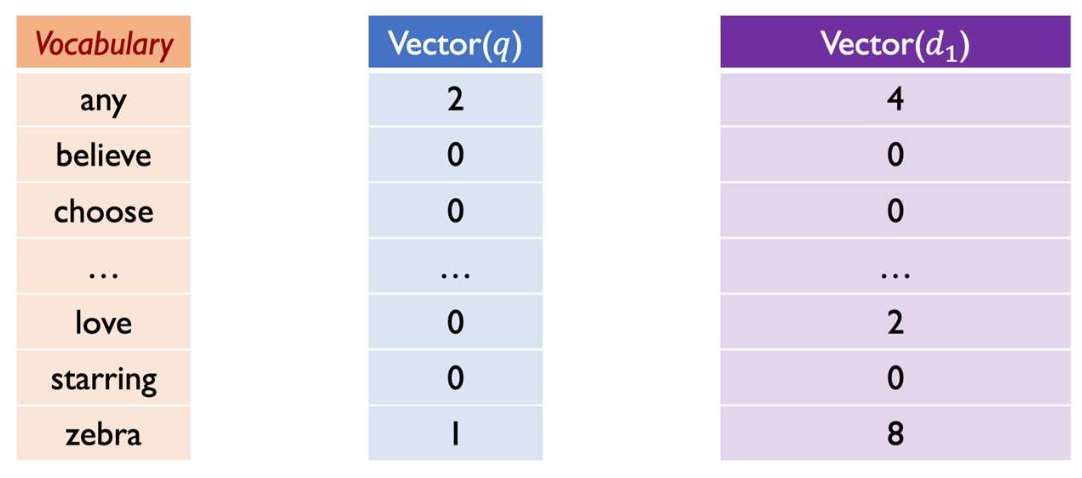
  • 수식 관계
    • $\text{Vector}(d_2) = 2 \, \text{Vector}(d_1)$

    • $\text{Vector}(q) \cdot \text{Vector}(d_2) = 2 \, \text{Vector}(q) \cdot \text{Vector}(d_1)$

    • $\text{Vector}(d_{100}) = 100 \, \text{Vector}(d_1)$
    • $\text{Vector}(q) \cdot \text{Vector}(d_{100}) = 100 \, \text{Vector}(q) \cdot \text{Vector}(d_1)$
  • 우리는 문서 $d$의 길이를 단순히 늘림으로써, 쿼리 $q$와 문서 $d$의 내적을 원하는 만큼 크게 만들 수 있다!

p33. 간단한 해결책: 코사인 유사도(Cosine similarity)

  • 이는 먼저 벡터를 단위 길이(unit length)로 정규화(normalizing) 한 다음,
    내적(dot product)을 계산하는 것과 동일하다.

  • 정의:

\[\mathbf{x} = [x_1, x_2, \ldots, x_N], \quad \mathbf{y} = [y_1, y_2, \ldots, y_N]\] \[\cos(\mathbf{x}, \mathbf{y}) = \frac{x_1 y_1 + x_2 y_2 + \cdots + x_N y_N}{\sqrt{x_1^2 + x_2^2 + \cdots + x_N^2} \times \sqrt{y_1^2 + y_2^2 + \cdots + y_N^2}} = \frac{\mathbf{x} \cdot \mathbf{y}}{\|\mathbf{x}\| \cdot \|\mathbf{y}\|} = \left(\frac{\mathbf{x}}{\|\mathbf{x}\|}\right) \cdot \left(\frac{\mathbf{y}}{\|\mathbf{y}\|}\right)\]

  • $\mathbf{x}$, $2\mathbf{x}$, $100\mathbf{x}$는 길이 정규화를 거치면 동일한 벡터가 된다.

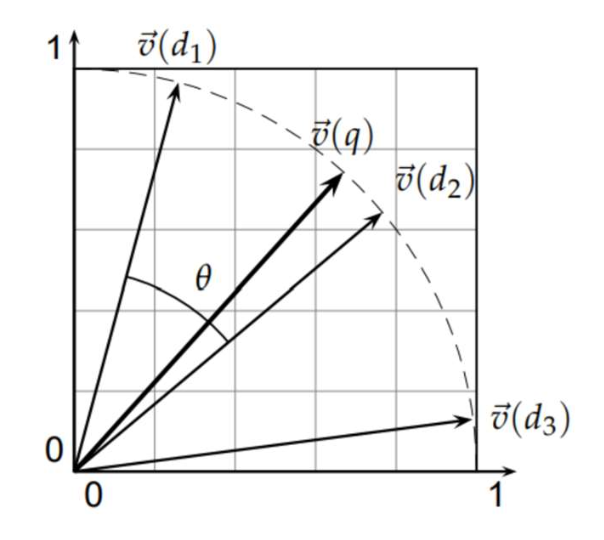
  • 코사인 유사도 값이 클수록 두 단위 벡터(unit vector) 사이의 각도는 작아지고,
    이는 곧 두 벡터가 더 “유사(similar)”하다는 것을 의미한다.

image

p34. 간단한 해결책: 코사인 유사도(Cosine similarity)

  • 요약하면, 희소 벡터(sparse vectors) 를 다룰 때는
    코사인 유사도(cosine similarity) 를 사용한다!

  • 희소 벡터(sparse vector)는 고차원(high-dimensional) 구조이며,
    차원 수는 어휘집(vocabulary)의 크기와 동일하다.

  • 더 긴 문서(longer documents)는 더 많은 단어(terms)와 더 큰 빈도(counts)를 포함하므로
    벡터 크기(vector magnitudes) 가 더 커지는 경향이 있다.

  • 코사인 유사도는 벡터들 사이의 각(angle) 을 비교한다.
    → 따라서 문서 길이(document length)에 대해 강건(robust) 한 유사도 측정을 가능하게 한다.

image

  • 계산 과정:
\[\|Vector(q)\| = \sqrt{2^2 + 1^2} = \sqrt{5}\] \[\|Vector(d_1)\| = \sqrt{4^2 + 2^2 + 8^2} = \sqrt{84}\] \[\cos(Vector(q), Vector(d_1)) = \frac{2 \times 4 + 0 \times 2 + 1 \times 8}{\sqrt{5} \times \sqrt{84}} \approx 0.781\]

p35. 복습: 희소 표현(Sparse representations)

  • BoW 표현
    문서(Document)와 단어(Term) 출현 빈도를 행렬로 표현한다.

    image

  • TF-IDF 표현
    단어의 빈도(frequency) 정보를 바탕으로 문서와 단어를 표현한다.

    image

  • 비교 요약

    • BoW와 TF-IDF는 둘 다 단어 빈도 정보를 기반으로 문서와 단어를 표현한다.
    • 그러나 BoW와 달리, TF-IDF는 자주 등장하는 단어(common words)의 가중치를 줄이고(downweights),
      문서를 구별하는 단어(terms that distinguish documents)를 강조(highlights)       한다.

p37. 복습: 희소 표현(Sparse representations)

  • 우리는 문서를 희소 벡터(sparse vectors)로 표현하는 방법과, 이들의 유사도를 계산하는 방법을 학습했다.

  • 장점:
    • 단순하고 계산하기 쉽다.
    • 작은/중간 규모의 어휘(vocabularies)에 효율적이다.
  • 단점:
    • 높은 차원(High dimensionality):
      • 어휘 크기가 쉽게 100k(10만)를 초과할 수 있다.
      • 이는 비효율적인 표현으로 이어진다.
    • 평탄화된 텍스트 뷰(Flattened view of text):
      • 문장의 구조와 단어 순서를 무시한다.
      • 예: “the horse ate” = “ate the horse” 로 처리된다.
    • 문맥에 둔감(Context-insensitive):
      • 단어의 의미 구분(word senses)을 하지 못한다.
      • 예: “bank” (강둑, river) vs. “bank” (금융, finance)를 동일한 토큰으로 취급한다.

image

p38. 다음: 밀집 표현 (Dense representations)

  • 희소 표현(sparse representation)에서 밀집 표현(dense representation)으로

    • 희소 벡터(sparse vectors): 매우 길다 (길이 = $ \mid V \mid $, 종종 10k 이상), 대부분의 항목 값 = 0
    • 밀집 벡터(dense vectors): 상대적으로 짧다 (50–1000 차원), 대부분의 항목 값 ≠ 0
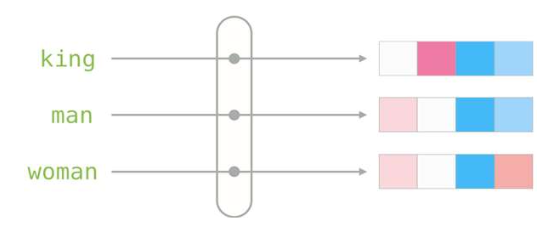
  • 정적 임베딩(Static embeddings)
    • 각 단어는 하나의 고정된 밀집 벡터(single fixed dense vector) 로 할당된다.
    • 주변 문맥(context)을 반영하지 않는다.
      • 예: “bank” → 항상 같은 벡터
    • 예시: Word2vec, GloVe

    image

  • 문맥 임베딩(Contextual embeddings)
    • 각 단어의 벡터는 주변 문맥(surrounding context) 에 따라 달라진다.
    • 단어의 의미가 문맥에 따라 변한다.
      • 예: “bank of the river” vs. “bank account”
    • 예시: BERT, LLM 기반 임베딩

    image

대학원 수업, 텍스트 마이닝
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.