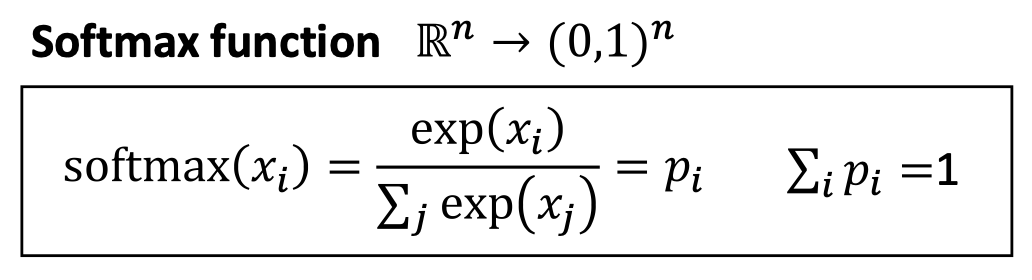포스트

[텍스트 마이닝] 6. Representing Texts with Vectors 2

게시 업데이트
By 김성진
37 분읽는 시간
[텍스트 마이닝] 6. Representing Texts with Vectors 2

밀집 고정 표현 (Dense static representation)

  • 간단히 하기 위해, 우리는 제품 설명(예: 제목, 특징)을 문서로 지칭한다.

p13. 문맥에 의한 단어 표현

  • 우리가 단어들을 벡터로 표현할 수 있다면, 어떤 텍스트든 그것들을 집계하여 벡터로 표현할 수 있다.

  • 분포 가설 (Distributional hypothesis)

    • 비슷한 문맥(context)에서 발생하는 단어들은 비슷한 의미를 가지는 경향이 있다.
    • 단어의 의미는 그것이 나타나는 문맥에 의해 크게 정의된다.

image

  • 예시: 우리가 “Ong choy”의 의미를 모른다고 가정하지만, 다음과 같은 문장을 본다고 하자:
    • Ong choy는 마늘과 함께 볶으면(sautéed with garlic) 맛있다.
    • Ong choy는 밥 위에(over rice) 얹으면 훌륭하다.
    • Ong choy는 잎(leaves)과 짠(salty) 소스와 함께한다.
  • 그리고 우리는 다음과 같은 문맥들을 보았다:
    • … 시금치가 마늘과 함께 볶아져 밥 위에(sautéed with garlic over rice) 올라간다.
    • … 근대 줄기와 잎(leaves)은 맛있다.
    • … 콜라드 그린과 다른 짠(salty) 잎채소들.
  • 이러한 문맥들로부터 우리는 다음을 추론할 수 있다:
    • Ong choy == water spinach (워터 스피니치, 즉 모닝글로리/공심채).

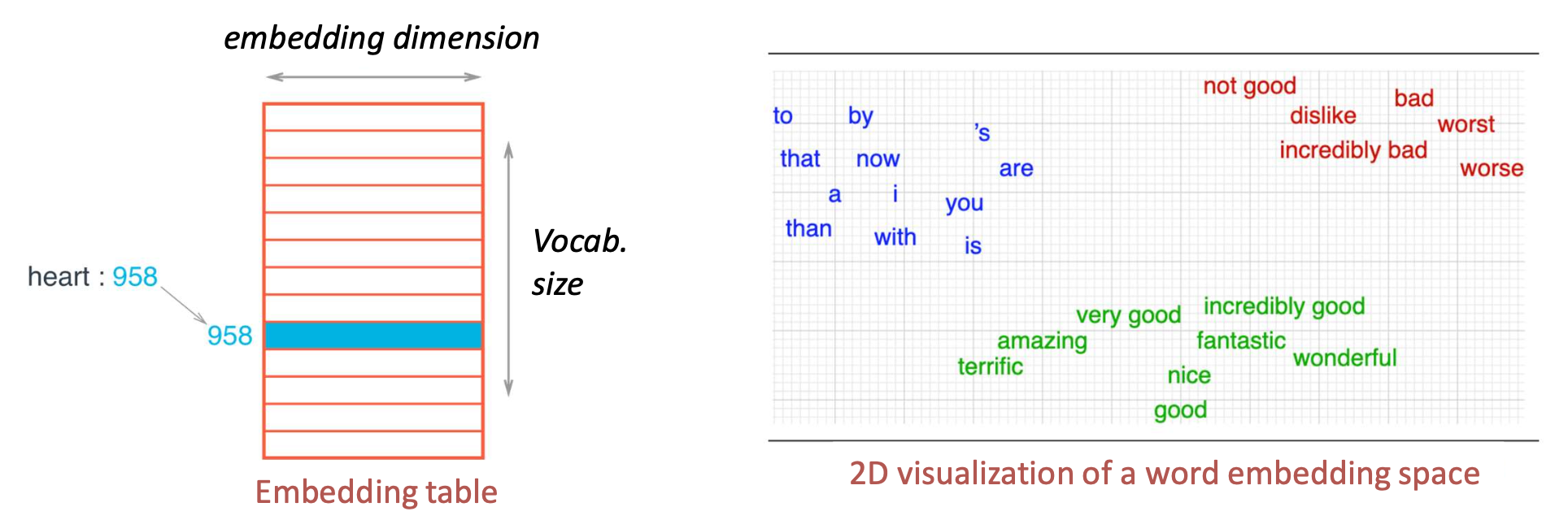
p14. 단어 임베딩: 일반적인 아이디어 (Word embeddings: general idea)

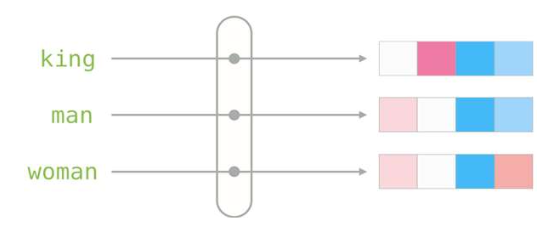
  • 목표는 분포 가설(distributional hypothesis) 에 기반하여 단어들의 밀집 벡터 표현(dense vector representations of words) 을 얻는 것이다.
    • 의미적으로 유사한 단어들(즉, 비슷한 문맥에서 발생하는 단어들)은 유사한 벡터 표현을 가지게 된다.
  • 단어 임베딩(word embeddings): 각 행이 하나의 단어에 대한 밀집 벡터에 대응하는 행렬.
    • 이는 한 공간(어휘, vocabulary)의 원소들을 다른 공간(벡터 공간, vector space)에서 표현하는 사상(mapping)으로 볼 수 있다.

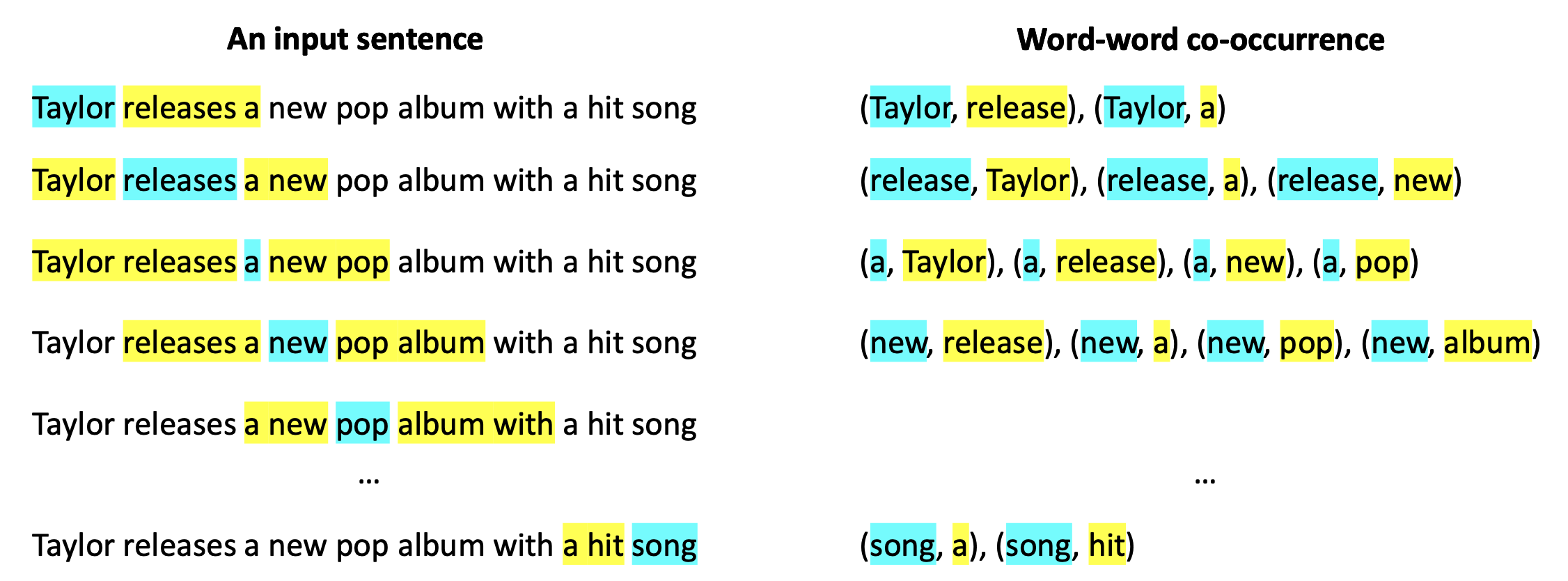
image

p15. 단어-문맥 정보 구성 (Constructing word-context information)

  • 우리는 단어가 문맥 윈도우(context window) 안에서 다른 단어와 함께 얼마나 자주 나타나는지를 센다.
    • 윈도우 크기: 타깃 단어(target word)의 좌우에 있는 문맥 단어(context words)의 최대 개수
    • 예시 (window size = 2)

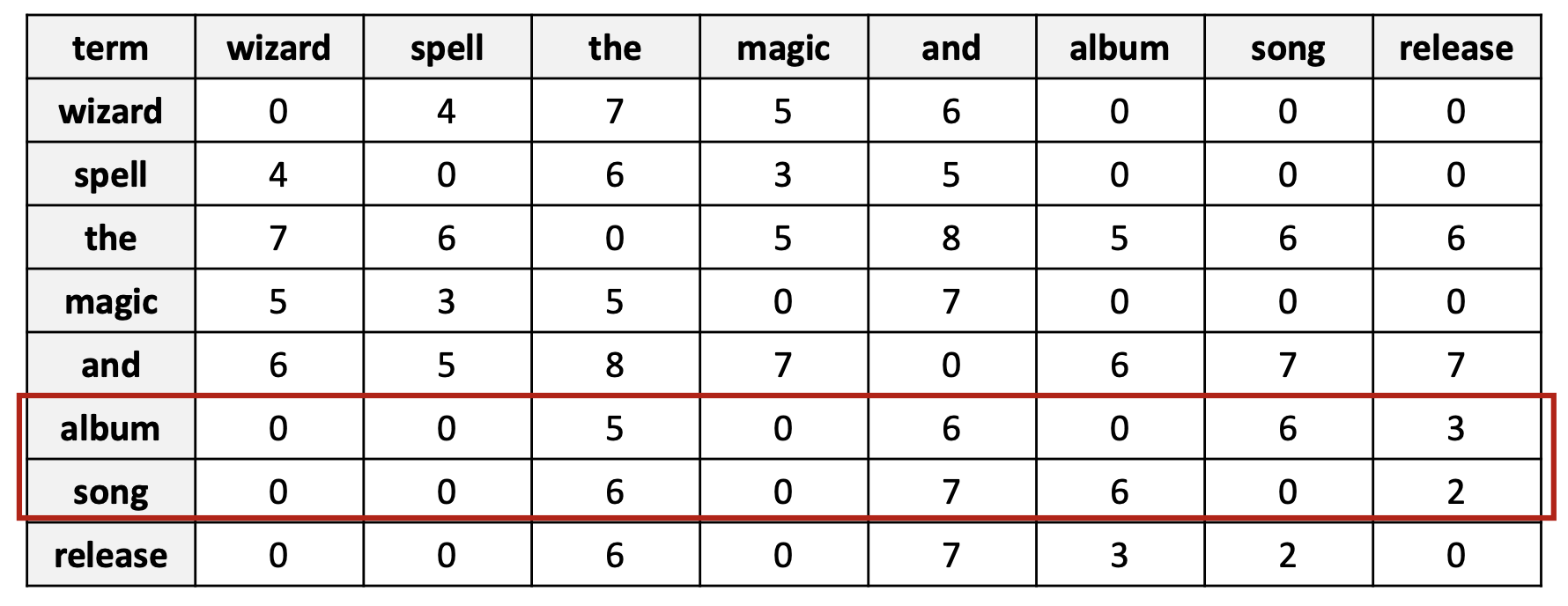
image

p17. 단어-문맥 정보 구성 (Constructing word-context information)

  • 공동 발생(co-occurrence) 횟수를 기반으로, 단어-단어 공동 발생 행렬(word-word co-occurrence matrix) 을 만든다.
    • 이 행렬의 크기는 $V \times V$이며, 여기서 $V$는 어휘집(vocabulary) 크기이다.
    • 각 항목은 문맥 윈도우(context window) 안에서 한 단어(행, row)가 다른 단어(열, column)와 함께 얼마나 자주 나타나는지를 센다.

image

이 벡터는 분포 가설(distributional hypothesis)을 반영한다:
의미적으로 유사한 단어들은 유사한 표현을 가진다.
그러나, 이 표현은 희소(sparse)하고 차원이 너무 높다(high-dimensional)!

p18. 밀집 단어 임베딩 생성 (Generating dense word embeddings)

  • 이제, 어떻게 이 크고 희소한 행렬을 밀집 단어 임베딩으로 바꿀 수 있을까?

  • 우리는 두 가지 접근법을 논의할 것이다:

  1. 차원 축소 (Dimensionality reduction)
    • 공동 발생 행렬(co-occurrence matrix)을 정규화한 후, truncated SVD를 적용하여 차원을 축소한다.
    • 각 행(필요에 따라 특이값(singular values)으로 스케일링됨)은 단어 임베딩으로 사용된다.
  2. 스킵그램 학습 (Skip-gram learning)
    • 행렬 분해(matrix factorization)를 수행하는 대신, 단어-문맥 쌍(word–context pairs)으로부터 직접 임베딩을 학습한다.
    • 주어진 타깃 단어의 문맥 단어들을 예측하는 모델을 학습한다.
    • Word2Vec으로 구현된다.
  • 실제로, 이 두 가지 접근법은 수학적으로 동등한 것으로 볼 수 있다.¹

¹ Neural Word Embedding as Implicit Matrix Factorization, NeurIPS, 2014

p19. 접근법 1: 차원 축소

  • 핵심 아이디어: 각 희소 벡터(sparse vector)를 저차원 공간으로 사영(projection)하되, 정보를 보존하면서 수행한다.

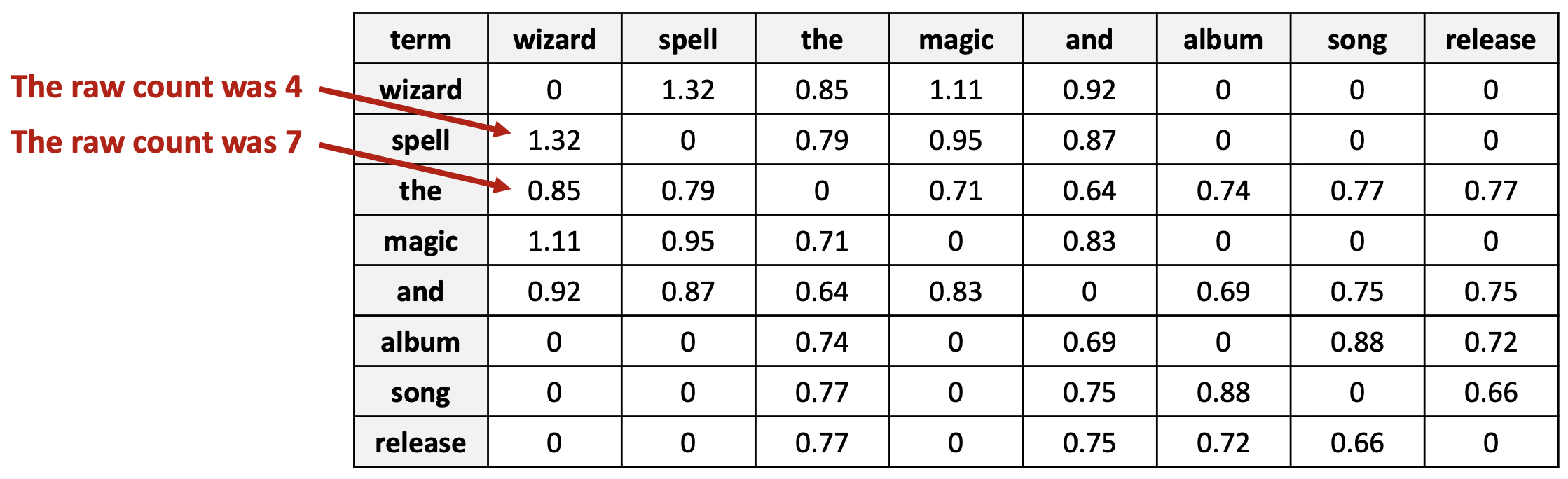
A. PMI (점별 상호정보량, Pointwise Mutual Information) 재가중치(re-weighting)

  • 앞서 논의했듯이, 단순 빈도(raw frequency)는 의미론을 잘 반영하지 못한다.
    • 일반적으로 자주 쓰이는 단어들(예: the, it)은 거의 정보를 제공하지 않는다.
  • PMI는 다음을 묻는다:
    단어 $w_1$ 과 $w_2$ 는 우연보다 더 자주 함께 등장하는가?
\[PMI(w_1, w_2) = \log \frac{P(w_1, w_2)}{P(w_1) P(w_2)}\] \[P(w_1, w_2) = \frac{\text{count}(w_1, w_2)}{N}\] \[P(w_1) = \frac{\text{count}(w_1)}{N}, \quad P(w_2) = \frac{\text{count}(w_2)}{N}\]
  • $N$: 모든 문맥 윈도우(context window)에서의 단어 쌍의 총 개수
  • $\text{count}(w_1, w_2)$: $w_1$ 과 $w_2$ 가 함께 등장한 횟수

  • $\text{count}(w)$: 단어 $w$ 가 등장한 횟수

  • $N$: 모든 문맥 윈도우에서의 단어 쌍의 총 개수
  • $\text{count}(w_1, w_2)$: $w_1$ 과 $w_2$ 가 함께 등장한 횟수
  • $\text{count}(w)$: 단어 $w$ 가 등장한 횟수

PMI(Pointwise Mutual Information)의 의미

  • PMI는 두 단어가 우연히 동시에 등장할 확률보다 실제로 얼마나 더 자주 함께 등장하는지를 측정하는 지표이다.

    \[PMI(w_1, w_2) = \log \frac{P(w_1, w_2)}{P(w_1)P(w_2)}\]
  • 분모 $P(w_1)P(w_2)$ 는 두 단어가 서로 독립일 때 공동으로 등장할 확률이다.
  • 분자 $P(w_1, w_2)$ 는 실제 문서에서 관찰된 공동 등장 확률(joint probability) 이다.

따라서

  • $PMI > 0$: 실제로 두 단어가 독립적일 때보다 더 자주 함께 등장한다.
  • $PMI < 0$: 두 단어가 거의 함께 등장하지 않는다는 뜻이다.

p20. 접근법 1: 차원 축소

  • 핵심 아이디어: 각 희소 벡터(sparse vector)를 저차원 공간으로 사영(projection)하되, 정보를 보존하면서 수행한다.

A. PMI (점별 상호정보량, Pointwise Mutual Information) 재가중치

\[PMI(w_1, w_2) = \log \frac{P(w_1, w_2)}{P(w_1) P(w_2)}\]

image

  • 관례적으로, $PMI < 0$ 인 값은 0으로 표기된다(clipped).

p21. 접근법 1: 차원 축소

  • 핵심 아이디어: 각 희소 벡터(sparse vector)를 저차원 공간으로 사영(projection)하되, 정보를 보존하면서 수행한다.

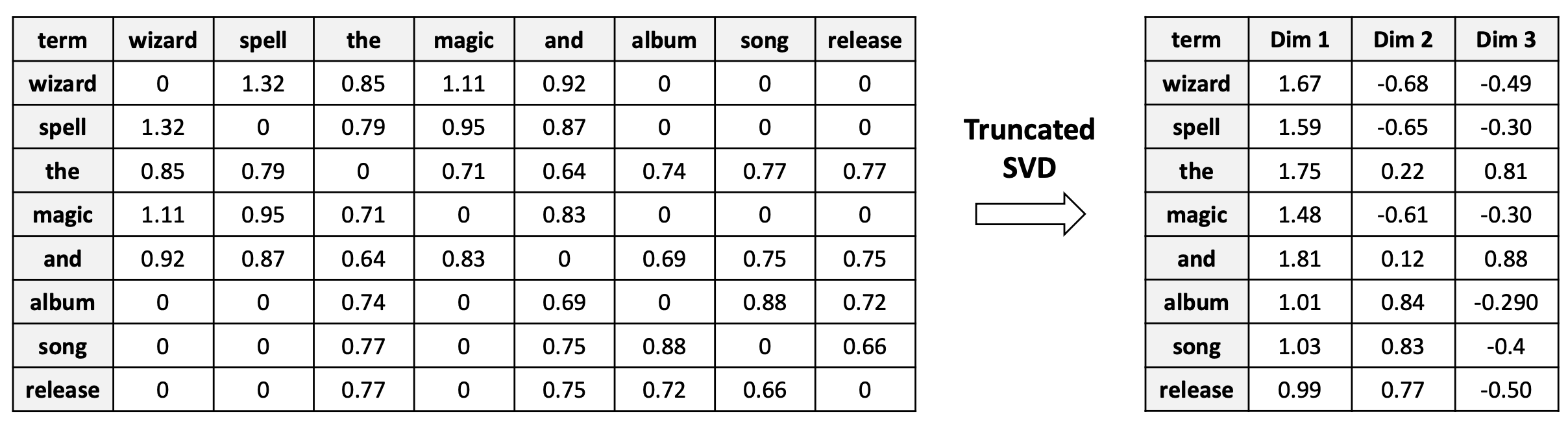
B. truncated SVD에 의한 차원 축소 (Dimensionality reduction by truncated SVD)

  • 축소된 행렬의 각 행(row)은 해당 단어(term)의 단어 임베딩(word embedding)이 된다.

image

  • $V \times V$ 희소 행렬(sparse matrix)
  • $V \times k$ 밀집 행렬(dense matrix)

우측 테이블이 단어의 임베딩 행렬(Embedding matrix)이 된다

p22. 배경 지식: 차원 축소

  • 차원 축소에 대한 직관적인 이해:
    • 원래 행렬의 값들이 그렇게 나타나는 이유를 근사적으로 설명해주는 숨겨진(latent) 차원들이 존재한다.

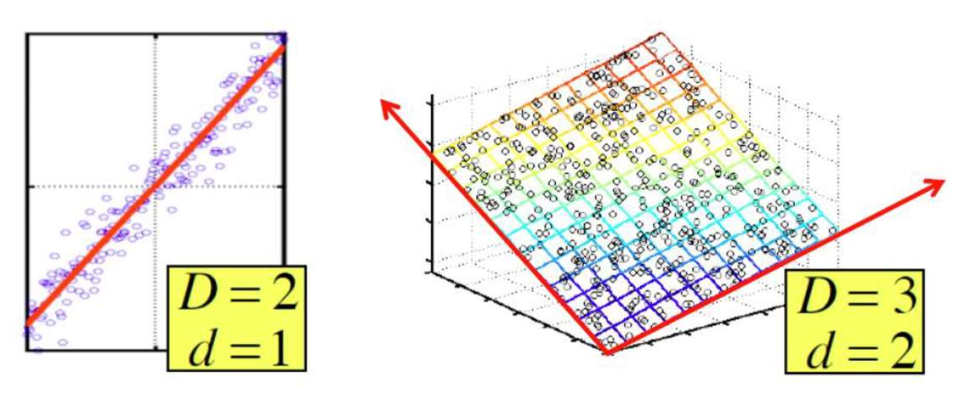
image

  • 이 차원들의 축(axes of these dimensions) 은 다음과 같이 선택될 수 있다:
    • 첫 번째 차원은 데이터가 가장 큰 분산(greatest variance) 을 보이는 방향이다.
    • 두 번째 차원은 첫 번째 차원과 직교하며, 두 번째로 큰 분산(second greatest variance) 을 포착한다.
    • 그리고 계속된다 (and so on).
  • Truncated SVD는 원래 행렬을 근사할 수 있도록 하며, 데이터를 설명하는 가장 중요한 분산을 포착하는 몇 개의 잠재 차원(latent dimensions)에 사영(projection)한다.

p23. 배경 지식: Truncated SVD

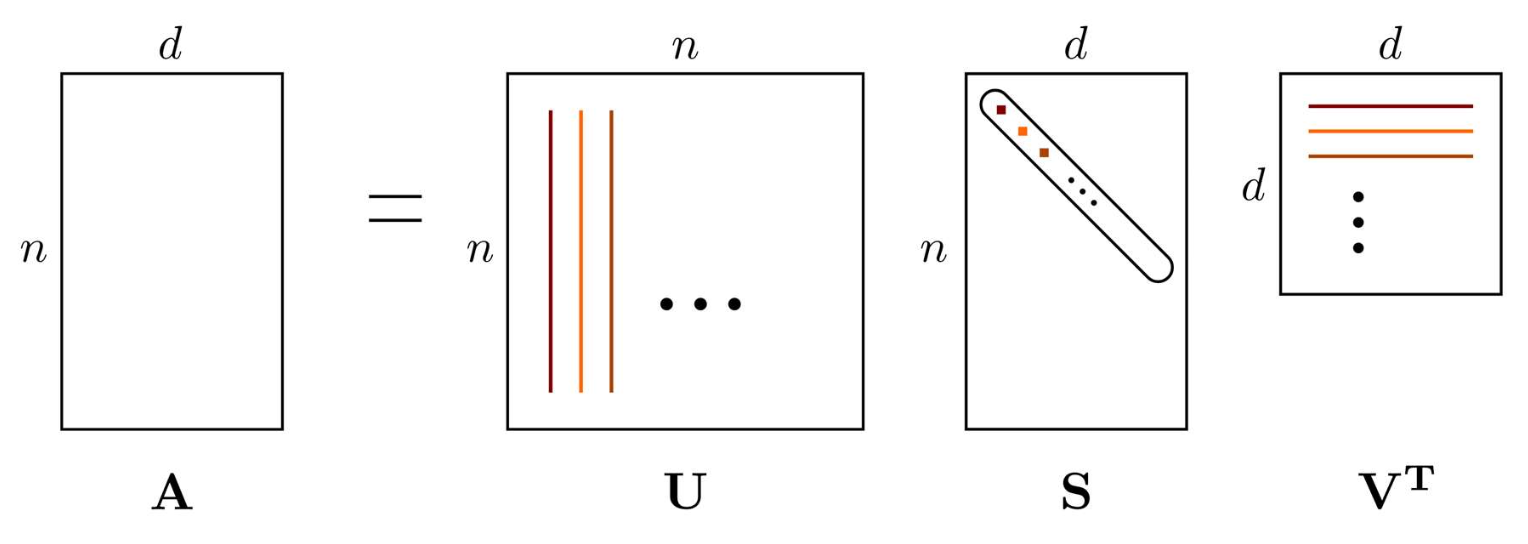
  • 특이값 분해(SVD, Singular Value Decomposition):
    데이터가 $n \times d$ 행렬 $A$로 표현될 때, 이는 세 개의 ‘단순한(simple)’ 행렬의 곱으로 나타낼 수 있다.
\[A = U S V^T\]

image

  • $n$: 데이터 인스턴스(data instances)의 개수
  • $d$: 원래 특성(original features)의 개수

SVD는 선형대수학 강의에서 다루어지는 내용이다. 혹시 잊었다면, 다음 참고 문헌을 보라 (for review):
Stanford CS168 강의노트

p24. 배경 지식: Truncated SVD

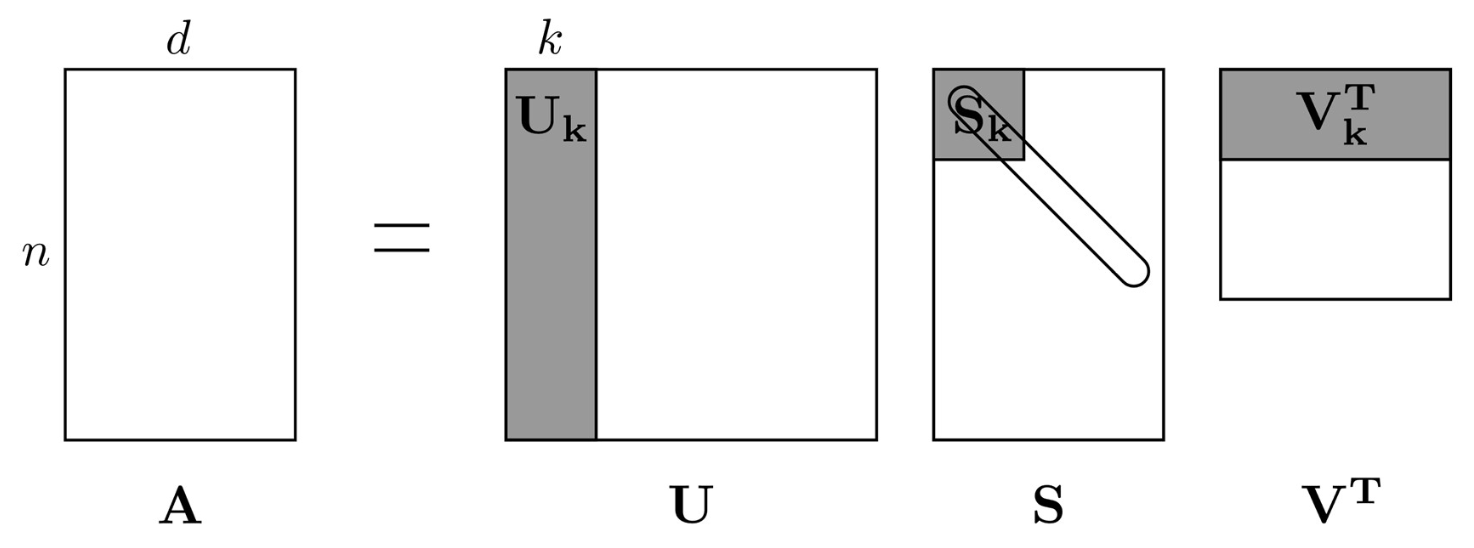
  • Truncated SVD:
    행렬 $A$는 세 개의 행렬 곱으로 가깝게 근사될 수 있다 (closely approximated).
    이때 세 행렬은 더 작은 공통 차원 $k$를 공유한다.
\[A \approx U_k S_k V_k^T\]

image

  • $n$: 데이터 인스턴스(data instances)의 개수
  • $d$: 원래 특성(original features)의 개수
  • $k$: 유지되는 잠재(latent) 차원의 개수 ($k < d$)

p25. 배경 지식: Truncated SVD

  • Truncated SVD: 행렬 A는 더 작은 공통 차원(k)을 공유하는 세 개의 행렬 곱으로 가까이 근사(closely approximated) 될 수 있다.

  • 예시 (Example):

image

p26. 밀집 단어 임베딩 생성 (Generating dense word embeddings)

  • 이제, 어떻게 이 크고 희소한 행렬을 밀집 단어 임베딩으로 변환할 수 있을까?

  • 우리는 두 가지 접근 방식을 논의할 것이다:

  1. 차원 축소 (Dimensionality reduction)
    • 동시발생 행렬(co-occurrence matrix)을 정규화한 후, Truncated SVD를 적용하여 차원을 축소한다.
    • 각 행은 (선택적으로 특이값으로 스케일된) 단어 임베딩으로 사용된다.
  2. Skip-gram 학습
    • 행렬을 인수분해하는 대신, 단어-문맥 쌍(word–context pairs)으로부터 직접 임베딩을 학습한다.
    • 주어진 목표 단어(target word)의 문맥 단어(context words)를 예측하는 모델을 훈련한다.
    • Word2Vec으로 구현된다.
  • 실제로, 이 두 가지 접근법은 수학적으로 동등한 것으로 볼 수 있다.¹

¹ Neural Word Embedding as Implicit Matrix Factorization, NeurIPS, 2014

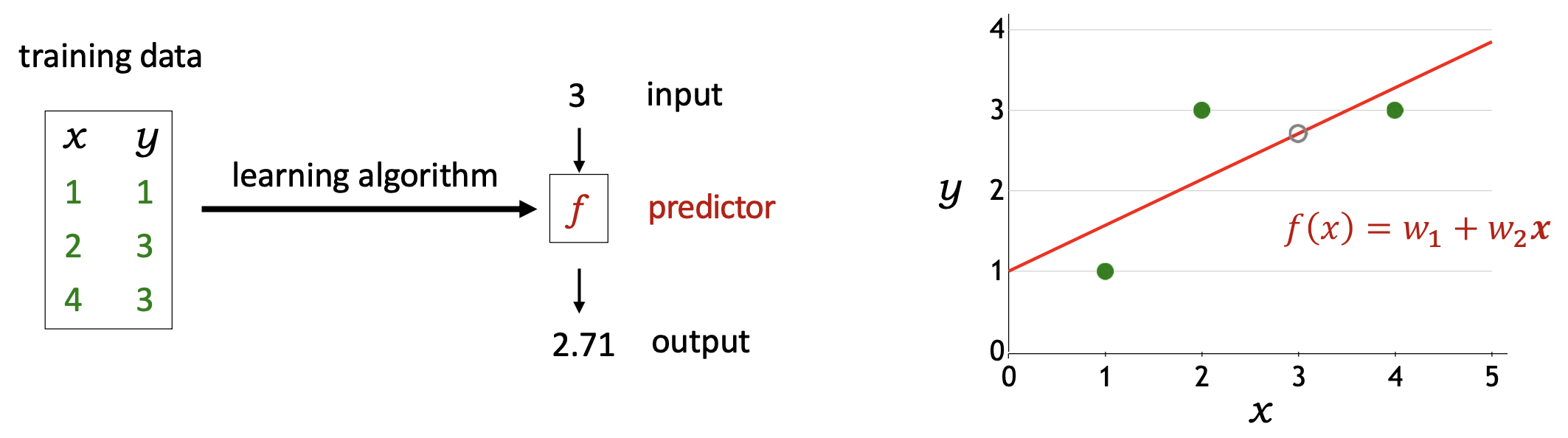
p27. 복습: 모델, 손실 함수, 최적화

image

  • 어떤 예측기(predictors)가 가능한가?

    • 가설 집합 (Hypothesis class)

      \[\mathcal{F} = \{ f_{\mathbf{w}}(x) = \mathbf{w} \cdot \varphi(x) \}\]
  • 예측기가 얼마나 좋은가?

    • 손실 함수 (Loss function)

      \[Loss(x, y, \mathbf{w}) = (f_{\mathbf{w}}(x) - y)^2\]
  • 예측기를 어떻게 최적화할 것인가?

    • 경사 하강법 (Gradient descent)

      \[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} \, TrainLoss(\mathbf{w})\]

p28. 접근 방식 2: Skip-gram 학습

  • 핵심 아이디어 (Key idea):
    맥락 단어들(the context words)을
    중심 단어(the center word)를 사용하여 예측한다.
    (의미적으로 유사한 중심 단어들은 유사한 맥락 단어들을 예측한다.)

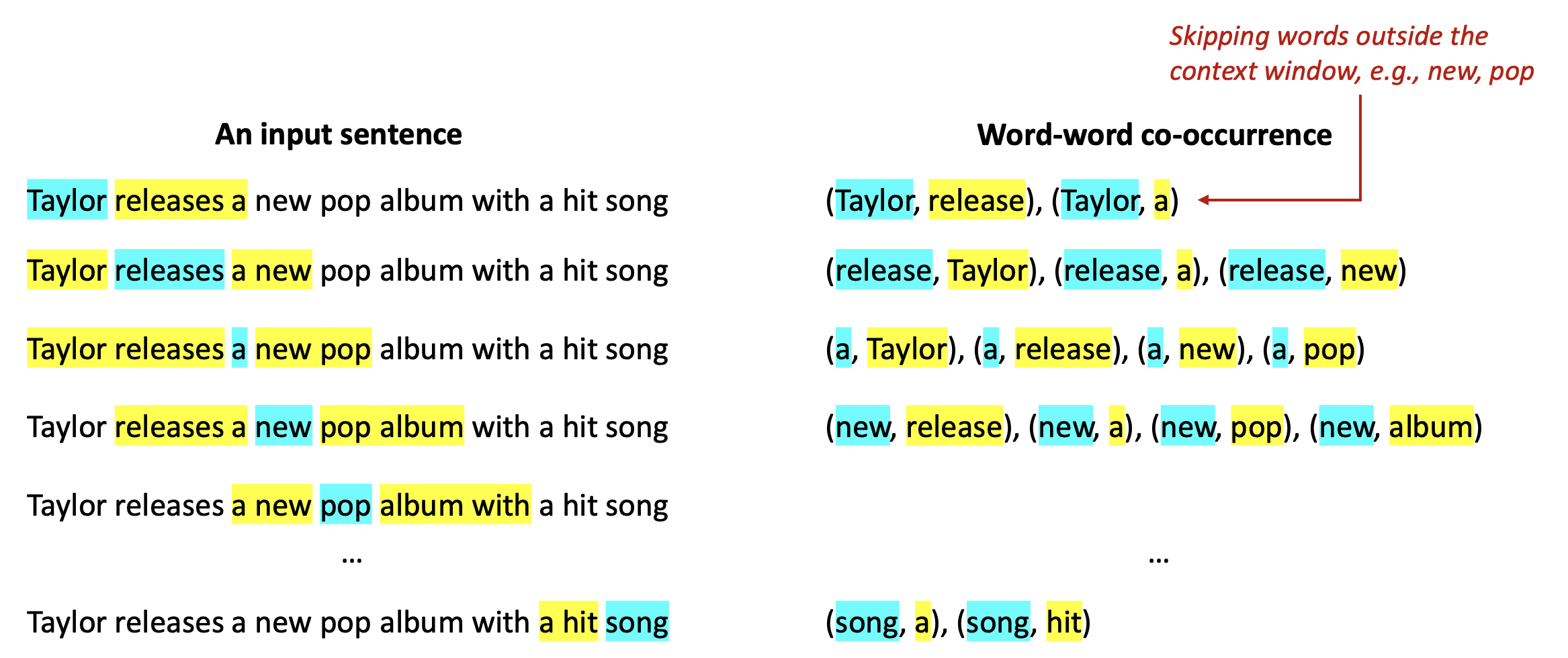
“Skip-gram”: 일부 맥락 단어들을 건너뛰고(context words), 나머지를 예측한다!

image

맥락 창(context window) 밖의 단어들을 건너뛰기, 예: new, pop

p29. 접근 방식 2: Skip-gram 학습

  • 핵심 아이디어 (Key idea):
    맥락 단어들(the context words)을
    중심 단어(the center word)를 사용하여 예측한다.
    (의미적으로 유사한 중심 단어들은 유사한 맥락 단어들을 예측한다.)

  • 목표 (Objective):
    맥락 단어 c(the context word c)를
    중심 단어 w(the center word w)를 사용하여 예측할 확률을 극대화한다.

\[\max_{\theta} \prod_{(w,c) \in D} p_{\theta}(c \mid w)\]
  • D: 전체 공기출현 쌍 집합 (total set of co-occurrence pairs)
  • θ: 최적화될 단어 임베딩들 (word embeddings to be optimized, model parameters)

image

  • 확률을 어떻게 표현할까? (How to express the probability?)

p30. 접근 방식 2: Skip-gram 학습

  • 핵심 아이디어 (Key idea):
    맥락 단어들(the context words)을
    중심 단어(the center word)를 사용하여 예측한다.
    (의미적으로 유사한 중심 단어들은 유사한 맥락 단어들을 예측한다.)

  • 목표 (Objective):
    맥락 단어 c(the context word c)를
    중심 단어 w(the center word w)를 사용하여 예측할 확률을 극대화한다.

\[\max_{\theta} \prod_{(w,c) \in D} p_{\theta}(c \mid w)\]
  • D: 전체 공기출현 쌍 집합 (total set of co-occurrence pairs)

  • θ: 최적화될 단어 임베딩들 (word embeddings to be optimized)
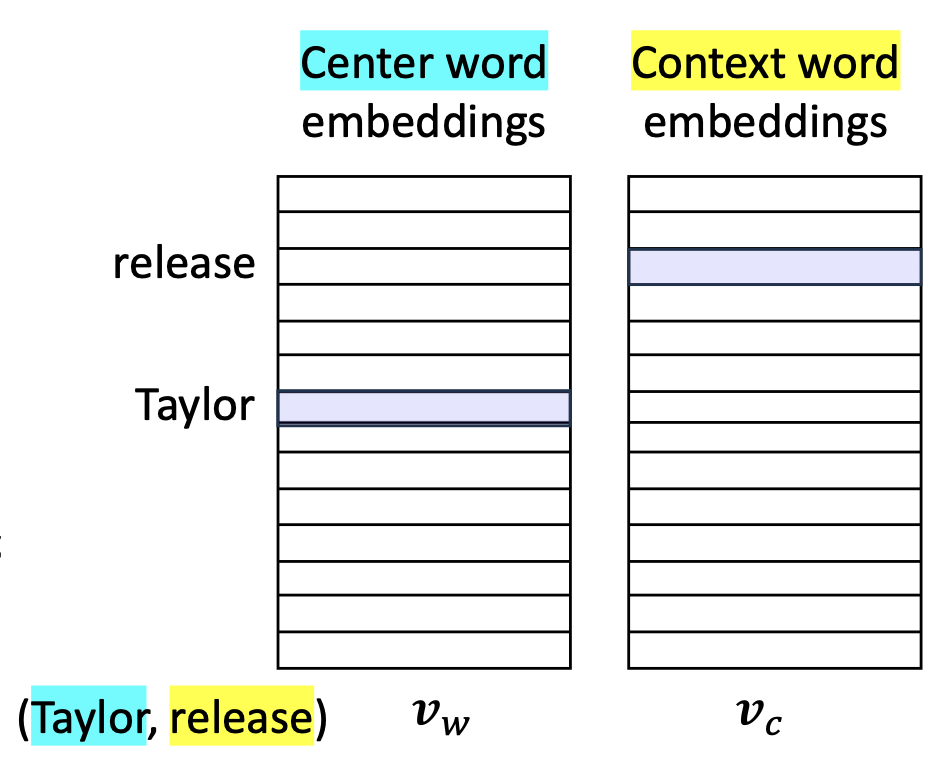
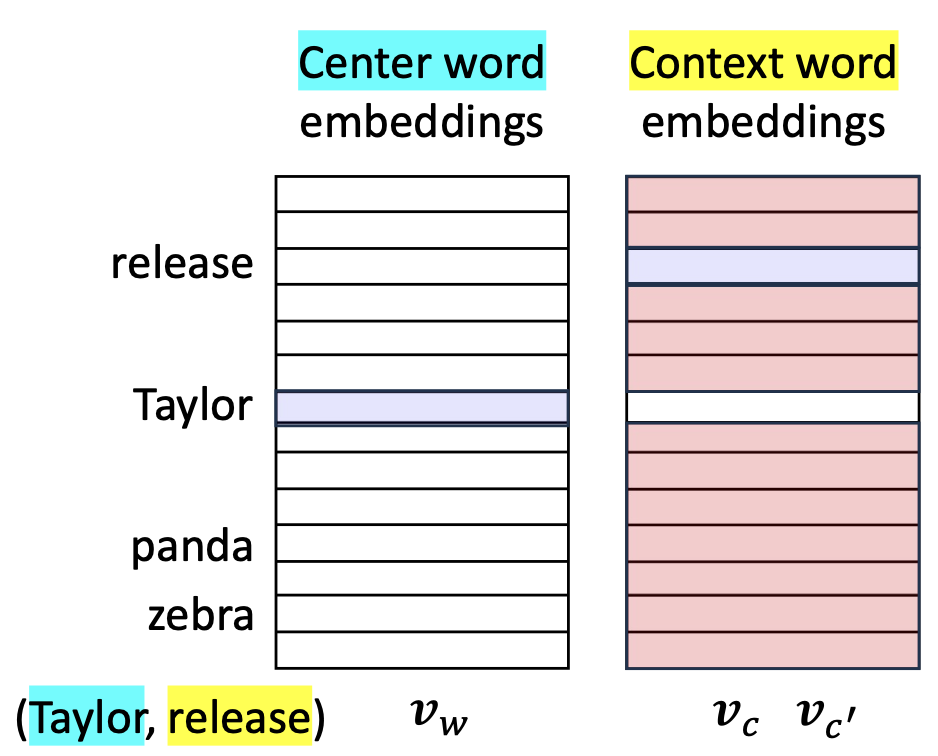
    { $v_w, v_c$ }

  • 각 단어는 두 개의 밀집 벡터(dense vectors)를 할당받는다:
    • 중심 단어 역할(center-word role)을 위한 것
    • 맥락 단어 역할(context-word role)을 위한 것
  • 로그 확률(log-probability)은 벡터 내적(vector inner product)에 비례한다고 가정한다:
\[\log p_{\theta}(c \mid w) \propto v_c \cdot v_w\]

image

p31. 접근 방식 2: Skip-gram 학습

  • 목표 (Objective):
    맥락 단어 c(the context word c)를
    중심 단어 w(the center word w)를 사용하여 예측할 확률을 극대화한다.
\[\max_{\theta} \prod_{(w,c) \in D} p_{\theta}(c \mid w)\]
  • D: 전체 공기출현 쌍 집합 (total set of co-occurrence pairs)

  • θ: 최적화될 단어 임베딩들 (word embeddings to be optimized)
    { $v_w, v_c$ }

  • 로그 확률(log-probability)은 벡터 내적(vector inner product)에 비례한다고 가정한다:

    • 각 $(w, c)$ 쌍에 대해:
    \[\log p_{\theta}(c \mid w) \propto v_c \cdot v_w\]
    • 다른 모든 맥락 단어들 $(c’)$에 대해:
    \[\log p_{\theta}(c' \mid w) \propto v_{c'} \cdot v_w\]

image

1. Skip-gram의 핵심 아이디어

  • Skip-gram 모델은 중심 단어(center word) $w$ 가 주어졌을 때
    주변 단어(context word) $c$ 를 예측하는 것을 목표로 한다.

  • 즉, “$w$ 가 주어진 조건에서 $c$ 가 등장할 확률” $p_\theta(c|w)$ 를
    가능한 한 크게 만드는 것이 목적이다.

    \[\max_{\theta} \prod_{(w,c)\in D} p_\theta(c|w)\]

2. 로그 확률의 내적 표현

  • Skip-gram에서는 두 단어의 로그 확률을 벡터 내적(inner product) 로 표현한다.

    \[\log p_\theta(c|w) \propto \mathbf{v}_c \cdot \mathbf{v}_w\]
  • $\mathbf{v}_w$: 중심 단어 임베딩
  • $\mathbf{v}_c$: 문맥 단어 임베딩
  • 두 벡터의 내적이 클수록 두 단어의 동시 등장 가능성(co-occurrence) 이 높다고 본다.

3. $(w,c)$ 와 $(w,c’)$ 의 의미적 차이

  • $(w,c)$: 실제로 문장에서 함께 등장한 단어쌍

    \[\log p_\theta(c|w) \propto \mathbf{v}_c \cdot \mathbf{v}_w \quad\text{(실제 문맥 단어)}\]

    → 내적을 크게 만들어야 한다.

  • $(w,c’)$: 함께 등장하지 않은 단어쌍(negative sample)

    \[\log p_\theta(c'|w) \propto \mathbf{v}_{c'} \cdot \mathbf{v}_w \quad\text{(잘못된 문맥 단어)}\]

    → 내적을 작게 만들어야 한다.

정리하면:

  • $(w,c)$ → 함께 등장한 적이 많을수록 내적 ↑
  • $(w,c’)$ → 등장하지 않을수록 내적 ↓

4. 요약

  • Skip-gram은 단어 쌍의 공동 등장 확률을 내적 형태로 근사한다.
  • 실제 문맥 단어는 내적을 크게, 비문맥 단어는 내적을 작게 학습함으로써
    단어의 의미적 유사도(semantic similarity) 를 반영하는 임베딩을 얻는다.

p32. 접근 방식 2: Skip-gram 학습

  • 목표 (Objective):
    맥락 단어 c(the context word c)를
    중심 단어 w(the center word w)를 사용하여 예측할 확률을 극대화한다.
\[\max_{\theta} \prod_{(w,c) \in D} p_{\theta}(c \mid w)\]
  • D: 전체 공기출현 쌍 집합 (total set of co-occurrence pairs)

  • θ: 최적화될 단어 임베딩들 (word embeddings to be optimized) { $v_w, v_c$ }

  • 최종 확률분포(final probability distribution)는 소프트맥스 함수(softmax function)로 얻어진다:
\[p_{\theta}(c \mid w) = \frac{\exp(v_c \cdot v_w)}{\sum_{c' \in |V|} \exp(v_{c'} \cdot v_w)}\]

어휘 전체(vocabulary)에 대해 정규화(normalize)하여 확률 분포를 만든다

image

image

1. Softmax의 역할

  • Skip-gram 모델은 중심 단어 $w$ 가 주어졌을 때
    주변 단어 $c$ 가 등장할 확률 $p_\theta(c|w)$ 를 계산해야 한다.
  • 가능한 모든 단어(어휘집 $\mathcal{V}$) 중 하나를 선택해야 하므로
    각 후보 단어의 점수를 0~1 사이의 확률로 정규화해야 한다.

  • Softmax 함수가 바로 이 정규화를 수행한다.

    \[p_\theta(c|w) = \frac{\exp(\mathbf{v}_c \cdot \mathbf{v}_w)} {\sum_{c' \in \mathcal{V}} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w)}\]
  • 분자: 단어쌍 $(w,c)$ 의 내적을 지수화해 “점수(score)”로 변환
  • 분모: 어휘 전체의 점수를 합하여 정규화
    → 전체 확률의 합이 1이 되도록 만든다.

2. 확률적 해석

  • $\exp(\mathbf{v}_c \cdot \mathbf{v}_w)$ 는
    중심 단어 $w$ 가 문맥 단어 $c$ 를 얼마나 선호하는지를 나타내는 양이다.
  • 값이 클수록 $p_\theta(c|w)$ 도 커지며,
    두 단어가 함께 등장할 가능성이 높다고 모델이 판단한다.

3. 예시 (직관적 이해)

  • 예: 중심 단어 $w =$ “Taylor”
  • 모든 후보 단어 $c’$ 에 대해
    \(\exp(\mathbf{v}_{c'} \cdot \mathbf{v}_{Taylor})\)
    값을 계산한다.
  • 그중 실제 문맥 단어 $c =$ “release” 의 내적이 가장 크면
    softmax 결과
    \(p_\theta(\text{release}|\text{Taylor})\)
    가 가장 크게 나온다.

4. 정리

  • Softmax는 내적 기반 점수를 확률 분포로 변환하는 함수이다.
  • 이를 통해 Skip-gram 모델은
    “가능한 모든 단어 중 실제 문맥 단어의 확률을 최대화”하도록 학습한다.

p33. 접근 방식 2: Skip-gram 학습

  • 우리는 단어 임베딩(word embeddings)을 최적화 문제(negative log)로 공식화(formulize)하였다:
\[\min_{\theta} \mathcal{L}(\theta) = - \sum_{(w,c) \in D} \log p_{\theta}(c \mid w) = - \sum_{(w,c) \in D} \left( v_c \cdot v_w - \log \sum_{c' \in |V|} \exp(v_{c'} \cdot v_w) \right)\]
  • D: 전체 공기출현 쌍 집합 (total set of co-occurrence pairs)
  • θ: 최적화될 단어 임베딩들 (word embeddings to be optimized) { $v_w, v_c$ }
\[p_{\theta}(c \mid w) = \frac{\exp(v_c \cdot v_w)}{\sum_{c' \in |V|} \exp(v_{c'} \cdot v_w)}\]

image

1. Skip-gram의 최적화 목표

  • Skip-gram 모델은 중심 단어 $w$ 가 주어졌을 때
    실제 문맥 단어 $c$ 가 등장할 확률 $p_\theta(c|w)$ 를 최대화한다.

    \[\max_\theta \prod_{(w,c)\in D} p_\theta(c|w)\]

  • 이를 로그 변환하고 부호를 반전하면 손실 함수 형태가 된다.

    \[\min_\theta \mathcal{L}(\theta) = - \sum_{(w,c)\in D} \log p_\theta(c|w)\]

→ 실제 등장한 단어쌍의 확률을 높이고, 그 부정확도를 최소화한다는 의미.

2. Softmax 확률을 대입한 형태

\[p_\theta(c|w) = \frac{\exp(\mathbf{v}_c \cdot \mathbf{v}_w)} {\sum_{c' \in \mathcal{V}} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w)}\]

로그를 취하면

\[\log p_\theta(c|w) = \mathbf{v}_c \cdot \mathbf{v}_w - \log \sum_{c' \in \mathcal{V}} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w)\]

따라서 최종 손실 함수는

\[\mathcal{L}(\theta) = - \sum_{(w,c)\in D} \left( \mathbf{v}_c \cdot \mathbf{v}_w - \log \sum_{c' \in \mathcal{V}} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w) \right)\]

3. 각 항의 의미

  • $\mathbf{v}_c \cdot \mathbf{v}_w$:
    실제 문맥 단어와 중심 단어의 유사도를 높이는 항 (positive pair 강화)

  • $\log \sum_{c’} \exp(\mathbf{v}_{c’} \cdot \mathbf{v}_w)$:
    모든 다른 단어의 점수를 정규화하는 항
    → 잘못된 문맥 단어(negative pair)를 억제하는 패널티

4. 직관적 이해

  • 모델은 실제 단어쌍 $(w,c)$ 의 내적을 크게 만들어
    $p_\theta(c|w)$ 를 키운다.
  • 동시에 등장하지 않은 단어 $c’$ 들의 내적은 작게 만들어야 한다.
  • 이 과정을 반복하면
    단어의 의미적 관계(semantic similarity) 가 반영된 임베딩이 형성된다.

p34. 접근 방식 2: Skip-gram 학습

  • 우리는 단어 임베딩(word embeddings)을 최적화 문제(negative log)로 정식화하였다:
\[\min_{\theta} \mathcal{L}(\theta) = - \sum_{(w,c) \in D} \log p_{\theta}(c \mid w) = - \sum_{(w,c) \in D} \left( v_c \cdot v_w - \log \sum_{c' \in |V|} \exp(v_{c'} \cdot v_w) \right)\]
  • 어떻게 최적화할까? (How to optimize?): 경사하강법(gradient descent)
    • 그래디언트 $\nabla_{\theta} \mathcal{L}(\theta)$는 훈련 손실을 가장 크게 증가시키는 방향이다.

💻 알고리즘 (Algorithm)

  • 무작위로 $\theta$ 초기화
  • 수렴할 때까지 반복:
\[\theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}(\theta)\]
  • $\theta$: 학습(또는 모델) 매개변수 (learning/model parameters)
  • $\eta$: 단계 크기(step size, 학습률 learning rate) → 하이퍼파라미터

image

p35. 배경 지식: 경사하강법 (Gradient descent)

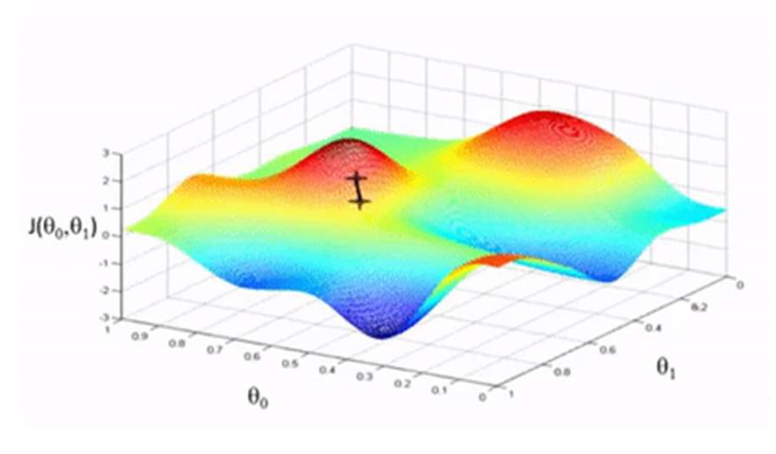
  • 우리는 목적 함수(손실 함수) $\mathcal{L}(\theta)$를 가진다.

  • 경사하강법(Gradient descent) 은 $\mathcal{L}(\theta)$를 최소화하기 위해 사용되는 반복적 최적화 알고리즘이다.

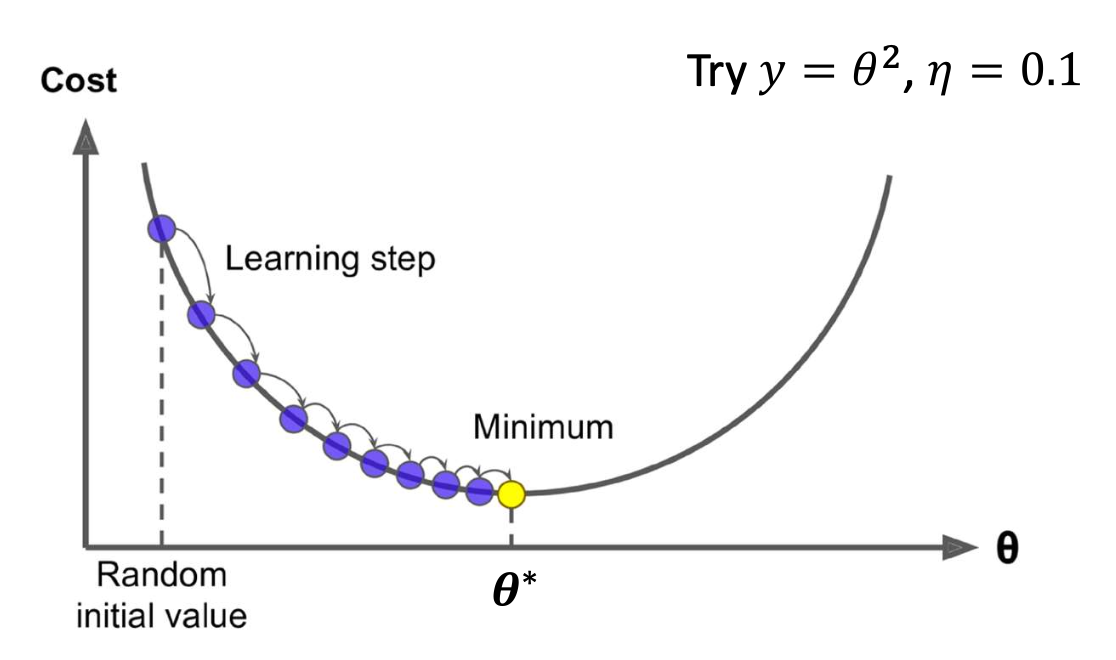
  • 어떻게 작동하는가? (How it works?)
    현재 값 $\theta$에 대해 $\mathcal{L}(\theta)$의 그래디언트를 계산한 다음, 음의 그래디언트 방향으로 작은 걸음을 이동한다.
    이를 반복한다.

💻 알고리즘 (Algorithm)

  • 무작위로 $\theta$ 초기화
  • 수렴할 때까지 반복:
\[\theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}(\theta)\]
  • $\theta$: 학습 매개변수 (learning parameters)
  • $\eta$: 단계 크기(step size, 학습률 learning rate) → 하이퍼파라미터
    image

📎 참고: Notes on derivatives (Stanford CS231n)

p36. 접근 방식 2: Skip-gram 학습

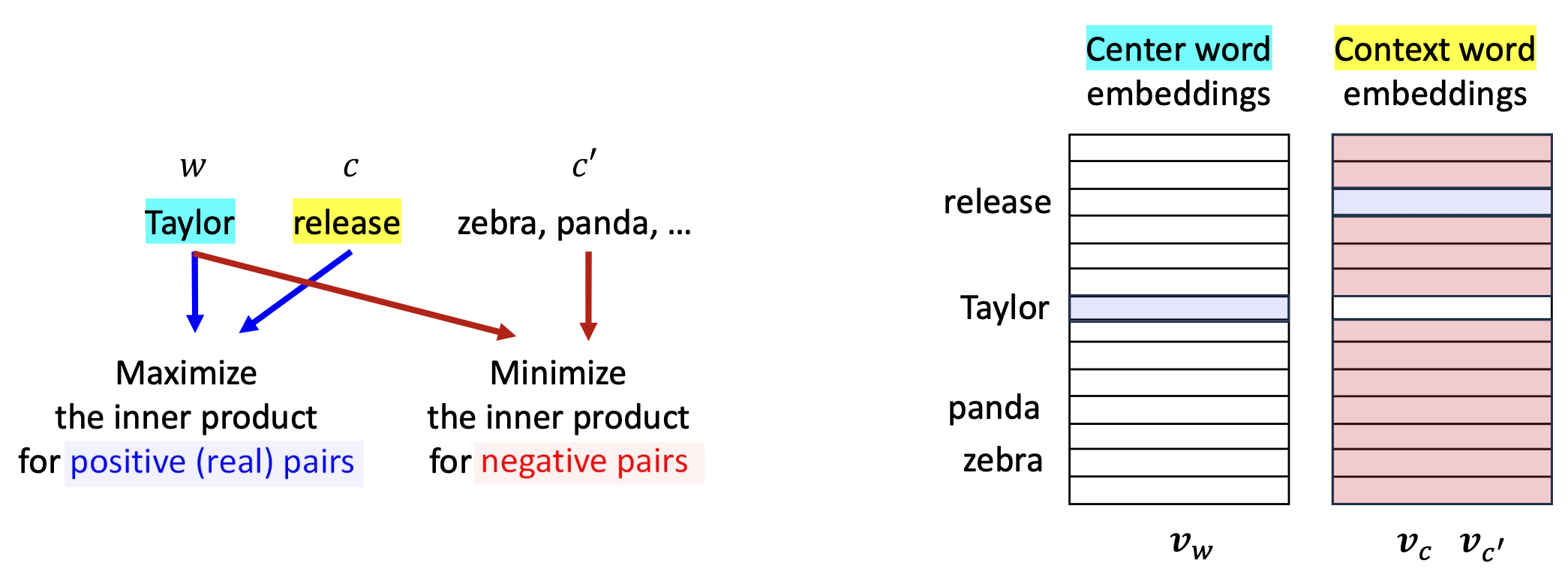
  • 우리의 문제로 돌아와서, 손실(loss)을 최소화하기 위해 학습 매개변수 $\theta$를 업데이트한다.
\[\min_{\theta} \; \mathcal{L}(\theta) = - \sum_{(w,c) \in D} \left( \mathbf{v}_c \cdot \mathbf{v}_w - \log \sum_{c' \in |\mathcal{V}|} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w) \right)\]

  • 예시 (E.g.), 쌍 ( Taylor, release ):

    • 양성(실제) 쌍(positive (real) pairs)의 내적(inner product)을 최대화한다.
    • 음성 쌍(negative pairs)의 내적(inner product)을 최소화한다.

image

p38. 접근 방식 2: Skip-gram 학습 (부정 샘플링, negative sampling)

  • 이전 해결책은 동작하지만, 비효율적이다.
\[\min_{\theta} \ \mathcal{L}(\theta) \;=\; - \sum_{(w,c) \in D} \Bigg( \, \mathbf{v}_c \cdot \mathbf{v}_w \;-\; \log \sum_{c' \in |\mathcal{V}|} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w) \,\Bigg)\]

어휘집 전체(vocabulary)에 대해 합산해야 함 → 비용이 큼 (expensive!)

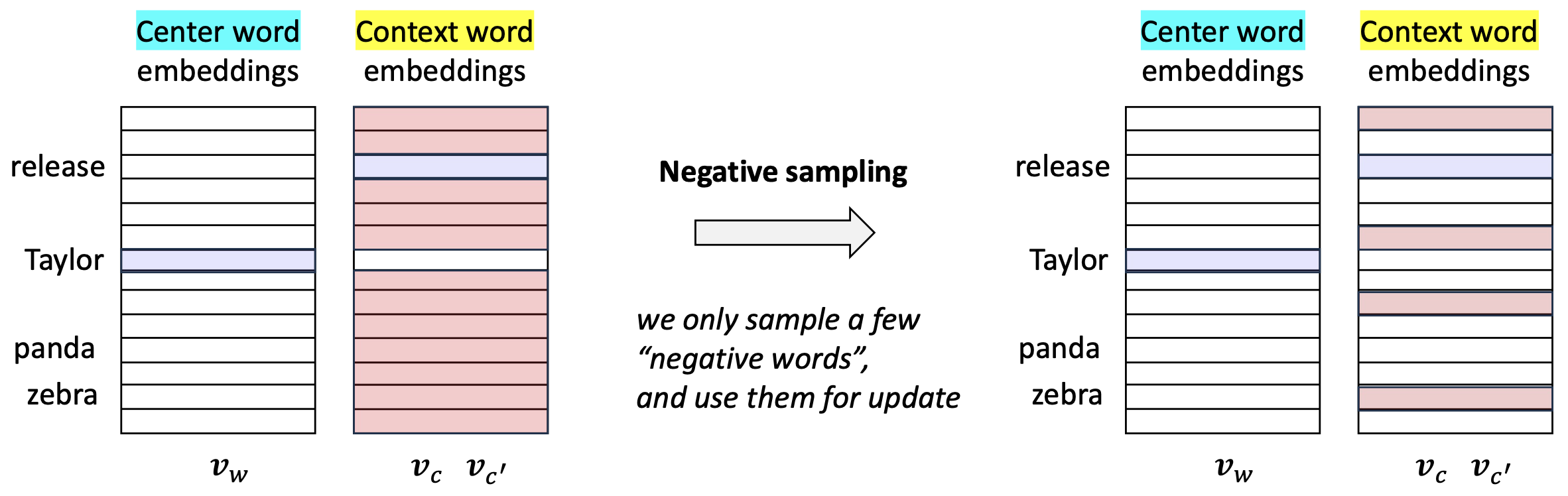
Negative sampling

  • 우리는 소수의 “부정 단어들(negative words)”만 샘플링하여 업데이트에 사용한다.

image

1. 기존 문제점

  • Skip-gram 손실 함수는 전체 어휘집 $\mathcal{V}$ 에 대해

    \[\sum_{c' \in \mathcal{V}} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w)\]

    를 매번 계산해야 한다.

  • 어휘 크기가 매우 클 때(수만~수십만 단어),
    이 계산은 매우 비효율적이다.

2. 근사의 핵심 아이디어

  • 전체 확률 분포를 계산하지 않고,
    Skip-gram 문제를 이진 분류 문제로 재해석한다.
  • 즉, 단어쌍 $(w,c)$ 가
    실제 문맥에서 등장한 참(true) 쌍인지,
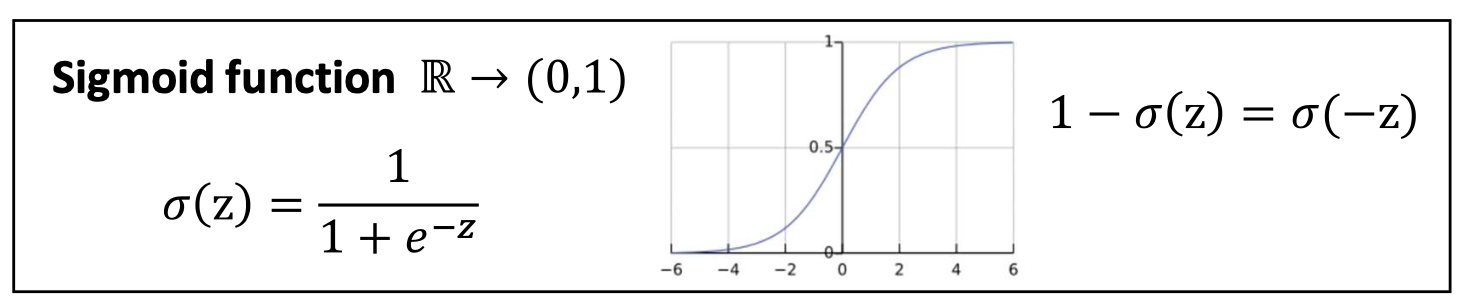
    아니면 무관한 거짓(false) 쌍인지 판별하도록 학습한다.

3. 시그모이드(Sigmoid)를 이용한 확률 표현

  • 두 단어 벡터의 내적을 시그모이드에 입력해
    단어쌍이 참인지의 확률로 변환한다.

    \[p_\theta(\text{True} \mid c,w) = \sigma(\mathbf{v}_c \cdot \mathbf{v}_w) = \frac{1}{1 + \exp(-\mathbf{v}_c \cdot \mathbf{v}_w)}\]
  • 내적이 클수록 두 단어가 자주 등장하는 관계라고 판단한다.

  • 거짓(false) 쌍의 확률은

    \[p_\theta(\text{False} \mid c,w) = 1 - \sigma(\mathbf{v}_c \cdot \mathbf{v}_w) = \sigma(-\mathbf{v}_c \cdot \mathbf{v}_w)\]

4. 직관적 이해

  • Softmax의 복잡한 정규화 계산을 피하면서도
    단어쌍 간의 관계를 학습할 수 있는 방식이다.
  • 실제 문맥 단어쌍 $(w,c)$ 는 “참(1)”으로,
    임의로 뽑은 단어쌍 $(w,c’)$ 는 “거짓(0)”으로 학습한다.
  • 결과적으로 Skip-gram은 이진 분류 형태로 단어 의미 관계를 학습하면서,
    계산 효율을 크게 향상시킨다.

p39. 접근 방식 2: Skip-gram 학습 (부정 샘플링, negative sampling)

  • 이전 해결책은 동작하지만, 비효율적이다.
\[\min_{\theta} \ \mathcal{L}(\theta) \;=\; - \sum_{(w,c) \in D} \Bigg( \, \mathbf{v}_c \cdot \mathbf{v}_w \;-\; \log \sum_{c' \in |\mathcal{V}|} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w) \,\Bigg)\]

어휘집 전체(vocabulary)에 대해 합산해야 함 → 비용이 큼 (expensive!)

  • 따라서 우리는 근사 목적 함수(approximate objective)를 사용하여 더 쉽게 최적화한다.
    • 목적 함수를 이진 분류(binary classification) 과제로 다시 정의한다:
      $(w, c)$가 진짜 쌍(true pair)인지 예측한다.
    • $(w, c)$가 진짜 쌍일 확률은 시그모이드 함수(sigmoid function)로 계산된다.
\[p_\theta(\text{True} \mid c, w) \;=\; \sigma(\mathbf{v}_c \cdot \mathbf{v}_w) \;=\; \frac{1}{1 + \exp(- \mathbf{v}_c \cdot \mathbf{v}_w)}\]

image

\[p_\theta(\text{False} \mid c, w) = 1 - p_\theta(\text{True} \mid c, w) = 1 - \sigma(\mathbf{v}_c \cdot \mathbf{v}_w) = \sigma(- \mathbf{v}_c \cdot \mathbf{v}_w)\]

p40. 접근 방식 2: Skip-gram 학습 (부정 샘플링, negative sampling)

  • 따라서 우리는 근사 목적 함수(approximate objective)를 사용하여 더 쉽게 최적화한다.
    • 양의 쌍(positive pairs, 실제로 함께 등장하는 단어들)의 확률을 최대화한다.
    • 음의 쌍(negative pairs, 무작위로 샘플링된 잡음)의 확률을 최소화한다.

Softmax vs. Sigmoid

  • Softmax: 가능한 모든 쌍들 중에서, 어떤 쌍이 가장 가능성이 높은가?
  • Sigmoid: 특정 쌍에 대해서, 이 쌍이 진짜인가 가짜인가?

목적 함수 변화

\[\min_{\theta} \ \mathcal{L}(\theta) \;=\; - \sum_{(w,c) \in D} \Bigg( \mathbf{v}_c \cdot \mathbf{v}_w \;-\; \log \sum_{c' \in |\mathcal{V}|} \exp(\mathbf{v}_{c'} \cdot \mathbf{v}_w) \Bigg)\] \[\Downarrow\] \[\min_{\theta} \ \mathcal{L}(\theta) \;=\; - \sum_{(w,c) \in D} \Bigg( \log \sigma(\mathbf{v}_c \cdot \mathbf{v}_w) \;+\; \sum_{c' \in \mathcal{N}} \log \sigma(- \mathbf{v}_{c'} \cdot \mathbf{v}_w) \Bigg)\]
  • positive pairs: $\log \sigma(\mathbf{v}_c \cdot \mathbf{v}_w)$

  • negative pairs: $\sum \log \sigma(- \mathbf{v}_{c’} \cdot \mathbf{v}_w)$

  • $\mathcal{N}$: 무작위로 샘플링된 음의 집합 (크기는 $ \mid \mathcal{V} \mid $보다 작음, 보통 5–10개)

p41. Word2Vec 시각화 (Word2Vec visualization)

image

p42. 복습: 밀집 고정 표현 (Dense static representation)

  • 분포 가설 (Distributional hypothesis)
    • 유사한 문맥(context)에서 나타나는 단어들은 유사한 의미를 가지는 경향이 있다.
  • 단어–문맥 쌍(word–context pairs) (혹은 행렬 형태) 이 주어졌을 때, 두 가지 주요 접근법이 있다:
  1. 차원 축소 (Dimensionality reduction)
    • 공출현 행렬(co-occurrence matrix)로부터 시작한다.
    • 정규화(normalize)하고 절단된 SVD (truncated SVD)를 적용하여 차원을 축소한다.
    • 각 행(필요시 특이값으로 스케일링된)은 단어 임베딩(word embedding)으로 사용된다.
  2. 스킵그램 학습 (Skip-gram learning)
    • 단어–문맥 쌍(word–context pairs)으로부터 직접 임베딩을 학습한다.
    • 주어진 목표 단어(target word)의 문맥 단어(context words)를 예측한다.
    • 학습을 효율적으로 만들기 위해 네거티브 샘플링(negative sampling)을 사용한다.
    • Word2Vec으로 구현된다.

p43. 밀집 표현들의 유사성 (Similarity of dense representations)

  • 단어 임베딩(word embeddings)을 사용하면, 어떤 텍스트든 이를 집계(예: 평균)하여 벡터로 표현할 수 있다.

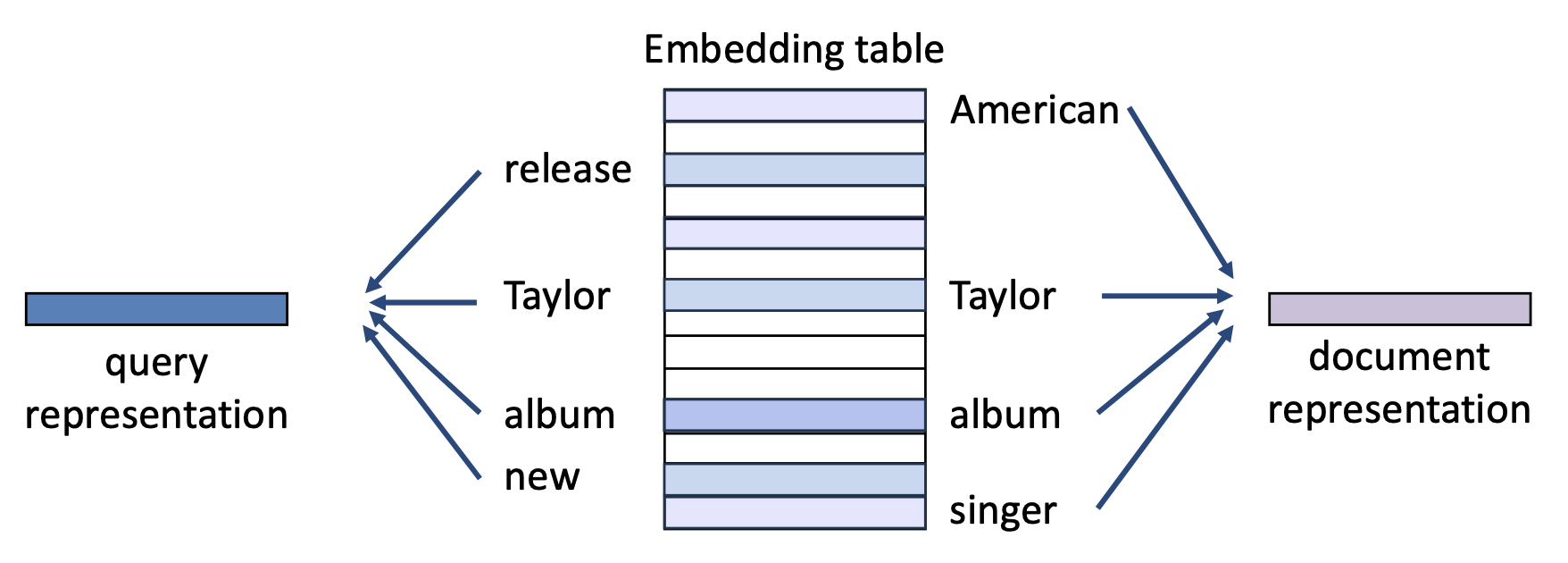
  • 쿼리(query)와 문서(document)가 주어졌을 때, 우리는 밀집 표현(dense representations)에 기반하여 그들의 유사성을 계산한다:

    • 쿼리 q: “Taylor release new album”
    • 문서 d: “American singer Taylor …”

image

p44. 밀집 표현들의 유사성 (Similarity of dense representations)

  • 단어 임베딩(word embeddings)을 사용하면, 어떤 텍스트든 이를 집계(예: 평균)하여 벡터로 표현할 수 있다.

  • 쿼리(query)와 문서(document)가 주어졌을 때, 우리는 밀집 표현(dense representations)에 기반하여 그들의 유사성을 계산한다.

  • 내적(inner product) 과 코사인 유사도(cosine similarity) 가 여기에서 널리 사용된다.

  • 희소 벡터(Sparse vectors):
    • 고차원이며, 대부분이 0
    • 크기는 문서 길이에 의존
    • 정규화 필요
    • ➤ 코사인 유사도가 선호됨
  • 밀집 벡터(Dense vectors):
    • 저차원, 연속적인 값
    • 노름(norms)은 훨씬 더 안정적
    • 단어 임베딩 풀링(pooling)은 → 길이의 영향을 덜 받음
    • ➤ 내적(inner product) 은 유사도 측정으로 사용될 수 있음
    • 노름 불변성을 선호하는 경우 코사인 유사도도 가능

p38. 다음: 밀집 “맥락” 표현 (Dense “contextual” representations)

  • 희소 표현(sparse representation)에서 밀집 표현(dense representation)으로

    • 희소 벡터(sparse vectors): 매우 길다 (길이 = $ \mid V \mid $, 종종 10k 이상), 대부분의 항목 값 = 0
    • 밀집 벡터(dense vectors): 상대적으로 짧다 (50–1000 차원), 대부분의 항목 값 ≠ 0
  • 정적 임베딩(Static embeddings)
    • 각 단어는 하나의 고정된 밀집 벡터(single fixed dense vector) 로 할당된다.
    • 주변 문맥(context)을 반영하지 않는다.
      • 예: “bank” → 항상 같은 벡터
    • 예시: Word2vec, GloVe

    image

  • 문맥 임베딩(Contextual embeddings)
    • 각 단어의 벡터는 주변 문맥(surrounding context) 에 따라 달라진다.
    • 단어의 의미가 문맥에 따라 변한다.
      • 예: “bank of the river” vs. “bank account”
    • 예시: BERT, LLM 기반 임베딩

    image

  • Speech and Language Processing: Chapter 5: Embeddings
대학원 수업, 텍스트 마이닝
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.