[텍스트 마이닝] 8. Text Classification 1

게시 2025/10/27 업데이트 2025/12/15

By 김성진

30 분읽는 시간

p9. 텍스트 분류 (Text classification)

왜 중요한가?
- 데이터 분석의 핵심 과제: 미리 정의된 레이블을 할당(assign predefined labels) (예: 브랜드, 감정, 주제 등)
- 검색 엔진, 추천 시스템, 스팸 탐지 등에서 폭넓게 사용된다.
- QA, 대화 시스템, 개인화(personalization) 등 다양한 고급 응용의 기초가 된다.

우리의 학습 경로:
- 텍스트를 벡터로 표현하였다.
- 다음으로, 이러한 표현을 이용하여 분류(classification) 를 수행할 것이다.
- 주로 사전학습(pretrain) - 미세조정(fine-tune) 패러다임 을 따라, 일반적인 언어 지식을 특정 분류 과제에 맞게 조정할 것이다.

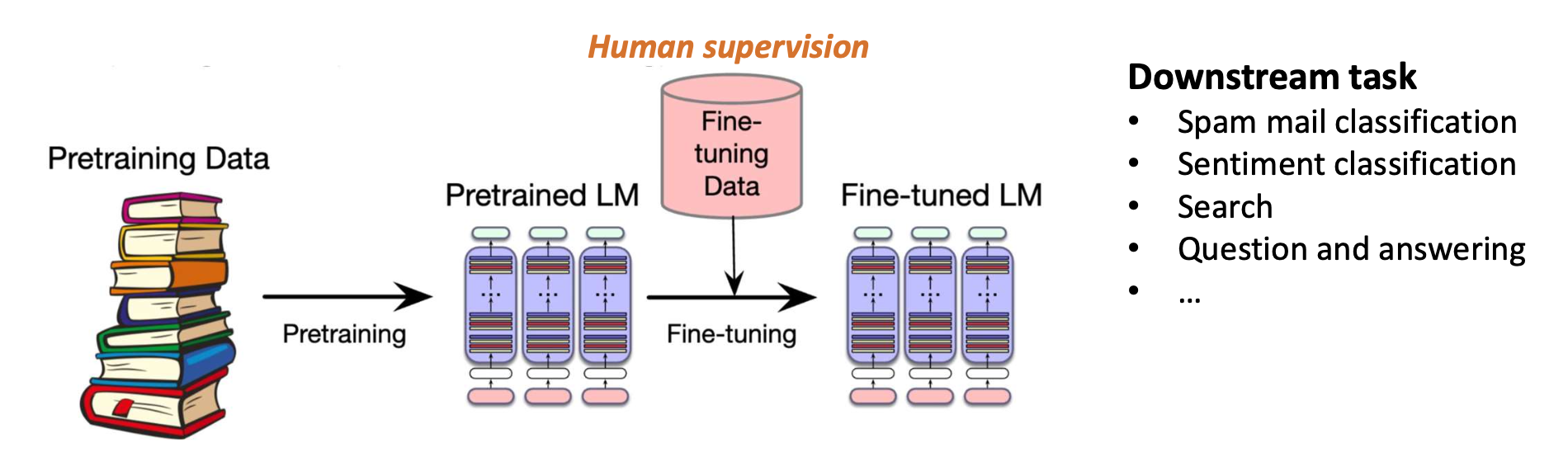
p10. 사전학습 및 미세조정

p11. 사전학습 + 미세조정 (Pretraining + Fine-tuning)

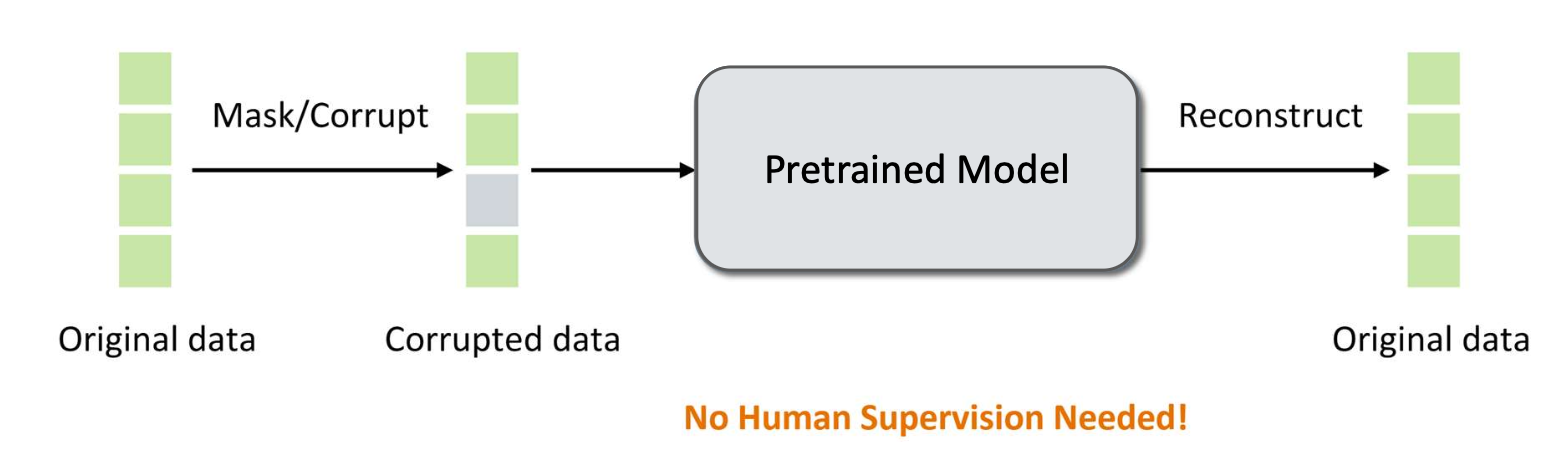
사전학습(Pretraining)
- 동기(Motivation): 웹에는 언어적 패턴과 세계 지식이 풍부하게 담긴 방대한 양의 텍스트 데이터가 존재한다.
- 목표: 사람의 레이블링 없이 일반적인 목적의 표현(general-purpose representations) 을 학습하는 것.
- 예시:
  - Word2Vec (인접 단어 예측)
  - BERT (마스크된 언어 모델링, 다음 문장 예측)

p12. 사전학습 + 미세조정

미세조정(Fine-tuning)
- 동기(Motivation): 사전학습된 모델은 일반적인 지식을 포착하지만, 분류와 같은 작업에는 과제(task) 특화 지식이 필요하다.
- 목표: 사전학습된 모델의 파라미터를 조정(adjust the pretrained model parameters) 하여 특정 목표(downstream) 과제 에서 좋은 성능을 내도록 하는 것.
  - 처음부터 학습하는 것보다 훨씬 적은 레이블된 데이터(labeled data)만 필요하다.
  - 사전학습 과정에서 학습된 지식을 활용한다.
- 예시:
  - BERT를 이용한 감정 분류(sentiment classification)

p13. 사전학습 + 미세조정

왜 사전학습 + 미세조정이 “최적화 관점(optimization perspective)”에서 도움이 되는가?
사전학습(Pretraining)
- 손실함수 $L_{\text{pretrain}}$ 을 최소화하여 파라미터 $\hat{\theta}$ 를 학습한다.
- 좋은 초기값(good initialization)을 제공한다.
미세조정(Fine-tuning)
- $\hat{\theta}$ 에서 시작하여 손실함수 $L_{\text{fine-tun}}$ 을 최소화한다.
- 사전학습된 모델을 목표 과제(target task)에 맞게 적응시킨다.
확률적 경사 하강법(SGD)은 초기값(initialization)에 크게 영향을 받는다.
사전학습으로부터 좋은 시작점을 얻으면,
모델은 효율적으로 수렴(converge efficiently)하며
더 적은 양의 데이터로도 잘 일반화(generalize well)되는 경향이 있다.

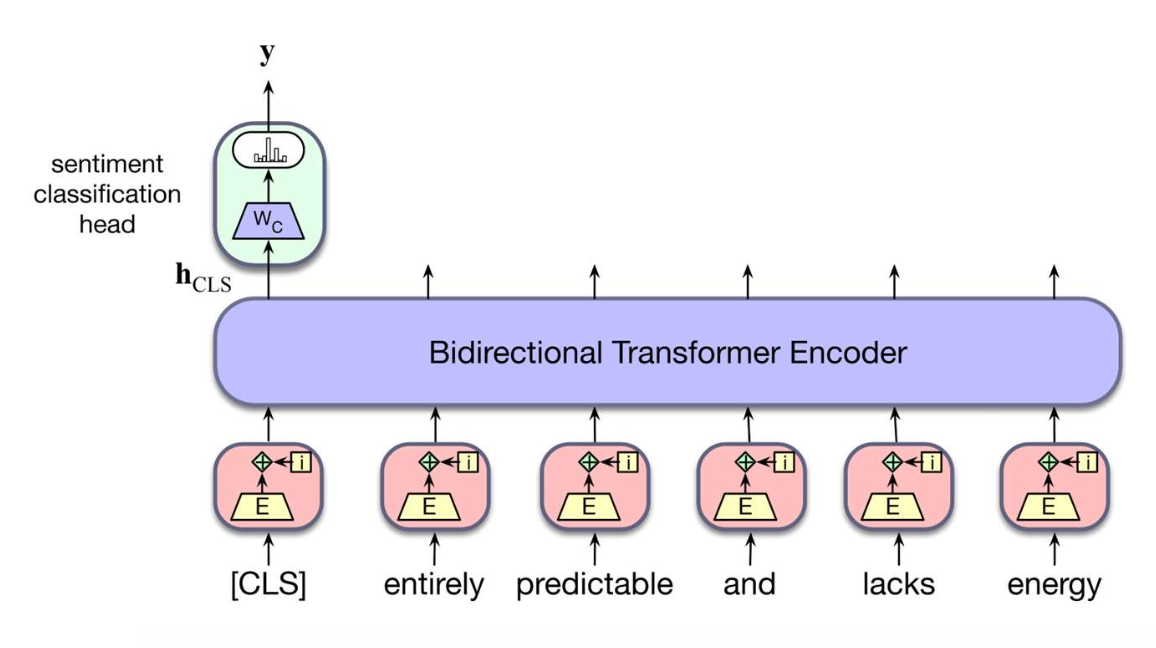
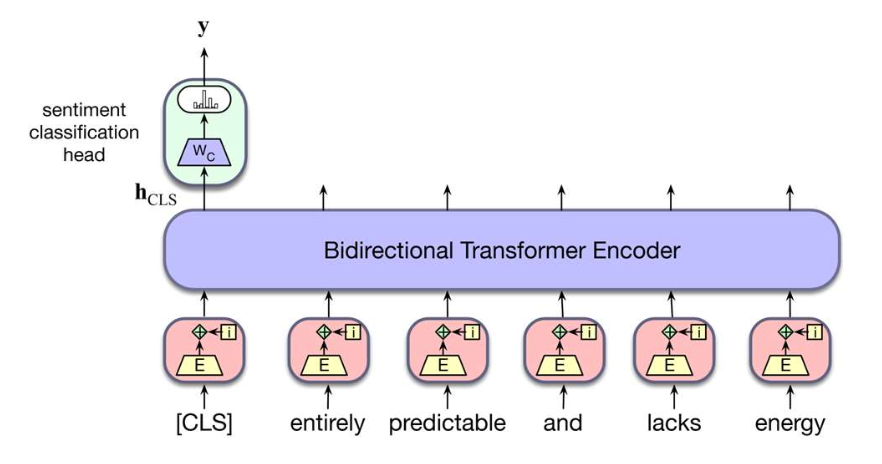
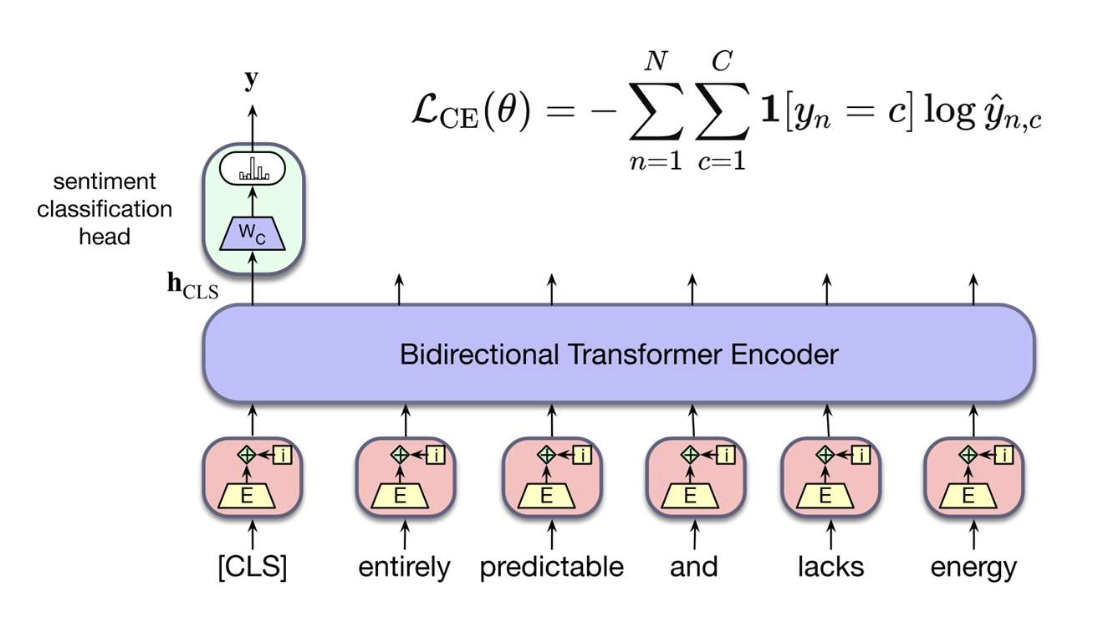
p14. 사전학습 + 미세조정 예시

Downstream task: 감정 분류
- 주어진 문장이 긍정(positive), 중립(neutral), 부정(negative)인지 예측한다.
작동 방식:
- 사전학습된 BERT를 이용해 각 문장을 벡터로 표현한다.
  - 일반적인 선택: CLS 표현(Representation) 또는 모든 문맥 임베딩의 평균.
- 작은 분류 헤드(classification head, 작은 신경망)를 추가한다.
- 이후 모델을 레이블이 있는 데이터(labeled data)로 미세조정(fine-tuning)한다.
학습 선택:
A. 전체 미세조정(Full fine-tuning): 모든 파라미터(all parameters)를 업데이트한다.
B. 부분 미세조정(Partial fine-tuning): 일부 파라미터(subset of parameters)만 업데이트한다.
- 인코더(encoder)를 고정(freeze)하고 헤드만 업데이트(only the head) 한다.
- 인코더 대부분을 고정하고 상위 층(top layers) 과 헤드(head) 를 함께 업데이트한다.

p15. 분류 작업(Classification task)

p16. 분류: 이진 분류 vs 다중 클래스 분류

분류(Classification): 미리 정의된 범주 집합 $C$에서 이산적인 레이블을 예측하는 것

\[x \;\longrightarrow\; f \;\longrightarrow\; y \in C\]

이진 분류 (Binary classification, $\mid C \mid = 2$)
- 예: 스팸 탐지 (스팸 / 정상 메일)
다중 클래스 분류 (Multiclass classification, $\mid C \mid > 2$)
- 예: 이미지 분류 (고양이, 개, 말)

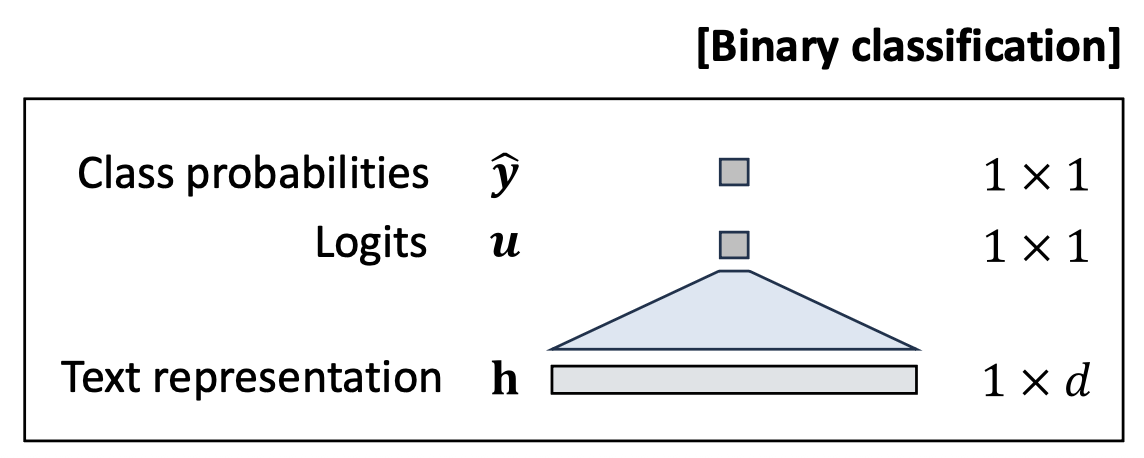
p18. 분류: 분류기(classifier)

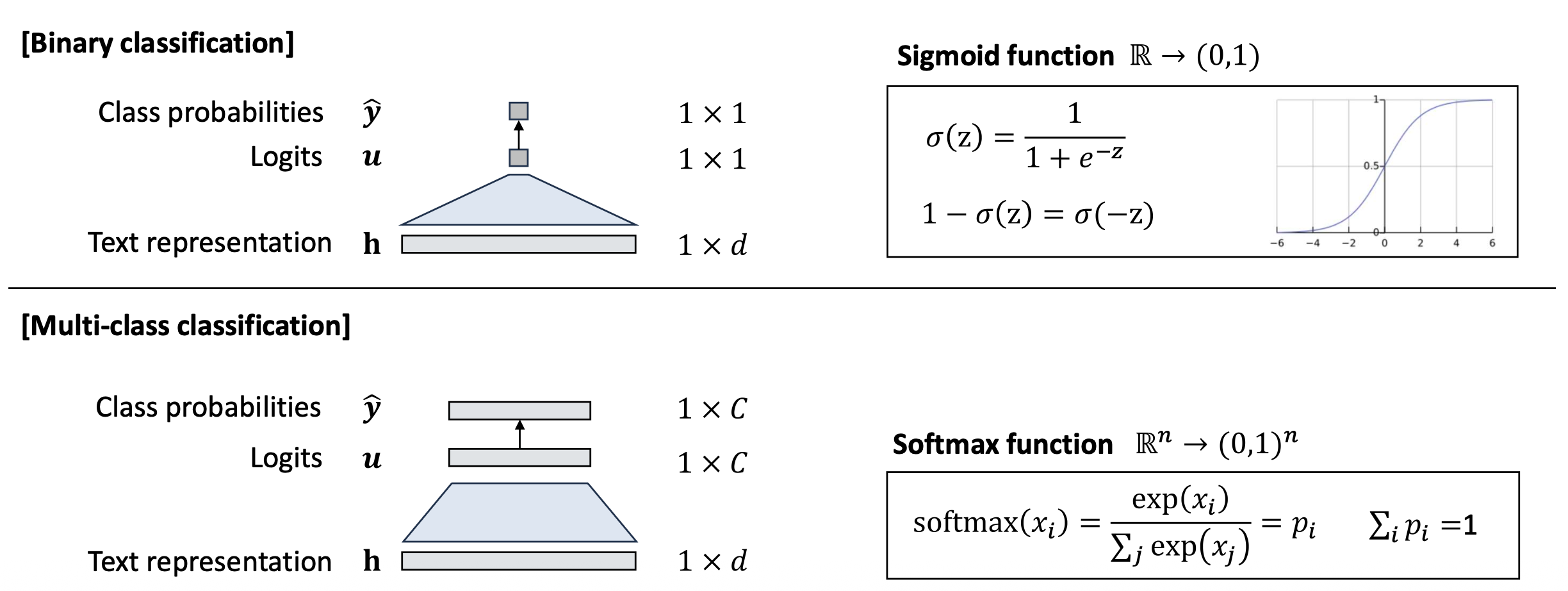
이제 우리는 (1) 사전학습된 모델을 사용하여 텍스트를 벡터 표현(vector representation) 으로 인코딩하고,
(2) 각 클래스에 대한 확률(probability) 을 계산할 수 있다.

p19. 분류: 손실 함수 (이진)

우리는 다음을 가진다
\[\mathcal{D} = \{(x_n, y_n) \mid n = 1, \ldots, N\}, \quad \text{where } y_i \in \{0, 1\}\]
손실 유도(Loss derivation):
- 각 레이블은 베르누이 확률변수(Bernoulli random variable)로 모델링될 수 있다.
  ✓ 베르누이 분포(Bernoulli distribution):
  - 확률변수 $y = 1$ 은 확률 $p$ 로, $y = 0$ 은 확률 $1 - p$ 로 발생한다.
  - 예시:
    \[p(Y = \{1,0,1,0,0\}) = p(1-p)p(1-p)(1-p) = p^2(1-p)^3\]
- 데이터셋 전체에 대한 우도(Likelihood)는 다음과 같이 표현된다:
  \[\prod_{n=1}^{N} \hat{y}_n^{y_n} (1 - \hat{y}_n)^{1 - y_n}, \quad \text{where } \hat{y}_n = p(y_n = 1 \mid x_n)\]
- 우도(Likelihood) = 모델 하에서 데이터셋(레이블)이 관측될 확률

p20. 분류: 손실 함수 (이진)

우리는 다음을 가진다
\[\mathcal{D} = \{(x_n, y_n) \mid n = 1, \ldots, N\}, \quad \text{where } y_i \in \{0, 1\}\]
손실 유도(Loss derivation):
- 데이터셋 전체에 대한 우도(Likelihood)는 다음과 같이 표현된다:
  \[\prod_{n=1}^{N} \hat{y}_n^{y_n} (1 - \hat{y}_n)^{1 - y_n}, \quad \text{where } \hat{y}_n = p(y_n = 1 \mid x_n)\]
  $\hat{y}_n$: 예측된 확률(sigmoid 출력)
- 우리는 로그 우도(log-likelihood)를 최대화(maximizing)하여 모델을 학습한다:
  \[\mathcal{L}_{\text{BCE}}(\theta) = -\sum_{n=1}^{N} \Big[ y_n \log \hat{y}_n + (1 - y_n)\log(1 - \hat{y}_n) \Big]\]
  - 이 손실 함수는 이진 교차 엔트로피(Binary Cross-Entropy, BCE)라고 불린다.

p21. 분류: 손실 함수 (다중 클래스)

https://en.wikipedia.org/wiki/Categorical_distribution

우리는 다음을 가진다
\[\mathcal{D} = \{(x_n, y_n) \mid n = 1, \ldots, N\}, \quad \text{where } y_i \in \{1, \ldots, C\}\]
손실 유도(Loss derivation):
- 각 레이블은 범주형 확률변수(Categorical random variable)로 모델링될 수 있다.
  \[P(y_n = c \mid x_n) = \hat{y}_{n,c}, \quad \sum_{c=1}^{C} \hat{y}_{n,c} = 1\]
  $\hat{y}_{n,c}$: 클래스 $c$ 에 대한 예측 확률(softmax 출력)
- 데이터셋 전체에 대한 우도(Likelihood)는 다음과 같이 표현된다:
  \[\prod_{n=1}^{N} \prod_{c=1}^{C} \hat{y}_{n,c}^{\,1[y_n = c]}\]
- 우리는 로그 우도(log-likelihood)를 최대화(maximizing)하여 모델을 학습한다:
  \[\mathcal{L}_{\text{CE}}(\theta) = -\sum_{n=1}^{N} \sum_{c=1}^{C} 1[y_n = c] \log \hat{y}_{n,c}\]
  - 이 손실 함수는 교차 엔트로피(Cross-Entropy, CE)라고 불린다.

p22. 이진 분류에서의 시그모이드 vs 소프트맥스

시그모이드(Sigmoid)와 소프트맥스(Softmax)는 서로 다른 가정에서 출발한다 (베르누이 vs. 범주형(Categorical)).
그러나 이진 분류(binary case)에서는 분자와 분모를 나누면 동일한 형태가 된다.
- 실제로는 구현상의 선택(implementation choice)의 문제이다.

주어진 로짓(logits) $u_1, u_2$ 에 대해:

\[p_1 = \frac{e^{u_1}}{e^{u_0} + e^{u_1}} = \frac{1}{1 + e^{u_0 - u_1}} = \sigma(u_1 - u_0)\] \[p_0 = \underbrace{\frac{e^{u_0}}{e^{u_0} + e^{u_1}}}_{\text{Softmax}} = \underbrace{\sigma(u_0 - u_1)}_{\text{Sigmoid}} = 1 - p_1\]

두 개의 로짓에 대한 소프트맥스는 로짓 차이 $(u_1 - u_0)$ 에 대한 시그모이드와 동일하다.
따라서 이는 같은 문제를 푸는 조금 다른 관점일 뿐이다.

교차 엔트로피(CE, Softmax)는 이진 교차 엔트로피(BCE)로 축소된다:

\[-\big[ y \log p_1 + (1 - y) \log(1 - p_1) \big]\]

p23. 다중 레이블 분류

다중 레이블 분류(Multi-label classification)

많은 실제(real-world) 사례에서, 각 인스턴스는 동시에 여러 클래스(multiple classes)에 속할 수 있다.
예시: 텍스트 주제 분류(Text topic classification), 객체 탐지(Object detection)

p24. 다중 레이블 분류

✓ 베르누이 분포(Bernoulli distribution):
확률변수 $y = 1$ 은 확률 $p$ 로, $y = 0$ 은 확률 $1 - p$ 로 발생한다.
예시:
\[p(Y = \{1,0,1,0,0\}) = p(1-p)p(1-p)(1-p) = p^2(1-p)^3\]

손실 유도(Loss derivation):
- 각 클래스 레이블 $y_c$ 는 독립적인 베르누이 확률변수로 모델링될 수 있다.
\[P(y \mid x) = \prod_{c=1}^{C} \hat{y}_c^{\,y_c} (1 - \hat{y}_c)^{\,1 - y_c}\]
- 여기에서, $\hat{y}_c = P(y_c = 1 \mid x) = \sigma(u_c)$, 클래스 c에 대한 sigmoid 출력

p25. 다중 레이블 분류

손실 유도(Loss derivation):
- 각 클래스 레이블 $y_c$ 는 독립적인 베르누이 확률변수로 모델링될 수 있다.
\[P(y \mid x) = \prod_{c=1}^{C} \hat{y}_c^{\,y_c} (1 - \hat{y}_c)^{\,1 - y_c}\]
- 여기에서, $\hat{y}_c = P(y_c = 1 \mid x) = \sigma(u_c)$, 클래스 c에 대한 sigmoid 출력
음의 로그 우도(negative log-likelihood)는 BCE 손실(binary cross-entropy loss)로 표현되며,
각 클래스에 독립적으로 적용(applied independently per class)된다.
\[\mathcal{L}_{\text{Multi-label}}(\theta) = - \sum_{n=1}^{N} \sum_{c=1}^{C} \Big[ y_{n,c} \log \hat{y}_{n,c} + (1 - y_{n,c}) \log(1 - \hat{y}_{n,c}) \Big]\]

✓ 주의(Note):

덜 일반적이지만(less common), 소프트맥스(Softmax)도 적용될 수 있다.
이 경우, 클래스 확률(class probabilities)은 반드시 합이 1이 되어야 하므로,
상호 배타적(mutually exclusive)인 레이블로 취급된다.

1. 다중 레이블 분류에서 소프트맥스의 제약
다중 레이블 분류(Multi-label classification)에서는
하나의 샘플이 여러 클래스에 동시에 속할 수 있다.
예: 이미지가 cat=1, dog=0, human=1 처럼 여러 레이블을 갖는다.
이런 경우 각 클래스의 확률을 독립적으로 계산해야 하므로
보통 시그모이드(Sigmoid)를 사용한다.
→ 확률의 합이 1일 필요가 없다.
2. 소프트맥스 적용 시의 의미
소프트맥스(Softmax)는 모든 클래스 확률의 합을 항상 1로 정규화한다.
\[\sum_{c=1}^{C} p(y=c \mid x) = 1\]
따라서 소프트맥스를 사용하면
“하나의 샘플이 오직 하나의 클래스에만 속할 수 있다”는
상호 배타적(mutually exclusive) 가정을 자동으로 따르게 된다.
즉, 소프트맥스는 다중 클래스 분류(Multi-class) 에 적합하고,
여러 레이블을 동시에 예측해야 하는 다중 레이블 분류(Multi-label) 에는 부적절하다.

p26. 분류 과제(Classification task): 요약

분류 유형과 손실:
- 이진 분류(Binary classification)
  \[\mathcal{L}_{\text{BCE}}(\theta) = -\sum_{n=1}^{N} \big[ y_n \log \hat{y}_n + (1 - y_n)\log(1 - \hat{y}_n) \big]\]
- 다중 클래스 분류(Multi-class classification)
  \[\mathcal{L}_{\text{CE}}(\theta) = -\sum_{n=1}^{N} \sum_{c=1}^{C} 1[y_n = c] \log \hat{y}_{n,c}\]
- 다중 레이블 분류(Multi-label classification)
  \[\mathcal{L}_{\text{Multi-label}}(\theta) = -\sum_{n=1}^{N} \sum_{c=1}^{C} \big[ y_{n,c}\log \hat{y}_{n,c} + (1 - y_{n,c})\log(1 - \hat{y}_{n,c}) \big]\]
전체 흐름을 생각하라!:
- 각 입력 텍스트는 사전학습된 모델(pretrained model)을 이용하여 벡터(vector)로 표현된다.
- 손실(loss)을 최소화함으로써 모델을 미세조정(fine-tuning)한다.
  (전체 파라미터를 조정할 수도 있고, 일부만 조정할 수도 있다 — full vs. partial fine-tuning)

p27. 분류: 평가(evaluation)

p28. 분류: 평가

우리의 분류기가 얼마나 잘 작동하는가?
먼저 이진 분류기(binary classifiers)부터 살펴보자:
- 이 이메일은 스팸인가?
  → spam (+) 또는 not spam (−)
- 이 게시글은 Pie 회사에 관한 것인가?
  → about pie (+) 또는 not about pie (−)
우리가 알아야 할 것들:
1. 분류기가 각 이메일 또는 게시글에 대해 무엇을 예측했는가?
2. 분류기가 무엇을 예측했어야 하는가?
  - 정답은 gold label 또는 ground-truth 라고 불린다.
  - 일반적으로 사람(human)에 의해 주석(annotated)된다.

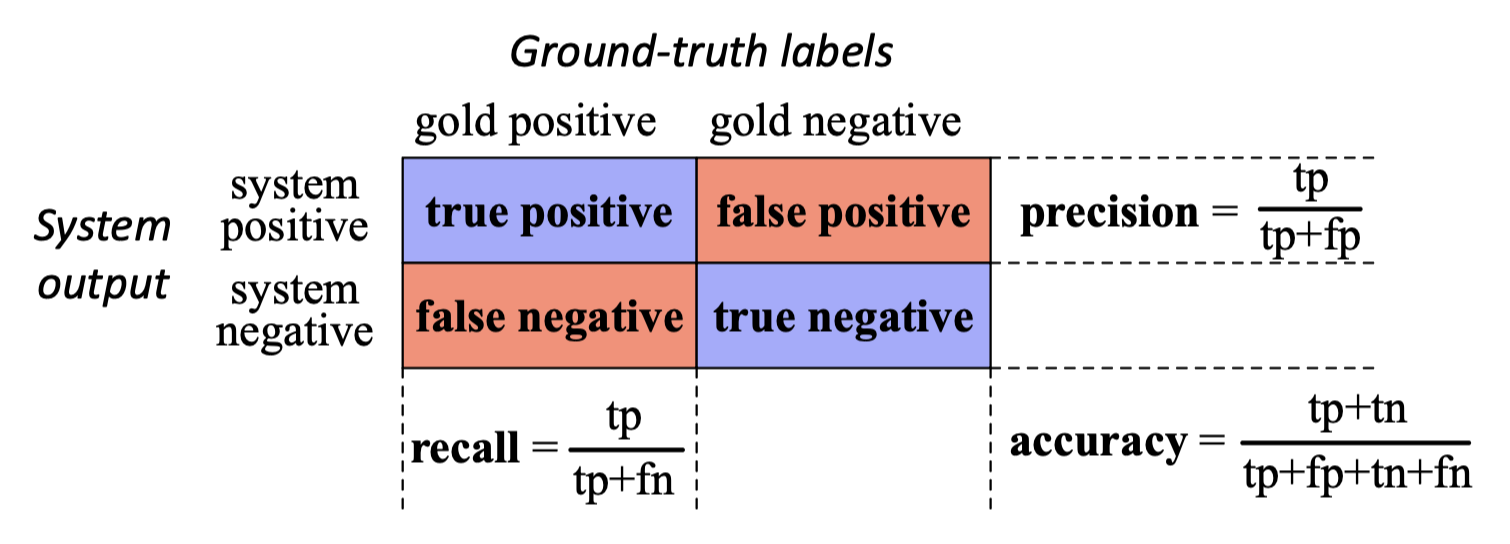
p29. 혼동 행렬

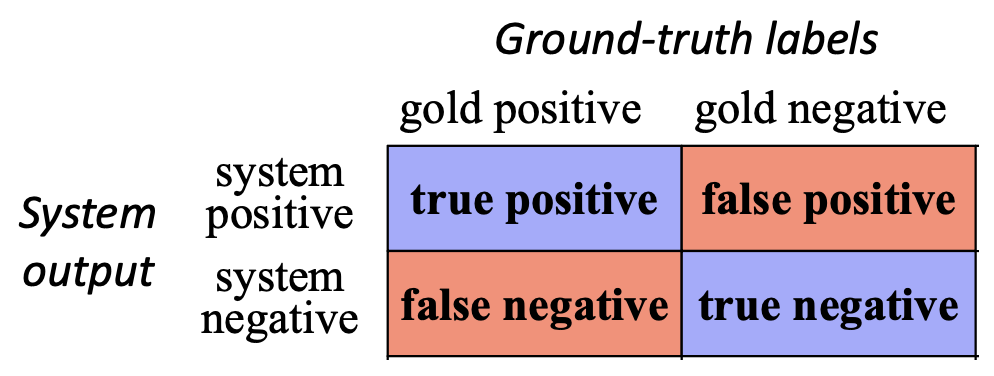
✓ 혼동 행렬(Confusion matrix)은
시스템이 정답 레이블(gold labels) 에 대해 얼마나 잘 동작하는지를 보여주는 표이다.

각 셀(cell)은 가능한 네 가지 결과 중 하나를 나타낸다:
- True Positive (TP): 실제로 긍정이고, 예측도 긍정
- False Positive (FP): 실제로 부정인데, 예측은 긍정
- False Negative (FN): 실제로 긍정인데, 예측은 부정
- True Negative (TN): 실제로 부정이고, 예측도 부정
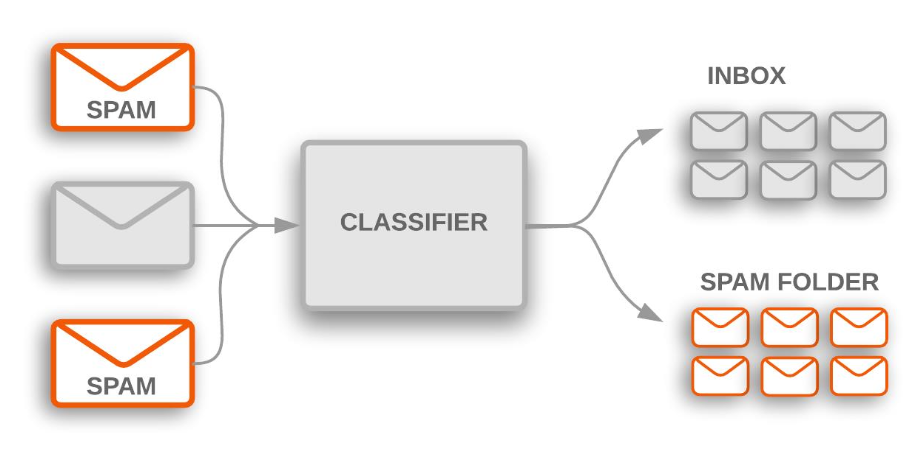
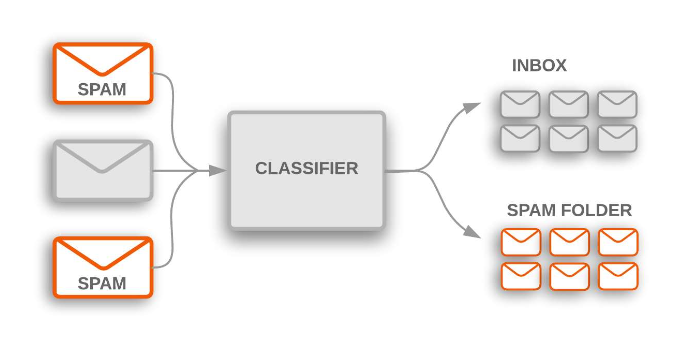
예시 (스팸 탐지, 총 100개의 이메일):
- 40개의 스팸이 정확히 스팸으로 탐지됨 → TP = 40
- 5개의 스팸이 잘못 비스팸으로 분류됨 → FN = 5
- 10개의 비스팸이 잘못 스팸으로 분류됨 → FP = 10
- 45개의 비스팸이 정확히 비스팸으로 분류됨 → TN = 45

p30. 혼동 행렬: 정확도

✓ 정확도(Accuracy)는 시스템이 정답으로 분류한 예측의 비율 을 나타낸다.
(the proportion of all predictions that the system labeled correctly)

\[\text{accuracy} = \frac{tp + tn}{tp + fp + tn + fn}\]

예시 (스팸 탐지, 100개의 이메일):
- 40개의 스팸이 정확히 스팸으로 탐지됨 → TP = 40
- 5개의 스팸이 비스팸으로 잘못 분류됨 → FN = 5
- 10개의 비스팸이 잘못 스팸으로 분류됨 → FP = 10
- 45개의 비스팸이 정확히 비스팸으로 분류됨 → TN = 45

\[\text{Accuracy} = \frac{(40 + 45)}{100} = 0.85\]

p31. 혼동 행렬: 정확도

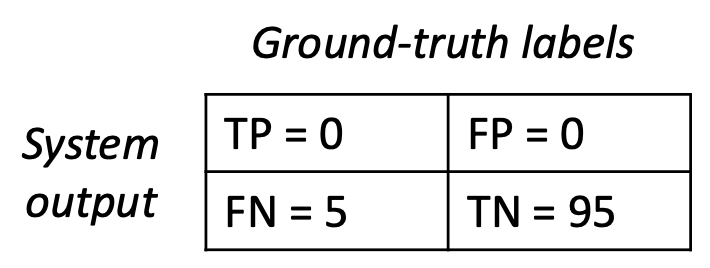
문제(Problem):
정확도(Accuracy)는 클래스가 불균형하거나 드문(imbalanced or rare) 경우
오해를 불러일으킬 수 있다(misleading).
예시 (스팸 탐지, 100개의 이메일):
- 스팸 5개, 비스팸(non-spam) 95개가 있다고 하자.
- 만약 어떤 분류기가 다음과 같이 낙관적으로 판단한다고 가정하면:
  → “모든 메일은 비스팸이다!”
\[\text{Accuracy} = \frac{(0 + 95)}{100} = 0.95\]
- 정확도는 95%로 높지만,
  실제로는 스팸 메일 탐지에는 전혀 쓸모없는(useless) 모델이다.
즉, 현실적인 많은 경우에서 정확도(accuracy)만으로는
시스템의 성능(performance)을 제대로 평가할 수 없다.

p32. 혼동 행렬: 정밀도와 재현율

✓ 정밀도(Precision) 는
예측된 긍정(predicted positives) 중에서 실제로 긍정인 것의 비율을 의미한다.

\[\text{precision} = \frac{tp}{tp + fp}\]

✓ 재현율(Recall) 은

실제 긍정(actual positives) 중에서 올바르게 예측된 것의 비율을 의미한다.

\[\text{recall} = \frac{tp}{tp + fn}\]

p33. 혼동 행렬: 정밀도와 재현율

사실, 정밀도(precision)와 재현율(recall)은 상충(trade-off) 관계 를 가진다.
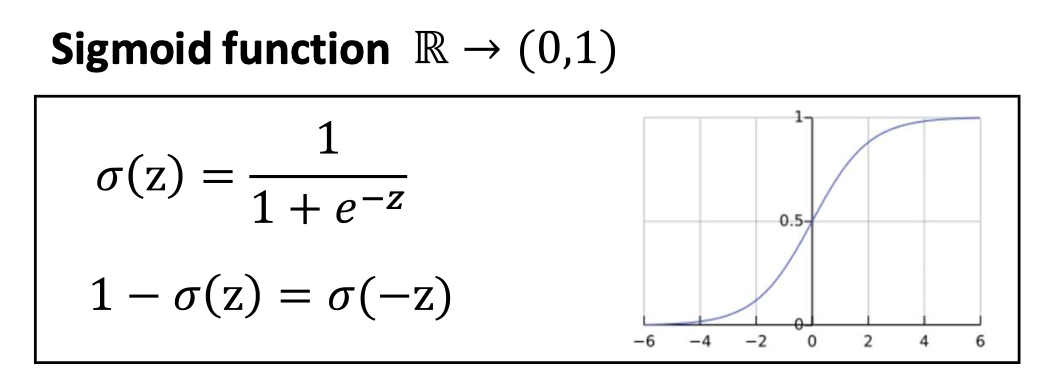
우리의 분류기가 메일이 스팸일 확률(시그모이드를 통해 0~1 로 변환됨)을 예측한다고 가정하자.
임계값(threshold, 예: 0.5)을 조정함으로써 분류기의 ‘민감도(sensitivity)’를 조절할 수 있다.
1. 임계값을 높이는 경우 (예: 0.8):
  - 우리는 더 엄격해진다. 매우 확신(confident)이 있는 예측만 스팸으로 간주된다.
  - 정밀도(Precision) ↑, 재현율(Recall) ↓
2. 임계값을 낮추는 경우 (예: 0.3):
  - 우리는 더 많은 항목을 스팸으로 분류한다.
  - 재현율(Recall) ↑, 정밀도(Precision) ↓

p34. 혼동 행렬: F1-점수

✓ F1 점수는 정밀도(Precision, P)와 재현율(Recall, R)의 조화 평균(harmonic mean) 이다.

두 값을 균형 있게 조정하며,
오직 정밀도와 재현율이 모두 높을 때만 높은 값을 가진다.

\[F_1 = \frac{2PR}{P + R}\]

예시 (스팸 탐지, 100개의 이메일):

p35. 다중 클래스(multi-class) 분류는 어떨까?

다중 클래스 설정(예: 3개 이상의 클래스)에서는
이진 혼동 행렬(binary confusion matrix)을 확장한다.
- 혼동 행렬(confusion matrix)은 $C \times C$ 표가 된다.
- 각 대각선 셀(diagonal cell) = 올바르게 분류된 샘플(클래스별 True Positive)
- 대각선이 아닌 셀(off-diagonal cell) = 잘못 분류된 샘플(클래스 간의 혼동)
- 각 클래스에 대해 정밀도(precision) / 재현율(recall) / F1 점수(F1) 를 계산할 수 있다.

예시 (메일 유형 분류: 긴급, 일반, 스팸)

Urgent class

Precision = 8 / (8 + 10 + 1) = 8 / 19 ≈ 0.421
Recall = 8 / (8 + 5 + 3) = 8 / 16 = 0.500
F1 = 2 × (0.42 × 0.5) / (0.42 + 0.5) ≈ 0.457

Normal class

Precision = 60 / (5 + 60 + 50) = 60 / 115 ≈ 0.522
Recall = 60 / (10 + 60 + 30) = 60 / 100 = 0.600
F1 = 2 × (0.52 × 0.60) / (0.52 + 0.60) ≈ 0.558

Spam class

Precision = 200 / (3 + 30 + 200) = 200 / 233 ≈ 0.859
Recall = 200 / (1 + 50 + 200) = 200 / 251 ≈ 0.797
F1 = 2 × (0.86 × 0.80) / (0.86 + 0.80) ≈ 0.827

p36. 다중 클래스(multi-class) 분류는 어떨까?

p37. 다중 클래스 분류는 어떨까?

전체 성능을 요약할 하나의 단일 지표(single metric) 가 필요하다.
- 클래스별(per-class) 지표는 두 가지 방식으로 결합된다:
1. Macro-averaging:
  각 클래스에 대해 Precision, Recall, F1을 계산한 뒤,
  이들을 클래스 전체에 걸쳐 평균을 낸다.
2. Micro-averaging:
  모든 클래스에 걸쳐 TP, FP, FN을 합산한 후,
  전체에 대해 Precision, Recall, F1을 계산한다.

예시 (Macro-averaging):

Urgent class
Precision ≈ 0.421
Recall = 0.500
F1 ≈ 0.457
Normal class
Precision ≈ 0.522
Recall = 0.600
F1 ≈ 0.558
Spam class
Precision ≈ 0.859
Recall ≈ 0.797
F1 ≈ 0.827
결합된 지표 (Macro-averaging):
Macro-Precision ≈ (0.421 + 0.522 + 0.859) / 3 ≈ 0.601
Macro-Recall ≈ (0.500 + 0.600 + 0.797) / 3 ≈ 0.632
Macro-F1 ≈ (0.457 + 0.558 + 0.827) / 3 ≈ 0.614

p38. 다중 클래스 분류는 어떨까?

전체 성능을 요약할 하나의 단일 지표(single metric) 가 필요하다.
- 클래스별(per-class) 지표는 두 가지 방식으로 결합된다:
1. Macro-averaging:
  각 클래스에 대해 Precision, Recall, F1을 계산한 뒤,
  이들을 클래스 전체에 걸쳐 평균을 낸다.
2. Micro-averaging:
  모든 클래스에 걸쳐 TP, FP, FN을 합산한 후,
  전체에 대해 Precision, Recall, F1을 계산한다.

예시 (Micro-averaging):

Combined metrics (Micro-averaging):
Micro-Precision ≈ 268 / (268 + 99) = 268 / 367 ≈ 0.730
Micro-Recall ≈ 268 / (268 + 99) = 268 / 367 ≈ 0.730
Micro-F1 ≈ 2 × 0.730 × 0.730 / (0.730 + 0.730) ≈ 0.730

p39. 다중 클래스 분류는 어떨까?

전체 성능을 요약하는 단일 지표(single metric) 가 필요하다.
- 클래스별(per-class) 지표는 두 가지 방식으로 결합된다.
  1. Macro-averaging:
    각 클래스에 대해 Precision, Recall, F1을 계산한 뒤,
    클래스 전체에 걸쳐 평균을 낸다.
  2. Micro-averaging:
    모든 클래스의 TP, FP, FN을 합산한 후,
    전체적으로 Precision, Recall, F1을 계산한다.

Macro- vs. Micro-averaging

Macro는 클래스의 크기(class size)와 관계없이 모든 클래스를 동일하게 취급한다.
- 장점(Pros):
  모든 클래스를 동일하게 다루며, 소수 클래스(minority class) 의 성능을 강조한다.
- 단점(Cons):
  희귀 클래스(rare class) 의 성능이 낮을 경우,
  전체 성능(overall performance)을 과소평가할 수 있다.
Micro는 클래스의 빈도(frequency) 에 따라 가중치를 부여하며,
큰 클래스(majority class)가 전체 지표에 더 큰 영향을 미친다.
- 장점(Pros):
  전체적인 성능을 잘 반영하며, 클래스 불균형(imbalance) 에 강하다.
- 단점(Cons):
  다수 클래스가 지표를 지배하므로, 소수 클래스의 성능을 가릴 수 있다.

예시 (메일 유형 분류: 긴급, 일반, 스팸)

Class	# of Samples	F1
Urgent	16	≈ 0.457
Normal	100	≈ 0.558
Spam	251	≈ 0.827

Macro-F1 ≈ 0.614
Micro-F1 ≈ 0.730

p40. 분류 평가: 요약

평가지표(Metrics):
- 정확도(Accuracy):
  전체 예측 중에서 올바르게 분류된 비율.
- 정밀도(Precision):
  모델이 양성이라고 예측한 것 중에서 실제로 양성인 비율.
- 재현율(Recall):
  실제 양성인 것 중에서 모델이 올바르게 양성으로 예측한 비율.
- F1-점수(F1-score):
  정밀도와 재현율의 조화 평균(harmonic mean).

평균화 방법(Averaging methods):
- 매크로 평균(Macro-averaging):
  각 클래스별로 정밀도, 재현율, F1을 계산한 후,
  이들을 클래스 전체에 대해 단순 평균한다.
  - 모든 클래스의 크기와 관계없이 동일한 비중(equal weight) 으로 취급한다.
- 마이크로 평균(Micro-averaging):
  모든 클래스의 TP(참양성), FP(거짓양성), FN(거짓음성)을 합산한 뒤,
  전체적으로 정밀도, 재현율, F1을 계산한다.
  - 클래스의 빈도(frequency) 에 따라 가중치가 부여되어,
    큰 클래스(majority class)가 결과에 더 큰 영향을 미친다.
활용 지침(Guideline):
클래스 불균형(class imbalance)이 이슈(concern)인 경우에는 매크로 평균(Macro) 을 사용하고,
전체적인 성능(overall performance)이 더 중요할 때는 마이크로 평균(Micro) 을 사용하는 것이 좋다.

p41. 다음: 제한된 레이블로 학습하기 (Learning with limited labels)

지금까지 우리는 레이블이 있는 데이터(labeled data) 를 사용하여
분류기(classifier)를 학습하는 방법 에 대해 논의하였다.
- 각 입력 텍스트 $ x $ 마다, 해당하는 클래스 레이블 $ y $ 가 주어진다고 가정하였다.
그러나 현실에서는 모든 데이터 인스턴스에 레이블이 존재할까?
이제 우리는 레이블이 부족한 데이터(scarcity of labeled data) 상황에서
이를 어떻게 다루는지를 살펴볼 것이다.

감정 분류(Sentiment classification) 예시

입력 텍스트	감정 레이블(Sentiment label)
문서 1	Positive
문서 2	Negative
문서 3	?
문서 4	…
문서 5	?

대학원 수업, 텍스트 마이닝