[텍스트 마이닝] 9. Text Classification 2
p10. 제한된 레이블로 학습하기 (Learning with limited labels)
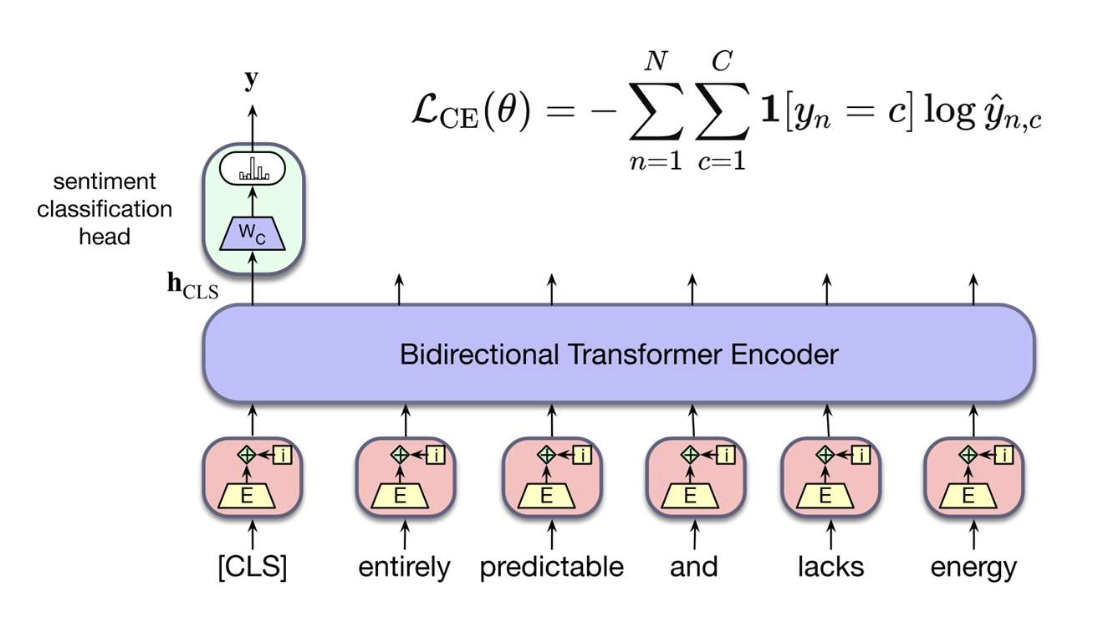
지금까지 우리는 레이블이 있는 데이터(labeled data) 를 사용하여
분류기(classifier)를 학습하는 방법 에 대해 논의하였다.- 각 입력 텍스트 $ x $ 마다, 해당하는 클래스 레이블 $ y $ 가 주어진다고 가정하였다.
그러나 현실에서는 모든 데이터 인스턴스에 레이블이 존재할까?
이제 우리는 레이블이 부족한 데이터(scarcity of labeled data) 상황에서
이를 어떻게 다루는지를 살펴볼 것이다.
감정 분류(Sentiment classification) 예시
| 입력 텍스트 | 감정 레이블(Sentiment label) |
|---|---|
| 문서 1 | Positive |
| 문서 2 | Negative |
| 문서 3 | ? |
| 문서 4 | … |
| 문서 5 | ? |
p11. 제한된 레이블로 학습하기 (Learning with limited labels)
지금까지 우리는 레이블이 있는 데이터(labeled data) 를 사용하여
분류기(classifier)를 학습하는 방법 에 대해 논의하였다.- 각 입력 텍스트 $x$ 마다, 해당하는 클래스 레이블 $y$ 가 주어진다고 가정하였다.
그러나 현실에서는 모든 데이터 인스턴스에 레이블이 존재할까?
- 이제 우리는 레이블이 부족한 데이터(scarcity of labeled data) 를
어떻게 다루는지를 살펴볼 것이다.
- 준지도 학습(Semi-supervised learning)
- “레이블이 없는 데이터를 어떻게 효과적으로 활용할 수 있을까?”
(How can we effectively leverage unlabeled data?)
- “레이블이 없는 데이터를 어떻게 효과적으로 활용할 수 있을까?”
- 다중 작업 학습(Multi-task learning)
- “하나의 작업에 레이블이 부족하다면,
관련된 다른 작업으로부터 신호를 가져올 수 있을까?”
(If one task doesn’t have enough labels, can we borrow signals from related tasks?)
- “하나의 작업에 레이블이 부족하다면,
- 적대적 학습(Adversarial learning)
- “레이블이 있는 데이터와 없는 데이터가 서로 다른 분포에서 왔다면 어떻게 할까?”
(What if labeled and unlabeled data come from different distributions?)
- “레이블이 있는 데이터와 없는 데이터가 서로 다른 분포에서 왔다면 어떻게 할까?”
p12. 준지도 학습 (Semi-supervised learning)
참고:
이 섹션의 많은 그림은 Mr. Baixu Chen과 Dr. Kevin Clark의 슬라이드에서 인용되었다.
p13. 레이블 가용성에 따른 학습 유형 (Learning types according to label availability)
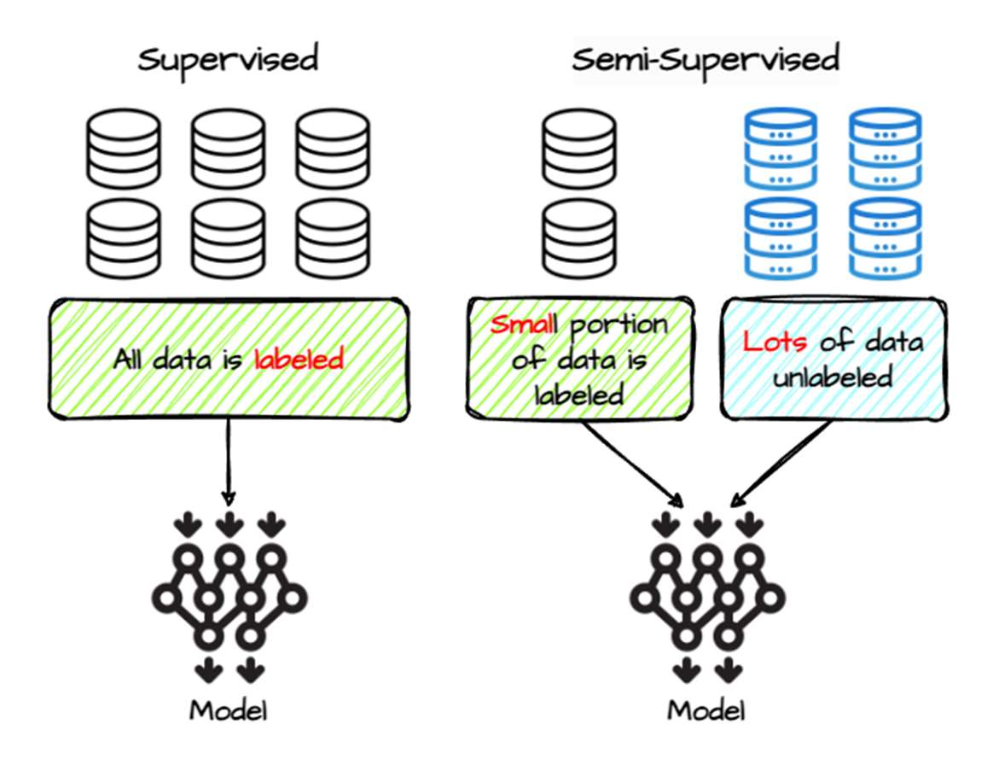
지도 학습 (Supervised learning)
\[\mathcal{D}_l = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\]- 모든 학습 샘플에는 정답 레이블 (ground-truth labels) 이 존재한다.
- 제한점 (Limitation):
레이블링(labeling)은 사람의 노력 (human effort) 을 필요로 하며
(종종 전문가의 지식이 요구됨),
매우 큰 규모의 레이블된 데이터셋을 확보하기 어렵다.
준지도 학습 (Semi-supervised learning)
\[\mathcal{D}_l = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\] \[\mathcal{D}_u = \{x_1, x_2, \ldots, x_m\}\]- 일부 샘플만 정답 레이블 을 가지고 있으며,
$m \gg n$ 이다. - 장점 (Advantage):
레이블이 없는 데이터 (unlabeled samples) 를 수집하는 것은
사람이 직접 레이블을 지정한 데이터 (human-labeled data) 를 모으는 것보다 훨씬 쉽다.
- 일부 샘플만 정답 레이블 을 가지고 있으며,
p14. 준지도 학습 (Semi-Supervised Learning, SSL)
목표 (Goal):
학습 과정에서 레이블된 데이터(labeled data) 와
비레이블 데이터(unlabeled data) 를 모두 사용하는 것이다.- 레이블된 데이터는 직접적인 감독 (direct supervision) 을 제공한다.
- 비레이블 데이터는 적절한 기법과 함께 사용될 때
모델이 더 잘 일반화 (generalize better) 하도록 돕는다.
p15. 준지도 학습 (Semi-Supervised Learning, SSL)
목표 (Goal):
학습 과정에서 레이블된 데이터(labeled data) 와
비레이블 데이터(unlabeled data) 를 모두 사용하는 것이다.- 레이블된 데이터는 직접적인 감독 (direct supervision) 을 제공한다.
- 비레이블 데이터는 적절한 기법과 함께 사용될 때
모델이 더 잘 일반화 (generalize better) 하도록 돕는다.
p16. 준지도 학습 (Semi-Supervised Learning, SSL)
목표 (Goal):
학습 과정에서 레이블된 데이터 (labeled data) 와
비레이블 데이터 (unlabeled data) 를 모두 사용하는 것이다.- 레이블된 데이터는 직접적인 감독 (direct supervision) 을 제공한다.
- 비레이블 데이터는 적절한 기법과 함께 사용될 때
모델이 더 잘 일반화 (generalize better) 하도록 돕는다.
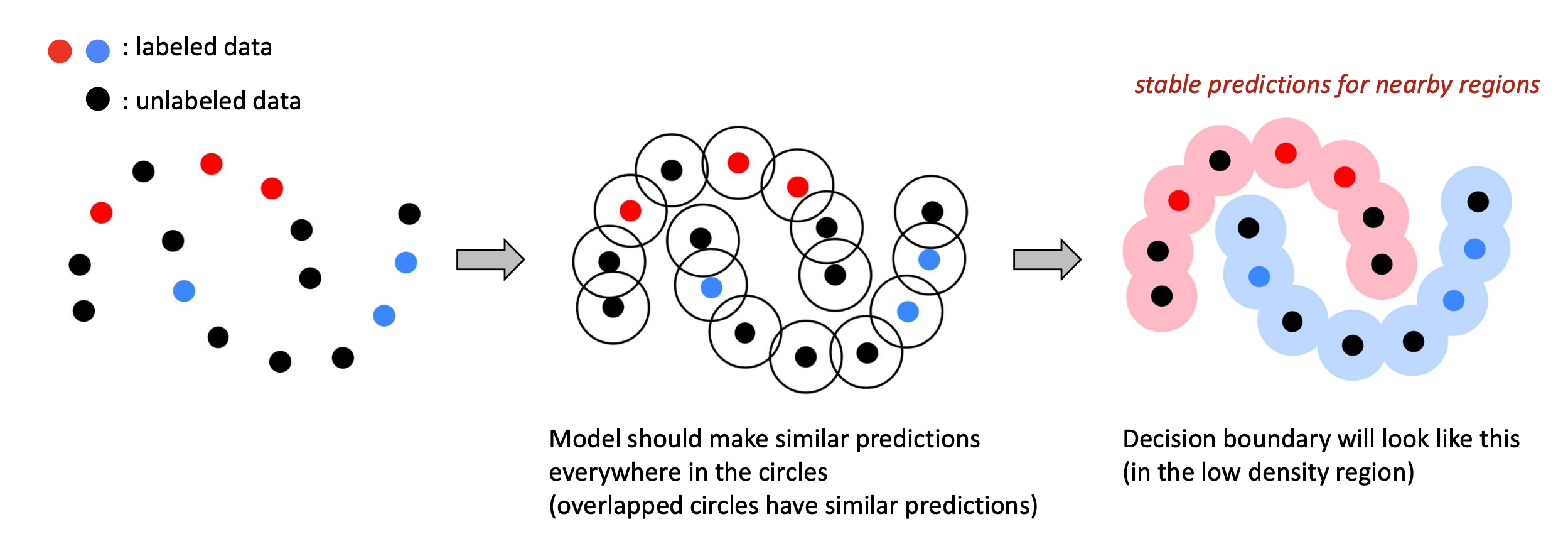
핵심 가정 (Key assumptions)
- 매끄러움 가정 (Smoothness assumption)
- 입력 공간에서 서로 가까운 데이터 포인트들은
같은 레이블 (same label) 을 가져야 한다. - “비슷하게 보이면, 실제로도 비슷하다 (If they look similar, they are similar).”
- 입력 공간에서 서로 가까운 데이터 포인트들은
- 저밀도 가정 (Low-density assumption)
- 클래스 간의 좋은 결정 경계 (decision boundary) 는
데이터가 많은 영역을 피해야 한다. - “결정 경계는 밀도가 낮은 영역을 통과해야 한다
(Boundaries should pass through low-density areas).”
- 클래스 간의 좋은 결정 경계 (decision boundary) 는
- 매끄러움 가정 (Smoothness assumption)
p17. 준지도 학습 (Semi-Supervised Learning, SSL)
- 두 가지 주요(그리고 기초적인) 접근법 (Two main and foundational approaches)
🟩 1. 의사 레이블링 (Pseudo Labeling) ← 이번 슬라이드에서 다룸
- 모델이 자신감(confidence)이 높은 예측을 사용하여
비레이블 데이터(unlabeled data) 에 레이블을 할당(assign labels) 하도록 한다. - 신뢰도가 높은 예측(confident predictions)은
모델이 유사한 레이블된 데이터(labeled examples) 로부터 이미 학습한 패턴과
대부분 일치한다.
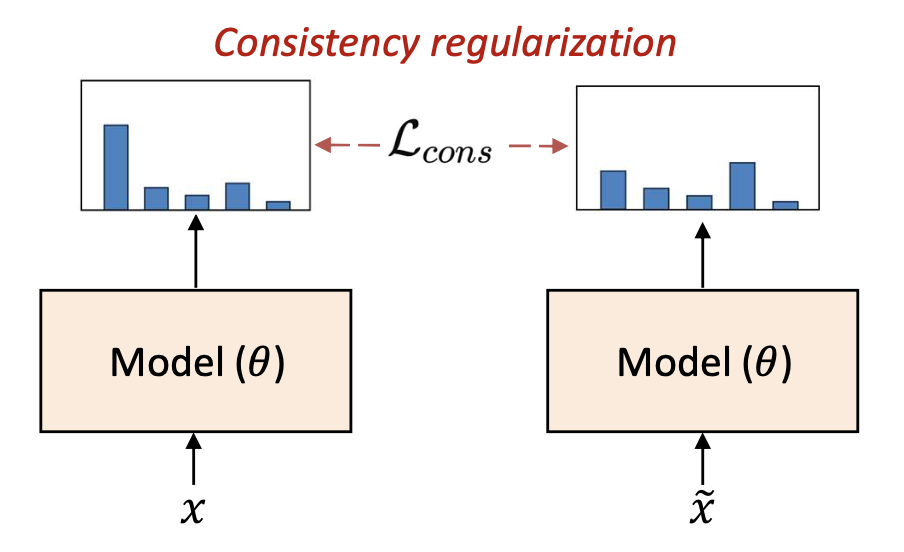
2. 일관성 정규화 (Consistency Regularization)
- 같은 입력(same input) 에 작은 변화(small changes) 를 주더라도
모델은 일관된 예측(consistent prediction) 을 해야 한다.- 예: 벡터에 작은 노이즈를 추가하거나 단어를 약간 변경하는 경우
- 이 접근법은 결정 경계(decision boundary) 가
저밀도 영역(low-density regions) 에 위치하도록 유도한다.
🔹 이번 장에서는 의사 레이블링 (Pseudo Labeling) 에 초점을 맞춘다.
다음 장에서 일관성 정규화 (Consistency Regularization) 를 다룬다.
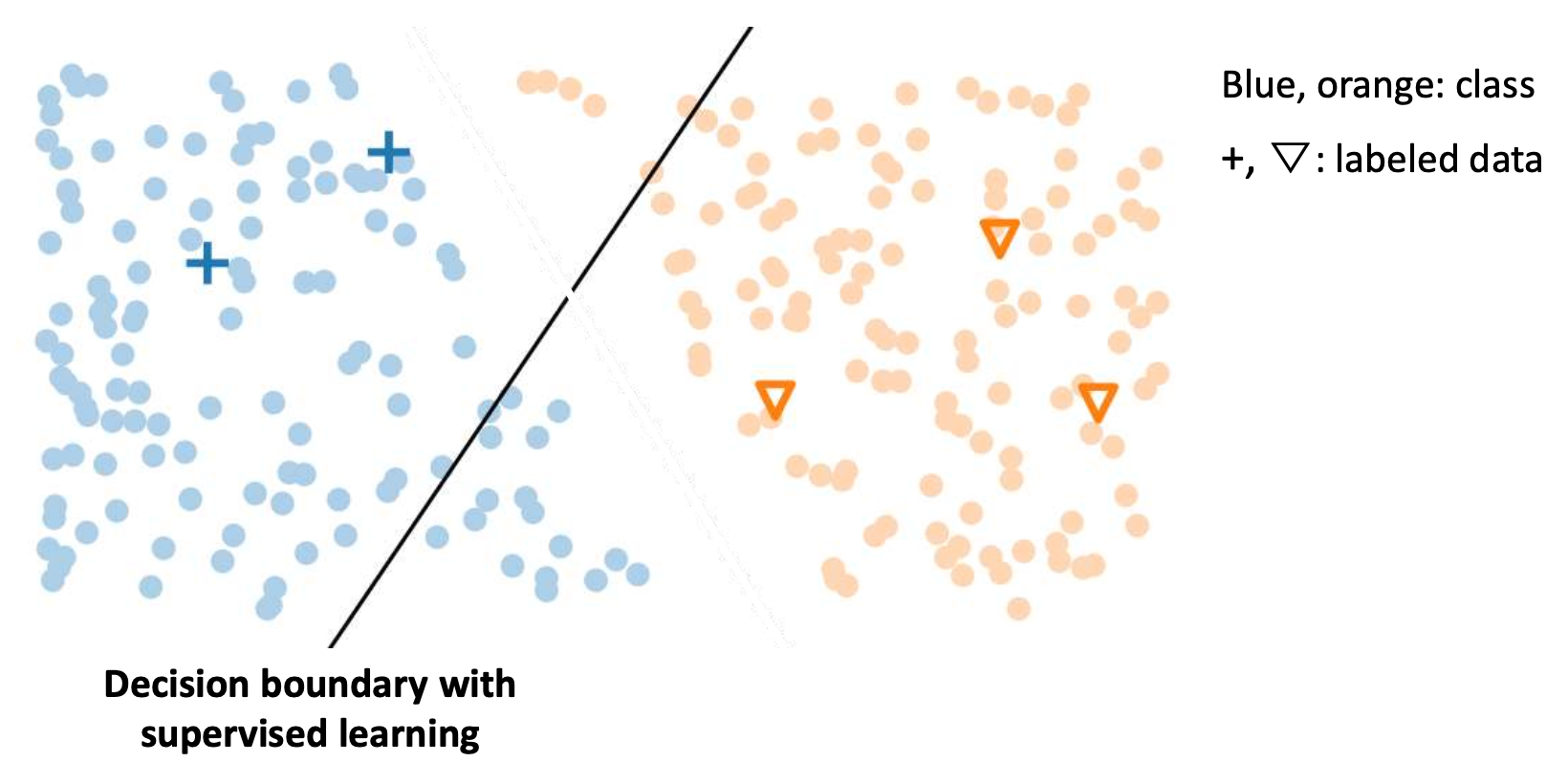
p18. 의사 레이블링 (Pseudo Labeling)
핵심 아이디어 (Key idea):
모델이 자신감(confidence) 있는 예측을 활용하여
비레이블 데이터(unlabeled data) 에 레이블을 부여(assign labels) 하도록 한다.훈련 과정에서 (During training)
레이블된 데이터(labeled data)로 학습한 모델은
특정 비레이블 샘플(certain unlabeled samples)에 대해 자신감(confident) 을 갖게 된다.- 이러한 자신감(confidence)은 모델이 이미 유사한 레이블된 샘플(similar labeled examples) 을
학습한 경험에서 비롯된다. - 이런 예측 결과(predictions)는 의사 레이블(pseudo-labels) 로 재사용되어
추가 학습에 활용될 수 있다.
- 이러한 자신감(confidence)은 모델이 이미 유사한 레이블된 샘플(similar labeled examples) 을
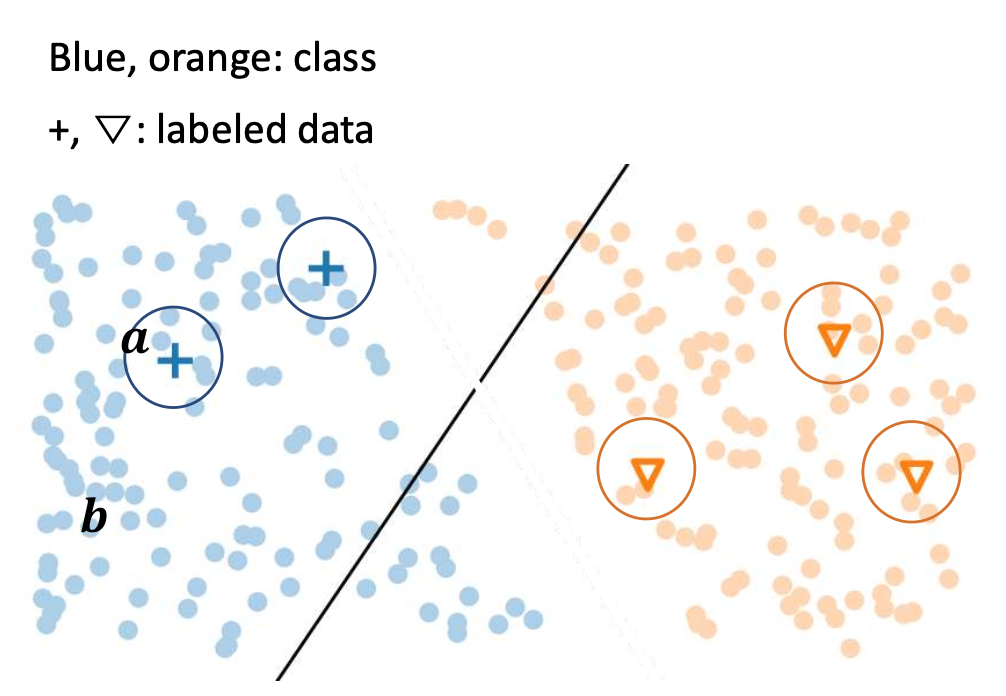
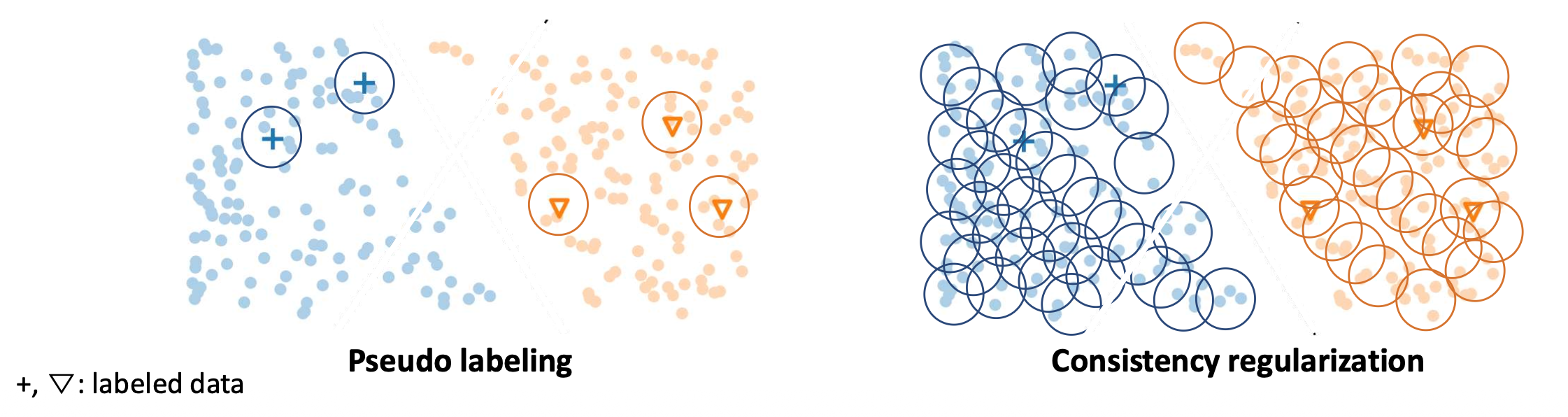
그림 설명:
파란색과 주황색 점은 클래스(class)를,
‘+’, ‘▽’ 기호는 레이블된 데이터(labeled data) 를 나타낸다.
데이터 $a$ 는 결정 경계(decision boundary)로부터 멀리 떨어져 있어
높은 확신(confidence) 을 가지며,
데이터 $b$ 는 경계 근처에 있어 낮은 확신(confidence) 을 가진다.
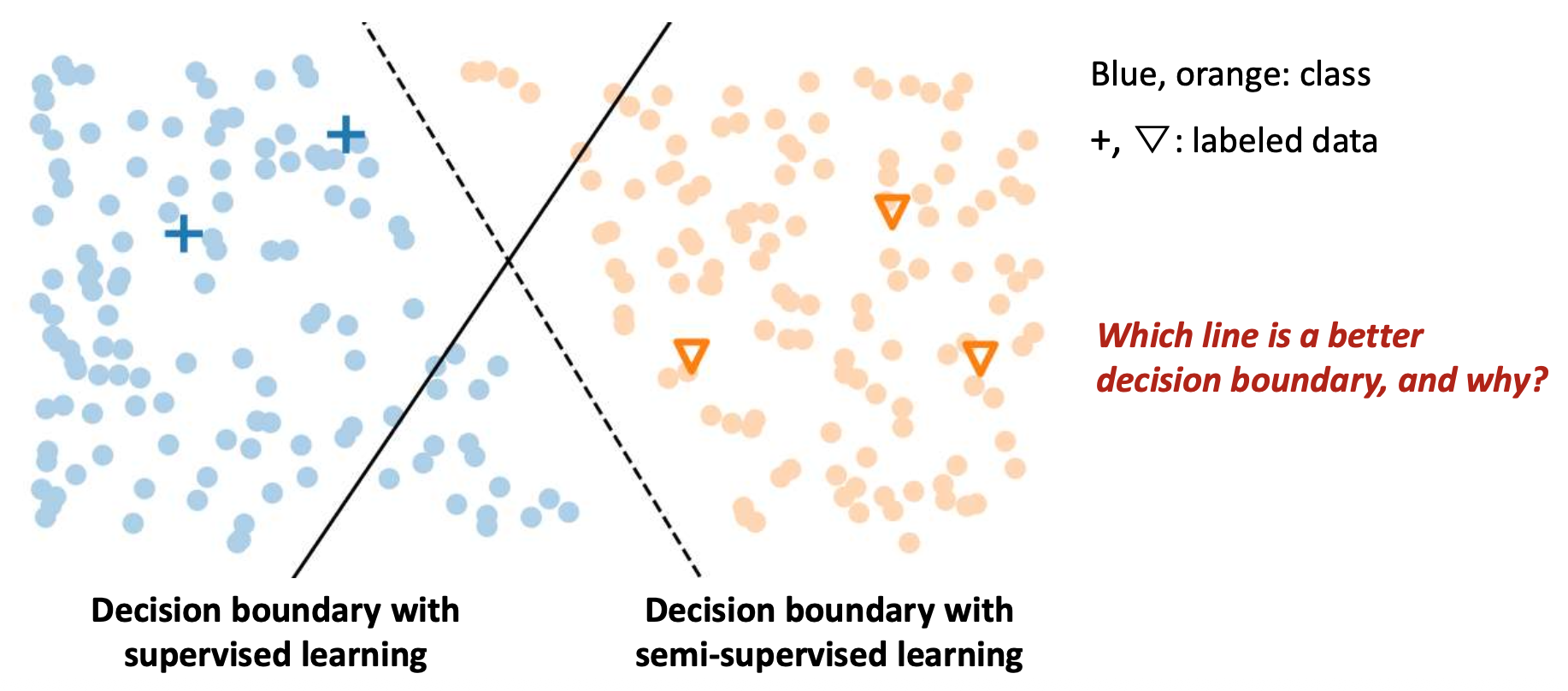
질문:
두 소프트맥스 결과 중 어느 쪽을 더 신뢰할 수 있을까?
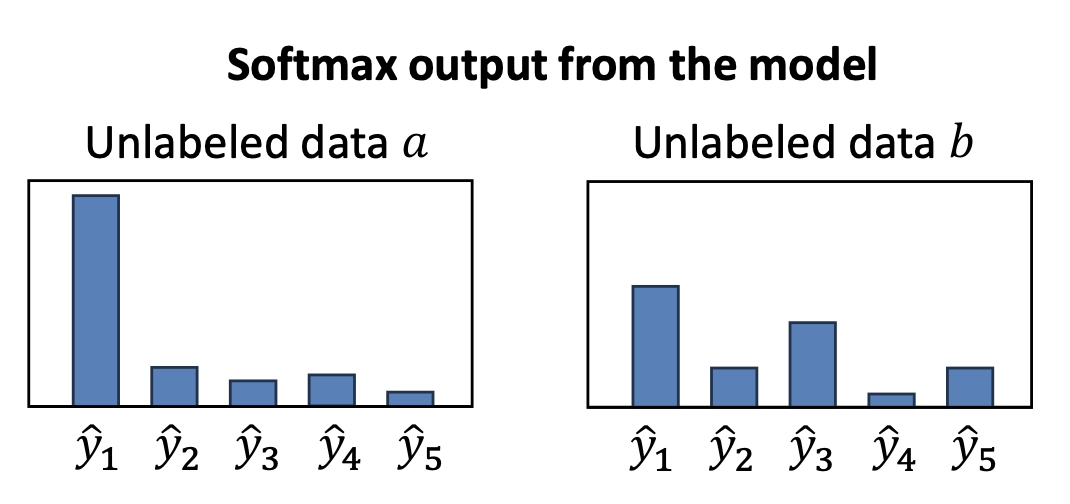
그림 설명: 각 데이터($a$, $b$)의 모델 소프트맥스 출력(softmax output) 을 보여준다.
데이터 $a$ 는 한 클래스($\hat{y}_1$)에 대해 매우 높은 확률을 가지므로
의사 레이블로 신뢰할 만하다,
반면 데이터 $b$ 는 여러 클래스에 확률이 분산되어 불확실성이 크다.
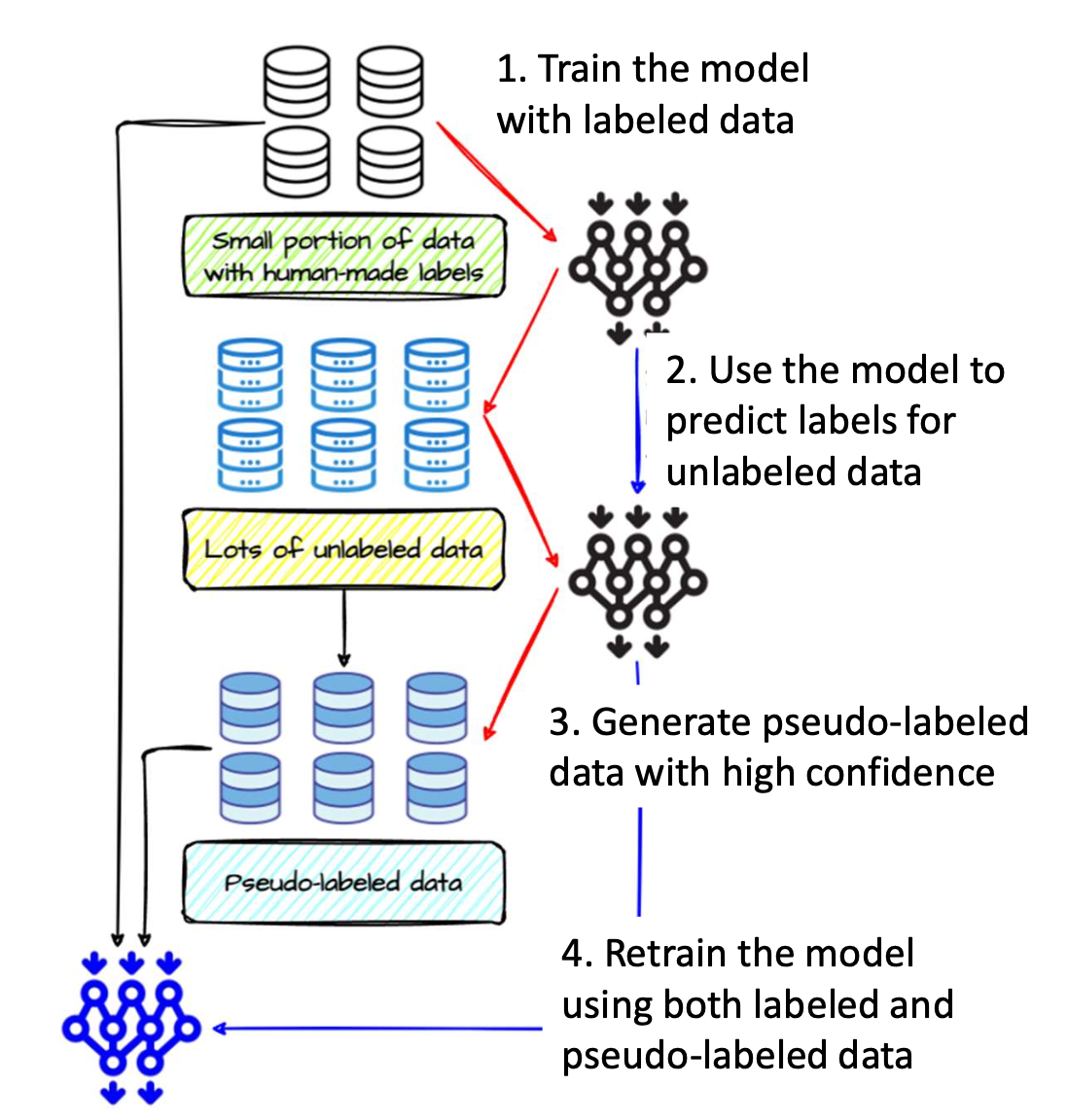
p19. 의사 레이블링 과정 (Pseudo Labeling: Process)
Step 1: 레이블된 데이터로 학습 (Train with labeled data)
- 소량의 레이블된 데이터(labeled data) 로 시작한다.
- 모델을 지도 학습(supervised way) 방식으로 학습시킨다.
Step 2: 비레이블 데이터에 대한 예측 (Predict labels for unlabeled data)
- 학습된 모델을 비레이블 데이터(unlabeled data) 에 적용한다.
- 예측 결과로부터 신뢰도(confidence) 가 서로 다른 예측 확률(max probability)을 얻는다.
Step 3: 의사 레이블 데이터 생성 (Generate pseudo-labeled data)
- 높은 신뢰도(high-confidence) 를 가지는 예측만을 의사 레이블(pseudo-label) 로 선택한다.
- 이 데이터를 진짜 레이블된 샘플(true labeled samples) 처럼 취급한다.
Step 4: 모델 재학습 (Retrain the model)
- 원래의 레이블된 데이터(labeled data) 와
새로 생성된 의사 레이블 데이터(pseudo-labeled data) 를 함께 사용하여
모델을 다시 학습시킨다.
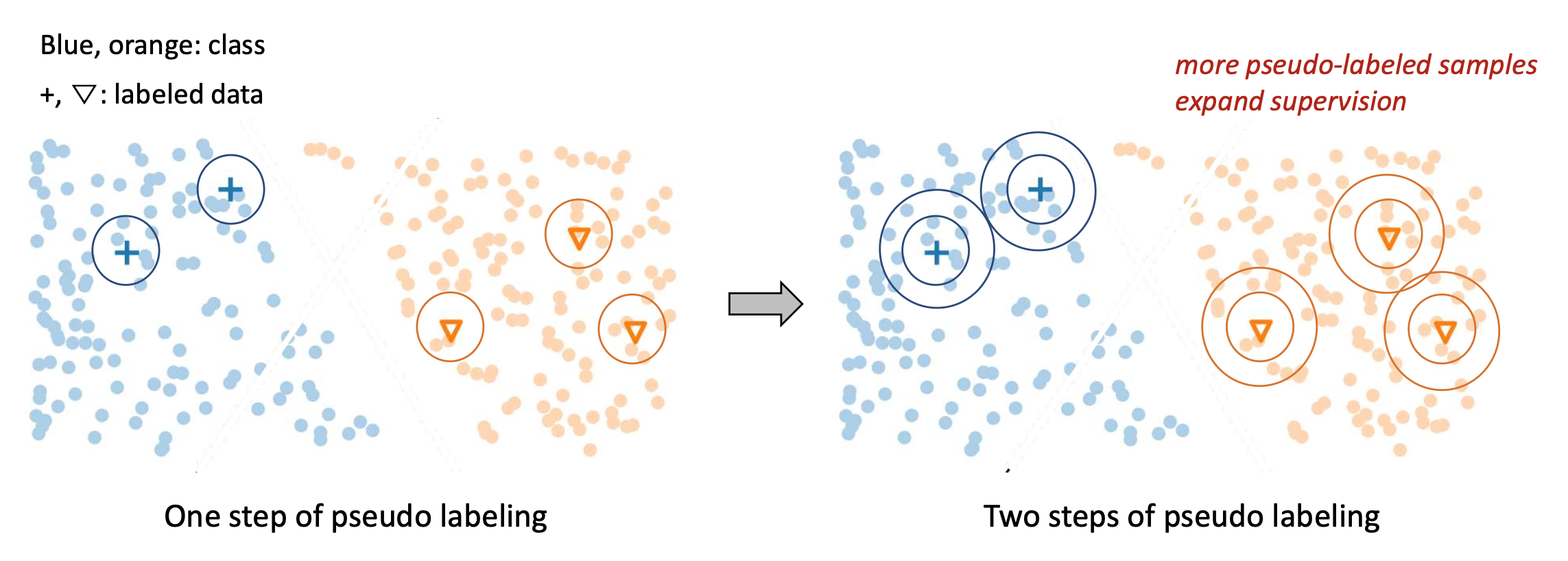
p20. 의사 레이블링: 자기 학습 (Pseudo Labeling: Self-Training)
의사 레이블로 학습함으로써, 모델은 점진적으로 비레이블 데이터에 대한 더 많은 지식을 얻게 된다.
자기 학습(Self-training):
의사 레이블링 과정을 반복하여 이 지식을 전파(propagate this knowledge) 하고 감독(supervision) 을 확장한다.- 자기 학습(Self-training) = 반복적 의사 레이블링(Iterative pseudo-labeling)
p21. 의사 레이블링: 자기 학습 (Pseudo Labeling: Self-Training)
의사 레이블로 학습함으로써, 모델은 점진적으로 비레이블 데이터(unlabeled data) 에 대한 더 많은 지식을 얻게 된다.
자기 학습(Self-training):
의사 레이블링 과정을 반복하여 이 지식을 전파(propagate this knowledge) 하고 감독(supervision)을 확장한다.- 자기 학습(Self-training) = 반복적 의사 레이블링(Iterative pseudo-labeling)
알고리즘 1. 의사 레이블링을 이용한 자기 학습(Self-training with Pseudo-Labeling)
- 입력(Input): 레이블된 데이터셋 $D_l$, 비레이블 데이터셋 $D_u$, 신뢰 임계값(confidence threshold) $\tau$
- 출력(Output): 학습된 모델 $f$
- 기본 모델 $f$ 를 $D_l$ 에서 학습한다.
- 수렴하지 않은 동안 while 루프 실행:
- $D_u$ 내의 샘플에 대해 모델 $f$ 를 사용하여 의사 레이블(pseudo-labels) 예측
- 신뢰도가 높은(high-confidence) 예측만 선택:
$D_p = \{ (x, \hat{y}) \mid \max f(x) \ge \tau \}$ - 학습 데이터셋 업데이트: $D_l \leftarrow D_l \cup D_p$
- 확장된 $D_l$ 로 모델 $f$ 업데이트
- while 루프 종료
- $f$ 반환(return)
p22. 의사 레이블링: 요약 (Pseudo Labeling: Summary)
의사 레이블링은 비레이블 데이터(unlabeled data) 를 활용하기 위한 단순하고 효과적인 방법(simple and effective way) 이다.
그러나 모델의 예측은 사람이 직접 단 레이블(human annotations) 만큼 정확하지 않다(not as accurate).
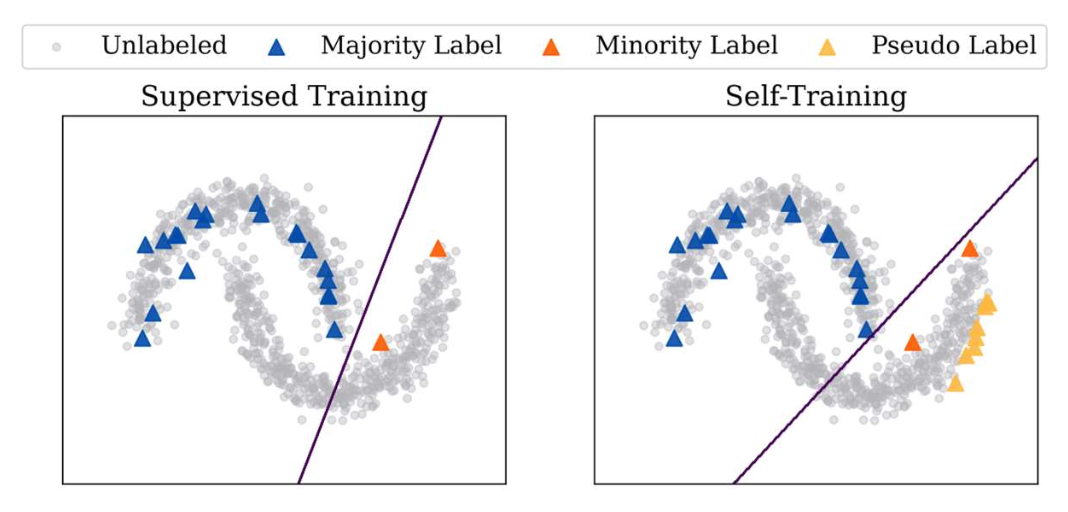
- 최악의 경우, 의사 레이블링은 오히려 레이블된 데이터만 사용하는 것보다 더 나쁜 성능(performance) 을 낼 수도 있다.
- 소수 클래스(minority class, 주황색) 의 레이블이 제한적인 경우,
모델은 전체 공간에서 정확한 예측을 수행하는 데 어려움을 겪는다. - 의사 레이블은 비레이블 데이터의 일부 패턴만(partial patterns) 포착할 수도 있다.
제한점(Limitations)
- 오류 전파(Error propagation): 잘못된 의사 레이블이 학습 과정에서 오류를 강화시킨다.
- 과잉 확신(Overconfidence): 모델이 자신의 잘못된 예측에 대해서도 과도하게 확신하게 될 수 있다.
p23. 준지도 학습 (Semi-Supervised Learning, SSL)
- 두 가지 주요(그리고 기초적인) 접근법 (Two main and foundational approaches)
1. 의사 레이블링 (Pseudo Labeling)
- 모델이 자신감(confidence)이 높은 예측을 사용하여
비레이블 데이터(unlabeled data) 에 레이블을 할당(assign labels) 하도록 한다. - 신뢰도가 높은 예측(confident predictions)은
모델이 유사한 레이블된 데이터(labeled examples) 로부터 이미 학습한 패턴과
대부분 일치한다.
🟨 2. 일관성 정규화 (Consistency Regularization) ← 이번 슬라이드에서 다룸
- 같은 입력(same input) 에 작은 변화(small changes) 를 주더라도
모델은 일관된 예측(consistent prediction) 을 해야 한다.- 예: 벡터에 작은 노이즈를 추가하거나 단어를 약간 변경하는 경우
- 이 접근법은 결정 경계(decision boundary) 가
저밀도 영역(low-density regions) 에 위치하도록 유도한다.
🔹 이번 장에서는 일관성 정규화 (Consistency Regularization) 에 초점을 맞춘다.
이전 장에서는 의사 레이블링 (Pseudo Labeling) 을 다뤘다.
p24. 일관성 정규화 (Consistency Regularization)
핵심 아이디어 (Key idea)
같은 입력(same input) 에 작은 변화(small changes) 를 주더라도
모델은 일관된 예측(consistent prediction) 을 해야 한다.- 작은 섭동(perturbation, 예: 노이즈 추가, 데이터 증강 등)을 적용해도
예측(prediction)은 안정적으로 유지되어야 한다. - 즉, 서로 가까운 데이터 포인트(nearby data points) 는
유사한 예측(similar predictions) 을 가져야 한다.
- 작은 섭동(perturbation, 예: 노이즈 추가, 데이터 증강 등)을 적용해도
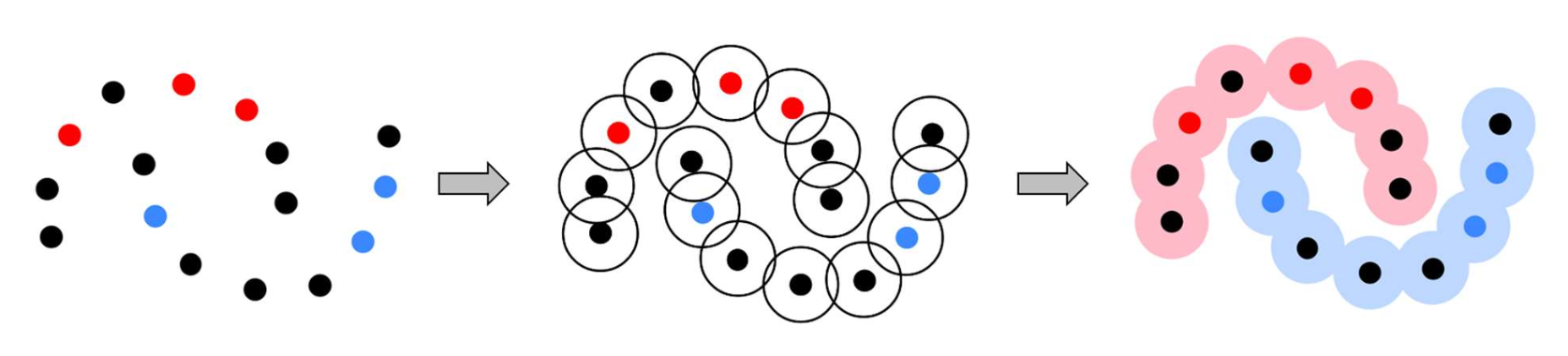
- 빨강 (red): 레이블된 데이터 (labeled data)
- 파랑 (blue): 레이블된 데이터 (labeled data)
검정 (black): 비레이블 데이터 (unlabeled data)
모델은 원 안에 있는 모든 포인트에서 유사한 예측(similar predictions) 을 해야 하며,
겹치는 원(overlapped circles) 은 서로 비슷한 예측을 갖게 된다.- 이렇게 되면 모델의 결정 경계(decision boundary) 는
저밀도 영역(low-density region) 에 형성된다.
p25. 일관성 정규화 (Consistency Regularization)
핵심 아이디어 (Key idea)
같은 입력(same input) 에 작은 변화(small changes) 를 주더라도
모델은 일관된 예측(consistent prediction) 을 해야 한다.- 작은 섭동(perturbation)을 추가한다. (예: 노이즈, 증강) → 예측은 안정적으로 유지되어야 한다.
구체화 (Instantiation):
\[\mathcal{L} = \mathcal{L}_{sup}(D_l) + \lambda \mathcal{L}_{cons}(D_u)\] \[\mathcal{L}_{cons} = \mathbb{E}_{x \in D_l \cup D_u} [ \| f(x; \theta) - f(\tilde{x}; \theta) \|^2 ]\]$ x $: 원래 입력 (original input),
$ \tilde{x} $: 섭동이 추가된 입력 (perturbed input)섭동을 추가하는 방법 (How to add perturbations):
- 임베딩에 작은 랜덤 노이즈 추가
- 단어 드롭아웃(word dropout) 또는 마스킹(masking)
- 데이터 증강(data augmentation, 예: 회전(rotation), 자르기(crop) 등)
- 그 외 여러 가지 방법
p26. 일관성 정규화: 통찰 (Consistency Regularization: Insights)
✓ 정규화는 모델이 데이터를 암기하지 않도록 하여 과적합(overfitting)을 방지한다.
구체화 (Instantiation):
\[\mathcal{L} = \mathcal{L}_{sup}(D_l) + \lambda \mathcal{L}_{cons}(D_u)\] \[\mathcal{L}_{cons} = \mathbb{E}_{x \in D_l \cup D_u} [ \| f(x; \theta) - f(\tilde{x}; \theta) \|^2 ]\]$ x $: 원래 입력 (original input),
$ \tilde{x} $: 섭동이 추가된 입력 (perturbed input)통찰 1 (Insight 1):
원래 입력과 섭동된 입력에 대해
예측된 확률 분포(predicted probability distributions) 가
유사하도록 강제한다.- 모델은 섭동된 입력에서 자연스럽게 신뢰도가 낮아지는 경향이 있다.
그 결과, 모델의 전반적인 신뢰도(confidence) 가 낮아진다.
- 정규화 효과 (Regularization effect):
모델이 데이터를 단순히 외우는 것(과적합, overfitting)을 방지하고,
과도한 자신감(overconfidence)을 갖지 않도록 한다.
p27. 일관성 정규화: 통찰 (Consistency Regularization: Insights)
구체화 (Instantiation):
\[\mathcal{L} = \mathcal{L}_{sup}(D_l) + \lambda \mathcal{L}_{cons}(D_u)\] \[\mathcal{L}_{cons} = \mathbb{E}_{x \in D_l \cup D_u} [ \| f(x; \theta) - f(\tilde{x}; \theta) \|^2 ]\]$ x $: 원래 입력 (original input),
$ \tilde{x} $: 섭동된 입력 (perturbed input)통찰 2 (Insight 2):
의사 레이블링(pseudo labeling) 은 신뢰도가 높은 샘플(high-confidence samples) 에만 의존하지만,
일관성 정규화(consistency regularization) 는 모든 비레이블 데이터(all unlabeled data) 를 사용한다.- 이는 데이터셋의 훨씬 더 큰 부분을 활용할 수 있게 한다.
p28. 일관성 정규화: 시간적 앙상블 (Consistency Regularization: Temporal Ensemble)
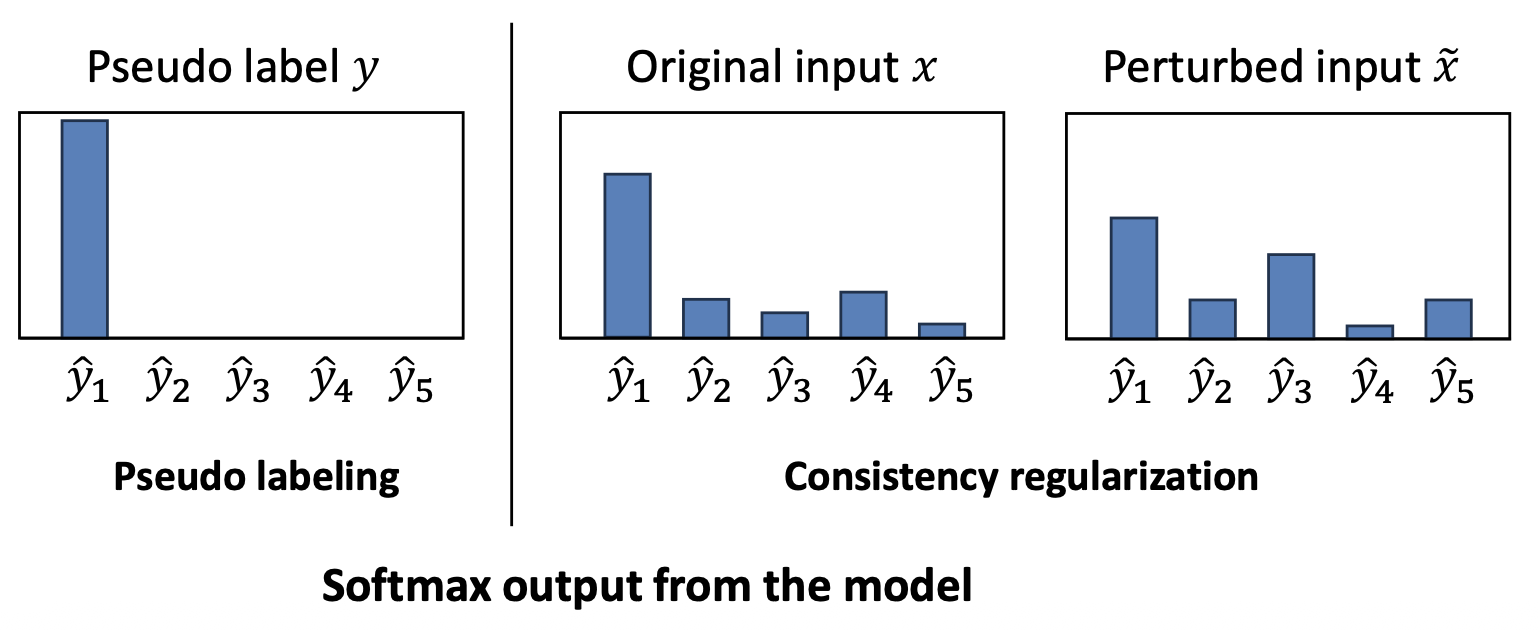
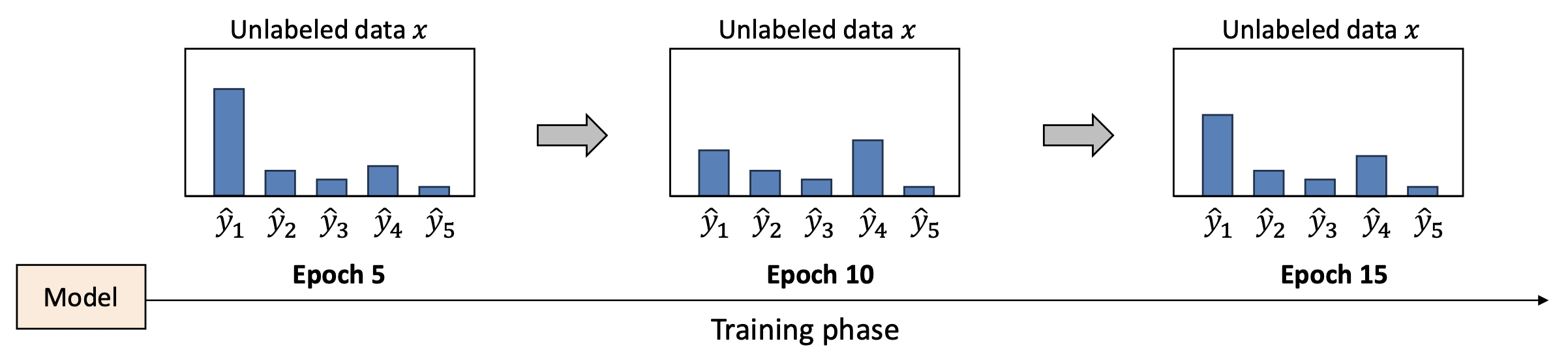
하나의 실제적인 문제 (One practical issue):
학습 과정에서 모델은 종종 비레이블 데이터(unlabeled data) 에 대해
불안정한 예측(unstable prediction) 을 한다.- 예측값은 섭동(perturbation)이 없더라도 에폭(epoch) 간에 변동한다.
- 섭동이 추가되면 이러한 불안정성은 더욱 심해지며,
이는 전체 학습을 불안정하게 만든다.
→ 비레이블 데이터의 경우, 실제 정답 레이블(gold label)이 존재하지 않는다.
→ 모델의 예측은 매우 불안정해지기 쉽다!
[모델의 Softmax 출력 예시 (Softmax output from the model)]
p29. 일관성 정규화: 시간적 앙상블 (Consistency Regularization: Temporal Ensemble)
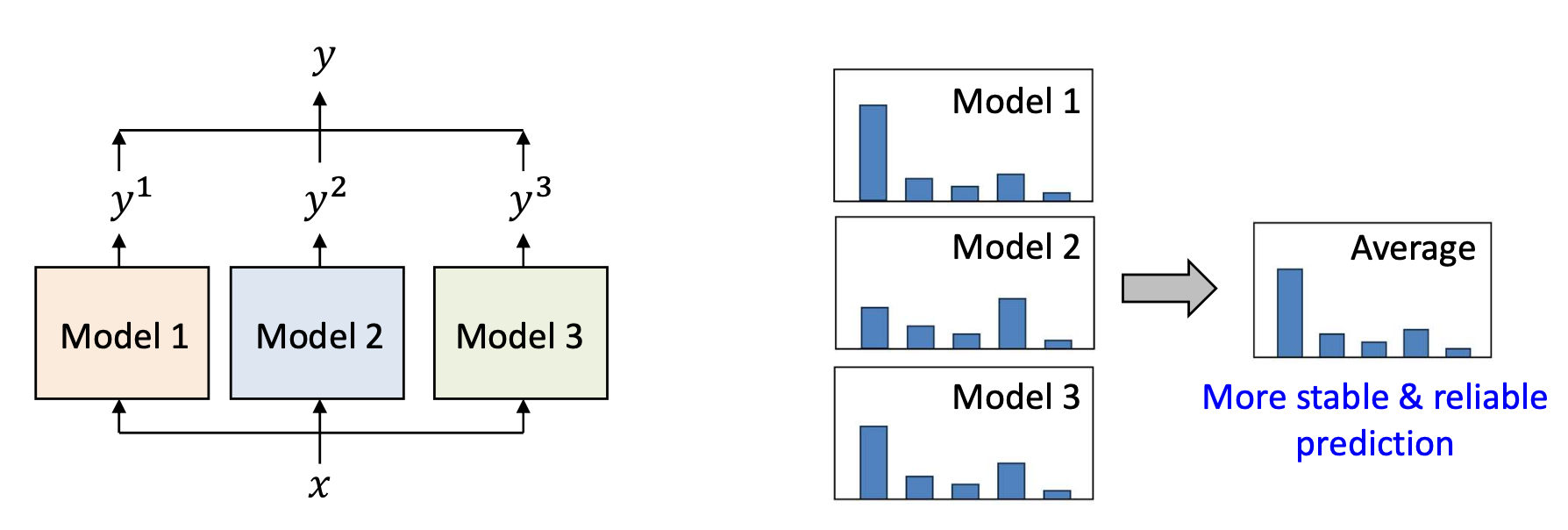
- 모델의 예측을 어떻게 안정화할 수 있을까?
✓ 모델 앙상블 (Model ensemble)
- 하나의 모델(single model)을 사용하는 대신,
여러 모델을 학습시키고 그들의 예측을 통합(aggregate) 한다.
이유 (Why?)
- 서로 다른 초기화(different initializations)는
서로 다른 수렴된 파라미터(converged parameters)를 만든다. - 예측을 평균(averaging)함으로써 분산(variance) 이 줄어들며,
더 안정적이고 신뢰할 수 있는 예측(more stable & reliable prediction) 이 가능해진다.
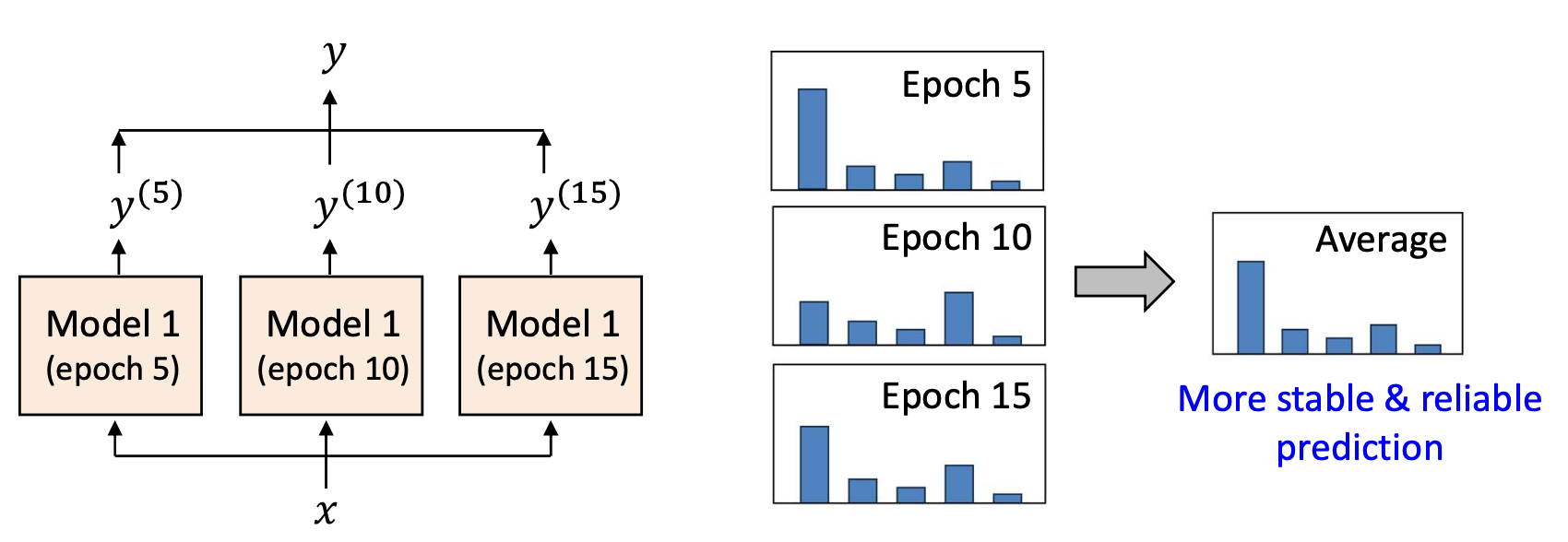
p30. 일관성 정규화: 시간적 앙상블 (Consistency Regularization: Temporal Ensemble)
- 모델의 예측을 어떻게 안정화(stabilize)할 수 있을까?
✓ 시간적 앙상블 (Temporal ensemble)
여러 모델을 독립적으로 학습시키는 것은 비용이 많이 든다.
“하나의 모델만으로 비슷한 효과를 얻을 수 있을까?”핵심 아이디어 (Key idea):
동일한 모델의 서로 다른 학습 시점(epoch) 에서의 예측값들을 통합(aggregate) 하는 것이다.시간에 따라 예측을 평균(averaging)하면, 변동(fluctuation) 이 줄어들고
예측이 더 안정적이고 신뢰할 수 있게(stable & reliable) 된다.
p31. 일관성 정규화: 시간적 앙상블 (Consistency Regularization: Temporal Ensemble)
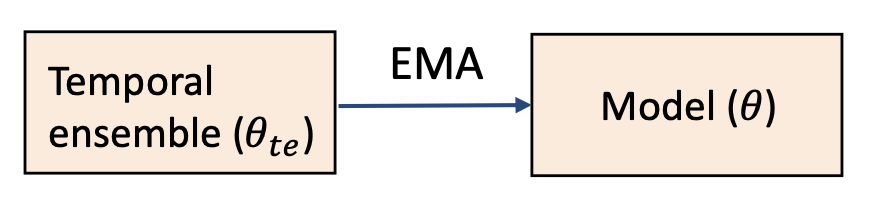
✓ 시간적 앙상블 (Temporal ensemble)
핵심 아이디어 (Key idea):
동일한 데이터에 대한 예측을 서로 다른 학습 시점(epoch) 에서 통합(aggregate) 한다.구현 방식 (Instantiation):
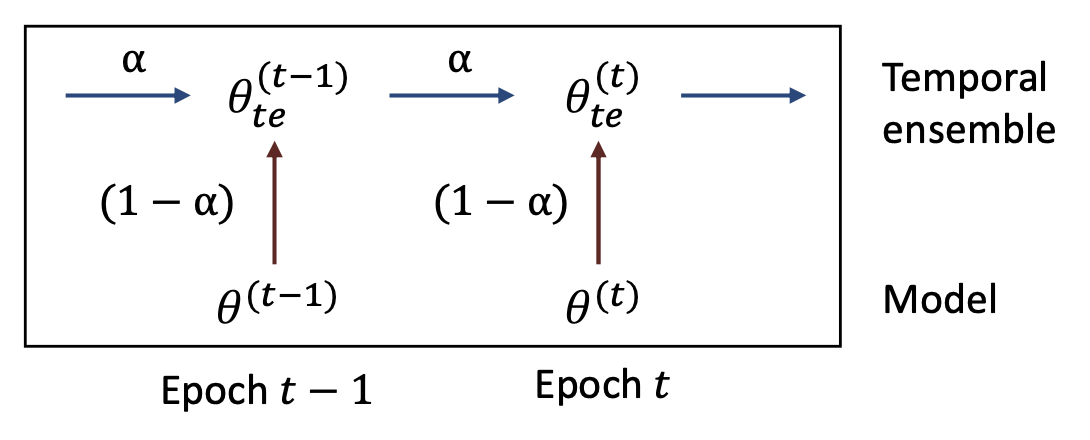
\[\theta_{te}^{(t)} \leftarrow \alpha \theta_{te}^{(t-1)} + (1 - \alpha)\theta^{(t)}\]
모델 파라미터를 지수이동평균(Exponential Moving Average, EMA) 으로 앙상블한다.$ \theta^{(t)} $: 학습 시점 $t$ 에서의 모델 파라미터
$ \theta_{te}^{(t)} $: 학습 시점 $t$ 에서의 시간적 앙상블 파라미터
$ \alpha $: 과거 지식을 얼마나 반영할지를 조절하는 하이퍼파라미터
- 시간적 앙상블은 학습 과정 동안 이전 모델 파라미터(past model parameters) 를 통합한다.
- 최신 모델(latest model)을 천천히 따라가면서(slowly follows),
에폭(epoch) 간의 예측 평균화(averaging predictions across epochs) 를 통해
훨씬 더 안정적인(stable) 결과를 얻는다.
시간적 앙상블 업데이트 프로세스(Temporal ensemble update process)
- 이전 앙상블 파라미터($\theta_{te}^{(t-1)}$)와
현재 모델 파라미터($\theta^{(t)}$)를
$\alpha$ 와 $(1 - \alpha)$ 가중합으로 결합하여
새로운 앙상블 파라미터($\theta_{te}^{(t)}$)를 생성한다.
p32. 일관성 정규화: 시간적 앙상블 (Consistency Regularization: Temporal Ensemble)
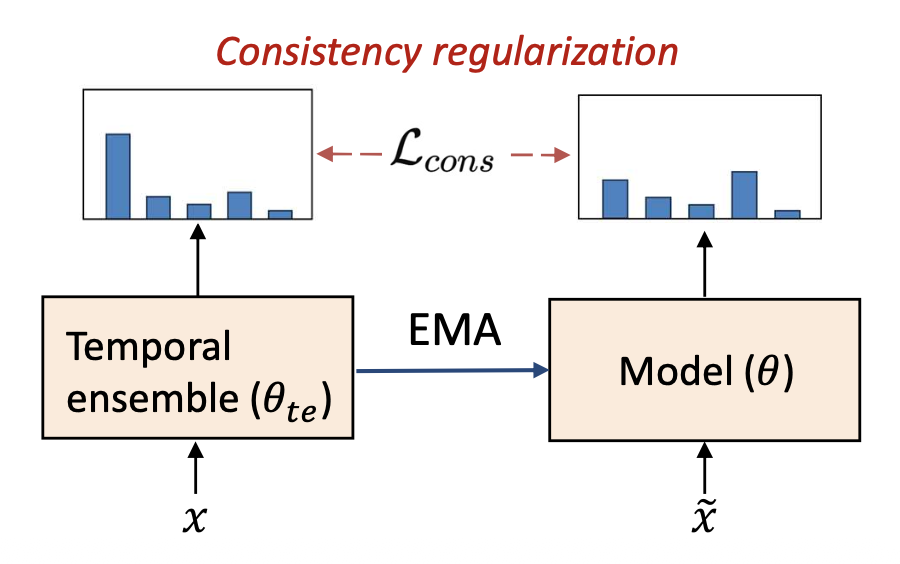
시간적 앙상블을 이용한 일관성 정규화 (Consistency regularization with temporal ensemble)
- 시간적 앙상블에서의 예측 $f(x; \theta_{te})$ 를 사용한다.
- 이는 더 신뢰할 수 있고 안정적인 가이드(more reliable and stable guidance) 를
비레이블 데이터(unlabeled data)에 제공한다.
원래 버전 (The original version):
\[\mathcal{L}_{cons} = \mathbb{E}_{x \in D_l \cup D_u} \left[ \| f(x; \theta) - f(\tilde{x}; \theta) \|^2 \right]\]
알고리즘 2 시간적 앙상블을 이용한 일관성 정규화 (Consistency Regularization with Temporal Ensemble)
- 입력 (Input): 레이블된 데이터셋 $D_l$, 비레이블 데이터셋 $D_u$
- 출력 (Output): 학습된 모델 $f(\cdot; \theta)$
- 파라미터 $\theta$, 앙상블 파라미터 $\theta_{te}$ 초기화: $\theta_{te} \leftarrow \theta$
- for epoch $t = 1$ to $T$ do
- $D_l$ 에 대해 지도 학습 손실 $ \mathcal{L}_{sup} $ 계산
- $D_u$ 에 대해 일관성 손실 \(\mathcal{L}_{cons} = \| f(x_u; \theta_{te}) - f(\tilde{x}_u; \theta) \|^2\) 계산
- \(\mathcal{L} = \mathcal{L}_{sup} + \lambda \mathcal{L}_{cons}\) 최소화를 통해 $\theta$ 업데이트
- 앙상블 파라미터 업데이트: $ \theta_{te}^{(t)} \leftarrow \alpha \theta_{te}^{(t-1)} + (1 - \alpha)\theta^{(t)} $
- end for
- 반환 (Return): $f(\cdot; \theta)$
p33. 일관성 정규화 (Consistency Regularization): 요약
핵심 아이디어:
동일한 입력(same input)에 작은 변화(small changes) 를 주더라도
모델은 일관된 예측(consistent predictions) 을 해야 한다.- 장점 (Pros)
- 비레이블 데이터(unlabeled data)의 효율적 활용:
작은 섭동(perturbations)만 필요하며, 다양한 비레이블 데이터에 적용 가능하다. - 단순한 개념(Simple concept):
기존 모델에 정규화 항(regularizer)으로 쉽게 추가할 수 있다.
- 비레이블 데이터(unlabeled data)의 효율적 활용:
- 단점 (Cons)
- 섭동 민감성(Perturbation sensitivity):
효과는 노이즈(noise)나 데이터 증강(augmentation)의 선택에 따라 달라진다.- 연구자들이 여전히 활발히 연구 중인 주제이다.
- 약한 직접적 지도(Weak direct guidance):
명시적인 레이블을 제공하지 않기 때문에
결정 경계(boundary)가 여전히 불확실할 수 있다.
- 섭동 민감성(Perturbation sensitivity):
p34. 준지도 학습 (Semi-Supervised Learning, SSL): 요약
- 우리가 다룬 두 가지 주요(그리고 기초적인) 접근법
- 의사 레이블링 (Pseudo Labeling)
- 강점 (Strength): 실제 레이블(ground truth)과 같은 직접적인 학습 신호(direct training signal) 를 제공한다.
- 한계 (Limitation): 모델이 잘못된 예측에 대해 과도하게 확신(overconfident) 할 경우,
오류를 증폭(amplify errors) 시킬 수 있다.
- 일관성 정규화 (Consistency Regularization)
- 강점 (Strength): 모델이 과도하게 확신(overconfident) 하는 것을 방지하는
정규화 항(regularizer) 로 작용한다. - 한계 (Limitation): 명시적인 레이블이 주어지지 않기 때문에
약한 지도(weak guidance) 를 제공한다.
- 강점 (Strength): 모델이 과도하게 확신(overconfident) 하는 것을 방지하는
- 이 두 접근법은 상호 보완적인 관계(complementary relationship) 를 가진다.
- 의사 레이블링은 강하지만 잡음이 많은 신호(strong but noisy signals) 를 제공하며,
일관성 정규화는 그것을 안정화(stabilizes them) 한다.
- 의사 레이블링은 강하지만 잡음이 많은 신호(strong but noisy signals) 를 제공하며,
- 거의 모든 최신 SSL(state-of-the-art SSL)은
이 두 접근법을 하나의 전체적인 프레임워크(holistic framework) 로 결합한다.
p35. (선택) 준지도 학습(SSL)의 개요 (Overview of SSL)
- 이번 강의에서는 2017년에 발표된 Mean Teacher 까지를 다루었다.
- 이후의 거의 모든 연구들은 우리가 학습한 두 가지 접근법(의사 레이블링, 일관성 정규화)을 기반으로 발전하였다.
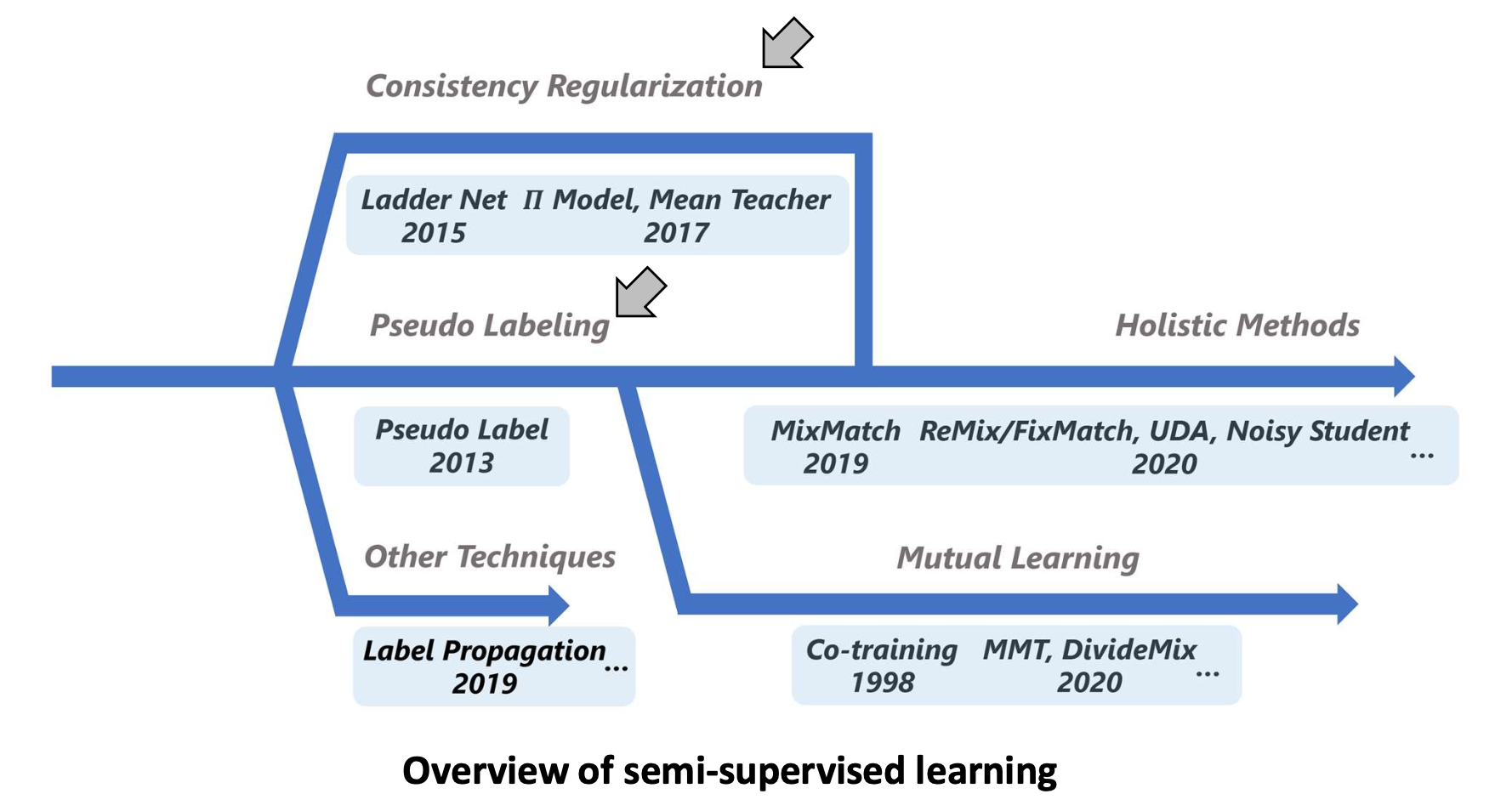
준지도 학습의 개요 (Overview of Semi-Supervised Learning)
- Consistency Regularization (일관성 정규화)
- Ladder Net (2015)
- Π Model (2015)
- Mean Teacher (2017)
- Pseudo Labeling (의사 레이블링)
- Pseudo Label (2013)
- Other Techniques (기타 기법)
- Label Propagation (2019)
- Mutual Learning (상호 학습)
- Co-training (1998)
- MMT, DivideMix (2020)
- Holistic Methods (통합적 방법)
- MixMatch (2019)
- ReMixMatch, FixMatch, UDA, Noisy Student (2020)
- …
p36. 추천 읽을거리 (Recommended Readings)
- 기사 (Articles):
- 인공지능의 우주 – 준지도 학습 (The Universe of AI – Semi-supervised learning)
- 한국어 버전: https://wikidocs.net/255169
- 영어 버전: https://wikidocs.net/255197
- 인공지능의 우주 – 준지도 학습 (The Universe of AI – Semi-supervised learning)
- 논문 (Papers):
- 시간적 앙상블을 이용한 일관성 정규화 (Consistency regularization with temporal ensemble)
- Mean teachers are better role models: 가중 평균된 일관성 목표(Weight-averaged consistency targets)가 준지도 학습된 심층 신경망의 성능을 향상시킨다, NeurIPS 2017
- (선택 사항, 본 강의 범위 밖)
- 편향 제거된 자기 학습(Debiased Self-Training)을 통한 준지도 학습, NeurIPS 2022
- 시간적 앙상블을 이용한 일관성 정규화 (Consistency regularization with temporal ensemble)