[논문] TranAD: Deep Transformer Networks for Anomaly Detection in Multivariate Time Series Data
논문 출처
Shreshth Tuli, Giuliano Casale, Nicholas R. Jennings.
TranAD: Deep Transformer Networks for Anomaly Detection in Multivariate Time Series Data.
Imperial College London / Loughborough University.
s.tuli20@imperial.ac.uk, g.casale@imperial.ac.uk, n.r.jennings@lboro.ac.uk
🔗 원문 링크 (arXiv: 2201.07284v6)
저자
- Shreshth Tuli
- Giuliano Casale
- Nicholas R. Jennings
(Imperial College London, Loughborough University)
초록 (Abstract)
다변량 시계열 데이터에서의 효율적인 이상 탐지와 진단은
현대 산업 응용에서 매우 중요한 문제이다.
그러나 이상 관측치를 빠르고 정확하게 식별할 수 있는 시스템을
구축하는 것은 도전적인 문제이다.
이는 이상 레이블의 부족, 데이터의 높은 변동성,
그리고 현대 응용에서 요구되는 초저지연 추론 시간 요구사항 때문이다.
최근 이상 탐지를 위한 딥러닝 접근법들이 개발되었음에도 불구하고,
이러한 모든 문제를 동시에 해결할 수 있는 방법은 소수에 불과하다.
본 논문에서는 TranAD를 제안하는데,
이는 데이터의 더 넓은 시간적 추세에 대한 지식을 바탕으로
어텐션 기반 시퀀스 인코더를 사용하여 신속하게 추론을 수행하는
딥 트랜스포머 네트워크 기반의 이상 탐지 및 진단 모델이다.
TranAD는 포커스 점수 기반 자기 조건화(self-conditioning)를
사용하여 강건한 멀티모달 특성 추출을 가능하게 하며,
적대적 학습을 통해 안정성을 확보한다.
또한 모델 비의존적 메타 학습(MAML, model-agnostic meta learning)을
적용하여 제한된 데이터만으로도 모델을 학습할 수 있도록 한다.
6개의 공개 데이터셋에 대한 광범위한 실험 결과를 통해,
TranAD는 데이터 효율적이고 시간 효율적인 학습을 유지하면서
탐지 및 진단 성능에서 최신 베이스라인 방법들을 능가함을 보였다.
구체적으로 TranAD는 베이스라인 대비 F1 점수를 최대 17%까지 향상시키고,
학습 시간을 최대 99%까지 감소시킨다.
1 서론 (Introduction)
현대 IT 운영 환경은 대규모 데이터셋의 지속적인 모니터링과
정상적인 동작을 위해 사용되는 고차원 센서 데이터의 막대한 양을 생성한다.
전통적으로 데이터 마이닝 전문가들은 일반적인 추세를 따르지 않는
데이터를 연구하고 강조함으로써 장애를 보고해 왔다.
이러한 보고는 반응적 장애 허용(reactive fault tolerance)과
견고한 데이터베이스 설계를 위한 시스템 관리 모델에서 핵심적인 역할을 해왔다 [47].
그러나 빅데이터 분석과 딥러닝의 등장과 함께,
이 문제는 데이터 마이닝 연구자들의 관심 대상이 되었으며
증가하는 데이터 양을 처리하는 데 있어 전문가들을 지원하는 데에도
중요한 주제가 되었다.
특히 하나의 중요한 활용 사례는 산업 4.0 데이터베이스를 위한 인공지능 분야로,
현대 시스템에서의 장애 탐지, 복구 및 관리를 자동화하는,
서비스 신뢰성에 대해 명확한 초점을 가진다 [38].
데이터 장애를 탐지하거나,
예상된 추세에 부합하지 않는 모든 형태의 행위를 탐지하는 것은
다변량 시계열에서의 이상 탐지라고 불리는 활발한 연구 분야이다 [11].
분산 컴퓨팅, 사물인터넷(IoT), 로보틱스, 도시 자원 관리와
관련된 산업을 포함한 다수의 데이터 기반 산업들은
이상 탐지를 위해 머신러닝 기반 비지도 학습 방법들을
현재 채택하고 있다 [4, 46].
도전 과제 (Challenges)
이상 탐지 문제는 데이터 모달리티의 증가로 인해
대규모 데이터베이스 환경에서 점점 더 어려워지고 있다 [18, 28, 54].
특히 현대 IoT 플랫폼에서 센서와 장치의 수가 증가하고
데이터 변동성이 커짐에 따라, 정확한 추론을 위해서는
상당한 양의 데이터가 요구된다.
그러나 지리적으로 분산된 클러스터를 기반으로 한
연합 학습 패러다임의 확산으로 인해,
장치 간 데이터베이스를 동기화하는 비용이 매우 크며,
이로 인해 학습에 사용할 수 있는 데이터의 가용성이 제한된다 [48, 57].
연합 학습 패러다임(federated learning paradigm)이란
데이터를 중앙 서버로 모으지 않고,
지리적으로 분산된 여러 장치나 클러스터가
각자 로컬 데이터로 모델을 학습한 뒤
학습된 모델 파라미터만을 공유·집계하는 학습 방식이다.이 방식은 데이터 프라이버시와 통신 비용 측면에서 장점이 있지만,
장치 간 모델 동기화와 업데이트에 따른 비용이 커질 수 있으며
학습에 활용 가능한 데이터의 일관성과 가용성이 제한될 수 있다.
더 나아가 차세대 응용에서는 빠른 복구와 최적의 서비스 품질(QoS)을 위해
초고속 추론 속도가 요구된다 [6, 49, 50].
시계열 데이터베이스는 환경, 인간, 또는 다른 시스템과 상호작용하는
여러 공학적 구성 요소들(서버, 로봇 등)에 의해 생성된다.
그 결과 데이터는 확률적 특성과 시간적 추세를
동시에 나타내는 경우가 많다 [45].
따라서 확률성으로 인해 발생한 이상치와,
관측된 시간적 추세를 따르지 않는 관측치를 구분하는 것이 중요해진다.
더욱이 레이블된 데이터의 부족과
이상의 다양성은 문제를 더욱 어렵게 만들며,
이는 다른 데이터 마이닝 영역에서 효과적임이 입증된
지도 학습 모델을 사용할 수 없기 때문이다 [12].
마지막으로, 이상을 탐지하는 것뿐만 아니라
비정상적인 행위를 유발한 근본 원인, 즉 구체적인 데이터 소스를
식별하는 것 또한 중요하다 [23].
이는 이상이 존재하는지 여부와, 존재한다면 어떤 소스에서 발생했는지를
동시에 예측해야 하는 다중 클래스 예측 문제를 필요로 하며,
문제를 더욱 복잡하게 만든다 [60].
기존 해법 (Existing solutions)
앞서 논의한 문제들은 자동화된 이상 탐지를 위한
다양한 비지도 학습 기반 해법(solution)들의 개발로 이어졌다.
연구자들은 주로 시간적 추세를 포착하고
비지도 방식으로 시계열 데이터를 예측한 뒤,
예측값과 실제 데이터 간의 편차를 이상 점수로 사용하는
재구성(reconstruction) 기반 방법들을 개발해 왔다.
다양한 극값(extreme value) 분석 방법에 기반하여,
이러한 접근법들은 높은 이상 점수를 갖는 타임스탬프를
비정상으로 분류한다 [4, 10, 14, 20, 28, 29, 45, 60, 62].
기존 연구들이 주어진 시계열로부터 예측 시계열을 생성하는 방식은
연구마다 상이하다.
SAND [10]와 같은 전통적인 접근법은
클러스터링과 통계적 분석을 사용하여 이상을 탐지한다.
openGauss [30] 및 LSTM-NDT [20]와 같은 현대적인 방법들은,
입력 시계열을 기반으로 데이터를 예측하기 위해
LSTM 기반 신경망을 사용하고,
예측 오차로부터 이상을 탐지하기 위해
비모수적 동적 임계값 설정 방식을 사용한다.
그러나 LSTM과 같은 순환 모델은 느리고
계산 비용이 크다는 한계가 있다 [4].
최근의 최신 기법들인 MTAD-GAT [62] 및 GDN [14]는
시계열 윈도우를 입력으로 사용하는 딥 신경망을 활용하여
보다 정확한 예측을 수행한다.
그러나 입력이 점점 더 데이터 집약적으로 변함에 따라,
작은 고정 크기의 윈도우 입력은,
모델에 제공되는 국소적 문맥 정보가 제한되기 때문에
탐지 성능을 제한한다 [4].
따라서 계산 오버헤드를 크게 증가시키지 않으면서
고수준의 추세를 포착할 수 있고 빠르게 동작하는 모델이 요구된다.
새로운 통찰 (New insights)
앞서 언급했듯이, 기존 방법에 기반한 순환 모델들은
느리고 계산 비용이 클 뿐만 아니라,
장기 추세를 효과적으로 모델링하지 못한다 [4, 14, 62].
이는 각 타임스탬프마다, 순환 모델이 다음 단계로 진행하기 전에
이전 모든 타임스탬프에 대해 추론을 수행해야 하기 때문이다.
최근 트랜스포머 모델의 발전은 위치 인코딩을 사용하여
전체 입력 시계열에 대해
단일 단계(single-shot) 추론을 가능하게 한다 [51].
트랜스포머를 사용하면 GPU 상에서 추론을 병렬화할 수 있어
순환 방법에 비해 훨씬 빠른 탐지가 가능하다 [19].
또한 트랜스포머는 시퀀스 길이에 거의 무관한 학습 및 추론 시간을 유지하면서
긴 시퀀스를 정확하게 인코딩할 수 있는 장점을 제공한다 [51].
따라서 우리는 계산 오버헤드를 크게 증가시키지 않으면서
이상 탐지기에 전달되는 시간적 문맥 정보를 확장하기 위해
트랜스포머를 사용한다.
우리의 기여 (Our contributions)
본 연구는 트랜스포머 신경망과 모델 비의존적 메타 학습을 포함한
다양한 도구들을 구성 요소로 사용한다.
그러나 이러한 기술들은 그 자체로는 직접 사용될 수 없으며,
이상 탐지를 위한 일반화 가능한 모델을 만들기 위해
필요한 수정이 요구된다.
구체적으로 우리는 자기 조건화와 적대적 학습 과정을 사용하는
트랜스포머 기반 이상 탐지 모델 TranAD를 제안한다.
이 아키텍처는 대규모 입력 시퀀스에서도 안정성을 유지하면서
학습과 테스트를 빠르게 수행할 수 있도록 한다.
단순한 트랜스포머 기반 인코더–디코더 네트워크는 편차가 매우 작은 경우,
즉 정상 데이터와 비교적 가까운 경우에 이상을 놓치는 경향이 있다.
우리의 기여 중 하나는
재구성 오류를 증폭시킬 수 있는 적대적 학습 절차를 통해
이 문제를 완화할 수 있음을 보이는 것이다.
또한 강건한 멀티모달 특성 추출을 위한 자기 조건화는
학습 안정성을 높이고 일반화를 가능하게 한다 [32].
이는 모델 비의존적 메타 학습(MAML)과 결합되어,
제한된 데이터 환경에서도 최적의 탐지 성능을 유지하는 데 도움을 주는데,
이는 이후 검증 과정에서 단순한 트랜스포머를 사용하는 방법들이
TranAD에 비해 11% 이상 성능이 저하됨을 보임으로써 확인된다 [15].
우리는 공개적으로 사용 가능한 데이터셋에 대해
광범위한 실증 실험을 수행하여,
TranAD를 최신 기법들과 비교·분석한다.
실험 결과, TranAD는
예측 점수를 최대 17%까지 향상시키는 동시에
학습 시간 오버헤드를 최대 99%까지 감소시켜
베이스라인들을 능가함을 보인다.
본 논문의 구성은 다음과 같다.
2장은 관련 연구를 개관한다.
3장은 다변량 이상 탐지 및 진단을 위한 TranAD 모델의 동작을 설명한다.
4장에서는 제안한 방법의 성능 평가를 제시한다.
5장은 추가 분석을 제공하며, 마지막으로 6장에서 결론을 맺는다.
2 관련 연구 (Related Work)
시계열 이상 탐지는 VLDB 커뮤니티에서 오랫동안 연구되어 온 문제이다.
VLDB 커뮤니티란
Very Large Data Bases(VLDB) 학회를 중심으로 형성된
대규모 데이터베이스 시스템, 데이터 관리, 데이터 마이닝 분야의
국제 연구자 및 실무자 공동체를 의미한다.
기존 문헌은 단변량(univariate)과 다변량(multivariate)이라는
두 가지 유형의 시계열 데이터를 다룬다.
전자의 경우, 단일 데이터 소스를 갖는 시계열 데이터에서
이상을 분석하고 탐지하는 다양한 방법들이 제안되었으며 [34],
후자의 경우에는 여러 시계열을 함께 고려하는 방법들이 사용된다 [14, 45, 62].
고전적 방법 (Classical methods)
이상 탐지를 위한 고전적인 방법들은 일반적으로
k-평균 클러스터링, 서포트 벡터 머신(SVM), 또는 회귀 모델과 같은
다양한 고전적 기법들을 사용하여 시계열 분포를 모델링한다 [10, 28, 43, 52].
다른 방법들로는 웨이블릿(wavelet) 이론이나 힐버트 변환과 같은
신호 변환 기법을 사용하는 방식이 있다 [25].
또한 다른 계열의 방법들은 주성분 분석(PCA),
공정 회귀(process regression), 또는 은닉 마르코프 체인을 사용하여
시계열 데이터를 모델링한다 [41].
GraphAn 기법 [9]은 시계열 입력을 그래프로 변환하고,
그래프 거리 지표를 사용하여 이상치(outlier)를 탐지한다.
또 다른 기법인 Isolation Forest는
여러 개의 분리(isolation) 트리로 구성된 앙상블을 사용하여
특성 공간을 재귀적으로 분할함으로써 이상치(outlier)를 탐지한다 [5, 31].
마지막으로 고전적 방법들은
Auto-Regressive Integrated Moving Average(ARIMA)의
변형을 사용하여 이상 행위를 모델링하고 탐지한다 [56].
그러나 자기회귀 기반 접근법들은
변동성이 큰 시계열을 효율적으로 포착하지 못하기 때문에,
고차원 다변량 시계열에서의 이상 탐지에는 거의 사용되지 않는다 [1].
SAND [10], CPOD [47], Elle [28]과 같은 다른 방법들은
클러스터링과 데이터베이스 읽기–쓰기 이력을 활용하여
이상치(outlier)를 탐지한다.
시계열 디스코드(discord) 탐지는
최근 제안된 또 다른 장애(fault) 예측 방법이다 [16, 37, 58, 59].
시계열 디스코드란
동일한 시계열 내의 다른 모든 부분 시퀀스들과 비교했을 때
가장 이례적인 부분 시퀀스를 의미한다.
일부 하위 방법들은 시계열 디스코드를 탐지함으로써
이상 및 모티프(motif, 반복 패턴)를 발견하기 위해
매트릭스 프로파일링 또는 그 변형을 사용한다 [16, 35, 63].
매트릭스 프로파일링 기법을 데이터 및 시간 효율적으로 만들기 위한
다수의 발전된 방법들이 제안되었다 [21].
다른 연구들은 매트릭스 프로파일링을 다양한 도메인에
적용 가능하도록 만드는 것을 목표로 한다 [64].
그러나 매트릭스 프로파일링은 이상 탐지 외에도 다양한 용도로 사용되며,
순수 디스코드 탐지 알고리즘보다 느린 것으로 알려져 있다 [37].
최근의 접근법인 MERLIN [37]은 길이가 서로 다른 부분 시퀀스를
인접한 이웃과 반복적으로 비교하는 방식의
파라미터 없는 시계열 디스코드 탐지를 사용한다.
MERLIN은 낮은 오버헤드를 가지는 최신 디스코드 탐지 기법으로 간주되며,
따라서 본 연구의 실험에서 베이스라인 중 하나로 사용된다.
딥러닝 기반 방법 (Deep Learning based methods)
대부분의 최신 기법들은 딥 신경망의 어떤 형태를 사용한다.
LSTM-NDT [20] 방법은 입력 시퀀스를 학습 데이터로 사용하고,
각 입력 시점마다 다음 시점의 데이터를 예측하는
LSTM 기반 딥 신경망 모델에 의존한다.
LSTM은 시퀀스 데이터에서의 순서 의존성을 학습하는 자기회귀 신경망으로,
각 시점의 예측은 이전 시점 출력의 피드백을 사용한다.
이 방법은 또한 오차 시퀀스의 이동 평균을 사용하여
이상 레이블링을 위한 임계값을 설정하는
비모수적 동적 오차 임계값 설정(NDT) 전략을 제안한다.
그러나 순환 모델인 LSTM은 긴 입력 시퀀스를 사용하는 경우
학습 속도가 느린 경우가 많다.
특히 LSTM은 데이터에 노이즈가 많은 경우
장기 시간 패턴을 모델링하는 데 비효율적인 것으로 알려져 있다 [62].
DAGMM [65]은 특성 공간에서의 차원 축소를 위해
딥 오토인코딩 가우시안 혼합 모델을 사용하고,
시간적 모델링을 위해 순환 신경망을 사용한다.
이 방법은 각 가우시안의 파라미터를 딥 신경망으로부터 얻는
가우시안 혼합(a mixture of Gaussians)을 사용하여 출력을 예측한다.
오토인코더는 입력 데이터를 잠재 공간으로 압축하며,
이 잠재 표현은 다음 데이터 포인트를 예측하기 위해
순환 추정 네트워크(recurrent estimation network)에 의해 사용된다.
두 네트워크를 분리하여 학습하는 방식은 모델을 더 강건하게 만들지만,
여전히 느리고 모달 간 상관관계를 명시적으로 활용하지 못한다 [14].
OmniAnomaly [45]는 확률적 순환 신경망과
평면 노멀라이징 플로우(planar normalizing flow)를 사용하여
재구성 확률을 생성한다.
확률적 순환 신경망이란
일반적인 순환 신경망이 각 시점의 상태를 하나의 값으로 결정하는 것과 달리,
은닉 상태를 확률 분포로 모델링하여
시계열 데이터에 내재된 불확실성과 잡음을 함께 표현하는 신경망 구조이다.즉, 같은 과거 관측이 주어지더라도
여러 가능한 미래 상태가 존재할 수 있음을 가정하며,
이는 변동성이 크고 예측이 불확실한 시계열을 다루는 데 유리하다.평면 노멀라이징 플로우(planar normalizing flow)란
단순한 확률 분포(예: 가우시안 분포)를
가역적이고 연속적인 비선형 변환을 통해
점점 더 복잡한 형태의 분포로 변형하는 기법이다.
또한 기존 NDT 접근법보다 성능이 우수한
자동화된 이상 임계값 선택을 위한
조정된 Peak Over Threshold(POT) 방법을 제안한다.
이는 기존 기법 대비 큰 성능 향상을 가져왔으나,
높은 학습 시간 비용을 요구한다.
다중 스케일 합성곱 재귀 인코더–디코더
(Multi-Scale Convolutional Recursive Encoder-Decoder, MS-CRED) [60]는
입력 시퀀스 윈도우를 정규화된 2차원 이미지로 변환한 뒤,
이를 ConvLSTM 계층에 통과시킨다.
이 방법은 보다 복잡한 모달 간 상관관계와 시간적 정보를 포착할 수 있지만,
학습 데이터가 부족한 환경에서는 일반화가 어렵다.
MAD-GAN [29]은 LSTM 기반 GAN을 사용하여 시계열 분포를 모델링한다.
이 방법은 이상 점수 계산에, 예측 오차뿐만 아니라 판별기 손실도 함께 사용한다.
MTAD-GAT [62]는 그래프 어텐션 네트워크를 사용하여
특성 및 시간적 상관관계를 동시에 모델링하고,
경량 GRU 네트워크를 통해 큰 오버헤드 없이 탐지를 수행한다.
전통적으로 어텐션 연산은 신경망으로 결정된 가중치를 사용한
볼록 결합(convex combination)을 통해 입력 압축을 수행한다.
GRU는 LSTM의 단순화된 버전으로, 더 적은 파라미터를 가지며
제한된 데이터 환경에서도 학습이 가능하다.
CAE-M [61]은 MS-CRED와 유사한 합성곱 오토인코딩 메모리 네트워크를 사용한다.
이 방법은 시계열을 CNN에 통과시킨 후,
양방향 LSTM으로 처리하여 장기 시간 추세를 포착한다.
그러나 이러한 순환 신경망 기반 모델들은
고차원 데이터셋에 대해 계산 비용이 높고
확장성이 낮은 것으로 알려져 있다 [4].
보다 최근의 연구들인 USAD [4], GDN [14], openGauss [30]는
자원 소모가 큰 순환 모델을 사용하지 않고,
어텐션 기반 네트워크 구조만을 사용하여 학습 속도를 개선한다.
USAD는 두 개의 디코더를 갖는 오토인코더와
적대적 게임 형태의 학습 프레임워크를 사용한다.
이는 단순한 오토인코더를 사용하여 낮은 오버헤드에 초점을 둔 초기 연구 중 하나로,
기존 기법 대비 학습 시간을 여러 배 단축할 수 있음을 보였다.
GDN(Graph Deviation Network)은 데이터 모드 간 관계 그래프를 학습하고,
어텐션 기반 예측과 편차 점수를 사용하여 이상 점수를 출력한다.
openGauss는 메모리 및 계산 비용이 낮은 트리 기반 LSTM을 사용하여,
노이즈가 있는 데이터에서도 시간적 추세를 포착할 수 있도록 한다.
그러나 작은 입력 윈도우와, 단순하거나 순환 모델을 사용하지 않는 구조로 인해,
최신 모델들은 장기 의존성을 효과적으로 포착하지 못한다.
최근 제안된 HitAnomaly [19]는
바닐라 트랜스포머를 인코더–디코더 구조로 사용하지만,
자연어 로그 데이터에만 적용 가능하며
일반적인 연속 시계열 데이터에는 적합하지 않다.
본 연구에서는
MERLIN, LSTM-NDT, DAGMM, OmniAnomaly,
MS-CRED, MAD-GAN, USAD, MTAD-GAT, CAE-M, GDN과 같은
최신 기법들과 TranAD를 비교한다.
이들 방법은 이상 탐지 및 진단에서 우수한 성능을 보이지만,
서로 다른 시계열 데이터셋 전반에서의 성능 측면에서는
상호 보완적인 특성을 가진다.
이들 중 USAD만이 학습 시간 감소를 명시적으로 목표로 하지만,
그 범위는 제한적이다.
재구성 기반 기존 연구들과 유사하게 [4, 29, 45, 60, 61],
우리는 학습 데이터를 사용하여 광범위한 수준의 추세를 학습하고,
테스트 데이터에서 이상을 탐지하는 TranAD 모델을 개발한다.
본 연구에서는 학습 시간을 줄이는 동시에
이상 탐지 및 진단 성능을 명확하게 향상시킨다.
3 방법론 (Methodology)
3.1 문제 정의 (Problem Formulation)
우리는 크기가 $T$인 관측치/데이터포인트의
타임스탬프가 부여된 시퀀스로 구성된 다변량 시계열을 고려한다.
여기서 각 데이터포인트 $x_t$는 특정 시점 $t$에서 수집되며,
$x_t \in \mathbb{R}^m$, $\forall t$이다.
이때 단변량 설정은 $m = 1$인 특수한 경우에 해당한다.
이제 우리는 이상 탐지와 이상 진단이라는 두 가지 문제를 정의한다.
이상 탐지(Anomaly Detection):
학습 입력 시계열 $\mathcal{T}$가 주어졌을 때,
길이가 $\hat{T}$이고 학습 시계열과 동일한 모달리티를 가지는
라벨이 없는 테스트 시계열 $\hat{\mathcal{T}}$에 대해,
$\mathcal{Y} = \lbrace y_1, \ldots, y_{\hat{T}} \rbrace$를 예측해야 한다.
여기서 $y_t \in \lbrace 0, 1 \rbrace$은
테스트 세트의 $t$번째 시점에 해당하는 데이터포인트가
이상인지 여부를 나타내며,
$1$은 이상 데이터포인트를 의미한다.
이상 진단(Anomaly Diagnosis):
위의 학습 및 테스트 시계열이 주어졌을 때,
$\mathcal{Y} = \lbrace y_1, \ldots, y_{\hat{T}} \rbrace$를 예측해야 하며,
여기서 $y_t \in \lbrace 0, 1 \rbrace^m$은 $t$번째 시점에서
데이터포인트의 어떤 모드(특성)가 이상인지 나타낸다.
3.2 데이터 전처리 (Data Preprocessing)
모델의 강건성을 높이기 위해, 우리는 학습과 테스트 모두에 대해
데이터를 정규화하고 이를 시계열 윈도우로 변환한다.
우리는 시계열 데이터를 다음과 같이 정규화한다:
\[x_t \leftarrow \frac{x_t - \min(\mathcal{T})}{\max(\mathcal{T}) - \min(\mathcal{T}) + \epsilon'} \tag{1}\]여기서 $\min(\mathcal{T})$와 $\max(\mathcal{T})$는
학습 시계열에서의 모드별 최소값 및 최대값 벡터이며,
$\epsilon’$은 0으로 나누는 것을 방지하기 위한 작은 상수 벡터이다.
값의 범위를 사전에 알고 있으므로,
데이터를 정규화하여 이를 구간 $[0,1)$에 위치하도록 한다.
시점 $t$에서의 데이터포인트 $x_t$의 의존성을 모델링하기 위해,
길이가 $K$인 국소 문맥(local contextual) 윈도우를 다음과 같이 정의한다.
$t < K$인 경우에는 복제 패딩(replication padding)을 사용하고,
입력 시계열 $\mathcal{T}$를 슬라이딩 윈도우 시퀀스 $\mathcal{W} = \lbrace W_1, \ldots, W_T \rbrace$로 변환한다.
복제 패딩은 각 $t < K$에 대해 윈도우 $W_t$를
길이가 $K-t$인 상수 벡터 $\lbrace x_t, \ldots, x_t \rbrace$로 확장하여
각 시점마다 윈도우 길이 $K$를 유지한다.
예를 들어 윈도우 길이가 $K = 5$이고,
현재 시점이 $t = 2$라고 가정하자.이때 실제로 존재하는 데이터는
$\lbrace x_1, x_2 \rbrace$ 두 개뿐이므로
그대로는 길이 5의 윈도우를 만들 수 없다.이 코드에서 사용하는 복제 패딩(replication padding)은
부족한 과거 데이터를
첫 시점 값 $x_1$로 반복해서 채우는 방식이다.즉, $W_2 = \lbrace x_1, x_1, x_1, x_1, x_2 \rbrace$와 같이
첫 값 $x_1$을 여러 번 복제하여
윈도우 길이를 항상 $K = 5$로 맞춘다.
학습 입력으로 $\mathcal{T}$를 직접 사용하는 대신,
모델 학습에는 $\mathcal{W}$를 사용하고,
테스트 시계열로는 $\hat{\mathcal{T}}$에 대응하는 $\hat{\mathcal{W}}$를 사용한다.
이는 기존 연구 [4, 45]에서 일반적으로 사용되는 방식으로,
단일 벡터 대신 국소 문맥을 포함한 데이터포인트를
제공할 수 있기 때문에 본 모델에서도 채택한다.
또한 우리는 시계열 $\mathcal{T}$의 현재 시점 $t$까지의 시간 구간을 고려하며,
이를 $C_t$로 표기한다.
이제 각 입력 윈도우 $W_t$에 대해 이상 레이블 $y_t$를 직접 예측하는 대신,
먼저 해당 윈도우에 대한 이상 점수 $s_t$를 예측한다.
과거 입력 윈도우들에 대한 이상 점수를 사용하여 임계값 $D$를 계산하고,
$s_t \ge D$인 경우 입력 윈도우를 이상으로 라벨링하여
$y_t = \mathbf{1}(s_t \ge D)$로 정의한다.
이상 점수 $s_t$를 계산하기 위해,
입력 윈도우를 재구성한 결과를 $O_t$로 두고,
$W_t$와 $O_t$ 간의 편차를 사용한다.
논의를 단순화하고 일반성을 해치지 않기 위해,
이후의 논의에서는 $W$, $C$, $O$, $s$를 사용한다.
3.3 트랜스포머 모델 (Transformer Model)
트랜스포머는 자연어 처리와 컴퓨터 비전 등
다양한 작업에서 사용되어 온 대표적인 딥러닝 모델이다 [51].
본 연구에서는 시계열 이상 탐지 작업에 맞게
트랜스포머 아키텍처를 의미 있게 재구성하여 사용한다.
다른 인코더–디코더 모델들과 마찬가지로,
트랜스포머에서 입력 시퀀스는 여러 어텐션 기반 변환을 거친다.
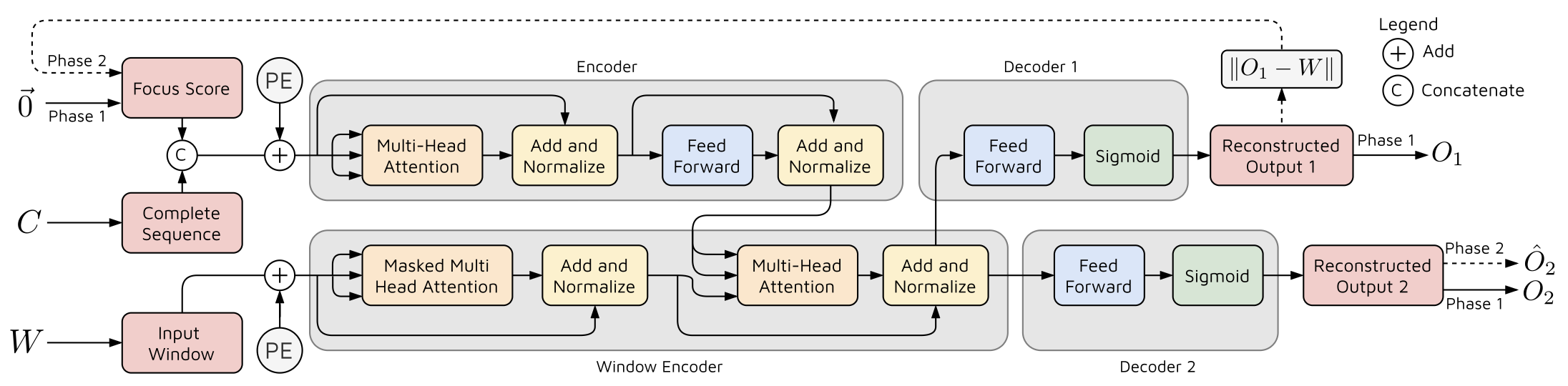
그림 1은 TranAD에서 사용되는 신경망 아키텍처를 보여준다.
인코더는 포커스 점수(focus score)를 사용하여
현재 타임스탬프까지의 전체 시퀀스 $C$를 인코딩한다
(자세한 내용은 이후에 설명한다).
윈도우 인코더는 이를 활용하여 입력 윈도우 $W$의 인코딩된 표현을 생성하며,
이는 두 개의 디코더로 전달되어 재구성을 수행한다.
그림 1. TranAD 모델
이제 TranAD의 동작을 상세히 설명한다.
$W$ 또는 $C$와 같은 다변량 시퀀스는
먼저 모달리티 $m$을 갖는 행렬 형태로 변환된다.
우리는 세 개의 행렬
$Q$(query), $K$(key), $V$(value)에 대해
스케일드 닷 프로덕트 어텐션을 정의한다 [51].
여기서 softmax는 $V$의 값들에 대한
볼록 결합(convex combination) 가중치를 형성하여,
행렬 $V$를 더 작은 표현 공간으로 압축함으로써
후속(downstream) 신경망 연산에서의 추론을 단순화한다.
기존 어텐션 연산과 달리, 스케일드 닷 프로덕트 어텐션은
가중치의 분산을 줄이기 위해 $\sqrt{m}$으로 스케일링하여
안정적인 학습을 가능하게 한다 [51].
입력 행렬 $Q$, $K$, $V$에 대해,
먼저 이를 $h$(헤드의 개수)개의 피드포워드 계층에 통과시켜
$i \in \lbrace 1, \ldots, h \rbrace$에 대해 $Q_i$, $K_i$, $V_i$를 얻은 뒤,
스케일드 닷 프로덕트 어텐션을 적용함으로써
멀티헤드 셀프 어텐션 [51]을 수행한다.
멀티헤드 어텐션은 서로 다른 표현 부분공간과 위치에서의 정보를
동시에 주목할 수 있도록 한다.
또한 [51]에서 정의된 바와 같이,
입력 행렬에 위치 인코딩(position encoding)을 사용한다.
GAN 모델이
입력이 이상인지 여부를 판단하는 특성 작업에서 우수한 성능을 보임에 따라,
본 연구에서는 시간 효율적인 GAN 스타일의 적대적 학습 방식을 활용한다.
우리 모델은 두 개의 트랜스포머 인코더와 두 개의 디코더로 구성된다 (그림 1).
우리는 모델 추론을 두 단계로 나누어 고려한다.
우리는 먼저 $W$와 $C$의 쌍을 입력으로 사용하고,
포커스 점수 $F$를 함께 입력으로 사용한다
($F$는 초기에는 $W$와 동일한 차원을 가지는 영 행렬이며,
자세한 내용은 다음 하위 절에서 설명한다).
적절한 제로 패딩을 적용하여
$F$를 $W$의 차원에 맞게 브로드캐스트한 뒤,
두 행렬을 연결(concatenate)한다.
그 후 위치 인코딩을 적용하여 첫 번째 인코더의 입력 $I_1$을 얻는다.
첫 번째 인코더는 다음 연산을 수행한다.
\[\begin{aligned} I_1^{(1)} &= \mathrm{LayerNorm}\!\bigl(I_1 + \mathrm{MultiHeadAtt}(I_1, I_1, I_1)\bigr), \\ I_1^{(2)} &= \mathrm{LayerNorm}\!\bigl(I_1^{(1)} + \mathrm{FeedForward}(I_1^{(1)})\bigr). \end{aligned} \tag{4}\]여기서 $\mathrm{MultiHeadAtt}(I_1, I_1, I_1)$는
입력 행렬 $I_1$에 대한 멀티헤드 셀프 어텐션 연산을 의미하며,
$+$는 행렬 덧셈을 나타낸다.
위의 연산들은 입력 시계열 윈도우와 전체 시퀀스를 함께 사용하여
입력 시퀀스 내의 시간적 추세를 포착하기 위한 어텐션 가중치를 생성한다.
이러한 연산들은 각 타임스탬프에서의 신경망 연산이
이전 타임스탬프의 출력에 의존하지 않도록 함으로써,
시계열 윈도우의 여러 배치에 대해 모델이 병렬로 추론할 수 있게 한다.
그 결과, 제안한 방법의 학습 시간이 현저하게 향상된다.
윈도우 인코더의 경우, 입력 윈도우 $W$에
위치 인코딩을 적용하여 $I_2$를 얻는다.
우리는 윈도우 인코더에서의 셀프 어텐션을 수정하여,
이후 위치(subsequent positions)의 데이터를 마스킹하도록 한다.
이는 학습 시 모든 $W$와 $C$가 한 번에 주어져
병렬 학습이 가능하도록 하면서도,
디코더가 미래 시점의 데이터포인트를
참조하지 못하도록 하기 위함이다.
윈도우 인코더는 다음 연산을 수행한다.
\[\begin{aligned} I_2^{(1)} &= \mathrm{Mask}\!\bigl(\mathrm{MultiHeadAtt}(I_2, I_2, I_2)\bigr), \\ I_2^{(2)} &= \mathrm{LayerNorm}\!\bigl(I_2 + I_2^{(1)}\bigr), \\ I_2^{(3)} &= \mathrm{LayerNorm}\!\bigl( I_2^{(2)} + \mathrm{MultiHeadAtt}(I_1^{(2)}, I_1^{(2)}, I_2^{(2)}) \bigr). \end{aligned} \tag{5}\]전체 시퀀스의 인코딩 결과 $I_1^{(2)}$는
윈도우 인코더에서 어텐션 연산을 수행할 때 value와 key로 사용되며,
인코딩된 입력 윈도우는 query 행렬로 사용된다.
식 (5)에 포함된 연산의 동기(motivation)는 식 (4)의 경우와 유사하다.
그러나 여기서는 동일한 입력 배치 내에서 미래 타임스탬프에 해당하는
윈도우 시퀀스를 숨기기 위해, 윈도우 입력에 마스킹을 적용한다.
현재 시점 $t$까지의 전체 입력 시퀀스가 모델에 입력으로 제공되기 때문에,
기존 연구들 [4, 45, 62]에서와 같이 제한되고 경계가 있는 문맥에 비해,
더 넓은 문맥을 포괄하고 이를 활용할 수 있다.
마지막으로, 동일한 두 개의 디코더를 사용하며,
이들은 다음 연산을 수행한다.
여기서 $i \in \lbrace 1, 2 \rbrace$는 각각 첫 번째 디코더와 두 번째 디코더를 나타낸다.
Sigmoid 활성화 함수는 출력을 구간 $[0,1]$로 생성하여,
정규화된 입력 윈도우와 일치하도록 한다.
따라서 TranAD 모델은 입력 $C$와 $W$를 받아
두 개의 출력 $O_1$과 $O_2$를 생성한다.
3.4 오프라인 2단계 적대적 학습 (Offline Two-Phase Adversarial Training)
이제 TranAD 모델에서 사용되는
적대적 학습 과정과 2단계 추론 접근법을 설명하며,
이는 알고리즘 1에 요약되어 있다.
단계 1 – 입력 재구성 (Phase 1 – Input Reconstruction)
트랜스포머 모델은
각 입력 시계열 윈도우의 재구성을 예측할 수 있게 해준다.
이는 각 타임스탬프에서
인코더–디코더 네트워크로 동작함으로써 수행된다.
그러나 전통적인 인코더–디코더 모델은
단기 추세를 포착하지 못하는 경우가 많으며,
편차가 너무 작을 경우 이상을 놓치는 경향이 있다 [29].
이 문제를 해결하기 위해,
우리는 재구성된 윈도우를 2단계로 예측하는
자기회귀적 추론 방식을 개발한다.
첫 번째 단계에서 모델은
입력 윈도우의 근사 재구성을 생성하는 것을 목표로 한다.
이 추론 결과와 입력 간의 편차는
앞서 언급한 포커스 점수(focus score)로 불리며,
이는 트랜스포머 인코더 내부의 어텐션 네트워크가
편차가 큰 부분 시퀀스에 집중하여 시간적 추세를 추출하도록 돕는다.
따라서 두 번째 단계의 출력은
첫 번째 단계에서 생성된 편차에 조건화된다(conditioned).
즉, 첫 번째 단계에서
인코더는 입력 윈도우 $W \in \mathbb{R}^{K \times m}$ (포커스 점수 $F = [0]_{K \times m}$)를
일반적인 트랜스포머 모델과 유사하게
문맥 기반 어텐션을 사용하여 압축된 잠재 표현 $I_2^{(3)}$으로 변환한다.
이 압축된 표현은 식 (6)을 통해 출력 $O_1$과 $O_2$를 생성하는 데 사용된다.
단계 2 – 포커스된 입력 재구성 (Phase 2 – Focused Input Reconstruction)
두 번째 단계에서는
첫 번째 디코더의 재구성 손실을 포커스 점수로 사용한다.
두 번째 단계의 포커스 행렬을 $F = L_1$로 두고,
모델 추론을 다시 수행하여 두 번째 디코더의 출력 $\hat{O}_2$를 얻는다.
첫 번째 단계에서 생성된 포커스 점수는
주어진 입력으로부터 재구성된 출력의 편차를 나타낸다.
이는 두 번째 단계에서
어텐션 가중치를 수정하기 위한 사전 정보(prior)로 작용하며,
특정 입력 부분 시퀀스에 대해 더 높은 신경망 활성화를 부여함으로써
단기 시간적 추세를 추출할 수 있게 한다.
이 접근법을 본 논문에서는
“자기 조건화(self-conditioning)”라고 부른다.
이러한 2단계 자기회귀 추론 방식은 세 가지 이점을 제공한다.
첫째, 재구성 오차가 그림 1에 제시된 인코더의 어텐션 부분에서
활성화로 작용하여 편차를 증폭시키고,
그 결과 이상 점수를 생성함으로써 고장 라벨링 작업을 단순화한다
(3.5절에서 논의됨).
둘째, 그림 1의 윈도우 인코더에서 단기 시간적 추세를 포착함으로써
거짓 양성(false positive)을 방지한다.
셋째, 적대적 스타일의 학습은 일반화 성능을 향상시키고
다양한 입력 시퀀스에 대해 모델을 강건하게 만드는 것으로 알려져 있다 [4].
진화하는 학습 목적 함수 (Evolving Training Objective)
앞서 설명한 모델은
다른 적대적 학습 프레임워크와 유사한 문제들에 직면할 수 있다.
그중 하나의 핵심 과제는 학습 안정성을 유지하는 것이다.
이를 해결하기 위해,
우리는 두 개의 분리된 디코더 (그림 1의 디코더 1과 디코더 2)의
출력을 사용하는 적대적 학습 절차를 설계한다.
초기에는 두 디코더 모두 입력 시계열 윈도우를
독립적으로 재구성하는 것을 목표로 한다.
[45]와 [39]를 따라,
첫 번째 단계의 출력을 사용하여 각 디코더에 대해
L2-노름 기반 재구성 손실을 다음과 같이 정의한다.
이제 우리는 두 번째 단계의 출력을 사용하는 적대적 손실을 도입한다.
여기서 두 번째 디코더는
첫 번째 단계에서 첫 번째 디코더가 생성한
재구성 후보와 입력 윈도우를 구분하기 위해,
$\lVert \hat{O}_2 - W \rVert_2$의 차이를 최대화하는 것을 목표로 한다.
반면 첫 번째 디코더는
입력을 완벽하게 재구성함으로써 (즉, $O_1 = W$)
영 벡터에 해당하는 퇴화(degenerate)된 포커스 점수를 생성하여
두 번째 디코더를 속이려 한다.
이는 이 단계에서
디코더 2가 1단계에서 입력과 일치시키고자 했던
$O_2$와 동일한 출력을 생성하도록 유도한다.
따라서 학습 목적은 다음과 같다.
\[\min_{\text{Decoder1}} \max_{\text{Decoder2}} \; \lVert \hat{O}_2 - W \rVert_2. \tag{8}\]즉, 첫 번째 디코더의 목적은
이 자기 조건화된 출력의 재구성 오차를 최소화하는 것이며,
두 번째 디코더의 목적은 이를 최대화하는 것이다.
이를 손실 함수로 표현하면 다음과 같다.
\[\begin{aligned} L_1 &= + \lVert \hat{O}_2 - W \rVert_2, \\ L_2 &= - \lVert \hat{O}_2 - W \rVert_2. \end{aligned} \tag{9}\]이제 두 단계 모두에 대한 손실 함수가 정의되었으므로,
각 디코더에 대한 누적 손실을 결정해야 한다.
이를 위해 두 단계의 재구성 손실과 적대적 손실을 결합하는
진화적(evolutionary) 손실 함수를 다음과 같이 사용한다.
여기서 $n$은 학습 에폭(epoch)이며,
$\epsilon$은 1에 가까운 작은 양의 학습 파라미터이다
(알고리즘 1의 7–8번째 줄).
초기에는 재구성 손실에 부여되는 가중치가 크다.
이는 디코더 출력이 입력 윈도우에 대한 열악한 재구성일 때에도
안정적인 학습을 보장하기 위함이다.
재구성이 부정확한 경우,
두 번째 단계에서 사용되는 포커스 점수는 신뢰할 수 없게 되며,
그 결과 입력 시퀀스와 크게 다른 재구성을
나타내는 사전 정보로 활용될 수 없다.
따라서 학습 초반에는
모델 학습의 불안정을 방지하기 위해
적대적 손실에 낮은 가중치를 부여한다.
재구성이 입력 윈도우에 가까워지고,
포커스 점수가 더 정밀해짐에 따라,
적대적 손실의 가중치는 점차 증가한다.
신경망 학습 과정에서의 손실 곡선은
일반적으로 지수 함수 형태를 따르므로,
우리는 작은 양의 상수 파라미터 $\epsilon$을 사용하여
학습 과정에서 $\epsilon^{-n}$ 형태의 가중치를 사용한다.
학습 과정은 데이터가 순차적으로 제공된다고 가정하지 않으므로
(온라인 과정과 달리),
전체 시계열은 $(W, C)$ 쌍으로 분할될 수 있으며,
모델은 입력 배치를 사용하여 학습될 수 있다.
마스킹된 멀티헤드 어텐션은
여러 배치에 대해 병렬 실행을 가능하게 하여,
학습 속도를 향상시킨다.
메타 러닝 (Meta Learning)
마지막으로, 우리의 학습 루프에서는
신경망의 빠른 적응을 위한 소수 샷(few-shot) 학습 모델인
모델 비의존적 메타 학습(MAML)을 사용한다 [15].
이는 제한된 데이터만으로도
TranAD 모델이 입력 학습 시계열에서
시간적 추세를 학습하도록 돕는다.
각 학습 에폭마다,
신경망 가중치(일반성을 해치지 않고 $\theta$라 가정)에 대한
그래디언트 업데이트는 다음과 같이 간단히 표현할 수 있다.
여기서 $\alpha$, $f(\cdot)$, $L(\cdot)$은
각각 학습률, 신경망의 추상적 표현, 손실 함수를 의미한다.
각 에폭의 끝에서
다음과 같은 메타 학습 단계를 수행한다.
메타 최적화는 메타 스텝 크기 $\beta$를 사용하여,
업데이트된 가중치 $\theta’$에 대해 목적 함수를 평가함으로써
모델 가중치 $\theta$에 대해 수행된다.
기존 연구에 따르면
이 방식은 제한된 데이터 환경에서도
모델을 빠르게 학습할 수 있게 해준다 [15].
우리는 이를 알고리즘 1의 한 줄(11번째 줄)로 요약하였다.
3.5 온라인 추론, 이상 탐지 및 진단
(Online Inference, Anomaly Detection and Diagnosis)
이제 학습된 트랜스포머 모델을 사용한 추론 절차를 설명하며,
이는 알고리즘 2에 요약되어 있다.
관측되지 않은 데이터 $(\hat{W}, \hat{C})$에 대해,
이상 점수는 다음과 같이 정의된다.
테스트 시점의 추론 역시 두 단계로 수행되며,
그 결과 단일 재구성 쌍 $(O_1, \hat{O}_2)$를 얻게 된다
(알고리즘 2의 2–3번째 줄).
테스트 시점에서는 현재 타임스탬프까지의 데이터만을 고려하므로,
연산은 온라인 방식으로 순차적으로 수행된다.
각 차원 $i$에 대해 타임스탬프별 이상 점수 $s_i$를 얻은 뒤,
이 점수가 임계값보다 크면 해당 타임스탬프를 이상으로 라벨링한다.
기존 연구 [9, 20, 45]와의 공정한 비교를 위해,
우리는 임계값을 자동적이고 동적으로 선택하는
Peak Over Threshold(POT) [44] 방법을 사용한다.
본질적으로 이는 “극값 이론(extreme value theory)”을 사용하여
일반화된 파레토 분포로 데이터 분포를 적합시키고,
적절한 위험 값(value at risk)을 식별함으로써
임계값을 동적으로 결정하는 통계적 방법이다.
또한 우리는 또 다른 널리 사용되는 EVT 방법인
연 최대값(annual maximum, AM) [7]도 실험하였다.
그러나 TranAD는 AM에 비해 POT를 사용할 경우
평균적으로 7.2% 더 높은 F1 점수를 보였다.
각 차원 $i$에 대한 이상 진단 레이블 $y_i$와
탐지 결과 $y$는 다음과 같이 정의된다.
따라서 $m$개의 차원 중 하나라도 이상으로 판단되면,
현재 타임스탬프를 이상으로 라벨링한다
(알고리즘 2의 5–6번째 줄).
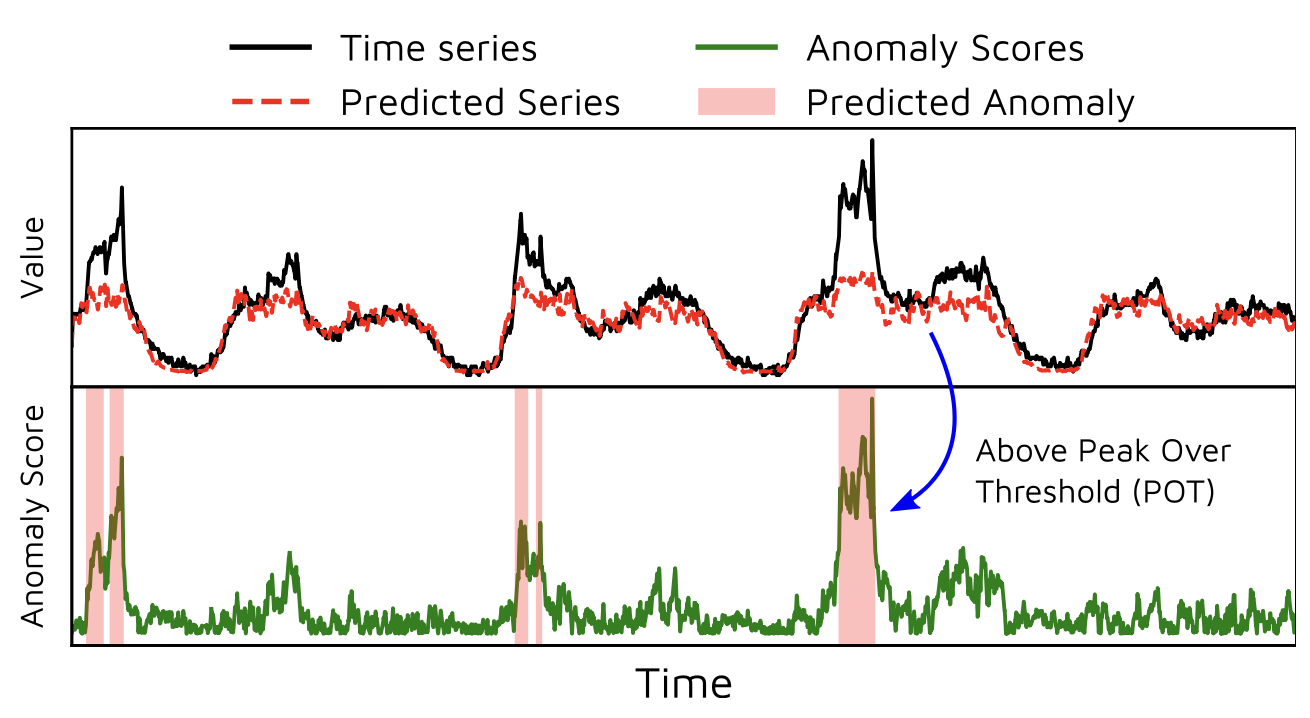
그림 2는 샘플 시계열에 대해 이 과정을 시각적으로 보여준다.
그림 2: 이상 예측의 시각화.
어텐션과 포커스 점수의 영향
(Impact of Attention and Focus Scores)
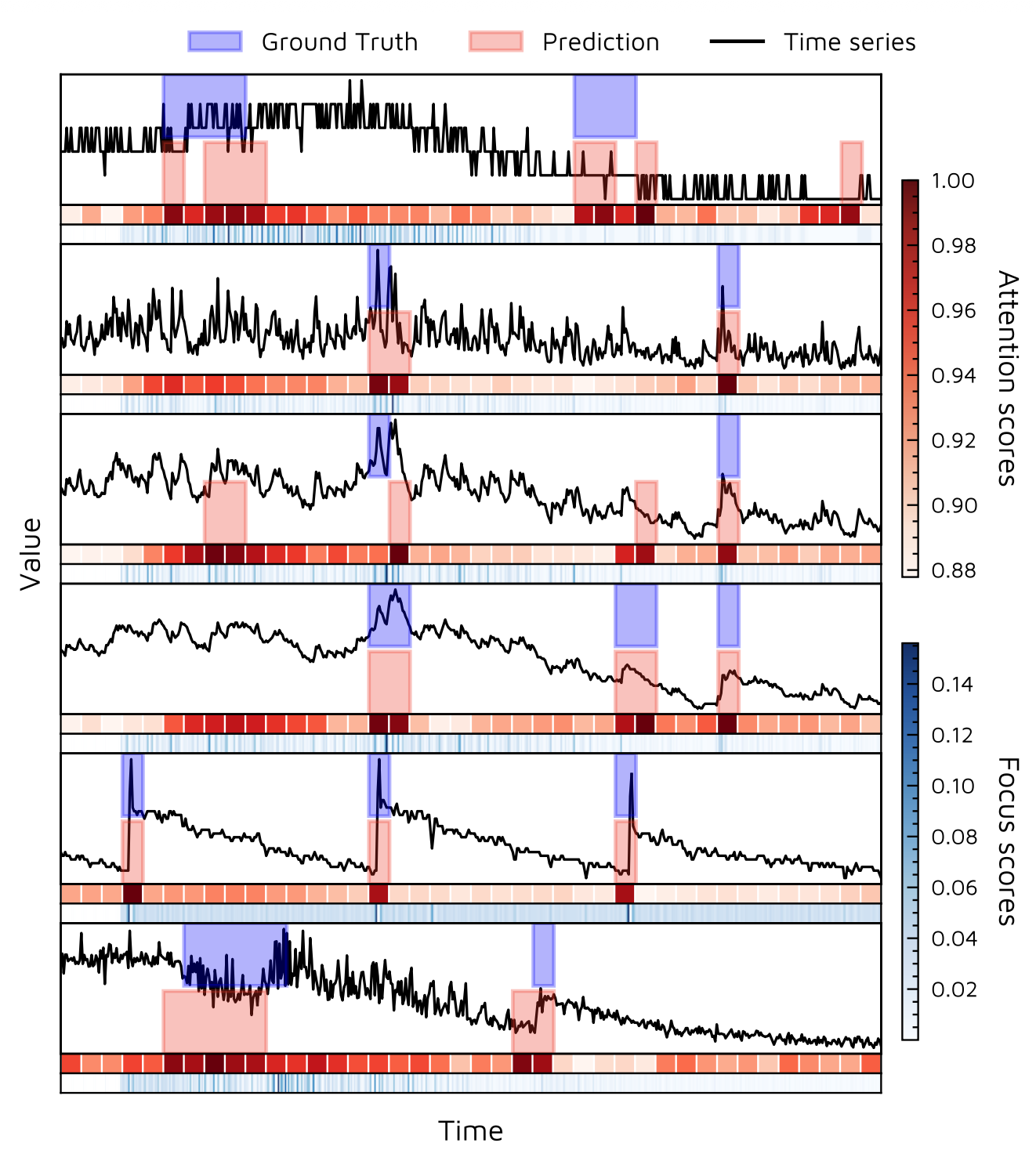
그림 3은 SMD 데이터셋으로 학습된 TranAD 모델의
어텐션과 포커스 점수를 시각화한다 (자세한 내용은 4.1절 참조).
그림 3: 포커스 점수와 어텐션 점수의 시각화.
우리는 시계열, 각 윈도우에 대한 평균 어텐션 가중치
(여러 헤드에 대해 평균됨),
그리고 데이터셋의 처음 6개 차원에 대한
포커스 점수를 함께 제시한다.
포커스 점수는 데이터의 피크와 노이즈와
높은 상관관계를 가지는 것이 분명히 드러난다.
또한 차원 간 포커스 점수 역시 높은 상관관계를 보인다.
시계열에서 급격한 변화가 발생하는 타임스탬프에서는
포커스 점수가 더 크게 나타난다.
더 나아가, 모델은 편차가 큰 시계열의
특정 차원에 더 높은 어텐션 가중치를 부여한다.
이는 전체 시퀀스의 문맥적 추세를 사전 정보로 활용하여,
각 차원별 이상을 개별적으로 정밀하게 탐지할 수 있도록 한다.