[논문] Auto-Encoding Variational Bayes
논문 출처
Kingma, D. P., & Welling, M.
Auto-Encoding Variational Bayes.
arXiv preprint arXiv:1312.6114 (2013).
🔗 원문 링크 (arXiv: 1312.6114)
저자
- Diederik P. Kingma (Machine Learning Group, Universiteit van Amsterdam) – dpkingma@gmail.com
- Max Welling (Machine Learning Group, Universiteit van Amsterdam) – welling.max@gmail.com
초록 (Abstract)
연속적인 잠재 변수(continuous latent variables)를 포함한
유향 확률적 모델(directed probabilistic models) 에서
계산 불가능한 사후분포(intractable posterior distributions) 와
대규모 데이터셋이 존재하는 상황에서
효율적인 추론(inference)과 학습(learning)을 수행하려면 어떻게 해야 할까?
본 논문에서는 대규모 데이터셋에 확장 가능하며,
약한 미분 가능성 조건하에서도(mild differentiability conditions)
계산 불가능한 경우(intractable case) 에도 동작하는
확률적 변분 추론(stochastic variational inference)과
학습 알고리즘을 제안한다.
우리의 기여는 두 가지로 요약된다.
첫째, 변분 하한식(variational lower bound)을
재매개변수화(reparameterization)함으로써
표준 확률적 경사 하강법(stochastic gradient methods)으로
간단하게 최적화할 수 있는 하한 추정량(lower bound estimator)을 제시한다.
둘째, i.i.d. 데이터셋에서 각 데이터 포인트마다 연속 잠재 변수가 존재할 경우,
제안된 하한 추정량(lower bound estimator)을 사용하여
계산 불가능한 사후분포를 근사 추론 모델(approximate inference model,
또는 recognition model) 에 적합시킴으로써
사후분포 추론(posterior inference)이 특히 효율적으로 수행될 수 있음을 보인다.
이론적 이점은 실험 결과를 통해 입증된다.
1. Introduction
연속적인 잠재 변수(continuous latent variables)나
모델 파라미터를 가진 유향 확률적 모델(directed probabilistic models) 에서
계산 불가능한 사후분포(intractable posterior distributions) 가 존재할 때,
효율적인 근사 추론(approximate inference)과 학습(learning)을
어떻게 수행할 수 있을까?
대부분의 확률적 그래프 모델에서 사후분포 $p(z \mid x)$ 는
\[p(z \mid x) = \frac{p(x, z)}{p(x)}\]
베이즈 정리로 표현된다.
\[p(x) = \int p(x, z)\,dz\]
그러나 여기서 정규화 상수(normalizing constant) 인는 고차원 잠재 변수 $z$ 에 대한 적분(integration) 을 포함하며,
일반적으로 닫힌 형태(closed-form)로 계산할 수 없다.
따라서 이 적분이 계산 불가능(intractable) 하기 때문에
사후분포 $p(z \mid x)$ 역시 직접 계산할 수 없게 된다.
변분 베이지안(Variational Bayesian, VB) 접근법은
계산하기 어려운 사후분포에 대한 근사치를 최적화하는 과정을 포함한다.
그러나 일반적인 평균장(mean-field) 접근법은
근사 사후분포에 대한 기댓값의 해석적 계산(analytical solution of expectations)을
필요로 하며, 이는 일반적인 경우 역시 계산 불가능하다(intractable).
우리는 변분 하한식(variational lower bound)을 재매개변수화(reparameterization) 함으로써,
간단하면서도 미분 가능한(differentiable) 불편 추정량(unbiased estimator) 을
얻을 수 있음을 보인다.
이 추정량은
SGVB (Stochastic Gradient Variational Bayes) 라고 불리며,
연속 잠재 변수나 파라미터를 포함하는 거의 모든 모델에서
효율적인 근사 사후추론(approximate posterior inference)을 수행할 수 있다.
또한, 표준 확률적 경사 상승법(stochastic gradient ascent techniques)을 이용해
간단히 최적화할 수 있다.
전통적인 평균장 변분추론(mean-field variational inference) 은
\[\mathcal{L}(x) = \mathbb{E}_{q(z)}[\log p(x, z) - \log q(z)]\]
근사 사후분포 $q(z)$ 를 단순한 형태(예: 독립 가우시안의 곱)로 가정하고,
ELBO의 기댓값을 해석적으로(analytically) 계산하려고 한다.
즉, 적분을 직접 풀어 닫힌 형태(closed form)로 얻어내야 한다.
하지만 대부분의 실제 모델에서는
$p(x, z)$ 가 복잡한 신경망 형태이거나 비선형 구조를 가지므로
이 적분을 정확히 계산할 수 없어 계산 불가능(intractable) 하다.반면 VAE (Variational Autoencoder) 에서는
사후분포를 신경망이 파라미터화한 근사 분포
$q_\phi(z \mid x)$ 로 표현하고,
이 분포로부터 샘플을 얻은 뒤
몬테카를로(Monte Carlo) 근사 를 사용해
위 기댓값을 수치적으로 근사한다.즉, VAE에서는
- 복잡한 적분을 직접 풀지 않고
- 샘플링을 통해 \(\mathbb{E}_{q_\phi(z \mid x)}[\cdot]\) 를 근사하고
- 재매개변수화 트릭(reparameterization trick)으로
이 과정에서 미분이 가능하도록 만들어
확률적 경사 하강법(SGD) 으로 ELBO를 최적화한다.따라서 평균장 접근법은 “기댓값을 직접 계산해야 해서 어렵고(intractable)”
VAE는 “기댓값을 샘플링 기반으로 근사해서 tractable하게 만든다”고 요약할 수 있다.
독립 동일 분포(i.i.d.) 데이터셋과
각 데이터 포인트마다 연속적인 잠재 변수(continuous latent variables)가 존재하는 경우,
우리는 Auto-Encoding Variational Bayes (AEVB) 알고리즘을 제안한다.
데이터 포인트(data point) 는 하나의 데이터 샘플(sample) 을 의미한다.
예를 들어,
- 이미지 데이터셋에서는 한 장의 이미지,
- 텍스트 데이터셋에서는 한 문장 또는 문서,
- 시계열 데이터에서는 한 시점의 관측값,
같은 개별 관측 단위를 가리킨다.“독립 동일 분포(i.i.d.) 데이터셋” 이란
각 데이터 포인트가 서로 독립적이며 동일한 확률분포에서 생성된다는 가정이다.
즉, 모든 샘플이 같은 확률적 메커니즘으로 만들어졌다고 보는 것이다.따라서 문장의 의미는,
“각 데이터 샘플마다 그 샘플을 설명하는 잠재 변수(latent variable)가 따로 존재하는 경우,
그런 데이터셋(i.i.d. 구조를 가진)에 대해
Auto-Encoding Variational Bayes(AEVB) 알고리즘을 제안한다”는 뜻이다.즉, 데이터 전체를 하나의 거대한 잠재 변수로 설명하는 것이 아니라,
각 샘플마다 독립적인 잠재 표현(latent representation)을 학습한다는 의미이다.
AEVB 알고리즘에서는
SGVB 추정량(SGVB estimator)을 이용하여
인식 모델(recognition model)을 최적화함으로써,
매우 효율적인 근사 사후 추론(approximate posterior inference)을
단순한 조상 샘플링(ancestral sampling) 을 통해 수행할 수 있다.
조상 샘플링(ancestral sampling) 은
유향 확률적 모델(directed probabilistic model) 에서
그래프의 위상 순서(topological order)에 따라
확률 변수들을 한 단계씩 순차적으로 샘플링하는 방법이다.
예를 들어, 잠재 변수 $z$ 가 먼저 샘플링되고
그 다음에 $x$ 가 $p(x \mid z)$ 로부터 샘플링되는 경우,
전체 데이터 생성 과정은
$z \sim p(z)$ → $x \sim p(x \mid z)$ 의 순서로 이루어진다.즉, 부모 변수(parent variable) 로부터
자식 변수(child variable) 를 순차적으로 샘플링하는 구조를
“조상(ancestral)”이라는 표현으로 설명한 것이다.VAE에서도 학습된 근사 사후분포 $q_\phi(z \mid x)$ 로부터
샘플을 뽑고, 이를 디코더 $p_\theta(x \mid z)$ 에 통과시키는 과정이
이러한 조상적 샘플링 절차(ancestral sampling process) 에 해당한다.
이 접근은 각 데이터 포인트마다
고비용의 반복적 추론(iterative inference) 절차(예: MCMC)를 수행하지 않고도
모델 파라미터를 효율적으로 학습할 수 있게 한다.
MCMC(Markov Chain Monte Carlo)란?
어떤 확률 분포(예: 사후확률 p(z|x))에서 무작위로 샘플을 뽑고 싶은데,
그 분포의 모양이 너무 복잡해서 직접 샘플링할 수 없을 때 사용하는 방법이다.MCMC의 기본 아이디어는 다음과 같다.
“복잡한 분포에서 바로 샘플을 뽑는 대신,
확률이 높은 쪽으로 조금씩 이동하면서 분포를 따라가자.”즉, MCMC는 하나의 “현재 위치”에서 시작해서
분포의 모양에 맞게 다음 위치를 하나씩 제안하고,
그 제안을 받아들일지 말지를 결정하면서
점점 분포 전체를 탐색해 나가는 방식으로 동작한다.
- 처음에는 임의의 위치에서 시작한다.
- 분포의 확률이 높은 방향으로 이동할 후보를 만든다.
- 후보가 더 가능성 높은 지점이면 이동하고,
그렇지 않아도 일정 확률로는 이동한다.- 이렇게 수천 번, 수만 번 반복하면
방문한 지점들의 분포가 우리가 구하고자 하는 복잡한 확률 분포와 비슷해진다.직관적 비유로 보면:
울퉁불퉁한 산 위를 “확률의 지형”이라고 생각하고,
한 사람이 그 위를 무작위로 걸어 다닌다고 하자.
그 사람은 높은 곳(확률이 높은 영역)에는 자주 머물고,
낮은 곳(확률이 낮은 영역)에는 가끔만 지나간다.오랫동안 걸어다니면, 그 사람의 발자국이 남은 위치들이
원래 우리가 알고 싶었던 확률 분포의 모양을 자연스럽게 닮게 된다.하지만 이 방법은 비효율적이다.
- 한 걸음씩 움직여야 하므로 시간이 오래 걸린다.
- 시작 위치가 나쁘면 오랫동안 엉뚱한 영역에 머무를 수 있다.
- 산이 여러 봉우리(모드)를 가지면,
다른 봉우리로 건너가기가 매우 어렵다.- 결국 정확한 결과를 얻으려면
수천, 수만 번의 반복이 필요해 계산 비용이 크다.VAE는 이 문제를 다르게 해결한다.
MCMC처럼 일일이 걸어 다니지 않고,
신경망이 “이 데이터라면 잠재변수 z는 이 근처일 것이다”라고
한 번에 예측하도록 학습한다.
따라서 VAE는 매번 긴 반복을 돌릴 필요 없이
한 번의 순전파로 근사 사후분포를 얻을 수 있어
훨씬 빠르고 효율적으로 동작한다.
또한 학습된 근사 사후 추론 모델은
인식(recognition), 노이즈 제거(denoising),
표현 학습(representation learning), 시각화(visualization) 등
다양한 작업에도 활용될 수 있다.
마지막으로,
인식 모델이 신경망(neural network) 으로 구현될 때
우리는 변분 오토인코더(Variational Auto-Encoder, VAE) 에 도달하게 된다.
2. 방법(Method)
이 절에서 제시하는 전략은
연속적인 잠재 변수(continuous latent variables)를 갖는
다양한 유향 그래프 모델(directed graphical models)에 대해
하한 추정량(lower bound estimator), 즉 확률적 목적 함수(stochastic objective function)를
유도하는 데 사용할 수 있다.
여기서는 각 데이터 포인트마다 잠재 변수가 존재하는
독립 동일 분포(i.i.d.) 데이터셋의 일반적인 경우에 국한한다.
이 경우 전역 파라미터(global parameters)에 대해서는
최대우도추정(ML) 또는 최대사후추정(MAP)을 수행하고,
잠재 변수(latent variables)에 대해서는
변분 추론(variational inference)을 수행한다.
각 데이터 포인트마다 잠재 변수가 존재한다는 뜻은,
예를 들어 여러 장의 이미지가 있을 때
각 이미지마다 그 이미지를 설명하는 ‘숨겨진 원인’(예: 조명, 각도, 표정 등)이
따로 존재한다는 의미이다.전역 파라미터(global parameters)는
모든 데이터에 공통으로 적용되는 값으로,
모델이 전반적으로 데이터를 어떻게 생성하는지를 결정한다.
예를 들어 신경망의 가중치나 분포의 평균·분산이 여기에 해당한다.최대우도추정(ML)이나 최대사후추정(MAP)은
이런 전역 파라미터를 전체 데이터셋을 보고
“가장 그럴듯한 값”으로 맞추는 과정이다.반면 변분 추론(variational inference)은
각 데이터의 잠재 변수를 직접 계산하기 어렵기 때문에,
복잡한 분포 대신 계산이 쉬운 근사 분포로 대신해서
그 값을 추정하는 방법이다.즉, 전역 파라미터는 전체 데이터를 보고 학습하고,
잠재 변수는 데이터마다 따로 근사해서 계산하는 것이다.
또한 이러한 설정은 전역 파라미터에 대해서도
변분 추론을 함께 수행하도록 확장하기 쉽다.
그 알고리즘은 부록(appendix)에 제시되어 있으며,
그 경우에 대한 실험은 향후 연구로 남겨 두었다.
본 방법은 온라인(online)이나 비정상(non-stationary) 환경,
예를 들어 스트리밍 데이터(streaming data)에도 적용할 수 있다.
그러나 여기서는 단순화를 위해
고정된 데이터셋(fixed dataset)을 가정한다.
2.1 문제 시나리오 (Problem scenario)
데이터셋 $\mathbf{X} = {\mathbf{x}^{(i)}}_{i=1}^N$ 가
$N$개의 연속형 혹은 이산형 변수 $\mathbf{x}$ 의
i.i.d. 표본들로 구성되어 있다고 가정한다.
이 데이터는 어떤 무작위 과정(random process)에 의해 생성된다고 가정하며,
그 과정에는 관찰되지 않는 연속형 잠재 변수 $\mathbf{z}$ 가 포함되어 있다.
이 생성 과정은 두 단계로 이루어진다.
(1) 잠재 변수 \(\mathbf{z}^{(i)}\) 는
어떤 사전분포(prior distribution) \(p_{\theta^*}(\mathbf{z})\) 로부터 생성되고,
(2) 관측 변수 \(\mathbf{x}^{(i)}\) 는
조건부 분포(conditional distribution) \(p_{\theta^*}(\mathbf{x} \mid \mathbf{z})\) 로부터 생성된다.
사전분포 \(p_{\theta^*}(\mathbf{z})\) 와 우도(likelihood) \(p_{\theta^*}(\mathbf{x} \mid \mathbf{z})\) 가
모두 매개변수화된(parametric) 확률분포 집합 \(p_\theta(\mathbf{z})\) 및 \(p_\theta(\mathbf{x} \mid \mathbf{z})\) 에 속하며,
이들의 확률밀도함수(PDF)는 \(\theta\) 와 \(\mathbf{z}\) 에 대해 거의 모든 곳에서 미분 가능하다고 가정한다.
하지만 실제로는 이 과정의 대부분이 관찰되지 않는다.
즉, 진짜 파라미터 \(\theta^*\) 와 각 데이터 포인트의 잠재 변수 값 \(\mathbf{z}^{(i)}\) 는
우리에게 알려져 있지 않다.
매우 중요한 점은, 우리는 주변 확률(marginal probabilities)이나
사후 확률(posterior probabilities)에 대해 흔히 사용하는
단순화 가정을 하지 않는다는 것이다.
대신, 우리는 다음과 같은 상황에서도 효율적으로 동작할 수 있는 일반적인 알고리즘에 관심을 둔다.
계산 불가능성(Intractability)
주변 우도(marginal likelihood)
$p_\theta(\mathbf{x}) = \int p_\theta(\mathbf{z})p_\theta(\mathbf{x}\mid \mathbf{z})\,d\mathbf{z}$
의 적분이 계산 불가능한 경우이다.
(즉, 주변 우도를 직접 계산하거나 미분할 수 없다.)
이때 사후 확률밀도
$p_\theta(\mathbf{z}\mid \mathbf{x}) = p_\theta(\mathbf{x}\mid \mathbf{z})p_\theta(\mathbf{z})/p_\theta(\mathbf{x})$
역시 계산 불가능하므로, EM 알고리즘을 사용할 수 없다.
또한 합리적인 평균장 변분 베이즈(mean-field VB) 접근에서도
필요한 적분들이 대부분 계산 불가능하다.
이러한 계산 불가능성은 꽤 일반적으로 나타나며,
예를 들어 비선형 은닉층을 포함한 신경망처럼
복잡한 우도 함수 $p_\theta(\mathbf{x}\mid \mathbf{z})$ 를 사용할 때 자주 발생한다.베이즈 정리에 따르면 사후분포는
$p_\theta(\mathbf{z}\mid \mathbf{x}) = p_\theta(\mathbf{x}\mid \mathbf{z})p_\theta(\mathbf{z})/p_\theta(\mathbf{x})$ 로 표현된다.
여기서 문제는 분모의 주변우도 $p_\theta(\mathbf{x})$ 이다.$p_\theta(\mathbf{x}) = \int p_\theta(\mathbf{x}\mid \mathbf{z})p_\theta(\mathbf{z})\,d\mathbf{z}$ 는
모든 가능한 $\mathbf{z}$ 에 대해 적분해야 하는데,
$\mathbf{z}$ 가 고차원이거나 $p_\theta(\mathbf{x}\mid \mathbf{z})$ 가 복잡한 비선형 함수일 경우
이 적분을 닫힌 형태로 계산할 수 없다.따라서 $p_\theta(\mathbf{x})$ 를 정확히 구할 수 없고,
결과적으로 사후분포 $p_\theta(\mathbf{z}\mid \mathbf{x})$ 도 계산할 수 없게 된다.EM 알고리즘(E-step)은 바로 이 사후분포 $p_\theta(\mathbf{z}\mid \mathbf{x})$ 의 기댓값을 계산해야 하는데,
그것을 구할 수 없으므로 EM 알고리즘을 적용할 수 없게 되는 것이다.대규모 데이터셋(A large dataset)
데이터가 너무 많아서 배치(batch) 단위로 최적화하기에는 계산 비용이 너무 크다.
따라서 작은 미니배치(minibatch)나
심지어 단일 데이터 포인트만을 사용해서
파라미터를 갱신할 수 있어야 한다.
예를 들어 Monte Carlo EM 같은 샘플링 기반 방법은
각 데이터 포인트마다 비싼 샘플링 루프가 필요하기 때문에
일반적으로 매우 느리게 동작한다.
우리는 위의 시나리오에서 세 가지 관련된 문제에 관심을 가지며,
그들에 대한 해결책을 제안한다.
파라미터 $\theta$ 에 대한 효율적인 근사 최대우도추정(ML) 또는 최대사후추정(MAP).
파라미터들은 그 자체로 흥미로운 대상일 수 있다.
예를 들어 우리가 어떤 자연적 과정을 분석하고 있다면 그렇다.
또한 이들은 숨겨진 확률적 과정을 모방하고
실제 데이터와 유사한 인공 데이터를 생성할 수 있게 해준다.주어진 관측값 $\mathbf{x}$ 에 대해
선택된 파라미터 $\theta$ 에 대한 잠재 변수 $\mathbf{z}$ 의
효율적인 근사 사후 추론(efficient approximate posterior inference).
이것은 부호화(coding)나 데이터 표현(data representation) 작업에 유용하다.변수 $\mathbf{x}$ 에 대한 효율적인 근사 주변 추론(efficient approximate marginal inference).
이는 $\mathbf{x}$ 에 대한 사전분포(prior)가 필요한
모든 종류의 추론 작업을 수행할 수 있게 해준다.
컴퓨터 비전의 일반적인 응용으로는
이미지 복원(denoising), 인페인팅(inpainting),
그리고 초해상도(super-resolution)가 포함된다.
위의 문제들을 해결하기 위한 목적으로,
우리는 인식 모델(recognition model) $q_\phi(\mathbf{z}\mid\mathbf{x})$ 를 도입한다.
이는 계산 불가능한 실제 사후분포(intractable true posterior)
$p_\theta(\mathbf{z}\mid\mathbf{x})$ 에 대한 근사(approximation)이다.
평균장 변분 추론(mean-field variational inference)의 근사 사후분포와 달리,
이 분포는 반드시 독립적(factorial)일 필요는 없으며,
그 파라미터 $\phi$ 또한 어떤 닫힌 형태의 기댓값(closed-form expectation)으로부터
계산되는 것은 아니다.
평균장(mean-field) 접근법에서는
복잡한 다변량 확률분포 $q(\mathbf{z})$ 를 단순화하기 위해
잠재 변수들 사이의 독립성(independence) 을 가정한다.
즉,
\(q(\mathbf{z}) = \prod_i q_i(z_i)\)
와 같이 각 잠재 변수 $z_i$ 가 서로 독립적으로 분포한다고 가정한다.이렇게 하면 원래는 고차원 공간에서의 복잡한 적분 문제를
각 변수별로 나눠서 계산할 수 있어 수학적으로 훨씬 단순해진다.
그러나 이 독립성 가정 때문에
실제 잠재 변수들 간의 상호 의존 관계(correlation)를 표현할 수 없게 되어
근사 성능이 떨어지는 단점이 있다.반면, VAE에서는 이런 인위적인 독립성 제약을 두지 않고
신경망이 학습을 통해
잠재 변수들 간의 의존 관계를 자연스럽게 학습하도록 한다.
대신, 우리는 생성 모델의 파라미터 $\theta$ 와 함께
인식 모델의 파라미터 $\phi$ 를 공동으로 학습(jointly learn) 하는 방법을 제시한다.
부호화 이론(coding theory)의 관점에서 보면,
관측되지 않은 변수 $\mathbf{z}$ 는
잠재 표현(latent representation) 또는 코드(code) 로 해석될 수 있다.
따라서 본 논문에서는 인식 모델 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 을
확률적 인코더(probabilistic encoder)라고 부르기로 한다.
이는 주어진 데이터 포인트 $\mathbf{x}$ 에 대해
그 데이터 포인트 $\mathbf{x}$ 가 생성되었을 법한
코드 $\mathbf{z}$ 의 가능한 값들에 대한 분포(예: 가우시안 분포)를
생성하기 때문이다.
비슷한 맥락에서,
$p_\theta(\mathbf{x}\mid\mathbf{z})$ 는 확률적 디코더(probabilistic decoder) 라고 부른다.
이는 주어진 코드 $\mathbf{z}$ 로부터
해당하는 데이터 $\mathbf{x}$ 의 가능한 값들에 대한 분포를
생성하기 때문이다.
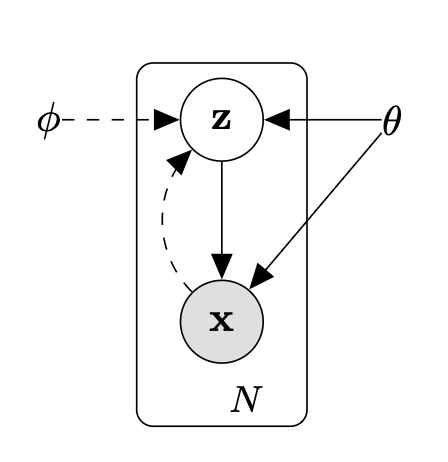
그림 1: 본 논문에서 다루는 유향 확률 그래프 모델(directed graphical model) 의 형태를 나타낸다.
실선(solid line)은 생성 모델 $p_\theta(\mathbf{z})p_\theta(\mathbf{x}\mid\mathbf{z})$ 을,
점선(dashed line)은 계산 불가능한 사후분포
$p_\theta(\mathbf{z}\mid\mathbf{x})$ 에 대한 변분 근사
$q_\phi(\mathbf{z}\mid\mathbf{x})$ 을 나타낸다.
변분 파라미터 $\phi$ 는 생성 모델의 파라미터 $\theta$ 와 함께
공동으로 학습된다(jointly learned).
2.2 변분 하한 (The variational bound)
주변 우도(marginal likelihood)는 각 데이터 포인트의 주변 우도의 합으로 구성된다.
\[\log p_\theta(\mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(N)}) = \sum_{i=1}^N \log p_\theta(\mathbf{x}^{(i)})\]각 항은 다음과 같이 다시 쓸 수 있다.
\[\log p_\theta(\mathbf{x}^{(i)}) = D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) \Vert p_\theta(\mathbf{z}\mid\mathbf{x}^{(i)})) + \mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) \tag{1}\]위 식은 변분 추론(variational inference) 의 기본적인 분해(분리) 과정을 통해 얻어진다.
주변 우도는 다음과 같이 정의된다.
\[p_\theta(\mathbf{x}) = \int p_\theta(\mathbf{x}, \mathbf{z})\,d\mathbf{z}\]이는 잠재 변수 $\mathbf{z}$ 를 적분하여 관측 데이터 $\mathbf{x}$ 의 확률을 구한 것이다.
직접 계산이 어려우므로, 계산 가능한 근사 분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 를 곱하고 나눈다.
\[\log p_\theta(\mathbf{x}) = \log \int q_\phi(\mathbf{z}\mid\mathbf{x}) \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z}\mid\mathbf{x})}\,d\mathbf{z}\]이렇게 하면 $q_\phi$ 를 기대값 형태로 활용할 수 있게 된다.
$\log p_\theta(\mathbf{x})$ 의 항을 분해하기 위해
\[D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z}\mid\mathbf{x})) = \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} \left[\log \frac{q_\phi(\mathbf{z}\mid\mathbf{x})}{p_\theta(\mathbf{z}\mid\mathbf{x})}\right]\]
KL 발산의 정의를 사용한다.베이즈 정리
\[p_\theta(\mathbf{z}\mid\mathbf{x}) = \frac{p_\theta(\mathbf{x}, \mathbf{z})}{p_\theta(\mathbf{x})}\]를 대입하면,
\[\begin{align*} D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z}\mid\mathbf{x})) &= \mathbb{E}_{q_\phi} \left[\log q_\phi(\mathbf{z}\mid\mathbf{x}) - \log p_\theta(\mathbf{x}, \mathbf{z}) + \log p_\theta(\mathbf{x})\right] \\ &= \mathbb{E}_{q_\phi} [\log q_\phi(\mathbf{z}\mid\mathbf{x}) - \log p_\theta(\mathbf{x}, \mathbf{z})] + \log p_\theta(\mathbf{x}) \end{align*}\]위 식을 $\log p_\theta(\mathbf{x})$ 에 대해 정리하면,
\[\log p_\theta(\mathbf{x}) = D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z}\mid\mathbf{x})) + \mathbb{E}_{q_\phi} [\log p_\theta(\mathbf{x}, \mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})]\]두 번째 항을
\[\mathcal{L}(\theta, \phi; \mathbf{x}) = \mathbb{E}_{q_\phi} [\log p_\theta(\mathbf{x}, \mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})]\]로 정의하면,
\[\log p_\theta(\mathbf{x}) = D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z}\mid\mathbf{x})) + \mathcal{L}(\theta, \phi; \mathbf{x})\]즉, 식 (1)이 도출된다.
오른쪽 첫 번째 항은 근사 분포와 실제 사후분포 간의 KL 발산(KL divergence) 이다.
이 KL 발산은 항상 0 이상이므로,
오른쪽 두 번째 항 $\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)})$ 는
데이터 포인트 $i$에 대한 주변 우도의 (변분) 하한(variational lower bound) 이 된다.
즉, 다음이 성립한다.
\[\log p_\theta(\mathbf{x}^{(i)}) \geq \mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) = \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [-\log q_\phi(\mathbf{z}\mid\mathbf{x}) + \log p_\theta(\mathbf{x}, \mathbf{z})] \tag{2}\]이 식은 다음과 같이 다시 표현할 수도 있다.
\[\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) = -D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) \Vert p_\theta(\mathbf{z})) + \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})] \tag{3}\]식 (2)에서 식 (3)으로 바꿔 쓸 수 있는 이유는
\[p_\theta(\mathbf{x}, \mathbf{z}) = p_\theta(\mathbf{z})\,p_\theta(\mathbf{x}\mid\mathbf{z})\]
결합 확률의 분해를 대입했기 때문이다.
이 항을 ELBO의 정의에 대입하면 다음과 같이 된다.
\[\begin{align*} \mathcal{L}(\theta, \phi; \mathbf{x}) &= \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{x}, \mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})] \\ &= \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{z}) + \log p_\theta(\mathbf{x}\mid\mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})] \end{align*}\]이 식을 두 개의 기대값으로 분리하면,
\[\mathcal{L}(\theta, \phi; \mathbf{x}) = \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{x}\mid\mathbf{z})] + \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})]\]두 번째 기대값 항은 바로
\[\mathcal{L}(\theta, \phi; \mathbf{x}) = -D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z})) + \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{x}\mid\mathbf{z})]\]
$-D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}) \Vert p_\theta(\mathbf{z}))$
와 동일하므로,를 얻는다.
우리는 변분 파라미터 $\phi$ 와 생성 파라미터 $\theta$ 에 대해
하한식 $\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)})$ 를 미분하고 최적화하고자 한다.
그러나 하한식의 $\phi$ 에 대한 그래디언트는 다소 문제가 있다.
일반적인 (단순한, naïve) 몬테카를로 그래디언트 추정식은 다음과 같다.
여기서 $\mathbf{z}^{(l)} \sim q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})$ 이다.
하지만 이러한 그래디언트 추정량은
분산(variance) 이 매우 크기 때문에 (참고: [BJP12])
실제 계산에서는 비효율적이며 본 연구의 목적에는 적합하지 않다.
이 식은 기대값 안에 파라미터 $\phi$ 가 포함되어 있을 때,
그 기대값을 미분하는 과정을 보여주는 것이다.먼저 기본 항등식은 다음과 같다.
\[\nabla_\phi \log q_\phi(\mathbf{z}) = \frac{\nabla_\phi q_\phi(\mathbf{z})}{q_\phi(\mathbf{z})}\]이는 고등학교 수준의 로그 미분 공식
\[(\log f(x))' = \frac{f'(x)}{f(x)}\]을 그대로 확률밀도 함수에 적용한 것이다.
양변에 $q_\phi(\mathbf{z})$ 를 곱하면,
\[\nabla_\phi q_\phi(\mathbf{z}) = q_\phi(\mathbf{z}) \nabla_\phi \log q_\phi(\mathbf{z})\]이 식은 항상 성립하는 로그 미분 항등식이다.
이 항등식을 기대값의 미분에 적용하면,
\[\mathbb{E}_{q_\phi}[f(\mathbf{z})] = \int f(\mathbf{z}) q_\phi(\mathbf{z})\, d\mathbf{z}\]와 같이 표현할 수 있으므로,
\[\nabla_\phi \mathbb{E}_{q_\phi}[f(\mathbf{z})] = \int f(\mathbf{z}) \nabla_\phi q_\phi(\mathbf{z})\, d\mathbf{z}\]
양변을 $\phi$ 로 미분하면가 된다.
\[\nabla_\phi \mathbb{E}_{q_\phi}[f(\mathbf{z})] = \int f(\mathbf{z}) q_\phi(\mathbf{z}) \nabla_\phi \log q_\phi(\mathbf{z})\, d\mathbf{z}\]
여기에 앞서의 항등식을 대입하면,적분 형태를 다시 기대값 형태로 쓰면,
\[\nabla_\phi \mathbb{E}_{q_\phi}[f(\mathbf{z})] = \mathbb{E}_{q_\phi}[f(\mathbf{z}) \nabla_\phi \log q_\phi(\mathbf{z})]\]이 된다.
실제 계산에서는 이 적분을 직접 구하기 어렵기 때문에,
분포 $q_\phi(\mathbf{z})$ 에서 샘플을 여러 개 뽑아 평균으로 근사한다.예를 들어,
\[\mathbb{E}_{q_\phi}[f(\mathbf{z}) \nabla_\phi \log q_\phi(\mathbf{z})] \approx \frac{1}{L} \sum_{l=1}^L f(\mathbf{z}^{(l)}) \nabla_\phi \log q_\phi(\mathbf{z}^{(l)}), \quad \mathbf{z}^{(l)} \sim q_\phi\]이렇게 적분 대신 분포에서 표본을 뽑아 평균을 내는 방법을
몬테카를로 근사(Monte Carlo approximation) 라고 한다.
즉, 적분을 직접 계산하지 않고
무작위 샘플링을 통해 기대값을 근사하는 방식이다.하지만 이 방법의 문제는 분산(variance) 이 크다는 것이다.
샘플마다 $f(\mathbf{z})$ 의 값이 들쭉날쭉하고,
$\nabla_\phi \log q_\phi(\mathbf{z})$ 의 크기와 방향도 불안정하다면,
그 곱의 평균이 쉽게 요동친다.예를 들어, 일부 샘플에서는 $f(\mathbf{z})$ 가 매우 크고
다른 샘플에서는 거의 0이라면
평균을 내도 결과가 크게 변동한다.이렇게 되면 학습 시 그래디언트가 불안정해지고,
학습 속도가 느려지며 최적화가 어렵게 된다.
2.3 SGVB 추정량과 AEVB 알고리즘
이 절에서 우리는 하한식(lower bound)의 실용적인 추정량(practical estimator)과
그 파라미터들에 대한 미분(derivatives)을 소개한다.
우리는 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 형태의
근사 사후분포(approximate posterior)를 가정한다.
그러나 이 기법은 $\mathbf{x}$ 에 조건화하지 않는,
즉 $q_\phi(\mathbf{z})$ 인 경우에도 적용될 수 있음을 주의하라.
파라미터들에 대한 사후분포를 추론하기 위한
완전한 변분 베이즈 방법(fully variational Bayesian method)은
부록(appendix)에 제시되어 있다.
특정한 완만한 조건들(under certain mild conditions) 하에서,
선택된 근사 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대해
우리는 보조 잡음 변수(auxiliary noise variable) $\boldsymbol{\epsilon}$ 의
미분 가능한 변환 $g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 을 이용하여
랜덤 변수 $\tilde{\mathbf{z}} \sim q_\phi(\mathbf{z}\mid\mathbf{x})$ 를
다시 매개변수화(reparameterize)할 수 있다.
“특정한 완만한 조건들(under certain mild conditions)” 이란,
함수 $g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 가
연속적이고 미분 가능한(smooth and differentiable) 형태를 가지며,
$\boldsymbol{\epsilon}$ 이 따르는 분포 $p(\boldsymbol{\epsilon})$ 가
충분히 단순하고 샘플링 가능한 경우를 의미한다.예를 들어, $\boldsymbol{\epsilon} \sim \mathcal{N}(0, I)$ 와 같이
정규분포를 사용하는 것이 일반적이다.
이러한 조건이 충족되어야
$\tilde{\mathbf{z}} = g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 의
미분 가능성이 보장되어,
역전파를 통해 $\phi$ 에 대한 그래디언트를 계산할 수 있다.즉, 확률적 샘플링 과정을
미분 가능한 결정적 함수 형태로 변환(reparameterize) 함으로써
학습 과정에서 안정적이고 효율적인 그래디언트 추정이 가능해진다.
적절한 분포 $p(\boldsymbol{\epsilon})$ 과 함수 $g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 를 선택하는
일반적인 전략에 대해서는 2.4절을 참조하라.
이제 우리는 함수 $f(\mathbf{z})$ 의 기댓값(expectation)을
$q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대해 몬테카를로 추정(Monte Carlo estimation)으로 근사할 수 있다.
우리는 이 기법을 변분 하한식(식 (2))에 적용하여,
일반적인 확률적 그래디언트 변분 베이즈(SGVB) 추정량
$\tilde{\mathcal{L}}^{A}(\theta,\phi;\mathbf{x}^{(i)}) \simeq \mathcal{L}(\theta,\phi;\mathbf{x}^{(i)})$ 를 얻는다.
여기서 $\mathbf{z}^{(i,l)} = g_\phi(\boldsymbol{\epsilon}^{(l)}, \mathbf{x}^{(i)})$ 이고,
$\boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})$ 이다.
$\tilde{\mathcal{L}}^{A}$ 는 재매개변수화로 얻은 샘플들을 사용해
ELBO(식 (2))의 기댓값을 몬테카를로 평균으로 근사한 추정치이다.
이 추정치는 샘플 수 $L$ 개를 사용한 불편향(unbiased) SGVB 추정값이며,
$L$ 을 늘릴수록 분산이 줄어들어
보다 안정적인 그래디언트 추정을 가능하게 한다.
종종 식 (3)의 KL 발산
$D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) \Vert p_\theta(\mathbf{z}))$ 은
분석적으로 적분(integrated analytically)될 수 있다(부록 B 참조).
따라서 기대 재구성 오차(expected reconstruction error)
\(\mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})} [\log p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})]\) 만이
샘플링을 통해 추정될 필요가 있다.
이때 KL 발산 항은
근사 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
사전분포 $p_\theta(\mathbf{z})$ 와 가깝도록 유도하는
정규화(regularization) 항으로 해석될 수 있다.
이로써 식 (3)에 대응하는,
두 번째 형태의 SGVB 추정량
을 얻으며,
이는 일반적인 추정량보다
보통 더 작은 분산을 갖는다.
여기서
$\mathbf{z}^{(i,l)} = g_\phi(\boldsymbol{\epsilon}^{(l)}, \mathbf{x}^{(i)})$,
$\boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})$ 이다.
$N$개의 데이터 포인트를 가진 데이터셋 $\mathbf{X}$ 로부터
여러 개의 데이터 포인트가 주어질 때,
우리는 미니배치(minibatch)에 기반하여
전체 데이터셋의 주변 우도 하한(marginal likelihood lower bound)의
추정량(estimator)을 구성할 수 있다.
식에서 $\frac{N}{M}$ 이 곱해지는 이유는,
전체 데이터셋의 하한값 $\mathcal{L}(\theta, \phi; \mathbf{X})$ 를
전체 $N$개의 데이터포인트에 대한 합으로 근사해야 하기 때문이다.하지만 실제 학습에서는 모든 데이터($N$개)를 한 번에 쓰기 어렵기 때문에,
대신 그중 $M$개만 임의로 뽑은 미니배치(minibatch) 로 계산한다.이때 미니배치의 합 $\sum_{i=1}^{M}\tilde{\mathcal{L}}(\theta, \phi; \mathbf{x}^{(i)})$ 은
전체 데이터셋의 일부($M/N$)에 해당하므로,
이를 전체 데이터에 맞게 스케일링하려면
$\frac{N}{M}$ 배를 곱해줘야 한다.즉, $\frac{N}{M}$ 은
“미니배치 평균을 전체 데이터셋 수준의 추정값으로 확장하는 비율”이며,
이렇게 하면 전체 데이터셋을 사용했을 때와
동일한 기댓값(expectation)을 가지게 된다.
여기서 미니배치 $\mathbf{X}^{M} = {\mathbf{x}^{(i)}}_{i=1}^{M}$ 는
$N$ 개의 데이터 포인트를 가진 전체 데이터셋 $\mathbf{X}$ 로부터
임의로 추출된 $M$ 개의 데이터 포인트 샘플이다.
실험에서는 데이터 포인트당 샘플 수 $L$ 을 1로 설정해도,
미니배치 크기 $M$ 이 충분히 클 경우(예: $M = 100$)
좋은 성능을 보였다.
여기서 데이터 포인트(data point)는 하나의 샘플(예: 한 장의 이미지, 한 문장 등)을 뜻한다.
미니배치(minibatch)는 이런 데이터 포인트 $M$개를 한 번에 묶어
모델이 동시에 학습하도록 만든 데이터의 묶음이다.반면 $L$은 “잠재 변수 샘플 수(number of latent samples per datapoint)”를 의미한다.
즉, 각 데이터 포인트 $\mathbf{x}^{(i)}$ 에 대해
잠재 변수 $\mathbf{z}$ 를 $L$번 샘플링하여
ELBO의 기댓값(재구성항)을 몬테카를로로 근사할 때 사용된다.요약하자면:
- $N$ : 전체 데이터셋의 샘플 개수
- $M$ : 한 번의 학습 단계에서 사용하는 미니배치 크기
- $L$ : 각 데이터 포인트당 샘플링하는 잠재 변수의 개수
따라서 실험에서 “$L=1$로 설정해도 충분히 좋은 성능을 보였다”는 말은,
각 데이터 포인트마다 잠재 변수를 한 번만 샘플링해도
미니배치 크기 $M$ 이 충분히 클 경우
전체적으로 기대값이 안정적으로 근사된다는 뜻이다.
$\nabla_{\theta,\phi}\tilde{\mathcal{L}}(\theta; \mathbf{X}^{M})$ 의
도함수를 계산하여 얻은 그래디언트는
SGD나 Adagrad [DHS10] 같은 확률적 최적화 방법과 함께 사용될 수 있다.
확률적 그래디언트를 계산하는 기본적인 접근법은 알고리즘 1에 제시되어 있다.
알고리즘 1
Auto-Encoding VB (AEVB) 알고리즘의 미니배치(minibatch) 버전
섹션 2.3에서 제시된 두 가지 SGVB 추정량 중 어느 것이든 사용할 수 있다.
실험에서는 $M = 100$, $L = 1$ 설정을 사용한다.
$\theta, \phi \; \leftarrow$ 파라미터 초기화
반복 (repeat)
$\mathbf{X}^{M} \; \leftarrow$ 전체 데이터셋에서 무작위로 선택된 $M$ 개의 데이터포인트
$\boldsymbol{\epsilon} \; \leftarrow$ 잡음 분포 $p(\boldsymbol{\epsilon})$ 로부터 무작위 샘플링
$\mathbf{g} \; \leftarrow \; \nabla_{\theta, \phi} \tilde{\mathcal{L}}^{M}(\theta, \phi; \mathbf{X}^{M}, \boldsymbol{\epsilon})$
(식 (8)의 미니배치 추정량(minibatch estimator)의 그래디언트 계산)
$\theta, \phi \; \leftarrow$ 그래디언트 $\mathbf{g}$ 를 사용하여 파라미터 갱신
(예: SGD 또는 Adagrad [DHS10])
until 파라미터 $(\theta, \phi)$ 가 수렴할 때까지
return $\theta, \phi$
오토인코더(auto-encoder)와의 연관성은
식 (7)에 주어진 목적함수를 살펴볼 때 명확해진다.
첫 번째 항은
“근사 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 와
사전분포 $p_\theta(\mathbf{z})$ 사이의 KL 발산(KL divergence)”으로,
정규화항(regularizer) 역할을 한다.
두 번째 항은
기대값 형태의 음의 재구성 오차(expected negative reconstruction error)이다.
ELBO는 최대화해야 하는 값이지만,
실제 학습에서는 손실(loss)을 최소화하도록 구현하기 때문에
부호를 반전시켜 $-\mathcal{L}$ 형태로 사용한다.따라서 \(\mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})}[\log p_\theta(\mathbf{x}\mid\mathbf{z})]\) 항은
원래는 커질수록 좋은 값(재구성 확률이 높을수록 좋음)이지만,
손실함수로 쓸 때는 부호가 바뀌어
음의 로그 우도(negative log-likelihood) 로 표현된다.이런 이유로 이 항을 “음의 재구성 오차(negative reconstruction error)”라고 부른다.
즉, 재구성 확률이 높을수록 오차는 작아지는 형태가 된다.
함수 $g_\phi(\cdot)$ 는
데이터 포인트 $\mathbf{x}^{(i)}$ 와
무작위 잡음 벡터 $\boldsymbol{\epsilon}^{(l)}$ 를
해당 데이터 포인트의 근사 사후분포로부터의 샘플에 매핑하도록 선택된다:
그 다음, 샘플 $\mathbf{z}^{(i,l)}$ 은
함수 $\log p_\theta(\mathbf{x}^{(i)} \mid \mathbf{z}^{(i,l)})$ 의 입력으로 주어진다.
이 함수는, 생성 모델 하에서
$\mathbf{z}^{(i,l)}$ 가 주어졌을 때
데이터 포인트 $\mathbf{x}^{(i)}$ 의
확률밀도(probability density) (또는 확률질량(probability mass))에 해당한다.
이 항은 오토인코더 용어로는
음의 재구성 오차(negative reconstruction error)이다.
2.4 재매개변수화 트릭(The reparameterization trick)
우리의 문제를 해결하기 위해
$q_\phi(\mathbf{z}\mid\mathbf{x})$ 로부터 샘플을 생성하기 위한
대체 방법(alternative method)을 도입하였다.
이 핵심적인 매개변수화 트릭(parameterization trick)은 매우 단순하다.
$\mathbf{z}$ 를 연속 확률변수(continuous random variable)라 하고,
$\mathbf{z} \sim q_\phi(\mathbf{z}\mid\mathbf{x})$ 가 어떤 조건부 분포라고 하자.
그러면 확률변수 $\mathbf{z}$ 를
결정론적 변수(deterministic variable)
$\mathbf{z} = g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 로 표현할 수 있는 경우가 자주 있다.
여기서 $\boldsymbol{\epsilon}$ 은
독립된 주변분포(independent marginal) $p(\boldsymbol{\epsilon})$ 를 가지는
보조 변수(auxiliary variable)이며,
$g_\phi(\cdot)$ 는 파라미터 $\phi$ 로 매개변수화된
벡터값 함수(vector-valued function)이다.
이 재매개변수화(reparameterization)는 우리의 경우에 유용하다.
그 이유는, 이것을 사용하여
$q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대한 기댓값(expectation)을 다시 쓸 수 있기 때문이다.
이로써 몬테카를로(Monte Carlo) 기댓값의 추정치가
$\phi$ 에 대해 미분 가능(differentiable)하게 된다.
증명(proof)은 다음과 같다.
결정론적 매핑(deterministic mapping)
$\mathbf{z} = g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 가 주어졌을 때, 우리는 다음을 알고 있다.1
1미소값(infinitesimal)에 대해서는
$dz = \prod_i dz_i$ 라는 표기 규칙(notational convention)을 사용한다.
이 관계식은 확률 질량(probability mass)의 보존 원리를 나타낸 것이다.
여기서 $\mathbf{z}$ 는 근사 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 에서 샘플링되는 변수이고,
$\boldsymbol{\epsilon}$ 은 더 단순한 분포(예: 표준 정규분포) $p(\boldsymbol{\epsilon})$ 에서
샘플링되는 보조 변수(auxiliary variable)이다.$\mathbf{z} = g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 로 정의된 결정론적 변환을 통해
두 변수의 공간이 서로 연결되므로,
한쪽 공간에서의 확률밀도와 미소부피의 곱은
다른 쪽 공간에서도 동일하게 유지되어야 한다.즉,
\[q_\phi(\mathbf{z}\mid\mathbf{x})\,dz = p(\boldsymbol{\epsilon})\,d\epsilon\]는 “변수 공간이 달라져도 전체 확률의 양은 변하지 않는다”는
확률 보존의 원리를 수학적으로 표현한 식이다.
따라서,
\[\int q_\phi(\mathbf{z}\mid\mathbf{x}) f(\mathbf{z}) \, d\mathbf{z} = \int p(\boldsymbol{\epsilon}) f(\mathbf{z}) \, d\boldsymbol{\epsilon} = \int p(\boldsymbol{\epsilon}) f(g_\phi(\boldsymbol{\epsilon}, \mathbf{x})) \, d\boldsymbol{\epsilon}\]이로부터 다음이 성립한다.
\[\int q_\phi(\mathbf{z}\mid\mathbf{x}) f(\mathbf{z}) \, d\mathbf{z} \simeq \frac{1}{L} \sum_{l=1}^{L} f(g_\phi(\mathbf{x}, \boldsymbol{\epsilon}^{(l)})) \quad \text{where} \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})\]섹션 2.3에서, 우리는 이 트릭을 변분 하한식(variational lower bound)의
미분 가능한 추정량(differentiable estimator)을 얻기 위해 적용하였다.
예를 들어, 단변량 가우시안(univariate Gaussian) 경우를 생각해 보자.
$z \sim p(z\mid x) = \mathcal{N}(\mu, \sigma^2)$ 라고 하자.
이 경우, 유효한 재매개변수화(reparameterization)는
$z = \mu + \sigma\epsilon$ 이며,
여기서 $\epsilon$ 은 $\epsilon \sim \mathcal{N}(0, 1)$ 을 따르는
보조 잡음 변수(auxiliary noise variable)이다.
따라서 다음이 성립한다.
\[\mathbb{E}_{\mathcal{N}(z; \mu, \sigma^2)}[f(z)] = \mathbb{E}_{\mathcal{N}(\epsilon; 0, 1)}[f(\mu + \sigma\epsilon)] \simeq \frac{1}{L}\sum_{l=1}^{L} f(\mu + \sigma\epsilon^{(l)}) \quad \text{where} \quad \epsilon^{(l)} \sim \mathcal{N}(0, 1)\]$q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대해
이러한 미분 가능한 변환 $g_\phi(\cdot)$ 과 보조 변수 $\boldsymbol{\epsilon} \sim p(\boldsymbol{\epsilon})$ 를
선택할 수 있는 경우는 언제인가?
세 가지 기본적인 접근법은 다음과 같다.
계산 가능한(intractable) 역누적분포함수(inverse CDF)
이 경우, $\boldsymbol{\epsilon} \sim \mathcal{U}(0, \mathbf{I})$ 로 두고,
$g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 를 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 의 역누적분포함수(inverse CDF)로 정의한다.
예시: Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal,
Gompertz, Gumbel, Erlang 분포.여기서 $\mathcal{U}(0, \mathbf{I})$ 는 균등분포(Uniform distribution) 를 의미한다.
즉, $\boldsymbol{\epsilon}$ 은 0과 1 사이에서 균등하게 샘플링된 값으로,
모든 값이 동일한 확률로 선택되는 분포를 따른다는 뜻이다.
(벡터인 경우, 각 차원이 독립적으로 0~1 사이의 균등분포를 따름.)역누적분포함수(inverse CDF, 또는 quantile function) 는
“누적된 확률값”을 입력받아 그에 해당하는 실제 데이터 값을 반환하는 함수이다.예를 들어,
- 누적분포함수(CDF) $F(z)$ 는 “값 $z$ 이하일 확률”을 계산한다.
즉, $F(z) = P(Z \le z)$ - 반대로 역누적분포함수 $F^{-1}(u)$ 는
“누적확률이 $u$일 때의 값 $z$”를 반환한다.
따라서
\[\epsilon \sim \mathcal{U}(0,1), \quad z = F^{-1}(\epsilon)\]라고 하면,
균등분포에서 샘플링한 $\epsilon$ 을
$F^{-1}$ 을 통해 변환함으로써
$z$ 가 $F$ 로 정의된 원래의 분포를 따르도록 만들 수 있다.즉, reverse CDF(역 CDF) 는
“균등한 확률 입력 → 해당 확률에 대응하는 분포 값 출력”의 역할을 하며,
복잡한 분포를 샘플링하기 쉽게 만들어 주는 함수이다.- 누적분포함수(CDF) $F(z)$ 는 “값 $z$ 이하일 확률”을 계산한다.
가우시안 예시와 유사한 방식
“location–scale” 계열의 분포에 대해서는
표준 분포(즉, location = 0, scale = 1)를 보조 변수 $\boldsymbol{\epsilon}$ 로 두고,
$g(\cdot) = \text{location} + \text{scale} \cdot \boldsymbol{\epsilon}$ 로 정의할 수 있다.
예시: Laplace, Elliptical, Student’s t, Logistic, Uniform,
Triangular, Gaussian 분포.합성(Composition)
랜덤 변수(random variables)는
보조 변수(auxiliary variables)의 다른 변환(different transformations)으로
표현되는 경우가 종종 있다.
예시: Log-Normal (정규분포 변수의 지수화),
Gamma (지수분포 변수의 합),
Dirichlet (Gamma 변수의 가중합),
Beta, Chi-Squared, F 분포.
세 가지 접근법이 모두 실패할 경우에도,
일부 방법에서는 PDF와 유사한 계산 복잡도로
역누적분포함수(inverse CDF)의 근사값을 효율적으로 계산할 수 있다
(예: [Dev86] 참조).
3. 예시: 변분 오토인코더 (Variational Auto-Encoder)
이 절에서는 확률적 인코더 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 에
신경망(neural network)을 사용하는 예시를 제시한다.
이 인코더는 생성 모델의 사후분포 $p_\theta(\mathbf{x}, \mathbf{z})$ 의
근사 형태(approximation)이며,
파라미터 $\phi$ 와 $\theta$ 는 AEVB 알고리즘을 통해 함께 최적화된다.
잠재 변수(latent variable)에 대한 사전분포(prior)는
중심화된 등방 다변량 가우시안 분포(centered isotropic multivariate Gaussian)
$p_\theta(\mathbf{z}) = \mathcal{N}(\mathbf{z}; \mathbf{0}, \mathbf{I})$ 로 둔다.
이 경우, 사전분포는 별도의 파라미터를 가지지 않는다.
$p_\theta(\mathbf{x}\mid\mathbf{z})$ 는 다변량 가우시안(multivariate Gaussian) (연속값 데이터의 경우)
또는 베르누이(Bernoulli) 분포 (이진 데이터의 경우)로 설정하며,
이 분포의 파라미터들은 MLP(완전연결 신경망, single hidden layer)로부터
$\mathbf{z}$ 를 입력받아 계산된다 (부록 C 참조).
진짜 사후분포 $p_\theta(\mathbf{z}\mid\mathbf{x})$ 는 이 경우 계산이 불가능(intractable)하다.
$q_\phi(\mathbf{z}\mid\mathbf{x})$ 의 형태에는 많은 자유도가 존재하지만,
진짜 사후분포는 대체로 근사적인 가우시안 형태를 가지며
대각 공분산(diagonal covariance)을 갖는다고 가정할 수 있다.
따라서 변분 근사 사후분포(variational approximate posterior)를
대각 공분산을 가진 다변량 가우시안으로 둘 수 있다.2
\[\log q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) = \log \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, {\boldsymbol{\sigma}^{2(i)}}\mathbf{I}) \tag{9}\]2이것은 단지 단순화(simplifying)를 위한 선택일 뿐이며,
본 방법론의 한계는 아니다.
여기서 근사 사후분포의 평균 $\boldsymbol{\mu}^{(i)}$ 와 표준편차 $\boldsymbol{\sigma}^{(i)}$ 는 인코딩 MLP의 출력값으로,
데이터 포인트 $\mathbf{x}^{(i)}$ 와 변분 파라미터 $\phi$ 의 비선형 함수로 주어진다 (부록 C 참조).
앞서 2.4절에서 설명한 것처럼,
사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})$ 로부터 샘플을 추출할 때
다음과 같은 재매개변수화(reparameterization)를 사용한다.
여기서 $\odot$ 는 요소별(element-wise) 곱을 의미한다.
이 모델에서 $p_\theta(\mathbf{z})$ (사전분포)와 $q_\phi(\mathbf{z}\mid\mathbf{x})$ (근사 사후분포) 모두 가우시안 분포이다.
이 경우, KL 발산(KL divergence)은
추정(estimation) 과정 없이도 계산 및 미분이 가능하므로
식 (7)의 추정량을 사용할 수 있다 (부록 B 참조).
이때, 데이터 포인트 $\mathbf{x}^{(i)}$ 에 대한 결과적인 추정량(estimator)은 다음과 같다.
\[\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) \simeq \frac{1}{2}\sum_{j=1}^{J} \left( 1 + \log\big((\sigma_j^{(i)})^2\big) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 \right) + \frac{1}{L}\sum_{l=1}^{L} \log p_\theta(\mathbf{x}^{(i)} \mid \mathbf{z}^{(i,l)}) \tag{10}\]여기서
\[\mathbf{z}^{(i,l)} = \boldsymbol{\mu}^{(i)} + \boldsymbol{\sigma}^{(i)} \odot \boldsymbol{\epsilon}^{(l)}, \quad \boldsymbol{\epsilon}^{(l)} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]출발점은 ELBO의 기본식이다.
\[\displaystyle \mathcal{L}(\theta,\phi;\mathbf{x}^{(i)}) = \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})}\!\big[\log p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})\big] - D_{KL}\!\big(q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) \,\Vert\, p_\theta(\mathbf{z})\big)\]여기서 첫 번째 항은 재구성 기댓값(reconstruction expectation),
두 번째 항은 근사 사후와 사전의 KL 발산(KL divergence) 이다.이제 KL 항을 구체적으로 전개한다.
\[\displaystyle D_{KL}(q\,\Vert\,p) = \frac{1}{2}\!\left[ \operatorname{tr}(\Sigma_p^{-1}\Sigma_q) + (\boldsymbol{\mu}_p - \boldsymbol{\mu}_q)^\top \Sigma_p^{-1}(\boldsymbol{\mu}_p - \boldsymbol{\mu}_q) - k + \log\frac{|\Sigma_p|}{|\Sigma_q|} \right]\]
두 다변량 가우시안 분포
$q=\mathcal{N}(\boldsymbol{\mu}_q,\Sigma_q)$,
$p=\mathcal{N}(\boldsymbol{\mu}_p,\Sigma_p)$ 의
KL 발산 일반식은 다음과 같다.여기서 $k$ 는 잠재 변수의 차원 수이다.
본 모델에서는
- $p_\theta(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I})$
- $q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) = \mathcal{N}\big(\boldsymbol{\mu}^{(i)}, \operatorname{diag}((\boldsymbol{\sigma}^{(i)})^2)\big)$
로 가정하므로
$\Sigma_p = \mathbf{I}$, $\Sigma_q = \operatorname{diag}((\boldsymbol{\sigma}^{(i)})^2)$,
$\boldsymbol{\mu}_p = \mathbf{0}$, $\boldsymbol{\mu}_q = \boldsymbol{\mu}^{(i)}$ 이다.각 항을 계산하면 다음과 같다.
- $\operatorname{tr}(\Sigma_p^{-1}\Sigma_q) = \sum_j (\sigma_j^{(i)})^2$
- $(\boldsymbol{\mu}_p - \boldsymbol{\mu}_q)^\top\Sigma_p^{-1}(\boldsymbol{\mu}_p - \boldsymbol{\mu}_q) = \sum_j (\mu_j^{(i)})^2$
- $\log\mid\Sigma_q\mid = \sum_j \log((\sigma_j^{(i)})^2)$
- $\log\mid\Sigma_p\mid = 0$
이를 대입하면 KL 항은 다음과 같이 닫힌형(closed form)으로 계산된다.
\[\displaystyle D_{KL}\big(q\,\Vert\,p\big) = \frac{1}{2}\sum_{j=1}^{J}\!\Big( (\mu^{(i)}_j)^2 + (\sigma^{(i)}_j)^2 - \log((\sigma^{(i)}_j)^2) - 1 \Big)\]ELBO에서는 $-D_{KL}$ 항이 포함되므로, 부호를 반전하면 다음을 얻는다.
\[\displaystyle -D_{KL} = \frac{1}{2}\sum_{j=1}^{J}\!\Big( 1 + \log((\sigma^{(i)}_j)^2) - (\mu^{(i)}_j)^2 - (\sigma^{(i)}_j)^2 \Big)\]이 항이 바로 식 (10)의 첫 번째 항에 해당한다.
이제 재구성 기댓값 항을 근사한다.
$\mathbf{z}$ 를 직접 샘플링하지 않고,
\[\mathbf{z}^{(i,l)} = \boldsymbol{\mu}^{(i)} + \boldsymbol{\sigma}^{(i)} \odot \boldsymbol{\epsilon}^{(l)}\]
재매개변수화 trick을 통해 $\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 에서 샘플링한다.이때, 기대값은 $L$개의 샘플 평균으로 근사된다.
\[\mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})}\!\big[\log p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})\big] \simeq \frac{1}{L}\sum_{l=1}^{L} \log p_\theta(\mathbf{x}^{(i)} \mid \mathbf{z}^{(i,l)})\]두 항을 합치면 다음의 최종 근사식을 얻는다.
\[\displaystyle \mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) \simeq \frac{1}{2}\sum_{j=1}^{J}\!\Big( 1 + \log((\sigma_j^{(i)})^2) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 \Big) + \frac{1}{L}\sum_{l=1}^{L} \log p_\theta(\mathbf{x}^{(i)} \mid \mathbf{z}^{(i,l)})\]여기서 $\odot$ 는 요소별 곱(element-wise product)을 의미한다.
앞서와 부록 C에서 설명한 것처럼,
디코딩 항 $\log p_\theta(\mathbf{x}^{(i)} \mid \mathbf{z}^{(i,l)})$ 는 모델링하는 데이터의 유형에 따라
베르누이(Bernoulli) 또는 가우시안(Gaussian) MLP로 구성된다.
4. 관련 연구 (Related Work)
웨이크-슬립 알고리즘(wake-sleep algorithm) [HDFN95]은
우리의 지식으로는,
연속적인 잠재 변수 모델(continuous latent variable models)의
동일한 일반적 범주에 적용 가능한
문헌상 유일한 다른 온라인 학습(on-line learning) 방법이다.
우리의 방법과 마찬가지로,
웨이크-슬립 알고리즘은
진짜 사후분포(true posterior)를 근사하는
인식 모델(recognition model)을 사용한다.
웨이크-슬립 알고리즘의 단점은
두 개의 목적함수를 동시에 최적화해야 한다는 점이며,
이 두 목적함수는 합쳐서도
주변우도(marginal likelihood)의 (하한에 대한) 최적화와
일치하지 않는다는 것이다.
웨이크-슬립 알고리즘의 장점은
이 방법이 또한
이산적인 잠재 변수(discrete latent variables)를 가진
모델에도 적용된다는 것이다.
웨이크-슬립 알고리즘은
데이터 포인트당 계산 복잡도(computational complexity)가
AEVB와 동일하다.
확률적 변분 추론(stochastic variational inference) [HBWP13]은
최근 점점 더 많은 관심을 받고 있다.
[BJP12]에서는
2.1절에서 논의된 나이브 그래디언트 추정량(naïve gradient estimator)의
높은 분산(variance)을 줄이기 위한
통제 변수(control variate) 기법을 도입하였으며,
이를 사후분포(posterior)의
지수족(exponential family) 근사에 적용하였다.
통제 변수(control variate) 는
“분산을 줄이기 위한 통계적 보정 기법”이다.예를 들어, 우리가 어떤 확률적 추정값을 계산할 때
그 결과가 매번 샘플링에 따라 크게 흔들린다면(즉, 분산이 크다면),
계산이 훨씬 불안정해진다.이때, 원래 계산하려는 값과 강하게 상관된 다른 변수를 하나 더 도입하고,
그 기대값(평균)을 미리 알고 있다면
두 값을 적절히 조합해 추정값의 흔들림을 줄일 수 있다.예를 들어,
“원래의 추정치 − 보정항 × (보조변수 − 보조변수의 평균)”
형태로 계산하면,
전체 분산이 줄어들면서도 기대값(평균)은 그대로 유지된다.즉, 통제 변수 기법은
“계산의 평균값은 유지하되, 변동성(variance)은 줄이는 방법”이다.논문 [BJP12]에서는 이 방법을
확률적 그래디언트 추정의 불안정성을 줄이기 위해 사용하였다.
[RGB13]에서는
원래의 그래디언트 추정량의 분산을 줄이기 위한
일반적인 방법들, 즉 통제 변수(control variate) 기법이 제안되었다.
[SK13]에서는
본 논문과 유사한 재매개변수화(reparameterization)를 사용하여,
지수족 근사 분포(exponential-family approximating distributions)의
자연 파라미터(natural parameters)를 학습하기 위한
효율적인 확률적 변분 추론 알고리즘의
한 형태를 제시하였다.
AEVB 알고리즘은
변분 목적식(variational objective)으로 학습된
유향 확률적 모델(directed probabilistic models) 과
오토인코더(auto-encoder) 사이의 연결점을 드러낸다.
선형 오토인코더(linear auto-encoder)와
특정 부류의 생성적 선형-가우시안 모델(generative linear-Gaussian models) 사이의
연결성은 오래전부터 알려져 있었다.
[Row98]에서는
PCA(주성분 분석, Principal Component Analysis)가
사전분포 $p(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I})$ 와
조건부 분포 $p(\mathbf{x}\mid\mathbf{z}) = \mathcal{N}(\mathbf{x}; W\mathbf{z}, \epsilon \mathbf{I})$ 를 가지는
특수한 형태의 선형-가우시안 모델에서,
$\epsilon$ 이 무한소(infinitesimally small)일 때의
최대우도추정(maximum-likelihood, ML) 해에
해당한다는 것이 보여졌다.
이 문장은 PCA(주성분 분석) 을
확률적 관점에서 해석한 결과를 설명하고 있다.일반적으로 PCA는 데이터를 저차원으로 압축하는
선형 변환(linear transformation) 방법이지만,
[Row98]에서는 이를 “확률 생성 모델(probabilistic generative model)”로
다시 해석했다.여기서의 모델은 다음과 같은 구조를 가진다.
- 잠재 변수 $\mathbf{z}$ 는 평균 0, 분산 1의 정규분포
$p(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I})$ 에서 생성된다.- 관측 데이터 $\mathbf{x}$ 는
$\mathbf{z}$ 에 선형 변환 $W$ 를 적용하고
여기에 작은 잡음 $\epsilon \mathbf{I}$ 를 더한
가우시안 분포
$p(\mathbf{x}\mid\mathbf{z}) = \mathcal{N}(\mathbf{x}; W\mathbf{z}, \epsilon \mathbf{I})$
에서 샘플링된다.이때 잡음의 세기 $\epsilon$ 을 거의 0에 가깝게(무한소로) 두면,
모델은 사실상 노이즈 없는 선형 변환으로 수렴하게 된다.즉, $\epsilon \to 0$ 인 경우에
이 생성 모델의 최대우도추정(Maximum Likelihood) 해가
바로 PCA 해와 동일함을 [Row98]에서 증명한 것이다.요약하자면,
PCA는 “가우시안 잡음이 매우 작은 선형 생성 모델”의
확률적 해석으로 볼 수 있다.
오토인코더(autoencoder)에 관한 최근의 관련 연구 [VLL+10]에서,
정규화되지 않은(unregularized) 오토인코더의 학습 기준(training criterion)이
입력 $X$ 와 잠재 표현 $Z$ 사이의
상호정보량(mutual information)에 대한
하한(lower bound)의 최대화(see the infomax principle [Lin89])에
해당한다는 것이 보여졌다.
상호정보량(mutual information)을
파라미터에 대해 최대화하는 것은
조건부 엔트로피(conditional entropy)를
최대화하는 것과 동등하며,
이 조건부 엔트로피는
오토인코딩 모델(autoencoding model) 하에서의
데이터의 기대 로그가능도(expected log-likelihood),
즉 음의 재구성 오차(negative reconstruction error) 에 의해
하한(lower bounded)된다 [VLL+10].
“하한(lower bounded)된다”는 말은,
어떤 값이 그보다 작아질 수는 없고, 더 커질 수만 있다는 뜻이다.여기서는 “조건부 엔트로피(conditional entropy)”의 실제 값이
“데이터의 기대 로그가능도(expected log-likelihood)”보다
항상 크거나 같다는 의미이다.즉,
\(\text{조건부 엔트로피} \ge \text{기대 로그가능도}\)
와 같은 관계가 성립한다는 뜻이다.따라서 “기대 로그가능도(=음의 재구성 오차)”는
조건부 엔트로피를 밑에서부터 근사하는 하한(lower bound) 으로 작용한다.오토인코더를 학습할 때 이 항을 최대화(=재구성 오차를 최소화)하면,
결과적으로 상호정보량을 간접적으로 높이는 효과가 있다.
그러나 이 재구성 기준(reconstruction criterion)만으로는
유용한 표현(meaningful representations)을 학습하기에
충분하지 않다는 것이 잘 알려져 있다 [BCV13].
이에 따라, 오토인코더가 유용한 표현을 학습할 수 있도록
정규화(regularization) 기법들이 제안되었다.
그 예로, 잡음 제거 오토인코더(denoising autoencoder),
수축 오토인코더(contractive autoencoder),
희소 오토인코더(sparse autoencoder) 등이 있다 [BCV13].
SGVB 목적식(SGVB objective)은
변분 하한(variational bound, 예: 식 (10))에 의해
결정되는 정규화 항(regularization term)을 포함하며,
유용한 표현(meaningful representations)을 학습하기 위해
일반적으로 필요한,
성가신 정규화 하이퍼파라미터(nuisance regularization hyperparameter) 를
필요로 하지 않는다.
이와 관련된 구조로는,
예측 희소 분해(predictive sparse decomposition, PSD) [KRL08]와 같은
인코더-디코더(encoder-decoder) 아키텍처가 있으며,
이는 본 연구에 영감을 주었다.
또한, 최근 제안된 생성 확률적 네트워크(Generative Stochastic Networks) [BTL13] 역시
관련이 있는데, 여기서는 잡음을 포함한 오토인코더(noisy auto-encoder) 가
데이터 분포로부터 샘플링하는 마르코프 연쇄(Markov chain)의
전이 연산자(transition operator)를 학습한다.
생성 확률적 네트워크(Generative Stochastic Networks, GSN) 는
오토인코더(autoencoder)의 학습 방식을 확률적(stochastic)으로 확장한 모델이다.여기서 “잡음을 포함한(noisy)” 오토인코더란
입력 데이터에 랜덤 잡음(random noise) 을 추가하거나,
은닉 표현(latent representation)을 생성할 때
확률적 샘플링(random sampling) 을 수행하는 방식을 의미한다.즉, 단순히 입력을 복원하는 것이 아니라
“잡음이 추가된 입력을 원래 데이터로 복원하도록” 학습되며,
이 과정이 마치 확률적 전이(stochastic transition)를 수행하는
마르코프 연쇄(Markov chain)의 한 단계처럼 작동한다.따라서 GSN은
오토인코더가 데이터를 단순히 인코딩–디코딩하는 데 그치지 않고,
데이터 분포에서 새로운 샘플을 생성할 수 있도록
이 확률적 전이 연산자(transition operator)를 학습한다는 점에서
일반적인 오토인코더보다 한 단계 확장된 개념이다.쉽게 말하면,
“잡음이 추가된 입력 → 복원”의 반복 과정을 통해
모델이 점점 더 데이터 분포 전체를 탐색하고
새로운 샘플을 생성할 수 있게 만드는 구조라고 볼 수 있다.
[SL10]에서는
인식 모델(recognition model)을 사용하여
딥 볼츠만 머신(Deep Boltzmann Machines)의
효율적인 학습을 수행하였다.
볼츠만 머신(Boltzmann Machine) 은
확률적 생성 모델(probabilistic generative model)의 한 종류로,
뉴런 간의 연결로 구성된 에너지 기반 모델(energy-based model) 이다.각 노드(뉴런)는 이진 상태(0 또는 1)를 가지며,
전체 시스템의 에너지(energy)가 낮을수록
해당 상태가 더 높은 확률로 선택되도록 설계되어 있다.모델은 확률분포를 다음과 같이 정의한다.
\[P(\mathbf{x}) = \frac{1}{Z} \exp(-E(\mathbf{x}))\]여기서 $E(\mathbf{x})$ 는 에너지 함수이고,
$Z$ 는 전체 확률이 1이 되도록 맞추는 정규화 상수(분배 함수, partition function)이다.딥 볼츠만 머신(Deep Boltzmann Machine, DBM) 은
이러한 구조를 여러 층으로 확장한 모델로,
각 층이 확률적으로 상호작용하면서
복잡한 데이터 분포를 학습할 수 있게 한다.다만, 이 모델은
에너지 함수의 정규화 상수 $Z$ 를 계산하기 어렵기 때문에
학습 과정이 매우 복잡하고 계산 비용이 높다.[SL10]에서는
이러한 계산 복잡성을 줄이기 위해
인식 모델(recognition model) 을 도입하여
사후분포를 근사하고,
이를 통해 딥 볼츠만 머신을 보다 효율적으로 학습하도록 하였다.
이러한 방법들은
정규화되지 않은 모델(unnormalized models, 즉 볼츠만 머신과 같은
무향 모델(undirected models))이나
희소 부호화(sparse coding) 모델에 국한되는 반면,
우리의 제안된 알고리즘은
일반적인 유향 확률적 모델(directed probabilistic models) 의
학습을 대상으로 한다.
최근에 제안된 DARN 방법 [GMW13] 또한
오토인코딩 구조(auto-encoding structure)를 사용하여
유향 확률적 모델(directed probabilistic model)을 학습하지만,
그들의 방법은 이진 잠재 변수(binary latent variables) 에 적용된다.
더 최근에, [RMW14]에서도
본 논문에서 설명한 재매개변수화 기법(reparameterization trick)을 이용하여,
오토인코더(auto-encoder),
유향 확률적 모델(directed probabilistic models),
그리고 확률적 변분 추론(stochastic variational inference) 사이의
연결 관계를 제시하였다.
그들의 연구는
우리의 연구와는 독립적으로 수행되었으며,
AEVB에 대한 또 다른 관점을 제공한다.
5. 실험 (Experiments)
우리는 MNIST와 Frey Face 데이터셋3의
이미지들로부터 생성 모델(generative models)을 학습하였으며,
변분 하한(variational lower bound)과
추정된 주변우도(estimated marginal likelihood)를 기준으로
학습 알고리즘들을 비교하였다.
3데이터셋은 https://www.cs.nyu.edu/~roweis/data.html 에서 이용할 수 있다.
3장에서 설명된 생성 모델(인코더, encoder)과
변분 근사(variational approximation) (디코더, decoder)를 사용하였으며,
여기서 인코더와 디코더는
동일한 수의 은닉 유닛(hidden units)을 가진다.
Frey Face 데이터는 연속형(continuous)이므로,
우리는 가우시안 출력(Gaussian outputs)을 가지는
디코더를 사용하였다.
이 디코더는 인코더와 동일하지만,
출력의 평균(mean)이 시그모이드 활성 함수(sigmoidal activation function)를 통해
(0,1) 구간으로 제한되었다(constrained).
참고로, “은닉 유닛(hidden units)”은
인코더와 디코더의 신경망(neural networks)에 존재하는
은닉층(hidden layer)을 의미한다.
모든 파라미터는
하한 추정량(lower bound estimator)
$\nabla_{\theta, \phi}\mathcal{L}(\theta, \phi; \mathbf{X})$ (알고리즘 1 참고)을
미분하여 계산된 그래디언트를 사용한
확률적 그래디언트 상승법(stochastic gradient ascent)을 통해 갱신되었다.
또한, 사전분포 $p(\theta) = \mathcal{N}(0, \mathbf{I})$ 에 대응하는
작은 가중치 감쇠 항(weight decay term)을 추가하였다.
변분 하한식(식 (3))에서
\[\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) = -D_{KL}(q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) \Vert p_\theta(\mathbf{z})) + \mathbb{E}_{q_\phi(\mathbf{z}\mid\mathbf{x})} [\log p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})]\]학습 초반에는 재구성항(reconstruction term)이 아직 충분히 학습되지 않아
KL 발산 항이 상대적으로 크게 작용한다.
이로 인해 사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
사전분포 $p_\theta(\mathbf{z}) = \mathcal{N}(0, \mathbf{I})$ 에
너무 빠르게 맞춰지며 “과도하게 수축(over-shrinking)”하는 현상이 발생한다.여기서 “사후분포가 수축한다”는 것은
입력 $x$ 와 무관하게 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
거의 모든 경우에서 평균이 0, 분산이 1인 정규분포 형태로 동일해지는 것을 의미한다.
즉, 잠재변수 $z$ 가 서로 다른 데이터를 구분하지 못하고
표현력이 사라지는 현상이 나타난다는 뜻이다.이를 완화하기 위해 작은 가중치 감쇠(weight decay)를 추가한다.
이는 사전분포 $p(\theta)$ 가 가우시안일 때 다음과 같은 관계로 표현된다.λ가 없는 기본 형태: \(\log p(\theta) = -\frac{1}{2}\|\theta\|^2 + \text{const.}\)
λ를 추가하여 정규화 강도를 조절하면: \(-\lambda \|\theta\|^2 \quad \leftrightarrow \quad \log p(\theta) = -\frac{1}{2}\|\theta\|^2 + \log \lambda + \text{const.}\)
여기서 λ는 정규화 정도를 조절하는 하이퍼파라미터로,
λ가 커질수록 상수항(const)이 커지고,
정규분포의 분산이 작아지며 파라미터 값이 더 작게 유지된다.결과적으로 가중치 감쇠는
학습 초기의 과도한 KL 수축을 완화하고
사후분포가 표준정규분포로 급격히 쏠리는 것을 방지하여
잠재변수가 충분히 표현력을 가질 수 있게 한다.
이 목적함수의 최적화는 근사적인 MAP 추정(approximate MAP estimation)과 동등하며,
여기서 우도(likelihood)의 그래디언트는
하한식(lower bound)의 그래디언트로 근사된다.
우리는 AEVB의 성능을
웨이크-슬립 알고리즘([HDFN95])과 비교하였다.
웨이크-슬립 알고리즘과 변분 오토인코더 모두에서
같은 인코더(인식 모델, recognition model)를 사용하였다.
모든 파라미터(변분 파라미터와 생성 파라미터)는
$\mathcal{N}(0, 0.01)$ 분포에서 무작위로 샘플링하여 초기화되었으며,
MAP 기준을 사용하여
확률적으로(stochastically) 공동 최적화(jointly optimized)되었다.
스텝 크기(stepsize)는
Adagrad([DHS10])를 사용하여 조정(adapted)되었으며,
Adagrad의 전역 스텝 크기 파라미터(global stepsize parameter)는
초기 학습 반복(iteration) 동안의
훈련 세트 성능에 따라 {0.01, 0.02, 0.1} 중에서 선택되었다.
미니배치 크기(minibatch size)는 $M = 100$으로 설정되었고,
각 데이터 포인트당 샘플 수는 $L = 1$로 두었다.
가능도 하한(Likelihood lower bound)
생성 모델(디코더)과 이에 대응하는 인코더(즉, 인식 모델, recognition model)를 학습시켰으며,
MNIST의 경우 은닉 유닛(hidden units)을 500개,
Frey Face 데이터셋의 경우 200개로 설정하였다
(후자는 데이터셋이 상대적으로 작기 때문에 과적합을 방지하기 위함이다).
선택된 은닉 유닛의 수는
기존 오토인코더(auto-encoder)에 관한 선행 연구를 기반으로 하였으며,
다양한 알고리즘 간의 상대적 성능은
이러한 설정 변화에 크게 민감하지 않았다.
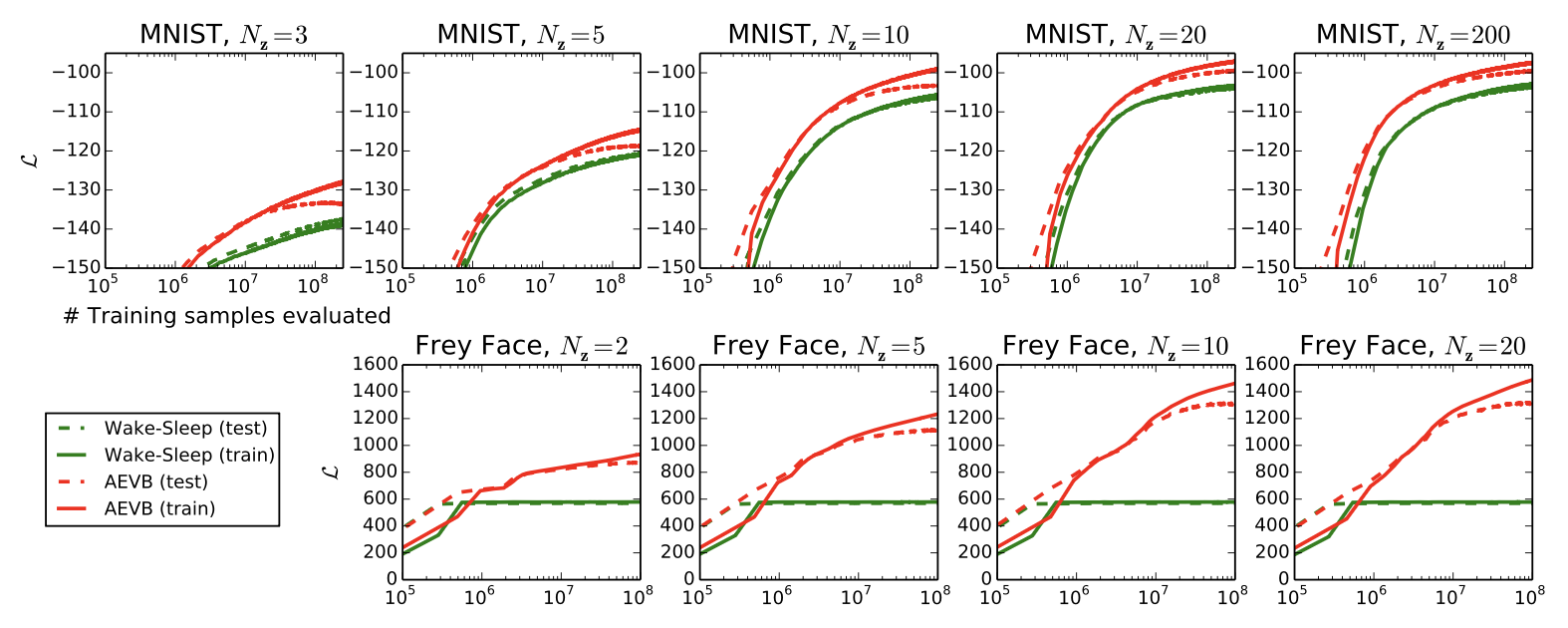
그림 2는 하한(lower bound)을 비교한 결과를 보여준다.
흥미롭게도, 불필요한(중복된) 잠재 변수(latent variables)의 추가는
과적합을 유발하지 않았으며,
이는 변분 하한의 정규화 성질(regularizing nature)에 의해 설명된다.
그림 2:
잠재 공간(latent space)의 차원 수 $N_z$ 가 다른 여러 실험에서,
하한(lower bound)의 최적화 관점에서
우리의 AEVB 방법과 wake-sleep 알고리즘을 비교하였다.
우리의 방법은 모든 실험에서 훨씬 더 빠르게 수렴하였으며,
더 나은 해(solution)에 도달하였다.
흥미롭게도, 잠재 변수(latent variables)의 수를 늘려도
과적합이 증가하지 않았는데,
이는 하한(lower bound)의 정규화 효과(regularizing effect)에 의해 설명된다.
세로축(vertical axis):
데이터 포인트당 추정된 평균 변분 하한(estimated average variational lower bound per datapoint).
추정량의 분산(estimator variance)은 매우 작았기 때문에 (< 1) 생략되었다.
가로축(horizontal axis):
평가된 학습 데이터 포인트의 개수(amount of training points evaluated).
연산은 Intel Xeon CPU (약 40 GFLOPS 효율) 환경에서
백만 개의 학습 샘플당 약 20~40분이 소요되었다.
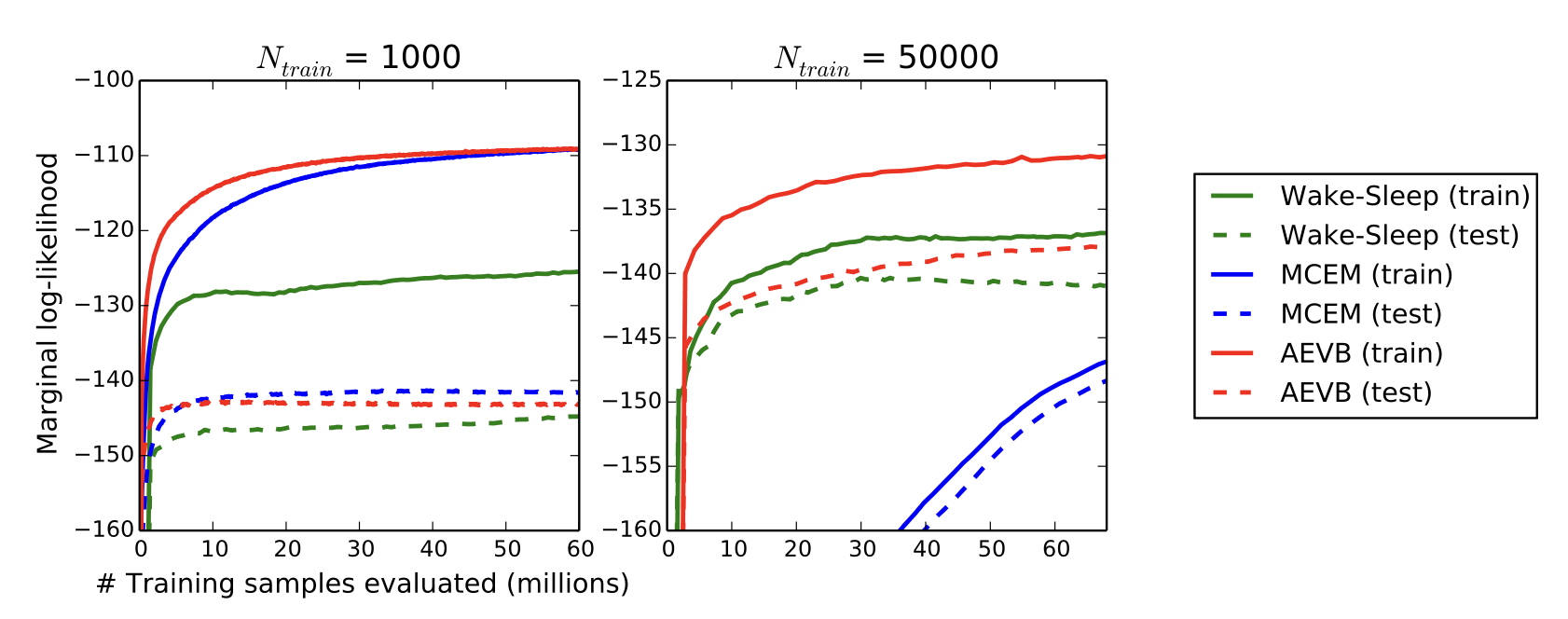
주변 가능도(Marginal likelihood)
잠재 공간(latent space)의 차원이 매우 낮을 경우,
학습된 생성 모델의 주변 가능도(marginal likelihood)를
MCMC 추정량(MCMC estimator)을 사용하여 추정하는 것이 가능하다.
주변 가능도 추정량에 대한 더 자세한 내용은 부록(appendix)에 제시되어 있다.
인코더와 디코더 모두에서
이번에는 은닉 유닛(hidden units) 100개와
잠재 변수(latent variables) 3개를 갖는 신경망을 사용하였다.
차원이 더 높아질 경우, 추정값(estimates)은 신뢰할 수 없게 되었다.
여기서도 MNIST 데이터셋이 사용되었다.
AEVB와 Wake-Sleep 방법은
하이브리드 몬테카를로(HMC, Hybrid Monte Carlo) 샘플러를 포함한
몬테카를로 EM(MCEM) [DKPR87] 방법과 비교되었으며,
세부 내용은 부록에 설명되어 있다.
우리는 세 알고리즘의 수렴 속도(convergence speed)를
작은 학습 세트와 큰 학습 세트의 경우 각각 비교하였으며,
그 결과는 그림 3에 제시되어 있다.
그림 3:
학습 데이터 포인트의 개수가 서로 다른 경우에 대해,
추정된 주변 가능도(estimated marginal likelihood)를 기준으로
AEVB, wake-sleep 알고리즘, 그리고 몬테카를로 EM(Monte Carlo EM)을 비교하였다.
몬테카를로 EM은 온라인(on-line) 알고리즘이 아니며,
AEVB나 wake-sleep 방법과 달리
전체 MNIST 데이터셋에 효율적으로 적용될 수 없다.
고차원 데이터의 시각화 (Visualisation of high-dimensional data)
만약 저차원(latent space)의 잠재 공간(예: 2차원)을 선택한다면,
학습된 인코더(즉, 인식 모델, recognition model)를 사용하여
고차원 데이터를 저차원 다양체(low-dimensional manifold)로 사상(project)할 수 있다.
MNIST 및 Frey Face 데이터셋의 2차원 잠재 공간 시각화 결과는
부록 A에서 확인할 수 있다.
6 결론 (Conclusion)
우리는 연속적인 잠재 변수(continuous latent variables)를 사용한 효율적인 근사 추론(approximate inference)을 위해, 변분 하한(variational lower bound)의 새로운 추정량(estimator)인 확률적 그래디언트 변분 베이즈(Stochastic Gradient VB, SGVB)를 소개하였다.
제안된 추정량은 표준 확률적 그래디언트 방법(standard stochastic gradient methods)을 통해
직접적으로 미분 및 최적화될 수 있다.
독립 동일 분포(i.i.d.) 데이터셋과
데이터 포인트마다 연속적인 잠재 변수(continuous latent variables)가 존재하는 경우에 대해,
우리는 효율적인 추론(inference)과 학습(learning)을 위한 알고리즘인
오토인코딩 변분 베이즈(Auto-Encoding VB, AEVB)를 제안한다.
이 알고리즘은 SGVB 추정량(estimator)을 사용하여
근사 추론 모델(approximate inference model)을 학습하며,
그 이론적 이점들은 실험 결과에 반영된다.
7 향후 연구 (Future work)
SGVB 추정량(estimator)과 AEVB 알고리즘은
연속적인 잠재 변수를 갖는 거의 모든 추론(inference) 및 학습(learning) 문제에
적용될 수 있으므로, 향후 연구 방향은 매우 다양하다.
(i) 인코더와 디코더에 사용되는
심층 신경망(예: 합성곱 신경망, convolutional networks)을 포함하는
계층적 생성 아키텍처(hierarchical generative architectures)를
AEVB와 함께 공동으로 학습하는 방법,
(ii) 시계열 모델(time-series models, 즉 동적 베이즈 네트워크, dynamic Bayesian networks),
(iii) SGVB를 전역 파라미터(global parameters)에 적용하는 방법,
(iv) 복잡한 잡음 분포(complicated noise distributions)의 학습에 유용한
잠재 변수를 포함하는 지도학습(supervised) 모델 등이 있다.
참고문헌 (References)
[BCV13] Yoshua Bengio, Aaron Courville, and Pascal Vincent. Representation learning: A review and new perspectives. 2013.
[BJP12] David M. Blei, Michael I. Jordan, and John W. Paisley. Variational bayesian inference with stochastic search.
In Proceedings of the 29th International Conference on Machine Learning (ICML-12), pages 1367–1374, 2012.
[BTL13] Yoshua Bengio and Éric Thibodeau-Laufer. Deep generative stochastic networks trainable by backprop.
arXiv preprint arXiv:1306.1091, 2013.
[Dev86] Luc Devroye. Sample-based non-uniform random variate generation.
In Proceedings of the 18th conference on Winter simulation, pages 260–265. ACM, 1986.
[DHS10] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization.
Journal of Machine Learning Research, 12:2121–2159, 2010.
[DKPR87] Simon Duane, Anthony D. Kennedy, Brian J. Pendleton, and Duncan Roweth. Hybrid monte carlo.
Physics Letters B, 195(2):216–222, 1987.
[GMW13] Karol Gregor, Andriy Mnih, and Daan Wierstra. Deep autoregressive networks.
arXiv preprint arXiv:1310.8499, 2013.
[HBWP13] Matthew D. Hoffman, David M. Blei, Chong Wang, and John Paisley. Stochastic variational inference.
The Journal of Machine Learning Research, 14(1):1303–1347, 2013.
[HDFN95] Geoffrey E. Hinton, Peter Dayan, Brendan J. Frey, and Radford M. Neal. The “wake-sleep” algorithm for unsupervised neural networks.
Science, pages 1158–1158, 1995.
[KRL08] Koray Kavukcuoglu, Marc’Aurelio Ranzato, and Yann LeCun. Fast inference in sparse coding algorithms with applications to object recognition.
Technical Report CBLL-TR-2008-12-01, Computational and Biological Learning Lab, Courant Institute, NYU, 2008.
[Lin89] Ralph Linsker. An application of the principle of maximum information preservation to linear systems.
Morgan Kaufmann Publishers Inc., 1989.
[RGB13] Rajesh Ranganath, Sean Gerrish, and David M. Blei. Black box variational inference.
arXiv preprint arXiv:1401.0118, 2013.
[RMW14] Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and variational inference in deep latent gaussian models.
arXiv preprint arXiv:1401.4082, 2014.
[Row98] Sam Roweis. EM algorithms for PCA and SPCA.
Advances in neural information processing systems, pages 626–632, 1998.
[SK13] Tim Salimans and David A. Knowles. Fixed-form variational posterior approximation through stochastic linear regression.
Bayesian Analysis, 8(4), 2013.
[SL10] Ruslan Salakhutdinov and Hugo Larochelle. Efficient learning of deep boltzmann machines.
In International Conference on Artificial Intelligence and Statistics, pages 693–700, 2010.
[VLL+10] Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio, and Pierre-Antoine Manzagol.
Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion.
The Journal of Machine Learning Research, 9999:3371–3408, 2010.
A 시각화 (Visualisations)
그림 4와 그림 5는
SGVB로 학습된 모델의
잠재 공간(latent space)과
그에 대응하는 관측 공간(observed space)의
시각화를 보여준다.
그림 4:
AEVB로 학습된, 이차원 잠재 공간(two-dimensional latent space)을 가지는
생성 모델의 학습된 데이터 다양체(data manifold) 시각화.
잠재 공간의 사전분포(prior)가 가우시안이기 때문에,
단위 정사각형(unit square) 위의 선형적으로 간격을 둔 좌표(linearly spaced coordinates)는
가우시안의 역누적분포함수(inverse CDF)를 통해 변환되어
잠재 변수 z의 값을 생성하였다.
이러한 각각의 z 값에 대해,
학습된 파라미터 $\theta$ 를 사용하여
해당하는 생성 분포 $p_\theta(\mathbf{x}\mid\mathbf{z})$ 를 시각화하였다.
그림 5:
잠재 공간(latent space)의
서로 다른 차원 수(dimensionalities)에 대해
학습된 MNIST 생성 모델(generative models)로부터의
무작위 샘플(random samples).
B $-D_{KL}(q_\phi(\mathbf{z}) \,|\, p_\phi(\mathbf{z}))$ 의 해, 가우시안 경우 (Gaussian case)
변분 하한(variational lower bound, 즉 최대화할 목적함수)은
종종 해석적으로 적분 가능한 KL 항(KL term)을 포함한다.
여기서는 사전분포(prior) $p_\theta(\mathbf{z}) = \mathcal{N}(0, \mathbf{I})$ 와
사후 근사분포(posterior approximation) $q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)})$ 가
둘 다 가우시안인 경우의 해를 제시한다.
$\mathbf{z}$ 의 차원 수를 $J$ 라 하자.
$\boldsymbol{\mu}$ 와 $\boldsymbol{\sigma}$ 는
데이터 포인트 $i$ 에서 계산된 변분 평균(variational mean)과
표준편차(standard deviation)를 나타내며,
$\mu_j$ 와 $\sigma_j$ 는 각각 이 벡터의 $j$번째 성분을 의미한다.
변분 평균 $\boldsymbol{\mu}$ 와 표준편차 $\boldsymbol{\sigma}$ 는
인코더(인식 모델) $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
입력 데이터 $\mathbf{x}^{(i)}$ 로부터 추정한
잠재 변수 분포의 평균과 표준편차를 의미한다.
즉, 인코더가 데이터 포인트마다
$\boldsymbol{\mu}^{(i)}$ 와 $\boldsymbol{\sigma}^{(i)}$ 를 출력하여
사후분포 $q_\phi(\mathbf{z}\mid\mathbf{x}^{(i)}) = \mathcal{N}(\boldsymbol{\mu}^{(i)}, (\boldsymbol{\sigma}^{(i)})^2\mathbf{I})$ 를 구성한다.
그렇다면 다음이 성립한다:
\[\begin{aligned} \int q_\theta(\mathbf{z}) \log p(\mathbf{z}) \, d\mathbf{z} &= \int \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2) \log \mathcal{N}(\mathbf{z}; \mathbf{0}, \mathbf{I}) \, d\mathbf{z} \\ &= -\frac{J}{2}\log(2\pi) -\frac{1}{2}\sum_{j=1}^{J}(\mu_j^2 + \sigma_j^2) \end{aligned}\]그리고 다음이 성립한다:
\[\begin{aligned} \int q_\theta(\mathbf{z}) \log q_\theta(\mathbf{z}) \, d\mathbf{z} &= \int \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2) \log \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2) \, d\mathbf{z} \\ &= -\frac{J}{2}\log(2\pi) -\frac{1}{2}\sum_{j=1}^{J}(1 + \log \sigma_j^2) \end{aligned}\]따라서,
\[\begin{aligned} - D_{KL}((q_\phi(\mathbf{z}) \,\|\, p_\theta(\mathbf{z}))) &= \int q_\theta(\mathbf{z}) (\log p_\theta(\mathbf{z}) - \log q_\theta(\mathbf{z})) \, d\mathbf{z} \\ &= \frac{1}{2}\sum_{j=1}^{J} \big(1 + \log((\sigma_j)^2) - (\mu_j)^2 - (\sigma_j)^2 \big) \end{aligned}\]인식 모델(recognition model) $q_\phi(\mathbf{z}\mid\mathbf{x})$ 을 사용할 때,
$\boldsymbol{\mu}$ 와 표준편차 $\boldsymbol{\sigma}$ 는
단순히 $\mathbf{x}$ 와 변분 파라미터 $\boldsymbol{\phi}$ 의 함수가 된다.
(본문의 예시 참고)
C 확률적 인코더와 디코더로서의 MLP들
변분 오토인코더(variational auto-encoders)에서는
신경망(neural networks)이 확률적 인코더(probabilistic encoders)와
디코더(decoders)로 사용된다.
데이터의 유형과 모델에 따라 인코더와 디코더에는
여러 가지 선택지가 존재한다.
우리의 예시에서는 비교적 단순한 신경망인
다층 퍼셉트론(MLP, multi-layered perceptrons)을 사용하였다.
인코더로는 가우시안 출력을 가지는 MLP를 사용하였으며,
디코더로는 데이터의 유형에 따라
가우시안 또는 베르누이 출력을 가지는 MLP를 사용하였다.
C.1 디코더로서의 Bernoulli MLP
이 경우,
$p_\theta(\mathbf{x}\mid\mathbf{z})$ 를
다변량 베르누이(multi-variate Bernoulli)로 두며,
그 확률은 $\mathbf{z}$ 로부터
단일 은닉층을 갖는 완전연결 신경망(fully-connected neural network)을 통해 계산된다.
여기서
\[\mathbf{y} = f_\sigma(\mathbf{W}_2 \tanh(\mathbf{W}_1\mathbf{z} + \mathbf{b}_1) + \mathbf{b}_2) \tag{11}\]이다.
여기서 $f_\sigma(\cdot)$ 는
요소별 시그모이드 활성함수(elementwise sigmoid activation function)를 의미하며,
$ \theta = \lbrace \mathbf{W}_1, \mathbf{W}_2, \mathbf{b}_1, \mathbf{b}_2 \rbrace $ 는
MLP의 가중치(weights)와 편향(biases)을 의미한다.
C.2 인코더 또는 디코더로서의 Gaussian MLP
이 경우, 인코더 또는 디코더를
대각 공분산(diagonal covariance) 구조를 가지는
다변량 가우시안(multi-variate Gaussian)으로 둔다.
여기서
$ \lbrace \mathbf{W}_3, \mathbf{W}_4, \mathbf{W}_5, \mathbf{b}_3, \mathbf{b}_4, \mathbf{b}_5 \rbrace $ 는
MLP의 가중치와 편향이며,
디코더로 사용될 때는 이들이 파라미터 $\theta$ 의 일부를 이룬다.
이 네트워크가 인코더 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 로 사용될 때는
$\mathbf{z}$ 와 $\mathbf{x}$ 의 역할이 서로 바뀌며,
가중치와 편향은 변분 파라미터 $\phi$ 가 된다.
D 주변가능도 추정량 (Marginal likelihood estimator)
우리는 다음과 같은 주변가능도 추정량을 유도하였다.
이 추정량은 표본공간의 차원이 낮을 경우(5차원 미만)
충분한 표본이 주어지면 주변가능도(marginal likelihood)의
좋은 추정값을 생성한다.
다음과 같이 두자:
$p_\theta(\mathbf{x}, \mathbf{z}) = p_\theta(\mathbf{z})p_\theta(\mathbf{x}\mid\mathbf{z})$
이는 우리가 표본을 생성하는 생성 모델이다.
주어진 데이터포인트 $\mathbf{x}^{(i)}$ 에 대해
우리는 주변가능도 $p_\theta(\mathbf{x}^{(i)})$ 를 추정하고자 한다.
추정 과정은 세 단계로 구성된다.
기울기 기반(gradient-based) MCMC(예: Hybrid Monte Carlo)를 사용하여
\[\nabla_\mathbf{z} \log p_\theta(\mathbf{z}\mid\mathbf{x}) = \nabla_\mathbf{z} \log p_\theta(\mathbf{z}) + \nabla_\mathbf{z} \log p_\theta(\mathbf{x}\mid\mathbf{z})\]
사후분포(posterior)로부터 $L$개의 값 $ \lbrace \mathbf{z}^{(l)}\ \rbrace $ 을 샘플링한다.
이때,를 사용한다.
기울기 기반 MCMC(gradient-based MCMC)는
확률분포로부터 샘플을 생성하기 위해 기울기 정보를 활용하는
마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo) 기법의 한 종류이다.대표적인 예로 하이브리드 몬테카를로(Hybrid Monte Carlo, HMC) 또는
해밀토니안 몬테카를로(Hamiltonian Monte Carlo)가 있다.이 방법은 단순한 무작위 이동(random walk) 대신,
확률분포의 로그 확률 밀도의 기울기(gradient)를 이용해
더 효율적으로 표본 공간을 탐색한다.이를 통해 고차원 공간에서도
상관성이 낮고 분산이 작은(high-quality) 샘플을 얻을 수 있다.아래의 식은 바로 이러한 기울기 기반 MCMC에서
사후분포의 기울기를 계산하기 위한 형태이다.사후분포는 베이즈 정리에 따라
\[p_\theta(\mathbf{z}\mid\mathbf{x}) = \frac{p_\theta(\mathbf{z})p_\theta(\mathbf{x}\mid\mathbf{z})}{p_\theta(\mathbf{x})}\]로 정의되며, 로그를 취하면
\[\log p_\theta(\mathbf{z}\mid\mathbf{x}) = \log p_\theta(\mathbf{z}) + \log p_\theta(\mathbf{x}\mid\mathbf{z}) - \log p_\theta(\mathbf{x})\]가 된다.
여기서 $\log p_\theta(\mathbf{x})$ 는 $\mathbf{z}$ 에 의존하지 않으므로
기울기를 계산할 때 상수항으로 간주되어 사라진다.따라서 사후분포의 로그 기울기는
\[\nabla_\mathbf{z} \log p_\theta(\mathbf{z}\mid\mathbf{x}) = \nabla_\mathbf{z} \log p_\theta(\mathbf{z}) + \nabla_\mathbf{z} \log p_\theta(\mathbf{x}\mid\mathbf{z})\]로 단순화된다.
이 표현은 MCMC 방법(특히 Hybrid Monte Carlo)에서
사후분포의 기울기를 계산할 때 매우 효율적이며,
사전분포(prior)와 우도(likelihood)의 기울기를 별도로 계산하여
각각의 항이 가지는 의미를 명확히 분리할 수 있다는 장점이 있다.이 샘플들 $\lbrace \mathbf{z}^{(l)}\ \rbrace$ 에 대해 밀도 추정량 $q(\mathbf{z})$ 를 적합(fit)한다.
이 단계에서는, 앞 단계에서 사후분포로부터 얻은 샘플들
$\lbrace \mathbf{z}^{(l)}\ \rbrace$ 의 분포 형태를 학습하기 위해
밀도 추정량(density estimator) $q(\mathbf{z})$ 를 적합(fit)한다.즉, 샘플링된 $\mathbf{z}$ 들이 따르는 확률 분포를
어떤 매개변수화된 모델(예: 가우시안 혼합 모델, 커널 밀도 추정,
또는 신경망 기반 확률 모델 등)로 근사하는 과정이다.이 과정의 목적은 사후분포의 복잡한 형태를
직접 다루지 않고도 근사 가능한 형태의 $q(\mathbf{z})$ 로 표현함으로써,
이후 단계에서 확률 계산(특히 주변가능도 추정)에
효율적으로 활용할 수 있도록 하는 것이다.다시 말해, $q(\mathbf{z})$ 는 사후분포로부터 얻은 샘플의
“경험적 분포(empirical distribution)”를 근사하는 역할을 하며,
나중에 등장하는 추정식에서 분모에 등장하는
$p_\theta(\mathbf{z})p_\theta(\mathbf{x}\mid\mathbf{z})$ 와의 비율 계산을
안정적으로 수행할 수 있게 한다.다시 사후분포(posterior)로부터 새로운 $L$개의 값을 샘플링한다.
\[p_\theta(\mathbf{x}^{(i)}) \simeq \left( \frac{1}{L} \sum_{l=1}^{L} \frac{q(\mathbf{z}^{(l)})} {p_\theta(\mathbf{z})p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z}^{(l)})} \right)^{-1} \quad \text{where } \mathbf{z}^{(l)} \sim p_\theta(\mathbf{z}\mid\mathbf{x}^{(i)})\]
이 샘플들과 적합된 $q(\mathbf{z})$ 를 다음 추정식에 대입한다:추정량의 유도는 다음과 같다:
\[\begin{aligned} \frac{1}{p_\theta(\mathbf{x}^{(i)})} &= \int \frac{q(\mathbf{z})}{p_\theta(\mathbf{x}^{(i)})} \, d\mathbf{z} \\ &= \int \frac{q(\mathbf{z}) \, p_\theta(\mathbf{x}^{(i)}, \mathbf{z})} {p_\theta(\mathbf{x}^{(i)}, \mathbf{z}) \, p_\theta(\mathbf{x}^{(i)})} \, d\mathbf{z} \\ &= \int \frac{p_\theta(\mathbf{x}^{(i)}, \mathbf{z})} {p_\theta(\mathbf{x}^{(i)}, \mathbf{z})} \frac{q(\mathbf{z})}{p_\theta(\mathbf{x}^{(i)})} \, d\mathbf{z} \\ &= \int p_\theta(\mathbf{z}\mid\mathbf{x}^{(i)}) \frac{q(\mathbf{z})} {p_\theta(\mathbf{z})p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z})} \, d\mathbf{z} \\ &\simeq \frac{1}{L} \sum_{l=1}^{L} \frac{q(\mathbf{z}^{(l)})} {p_\theta(\mathbf{z})p_\theta(\mathbf{x}^{(i)}\mid\mathbf{z}^{(l)})} \quad \text{where } \mathbf{z}^{(l)} \sim p_\theta(\mathbf{z}\mid\mathbf{x}^{(i)}) \end{aligned}\]
E 몬테카를로 EM (Monte Carlo EM)
몬테카를로 EM 알고리즘은 인코더를 사용하지 않으며,
대신 사후분포(posterior)로부터 잠재 변수(latent variables)를 샘플링한다.
이때 다음 식으로 계산된 사후분포의 기울기를 사용한다:
몬테카를로 EM 절차는 10회의 HMC(하이브리드 몬테카를로) leapfrog 단계를 포함하며,
승인율(acceptance rate)이 90%가 되도록 자동으로 조정된 단계 크기(step size)를 사용한다.
그 후, 획득된 샘플을 이용하여 5회의 가중치 갱신(weight update) 단계를 수행한다.
모든 알고리즘에서 파라미터들은 Adagrad 단계 크기(step size)를 사용하여
(냉각 스케줄(annealing schedule)을 동반하여) 갱신되었다.
주변가능도(marginal likelihood)는
훈련 세트와 테스트 세트에서 처음 1000개의 데이터 포인트를 사용하여 추정되었으며,
각 데이터 포인트마다 잠재 변수의 사후분포로부터
하이브리드 몬테카를로(Hybrid Monte Carlo)를 이용해
4회의 leapfrog 단계를 거쳐 50개의 값을 샘플링하여 계산되었다.
F 완전 변분추론 (Full VB)
논문에서 기술된 바와 같이,
잠재 변수 $\mathbf{z}$ 에 대해서만 변분추론을 수행하는 대신
파라미터 $\boldsymbol{\theta}$ 와 잠재 변수 $\mathbf{z}$ 모두에 대해
변분추론(variational inference)을 수행하는 것이 가능하다.
여기에서는 그 경우에 대한 우리의 추정량(estimator)을 유도한다.
앞에서 소개한 파라미터들에 대한 하이퍼사전분포(hyperprior)를
$\boldsymbol{\alpha}$ 로 매개변수화하여 $p_{\boldsymbol{\alpha}}(\boldsymbol{\theta})$ 라 하자.
그렇다면 주변가능도(marginal likelihood)는 다음과 같이 쓸 수 있다:
사후분포의 정의
\[p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X}) = \frac{p_{\boldsymbol{\alpha}}(\mathbf{X}, \boldsymbol{\theta})}{p_{\boldsymbol{\alpha}}(\mathbf{X})}\]에 따라서,
\[\begin{aligned} \log p_{\boldsymbol{\alpha}}(\mathbf{X}) &= \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log p_{\boldsymbol{\alpha}}(\mathbf{X}) \, d\boldsymbol{\theta} \\ &= \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log \frac{p_{\boldsymbol{\alpha}}(\mathbf{X}, \boldsymbol{\theta})} {q_{\boldsymbol{\phi}}(\boldsymbol{\theta})} \, d\boldsymbol{\theta} + \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log \frac{q_{\boldsymbol{\phi}}(\boldsymbol{\theta})} {p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X})} \, d\boldsymbol{\theta} \end{aligned}\]두 번째 적분항은 바로
\[D_{KL}(q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \,\|\, p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X})) = \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log \frac{q_{\boldsymbol{\phi}}(\boldsymbol{\theta})} {p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X})} \, d\boldsymbol{\theta}\]
KL 발산(Kullback–Leibler divergence) 으로 정의된다:따라서 위 식을 정리하면,
\[\log p_{\boldsymbol{\alpha}}(\mathbf{X}) = D_{KL}(q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \,\|\, p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X})) + \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log \frac{p_{\boldsymbol{\alpha}}(\mathbf{X}, \boldsymbol{\theta})} {q_{\boldsymbol{\phi}}(\boldsymbol{\theta})} \, d\boldsymbol{\theta}\]여기서 두 번째 항을
\[\mathcal{L}(\boldsymbol{\phi}; \mathbf{X}) = \int q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \log \frac{p_{\boldsymbol{\alpha}}(\mathbf{X}, \boldsymbol{\theta})} {q_{\boldsymbol{\phi}}(\boldsymbol{\theta})} \, d\boldsymbol{\theta}\]
변분 하한(variational lower bound, 혹은 ELBO)으로 정의하면:최종적으로 다음 식이 얻어진다:
\[\log p_{\boldsymbol{\alpha}}(\mathbf{X}) = D_{KL}(q_{\boldsymbol{\phi}}(\boldsymbol{\theta}) \,\|\, p_{\boldsymbol{\alpha}}(\boldsymbol{\theta}\mid\mathbf{X})) + \mathcal{L}(\boldsymbol{\phi}; \mathbf{X})\]
여기서 우변의 첫 번째 항은
근사분포(approximate distribution)와 실제 사후분포(true posterior) 사이의
KL 발산을 의미하며,
$\mathcal{L}(\boldsymbol{\phi}; \mathbf{X})$ 는
주변가능도에 대한 변분 하한(variational lower bound)을 나타낸다.
KL 발산은 0 이상이므로,
이 항은 항상 하한(lower bound)을 형성한다.
근사분포와 실제 사후분포가 정확히 일치할 때,
이 하한은 실제 주변가능도와 같아진다.
$\log p_{\boldsymbol{\theta}}(\mathbf{X})$ 항은
각 데이터포인트의 주변가능도 합으로 구성되며,
각 항은 다음과 같이 다시 쓸 수 있다:
\[\log p_{\boldsymbol{\theta}}(\mathbf{x}^{(i)}) = D_{KL}(q_{\boldsymbol{\phi}}(\mathbf{z}\mid\mathbf{x}^{(i)}) \,\|\, p_{\boldsymbol{\theta}}(\mathbf{z}\mid\mathbf{x}^{(i)}))) + \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\phi}; \mathbf{x}^{(i)}) \tag{15}\]여기서 우변의 첫 번째 항은
근사분포와 실제 사후분포 간의 KL 발산을 의미하며,
$\mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\phi}; \mathbf{x})$ 는
데이터포인트 $i$ 의 주변가능도에 대한 변분 하한이다.
오른쪽 항(식 (14) 및 (16))에 있는 기댓값들은
명백히 세 개의 별도 기댓값들의 합으로 표현될 수 있으며,
이 중 두 번째와 세 번째 항은
$p_\theta(\mathbf{x})$ 와 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
가우시안(Gaussian)일 때 해석적으로 계산될 수 있다.
일반성을 위해, 여기서는 이러한 기댓값들이 계산 불가능한(intractable) 경우를 가정한다.
논문의 해당 절(section)에 제시된 몇 가지 완화된 조건들(certain mild conditions) 하에서,
선택된 근사 사후분포들 $q_\phi(\boldsymbol{\theta})$ 와 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 에 대해
조건부 샘플 $\tilde{\mathbf{z}} \sim q_\phi(\mathbf{z}\mid\mathbf{x})$ 을 다음과 같이 재매개변수화할 수 있다:
여기서 우리는 사전분포(prior) $p(\boldsymbol{\epsilon})$ 와 함수 $g_\phi(\boldsymbol{\epsilon}, \mathbf{x})$ 를 선택하여
다음이 성립하도록 한다:
근사 사후분포 $q_\phi(\boldsymbol{\theta})$ 에 대해서도 동일한 작업을 수행할 수 있다:
\[\tilde{\boldsymbol{\theta}} = h_\phi(\boldsymbol{\zeta}) \quad \text{with} \quad \boldsymbol{\zeta} \sim p(\boldsymbol{\zeta}) \tag{19}\]이와 유사하게, 사전분포 $p(\boldsymbol{\zeta})$ 와 함수 $h_\phi(\boldsymbol{\zeta})$ 를 선택하여
다음이 성립하도록 한다:
표기상의 간결함을 위해, 다음과 같은 단축 표기법을 도입한다:
\[f_\phi(\mathbf{x}, \mathbf{z}, \boldsymbol{\theta}) = N \cdot \big(\log p_\theta(\mathbf{x}\mid\mathbf{z}) + \log p_\theta(\mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})\big) + \log p_\alpha(\boldsymbol{\theta}) - \log q_\phi(\boldsymbol{\theta}) \tag{21}\]이 식은 앞서 정의된 변분 하한(ELBO)들의 항들을
하나의 함수 형태로 묶어 표기하기 위해 도입된 것이다.구체적으로, 식 (18)과 (20)에서
$\mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\phi}; \mathbf{x}^{(i)})$ 와
$\mathcal{L}(\boldsymbol{\phi}; \mathbf{X})$ 는 각각
데이터 포인트 수준(local term)과
전체 데이터 세트 수준(global term)의 변분 하한을 나타낸다.두 식을 보면 공통적으로 다음 항들이 반복된다:
- 우도 항: $\log p_\theta(\mathbf{x}\mid\mathbf{z})$
- 잠재 변수의 사전분포 항: $\log p_\theta(\mathbf{z})$
- 근사 사후분포 항: $-\log q_\phi(\mathbf{z}\mid\mathbf{x})$
- 파라미터의 사전분포 항: $\log p_\alpha(\boldsymbol{\theta})$
- 파라미터 근사분포 항: $-\log q_\phi(\boldsymbol{\theta})$
따라서 이 다섯 항을 모두 포함하는 하나의 통합된 함수
$f_\phi(\mathbf{x}, \mathbf{z}, \boldsymbol{\theta})$ 를 정의하면
나중에 식을 단순하게 표현할 수 있다.또한 데이터가 $N$개 있다고 가정할 때,
각 데이터포인트의 기여도를 합산하는 형태를 반영하기 위해
앞에 $N$을 곱해준다.결과적으로 다음과 같은 단축 표기가 생긴다:
\[f_\phi(\mathbf{x}, \mathbf{z}, \boldsymbol{\theta}) = N \cdot \big(\log p_\theta(\mathbf{x}\mid\mathbf{z}) + \log p_\theta(\mathbf{z}) - \log q_\phi(\mathbf{z}\mid\mathbf{x})\big) + \log p_\alpha(\boldsymbol{\theta}) - \log q_\phi(\boldsymbol{\theta})\]즉, $f_\phi$ 는 “데이터 샘플 $\mathbf{x}$, 잠재 변수 $\mathbf{z}$,
그리고 모델 파라미터 $\boldsymbol{\theta}$” 가 함께 등장하는
전체 변분 하한 계산의 핵심 항들을 하나로 묶은 표현이다.
식 (20)과 (18)을 이용하면,
주어진 데이터포인트 $\mathbf{x}^{(i)}$ 에 대한 변분 하한의 몬테카를로 추정치는 다음과 같다:
여기서
$\boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})$ 이고
$\boldsymbol{\zeta}^{(l)} \sim p(\boldsymbol{\zeta})$ 이다.
이 추정량은 $p(\boldsymbol{\epsilon})$ 과 $p(\boldsymbol{\zeta})$ 로부터의 샘플에만 의존하며,
이들은 $\boldsymbol{\phi}$ 와 무관하므로
이 추정량은 $\boldsymbol{\phi}$ 에 대해 미분 가능하다(differentiable).
이렇게 얻어진 확률적(stochastic) 그래디언트들은
확률적 최적화(stochastic optimization) 기법들,
예를 들어 SGD나 Adagrad [DHS10] 등과 함께 사용할 수 있다.
확률적 그래디언트 계산의 기본 접근법은 알고리즘 1을 참고한다.
F.1 예시 (Example)
파라미터와 잠재 변수들에 대한 사전분포(prior)는
중심화된 등방성 가우시안(centered isotropic Gaussian)으로 두자:
이 경우, 사전분포는 파라미터를 포함하지 않는다는 점에 유의하라.
또한, 실제 사후분포(true posterior)가
대각 공분산(diagonal covariance)을 갖는 가우시안에 가깝다고 가정하자.
이 경우, 변분 근사 사후분포(variational approximate posterior)도
대각 공분산 구조를 갖는 다변량 가우시안(multivariate Gaussian)으로 둘 수 있다:
여기서 $\boldsymbol{\mu}_z$ 와 $\boldsymbol{\sigma}_z$ 는
아직 명시되지 않은 $\mathbf{x}$ 의 함수이다.
이들이 가우시안이므로, 변분 근사 사후분포는 다음과 같이 매개변수화할 수 있다:
여기서 $\odot$ 기호는 원소별 곱(element-wise product)을 나타낸다.
이 표현들은 앞서 정의된 하한식(식 (21), (22))에 대입될 수 있다.
이 경우, 더 낮은 분산을 갖는 대체 추정량(alternative estimator)을 구성할 수 있다.
이는 모델 $p_\alpha(\boldsymbol{\theta})$, $p_\theta(\mathbf{z})$,
$q_\phi(\boldsymbol{\theta})$, 그리고 $q_\phi(\mathbf{z}\mid\mathbf{x})$ 가
모두 가우시안이기 때문이다.
따라서 $f_\phi$ 의 네 개 항은 해석적으로(analytically) 풀 수 있다.
그 결과 얻어지는 추정량은 다음과 같다:
여기서 $\mu_j^{(i)}$ 와 $\sigma_j^{(i)}$ 는
각각 벡터 $\boldsymbol{\mu}^{(i)}$ 와 $\boldsymbol{\sigma}^{(i)}$ 의 $j$번째 원소를 나타낸다.
알고리즘 2
우리의 추정량(estimator)을 사용하여 확률적 그래디언트(stochastic gradient)를 계산하는 의사코드(pseudocode)
함수 $f_\phi$, $g_\phi$, $h_\phi$ 의 의미는 본문을 참조하라.
입력 (Require): $\boldsymbol{\phi}$ (현재 변분 파라미터의 값)
$\mathbf{g} \leftarrow 0$
for $l$ = 1 to $L$ do
$\mathbf{x} \leftarrow$ 데이터셋 $\mathbf{X}$ 로부터 무작위 추출 (random draw)
$\boldsymbol{\epsilon} \leftarrow$ 사전분포(prior) $p(\boldsymbol{\epsilon})$ 로부터 무작위 추출
$\boldsymbol{\zeta} \leftarrow$ 사전분포(prior) $p(\boldsymbol{\zeta})$ 로부터 무작위 추출
$\mathbf{g} \leftarrow \mathbf{g} + \frac{1}{L}\nabla_\phi f_\phi(\mathbf{x}, g_\phi(\boldsymbol{\epsilon}, \mathbf{x}), h_\phi(\boldsymbol{\zeta}))$
end for
return $\mathbf{g}$